Neuroscience-Based Information and Communication Technologies Development in Elementary School Mathematics through Games: A Case Study Evaluation

Abstract

Universities play a pivotal role in knowledge production and in transforming teaching methodologies across various subjects. This research is a case study detailing the pedagogical implementation of a game-based methodological approach in a dual-degree program for primary and early childhood education teachers. The focus is on integrating information and communication technologies (ICT) tools for mathematics, specifically Scratch and GeoGebra, underpinned by principles of neuroscience. Based on a sample of 28 students, this study adopted game-based learning (GBL) in mathematics exercises, aimed at equipping student-teachers with strategies for educating future students (ages 7 to 11) in the 3rd to the 6th grade. Key areas of focus included plane and spatial geometry, requiring student-teachers to design game-like activities, emulating the problem-solving approaches of children. The culmination of this study involved presentations by the student-teachers, demonstrating how neuroscience principles can enhance the creation of educational games for primary school students. The findings highlight a significant divergence between the reality of teaching mathematics and the preconceived notions held by the student-teachers. This study opens avenues for integrating neuroscience into education, particularly through GBL, but also highlights the need for comprehensive understanding and application of neuroscientific principles to maximize learning outcomes.

1. Introduction

The working world is increasingly demanding a range of professional skills. In the case of the teaching profession for elementary education, university students need to adapt to an environment by developing their competencies in critical thinking, creativity, collaboration, and communication. These skills enable them to act decisively in addressing problem solving and decision making [1,2].

In research aimed at understanding the development of these cross-cutting skills, it is necessary to incorporate how the brain functions at the very moment of learning, which falls within the realm of educational neuroscience or neuroeducation. Thus, it can be said that neuroeducation has a greater ability to align learning with the neurocognitive development of human beings. Neuroscience shows that learning is much more effective when games are used as an interface in the teaching–learning process along with playful methodologies [3].

Therefore, games act as novel methodologies supporting the teaching and learning of mathematics by developing specific skills necessary for effective learning. Promoting such skills is challenging in traditional classes, as the teaching strategies and techniques used do not allow students to delve into or focus on the need for decision making, recognizing potential errors or necessary changes, or observing occurrences in the classroom environment [4].

One teaching strategy considered within active methodologies that foster mathematical learning is game-based learning (GBL). Game-based learning can develop skills involving not only cognitive but also affective, emotional, and behavioral dimensions, which are essential for learning mathematics. This methodology stimulates imagination, contributing to a greater assimilation of reality [5], and offers students a collaborative, challenging, and feedback-rich environment [2].

Considering all of this, this paper aims to answer the following research question: are future teachers capable of carrying out mathematics didactic proposals through GBL that are oriented according to neuroeducation guidelines? This paper presents a proposal based on gaming as a teaching methodology used with students in the 5th year of the dual-degree in primary and pre-primary education, specifically in the ICT for Primary Mathematics course focused on Scratch and GeoGebra, applying principles of neuroscience. In addition to the methodology used in the planning of the course, the results demonstrated by one group of students and future teachers as well as the video game methodology used to teach mathematical content with the support of ICT tools and neuroscience will be presented.

2. Theoretical Foundations

“Teaching without an awareness of how the brain learns is like designing a glove with no sense of what the hand looks like” [6]. This is one of the core principles of neuroeducation, involving the direct application of neuroscience to education, highlighting the importance of understanding the human brain to teach effectively. This underlines the current significance of neuroeducation as a novel aspect of education, offering support through insights into how the brain functions.

From this, a certain advantage is derived, as it allows for the integration of other disciplines (psychology, sociology, and medicine), enhancing both learning and teaching processes. This fosters improvement for both students and teachers [7]. Therefore, learning is more than just absorbing knowledge [8]; fundamentally, learning enables or induces specific changes in the brain [9].

Learning can be understood through what individuals express, as everything is a manifestation of brain function, such as how they think, feel, or behave. The brain constantly communicates with all the body’s organs and the surrounding environment [7].

From this perspective, learning occurs precisely when certain brain changes take place [9], meaning that the dialogue maintained by the brain leads to neuroplasticity. This is the process of generating neurons anatomically and functionally, thereby creating new synaptic connections.

Domínguez Márquez [10] notes that neuroplasticity is a lifelong condition; thus, learning also occurs throughout life. However, this requires activating the attention mechanism, which functionally occurs between the neurons of the cerebral cortex and the thalamus, where consciousness is activated, as learning and memorizing, at least in terms of teaching, require that precise focus which is attention [7].

Learning is a constant challenge for the brain, activating the amygdala, part of the limbic system, which produces dopamine. This acts as a reward, generating pleasure the brain seeks to replicate due to the positive experience. Consequently, it enhances prefrontal performance and all attentional processes, without which learning does not occur [11].

This positive experience that the brain seeks to replicate culminates in positive emotions that sustain curiosity and attention, besides evoking desire. Thus, the emotion–cognition assembly in the learning process is indissoluble. For Mora [7], any event linked to episodes associated with an emotion, whether positive or negative, facilitates better and more extensive information storage and learning.

As we have seen, learning is directly linked to emotion, curiosity, attention, and the reward system. Therefore, games might be the most conducive environments for incorporating all elements of neuroeducation, as the link between brain parts can stimulate one function and enhance others, leading to learning. Games can be used to design activities that facilitate learning a skill, enabling the development of others.

Consequently, games could be the backdrop of the neuroeducation stage, allowing for a learning process which focuses on students’ strengths rather than their weaknesses. According to Hamari et al. [12], games positively impact the development of students’ skills and competencies.

Various authors [13,14,15] assessed participation, motivation, knowledge acquisition, and development by considering the impact of games on student performance and found a positive increase in both motivation and performance. Developing such activities generates unintentional learning, stimulating student engagement in the educational process [16].

Gallardo-López and Gallardo-Vázquez [17] highlight the significance of play and culture as educational tools. Olivares et al. [18] conducted a literature review, revealing insights into the meaningful contributions of play in the mathematics learning process. Valles-Pereira and Motta-Villegas [19] aimed to spark interest in mathematics among students by using a technological tool, Kahoot, as an alternative to traditional exams. Their findings suggest that such tools can alleviate tension, stress, and the high anxiety levels typically associated with written exams.

Another study focused on student perceptions of interactive games in education and their impact on motivation in learning mathematics was conducted by Cruz-Vitorino and Alvites-Huamaní [20]. They found that the use of interactive games in math classes enhances understanding of the subject matter, allowing students to develop their mathematical skills. This approach is seen as an effective pedagogical strategy that fosters student learning. San Andrés-Soledispa et al. [21] analyzed games as a motivational strategy in math education using a Likert scale-designed survey. Their research revealed an increased interest and attention in mathematics among students when new elements like games were introduced. These games were credited with boosting motivation and promoting meaningful learning, provided there is timely planning based on cognitive parameters and supportive teacher involvement.

Student performance in mathematics can be improved [22]. Therefore, it is necessary to create classroom dynamics that significantly enhance the teaching of mathematics. Technological contexts involving games can contribute as knowledge-building strategies [23,24].

For Shemran et al. [25], games can better engage students in developing skills in science, technology, engineering, and mathematics. González-Tablas [26] suggests that one way to reinforce mathematical skills is through games so as to mitigate certain disadvantages in interpersonal competencies and motivate student participation.

It is important to consider that using games for teaching demonstrates that mathematics is more than operational knowledge. This subject is used as a support tool in almost all areas of knowledge, such as administration, finance, and medicine, among others [3]. Therefore, in education, mathematics is more than just a tool; this science enables answering most of the problematic questions in teaching.

The use of games in learning mathematics is of significant relevance, as they represent an increase in student motivation [27]. Luo [28] points out that engagement, participation, motivation, and goal achievement, among others, are just some of the educational outcomes associated with mathematics strengthened by the use of games.

Finally, as evidenced so far, the importance of an approach such as game-based learning is clear, enabling students to acquire specific mathematical knowledge through games, providing them with a higher level of retention and understanding. According to Waiyakoon et al. [29], this process will help students learn independently.

This research addresses the role of neuroeducation in understanding brain functioning and how this knowledge is essential for future primary and early childhood educators. It focuses on analyzing how the implementation of specifically designed games can facilitate and improve the teaching and learning process in mathematics.

3. Materials and Methods

3.1. Participants

The participants were 28 students, all of whom attended classes regularly, consisting of 23 females and 5 males. The students were enrolled in the fifth year of a dual-degree program in Early Childhood and Primary Education at a public Spanish university, in a semester-long course on ICT for Mathematics in Primary Education. To ensure that participation met all the ethical criteria for social research, approval was obtained from the Social Sciences Research Committee of the University of Castilla-La Mancha under code CEIS-634122-B5K2.

3.2. Research Design

As a procedure, the decision was made to work with the existing base groups, which were seven in total, each comprising between three and five members. This was to ensure that the content and objectives of the course were effectively developed. Each group was responsible for developing a practical project at the end of each theoretical block, using Scratch for the content of the four basic operations and plane geometry and GeoGebra for the geometry of space content. At the end of the course, the groups had to develop a series of games using Scratch and GeoGebra, at their discretion. Each of the blocks was named according to the topics chosen by the teacher, thus encompassing all the content worked on during the semester, as shown in

Table 1. Distribution of the blocks in the subject ICT for Mathematics in Primary Education.

Blocks
Scratch—Plane Geometry: 1 Square 2 Rectangle 3 Triangle 4 Pentagon and Hexagon Scratch—Operations: 5 Operations (addition, subtraction, division and multiplication, greater than, and less than and equal to) GeoGebra—Geometry of Space: 6 Construction of Polyhedra 7 Construction of a Barycenter, Orthocenter, and Incenter.

.

The blocks were structured so that one or several contents presented in the teaching guide could be worked on in each of them. In block 1, the content related to plane geometry was covered; in block 2, operations; and, in block 3, the geometry of space. For the development of the projects, a structure was proposed that was analyzed and modified by the participants until reaching the final form shown in

Table 2. Didactic guide used for the development of the internships.

Title It Should Be Creative and Motivate Students to Want to Take Part in Projects

Introduction Justification of the proposal Theoretical framework The theoretical framework should provide support for all work based on older and more recent authors and neuroscience contributions. Objectives Programming objectives Contents Programming contents based on the procedures and sub-procedures Recipient It will indicate the learners targeted and describe the difficulties that may be encountered in classes for them. Proposed activity The activity should contain all the activities you intend to develop in class in an explanatory way and how you will work with the students. Teaching strategies Here you should explain how you are going to develop what you set out to complete in your class and list how you are going to achieve it. Bibliography

. The goal was for the work guide to be a living document adapting to the needs of each practice.

3.3. Procedure

The future teachers were required to research what neuroscience says about how primary-aged students learn mathematics, as this ICT course for mathematics is focused on training educators in this educational stage. Based on the scientific knowledge gathered, they had to create practical activities using ICT tools.

From this proposal offered by the university faculty, seven practices emerged, one per group, where the future teachers had to prepare activities using Scratch or GeoGebra for the chosen student age group (between 6/7 and 11/12 years old) as well as create games adapted to the contents with the objective of enhancing learning. The contents were plane geometry, operations, and space geometry. All the practices were followed by group tutorials and/or online tutorials, depending on the needs of each group, to verify the degree of the scope and adaptation of the approaches to the ages of primary education students. Additionally, communication was maintained fluently through a WhatsApp group so that all groups could participate and assist in solving any group’s problems and ensure the theoretical learning of mathematics by the future teachers.

On the other hand, the strategies employed for the development of the games were based on studies indicating how the human brain behaves when engaging with a game. These strategies encompassed the duration of each phase, the difficulty level appropriate for elementary school students, the appeal of the content to foster interest in playing, and the sequencing of phases according to the introduction of mathematical content. All games were designed to include three to four phases to thoroughly cover any content.

Testing of the games occurred in two stages: initially, by university peers from different groups who played games created by others; and, subsequently, by elementary school children, as each group was responsible for bringing them to the university to play and provide feedback on the games.

3.4. Instrument for the Evaluation

To assess the final products of the groups, an interactive dynamic was organized where each team presented their project to the other students. During these presentations, both peers and the teacher evaluated the developed games using a detailed rubric (Figure 1). This rubric consisted of six essential criteria, each rated as “Satisfactory” (S), “Unsatisfactory” (U), and “Underdeveloped” (UD). These criteria encompassed the following aspects: (1) the appropriateness of the interface, (2) the interactivity of the characters, (3) the accuracy of the mathematical concepts, (4) the quality of the operations, (5) the ability to keep the player engaged, and (6) the quality of the challenges presented.

The grading of the games (“Assessment” column in the rubric) was based on a clear system: those with more than two “Unsatisfactory” ratings were considered “In Development”; those receiving fewer than two “Unsatisfactory” ratings were categorized as “Ready with Modifications”; and those with only one “Underdeveloped” rating were deemed “Ready for Use”. Appendix A displays the evaluation of Group 1 as an example. Each group assessed the others using a similar template.

4. Results

All the groups had to present as a final product structured games designed using Scratch or GeoGebra. The activity’s objective was to enhance learning and provide a meaningful and satisfying experience for students based on the principles of neuroscience, emotion, curiosity, attention, and reward systems.

Table 3. Summary of the evaluation of nonconformities obtained by the groups.

Groups	Title of the Work	Number of Members	Topics	Specific Criteria Not Presented or Underdeveloped
1	Hansel and Gretel and the Witch of Operations	4	Operations	(1), (3), (6)
2	Jumanji and the portals of Geometry	5	Geometry of Space	(1), (2), (3), (6)
3	Little Spies vs. Doctor Polyhedron	3	Geometry of Space	(2), (4), (5), (6)
4	Tadeo Jones and the kingdom of the flat figures	4	Plane Geometry	(1), (2), (3), (6)
5	Lightning MacQueen and the race of the 4 challenges	4	Operations	(3), (4), (5), (6)
6	Snow White and the Huntsman in the Geometric Forest	3	Plane Geometry and Space	(1), (2), (6)
7	Mario Bross in the World of Mathematics	5	Operations	(5)

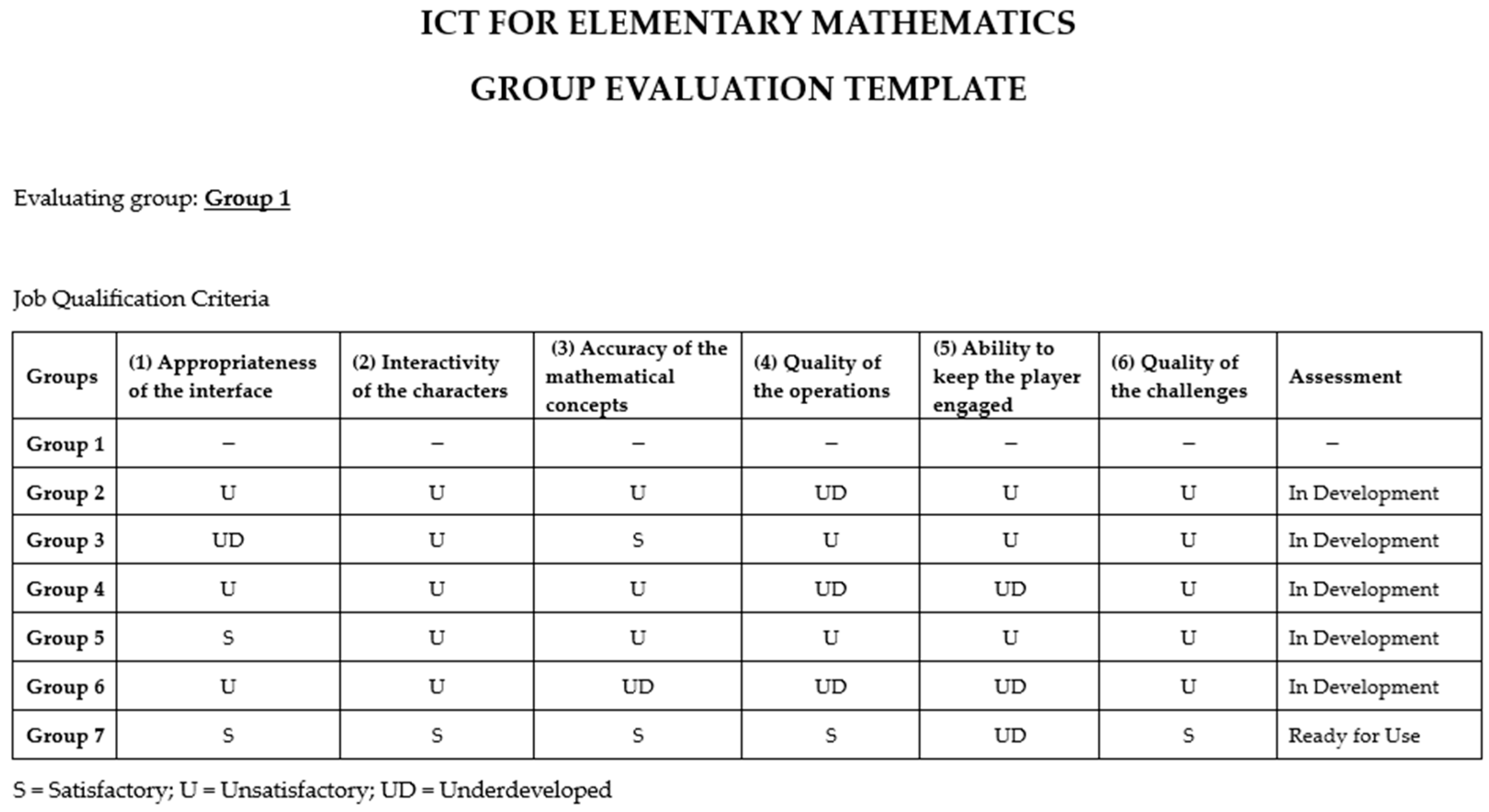
(1) Appropriateness of the interface, (2) interactivity of the characters, (3) accuracy of the mathematical concepts, (4) quality of the operations, (5) ability to keep the player engaged, and (6) quality of the challenges.

shows a summary of the evaluation of nonconformities obtained by the groups. This table reveals details such as the titles of the works, the number of members per team, the topics chosen for game development, and the specific criteria that led to the disqualification of some projects.

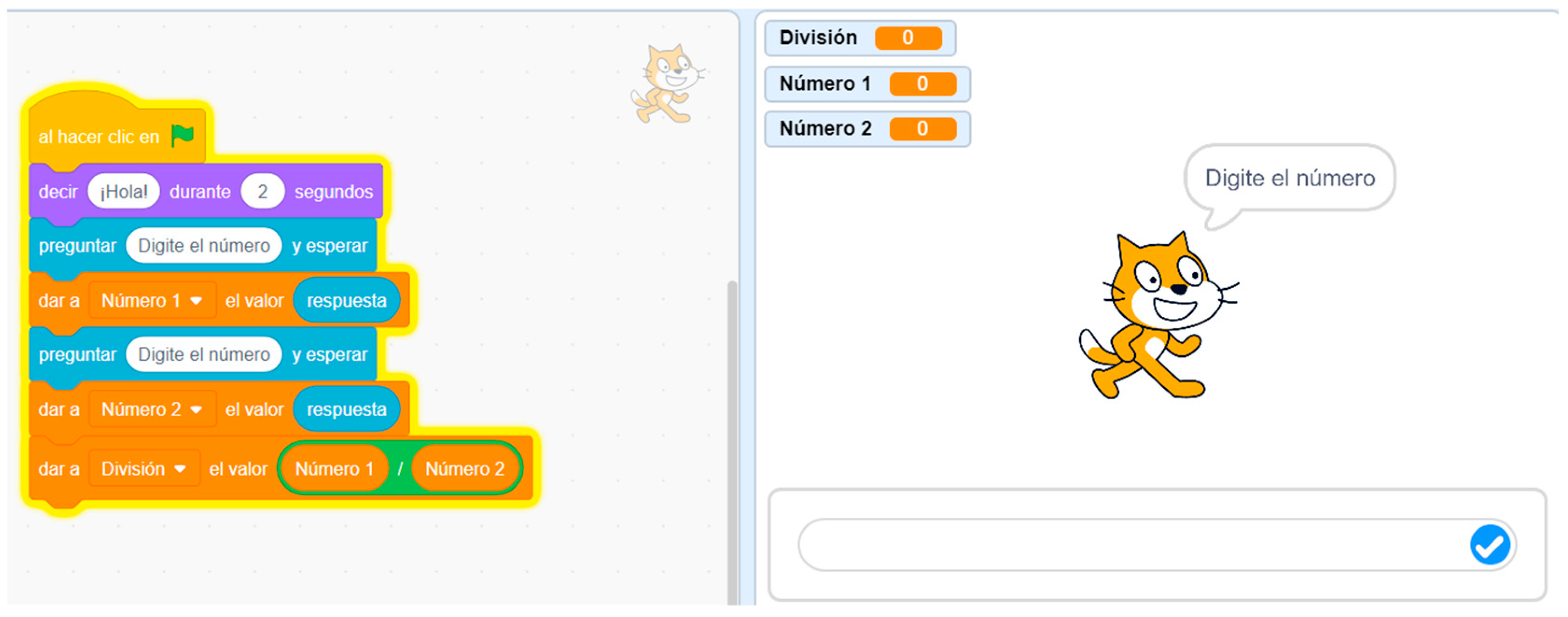
Of the seven projects created by the seven groups, the one chosen for presentation in this paper had a solid foundation in neuroscience and a structured routine in the four principles: cognitive, affective, emotional, and behavioral. The other groups, in contrast, faced difficulties both in the structure and in the application of the essential mathematical concepts for the development of their projects. This prevented them from adequately integrating these four principles into their work. As an illustrative example, we consider the project of group 5. Their goal was to develop a game based on mathematical operations (see Figure 2). However, the group made several errors. They developed four different procedures, one for each mathematical operation. This resulted in a less fluid gameplay dynamic, as students had to switch files after completing each challenge, interrupting the sense of achievement at the end of each stage. For the brain to want to store or repeat an experience pleasurably, it is crucial that the challenges be continuous [26]. Additionally, the interaction between the game character and the player was limited, as was the interface, which was not engaging. These elements are crucial for the development of an effective educational product. According to neuroscience, to facilitate the transmission of information between the hippocampus and the prefrontal cortex, it is essential to arouse satisfaction in the user. This is achieved through the release of higher amounts of dopamine, a process which is activated when the game fully engages the player [27].

The detected errors in group 5’s work included the following: creating four separate procedures, one for each operation, requiring students to switch files upon completing the challenges. This approach failed to offer a dynamic game experience, hindered the brain’s desire to store or repeat the process enjoyably, as challenges should be continuous [26] and were not in this case. Interaction between the chosen character and the player was limited, as was the interface’s appeal—crucial aspects when aiming to develop an educational product. That is, leveraging neuroscience to facilitate information transmission between the hippocampus and the prefrontal cortex is essential for awakening satisfaction, necessitating high dopamine release [27], which occurs when a game successfully engages the player; this was not achieved when players felt interrupted and disengaged from the game, as it was observed here.

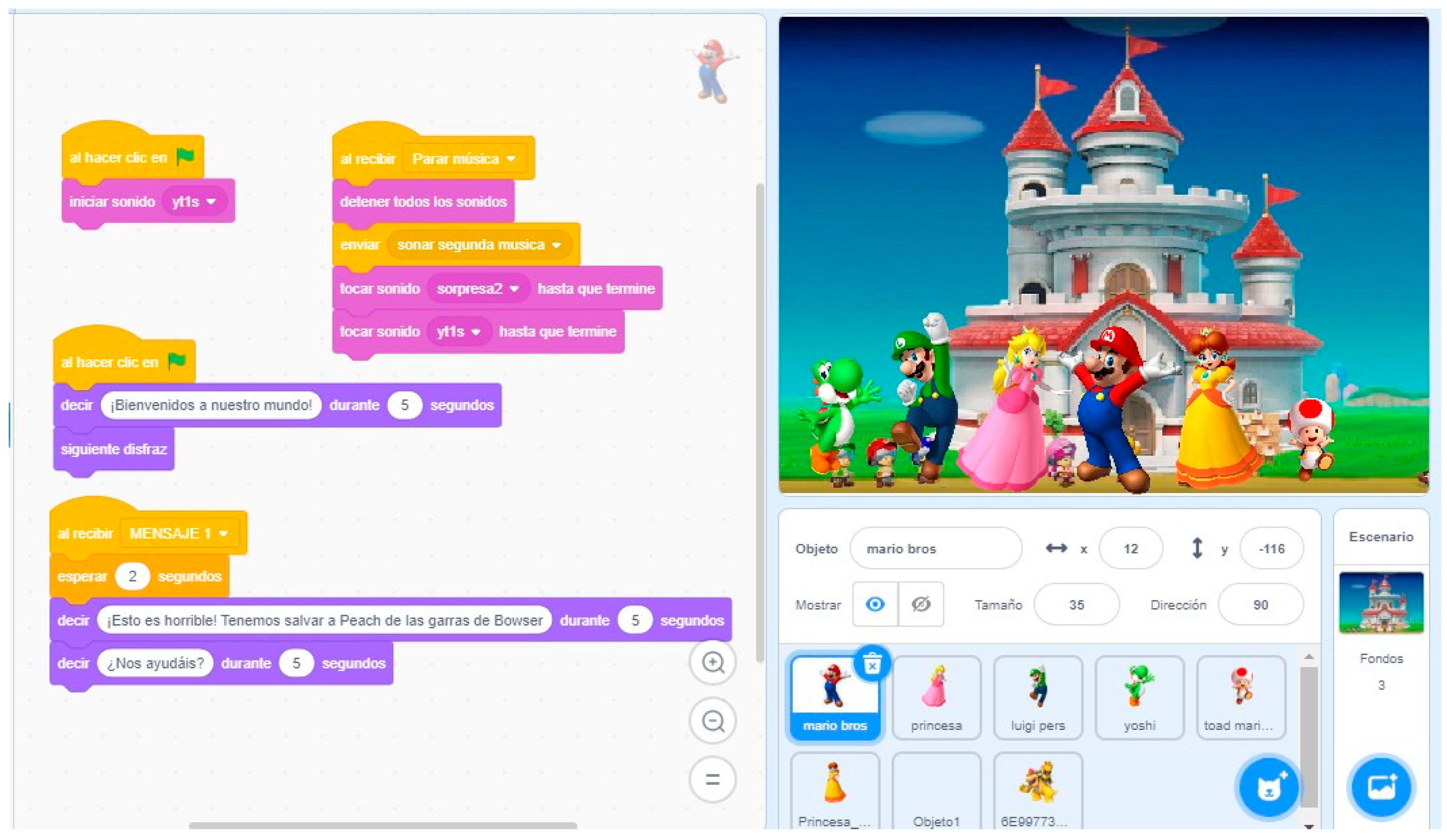
The work selected for further discussion is a video game titled “Mario Bross in the World of Mathematics”, prepared by group 7. The group, composed of five students and future primary education teachers, contextualized a usual task in a video game format. The activity is presented in a novel, motivating format that captures students’ attention, thus provoking the emotion–cognition assembly [7], facilitating the learning of mathematics. Even among university peers, a significant change in motivation, interest, and learning was noted compared to those observed in other presentations. The only negative point that was attributed to the game was the ability to keep the player engaged, but it was evaluated as underdeveloped, not declassifying the game.

The programmed Mario Bross game features various phases, each corresponding to exercises on the contents chosen by the group: addition, subtraction, division and multiplication, greater than, and less than and equal to.

The routines created were developed to allow socialization among group members, creating a relaxed atmosphere of interaction among all players. It is known that the integration of group members and the way they interact through a game promotes certain changes, as the brain maintains constant dialogue with the entire body and the environment it is in [7], thus facilitating learning.

The following figures present the phases of the game “Mario Bross in the World of Mathematics.” The examples shown in the figures do not represent the entirety of the developed phases, as they are screenshots of parts of the game. The first phase is the presentation of the game rules and the choice of characters (Figure 3).

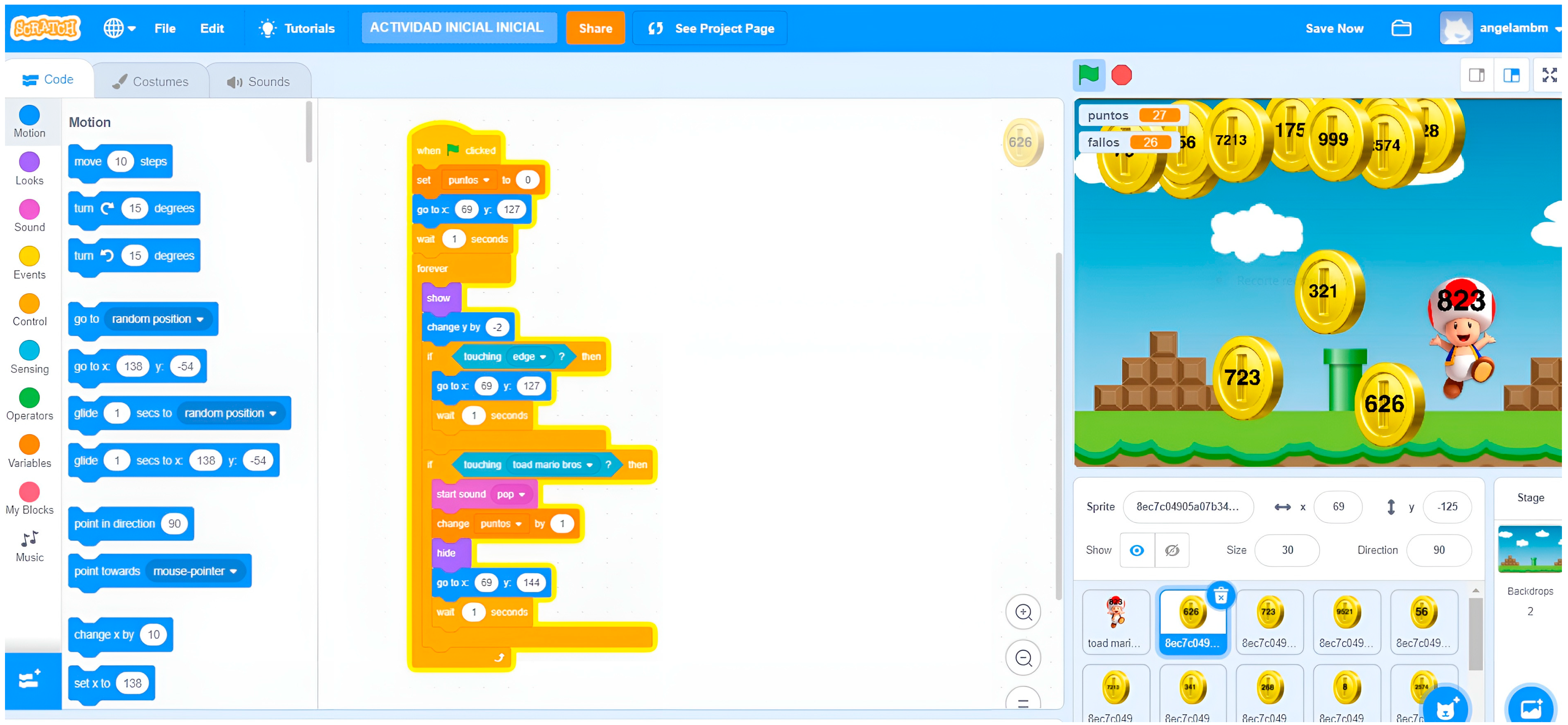
In the second phase (Figure 4), the routines of the character (Toad) and the 17 total coins are presented. In this phase, the objective of the game is to work on the subtraction operation, for which the player should be attentive to the values of each coin, since each coin varies in value and moves randomly. The value of each coin can be either greater or less than that of the character it interacts with. When a character is touched with a coin of a lesser value, the player earns a point, accompanied by a sound effect. Conversely, touching a character with a coin of a higher value is marked as a mistake and triggers a different sound. This game conveys to elementary students the concept that not all pairs of numbers can be subtracted from one another; it is crucial to discern which number is smaller and which one is larger. The second phase finishes once the player navigates through all the challenges corresponding to each of the four operations, always adhering to the mathematical principles, as demonstrated in the case of subtraction.

In the third phase, Mario Bross aims to rescue the character Peach. The procedures created in Scratch enable Mario to move and prevent his enemy Browser from continuing. For this, he must answer a question related to arranging numbers in ascending or descending order. If Mario, represented by the playing group, answers correctly, he moves to another world, repeating the routine. Upon overcoming all the challenges in the final routine, Browser is defeated, and Peach is rescued by Mario. However, if Mario answers incorrectly three times, the game restarts.

5. Discussion

This study tries to shed light on the research question, which is whether future teachers are capable of carrying out mathematics didactic proposals through GBL which are oriented according to neuroeducation guidelines. For that purpose, a case study was carried out with 28 students enrolled in the fifth year of a dual-degree program in Early Childhood and Primary Education at a public Spanish university, in a semester-long course on ICT for Mathematics in Primary Education, who created a mathematics game with unequal achievements.

The game presented by one of the groups (group 7) of fifth-year students of the dual degree in Primary and Early Childhood Education is almost as engaging as the original video game. This demonstrates one of the clear reasons why learning can occur through play, as it is a tool which reflects the world of children [2,5]. This type of activity can engage students because it showcases a dynamic, magical world full of action, challenges, and significance as educational tools, as highlighted by Gallardo-López and Gallardo-Vázquez [17]. In addition, the implementation of a game-based methodology has contributed to the improvement of coexistence and learning in a collective way, enhancing the expansion of the knowledge involved, fostering the interest on mathematics knowledge through neuroeducation and ICT [19,20]. Visually captivating, the game features sounds, movements, and realism [5]. Moreover, it always includes instant feedback, letting players know if they have achieved the objective of the challenge, thereby boosting self-esteem and earning recognition from peers [30] and dopamine generation as a reward which produces pleasure [11].

Therefore, in testing the game among university students who will become educators, to assess whether it met its objectives, these students critically evaluated it based on neuroscience’s positive elements. An entertainment video game provides specific qualities such as player interactivity, a suitable interface, an interactive character, the ability to keep the player engaged, and the ability to maintain challenges, as González-Tablas et al. informed [26]. These points were considered by the university students when creating the games, forming the evaluation rubric for their peers’ projects, to verify whether they aligned with neuroscience’s claims regarding learning. Hence, using this rubric helped future educators solidify their understanding of the elements valued in their peers’ games, achieving one of the didactic objectives of the proposal: to assess learning in relation to brain functioning, which is the only way to learn, aligned with Hart statements [6]. In this case, the game served as a mediating role in making the teaching of mathematics more accessible to university students, by connecting teaching with learning mathematics, as suggested by Brennan and Vos [4].

Additionally, when a student overcomes each challenge (phase) of the game, it brings pleasure. In this process, the reward system generates dopamine, a neurotransmitter which improves neuron communication, which facilitates learning [7]. This dopamine release also occurred among university students when they overcame a challenge in the game creation process, aiding their understanding of the mathematical content involved [4]. Thus, the pedagogical approach of GBL has shown an improvement in mathematics comprehension aligned with Zabala-Vargas et al. [3], the enhancement of coexistence, and collective learning fostered by this methodology’s implementation, in addition to broadening knowledge about ICT and understanding neuroeducation’s contributions to the teaching–learning process [6]. Thus, the motivation arising from accumulating rewards is sustained when the brain receives a positive outcome after a specific choice, encouraging the brain to repeat the experience for the pleasure it generates [31]. This enhances the capacity to store information in one’s memory.

Memory, defined as the ability to acquire and retain information, treats content as an element that is maintained based on its frequency of use. According to López-Marí et al. [32], this information, represented through concepts, principles, and problem solving, is optimally assimilated in playful environments, as reported by other authors in the literature [17,18,19]. This characteristic, inherent to video games and games, ensures that students not only learn and memorize but also explore, creating a more stimulating and effective environment for learning.

Consequently, in mathematics education, it is essential to incorporate specific pedagogical actions that enhance student learning. The use of computational tools to improve interaction, feedback, and self-assessment is crucial [16]. Additionally, it is vital to develop teaching competencies, explore new didactic methodologies, and seek innovative learning environments, as all these aspects significantly influence the dynamics of teaching processes [33,34].

Effective learning in mathematics requires careful attention to the emotional component [7]. Employing games as a methodology, especially those resembling video games, can intensify the emotional charge of the content. This strategy directly influences memory, thereby significantly enhancing the retention and understanding of mathematics. Joy, sadness, empathy, success, and frustration are some of the emotions students experience while engaging in mathematics learning, similar to the feelings elicited by games [3,27].

Our results are aligned with the research conducted by authors such as Clarke et al. [15] and Goehle [35], who have evaluated student participation in games designed to facilitate learning. The findings indicate that these games generate positive motivation and improve academic performance, as was found by us in all the students involved in this study, although in unequal extents. Therefore, we can state, based on the results shown in the previous section, that educational games impact two fundamental domains: firstly, they positively influence students’ skills and competencies, as reported by Olivares et al. in their literature review [18]; secondly, they increase their motivation [12,20,21]. According to Connolly et al. [16], fostering this latter aspect leads to unintentional learning, encouraging students to take responsibility for their educational process, as we have experienced with our students and future teachers.

It has been observed that, when playing to evaluate these games, the students showed sustained attention and concentration [7], required to learning. This is because the novel elements, relevance, visual stimuli, and rewards present in video games captured their attention and interest, as proposed by San Andrés-Soledispa et al. [21]. This occurs because the brain, when surprised and captivated, activates the reward and pleasure circuits known as the mesolimbic pathway, a typical effect of video games [35,36]. Therefore, video games can keep the player in a state of constant alertness, thanks to the visual and auditory stimuli which provoke various emotions, contributing to the activation of the neuronal connections fostering learning [11].

These reactions are driven by emotions, which directly affect learning [36]. That is, the way in which a teacher transmits knowledge can decisively influence the teaching–learning process. Managing emotions in this process is key to improving learning, making it more meaningful and allowing students to effectively internalize concepts.

Mora [7] notes that, when students experience emotions, learning is accompanied by immediate action that maintains high levels of attention. This is evident in video games, as they generate a range of emotions in students.

Therefore, the emotions experienced during gameplay facilitate students’ ability to remember facts, memorize processes, and improve their self-esteem. Thus, the use of games maintains the stimulus that allows the process culminating in the learning of mathematics to occur.

5.1. Theoretical and Practical Implications

This study explored how employing game-based methodologies by students in primary and early childhood education, supported by neuroeducation principles, can align with the brain’s learning processes, particularly in the context of mathematics learning. This is a novel contribution of the first order.

This article enriches the theoretical framework on the integration of ICT tools in mathematics education, particularly through the lens of neuroeducation. It contributes to the specialized literature by exploring how game-based learning, supported by tools like Scratch and GeoGebra, can align with cognitive processes to enhance mathematical understanding in primary and early childhood education. This work underscores the interplay between educational technology and neuroscientific insights, offering a novel perspective on designing pedagogical strategies which cater to diverse learning needs.

The practical contribution of this research extends to the innovative application of neuroeducation principles in mathematics education through ICT tools. By grounding teaching strategies in neuroscience, this study offers insights into how learning activities can be designed to align with the way in which the brain processes and retains mathematical concepts. This neuroeducational approach provides a framework for developing engaging and brain-compatible learning experiences, enhancing student-teachers’ ability to create effective, neuroscience-informed educational practices. Such contributions are pivotal for improving students’ engagement, understanding, and retention of mathematical concepts, demonstrating a practical pathway for incorporating neuroscientific insights into everyday teaching methodologies.

This dual contribution underscores this manuscript’s significance in both advancing academic discourse and offering actionable insights for educators seeking to leverage technology to improve mathematics education, through a neuroscience-based approach.

5.2. Limitations and Further Research Directions

This research focuses on the integration of neuroscience and mathematics education to enhance learning through the use of games and video games. The journey was not without its challenges. Firstly, this being a case study conducted at a single institution may limit the generalizability of the findings [37]. Obviously, the proposal needs to be tested with bigger groups to compare effectiveness. Secondly, this study revealed a varied success rate among student groups in creating effective educational games, highlighting the intricate balance between game design and neuroeducational objectives. This variability underscored the need for a more structured approach to applying neuroscientific insights to educational tools.

Furthermore, this study brought to light the complexities in understanding how the brain engages with and responds to learning stimuli, particularly through emotions like joy and frustration. It became evident that a deeper foundational knowledge of neuroscience was crucial for students to effectively translate these principles into practical learning applications. This research, while opening new horizons in educational methodologies, also beckoned future explorations. It suggested a rich field for further inquiry, ranging from longitudinal studies on the long-term impacts of game-based learning to comparative analyses across different subjects and educational settings.

6. Conclusions

This research, although being a case study, allows for reflection on how the union of two different areas of knowledge, neuroscience and mathematics education, can cooperate to develop learning. With the contribution of neuroeducation, it is possible to observe that certain manifestations of the human brain align with some strategies used for learning, suggesting that employing a methodology like the use of games or video games for teaching mathematics enhances learning, and make future teachers to realize this fact.

From this perspective, the students of the dual degree in Primary and Early Childhood Education were challenged to develop games using two technological tools, Scratch and GeoGebra, supported by the knowledge of neuroeducation combined with how games affect the human brain.

It is important to note that all the students could appreciate how games interact with the human brain through a pleasure-generating system, but, unfortunately, not all groups were able to develop games that met those objectives.

By becoming aware of the complexity involved in learning, in this case mathematics learning, some students failed to understand that the same reward system that makes the brain want to repeat certain actions (when feeling pleasure) is the same one that occurs at the moment of learning. The brain is stimulated through challenge, joy, sadness, empathy, success, and frustration and also when it perceives the possibility of achieving success in a particular task [38]. Games also have the same capacity to stimulate the human brain, generating a learning act, but through more pleasurable pathways that lead the human brain to repeat the same action, implying that memory then stores all the information, which, in this case, results in learning.

In proposing the creation of games using ICT tools for the fifth-grade students of the dual degree in Primary and Early Childhood Education, it was anticipated that the students would integrate specific mathematical concepts, leading to a new level of knowledge for them. Furthermore, by addressing how the brain learns in relation to neuroeducation, it was expected that they could tailor their designs to facilitate a more enjoyable learning experience in mathematics. This initiative resulted in, on the one hand, an increase in the learning of the mathematical concepts chosen for game creation and the integration of new knowledge (neuroeducation), which took students beyond the separate subjects taught at the university. On the other hand, testing all the games revealed that there was learning among each student with the topics covered by the games created by other groups.

In this teaching experience, this group of students made a difference, as they were able to understand that simple technological resources can be used, supported by neuroeducation, to provoke learning in line with the reality of children, who primarily play. This study sheds light on the need to avoid the treatment of areas such as neuroeducation and mathematics on a separate base. The combination of the two has positive effects on preservice teachers’ learning, which could later contribute to a better teaching of mathematics.