Design and Validation of a Classroom Observation Instrument to Evaluate the Quality of Mathematical Activity from a Gender Perspective

Abstract

This study aimed to design and validate an instrument as a guideline for classroom observation and analysis of teaching–learning process in mathematics. The instrument considers 3 dimensions and 16 subdimensions with a gender perspective. A content validity process by eight expert judges is presented, built from a dialectical work between theory and empirical evidence from more than 100 classes observed and recorded on video from 19 educational centers. The degree of agreement between experts was determined with Fleiss Kappa and Kendall coefficients. Experts’ judgement scored each dimension from 1 to 3. Globally, an almost perfect strength of agreement was obtained in 6 of 16 dimensions with $\stackrel{-}{x}>2.5$, and in the other 10 dimensions, a strength of agreement was obtained between moderate and almost perfect, $\mathrm{2,14}\le \stackrel{-}{x}\le \mathrm{2,5}$. Fleiss Kappa coefficients were highest in relevance and clarity, $\kappa$ = 0.425, 95% CI [0.344, 0.506], p < 0.001 and, $\kappa$ = 0.461, 95% CI [0.375, 0.548], p < 0.001, respectively. Moreover, the degree of clarity, coherence, sufficiency, and relevance was statistically moderately agreed upon in their assessments, with an overall Kendall’s W = 0.489, p < 0.001.

1. Introduction

One of the basic principles of didactics in mathematics is that students’ mathematical understanding is primarily determined by the educational and mathematical structure and the interactions between the teacher and students during class related to the study of mathematics [1,2]. Along these lines, in recent years, the theoretical and empirical evidence on teaching and learning in mathematics has revealed the central role played by the knowledge and specific didactic skills of teachers in their way of teaching and hence its importance for understanding in-depth teacher–student interactions [3,4,5].

The literature on interactions is abundant and centers primarily on observations in the classroom setting. Studies have shown the crucial role of interactions in shaping students’ learning experiences [6,7]. As such, interactions have become a key aspect of research in mathematics education [8]. Furthermore, some studies indicate that these instructional practices and expectations may have a gender-differentiated impact on learning [9,10,11,12,13]. Along these lines, ref. [7] proposes that all human beings should have access to the same opportunities in education regardless of their gender. Providing quality, inclusive, and unbiased education is vitally important in any modern society. However, despite significant improvements in recent decades, education is not universally available, and gender inequalities persist. In particular, the gender disparity in careers related to Science, Technology, Engineering, and Mathematics (STEM, for the English term used to group these academic disciplines) is alarming [11].

Based on this last discipline, gender gaps and difficulties around school mathematics comprise a highly complex framework in which various actors and actions of society intervene [12]. Gender gaps on various math tests correlate with gender equality in societies [13]. More equitable societies have shown smaller gaps.

Although the theories that explain gender differences in students’ academic performance in mathematics are numerous [14,15], no single theory can explain all the dimensions and causes of gender gaps [16].

To analyze classroom interactions, various authors have shown a greater interest in the construction of instruments for classroom observation and multiple investigations have tried to identify attributes of teaching and pedagogical dimensions within the classroom that make the students achieve more and better learning [17,18]. However, although these instruments offer essential information on the quality of the interactions, the experiences of the different students in the classroom are standardized and homogeneous [19], and very few results based on the observation evidence in the classroom have examined and evaluated both analytically and critically the nature of interactions and mathematical activity from a gender perspective. Moreover, the preceding adds to a disconnection of said analyses from the perspective of specific didactics.

Consequently, there is a need to design validated observational instruments focused on effective practices for mathematics instruction in interventions and settings that explore the role of gender within other factors that affect the quality and equity of mathematics teaching practices. Thus, considering the gender variable and its synchrony with the development of specific mathematical skills and competencies in Chilean students, the general objective of this research was to design and validate an instrument that operates as an instrument for observation and analysis of teaching practices in the classroom, considering: i) the specificity of the mathematical knowledge that is the object of learning and ii) the specificity of knowledge in the teaching–learning process with a gender perspective. For this, we propose an instrument validated by expert judges. This instrument is built from a dialectical process between theoretical and empirical criteria agreed at national and international levels from math classroom observation.

Based on all these last elements, this study aimed to answer the following research questions:

• What dimensions and/or relevant factors of teaching practices, referring mainly to pedagogical, didactic, and disciplinary skills, influence the quality and equity of said practices?
• Which of these dimensions and/or factors would allow identifying gender biases in classroom interactions?

1.1. Quality and Equity of Mathematical Activity in the Classroom

The theoretical position assumed to elaborate our instrument emerged from the perspective of quality and equity of mathematical activity results from local integration [20]. This approach arises from two theoretical perspectives in education: the Epistemological Approach in Mathematics Didactics, especially the Anthropological Theory of Didactics (ATD) [21,22,23,24], and the Sociological Approach of Education, particularly the Theory of Pedagogical Codes (TPC) [25]. However, given our research purpose and the specific conditions of our object of study, we can analyze from a more complex perspective different phenomena associated with the quality and equity of the teaching and learning processes of mathematics in the classroom. Said local integration of theories [26] has already been used to analyze mathematics classes, focusing on quality, equity, and the access that students have to resources.

The ATD postulates that mathematical activity, whether of creation, use of known mathematics of diffusion, or teaching and/or learning of mathematics, is essentially an activity of studying fields of mathematical problems. A person’s construct uses or learns mathematics when they are substantively involved in the process of addressing and solving real and significant problem questions for him or her [23,27].

Even though some studies show that there are not statistically significant differences in the quality and quantity of participation for male and female students in math classes [28], there is strong evidence that mathematics teachers tend to pay greater attention and grant greater responsibilities within the study processes to men than to women at the international level. Other studies indicate how systematically high-level cognitive questions are directed in a notoriously higher proportion to male students than female students [29,30,31]. Likewise, male students receive more significant support and attention from male teachers in solving problems, and it is male students who predominantly participate in mathematical discussions [32]. Other studies suggest that women are at a clear disadvantage compared to men in math classes because teachers interact more with men [33].

Chile is no exception, as reflected in a relatively recent study that concludes that female students are at a disadvantage in terms of opportunities for interaction with the teacher when studying mathematics [34]. It can be deduced that female students’ lower mathematical proficiency stems from their lack of significant opportunities to participate in mathematical learning activities, which may be due to gender-related factors.

In this way, our observation instrument places the study and resolution of problems at the heart of the mathematical work from which learners are taught, consistent with the principles of mathematics didactics shared by the international community [35,36,37,38]; Consequently, ATD describes mathematical activity in terms of praxeologies and generalizes this principle for any human activity [21].

Our theoretical stance integrates equity aspects in the mathematical teaching–learning process from the Sociological Approach to Education [25]. Equal measures for all can generate inequality and gaps in the classroom [39]. We argue that the purpose of learning activities must be recognized and understood by all students in the class, without biases of any kind (particularly gender); that, depending on the needs of each one, there must be a pertinent and adequate regulation between what is explicit and what is implicit; that the socialization of mathematical knowledge is under construction; and that there must be equal opportunities for the appropriation of the evaluation criteria by all students [40].

This brief description of the process of learning mathematics highlights several important implicit concepts. Firstly, the process of studying and solving problems requires the utilization of various mathematical thinking skills that are adjusted, related, and applied until the problem is resolved [35,36,37]. Secondly, the type of problems and their contextual significance play a crucial role in the learning process [27]. The context and connections that give meaning to the problem must be accurate and relevant. Lastly, it is emphasized that one cannot become a competent solver and learner of mathematical problems without consistently practicing the procedures necessary to solve them [41]. The last idea is related to the fact that teachers must build a relationship between what has been built in processes based on mathematical knowledge already previously learned by the students and the knowledge that they will learn later [42].

In this way, by a quality, equitable mathematical learning–teaching process, the assumed theoretical perspective is understood as one that, in its didactic management, preserves all the dimensions of the mathematical activity described above, without gender or other biases.

1.2. Gender Stereotypes in the Math Classroom

Of the many stereotypes that have been studied, the stereotype that women are not as good at math as men [43] is one of the most studied. International evidence shows that girls’ self-efficacy and attitudes related to mathematics are strongly influenced by their immediate family environment, especially parents, and the broader social context: school.

Specifically, performance in mathematics is affected by stereotypes and expectations on the part of teachers [30] in identifying female students with mathematics and, therefore, in their subsequent performance. Female students also appear to perform better when teaching strategies consider their learning needs and teachers have high expectations and treat them equally [7]. In contrast, female students’ learning experience in mathematics is compromised when teachers have stereotypical beliefs about ability based on sex or treat men and women unequally in the classroom. Thus, performance in mathematics is affected by the stereotypes and expectations of teachers who believe that mathematics comes more easily to men than to women [30]. However, this gap can be addressed with practice, regardless of gender, especially during the first years of life.

At the Latin American level, various studies agree that the gender gap in student performance in mathematics favors males and increases throughout the academic trajectory of the students [31]. In a study on gender differences in the mathematics classroom, ref. [44] investigate the gender relations between teachers and students through observations, based on interactions, language used by teachers, and the focus of attention and participation that they give to their students. Male and female teachers direct their attention to the most outstanding students, seeking responses and participation. Similarly, when female teachers manage or conduct the class, female students tend to participate more in the mathematical activity. This problem is consistent with other studies in terms of how and how much teachers interact with students [45]. Similarly, male students tend to perform better than their peers when the teacher is male because they feel more secure, and usually when women succeed in mathematics, it is associated with effort and dedication, not with cognitive abilities [46].

In the case of Chile, ref. [47] report that there is a gap in standardized tests such as the University Selection Test (PSU) in mathematics. In addition, the gender gap affects women with higher self-efficacy in math and better math grades. According to the evidence from the Program for the International Assessment of Adult Competencies (PIAAC), in contrast with the gap in reading performance, differences in mathematics in Chile persist until later in life [48].

At the national level, ref. [33] state that few studies have focused on analyzing and observing interactions in the mathematics classroom with a focus on gender. Therefore, new studies become imperative considering that after family social variables, the school is the one that reproduces and enhances gender gaps.

1.3. Classroom Math, Classroom Observation, and Classroom Observation Instruments

According to certain authors, class observation is a common empirical research method for assessing teacher performance [49]. However, other authors suggest that class observation presents an opportunity for teachers to engage in reflective learning as part of their professional training [50]. Although from an instrument it is impossible to address the immense variety of observable elements, we focus on the pedagogical, didactic, and disciplinary skills of teachers that influence the quality and equity of said practices by analyzing possible gender biases emerging in work–classroom interactions. In this way, class observation is a pivotal input to promote teachers’ professional development and support training processes in both initial and ongoing teacher training.

As references for the design of our instrument, we base ourselves on other class observation instruments used widely internationally, such as the component and indicator observation protocols developed within the framework of the TALIS Video-Study project and the MQI instrument, developed by researchers from the University of Michigan and Harvard University to reliably measure various dimensions of teaching work around mathematical content. Some national references were also considered, such as the Framework for Good Teaching; MateO, designed within the framework of the Best Mathematics Program of the Center for Advanced Research in Education of the University of Chile (CIAE); the class observation instrument developed and validated by the authors, and the classroom observation instruments for detecting gender biases and stereotypes, prepared by the Center for Comparative Education Policies (CPCE) of the Diego Portales University, the United Nations Development Program (UNDP), and the Chilean Ministry of Education (MINEDUC).

2. Methodology

This research is a descriptive, psychometric, and content validity study through expert judgment. The instrument was developed in a Chilean university using an external language of description constructed “ad hoc” by a dialectical iterative process.

In addition, previous instruments to observe classroom interactions from a gender perspective were considered, particularly some theoretical elements indicated in the literature for the design of classroom observation instruments. Furthermore, a review of specific classroom observation instruments or guidelines for mathematics education in Chile was made. In addition, previous instruments to observe classroom interactions from a gender perspective were considered.

It should be noted that in the instrument’s design, in addition to considering criteria that emerged from the literature review, we considered a prior inductive process. The design of each item and subdimension emerged from the observation of videos of more than 100 classes videotaped from 15 educational centers; these were taken as a reference. Teaching practices in the classroom were analyzed based on quality and equity of opportunities to learn. 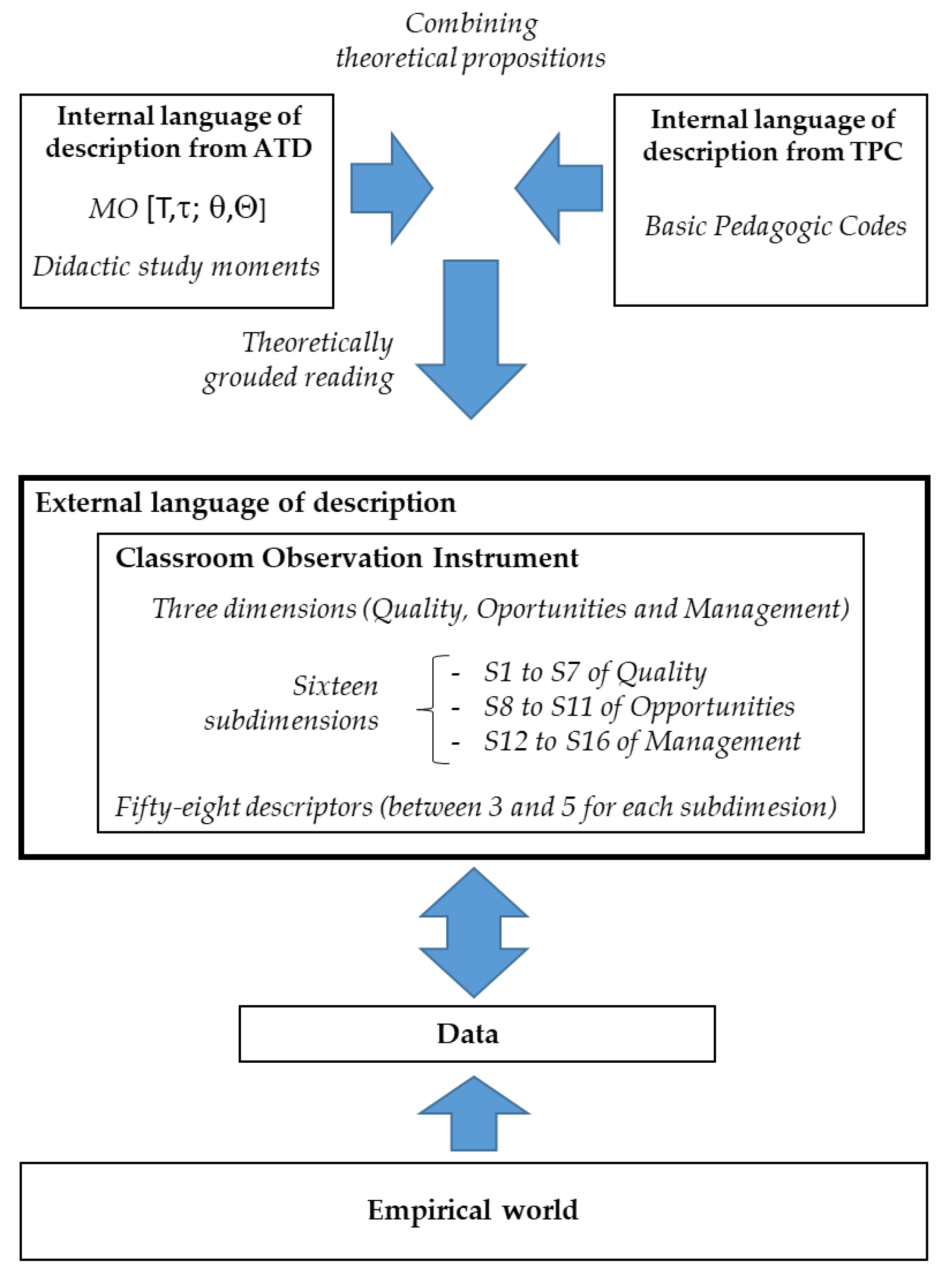Figure 1 shows a diagram of the main methodological aspects of the construction process of the language used to design the classroom observation instrument. The process is an adaptation that the authors used in a previous work [26].

The antecedents of ATD and TPC theories provide internal languages of description. These internal languages consist of theoretical propositions that, from our point of view, are the corpus to cover the dimensions of the empirical world that seem essential to evaluate the quality of mathematical activity in the classrooms. An external language of description was constructed in order to produce the descriptions of empirical settings. This construction was carried out by a dialectical process between a theoretically grounded reading of data and a continuously refining grasp of the data (observed lessons).

The external language provides a structure to design the classroom observation instrument. The three dimensions of the instrument (Quality of mathematical activity, Opportunities for mathematical learning, and Management and socio-emotional support) can be traced back to the background theories. Every dimension refers to main aspects of the study process, which can be separated analytically into different domains. In order to provide a set of descriptors to evaluate mathematics classroom activity, these three dimensions were broken down into sixteen subdimensions, seven related to Quality (S1 to S7), four related to Management (S8 to S11), and five related to Socio-emotional support (S12 to S16). Each subdimension refers to an aspect of the dimension that, in the iterative refined process between external language and data observations (videotaped mathematics lessons), we found it essential to take into account for its description. In addition, elements that allowed the observation of gender biases were integrated into this stage, specifically in the mathematics classroom. In order to assess the level of achievement of subdimensions, a set between three and five descriptors (based on the lesson observations) was established for each subdimension.

For example, the aim of subdimension S3 (Coherence, sufficiency, and articulation between arguments and mathematical activity) is to characterize (in terms of ATD) whether, in the teacher’s discourse and in the students’ argumentations, there appear the appropriate theorical [Θ] and technological [θ] arguments to understand and justify the techniques [τ] that are being used to solve the problems [T]. Furthermore, it aims to characterize whether the students have the opportunities (between students and between students and the teacher) for exteriorization and interchange of thoughts to develop mathematical knowledge in terms of the argumentation [θ/Θ]. Related to S3, from the ATD point of view, a teaching strategy to solve problems centered only on the techniques [t], ignoring the technologies [θ] and the theory [Θ] aspects that explain them, cannot be considered quality instruction. In this sense, is very important that all essential ingredients [T,τ; θ,Θ] of each mathematical organization (MO) that has been studied are present. From the TPC view, is very important that the interactions between students and between teacher and students in the classroom promote access and appropriation of the argumentative discourse by all students. It is also important to consider the participation of students in the development of that argumentative discourse.

The instrument had an internal piloting process, where the descriptors and dimensions to be observed were calibrated using the observations of another set of videos to shape it. After the pilot, the instrument was submitted to expert judgment for validation.

Finally, after the comments received from the judges, seventeen of fifty-eight descriptors were adjusted.

2.1. Validation Process

The validation of the instrument was carried out by peer expert judgment of a measurement instrument [51]. The eight judges were asked to rate the 58 items that made up the original instrument from 1 to 3 (1 does not comply, 2 partially complies, and 3 fully complies) with respect to four pre-established categories: sufficiency, coherence, relevance, and clarity. In turn, in those evaluations rated less than 3, the judges were asked for a short description of why items did not meet the defined criteria or what should be added so that said criteria were fully met.

To calculate and measure the degree of agreement between experts, we calculated the means and standard deviations of the judges’ scores given to each subdimension of the instrument. Then, to measure the degree of correlation, concordance, and internal consistency of the variables between the experts, we applied the Fleiss Kappa index and W Kendall coefficients. The Fleiss Kappa coefficient is a statistical analysis used to evaluate the agreement between three or more evaluators who independently judge measurement criteria through an instrument consisting of a certain number of ordinal categories. The minimum value assumed by the coefficient is 0, and the maximum is 1. For the interpretation of this coefficient, the scale established by [52] was considered, which qualitatively expresses the strength of agreement between the evaluators (originally in English), detailed in

Table 1. Interpretation of the kappa coefficient [52].

Fleiss Kappa Coefficient Force of Agreement	Value
(Poor)	0
(Slight)	0.1–0.20
(Fair)	0.21–0.40
(Moderate)	0.41–0.60
(Substantial)	0.61–0.80
(Almost perfect)	0.81–1.0

.

Kendall’s W concordance coefficient is used to determine the degree of association between k sets of ranges [53], which is why it is advantageous when experts are asked to evaluate an instrument and assign values in ranges, for example, from 1 to 4. In this study, for the evaluation and assessment of the instrument, the analytical categories used by [54] were adapted in the range 1 to 3, and to calculate the coefficient of Kendall’s W, the study used by [55] was used as a frame of reference. Kappa statistics show the exact agreement between ratings, whereas Kendall’s coefficients assess the relationships between ratings. Thus, Kappa statistics consider all incorrect classifications as equal, whereas Kendall’s coefficients distinguish between different misclassifications. To analyze the data, SPSS Statistics v.26 software was used.

The expert judges were professionals with experience in mathematics didactics and teacher training, with ten or more years in teaching or research in mathematics teaching and learning. Another criterion in selecting experts was also demonstrable professional and academic training, either with a master’s or doctorate. The call was made to ten experts, and finally, the intended sample included eight experts from both Chilean and Spanish universities. Regarding ethical issues, informed consent, and other formal issues, the requirements of the ethics committee of the university where this study is hosted were met.

2.2. Instrument

The design of the instrument’s dimensions and subdimensions emerges from the didactic praxeologies of teachers and students, mathematical praxeologies constructed by teachers and students and the Theory of Didactic Study Moments [22], and the notions of didactic contract [1] and school contract [27]. Likewise, domains and dimensions of quality and equity of teaching processes constructed by [26] and specific analysis criteria on gender [10] are used. The instrument is grouped into 16 subdimensions and 3 large dimensions (see

Table 2. Dimensions and subdimensions of instrument.

Dimensions	Subdimensions
1. Quality of mathematical activity	S1. Relevance, richness, and variability of learning situations. S2. Variety of techniques and representations. S3. Coherence, sufficiency, and articulation between arguments and mathematical activity. S4. Disciplinary rigor of the teacher’s speech. S5. Articulation between mathematical activity and the natural world. S6. Stereotyped mathematical content (situations, contexts, arguments, others). S7. Bias in the teacher’s management towards students; bias in student participation and its distribution in mathematical discourses.
2. Opportunities for mathematical learning for all students, without gender or other biases	S8. Access to the meaning and purpose of activities without gender or other biases. S9. Regulation between the explicit and the implicit. S10. Socialization of mathematical knowledge under construction without gender or other biases. S11. Opportunities for participation and appropriation of evaluative criteria without gender biases or of any other kind.
3. Management and socio-emotional support within the mathematical activity in the classroom	S12. Inclusive distribution of responsibilities without gender bias in the teaching–learning process. S13. Management and handling of the rhythm of the teaching–learning process, adapted to the needs of its students. S14. Use of time focused on the task of teaching/learning. S15. Proper handling of disruptions and conflicts. S16. Socio-emotional climate that motivates, unites, and secures students in the face of learning tasks without gender or other biases.

). In addition, two subdimensions with their respective items/descriptors are presented as examples in

Table 3. Example of subdimension 6 and descriptors.

Subdimension 6. Stereotyped mathematical content (situations, contexts, arguments, others). We want to observe the situations, arguments, and contexts related to the adaptation to socially accepted gender roles and activities and the dichotomies based on the gender variable (e.g., women take care of children, cook; men work outside the home).
Descriptor 1	Teachers regularly use situations, contexts, and/or arguments related to mathematical activity with gender biases.
Descriptor 2	Teachers allow situations, contexts, and/or arguments to appear by students with gender bias and/or they do not comment on stereotypes that emerge in the contexts of mathematical activity.
Descriptor 3	Teachers are concerned that the situations, contexts, and/or arguments they present do not have gender biases.
Descriptor 4	Teachers are concerned about the situations, contexts, and/or arguments used in the mathematical activity without gender biases or other stereotypes. In addition, teachers intervene proactively and explicitly encourage gender biases not to be generated among students.

and

Table 4. Example of subdimension 7 and descriptors.

Subdimension 7. Bias in the teacher’s management towards students; bias in student participation and its distribution in mathematical discourses. We want to observe the teacher’s management towards the students regarding the assignment of responsibilities or tasks based on stereotyped gender roles (e.g., allows participation and/or assignment of responsibilities or tasks in a biased way. For example, women distribute math guides, collect or order material, take care of the course for a moment; men demonstrate in public, carry out homework involving force, etc.).
Descriptor 1	Teachers assign and manage responsibilities or tasks with a strong gender bias and/or teachers assert or reinforce gender bias situations that exist among students.
Descriptor 2	Teachers allow or do not intervene when assignments of responsibilities or tasks appear between students with gender bias.
Descriptor 3	Teachers assign and manage responsibilities or tasks without gender or other biases.
Descriptor 4	Teachers assign and manage responsibilities or tasks without gender or other biases. In addition, teachers intervene proactively and explicitly encourage avoiding the generation of gender biases among students.

.

3. Results

To start the first stage of the validation process and analysis of our instrument, descriptive statistics were run to identify subdimensions with low- and high-ranking punctuation in each category (sufficiency, coherence, relevance, and clarity). Results are shown in

Table 5. Descriptive statistics in each category of subdimensions rated.

Subdimensions		Categories								Mean of Each Subdimension
		Sufficiency		Coherence		Relevance		Clarity
		${\stackrel{-}{x}}_{i1}$	$\pm {\sigma }_{i1}$	${\stackrel{-}{x}}_{i2}$	$\pm {\sigma }_{i2}$	${\stackrel{-}{x}}_{i3}$	$\pm {\sigma }_{i3}$	${\stackrel{-}{x}}_{i4}$	$\pm {\sigma }_{i4}$	${\stackrel{-}{x}}_i$
Quality	S1	2.43	0.53	2.71	0.49	2.43	0.79	2.29	0.95	2.46
	S2	2.57	0.53	2.43	0.79	2.71	0.49	2.29	0.95	2.50
	S3	2.29	0.49	2.14	0.69	2.29	0.76	2.29	0.76	2.25
	S4	2.86	0.38	2.71	0.49	2.71	0.76	2.71	0.49	2.75
	S5	3.00	0.00	2.86	0.38	3.00	0.00	2.71	0.76	2.89
	S6	2.71	0.49	3.00	0.00	3.00	0.00	2.71	0.49	2.86
	S7	2.86	0.38	2.43	0.53	3.00	0.00	2.71	0.49	2.75
Opportunities	S8	2.71	0.49	2.57	0.79	3.00	0.00	2.57	0.53	2.71
	S9	2.14	0.69	2.57	0.79	2.57	0.79	2.57	0.79	2.46
	S10	2.86	0.38	3.00	0.00	3.00	0.00	2.86	0.38	2.93
	S11	2.71	0.49	2.86	0.38	2.86	0.38	2.86	0.38	2.82
Management	S12	2.43	0.53	2.43	0.53	2.57	0.53	2.29	0.76	2.43
	S13	2.43	0.53	2.43	0.53	2.57	0.53	2.57	0.53	2.50
	S14	2.43	0.53	2.57	0.53	2.57	0.53	2.57	0.53	2.54
	S15	2.43	0.53	2.71	0.49	2.57	0.53	2.71	0.49	2.61
	S16	2.71	0.49	2.57	0.53	2.71	0.49	2.57	0.53	2.64
Mean of each category *		2.51		2.63		2.73		2.60		2.64

* Note: All mean values were calculated using weighted average values of each mean dimension.

. It should be noted that the judges, when assessing compliance with each subdimension, had to define whether their items did not comply (1 pts.), partially complied (2 pts.), or fully complied (3 pts.), for the four considered categories.

For the process and analysis of the information, the results of the judges’ assessments were synthesized in the 16 subdimensions of the instrument. The mean ${\stackrel{-}{x}}_{ij}$ and the standard deviation ${\sigma }_{ij}$ of each subdimension (represented by the subscript $i$) and values were calculated for each category (represented by the subscript $j$). When analyzing the means ${\stackrel{-}{x}}_{ij}$ (subdimensions/categories), results were split into two groups according to mean values ${\stackrel{-}{x}}_{ij}\le 2.5$ or ${\stackrel{-}{x}}_{ij}>2.5$. The first group (group A) contains the subdimensions/categories where most of judges scored with 2 pts. The second group (group B) contains the subdimensions/categories where judges scored with 3 pts.

As can be seen in Table 5, 46 ${\stackrel{-}{x}}_{ij}$ were values greater than 2.5 (group B), while the other 18${\stackrel{-}{x}}_{ij}$ were in the range $2.14\le {\stackrel{-}{x}}_{ij}\le 2.5$ (group A). The subdimensions and/or their items in group A were reviewed, and small modifications were made, based on the comments of the judges, without altering their structure.

As an example, in the case of “Quality of mathematical activity”, we were able to establish two groups. Group A is made up of subdimensions 1, 2, and 3 in which nine of the twelve ${\stackrel{-}{x}}_{ij}$ of this group are in the range $2.14\le {\stackrel{-}{x}}_{ij}\le 2.5$. Therefore, these dimensions were modified based on comments. When analyzing the means of subdimensions 4, 5, 6, and 7 of “Quality of mathematical activity”, all ${\stackrel{-}{x}}_{ij}$ except one (${\stackrel{-}{x}}_{72}=2.43$)) were in the range $2.71\le {\stackrel{-}{x}}_{ij}\le 3$. In this case, we decided to make a small modification to one of the descriptors of subdimension 7, which, in terms of coherence, was evaluated by most of the judges with a 2.

Following the same procedure, the dimension “Opportunities for mathematical learning for all students, without gender or other biases” was assessed. However, of the 16 averages ${\stackrel{-}{x}}_{ij}$ associated with subdimensions 8, 9, 10, and 11, only one of them (${\stackrel{-}{x}}_{91}=2.14$) resulted in ${\stackrel{-}{x}}_{ij}\le 2.5$. Therefore, we decided to make slight modifications to some of the descriptors of subdimension 9 to increase their sufficiency.

Regarding the dimension “Management and socio-emotional support within the mathematical activity in the classroom”, following the recommendations of the judges, some of its descriptors were modified. Some subdimensions, e.g., subdimension 12 required quite a few modifications because the ordering of the words and their meaning make it difficult to understand the full dimension or some items were disarticulated syntactically and semantically. In addition, small changes were introduced in the descriptors related to subdimensions 13, 14, and 15 to improve sufficiency.

After doing some modifications to the items following the analysis of the results from Table 5, Fleiss Kappa was run to determine if there was agreement between the eight experts’ judgement on whether our instrument was sufficient, coherent, relevant, and clear to evaluate the quality of mathematical activity in Chilean classrooms from a gender perspective.

In terms of the sufficiency of the items, there was overall fair agreement between the officers’ judgements (κ = 0.251, 95% CI [0.163, 0.339], p < 0.001). Individual kappa values for the “not enough”, “only some aspects”, and enough categories were 0.235, 0.168, and 0.331, respectively. In terms of the coherence of the items to measure the dimension, there was overall moderate agreement between the experts’ judgements (κ = 0.425, 95% CI [0.344, 0.506], p < 0.001). Individual kappa values for the “not logic connection with dimension”, “require some adaptation”, and “clearly connected” categories were 0.556, 0.414, and 0.745, respectively. In terms of the clarity of the items to measure the dimension, there was also an overall moderate agreement between the experts’ judgements (κ = 0.461, 95% CI [0.375, 0.548], p < 0.001). Individual kappa values for the “not clear”, “item requires modification”, and “clear” categories were 0.600, 0.657, and 0.753, respectively. In terms of the relevance of the items to measure the dimension, there was a fair agreement between the experts’ judgements (κ = 0.232, 95% CI [0.141, 0.323], p < 0.001). Individual kappa values for the “item can be eliminated, “not relevant”, and “relevant to be included” categories were 0.556, 0.414 and 0.745, respectively.

Kendall’s W was run to determine if there was agreement between the eight experts’ judgement among the 16 subdimensions (see

Table 6. Kendall’s W, agreement between eight experts’ judgement.

	Related-Samples Kendall’s Coefficient of Concordance Summary
Total N	7
Kendall’s W	0.489
Test Statistic	51,346
Degree of Freedom	15
Asymptotic Sig. (2-sided test)	<0.001

). In a similar way with Fleiss Kappa, overall, the eight experts statistically moderately agreed in their assessments (W = 0.489, p < 0.001).

Specifically, in each of the categories punctuated, Kendall’s W values are presented in

Table 7. Kendall’s W, agreement between eight experts’ judgement in each category.

	D1. Quality (Sub 1–7)	p	D2. Opportunities (Sub 8–11)	p	D3. Management (Sub 12–16)	p
Sufficiency	0.502	<0.001	0.606	0.002	0.401	0.012
Coherence	0.604	<0.001	0.657	0.003	0.789	<0.001
Relevance	0.465	0.002	0.400	0.003	0.843	0.002
Clarity	0.459	0.004	0.714	0.002	0.564	0.003

.

4. Discussion

The findings of this study show that Fleiss Kappa and Kendall’s W coefficients are useful in assessing the reliability and validity of an instrument. Both measures are beneficial in evaluating the inter-rater agreement or consistency of multiple raters’ assessments of the same set of data. The quantitative analysis of the data revealed strengths and weaknesses of the instrument, and adjustments were made based on the results, as well as the qualitative observations and recommendations issued by the experts, particularly regarding the clarity and precision of the items. After the evaluation and comments, multiple items of the instrument were adjusted to increase clarity and improve their writing. Different subdimensions within three dimensions were modified, including categories where judges scored with ${\stackrel{-}{x}}_{ij}\le 2.5$, to improve sufficiency, coherence, relevance, and clarity. These dimensions included mainly subdimensions 1, 2, and 3 (S1. Relevance, richness, and variability of learning situations; S2. Variety of techniques and representations used in teaching; S3. Coherence, sufficiency, and articulation between arguments and mathematical activity). For example, the drafting version of subdimension 12 required significant changes due to challenges in comprehending the entire dimension. Certain words’ phrasing and meaning were causing difficulties, and some items were disjointed both syntactically and semantically. Similarly, we made a minor adjustment to one of the descriptors of subdimension 7, which most judges evaluated as having a coherence score of 2. The final validated version of the instrument can be a contribution to previous studies about classroom observation in mathematics, specifically in Chile, e.g., [31,34].

Although it is complex to reach agreements in the social sciences due to the nature and length of the descriptors, there was strong agreement among the judges in most cases. However, some limitations of the study might be the scarcity of knowledge of the context of Chilean teachers by some international judges or the ambiguity of some concepts utilized in the design of the instrument.

The design and validation of content by expert judgment of an instrument that addresses dimensions and subdimensions corresponding to relevant teaching practices in the mathematical classroom are presented. This validation process aims to design an instrument to observe essential aspects of the pedagogical, didactic, and disciplinary competencies of teachers and their attitudes, which influence the quality and equity of these practices [26]. It is expected that these dimensions and/or factors will also make it possible to identify possible gender biases that exist in classroom interactions.

The strength of this study is that it proposes a classroom observation instrument that focuses on effective practices for mathematics instruction in interventions and settings that explore the role of gender within other factors that affect the quality and equity of teaching practices in mathematics. The instrument design arises from a dialectical process between theory and observation. It is worth mentioning that the application of the instrument could require a certain degree of expertise or familiarization with the concepts that are the basis of its design. For this reason, we are developing a protocol that incorporates more detailed descriptions of the descriptors and examples of the use of the instrument based on real cases. The final version of the validated instrument can be found as Supplementary Material. A Spanish version of the final version of the instrument is also available.

5. Conclusions

This research aimed to design and provide content-related evidence as a source of validation for an instrument that serves as a guideline for observing and analyzing teaching practices in the mathematics classroom, taking into consideration the specificities of the teaching–learning process with a gender perspective. We had an initial evaluation where several items were highly evaluated. Subsequently, the instrument was adapted, and the judges were consulted to raise the rating. The validation by judges and the statistical analysis substantially contributed to improving the instrument. Therefore, these types of coefficients are useful in social sciences. Thus, the methodology of this study made it possible to achieve statistical validation, allowing decisions to be made to improve the coherence, relevance, clarity, and sufficiency of items in an instrument and thereby satisfactorily validate the classroom observation instrument. The validated instrument can be explored and applied to favor and evaluate the quality of mathematical activity in Chilean classrooms with a gender perspective.

By providing content-related evidence as a source of validation, this study contributes to research in mathematics didactics by integrating the quality of mathematical activity and equity and a gender perspective, which are usually studied separately. Furthermore, the classroom observation instrument is expected to contribute to public policy regarding improving mathematics teaching by paying attention to interactions, particularly concerning gender. At the same time, it contributes to teachers because it guides improvement towards their performance in the classroom and as an instrument to promote pedagogic reflection.

We acknowledge that this study is focused on providing content-related evidence. This is just one of the five sources of evidence that, according to the Standards for Educational and Psychological Testing, can be used to validate in terms of interpretation and use arguments [56]. Specifically, the research provides evidence for a claim that the dimensions, subdimensions, and descriptors defined in the instrument are sufficient, coherent, relevant, and clear. In the future, the ongoing project will be enriched by providing the other sources of validity stated in the Standards.

Finally, we thank the Universidad de Santiago de Chile for supporting this research through the project DICYT 031933es, as well as the eight judges to their opinions on the instrument and the constructive criticism received from the reviewers.