Abstract
The International Commission for the Study and Improvement of Mathematical Education (1950) was interested in updating and developing teaching resources to address the pedagogical problems of mathematics teaching in the mid-1950s. As a result of this concern, the First International Exhibition of Mathematical Teaching Material was held in Spain in 1957, an event that had great international repercussions. This work is situated in the field of the history of mathematics education, so the research method used is historical. The aim is to study those mathematical didactic models which, due to their dynamic and multipurpose nature, stood out at the Exhibition. The results show that these materials contributed favorably to the teaching of mathematics, as they made it possible to work on a wide variety of topics and provided numerous advantages over traditional material. The use of these models meant that the mathematical notions or ideas generally arose from the action that the child carried out with the material; they also made the student the main protagonist of their learning.
1. Introduction
The International Commission for the Study and Improvement of Mathematics Teaching (CIEAEM) was created in 1950 with the goal of addressing problems encountered in teaching mathematics at the time, mainly in primary and secondary education. The CIEAEM was not linked to official institutions; it was created at the instigation of Caleb Gattegno, a professor at Teacher’s College, University of London, who was its secretary and animator until 1960. After the Second World War, international relations in the field of mathematics were not quickly re-established; it was not until 1953 that the ICMI meetings were resumed [1,2] (p. 32). Thus, in the years of its creation, the CIEAEM was a reference for mathematics education.
Lucienne Felix, a French secondary school teacher and disciple of Lebesgue, belonged to the CIEAEM from the beginning and wrote a report on its first 35 years [3]. It lists the themes of the 36 congresses held up to 1984. The first ten took place between 1950 and 1955; the eleventh was held in Madrid in 1957, together with an exhibition of didactic material for the teaching of mathematics, the study of which is the subject of this work. In the same year (1957), the USSR launched the first Sputnik, an event which led to an awareness of the importance of mathematics and science education and the need for reforms in these fields [1].
Among the members of the CIEAEM are key international players from different fields [1,2,3]: epistemologists and psychologists such as Jean Piaget and Ewart W. Beth; mathematicians such as Gustave Choquet, Jean Dieudonné, and André Lichnerowicz; and educators such as Caleb Gattegno, Emma Castelnuovo, and Willy Servais [4]. To bring about effective and fundamental reforms of the programs, methods, and approaches used in teaching mathematics, the Commission believed two things were necessary:
First, a deep understanding of mathematical structures; and second, which is no less important, knowledge of childhood intelligence and emotional developmental processes. The reason was not only to understand the origins of mathematical concepts and reasoning in their minds but also to consider the factors that attract and create interest so as to stimulate and encourage them [4] (p. 96).
In the early years, the commission’s meetings were rather informal and no minutes or reports were produced [3] (p. 17). However, two books were published, which can be related to the dual purpose of study and improvement of the Commission. In L’Enseignement des Mathematiques [5,6], its authors, members of the CIEAEM, deal with psychological, epistemological, mathematical, or pedagogical aspects that have an impact on the teaching of mathematics. The other book, Le materiel pour l’ensegneiment des mathematiques [7,8], “was strongly oriented towards classroom practices by presenting concrete materials for mathematics teaching” [9] (p. 3) and collected reflections on the meaning of the use of didactic materials as well as experiences and proposals from the authors on the elaboration and use of different materials. These are two lines that were maintained, with greater or lesser preponderance, throughout the history of the CIEAEM. One of the most important representatives of this second line over time was Emma Castelnuovo [9].
Didactic material was the subject addressed in the 11th CIEAEM Meeting and the First International Exhibition of Mathematics Teaching Material, held from the 21st to the 27th of April, 1957 in Madrid (Spain). Both events were held jointly, and the later received broad interest among the educational community given that it was “the first international event recorded in history on mathematics teaching material” [10] (p. 7).
Multiple foreign media sources—specializing in mathematics—reported on the event, such as the French journal Bulletin de l’Association des Professeurs de Mathematiques, the publication Mathematica & Paedagogia (associated with the Belgian Society of Math Teachers), the English newsletter Mathematics Teaching, and Archimede, an Italian journal [10,11]. The contribution of the journal Enseñanza Media stands out, which published the book El Material Didáctico Matemático Actual in 1958. Puig Adam was the author, and in it, he provided an extensive chronicle of the 11th CIEAEM meeting and the First International Exhibition of Mathematics Teaching Material [10].
Against this background, the question posed for this work was the study of the mathematical teaching models that were presented at the First International Exhibition of Mathematical Teaching Material, which was held in Madrid in 1957. In order to answer this question, this research aimed to identify and describe the mathematical models that were presented at the exhibition and which were cited in the reports on the exhibition, and to study some of the didactic applications that their creators devised for these materials.
It analyses the material culture of educational institutions, which has also been expressed as school materiality. This focus emerged from changes in the field of historiography brought about by interest in school culture [12], which produced a broadening in the field of history of education and the development of new problems, new sources to study them, and new survey instruments [13,14,15]. Notably, interest in studying teaching practices and what happens in classrooms increased; this aspect has been termed the “black box” of schools given its opaque nature and the difficulty in accessing teaching practices. One way to approach this black box is to study objects present in the classroom, “cultural artifacts that refer to things created by human beings (outside the classroom) that provide information about the culture of their creator and users” [16] (pp. 16–17).
Interest in material culture has resulted in research, specialized meetings, and numerous monographs in journals, such as the one from 2021 in the journal Educació i Història: Revista d’Història de l’Educació, dedicated to the “material change in the history of education” that included contributions by researchers from different countries: Spain, France, the UK, Italy, Brazil, and Greece. Related scientific societies have been created, such as the Spanish Society for the Study of Historical-Educational Heritage (SEPHE), created in 2004; the Iberoamerican Network for the Study and Dissemination of Historical-Educational Heritage (RIDPHE), created in 2008; and more recently, the Italian Society for the Study of Historical-Educational Heritage (SIPSE) created in 2018 [17]. The search for, conservation, and study of new sources boosted the creation of new school life museums and centers dedicated to the history of education [18], including some notable examples: the GHEMAT in Brazil, with a foundation related to the history of mathematics education [19]; the Guy Broussea Center for Mathematics Teaching Resources at the University Jaime I in Castellón (Spain), which houses the COREM archives (Centre d’Observation et de Recherche pour l’Enseignement des Mathematiques) [20]; and the Center for Studies on School Memory at the University of Murcia (Spain) [21].
In the field of mathematics education history, research on locating and using mathematics textbooks provides insight into the material culture of educational institutions; however, the most distinctive studies in this area focus on objects present in the classroom and their use. These questions also appear in broader studies such as Carrillo [22] or Sánchez-Jiménez [23], as well as inspiring research focused on what objects used in mathematics teaching and learning processes contributed to the history of mathematics education [24,25,26,27].
2. Materials and Methods
This study focuses on the history of mathematics education (HME), a sub-segment in the area of the history of education [28]; as a result, the historical method was used. As noted by Karp [29], research on the history of mathematics education “inevitably inherits techniques and methods developed in both mathematics education and history (including the history of science)”. Priority was given to consulting primary sources that addressed the event being analyzed.
Among the primary sources analyzed, emphasis was given to professional journals and methodological textbooks directed, generally, at high school teachers. Information about the exhibition has been found in the professional journals Enseñanza Media (a “didactic information” journal published by the Ministry of Education and aimed at secondary school teachers), Revista de Educación (a scientific publication of the Ministry of Education which aims to disseminate educational research and innovation both nationally and internationally), and Mathematica & Paedagogia (founded by Willy Servais, a member of the CIEAEM since the beginning and Gattegno’s successor in the direction; the voice of the Belgian Society of Mathematics Teachers) [30]. Mainly the following two types of document have been used: published chronicles about the meeting-exhibition, which allowed us to evaluate teachers’ opinions on the event at the time; and methodological articles that were published by various teachers who participated in the exhibition, in which they revealed—through model lessons—the teaching approaches for the mathematics material they had created.
Regarding the methodological textbooks analyzed, El Material Didáctico Matemático Actual [10] is noteworthy; its main objective was to disseminate what happened at the 11th CIEAEM meeting and the First International Exhibition of Mathematics Teaching Material. Also notable was the collective work of the CIEAEM, El material para la enseñanza de las matemáticas [8], which sought to study material intended for use in teaching mathematics and to bridge the gap in the teaching literature on this topic that existed at the time. Moreover, the publication of this book coincided with the 11th CIEAEM meeting, by design, as they both addressed the same topics [10].
3. Results
The 11th CIEAEM Meeting was held in conjunction with the 1st International Exhibition of Mathematical Educational Materials. For this reason, there was a considerably larger number of participants than at previous editions of the meeting. Nearly 50 foreign teachers attended the meeting in addition to nearly 200 Spanish teachers. Ten countries were represented at the meeting-exhibition, including the following individuals: from England, among others, professor Gattegno (from the Institute of Education at the University of London) and two members of the Mathematical Association (Fletcher and Harris); from France, Choquet, Walusinsky (from the Association of Professors), Biguenet, and Lucienne Félix; from Belgium, Servais (from the Association of Professors), Carleer, and Langer; from Italy, Castelnuovo and Campedelli (from the Teaching Center), Pescarini, Ragusa, and Gianarelli; from Germany, Wolf and Pauls; from Austria, Mr. Staber; from Portugal, Mr. Silva; from Yugoslavia, Mr Kurepa; from Uruguay, Mr. Galli; and from Switzerland, Nicolet, Schilt, and Roth [31]. From Spain, various teachers participated in representation of different educational centres (both official and unofficial), such as the mathematics catedráticos de instituto (in Spain, a catedrático de instituto is the highest rank a secondary school teacher can achieve.) Puig Adam (from the San Isidro of Madrid Secondary School), Pascual Ibarra (from the Valladolid Secondary School), Fernández de Trocóniz (from the girls’ Secondary School of Bilbao) and the primary school teacher María Dolores Puig Sabadell (from the Sacred Heart of Jesus Primary School in Valladolid) [10].
The opening session of the meeting-exhibition was held at San Isidro Secondary School, and Gustave Choquet (professor at the Faculty of Sciences at La Sorbonne and president of the Commission) presided over the ceremony. Together with him were Professor Gattegno, who acted as secretary at the meeting, and Puig Adam (professor of mathematics teaching at the University of Madrid and catedrático de instituto at the San Isidro Secondary School). Puig Adam was a member of the CIEAEM from 1955 and played a leading role in the decision to hold the meeting in Spain. The scheduled activities included scientific-teaching conferences, practical lessons, working seminars, showings of films on mathematics teaching, and visits to the exhibition [32].
The First International Exhibition of Mathematics Teaching Material was held in the galleries of the San Isidro Secondary School in Madrid. The material presented was classified into two groups based on its origin: foreign or domestic. The majority of the teaching materials from the first group came from Belgium, specifically, the Belgian Society of Mathematics Teachers. As for the second group, the contribution from the San Isidro Secondary School in Madrid represented a significant portion of the sample, and the largest part was created by Puig Adam. Mariano Fernández Gómez, a primary school teacher, who was very artful and taught at the intermediate school of this educational center, supported him in the creation of this material. Puig Adam noted that in the creation of these models, they had sought, principally, the following characteristics: “simplicity, a multipurpose nature, to provoke action, and real life application” [10] (p. 61).
In the months prior to the meeting, official Spanish organizations, such as the Center for Teaching Guidance (COD), encouraged mathematics teachers and catedráticos de instituto to participate in and submit their teaching models to the International Exhibition of Mathematics Teaching Material. On occasion, these calls were made through advertisements in professional journals that published material on events of this type. In the journal Enseñanza Media, it was noted that only novel materials that evinced quality and ingenuity would be considered. Another desirable characteristic was the multipurpose nature of the models submitted. To guide teachers in the creation of this type of teaching material, the COD suggested interested parties consult the book Didáctica matemática eurística [33], as they considered the examples in that work to be of sufficient inspiration for those who wished to participate in the exhibition [34].
The following is a description of the mathematical models that were presented at the exhibition and that were included in the reports on the exhibition, especially in the book written by Puig Adam [10], which is the most extensive report on the exhibition. The didactic applications proposed for them are also presented.
3.1. Examples of Dynamic and Multipurpose Teaching Models Presented at the First International Exhibition of Mathematics Teaching Material
Puig Adam believed that several proposals for teaching material presented at the exhibition for teaching mathematics were “interesting samples of effective, simple, and multipurpose materials” [10] (p. 64). He also noted that the effectiveness of these models was widely demonstrated in these areas of mathematics, and that, given their versatility, they were also appropriate for other mathematics content [35] (p. 245). In this section, we describe these materials, as well as some of the mathematics content that could be covered in the classroom using them, with special emphasis given to the 3D models designed by the mathematics catedráticos de instituto Puig Adam and Fernández de Trocóniz.
María Dolores Puig Sabadell, from the Sacred Heart of Valladolid School, designed a teaching aid, which she called a ‘mathematics board’. It consisted of a square board with circular holes, where different colored pieces, similar to those used to play checkers, could be inserted (Figure 1). In early 1959, Puig Sabadell published the article “Modelo multivalente para demostraciones de matematicas” in the journal Enseñanza Media. In this article, she described several classroom activities that could be performed with this device in the first sessions of high school mathematics classes, adequate for both arithmetic and geometry. The following are some examples of the arithmetic activities: demonstrate some of the formal properties of addition or multiplication (associative and commutative properties of addition, associative property of multiplication, etc.); interpret the product as a representation multiplication, etc.); interpret the product as a representation of a rectangle; and calculate the remainder of a square root as the difference between two consecutive square roots. Among the geometry activities were demonstrating that the areas of a parallelogram and a rectangle with the same base and height are equivalent, and deducing that the ratio of the areas of two similar figures is the square of their similarity ratio [36].

Figure 1.
Puig Sabadell’s ‘mathematics board’ [10] (p. 121).
Another teaching aid that was positively evaluated by Puig Adam was the use of Cuisenaire rods (Figure 2); he believed that the use of colored number rods significantly improved the teaching of elemental arithmetic [10,35,37]. The aid consisted of prismatic rods that were 1 cm and ranged from 1 to 10 centimeters in length. Moreover, the color of each rod varied in accordance with its length: white (1 cm); red (2 cm); light green (3 cm); pink (4 cm); yellow (5 cm); dark green (6 cm); black (7 cm); brown (8 cm); blue (9 cm); and orange (10 cm). This teaching method of Belgian origin transcended borders and was used by teachers in many different countries. Gattegno contributed significantly to the dissemination of this teaching aid. After meeting with Cuisenaire in Thuin, Belgium in the early 1950s, he dedicated the majority of his investigative efforts to studying how this material could be used to teach mathematics content beyond primary school levels [35].

Figure 2.
Professor Gattegno explaining how to use Cuisenaire rods to the Spanish Director General of Primary Education (Joaquín Tena) and other participants at the 11th CIEAEM meeting [10] (p. 99).
According to Gattegno [38], the multipurpose nature of these rods contributed notably to their value as a teaching tool. This was attested to by the huge variety of mathematics topics that could be addressed using the rods: whole numbers and operations with whole numbers; fractions and operations with fractions; arithmetic and geometric progressions; combinatorics; the calculation of areas and volumes; and solving systems of equations. Below is an example where professor Gattegno shows how to use this teaching aid to find the value of two lengths (x and y), where their sum and difference is known (a system of two equations with two unknowns):
For instance, starting with an orange rod: it is equal to one black and one light green rod. However, the black rod is equal to one light green and one pink rod. As a result, the orange rod is equal to a pink rod and two light green rods, but the pink rod is also equal to the difference between the black and the light green rods, while the orange is their sum. With this information, we can pose the following question: If we have the orange and pink rods and we know that the orange rod is equal to the sum of two unknown rods and the pink rod is equal to the difference of those same two rods, what are the two rods? [38] (p. 218).
Another resource that contributed favorably to the study of mathematics, in this case—plane geometry, was the use of geometric mosaics and puzzles. The different actions that students could perform with this type of material (adjusting, connecting, etc.) were seen as a motivating element and suggestive of mathematics concepts [35]. An example of this type of material is the one that the catedrático de instituto Pascual Ibarra [39] created to study, heuristically, the similarity of triangles with students from the later years of secondary education (Figure 3).

Figure 3.
Material provided by José Ramón Pascual Ibarra [10] (p. 107).
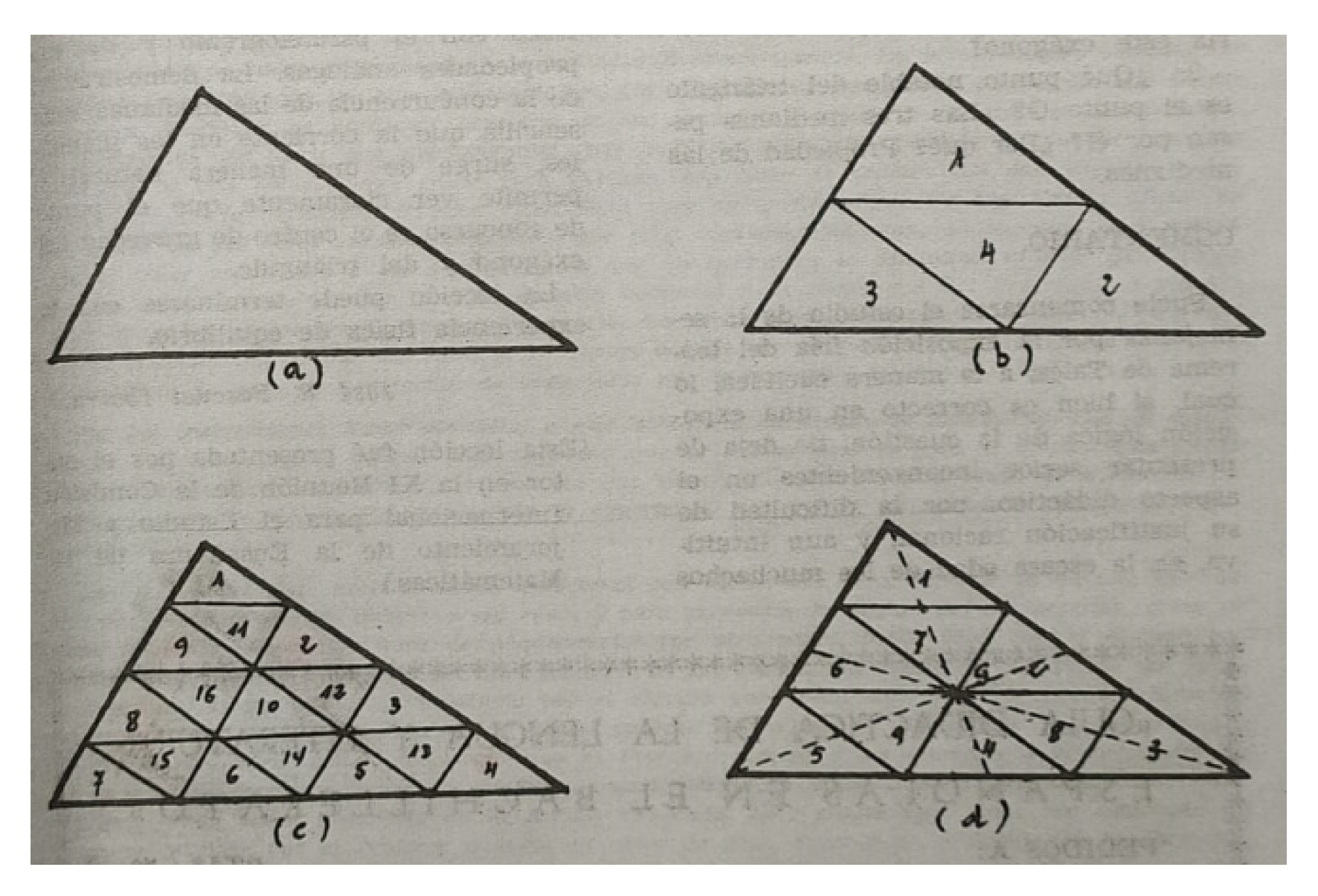
The typical approach to introducing the study of similarity at the end of high school using Thales’s theorem (Euclid’s Elements) presented serious teaching issues for students of this age, especially due to the difficulty students had in rationalizing the end result. To improve this situation, Pascual Ibarra based his proposal on a dynamic approach using four triangles made out of thin wooden board. As can be seen in Figure 4, the second triangle (b) is obtained by decomposing the first triangle (a) using its midsegments. Triangle (c) is found by dividing the first triangle into 16 triangles and triangle (d) is found by doing the same using nine triangles.
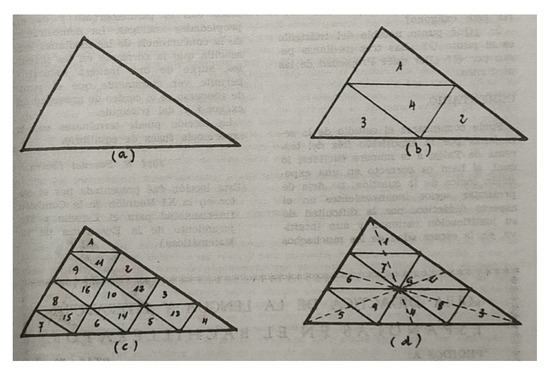
Figure 4.
Material given to students during a lesson with J.R. Pascual [39] (p. 55).
Some of the activities suggested in this lesson are described below:
1. Students are given four triangles (b). Describe these triangles. They are given triangle (a). They are asked to place the four triangles from (b) on (a). How much bigger is triangle (a) than one from (b)? Its area? Its sides?
2. The process is repeated with the 16 triangles (c) and triangle (a): How much bigger is triangle (a) than one from (b)? Its area? Its sides?
3. How much bigger is triangle (b) than one from (c)?
4. What do all these triangles have in common? Their shape. What about them is different? Their size [39] (p. 55).
Gattegno [38] also participated in the exhibition and presented his geoplane model. He believed that the majority of the fundamental content for Euclidean plane geometry could be addressed using his model. He pointed out that stretching rubber bands between the nails set in the geoplane model to represent geometric figures provided several benefits in comparison with the traditional method of using the blackboard to draw them:
The polygons were always clear, and this did not depend on the teacher’s artistic ability; since the geoplane was relatively small, it could be rotated to change the orientation of the figure, demonstrating that the properties of that figure were invariable regardless of movement in the plane; and students that used the geoplane model would create the habit of rotating it in order to view the figure from different angles [38] (p. 210).
Gattegno asserted that his model could be used in a wide variety of learning experiences and was viable for all levels of education. He grouped the types of lessons that could be taught with it into three categories: (a) those where the teacher used the geoplane model as a substitute for the chalkboard; (b) lessons where the students used the geoplane model individually to solve a specific problem; and (c) lessons where using the geoplane model allowed students to investigate all solutions until all possibilities had been exhausted. He believed that this last type of exercise contributed in the most profound manner to the “education of the mathematician located inside every student” [38] (p. 214).
Various teachers created different types of geospace models based on Gattegno’s geoplane model to address spatial geometry. This type of teaching aid consisted of a cube that allowed for the construction of different spacial figures inside it using string or rubber bands. Pescarini (from Italy) participated in the exhibition, presenting a geospace model constructed from clear plastic board (Figure 5). This had different orifices on the lateral faces and hooks on the base that facilitated illustrating spatial figures and their properties [10].

Figure 5.
Pescarini’s geospace model [10] (p. 79).
Another Italian submission was created by the School of Secondary Teaching in Rome, which participated by submitting a metallic geospace model (Figure 6) whose walls were formed of metal bars [10].

Figure 6.
Metallic geospace model from the School of Secondary Teaching in Rome [10] (p. 79).
The Spanish proposals related to geospace models were submitted by the mathematics catedráticos de instituto, Puig Adam and Fernández de Trocóniz [10] (p. 62). According to Puig Adam, these models surpassed other geospace models on display at the exhibition due to their simplicity and versatility, as their structures, which could be dismantled, were made of hooks, and had barred walls, among other things, allowed for “the most ample variety of perspectives and uses”.
3.2. Puig Adam’s Geospace Model
Puig Adam believed that the new concept of teaching—student-centered spatial geometry—required updating mathematics models. Materials were needed that the students would use and which allowed them to “make” geometry, something Puig felt was impossible to do with the classical materials that he called “display case models”. Adam Puig’s geospace model (Figure 7) consisted of a box whose sides were made of thin, wooden slats. This allowed students to see the configurations represented inside the box from any perspective. Puig created various types of geospace model, some of which were made from solid boxes while others could be dismantled [10,40].

Figure 7.
Several geospace models designed by Puig Adam [10] (p. 114).
As for the other materials necessary to use the model, he stated that, while rubber bands (as in the case of the geoplane model) could be used, he preferred using twine because it allowed you to create spatial figures with many edges more quickly. He also suggested using rigid bars in combination with twine to introduce the concept of continuous variations. To demonstrate how to use the geospace model in the classroom, Puig Adam detailed various examples of how to address specific content from different course levels in high school. By way of example, he mentions the construction of a variable parallelepiped (Figure 8) using rubber bands placed on rigid bars [40]. He pointed out that after interacting with the model, several students were able to deduce the rule used to calculate the volume of the figure:

Figure 8.
Representation of a parallelepiped in Puig Adam’s geospace model [10] (p. 115).
The parallelepiped starts as a right-angled rectangle; however, after first moving the rubber bands and later the rigid bars, it becomes oblique, with the base of a parallelogram. After each change to the figure, the students clearly see how the same volume that is removed from one side is added to the other. In this way, the total volume of the parallelepiped and the law which governs its calculation (base × height) is maintained [40] (p. 24).
Puig Adam [40] believed that another advantage of this model, related to its simplicity, was the ability for students to build their own models using everyday objects (packing boxes, screws, rubber bands, twine, etc.). With the goal of promoting this practice, he provided teachers with the following guidelines:
Any packing box that was at least 25 cm long/tall will suffice. After removing one of the largest sides, which facilitates access to the interior of the box, attach a uniform array of screws on each of the remaining sides (or place them in specific locations if you wish to achieve spatial figures of a predetermined size). In this way, the entire interior surface of the box will be covered with a collection of points where we can connect rubber bands or twine that can just as easily represent lines in projection problems as they could represent the edges of a transparent polyhedron, appropriate for measured study [40] (p. 23).
To demonstrate the versatility of the model created by Puig Adam, two modifications the author pointed out are described. The first of these modified the geospace model to study descriptive geometry. It entails covering three of the faces (the bottom, the back, and one side) with cardboard. Puig indicated that this simple gesture allows you to project (using lights) figures constructed in the geospace model, and in this way bring the characteristics of the projections into being in front of the students [40] (p. 23). The second entails substituting the wooden slats on the geospace model for wire mesh (Figure 9). According to Puig Adam, this modification did not compromise visibility in the model and allowed the creation of warped and circumscribed curves, which revealed the intrinsic trihedron of a point on a curve [10,40].

Figure 9.
Geospace model created by Puig Adam using wire mesh [10] (p. 114).
3.3. Fernández de Trocóniz’s Geospace Model
Fernández de Trocóniz, mathematics catedrático de instituto at the girls’ Secondary School of Bilbao, also participated in the exhibition and presented a geospace model. This teaching aid was positively evaluated by important figures in the mathematics teaching community:
perfectly executed with a system of orifices and hooks located on three clear plastic plates and a collection of supplementary pieces that enable representation of the majority of the figures and shapes that constitute the content of current spatial geometry course [10] (p. 60).
This simple to construct geospace model was made from everyday objects (a box, two pieces of plastic, four stamped pieces as columns, knitting needles, elastic thread, etc.) and could be fully dismantled (Figure 10). Fernández de Trocóniz believed that the ability to accurately reproduce spatial figures contributed to overcoming some of the problems students typically encountered when studying three-dimensional space [41].

Figure 10.
Fernández de Trocóniz showing how his geospace model works at the exhibition of teaching material [10] (p. 107).
Students progress through plane geometry with definitions, problems, and theorems supported by the foundation of teaching aids that allow them to ‘authentically’ represent the figures and concepts they are dealing with. These aids are paper and a blackboard.
It is a very different thing when dealing with the third dimension. Representations are no longer ‘authentic’ for children. This is the start of a symbolism that, at first glance, is difficult to understand. We speak to them about right angles or perpendicular lines, and we draw oblique lines; we talk about equal segments, but the ones that we draw could not be more dissimilar; the same thing occurs with the polygons we draw when we talk about regular polygons, which could not be considered regular by any criteria. Children at this age find no help on the blackboard or on paper; we could almost say that, initially, these tools help them to fail [41] (p. 155).
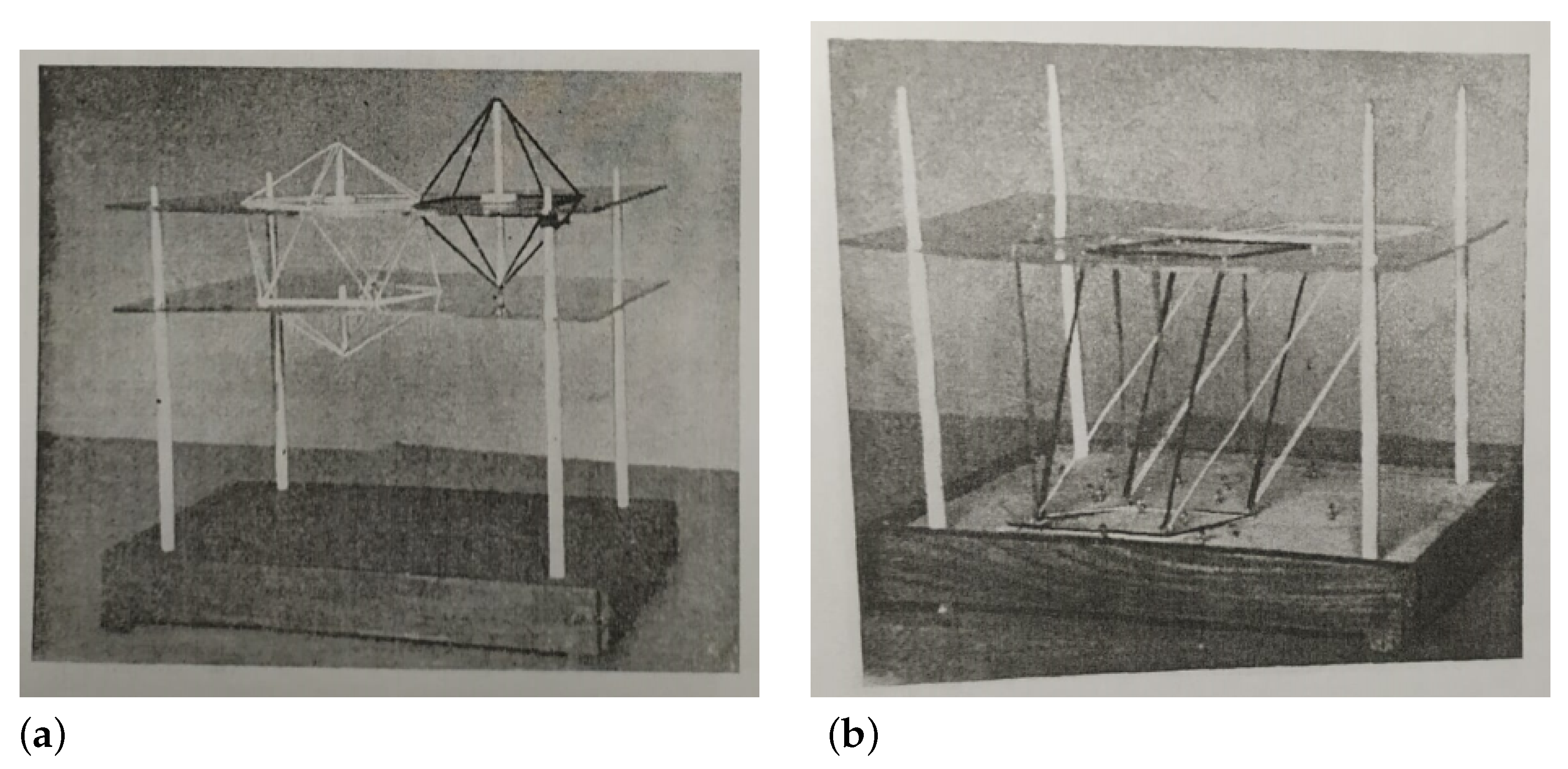
Fernández de Trocóniz created several examples of how to use the model, such as the representation of a regular icosahedron and a regular octahedron, as well as the study of the equivalence of parallelepipeds (Figure 11). He did not feel, however, that the use of this model conflicted with teaching students how to graphically represent spatial elements. To the contrary, he believed it could be used as a corrective measure: “How instructive it will be to compare such disparate drawings obtained from different perspectives with the same figure!” [41] (p. 159).
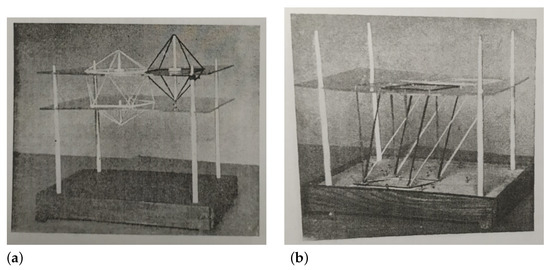
Figure 11.
(a) Representation of a regular icosahedron and a regular octahedron in Fernández de Trocóniz’s geospace model. (b) Equivalence of parallelepipeds in Fernández de Trocóniz’s geospace model [41] (pp. 155–156).
4. Discussion
Since the 19th century, proposals for teaching mathematics have been made with the help of concrete models and other teaching materials that allow an intuitive approach to mathematics teaching. In this way,
Instead of prematurely confronting students with finalized mathematical structures or theorems, they first have to build an intuitive understanding of the basic mathematical ideas and properties by observing, manipulating, and constructing models. Only by perception and action, seen as inseparable parts of the mathematical activity itself, can students achieve higher levels of mathematical understanding [2] (p. 33).
As noted above, one of the topics of debate and investigation of the CIEAEM was the use of concrete models, teaching materials, or teaching aids [2] (p. 33). One of the two books published in the 1950s was devoted to teaching materials [7,8].
Puig Adam, as a member of the CIEAEM, was aware of the advances taking place in different countries in this regard and actively collaborated in disseminating novel teaching material among Spanish teachers. As proposed by him, the 11th CIEAEM meeting and the First International Exhibition of Mathematics Teaching Material was held in Madrid; Puig Adam was a prominent figure in these events as the key organizer. This meeting-exhibition had significant international impact and benefited from the participation of delegates from various countries who came to Madrid to present their proposals. These materials were characterized by their simplicity, multipurpose nature, call to action, and real-life application, and they sparked great interest when compared with stationary models.
Lucienne Felix [3] assessed the meeting and the exhibition in the following way:
This is a strangely provocative moment for teachers who are at once searching for, discovering, and experimenting with materials created by themselves or by other colleges or by their own students. One also becomes aware of the multivalence of some of these materials (p. 49).
Later on, he pointed out the role of these teaching materials when commenting on the conclusions of the meeting:
Our conclusions on this meeting: To help the acquisition of any mathematical concept one should avoid unprepared recourse to abstraction. An intuitive basis must be given. Abstract notions will be reached all the better if they have been freed from concrete situations (p. 50).
Puig Adam’s interest in these teaching materials is related to the defense and application of active teaching methods in mathematics throughout his professional career, specifically the heuristic method [33]. An example of this is that two of the rules on his ’List of Ten Rules for Secondary Mathematics Teaching’ reference the same: “V.- Teach by guiding creative activity and student discovery” and “VI.- Stimulate this activity by encouraging direct and functional interest in the object of knowledge” [42] (p. 130). This list of ten rules was used broadly for teaching activities by Spanish teachers [43] and was used as an example of the state of education in Spain at the 19th International Conference of Public Instruction celebrated in Geneva in 1956, together with other teaching models created by Puig Adam. This event was organized by UNESCO and the International Bureau of Education (IBE), which Piaget headed at the time; various countries (Spain, Belgium, Italy, Austria, the United States, France, etc.) participated, putting different aspects of their educational system on display (curricula, publications, advances in teaching methods, etc.) [44].
The large number of teaching models that Puig Adam presented at the exhibition, as a representative of the San Isidro Secondary School, testifies to the educational importance that teachers gave to mathematics materials. He believed that the use of dynamic models promoted learning that resulted from the child taking action and handling the material, and, more specifically, from considering those mathematical concepts that were not affected by movements (above all, if these transformations took place in a continuous context). The nature and versatility of the models examined in this study caused Puig Adam to consider them the most appropriate for modern teaching perspectives, in which the child was the center of the teaching–learning process. Furthermore, he inspired teachers to encourage their students to create new models and believed that designing such models trained the students in the functions of abstraction and concreteness, which are fundamental to learning mathematics. To build these models, he recommended using everyday objects (tape, rubber bands, boxes, etc.) because he believed that they resulted in a very simple model at a low cost. The use of models from daily life to teach mathematics was a recurring theme in the teaching proposals Puig Adam created, as he believed that “the most fertile and instructive source of mathematical models is daily life” [45] (p. 19). In the first educational writings he authored for secondary education, together with Julio Rey Pastor, he mentioned these items (boxes, bottles, knitting needles, folders, etc.) [46,47] and the majority of them continued to appear in later works and adaptations [33,35,45].
Puig Adam asserted that the use of building components and models that could be dismantled (rods, tokens, slats, mosaics, bars, etc.) strongly favored creative activity in children because these elements could typically be joined and interlock, which allowed them to be used in numerous activities and even facilitated learning how to use them during free play. This last point enabled teachers to steer students’ initial interest from simply handling the material (organizing them by length, building things with them, etc.) towards activities focused on mathematics content [10]. The aforementioned considerations on the use of models to teach mathematics substantiate some of the key conclusions from the CIEAEM meeting-exhibition. Interest was expressed in using models to build knowledge of abstract mathematical concepts and also to prevent the overuse of models that would limit the scope and characteristics of the mathematical concepts they refer to:
Avoid personal a priori reasoning in determining the effectiveness of a model; children are full of surprises and, ultimately, they are the ones that will make the final judgment on the model’s effectiveness. Do not use models where they seem unnecessary nor prolong their use beyond what is strictly essential. Make the jump to abstraction gradually by moving first from tangible and concrete ideas to concrete imaginable ones. Let the model perform its function as spontaneously as possible in dialog with the child, allowing the teacher to get used to to not interfering or forcing this interaction with the goal that the model not be just a simple means for transmission but rather a thought-provoking factor in knowledge acquisition and attainment [10] (pp. 28–29).
Proposals for active teaching that would lead pupils to construct knowledge through observation and experimentation are characteristic of the new schools movement that developed between 1889 and 1940, as reflected in the Principles of New Education formulated by Ferrière [48]. It should be noted that some of the leading members of the ICIEAEM had been associated with the new schools movement and with the teaching materials created in that field. For example, Piaget used the school Maison des Petits, attached to the J.J. Rousseau Institute in Geneva, for his studies on the development of children’s thinking. In this school, children carried out activities in a fairly free way with material created by the teachers Audemars and Lefendel [49,50]. For her part, Emma Castelnuovo maintained contact over the years with the Decroly School, through Libois, who attached great importance to mathematical modeling by both teachers and pupils and organized several exhibitions of such material in Brussels [2] (p. 19); Castelnuovo was inspired by this experience to hold similar exhibitions in Italy, which he recorded in his work Matematica nella realtat [51].
As Roberts points out [24] (p. 565), “The employment of tools to assist teaching and learning of mathematics in fact has a history long predating electronic technology, and some of them have been proclaimed as revolutionary”.
5. Conclusions
In conclusion, as we have seen, models of different mathematical concepts, mainly geometrical ones, have been commercialized since the end of the 19th century [1]. At the level of international meetings, Ruthven [52] has shown that the interest in technologies that could enable intuitive and experimental teaching of mathematics was already evident at the ICMI in 1912 and has continued since. The creation of new materials adapted to classroom conditions involved people connected with the CIEAEM, such as Emma Castelnuovo, Caleb Gattegno, who created software for learning numeracy, or Emma Castelnuovo’s collaborator, Mario Barra, who is currently studying the use of Dynamic Geometry Software in the teaching of mathematics [53]. The manipulative teaching materials created active learning environments and prepared the conditions for the school use of mathematical technology [1,52].
Finally, this paper shows the variety and relevance of the mathematical models that were presented at the exhibition and their link to active mathematics teaching approaches up to the present day.
Author Contributions
All authors contributed equally. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CEME | Centro de Estudios sobre la Memoria Educativa de la Universidad de Murcia |
| (Center for Studies on School Memory at the University of Murcia) | |
| CIEAEM | Commision Internationale sur l’Etude et l’Amélioration de l’Enseignement des |
| Mathématiques (International Commission for the Study and Improvement of | |
| Mathematics Teaching) | |
| COD | Centro de Orientación Didáctica (Center for Teaching Guidance) |
| HME | History of Mathematics Education |
References
- Furinghetti, F.; Matos, J.M.; Menghini, M. From mathematics and education, to mathematics education. In Third International Handbook of Mathematics Education; Clements, M.A., Bishop, A., Keitel, C., Kilpatrick, J., Leung, F.K.S., Eds.; Springer: Cham, Switzerland, 2013; pp. 273–302. [Google Scholar]
- De Bock, D.; Vanpaemel, G. Rods, Sets and Arrows: The Rise and Fall of Modern Mathematics in Belgium; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Felix, L. Aperçue Historique (1950–1984) sur la Commision Internationale sur l’Etude et l’Amélioration de l’Enseignement des Mathématiques (CIEAEM); IREM de Bordeaux: Bordeaux, France, 1986. [Google Scholar]
- Puig-Adam, P. La Comisión Internacional para el estudio y mejoramiento de la enseñanza matemática. Proyecto de una interesante reunión en Madrid, abril de 1957. Rev. Educ. 1955, 38, 96. [Google Scholar]
- CIEAEM. l’Enseignement des Mathématiques; Delachaux & Niestlé: Paris, France, 1960. [Google Scholar]
- CIEAEM. La Enseñanza de las Matemáticas; Aguilar: Madrid, Spain, 1965; Available online: https://www.redalyc.org/pdf/1794/179414894008.pdf (accessed on 17 February 2023).
- CIEAEM. Le Materiel pour l’Enseignement des Mathématiques; Delachaux & Niestlé: Paris, France, 1958. [Google Scholar]
- CIEAEM. El Material para la Enseñanza de las Matemáticas; Aguilar: Madrid, Spain, 1964. [Google Scholar]
- Furinghetti, F.; Menghini, M. The role of concrete materials in Emma Castelnuovo’s view of mathematics teaching. Educ. Stud. Math. 2014, 87, 1–6. [Google Scholar] [CrossRef]
- Puig-Adam, P. El Material Didáctico Matemático Actual; Publicaciones de la Revista Enseñanza Media, Ministerio de Educación Nacional: Madrid, Spain, 1958. [Google Scholar]
- Puig-Adam, P. Les mathématiques et le concret. Math. Paedagog. 1956, 12, 62–65. [Google Scholar]
- Juliá, D. La culture scolaire comme objet historique. Paedagog. Hist. 1995, 31, 353–382. [Google Scholar] [CrossRef]
- Moreno-Martinez, P.L. History of School Besk Development in Terms of Hygiene and Pedagogy in Spain (1838–1936). In Materialities of Schooling: Design—Tecnology—Objects—Routines; Lawn, M., Grosvenor, I., Eds.; Symposium Books: Oxford, UK, 2005; pp. 71–95. [Google Scholar]
- Herman, F.; Van Gorp, A.; Simon, F.; Depaepe, M. The School Desk: From Concept to Object. Hist. Educ. 2011, 40, 97–117. [Google Scholar] [CrossRef]
- Viñao, A. La historia material e inmaterial de la escuela: Memoria, patrimonio y educación. Educacion 2012, 31, 7–17. [Google Scholar]
- Braster, S.; Grosvenor, I.; del Pozo Andrés, M.M. Opening the Black Box of Schooling Methods, Meanings and Mysteries. In The Black Box of Schooling. A Cultural History of the Classroom; Braster, S., Grosvenor, I., del Pozo Andrés, M.M., Eds.; Peter Lang: Bruxelles, Belgium, 2011; pp. 9–18. [Google Scholar]
- Vidal, D.; Alcântara, W. The material turn in the History of Education. Educ. Hist. Rev. d’Hist. l’Educ. 2021, 38, 11–32. [Google Scholar]
- Lawn, M. Modelling the Future: Exhibitions and Materiality of Education; Symposium Books: Oxford, UK, 2009. [Google Scholar]
- Valente, W.R. O GHEMAT Brasil e a pesquisa coletiva em história da educação matemática. Hist. Mem. Educ. 2020, 11, 595–613. [Google Scholar] [CrossRef]
- Orús, P.; Fregona, D. Huellas del COREM y la TSD en el desarrollo de la didáctica de la matemática en España y Argentina. Hist. Mem. Educ. 2020, 11, 553–594. [Google Scholar]
- Carrillo-Gallego, D.; Moreno-Martínez, P.L.; Sánchez-Jiménez, E. El Centro de Estudios sobre la Memoria Educativa (CEME) de la Universidad de Murcia y la investigación en historia de la educación matemática. Hist. Mem. Educ. 2020, 11, 615–646. [Google Scholar] [CrossRef]
- Carrillo-Gallego, D. La Metodología de la Aritmética en los Comienzos de las Escuelas Normales (1838–1868) y sus Antecedentes. Ph.D. Thesis, Universidad de Murcia, Murcia, Spain, 2005. [Google Scholar]
- Sánchez-Jimenez, E. Las Escuelas Normales y la renovación de la enseñanza de las matemáticas (1909–1936). Ph.D. Thesis, Universidad de Murcia, Murcia, Spain, 2015. [Google Scholar]
- Roberts, D. History of Tools and Technologies in Mathematics Education. In Handbook on the History of Mathematics Education; Karp, A., Schubring, G., Eds.; Springer: New York, NY, USA, 2014; pp. 565–578. [Google Scholar]
- Volkov, A. Visual Representations of Arithmetical Operations Performed with Counting Instruments in Chinese Mathematical Treatises. In Researching the History of Mathematics Education. An International Overview; Furinghetti, F., Karp, A., Eds.; Springer: New York, NY, USA, 2018; pp. 279–304. [Google Scholar]
- Carrillo-Gallego, D. Los catálogos de material escolar como fuente de la historia de la educación matemática: El caso de los ábacos. Hist. Mem. Educ. 2018, 7, 573–613. [Google Scholar] [CrossRef]
- Carrillo-Gallego, D.; Maurandi-López, A.; Olivares-Carrillo, P. From Pestalozzi’s intuition principle to classrooms: The counting frame and innovations in the teaching of mathematics (Spain, nineteenth century). Paedagog. Hist. 2021, 1–21. [Google Scholar] [CrossRef]
- Valente, W.R. Oito temas sobre história da educação matemática. REMATEC 2013, 8, 22–50. [Google Scholar]
- Karp, A. The History of Mathematics Education: Developing a Research Methodology. In Handbook on the History of Mathematics Education; Karp, A., Schubring, G., Eds.; Springer: New York, NY, USA, 2014; pp. 9–24. [Google Scholar]
- De Bock, D.; Vanpaemel, G. The belgian journal Mathematica & Paedagogie (1953–1974): A forum for the national and international scene in mathematics education. In History and Epistemology in Mathematics Education. Proceedings of the Seventh European Summer University (ESU 7); Barbin, E., Jankvist, U., Kjeldsen, T., Eds.; Aarkus University: Aarkus, Norway, 2015; pp. 723–734. [Google Scholar]
- Redacción. XI Reunión de la Comisión Internacional para el estudio y mejoramiento de la enseñanza matemática. Enseñ. Media 1957, 7–8, 92–94.
- Pascual-Ibarra, J.R. Reunión en Madrid de la Comisión internacional para el estudio y mejoramiento de la enseñanza de las Matemáticas. Revista Educ. 1957, 64, 40–43. [Google Scholar]
- Puig-Adam, P. Didáctica Matemática Eurística; Instituto de Formación del Profesorado de Enseñanza Laboral: Madrid, Spain, 1956. [Google Scholar]
- Redacción. Anuncio sobre la Reunión-Exposición de Material Didáctico de Matemáticas publicado en la revista Enseñanza Media. Enseñ. Media 1957, 3, 26.
- Puig-Adam, P. La Matemática y su Enseñanza Actual; Ministerio de Educación Nacional: Madrid, Spain, 1960; Available online: https://scholar.google.com.hk/scholar?hl=zh-CN&as_sdt=0%2C5&q=Puig-Adam%2C+P.+La+Matem%C3%A1tica+y+su+Ense%C3%B1anza+Actual%3B+Ministerio+de+Educaci%C3%B3n+Nacional%3A+Madrid%2C+Spain%2C+1960&btnG= (accessed on 17 February 2023).
- Puig-Sabadell, M.D. Modelo multivalente para demostraciones de Matemáticas. Enseñ. Media 1959, 33–36, 41–44. [Google Scholar]
- Puig-Adam, P. Sobre la enseñanza de la Aritmética en la Escuela Primaria. Vida Escolar 1959, 9–10, 2–7. [Google Scholar]
- Gattegno, C. Materiales multivalentes. In El Material para la Enseñanza de las Matemáticas; CIEAEM, Ed.; Aguilar: Madrid, Spain, 1967; pp. 210–226. [Google Scholar]
- Pascual-Ibarra, J.R. Una lección sobre iniciación en la semejanza de triángulos (para alumnos de 11 a 12 años). Enseñ. Media 1957, 11, 55–56. [Google Scholar]
- Puig-Adam, P. Un nuevo material para la enseñanza eurística de la Geometría del Espacio. Enseñ. Media 1957, 3, 22–26. [Google Scholar]
- Fernández de Trocóniz, A. El material didáctico en la enseñanza de la Geometría del Espacio. Enseñ. Media 1958, 17, 155–159. [Google Scholar]
- Puig-Adam, P. Decálogo de la didáctica matemática media. Gac. Mat. 1955, 5–6, 130–135. [Google Scholar]
- Redacción. Renovación de los métodos didácticos en España: Matemáticas. Enseñ. Media 1956, 2, 47–49.
- Lozano, J. La XIX Conferencia Internacional de Instrucción Pública de Ginebra. Rev. Educ. 1956, 51, 16–19. [Google Scholar]
- Puig-Adam, P. Modelos matemáticos extraidos de la vida. Arquímedes 1958, 3, 19–23. [Google Scholar]
- Rey-Pastor, J.; Puig-Adam, P. Elementos de Aritmética. Colección Elemental Intuitiva, Tomo I; Imprenta de A. Marzo: Madrid, Spain, 1927. [Google Scholar]
- Rey-Pastor, J.; Puig-Adam, P. Elementos de Geometría. Colección Elemental Intuitiva, Tomo II; Imprenta de A. Marzo: Madrid, Spain, 1928. [Google Scholar]
- Ferrière, A. L’École nouvelle et le Bureau international des Écoles nouvelles. Pour l’Ére Nouv. 1925, 15, 2–8. [Google Scholar]
- Audemars, M.; Lafendel, L. La Maison des Petits de l’Institut J.J. Rousseau; Delachaux & Niestlé: Neuchâtel, Switzerland, 1923. [Google Scholar]
- Carrillo-Gallego, D.; Olivares-Carrillo, P. La difusión de los juegos de la Maison des Petits en España. Rev. Hist. Educ. 2020, 24, e99354. [Google Scholar] [CrossRef]
- Castelnuovo, E.; Barra, M. Matematica nella Realtá; Paolo Boringhieri: Torino, Italy, 1983. [Google Scholar]
- Ruthven, K. Mathematical Technologies as a Vehicle for Intuition and Experiment: A Foundational Theme of the International Commission on Mathematical Instruction, and a Continuing Preoccupation. Int. J. Hist. Math. Educ. 2008, 3, 91–102. [Google Scholar]
- Barra, M. Fusionismo Olistico e Software per la Geometria Dinamica. 2017. Available online: http://www.educationduepuntozero.it/didattica-e-apprendimento/fusionismo-olistico-software-la-geometria-dinamica-3081635564.shtml (accessed on 17 February 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).