Achieving Transfer from Mathematics Learning

Abstract

The question of transfer is a special challenge in mathematics teaching because the wide range and fragmentation of the curricula have in many cases fostered an instrumental understanding, which makes transfer difficult for the students. Although promoting a relational learning has been a huge step forward in achieving transfer, understanding usually remains at the technical level of learning. Fostering critical thinking and metacognition raises learning to the psychological level, as students are encouraged to analyse their own thinking. Despite this, our hypothesis is that transfer will only be achieved when students are helped to reach a personal dimension, being encouraged to discover their own way of approaching the global reality of their lives beyond the subject. Learning, for instance, the greatest common divisor should be an opportunity to discover that, as numbers can be presented by their prime factors, people can be recognised by their features and interests. As such, looking for the greatest common divisor should not differ from discovering common interests with friends. Integrating specific and general learning will make transfer no longer unattainable. Personalising learning means discovering how one specific learning impacts on the personal way of understanding reality (oneself, others, and the world), thus making transfer natural.

1. Introduction

Research into transfer has been gaining ground in the literature, especially with the current focus on increasing the impact of a given educational intervention. Transfer of learning occurs when learning in one context enhances (positive transfer) or undermines (negative transfer) a related performance in another context, whether a closely related context (near transfer) or a context further removed (far transfer) [1]. For these authors, a “low road transfer” consists of practicing—in a new context—routines similar to those which have been learnt in a previously known context, whereas a “high road transfer” involves deliberate effortful abstraction and a search for connections between different contexts of learning.

The question of transfer is a special challenge in mathematics teaching because the wide range and fragmentation of the curricula—together with a search for effectiveness—have in many cases fostered an instrumental understanding, which makes transfer difficult for the students. Since instrumental understanding consists of learning protocols or routine procedures, it is not surprising that extrapolating these to contexts different from those in which they were formulated leads to a significant number of mistakes. In fact, one of the reasons why Richard Skemp [2] advocated a relational understanding over an instrumental one is its adaptability to new tasks. Relational understanding includes knowing why a certain method works, enabling students to assess its suitability for a given problem, and possibly to adapt the method to new problems. Moreover, relational understanding involves comprehending a general law beyond the specific method which is being learned, such comprehension being necessary for the learning of other topics beyond the one being studied. The apparent easiness of learning protocols, without having to go deeper into the grounding of the theory, becomes a disadvantage when faced with the sheer number of protocols to be learned. Skemp concludes his argumentation describing relational understanding as an organic system, i.e., a system which acts as an agent of its own growth. Students who have built a relational schema in their minds will actively explore new areas to widen the initial schema, thus guaranteeing a long-term learning. Developing schemas in one’s mind is the true goal of relational understanding, enabling students to solve new problems by themselves. These schemas make transfer unnecessary when it comes to problems of a similar nature.

Not all researchers agree on the nature of these schemas. For some, they consist of abstract structures, more or less rigid, which the learner constructs through finding the common elements between different problems. For other researchers [3,4], they are flexible learned ways of seeing the world that vary across situations and yet permit overall coherent understandings. The latter perspective—termed “transfer in pieces”—is more consonant with the notion of organic systems described by Skemp. Transfer does not stem from the learner’s ability to state a general rule:

At the heart of a knowledge-in-pieces approach to transfer is the expectation that different knowledge resources and patterns of readout and coordination might be used at different times and with respect to specific contextual differences, all in the service of a single concept or principle [4].

For these authors, transfer is understood, not as the all-or-nothing transportation of an abstract knowledge structure across situations, but as the incremental growth, systematization, and organization of knowledge resources that only gradually extend the span of situations in which a concept is perceived as applicable [3]. For this approach, a wide range of examples should be used in instruction (e.g., differences in problem type, aspect, and context), in order to enable students to acquire a range of appropriate strategies and explanatory resources for reasoning about a concept. “The more complex and varied a particular knowledge frame grows, the more likely it is to be cued across many situations, and the more readily and flexibly it can be used to interpret any situation in which it is applied” [4].

Baroody [5] refers to relational understanding as meaningful knowledge. The question of meaning has been traditionally related to the search of coherence between previously learned concepts and new concepts [6], as well as to the comprehension of the contexts in which these concepts are useful or applicable [7]. Transfer cannot be achieved without taking the question of meaning into account.

Moreover, to foster a far transfer, it has also been proposed that critical thinking and other transferable skills be worked on, leading to debates regarding whether knowledge includes these skills or otherwise [8]. Besides these cognitive or intellectual skills, Humphrey et al. [9] define social and emotional learning as a set of social, emotional, behavioural and character skills that support success in school, the workplace, relationships, and the community. They are considered soft skills because they are not explicitly addressed, although they are always communicated by teachers [10]. Similarly, Frey et al. [11] assert that classroom learning always includes cognitive, social and emotional issues. Referring to scientific education, Whitehead [12] considers that ideas are helpful only if they are presented in relation to sense perceptions, feelings, hopes, desires and to the mental activities which form our life. For this author, there is only one subject-matter for education, which is life in all its manifestations. As such, he proposes the eradication of the “fatal disconnection of subjects which kills the vitality of our curricula”, in order to help students see the wood by means of the trees. What he is proposing goes beyond the psychological level of learning to reach the personal level.

This brief journey shows that transfer requires that the learner go beyond the concrete to enter into his or her interiority. Abstract knowledge, meaning, emotional experience, metacognition, criteria of knowledge, critical thinking—in relation to the way of knowing rather than what is known—have as their reference the interiority of the person. Our hypothesis is that transfer will only be achieved when students are helped to discover their own way of approaching reality (oneself, others and the world), i.e., life, not only through metacognition—studying how they think—but also through “metacognition of metacognition”. Through seeking to discover why they think as they do, learners will integrate specific and general learning.

2. Methodology

In order to support our main hypothesis—the necessity of reaching the inner dimension of the person for transfer to take place—we will carry out a narrative review of several recognized scholars’ research in which knowledge is regarded as emerging in the human being from the interiority, as an existential inter-relational process. These researchers show the young child as an active author and constructor of his or her meaningful world through the interpersonal relationship. If knowledge emerges in the human being as an existential inter-relational process, this process is the ‘place’ from which all knowledge emanates and converges. As such, knowledge involves the inner dimension of the person and, from this dimension, all his or her capacities are put into play. In this paper, we will present all these different levels of the human act and their relationship with transfer, seeking to show the implications of taking all of them into account for transfer to take place (Section 3). Section 4 is devoted to presenting specific ways of bringing the inner dimension of the students into play in the mathematics classroom, which may be achieved by applying the pedagogical approach proposed by Orón [13,14] to the subject of mathematics. Finally, an application of this to a specific mathematical topic is presented.

3. Different Levels of the Human Act and Its Relationship with Transfer

Before introducing the inner dimension of learning, we analyse the different levels of the human act and the corresponding levels of transfer. As an example, we will show how a common topic in mathematics, finding out the greatest common divisor of several whole numbers, may be linked with the understanding of oneself and one’s personal relationships.

The most external aspects of the human act—those which are identified as behaviours—are apparently very different from each other. At this level, the procedures which are necessary to find out the greatest common divisor of several numbers have nothing to do with, for example, those involved in decomposing a polygonal shape into smaller polygons but neither of these seem to be related to the tasks involved in a personal activity such as arranging to meet friends. The different procedures, protocols and behaviours related to these tasks make transfer difficult, if not impossible.

However, when we delve a little deeper into the human act, we find a certain commonality between the aforementioned actions. The tasks of finding the greatest common divisor and decomposing a polygonal shape into smaller polygons share at the very least certain capacities of analysis. Given this fact, by abandoning the level of a specific object on which to act and focusing instead on the requisite capacities, the issue of transfer is already being facilitated. A recognition of this has led some researchers to propose the learning of soft skills as the ‘royal road’ to transfer. At this level, the key question would be what skills are required of the person, irrespective of the object to which they are going to be applied. However, it will be seen that this is still insufficient for transfer to take place.

Developing the capacity of analysis in a given curricular subject enables the application of this capacity to another field. This is certainly positive, but it does not guarantee transfer, nor is it transfer per se. Working at this level is similar to what neuroscience calls working on motor programmes. For example, whether we sign our name on a piece of paper, on a blackboard or in the sand, the signature is the same although the motor executions are quite different. The common element is their underlying motor programme [15]. Something analogous can be seen in the case of the analytical capacity, although, rather than a motor programme, we are dealing with a mental programme.

Just as the efficacy of training motor programmes is proven [15], so is the development of mental programmes; not only of the capacity of analysis—which is an activity of intelligence—but also of mental acts of the will, the memory and the imagination among others. However, all these acts—situated at the mental level—cannot be exercised without an object: memory requires something to be remembered; imagination needs something to be imagined and so on.

We thus observe that the mental level is an inner activity of the person which still refers to a given object, but does the human act involve something more than behaviour and mental activity? According to the model of the human act presented in [16] there is a further aspect of the human act, an inner dimension which, instead of referring to a particular object, refers to the subject itself. This inner dimension, far from being new, has been present in philosophy since ancient times. Aristotle [17] speaks about interiority in relation to virtue, which he considers “a way of being”, which includes the more behavioural and external dimensions of the person and also his or her interiority. For Spanish philosopher Leonardo Polo [18], the special relationship which takes place between two people (from interiority to interiority) is precisely what constitutes the human being as a person. Only the human being has this intimate relational dynamic. Similar ideas are held by Spaeman [19] and Whitehead [12] (p. 68): “Despite all external stimuli and guidance, the creative impulse towards growth comes from within and is intensely characteristic of the individual”.

Focusing on educational activity, we find this dimension of interiority in Pestalozzi [20]—who sees the child’s interiority as the true source of the novelty and growth involved in becoming a person with a sense of order and beauty—and in Fröbel [21], who affirms that the educator has to help the child to discover the inner connection of everything; only then will the child unfold all his or her activity and proactivity. Montessori [22] also believes in the inner richness of the child, which is unique and distinct from that of the adult. Only being aware that human action arises from the interiority, from the existential positioning of the person—who is capable of mobilising all his or her faculties and thus transforming the world—will the reduction of human action to mere behaviours be avoided.

This allows us to hypothesise that this personal level is that which must be reached for the phenomenon of transfer to occur naturally. This level should not be confused with what we have called the mental level or with soft skills, as both refer to the object and not to the person per se. Working on the ability per se rather than on the mastery of a given object is an improvement on the mere teaching of protocols and procedures, but there is still a long way to go. The same applies to soft skills, which also focus on operability and efficiency. These are the personal skills that help interaction with others and with objects beyond the subject in question. Among these figure the capacity for dialogue and perseverance, something which may be acquired through working on the object. Even widening the scope thus, we are still focused on the object, either a specific object or a generic object. The personal level, however, refers to the person per se, who is not an object, but rather a subject.

As has been shown, knowing is not a technical matter that can be achieved independently of the most internal realities of the person. Understanding knowing as such requires a dynamic vision of human knowledge in which there is interaction between the person and what is known. It is therefore necessary to go beyond representationist visions of reality—which assume a more passive or sequential way of achieving knowledge—to very dynamic conceptions, following Dewey, Dennet, Whitehead, Wang Yang-Ming, among others [23].

In other words, knowing the world requires knowing oneself and knowing others. These three dimensions of knowing are intertwined from the very origin of our lives, as psychoanalysis has shown [24,25,26].

Bowlby’s attachment theory [27] shows that the way of projecting oneself onto the world, onto others, and the understanding of oneself have been shaped by one’s childhood relational style. An acceptance and welcome relationship in which the child’s physical, psychological and relational needs are met leads him or her to develop a secure attachment which enables him or her to open up to reality. If another kind of attachment has been developed—one that is insecure for the child—the child may sometimes perceive reality as a danger.

Similarly, Erikson [28] found that, during the first two years of life, a child may develop two alternative basic relational styles: trust or distrust. In trust, one is open to others, to the world and to oneself—all these constituting reality—and wants to know it. In distrust, one seeks—instead of knowing in an open way—to identify points of danger in order to protect oneself.

Theories of social reference [29,30,31] have shown that what children do is much more complicated than imitating adult behaviors, as is usually said. What a child actually does is learn meanings. As such, it can be said—quite literally—that parents lend their minds to their children. Moreover, knowing any new reality in a meaningful way requires that this reality be introduced into a satisfying interpersonal experience, which is the reference point the person uses to make meaning out of reality [24,32,33,34].

We hypothesise that, if all new knowledge manages to reach this level of interiority, which we might call ‘originary’, such knowledge will be truly integrated into the person’s life and then naturally transferable because the knowledge has been installed in the ‘from where’ the person accesses and knows the world. Moreover, this will not only enable transfer, but also the creation of new knowledge, as already suggested in [35].

According to the papers cited above, the child in his or her first access to the world simultaneously answers three questions: Who am I? Who is the other? What is the world? [26]. We may thus formulate [16] the inner dimension in terms of:

• Personal identity: the understanding of oneself.
• Relational intention: ranging from the intention to trust the other to attempts to make the other conform to our expectations.
• Existential positioning: the way of understanding oneself in this world and what one thinks one can do with this world.

Every act presupposes a starting point from which one acts and promotes a way of wanting to live and be [36], bringing all these personal dimensions into play.

It is, thus, necessary to know one’s way of being positioned towards oneself, others and the world, in order to know why one knows in the way one does. We consider it necessary to reach these levels of personal knowledge for transfer to be carried out. Moreover, we think that it is necessary to reach this point in order to truly say that one knows what one claims to know.

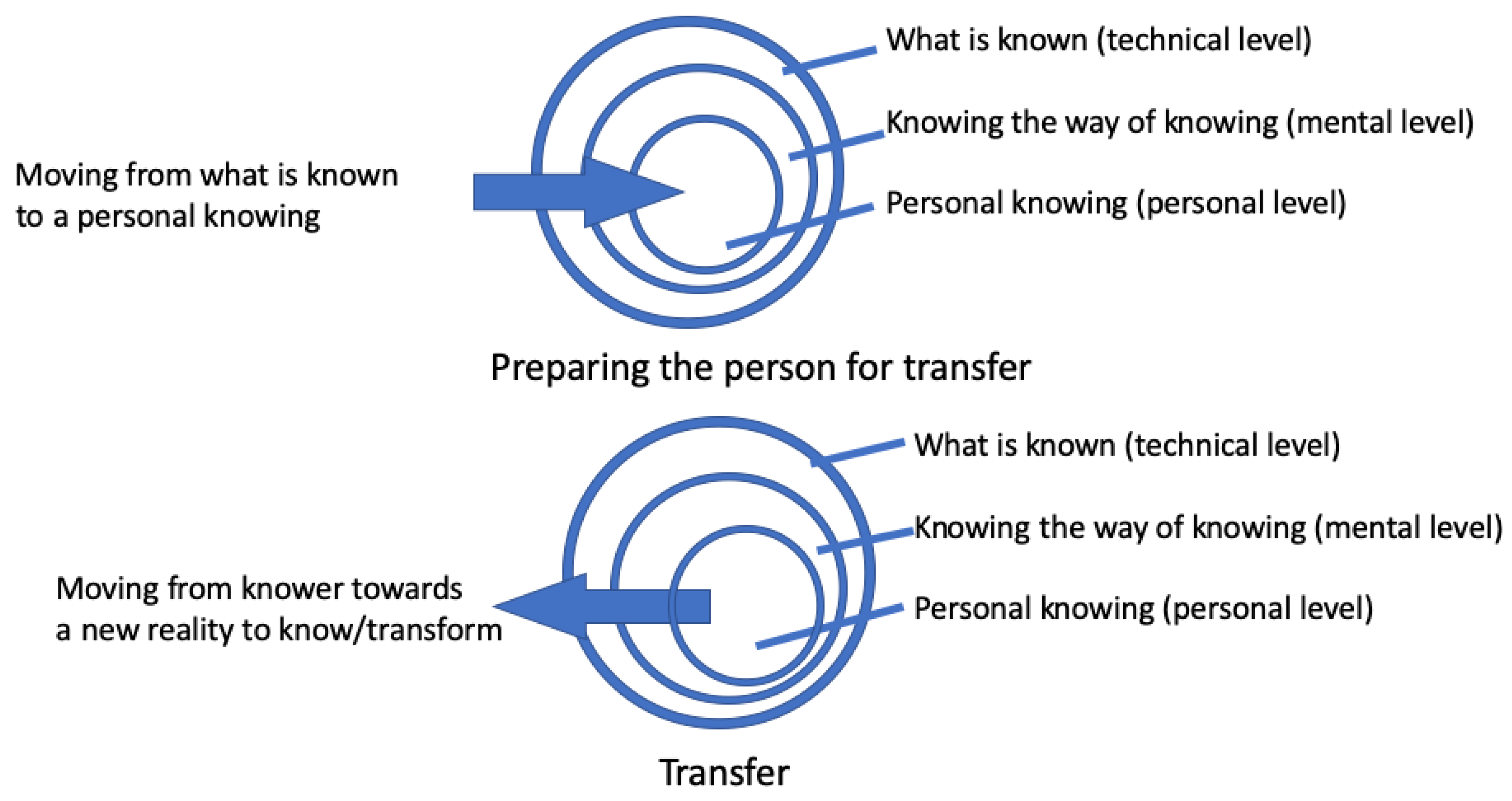
The aim of the next section is to show how to move, in a mathematical classroom, from what is known into personal levels, transfer then occurring when the learner moves—from the interiority reached—towards either new knowledge or an action which applies what is initially known.

4. Working on Mathematics Taking the Inner Dimension into Account

In a mathematics classroom, aside from learning procedures and protocols, it is possible to work on skills. For instance, following Bloom’s scale [37], working on the ability to analyse different objects would help students to learn how to analyse. This is certainly a good thing, because it takes one beyond merely learning protocols and procedures. Sadly, however, teachers often provide thoughts but do not teach how to think, or they provide evaluations (whether something is correct or otherwise) but do not teach how to evaluate, or—moving to the emotional sphere—they give names to feelings but do not help to feel, and so on with every possible mental activity. This way of teaching disintegrates human action, leaving aside the interiority of the person and asking students to act from the mental level, often focusing on a specific psychological activity. However, if human action stems from the interiority of the person and embraces all his or her potentialities in a unified way, each behaviour or performance of a task is an expression of both the person’s interiority and his or her mental activity. The term growth gains relevance in this vision since the development of any human faculty, including cognition, serves growth. From this perspective, the various human faculties and realities cannot be educated separately, because working on one of them affects the whole person. Even in a mathematics classroom, the whole reality of the person should be worked with, including his or her interiority, by simultaneously attending to the internal dimensions of the human act, which are present in every act and do not refer to a specific object of knowledge:

• Personal identity: Being aware of the relevance of the human act entails giving the students opportunities to develop their authorship. Presenting mathematics as a collection of definitions, procedures, rules, and formulae, something that one only has to learn and then apply in different exercises and problems, leaves little room for human growth [38]. As such, mathematical tasks should give students room for choice, thus enabling them to decide, not only what to do, but also who they want to be, thus, working on personal identity.
• Relational intention: Deciding who one wants to be entails defining one’s personal relationship style, whether trusting the other or trying to make the other conform to our intentions. In order to facilitate this decision, mathematics should be presented in a human way, as a subject anchored in human perception, movement, intentions and actions [39]. Introducing maths as a dynamic subject, which has evolved in line with the concerns of humanity—as is the case with all the cultural creations—will help students to discover the processes and the genesis of the discipline. Such a presentation will enable students to insert mathematics into their life, including personal relationships, these being understood as the source of all novelty, growth and innovation [35].
• Existential positioning: Life is complex and knowing reality in all its complexity requires not separating the world from the human being. As such, mathematics should be studied in relation to reality, being presented as an interconnected network—rather than a pyramidal structure whose layers need to be covered to reach the top [38]—and taking into account that the learner is also part of this reality. It has been shown that, even with a highly standardized curriculum, mathematical experience is unique for each student, intrinsically related to personal circumstances [38]. This means that the way in which the learner projects him or herself onto reality determines to a great extent what he or she knows and how he or she knows.

In order to take all these parameters into account, we will apply the pedagogical approach of Orón [13,14], which was specially designed to foster personal growth. Orón’s approach consists of two steps: (1) growing in knowing reality, including self-knowledge and (2) making decisions aimed at personal growth, which is understood as inseparable from the improvement of interpersonal relationships. We study how to implement these two steps within a mathematical activity:

(1)

Although reality is a whole, parceling it facilitates a better understanding of its complexity. Mathematics can contribute to a better knowing of the following ‘realities’ distinguished by Orón:

• Realities of nature: Nature should be understood as it is really is, its knowledge being guided by the awe or surprise of contemplating something new. Geometry is the area of maths which is closest to nature: it describes shapes and movement. A presentation of this area in relation to the physical world—instead of as an artificial body of knowledge—will help students to know nature in an open and trustful way, going beyond a mere classification of geometrical shapes. The teacher should present the contents in the closest possible way to what our senses show to us, giving the learners opportunities to perceive curves, lines, shapes, angles, movement and so on, as well as chances to reflect on the mathematical ways of describing these.
• Man-made realities: In this case, knowing is knowing the intention that explains the existence of each reality. Knowing intentions will allow learners to evaluate whether each man-made reality serves to improve personal relationships or otherwise. Mathematics should be presented as a human construction which has always been linked to the concerns and preoccupations of civilizations throughout history [40].
• Realities of personal history: These refer to learners’ experiences. Mathematical tasks may serve for students to discover their own way of facing problems and dealing with the difficulties they encounter, as well as to learn how to relate this knowing to their personal way of understanding both the world and themselves. When students make an analysis of these issues in the classroom, the question of their personal relationships often comes to the surface, preparing them for making decisions in this regard.
• Relational realities: Interpersonal relations are the basis of all experience and contrast. As has been seen [41], self-knowledge occurs because the encounter with the other allows us to know about ourselves. These relationships are also the finality of our acts if they are true human acts [26]. Mathematical tasks are full of opportunities for students to contrast their thinking with others’ thinking, thus, analysing the flexibility of their mental schemas and their capacity for accepting those of others. Moreover, the educational act should not focus on merely mastering the mathematical tasks, but also on understanding the underlying criteria, using the curricula contents as a means of transforming the world into a more human place.

(2)

This presentation of maths as something flexible and dynamic—rather than a rigid schema—will help learners to make decisions aimed at transforming reality. In some cases, the decision may consist of a change of intentionality in the use of a man-made reality rather than to a transformation of reality itself; in others, the decisions may be put at the service of the improvement of personal relationships. In order to prepare these decisions, when designing a mathematical activity, a teacher must identify the student’s starting point, not only in terms of what the student’s knowledge of the subject is, but also in terms of the thematic proximity between what is being learned and what the student is living. To the extent that the learner discovers that the educator is concerned with his or her person, over and above the subject matter, the learner will be able to open up to his or her own interiority and initiate processes of growth in relation to the subject or topic in question [14]. At this point, the question of meaning does not only arise with reference to the context in which the mathematical activities are presented, but also in relation to the challenges that each person is facing at each stage of his or her life, in particular the challenge of personal identity. If the mathematical activities are presented as true human acts, they will start from the most general and move towards the particular, as such involving the whole person. The most general thing is to decide who one wants to be in relation to others, and the particular thing is to make a concrete decision and carry out an action, using the learned contents in such a way that it impacts on the transformation of the world. This way of promoting global growth, stemming from interiority, will make transfer natural.

The following table (

Table 1. Relation between the different levels of the human act and the corresponding mathematical knowledge and transfer.

Levels of the Human Act	Mathematical Knowledge Which Is Working on	Kind of Understanding Which Is Promoted	Transfer Level	How to Achieve Transfer	References
Most external level	Behaviors Protocols Routine procedures	Instrumental understanding: What to do and how to do it	Low road transfer: Practicing—in a new context—routines similar to those which have been learnt in a previously known context	Teaching of protocols and routines	This perspective can be seen in the traditional official curricula
Psychological or mental level (rational and emotional)	Effortful abstraction Comprehension of general laws Problem solving Critical thinking Metacognition Soft skills (capacity of analysis, creativity, communication skills, perseverance, etc.)	Relational understanding: Why to do it Meaningful learning Social and emotional learning	High road transfer: Incremental growth, systematization, and organization of knowledge resources Development of general schemas Search of rational coherence	Working on a wide range of examples Delving into the theory in a related way, also in connection with other subjects Presented in relation with perceptions, feelings, hopes and desires Working cooperatively	This perspective can be found in [1,2,3,4,5,6,7,8,9,10,11,12]
Inner level	Metacognition of metacognition Knowledge of oneself and one’s interpersonal relationships starting from the mathematical content Knowledge of the world	Personal understanding: For what purpose and for whom to do it Discovery of one’s own way of approaching reality	Personal road transfer: Personal knowledge integrated with that of the world in a meaningful way, thus transferable to both other knowledge and action	Presenting the subject in a dynamic and human way Providing the underlying criteria of the theory Working on personal identity, interpersonal relationships and existential positioning Making decisions at a personal level	Antecedents of this perspective can be found in [42,43,44,45,46,47]

Remark: Working on maths at a given level entails also working on all the skills which are described in the lower levels boxes, but with a wider perspective.

) shows the different aspects of mathematical learning in relation to the levels of the human act and the diverse ways to promote transfer.

Let us look at a specific example and find out what looking for the greatest common divisor, decomposing a polygonal shape into smaller parts and meeting with friends mean on a personal level, thus making transfer natural.

The calculation of the greatest common divisor of several whole numbers requires factoring each of them as the product of prime numbers, something which is often presented to children in late primary and/or early secondary school as a mere technical task. Taking care to present a graduated and varied collection of examples will help the students to build a relational schema of this topic in their minds, especially if these are presented in diverse contexts such as the area of a rectangle decomposed as the product of its possible width and height, or a whole number of cookies decomposed as the product of the possible number of packs and its capacity, all these contexts being representable by means of polyominoes or polycubes. An expansion of these mental schemas could be facilitated by presenting a posteriori the decomposition of polynomials as the product of irreducible ones. However, this secondary school task is seldom presented in relation to the decomposition of numbers and the parallelism between both decompositions is often hidden to students. We are not saying that the abstract structure which embraces both whole numbers and polynomials—that of the unique factorization domain—should be introduced at this stage, but rather that the communalities of both decompositions should be shown. Moreover, it would be possible to go beyond arithmetic to work on the decomposition of polygonal shapes as the disjoint union of ‘irreducible’ ones, highlighting both the similarities and the differences between this geometrical decomposition and the arithmetical ones. Every polygonal shape may be expressed as the disjoint union of triangles with vertices belonging to the initial polygon (these being the irreducible polygonal shapes). However, this decomposition is far from unique.

Finding out the greatest common divisor of several whole numbers consists in identifying the greatest whole number which occurs in the decomposition of all of them. What does this task mean in each of the contexts in which it has been presented? When may this be helpful? Is this task possible when we deal with polynomials instead of numbers, and when the entities to be decomposed are polygonal shapes as the disjoint union of triangles? What has this task to do with arranging to meet friends?

As numbers can be presented by their prime factors, people can be recognised by their features and interests, although in this case the decomposition is not unique. The students may be asked to express their own factorization following this model and some of them might decide to express one or more of ‘their factors’ up to a certain exponent, as occurs with some numbers. If several friends are arranging a meeting, they should find out their common interests and, if possible, their greatest common interests. It may also be considered what finding out the least common multiple means in the activity of arranging to meet friends. The students might discover, for instance, that finding an activity which embraces all their interests is more interesting than settling for what they have in common.

While these activities are being carried out, processes of metacognition may be fostered in the classroom: what difficulties does one encounter? Do these difficulties have something to do with a lack of depth in understanding numbers or do they reflect a lack of development of one’s capacity of analysis? We are still on the mental or psychological level.

Going deeper than the mental sphere—where we have been able to find many commonalities between all the above presented tasks—it is now the moment to enter the personal dimension, carrying out processes of metacognition of metacognition.

At this step, one may ask oneself why one’s factorization happens to be difficult and perhaps discover that one—and thus anyone—cannot be reduced to their features and interests; but what else is a person? Only another person can discover this extra dimension in oneself. The role of the teacher at this step is fundamental in order to help students to discover their interiority. Students may also be helped to wonder what they are looking for when meeting with friends, whether carrying out activities related to what all of them have in common or otherwise opening up to look for further interests. Each student may be also encouraged to make specific decisions about his or her next meeting with friends, bringing their relational intentions into play. These actions can be already considered transfer (see Figure 1), but also contribute to making transfer natural when it comes to learning new contents which are close to the decomposition of a number as the product of its prime factors.

5. Conclusions and Discussion

The difficulties which are commonly encountered in achieving a natural transfer in mathematical learning may be partly caused by a lack of consideration of the inner dimension of the person in the activities developed in the mathematics classroom. The human being seeks to know the complexity of reality, including him or herself. His or her openness to knowing reality in its complexity prevents the person from being understood as an object (reduced to his or her characteristics). Only an education that helps the person to be the author of his or her own life will enable both personal and social growth.

If education is understood as a mere improving of intellectual, social and emotional skills, transfer will have to be specifically fostered and worked on. Conversely, if education is understood as holistic growth, stemming from the interiority and embracing all the personal dimensions, transfer will arise in a natural way.

Mathematics is full of opportunities to help students to discover this inner dimension by bringing into play issues such as the search of identity, personal relationships and existential positioning within the ordinary activities. In this way, the learning of procedures and contents may be carried out taking the inner dimension into account, both at the step of knowledge and at that of decision-making, these being the two steps in the pedagogical approach presented by Orón in [13,14].

Since human decisions come back to the person, configuring his or her way of living [36], this education will promote true personal growth and a facilitation of transfer. The person is a personal subject. Working only at the mental level, mathematics is not helping students to discover their interiority. At this point, the role of the teacher is central because the inner dimension can be discovered only in the presence of others [40]. If the teacher fosters the analysis of students’ way of thinking (metacognition) but does not help them to wonder why or how this way of thinking has been formed, the inner level is not being reached. Conversely, if the students are helped to discover the personal dimension when performing a mathematical task, this task will be dealt with as a true human act, preparing students for a metacognition of metacognition. Such an activity—and the existential questions which it involves—often bring interpersonal relationships to the surface. Introducing novelty into one’s relationships leads to a new way of thinking: we are entering the personal sphere and thus making transfer natural.

A mere technical education is not able to bring about a new way of either being in the world or relating to others. The world cannot break the person’s self-consciousness either. Only the fact that the other thinks in a different way breaks it. Through trying to understand the other, the person discovers that the other—and also him or herself—is more than his or her mental activity. The other has given the person access to his or her inner self. Now the person’s acts and decisions come from within: firstly, deciding who one wants to be and then, little by little, making decisions regarding what to do, bringing into play all one’s mental activity.

The hypothesis presented in this paper clearly needs to be verified and would require an experimental implementation in which the teaching-learning process is carried out as a process that starts from the encounter with the reality of study and reaches the most intimate levels. This process could include a series of questions which gradually delve into reality starting from the object of study. For example, we might start by asking about the object in the simplest way: “What is it?”. Then, about the object in its context, by increasing the number of related variables: “What is it in this or that context?”. After that, we might ask about the psychological processes involved in one’s way of knowing: “How do I think when answering the question regarding what it is in this or that context?“, in order to know one’s habits of thought. Another question might deal with personal relevance: “What does the experience of knowing the object in its context mean in my life?”. Finally, we return to self-knowledge by asking oneself: “What do I discover in my way of understanding myself and my relations with others, and what can be done in this world by knowing all of the above?”

We believe that precedents for this proposal can be found in the understanding that learning is: meaningful learning [42], cooperative learning [43,44], relational learning [45], learning in complexity rather than in simplicity [46,47] (a requirement for transfer [1]). However, we think it is necessary to go deeper along these lines to the most personal levels—the interiority or intimacy of the person, since the above cited papers often give the interpersonal relationship a medial value for learning, while, in our approach, it is learning that truly has a medial value for the improvement of relationships. In this regard, Tomasello, a renowned anthropologist, clearly asserts that cooperation is not possible without presupposing interpersonal trust and seeking to increase and deepen this trust [48,49].

Designing mathematical activities which embrace all the dimensions of each human act is a significant challenge, but no less significant is the challenge of involving teachers in this new way of understanding education. Finding proposals for preparing teachers for this exciting task comprises a challenging area for future research.