Incorporating Problem-Posing into Sixth-Grade Mathematics Classes

Abstract

Problem-posing is an essential component of mathematics education because, among other reasons, when students are given the opportunity to pose their problems, they can take ownership of their learning and become more engaged in the given subject. Thus, problem-posing can lead to a deeper understanding of the studied mathematical concepts. In a collaborative action research study, the authors explored whether well-structured problem-posing activities could be incorporated into classes with students of mixed ability in mathematics. This question is addressed by examining the correlation between students’ mathematics grades and problem-posing success. The problem-posing approach used in this paper relies on problem solving as a parallel activity. Hence, the study also focuses on the relationship between problem posing and problem solving. The paper presents the results of a classroom experiment with 86 sixth-grade students and their teachers from Hungary and Romania. After evaluating the students’ problem-posing products and problem-solving performances, the results show that problem posing, based on a worked-out model problem, is a feasible challenge for most students. Moreover, this experiment identified a direct relationship between successful problem posing and problem solving.

1. Introduction

Problem-posing is an important aspect of mathematics education because, when students are given the opportunity to pose their problems, they can take ownership of their learning and become more engaged in the material, with a deeper understanding of the concepts they are learning. Additionally, problem posing allows students to see the relevance of mathematics in the real world, as they can apply the concepts they have learned to real-life situations. Experiencing the connection between mathematics and everyday life can increase their motivation to learn and help them see the value of mathematics beyond only being a subject they are required to study in school. Overall, problem posing seems to be an effective teaching strategy that can help primary school students develop essential skills and a deeper understanding of mathematics.

The relationship between mathematical skills and problem posing has long been a research focus. English writes, “We know comparatively little about children’s abilities to create their own problems in both numerical and non-numerical contexts, and the extent to which these abilities are linked to their competence in other domains such as number sense or novel problem-solving” [1] (p. 184). Although Cai et al. [2] assert that considerable progress has been made in this area, research on the subject is far from complete. By analyzing problem-posing products and comparing the results of high and low mathematical achievers, the authors intend to expand on previous research findings.

The authors approached the introduction of problem posing in the classroom based on Ellerton’s active learning framework [3]. This approach seemed successful when introduced in classrooms with no problem-posing practice, as the method included even traditional elements and relied on problem solving. Moreover, it seemed feasible to implement it in an online learning environment. Ellerton argues that the paradigm is simple and basic, yet stresses that further study is needed to extend and apply this framework to mathematics lessons for all ages. Nonetheless, the authors found limited results with the active learning framework’s application and efficiency in the age range they analyzed. A few publications focus on mathematics teacher education [4,5]. The present research contributes to filling a gap in the literature by investigating the framework’s applicability in sixth-grade mixed-ability classrooms.

The action research reported here involves two mathematics teacher–researchers from Hungary and Romania teaching sixth graders, and two university experts in mathematics education. The primary concerns of the researchers were integrating problem posing based on research findings in a typical classroom for 11- to 12-year-olds, and determining if students could perform this activity without prior experience. Thus, the first research question in this article is informed by two interrelated factors: the characteristics of the students’ problem-posing products and the relationship of the activity with mathematical ability.

RQ1. Is there a relationship between students’ mathematical ability and the quality of the problems they pose?

To answer RQ1, the authors use a code system to assess the quality of the problems that students formulate and compare the result to their mathematics grades. The problem-posing quality can be investigated by assessing the mathematical validity of the posed problem, i.e., the clarity of the problem formulation and its solvability [6]. In this study, the authors complement this perspective by determining whether the learner correctly interprets the problem-posing task. This facet is part of the poser’s aptness, as considerations of aptness include the poser’s comprehension of explicit and implicit requirements of the problem-posing task.

Problem posing and problem solving are deeply connected; problem posing can be viewed as a particular type of problem solving [7]. Perhaps the most widely cited reason for curricular and educational involvement in problem posing is its perceived value in motivating students to become better problem solvers [8]. As the problem-posing approach in this research relies primarily on problem solving as a parallel activity, the second research question narrows the relationship between problem posing and the problem-solving performance in the same mathematical topic.

RQ2: Is there any connection between the quality of the problem posing and the success in the problem solving?

To answer this question, the authors explore problem-solving efficacy concerning the students’ and their classmates’ problems.

In summary, the paper investigates the quality of the students’ problem-posing products and the effect of problem posing on problem solving.

Crucially, although the initial study design assumed a stable school environment, the experiment was conducted in 2020 in an online environment, triggered by the COVID-19 pandemic.

2. Theoretical Background

2.1. Problem-Posing

For several decades, there has been an increased interest in problem posing [9,10]. Various definitions of problem-posing have appeared in the literature [11]. Silver’s traditional approach [8] has been widely cited. It includes the invention of new problems based on individual situations and the reformulation of existing problems. Papadopoulos et al. enhanced the problem-posing concept by categorizing it into five categories: exclusively producing new issues, exclusively reformulating existing or provided problems, simultaneously generating and reformulating problems, raising questions, and modeling [12].

Identifying these approaches, while also considering the circumstances of the classroom environment, in this paper, the authors share the view of Cai and Hwang [13] (p. 2).

By problem posing in mathematics education, we refer to several related types of activity that entail or support teachers and students formulating (or reformulating) and expressing a problem or task based on a particular context (which we refer to as the problem context or problem situation).

An early systematic analysis by Kilpatrick outlined some directions for research, i.e., problem structuring, problem formulating, and problem-formulating instructions [14]. Since then, a primary focus of educational studies in problem posing has been on prospective teachers [13,15]. Simultaneously, the field of school applications continues to be an essential component. Hence, a critical mass of activities for teachers and students was devised and termed “problem-posing tasks” [9]. However, while official curriculum materials make vague reference to the importance of problem posing in school mathematics, problem posing is rarely included in implemented or assessed programs [3]; thus, classroom research is becoming increasingly important.

2.2. The Active Learning Framework for Problem-Posing

Problem posing is a learnable activity [16,17], and conceptualizing it improves the process [18]. Problem-posing can be implemented in the classroom in a variety of ways. For example, Cai and Brook directly connect problem posing with Polya’s four-phase problem-solving model, emphasizing the “looking back” phase [19,20]. Ellerton proposes a phased model called the active learning framework (ALF) for incorporating problem posing into mathematics classes [3]. This approach also combines problem posing and problem solving.

Ellerton’s framework distinguishes between classroom and student actions. With the shift in the teacher’s position, the learner’s involvement in the learning process becomes more active. The teacher introduces the session by presenting a worked-out model problem. At this level, the learner remains receptive, and the primary activities of the learners are listening, memorizing, and observing. Following the model problem, the learner’s activity level increases as they recognize solution patterns and recreate the experience of comprehending the model problem through practice exercises. The teacher’s role diminishes in the last phase, while the learner’s activity increases. The student takes the initiative with problem posing; the teacher’s responsibility is to supervise and organize the classroom activity that closes the process, for example, by selecting the problems to be discussed in the final phase (

Table 1. Classroom actions in the ALF framework.

Model	Practice	Problem-Posing	Problem-Solving
Processing the new content, the teacher models examples and draws attention to the textbook	Students locate examples and solve problems based on the model	Students pose problems with the same structure as the model	The class discusses and solves problems posed by students

). Note that Ellerton’s original work lists classroom actions in six steps. The authors adapted the model for the present research by dividing Ellerton’s sequence into four key phases. In particular, the first two stages (teacher models examples, teacher draws attention to the textbook) and the third and fourth stages (students locate examples, students solve problems based on model problems) of the original model were combined into one phase each.

According to Cai et al. [2], the ALF paradigm treats problem posing in the classroom as a capstone activity that allows students to consolidate and think critically about what they have learned. Analyzing the different phases of the ALF approach, the first two phases are very similar to the traditional teaching approach. The main difference is the third phase, which is novel; the fourth phase is also novel because the source of the mathematical problem is not the textbook, but a student. This characteristic of the ALF approach makes it suitable for introducing problem posing into classrooms where problem-posing was not part of the classroom practice; this is because this method does not include many new features. Furthermore, no extra training is required for students because the model problem and practicing activities structure the problem-posing process. At the same time, creating a mathematical problem reinforces active learning. Furthermore, solving “my classmate’s problem” may increase engagement in the task, as it may stimulate the learner’s natural aspiration to create a problem that pleases not only themselves, but also the teacher and their classmates.

Since the authors expect students to ask questions based on a known model problem, the result may not necessarily be interpreted as a mathematical problem, at least in thesense used in the problem-solving literature. However, in this article, the authors refer to the mathematical questions asked by the students following the ALF activity as “problem-posing products”.

2.3. Problem-Posing and Problem-Solving

Investigating the links between problem posing and problem solving is essential for problem-posing research [2]. Pólya highlights that problem posing is a natural part of problem solving, as problem solving often means the successive reformulation of the original problem [19]. Kilpatrick claimed that the nature of the problems people can pose could indicate how well they solve a problem [14]. Some empirical studies have explored possible relations between problem posing and problem solving [21]. However, based on research until the nineties, Silver claims no clear, direct connection has been identified between the competence to pose and solve problems [8]. In a later study, Cai and Hwang found a good connection between seventh-grade students’ problem-solving skills and their ability to formulate new problems [22]. However, the researchers did not obtain this relationship in earlier research. Moreover, cross-national studies obtained different results in the US and China [23].

The disparities in results could be attributed to different problem-posing circumstances. Zhang et al. emphasize the significance of the task format [24]. In their research, students performed better during the problem-posing stages when numerical information was placed in context. The task format with context allowed them to express problems more clearly. In addition to investigating the direct impact of problem posing on the success of problem solving (and vice versa), research has introduced a new paradigm, namely, the study of the cognitive process of problem posing. Cai and Hwang envisioned that students engage in problem-solving activities while thinking about posing a problem [25].

2.4. A Framework for Interpreting the Problem-Posing Process and Product

Kontorovich et al. proposed a framework for interpreting the problem-posing process [6]. The framework is given as a modular structure that can be used in various contexts and with various subjects to understand the main factors involved in mathematical problem posing. Although the conditions of problem posing in the present article vary from those in the cited study, the authors believe that most of its components are applicable in general.

The problem-posing situation involves interactions between several complex subsystems. The framework deduces the following subsystems for studying problem-posing processes: (1) task organization; (2) knowledge base, including mathematical schemes; (3) problem-posing heuristics and schemes; (4) group dynamics, and (5) individual considerations of aptness. The subsystems are briefly described below.

The task organizing facet accounts for all didactical considerations when constructing a problem-posing activity. The teacher should plan the lesson ahead of time, deciding on the educational objectives, oral or written instructions, and lesson structure.

Based on Schoenfeld’s problem-solving model, the knowledge base encompasses mathematical facts, definitions, algorithmic procedures, routine operations, a system of archetypal problems, and the related mathematical discourse and writing skills needed for composing a new problem [26]. The knowledge base of the poser(s) can be determined by assessing the mathematical validity of the posed problem, i.e., the clarity of the problem formulation and its solvability. In addition, these evaluations can illuminate the existing aspects of the posers’ knowledge bases and those aspects that are lacking.

Heuristics are helpful problem-solving organizational units and are typically treated analogously in the problem posing. However, sometimes, they are interpreted as schemas or “cosmetic changes” [27], rather than heuristics. Examples of problem-posing heuristics and schemas are numerical variation, goal manipulation, generalization, and the what-if-not strategy [28].

Group members have different functional roles in organized problem posing in a learning group; these include, for example, idea generation, combining and enriching the ideas offered, and mediation.

The poser’s interpretation of the problem statement and the assumption of the requirements are aptitude factors. Aptness considerations in problem posing include aptness to themselves, i.e., the degree to which a poser feels satisfied with the quality of the presented problem, aptness to possible evaluators, and aptness to possible solvers of a posed problem.

The involvement of all of these subsystems demonstrates the complexity of problem posing, although the role and weight of some subsystems may vary depending on the problem-posing settings and conditions. In fact, not all subsystems are always present; for example, in the present research, group dynamics do not play a relevant role.

3. The ALF Research Project

3.1. Subjects

Two schools from Hungary and Romania took part in the experiment, with two sixth-grade classes from each school. The teacher of the two classes in Hungary was the same person. Similarly, the two classes in Romania were taught by the same mathematics teacher.

Although the two countries’ educational systems differ, the 11- to 12-year-old students in our experiment, in grade 6, are both at ISCED level 2 [29]. In Hungary, primary and lower secondary education (ISCED 1, 2) is arranged as a unified structure in eight-grade schools, typically for children aged 6–14, and covering grades 1–8. However, secondary schools are also permitted to provide lengthier programs that begin from grade 5 or 7. In Romania, the fifth through eighth grades are included in secondary lower education (ISCED 2).

The authors judged the overall mathematics performance of the students by the mathematics grades they received at the end of the semester preceding the experiment. It was considered possible to accurately assess the pupils’ mathematical abilities based on their mathematical grades due to their summative nature. The Hungarian education system employs a five-point scale, with five being the best. The Romanian classification is a ten-degree system. For comparability, this paper assigns mathematics grades with the Hungarian equivalent. The grades were converted according to the official table of the Hungarian government; see

Table 2. Conversion of grades.

Romanian grades	1, 2, 3, 4	5	6, 7	8	9, 10
Hungarian grades	1	2	3	4	5

.

In the Hungarian school (from now on, School 1), the students’ mathematics grades were 4 or 5, and only one student received a 2 in mathematics. The other school (from now on, School 2) is a Hungarian language school in Romania. The students’ mathematical abilities were average in the Romanian school, and the mathematics grades were scattered; see

Table 3. Math grades in School 1 and School 2.

	The Number of Students	The Number of the Students Who Received a 4 or 5	The Number of the Students Who Received a 2 or 3
School 1	44	43	1
School 2	42	29	13
Sum	86	72	14

.

In what follows, students who received grades of 4 and 5 are referred to as high achievers, while students who received grades of 2 and 3 are referred to as low achievers.

3.2. The Impact of the COVID-19 Pandemic on the Experiment

The authors designed the experiment before the COVID pandemic, and the intervention was planned to be conducted in classroom lessons. However, both countries switched to online education shortly before the experiment started. Thus, the authors conducted the experiment during the online education period in 2020. The distribution of lessons to pupils took the form of online presentations, which included audio recordings of the teachers’ explanations. This method allowed students to progress at their own pace, as they could stop, resume, and repeat the presentations several times. In addition, the students sent their work to the teachers, either photographed or scanned. What we call a lesson in this online context consists of an action by the teacher (giving an audio online presentation or assignment), and an action by the student in response.

The unanticipated event caused by the pandemic was that the experiment was initially planned for 3–3 teaching units, but that only 2–2 units could be fully implemented, so the authors excluded the experience of the incomplete unit from the analysis. Furthermore, not all students in the classes completed the whole experiment. Therefore, the authors used only data from students who submitted all the problem-posing assignments.

This environment also made it infeasible to study group dynamics.

3.3. Task Organization

The experiment included six lessons in both schools. The curricula and syllabi are different in the two countries, so the two schools’ curricula were not the same in the experiment. However, although the course material was not the same across the two sets of schools, all the tasks were based on the premise that the arithmetic level of thinking was sufficient to solve them.

The authors applied the ALF method to two teaching units of the teachers’ syllabi in both schools. Following the ALF approach, the planned structure was the same (

Table 4. The structure of the experiment.

Lesson	Activity	The Topic of the Teaching Unit in School 1	The Topic of the Teaching Unit in School 2
1.	M, P, PP + PS	Proportional division	Addition and subtraction of fractions
2.	M, P, PP + PS
3.	PS
4.	M, P, PP + PS	Direct and inverse proportionality	Multiplication and division of fractions
5.	M, P, PP + PS
6.	PS

, and for the wording of problems, see Appendix A). The introduction of the model problem (M) and practicing based on the usual textbook exercises (P) was followed by problem-posing tasks, including solving the proposed problems (see the “PP + PS” labels in Table 4).

Each teaching unit ends with “my classmate’s problem” (PS), organized as follows. First, the teachers selected one or two “capstone” problems from problems previously posed by the students. The selection criteria were that the chosen problem’s mathematical background should be similar to the model problem, but that the text should be as intriguing as possible and specific to the student who formulated the problem. Second, the teachers asked students to solve one of the proposed problems independently.

In the following, we refer to the students’ activities by specifying the activity type (PS or PP) and the lesson number. For example, PS2 means that the activity is the solution to the second problem-posing task. If necessary, the authors also indicate the school.

4. Data Collection and Analysis

The research material consists of students’ written work, i.e., submissions of problem-posing and problem-solving tasks sent to teachers via email.

In action research, the research’s validity is always questioned [30]. Triangulation is a way of improving the consistency and validity of action research. The authors collected and compared data from the two sets of schools using the same method, i.e., they triangulated the sources. Analyst triangulation means that all research group members code the sources and analyze the results. Additionally, triangulation can open up multiple perspectives to interpret the data [31].

The two-tailed Fisher exact test [32] was performed for the quantitative analysis. The significance level in this study was set at the 0.05 level. The null hypothesis was that there was no difference in performance between the two groups of students. The null hypothesis was rejected if p < 0.05, and the fact that the groups differ is considered statistically significant.

The authors processed the students’ related documents through a qualitative content analysis. First, the authors developed a coding frame for evaluating the students’ outcomes, including two main dimensions: the quality of problem-posing and the quality of problem-solving (

Table 5. Coding of students’ work.

Main Dimension	Corpus Includes	Codes	Definition
Quality of problem posing	Problem-posing tasks	Competent (C)	The student submitted their work following the teacher’s instructions. The student understood the model problem; the mathematical background is appropriate. Decision rule: If the student provided redundant but not contradictory data, their work is still classified in this category.
		Incompetent (IC)	The student submitted an uninterpretable task or a meaningful math task, but not as instructed by the teacher. Decision rule: If the student included contradictory data, their work is classified as incompetent.
Quality of problem solving	The solution to the student’s “competent” tasks and classmates’ tasks	Correct solution (CT)	The student solved the problem correctly. This category also includes work where the student applied the mathematical model correctly but made a calculation or scaling error.
		False solution (F)	The learner misapplied the new material.
		No solution	The student did not submit a solution.

). A complementary analysis of the personalization of problem-posing products was reported in the paper [33].

• Example 1 (School 1, Topic 1, proportional division, lesson 2).
• Model problem (M2). Rita and Eva bought 18 dragon fruits. Rita gave € 8, and Eve € 28 for the fruit. How many dragon fruits did a girl get if the fruit was distributed in proportion to the money paid?
• Problem-posing assignment with problem solving (PP2 + PS2). Create a word problem for proportional division. Additionally, write the text of the task and the detailed solution.

Two answers to this assignment demonstrate the use of the code table. The problem proposed by Student 50 from School 1 is presented (Figure 1): The total mass of two cars is 480 kg. Their ratio is 4:2. How many kilograms are each of the two cars?

The coding of the former work according to the code system is shown in

Table 6. Coding PP2 + PS2 by Student 50 from School 1.

Dimension	Code	Explanation
Quality of problem posing	C	The task corresponds to the mathematical description.
Quality of problem solving	CT	The solution is correct.

.

The problem proposed by Student 26 from School 1 (Figure 2).

The coding of the former work according to the code system is shown in

Table 7. Coding PP2 + PS2 by Student 26 from School 1.

Dimension	Code	Explanation
Quality of problem posing	IC	The task does not correspond to the requirement. Moreover, it contains contradictory data: $80\ne 11+5+4$. The student probably wanted to split the 80 km distance in the ratio of $11:5:4$. The student drew accordingly; the $80:20$ division in his work also indicates this. However, the student’s question is not about proportional division.
Quality of problem solving	-	The student answered his question correctly $\left(11+5+4=20\right)$. The coder does not code the solution because the problem posing was assigned the “incompetent” code.

.

In the first phase of the coding process, two raters coded the corpus independently. Next, the authors measured the interrater’s agreement with Cohen’s kappa [34].

Table 8. Interrater agreement.

	Cohen’s Kappa
Quality of problem posing	0.89
Quality of problem solving	0.88

contains the result. Cohen’s kappa values indicate a strong interrater agreement. Later, the raters reached a consensus on the open points used in the remainder of this paper.

5. Results and Discussion

The authors discuss the findings in two subsections related to the two research questions.

5.1. The Problem-Posing Performance

The students were asked to solve four problem-posing tasks (PP1, PP2, PP4, PP5). These tasks were assessed as either competent or incompetent. The results are shown in

Table 9. Problem-posing performance of students in School 1.

	Competent (C)	Incompetent (IC)	Sum (N)	C/N
PP1	38	6	44	0.86
PP2	37	7	44	0.84
PP4	41	3	44	0.93
PP5	32	12	44	0.73
Sum	148	28	176	0.84

and

Table 10. Problem-posing performance of students in School 2.

	Competent (C)	Incompetent (IC)	Sum (N)	C/N
PP1	37	5	42	0.88
PP2	35	7	42	0.83
PP4	25	17	42	0.60
PP5	22	20	42	0.52
Sum	119	49	168	0.71

.

The results of the assessment show the following.

(1)

The two schools perform differently. The percentage of competent tasks is 84% in School 1 and 71% in School 2. The difference between the two schools is significant, according to Fisher’s exact test at the $p=0.04$ level; see contingency

Table A3. Comparison of students’ problem-posing performances in Schools 1 and 2.

	Competent	Incompetent	Sum
School 1	148	28	176
School 2	119	49	168
Sum	267	77	344

of Appendix B.

(2)

Students from School 2 are less successful in the second teaching unit (i.e., in PP4 and PP5) than in the first (i.e., in PP1 and PP2). Moreover, the difference is significant with $p<0.01$; see contingency

Table A4. Students’ performances in problem-posing tasks in School 2.

	Competent	Incompetent	Sum
PP1 and PP2	72	12	84
PP4 and PP5	47	37	84
Sum	119	49	168

in Appendix B.

(3)

Students from School 1 are less successful in PP5 than in the other tasks, and the difference is significant with $p=0.03$; see contingency

Table A5. Students’ performances in problem-posing tasks in School 1.

	Competent	Incompetent	Sum
PP1, PP2 and PP4	116	16	132
PP5	32	12	44
Sum	148	28	176

in Appendix B.

This fine structure of results is discussed below, based on Kontorovich et al.’s framework.

Ad. 1. The analysis reveals that the students’ mathematical knowledge base, measured by their school mathematics grades, influences their problem-posing success. Comparing the students’ performance from School 1, where all but one of the students are regarded as high achievers, to that of School 2′s high achievers, our measure indicates that the difference is marginal (84% vs. 81%). See

Table 11. Problem-posing performance in School 2, only high achievers.

	Competent (C)	Incompetent (IC)	Sum (N)	C/N
PP1	29	0	29	1.00
PP2	26	3	29	0.90
PP4	19	10	29	0.65
PP5	20	9	29	0.69
Sum	94	22	116	0.81

.

In other words, although the curricula were different in the two schools, high achievers had nearly equal success with problem posing.

The disparity between high and low mathematical achievers is apparent in School 2 (

Table 12. Problem-posing performance of high achievers and low achievers in School 2.

	Competent (C)	Incompetent (IC)	Sum (N)	C/N
High achievers	94	22	116	0.81
Low achievers	25	27	52	0.48
Sum	119	49	168	0.71

); Fisher’s exact test shows a high correlation between problem-posing success and general mathematical performance with $p<0.01$. Math grades, indicating mathematical knowledge and ability, were strong predictors of problem-posing success in our study.

Ad 2. The mathematical knowledge base also played a role in other aspects of the experiment. The first topic is the addition and subtraction of fractions in School 2, while the second is the multiplication and division of fractions (Table 4; for the wording of problems, see Appendix A). The contrast between the two sets of curriculum materials is also reflected in the problem-posing success rate, which means that the multiplicative structure was significantly more difficult for students, particularly those with lower mathematical abilities. On the other hand, low achievers were also more often successful in tasks requiring additive thinking than not: they scored 65% in PP1 + PP2 (17 competent and 9 incompetent), but only 30% in PP4 + PP5 (8 competent and 18 incompetent products).

Ad 3. Students in School 1 are less successful in PP5 than in the other tasks, and the authors attribute this difference to inadequate task organization.

• Example. (School 1, PP5. The lesson topic is direct and inverse proportionality).
• Previously, the model problem required students to classify the connection between two variable quantities as direct proportionality, inverse proportionality, or neither. For the nonproportional relationship, the following model problem was provided:
• Model problem. A 5-year-old boy weighs 18 kg. How many kg will he weigh at the age of 65?
• Assignment. Create a word problem. There should be no proportionality in this task. Provide a solution to this problem as well.

In the case of students who inappropriately solved the problem, the two variables were not apparent in their problem suggestion, as the following example shows.

The problem posed by Student 53 from School 1 is presented: Béla is three years old, and Feri is ten years old. How much older is Feri?

The objective of the assignment was to emphasize the limitations and critical application of various mathematical models. Many incompetent answers may be attributed to students’ misinterpretation of the task. The phrasing did not explicitly refer to the model problem. A more explicit wording of the assignment may have specified the two variables to be included. However, because of the lack of a solid function concept in this age group, the reference to two variables may not positively influence the understanding. Thus, inappropriate task organization may have contributed to a weaker performance.

Since problem posing is seen as a specific problem-solving activity, the difference in problem-posing performance between high and low achievers may be due to a more conscious use of heuristic strategies and schemas. The ALF approach is conducive to such schemas, as changing the context, the numerical data, or both, was a typical pattern in the experiment. Additionally, some common problem-solving strategies also appeared. For example, the appearance of the backward thinking strategy was prevalent in PP1 in School 1.

• Example. (School 1, Topic 1, proportional division, lesson 1).
• Problem-posing assignment with problem solving (PP1 + PS1). Laci and Robi received a large box of jam Linzer cookies from their grandmother. All 60 Linzers should be distributed between the two boys to ensure they do not receive the same number of cookies. Guess on what basis and in what ratio they should distribute the cookies. How many cookies did each of the boys receive? Write a word problem, and describe a detailed solution as well.

The activity is moderately structured: the teacher prescribed that 60 pieces of Linzers should be divided into two parts. The students’ guessed principle had to be invented, and the learned mathematical procedure had to be applied. When choosing the data, the teacher tried to be realistic (60 Linzer cookies means approximately two oven pans), but at the same time, the number given has many divisors. It is assumed that the fact that the distribution principle had to be invented contradicts the obvious solution: the sum of the numbers in the ratio pair was already 60. Indeed, only four students stopped at the decomposition of 60 into a sum of two numbers, saying that these numbers define the ratio in question (e.g., 20 + 40 = 60, and the ratio is 20:40, as S10 submitted in their solution to the task). Others started from the sum but set the task after simplification. Some students documented their reasoning accurately; see, for example, the work of Student 19 (Figure 3).

The submission by Student 19 in School 1 is presented (Figure 3): Laci and Robi received 60 Linzers from their grandmother. The cookies should be divided 2:3 so that Laci gets less because he is on a diet.

The problem formulation is preceded by describing how they arrived at the problem and the numbers in the text. The student

• decomposes 60 by the sum of two numbers: $24+36=60$;
• simplifies the fraction: $24:36=12:18=6:9=2:3$;
• checks who obtains 24 and 36 pieces if dividing the Linzers in the ratio of $2:3$: $2+3=5, 60:5=12, 12·2=24, 12·3=36;$
• sets the task: Laci and Robi got 60 Linzers from their grandmother. It should be divided 2:3 so that Laci gets less because he is on a diet.

In the practicing exercises, the teacher always used a straightforward way of solving the problem, so the student used thinking backward as a conscious strategy.

5.2. Problem-Solving Performance and its Relationship with the Quality of Problem-Posing

During the experiment, the students had to solve six problems. They solved four problems of their construction and two problems chosen by the teacher from a classmate. The proportion of correct solutions to their task was 95% in School 1 and 87% in School 2 (

Table 13. Solutions to problem-solving tasks in School 1. (* indicates the “classmate’s problem.”).

Task	CT	F	No Solution	N	CT/N
PS1	35	3	0	38	0.92
PS2	35	2	0	37	0.95
PS3 (*)	33	8	3	44	0.75
PS4	40	0	1	41	0.98
PS5	31	1	0	32	0.97
PS6 (*)	36	4	4	44	0.81
Sum	210	18	8	236	0.89

and

Table 14. Solutions to problem-solving tasks in School 2. (* indicates the “classmate’s problem.”).

Task	CT	F	No solution	N	CT/N
PS1	29	8	0	37	0.78
PS2	34	0	1	35	0.97
PS3 (*)	34	6	2	42	0.81
PS4	19	5	1	25	0.76
PS5	21	1	0	22	0.95
PS6 (*)	32	7	3	42	0.76
Sum	169	27	7	203	0.83

). In classes with good mathematical results (School 1), the success of the two exercises on one topic was close; however, in classes with mixed-ability students (School 2), the result of the second exercise was always better than the first. Moreover, the success rate for the second exercise in the topics matched that of the first school. Note that the correctness of solving one’s own problem was examined if the related problem posing was competent. The proportion of correct solutions was lower for the classmate’s problem. However, this percentage did not differ significantly between the two schools, i.e., 78% in School 1 and 79% in School 2.

According to [26], problem solving is influenced by five main factors: (1) knowledge base, (2) problem-solving strategies, (3) monitoring and control, (4) beliefs and affect, and (5) practices. In this experiment, the increased role of monitoring and control was noticeable. The following task illustrates this finding:

• Example. (School 2, Topic 1, adding and subtracting fractions, lesson 1).
• Model problem (M1). Kati and Laci are sixth graders, and they start their school day. In their math class, they need to solve a number pyramid. Help them: add up two adjacent numbers and write the result in the cell above them. Continue until the pyramid is complete. Tip: You can also use the reverse operation of addition.

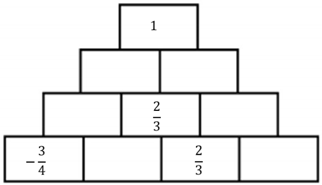
• The problem-posing assignment with problem solving (PP1 + PS1). Make a new pyramid for Kati and Laci with the following three numbers: $\frac{4}{5};-\frac{1}{2}; \frac{1}{3}$. Your task is to draw a pyramid in your notebook with three levels and put the given numbers in it. Write the given numbers in red and the calculated numbers in blue. After solving the first pyramid, draw another pyramid, put the given number into it differently, and solve the pyramid again.

This problem-posing task also represents a problem situation, and the learner needs some monitoring to solve the problem. For example, it is possible that the student creates a contradictory pyramid from the numbers or that the student’s knowledge is not sufficient to find a solution. Thus, students need some control to complete the task. For example, Student 34 created a “blind pyramid” (Figure 4). The given numbers are in the top, leftmost and rightmost positions.

Most likely, the student first divided $4/5$ (top position) into the sum of two fractions, $2/5+2/5,$ and determined the missing number by subtraction: $2/5-1/3=1/15$. Some strategy devising process is present, but the monitoring is lacking: $1/15+\left(-1/2\right)$ is not equal to $2/5$. The authors used the phrase “blind problem” because the student did not realize the problem’s difficulty. The student needed to form an equation for the right solution and was not ready for this level of difficulty. If we denote the middle element in the bottom row by $x$, then $1/3+2x-1/2=4/5$, and we obtain $x=29/60$. In other words, the combination of the missing look-back phase and the lack of mathematical resources led to the erroneous solution.

The problem-solving indicators show many similarities between the two schools, as well as differences. Even though the ALF approach provides a conceptual structure for task organization, the setting of individual tasks impacted problem-solving effectiveness. The problem-solving success in School 1 was influenced by whether the problem was unknown (i.e., a classmate’s problem had to be solved) or not (i.e., the student solved his or her own problem). Fisher’s exact test for the contingency table in

Table 15. Problem-solving performance in School 1.

	Correct Solution (CT)	False Solution (F)	Sum
Solving own problem	141	6	147
Solving classmate’s problem	69	12	81
Sum	210	18	228

is $p=0.01$. In contrast, in School 2, problem-solving success depends on whether the problem contains operations embedded in the text or without text (

Table 16. Problem-solving performance in School 2.

	Correct Solution (CT)	False Solution (F)	Sum
Only numerical information (PS1, PS4)	48	13	61
Numerical information placed in context (PS2, PS5, PS3, PS6)	121	14	135
Sum	169	27	196

, $p=0.046$). For example, deciding on addition or subtraction in the number pyramid was more difficult than in the text problems. There was no significant difference between solving one’s own and a classmate’s problem in the second school. These observations show that a combination of factors determines problem-solving success.

Finally, the authors also examined the relationship between the success of problem solving and problem posing. The authors measured a student’s success in problem-posing by the ratio of the number of competent solutions and all four problem-posing tasks. That is, the success ratio for a student is $pp=n_c/4$, where $n_c$ is the number of competent proposals. Similarly, the authors measured a student’s success in problem solving by the ratio of the number of correct solutions and all six problem-solving tasks. That is, the success ratio for a student is $ps=n_{CT}/6,$ where $n_{CT}$ is the number of correct solutions to problem-posing tasks provided by the student. The median scores for the different groups of students are shown in

Table 17. The relationship between the success of problem solving and problem posing.

	Median for $\mathit{p}\mathit{p}$	Median for $\mathit{p}\mathit{s}$
School 1	0.75	0.83
School 2 (all students)	0.75	0.67
School 2 (high achievers)	0.75	0.83
School 2 (low achievers)	0.50	0.50

.

The problem-solving results of the more successful problem posers were better in both schools. The results are provided in contingency tables, which compare students to the school medians for problem posing and problem solving (

Table 18. Comparison of PP and PS performance in School 1.

	$\mathit{p}\mathit{p}<0.75$	$\mathit{p}\mathit{p}\ge 0.75$	Sum
$ps<0.83$	3	11	14
$ps\ge 0.83$	0	30	30
Sum	3	41	44

and

Table 19. Comparison of PP and PS performance in School 2.

	$\mathit{p}\mathit{p}<0.75$	$\mathit{p}\mathit{p}\ge 0.75$	Sum
$ps<0.67$	13	3	16
$ps\ge 0.67$	2	24	26
Sum	15	27	42

). We implemented the same for high math performers in the second school (

Table 20. Comparison of PP and PS performance in School 2, only high achievers in mathematics.

	$\mathit{p}\mathit{p}<0.75$	$\mathit{p}\mathit{p}\ge 0.75$	Sum
$ps<0.83$	6	4	10
$ps\ge 0.83$	0	19	19
Sum	6	23	29

). According to the contingency tables, successful problem solvers are also successful problem posers, and vice versa. Fisher’s exact test confirms the significant correlation in the second school $(p<0.01$). Because of the small number of elements in the first column, the Fisher test was not performed on contingency tables Table 18 and Table 20, but the pattern is instructive. In students with good mathematical performance, successful problem solving was not associated with poor problem-posing performance.

6. Conclusions

The authors investigated how sixth graders cope with problem posing when it is introduced using the active learning framework. They were interested in the quality of the problems students created, the relationship between problem-posing performance and the students’ mathematics grades, and the connection between problem posing and problem solving during the activity.

The action research involved schools from Hungary and Romania with two different curricula, which allowed the authors to consider the students’ age (11–12 years) as a common factor. At the same time, however, the study of ALF-based problem formulation at this age is where the authors found a gap in the literature.

The authors hypothesized that the ALF problem-posing model provides a sufficient structure for problem posing to be implemented in mixed-ability classrooms where problem posing is not part of everyday mathematics teaching practice. In addition, through the embedded problem-solving stages, the ALF activity contributes to learning outcomes.

The authors conclude their research by summarizing the answers to the research questions.

RQ1. Is there a relationship between students’ mathematical ability and the quality of the problems they pose?

In the experiment presented here, three main factors influenced the quality of problem posing, namely, (1) the students’ mathematical abilities, (2) the mathematical background of the task, and (3) task organization, i.e., the way the task was formulated.

Ad 1. The results indicate a correlation between the success of problem posing and mathematics grades. The success rate of the students with a lower math performance was considerably weaker, while high achievers performed at nearly the same level in both schools. Thus, the mathematics grades, which express mathematical knowledge and ability, were good predictors of problem-posing success in the research. The data reinforce and complement Ellerton’s earlier findings (for the same age group), which suggest that high-ability learners can develop more complex problems [21].

Ad 2. The importance of the mathematical background of the tasks was apparent because problem-posing based on the multiplicative structure of rational numbers was more difficult for students than that based on the additive structure.

Ad 3. The ALF approach builds on the model problem. However, if the task was ill-defined and the model problem was not clearly identifiable, students were less successful, including those with above-average mathematics abilities. This observation confirms the importance of work organization in the process [6].

RQ2: Is there any connection between the quality of the problem-posing and the success in the problem-solving?

The results confirmed that problem posing could be seen as an open problem-solving activity [7]. When creating a problem, students often use heuristic strategies, such as thinking backward; furthermore, Pólya’s look-back phase and other control processes are also observed.

Concerning the success of problem solving, three phenomena were revealed in the experiment. First, in high-ability classrooms, the factor influencing problem-solving success was whether the student solved their own problem or a classmate’s problem set by the teacher. The authors argue that this result was natural because of the students’ problem-posing strategies and schemas, including minimal changes to the model problem. In contrast, in the case of the unknown problem (classmate’s problem), the teacher tried to select a more original setting. The second phenomenon was that the problems embedded in the text were solved more successfully than the problems containing only numbers. This phenomenon is also known from the literature [24].

Finally, in this experiment, the problem-posing quality predicted the problem-solving success; better problem posers were more successful in problem solving.

The pedagogical implication of this research is that problem-posing based on the ALF model can be implemented for 11- to 12-year-old students, albeit with care. The teacher should specify the expectation when constructing the assignment and precisely which model problem the posed problem should be similar to. Differentiation in the mathematical background is also recommended. For students with weaker mathematical abilities, given that they are already poorer problem solvers, the mathematical complexity of the work should be adjusted to their level of ability. Nonetheless, problem posing by differentiation could be a future research topic.

The research also indicates that the ALF approach was feasible during the closure period, as the authors were able to perform all the process steps online.

7. Limitations

Action research, as a research method, has known limitations. Using the triangulation method, the authors tried to increase the reliability of the research findings. Moreover, the pandemic situation constrained the research in several respects. Missing data were a factor, which the authors addressed in the study by excluding students with missing data. Unfortunately, this treatment of missing data reduced the number of children participating in the experiment. Additionally, students worked from home in uncontrolled settings.

Another constraint in this study was the time limit, the half-year duration of the experiment, and the four problem-posing tasks that were too few to determine the method’s effectiveness. However, the authors believe that they gained experience in the method’s applicability.