Describing and Interpreting the Space of Classroom Learning in Problem-Solving-Based Mathematics Instruction: Variation as an Analytical Lens
Abstract
1. Introduction
2. Variation and Space of Learning
3. Problem-Solving-Based Mathematics Instruction
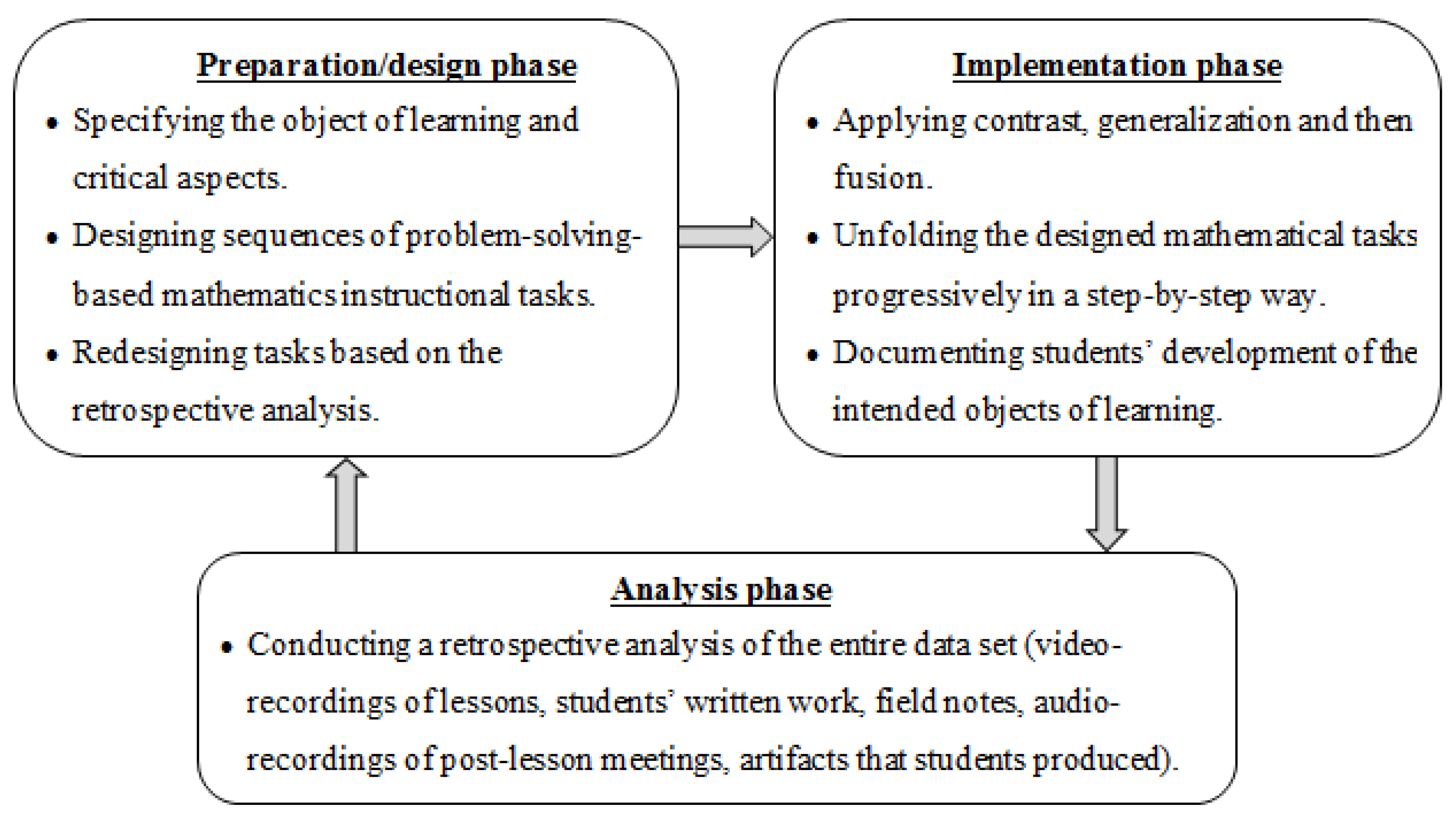
4. Methods
5. Results
5.1. The Space of Learning in Classroom 1
5.1.1. Lesson Structure
5.1.2. Mathematical Tasks Presented to Students
5.1.3. Patterns of Classroom Interaction
- (1)
- T: Why did you add 3 to both sides of the inequality x − 3 > 10?
- (2)
- S: To remove 3.
- (3)
- T: Is it to remove 3 or −3?
- (4)
- S: −3.
- (5)
- T: Why did the inequality sign not change?
- (6)
- S: Because that is the addition rule.
- (7)
- T: You are right. How do you determine the final solution set {14, 15, 16, …}?
- (8)
- S: Because x > 13.
- (9)
- T: Right, but it is also because the given working region (domain) is the set of natural numbers.
| Episode | Instructional Activities | Dimensions of Variation |
|---|---|---|
| Episode 1: Reviewing/Introducing (5 min) | After checking students’ homework given in the previous day’s lesson, the teacher asked: Who can remember what you have learned last period? One student gave a response: We learned about linear equations. She then asked: What is a linear equation? Another student said: That which involves an equal sign. The teacher then said: A linear equation is an equation which can be written as ax + b = 0. She gives two sample linear equations emphasizing that a and b are constants, x is a variable and the value of x is a solution. The teacher announces the title of the lesson: Solving linear inequalities. She then asked: Do you remember the meaning of the signs ? One student gave a response. She then said: An algebraic expression involving one of these mathematical signs is said to be an inequality. | DoV1: General form of linear equation
|
| Episode 2: Discussing (teacher-led + whole-class) (20 min) | The teacher wrote the following definition: Definition: An inequality is said to be a linear inequality if it is written in one of the following forms: ax + b < 0, ax + b ≤ 0, ax + b > 0, or ax + b ≥ 0, for a ≠ 0. She then provided examples to support the definition. x + 3 > 0, x + 4 ≤ 0, 2x + 1 < 0 and 3x + 7 ≥ 0 are linear inequalities. She worked on another example from the textbook: Which of the following numbers make the inequality x + 3 < 5 true? (a) −4 (b) −1 (c) 0 (d) 2 (e) 3 She demonstrated how to find solutions by substituting the given numbers. She said: The numbers −4, −1 and 0 make the inequality true. They are solutions to the inequality. There are also other solutions to it. How can we find them? She wrote the addition, subtraction, multiplication and division properties of inequalities on the blackboard. She then demonstrated the properties as follows. and 4 2 and 4 × 3 2 × 3 10 15 and 10 ÷ 5 15 ÷ 5 The teacher then provided the following example: Find the solution set for the inequality x + 4 < 7 in the given regions. (a) Set of whole numbers (b) Set of natural numbers She then found the solution interacting with students. x + 4 < 7 x + 4 − 4 < 7 − 4 x < 3 (a) solution set = {0, 1, 2} in the set of whole numbers (b) solution set = {1, 2} in the set of natural numbers | DoV3: General form of linear inequalities
DoV5: Properties of inequality
DoV7: Solution of inequalities within a specified set |
| Episode 3: Discussing (group work + teacher-led demonstration) (20 min) | The teacher provided the following textbook examples: Find the solution set of each of the following inequalities. (a) x − 2 5, x is a whole number (b) 2x 10, x is a natural number (c)x 3, x is in {0, 1, 2, …, 20} (d) x + 1, x is in {1, 2, 3, … } The teacher demonstrated all the examples to the whole class. (a) x − 2 5 (b) x − 2 + 2 5 + 2 x 7 S.S = {8, 9, 10, …} S.S = {1, 2, 3, 4} (c) x 3 (d) 4(x) 4(3) x 12 S.S = {13, 14, 15, …, 20} S.S = { } | DoV8: Applying the addition property of inequalities DoV9: Applying the multiplication property of inequalities DoV10: Applying the division property of inequalities DoV7: Solution of inequalities within a specified set |
| Episode 4: Practicing (15 min) | She provided the following exercises from the textbook for the students to work first in small groups and then to show to the whole class. (a) x + 4 < 8, x is in the set of whole numbers. (b) x − 2 < 7, x is in the set of integers. (c) x − 3 > 10, x is in the set of natural numbers. (d) , x is in the set of negative integers. The teacher walked around each group to check their progress. The teacher then invited four students to show their work on the black board, in parallel, and provided feedback on the four tasks. | DoV6: Applying properties of inequality DoV7: Solution of inequalities within a specified set |
| Summarizing (5 min) | The teacher provided a short summary. She gave emphasis on the form of writing inequalities, properties of inequalities and the nature of a solution set. At the end, she provided homework exercises from the textbook. | DoV3: The general form of linear inequalities DoV5: Properties of inequality |
5.2. The Space of Learning in Classroom 2
5.2.1. Lesson Structure
5.2.2. Mathematical Tasks Presented to Students
5.2.3. Patterns of Classroom Interaction
- (1)
- T: What is Mahlet’s amount of money at the end of the 5th week?
- (2)
- S: 425 birr.
- (3)
- T: How do you get it?
- (4)
- S: By adding 5 to 400 five times.
- (5)
- T: Why do you add 5 five times?
- (6)
- S: Because Mahlet saves 5 birr per week.
- (7)
- T: Why do you add to 400?
- (8)
- S: Initially she has 400 birr in her account.
- (9)
- T: What is her amount of money at the end of the 10th week?
- (10)
- S: 450 birr.
- (11)
- T: How about at the end of 20th week? Does the use of variables help to get the answer?
- (12)
- T: When does Mahlet’s amount of money equal 565?
- (13)
- S: At week 33.
- (14)
- T: How do you get it?
- (15)
- S: By dividing 156 by 5.
- (16)
- T: What is 156?
- (17)
- S: 565 − 400 = 156.
- (18)
- T: So, when does it become greater than 565?
- (19)
- S: At week 34.
- (20)
- T: Why?
- (21)
- S: She saves an additional 5 birr.
- (22)
- T: Is there any other answer to it?
- (23)
- S: Yes, 35.
- (24)
- T: How about at week 37?
- (25)
- S: It is greater.
- (26)
- T: How many answers does it have?
- (27)
- S: Many.
- (28)
- T: Is there any other approach to find the answer?
| Episode | Instructional Activities | Dimensions of Variation | ||||||
|---|---|---|---|---|---|---|---|---|
| Episode 1: Reviewing/Introducing (10 min) | The teacher started the lesson by providing the following exercises to students to work in pairs. 1. Simplify each of the following algebraic expressions into their lowest terms. (a) 12y + 12 − 6y (b) 2x + 7 + 5x − 15 + 6 − x 2. Solve each of the following equations. (a) z + 5 = 9 (b) 7n = 14 (c) 2m − 4 = 6 After checking students’ work, she summarized students’ answers to the whole class. She gave emphasis on the nature of algebraic terms, the change in variables and the use of properties of equality to solve one-step and two-step equations. The teacher announced the title of the lesson: solving linear inequalities. She then asked: What is an inequality? What is the difference b/n an equation and an inequality? Two students gave responses. In her feedback, she emphasized the difference in the meaning of the signs. She asked: What do you know about bank accounts? One student gave a response. She emphasized the key terms saving and withdrawing. She then provided the following tasks written on a piece of paper: Mahlet had 400 birr in her bank account. She saves an additional 5 birr each week in her account. Her brother Yonas had 582 birr in his account. He withdraws 8 birr each week from his savings. (a) How much money does Mahlet have in her account in the fifth week? How about in the tenth week? (b) In which week does Mahlet have 565 birr in her account? In which week is it greater than 565 birr? (c) In which week does Yonas have 422 birr in his account? In which week is it less than 422 birr? (d) At what week do Mahlet and Yonas have the same amount of money in their accounts? In which week is Mahlet’s money greater than Yonas’s money? She then announced: You can start working only on the first two. | DoV1: Adding/subtracting like terms DoV2: Change in variables
| ||||||
| Episode 2: Discussing (individual + group work + whole-class) (25 min) | The teacher asked questions while checking students work as they worked individually and in small groups, encouraging them to try more than one method. She took note of some students’ work as she checked. After some time had passed, the teacher invited students to present their solutions to the whole class. She organized and orchestrated the presentation in the following way: (a) Strategy 1: 5th week: 400 + 5 + 5 + 5 + 5 + 5 = 425 birr. 10th week: 400 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 = 450 birr. Strategy 2: 5th week: 5× 5 = 25 birr, so 400 + 25 = 425 birr 10th week: 5× 10 = 50 birr, so 400 + 50 = 450 birr | DoV7: Multiple solution strategies
DoV10: Number of solutions
DoV12: Representations of inequalities
subtraction, addition multiplication, division DoV6: Context
| ||||||
| Strategy 3: | ||||||||
| Week | Money | Week | Money | |||||
| 1st | 405 | 6th | 430 | |||||
| 2nd | 410 | 7th | 435 | |||||
| 3rd | 415 | 8th | 440 | |||||
| 4th | 120 | 9th | 445 | |||||
| 5th | 425 | 10th | 450 | |||||
| (b): | ||||||||
| Strategy 1: 400 + 5 + 5 + 5 + … + 5 = 565 1w 2w 3w 33w Strategy 2: 400 + 50 + 50 + 50 + 15 = 565 10w 20w 30w 33w Strategy 3: 565 − 400 = 165. So, 165 ÷ 5 = 33. The teacher asked questions to the presenting students. | ||||||||
| The teacher then connected their solution strategies and produced the following answer: | ||||||||
| Week | Amount in her account | |||||||
| 1st | 400 + 5 | 400 + 1 × 5 | ||||||
| 2nd | 400 + 10 | 400 + 2 × 5 | ||||||
| 3rd | 400 + 15 | 400 + 3 × 5 | ||||||
| 4th | 400 + 20 | 400 + 4 × 5 | ||||||
| 5th | 400 + 25 | 400 + 5 × 5 | ||||||
| 6th | ||||||||
| 400 + w × 5 400 + 5w | ||||||||
| 400 + 5w = 565 | ||||||||
| 400 + 5w − 400 = 565 − 400 5w + 400 − 400 = 565 − 400 5w = 165 5w/5 = 165/5 w = 33 weeks. So, the money in her account is equal to 565 at the 33rd week and is greater than it at weeks 34, 35, 36, and so on. That is, 400 + 5w > 565 400 + 5w − 400 > 565 − 400 5w + 400 − 400 > 565 − 400 5w > 165 5w/5 > 165/5 So, w > 33 week. | ||||||||
| Episode 3: Discussing (group work + whole class) (25 min) | The teacher then asked: Now do the remaining two questions (c and d) in your groups. She invited three students to present their work to the whole class. She organized and orchestrated the presentation in the following way:: (c): Strategy 1: 58 − 8 − 8 − 8 − … − 8 = 422 1w 2w 3w 20w So, his amount of money is equal to 422 at the 20th week and less than it at week 21, 22, 23, and so on. Strategy 2: 582 − 422 = 160. So, 160 ÷ 8 = 20. Strategy 3: 582 − 8w = 422, so w = 20 weeks. 582 − 8w < 422, so w < 20 weeks. (d): | DoV15: Type of linear inequality
DoV10: Number of solutions
DoV12: Representations of inequalities
subtraction, addition multiplication, division DoV14: Properties of inequality
| ||||||
| Strategy 1: | ||||||||
| Week | Mahlet | Yonas | Week | Mahlet | Yonas | |||
| 400 | 582 | 11th | 455 | 494 | ||||
| 1st | 405 | 574 | 12th | 460 | 486 | |||
| 2nd | 410 | 566 | 13th | 465 | 478 | |||
| 3rd | 415 | 558 | 14th | 470 | 470 | |||
| 4th | 420 | 550 | 15th | 475 | 462 | |||
| 5th | 425 | 542 | ||||||
| 6th | 430 | 534 | ||||||
| 7th | 435 | 526 | ||||||
| 8th | 440 | 518 | ||||||
| 9th | 445 | 510 | ||||||
| 10th | 450 | 502 | ||||||
| Strategy 2: | ||||||||
| 400 + 5w = 582 − 8w 5w + 8w = 582 − 400 13w = 182 w = 182/13 = 14 week Through discussion, the teacher then provided full solution steps to the whole class. (c) 582 − 8w < 422 582 − 8w +8w < 422 + 8w 582 < 422 + 8w 582 − 422 < 422 − 422 + 8w 160 < 8w 160/8 < 8w/8 20 < w That is, w > 20 weeks. Hence, his money in his account is less than 422 after the 20th week. At the 72nd week, the money in his account will be: 582 − 8w = 582 − 8 (72) = 6 birr. That is, at w > 72 weeks, he cannot withdraw 8 birr per week for his account. (d) 400 + 5w > 582 − 8w 5w + 8w > 582 − 400 13w > 182 w > 182/13 w > 14 week Mahlet’s money is equal to Yonas’s money at week 14 and is greater at week 15 and later. | ||||||||
| Episode 4: Practicing (15 min) | The teacher provided the following exercises and ordered students to work individually. Solve each of the following inequalities. (a) x + 5 < 8 (b) y − 3 > 2 (c) 2z < 10 (d) 2x − 3 > 7 (e) 4y − 1 < 3y + 8 The teacher walked around the classroom to check every student’s work. | DoV15: Type of linear inequality
subtraction, addition, multiplication, division | ||||||
| Episode 5: Summarizing (5 min) | The teacher orally provided a summary through questioning in 5 min. She gave emphasis on comparing solving equations and inequalities based on the number of solutions and solution strategies. | DoV18: Difference b/n an equation and an inequality
| ||||||
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cai, J.; Morris, A.; Hohensee, C.; Hwang, S.; Robison, V.; Cirillo, M.; Kramer, S.L.; Hiebert, J.; Bakker, A. Maximizing the Quality of Learning Opportunities for Every Student. J. Res. Math. Educ. 2020, 51, 12. [Google Scholar] [CrossRef]
- Hiebert, J.; Grouws, D. The effects of classroom mathematics teaching on students’ learning. In Second Handbook of Research on Mathematics Teaching and Learning; Lester, F.K., Ed.; Information Age: Charlotte, NC, USA, 2007; pp. 371–404. [Google Scholar]
- Killpatrick, J.; Swafford, J.; Findell, B. Adding It Up: Helping Children Learn Mathematics; National Academy Press: Washington, DC, USA, 2001. [Google Scholar]
- Cai, J. What research tells us about teaching mathematics through problem-solving? In Research and Issues in Teaching Mathematics through Problem-Solving; Lester, F., Ed.; NCTM: Reston, VA, USA, 2003; pp. 241–254. [Google Scholar]
- Lesh, R.; Zawojewski, J.S. Problem-solving and modeling. In Second Handbook of Research on Mathematics Teaching and Learning; Lester, F., Ed.; Information Age Publishing: Charlotte, NC, USA, 2007; pp. 763–804. [Google Scholar]
- Lester, F.K., Jr. Thoughts About Research On Mathematical Problem- Solving Instruction. Math. Enthus. 2013, 10, 245–278. [Google Scholar] [CrossRef]
- Lester, F.K., Jr.; Cai, J. Can mathematical problem-solving be taught? Preliminary answers from 30 years of research. In Posing and Solving Mathematical Problems: Advances and New Perspectives; Felmer, P., Pehkonen, E., Kilpatrick, J., Eds.; Springer: New York, NY, USA, 2016; pp. 117–135. [Google Scholar]
- National Council of Teachers of Mathematics [NCTM]. Principles and Standards for School Mathematics; National Council of Teachers of Mathematics [NCTM]: Reston, VA, USA, 2000. [Google Scholar]
- National Council of Teachers of Mathematics [NCTM]. Principles to Actions: Ensuring Mathematical Success for All; National Council of Teachers of Mathematics [NCTM]: Reston, VA, USA, 2014. [Google Scholar]
- Marton, F.; Tsui, A. Classroom Discourse and the Space of Learning; L. Erlbaum Associates: Mahwah, NJ, USA, 2004. [Google Scholar]
- Marton, F. Necessary Conditions of Learning; Routledge: New York, NY, USA, 2015. [Google Scholar]
- Marton, F.; Booth, S. Learning and Awareness; L. Erlbaum Associates: Mahwah, NJ, USA, 1997. [Google Scholar]
- Al-Murani, T.; Kilhamn, C.; Morgan, D.; Watson, A. Opportunities for learning: The use of variation to analyse examples of a paradigm shift in teaching primary mathematics in England. Res. Math. Educ. 2019, 21, 6–24. [Google Scholar] [CrossRef]
- Huang, R.; Barlow, A.T.; Prince, K. The same tasks, different learning opportunities: An analysis of two exemplary lessons in China and the U.S. from a perspective of variation. J. Math. Behav. 2016, 41, 141–158. [Google Scholar] [CrossRef]
- Kullberg, A.; Runesson, K.U.; Marton, F. What is made possible to learn when using the variation theory of learning in teaching mathematics? ZDM Math. Educ. 2017, 49, 559–569. [Google Scholar] [CrossRef]
- Olteanu, L. Opportunity to communicate: The coordination between focused and discerned aspects of the object of learning. J. Math. Behav. 2016, 44, 1–12. [Google Scholar] [CrossRef]
- Runesson, U. Beyond discourse and interaction. Variation: A critical aspect for teaching and learning mathematics. Camb. J. Educ. 2005, 35, 69–87. [Google Scholar] [CrossRef]
- Watson, A.; Mason, J. Seeing an Exercise as a Single Mathematical Object: Using Variation to Structure Sense-Making. Math. Think. Learn. 2006, 8, 91–111. [Google Scholar] [CrossRef]
- Marton, F.; Pang, M.F. On Some Necessary Conditions of Learning. J. Learn. Sci. 2006, 15, 193–220. [Google Scholar] [CrossRef]
- Gu, L.; Huang, R.; Marton, F. Teaching with variation: An effective way of mathematics teaching in China. In How Chinese Learn Mathematics: Perspectives from Insiders; Fan, L., Wong, N., Cai, J., Li, S., Eds.; World Scientific: Singapore, 2004; pp. 309–345. [Google Scholar]
- Gu, F.; Huang, R.; Gu, L. Theory and development of teaching through variation in mathematics in China. In Teaching and Learning Mathematics through Variation; Huang, R., Li, Y., Eds.; Sense: Boston, MA, USA, 2017; pp. 13–41. [Google Scholar]
- Pang, M.; Bao, J.; Ki, W. “Bianshi” and the variation theory of learning: Illustrating two frameworks of variation and invariance in the teaching of mathematics. In Teaching and Learning Mathematics through Variation: Confucian Heritage Meets Western Theories; Huang, R., Li, Y., Eds.; Sense: Rotterdam, The Netherlands, 2017; pp. 43–68. [Google Scholar]
- Marton, F.; Runesson, U.; Tsui, A. The space of learning. In Classroom Discourse and the Space of Learning; Marton, F., Tsui, A.B.M., Eds.; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 2004; pp. 3–42. [Google Scholar]
- Kullberg, A. Students’ open dimensions of variation. Int. J. Lesson Learn. Stud. 2012, 1, 168–181. [Google Scholar] [CrossRef]
- English, L.D.; Gainsburg, J. Problem-solving in a 21st-century mathematics curriculum. In Handbook of International Research in Mathematics Education, 3rd ed.; English, L.D., Kirshner, D., Eds.; Routledge: New York, NY, USA, 2016; pp. 313–335. [Google Scholar]
- Henningsen, M.; Stein, M.K. Mathematical tasks and student cognition: Classroom- based factors that support and inhibit high-level mathematical thinking and reasoning. J. Res. Math. Educ. 1997, 28, 524–549. [Google Scholar] [CrossRef]
- Stein, M.K.; Grover, B.W.; Henningsen, M. Building student capacity for mathematical thinking and reasoning: An analysis of mathematical tasks used in reform classrooms. Am. Educ. Res. J. 1996, 33, 455–488. [Google Scholar] [CrossRef]
- Kapur, M. Productive Failure in Learning Math. Cogn. Sci. 2014, 38, 1008–1022. [Google Scholar] [CrossRef] [PubMed]
- Loibl, K.; Roll, I.; Rummel, N. Towards a Theory of When and How Problem Solving Followed by Instruction Supports Learning. Educ. Psychol. Rev. 2017, 29, 693–715. [Google Scholar] [CrossRef]
- Schalk, L.; Schumacher, R.; Barth, A.; Stern, E. When problem-solving followed by instruction is superior to the traditional tell-and-practice sequence. J. Educ. Psychol. 2018, 110, 596–610. [Google Scholar] [CrossRef]
- Stein, M.K.; Engle, R.A.; Smith, M.S.; Hughes, E.K. Orchestrating Productive Mathematical Discussions: Five Practices for Helping Teachers Move Beyond Show and Tell. Math. Think. Learn. 2008, 10, 313–340. [Google Scholar] [CrossRef]
- Chen, O.; Kalyuga, S.; Sweller, J. The worked example effect, the generation effect, and element interactivity. J. Educ. Psychol. 2015, 107, 689–704. [Google Scholar] [CrossRef]
- Chen, O.; Kalyuga, S.; Sweller, J. Relations between the worked example and generation effects on immediate and delayed tests. Learn. Instr. 2016, 45, 20–30. [Google Scholar] [CrossRef]
- Kirschner, P.A.; Sweller, J.; Clark, R.E. Why Minimal Guidance During Instruction Does Not Work: An Analysis of the Failure of Constructivist, Discovery, Problem-Based, Experiential, and Inquiry-Based Teaching. Educ. Psychol. 2006, 41, 75–86. [Google Scholar] [CrossRef]
- Sweller, J.; Ayres, P.; Kalyuga, S. Cognitive Load Theory, Explorations in the Learning Sciences Instructional Systems; Springer: New York, NY, USA, 2011. [Google Scholar]
- Prusak, N.; Hershkowitz, R.; Schwarz, B.B. Conceptual Learning in A Principled Design Problem Solving Environment. Res. Math. Educ. 2013, 15, 266–285. [Google Scholar] [CrossRef]
- Russo, J.; Hopkins, S. Teachers’ Perceptions of Students When Observing Lessons Involving Challenging Tasks. Int. J. Sci. Math. Educ. 2019, 17, 759–779. [Google Scholar] [CrossRef]
- Anthony, G.; Walshaw, M. Characteristics of effective teaching of mathematics: A view from the West. J. Math. Educ. 2009, 2, 147–164. [Google Scholar]
- Lo, M.L.; Marton, F. Towards a science of the art of teaching: Using variation theory as a guiding principle of pedagogical design. Int. J. Lesson Learn. Stud. 2012, 1, 7–22. [Google Scholar] [CrossRef]
- Cobb, P.; Confrey, J.; Disessa, A.; Lehrer, R.; Schauble, L. Design Experiments in Educational Research. Educ. Res. 2003, 32, 9–13. [Google Scholar] [CrossRef]
- Cobb, P.; Jackson, K.; Dunlap, C. Design research: An analysis and critique. In Handbook of International Research in Mathematics Education, 3rd ed.; English, L.D., Kirshner, D., Eds.; Routledge: New York, NY, USA, 2016; pp. 481–503. [Google Scholar]
- McMillan, J.H.; Schumacher, S. Research in Education: Evidence-Based Inquiry, 7th ed.; Pearson: Harlow, UK, 2014. [Google Scholar]
- Sullivan, P.; Askew, M.; Cheeseman, J.; Clarke, D.; Mornane, A.; Roche, A.; Walker, N. Supporting teachers in structuring mathematics lessons involving challenging tasks. J. Math. Teach. Educ. 2014, 18, 123–140. [Google Scholar] [CrossRef]
- Sullivan, P.; Borcek, C.; Walker, N.; Rennie, M. Exploring a structure for mathematics lessons that initiate learning by activating cognition on challenging tasks. J. Math. Behav. 2016, 41, 159–170. [Google Scholar] [CrossRef]
- Franke, M.L.; Webb, N.M.; Chan, A.G.; Ing, M.; Freund, D.; Battey, D. Teacher Questioning to Elicit Students’ Mathematical Thinking in Elementary School Classrooms. J. Teach. Educ. 2009, 60, 380–392. [Google Scholar] [CrossRef]
- Hufferd-Ackles, K.; Fuson, K.C.; Sherin, M.G. Describing Levels and Components of a Math-Talk Learning Community. J. Res. Math. Educ. 2004, 35, 81. [Google Scholar] [CrossRef]
- Wood, T. Patterns of Interaction and the Culture of Mathematics Classrooms. In Cultural Perspectives on the Mathematics Classroom; Mathematics Education Library; Springer: Dordrecht, The Netherlands, 1994; Volume 14. [Google Scholar]
| Classroom 1 | CA1: Understanding the structure of linear inequalities; CA2: Understanding properties of inequalities; CA3: Applying properties of inequalities to find solution sets of linear inequalities within a specified set. |
| Classroom 2 | CA1: Solving real-life problems involving linear inequalities and interpreting the results; CA2: Developing algebraic representations of linear inequalities from the patterns of arithmetic representations of linear equations; CA3: Applying properties of inequalities to solve linear inequalities. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kassa, B.G.; Ding, L.; Tamiru, A.B. Describing and Interpreting the Space of Classroom Learning in Problem-Solving-Based Mathematics Instruction: Variation as an Analytical Lens. Educ. Sci. 2023, 13, 111. https://doi.org/10.3390/educsci13020111
Kassa BG, Ding L, Tamiru AB. Describing and Interpreting the Space of Classroom Learning in Problem-Solving-Based Mathematics Instruction: Variation as an Analytical Lens. Education Sciences. 2023; 13(2):111. https://doi.org/10.3390/educsci13020111
Chicago/Turabian StyleKassa, Berie Getie, Liping Ding, and Alemayehu Bishaw Tamiru. 2023. "Describing and Interpreting the Space of Classroom Learning in Problem-Solving-Based Mathematics Instruction: Variation as an Analytical Lens" Education Sciences 13, no. 2: 111. https://doi.org/10.3390/educsci13020111
APA StyleKassa, B. G., Ding, L., & Tamiru, A. B. (2023). Describing and Interpreting the Space of Classroom Learning in Problem-Solving-Based Mathematics Instruction: Variation as an Analytical Lens. Education Sciences, 13(2), 111. https://doi.org/10.3390/educsci13020111






