Lossless Encoding of Mental Cutting Test Scenarios for Efficient Development of Spatial Skills
Abstract
1. Introduction
1.1. Measuring Spatial Skills
1.2. Our Dataset of MCT Scenarios
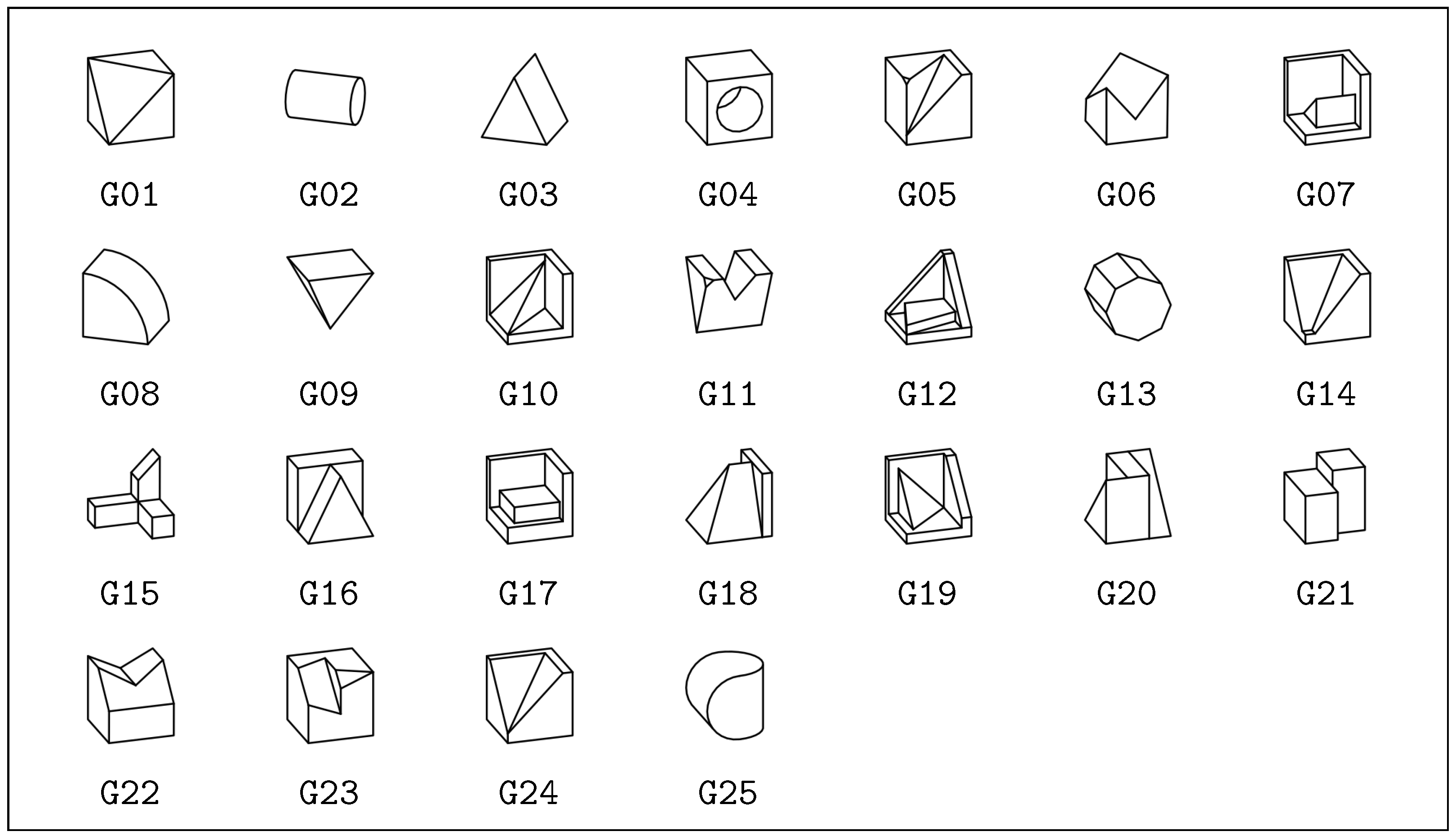
- We have developed additional, manually permuted meshes for each classic mesh. Without using groups G02, G04, G08, and G25, a total number of 205 different manually designed meshes are available (see Figure 1).
- Thirty-one cutting planes are combined with each mesh (see Figure 2).
- Twenty-four rotation vectors are used to rotate each mesh to each possible orientation using Euler rotation (note that multiple orientations of symmetric shapes can be considered the same).
- Seven scaling vectors yield various meshes, applying a multiplier of 0.7 in one or two dimensions.
1.3. Our Vision
2. Creation and Structure of the Graphical Assets
- Each model has the UV map due to the behavior of Blender;
- The UV map of each model was removed before the processing.
2.1. Properties of the JSON Chunk
2.1.1. Property Asset
2.1.2. Properties Scene and Scenes
2.1.3. Property Nodes
2.1.4. Property Meshes
2.1.5. Property Materials
2.1.6. Property Accessors
2.1.7. Properties BufferViews and Buffers
2.2. Permutation-Based Features
2.2.1. Property Nodes
- Each 3D mesh is rotated using 24 different rotation vectors.
- Each 3D mesh is scaled using seven different scaling vectors.
- A total number of 31 cutting planes are combined with each 3D mesh. On the other hand, four different meshes represent a cutting plane. The rest of them can be yielded by applying transformation operators on the set of selected frames.
- A cleaned Node object for each cutting plane(a total number of 31 objects);
- A cleaned Node object for each rotation vector(a total number of 24 objects).
2.2.2. Property Accessors
2.2.3. Properties BufferViews and Buffers
2.2.4. Data Chunk
3. Reduced Storage of the Dataset for Efficient Use in Application
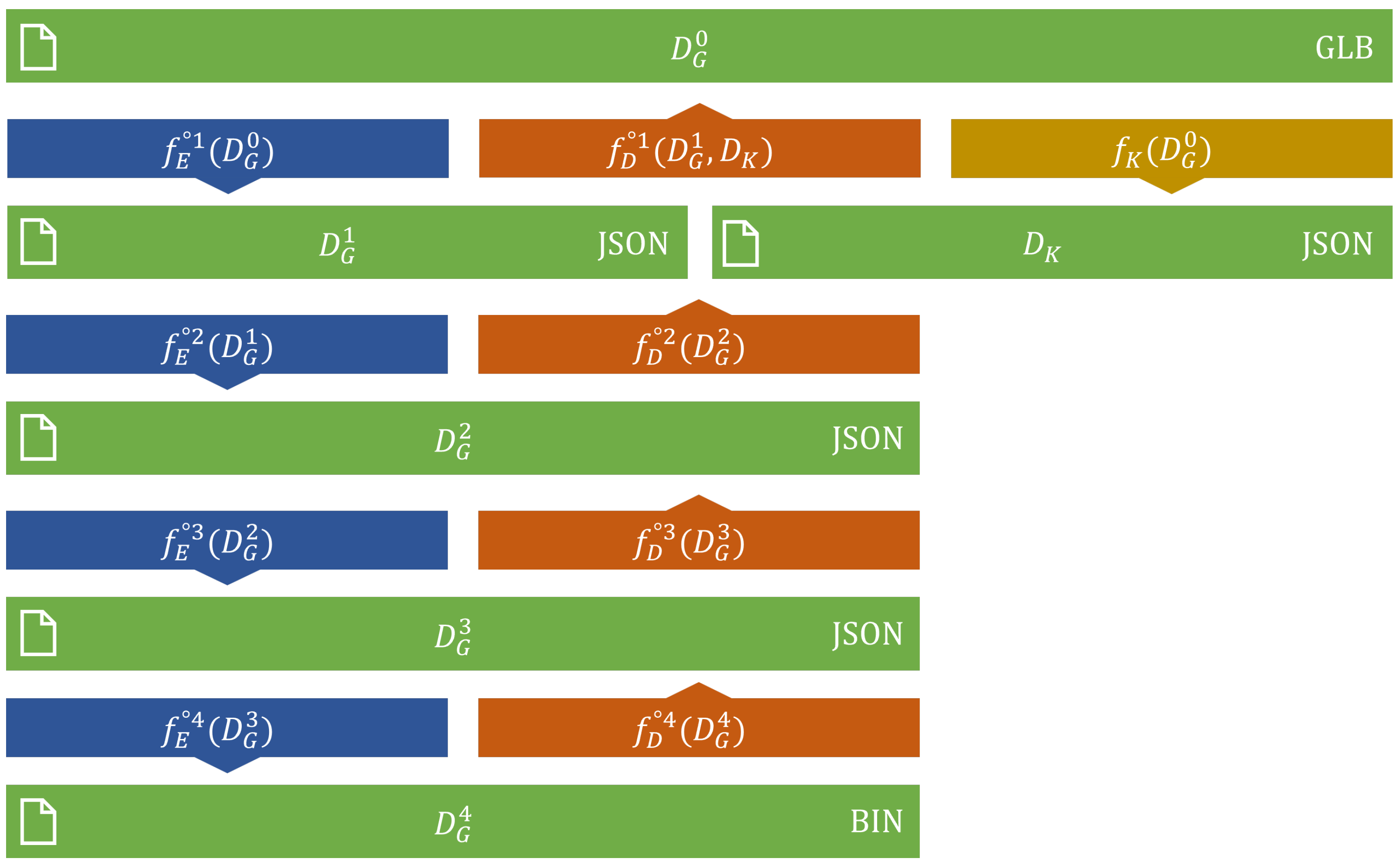
3.1. Key Document
3.2. First Level
3.3. Second Level
3.4. Third Level
3.5. Fourth Level
3.6. Evaluation
3.6.1. Verification
- Each calculation with an IEEE 754 type increases the probability of a higher error in the result.
- Moreover, the original mesh is designed manually. Thus, designers may make minor errors in setting the coordinates of vertices. Consequently, minor errors occur in the bytes of the data chunk and the values of the JSON chunk.
- Finally, our decoding algorithm applies a multiplication on the min and max properties of Accessor objects to simulate the scaling operation.
- The properties of their JSON chunks should be compared recursively. In the case of floating values, their difference should be above a given threshold . Objects must contain the same key-value pairs, while the order of the elements in two arrays should also be the same.
- The binary chunks can be compared bitwise, except the sequences that belong to a buffer using floating values. In that case, the comparison must be performed using the given threshold .
- Only globally unique metadata (such as property asset) can be reconstructed and checked since the algorithm does not code any metadata in but in .
3.6.2. Analysis
- Export only the subset of assets from Blender, which is required as an input of and . Denote the set of assets with .
- Create with function call .
- Encode each group to retrieve with a function call .
- Decode each document to retrieve the full dataset with a function call .
3.6.3. Remarks
- Each calculation was performed on a Zenbook UX433FA-A5082T notebook with an SSD and OS Windows 11.
- During the measurements, only our Blender script or standalone Python scripts were executed on the computer. All the other non-essential processes had been stopped, including Windows Defender.
- The Blender script was executed using the built-in interpreter of Blender 3.3, using our wrapper script.
- The wrapper script and encoding process were interpreted with Python version 3.10.6 in a Miniconda 4.14.0 environment.
- Each mentioned runtime is an average of processes in the case of our Blender script, and five processes in the case of our encoding and decoding functions.
- A pre-processing step was executed before the encoding process to guarantee that all the shapes had the same materials without precision errors that affected the calculations. The material shown in Figure 7 has been added to all the assets in this step.
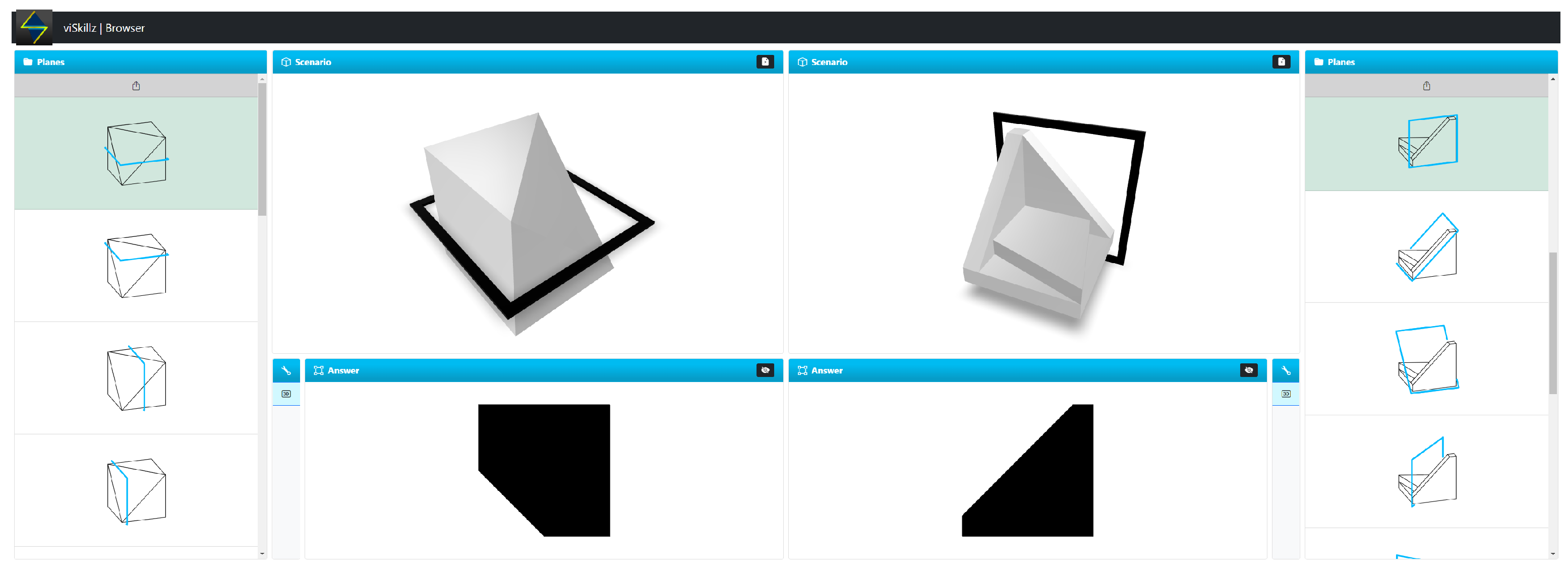
3.7. Applications
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MCT | Mental Cutting Test |
| GLB | GL Transmission Format Binary file |
References
- Bohlmann, N.; Benölken, R. Complex Tasks: Potentials and Pitfalls. Mathematics 2020, 8, 1780. [Google Scholar] [CrossRef]
- Bishop, A.J. Spatial abilities and mathematics education—A review. Educ. Stud. Math. 1980, 11, 257–269. [Google Scholar] [CrossRef]
- Tosto, M.G.; Hanscombe, K.B.; Haworth, C.M.; Davis, O.S.; Petrill, S.A.; Dale, P.S.; Malykh, S.; Plomin, R.; Kovas, Y. Why do spatial abilities predict mathematical performance? Dev. Sci. 2014, 17, 462–470. [Google Scholar] [CrossRef] [PubMed]
- Cole, M.; Wilhelm, J.; Vaught, B.M.M.; Fish, C.; Fish, H. The Relationship between Spatial Ability and the Conservation of Matter in Middle School. Educ. Sci. 2021, 11, 4. [Google Scholar] [CrossRef]
- Zimmermann, W.; Cunningham, S. (Eds.) Visualization in Teaching and Learning Mathematics; Mathematical Association of America: Washington, DC, USA, 1991. [Google Scholar]
- Presmeg, N. Visualization and Learning in Mathematics Education. In Proceedings of the Encyclopedia of Mathematics Education; Springer International Publishing: Cham, Switzerland, 2020; pp. 900–904. [Google Scholar]
- Presmeg, N. Spatial Abilities Research as a Foundation for Visualization in Teaching and Learning Mathematics. In Proceedings of the Critical Issues in Mathematics Education; Springer: Boston, MA, USA, 2008; pp. 83–95. [Google Scholar]
- Gerber, A. (Ed.) Spatial Abilities. A Workbook for Students of Architecture; Birkhauser Verlag GmbH: Basel, Switzerland, 2020. [Google Scholar]
- Katsioloudis, P.; Bairaktarova, D. Impacts of Scent on Mental Cutting Ability for Industrial and Engineering Technology Students as Measured Through a Sectional View Drawing. In Proceedings of the Spatial Cognition XII; Šķilters, J., Newcombe, N.S., Uttal, D., Eds.; Springer: Cham, Switzerland, 2020; pp. 322–334. [Google Scholar]
- Estapa, A.; Nadolny, L. The effect of an augmented reality enhanced mathematics lesson on student achievement and motivation. J. Stem Educ. 2015, 16, 40–48. [Google Scholar]
- Chen, Y. Effect of mobile augmented reality on learning performance, motivation, and math anxiety in a math course. J. Educ. Comput. Res. 2019, 57, 1695–1722. [Google Scholar] [CrossRef]
- del Cerro Velázquez, F.; Morales Méndez, G. Application in Augmented Reality for Learning Mathematical Functions: A Study for the Development of Spatial Intelligence in Secondary Education Students. Mathematics 2021, 9, 369. [Google Scholar] [CrossRef]
- Petrov, P.D.; Atanasova, T.V. The Effect of Augmented Reality on Students’ Learning Performance in Stem Education. Information 2020, 11, 209. [Google Scholar] [CrossRef]
- Flores-Bascuñana, M.; Diago, P.D.; Villena-Taranilla, R.; Yáñez, D.F. On Augmented Reality for the learning of 3D-geometric contents: A preliminary exploratory study with 6-Grade primary students. Educ. Sci. 2020, 10, 4. [Google Scholar] [CrossRef]
- Suselo, T.; Wünsche, B.C.; Luxton-Reilly, A. Using Mobile Augmented Reality for Teaching 3D Transformations. In Proceedings of the 52nd ACM Technical Symposium on Computer Science Education, Virtual Event, 13–20 March 2021; pp. 872–878. [Google Scholar]
- CEEB Special Aptitude Test in Spatial Relations; College Entrance Examination Board: New York, NY, USA, 1939.
- Bölcskei, A.; Gál-Kállay, S.; Kovács, A.Z.; Sörös, C. Development of Spatial Abilities of Architectural and Civil Engineering Students in the Light of the Mental Cutting Test. J. Geom. Graph. 2012, 16, 103–115. [Google Scholar]
- Šipuš, Ž.M.; Cižmešija, A. Spatial ability of students of mathematics education in Croatia evaluated by the Mental Cutting Test. Ann. Math. Informaticae 2012, 40, 203–216. [Google Scholar]
- Németh, B.; Sörös, C.; Hoffmann, M. Typical mistakes in Mental Cutting Test and their consequences in gender differences. Teach. Math. Comput. Sci. 2007, 5, 385–392. [Google Scholar] [CrossRef]
- Németh, B.; Hoffmann, M. Gender differences in spatial visualization among engineering students. In Proceedings of the Annales Mathematicae et Informaticae; Institute of Mathematics and Informatics of Eszterházy Károly University: Eger, Hungary, 2006; pp. 169–174. [Google Scholar]
- Ballatore, M.G.; Duffy, G.; Sorby, S.; Tabacco, A. SAperI: Approaching Gender Gap Using Spatial Ability Training Week in High-School Context. In Proceedings of the Eighth International Conference on Technological Ecosystems for Enhancing Multiculturality, Salamanca, Spain, 21–23 October 2020; TEEM’20. pp. 142–148. [Google Scholar] [CrossRef]
- Tóth, R.; Zichar, M.; Hoffmann, M. Improving and Measuring Spatial Skills with Augmented Reality and Gamification. In Proceedings of the International Conference on Geometry and Graphics, Sao Paulo, Brazil, 18–22 January 2021; pp. 755–764. [Google Scholar]
- Guzsvinecz, T.; Szeles, M.; Perge, E.; Sik-Lanyi, C. Preparing spatial ability tests in a virtual reality application. In Proceedings of the 2019 10th IEEE International Conference on Cognitive Infocommunications (CogInfoCom), Naples, Italy, 23–25 October 2019; pp. 363–368. [Google Scholar]
- Tóth, R.; Zichar, M.; Hoffmann, M. Gamified Mental Cutting Test for enhancing spatial skills. In Proceedings of the 2020 11th IEEE International Conference on Cognitive Infocommunications (CogInfoCom), Mariehamn, Finland, 23–25 September 2020; pp. 299–304. [Google Scholar]
- Rizzo, A.A.; Buckwalter, J.G.; Neumann, U.; Kesselman, C.; Thiébaux, M.; Larson, P.; van Rooyen, A. The virtual reality mental rotation spatial skills project. Cyberpsychol. Behav. 1998, 1, 113–119. [Google Scholar] [CrossRef]
- Lochhead, I.; Hedley, N.; Çöltekin, A.; Fisher, B. The Immersive Mental Rotations Test: Evaluating Spatial Ability in Virtual Reality. Front. Virtual Real. 2022, 3. [Google Scholar] [CrossRef]
- Hartman, N.W.; Connolly, P.E.; Gilger, J.W.; Bertoline, G.R.; Heisler, J. Virtual reality-based spatial skills assessment and its role in computer graphics education. In Proceedings of the ACM SIGGRAPH’06 Proceedings, Boston, MA, USA, 30–31 July 2006; p. 46. [Google Scholar]
- Safadel, P.; White, D. Effectiveness of computer-generated virtual reality (VR) in learning and teaching environments with spatial frameworks. Appl. Sci. 2020, 10, 5438. [Google Scholar] [CrossRef]
- Saredakis, D.; Szpak, A.; Birckhead, B.; Keage, H.A.D.; Rizzo, A.; Loetscher, T. Factors associated with virtual reality sickness in head-mounted displays: A systematic review and meta-analysis. Front. Hum. Neurosci. 2020, 14, 96. [Google Scholar] [CrossRef] [PubMed]
- Chang, E.; Kim, H.T.; Yoo, B. Virtual reality sickness: A review of causes and measurements. Int. J. Hum. Comput. Interact. 2020, 36, 1658–1682. [Google Scholar] [CrossRef]
- The Khronos® 3D Formats Working Group. GlTF™ 2.0 Specification-Version 2.0.1. 2021. Available online: https://registry.khronos.org/glTF/specs/2.0/glTF-2.0.html (accessed on 11 September 2022).
- Fedyukov, M. IEEE Industry Connections (IEEE-IC) File Format Recommendations for 3D Body Model Processing; IEEE: New York, NY, USA, 2019; pp. 1–38. [Google Scholar]
- Yang, Q.; Dong, X.; Cao, X.; Ma, Y. Adaptive compression of 3D models for mobile web apps. In Proceedings of the 20th Annual International Conference on Mobile Systems, Applications and Services, Portland, OR, USA, 27 June–1 July 2022. [Google Scholar]
- Possemiers, A.L.; Lee, I. Fast OBJ file importing and parsing in Cuda. Comput. Vis. Media 2015, 1, 229–238. [Google Scholar] [CrossRef]
- Tuker, C. Training Spatial Skills with Virtual Reality and Augmented Reality. In Encyclopedia of Computer Graphics and Games; Springer International Publishing: Cham, Switzerland, 2018; pp. 1–9. [Google Scholar] [CrossRef]
- Tóth, R.; Tóth, B.; Zichar, M.; Fazekas, A.; Hoffmann, M. Educational Applications to Support the Teaching and Learning of Mental Cutting Test Exercises. In Proceedings of the ICGG 2022–Proceedings of the 20th International Conference on Geometry and Graphics, Sao Paulo, Brazil, 15–19 August 2022; pp. 928–938. [Google Scholar] [CrossRef]
- Tóth, R. Script-aided generation of Mental Cutting Test exercises using Blender. Ann. Math. Inform. 2021, 54, 147–161. [Google Scholar] [CrossRef]
- Python Software Foundation. Struct—Interpret Bytes as Packed Binary Data—Python 3.10.7 Documentation. 2022. Available online: https://docs.python.org/3/library/struct.html (accessed on 11 September 2022).












| Group | ||||||||
|---|---|---|---|---|---|---|---|---|
| 01 | 23.89 | 24.38 | 23.98 | 24.47 | 22.89 | 22.71 | 23.48 | 23.88 |
| 03 | 24.08 | 23.90 | 23.75 | 24.43 | 22.99 | 22.97 | 23.42 | 23.51 |
| 05 | 19.38 | 19.13 | 19.64 | 19.27 | 18.67 | 18.38 | 19.18 | 18.75 |
| 06 | 19.52 | 19.50 | 19.90 | 19.17 | 18.66 | 18.50 | 19.30 | 19.04 |
| 07 | 24.35 | 24.65 | 25.39 | 24.27 | 22.70 | 23.34 | 23.67 | 23.67 |
| 09 | 24.29 | 24.87 | 24.65 | 24.80 | 23.23 | 23.18 | 23.68 | 23.84 |
| 10 | 24.88 | 24.93 | 24.63 | 24.26 | 23.53 | 23.01 | 24.04 | 24.09 |
| 11 | 27.13 | 26.86 | 27.61 | 26.35 | 25.76 | 26.15 | 26.38 | 26.49 |
| 12 | 24.28 | 24.83 | 24.43 | 24.46 | 23.58 | 23.47 | 23.92 | 23.96 |
| 13 | 19.40 | 20.17 | 19.76 | 19.53 | 18.53 | 18.73 | 19.26 | 19.08 |
| 14 | 24.21 | 24.64 | 25.35 | 24.47 | 23.23 | 23.48 | 24.13 | 23.91 |
| 15 | 24.30 | 24.99 | 25.28 | 24.45 | 23.25 | 23.93 | 23.60 | 24.29 |
| 16 | 23.94 | 24.90 | 24.69 | 24.27 | 23.35 | 23.83 | 23.79 | 23.84 |
| 17 | 24.45 | 25.05 | 25.21 | 24.17 | 23.25 | 23.80 | 24.14 | 24.18 |
| 18 | 24.29 | 24.66 | 24.94 | 24.32 | 23.13 | 23.38 | 23.78 | 23.93 |
| 19 | 24.70 | 25.01 | 24.92 | 24.03 | 23.09 | 23.91 | 24.21 | 23.96 |
| 20 | 24.43 | 25.47 | 25.28 | 24.48 | 23.10 | 24.14 | 24.03 | 23.77 |
| 21 | 24.48 | 24.74 | 25.12 | 24.60 | 23.38 | 23.81 | 23.92 | 23.87 |
| 22 | 24.29 | 24.83 | 24.93 | 24.11 | 23.47 | 23.52 | 23.50 | 23.57 |
| 23 | 24.08 | 24.82 | 24.97 | 24.09 | 23.23 | 24.14 | 24.10 | 24.33 |
| 24 | 24.37 | 25.06 | 24.56 | 24.43 | 23.18 | 23.91 | 23.94 | 23.74 |
| Total | 498.75 | 507.38 | 508.98 | 498.42 | 476.20 | 482.30 | 489.46 | 489.71 |
| Group | Original (s) | Enhanced (s) | Ratio (%) | |||
|---|---|---|---|---|---|---|
| Exporting | Encoding | Decoding | Sum | |||
| 01 | 1624.3172 | 22.7412 | 0.0158 | 23.8874 | 46.6444 | 2.8716 |
| 03 | 1636.5026 | 23.3132 | 0.0162 | 24.0778 | 47.4072 | 2.8969 |
| 05 | 1307.6983 | 19.1244 | 0.0082 | 19.3816 | 38.5143 | 2.9452 |
| 06 | 1300.7097 | 18.7861 | 0.0112 | 19.5166 | 38.3140 | 2.9456 |
| 07 | 1633.5453 | 23.3287 | 0.0124 | 24.3548 | 47.6960 | 2.9198 |
| 09 | 1632.9955 | 23.1342 | 0.0125 | 24.2930 | 47.4398 | 2.9051 |
| 10 | 1671.4794 | 23.1511 | 0.0083 | 24.8838 | 48.0431 | 2.8743 |
| 11 | 1839.2504 | 25.4292 | 0.0156 | 27.1265 | 52.5714 | 2.8583 |
| 12 | 1638.0409 | 23.4728 | 0.0121 | 24.2773 | 47.7622 | 2.9158 |
| 13 | 1321.5149 | 19.1439 | 0.0062 | 19.4022 | 38.5523 | 2.9173 |
| 14 | 1633.9655 | 23.8631 | 0.0125 | 24.2062 | 48.0819 | 2.9426 |
| 15 | 1654.7123 | 23.3419 | 0.0156 | 24.3038 | 47.6613 | 2.8803 |
| 16 | 1657.0160 | 23.2236 | 0.0094 | 23.9401 | 47.1731 | 2.8469 |
| 17 | 1672.3261 | 23.3899 | 0.0156 | 24.4518 | 47.8574 | 2.8617 |
| 18 | 1656.3157 | 23.4130 | 0.0110 | 24.2897 | 47.7137 | 2.8807 |
| 19 | 1686.8150 | 23.1013 | 0.0156 | 24.7023 | 47.8192 | 2.8349 |
| 20 | 1680.0384 | 23.1084 | 0.0094 | 24.4292 | 47.5470 | 2.8301 |
| 21 | 1684.0271 | 23.4228 | 0.0156 | 24.4811 | 47.9195 | 2.8455 |
| 22 | 1651.6237 | 23.2053 | 0.0183 | 24.2945 | 47.5181 | 2.8771 |
| 23 | 1649.9467 | 23.2368 | 0.0094 | 24.0782 | 47.3244 | 2.8682 |
| 24 | 1654.0871 | 23.2149 | 0.0094 | 24.3676 | 47.5919 | 2.8772 |
| Total | 33,886.9280 | 478.1459 | 0.2605 | 498.7456 | 977.1520 | 2.8836 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tóth, R.; Hoffmann, M.; Zichar, M. Lossless Encoding of Mental Cutting Test Scenarios for Efficient Development of Spatial Skills. Educ. Sci. 2023, 13, 101. https://doi.org/10.3390/educsci13020101
Tóth R, Hoffmann M, Zichar M. Lossless Encoding of Mental Cutting Test Scenarios for Efficient Development of Spatial Skills. Education Sciences. 2023; 13(2):101. https://doi.org/10.3390/educsci13020101
Chicago/Turabian StyleTóth, Róbert, Miklós Hoffmann, and Marianna Zichar. 2023. "Lossless Encoding of Mental Cutting Test Scenarios for Efficient Development of Spatial Skills" Education Sciences 13, no. 2: 101. https://doi.org/10.3390/educsci13020101
APA StyleTóth, R., Hoffmann, M., & Zichar, M. (2023). Lossless Encoding of Mental Cutting Test Scenarios for Efficient Development of Spatial Skills. Education Sciences, 13(2), 101. https://doi.org/10.3390/educsci13020101







