Contextual Mathematical Modelling: Problem-Solving Characterization and Feasibility
Abstract
:1. Introduction
Mathematical Problem-Solving
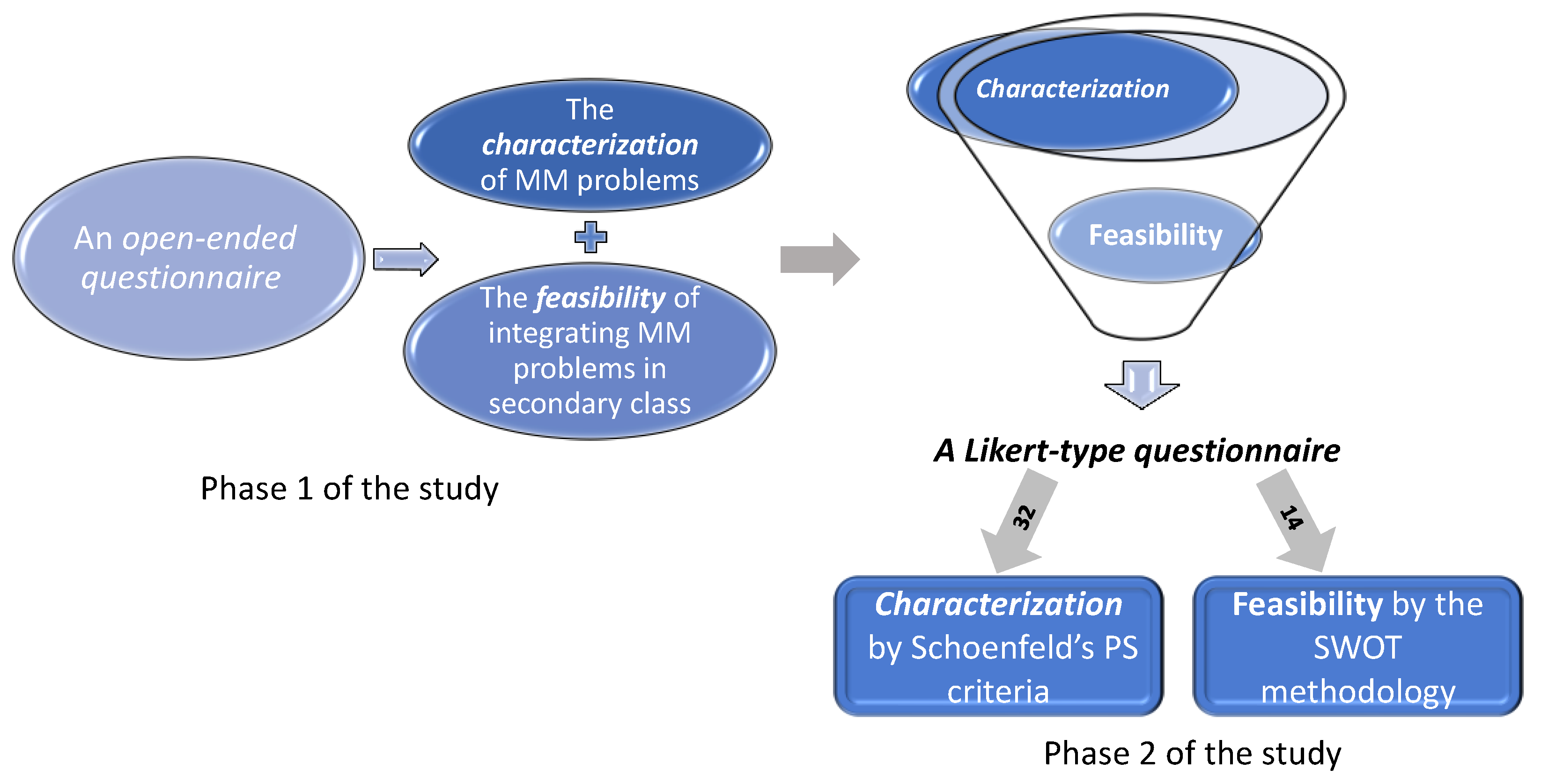
2. Materials and Methods
2.1. The Context of the Study
2.2. Participants and Procedures
2.3. Research Tools
2.4. Data Analysis
3. Results
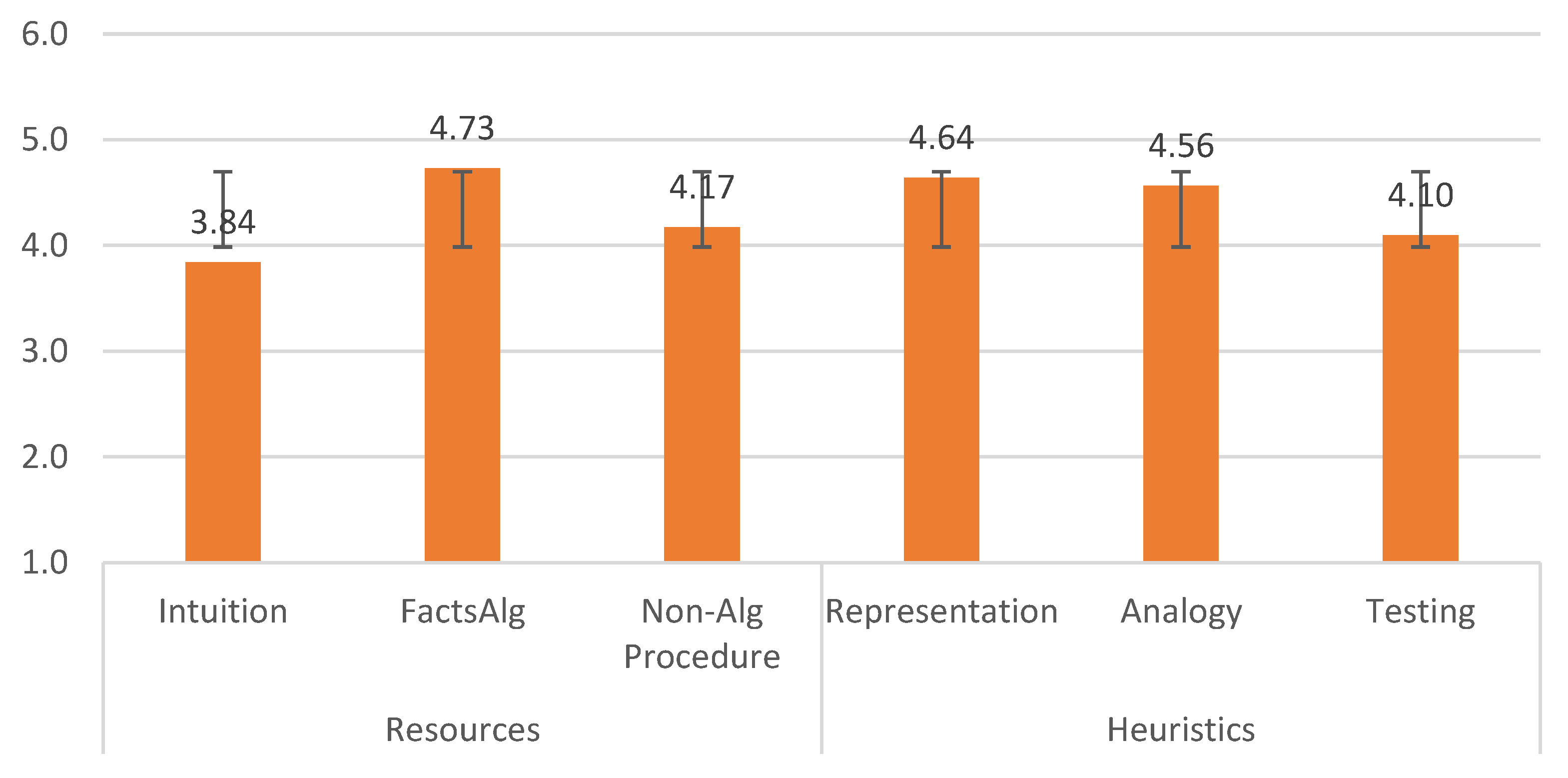
3.1. The Characteristics of the Contextual MM Problems
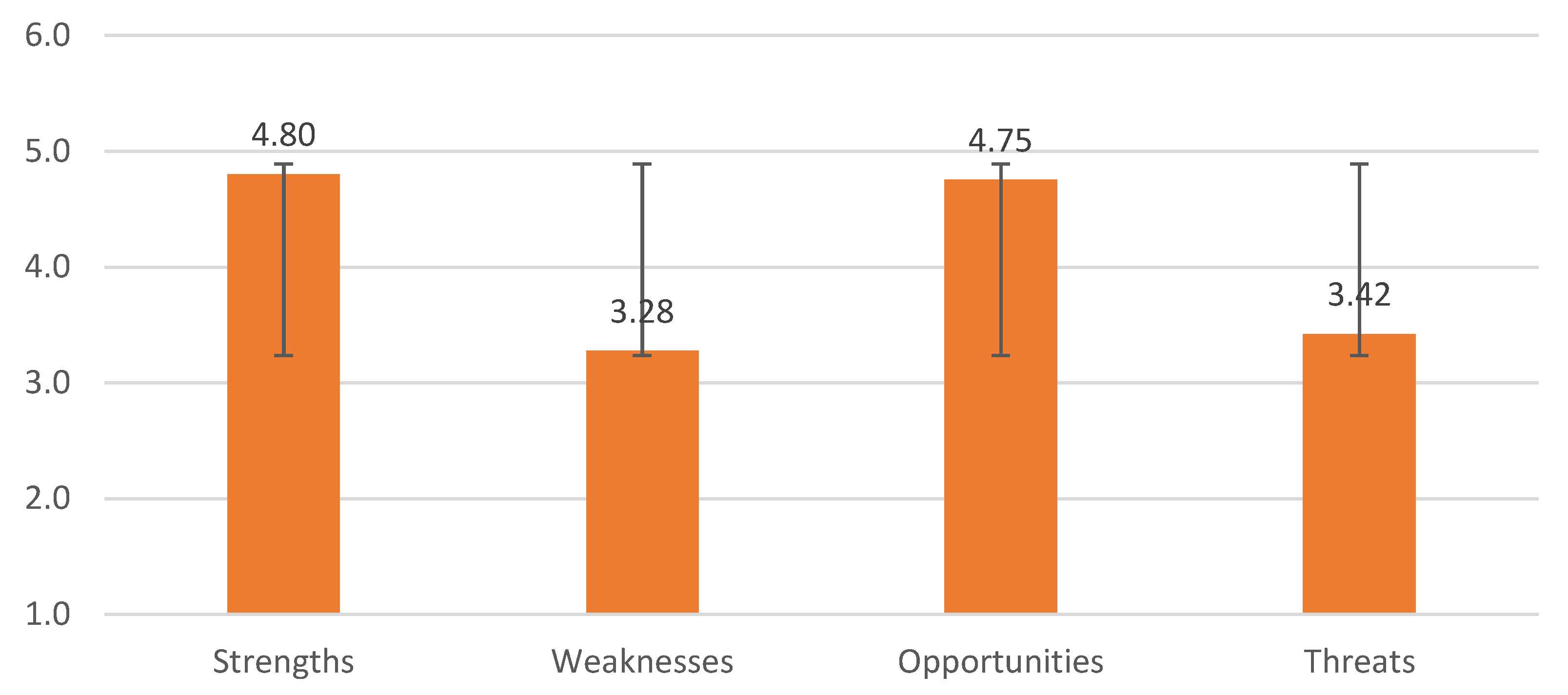
3.2. The Feasibility of Incorporating the Contextual MM Problems in Classes
4. Discussion
The Study’s Contribution
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| PS Criteria | PS Sub-Criteria | Gender | Level of Education | STEM Background | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M | F | B.A. | M.A. or Ph.D. | Engineering | STEM | None | |||||||||
| M | SD | M | SD | M | SD | M | SD | M | SD | M | SD | M | SD | ||
| Resources | Intuitions and informal knowledge regarding the domain | 3.95 | 0.51 | 3.82 | 0.57 | 3.79 | 0.53 | 3.86 | 0.58 | 3.97 | 0.53 | 3.87 | 0.54 | 3.79 | 0.54 |
| Facts, rules and algorithmic procedures | 4.67 | 0.63 | 4.76 | 0.69 | 4.78 | 0.70 | 4.69 | 0.66 | 4.75 | 0.62 | 4.83 | 0.66 | 4.68 | 0.72 | |
| “Routine” nonalgorithmic procedures | 3.99 | 0.59 | 4.22 | 0.69 | 4.11 | 0.73 | 4.24 | 0.61 | 4.22 | 0.69 | 4.17 | 0.58 | 4.20 | 0.69 | |
| Heuristics | Appropriate representations | 4.43 | 0.80 | 4.69 | 0.76 | 4.63 | 0.87 | 4.67 | 0.70 | 4.67 | 0.73 | 4.73 | 0.67 | 4.56 | 0.86 |
| Analogies and exploiting related problems | 4.55 | 0.84 | 4.57 | 0.82 | 4.56 | 0.85 | 4.58 | 0.79 | 4.56 | 0.87 | 4.68 | 0.62 | 4.52 | 0.93 | |
| Testing and verification procedures | 4.13 | 1.13 | 4.09 | 1.03 | 4.11 | 0.98 | 4.10 | 1.06 | 4.00 | 0.88 | 4.04 | 0.97 | 4.19 | 1.16 | |
Appendix B
| SWOT Criteria | Gender | Level of Education | STEM Background | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M | F | B.A. | M.A. or Ph.D. | Engineering | STEM | None | ||||||||
| M | SD | M | SD | M | SD | M | SD | M | SD | M | SD | M | SD | |
| Strength | 4.82 | 0.85 | 4.80 | 0.79 | 4.74 | 0.91 | 4.85 | 0.74 | 5.07 | 0.80 | 4.91 | 0.74 | 4.59 | 0.81 |
| Weakness | 3.33 | 0.78 | 3.27 | 0.86 | 3.31 | 0.80 | 3.27 | 0.90 | 3.37 | 0.82 | 3.38 | 0.71 | 3.10 | 0.96 |
| Opportunity | 4.66 | 0.64 | 4.78 | 0.74 | 4.59 | 0.80 | 4.88 | 0.64 | 4.86 | 0.61 | 4.78 | 0.65 | 4.69 | 0.82 |
| Threat | 3.39 | 0.80 | 3.42 | 0.75 | 3.40 | 0.79 | 3.41 | 0.75 | 3.52 | 0.65 | 3.36 | 0.75 | 3.39 | 0.82 |
References
- Li, T. Mathematical Modeling Education Is the Most Important Educational Interface Between Mathematics and Industry. In New ICMI Study Series; Springer: Berlin/Heidelberg, Germany, 2013; Volume 16, pp. 51–58. [Google Scholar]
- Maaß, J.; O’Meara, N.; Johnson, P.; O’Donoghue, J. Mathematical Modelling for Teachers A Practical Guide to Applicable Mathematics Education; Springer: New York, NY, USA, 2018. [Google Scholar]
- Schoenfeld, A.H. Making Sense of “out Loud” Problem-Solving Protocols Teaching for Robust Understanding View Project. J. Math. Behav. 1985, 4, 171–191. [Google Scholar]
- Kohen, Z.; Orenstein, D. Mathematical Modeling of Tech-Related Real-World Problems for Secondary School-Level Mathematics. Educ. Stud. Math. 2021. [Google Scholar] [CrossRef]
- van der Wal, N.J.; Bakker, A.; Drijvers, P. Teaching Strategies to Foster Techno-Mathematical Literacies in an Innovative Mathematics Course for Future Engineers. ZDM-Math. Educ. 2019, 51, 885–897. [Google Scholar] [CrossRef] [Green Version]
- van der Wal, N.J.; Bakker, A.; Drijvers, P. Which Techno-Mathematical Literacies Are Essential for Future Engineers? Int. J. Sci. Math. Educ. 2017, 15, 87–104. [Google Scholar] [CrossRef] [Green Version]
- Blum, W.; Leiss, D. How Do Students and Teachers Deal with Modelling Problems? The Example “Sugarloaf” and the DISUM Project. In Mathematical Modelling (ICTMA12)—Education, Engineering and Economics; Woodhead Publishing: Cambridge, UK, 2007. [Google Scholar]
- Ferri, R.B. Theoretical and Empirical Differentiations of Phases in the Modelling Process. ZDM-Int. J. Math. Educ. 2006, 38. [Google Scholar] [CrossRef]
- Lesh, R.; Doerr, H.M.; Carmona, G.; Hjalmarson, M. Beyond Constructivism. Math. Think. Learn. 2003, 5. [Google Scholar] [CrossRef]
- Niss, M.; Blum, W.; Galbraith, P. Introduction. In New ICMI Study Series; Springer: Berlin/Heidelberg, Germany, 2007; Volume 10, pp. 3–32. [Google Scholar]
- Borromeo Ferri, R.; Blum, W. Mathematical Modelling in Teacher Education–Experiences from a Modelling Seminar. In Proceedings of the CERME 6, Lyon, France, 28 January–1 February 2010. [Google Scholar]
- English, L.D.; King, D.T. STEM Learning through Engineering Design: Fourth-Grade Students’ Investigations in Aerospace. Int. J. STEM Educ. 2015, 2, 1–18. [Google Scholar] [CrossRef]
- Hoyles, C.; Noss, R.; Kent, P.; Bakker, A. Mathematics in the Workplace: Issues and Challenges. In New ICMI Study Series; Springer: Berlin/Heidelberg, Germany, 2013; Volume 16, pp. 43–50. [Google Scholar]
- Koichu, B.; Cooper, J.; Widder, M. Implementation of Problem Solving in School: From Intended to Experienced. Implement. Replication Stud. Math. Educ. 2022, 2, 76–106. [Google Scholar] [CrossRef]
- Mason, J. Part 1 Reaction: Problem Posing and Solving Today. In Posing and Solving Mathematical Problems; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Schoenfeld, A.H. Why Are Learning and Teaching Mathematics So Difficult? In Handbook of Cognitive Mathematics; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar]
- Pellegrino, J.W.; Hilton, M.L. Education for Life and Work: Developing Transferable Knowledge and Skills in the 21st Century; National Academies Press: Washington, DC, USA, 2013. [Google Scholar]
- Cobb, P.; Jackson, K.; Dunlap, C. Design Research: An Analysis and Critique. In Handbook of International Research in Mathematics Education, 3rd ed.; Routledge Press: London, UK, 2015. [Google Scholar]
- Stanic, G.; Kilpatrick, J. Historical Perspectives on Problem Solving in the Mathematics Curriculum. Teach. Assess. Math. Probl. Solving Res. Agenda Math. Educ. 1989, 3, 1–12. [Google Scholar]
- García, F.J.; Maass, K.; Wake, G. Theory Meets Practice: Working Pragmatically within Different Cultures and Traditions. In Modeling Students’ Mathematical Modeling Competencies; Springer: Boston, MA, USA, 2010. [Google Scholar]
- Borko, H. Professional Development and Teacher Learning: Mapping the Terrain. Educ. Res. 2004, 33, 3–15. [Google Scholar] [CrossRef]
- Kohen, Z.; Borko, H. Classroom Discourse in Mathematics Lessons: The Effect of a Hybrid Practice-Based Professional Development Program. Prof. Dev. Educ. 2019. [Google Scholar] [CrossRef]
- Gainsburg, J. Why New Mathematics Teachers Do or Don’t Use Practices Emphasized in Their Credential Program. J. Math. Teach. Educ. 2012, 15, 359–379. [Google Scholar] [CrossRef]
- Remillard, J.T.; Bryans, M.B. Teachers’ Orientations toward Mathematics Curriculum Materials: Implications for Teacher Learning. J. Res. Math. Educ. 2004, 35, 352–388. [Google Scholar] [CrossRef]
- Polya, G. How to Solve It: A New Aspect of Mathematical Method Second Edition. Math. Gaz. 1978, 30. [Google Scholar]
- Schoenfeld, A.H. Learning to Think Mathematically: Problem Solving, Metacognition, and Sense Making in Mathematics (Reprint). J. Educ. 2016, 196, 1–38. [Google Scholar] [CrossRef] [Green Version]
- Damlamian, A.; Rodrigues, J.F.; Sträßer, R. Report on the Study. In New ICMI Study Series; Springer: Cham, Switzerland, 2013; Volume 16. [Google Scholar]
- Reeff, J. New Assessment Tools for Cross-Curricular Competencies in the Domain of Problem Solving. 1999. Available online: https://cordis.europa.eu/docs/projects/files/SOE/SOE2982042/70781411-6_en.pdf (accessed on 30 May 2022).
- Lesh, R.; Post, T.; Behr, M. Representations and Translations among Representations in Mathematics Learning and Problem Solving. In Problems of Representations in the Teaching and Learning of Mathematics; Lawrence Erlbaum: Mahwah, NJ, USA, 1987. [Google Scholar]
- Kohen, Z.; Amram, M.; Dagan, M.; Miranda, T. Self-Efficacy and Problem-Solving Skills in Mathematics: The Effect of Instruction-Based Dynamic versus Static Visualization. Interact. Learn. Environ. 2019, 20. [Google Scholar] [CrossRef]
- Ben-Chaim, D.; Lappan, G.; Houang, R.T. Adolescents’ Ability to Communicate Spatial Information: Analyzing and Effecting Students’ Performance. Educ. Stud. Math. 1989, 20, 121–146. [Google Scholar] [CrossRef]
- Yerushalmy, M.; Nagari-Haddif, G.; Olsher, S. Design of Tasks for Online Assessment That Supports Understanding of Students’ Conceptions. ZDM-Math. Educ. 2017, 49, 701–716. [Google Scholar] [CrossRef]
- Murry, J.W.; Hammons, J.O. Delphi: A Versatile Methodology for Conducting Qualitative Research. Rev. High. Educ. 1995, 18, 423–436. [Google Scholar] [CrossRef]
- Skulmoski, G.J.; Skulmoski, G.J.; Hartman, F.T.; Krahn, J. The Delphi Method for Graduate Research. J. Inf. Technol. Educ. Res. 2007, 6, 1–21. [Google Scholar] [CrossRef]
- Dyson, R.G. Strategic Development and SWOT Analysis at the University of Warwick. Eur. J. Oper. Res. 2004, 152, 631–640. [Google Scholar] [CrossRef]
- Thomas, S.; Chie, T.; Abraham, M.; Raj, S.J.; Beh, L.-S. A Qualitative Review of Literature on Peer Review of Teaching in Higher Education: An Application of the SWOT Framework. Rev. Educ. Res. 2014, 84, 112–159. [Google Scholar] [CrossRef]
- Braun, V.; Clarke, V. Using Thematic Analysis in Psychology. Qual. Res. Psychol. 2006, 3. [Google Scholar] [CrossRef] [Green Version]
- Bakker, A.B.; Schaufeli, W.B.; Leiter, M.P.; Taris, T.W. Work Engagement: An Emerging Concept in Occupational Health Psychology. Work Stress 2008, 22. [Google Scholar] [CrossRef]
- Kaiser, G.; Blum, W.; Ferri, R.B.; Stillman, G. Trends in Teaching and Learning of Mathematical Modelling–Preface. In International Perspectives on the Teaching and Learning of Mathematical Modelling; Springer: Cham, Switzerland, 2011; Volume 1. [Google Scholar]
- English, L.D.; Kirshner, D. Handbook of International Research in Mathematics Education, 3rd ed.; Lawrence Erlbaum: Mahwah, NJ, USA, 2016; ISBN 978-0-41-583204-5. [Google Scholar]
- Schoenfeld, A.H. Toward Professional Development for Teachers Grounded in a Theory of Decision Making. ZDM-Int. J. Math. Educ. 2011, 43, 457–469. [Google Scholar] [CrossRef] [Green Version]
- Burkhardt, H.; Schoenfeld, A. Not Just “Implementation”: The Synergy of Research and Practice in an Engineering Research Approach to Educational Design and Development. ZDM-Math. Educ. 2021, 53, 991–1005. [Google Scholar] [CrossRef]
- English, L.D.; Gainsburg, J. Problem Solving in a 21st-Century Mathematics Curriculum. In Handbook of International Research in Mathematics Educatio; Routledge: Oxford, UK, 2015; pp. 313–335. [Google Scholar]
- Kohen, Z.; Nitzan, O. Excellence in Mathematics in Secondary School and Choosing and Excelling in STEM Professions over Significant Periods in Life. Int. J. Sci. Math. Educ. 2022, 20, 169–191. [Google Scholar] [CrossRef]
- Dierdorp, A.; Bakker, A.; van Maanen, J.A.; Eijkelhof, H.M. Meaningful Statistics in Professional Practices as a Bridge between Mathematics and Science: An Evaluation of a Design Research Project. Int. J. STEM Educ. 2014, 1, 1–15. [Google Scholar] [CrossRef] [Green Version]

| Background Variables | Frequency | % | |
|---|---|---|---|
| Gender | Male | 24 | 19.7% |
| Female | 98 | 80.3% | |
| STEM background | Engineering | 28 | 24.1% |
| STEM | 41 | 35.3% | |
| None | 47 | 40.5% | |
| Level of education | B.A. | 48 | 40.3% |
| M.A. or Ph.D. | 71 | 59.7% | |
| Criteria (by Schoenfeld [3]) | Sub-Criteria (by Schoenfeld [3]) | Examples of Categories Retrieved in This Study | |
|---|---|---|---|
| Experts and Policy-Makers | Teachers | ||
| Resources | Intuitions and informal knowledge regarding the domain | Suitable for high-level students | Suitable for high-level students |
| Facts, rules, and algorithmic procedures | Being precise in sketches | Being precise in sketches | |
| “Routine” non-algorithmic procedures | Suitable as a summary, enrichment, or research question | Suitable as a summary or as enrichment | |
| Heuristics | Appropriate representations | The use of dynamic illustrations | The use of dynamic illustrations |
| Analogies and exploiting-related problems | Using a relevant analogy and a story that will motivate students | Using a relevant analogy and a story that will motivate students | |
| Testing and verification procedures | Using a real scale in building the mathematical problem | Attach a student help page | |
| Criteria | Examples of Categories Retrieved in This Study | |
|---|---|---|
| Experts and Policymakers | Teachers | |
| Strengths | Authenticity and relevancy | Increasing students’ motivation |
| Weaknesses | Convincing teachers that they can use the contextual MM problems | Teachers’ lack of confidence in explaining the related scientific knowledge of the contextual MM problems |
| Opportunities | Teacher training sessions | Teacher training sessions |
| Threats | Availability of teachers to apply the contextual MM problems | Conservative view of the education system and the teachers |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kohen, Z.; Nitzan-Tamar, O. Contextual Mathematical Modelling: Problem-Solving Characterization and Feasibility. Educ. Sci. 2022, 12, 454. https://doi.org/10.3390/educsci12070454
Kohen Z, Nitzan-Tamar O. Contextual Mathematical Modelling: Problem-Solving Characterization and Feasibility. Education Sciences. 2022; 12(7):454. https://doi.org/10.3390/educsci12070454
Chicago/Turabian StyleKohen, Zehavit, and Ortal Nitzan-Tamar. 2022. "Contextual Mathematical Modelling: Problem-Solving Characterization and Feasibility" Education Sciences 12, no. 7: 454. https://doi.org/10.3390/educsci12070454
APA StyleKohen, Z., & Nitzan-Tamar, O. (2022). Contextual Mathematical Modelling: Problem-Solving Characterization and Feasibility. Education Sciences, 12(7), 454. https://doi.org/10.3390/educsci12070454






