Walking through Algebraic Thinking with Theme-Based (Mobile) Math Trails
Abstract
1. Introduction
2. Theoretical Framework
2.1. Task Design in Mathematics Education
2.2. A Didactical Sequence to Develop Algebraic Thinking
2.3. Outdoor Mathematics in a Digital Context
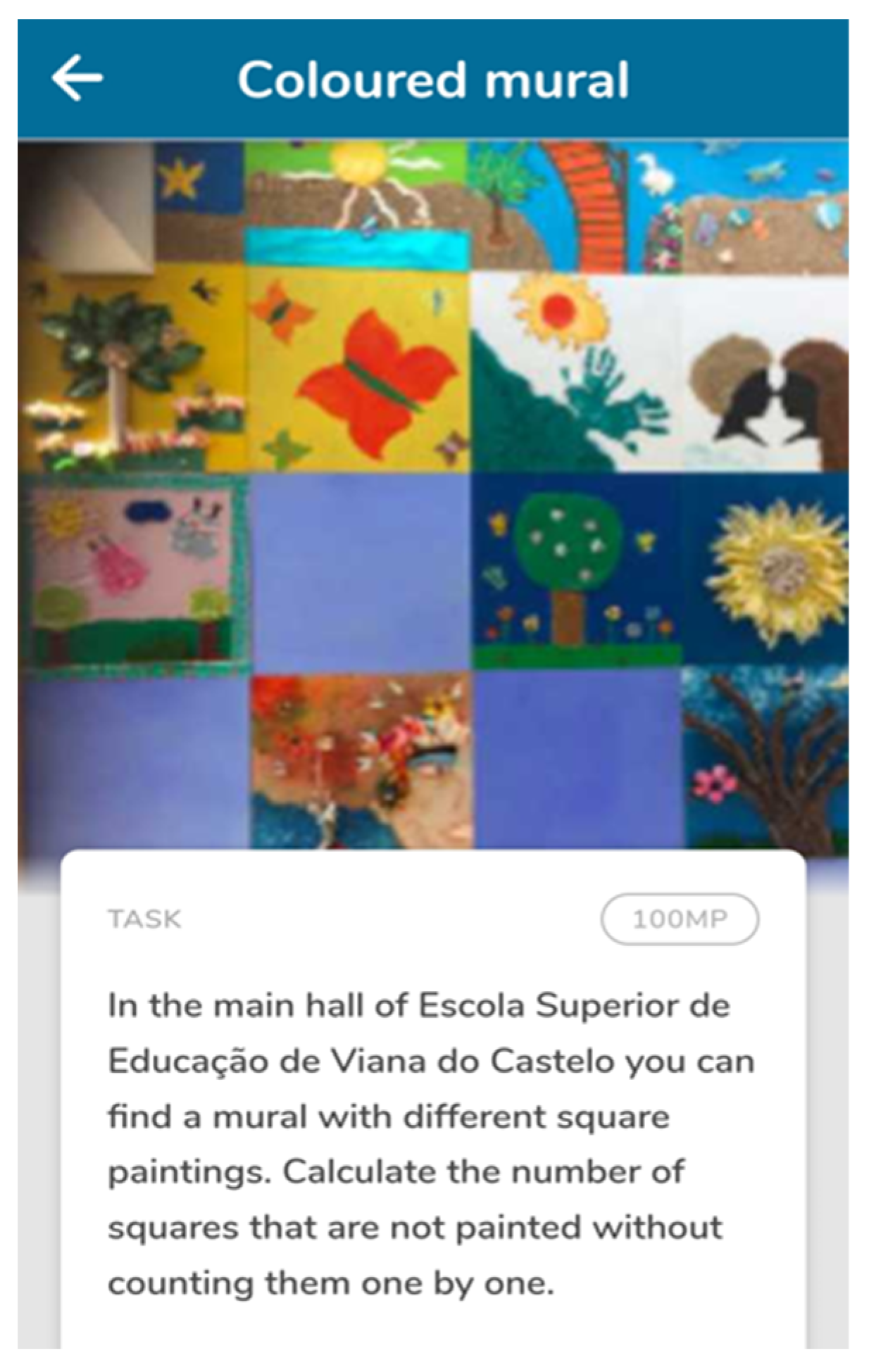
- Uniqueness: “To make clear which object is meant, every task should provide a picture that helps identify the object of the task and what the task is about” [47] (p. 118).
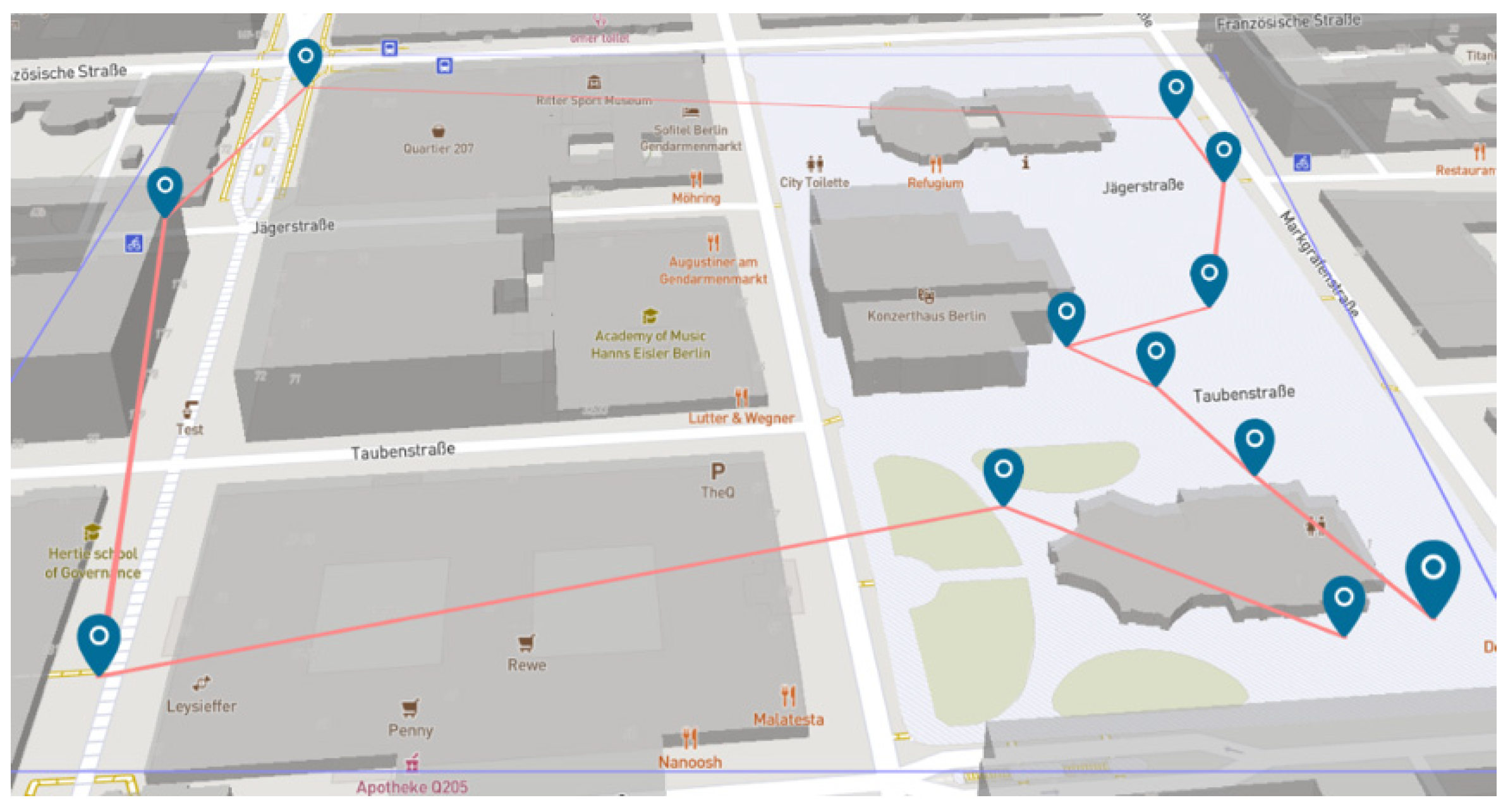
- Attendance: “A task should be authentic, i.e., leaving the educational context and having a certification. Thus, the task can only be solved at the object location and its description should never be enough to solve it” [47] (p. 118).
- Activity: “Physical activity has a positive effect on learning, implying the idea of embodied mathematics, i.e., mathematics can only be fully comprehended through an active experience (Tall, 2013). The task solver should therefore become active and do something in order to solve the task, e.g., measure and count” [47] (p. 118).
3. Method, Context and Participants
4. Results and Discussion
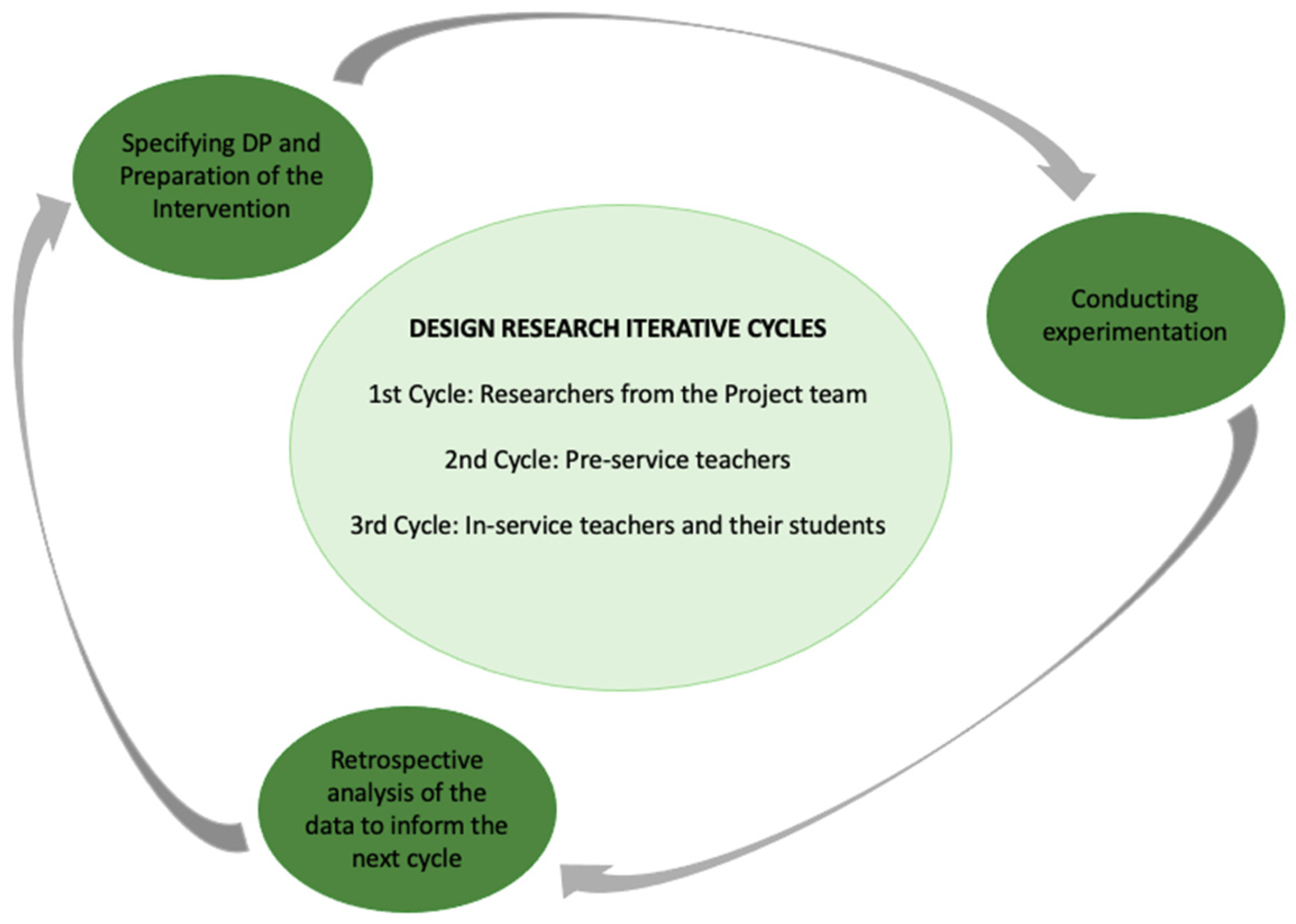
4.1. 1st Cycle
- DP1—Formulate a catalog of generic tasks based on objects/phenomena that might be found in schools or in the surrounding environment, to inspire teachers to more easily adapt the proposals to their educational context [46].
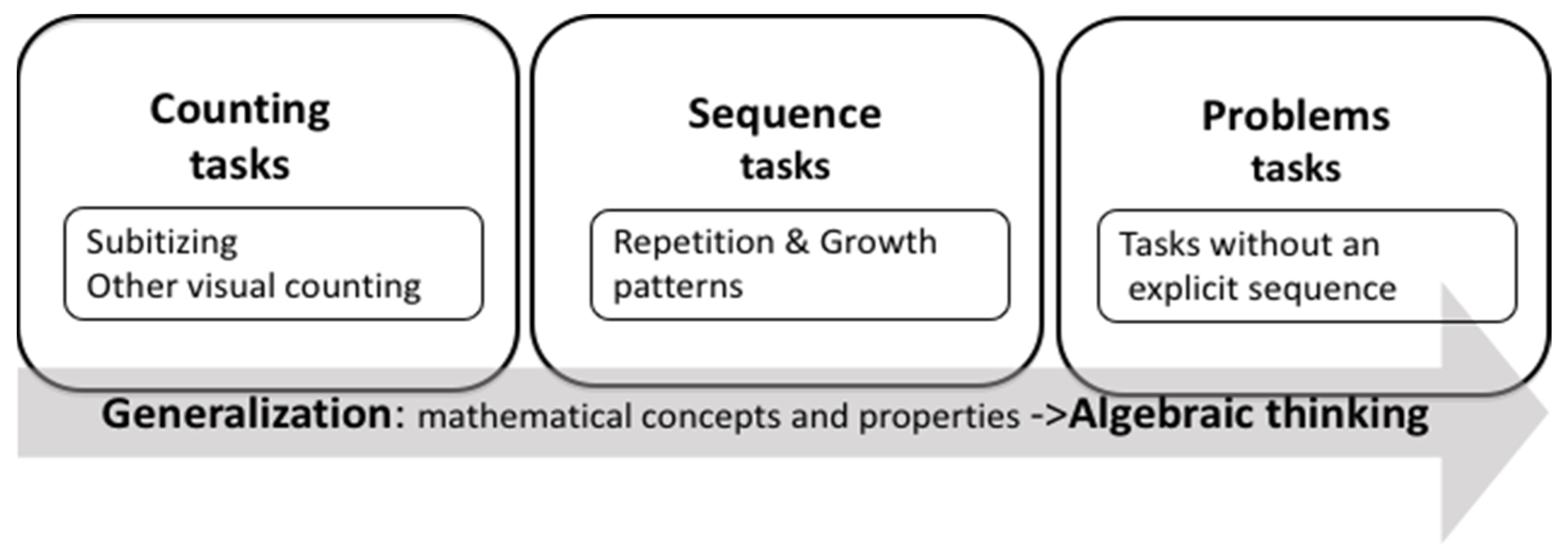
- DP2—In order to develop algebraic thinking in elementary grades, tasks should contemplate the following concepts: counting in visual contexts (subitizing); combinatorial counting; repetition patterns; growth patterns. This learning trajectory is sustained by research and can be considered as a possible pathway to work on generalization [28].
- DP3—Differentiate the tasks’ features in order to diversify the level of cognitive demand [9]. Lower-level and higher-level tasks imply different procedures and reasoning, routine and non-routine approaches, which contribute to a more interconnected mathematical understanding.
- DP4—Formulate the tasks according to the MCM portal features, namely available answer formats and quality criteria [47].
4.2. 2nd Cycle
- DP1—Formulate a set of particular tasks, organized in the form of a math trail, based on specific objects/phenomena that can be found in schools, to inspire teachers to more easily adapt the proposals to their educational context [46].
- DP3—Differentiate the tasks’ features in order to diversify the level of cognitive demand [9]. Lower-level and higher-level tasks imply different procedures and reasoning, routine and non-routine approaches, which contribute to a more interconnected mathematical understanding. Balance the level of challenge of the tasks, introducing more lower-level tasks than higher-level ones.
4.3. 3rd Cycle
- DP1—Formulate a set of particular tasks, in a clear and objective manner, organized in the form of a math trail, based on specific objects/phenomena that can be found in schools, in order to inspire teachers to more easily adapt the proposals to their educational context [46].
- DP3—Differentiate the tasks’ features in order to diversify the level of cognitive demand [9]. Lower-level and higher-level tasks imply different procedures and reasoning, routine and non-routine approaches, which contribute to a more interconnected mathematical understanding. Balance the level of challenge of the tasks, introducing more lower-level tasks than higher-level ones, and establish connections between the main theme and other mathematical themes.
- DP1—Formulate 7–8 particular tasks, in a clear and objective manner, organized in the form of a math trail, based on specific objects/phenomena that can be found in schools, to inspire teachers to more easily adapt the proposals to their educational context [46].
- DP2—In order to develop algebraic thinking in elementary grades, tasks should contemplate the following concepts: counting in visual contexts (subitizing); combinatorial counting; repetition patterns; and growth patterns. This learning trajectory is sustained by research and can be considered as a possible pathway to work on generalization [28].
- DP3—Differentiate the tasks’ features in order to diversify the level of cognitive demand [9]. Lower-level and higher-level tasks imply different procedures and reasoning, routine and non-routine approaches, which contribute to a more interconnected mathematical understanding. Balance the level of challenge of the tasks, introducing more lower-level tasks than higher-level ones, and establish connections between the main theme and other mathematical themes.
- DP4—Formulate the tasks according to the MCM portal conditions, namely the available answer formats and quality criteria [47].
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- NCTM. Principles to Actions: Ensuring Mathematical Success for All; NCTM: Reston, VA, USA, 2014. [Google Scholar]
- Vale, I.; Barbosa, A. Photography: A Resource to Capture Outdoor Math. In Research on Outdoor STEM Education in the digiTal Age. Proceedings of the ROSETA Online Conference, Online, 16–19 June 2020; Ludwig, M., Jablonski, S., Caldeira, A., Moura, A., Eds.; WTM: Münster, Germany, 2020; pp. 179–186. [Google Scholar]
- Kenderov, P.; Rejali, A.; Bartolini Bussi, M.; Pandelieva, V.; Richter, K.; Maschietto, M.; Kadijevich, D.; Taylor, P. Challenges Beyond the Classroom—Sources and Organizational Issues. In Challenging Mathematics In and Beyond the Classroom—New ICMI Study Series 12; Barbeau, E., Taylor, P., Eds.; Springer: Cham, Switzerland, 2009; pp. 53–96. [Google Scholar]
- Zender, J. Mathtrails in der Sekundarstufe I. Der Einsatz von MathCityMap bei Zylinderproblemen in der Neunten Klasse; WTM: Münster, Germany, 2019. [Google Scholar]
- Ludwig, M.; Jablonski, S. Step by Step – Simplifying and Mathematizing the Real World with MathCityMap. Quadrante 2021, 30, 242–268. [Google Scholar]
- Vale, I.; Barbosa, A.; Pimentel, T. Math trails a rich context for problem posing—An experience with pre-service teachers. Quad. Di Ric. Didat. (Mathematics) 2015, 25, 221–227. [Google Scholar]
- Gurjanow, I.; Ludwig, M.; Zender, J. Why do in-service teachers and student teachers use MathCityMap and why don’t—A short survey on acceptance and user behavior of MathCityMap. In Proceedings of the CERME, Dublin, Ireland, 1–5 February 2017. [Google Scholar]
- Doyle, W. Work in Mathematics Classes: The Context of Students’ Thinking During Instruction. Educ. Psychol. 1988, 23, 167–180. [Google Scholar] [CrossRef]
- Smith, M.S.; Stein, M.K. Selecting and Creating Mathematical Tasks: From Research to Practice. Math. Teach. Middle Sch. 1998, 3, 344–350. [Google Scholar] [CrossRef]
- Stein, M.K.; Smith, M.S. Mathematical Tasks as a Framework for Reflection. Math. Teach. Middle Sch. 1998, 3, 268–275. [Google Scholar] [CrossRef]
- Vale, I.; Barbosa, A. Visualization: A pathway to mathematical challenging tasks. In Mathematical Challenges for All; Zazkis, R., Leikin, R., Eds.; Springer International Publishing: Cham, Switzerland, 2022; Volume 10, in press. [Google Scholar]
- NCTM. Principles and Standards for School Mathematics; NCTM: Reston, VA, USA, 2000. [Google Scholar]
- Barbeau, E.J.; Taylor, P.J. Challenging Mathematics In and Beyond the Classroom—New ICMI Study Series 12; Springer: New York, NY, USA, 2009. [Google Scholar]
- Hartmann, L.M.; Schukajlow, S. Interest and emotions while solving real-world problem inside and outside the classroom. In Mathematical Modelling Education in East and West. International Perspectives on the Teaching and Learning of Mathematical Modelling; Leung, F.K.S., Stillman, G., Kaiser, G., Wong, K.L., Eds.; Springer: Cham, Switzerland, 2021; pp. 153–164. [Google Scholar]
- Mullis, I.; Martin, M. TIMSS 2019 Assessment Frameworks; TIMSS & PIRLS International Study Center: Chestnut Hill, MA, USA, 2017. [Google Scholar]
- Ferreira, P.; Buriasco, R. Math Tasks Instructions Based on the Realistic Mathematics Education Perspective. Bolema 2015, 29, 452–472. [Google Scholar] [CrossRef][Green Version]
- Borasi, R. On the nature of problems. Educ. Stud. Math. 1986, 17, 125–141. [Google Scholar] [CrossRef]
- van den Heuvel-Panhuizen, M. The role of contexts in assessment problems in mathematics. Learn. Math. 2005, 25, 2–9. [Google Scholar]
- Silver, E. Fostering creativity through instruction rich in mathematical problem solving and problem posing. ZDM 1997, 3, 75–80. [Google Scholar] [CrossRef]
- Stoyanova, E. Problem posing in mathematics classrooms. In Research in Mathematics Education: A Contemporary Perspective; McIntosh, A., Ellerton, N., Eds.; MASTEC: Perth, Australia, 1998; pp. 164–185. [Google Scholar]
- Baumanns, L.; Rott, B. The process of problem posing: Development of a descriptive phase model of problem posing. Educ. Stud. Math. 2021, 110, 251–269. [Google Scholar] [CrossRef]
- Brown, S.; Walter, M. The Art of Problem Posing; Erlbaum: Mahwah, NJ, USA, 2005. [Google Scholar]
- Vale, I.; Barbosa, A. Outdoor photography: A resource teacher training. In Mathematics Education in the Digital Age (MEDA)—Proceedings; Donevska-Todorova, A., Faggiano, E., Trgalova, J., Lavicza, Z., Weinhandl, R., Clark-Wilson, A., Weigand, H.G., Eds.; Johannes Kepler University: Linz, Austria, 2020; pp. 327–334. [Google Scholar]
- Sullivan, P.; Liburn, P. Good Questions for Math Teaching; Math Solutions Publications: Sausalito, CA, USA, 2002. [Google Scholar]
- Bragg, L.; Nicol, C. Seeing mathematics through a new lens: Using photos in the mathematics classroom. Aust. Math. Teach. 2011, 67, 3–9. [Google Scholar]
- Richardson, K. Designing math trails for the elementary school. Teach. Child. Math. 2004, 11, 8–14. [Google Scholar] [CrossRef]
- Devlin, K. Mathematics: The Science of Patterns; Scientific American Library: New York, NY, USA, 2003. [Google Scholar]
- Vale, I.; Pimentel, T.; Barbosa, A.; Borralho, A.; Barbosa, E.; Cabrita, I.; Fonseca, L. Padrões em Matemática—Uma Proposta Didática no Âmbito do novo Programa Para o Ensino Básico. [Mathematical Patterns—A didactical Propose in the Scope of the Elementary Education Curriculum]; Texto Editores: Lisboa, Portugal, 2011. [Google Scholar]
- Barbosa, A.; Vale, I. Visualization in pattern generalization. J. Eur. Teach. Educ. Netw. 2015, 10, 57–70. [Google Scholar]
- Blanton, M.; Kaput, J. Functional thinking as a route into algebra in the elementary grades. In Early algebraization. A Global Dialogue from Multiple Perspectives; Cai, J., Knuth, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 5–23. [Google Scholar]
- Kieran, C. Overall commentary on early algebraization: Perspectives for research and teaching. In Early algebraization. A Global Dialogue from Multiple Perspectives; Cai, J., Knuth, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 557–577. [Google Scholar]
- Warren, E. Generalising the pattern rule for visual growth patterns: Actions that support 8 year olds’ thinking. Educ. Stud. Math. 2008, 67, 171–185. [Google Scholar] [CrossRef]
- Blanton, M.; Kaput, J. Characterizing a classroom practice that promotes algebraic reasoning. J. Res. Math. Educ. 2005, 36, 412–446. [Google Scholar]
- Rivera, F. Toward a Visually-Oriented School Mathematics Curriculum: Research, Theory, Practice, and Issues; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Blanton, M. Algebra and the Elementary Classroom: Transforming Thinking, Transforming Practice; Heinemann: Portsmouth, NH, USA, 2008. [Google Scholar]
- Arcavi, A. The role of visual representations in the learning of mathematics. Educ. Stud. Math. 2003, 52, 215–241. [Google Scholar] [CrossRef]
- Ball, D.L. Prospective elementary and secondary teachers’ understanding of division. J. Res. Math. Educ. 1990, 21, 132–144. [Google Scholar] [CrossRef]
- Vale, I.; Pimentel, T.; Barbosa, A. The power of seeing in problem solving and creativity: An issue under discussion. In Broadening the Scope of Research on Mathematical Problem Solving: A Focus on Technology, Creativity and Affect; Amado, N., Carreira, S., Jones, K., Eds.; Springer: Cham, Switzerland, 2018; pp. 243–272. [Google Scholar]
- Rivera, F.; Becker, J. Middle school children’s cognitive perceptions of constructive and deconstructive generalizations involving linear figural patterns. ZDM—Int. J. Math. Educ. 2008, 40, 65–82. [Google Scholar]
- Shoaf, M.M.; Pollak, H.O.; Schneider, J. Math Trails; COMAP Incorporated: Bedford, MA, USA, 2004. [Google Scholar]
- Ludwig, M.; Jesberg, J.; Weiß, D. MathCityMap—eine faszinierende Belebung der Idee mathematischer Wanderpfade. Praxis der Mathematik 2013, 53, 14–19. [Google Scholar]
- Cross, R. Developing Math Trails. Math. Teach. 1997, 158, 38–39. [Google Scholar]
- Barbosa, A.; Vale, I. Math trails: Meaningful mathematics outside the classroom with preservice teachers. J. Eur. Teach. Educ. Netw. 2016, 12, 49–63. [Google Scholar]
- Blane, D.C.; Clarke, D. A Mathematics Trail Around the City of Melbourne; Monash University, Monash Mathematics Education Centre: Monash, Australia, 1984. [Google Scholar]
- Buchholtz, N. Mathematische Wanderpfade unter einer didaktischen Perspektive. Math. Didact. 2020, 43, 1–16. [Google Scholar]
- Ludwig, M.; Jablonski, S. MathCityMap-Mit mobilen Mathtrails Mathe draußen entdecken. MNU J. 2020, 1/2020, 29–36. [Google Scholar]
- Jablonski, S.; Ludwig, M.; Zender, J. Task Quality vs. Task Quantity. A dialog-based review system to ensure a certain quality of tasks in the MathCityMap web community. In Proceedings of the Fifth ERME Topic Conference (ETC 5) on Mathematics Education in the Digital Age (MEDA), Copenhagen, Denmark, 5–7 September 2018; Weigand, H.G., Clark-Wilson, A., Donevska-Todorova, A., Faggiano, E., Grønbæk, N., Trgalova, J., Eds.; University of Copenhagen: Copenhagen, Denmark, 2018; pp. 115–122. [Google Scholar]
- Barlovits, S.; Baumann-Wehner, M.; Ludwig, M. Curricular learning with MathCityMap: Creating theme-based math trails. In Mathematics Education in the Digital Age (MEDA)—Proceedings; Donevska-Todorova, A., Faggiano, E., Trgalova, J., Lavicza, Z., Weinhandl, R., Clark-Wilson, A., Weigand, H.G., Eds.; Johannes Kepler University: Linz, Austria, 2020; pp. 143–150. [Google Scholar]
- Erickson, F. Qualitative Methods in Research on Teaching. In Handbook of Research on Teaching; Wittrockk, M., Ed.; MacMillan: New York, NY, USA, 1986; pp. 119–161. [Google Scholar]
- van der Akker, J.; Gravemeijer, K.; McKenney, S.; Nieveen, N. Educational Design Research; Routledge: London, UK, 2006. [Google Scholar]
- Prediger, S.; Gravemeijer, K.; Confrey, J. Design research with a focus on learning processes: An overview on achievements and challenges. ZDM 2015, 47, 877–891. [Google Scholar] [CrossRef]
- McKenney, S.; Reeves, T. Conducting Educational Design Research: What It Is, How We Do It, and Why; Routledge: London, UK, 2012. [Google Scholar]
- Cobb, P.; Jackson, K.; Dunlap, C. Design research: An analysis and critique. In Handbook of International Research in Mathematics Education; English, L.D., Kirshner, D., Eds.; Routledge: London, UK, 2016; pp. 481–503. [Google Scholar]



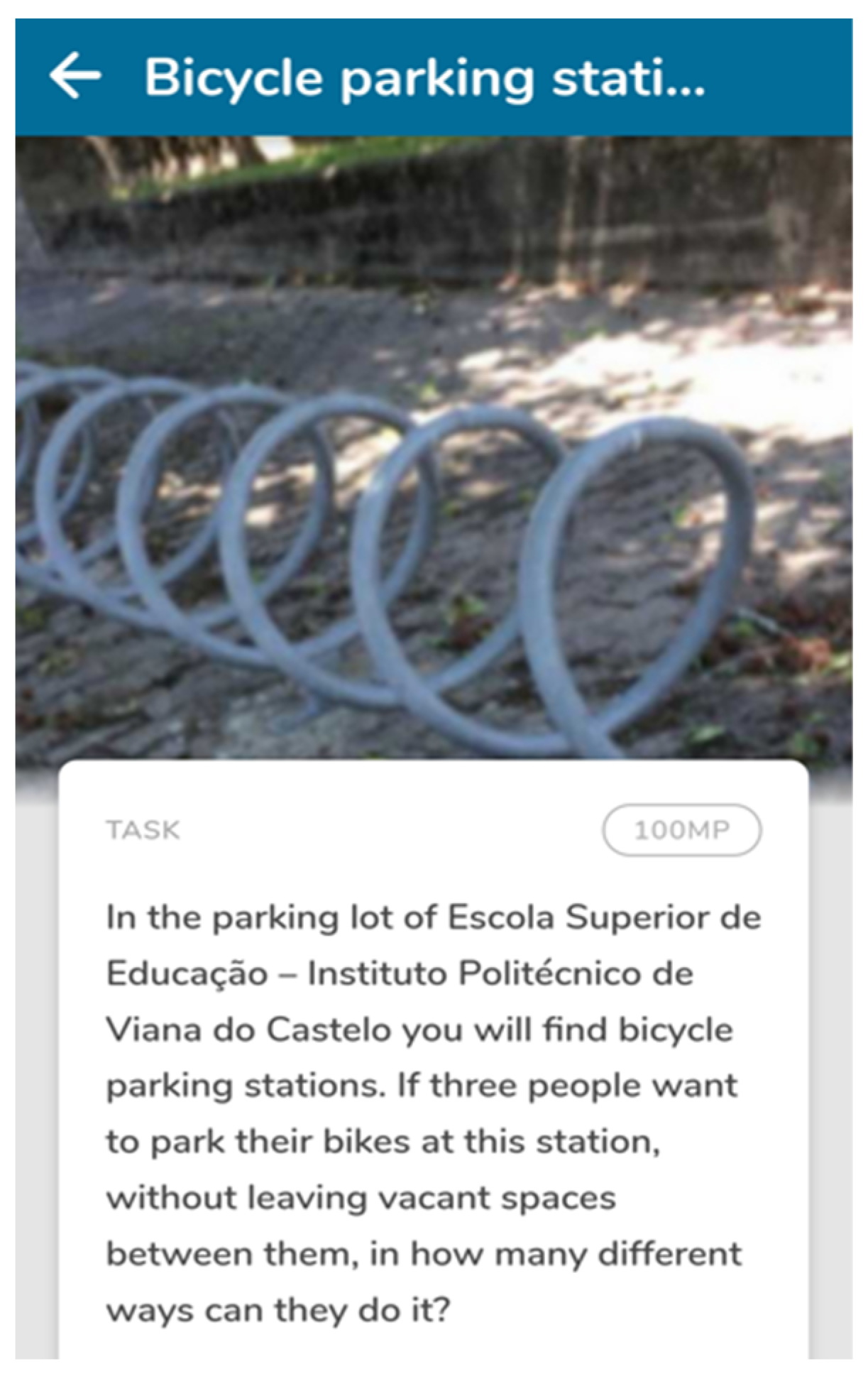

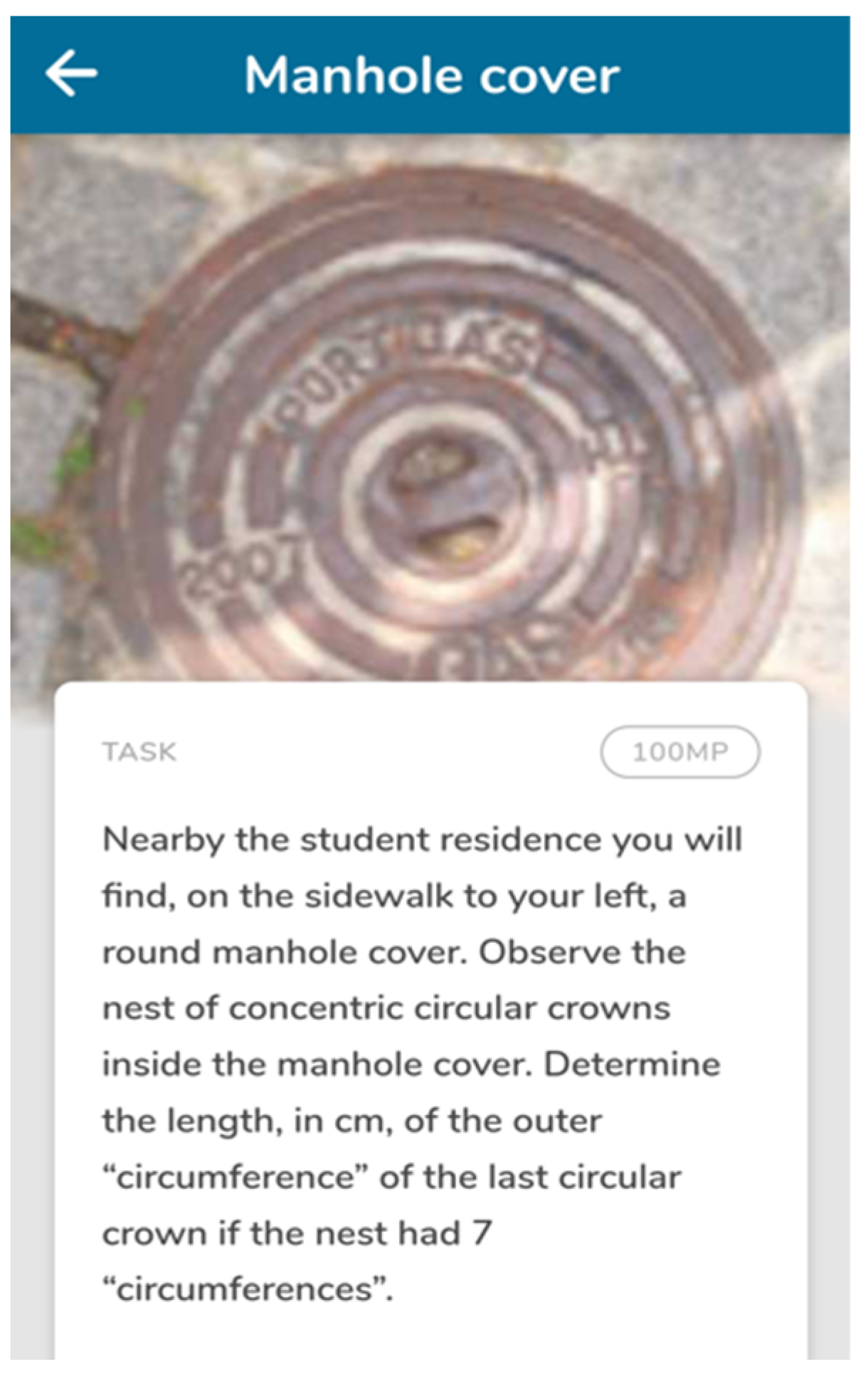


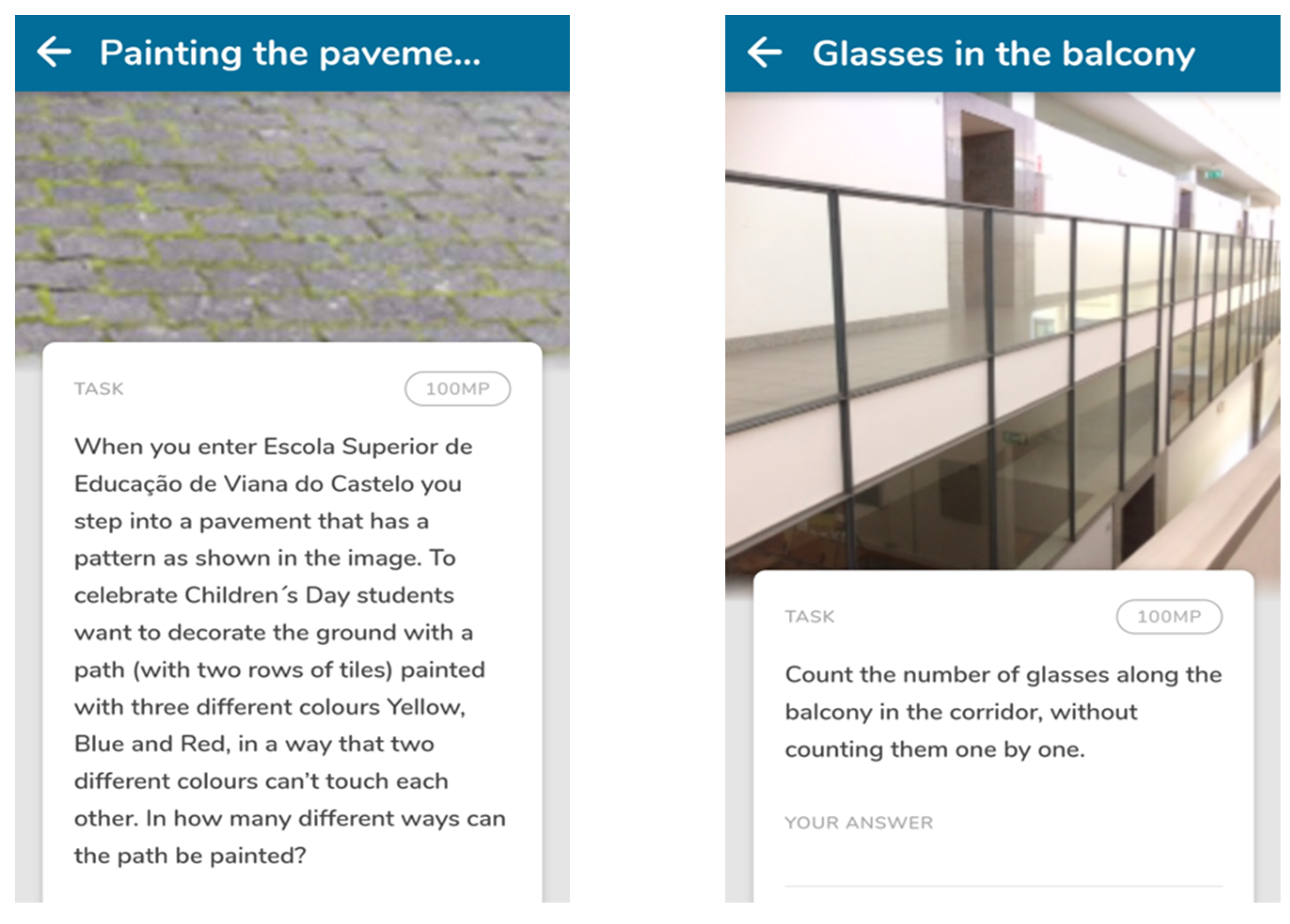
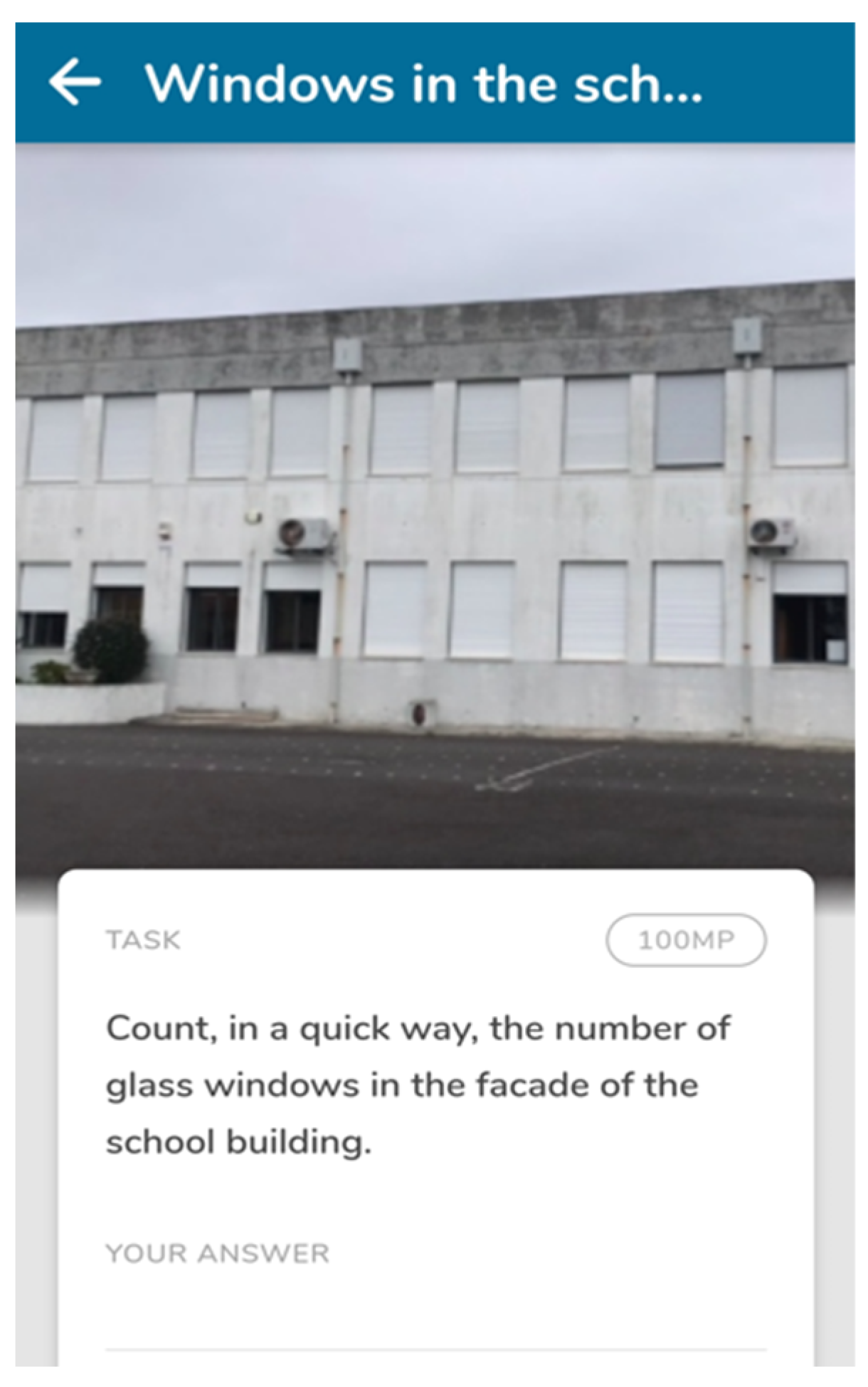

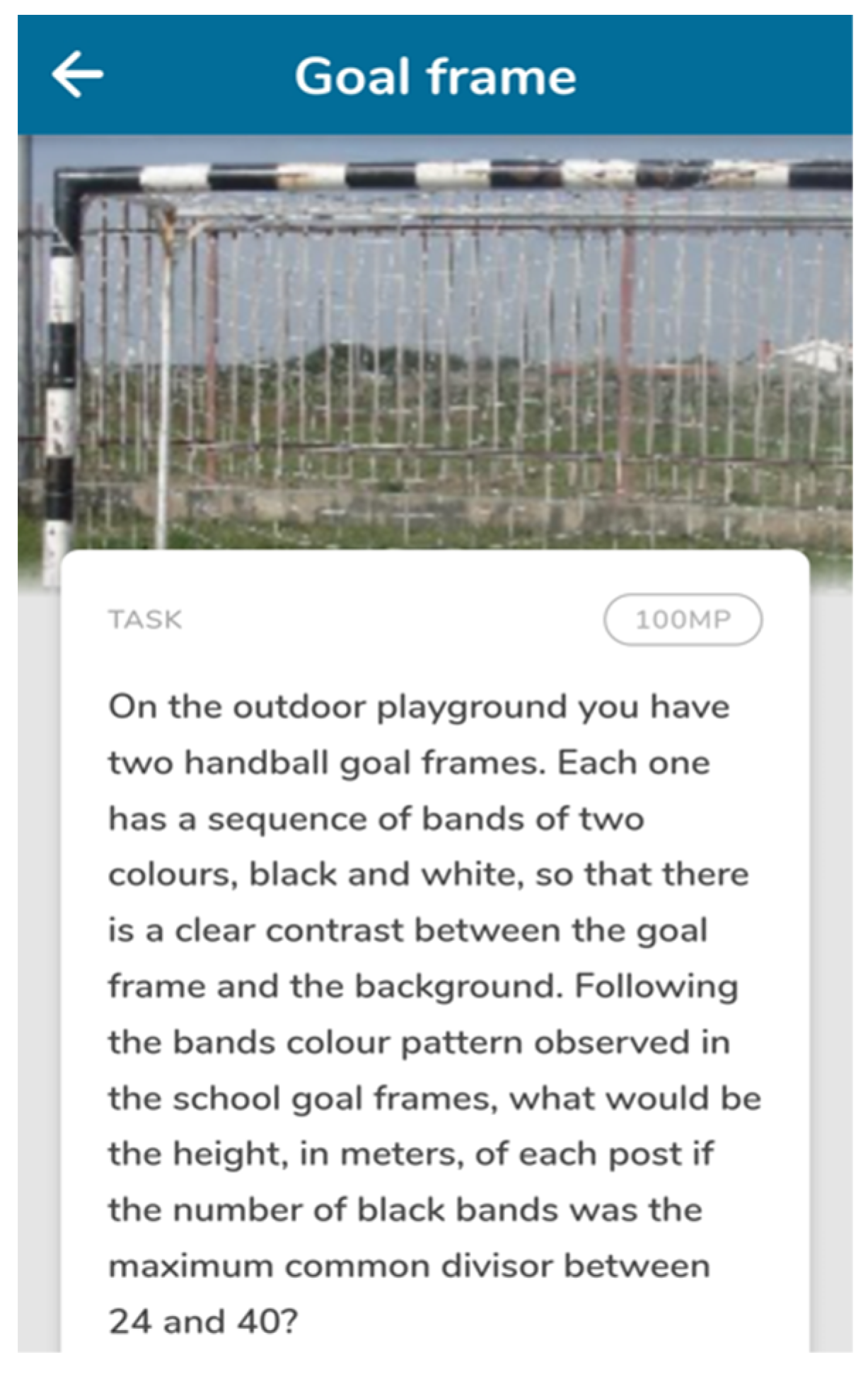
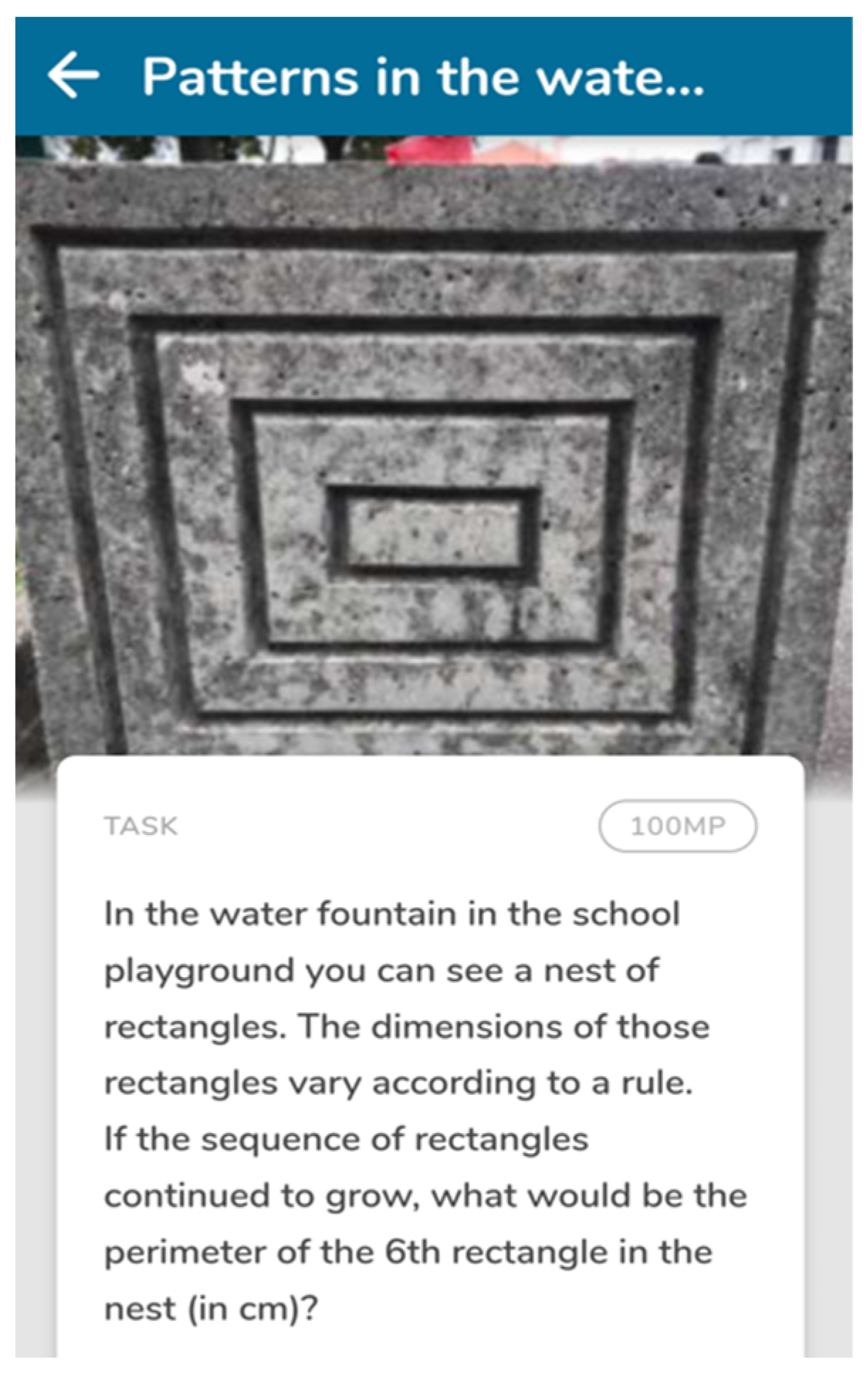


| Lower-Level Demand | Higher-Level Demand |
|---|---|
| (1) Memorization | (3) Procedures with connections |
| Involves the reproduction of previously memorized facts as rules, formulas, facts or definitions. | Focus students’ attention on the use of procedures for the purpose of developing deeper levels of understanding of mathematical concepts and ideas. |
| (2) Procedures without connections | (4) Doing mathematics |
| Involves the use of algorithmic procedures that are evident in the task statement. | Requires complex thinking instead of algorithmic procedures and strategies in solving the tasks. Students have to access relevant knowledge and experiences and make appropriate use of them in working through a task. |
| Knowing | Applying | Reasoning |
|---|---|---|
| Imply the evocation and repetition of knowledge that has already been taught, cover the facts, concepts, and procedures students need to know. | Requires the integration and relationship of diverse mathematical knowledge, based on knowing and framed in non-routine situations, related to familiar settings, focuses on the ability of students to apply knowledge and conceptual understanding to solve problems or answer questions. | Demand reasoning and reflection to achieve the solution and to go beyond the solution of routine problems to encompass unfamiliar situations, complex contexts, and multi-step problems. |
| Answer Format | Description | Use Cases |
|---|---|---|
| Exact value | The exact value is only one number as the correct answer. | It can be used for tasks in which definitely only one correct answer exists, e.g., for counting tasks or for combinatorial problems. |
| Interval | By setting up an interval, teachers define a green branch for “good” solutions and an orange branch for “acceptable” solutions. Everything outside the green and orange branches is validated as “wrong”. | The interval used whenever measurements are necessary, e.g., to determine a length, an area, or a volume. |
| Multiple choice | Available data can be queried within the Multiple Choice format like in a quiz. Thereby, at least two answer options must be given, of which at least one is correct. | The multiple choice answers are open to every situation. It is especially recommended for recognizing mathematical characteristics. |
| Fill-in-the-blanks | Within this format, gap texts can be easily worked on outside the classroom. | The fill-in-the-blanks format is useful to analyze objects outdoors in technical language, to deal with data from information boards or to raise questions on data of historical realities. |
| Set | If several numbers are the expected solution in a task, but the order in which the numbers are to be entered is not important, the set task format can be used. | The set answer format can be used for tasks in which more than one correct answer exists and all of them can be clearly identified. |
| Vector | To raise more than one question on a measuring activity, the task format vector (interval) can be used. Analogously, we offer the vector (exact value) format, which can be used to set several counting tasks or combinatorial problems at once. | The vector can be used to check several measurements. Moreover, the task format can be applied for questions concerning spatial geometry. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barbosa, A.; Vale, I.; Jablonski, S.; Ludwig, M. Walking through Algebraic Thinking with Theme-Based (Mobile) Math Trails. Educ. Sci. 2022, 12, 346. https://doi.org/10.3390/educsci12050346
Barbosa A, Vale I, Jablonski S, Ludwig M. Walking through Algebraic Thinking with Theme-Based (Mobile) Math Trails. Education Sciences. 2022; 12(5):346. https://doi.org/10.3390/educsci12050346
Chicago/Turabian StyleBarbosa, Ana, Isabel Vale, Simone Jablonski, and Matthias Ludwig. 2022. "Walking through Algebraic Thinking with Theme-Based (Mobile) Math Trails" Education Sciences 12, no. 5: 346. https://doi.org/10.3390/educsci12050346
APA StyleBarbosa, A., Vale, I., Jablonski, S., & Ludwig, M. (2022). Walking through Algebraic Thinking with Theme-Based (Mobile) Math Trails. Education Sciences, 12(5), 346. https://doi.org/10.3390/educsci12050346






