1. Introduction
Project-Based Instruction (PBI) is more prevalent in science classrooms, focusing on real-world tasks as a vehicle for learning. Students’ investigations are organized around a driving question, which is authentic and encompasses substantial content. Project-based Instruction (PBI) advocates a student-centered and experiential approach that supports “deeper learning” based on students’ interests and real-world problems [
1,
2,
3,
4,
5]. Benefits for students learning through the PBI approach were clearly spelled out in the literature: enhancing students’ motivation, conceptual knowledge, and problem-solving skills [
1,
6,
7,
8], which are well-aligned with the goals of the Common Core State Standards and the Next Generation Science Standards in the U.S.
A student learning through PBI is driven by challenging, complex, and open-ended problems that are embedded in real-world situations. Unlike traditional problem-solving, as not all the information is given, designing scaffolding questions for the PBI lessons is essential for students to engage in the “authentic practice” but “reducing the complexity of the practices, while retaining their key elements” [
9] (p. 336). A problem-solving approach can be served as a strategy for scaffolding while completing a targeted project.
While studies report the benefits of PBI instructions for students’ STEM learning, there is a lack of consensus on the PBI concept, defining features, and what and how to be presented in a classroom [
1]. Some studies suggested that the design principles need to be adapted to their local context, and thus, teacher adaptation of the curriculum is essential [
1,
10]. There is a need to study how teachers interpret and adapt the PBI design principles. Most studies focus on teachers’ cognition or behavior relevant to teaching, but there is a lack of studies on how pre-service teachers design and implement PBI in their classroom, particularly in mathematics.
This case study attempted to explore how pre-service secondary mathematics teachers designed and implemented project-based instruction with mathematics problem-solving. The underlying questions were how the project-based instruction could be designed and implemented with mathematics problem-solving by pre-service teachers and how the teachers guided problem-solving process toward the project’s goals. In the following sections, the author discusses the common features of the research-based PBI that guided the pre-service teachers’ lesson and the problem-solving process in this study and presents the results from the analysis of the pre-service teachers (PSTs)’ intended and enacted lessons.
2. Project-Based Instruction (PBI) Design Principles and Problem-Solving Process for Scaffolding
Studies suggested that PBI design principles should address both content and assessment, should be measurable, and should investigate adaptation [
1,
2,
10,
11]. The literature identified key design principles such as (1) defining learning appropriate goals that lead to deep understanding; (2) providing scaffoldings such as “embedded teaching”, “teaching tools”, and beginning with problem-based learning activities before initiating projects; (3) ensuring multiple opportunities for formative self-assessment and revision; and (4) developing social structures that promote participation and a sense of agency [
11] (p. 1).
The essential elements of PBI may vary, but there were substantial overlaps among several of those elements. As a framework for interpreting the PSTs’ lessons, this study identified well-defined and research-based components of PBI [
1,
11]:
driving question, learner product, assessment, tools, collaboration, and scaffolding. The driving question is a guiding question for the project that connects activities and underlying concepts in authentic open-ended, real-world problems.
A learner product is a project outcome that can be tangible and applicable in real-world settings.
The investigation is a project component that aims to lead students’ authentic practice with a complex inquiry. Ongoing formative
assessments while reflecting the PBI principles are encouraged.
Tools such as technologies or cognitive tools can help students to understand the complex problems and concepts. PBI encourages students to create their learning communities and
collaborative activities. By creating project outcomes and products in collaborative activities, students can play a role as active learners. Lastly,
scaffolding is one of the key features of PBI. Given students’ prior knowledge and background, teachers can provide them with simulated constraints of problems to help unstuck any blockages along the way to complete students’ projects.
For the PSTs’ lesson plans and analysis framework for this study, the author utilized problem-solving heuristics [
12,
13]. Problems, defined as “a situation that requires a decision and/or answer, no matter the solution is readily available or not” [
12] (pp. 3–4). Fan and Zhu (2004) [
12] classified problems: routine versus non-routine, traditional versus non-traditional, open-ended versus closed-ended, application versus non-application, single-step versus multi-step, sufficient data, extraneous data, and insufficient data, and pure mathematical form, verbal form, visual form, and combined form.
The problem-solving processes are divided into the stages of understanding the problem, devising a plan, carrying out the plan and looking back [
12,
13,
14] as follows:
- [PS1]
Understanding the problem: rephrase it in the students’ own words.
- [PS2]
Devising a plan: Making a general plan, select relevant methods (heuristics); describe assumptions and plan future calculations.
- [PS3]
Carrying out the plan: perform calculations and manipulations.
- [PS4]
Looking back: check results, reflecting on key ideas and processes of problem solutions, generalizing or extending the methods or results.
Table 1 provides descriptions of problem-solving heuristics by Fan & Zhu [
12].
The theoretical foundations of PBI and problem-solving process with heuristics guided the PSTs’ PBI lesson design for supporting students’ learning mathematics. As described in the PBI features, a project lesson starts with a driving question grounded in real-world contexts for students to engage, explore, and learn through mathematical problem-solving activities. The lessons target learning goals so that students can master the content and problem-solving skills while creating a tangible outcome situated in the real world at the end of the lessons. Students are to engage in problem-solving activities by exploring and exercising the various heuristics (e.g., understanding the problem, checking assumptions, developing and using models, engaging in the investigation, finding mathematics, explaining the results, and checking the results and approach), and the lessons aim to connect those activities to an everyday life situation. Teachers can plan and conduct a frequent formative assessment by engaging in group discussions and activities to reflect the design principles.
3. Method
This study was conducted using a design-based research methodology [
16]. All design research methods are characterized by iterative design and formative research in real-world settings concerning the following aspects: (1) collaboration between practitioners and researchers, (2) implementation of theories for testing or developing and refining of theories, (3) the possibility of contributing to the growth of educational reform. The author, as a researcher, collaborated with the pre-service teachers in developing and implementing the PBI lessons by providing the design principle of the PBI lessons and the feedback. However, the pre-service teachers played their role as designers and practitioners and the researcher supported them. This case study focused on two pre-service mathematics teachers’ who intended and enacted the PBI lessons with problem-solving activities. Case study research is well suited to addressing the critical problems of practice (e.g., implementing project-based mathematics in secondary schools) and extending the knowledge base of various aspects of education [
17]. Case study consists of a detailed investigation, often with empirical material collected over a period from a well-defined case to analyze the context and processes involved in the phenomenon [
18]. The unit of analysis is defined by what the case is [
18]. In this study, the case was the pre-service teachers’ who intended and enacted the PBI mathematics lessons with problem-solving. The individual case was selected based on convenience as it was expedient for data collection purposes [
19].
3.1. Participants and Research Setting
Jesse and Conan were STEM (Science, Technology, Engineering, and Mathematics) pre-service teachers (PST)s who enrolled in a Project-Based Instruction class, a required method course for STEM pre-service teachers. Jesse was majoring in mathematics, whereas Conan was an aerospace engineering major. Both enrolled in STEM education dual-degree programs. The PSTs designed and implemented their PBI lessons as a team. The focus of this study is not on individual teachers’ behavior but the design of the team lesson and its implementation. Those two PSTs were chosen as part of this study since their lessons were based on mathematics problem-solving with PBI. Given the guiding principles of PBI, the participating pre-service teachers developed project-based units as part of the course requirements. The project-based lesson units were developed over a month, and the participants implemented the instruction for a five-day lesson in high school classrooms as apprentice teachers. Students were asked to present their project product after the five-day lesson.
3.2. Data Collection and Analysis
Data sources for this study were lesson plans with relevant handouts and video-recorded classroom observations. Participants’ modeling lesson units served as artefacts for examining how closely their planning linked to the ideas represented in the frameworks and their experiences in the PBI class. Observation field notes provided detailed descriptions of activities and the pre-service teachers’ engagement and participation patterns. The study used content analysis, and the author created a coding scheme based on the PBI design principle and problem-solving heuristics to code components in each lesson unit. Out of five lessons and 260 minutes of video-recordings, the inter-rater agreement was 83%.
The video coding scheme was modified from the one developed by Ho and Hedberg (2005) [
20] to look for the main pedagogical features of classroom practices with PBI and problem-solving using the Grounded Theory approach [
18]. For the analysis of video-recordings, a coding scheme divided each lesson into phases comprising
problem-solving activities, teaching skills and concepts, group activities, assessment, driving questions, and other events. The
problem-solving phase happens when the teacher presents a problem to teach problem-solving. It usually involves teacher’s explication or teacher-initiated question-and-answer. This phase is further broken into Polya (1973)’s [
13] four stages of problem-solving: understanding, devising a plan, carrying out the plan, and reflecting.
Teaching skills and concepts means that the teacher uses an example of closed-end problems to teach specific skills such as arithmetic or algebraic manipulation, use of mathematical formulas, handling data, etc.
Teaching skills and concepts is to be distinguished from the problem-solving phase (carrying out the plan), where skills are used to solve a problem. For teaching of concepts, instruction time is spent showing, demonstrating, defining, and explaining a numerical, geometrical, and algebraic concept.
Group work occurs when groups of students are given tasks to do as a group. Teachers sometimes help students during the group work by answering students’ questions.
Driving questions means when teachers introduce the questions and engage in discussions by elaborating the questions. Coders differentiated it from the problem-solving phase (understanding the problem). The purpose of coding these two phases is to examine what extent the PSTs engage in and focus on driving questions as a key component of PBI. The phrase of
Other events indicates a catch-all category to include all other events not listed in the categories.
3.3. PBI Lesson: Mission on Mars
The participating PSTs (Jesse and Conan) designed the five-day-long lesson plans (see
Figure 1 for the overview) based on the PBI design principles. The primary content state standards covered by the lesson were:
Apply geometric methods to solve design problems (e.g., designing an object or structure to satisfy physical constraints).
Understand and evaluate the inverse trigonometric function of a tangent.
Understand the inverse trigonometric function of tangent ratios using the adjacent and opposite sides.
The big idea of these standards is for students to be able to solve a triangle with missing sides or missing angles. Both trigonometric ratios and the Pythagorean Theorem provide students with the tools needed to solve a right triangle given different forms of information.
4. Results
As seen in the Day 1 lesson (see
Figure 1), the driving question for the project was explicitly stated along with the project goals in the overview. On the first day of the lesson, the PSTs introduced the driving question in class,
“How can we determine the most efficient path for a Mars Rover?” After showing a short video clip on a Mars Rover, the PSTs provided students with the project overview. Jesse asked students, “What do we need to know?”, “Mars, the rover, path, anything else?”, “What does ‘efficient’ mean?” “What elements should you think about when considering efficiency?” A few relevant questions were posed: however, instead of extending their discussions by unpacking those questions, the PSTs gave students the project goals to answer the driving question (see
Figure 1). Each lesson unit aimed to focus on each stage of problem-solving. Throughout the lesson, the PSTs used the strategies of solving a simplified problem and visual representation in the “planning for solution” stage (See
Figure 2).
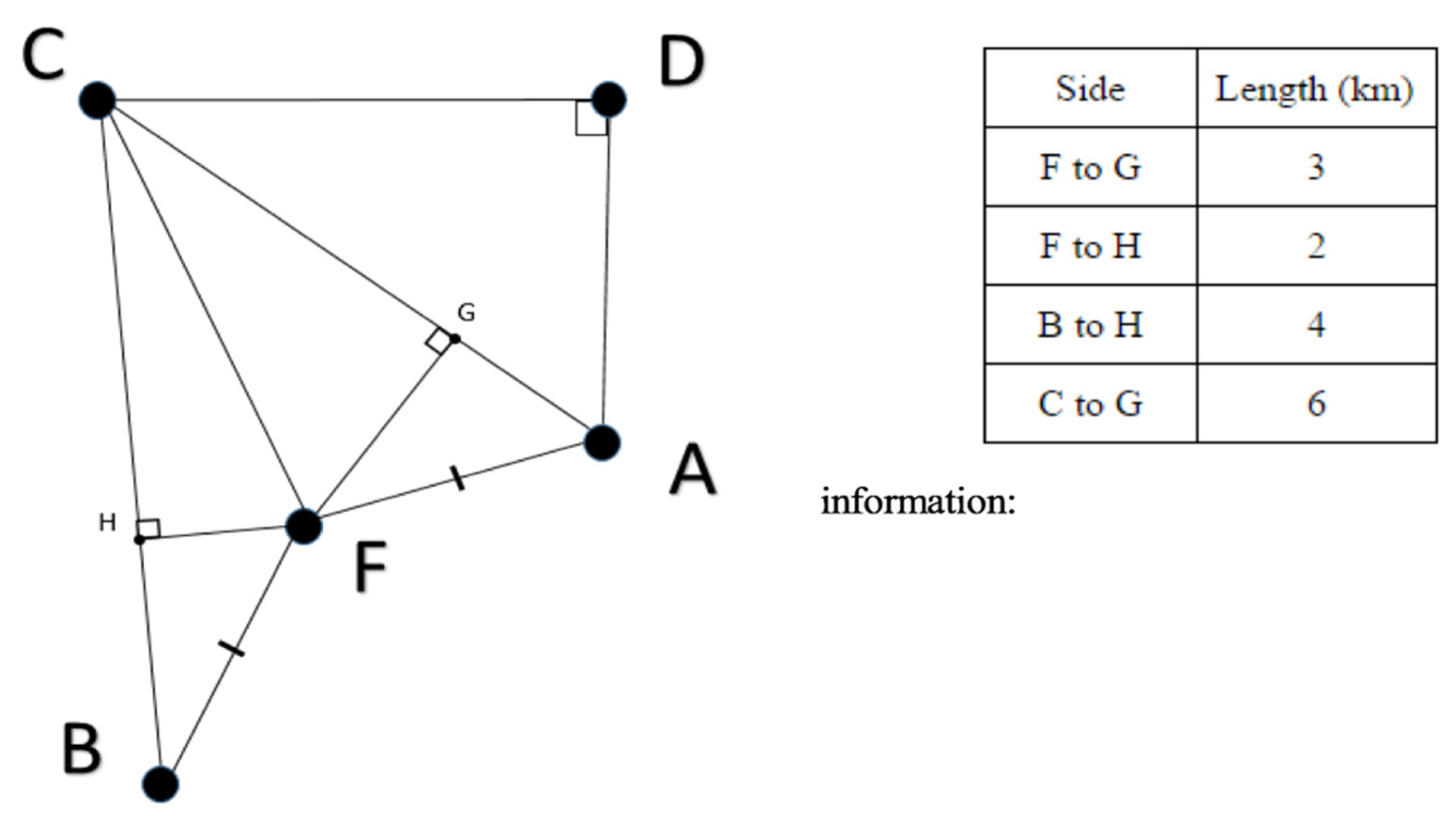
Students were asked to fill out missing components in the provided tables below (see
Table 2 and
Table 3) based on Diagram 2 (See
Figure 2).
In
Figure 2 and
Figure 3, the PSTs simplified diagram 1 and translated it into geometrical tasks using diagrams and tables.
Table 1 indicated
simplifying problems by ‘changing the complex numbers or situations in the problem into simpler ones without altering the problem mathematically’. With the tasks, scaffolding questions were listed to guide students toward meeting their project goals: How do we find the angles CBA, ACB, ACD? Is there more than one way to solve for these angles? Which method/equation is best for solving each angle? Do we have enough information to solve? This set of metacognitive questions was intended for students to evaluate methods to solve the problems. Subsequently, in the same tasks, the following sub-questions were asked: To determine the path, Where do we begin, and where do we end? Is there only one path? How many paths could you take? How do you find the angle you need to turn each time? How do you know how efficient your path is? The last four questions were related to assumptions for the problem so that students could plan for problem-solving. Going back to the driving questions, the PSTs presented determining factors and facts for students’ engagement while aiming to reach the project goal by structuring and simplifying the problem. The questions utilized all the heuristics listed in
Table 1. As students struggled with finding essential information on their own, the PSTs provided students with relevant facts on the rover: for example, the rover takes 12 J to go 5 km, (124 J per full charge, 52 km going 6.5 km/h), the rover must shut down and stay charged for six consecutive hours for the full charge (the rover is solar-powered).
Table 4 illustrates how the lesson components were connected with the PBI features and relevant problem-solving activities to those components. The overall lesson was designed based on PBI principles, and each lesson contained problem-solving activities based on the stages of problem-solving ([PS1]–[PS4]).
The driving questions lead to accomplishing an overarching goal of the project in real-world contexts and connecting underlying concepts to subject matter. This requires the first step for the lessons to determine targeting content standards within a big idea of the real-world problem setting. The PBI lesson was then unpacked with the content standards to design a sequence of the lessons by setting manageable goals. Parallel to the driving question feature, Lesson 1 focused on having students “understand a problem” using various means such as rephrasing, drawing diagrams, and underscoring keywords in the problem.
According to the overarching goal, the lessons move to the stage of [PS2] Devising a plan: Making a general plan, selecting suitable methods (heuristics); describing assumptions, and planning future calculations; each lesson unit was designed to target the subgoals using appropriate problem-solving heuristics. Both intended and enacted lessons lead learners to consider the assumptions through scaffolding questions, which is part of the investigation to tackle the complex problems. A sequence of questions was posed to assess learners to see if they meet the subgoals that can allow them to reach the project goal. Anticipating students’ cognitive blockages, lesson units asked students to work on necessary calculations [PS3]. Each lesson unit consists of constrained problems and serves as scaffolding questions [e.g.,
Figure 2 and
Figure 3]. For Day 4, the lesson unit revisited the driving question, the assumptions to be considered, and the relevant information for the students to reach the project goal. This is related to the last stage of problem-solving [PS4] Looking back: check results, reflecting on key ideas and processes of problem solutions, generalizing or extending the methods or results. In each stage of problem-solving, a wide range of heuristics was observed in each lesson. The problem-solving heuristics utilized in each lesson are summarized in
Table 5.
As
Table 5 indicates, the PSTs predominantly used Draw a Diagram/Model, Making suppositions, Simplifying, Restating the problem in another way, and Solving sub-problems heuristics. The heuristics were employed during the whole class instruction time when the PSTs addressed and discussed the project driving question. Those strategies were prevalent in both written and enacted lessons. At times, such as when the PSTs introduced the driving question, engaged in the clinometer outdoor activity, and explained the model of how a Mars Rover turned around the corner, the PSTs demonstrated using the “Act it out” strategy. For example, Jesse pretended to be a Mars Rover, turned around a corner physically, and demonstrated how to measure the exterior angle of a triangle in class. At the beginning and the end of the five-day lesson, the PSTs revisited the driving question and underscored the assumptions and relevant information while using the “Making a systemic list” strategy in both the written and the enacted lessons. During the “teaching skills and concepts” activities, the PSTs used closed routine problems that students may be familiar with so that they can help students’ understanding of relevant mathematical concepts. The five-day lessons were recorded over the two weeks. The following
Table 6 summarizes the time the PSTs spent on each phase.
Focusing on the problem-solving phase, the proportion of time the teachers spent giving instructions via Pólya’s four stages of problem-solving was about 6%. Unlike intended lesson units that were designed based on each stage of problem-solving, instruction time for engaging in problem-solving activities with the whole class was relatively limited. The main focus of the whole class lessons was not on problem-solving per se (in Pólya’s sense). On the other hand, lesson units were intended for students to engage in problem-solving activities. The PSTs spent relatively more time engaging in the driving question than other activities in Lesson 1 and spent some time revisiting it in the last lesson unit. As described in coding procedures, the category of driving questions was distinguished from the phase of problem-solving activities. Based on the proportion of time for giving instructions on problem-solving, the teachers seemed to approach it through group work with assigned worksheets. About half of the total instructional time was spent on group activities. Teachers also spent about 30% of their time teaching concepts and skills needed to solve the problems.
5. Discussion and Conclusions
The key elements of PBI that the two PSTs implemented were consistent with what other studies identified [
8,
11]. For example, the driving question was an authentic, real-world problem that connects math problem-solving activities and underlying mathematical concepts [
11]. The learner outcome requires culminating product and represents a response to the driving question [
8]. Students primarily engaged in collaborative group activity and prepared for the final presentation as a group. Each lesson unit and the worksheets served as scaffolding problem-solving activities and benchmarks toward completing the project.
The PSTs mentioned that “doing with understanding” is essential [
11] (p. 272). The PSTs spent substantial instructional time teaching mathematics concepts and skills. For that, they adopted closed-ended questions from a textbook for the whole-classroom instruction: however, as the nature of driving question was somewhat open-ended and required multiple steps, it facilitated teacher-student discussions on problem-solving processes and strategies. The PSTs emphasized and revisited the driving question in their intended lessons and enacted lessons so that students could elaborate, explore and answer the question throughout the project, which was identified as a critical element in the literature [
8,
11].
Throughout the PBI lessons, the wide range of problem-solving heuristics that the teachers employed was highlighted in this study. The author, as a researcher, did not provide any feedback on the PST’s choices of problem-solving heuristics in the lesson design process. However, as the current study indicated, it is plausible that the PBI design principles allowed the PSTs to use a wide range of heuristics in their intended lessons and spend ample instruction time for group activity compared to direct instruction.
This study explored how pre-service teachers can plan and enact project-based instruction (PBI) in mathematics with problem-solving strategies: it provides example lessons designed with PBI principles and problem-solving heuristics. Such PBI can be served as a Choice-Based Pedagogy (CBP) [
21,
22] in an open-ended mathematics problem situation, as illustrated in this study. Students have choices to extend their collaboration and mode of interaction and become agents who explore various problem-solving activities while engaging in challenging and complex problems. It often appears that cognitive blockages can impede engaging students in such complex and challenging problem-solving; as a result, students may not continue their efforts to persevere along the way to solve problems. The study has demonstrated how PBI can be designed with mathematics problem-solving activities so that students can persevere and engage in the tasks, allowing teachers to exercise various problem-solving heuristics.
As studies explained that productive struggle could be manifested as problem-solving actions, problem-solving could therefore be a means for students to actively engage in productive struggle and perseverance, primarily through exercising heuristics toward a mathematical goal [
14,
23]. The complexity and openness of mathematical problem tasks can contribute to whether students engage in deeper learning or persevere toward the learning goal. In the PSTs’ lessons for this study, they provided multiple-entry points that students may be familiar with, but still retained the complex structure as a whole to accomplish the project goal. Students may be unable to engage in such an ill-structured problem without the scaffolding questions. Especially, the scaffolding questions with various problem-solving heuristics might have assisted students in sustaining their efforts while engaging in a productive struggle of mathematical thinking. Supporting such activity with scaffolding is well documented in the literature, but in order to maintain the integrity of a task’s perseverance requirements, a scaffold must “[simplify] the task so that it could be solved while maintaining task complexity” [
24] (p. 467). Given the argument, planning scaffolding questions with problem-solving under the overarching project goal with a driving question seems to be a fitting approach, as shown by the findings of this study. The scaffolding can assist students in connecting their prior knowledge to the tasks embedded in complex problems by offering procedures to follow and reducing the level of cognitive demand of the tasks.
Research suggested that students seldom apply general heuristics in unfamiliar situations [
21,
22]. This study highlights the PST’s PBI mathematics scaffolding lessons with problem-solving heuristics. The teachers could sustain the efforts to keep students engaged in problem-solving amid challenges and persevere toward reaching goals. On the other hand, the PBI can be used as a platform for expanding students’ choices while engaging in open-ended problems.
This study focused on the pre-service teachers’ lessons, and future study can further examine how students respond to those lessons by engaging in problem-solving activities. The findings of this study are limited to lessons designed and enacted by one pair of the PSTs, a case selected based on convenience. The literature suggested that teachers’ task design and its implementation could be affected by teachers’ views and belief systems, but that was not within the scope this study. Accordingly, cases with the PSTs’ views and how the findings may be altered could be further examined. The current study did not investigate the discourses between students and the teachers during group activities, but that could inform how and to what extent teachers guided students using problem-solving heuristics in the groups. The PSTs introduced the project driving question without engaging in extensive discussions in class. They gave the relevant information in worksheets (see
Table 4, e.g., the rover’s joules and how much time it will take to complete). To what extent students would engage in the tasks without those constraints could be an open question. The length of the PBI lesson was only about a week; thus, the time constraint was one of the barriers that the PSTs identified. Providing extended periods such as a month or a semester-long duration with benchmark lesson units along the way to complete the project may give the PSTs more time and opportunities to engage in problem-solving activities during a whole-group instruction.