Abstract
Pregraduate students often have low success expectations toward their thermodynamics courses, which are often considered too abstract and remarkably difficult to understand. For this reason, they may not even try to reach any level of comprehension while settling for reproducing mathematical calculations and memorizing definitions to pass the exams. Traditional lectures on thermodynamics, focusing on mathematical deductions while neglecting the qualitative characterization of the concepts behind the equations, do not help in this respect. Aiming at a change in the teaching practice and focused on the second law of thermodynamics, the main goals of this work are to characterize the way of reasoning of the expert; to present a review on the most important learning difficulties encountered by students and categorize them into three groups: the disregard of qualitative understanding, the inherent conceptual difficulties, and those related to the students’ previous knowledge; and to propose some suitable teaching practices to assist instructors in this difficult but rewarding task.
1. Introduction
The second law of thermodynamics (SLT) limits the direction of natural processes, which are only possible in the direction in which the entropy of the universe increases. This law applies to any process and explains in a remarkably simple way how the universe works. Reference [1] remarked its importance in his famous quote: “the law that entropy always increases holds, I think, the supreme position among the laws of Nature. […] if your theory is found to be against the Second Law of Thermodynamics I can give you no hope; there is nothing for it to collapse in deepest humiliation”. Both the SLT and the concept of entropy are key to the academic formation of university students in diverse science and engineering fields.
Moreover, thermodynamics students often approach this discipline with low success expectations [2]. Given that perceptions of difficulty are central to the classroom [3] and keeping in mind that thermodynamics is often programmed in the first or second year of university studies, we consider that offering effective learning experiences to seek academic success is highly advisable and will probably reduce the dropout rate.
Although a discussion on the teaching and learning of the SLT may not seem innovative in today’s context on education research, the reality is that still nowadays, this is an unresolved problem in the classroom. Very often, the true comprehension of thermodynamic concepts is not the highest priority; hence, the evaluation is limited to the repetition of mathematical calculations, which does not request conceptual mobilization [4]. Therefore, it could be stated that there are two different ways to define academic success in thermodynamics studies. On the one hand, if deep understanding is not promoted, students may perceive that this study consists of using equations they do not understand and must memorize in order to make calculations and pass the exam [4,5]. They will hence adopt a survival approach in which mechanical repetition, instead of deep conceptual understanding, is the key to success. Probably these students do not even feel that they truly need to understand anything in order to pass. On the other hand, and in order to avoid students’ misinterpretation of success, teaching staff should favor the deep understanding and assess coherently. This obviously implies that exams must feature qualitative deductions along with numerical calculations, hence valuing critical thinking over memorization. By doing this both in the classroom and over assessment, students will link academic success to true comprehension.
The first step to address the SLT learning problem is to answer the question: what does it mean to deeply understand the SLT? Deeply understanding of one concept implies acquiring a new way of thinking, the way in which an expert reasons. Understanding means, in short, entering into the particular ways of thinking of a discipline [6]. These ways of thinking, characteristic of each discipline, are organized around certain key concepts that provide meaning to determined phenomena, observations, or practices, and that constitute the main structural nodes of the network of concepts that sustains the dialogue and research in the discipline [7,8]. Characterizing this way of reasoning in a particular discipline is the starting point to analyze the difficulties impeding new learning and seeking the best way to teach a specific topic. We should then ask: What actually makes one an expert in this field? And in our specific case: When does it become noticeable that somebody deeply understands the SLT? How does he/she establish relationships between the concepts of SLT? To put it in more practical terms: What should our students be able to do in order to show that they have deeply understood the SLT?
Once the expert way of reasoning has been characterized, the next step is to describe the learning difficulties that students encounter to address their misunderstanding and improve the teaching/learning process. Instructors tend to overestimate the students’ conceptual understanding while underestimating their difficulties in acquiring them [9]. In the last two decades, some articles have been published dealing with learning difficulties in thermodynamics, such as the works of [4,10,11,12], but to the best of our knowledge, no paper compiles the specific difficulties that pregraduate students experience on the study of the SLT. Therefore, in this paper, we aim to answer the following research questions:
- What characterizes the deep understanding of the SLT in pregraduate students?
- Which are the main learning difficulties encountered by pregraduate students while approaching the SLT?
- Based on the previous, which suitable teaching practices could instructors adopt to help students understand the SLT deeply?
2. What Does It Mean to Deeply Understand the SLT?
Before compiling the learning difficulties on the SLT, we should address the critical points that actually let instructors perceive the deep understanding of these concepts. Understanding is an unceasing process that continues after instruction. Keeping this in mind, we must match our expectations to that which is achievable by pregraduate students. At this point of their academic formation, it is expected that they abandon their previous misconceptions and adopt reasonable expert thinking.
Figure 1 represents this expert thinking on entropy (S), which is characterized by the following points:
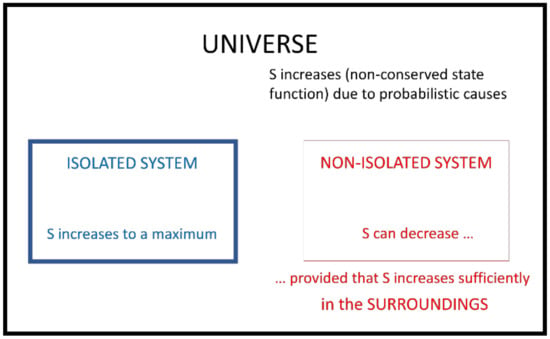
Figure 1.
Expert thinking on entropy (S).
- Entropy is, unlike energy, a non-conserved property.
The first law of thermodynamics states that energy is a conserved property; hence, it cannot be destroyed or generated, it can only be transformed. Therefore, the energy in an isolated system (i.e., a system that is unable to gain or lose energy) will always remain constant. This is not the case of entropy, which is spontaneously generated and will ultimately reach a maximum in the system. When asked about the entropy progression in an isolated system undergoing any process, the student who understands the SLT will not assume that entropy is constant, rather that its natural tendency is a spontaneous increase and that it will only remain invariable once it has reached its maximum.
- Isolated systems and the universe behave the same way, and their entropy will naturally increase to a maximum. Processes leading to the reduction in universal entropy are impossible.
When asked about the universe and having understood that it is the ultimate isolated system, the student would apply the same reasoning. When facing a hypothetical process taking place in an isolated system and asked about its spontaneity or impossibility, a student who has reached a deep understanding of SLT will indistinctly focus on the progression of entropy of the universe (system plus surroundings) or that of the system.
- The spontaneity of a process taking place in any system is linked to the increase in universal entropy. Therefore, it is the entropy of the universe, and not necessarily that of the system, which increases continuously and will ultimately reach a maximum.
When facing a hypothetical process taking place in a non-isolated system and asked about its spontaneity or impossibility, a student who has reached a deep understanding of SLT will focus on the progression of entropy of the universe (system plus surroundings) rather than on the entropy of the system where the process is taking place. Students who still have not reached a deep understanding would focus on the entropy of the system where the process is taking place.
- Entropy can be reduced locally in a non-isolated system.
Students who have understood the SLT accept that the entropy can be reduced in non-isolated systems. Irreversible processes are accompanied by the increase in universal entropy, which does not imply that entropy must increase in all locations. Hence, when asked about a generic system (not labeled as isolated), they do not reject the possibility of entropy decrease.
- The local reduction in entropy must be accompanied by an entropy increase in the rest of the universe so that the entropy of the universe is increased.
A deep understanding of SLT is revealed when, after accepting the possible entropy reduction in a non-isolated system, students point to the necessary entropy increase in the surroundings. This increase must take place so that the entropy of the universe (system plus surroundings) increases.
- The natural tendency to higher entropy is linked to a probabilistic explanation based on a microscopic approach.
Entropy becomes somewhat more tangible to students when related to the microscopical arrangement of molecules. A comparison could be established in which an isolated system is presented in two different states having different numbers of arrangements. A student who has reached a deep understanding of this concept is able to relate a higher number of molecular arrangements in a system with higher probability and higher entropy.
- Entropy is a state function.
The entropy of a system is defined as soon as the state is defined. It can only vary if the state is modified. Entropy variations are path-independent. Students who have deeply understood the concept of entropy will recognize that, once the initial and final states of a system are defined, the entropy variation is defined. When asked about the entropy variations of any other process connecting the same two states, they will sustain that no more calculations need to be performed since entropy change remains invariable.
3. An Overlook on the Learning Difficulties in the SLT
Starting from the obvious, entropy is a remarkably difficult concept to teach because it is extremely challenging to understand. This intrinsic feature has been repeatedly asserted in the literature [13,14,15,16,17]. The SLT, being based on this elusive property, is also troublesome. Apart from the inherent difficulties linked to the concept itself, and to some point as a consequence of it, some other challenges arise in the academic context as related to the teaching approach. The inherent difficulties linked to the SLT may discourage the qualitative understanding of the concepts. This can be aggravated depending on the teaching approach, especially when instructors focus on mathematical procedures instead of true learning. Additionally, the student’s previous knowledge often plays a key role in the STL learning process. Figure 2 maps these difficulties, all of which will be described below.
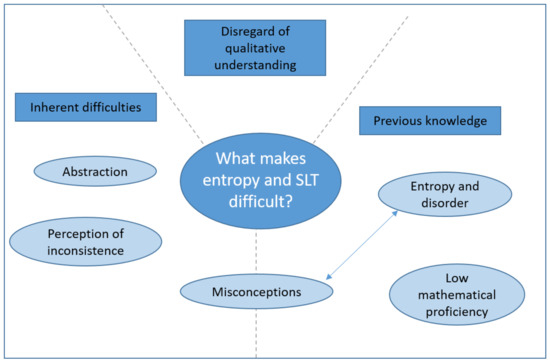
Figure 2.
Main learning difficulties experienced by thermodynamics students.
3.1. Disregard of Conceptual Understanding
This poor practice entails one of the main difficulties reported by students. In a study by Sözbilir [4], students complained that they had to simply memorize the definitions and equations in order to pass the exams. Some of them argued that the exams merely tested how to manipulate data and resolve problems. They also stated that if more attention was given to the confusing concepts, their understanding might be improved.
Although it can be considered as a brake to true learning in any area, this wrong prioritization can be especially unhelpful to understand the SLT since it will likely result in a complete disengagement between qualitative comprehension and quantification of thermodynamic properties. In fact, thermodynamics students can be competent in the solution of numerical problems such as the calculation of entropy variations, even though the concept has not been understood.
If conceptual understanding is disregarded, students will most likely adopt a “survival mode” where deep comprehension is not only unnecessary but a waste of time. The effort would then be put into memorization and mechanical problem solving. For this reason, it is important to define qualitatively conceptual entities and discuss their effects before defining them quantitatively [4].
3.2. Inherent Difficulties to the Concepts of Entropy and the SLT
In the following sections, some inherent difficulties to the concept of entropy and the second law of thermodynamics are addressed.
3.2.1. The Abstract Nature of Thermodynamic Concepts
It is generally accepted that thermodynamic concepts are highly abstract [7,18], which makes them difficult to understand [6]. Among them, entropy is more cognitively demanding than others and hence harder to explain [17,19]. As the laws of thermodynamics syllabus progresses, the SLT and the entropy come up after dealing with heat, temperature, work, and energy. Students can easily relate all these concepts to their everyday life, which is not the case of entropy, which they do not encounter outside an academic context [15]. This abstract nature makes high demands on the cognitive processing of students when constructing new meanings [5].
In a study by the authors of [4], students found it hard to visualize abstract concepts and to make them understandable and applicable to the macrophysical world. Aiming to overcome this difficulty, a significant number of students (56%) proposed that if links could be made between the concepts and their applications to everyday life, understanding would be easier. Consequently, it is accepted that using pseudo-examples, designed to reveal the critical and variable attributes of an abstract concept, would help learners [18]. However, care should be taken not to provide an incorrect impression or wrong information about the represented concepts when using the analogy. Students should always be able to appreciate that the characteristics of the analogy are not attributable to the concept being taught. In the specific case of entropy, a frequent analogy is that which relates this property to the disorder or chaos in the thermodynamic system, and it is one of the reasons for some student’s misconceptions.
3.2.2. Perception of Inconsistence
Leaving the system’s disorder aside, there are other correct definitions of entropy, as unquestionably, it is a polysemic term [17]. Entropy has been defined as the property defining the direction of the spontaneous processes, a concept arising from the need to explain spontaneous processes, a criterion to decide if some transformation between two states can take place or not, the quality of the available energy, a measure for the degradation of energy or for the dispersal of energy. Entropy variations equal the ratio of heat reversibly exchanged to temperature. It has also been defined as the heat available to do work or a mathematical expression of all the transformations taking place in a system. On a molecular level, it is correlated to the system’s loss of restrictions, the loss of information, and disorganization (meaning that a system is more organized if more restrictions are imposed on it).
Several studies have reported on the definitions of entropy used by university instructors and texts. The authors of [19] identified 5 definitions and 7 physical representations of entropy after interviewing 12 lecturers, which illustrates the wide variety of entropy conceptions in the teaching practice. This diversity stems from the efforts of scientists and teachers to make this property understandable, but unfortunately, it results in the perception of inconsistency since students do not receive a simple and univocal answer to what entropy really is. In light of this, it is frequent that instructors resign from assigning any physical meaning to entropy or resort to the analogy of disorder to put a brake on student’s frustration while focusing on mathematical calculations.
Another reason for the perceived inconsistency is the multiple statements of the SLT. This law has been phrased in various ways by different authors over history. At first sight, students cannot see the link between the different statements, but these links arise and become more comprehensible as the qualitative understanding of entropy and the SLT progresses.
3.2.3. Misconceptions
The construction of new knowledge is affected by previous conceptions, which can be wrong [20]. As described by reference [5], new knowledge is constructed through an interactive process between conceptions that already exist in the learner’s memory and a new stimulus. Therefore, when a student is listening to a lecture, he/she holds previously constructed conceptions in his/her memory and recalls these in order to interpret the new stimulus. This interaction process can cause existing conceptions to be modified or new ones to be created. Obviously, if students lack the required prior knowledge or have constructed/arranged understandings in ways that are incompatible with the accepted scientific concepts, then building new concepts will be difficult [5,21]. As reported in the literature, undergraduate students have already formed misconceptions related to thermodynamics before they begin their university studies, and these will have a significant impact on their further understanding [5]. Table 1 shows the most common misconceptions related to the SLT.

Table 1.
Reported misconceptions on the SLT.
Spontaneous processes are accompanied by an increase in the entropy of the universe (system plus surroundings). Only if the entropy of the surroundings is not modified by the process could it be stated that the entropy of the system increases in spontaneous processes. This is a source of confusion for students, who could wrongly believe that it is the entropy of the system that will always increase. This may primarily be a problem of nomenclature if the symbol S is used without specifying universe or system [24]. Reference [22] found that the students of an introductory course tended to argue that the entropy of the system must increase, even in cases where inadequate information is available to make such a determination. Moreover, these students were reluctant to accept the idea that the total entropy must increase during spontaneous processes. The same misconception was found in students enrolled in a thermal physics course. Incoherently, Reference [10] observed that many students did not seem to know that the entropy of isolated systems undergoing spontaneous processes must increase.
The misconception that links entropy and disorder is closely related to another stating that entropy depends solely on the spatial distribution of the molecules. From its initial definition [28], entropy consists of two components, namely kinetic entropy, depending on temperature and hence the kinetic energy of the molecules, and spatial entropy, affected by the location of the molecules and hence by the volume [27]. If entropy were only related to spatial distribution and solely dependent on volume, the kinetic component of entropy would be neglected, and comprehension is incomplete [19].
Misconceptions are highly persistent and hinder the acquisition of new knowledge, as reported by previous studies. Reference [22] reported that most of the students of an advanced physical chemistry course believed that the entropy of the universe remains constant in spontaneous processes, just as the students of an introductory physics course did. In a study by Carson and Watson [5] conducted on first-year undergraduate chemistry students, both the number of correct conceptions and misconceptions were increased at the end of the course. Reference [25] found that only 6% of their students in an introductory physics course correctly answered questions about entropy in a pretest. Nearly two-thirds of the students showed clear evidence of conservation-type reasoning regarding entropy. This barely changed after instruction.
Some action proposals have been put forward to counter the persistence of misconceptions. The authors of [22] points out the need for a strong focus on fundamental concepts and qualitative reasoning, at least at the beginning of the course. The authors of [5] suggested that some seminar might be held at the beginning of the course where students should write or talk about their previous knowledge. This would help reveal the major misconceptions held by them. The same authors point out that it would be profitable to challenge students with some already known alternative conceptions, asking them to support or deny these conceptions and explain their answers.
3.3. Difficulties Stemming from Student’s Previous Knowledge
3.3.1. Entropy and Disorder
The misconception that tightly associates entropy with “randomness”, “chaos”, or metaphors of “disorder” is probably one of the most frequently held by pregraduate students. In a study by the authors of [11], students were asked before instruction about entropy and used terms such as “disorder” with no evidence of reasoning that links “disorder” to entropy. Although the meaning of entropy is often linked with both macroscopic and microscopic notions of disorder, more precise definitions are often omitted [25]. This analogy may seem helpful, and in fact, “orderly–disorderly” seems to be an easy visual support, but it can be so grievously misleading as to be characterized as a failure-prone crutch rather than a reliable aid [29,30]. This is supported by studies describing the students’ difficulties for correct interpretation. Reference [5] reported that students described entropy in vague terms such as chaos and randomness without specifying what was chaotic or random. When students tried to be more specific, they related entropy variations to changes of state rather than to the distribution of energy in microstates.
3.3.2. Low Mathematical Proficiency
Mathematics understanding and proficiency are connected to student success in physical chemistry [11], and having insufficient skills has been reported as one of the most relevant learning difficulties for thermodynamics students. Reference [4] stated that the two main learning difficulties reported by thermodynamics students are abstraction and mathematics.
Some studies report on students’ struggles while solving numerical problems of thermodynamics. Reference [31] examined students’ understanding of the work concept in a physics context and path-dependent functions in a mathematics context. The results showed that students hold an isolated understanding of the two subjects rather than an integrated framework. Work was described as path-independent (state function). Students found it difficult to relate the work performed on P–V diagrams (bidimensional graphs where the pressure of the system is represented as a function of its volume) and definite integrals. The results were interpreted as low mathematical proficiency rather than a lack of physics conceptual understanding.
Whenever the goal is assisting students’ understanding of thermodynamic concepts through mathematical relationships, we must help them learn the meanings of mathematical concepts (derivatives, partial derivatives, integrals, state functions, etc.) in the context of thermodynamics [11]. It should, however, be pointed out that students may demonstrate mathematical proficiency even though they lack a conceptual understanding of mathematical concepts [32,33,34]. Furthermore, while suitable mathematical skills are necessary for correct problem solving and academic success, it is not necessarily linked to conceptual understanding. Therefore, mathematical proficiency is a necessary but not sufficient condition for success in an undergraduate thermodynamics course.
4. Suitable Teaching Practices for Instructors
As concluded from the previous sections, a new teaching approach is necessary where qualitative ideas of the SLT should be a central and integral part from the beginning of instruction. In the literature, different suggestions have been made on how to teach the topics at hand. Reference [15] proposed a three-step method to explain entropy to undergraduate students where residual entropy was introduced after thermal entropy. Reference [33] stressed the multiplicity of a macrostate to help students understand entropy. Other examples are [19,32,33,34,35,36]. However, to the best of our knowledge, no studies have been published that describe the sequence to be followed in order to stress the qualitative understanding of SLT while also addressing the difficulties and misconceptions in the most appropriate moments. Therefore, we made our own proposal in this field to assist practitioners of thermodynamics introductory courses. Our proposal does not require a specific teaching methodology and could be adapted to different learning contexts, according to the practitioner’s best judgment. Moreover, it is always advisable to adjust the teaching strategy to the wrong ideas that the group of students hold, which could be detected by having an initial seminar [5]. Revising their mathematical skills before and over instruction is, of course, advisable as well. Next, we detail a series of suitable practices for students to: (1) understand SLT and entropy qualitatively; and (2) properly quantify entropy variations.
4.1. Understanding the SLT and Entropy Qualitatively
Thermodynamics lecturers should prioritize conceptual understanding and address it sufficiently before moving on to numerical problems. Deep understanding could be promoted by presenting some qualitative questions about the concept before tackling problem solving. This approach promotes deep understanding, as opposed to traditional lectures on thermodynamics, where mathematical deductions take most of the student’s attention and obscure the concept behind the equation. Coherently, the evaluation must be focused on understanding rather than reproduction, or otherwise, the exams could distort the efforts of students to achieve personal understanding [37]. We propose to follow the next sequencing:
4.1.1. How Important Is the SLT? Catching Students’ Attention
If students do not perceive new knowledge as highly valuable, they may not show any interest in acquiring it, thus affecting their motivation level. In order to make new concepts interesting to students, it is important to justify their importance, either in a professional context or in everyday life, or both.
Before exposing our students to the remarkable scope of the SLT, they should first see the gap left by the first law. It states that energy is a conserved property but does not provide any information about the direction of spontaneous change. However, many processes that we observe daily take place only in one direction (gravity, chemical reactions, biological processes…). This idea could be phrased in questions such as: Why is the air in this room taking up all the space available, and it is not packed in one corner? Why does the heat always flow from hot to cold and never backward? Making these connections between the topic of the lecture and everyday observations will help to reduce the abstraction of the concepts involved. Students may then claim that these are weird questions to make, which gives the teacher the opportunity to let them note that they have always observed that nature behaves this way, but they have never wondered why it behaves this way. The SLT is the answer to this, stating the reason why all spontaneous processes take place only in one direction and never backward. It is expected that this foreword on the SLT grasps the attention of our students and keeps them motivated.
4.1.2. The Entropy of the Universe Is Always Increasing
The reason behind the unique direction of spontaneous processes is that, by taking place in this direction, they cause an increase in the entropy of the universe (SU). This should be accompanied by some clarifications:
- (a)
- This universal entropy increase is contrary to the widely accepted misconception that entropy, like energy, is a conserved property. Some properties of the universe must change over time, or spontaneous changes could take place in both directions.
- (b)
- The SU increase principle constitutes one of the statements of the SLT, which has been phrased in several forms. The rest of the statements (which could be referred to as engineering statements and will gain focus later on) are practical observations performed by engineers while trying to improve the efficiency of steam engines, and they are nothing but manifestations of the SU increase.
- (c)
- It should be stressed that it is the entropy of the universe, which is continuously increasing, and this does not imply that the entropy is always increasing in every part of the universe. The continuous increase in SU is perfectly compatible with a local entropy reduction (in a system), provided that it is accompanied by a sufficient entropy increase in the rest of the universe (surroundings). To illustrate this, an example could be given in which some beverage is cooled down in a fridge while its entropy is being reduced. This must be compatible with the universal entropy increase principle, or this process would not be possible. Students would then be confronted with a riddle to solve, where the missing piece is the entropy increase in the surroundings. If this increase is big enough, the entropy decrease in the beverage can take place while the entropy of the universe increases. It could be said then that the surroundings are “paying the price” for the entropy decrease in the beverage. This reasoning could be then reinforced with numerical examples where the students would realize that, in order to identify a spontaneous process taking place in a system, they have to actually look away from the system and shift their focus to the universe, in spite of the process taking place in the system.
- (d)
- The specific case of an isolated system should be addressed here. Being unable to interact with the rest of the universe when a process takes place in an isolated system will not affect the entropy of the rest of the universe. In this case, the entropy variations of the system will equal the entropy variations of the universe, which is not the case in non-isolated systems. Some activities could be proposed here where the students practice the new reasoning, consisting of labeling hypothetical processes as spontaneous/impossible in non-isolated/isolated systems, on the basis of the timely progression of the entropies of the surroundings and the universe.
- (e)
- It could be interesting to comment on the contrast between the apparent simplicity of the SLT and its enormous scope, given that it justifies why the universe behaves as it does. Unfortunately, in order to do this, it is based on entropy, a thermodynamic property that is not easily relatable to our everyday life, unlike others such as heat, energy, or work.
4.1.3. A Quick Look at How the SLT Was Discovered
Probably students will wonder how it was possible that the SLT could even be stated, given that entropy is a non-directly experiential or measurable property. At this point, some historical context could be given by commenting that, before Clausius could postulate the continuous increase in SU, some scientists and engineers such as Carnot made some observations while trying to improve the efficiency of steam engines. These empirical observations constitute the engineering statements of the SLT. They relate between them and are also related to the SU increase principle. Later on, these connections could be demonstrated.
4.1.4. Carnot Engine and the Discovery of a New State Function: Entropy
Before presenting the Carnot engine, it should be checked that students are familiar with the depiction of a heat engine and the definition of the engine efficiency (η = work out divided by heat in). Once the idealized Carnot cycle has been presented, it can be demonstrated that η can be expressed both as a function of the heat flows and of the temperatures of the sources. At this point, the new state function entropy emerges, whose increments are defined as the ratio between the heat exchanged reversibly and temperature. In the idealized Carnot engine, this ratio cancels over the cycle, which demonstrates that entropy is a state function. On the contrary, real engines work irreversibly and have lower efficiency; hence, the Clausius inequality is deduced. This equation can be applied to hypothetical engines to label them as real, idealized, or impossible, and finally to demonstrate the engineering statements of the SLT, as well as their relationship with the SU increase principle.
Students should now be guided to notice that thermal engines actually need to lose some heat in order to produce work. The same reasoning that was earlier applied to the beverage in the fridge could, in this context, be used to justify the need for heat losses. Three actors must be taken into account: the hot source, the engine, and the cold sink. As the hot source is providing heat, its entropy is being reduced. Who pays the price for this entropy reduction? It is not the engine whose entropy gets back to the initial value every time a cycle is completed, but the cold sink, which receives the heat, loses and undergoes an entropy increase. In real machines, working irreversibly, the entropy increase in the cold sink is higher than the entropy loss of the hot source, as expressed mathematically by Clausius inequality. Repeating the paying the price reasoning, this time in the context of thermal machines would reinforce the idea that it is the entropy of the universe and not that of one part of it, which determines if a process can actually take place.
4.1.5. Molecular Interpretation of Entropy
Addressing the molecular interpretation of entropy prior to expose how to calculate entropy variations completes the qualitative description of this concept and favors the understanding of the subsequent quantification. Moreover, the schematic figures of thermodynamic systems with different values of entropy will probably help to reduce the inherent abstraction of this concept.
As an introduction, it could be said that in the late 1800s, the scientific community had not fully accepted the existence of atoms while wondering the cause of the increasing tendency of entropy. At that time, Boltzmann put forward his theory that explained entropy from a probabilistic perspective by directly linking this property with the number of microstates Ω (microscopical configurations) of a specific macrostate. According to this link, a system has the highest possible entropy when it is in the most likely macrostate, that is, the state that has the highest number of microscopical configurations. This explains the increasing tendency of entropy in probabilistic terms. For instance, a gas expands to take all the available volume just because there are much more microstates for this state than for any other state where the gas takes only part of the volume. No other cause than probability makes it be this way.
This reasoning can be further explained using Figure 3, which shows two macrostates of a gas system. In macrostate 1 (compressed), the gas is taking only part of the available volume, and in macrostate 2 (dispersed), it is taking all the volume. Since more space available for the gas implies a larger number of microstates, macrostate 2 can take place through much more microstates than macrostate 1. Therefore, macrostate 2 is much more likely to happen than macrostate 1. For this reason, a gas initially compressed will spontaneously progress to occupy all the available volume, but this process will never take place in the opposite direction. Given the direct link between the number of microstates and entropy, and the fact that macrostate 2 has the highest number of microstates, it has also the maximum entropy.
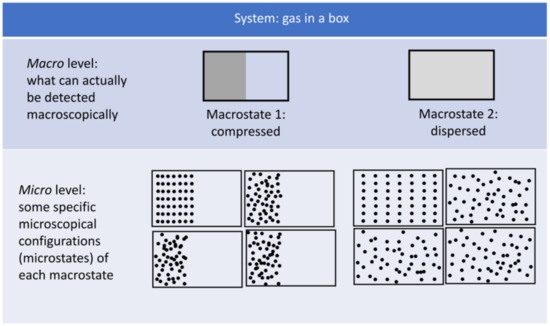
Figure 3.
Different microstates of two (macro)states. Macrostate 1 has low entropy, whereas macrostate 2 has the highest entropy. In both cases, some microstates could be described as more ordered, which does not imply any entropy variations as compared to disordered microstates.
The misconception that relates entropy with disorder should be addressed at this point. As students link entropy with disorder due to entropy’s everyday meaning, they normally relate entropy and hence disorder with visual chaos. Aiming to address this misconception and detach entropy from the specific molecular arrangement in the system, some microstates have been represented in Figure 3 for both selected macrostates (1, low entropy and 2, maximum entropy). In each case, different microstates could be described as either ordered or disordered, using the common non-scientific meaning of this term. Describing the microstate in one way or another relates only to the observer’s perception and does not imply any difference in the probability or in entropy. All these microstates are equally probable since the gas particles move freely, and the system has no preference for a particular configuration. Therefore, when the system goes from a disordered microstate to an ordered microstate and back to a disordered microstate, it does not experience any entropy changes. This should also be connected to the fact that entropy is a state function; therefore, it has a defined value once the state of the system is defined, independently of the particular molecular arrangement of a microstate.
The class could then be asked about how correct it is to link entropy and disorder. How could a state of high entropy be labeled? Would it be more accurate to describe it as homogeneous or non-compartmented, as compared to disordered or chaotic? While engaging in this debate, our students will experience difficulties in finding an easy description for high entropy and why it should not be identified with disorder. This would also be a suitable moment to address the polysemy of the term entropy while presenting comparisons between the two states. In which state could the system do more work? In which case is the energy of the system more disperse? When does the system have more restrictions on it? In which state do we have more information about the system?
So far, the molecular interpretation of entropy has been explained on the basis of the spatial distribution of gas particles, which was necessary to address the misconception that links entropy and disorder. However, this part of the lecture on the qualitative description of entropy should be completed with the effect of temperature on this property. At this point, it should be stressed that it is the number of microstates and not merely the spatial distribution of the particles, which is directly related to the entropy of the system. When a system undergoes a process in which the temperature increases, the molecules reach higher levels of kinetic energy, and the number of microstates is increased. Therefore, the number of microstates does not only depend on the volume but also on the temperature [27]. This is coherent with the equations to calculate entropy variations, which will be studied later on.
4.1.6. Final Comments on the Qualitative Discussion about Entropy
Finally, for a high-level qualitative discussion about entropy, a comment could be done on a third approach that does not refer to either heat engines or statistical mechanics. This reasoning has the advantage that temperature is eliminated as an a priori concept and emerges as a quantity derived from entropy rather than the other way around. Following this approach, Lieb and Yngvason [38] proved the differentiability of S as a function of energy and work coordinates and that temperature can be derived from entropy.
4.2. Quantification of Entropy Variations
Once instructors have addressed the main student’s misconceptions and students know the qualitative meaning of STL and entropy, we suggest the following best practices to teach them how to quantify entropy variations.
4.2.1. Entropy Is a State Function. What Does This Imply When Solving Problems?
Before deducing or showing the mathematical equations to calculate entropy increments of the system (ΔS), it should be reminded that entropy is a state function, and hence its variations are path-independent and defined solely by the initial and final states. All processes connecting states 1 and 2 will have the same ΔS, and consequently, ΔS can be calculated for irreversible processes despite it is equal to q/T only for reversible processes. This strategy, connecting the two states with a reversible process, even though the statement of the problem describes an irreversible process, is highly useful for problem solving, and students tend to forget this possibility [23]. The students could practice this by thinking about ΔS of a system undergoing several processes on a P-V diagram. By comparing them, the students would become aware that only the initial and final states matter.
4.2.2. How to Calculate Entropy Variations of the System over Different Processes
At this point, the quantification of ΔS in different processes can be addressed. Before presenting the equations, an activity where the students are asked to predict the sign of ΔS is highly recommendable since answering correctly would request for the mobilization of previous conceptions (entropy as a function state and as an indicator of the number of microstates). The students would also become aware that adiabatic reversible processes are isentropic.
Finally, problem resolution should be practiced. A prediction of the sign of ΔSsystem and the corresponding justification should be asked before even starting the calculations. This will invite students to qualitatively reflect on the expected result and critically analyse it once it has been obtained. By doing this, our students are being trained in critical thinking and provided with tools to detect mistakes in their mathematical calculations.
Problem resolution is the perfect context where some misconceptions can be argued. Misconceptions are highly persistent, and addressing them in a quantitative way (e.g., with actual indisputable numbers) will provide our students with irrefutable arguments to initiate the process where they substitute them with correct conceptions. With this philosophy, we could put forward problems in which the entropy of a system is decreased in a spontaneous process, whereas that of the surroundings increases in a greater amount. To promote awareness, the statements should request a qualitative description of what is going on in the system, the surroundings, and the universe. Problems on impossible processes could also be presented, where their feasibility is questioned. Lastly, assessment should be coherent with the proposed approach in the classroom, and qualitative descriptions should be requested in order to test understanding.
5. Conclusions
Thermodynamics is regarded by pregraduate students as a difficult topic, packed with complicated equations and abstract concepts. The traditional way to lecture, based on mathematical calculations, does not promote deep understanding, and over many years thermodynamics students have settled for reproducing calculations to pass the exams. Conceptual understanding must be promoted to reach actual academic success.
In this paper, we have characterized the deep understanding of the second law of thermodynamics and entropy for pregraduate students in introductory thermodynamics courses. We have presented a review on the difficulties affecting the understanding of these concepts, which, to the best of our knowledge, was missing in the literature. A classification of these difficulties into three groups was made, namely the disregard of conceptual understanding, the inherent difficulties of the concepts, and the difficulties related to the student’s previous knowledge. In accordance with our findings, some guidelines on suitable teaching practices are proposed for instructors. These include sequencing of the introduction of concepts and addressing misconceptions for students both to understand SLT and entropy qualitatively and properly quantify entropy variations. This proposal will probably assist instructors in their teaching practice, hence ultimately help students to deeply comprehend these concepts. The real impact of the teaching practices proposed in this paper needs to be evaluated in some future research.
Author Contributions
Conceptualization, L.A.; original draft preparation, L.A., M.J.C. and M.T.; review and editing: J.V.B.-D., J.P.R. and A.F.-M.; supervision, J.P.R.; project administration, J.P.R. and A.F.-M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Eddington, A.S. The Nature of the Physical World; Cambridge University Press: Cambridge, UK, 1928. [Google Scholar]
- Nicoll, G.; Francisco, J.S. An investigation of the factors influencing student performance in physical chemistry. J. Chem. Educ. 2001, 78, 99–102. [Google Scholar] [CrossRef]
- Carter, C.S.; Brickhouse, N.W. What makes chemistry difficult? J. Chem. Educ. 1989, 66, 223–225. [Google Scholar] [CrossRef]
- Sözbilir, M. What makes physical chemistry difficult? Perceptions of Turkish Chemistry Undergraduates and Lecturers. J. Chem. Educ. 2004, 81, 573–578. [Google Scholar] [CrossRef]
- Carson, E.M.; Watson, J.R. Undergraduate students’ understandings of entropy and Gibbs free energy. Univ. Chem. Educ. 2002, 6, 4–12. [Google Scholar]
- Donald, J.G. Learning to Think: Disciplinary Perspectives; Jossey-Bass: San Francisco, CA, USA, 2002. [Google Scholar]
- Meyer, J.H.F.; Land, R. Threshold Concepts and Troublesome Knowledge: Linkages to Ways of Thinking and Practising within the Disciplines; ETL Project; University of Edinburgh: Edinburgh, UK, 2003. [Google Scholar]
- Entwistle, N. Threshold Concepts and Transformative Ways of Thinking within Research into Higher Education. In Threshold Concepts within Disciplines; Land, R., Meyer, J.H.F., Smith, J., Eds.; Sense Publishers: Rotterdam, The Netherlands, 2008. [Google Scholar]
- Sözbilir, M. What students’ understand from entropy? A review of selected literature. J. Baltic Sci. Educ. 2003, 2, 21–27. [Google Scholar]
- Sözbilir, M.; Bennett, J.M. A study of Turkish chemistry undergraduates’ understanding of entropy. J. Chem. Educ. 2007, 84, 1204. [Google Scholar]
- Bain, K.; Moon, A.; Mack, M.R.; Towns, M.H. A review of research on the teaching and learning of thermodynamics at the university level. Chem. Educ. Res. Pract. 2014, 15, 320–335. [Google Scholar] [CrossRef]
- Cotignola, M.I.; Bordogna, C.; Punte, G.; Cappannini, O.M. Difficulties in learning thermodynamic concepts are they linked to the historical development of this field? Sci. Educ. 2002, 11, 279–291. [Google Scholar] [CrossRef]
- Amin, T.G.; Jeppsson, F.; Haglund, J.; Strömdahl, H. Arrow of time: Metaphorical construals of entropy and the second law of thermodynamics. Sci. Educ. 2012, 96, 818–848. [Google Scholar] [CrossRef] [Green Version]
- Styer, D.F. Insight into entropy. Am. J. Phys. 2000, 68, 1090–1096. [Google Scholar] [CrossRef] [Green Version]
- Popovic, M. Explaining the entropy concept and entropy components. J. Subj. Didact. 2017, 2, 73–80. [Google Scholar]
- Dixon, J.R.; Emery, A.H. Semantics, operationalism, and the molecular-statistical model in thermodynamics. Am. Sci. 1965, 53, 428–436. [Google Scholar]
- Haglund, J.; Jeppsson, F.; Strömdahl, H. Different senses of entropy—Implications for education. Entropy 2010, 12, 490–515. [Google Scholar] [CrossRef]
- Herron, J.D. The Chemistry Classroom; American Chemical Society: Washington, DC, USA, 1996. [Google Scholar]
- Ulloa-Lugo, N.Y. Origen y Evolución del Concepto de Entropía. Representaciones e Implicaciones para la Enseñanza. Ph.D. Thesis, Universidad Pedagógica Nacional, Bogotá, Colombia, 2006. [Google Scholar]
- Osborne, R.; Wittrock, M. The generative learning model and its implications for science education. Stud. Sci. Educ. 1985, 12, 59–87. [Google Scholar] [CrossRef]
- White, R.T. Learning Science; Blackwell: Oxford, UK, 1988. [Google Scholar]
- Meltzer, D.E. Investigation of student learning in thermodynamics and implications for instruction in chemistry and engineering. AIP Conf. Proc. 2007, 883, 38–41. [Google Scholar]
- Smith, T.I.; Christensen, W.M.; Thompson, J.R. Addressing student difficulties with concepts related to entropy, heat engines and the Carnot cycle. AIP Conf. Proc. 2009, 1179, 277–280. [Google Scholar]
- Granville, M.F. Student misconceptions in thermodynamics. J. Chem. Educ. 1985, 62, 847. [Google Scholar] [CrossRef]
- Christensen, W.M.; Meltzer, D.E.; Ogilvie, C.A. Student ideas regarding entropy and the second law of thermodynamics in an introductory physics course. Am. J. Phys. 2009, 77, 907–917. [Google Scholar] [CrossRef] [Green Version]
- Sreenivasulu, B.; Subramaniam, R. University students’ understanding of chemical thermodynamics. Int. J. Sci. Educ. 2013, 35, 601–635. [Google Scholar] [CrossRef]
- Brosseau, C.; Viard, J. Quelques reflexions sur le concept D’entropie issues d’un enseignement de thermodynamique. Enseñanza Cienc. 1992, 10, 013–016. [Google Scholar]
- Clausius, R.J.E. Théorie Mécanique de la Chaleur; Lacroix, E., Ed.; Libraire de la Société des Ingénieurs Civils: Paris, France, 1868; Volume 1. [Google Scholar]
- Lambert, F.L. Disorder—A cracked crutch for supporting entropy discussions. J. Chem. Educ. 2002, 79, 187. [Google Scholar] [CrossRef]
- Lambert, F.L. Shuffled cards, messy desks, and disorderly dorm rooms—Examples of entropy increase? Nonsense! J. Chem. Educ. 1999, 76, 1385. [Google Scholar] [CrossRef]
- Pollock, E.B.; Thompson, J.R.; Mountcastle, D.B. Student Understanding of The Physics and Mathematics of Process Variables In P-V Diagrams. AIP Conf. Proc. 2007, 951, 168–171. [Google Scholar]
- Becker, N.; Towns, M. Students’ understanding of mathematical expressions in physical chemistry contexts: An analysis using Sherin’s symbolic forms. Chem. Educ. Res. Pract. 2012, 13, 209–220. [Google Scholar] [CrossRef]
- Baierlein, R. Entropy and the second law: A pedagogical alternative. Am. J. Phys. 1994, 62, 15–26. [Google Scholar] [CrossRef]
- Morikawa, T.; Williamson, B.E. A chemically relevant model for teaching the second law of thermodynamics. J. Chem. Educ. 2002, 79, 339. [Google Scholar] [CrossRef]
- Abreu, R.; Guerra, V. Introducing thermodynamics through energy and entropy. Am. J. Phys. 2012, 80, 627–637. [Google Scholar] [CrossRef]
- Fuchs, H.U. Entropy in the teaching of introductory thermodynamics. Am. J. Phys. 1987, 55, 215–219. [Google Scholar] [CrossRef]
- Entwistle, N.J.; Entwistle, A. Contrasting forms of understanding for degree examinations: The student experience and its implications. High. Educ. 1991, 22, 205–227. [Google Scholar] [CrossRef]
- Lieb, E.H.; Yngvason, J. The physics and mathematics of the second law of thermodynamics. Phys. Rep. 1999, 310, 1–96. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).