Teaching Congruences in Connection with Diophantine Equations

Abstract

The presented paper is devoted to the new teaching model of congruences of computer science students within the subject of discrete mathematics at universities. The main goal was to create a new model of teaching congruences on the basis of their connection with Diophantine equations and subsequently to verify the effectiveness and efficiency of the proposed model experimentally. The teaching of congruences was realized in two phases: acquisition of procedural knowledge and use of Diophantine equations to obtain conceptual knowledge of congruences. Experiments confirmed that conceptual understanding of congruences is positively related to increasing the procedural fluidity of congruence resolution. Research also demonstrated the suitability of using Diophantine equations to link congruences and equations. Among other things, the presented research has confirmed the justification of teaching mathematics in computer-oriented study programs.

1. Introduction

Society is currently being intensively digitized, and the ongoing COVID-19 pandemic has increased that need. With the transfer of work activities to the online space, the requirements for the security of virtual space are also increasing, which should also be ensured by high-quality encryption of the content of messages transmitted within the Internet networks. It is a challenge also for the field of education, which often faces criticism from the employers of school graduates themselves. Various employers claim that schools do not pay enough attention to understanding and developing the skills that graduates need to succeed outside school [1]. The World Economic Forum (2016) identified, among other things, the skills that students should have after completing their university studies. These are, for example, the ability to solve problems comprehensively, the ability to think critically, the ability to creatively use already acquired knowledge in various contexts and cognitive flexibility enabling insight into the problem to be solved from different perspectives. For these reasons, too, we consider it necessary to explore the possibilities of teaching mathematics with regard to the understanding and interconnection of individual knowledge. At the same time, it is necessary for students to gain experience in the diverse use of mathematics from the teaching of mathematics. According to Prawat [2], the assignment of diverse tasks is beneficial for the student, as necessary knowledge and skills are built up when the student has to deal with rich information and by resolving cognitive conflicts, instead of using ready-made algorithms to solve standard tasks. Applying knowledge in a variety of situations is a convenient way to combine the process of remembering and understanding. According to Marton et al. [3], it is necessary to combine these two processes in the teaching mathematics. Research also suggested that practitioners draw on interdisciplinary knowledge in problem solving ([4,5,6]). Given the difficulty and complexity of the problems that need to be addressed today, interdisciplinary knowledge is a natural requirement for school leavers. The accelerated development of scientific knowledge creates a natural requirement and a precondition to manage the teaching process through interdisciplinary relationships [7]. For example, regarding machine learning, in addition to programming skills the solver of a real problem needs a relatively broad knowledge of various areas of mathematics.

The above-mentioned need for cyber security requires quality computer experts and computer scientists. Informatics and mathematics have really strong ties and a common history [8]. Mathematics provides a theoretical basis for many sub-areas of computer science. It also provides important analytical tools that computer scientists apply to specific computational problems. For example, the study of ciphers and the search for possibilities to break them has an incredibly large amount of synergy with mathematics [9]. This link between mathematics and computer science and practice could serve as a strong motivating factor for students to acquire the mathematical knowledge needed to understand the nature of encryption. The basic precondition for mastering the problem of encryption is the acquisition of knowledge in the field of congruences. When teaching students how to solve linear congruences, it might be useful to consider these congruences as analogous to equations [10]. To achieve this goal, Diophantine equations, which can also be solved using congruences, prove to be a suitable tool. According to [11] the development of quality procedural lessons in order to create basic procedural knowledge in conjunction with pointing out the basic concepts is a prerequisite for later improvement of procedural knowledge and gaining the necessary conceptual knowledge. The search for ways to combine the isolated requirements of professional subjects with a conceptual understanding of mathematical concepts or procedures could contribute to the streamlining of mathematical courses in non-mathematical study fields of universities. To understand professional problems, computer science students to a large extent need a conceptual understanding of the mathematical background of a given issue. On the basis of the above research objectives, the aim was to find out whether the connection of knowledge about congruences with the solution of Diophantine equations will increase the success of students in solving problems related to congruences. At the same time, we experimentally verified the assumption that improving procedural knowledge of congruences can support the improvement of conceptual knowledge of congruences.

2. Cryptography and Congruences

The problem of encrypting a message so that the enemy does not understand it and the ally can decrypt it again has been important since ancient times. It is known that Gaius Julius Caesar already used a simple code in which each letter was replaced by a different one found in the Latin alphabet “three places further”, i.e., $A\to D$, $B\to E$, $C\to F$, etc. Important mathematicians took part in solving codes. For example, François Viète (1540–1603) deciphered the code used by Spanish troops in France. During World War II, the Germans used an encryption machine called ENIGMA. The breaking of this code by a group of British correspondents led by Alan Turing [12] was essential for the Allied victory in the North Atlantic, where German submarines threatened the convoys of Allied ships. In the Pacific, the decipherment of the Japanese code before the Battle of Midway Roundtable brought the Americans a great advantage when they managed to sink four Japanese aircraft carriers and lost only one themselves.

It can be said that until the early 1970s, cryptography was more or less a military matter and not much was published about the theory of coding. However, the civilian, commercial and banking sphere began to make more and more use of wireless data transmission, which could also be “sensitive”. Therefore, there arose the need to find a simple cryptographic algorithm used for secure and fast data transmission. In November 1976, it was formally adopted in the USA as a federal standard called DES (Digital Encryption Standard) [13]. It was a cryptographic system with a secret key, where any two users had to exchange this key before they could exchange encrypted messages. The encrypted message was very difficult to decipher for those who did not know the key.

In 1976, Diffie and Hellman proposed a fundamentally new method using the so-called public key for encryption systems. However, the system also has a secret key, and only those who know it are able to easily decrypt the text encrypted with the public key. The implementation of this system was proposed by Rivest, Shamir and Adleman (a so-called RSA system) [14]. This method is related to the issue of electronic signatures or trading on the Internet. It is based on the mathematical apparatus (factorization) of natural numbers into powers of prime numbers. It is an encryption in which each of its principles is known and is public, but no one decrypts the encrypted information, because the public key only (i.e., knowledge of the encryption principle) is not enough. To decipher the cipher and read the message, it is necessary to obtain prime number elements of prime factorization that can only be obtained by the recipient of the message who also knows the private key (that is, some necessary information on how the product originated). One of the first standards was RSA-768 [15], which represents a 232-digit number. The standard has been broken by scientists by bringing together hundreds of computers that have been working for a period representing 2000 years of one computers work. Later, the RSA-1024, RSA-2048 or RSA-4096 standards have been developed which are used today. The use of linear congruences for coding problems stems from knowledge from the 18th century, which has started to be used practically now in the 20th century.

Thus, we can easily algorithmically decompose only numbers of a certain “small” size into the product of prime numbers and this fact is the basis of virtual security. If we take two very large prime numbers, where both the first and the second represent some information, it is easy to multiply them with each other, giving a very large composite number practically decomposable (unless we know the so-called private key, i.e., some necessary information how the large number came up). Algorithms that would look for the factors of a product by “brute force”, i.e., by trying all possibilities, would have a tremendous time complexity [16]. The principle of coding a given message $x$ using the RSA method is that we take two large primes $p$ and $q$, which mutually different such that $x<p·q$ and $p\nmid x$, $q\nmid x$. We create their product $p·q$, which is publicly accessible. However, only one who knows both primes $p$ and $q$ can easily calculate the value of the Euler function $\phi \left(p·q\right)=\left(p-1\right)\left(q-1\right)$. For those who do not know from which primes the product originated, it is very difficult to calculate the value of $\phi \left(p·q\right)$ because the decomposition of the large number which originated as a product of prime numbers is demanding. Now we choose any number $e$, incommensurable with $\phi \left(p·q\right)$, except $e=1$ and $e=\left(p-1\right)\left(q-1\right)-1$. This number, a so-called encryption exponent, shall also be disclosed. Anyone who knows the numbers $p·q$ and $e$ can encrypt their message by calculating the number $y$ for which $y\equiv x^e\left(\mathrm{mod} p·q\right)$ holds true. The author of the message must calculate the so-called decoding exponent $f$, presented by a private key. It can be found as a solution of the congruence $e·f\equiv 1\left(\mathrm{mod} \phi \left(p·q\right)\right)$. It holds true that $\left(e,\phi \left(p·q\right)\right)=1$ and the search for the number $f$ is performed by Euclid’s algorithm [17], so there exist integers $f$, $h$ such that $e·f+\phi \left(p·q\right)·h=1$. Then, $e·f=1-\phi \left(p·q\right)·h$ and thus $e·f-1$ is divisible by $\phi \left(p·q\right)$ and $e·f\equiv 1\left(\mathrm{mod} \phi \left(p·q\right)\right)$. The decryption of the encoded word $y$ consists of the following steps. We know that $e·f=1-\phi \left(p·q\right)·h$. Let $k=-h$, then $e·f=1+\phi \left(p·q\right)·k$. As $\left(x,p·q\right)=1$, then according to Euler’s theorem [18],

$$x^{\phi \left(p·q\right)}\equiv 1\left(\mathrm{mod} p·q\right),$$

(1)

and also

$$x^{k·\phi \left(p·q\right)}={\left(x^{\phi \left(p·q\right)}\right)}^k\equiv 1\left(\mathrm{mod} p·q\right),$$

(2)

then

$$y^f=x^{e·f}=x·x^{k·\phi \left(p·q\right)}\equiv x\left(\mathrm{mod} p·q\right).$$

(3)

The last relation describes that in order to decrypt the encoded word $y$, it is sufficient to calculate the smallest non-negative remainder by dividing the power $y^f$ by the number$p·q$, which is an easily solvable task. The RSA method is the simplest one and it shows how modular arithmetic has a practical application. The RSA method has become very widespread in e-banking, online shopping, electronic signatures, etc. [19].

We will show the RSA encryption principle using the congruences on a specific example. We will encrypt (and decrypt) the name (message) “REX” by RSA method using prime numbers $p=7$, $q=11$. We will work with the letters of English alphabet, A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y, and Z, assigning each letter a numeric two-digit number, sequentially to letter A—01, to letter B—02 etc. to letter Z—26.

Then the word “REX” in numeric form will presented by number $x=180524$. Now, we will encrypt letter by letter. The product $p·q=77$, hence $\phi \left(p·q\right)=\phi \left(77\right)=77·\left(1-\frac{1}{7}\right)·\left(1-\frac{1}{11}\right)=77·\frac{6}{7}·\frac{10}{11}=6·10=60$ [20]. Let us choose, e.g., $e=43$ as the encryption exponent so that $\gcd \left(60,43\right)=1$. Now we have to calculate the number $f$ that $e·f\equiv 1\left(\mathrm{mod} 60\right)$. Using the Euclidean algorithm, we get $60=43·1+17$, $43=17·2+9$, $17=9·1+8$ a $9=8·1+1$. Next $\gcd \left(60,43\right)=1=9-8=9-\left(17-9\right)=17·\left(-1\right)+9·2=17·\left(-1\right)+\left(43-17·2\right)·2=43·2+17·\left(-5\right)=43·2+\left(60-43\right)·\left(-5\right)=60·\left(-5\right)+43·7$. From that we see $43·7=1+60·5$, and therefore $43·7\equiv 1\left(\mathrm{mod} 60\right)$. Then the decryption exponent is $f=7$.

As we encrypt letter by letter, we now have to calculate the numbers $y$ such that $y\equiv a^{43}\left(\mathrm{mod} 77\right)$ (resp. we solve the Diophantine equation $-77x+y=a^{43}$, because $77|y-a^{43}\Rightarrow y-a^{43}=77x$) sequentially for $a=18, 5, 24$. Now we calculate $y\equiv {18}^{43}\left(\mathrm{mod} 77\right)$, so we’re searching such $y$ that belong to the same residual class as the number ${18}^{43}$ modulo $77$. It holds ${18}^{43}=18·{18}^{42}=18·{\left({18}^6\right)}^7\equiv 18·{15}^7=270·{15}^6=270·{\left({15}^3\right)}^2\equiv 270·{64}^2\equiv 46\left(\mathrm{mod} 77\right).$ Analogously from congruences $y\equiv 5^{43}\left(\mathrm{mod} 77\right)$ and $y\equiv {24}^{43}\left(\mathrm{mod} 77\right)$ we get the remaining values 26 and 52 for $y$. To decrypt the message back with the private key $f=7$ letter by letter, we first calculate the congruence $x\equiv {46}^7\left(\mathrm{mod} 77\right)$ and we get $x=18$, which represents the letter R. The same way we calculate the remaining two congruences $x\equiv {26}^7\left(\mathrm{mod} 77\right)$ and $x\equiv {52}^7\left(\mathrm{mod} 77\right)$. The results obtained are shown in

Table 1. RSA encryption principle.

Message from Sender	x	y Encrypted Message	Decrypted Message	Message at the Recipient
R	18	46	18	R
E	5	26	5	E
X	24	52	24	X

.

More information on RSA cryptosystems using congruences can be found, e.g., in [21].

3. Results

Consider $a,b,m\in \mathbb{Z}$, while $m>1$. Then we say that number $a$ is congruent with number $b$ by module $m$ (or we call it modulo $m$), if $m|\left(a-b\right)$. Additionally, we note

$$a\equiv b\left(\mathrm{mod} m\right).$$

(4)

The number $a$ is called the left side, the number $b$ the right side of congruence. The notation $a\not\equiv b\left(\mathrm{mod} m\right)$ means that the number $a$ is not congruent with number $b$ by module $m$., i.e., $m\nmid \left(a-b\right)$ [22].

The relation of congruence is:

• reflex: $a\equiv a\left(\mathrm{mod} m\right)$
• symmetric: $a\equiv b\left(\mathrm{mod} m\right)\Rightarrow b\equiv a\left(\mathrm{mod} m\right)$
• transitive: $a\equiv b\left(\mathrm{mod} m\right)\wedge b\equiv c\left(\mathrm{mod} m\right)\Rightarrow a\equiv c\left(\mathrm{mod} m\right)$

Now we show that if $a+b\equiv c\left(\mathrm{mod} m\right)$ and $a\equiv d\left(\mathrm{mod} m\right),$ then $d+b\equiv c\left(\mathrm{mod} m\right)$. From $a+b\equiv c\left(\mathrm{mod} m\right)$ it applies $m|a+b-c$ and from $a\equiv d\left(\mathrm{mod} m\right)$ it applies$m|a-d$. Then $a+b-c=k_{1}m$ and $a-d=k_{2}m$, thus $d-a=-k_{2}m$. Then $a+b-c+d-a=k_{1}m-k_{2}m$, and therefore $d+b-c=\left(k_1-k_2\right)m$. Out of previous $d+b\equiv c\left(\mathrm{mod} m\right)$.

Furthermore, if $a\equiv b\left(\mathrm{mod} m\right)$ and $c$ is any integer, then:

$$a+c\equiv b+c\left(\mathrm{mod} m\right).$$

(5)

Because if $a\equiv b\left(\mathrm{mod} m\right)$, then $m|\left(a-b\right)$. As $\left(a+c\right)-\left(b+c\right)=a-b$, then $m|\left[\left(a+c\right)-\left(b+c\right)\right]$, out of which $a+c\equiv b+c\left(\mathrm{mod} m\right)$.

Now consider the congruence system:

$$\begin{gathered} \left(\mathrm{mod} m\right) \\ {a}_2\equiv b_2\left(\mathrm{mod} m\right) \\ \cdots \\ {a}_k\equiv b_k\left(\mathrm{mod} m\right) \end{gathered}$$

(6)

Then $a_1{a}_2\dots a_k\equiv b_1{b}_2\dots b_k\left(\mathrm{mod} m\right)$. The formula can be proved by mathematical induction. First let $k=2$. Then we must show that $a_1{a}_2\equiv b_1{b}_2\left(\mathrm{mod} m\right)$. Let us denote $M=a_1{a}_2-b_1{b}_2=a_1{a}_2-a_1{b}_2+a_1{b}_2-b_1{b}_2=a_1\left(a_2-b_2\right)+b_2\left(a_1-b_1\right)$. From the assumptions of the first and second congruence the following applies $m|\left(a_1-b_1\right)$ and $m|\left(a_2-b_2\right)$, and thus $m|M$. The second step is analogous.

From the last statement we can deduce the result that if $a\equiv b\left(\mathrm{mod} m\right)$ and $c$ is any integer, then:

$$ac\equiv bc\left(\mathrm{mod} m\right).$$

(7)

Next, let $a\equiv b\left(\mathrm{mod} m\right)$. Let $d$ be an integer with properties $d|a$, $d|b$, $\left(d,m\right)=1$. Then:

$$\frac{a}{d}\equiv \frac{b}{d}\left(\mathrm{mod} m\right).$$

(8)

To prove the validity of this formula, let us denote $a=a_{1}d$, $b=b_{1}d$. Based on the assumption $m|\left(a-b\right)$, it is valid that $m|d\left(a_1-b_1\right)$. As $\left(d,m\right)=1$, it is valid that $m|\left(a_1-b_1\right)$. Then $a_1\equiv b_1\left(\mathrm{mod} m\right)$, thus $\frac{a}{d}\equiv \frac{b}{d}\left(\mathrm{mod} m\right)$.

Again, let $a\equiv b\left(\mathrm{mod} m\right)$ and $d>0$ be a common divisor of numbers $a$, $b$, $m$. Then:

$$\frac{a}{d}\equiv \frac{b}{d}\left(\mathrm{mod} \frac{m}{d}\right).$$

(9)

If it is true that$a\equiv b\left(\mathrm{mod} m\right)$, then there is such an integer $c$, that $a-b=mc$. After dividing by number $d$ we get $\frac{a}{d}-\frac{b}{d}=\frac{m}{d}c$, which means that $\frac{m}{d}|\left(\frac{a}{d}-\frac{b}{d}\right)$, and thus $\frac{a}{d}\equiv \frac{b}{d}\left(\mathrm{mod} \frac{m}{d}\right)$.

Next consider any natural number $m>1$. According to the division with remainder theorem [23], we can write every integer $n$ in the form:

$$n=m·q+r, 0\le r<m$$

(10)

While the number $r$ is called the remainder of division of the number $n$ by number $m$. Now let us decompose the set $\mathbb{Z}$ to subsets $R_0\left(m\right), R_1\left(m\right),\dots ,R_{m-1}\left(m\right)$ in such a way that $R_i$ is the set of all those integers whose remainder after dividing by a number $m$ is $i$.

Then the sets $R_i\left(m\right)$ are called the residual classes according to a module (or we talk about modulo) $m$. The residual classes are disjoint by pairs and each integer belongs to one of them. At the same time the set $R_i\left(m\right)$ is a set of all integers $x$, to which it applies that $x\equiv i\left(\mathrm{mod} m\right)$. If modulo is known, we simply refer $R_i$ instead of $R_i\left(m\right)$.

Integers $a$ and $b$ belong to the same modulo class $m$ if and only if $a\equiv b \left(\mathrm{mod} m\right)$. We can prove the validity of the statement from both sides.

I. Let us express the numbers $a, b\in R_i$ in the form:

$$a=m·q+i, b=m\cdot p+i.$$

(11)

Then $a-b=m\left(q-p\right)$, i.e., $m|a-b$, and then $a\equiv b\left(\mathrm{mod} m\right)$.

II. Now let $a\equiv b \left(\mathrm{mod} m\right)$ and $a=mq+i, b=mp+j (0\le i, j<m)$. Suppose for example that $i>j$. As $a\equiv b \left(\mathrm{mod} m\right)$, then $m|a-b$. However, then $m|\left(a-b\right)=\left[m\left(q-p\right)+\left(i-j\right)\right]$, out of which $m|\left(i-j\right)$, but that is a contradiction because $0<i-j<m$. Similarly, a contradiction arises from the assumption $i<j$. It must therefore apply $i=j$, and then numbers $a$ a $b$ belong to the same residual class.

The $m$-tuple of numbers $x_0,\dots ,x_{m-1}$is called a complete residual modulo system $m$, if $x_i\in R_i$ for $i=0, \dots , m-1$. We say that the residual class $R_i$ by module $m$ is reduced if $\left(i, m\right)=1$. For example, the residual class $R_2$ is reduced modulo 7, because $\left(2, 7\right)=1$. The class $R_0$ it is not reduced by any module.

If $R_i$ is a reduced residual class modulo $m$, then for any $x\in R_i$ it applies $\left(x,m\right)=1$. Because it is valid that $x\equiv i\left(\mathrm{mod} m\right)$, thus $m|\left(x-i\right)$, and therefore there exists such an integer $c$ that $x-i=mc$, thus $x-mc=i$. Then every common divisor of numbers $x$ and $m$ would also be a divisor of number $i$, and thus the common divisor of $i$ and $m$. However, as $\left(i, m\right)=1$, it is valid that $\left(x,m\right)=1$.

There exist $\phi \left(m\right)$ reduced residual classes of modulo $m$ [23]. We say that $\phi \left(m\right)$-tuple of numbers $y_1,\dots ,y_{\phi \left(m\right)}$ forms a reduced residual modulo system $m$ if numbers $y_i$ are selected one by one from the reduced residual classes. The elements of the reduced system are coprime with $m$. The reduced residual system can be obtained by omitting numbers that are commensurable with the module, from the complete. E.g., if $m=8$. The complete residual system consists e.g., of numbers $0, 1, 2, 3, 4, 5,6,7$. We will choose $0, 2, 4$ 6 from those because they are commensurable with $m$, so we get a reduced residual system of 1,3,5,7. It is valid that $\phi \left(8\right)=8\left(1-\frac{1}{2}\right)=4$.

Generally, all non-negative numbers less than $m$ coprime with $m$ form the smallest non-negative reduced residual system.

If $y_1,\dots ,y_{\phi \left(m\right)}$ is a reduced residual system modulo $m$ and $\left(m, c\right)=1$, then $c{y}_1,\dots ,c{y}_{\phi \left(m\right)}$ is a reduced residual system too, by module $m$. Numbers $y_1,\dots ,y_{\phi \left(m\right)}$ belong to different residual classes and the same can be said of numbers $c{y}_1,\dots ,c{y}_{\phi \left(m\right)}$ because of congruence $c{y}_i\equiv c{y}_j\left(\mathrm{mod} m\right)$ under the condition $\left(m,c\right)=1$ the following results:

$$y_i\equiv y_j\left(\mathrm{mod} m\right).$$

(12)

The count of numbers $c{y}_i$ is $\phi \left(m\right)$ while $\left(c{y}_i, m\right)=1$. It means the numbers $c{y}_i$ are selected one by one out of the reduced residual classes.

Let $x_1,\dots ,x_{\phi \left(m\right)}$ and $y_1,\dots ,y_{\phi \left(m\right)}$are any reduced residual systems modulo $m$. Then

$$x_1\dots x_{\phi \left(m\right)}\equiv y_1\dots y_{\phi \left(m\right)} \left(\mathrm{mod} m\right).$$

(13)

Each $x_i$is congruent with just one $y_j$ because both groups are selected one by one from the reduced classes. Additionally, the evidence then results directly from the properties of the congruences, while if:

$$\begin{gathered} a_1\equiv b_1\left(\mathrm{mod} m\right) \\ {a}_2\equiv b_2\left(\mathrm{mod} m\right) \\ \cdots \\ {a}_k\equiv b_k\left(\mathrm{mod} m\right) \end{gathered}$$

(14)

then $a_1{a}_2\dots a_k\equiv b_1{b}_2\dots b_k\left(\mathrm{mod} m\right)$.

A linear congruence with one unknown is a congruence in the form:

$$ax\equiv b \left(\mathrm{mod} m\right).$$

(15)

The solution of linear congruence is such a residual class $R_i\left(m\right)$ that $m|\left(ax-b\right)$ applies. A congruence is called solvable if it has at least one solution.

Congruence $ax\equiv b \left(\mathrm{mod} m\right)$ can also be written in the form:

$$ax=b+my,$$

(16)

which actually gives a linear Diophantine equation with two unknowns [17].

A linear congruence $ax\equiv b \left(\mathrm{mod} m\right)$ is solvable if and only if $\left(a,m\right)|b.$ If module $m$ and coefficient $a$ are coprime, then linear congruence is always solvable and the elements of one residual class are the solution.

Let $y\in \mathbb{Z}$ is a solution to congruence $ax\equiv b \left(\mathrm{mod} m\right)$ and let $y\in R_i\left(m\right)$. Then all the elements of the set $R_i$are a solution to congruence $ax\equiv b \left(\mathrm{mod} m\right)$. Thus, a solvable linear congruence has infinitely many solutions. This follows directly from the basic properties of congruences and residual classes. If $z\in R_i$, then $z\equiv y\left(\mathrm{mod} m\right)$ and $az\equiv ay\equiv b\left(\mathrm{mod} m\right)$.

If $\left(a,m\right)|b$, then congruence $ax\equiv b \left(\mathrm{mod} m\right)$ has just $\left(a,m\right)$ mutually non-congruent (or we talk about incongruent) solutions. Let us denote $d=\left(a,m\right), z=\frac{m}{d}$. Let $y$ is such a congruence solution $ax\equiv b \left(\mathrm{mod} m\right)$ to which it applies $0\le y<m$. Additionally, let us examine numbers that are in the form:

$$y+zs, \mathrm{where} s=0,1,\dots ,d-1.$$

(17)

These numbers are congruent $ax\equiv b \left(\mathrm{mod} m\right)$ because it is true that $a\left(y+zs\right)=ay+a\frac{m}{d}s\equiv b\left(\mathrm{mod} m\right)$ because $\frac{a}{d}s$ is an integer, and thus $a\frac{m}{d}s$ is a multiple of the number $m$. Now we indirectly prove that the numbers $y+zs$ are non-congruent with each other according to modulo $m$. Suppose:

$$y+z{s}_1\equiv y+z{s}_2\left(\mathrm{mod} m\right).$$

(18)

From this, based on common congruence simplifications, we get:

$$s_1\equiv s_2\left(\mathrm{mod} m\right),$$

(19)

which is not possible, because $s_1\ne s_2$ while $0\le s_1, s_2<m$. Vice versa, if $u$ and $v$ are different solutions to congruence $x\equiv b \left(\mathrm{mod} m\right)$, then the following applies:

$$au\equiv av\left(\mathrm{mod} m\right).$$

(20)

Then:

$$\frac{a}{d}u\equiv \frac{a}{d}v\left(\mathrm{mod}\frac{m}{d}\right).$$

As $\left(\frac{a}{d},\frac{m}{d}\right)=1$, it is valid that:

$$u\equiv v\left(\mathrm{mod} \frac{m}{d}\right).$$

(21)

So, all solutions of congruence $ax\equiv b \left(\mathrm{mod} m\right)$ that belong to the interval $\langle 0, m-1\rangle$ are congruent with $y$ by module $\frac{m}{d}$ and are in form of $ax\equiv b \left(\mathrm{mod} m\right)$ and all remaining solutions are congruent with some of the solutions.

A linear congruence can also be solved using Euler’s theorem [18]. If we have a congruence $ax\equiv b \left(\mathrm{mod} m\right)$ where $\left(a, m\right)=1$, then the number

$$a^{\phi \left(m\right)-1}b$$

(22)

is one of its solutions. Because it is true that $a\left(a^{\phi \left(m\right)-1}b\right)=a^{\phi \left(m\right)}b\equiv b\left(\mathrm{mod} m\right)$.

4. Research Methodology

The research was carried out at a selected university in the Slovak Republic with the knowledge and consent of the faculty management. Before the start of the research, all students of the 1st year of bachelor’s study in computer science study fields were addressed. A total of 38 students volunteered for the research. All participants in the research were informed about the anonymity of the obtained data. The methodological research is based on the claims of Dahlin and Watkins [24], according to which the connecting point between memorization and comprehension is meaningful repetition. 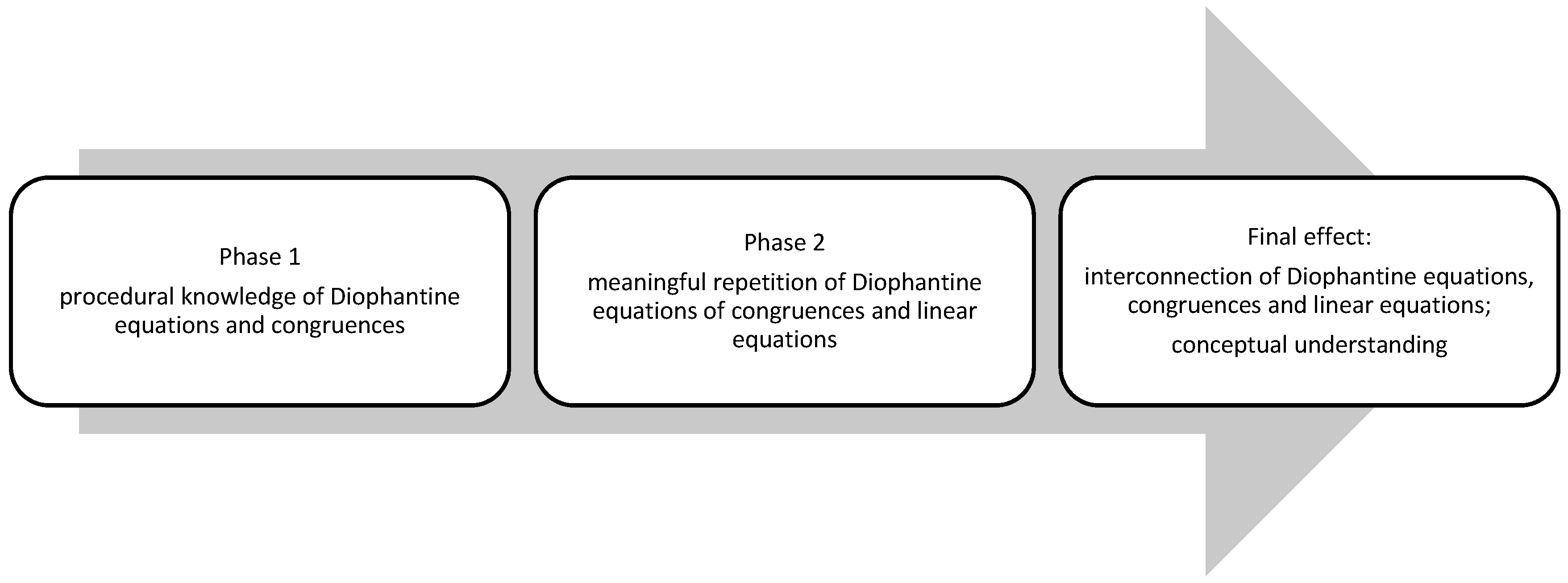Meaningful repetition creates a deep impression, which leads to memorization and can also lead to the “discovery of a new meaning”, which leads to understanding [25]. Therefore, we divided the teaching of congruences into two phases (Figure 1):

Phase 1—teaching congruences with a focus on the development of procedural knowledge about congruences, Phase 2—“meaningful repetition” of congruences in order to create a conceptual understanding of the concept of congruence in students. This division is theoretically based on the finding that improving procedural knowledge can support the improvement of conceptual knowledge. Evidence comes from studies of carefully constructed practical problems [26,27,28,29]. We used the solution of Diophantine equations in the second phase as a “tool” to connect between congruences and linear equations. According to [30], this connection is very important for the successful solution of congruences.

In the first phase of the research, students completed a seminar on mathematics consisting of two parts: (a) solving Diophantine equations, and (b) congruences. The seminar was realized in the form of full-time teaching. In this phase, students became acquainted with the basic algorithm for solving Diophantine equations. We solved linear Diophantine equations with two unknowns in the form $ax+by=c$, $a, b\ne 0$, while explaining the algorithmic solution procedure. As the solution procedure required knowledge of the Euclidean algorithm, this was taken over separately [31]. Subsequently, they adopted the concept of “congruence” and their basic properties. Then simple congruences (equations on the set $Z_n$) were solved. Within the curriculum of congruences, we first took over the basic properties of congruences and the basic theorems for working with congruences. We have separately explained the residual classes and definitions as a complete or reduced residual system. We have defined a linear congruence with one unknown in the form $ax\equiv b \left(\mathrm{mod} m\right)$ and showed an algorithm for its solution. We explained conditions for solvable congruence and what congruent and incongruent solutions mean (Section 3, part Equations (15)–(22)). The same time was devoted to both parts of the seminar. After completing the seminar, a pre-test was carried out, in which tasks from both parts of the seminar were equally represented (two tasks from each thematic area). Students had 60 min to solve the four tasks. We asked students to measure the real time they needed to solve each task in addition to solving the given tasks. In the second phase of the research, after passing the pre-test, the same students completed another part of the mathematics seminar, where attention was paid to the connection between congruences and Diophantine equations. In this part of the seminar, students were introduced to the method of using congruences to solve Diophantine equations (Section 3, Equation (16)). This can be considered a meaningful repetition in order to link the solution of congruences with the solution of equations. Thus, students can use already acquired algebraic knowledge and skills in solving congruences. After the second part of the mathematics seminar, students completed a post-test, which included two problems to be solved by Diophantine equations and two problems for congruences (as in the pre-test). In addition to solving the problems, they also recorded the time needed for solving.

We sought answers to the following research hypotheses by content analysis of respondents work and statistical analysis of respondents success in pre-test and post-test:

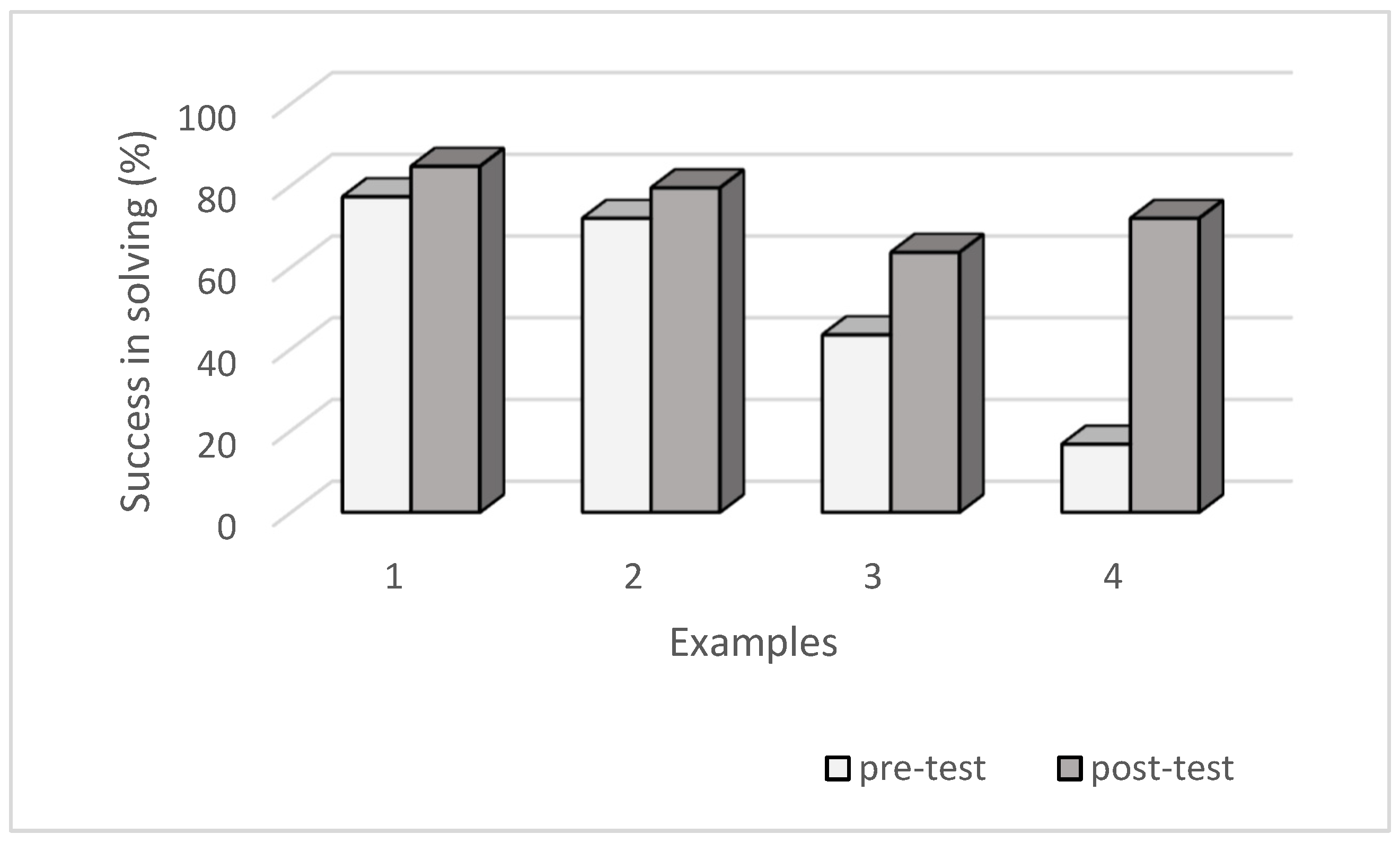
Hypothesis (H1):

Linking congruences with the solution of Diophantine equations and linear equations will increase the success of students in solving congruences.

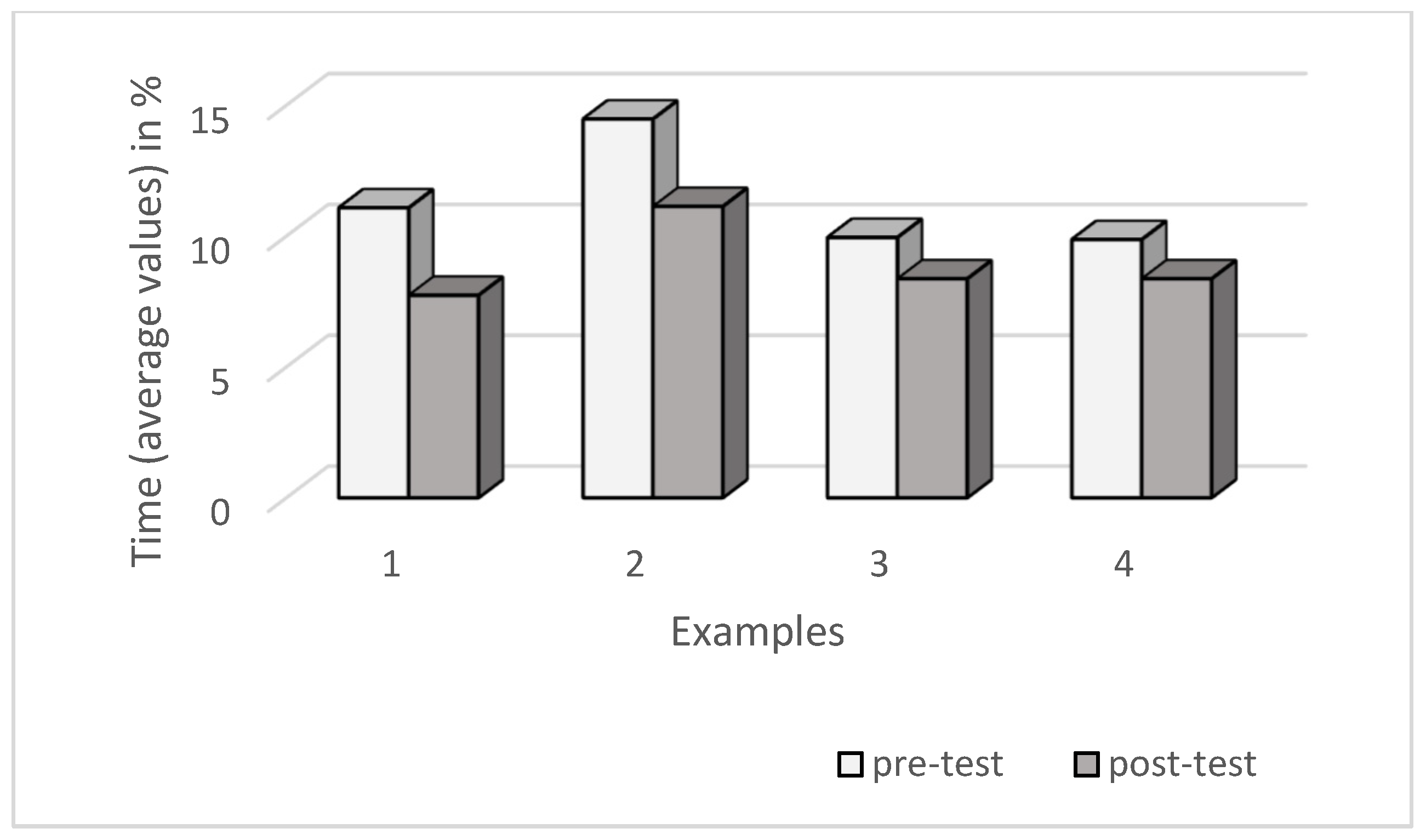
Hypothesis (H2):

Conceptual understanding of congruences will reduce students’ time to solve congruent problems.

5. Research Results

5.1. Analysis of the Success of Respondents in Solving Tasks

The results (number of points) that the students achieved in the pre-test and in the post-test are shown in Figure 2.

In Figure 2 we can see that the students in the pre-test and in the post-test achieved different results (number of points). We wondered if these differences were also statistically significant. A parametric paired t-test can be used to verify the statistical significance of the differences between the two tests in the results obtained. A prerequisite for its correct use is the fulfillment of the assumption of a normal distribution of the observed feature. In our case, we verified the assumption of a normal distribution of both sets by the Shapiro–Wilk test.

As the assumption of a normal distribution of observed traits is not substantiated, we used the nonparametric Wilcoxon signed rank test, which is a nonparametric analogy of a paired parametric t-test, to verify the statistical significance of differences in the level of observed traits.

In our case, the observed characters were X, Y, where X is the number of points that students gained in the pre-test and Y is the number of points that students gained in the post-test. Because we assume that students received higher scores in the post-test, in this case we will use the one-sided Wilcoxon test. We tested hypothesis ${\mathrm{H}}_0$: the medians X, Y are equal to the one-sided alternative hypothesis H₁ that the median Y is greater. We implemented the test in the STATISTICA program. After entering the input data, we got the following results into the output set of the computer: the value of the test criterion of the one-sample Wilcoxon test (Z = 5.373) and the value of the probability p (p = 0.000). We evaluated the test using the value of p (p is the probability of an error we make when we reject the tested hypothesis). If the calculated value of the probability p is sufficiently small (p < 0.05 or p < 0.01), we reject the tested hypothesis (at the significance level 0.05 or 0.01). As the calculated value of the probability p < 0.01, at the level of significance α = 0.01 we reject the tested hypothesis H₀. This means that by taking over or by supplementing the curriculum focused on the relationship between Diophantine equations and congruences in the optional seed, the level of students’ knowledge in the field of congruences increased statistically significantly.

Subsequently, we were interested in whether knowledge in solving problems in the field of congruences statistically significantly improved, and also whether it improved for Diophantine equations. For this reason, we verified the statistical significance of the differences in the success of solving each of the four pre-test and post-test tasks by using the Wilcoxon one-sample test. The obtained results are clearly recorded in

Table 2. Wilcoxon signed rank test (success in pre-test and post-test).

Problem	Z	p-Value
1	2.950	0.003 *
2	2.094	0.036 *
3	4.372	0.000 *
4	5.232	0.000 *

Note. Statistically significant values are marked with an asterisk in the table.

.

The results of the test showed that in all four tasks, students achieved a statistically significantly higher success rate in the post-test than in the pre-test. This confirmed the validity of the research Hypothesis (H1).

5.2. Analysis of the Length of Time Required to Solve Tasks

Average number of minutes that the students needed in the pre-test and in the post-test are shown in Figure 3.

In Figure 3 we can see that there are differences between the average time that students needed to solve the problems in pre-test in post-test. We also verified whether these differences are statistically significant in the case of using the Wilcoxon signed rank test. We proceeded analogously as in the previous case—when analyzing the success of solving problems in the pre-test and post-test. We calculated the value of the single-sample Wilcoxon test criterion (Z = 4.839) and the probability value p (p = 0.000). We also evaluated the test when using the value of the probability p. As the calculated value of the probability p < 0.01, at the level of significance α = 0.01 we reject the tested hypothesis H₀. This means that by teaching the curriculum focused on the relationship between Diophantine equations and congruences in the selective seminar, the time that students needed in the post-test to solve problems was statistically significantly reduced.

Subsequently, we were interested in whether time decreased statistically significantly not only in solving problems in the field of congruences but also Diophantine equations. For this reason, we used the Wilcoxon single-sample test to verify the statistical significance of the differences in time that students needed to solve each of the 4 pre-test and post-test problems. The obtained results are clearly recorded in

Table 3. Wilcoxon signed rank test (time required to solve pre-test and post-test tasks).

Problem	Z	p-Value
1	4.022	0.000 *
2	3.456	0.001 *
3	2.187	0.029 *
4	2.113	0.035 *

Note. Statistically significant values are marked with an asterisk in the table.

.

The results of the test showed that in all four problems, students achieved a statistically significantly shorter time in the post-test than in the pre-test. In other words, the difference between the time that students needed to solve a given problem (each) in the post-test is statistically significantly shorter than the students needed to solve an adequate problem in the pre-test. This confirmed the validity of the research Hypothesis (H2).

6. Discussion

In the pre-test, which followed the first phase of teaching congruences, students recorded very low success in solving problems focused on congruences (success rate was 43% or 17%). Congruences were a new concept for them and, according to students, it was an isolated concept for them (72% of students). Isolated knowledge leads to the acquisition of skills without understanding [32]. The solution of congruences was for them a “branched” algorithm, the memory of which caused them problems. This was evidenced by the large number of unresolved problems. Our findings confirmed the fact that learning new concepts is difficult for students if there is no network of previously learned concepts and skills with which to combine a new topic [33]. Despite sufficient time to solve the pre-test, the students were unable to reconstruct the insufficiently memorized algorithm. This indicates their focus on acquiring procedural skills without understanding the individual steps of the algorithm [34]. However, a conceptual understanding of a new concept is also necessary for the successful solution of problems, and this requires the connection of new knowledge with already acquired knowledge [35]. In our case.

There is a need to link the concept of “congruence” with knowledge of equations and their solutions. Based on the results of the pre-test, students did not find this connection. The same conclusion was found out by [36], according to who university students in the USA, future teachers of mathematics did not find linear congruences analogous to equations. The high success of students in the pre-test in solving Diophantine equations was probably conditioned by the existing connection with the term “equation” and students learned a new algorithm for solving another type of equation. It is also evidenced by the fact that some students solved Diophantine equations by choosing one unknown as a parameter and then expressing the other unknown depending on the value of the parameter. In rare cases, we also recorded a solution by trial and error. When solving Diophantine equations, students showed faith in their own ability to solve the equation, because they could use their already acquired knowledge and skills in solving equations. In solving the congruences, the students relied on the limited possibilities of the memorized “branched” algorithm. In the post-test, the students were divided into two groups for Diophantine equations. One group of students (mainly those students who successfully solved both problems on Diophantine equations in the pre-test) did not use congruence to solve a simpler problem. They preferred the already “proven” way of solving Diophantine equations. This approach of students corresponds to the knowledge that when students learn a new, more effective procedure, they do not always abandon the old procedure. Instead, they use either the old procedure or the new one, depending on the situation. Only with time and practice they stop using fewer effective methods [37,38]. In the second (more complex) problem, they considered a method of solution—to use or not to use congruences. According to their own statements, they considered which of the procedures would lead to the result in a shorter way. In determining how to use as few computational steps as possible, students analyzed the problem, demonstrating the ability to think of higher order [39]. These students mastered the solution of congruences at a higher level of knowledge, such as understanding, because they were able to evaluate the suitability of using congruences to solve a given problem [40]. The second group (most students) solved Diophantine equations using congruences, i.e., they evaluated the use of congruences as a more efficient way of solving Diophantine equations. Replacing learned practices with new more effective solutions are part of the development of strategic skills [33]. This group of students was also more successful in solving congruences. Overall, in the post-test, the success of students in solving congruences increased significantly, mainly due to their connection with the solution of equations. The number of unresolved tasks decreased significantly.

In the post-test, there was also a statistically significant decrease in the time that students needed to solve particular problems, which indicates an increase in the procedural fluency of the use of learned algorithms. Procedural fluency is the ability to flexibly, accurately, and efficiently perform learned problem-solving procedures (mostly algorithms) in conjunction with the ability to assess the appropriateness of using a given procedure [33]. Students will acquire procedural fluency in the use of their strategic abilities to choose between effective procedures. This finding indicates an increase in the conceptual understanding of the concept of “congruence” and also an understanding of the algorithm for solving congruences. According to [41], experience in solving diverse problems using developed procedural fluency in conjunction with experience in solving problems help students gain new conceptual knowledge. The flexibility of procedural knowledge is positively related to conceptual knowledge [42].

7. Conclusions

To understand professional problems, computer science students need a conceptual understanding of the mathematical background of a given issue. This mathematical knowledge is often far removed from the mathematical knowledge that students acquired in previous mathematical education. In such a case, the teacher faces the problem of how to present the new subject to students, because conceptual understanding requires the connection of new knowledge with already acquired knowledge. Based on the results of our research, one of the possible ways is to divide teaching into two phases. First, to create an isolated island of procedural skills related to the subject matter and then, by “meaningful” repetition, to create a link between the new and the already acquired, thus ensuring the necessary conceptual understanding. In teaching congruences, we confirmed that Diophantine equations are a suitable tool to support the development of conceptual understanding of congruences. A certain degree of acquisition of procedural skills in solving congruences, which students acquired in the first phase of the seminar, was a suitable springboard for the use of congruences in solving equations. The search for similar possibilities to connect the isolated requirements of professional subjects for the conceptual understanding of mathematical concepts or procedures could contribute to the streamlining of mathematical courses in non-mathematical study fields of universities.