Teacher Interventions for Advancing Students’ Mathematical Understanding

Abstract

The relationship between teacher interventions and students’ mathematical thinking has been the subject of inquiry for quite some time. Using the Pirie–Kieren theory for dynamic growth in mathematical understanding, this study documents teacher interventions that support students’ growth toward developing a general understanding of a mathematical idea in a designed learning environment. By studying the interactions of seven middle school students and the teacher-researcher working on a two-week unit on geometric transformations within a dynamic geometry environment, this study identified nine major categories of teacher interventions that support and extend students’ investigations of mathematical ideas around geometric transformations. The typology of teacher interventions reported in this study provides a cognition-based framework for teacher moves that extend and advance students’ mathematical understanding.

1. Introduction

The relationship between teacher interventions and students’ mathematical thinking has been the subject of inquiry for quite some time [1]. There is a consensus that the teacher plays a crucial role in guiding students towards developing a deeper understanding of mathematical ideas [2], relying on approaches and tools that support mathematical reasoning [3,4]. Indeed, a variety of metaphors have been introduced to describe multiple roles that the teacher plays in the process of advancing children’s mathematical thinking, which amongst many include the teacher as a facilitator, the teacher as an orchestrator of learning, the teacher as a co-learner, and the teacher as a responder to students’ thinking. Common to all these various characterizations are three specific teaching actions that are assumed to optimize both student autonomy and their mathematical advancement. These include eliciting, supporting, and extending [5,6,7]. Eliciting actions invite students to share their ideas and encourage elaborations on and comparison of solution methods. Supporting actions attempt to coordinate and manage students’ work. Here, the teacher may suggest strategies, offer interpretations, and record and/or re-voice student ideas. Extending actions are considered to be interventions that extend mathematical reasoning, particularly in terms of generalizing their strategies or ideas and developing mathematically appropriate justifications [6,7].

There is evidence that in classrooms that tend to support inquiry, teachers frequently exhibit eliciting actions, as they ask students to share ideas and then use them to encourage group discourse. The most prevalent supporting actions reported in the literature include reminding students of task goals and what they already know, revoicing learners’ ideas, and introducing alternative strategies and conceptual explanations [6,8,9]. Although common practices associated with extending have been conceptualized to include encouraging reasoning, encouraging reflection, pressing for justification and generalization, and creating a space for the development of new mathematical insights [6,7,9], the potential outcome of these actions relative to learners’ mathematical cognition remains unclear. In this work, we examined the types of teacher interventions that seemingly assisted a cohort of middle school students in discovering and generalizing the properties of geometric transformations in a dynamic geometry environment. Relying on the Pirie–Kieren theory of growth in mathematical understanding, we traced the specific domains of mathematical understanding that were provoked, promoted, or established in the presence of these interventions. Our data analysis focused on identifying teacher intervention types and their impact on students’ mathematical development. Specific questions guiding our analysis included: (1) What are the types of teacher interventions that support students in discovering and generalizing the properties of geometric transformations in a dynamic geometry environment? (2) How does students’ mathematical understanding evolve in the presence of these types of interventions?

2. Review of Literature on Teacher Moves

The literature on classroom discourse has identified teacher’s verbal and non-verbal moves that fall in a range of effectiveness in supporting students’ growth in mathematical understanding and discussed the differences between less-productive and more-productive discourse patterns. In this section, we will first review studies that examine particular teacher moves and frameworks that categorize teacher moves from a variety of perspectives. We will then address how the use of the Pirie–Kieren theory offers a new perspective by connecting the teacher act to the particular level of student understanding that it activates, supports, or extends.

One genre of research on teacher’s pedagogical actions examines individual teacher acts, such as re-voicing (repeating and possibly reformulating student’s utterances through repetition, expansion, or rephrasing [10]), eliciting (the act of determining what students know and how they think [5,6]), and questioning [11]. Another body of work depicts a variety of dichotomous interaction patterns that differ in their potential to foster student reasoning. For instance, Wood [12] distinguished between the funneling pattern, in which a teacher provides a series of leading questions in an attempt to guide students to a predetermined solution procedure, and the focusing pattern, in which teachers’ questions serve as attempts to orient the conversation to aspects of student thinking, where students are encouraged to explain their thinking. Similarly, Knuth and Peressini [13] differentiated between univocal and dialogic discourse. In univocal discourse, the teacher is the sole authority to evaluate all contributions, whereas in dialogic discourse the teacher and students share authority in class discussion. Although the studies on individual teacher acts identify some powerful teacher moves that foster student mathematical understanding, they do not offer a detailed account of the complexity of teacher moves.

A number of studies have organized teacher moves into frameworks for different purposes. A subset of the frameworks emphasizes pedagogical actions that support conceptual understanding and mathematical meaning-making. For instance, Anghileri [14] described environmental provisions; explaining, reviewing, and restructuring; and developing conceptual thinking as three levels of teacher scaffolding that support children’s mathematical development. Environmental provisions are not direct interactions between the teacher and students, but instead are decisions that the teacher makes about the structure and environment of the classroom. Scaffolding techniques at this level include organizing the classroom, the sequencing and pacing of classroom events, grouping children during work time, selecting tasks and tools, and providing emotive feedback. The next level of teacher scaffolding directs toward the mathematical ideas the students are to learn and understand. Explaining, reviewing, and restructuring are three types of teacher scaffolding at this level, each of which includes a set of teacher moves. Scaffolding at the level of developing conceptual thinking aims to create opportunities to promote conceptual understanding. Teacher moves at this level include developing visual or verbal representational tools; making connections among different mathematical ideas and concepts; and facilitating discussion, in which students engage in meaningful mathematical discussions that expand their conceptual understanding. Cengiz, Kline, and Grant [6] extended the work of Fraivillig et al. [5] and developed the Extending Student Thinking (EST) framework, which examines the instructional actions teachers implement during extending episodes that encourage reflection, reasoning, and justification. The framework clusters teacher moves into eliciting, supporting, and extending. Teacher eliciting actions aim to draw out, identify, clarify, and understand students’ ideas and contributions. Supporting actions are to support students’ conceptual understanding. Examples of supporting actions include suggesting an interpretation of a claim/observation; reminding students of the goal of the discussion, the problem, or other information; repeating a claim; recording student thinking; and introducing different representations/contexts. Extending actions are instructional actions that allow students to further develop connections among ideas and solution methods and move beyond their existing mathematical knowledge. Inviting students to evaluate a claim or an observation, providing reasoning for a claim, comparing different methods, using the same method for new problems, and providing counter speculation for a claim are examples of teacher’s extending actions. More recently, Ellis, Özgür, and Reiten [7] developed the Teacher Moves for Supporting Student Reasoning (TMSSR) framework to examine teacher moves specific to inquiry-oriented instruction. Eliciting, responding, facilitating, and extending are four categories of teacher moves in this framework. The teacher moves in each category are organized based on their level of potential for supporting student reasoning. Eliciting answers, eliciting facts or procedures, asking for clarification, figuring out student reasoning, and checking for understanding are examples of lower-potential moves for eliciting student reasoning, whereas eliciting ideas, eliciting understanding, and pressing for explanation are examples of higher-potential eliciting moves. When responding to student reasoning, lower-potential moves include correcting student errors, re-voicing, encouraging student re-voicing, and validating a correct answer, and higher-potential moves include promoting error correction and re-presenting. The lower-potential moves in facilitating student reasoning include cueing, funneling, Topaze effect, providing information, providing procedural explanation, and providing summary explanation, whereas the higher-potential moves in this category include providing guidance, encouraging multiple solution strategies, providing alternative solution strategies, and providing conceptual explanation. When extending student reasoning, encouraging evaluation, pressing for precision, and Topaze for justification fall into the lower-potential moves, and encouraging reflection, encouraging reasoning, pressing for justification, and pressing for generalization are examples of higher-potential moves. Although frameworks similar to the above ones emphasize teacher moves that support and extend conceptual understanding and mathematical reasoning, they are not developed to capture a specific level of mathematical understanding a teacher move aims to activate, support, or extend. Therefore, there is a need to develop frameworks that characterize teacher moves based on their potential to support students’ cognitive actions.

The development of cognition-based frameworks of teacher moves relies on robust theories on student cognition. The Pirie–Kieren theory [15] perceives student understanding as a dynamic, leveled but nonlinear recursive process, and describes eight potential layers of cognitive actions associated with the growth in mathematical understanding. Each level of understanding is contained with succeeding levels and is dependent on the forms and processes within and, further, is constrained by those without. The theory has been proved useful to capture the growth in mathematical understanding at different grade levels across mathematical contexts [16,17,18]. Moreover, the theory acknowledges the importance of social interactions and tools in students’ growth in mathematical understanding. Therefore, it provides a viable framework to examine teacher moves that support students’ growth in mathematical understanding.

3. Theoretical Framework

The Pirie–Kieren theory [15] contains eight potential layers of action for describing a person’s growth in understanding of a specified concept (Figure 1). The eight nested circles provide a two-dimensional diagrammatic representation of the theory. This nesting illustrates that each layer contains all previous layers and is included in all subsequent layers to emphasize the embedded nature of mathematical understanding. Although the more abstract and general understanding becomes as the rings of the model expand outward, growth in understanding is not seen to happen in such a linear way. Instead, growth occurs through a continual movement back and forth within the layers of knowing.

According to this theory, the process of coming to understand starts with Primitive Knowing, which connotes a starting place for growth in any particular mathematical understanding rather than low-level mathematics. Its core content is all the information brought to the learning situation by a learner, including both appropriate and inadequate or even misconceived knowledge. At the second level, called Image Making, the learner is engaged in specific physical actions that aim at helping him/her to develop a mental image about the concept. Prominent in this layer is the need to “act” on actual models as a way of gaining a sense of the concept under consideration. The images about the concept developed at this level cannot be separated from the specific actions that produce them. By the level of Image Having, single activity-associated images are replaced by a mental picture which frees the mathematical activity of the learner from the need for particular actions or examples. The learner at this level is able to imagine a concept unconstrained by the physical processes that produced the image and carry out specific mathematical actions with a general mental plan. At the level of Property Noticing, the learner is able to reflect on his/her mental image and recognize the attributes and features of it. Besides noticing the properties internal to a specific image, the learner is capable of noticing the distinctions, combinations, or connections between multiple mental images. When Formalizing, the learner abstracts a method or common quality from classes of mental images. The person at this level has class-like mental objects built from the noticed properties, the abstraction of common qualities, and the abandonment of the origins of one’s mental action. The description of these class-like mental objects results in the production of mathematical definitions or algorithms. The level of Observing entails the ability to consider and reference one’s own formal thinking. The learner at this level is able to observe, structure, and organize personal thought processes and recognize the ramifications of thought processes. Structuring occurs when the learner attempts to think about his/her formal observations as a theory. This means that the learner is aware of how a collection of theorems is connected and seeks the justification of statements through logical or meta-mathematical argument. A person at the level of Inventising is able to break free of structured knowledge and create new questions that result in the learner’s use of the structured knowledge as primitive knowing when investigating beyond the initial domain of investigation.

Although developed to describe the learner’s growth in mathematical understanding, the theory acknowledges the importance of social interaction in students’ growth in mathematical understanding. Indeed, Pirie and Kieren [15] outlined three classes of teacher interventions. Teacher’s provocative actions have the effect of moving students to an outer layer of understanding, teacher’s invocative actions cause students to fold back to an inner layer of understanding in order to enlarge or alter their understanding, and teacher’s validating actions allow students to confirm existing understanding. These classes of teacher interventions, however, were not further explored in the original model. To date, only a handful of studies have utilized this theory to examine teacher actions that seem to advance or inhibit the development of students’ mathematical understanding [19,20]. Therefore, further research that utilizes this theory to examine teacher interventions not only has the potential to deepen our understanding of the impact of particular teacher moves on student cognition but also enrich the theory itself.

4. Methodology

4.1. Method and Participants

The data for this study come from existing videos and the associated verbatim transcripts collected by the authors through a constructivist teaching experiment [21] that aimed to investigate students’ construction of mathematical generalizations in a technology-rich learning environment. In designing the teaching experiment, we considered four aspects of the instructional environment that are critical in supporting students’ mathematical development, including mathematical tasks, the structure of classroom activity, the computer-based tools students use, and classroom discourse [22]. The use of technology in the teaching experiment was conceptualized to serve at least three functions—(1) a scaffolding tool that could be used by the teacher to provoke reflection, (2) a semiotic/communication media that could promote focused discussions between the teacher and students as the properties of mathematical objects were observed, (3) an amplifier of cognition—giving both the researchers and the learners means for observing patterns of actions.

The teaching experiment included 10 sessions, each of which lasted for approximately two hours. The participants were seven middle school students enrolled in a summer enrichment program taught by the authors, where they engaged in exploring the properties of geometric transformations with the Geometer’s Sketchpad (GSP). Five of the participants were rising 8th graders and two were rising 9th graders when they participated in the summer enrichment program. Consistent with the principles of the teaching experiment methodology, the co-authors served as teachers and witnesses to the events and analyzed the data at each stage in preparation for subsequent activities. Each author took part in instructing or witnessing the sessions. Yao and Manouchehri [23] provided more information about the teaching experiment.

The tasks in the teaching experiment focused on exploring the properties of geometric transformations and the compositions of geometric transformations. Each task only served as an initial problem for exploration and was further extended by the teacher-researchers during the subsequent class discussion to generalize the mathematical ideas developed by the students.

Table 1. Mathematical tasks in the teaching experiment.

Day #	Mathematical Topic	Description of Mathematical Tasks
Day 1	Properties of geometric transformations	Task 1: What do you know about geometric transformations? Task 2: Can the image under a rotation be produced by a composite reflection?
Day 2	Properties of geometric transformations	Task 3: Decide whether each given statement is sometimes/always/never true for each isometry. Task 4: Find the center of rotation given a preimage and its image under rotation.
Day 3	Defining parameters of geometric transformations	Task 5: Find the line of reflection given a preimage and its image under reflection. Task 6: Can you find the center of rotation and the line of reflection given a preimage and its image resulting from the composition of rotation and reflection?
Day 4	Application of geometric reflection	Task 7: Telephone pole problem: A length of wire is attached to the top of each pole and it is also staked to the ground somewhere between the two poles. Where should the wire be staked so that the minimum amount of wire is used?
Day 5	Composition of transformations	Task 8: Telephone pole problem extension. Task 9: Explore the results of compositions of transformations. Task 10: Make statements about the results of compositions of transformations that contain “never” or “always”.
Day 6	Order of composite transformations	Task 11: Does order matter when composing transformations?
Day 7	Composition of reflections	Task 12: Given a preimage and its image resulting from the composition of reflections over two parallel lines, can you find the two reflections? Task 13: Given a preimage and its image resulting from the composition of reflections over two intersecting lines, can you find the two reflections?
Day 8	Properties of transformations	Task 14: Generate statements that are always true for one type of transformation but not necessarily true for other types of transformations. Task 15: One student claims that all translations and rotations can be decomposed into two reflections. Do you believe him?
Day 9	Composition of transformations	Task 16: Find all the possible compositions of I, R, and S, where I is an identity, R is a reflection over the y-axis, and S is a counterclockwise 90° rotation.
Day 10	Application of geometric reflection	Task 17: Explore coordinate rules for reflection. Task 18: Explore the relationship between the reflectional and rotational symmetries of regular polygons.

offers a brief description of the tasks developed and implemented during the teaching experiment. Whole group discussions surrounding the lessons served as data for the current study.

4.2. Data Analysis

The data processing and analysis consisted of two phases. During the first phase, the videos of each session were first segmented into episodes based on transitions in mathematical activities. The Pirie–Kieren theory was then used to trace the students’ growth in mathematical understanding in each episode. A coding framework was developed to facilitate the creation of understanding maps (

Table 2. Coding framework developed for the levels of understanding of transformations.

Level of Understanding	Actions Associated with Transformations	Example Action from the Data
Primitive Knowing	Know how to perform transformation actions with GSP; Be able to recognize a transformation given a preimage and its image.	Recall their knowledge of rotation in order to develop an idea for finding the center of rotation given a preimage and its image.
Image Making	Perform transformation actions in order to decide its result; Make conjectures or observations about the result of a single or composite transformation based on visual clue on the screen.	Match the image under rotation and the image resulting from the composition of two reflections over two intersecting lines by continuously dragging.
Image Having	Imagine/describe the possible or impossible results of a single or composite transformation without performing the associated transformation action(s); Represent a mental image about the result of a single or composite transformation with GSP.	Hold the mental image that corresponding points under reflection are equidistant to the reflection line when asked to find the coordinates of a point reflected over a line.
Property Noticing	Abstract properties from dynamic images about a single or composite transformation through dragging or visual perception; Search for numeric pattern regarding a single or composite transformation through performing repeated computing or measuring actions with GSP.	Observe that the angle between the two reflection lines is half of the angle of rotation when the image under rotation and the image resulting from a composite reflection are coincident.
Formalizing	Develop/apply/describe a construction of a defining parameter of a transformation; Develop/apply/describe a construction of a transformation equivalent to a given composite transformation; Express/extend the generality of a property about a transformation.	Develop a formal construction of a composite reflection equivalent to a single rotation.
Observing	Connect one transformation with another transformation; Connect the use of transformations and their compositions in different mathematical contexts such as geometry, function, and matrix.	Reason that the image resulting from the composition of a rotation and a translation can be produced with four reflections after formalizing the procedures for finding a composition reflection equivalent to a single rotation and a composite reflection equivalent to a single translation.
Structuring	Develop theories that connect multiple mathematical relationships/properties of transformations; Justify mathematical statements about transformations through a chain of deductive reasoning.	Formally justify why the composition of two translations can never be a single rotation.
Inventizing	Create new concepts as a result of fully understanding of transformations and their compositions.	Not observed from the data.

). Analysis at this phase resulted in an understanding map for each episode.

The second phase involved the analysis of teacher interventions. When analyzing the properties and generalizations emerging in each episode, we observed an explicit connection between the teacher moves and students’ understanding activities. The prominence of teacher interventions made the data viable for investigating teacher actions and their impact on students’ understanding activities. A typology was developed to categorize the teacher interventions that seemingly supported and extended students’ understanding activities. When developing the typology, we considered the intent behind each teacher intervention relative to students’ cognition as evident in their work and the specific level of understanding that the intervention targeted, activated, or supported.

5. Results

In this section, we will first offer a typology that categorizes teacher interventions into different types based on their intentions relative to students’ actions and the targeted layer of understanding. The sample vignettes focused on sessions during which the learners examined the defining properties of transformations (Task 3) and the composition of transformations (Tasks 2, 9, 10, and 12). We will then share two sample episodes of understanding events, relying on the Pirie–Kieren theory to demonstrate how different types of teacher interventions work together to support students’ investigations of mathematical ideas and the development of generalizations around geometric transformations.

5.1. Types of Teacher Interventions for Advancing Mathematical Understanding

The analysis of interactions between the teacher and students revealed nine categories of teacher interventions. Each category describes a type of intervention that appeared to foster the construction, refinement, or justification of a mathematical idea by the students. We will elaborate on each intervention type and provide illustrative examples from the data to illuminate the content and outcomes of each.

5.1.1. Activating Primitive Knowing

Activating Primitive Knowing accounts for teacher actions that prompted students to search for and collect usable knowledge that was needed to move to an outer layer understanding. Primitive Knowing is the starting place for growth in any particular mathematical understanding. It is observed to be everything that a learner knows and can do except the knowledge about the particular concept that is being considered by the observer. When building an understanding of a particular topic, a learner needs to search usable knowledge from his Primitive Knowing domain and decide what specific piece might be relevant to the current problem situation. The process of searching for usable knowledge is cognitively demanding because a learner might not realize what previous knowledge might be useful or applicable to a new problem situation. Assuming this to be the case, the teacher may need to help students retrieve what they know that might apply. Such was the case in our data. The teacher in this study used different actions to elicit students’ previous knowledge, relying on either clue giving or questioning techniques. She directed students to a particular piece of knowledge that she considered useful in thickening learners’ understanding. The following vignette illustrates the teacher’s efforts towards activating Primitive Knowing. In this vignette, students were asked to find the center of rotation given a pre-image and an image. Students in turn asked the teacher to tell them the angle of rotation first. Rather than giving them an answer, the teacher provoked the students to use an idea from their previous conversation to find the angle of rotation.

Vignette 1

Student 4: Do you know how many degrees it rotates?

Teacher: I don’t know how many degrees, but based on your previous conversation, can you figure it out?

Student 6: You just do the opposite of what we did.

Teacher: Yeah, you just do the opposite of what we did, but how can you find it?

Student 1: Move the corresponding line segments to where they intersect and use that angle as the angle of rotation.

The teacher’s questioning triggered students to consider a generalization they had previously constructed, which states that the angle between a pair of corresponding sides under rotation and the angle of rotation are congruent. The students applied this generalization and suggested finding the angle of rotation by measuring the angle of a pair of corresponding sides. One student’s comment, “do the opposite of what we did”, indicates that this method was not just a simple recall of an existing idea. Rather, it involves inserting the idea into the new problem. After finding the angle of rotation, the students formulated an idea for finding the center of rotation. The idea involves drawing a line from a point and another line from its corresponding point and then adjusting the angle between the two lines to make it equal to the angle of rotation.

5.1.2. Refining Primitive Knowing

Refining Primitive Knowing accounts for instances in which the teacher identified and took actions to refine the students’ incomplete or inappropriate understanding of a mathematical idea at the Primitive Knowing level. When building an understanding of a specific mathematical idea, students bring their previous knowledge and experiences into the process, some of which may not be helpful in advancing their understanding due to flawed mental images, incomplete definitions, or the limited scope of the knowledge itself. To deepen their understanding of the current mathematical idea, the teacher takes actions to address gaps in learners’ previous knowledge (e.g., asking questions to make students realize the flaw or incompleteness in their previous knowledge, introducing a precise mathematical definition). Refining Primitive Knowing is an invocative action in that it often causes students to fold back from their current layer of understanding to Primitive Knowing. Students might use the refined idea at the Primitive Knowing level to modify a mathematical idea constructed at an outer layer of understanding or to construct a new mathematical idea. The following excerpt exemplifies a teacher intervention that aimed at refining Primitive Knowing. In this vignette, the students were asked to generate a list of statements that they had known about isometries. A few students stated that rotation and reflection change orientation and that translation moves a figure without altering its orientation. This indicated the students used orientation to mean the direction of a figure. After understanding students’ use of the word “orientation”, the teacher introduced the mathematical definition of the orientation of the vertices and used reflection as an example to illustrate the concept of orientation reversing relying on images she had created on the board.

Vignette 2

Teacher: How about rotation? I’m really curious about what you mean by changing the orientation. What did you mean? When you said it changes the orientation, what do you mean by orientation?

Student 3: When I said changes the orientation, I meant kinda like a flip, well, not a flip, but a turn. For example, your head is at your feet.

Teacher: Mathematically, when we say something changes the orientation, it’s a little bit different. So, I was trying to understand what you meant. (Moves closer to the blackboard) if I start at this point (referring to $A$ in Figure 2), and move along that path, then the image of that motion would just be reversed. So, if this is $A$, that’s $A^{\prime }$; if this is $B$, it’s $B^{\prime }$, right? If this is $C$, where’s $C^{\prime }$ ? Here? (Students agree). When this is $D$, this is $D^{\prime }$. Now, let’s read. $A, B, C, D,$ clockwise. Here, $A^{\prime }, D^{\prime }, C^{\prime }, B^{\prime }$. That’s what we mean mathematically when you said orientation changes. With reflection, notice that we said my left was her right and that her right was my left. We say the orientation changes. But with rotation, it stays the same. I’m telling you that because I want us to have the same language.

The students appeared to have grasped the notion of orientation reversing, since they used it to reason about the results of compositions of transformations in later discussions. For instance, when the teacher asked students about the possible results of a reflection followed by a rotation, they argued it could only be a reflection, as the preimage and its image would have reversed orientations.

5.1.3. Encouraging Image Reviewing

Encouraging image reviewing consists of teacher interventions that engaged students in reviewing and reflecting on their current mathematical activities. Developing mathematical understanding frequently involves carrying out specific activities to form an initial conception for the meaning of a mathematical concept or a preliminary idea for solving a particular mathematical problem. However, learners, who are simply taking actions on mathematical objects, might see their previous actions as completed and, therefore, might not automatically look back and reflect on their current work. External interventions might be necessary to engage learners in reviewing and reflecting on actions taken on mathematical objects and the product resulting from those actions. Through reviewing and reflecting on their current work, students might adjust their behavior and form a tentative idea regarding how to solve the problem at hand. This type of teacher intervention allowed students to alter their actions without having yet developed a clear mental plan for solving a problem. Vignette 3 presents an illustrative example of teacher engaging students in reviewing and reflecting on their current mathematical work in their process of developing a procedure for finding two reflections whose composition would produce the same image as a given rotation. The event started with the teacher asking students to find two reflections whose composition would produce the same image as 180$°$ rotation. Although the two reflections that students suggested to use did not produce the desired image (Figure 3), the teacher engaged them in reviewing the diagram on the screen, hoping that they would extract information to guide their subsequent actions.

Vignette 3

Teacher: Well, one thing we noticed is that the labels match now. The orientation. Do you notice it? $E^{\prime }$, $E″$, etcetera, etcetera. So we have the orientation fixed. Now the question is moving this guy. How? (S3 raises her hand) Go!

Student 3: To make it like that, I guess you can draw a line here, so this entire thing will flip.

Teacher: (Moves the second line segment so that it intersects with the first line segment) Like that?

Student: Yeah.

Teacher: It’s not there. What now?

Student 1: You can just slide it over.

Teacher: How?

Student 1: Translation.

In the above vignette, the teacher engaged students in reviewing the diagram on the screen and pointed out that the image under rotation and the image resulting from the composition of the two reflections had the same orientation. The students proposed matching the two final images by a translation, an idea that was likely informed by the act of image reviewing. Although the students had not developed a construction of the two reflections, the act of image reviewing helped them develop a tentative idea for matching the two final images by continuously dragging and adjusting the two reflection lines. Later, the matched images allowed them to notice the properties of the “desired” diagram, which eventually contributed to the formation of a formal construction.

5.1.4. Externalizing Mental Images

Externalizing mental images consists of teacher actions that externalized students’ mental representations of a mathematical idea. It occurred when the students seemed to have maintained or developed a particular mental image of a mathematical idea and the teacher took actions to elicit and represent it. Tall and Vinner [24] coined the construct of a concept image to describe the total cognitive structure that is associated with the concept, which includes all the mental pictures and the associated properties and processes. Although a mental image is the internal representation of a mathematical idea, it can be modeled with an external representation. The externalized mental image might become an object in subsequent discussions. This might lead students to refine their mental image, observe new properties of the mental image, formalize an idea extracted from the mental image, or justify the validity of the idea. When a mental image is represented on the GSP screen, the elements of the externalized mental image become dynamically linked and manipulatable. This allows students to take actions on the externalized mental image and notice its properties. The following vignette illustrates how externalizing mental images fostered generalizations. In this vignette, although the students initially stated that all pairs of corresponding sides under 180$°$ rotation are parallel, when the teacher planned to rotate a triangle 180$°$, they requested to set the preimage figure at a specific orientation and the center at a particular location before executing the 180$°$ rotation. In order to extract the students’ mental images, the teacher took the effort to understand their request and represent their idea with the GSP.

Vignette 4

Teacher: Okay. So here is the line (constructs a line from A). And now you want the center to be here (moves C to the line and moves it back)?

Student 3: No. A, C, and that dot have to be on the same line.

Teacher: Ah, (moves C so that AC is on the horizontal line) so you want it to be like this.

Students: Yes.

Teacher: Now what?

Students: Put the center on the line.

Teacher: (Brings the center to the line) Now what?

Students: Now rotate it.

Teacher: Now rotate it. How many degrees?

Students: 180 degrees.

Teacher: Are you sure?

Students: Yes.

Teacher: Okay (rotates triangle ABC 180$°$ about the center as shown in Figure 4).

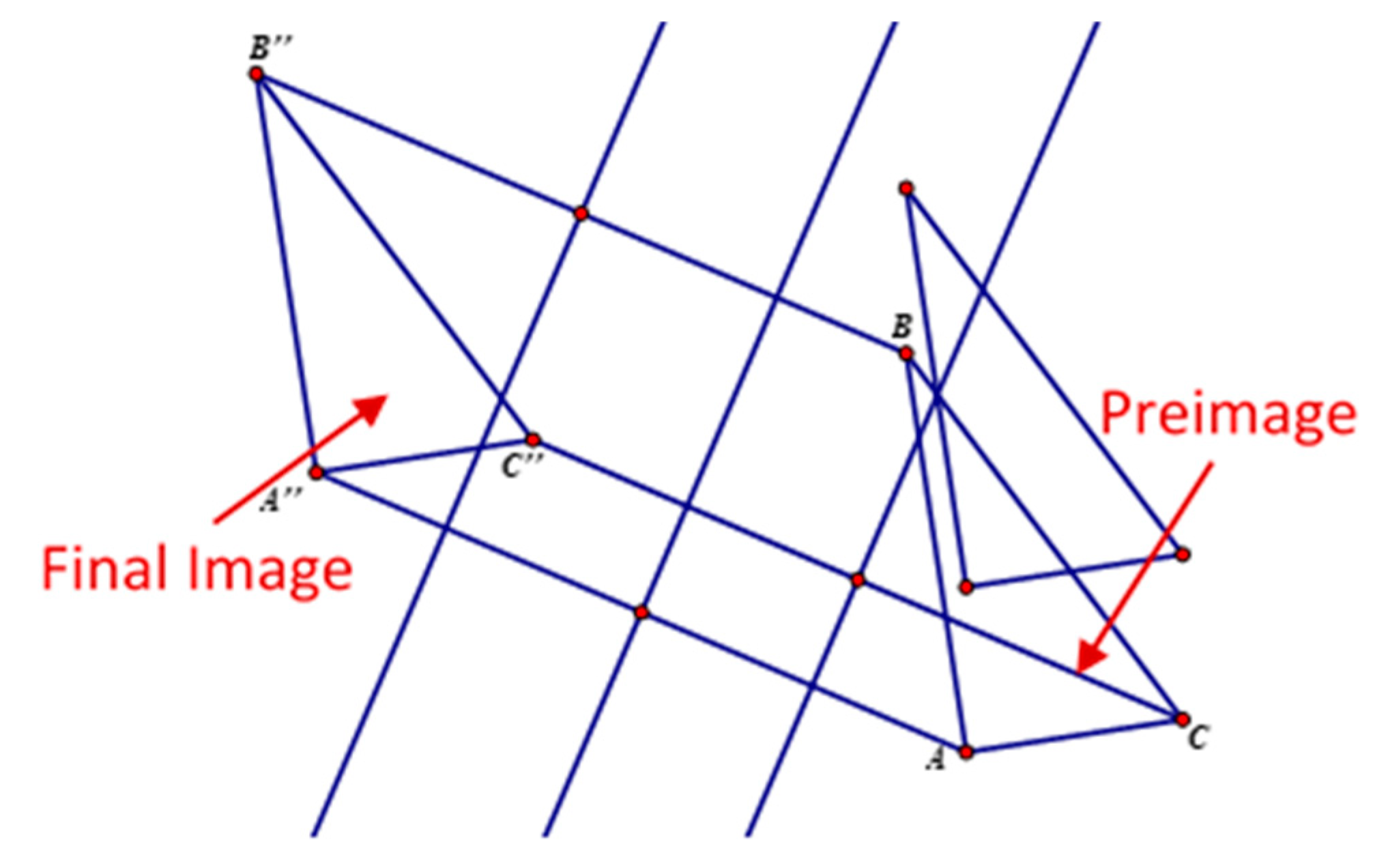
In the above vignette, the students’ request suggested that they held a mental image that all pairs of corresponding sides under a 180$°$ rotation were parallel only when the center was on the horizontal line containing one side of the preimage. In the course of interaction, the teacher elicited this mental image and represented it on the GSP screen. Later, the teacher dragged the rotation center and vertices of the preimage. The students observed that the corresponding sides of the preimage and its image were always parallel under 180$°$ rotation regardless of the orientation of the preimage and the location of the center of rotation.

5.1.5. Focusing Attention on Mathematical Properties/Relationships

Focusing attention on mathematical properties/relationships refers to teacher interventions that directed students’ attention to the specific mathematical features of a problem, idea, or representation. A similar type of teacher intervention has been discussed in the literature. For instance, Boaler and Brodie [11] identified “orienting and focusing” as an important type of teacher questioning strategy that directed students’ attention to key aspects of a problem situation. In this study, the most common type of focusing action took the form of the teacher directing students’ attention to specific relationships or elements in a diagram both verbally and/or by GSP-based actions. As a proactive action, a successful focusing action often moved the students to the stage of Property Noticing as they observed and expressed a new property or relationship. The following vignette illustrates the teacher’s use of questions to direct students’ attention to a specific mathematical relationship. In this vignette, the teacher directed students’ attention to the relationship between the two reflection lines after they matched the image under 180$°$ rotation and the image resulting from the composition of two reflections.

Vignette 5

Teacher: You got it. Very nice! (Students cheering). (Refers to reflection lines in Figure 5) what do you guys notice about the mirrors?

Student 3: They are sort of perpendicular.

Prior to the teacher intervention, the students solely focused on dragging the two reflection lines in order to match the two images. They used the immediate feedback from each dragging action to inform their subsequent dragging moves without considering the relationship between the two reflection lines. The teacher’s question directed the students’ attention to the relationship between the two reflection lines. Based on the visual clue of the diagram, the students noticed that the two reflection lines were perpendicular, a property that they immediately verified by measurement. This property became crucial in assisting the students to formulate the conjecture that the angle of the two reflection lines was half the rotation angle.

5.1.6. Encouraging Extending Mathematical Ideas

Encouraging extending mathematical ideas accounts for instances in which the teacher encouraged students to extend a mathematical idea beyond the problem, situation, or case in which it originated. When encouraging extending mathematical ideas, the teacher might intend for students to extend the domain of validity of the idea, synthesize previously explored mathematical ideas, discover a new mathematical relationship, and/or subsume the idea to a more generalized idea. As a result, the students generate something new, such as a new domain of the validity of an idea, new members of a class, a new relationship, or a new structure. This type of teacher interventions can make students move toward Property Noticing or Formalizing when the idea can be applied to solve the new problem. It can also make students fold back to an inner layer of understanding, such as Image Having or Image Making, when the idea is insufficient to solve the new problem. The teacher interventions can expand the domain of the validity of an idea, as illustrated in the following vignette. It occurred in the context where the students were asked to find the two reflections given a preimage and its image resulting from the composite reflection over a pair of vertical parallel lines. Initially, the students held the conception that the two reflection lines had to be in between the preimage and its image.

Vignette 6

Teacher: So you said as long as the two mirrors are six units away from each other it is going to work.

Student 1: Hmm, well, I mean it has to be in between.

Teacher: So you think the two mirrors have to be in between the two figures.

Student 2: They can be on the figure.

Teacher: Okay, so the mirrors have to be inside or on the figure. If it’s outside the figures, it wouldn’t be possible. Do you all believe that’s true?

Students: (Students in silence for about 30 s) I don’t know. I want to try this again.

[Students work individually for about 5 min]

Teacher: So, tell me which case you tried?

Student 1: (Points to the screen) I did that one, and it worked. And then I did a case where both lines were on the opposite side of the image.

Teacher: (Moves the two mirrors to the left of the preimage) how far are the two mirrors?

Student 1: Six.

Teacher: Six. (Makes the two reflection lines six units apart and then reflects the preimage over the two reflection lines) What do you notice? So the distance between the two mirrors is still six. What if I move the two mirrors? (Moves the two reflection lines but keep their distance fixed, see Figure 6) what do you notice? (After a few seconds) let me move them again. What conclusion can you draw?

Student 2: As long as the mirrors are equidistant to each other, no matter where the two reflection lines are, the figure will not change.

In the above vignette, the teacher’s questions and dragging actions were crucial in assisting the students to extend this initial idea to a broader mathematical context. By asking whether or not the reflection lines had to be in between the two images, the teacher promoted students to reconsider their initial idea. After trying out cases with their own computer, the students found that the reflection lines could be outside the two images. By moving around the two reflection lines while keeping their distance fixed, the teacher made the students realize that the two reflections could be anywhere as long as their distance was fixed. This indicates that the students had extended the domain of validity of their initial idea.

5.1.7. Encouraging Formalizing Mathematical Ideas

Encouraging formalizing mathematical ideas refers to teacher interventions that encouraged students to formally express a mathematical idea that they applied to solve problems but not yet explicitly articulated with formal language. An analysis of the data in this study indicates that sometimes students may not formally articulate a mathematical idea without external prompts. Therefore, teacher intervention became crucial in assisting students to formalize their mathematical ideas. As a proactive action, encouraging formalizing mathematical ideas intends to move students’ understanding to Formalizing. The following vignette is an illustrative example in which the teacher encouraged students to formalize their generalization that the angle of a pair of corresponding sides of a preimage and its image under rotation is congruent to the angle of rotation. It occurred after the students explored 180°, 90°, and 60° rotations and discovered that the angle of a pair of corresponding sides was 180°, 90°, and 60°, respectively. Although the students seemed to have already developed the idea that the angle of a pair of corresponding sides of a preimage and its image under rotation was congruent to the angle of rotation, this generalized idea was not explicitly stated. The teacher encouraged the students to articulate this generalized idea.

Vignette 7

Teacher: Can you make a generalized statement based on what we have done?

Student 2: A more generalized statement?

Teacher: Yes, a more generalized statement.

Student 1: If the angle of rotation is whatever degree then the corresponding lines would intersect at the same angle.

Student 3: X degrees or the same degrees. So, the angle rotation determines the angle of intersection.

In the above vignette, by asking students to make a generalized statement the teacher provided the students an opportunity to articulate the generalization emerging from their exploration of different cases. The students were aware that the statement subsumed their previous statements.

5.1.8. Synthesizing Mathematical Ideas

Synthesizing mathematical ideas accounts for instances in which the teacher directly formalized a mathematical idea that the students had constructed but not yet formally articulated. Mathematical ideas might be expressed with informal, pre-formal, and formal representations. When synthesizing mathematical ideas, the teacher takes an active role and uses formal mathematical language to describe the mathematical ideas that students have expressed. This type of teacher intervention is different from encouraging formalizing mathematical ideas in that it is the teacher rather than the students who offers the formal statement. As a proactive action, synthesizing mathematical ideas often intends to move the students from an inner layer of understanding to Formalizing. It creates a generalized statement that includes a class of objects. The following vignette exemplifies the teacher’s synthesis of a mathematical idea. Prior to the vignette, through exploring the cases of 180$°$, 75$°$, and 125$°$ rotations, the students developed a constructible procedure for finding a composite reflection that produces the same image as a given rotation.

Vignette 8

Teacher: So here is my preimage and here is a center. Let’s mark the center and let’s rotate this guy. And this time, I’m not going to even care about the labeling. How many degrees do you want to rotate?

Student 3: 666.

Teacher: 666 degrees, rotate. Now let’s find the two reflections. I know that I need two intersecting lines and the center is at the point of intersection of the two lines. Fair enough? So this is what I will do. I will get a line going through that point. That’s my first mirror. How to get my second mirror?

Student 3: Rotate the mirror 333 degrees from the center.

Teacher: 333 degrees, rotate (rotates the first reflection line about the center 333$°$). Okay, let’s see now. let’s reflect this one (reflects the figure across the first reflection line). Let’s change the color a little bit. Now let’s reflect it about the second mirror. If you guys are right, the two images should match. Do you think it’s going to match?

Students: Yes.

Teacher: Okay, reflect it (reflects the resulting image over the second reflection line). They matched! This is fascinating you guys. So, what happened? Pick whatever angle you wish as your angle of rotation, rotate the object about some arbitrary center at that angle of measure, pick the center as the intersection of the two intersecting mirrors where the angle of the mirrors is going to be half of the rotation. Are we good? Draw a picture to capture all the information.

Although the students applied the procedure to find a composite reflection that produced the same image as a 666$°$ rotation, this general procedure had not yet been formally articulated thus far. By describing the generalized procedure, the teacher articulated the construction of a composite reflection equivalent to a given rotation.

5.1.9. Encouraging Justifying Mathematical Ideas

Encouraging justifying mathematical ideas consists of teacher actions that engaged students in explaining the validity of a mathematical idea relying on the properties of a mathematics object or through creating an argument consisting of several connected statements. This type of teacher intervention might take different forms: requesting that students explain a generalization, engaging the students in connecting a generalization with known mathematical properties, or engaging students in building a chain of logical reasoning. The levels of formality of the justification might also vary. The amount of support the teacher provides also varies by episode. Although this type of intervention did not happen in all the episodes, it was intended to move the students to the Structuring stage. The following vignette illustrates how the teacher engaged students in using geometric properties and chains of logical reasoning to justify newly constructed generalizations. It occurred when the teacher asked students to justify their claim that a translation followed by a translation could never be a rotation. The teacher then engaged students in using the procedure of finding the center of rotation and proof by contradiction to prove their statement.

Vignette 9

Teacher: What’s your guess as to predict my behavior? One approach is a lazy approach, which is putting a point as the center and then experimenting on it to see under what conditions the image under rotation matches with the images resulting from the composition of the two translation. But you guys had a very important and fruitful discussion a couple of days ago about given an image and its preimage how I am going about finding the center of rotation.

Student 5: Oh, connecting the corresponding points and then you find the perpendicular bisector.

Teacher: Okay, see, you can predict what I may do. And then we can test to see whether we can indeed rotate the object. So let’s do that. In fact, you can replicate it on your own computers. So $B$ to $B″$, construct a segment; $A$ to $A″$, construct a segment; and $C$ to $C^{\prime }$, construct a segment. And then, what did you say? Find a perpendicular bisector?

Students: Yes.

Teacher: Okay, so here construct the midpoints and the perpendicular lines. (Constructs perpendicular bisectors of line segments connecting the corresponding points one by one, see Figure 7). What’s happening here?

Student 5: They’re on the same angles, so you can’t find one.

Student 1: All lines are parallel lines. Here it is. We have a proof!

Teacher: So, there is no center?

Student 3: Therefore, you can’t rotate it, aha!

In the above vignette, the teacher reminded the students of the discussion they had had on how to find the center of rotation. The students recalled a procedure that they had constructed previously for finding the center of rotation. To find the hypothetical center, the students suggested constructing perpendicular bisectors of the lines connecting the corresponding points of the preimage and final image. The teacher carried out those actions with GSP. The students noticed that all the perpendicular bisectors were parallel and concluded that the rotation did not exist. Here, the teacher essentially engaged students in proving by contradiction. When she asked the students to find the center, the teacher essentially made them assume that a translation followed by a translation could be a rotation. The students and teacher then attempted to find a center by using the procedure for finding the center of rotation. However, the construction revealed that all of the perpendicular bisectors were parallel, and, therefore, there was no center, which contradicted the fact that any rotation has a center.

5.2. Interactions in Growth in Mathematical Understanding

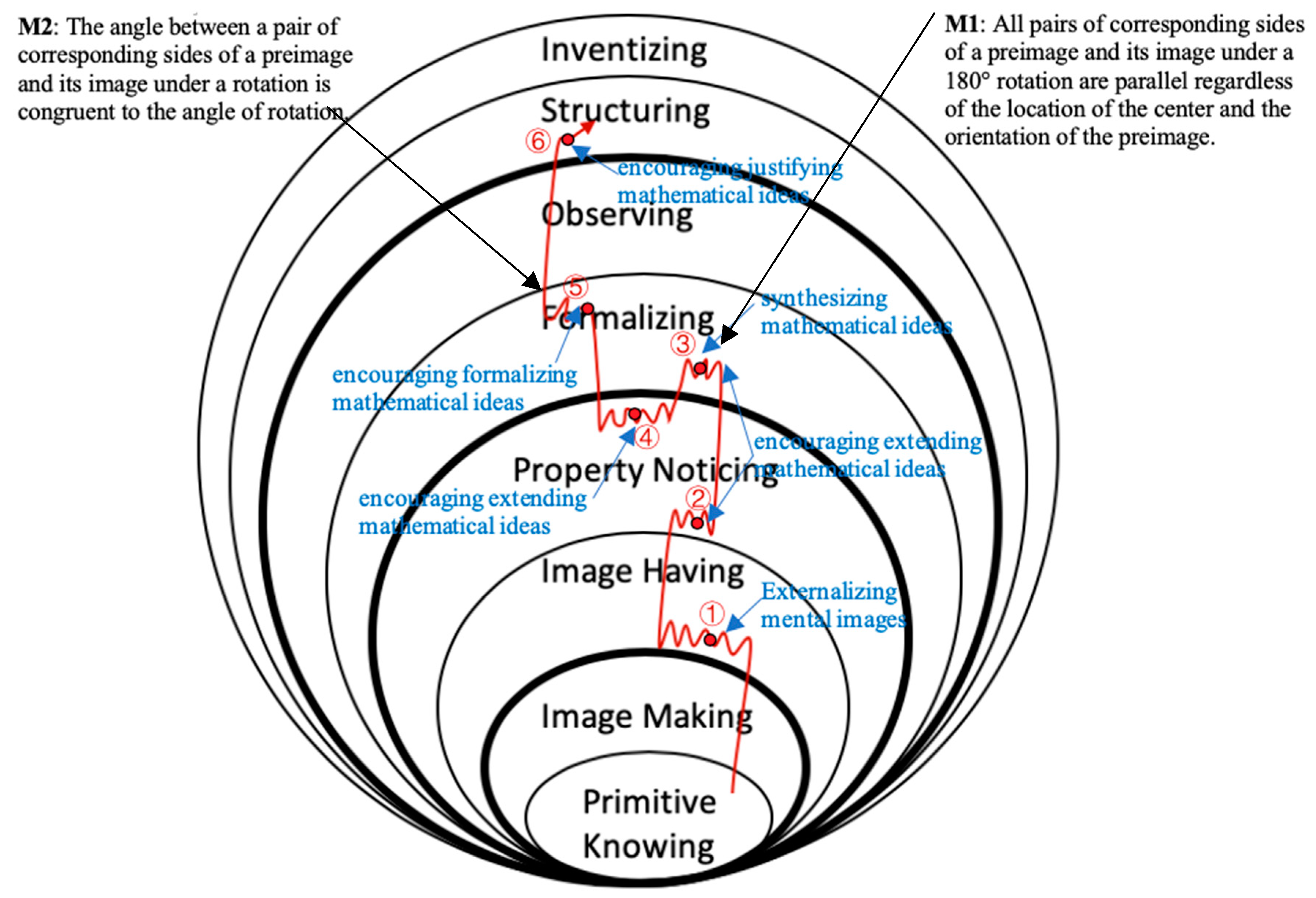
The analysis revealed patterns of students creating and refining their mathematical ideas through cyclical interactions, in which each round of interaction supported the growth in mathematical understanding. This section presents two episodes that demonstrate the manner in which teacher interventions supported students’ construction, refinement, and justification of mathematical ideas. The first episode describes the students’ process of formalizing a construction of two reflections whose composition produces the same image as a given rotation. The second episode describes the process of formalizing a general relationship, which states that the angle between a pair of corresponding sides under rotation is congruent to the angle of the rotation. Although one is a construction procedure and the other is a general property, their emergence and evolution were shaped by interactions between the students and teacher. Note that each understanding map includes a path of understanding and teacher interventions along the path. A serrated line along a path indicates extensive work at a particular level. The more serrations there are, the more arduous the understanding process. The important mathematical ideas students constructed were identified along the path. A red point indicates the presence of a certain type of teacher intervention, which often consisted of a series of teacher actions.

Episode I: When exploring the relationship between reflection and rotation, the students formalized a procedure for constructing a composite reflection equivalent to a given rotation. Figure 8 represents the process to gain this understanding.

The episode started by the teacher creating an image under 180$°$ rotation and an image under reflection and then asking students whether the image under 180$°$ rotation could be obtained by reflection. The students made a conjecture that the composition of two reflections might produce the same image as the 180° rotation. The teacher then asked the students where to place the second reflection line. One student suggested drawing a horizontal segment at the bottom of the GSP screen as the second reflection line. It turned out that the two images did not match (see Figure 3). The teacher engaged the students in reviewing the image under the composite reflection and the image under the 180° rotation (encouraging image reviewing). The teacher intervention made the students realize that the image under the composite reflection could be translated to the image under the 180° rotation. Relying on the immediate feedback from the GSP screen, the students then matched the two images by continuously dragging and adjusting the two reflection lines. The students’ actions with GSP indicated that they were Image Making. After students matched the two images, the teacher asked what they noticed about the two reflection lines (focusing attention on mathematical properties). The teacher intervention moved students to Property Noticing (①→②). The students observed that the two segments seemed to be perpendicular and verified this observation with an angle measurement (see Figure 5).

The teacher then asked the students how to find the two reflections if the angle of rotation is 75$°$ (encouraging extending mathematical ideas). The students made a conjecture that the angle of the two reflection lines might be 37.5$°$ since, in the previous case, 90$°$ was one half of 180$°$. In an attempt to find the two reflection lines, the students folded back from Property Noticing to Image Having (②→③) and suggested drawing two segments whose angle was 37.5$°$. The teacher used rotation to construct two segments with a fixed angle of 37.5$°$ and then carried out the two reflections (externalizing mental images). It turned out that the two images did not match. The students then suggested moving the two reflection lines to match the two images, which indicated that they moved from Image Having back to Image Making (③→④). The teacher dragged the point of intersection of the two reflection lines and moved it toward the center of rotation (focusing attention on mathematical properties). The students noticed the center of rotation was the point of intersection of the two reflection lines when the two images matched (④→⑤).

The teacher then asked the students to find two reflections whose composition would produce the same image as a 125$°$ rotation relying on a minimum number of guesses and checks. In doing so, the teacher aimed to move the students in the direction of formalizing a general construction of the two reflections (encouraging formalizing mathematical ideas). The students suggested drawing two segments passing through the center of rotation with a fixed angle of 62.5$°$, which indicates that the students had started to formalize a construction of the two reflections, although a formal construction was not explicitly articulated. Since the reflection lines were drawn as segments rather than as straight lines in all three cases, the position of the center of rotation in the three cases triggered one student to conjecture that the center of rotation seemed to be the midpoint of the two reflection lines. The class debated on this conjecture and used the case of a 666$°$ rotation to test this conjecture. In the diagram of the 666$°$ rotation, the teacher moved the center of rotation along the two reflection lines and pointed out that a line of reflection is not a segment but a straight line and, therefore, it does have a midpoint (refining Primitive Knowing). Here, the teacher folded back to Primitive Knowing to address the students’ misconception about reflection lines (⑥→⑦). The teacher then synthesized this formal procedure and asked the students to draw a picture to capture this generalization (synthesizing mathematical ideas).

Episode II: In this episode the students formalized and justified the relationship that the angle between a pair of corresponding sides under rotation is congruent to the angle of the rotation. Figure 9 represents the process to gain this understanding.

The episode occurred in a context where the students were asked to decide the truth of a given list of statements for each type of transformation. One of the statements was that all the corresponding sides of a preimage and its image are parallel. When considering the truth of the statement for rotation, the teacher took actions to elicit students’ mental images by asking students to direct her interaction with the GSP (externalizing mental images). The way the class interacted with the GSP indicated that they held the conception that all pairs of corresponding sides of a polygon and its image under 180$°$ rotation were parallel only when the center of rotation was on the line containing one side of the preimage (see Figure 4). To extend this mental image, the teacher first moved the center of rotation off the line that contains one side of the preimage and then dragged the vertices of the preimage to change its orientation (encouraging extending mathematical ideas). The students moved to Property Noticing (①→②) and observed that all the corresponding sides remained parallel regardless of the location of the center of rotation and the orientation of the preimage. When the teacher asked the students to predict what would happen if the angle of rotation was not 180$°$ (encouraging extending mathematical ideas), one student said the property would hold for a 540$°$ rotation. The teacher formalized this idea and concluded that the property would hold for any multiple of 180$°$ (synthesizing mathematical ideas, ②→③). Another student then conjectured that all the pairs of corresponding sides in a 90$°$ rotation would be perpendicular. After creating a diagram of a 90$°$ rotation, the class verified the conjecture by measuring the angles of pairs of corresponding sides of the preimage and its image. The teacher asked the students what would happen if the angle of rotation was 60$°$ (encouraging extending mathematical ideas). The students stated that the angle between the corresponding sides of a preimage and its image under a 60$°$ rotation would be 60$°$. The statement was verified in a similar fashion to the case of the 60$°$ rotation. The teacher encouraged the students to make a more generalized statement (encouraging formalizing mathematical ideas, ④→⑤). The students generalized that the angle of any pair of corresponding sides under rotation is congruent with the angle of rotation. The teacher then engaged students in justifying the generalization, which moved the class to Structuring (⑤→⑥). She drew a quadrilateral ABCD, rotated it around a center, and constructed four concentric circles using the center of rotation as the center of the circles and the distances between the center and the vertices as the radii. The teacher explained to the students that, under rotation, all parts move at the same angle around those concentric circles (encouraging justifying mathematical ideas).

6. Discussion and Conclusions

Pirie and Kieren [15] suggested classifying teacher interventions as provocative, invocative, and validating based on their immediate impact on the direction (inward or outward) of an understanding activity. In this study, we observed teacher–students interactions in whole-class discussions and identified nine types of teacher interventions that seemingly supported students in the course of developing a more general understanding of mathematical ideas. Each of the nine types of teacher interventions identified in this study might roughly fall into one of the three classes. Since both activating primitive knowing and refining primitive knowing draw attention to students’ Primitive Knowing from an outward understanding level, they are instances of the teacher’s invocative actions. Encouraging image reviewing, externalizing mental images, encouraging expressing generalizations, and synthesizing mathematical ideas are instances of the teacher’s validating actions because they frequently aim to support activity within a particular level of understanding. The actions of focusing attention on mathematical properties/relationships, encouraging extending mathematical ideas, and encouraging justifying generalizations intend to move students’ understanding activities to an outward level and are, therefore, instances of teacher’s provocative actions. By specifying the possible types of teacher interventions, this study enriched the classes of teacher interventions described in the Pirie–Kieren theory. These types of teacher interventions can be used to further examine teacher–students interactions in regard to growth in mathematical understanding within the Pirie–Kieren theory.

Different frameworks have been developed to characterize teacher moves [6,7,14]. The types of teacher interventions identified in this study are different from the current frameworks of teacher moves in at least two ways. First, the typology was built upon a widely used theory of mathematical understanding. Each type of intervention considers a particular layer of students’ mathematical understanding that teacher actions intend to act upon. These cognition-based interventions represent the ways in which the teacher, students, and mathematical task interact with each other to advance mathematical understanding. When developing the typology, we considered both the form and the content of teacher actions. As a result, the same teacher action could fall into different intervention categories depending on the particular level of understanding the action attends to at a particular moment. Moreover, the teacher interventions in this typology spread levels of mathematical understanding. It includes not only teacher actions that directly engage students in extending, formalizing, and justifying mathematical ideas but also those that set the stage for students to begin to explore the generality of a mathematical idea. It demonstrates how teacher interventions can support students throughout their process of developing a general and structural understanding of a mathematical idea.

Although the typology that we proposed in this study does not stipulate the specific actions that a teacher should take at different levels of understanding, it describes what a teacher could do to advance mathematical understanding to a higher level based on his/her knowledge of student thinking. When students are building mental images for a problem, a teacher can productively guide them in retrieving and refining their previous knowledge, reviewing and reflecting on their current mathematical activities, and representing their mental images. Following the construction of a mental image, a teacher can focus learners’ attention on mathematical relationships and encourage them to extend and formalize mathematical ideas. Once students formalize a mathematical idea, a teacher can engage them in justifying it. Therefore, the typology can enhance teachers’ pedagogical repertoire to guide students towards discovering and justifying mathematical ideas.

In this work, we relied on data from a teaching experiment involving seven middle school students. Unlike typical classrooms where teachers are constrained by factors such as time, content coverage, and testing, we (teacher-researchers) were free to design pedagogical interventions that supported students’ mathematical investigations. Although this setting differed significantly from what typically occurs in mathematics classrooms globally, it certainly provides an important view of the types of teacher interventions that can support and extend students’ investigations of mathematical ideas and development of generalizations. Future work is needed to consider the ways in which these actions could translate to regular classrooms.