Are Physical Experiences with the Balance Model Beneficial for Students’ Algebraic Reasoning? An Evaluation of two Learning Environments for Linear Equations
Abstract
1. Introduction
1.1. Using the Balance Model for Linear Equations Solving
1.2. Current Study
2. Materials and Methods
2.1. Participants
2.2. Conditions
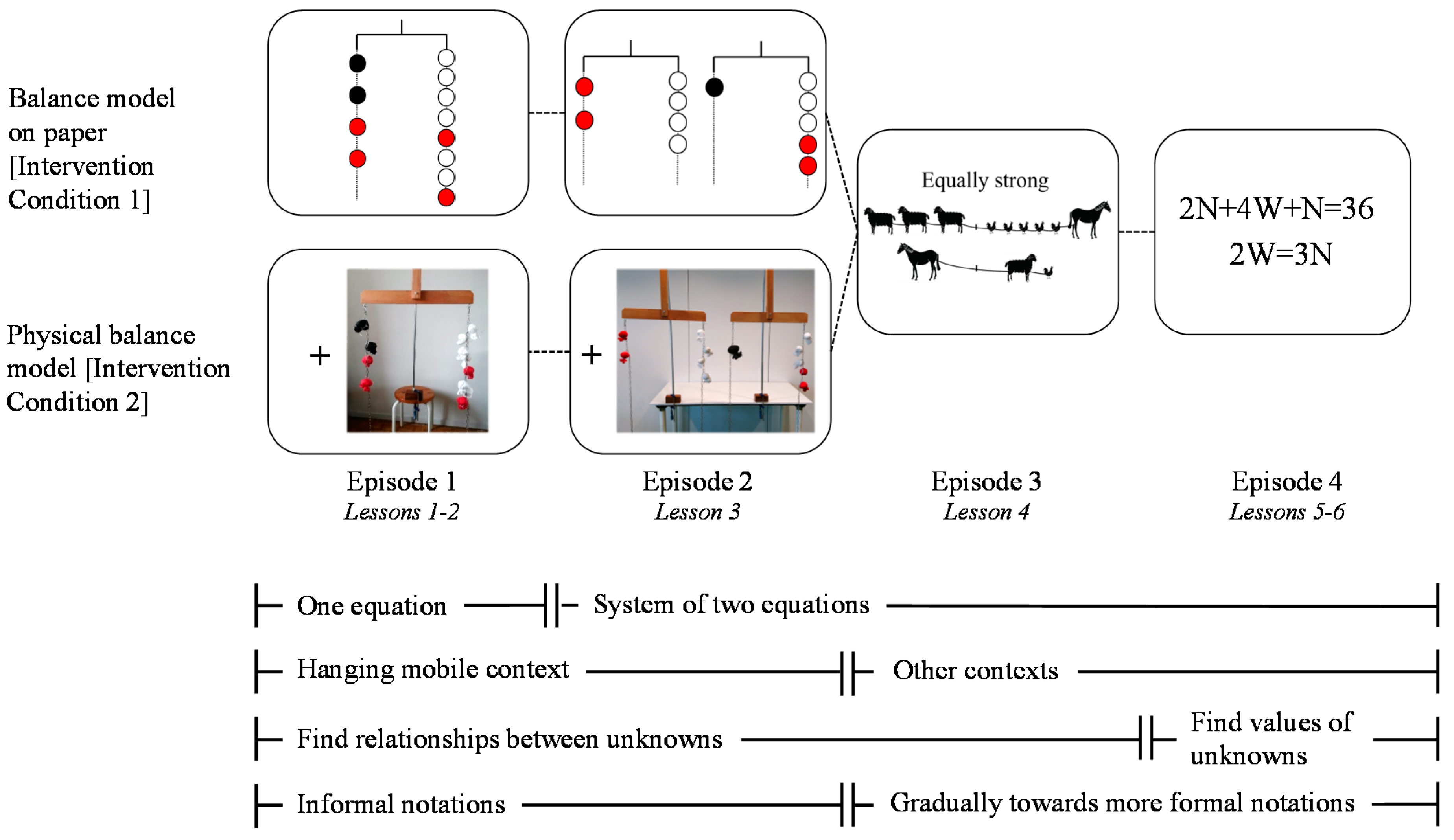
2.3. Intervention Program
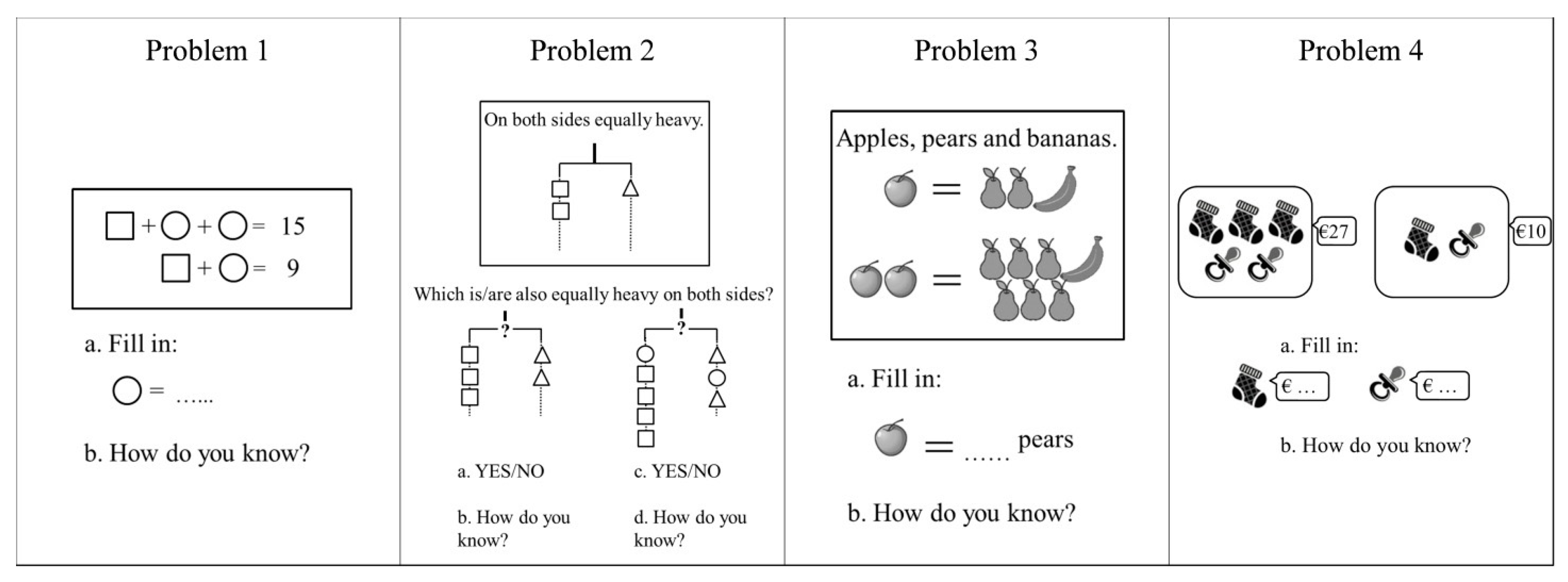
2.4. Measures
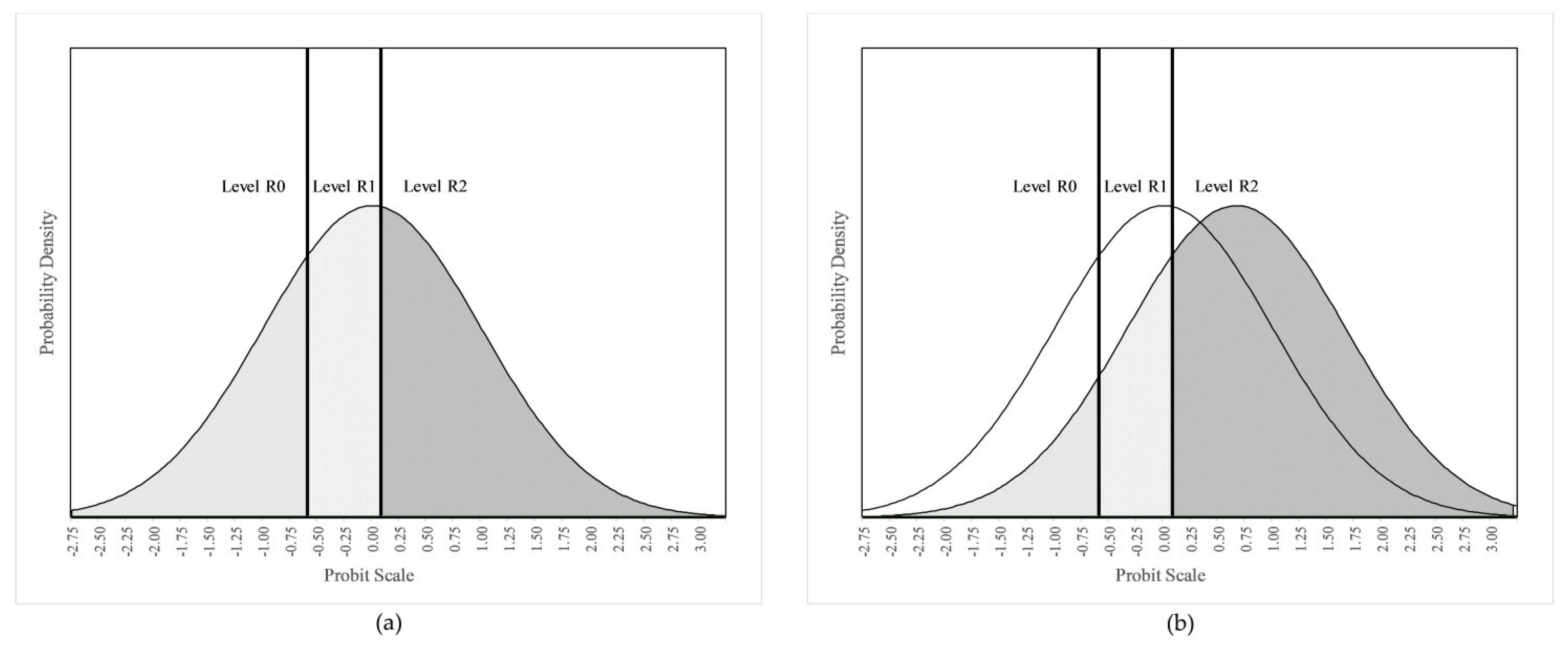
2.4.1. Algebraic Reasoning
Coding
2.4.2. General Reasoning Ability
2.4.3. General Mathematics Performance
2.5. Research Design and Procedures
2.6. Data Analysis
2.6.1. Qualitative Analysis
2.6.2. Quantitative Analysis
Descriptive Statistics
Multi-Group Latent Variable Growth Curve Modeling
2.6.3. Missing Data
3. Results
3.1. Results from the Qualitative Analysis of Students’ Reasoning
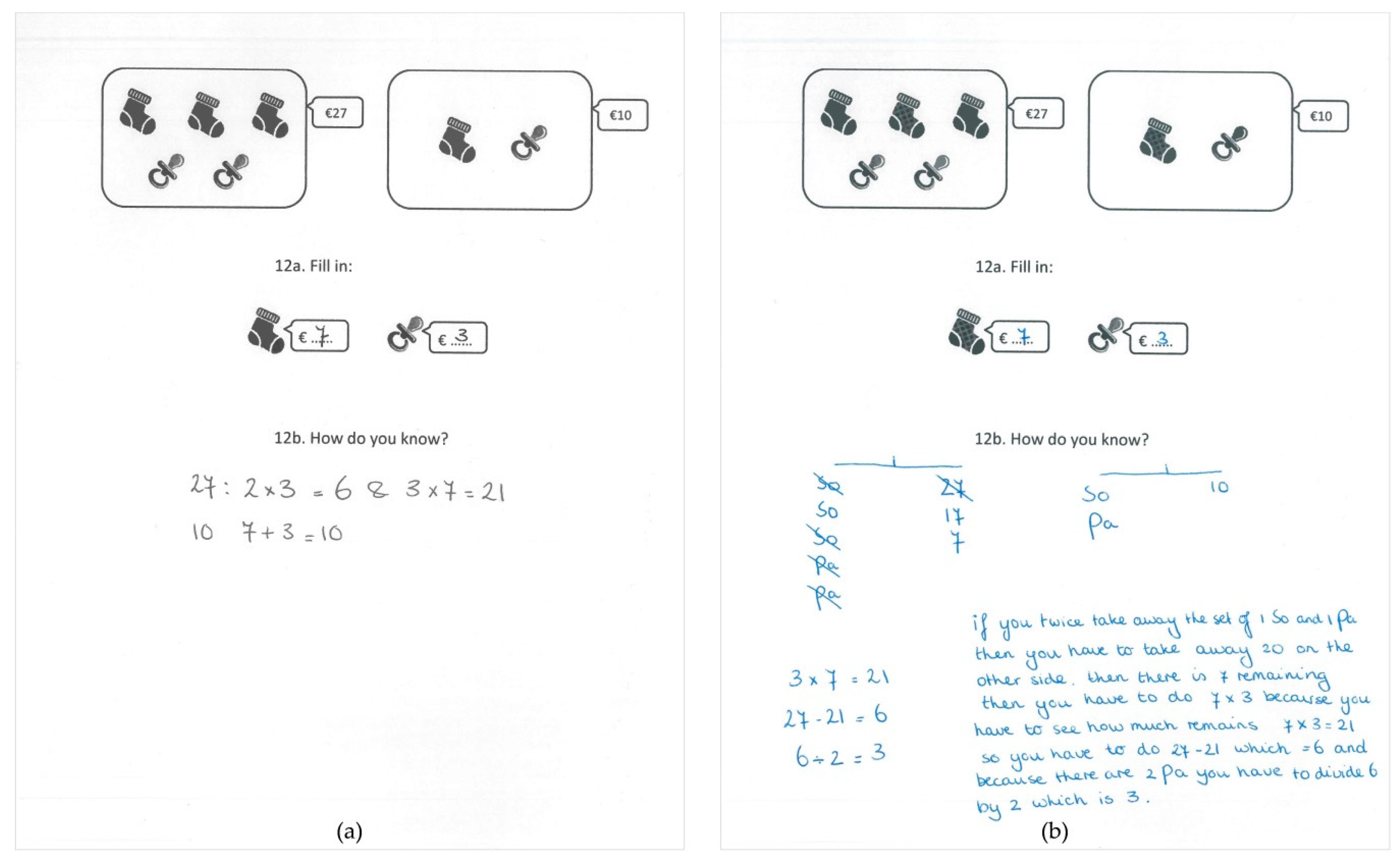
3.1.1. Case 1—Noah
3.1.2. Case 2—Lea
3.2. Results from the Quantitative Analysis of Students’ Reasoning
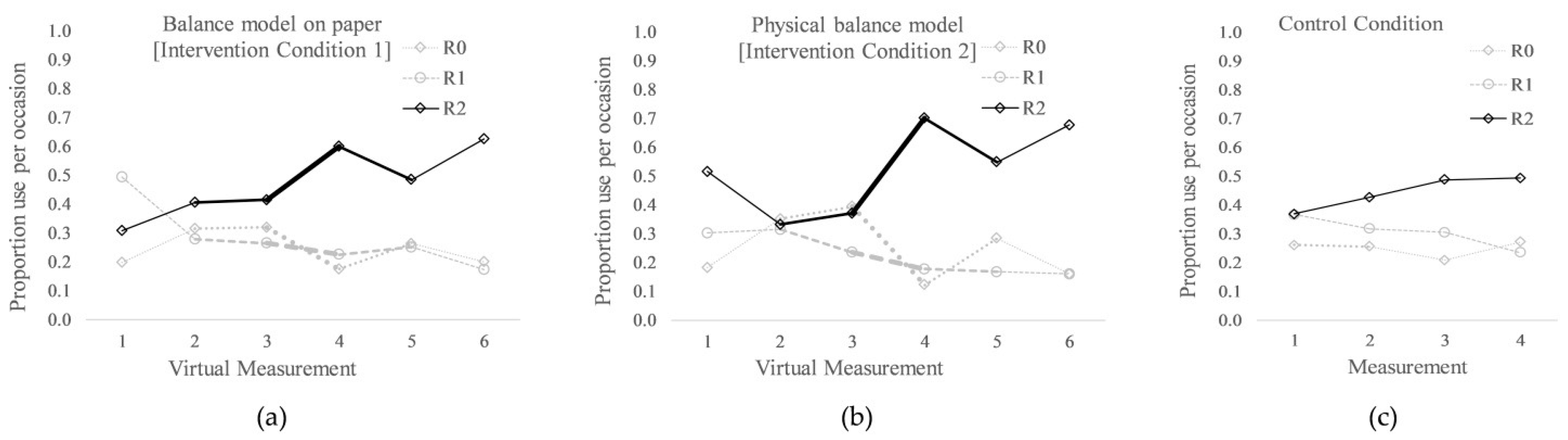
3.2.1. Descriptive Statistics
3.2.2. Multi-Group Latent Growth Model
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Level of Reasoning | Description | Subtypes | Problem 1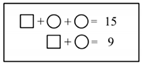 | Problem 2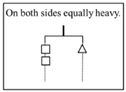 | Problem 3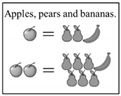 | Problem 4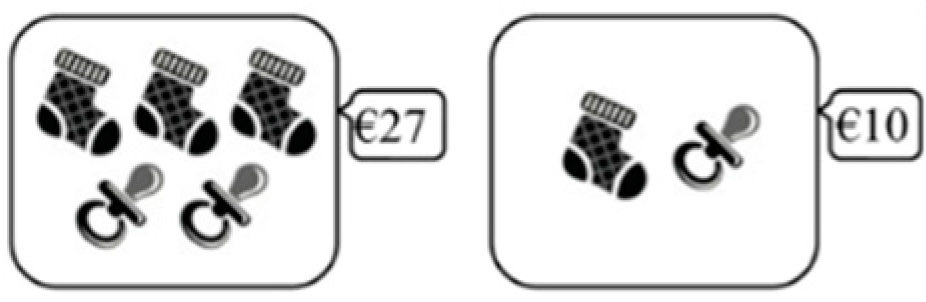 |
|---|---|---|---|---|---|---|
| R0 | Student does not use one any of the given equations | R0_empty | [no response] | Idem | Idem | Idem |
| R0_don’t know |
| Idem | Idem | Idem | ||
| R0_just know |
| Idem | Idem | Idem | ||
| R0_repeat given equation(s) or question(s) | - |
|
| - | ||
| R0_repeat answer(s) | - | - |
|
| ||
| R0_general description |
| Idem | Idem | Idem | ||
| R1 | Student reasons on the basis of only one of the two given equations | R1_without showing strategy |
|
|
|
|
| R1_with showing strategy |
|
|
|
| ||
| R2 | Student reasons on the basis of both given equations by combining the information of both of them | R2_without showing strategy |
|
|
|
|
| R2_with showing strategy |
|
|
|
|
References
- Cai, J.; Jakabcsin, M.S.; Lane, S. Assessing students’ mathematical communication. Sch. Sci. Math. 1996, 96, 238–246. [Google Scholar] [CrossRef]
- National Council of Teachers of Mathematics [NCTM]. Principles and Standards for School Mathematics; NCTM: Reston, VA, USA, 2000. [Google Scholar]
- Stein, M.K.; Grover, B.W.; Henningsen, M. Building student capacity for mathematical thinking and reasoning: An analysis of mathematical tasks used in reform classrooms. Am. Educ. Res. J. 1996, 33, 455–488. [Google Scholar] [CrossRef]
- Thom, J.S. Nurturing mathematical reasoning. Teach. Child. Math. 2011, 18, 234–243. [Google Scholar] [CrossRef]
- Kilpatrick, J.; Swafford, J.; Findell, B. Adding it up: Helping Children Learn Mathematics; National Research Council: Washington, DC, USA, 2001. [Google Scholar]
- Blanton, M.; Stephens, A.; Knuth, E.; Gardiner, A.M.; Isler, I.; Kim, J.S. The development of children’s algebraic thinking: The impact of a comprehensive early algebra intervention in third grade. J. Res. Math. Educ. 2015, 46, 39–87. [Google Scholar] [CrossRef]
- Brizuela, B.; Schliemann, A. Ten-year-old students solving linear equations. Learn. Math. 2004, 24, 33–40. [Google Scholar]
- Kaput, J.J.; Carraher, D.W.; Blanton, M.L. Algebra in the Early Grades; Lawrence Erlbaum Associates: New York, NY, USA, 2008. [Google Scholar]
- Blanton, M.L.; Kaput, J.J. Characterizing a classroom practice that promotes algebraic reasoning. J. Res. Math. Educ. 2005, 36, 412–446. [Google Scholar] [CrossRef]
- Cai, J.; Knuth, E. A global dialogue about early algebraization from multiple perspectives. In Early algebraization; Cai, J., Knuth, E., Eds.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Blanton, M.; Schifter, D.; Inge, V.; Lofgren, P.; Willis, C.; Davis, F.; Confrey, J. Early algebra. In Algebra: Gateway to a Technological Future; Katz, J., Ed.; The Mathematical Association of America: Washington, DC, USA, 2007; pp. 7–15. [Google Scholar]
- Smith, J.P.; Thompson, P.W. Quantitative reasoning and the development of algebraic reasoning. In Algebra in the Early Grades; Kaput, J.J., Carraher, D.W., Blanton, M.L., Eds.; Lawrence Erlbaum Associates: New York, NY, USA, 2008; pp. 95–132. [Google Scholar]
- Stephens, A.C.; Fonger, N.; Strachota, S.; Isler, I.; Blanton, M.; Knuth, E.; Gardiner, A. A learning progression for elementary students’ functional thinking. Math. Think. Learn. 2017, 19, 143–166. [Google Scholar] [CrossRef]
- Goldenberg, P.E.; Mark, J.; Kang, J.; Fries, M.; Carter, C.J.; Cordner, T. Making Sense of Algebra: Developing Students’ Mathematical Habits of Mind; Heinemann: Portsmouth, NH, USA, 2015. [Google Scholar]
- Otten, M.; Van den Heuvel-Panhuizen, M.; Veldhuis, M.; Heinze, A. Developing algebraic reasoning in primary school using a hanging mobile as a learning supportive tool. J. Study Educ. Dev. 2019, 42, 615–663. [Google Scholar] [CrossRef]
- Jones, I.; Inglis, M.; Gilmore, C.; Dowens, M. Substitution and sameness: Two components of a relational conception of the equals sign. J. Exp. Child. Psychol. 2012, 113, 166–176. [Google Scholar] [CrossRef]
- Kieran, C. Concepts associated with the equality symbol. Educ. Stud. Math. 1981, 12, 317–326. [Google Scholar] [CrossRef]
- Bush, S.B.; Karp, K.S. Prerequisite algebra skills and associated misconceptions of middle grade students: A review. J. Math. Behav. 2013, 32, 613–632. [Google Scholar] [CrossRef]
- Kieran, C.; Pang, J.; Schifter, D.; Ng, S.F. Early Algebra: Research into its Nature, its Learning, its Teaching; Open access eBook; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Behr, M.; Erlwanger, S.; Nichols, E. How children view the equals sign. Math. Teach. 1980, 92, 13–15. [Google Scholar]
- Carpenter, T.P.; Franke, M.L.; Levi, L. Thinking Mathematically: Integrating Arithmetic and Algebra in Elementary School; Heinemann: Portsmouth, NH, USA, 2003. [Google Scholar]
- Falkner, K.P.; Levi, L.; Carpenter, T.P. Children’s understanding of equality: A foundation for algebra. Teach. Child. Math. 1999, 6, 232–236. [Google Scholar]
- Knuth, E.J.; Stephens, A.C.; McNeil, N.M.; Alibali, M.W. Does understanding the equal sign matter? Evidence from solving equations. J. Res. Math. Educ. 2006, 37, 297–312. [Google Scholar] [CrossRef]
- McNeil, N.M.; Alibali, M.W. Why won’t you change your mind? Knowledge of operational patterns hinders learning and performance on equations. Child Dev. 2005, 76, 883–899. [Google Scholar] [CrossRef]
- Antle, A.N.; Corness, G.; Bevans, A. Balancing justice: Comparing whole body and controller-based interaction for an abstract domain. Int. J. Arts Technol. 2013, 6, 388–409. [Google Scholar] [CrossRef]
- Figueira-Sampaio, A.S.; Santos, E.E.F.; Carrijo, G.A. A constructivist computational tool to assist in learning primary school mathematical equations. Comput. Educ. 2009, 53, 484–492. [Google Scholar] [CrossRef]
- Papadopoulos, I. Using mobile puzzles to exhibit certain algebraic habits of mind and demonstrate symbol-sense in primary school students. J. Math. Behav. 2019, 53, 210–227. [Google Scholar] [CrossRef]
- Suh, J.; Moyer, P.S. Developing students’ representational fluency using virtual and physical algebra balances. J. Comput. Math. Sci. Teach. 2007, 26, 155–173. [Google Scholar]
- Warren, E.; Cooper, T.J. Young children’s ability to use the balance strategy to solve for unknowns. Math. Educ. Res. J. 2005, 17, 58–72. [Google Scholar] [CrossRef]
- Alibali, M.W. How children change their minds: Strategy change can be gradual or abrupt. Dev. Psychol. 1999, 35, 127–145. [Google Scholar] [CrossRef] [PubMed]
- Kaplan, R.G.; Alon, S. Using technology to teach equivalence. Teach. Child. Math. 2013, 19, 382–389. [Google Scholar] [CrossRef]
- Bajwa, N.P.; Perry, M. Features of a pan balance that may support students’ developing understanding of mathematical equivalence. Math. Think. Learn. 2019. advance online publication. [Google Scholar] [CrossRef]
- Mann, R.L. Balancing act: The truth behind the equals sign. Teach. Child. Math. 2004, 11, 65–70. [Google Scholar]
- Anthony, G.; Burgess, T. Solving linear equations. In Algebra Teaching around the World; Leung, F., Park, K., Holton, D., Clarke, D., Eds.; Sense Publishers: Rotterdam, The Netherlands, 2014; pp. 17–37. [Google Scholar]
- Vlassis, J. The balance model: Hindrance or support for the solving of linear equations with one unknown. Educ. Stud. Math. 2002, 49, 341–359. [Google Scholar] [CrossRef]
- Cheeseman, J.; McDonough, A.; Golemac, D. Investigating children’s thinking about suspended balances. N. Z. J. Educ. Stud. 2017, 52, 143–158. [Google Scholar] [CrossRef]
- Otten, M.; Van den Heuvel-Panhuizen, M.; Veldhuis, M. The balance model for teaching linear equations: A systematic literature review. Int. J. STEM Educ. 2019, 6, 30–51. [Google Scholar] [CrossRef]
- Fyfe, E.R.; McNeil, N.M.; Borjas, S. Benefits of “concreteness fading” for children’s mathematics understanding. Learn. Instr. 2015, 35, 104–120. [Google Scholar] [CrossRef]
- Alibali, M.W.; Nathan, M.J. Embodiment in mathematics teaching and learning: Evidence from learners’ and teachers’ gestures. J. Learn. Sci. 2012, 21, 247–286. [Google Scholar] [CrossRef]
- Núñez, R.E.; Edwards, L.D.; Matos, J.F. Embodied cognition as grounding for situatedness and context in mathematics education. Educ. Stud. Math. 1999, 39, 45–65. [Google Scholar] [CrossRef]
- Wilson, M. Six views of embodied cognition. Psychon. Bull. Rev. 2002, 9, 625–636. [Google Scholar] [CrossRef] [PubMed]
- Alessandroni, N. Varieties of embodiment in cognitive science. Theory Psychol. 2018, 28, 1–22. [Google Scholar] [CrossRef]
- Gibbs, R.W., Jr. Embodiment and Cognitive Science; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Carbonneau, K.J.; Marley, S.C.; Selig, J.P. A meta-analysis of the efficacy of teaching mathematics with concrete manipulatives. J. Educ. Psychol. 2013, 105, 380–400. [Google Scholar] [CrossRef]
- Kindt, M.; Abels, M.; Meyer, M.R.; Pligge, M.A. Comparing Quantities. In Mathematics in Context: A Connected Curriculum for Grades 5–8; National Center for Research in Mathematical Sciences Education, Freudenthal Institute, Ed.; Encyclopedia Brittanica Educational Corporation: Chicago, IL, USA, 1998. [Google Scholar]
- Glaser, B.G. The constant comparative method of qualitative analysis. Soc. Probl. 1965, 12, 436–445. [Google Scholar] [CrossRef]
- Raven, J.C.; Court, J.H.; Raven, J. Manual for Raven’s Standard Progressive Matrices and Vocabulary Scales; Oxford Psychologists Press: Oxford, UK, 1996. [Google Scholar]
- Bilker, W.B.; Hansen, J.A.; Brensinger, C.M.; Richard, J.; Gur, R.E.; Gur, R.C. Development of abbreviated nine-item forms of the Raven’s standard progressive matrices test. Assessment 2012, 19, 354–369. [Google Scholar] [CrossRef]
- Janssen, J.; Scheltens, F.; Kraemer, J.M. Leerling- en Onderwijsvolgsysteem Rekenen-wiskunde [Student Monitoring System Mathematics]; Cito: Arnhem, The Netherlands, 2005. [Google Scholar]
- Bollen, K.A.; Curran, P.J. Latent Curve Models; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Duncan, T.E.; Duncan, S.C.; Strycker, L.A. An Introduction to Latent Variable Growth Curve Modeling, 2nd ed.; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 2006. [Google Scholar]
- Muthén, L.K.; Muthén, B.O. Mplus User’s Guide, 8th ed.; Muthén & Muthén: Los Angeles, CA, USA, 1998–2017. [Google Scholar]
- Little, T.D. Longitudinal Structural Equation Modeling; Guildford Press: New York, NY, USA, 2013. [Google Scholar]
- Van Amerom, B.A. Focusing on informal strategies when linking arithmetic to early algebra. Educ. Stud. Math. 2003, 54, 63–75. [Google Scholar] [CrossRef]
- Van Reeuwijk, M. The role of Realistic Situations in Developing Tools for Solving Systems of Equations; Annual Meeting of the American Educational Research Association: San Francisco, CA, USA, 1995. [Google Scholar]
- Van den Heuvel-Panhuizen, M. The didactical use of models in realistic mathematics education: An example from a longitudinal trajectory on percentage. Educ. Stud. Math. 2003, 54, 9–35. [Google Scholar] [CrossRef]
- McCaffrey, T.; Matthews, P.G. An emoji is worth a thousand variables. Math. Teach. 2017, 111, 96–102. [Google Scholar] [CrossRef]
- Cook, T.D.; Campbell, D.T. Quasi-experimentation: Design and Analysis Issues for Field Settings; Rand McNally: Chicago, IL, USA, 1979. [Google Scholar]

| Cohort | n | Measurement 1 October 2016 | November–December 2016 | Measurement 2 December 2016 | February–March 2017 | Measurement 3 March 2017 | May–June 2017 | Measurement 4 June 2017 | |
|---|---|---|---|---|---|---|---|---|---|
| Balance model on paper [Intervention Condition 1] | 1 | 22 | M1 | Teaching sequence (6 lessons) | M2 | M3 | M4 | ||
| 2 | 21 | M1 | M2 | Teaching sequence (6 lessons) | M3 | M4 | |||
| 3 | 24 | M1 | M2 | M3 | Teaching sequence (6 lessons) | M4 | |||
| Physical balance model [Intervention Condition 2] | 1 | 22 | M1 | Teaching sequence (6 lessons) | M2 | M3 | M4 | ||
| 2 | 18 | M1 | M2 | Teaching sequence (6 lessons) | M3 | M4 | |||
| 3 | 25 | M1 | M2 | M3 | Teaching sequence (6 lessons) | M4 | |||
| Control Condition | 4 | 80 | M1 | M2 | M3 | M4 |
| General Reasoning Ability | General Mathematics Performance | ||
|---|---|---|---|
| Cohort | M (SD) | M (SD) | |
| Balance model on paper [Intervention Condition 1] | 1 | 11.18 (2.84) | 102.05 (9.48) |
| 2 | 11.00 (2.17) | 96.57 (9.19) | |
| 3 | 10.08 (2.59) | 87.00 (10.82) | |
| Mean | 10.73 (2.56) | 94.94 (11.65) | |
| Physical balance model [Intervention Condition 2] | 1 | 9.95 (2.01) | 95.76 (9.49) |
| 2 | 8.94 (2.78) | 92.82 (9.21) | |
| 3 | 10.92 (2.97) | 92.48 (9.38) | |
| Mean | 10.05 (2.71) | 93.69 (9.35) | |
| Control Condition | 4 | 10.49 (2.74) | 97.32 (12.62) |
| Model Parameter | M | p-value | var |
|---|---|---|---|
| Intercept | |||
| Cohort 1 | @0 | 0.59 | |
| Cohort 2 | −0.44 | .013 | 0.59 |
| Cohort 3 | 0.14 | .399 | 0.59 |
| Control Cohort | 0.10 | .534 | 0.59 |
| Slope (mean) | 0.06 | .048 | 0.05 |
| Intervention (mean) | 0.67 | <.001 | 0.09 |
| Weaken (mean) | −0.31 | .001 | @0 |
| Predictor regressions (β) | |||
| General reasoning ability on intercept | .34 | <.001 | |
| Condition on intervention | .33 | .136 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otten, M.; van den Heuvel-Panhuizen, M.; Veldhuis, M.; Boom, J.; Heinze, A. Are Physical Experiences with the Balance Model Beneficial for Students’ Algebraic Reasoning? An Evaluation of two Learning Environments for Linear Equations. Educ. Sci. 2020, 10, 163. https://doi.org/10.3390/educsci10060163
Otten M, van den Heuvel-Panhuizen M, Veldhuis M, Boom J, Heinze A. Are Physical Experiences with the Balance Model Beneficial for Students’ Algebraic Reasoning? An Evaluation of two Learning Environments for Linear Equations. Education Sciences. 2020; 10(6):163. https://doi.org/10.3390/educsci10060163
Chicago/Turabian StyleOtten, Mara, Marja van den Heuvel-Panhuizen, Michiel Veldhuis, Jan Boom, and Aiso Heinze. 2020. "Are Physical Experiences with the Balance Model Beneficial for Students’ Algebraic Reasoning? An Evaluation of two Learning Environments for Linear Equations" Education Sciences 10, no. 6: 163. https://doi.org/10.3390/educsci10060163
APA StyleOtten, M., van den Heuvel-Panhuizen, M., Veldhuis, M., Boom, J., & Heinze, A. (2020). Are Physical Experiences with the Balance Model Beneficial for Students’ Algebraic Reasoning? An Evaluation of two Learning Environments for Linear Equations. Education Sciences, 10(6), 163. https://doi.org/10.3390/educsci10060163






