Abstract
The research on deductive reasoning in mathematics education has been predominantly associated with the study of proof; consequently, there is a lack of studies on logical reasoning per se, especially with young children. Analytical reasoning problems are adequate tasks to engage the solver in deductive reasoning, as they require rule checking and option elimination, for which chains of inferences based on premises and rules are accomplished. Focusing on the solutions of children aged 10–12 to an analytical reasoning problem proposed in two separate settings—a web-based problem-solving competition and mathematics classes—this study aims to find out what forms of deductive reasoning they undertake and how they express that reasoning. This was done through a qualitative content analysis encompassing 384 solutions by children participating in a beyond-school competition and 102 solutions given by students in their mathematics classes. The results showed that four different types of deductive reasoning models were produced in the two venues. Moreover, several representational resources were found in the children’s solutions. Overall, it may be concluded that moderately complex analytical reasoning tasks can be taken into regular mathematics classes to support and nurture young children’s diverse deductive reasoning models.
1. Introduction
Logical reasoning, namely deductive reasoning, is one of the recognized and celebrated pillars of mathematical reasoning, whether linked to proof and argumentation or communication and problem-solving, which makes it meaningful to school mathematics worldwide (e.g., [1,2]). Despite its relevance in the learning of mathematics from early ages, the difficulties related to the use of deductive reasoning are well known; not only are such difficulties found in students across the various levels of education, but also in the general population when individuals are given logic problem situations from different domains. However, relatively little is known about effective and adequate teaching of logic, and there is much evidence that, even with specific training in mathematics, many students continue to fail in formal proofs [3,4,5,6].
A question that is far from resolved in the available research is whether deductive reasoning has the potential to be cultivated in activities such as word problems or challenging situations, sometimes referred to as puzzles or brain-teasers. Another open question is that of the ability of school-aged children to deal with logical forms of reasoning because it is uncertain when the mastery of different forms of deductive reasoning is achieved [7]. There is, however, a general tendency to look at deductive reasoning as a high-level skill, which will only be available to students of advanced years [8].
Knowing more about the ways that children deal with word problems requiring deductive reasoning and their ability to express that reasoning is important to improve our understanding of children’s engagement with that kind of logical thinking from an early age. This interest in children’s deductive reasoning stems from an extensive assessment of the solutions to several analytical reasoning problems, which are part of the collection of problems proposed in a web-based problem-solving competition (addressing students aged 10–12) promoted by the University of Algarve, in Portugal [9]. Analytical reasoning problems, also referred to as constraint-satisfaction problems [10,11], have a strong relationship with logical reasoning and hold an important place in various areas of knowledge.
Rationale and Aims
The present study focuses on the deductive reasoning of children aged 10–12 when solving an analytical reasoning problem of a moderately challenging level. Two very different settings were contemplated for data collection. The reason for this decision is related to the contrasting conditions between both, namely the condition of limited against extended time and the condition of possible help from adults against no aid provided. The inclusion of the two settings was designed as a way of ascertaining whether children are capable of producing effective deductive reasoning in both cases, thus proposing two contrasting venues for deductive reasoning within problem-solving activities. In the first case, we gathered students’ solutions to an analytical reasoning problem in the course of their participation in a web-based mathematical problem-solving competition, which took place online in a beyond-school environment. In the second case, we collected the solutions produced by other students who solved the same problem in the mathematics classroom during a regular class. In the case of the children who participated in the competition, their success in solving the analytical reasoning problem was evident; they worked on the problem outside of school, mostly at home, with extended time (two weeks) to think about the problem and develop ways of communicating the solution, with possible help and guidance from others (family, teachers, and friends). In the case of children who solved it in the classroom, the work was done individually in a limited time (defined by their teacher, but roughly 30 min), and the answers were written on paper, using only a pencil or pen to express the reasoning. The success rate of the latter was clearly lower, and there were also signs of there being little time to improve the written explanations of the solution process.
The empirical study material is composed of the solutions obtained in the two settings. The research questions were as follows: (i) What are the types of deductive reasoning that can be found in the children’s solutions? (ii) How is deductive reasoning expressed by children in their solutions? (iii) Do the same types of deductive reasoning appear in the two settings in which the solutions were created?
2. Theoretical Background
From a theoretical point of view, the study acknowledges the research debate between two opposing theories in explaining the psychological mechanisms of deductive reasoning: The mental logic theory and the mental models theory. As they are theories about pure logical reasoning, the theoretical framework also reviews the research on how logical reasoning and mathematical reasoning interrelate, particularly in the case of school-aged children, and finally discusses analytical reasoning problems (also known as relational reasoning problems) as special problems that surround many knowledge domains, from law to mathematics, including many everyday situations that children can be challenged to solve from young ages.
2.1. Theoretical Approaches to the Psychology of Deduction
Two major competing theories in the psychology of deduction have been proposed over the last few years: The mental models theory and the mental logic theory. The debate between the proponents of each of them has engendered consecutive empirical investigations attempting to confirm their distinct theoretical assumptions. In the work of Schroyens, Schaeken, and D’Ydewalle [12], a synthesis of the starting points of each of the two opposing theories is presented, as well as the acknowledgement that the results of various investigations could be effectively explained by either theory.
The theorists of the mental logic approach assume that the mental apparatus underlying deduction consists of applying mental inference rules (inference schemata) to the premises. Theorists who support this position postulate that individuals use a mental logic that is similar to propositional calculus. They claim that deductive thinking consists of applying a set of formal rules that allow derivation of a conclusion from given premises, regardless of the meaning of the propositions. In other words, individuals make use of formal inferential rules free of content when reasoning deductively. According to this perspective, when people fail in logical reasoning problems, it is not because they are devoid of mental logic, but because the demands of the situation exceed their logical skills, because they make inferences from non-logical sources, or because they are reasoning on a non-logical matter. Thus, the difficulty of a problem would mainly be a consequence of the number and/or availability of inference rules to be applied. Moreover, the theorists of mental logic consider the importance of the reductio ad absurdum argument in many logic problems, especially in those that include some form of conditional reasoning.
The mental models theory, largely developed by Johnson-Laird and colleagues (e.g., [13,14]), conceptualizes logical reasoning, similarly to other fields of reasoning, as a processing schema in three phases. In the first phase—the construction of the model—various mental models that represent, to the individual, the truth of the premises are constructed. Mental models essentially represent possible worlds, i.e., possibilities of meanings given to the premises in light of relevant knowledge that is triggered during the process of interpretation. In the second phase—the formulation of the conclusion—individuals integrate the mental models of the premises. The inconsistent models are eliminated and the consistent ones are combined in the creation of an integrated model. The resulting model allows people to form a putative conclusion. In the third phase—the validation of the conclusion—people seek alternative models of the premises, which may falsify the putative conclusion. In fact, based on the limitations of the working memory, it is assumed that people do not initially represent all the possibilities consistent with the premises. Developments of the theory related to the validation process suggest that the search for counterexamples is a crucial element, namely in using the reductio ad absurdum form of reasoning, which roughly means avoiding contradictions at all costs. The availability of counterexamples seems to be related to the semantic content of the problem, as the following claim suggests: “The less semantically impoverished the materials are, the stronger a search for counterexamples might be driven by our background knowledge associated with and triggered by the given information” [12] (p. 161). The theory of mental models predicts that the difficulty of a problem increases with the number of models that are compatible with the problem.
Put briefly, a clear distinction between the two opposing theories refers to the semantics of a problem, namely when generating indeterminacy [15], and to its role in the difficulty of a problem: Minimized by the theory of mental logic and emphasized by the theory of mental models.
2.2. Logical Reasoning and Mathematics Learning
It is generally accepted that individuals’ ability to use logical–deductive reasoning is an important element for success in mathematics learning, and several studies have supported the claim that such an ability can and should be strengthened and developed [6,7,16,17,18,19].
In the field of mathematics education, the study of deductive reasoning has been mainly associated with mathematical proof, leaving the understanding of deductive reasoning, per se, in the background [20,21]. This may have to do with the diverse ways of conceiving deductive thinking by the protagonists involved in mathematics education. The study by Ayalon and Even [20] offers a picture of that diversity. It looked at the core conceptions on deductive reasoning held by a heterogeneous group of people engaged in mathematics education (teachers, mathematicians, researchers in mathematics education, curriculum designers, and teacher educators). Two different approaches to the meaning of deductive reasoning were identified: The systematic approach, which considered deductive reasoning as a systematic problem-solving approach regardless of whether it is used in mathematics or in various other areas, and the logical approach, which emphasizes logic in mathematics as distinct from logic in other domains.
Research on students’ logical reasoning is even sparser when it comes to young children. Nevertheless, some studies (namely those revised in Stylianides and Stylianides [7]) have already revealed that children are able to develop logical reasoning in various deductive reasoning tasks and problems. In light of such evidence, the research in mathematics education needs to know more about the ways in which schoolchildren can develop their deductive reasoning, namely under what circumstances and with what kind of tasks.
Authors such as Hoyles and Küchmann [19], Epp [17], Lee [4], Nunes et al. [16], Stylianides and Stylianides [7], and Lommatsch [22], among others, have advocated an explicit teaching of deductive reasoning in school mathematics. In general, they have criticized the teaching of propositional logic as an empty unit, considering the weak transfer of that learning to mathematics and problem-solving.
Hoyles and Küchmann [19] developed a study with a large sample of students in the eighth and ninth grades (ages 12–13) on the use of conditional reasoning in tasks involving properties of number sums and products. Students were presented with two statements: An implication and its converse. They were then asked to: Decide whether the two statements said the same thing, draw a conclusion assuming that one of the statements was true, and assess the validity of each statement in turn. Overall, the research showed that even students with high performance in mathematics cannot fully understand how to determine the truth of “if p then q”. This supported a recommendation for school mathematics: The design of activities that focus on giving meaning to the structural properties of logical implication and encourage education to strengthen and refine those meanings over time.
Nunes et al. [16] investigated the causal relationship between the logical–deductive performance of children and their learning of mathematics. In adopting an experimental design with six-year-old children attending the first grade, the researchers implemented an educational program in the regular period of mathematics classes. The results showed a beneficial effect on children’s mathematics learning that persisted after several months following the intervention. The teaching on logical principles related to quantities and operations even improved the learning of children whose levels of logical competence were consistent with their difficulties in mathematics. Nunes et al. [16] derived important consequences about the value of time invested in developing logical competence in school mathematics and on the advantage of giving children opportunities to achieve a logical understanding of arithmetic operations.
The study by Stylianides [8] focused on a class of third graders where the use of a representational model—the “building model”—was investigated. The task required the students to find out how many ways there were for a person to get to the second floor, and asked them to prove their answer. Depending on the assumption the student would make, the task would lead to proving the existence of a finite number of ways or infinitely many ways. The results of the study highlighted the fundamental role of assumptions in proving with children from early grades. Evidence was also produced on the abilities of young children in dealing with mathematical situations that are related to assumptions and proofs, which, in many aspects, resembled the way of thinking of mathematicians.
From these studies, it may be inferred that the richness of the tasks (both inquiring and challenging) and the way they are used to trigger students’ logical and deductive forms of reasoning are common traits in eliciting and developing the ability to reason deductively. In addition, it seems that students’ use of different strategies and reasoning models offers opportunities for them to understand what it means to engage in logical arguments and to explicitly explore such reasoning in mathematics education.
2.3. Analytical Reasoning Problems
Among the problems that require deductive reasoning processes are those known as analytical reasoning problems or relational reasoning problems (e.g., determine the layout of seats at a table, subject to a number of conditions and restrictions, such as protocol rules). Such problems involve reasoning deductively from a set of instructions, rules, or principles that describe relationships between people, things, or events. They require the ability to consider a set of facts and conditions, and to determine, based on logical principles, which may or must be true. Sometimes, such problems are also described as puzzles based on constraint satisfaction [10,11,23].
Analytical reasoning problems involve a wide variety of deductive reasoning skills, which include: (i) Understanding the basic structure of a set of relations in order to find a complete solution to a given problem; (ii) using conditional reasoning of the form “if–then” and recognizing logically equivalent formulations of such conditional statements; (iii) deducing what may be true or must be true from certain facts and rules by removing contradictions or generating new information in the form of an additional or substitute rule; (iv) deciding when two statements are logically equivalent in the context by identifying the rule that corresponds to one or more of the original conditions. Not surprisingly, analytical reasoning problems are quite common in many areas of study, such as law, management, planning, military defense, security, network operations, and medicine, not to mention mathematics.
According to the literature, the difficulty of such problems depends on the number of dimensions and on the number of values along each dimension. Problems containing statements in the negative form are also perceived as being more difficult than those in which all the information is given in the affirmative form. Finally, problems involving reasoning with quantifiers were also considered as having a high level of difficulty. The study by Cox and Brna [23] examined the effects of the choice and use of external representations by university students in solving problems of analytical reasoning with different degrees of difficulty. This study revealed several types of external representations performed by the subjects, which were analyzed in detail as to their benefits and limitations. The results showed that: Some individuals may not have ways to represent more abstract relationships, such as those involving quantifiers; the use of multiple representations appears generally associated with good performance (including tables, ordered text or lists, free text, tree diagrams, set diagrams); the tabular representation was the predominant external representation; and the cognitive load associated with the choice and construction of external representations is compensated by the relief of cognitive load in the subsequent use of those representations to infer conclusions.
The selection of one or more external representations emerges as a crucial stage of the reasoning process, as it is often difficult because the requirements of representation vary with the problems. The expressive properties of the external representation chosen should allow representation of the semantics of the problem. Thus, the subject must correctly understand the essential characteristics of the problem, namely the dimensionality and the level of determination, and then select a suitable form of representation from her/his repertoire. A significant amount of information provided in analytical reasoning problems is given implicitly and, therefore, must be inferred before it can be represented. An important function of external representations appears to be the guiding of the search for implicit information. However, the combination of producing representations and creating inferences brings a high cognitive demand to the subject.
The work of English [24] focused on another aspect of solving analytical reasoning problems—the reasoning processes used by young students attending primary school (9–12 years old). Its main purpose was to investigate the reasoning processes of children in a set of problems presented in writing and complemented by manipulatives. The research involved a detailed analysis of the protocols obtained from the verbalization of children’s thinking as they solved the problems. The study included a large sample of children from fourth to seventh grade, and this allowed the exploration of all the general trends of their reasoning processes. The theoretical perspective adopted was the mental models theory, according to which a sound logical reasoning is not equal to the application of the formal rules of logic. The results of the study showed a strong correlation between success in the problem-solving and the choice of assumptions that more easily contribute to the construction of an initial model and its development. The less efficient solvers tended to avoid the relational complexity of the premises, and instead used processes of segmentation of the relations.
Newstead et al. [25] argue that analytical reasoning problems are deductive reasoning problems in that they can be solved completely based on the information presented, and their solutions can be obtained and verified by formal logic. However, they are much more complex than the tasks traditionally used by psychologists in the investigation of deductive reasoning and, in a sense, may be more representative of logical reasoning in the real world. Their greater difficulty is often related to the kind of inferences involved: Necessary, possible, or impossible. During the solving process, there are situations in which multiple consequences are possible, thus making the problem more difficult.
Two main strategies were used by the participants in their study, which are described as rule checking and option elimination. These strategies consist of choosing one of the dimensions of the problem and testing all possible assumptions for a given rule, or, systematically, for each of the rules, seeking contradictions in order to discard hypotheses and draw necessary conclusions.
The study involved undergraduate and graduate students in solving complex analytical reasoning problems, which included many rules and conditions to be met. The research was designed to provide a model for the predictive characteristics of the difficulty of analytical reasoning problems. At the same time, it sought to understand which of the two major theories about the nature of logical thinking (mental models theory or mental logic theory) was best suited to assess the difficulty of the problems. From the results, it may be highlighted that the difficulty of the rules is the feature that most contributes to the difficulty of the problem. Moreover, the predominant strategy was the systematic checking of hypotheses against the rules available. This suggested the construction of models of the situation based on the given premises, followed by their validation through a procedural form of checking. In some cases, the subjects also combined rules in order to derive logical conclusions from them. In this particular point, the authors also found a resonance with the mental logic theory.
A relevant discussion for the present investigation is brought by the work of Van der Henst [15], which analyzes the assumptions of each of the theories to explain an element that generates greater difficulty in analytical reasoning problems: The indeterminacy factor. This means the existence of premises that, while not being irrelevant per se, introduce an element of indeterminacy in the conclusions derived from the premises. Thus, proponents of the mental models theory consider that such problems contain a higher level of complexity because the solvers will have more than one possible model to obtain the answer; this could arguably not be explained by the theory of mental logic, which would only take into account the inferential rules derived from the premises, which do not change due to the fact that there is an indeterminacy factor. On the other hand, the theory of mental logic may also explain the higher degree of complexity by claiming that the reasoner does not know in advance what information is necessary for solving the problem (determinate relations) and what information is not (indeterminate relations). Thus, the higher level of complexity could also be explained by the greater number of relationships to be stored mentally. As the author, concludes: “According to MMT [Mental Model Theory], indeterminacy involves the construction of several models. According to a rule approach, it involves more propositional information to store and manipulate in memory. Although empirical data in relational reasoning are neatly described by MMT, they do not exclude a description based on inference rules” [15] (p. 200).
3. Methodology
3.1. Participants
The study comprises two settings where children aged 10–12 solved an analytical reasoning problem: (i) Beyond-school mathematics and (ii) the regular math class.
In the first case, the students were voluntarily participating in a mathematical problem-solving competition taking place over the Internet. This was an inclusive competition, where non-routine and moderate mathematical challenges were proposed, and students sent their solutions by email. The requirement of explaining the problem-solving process was always emphasized. Participants could compete individually or in pairs. Some of the presented problems were analytical reasoning problems. One of those problems was selected for the present study.
The second setting consisted of regular math classes of students of the same age (attending the fifth or sixth grade). Three mathematics teachers, all from different public middle schools, agreed to propose the chosen analytical reasoning problem to different classes, allowing students the appropriate time for their resolution (which they planned to be around 30–45 min). Across the three schools, two fifth-grade classes and four sixth-grade classes participated. All of the teachers decided to deliver the problem as the final task of a lesson. They also emphasized the requirement of explaining the problem-solving process when they handed the task. The students solved the problem with paper and pencil and delivered their solutions at the end. The problem was solved individually, without any intervention or help from the teacher.
Several important distinctions between the two settings must be noted. In the competition scenario, the participating students had substantial time (two weeks) to solve the problem and submit the solution; the final product was sent in digital format, and the participants were free to choose any digital tools that would suit them to describe and express their ways of reasoning tidily and cleanly; the participants could count on possible help and guidance from parents, teachers, and friends. In the mathematics classroom scenario, students had limited and significantly less time (about half an hour); the solution was produced on paper and pencil, and it was not feasible in the time available to improve the presentation of the reasoning in their final answers; the students worked individually and received no help from the teacher.
3.2. Materials and Data Collection
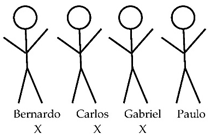
The following is the analytical reasoning problem that was given to both sets of young children (Figure 1):

Figure 1.
Analytical reasoning problem proposed.
The goal is to know which of the friends spilled the popcorn, drawing on various premises and rules:
- There are four friends: Bernardo, Carlos, Gabriel, and Paulo.
- Each of the four friends makes a statement (three refer to who spilled the popcorn and the latter refers to the truth of one of the statements).
- One—and only one—of the friends spilled the popcorn.
- One—and only one—of the friends lied.
Based on the given information, it is possible to isolate the following atomic propositions involved in the problem (Table 1), divided according to the two dimensions of the problem situation (lying and spilling popcorn). Among the propositions P1, P2, P3, and P4, only one is true, and among the propositions Q1, Q2, Q3, and Q4, also only one is true.

Table 1.
Sets of propositions on the dimensions “lying” and “spilling popcorn”.
According to the rule that only one of the friends lied, one can make an exhaustive analysis, assuming that each of them, in turn, was the one who lied.
Thus, there are four cases, as follows:
(1) Let P1 be true.
If P1, then we have: Q1 and not-P2, not-P3, and not-P4 (Bernardo was the dropper and none of the others lied). However, the two propositions not-P3 and not-P4 are contradictory (if Gabriel is telling the truth, then Paulo is lying, and vice versa). Therefore, P1 is false.
(2) Let P2 be true.
If P2, then we have: Not-Q4, not-P1, not-P3, and not-P4 (Paulo was not the dropper, and none of the others lied). However, again, the two propositions not-P3 and not-P4 are contradictory. Therefore, P2 is false.
(3) Let P3 be true.
If P3, then we have: Not-Q2, not-P1, not-P2, and not-P4 (Carlos was not the dropper, and none of the others lied). Therefore, we conclude: Not-Q1, not-Q2, and Q4 (Bernardo was not the dropper and Paulo was the dropper). As there is only one that is guilty, we may deduce not-Q3. This means that Paulo spilled the popcorn and Gabriel was the liar.
(4) Let P4 be true.
If P4, then we have: Not-P3, not-P1, and not-P2 (Bernardo is true, Carlos is true, and Gabriel is true). Then, we have Q2 and Q4 (Paulo was the dropper and Carlos was the dropper). This is not true because Q2 and Q4 cannot both be true (only one has spilled the popcorn). Therefore, P4 is false.
Similarly, according to the rule that only one of the friends spilled the popcorn, one can make an exhaustive analysis, assuming that each of them, in turn, was the one who spilled it.
The solutions from the participants in the web-based competition were collected in the first place. All of those solutions were received in a digital form via email, and were collected over a period of fifteen days since the problem was posted. The email messages with the solutions all indicated: Name, school, and class. Many of the solutions were presented in the email message window, but some came enclosed in attached files, such as Word, PowerPoint, Excel, or scanned images of paper-and-pencil work. The total of those solutions was 384. The solutions given by the students who solved the problem in the class were collected at a later time. All of them were written on paper and delivered to the teacher after completion. Depending on the schools, the students used a blank A4 sheet or half a sheet to present their solutions. The students only indicated the school and the class on their worksheets. The total of solutions collected was 102 (the amounts per school were 25, 35, and 42). In the study, ethical standards were ensured, namely by keeping the anonymity of the students and teachers involved.
3.3. Data Analysis
The data were analyzed based on qualitative content analysis. The method is suitable for the analysis of recorded material, namely written documents or digital files that contain written information, including text and forms of visual communication. The method is equally suited to the research questions that seek to know what the world of children’s deductive reasoning “looks like” [26] (p. 29) by identifying and describing, in as efficient and clear ways as possible, the deductive reasoning produced and expressed by young children in solving the problem, both in the context of a beyond-school competition as well as in the classroom context.
The expectation, with regard to the more likely forms of reasoning, was that students would test systematic hypotheses and look for contradictions. In that sense, they would probably elect one of the two dimensions of the problem for their hypothesis testing (as suggested in the presentation of the problem in Section 3.2). Thus, the coding frame used for the preliminary analysis [27] consisted of classifying the solutions under two major concept-driven categories: Focusing on the rule that one—and only one—of the friends lied, or focusing on the rule that one—and only one—of the friends spilled the popcorn. Solutions that did not fit into either category would be cataloged according to their specific approach. After that separation, a data-driven categorization process followed, in which the various solutions from each category were reviewed, and patterns were searched to provide a finer subdivision of the forms of deductive reasoning according to different types of conceptual models or approaches (Figure 2).
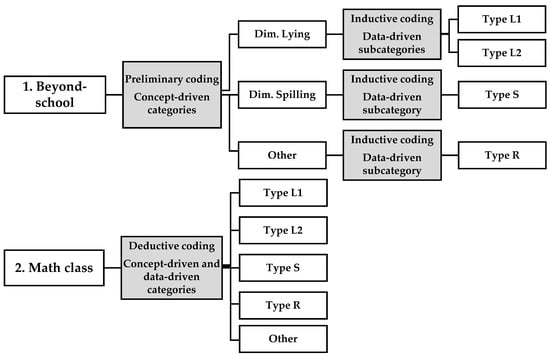
Figure 2.
Steps of the qualitative content analysis of each set of data.
Following this procedure, it was possible to identify types and subtypes of solutions to the problem, each of which corresponded to a specific form of deductive reasoning. In a subsequent stage, we chose prototypical examples of the different types of solutions, which were the object of a more detailed analysis and led to the identification of the supporting structures of the deductive reasoning developed. Those prototypes were also scrutinized for the students’ kinds of expression of deductive reasoning, including representational features.
The coding process was firstly applied to the body of solutions from the beyond-school scenario because their number was higher and, therefore, they could be more diverse. Next, using the obtained categories and subcategories as the established coding frame, the analysis was applied to the body of solutions from the mathematics class (Figure 2). Finally, a comparison was made between the results from the two bodies of data.
4. Results and Findings
In this section, the results are presented and empirical evidence of the findings is provided from a selection of prototypes of solutions pertaining to each type and subtype. The originals in Portuguese were transcribed and translated. The translation aimed to be as faithful as possible to the original text, with the utmost concern of preserving the meaning and the style of the written text used by the students. The language used by most students was quite simple and was usually filled with the very words that the problem itself contains: The names of the characters in the story, the verbs to lie and tell the truth, the adjectives of guilty and liar. Another type of word that frequently appeared included expressions like: Supposing that; we know that; therefore.
First, the results of the analysis of the solutions from the beyond-school setting are presented as a result of which three types of logical reasoning were identified, one of them subdivided into two sub-types. Each form of reasoning is concisely described and illustrated with two examples of students’ productions. Next, based on the previous categories, the results from the coding of the classroom solutions are presented, and an example of an answer for each type of reasoning is given.
4.1. Results from the Beyond-School Scenario
The first reading of the data allowed identification of the correct, incorrect, and partially correct answers. The latter consisted of solutions that presented an insufficient or unclear explanation of the reasoning that led to the answer to the problem. As can be seen in Table 2, which presents the numbers obtained, the success rate of the students who participated in the problem-solving competition was quite high.

Table 2.
Success summary from the beyond-school body of solutions.
The two main approaches identified in the solutions were each associated with one of the dimensions of the problem: (a) Who lied and (b) who spilled the popcorn (Table 3). Looking for necessary inferences about the one who lied was the most used approach. The two cases involved the testing of hypotheses and the elimination of options due to contradictions with the premises: Only one friend lied; only one friend spilled the popcorn; or one or more of the statements uttered by the characters. In addition to the two main approaches, some solutions adopted an alternative strategy. In a much smaller number, such solutions concentrated on the reduction of the conditions through the previous establishment of relations between the given constraints. In particular, some were based on realizing that two of the boys accused different people, which made it possible to deduce that one of them was necessarily the liar, and some were based on noticing that two of the boys could not both be lying (or telling the truth), as one states that the other lies, which made it possible to infer that one of them was necessarily the liar.

Table 3.
Main categories from the beyond-school body of solutions.
In many cases, the checking of hypotheses was indicated in an organized manner. The ways in which students solved the problem allowed their classification into three different types: Lying (L), spilling (S), and relations (R). In the case of the deductive reasoning focusing on the dimension “lying”, two subtypes of reasoning were then identified in the data (labeled as L1 and L2) and categorized according to the underlying form of logical reasoning.
4.1.1. Dimension “Lying”: The L1 Type of Deductive Reasoning
Based on their common features, the first type of solution under the general approach of checking all the options for the dimension “X lies” is illustrated by the Examples 1 and 2, and is characterized as the L1 type of deductive reasoning.
L1 Deductive Reasoning (Example 1)
Hypothesis 1.
Bernardo is lying—then it was Bernardo who spilled the popcorn. This cannot be the case because Gabriel and Carlos would also be lying.
Hypothesis 2.
Paulo is lying—then Gabriel is telling the truth and it was Carlos who spilled the popcorn. This cannot be the case because Carlos would also be lying, and there cannot be two lying.
Hypothesis 3.
Carlos is lying—then Paulo speaks the truth and, therefore, Gabriel has to be lying, which cannot be the case because there would be two of them lying.
Hypothesis 4.
Gabriel is lying—so it was not Carlos [who spilled the popcorn] and, therefore, Paulo speaks the truth. Since Bernardo is also speaking the truth and Carlos too, it was Paulo who spilled the popcorn.
L1 Deductive Reasoning (Example 2)
- If it was Bernardo lying, then he was the one who spilled the popcorn; therefore, Carlos had to be lying, and Gabriel too. This hypothesis is not true because there are three of them lying.
- If it was Gabriel lying, then it was not Carlos [who spilled the popcorn], and the others are telling the truth; therefore, the one who spilled the popcorn was Paulo, and that is the true hypothesis because only one is lying.
- If it was Carlos lying, Paulo did not spill the popcorn on the floor, and then it was Carlos [who spilled the popcorn], because Gabriel is telling the truth. However, Paulo says that Gabriel is not telling the truth, so one just cannot figure out, but there are two of them lying.
- If it was Paulo lying, Carlos and Gabriel were telling the truth, and this cannot be the case because they say different names, and only one spilled the popcorn.
This pattern of deductive reasoning corresponds to trying the falsification of hypotheses on the dimension “X lies” against the premise of having exactly one person lying or by the emergence of conflicting inferences, and can be summarized as follows:
L1 Deductive Reasoning
- Suppose X lies, then…; therefore, there is more than one lying (Eliminate).
- Suppose X lies, then…; therefore, conflicting inferences (Eliminate).
- Suppose X lies, then…; therefore, there is only one liar (Accept).
4.1.2. Dimension “Lying”: The L2 Type of Deductive Reasoning
A different version of the reasoning that focused on checking all the values of the dimension “X lies” applies the assumption that only one character is lying, and immediately establishes that all the others tell the truth. Thus, the checking is not concerned with ruling out the cases of more than one liar; instead, the checking is done sometimes against the assumption that only one person spilled the popcorn, and, other times, by the contradiction among conflicting inferences (a statement and its negation). The following two are examples of solutions that illustrate the L2 type of deductive reasoning.
L2 Deductive Reasoning (Example 1)
Scenario 1
- [Bernardo]—lies
- [Carlos]—tells the truth
- [Gabriel]—tells the truth
- [Paulo]—tells the truth
It is impossible because Carlos and Gabriel accuse different people.
Scenario 2
- [Bernardo]—Tells the truth
- [Carlos]—Lies
- [Gabriel]—Tells the truth
- [Paulo]—Tells the truth
It is impossible because Gabriel and Paulo cannot both be telling the truth, since Paulo says that Gabriel is lying.
Scenario 3
- [Bernardo]—Tells the truth
- [Carlos]—Tells the truth
- [Gabriel]—Lies
- [Paulo]—Tells the truth
It is possible because we conclude that it was not Bernardo and it was not Carlos, and Paulo confirms that Gabriel lies. So, it was Paulo.
Scenario 4
- [Bernardo]—Tells the truth
- [Carlos]—Tells the truth
- [Gabriel]—Tells the truth
- [Paulo]—Lies
It is impossible because Carlos and Gabriel accuse different people.
Answer: It was Paulo who spilled the popcorn.
L2 Deductive Reasoning (Example 2)
Hypothesis H1.
(Bernardo lies)
| Statement | Bernardo | False | Therefore, he is guilty. | Accept |
| Carlos | True | Therefore, it was Paulo. | Contradiction | |
| Gabriel | True | Therefore, it was Carlos. | Contradiction | |
| Paulo | True | Therefore, Gabriel is not telling the truth and it was not Carlos. | Contradiction |
Conclusion: Hypothesis not accepted.
Hypothesis H2.
(Carlos lies)
| Statement | Bernardo | True | Therefore, it was not him | Accept |
| Carlos | False | Therefore, it was not Paulo | Accept | |
| Gabriel | True | Therefore, it was Carlos | Accept | |
| Paulo | True | Therefore, Gabriel is not telling the truth and it was not Carlos | Contradiction |
Conclusion: Hypothesis not accepted.
Hypothesis H3.
(Gabriel lies)
| Statement | Bernardo | True | Therefore, it was not him | Accept |
| Carlos | True | Therefore, it was Paulo | Accept | |
| Gabriel | False | Therefore, it was not Carlos | Accept | |
| Paulo | True | Therefore, Gabriel is not telling the truth and it was not Carlos | Accept |
Conclusion: Hypothesis accepted, that is, Gabriel lied and Paulo spilled the popcorn.
Hypothesis H4.
(Paulo lies)
| Statement | Bernardo | True | Therefore, it was not him | Accept |
| Carlos | True | Therefore, it was Paulo | Accept | |
| Gabriel | True | Therefore, it was Carlos | Contradiction | |
| Paulo | False | Therefore, Gabriel is telling the truth and it was Carlos | Contradiction |
Conclusion: Hypothesis not accepted.
This form of reasoning also corresponds to the intention of falsifying hypotheses under the dimension “X lies”, and can be translated as follows, where the checking is based on the existence of a single guilty person or else on contradictory inferences about who has dropped the popcorn on the floor:
L2 Deductive Reasoning
- Suppose X is the only liar, then…; therefore, there is more than one guilty (Eliminate).
- Suppose X is the only liar, then…; therefore, conflicting inferences (Eliminate).
- Suppose X is the only liar, then…; therefore, there is only one guilty (Accept).
4.1.3. Dimension “Spilling”: The S Type of Deductive Reasoning
Another route for solving the problem, corresponding to a smaller percentage of answers, took the dimension “who spilled the popcorn” for the construction of hypotheses. This kind of solution stands out in that it presents a much more condensed explanation and more simple and direct deductions, indicating an apparent simplification of the problem-solving process. Some of these solutions include a double-entry table, where one of the dimensions is attributed to the person that spilled the popcorn and the other dimension to the statement of each of the characters, aiming for cross-checking and determining the option consistent with one single person lying. The following two examples illustrate the reasoning of Type S.
S Deductive Reasoning (Example 1)
Assuming that Bernardo spilled the popcorn, then all lied (L), except Gabriel, who told the truth (T) (see table, first column). If it was Carlos, then Carlos and Paulo were lying. If it was Gabriel who spilled the popcorn, then Carlos and Gabriel were lying. If it was Paulo, then only Gabriel lied. So, it was Paulo who spilled the popcorn, and Gabriel lied.
| B. | C. | G. | P. | |
| - It was not me, said Bernardo. | L | T | T | T |
| - It was Paulo, said Carlos. | L | L | L | T |
| - It was Carlos, said Gabriel. | L | T | L | L |
| - Gabriel is not telling the truth, said Paulo. | T | L | T | T |
| N. of lies | 3 | 2 | 2 | 1 |
S Deductive Reasoning (Example 2)
Let us suppose that Bernardo spilled the popcorn. Then, Bernardo lied. Then, Paulo lied. However, as there was only one who lied, IT WAS NOT BERNARDO.
Let us assume that it was Carlos. Then, Carlos lied. Then, Paulo lied. However, as there was only one who lied, IT WAS NOT CARLOS.
Let us suppose that it was Gabriel. Then, Carlos lied. Then, Gabriel lied. However, as there was only one who lied, IT WAS NOT GABRIEL.
As there is only one left, it was Paulo who spilled the popcorn.
Let us check: Bernardo did not lie. Carlos did not lie. Gabriel lied. Paulo did not lie. Conclusion: IT WAS PAULO THAT SPILLED THE POPCORN.
In the case of the S Type of solution, as shown in the examples, the reasoning is built on the falsification of assumptions about the dimension “X spills the popcorn”, as these are confronted with the premise that there is only one person who is lying. The hypothesis that leads to only one lying is accepted. The schema of reasoning has a simple structure, and it does not yield contradictory inferences, as summarized below:
S Deductive Reasoning
- Suppose X spills, then…; therefore, there is more than one lying (Eliminate).
- Suppose X spills, then…; therefore, there is only one liar (Accept).
4.1.4. Using Relations between the Premises: The R Type of Deductive Reasoning
The solutions of Type R, even less frequent than the former, draw necessary conclusions from relationships between some conditions of the problem, as illustrated below in Examples 1 and 2. In this type of solution, students use combinations of rules to produce new inferences, thus generating new information from the relations devised among the statements provided.
R Deductive Reasoning (Example 1)
- There is only one liar and only one who spilled the popcorn.
- From the two middle sentences, I concluded the following:
- -
- Carlos says: It was Paulo who spilled the popcorn.
- -
- Gabriel says: It was Carlos who spilled the popcorn.
As only one spilled the popcorn, then Carlos and Gabriel cannot both speak the truth because they say different things. So, one of them lies, and thus the liar is either Carlos or Gabriel. So, Paulo speaks truth.
- 3.
- Paulo speaks the truth and says that Gabriel is lying; therefore, if Gabriel lies, then Carlos speaks the truth, and he says it was Paulo who spilled the popcorn.
R Deductive Reasoning (Example 2)
The statements of Gabriel and Paulo cannot both be true, which means that one of them is lying. So we raised two hypotheses:
Hypothesis A.
If Gabriel tells the truth, then it was Carlos, and Paulo lies (because he says Gabriel lied); then, Carlos lies because he says that it was Paulo (and it was not, since it was Carlos according to this hypothesis), and Bernardo tells the truth (because he says it was not him).
The Hypothesis A is not right because, according to the data of the problem, only one can lie, but in this case, Paulo and Carlos are both lying.
Hypothesis B.
If Gabriel lies, then it was not Carlos (because he says it was Carlos), and Paulo tells the truth (because he says Gabriel lies); as only one of the four friends is lying, then Carlos tells the truth (so it was Paulo) and Bernardo tells the truth (because it was not him, but Paulo).
The conclusion is that the Hypothesis B is correct, so Gabriel was the one who lied and it was Paulo who spilled the popcorn.
This type of reasoning means checking the validity of one of two mutually exclusive assumptions. In a simplified form, this consists of testing two conflicting hypotheses (in referring to the codes used in Section 3.2, that means testing the assumptions P2 and P3 or the assumptions P3 and P4) by admitting the truth of one and the consequent falsity of the other. Considering P3 and P4, one may conclude that one of them has to be false, since Carlos and Gabriel are indicating different names for the guilty one. Likewise, if we consider P3 and P4, one may deduce that one of them has to be false, since Paulo asserts that Gabriel is lying.
In this case, we may describe the R type of deductive reasoning as follows:
R Deductive Reasoning
- Either P2 or P3; suppose not-P2 and P3…; therefore, conflicting inferences (Eliminate).
- Either P2 or P3; suppose not-P3 and P2…; therefore, one guilty and one liar (Accept).
Or else
- Either P3 or P4; suppose not-P3 and P4…; therefore, one guilty and one liar (Accept).
- Either P3 or P4; suppose not-P4 and P3…; therefore, conflicting inferences (Eliminate).
4.2. Results from the School Scenario
In analyzing the data from the mathematics class scenario, the first step was to classify the answers as correct, incorrect, or partially correct. As can be seen from the summary in Table 4, it is clear that the success rate of this group of students in the problem was much lower.

Table 4.
Success summary from the school body of solutions.
The next step was to examine the 31 correct solutions that were obtained. One aspect that stood out was the fact that several resolutions were apparently produced by the students directly on the answer sheet. The written answers showed numerous erasures and, in some cases, there were signs of a lack of space to make multiple attempts, as well as areas of the paper that were written upon and then crossed out by the student.
This time, the data analysis applied the categories already identified in the analysis of the previous body of solutions, that is, each of the resolutions was assessed for its adjustment to any of the identified types of deductive reasoning, including the two subtypes. After careful reading of the answers, it was observed that every solution could be assigned to one of the previous categories, with no other strategy or alternative resolution scheme having emerged, as shown in Table 5.

Table 5.
Categories from the school body of solutions.
Interestingly, the results show a more even distribution among the various types of reasoning, the most frequent (albeit with a slight advantage) being the one where students focused on the dimension “who spilled the popcorn”, that is, the Type S deductive reasoning. The vast majority of solutions present the reasoning in textual form, with some specific cases using tables and even some quick drawings. Apparent hesitations were observed in the elaboration of the written text (as already stated), with several responses showing crossed-out and then redone text. Prototypical examples were identified and compared with those that had been selected in the analysis of the solutions produced outside of school. The fundamental characteristics of each pattern of deductive reasoning were found and confirmed. Below is an example for each pattern of deductive reasoning selected from the students’ solutions to the problem in the mathematics class.
L1 Deductive Reasoning (Example)
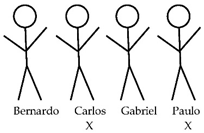
If Paulo is lying, then it was Carlos who spilled the popcorn. However, Carlos is telling the truth and says it was Paulo. So it is wrong.
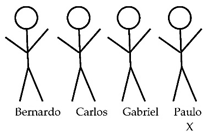
If Gabriel is lying, then it was not Carlos who spilled the popcorn. So, it was Paulo because Carlos is telling the truth. This has no errors (Paulo).
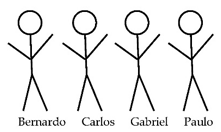
If Carlos is lying, then it was not Paulo. So, it was Carlos because Gabriel is telling the truth. However, Paulo is also telling the truth. So, it is wrong.
If Bernardo is lying, then it was him. However, it was also Paulo and it was also Carlos, because Carlos and Gabriel are telling the truth. So, it is wrong.
L2 Deductive Reasoning (Example)
| Bernardo | Carlos | Gabriel | Paulo |
| He said it was not him | He said it was Paulo | He said it was Carlos | He said that Gabriel lied |
| True | True | True | Lie |
| NO. Carlos is true. Gabriel cannot be true. | |||
| True | True | Lie | True |
| YES. Bernardo is true. Carlos is true. Paulo is true. | |||
| True | Lie | True | True |
| NO. Gabriel is true. Paulo cannot be true. | |||
| Lie | True | True | True |
| NO. Bernardo is not true. Carlos cannot be true. |
Answer: Gabriel lied and Paulo spilled the popcorn.
S Deductive Reasoning (Example)
It was not Bernardo. It was not Paulo. It was not Carlos. It was Gabriel. This possibility is false because there are two liars here.
It was not Bernardo. It was not Paulo. It was Carlos. It was not Gabriel. This possibility is false because there are two liars here.
It was not Bernardo. It was Paulo. It was not Carlos. It was not Gabriel. This possibility is true because there is only one liar here.
It was Bernardo. It was not Paulo. It was not Carlos. It was not Gabriel. This possibility is false because there are three liars here.
Correct possibility: It was Paulo, because Bernardo was telling the truth, Carlos was telling the truth, Gabriel was lying, and Paulo was telling the truth.
R Deductive Reasoning (Example)
Only one of those four friends lied, and only one of those four friends dropped the bucket of popcorn.
It could only have been Paulo or Carlos because they were both accused and because only one of the accusations is a lie.
It could not be Carlos, because if it were Carlos, two of the friends were lying (Carlos and Paulo).
So, it turns out that it was Paulo; therefore, only one of them was lying (Gabriel).
The four examples displayed above effectively substantiate the four reasoning models that were previously described and outlined, and confirm the logical structure that distinguishes them. This leads us to state with reasonable confidence that 10–12 year old students are able to reason deductively and that several models of deductive reasoning are, in fact, plausible among young children.
4.3. Comparative and Interpretative Analysis of the Two Scenarios
When confronting the results obtained in the two scenarios, it is possible to perceive commonalities and dissimilarities.
In terms of common results, it stands out that the four patterns of deductive reasoning were found in both groups of subjects. This indicates that children aged 10–12, in different contexts of activity, reason logically and are able to produce adequate and solid deductive reasoning to solve a moderately complex analytical reasoning challenge. Another aspect to be noted is that the R type of deductive reasoning was observed in both cases, especially focusing on dichotomous conditions that entail the use of exclusive disjunction. A third point to be highlighted has to do with the representational resources that were displayed in both groups. The majority of solutions produced by the children reveal the use of free written text with an argumentative spirit, in which the steps of the reasoning appear in a generally sequential and organized way. The use of text lists was also observed, which usually included abbreviations of sentences and use of expressive linguistic elements (e.g., therefore, however, assume, either, or). Other types of notations were observed; for example, the initials of the names of the friends referred to in the problem, as well as the letters T and F to mean true and false, or the letter L to mean lie or liar. In a smaller number, although in both contexts, children used tables as a way to record and organize the production of inferences and the elimination of options. Some examples of simple drawings were also seen, typically used as a way to express the situation in terms of its logical components (e.g., schematic faces or humans to represent the four characters), which were used to highlight the utterances made or to denote inferences (namely, crossing them out when options were eliminated).
As for the contrasts that emerged in the comparison, one of the most obvious has to do with the success rates in the two groups. The notable difference between the higher success of the participants in the beyond-school competition and the lower success of the students in the classroom leads to the consideration of several important conditions for working on analytical reasoning problems. One of them is the existence of possible aid, ranging from adult guidance to the use of resources in solving and expressing the solution. Students in the beyond-school scenario, in many cases, used digital tools to present their solution process, and were able to take advantage of the affordances of those tools. On the contrary, students in the classroom only had paper and pencils at their disposal. Another important condition is linked to the time available to work on the problem. This condition seems relevant not only to interpret the difference in the number of correct answers, but also to justify the most frequent type of reasoning (focused on the dimension “lying”) among students who solved the problem in the beyond-school scenario. As the results demonstrated, both the L1 type and the L2 type of deductive reasoning require a more laborious construction of inferences, not because of the number, but because of its extent and its nature. These are the answers that tended to use more space and that appeared to involve longer solution processes. The apparent prevalence of these types of reasoning among students in the beyond-school scenario may be in line with some of their probable characteristics—they usually like to solve challenges, persist in looking for solutions, invest time and work to arrive at an answer, accept more easily the complexity of a problem, and value the quality of the explanation of the solution. Furthermore, unlike students in the classroom, they had the possibility to do and redo several attempts to solve the problem and to choose what seemed to them the most explicit and complete way of showing the reasoning, which may not be the most shortened one. In the case of the students in mathematics classes, not only the more reduced time, but also the reduced resources may inhibit the development of long or more difficult inferences. They could be more disposed to get easy and swift answers. The expression of reasoning seems to be less essential to them because they had fewer opportunities to do and redo attempts. This was perceptible from some messiness in the students’ answers and the lack of space that they possibly struggled with.
5. Discussion
The present study aimed at getting a fine-grained picture of how young children (aged 10–12), in different scenarios, solve an analytical reasoning problem based on deductive reasoning, and to know about the ways in which that reasoning was expressed. The empirical data consisted of 384 solutions from children participating in a beyond-school problem-solving competition taking place through the Internet, and 102 solutions produced by students from the fifth and sixth grades in their mathematics classrooms without any help from others.
5.1. Models of Deductive Reasoning in Problem-Solving
Two main approaches to the problem were identified in the solutions collected. One approach focuses on the dimension “who lied”, and the other on the dimension “who spilled the popcorn”. It is possible to consider four atomic propositions related to the act of lying and four others related to the act of dropping the popcorn, as well as a set of relations between these, as described earlier. Thus, the approach of looking for who lied directs attention to the goal of determining which of the four friends lied, whereas the approach of looking for who dropped the popcorn sets the objective of finding the dropper, in both cases keeping in mind that only one lied and only one spilled the popcorn. Clearly, in either approach, both dimensions were involved, since the relational structure of the problem entails that.
In those two approaches, the predominant strategy for solving the problem is consistent with the one discussed by Newstead et al. [25], that is, participants showed a systematic use of rule checking and option elimination. So, they worked systematically in testing hypotheses, looking for contradictions, and discarding those generating conflicting inferences. The general structure of the reasoning developed consists of assuming an option and testing it against all the given premises, using different control criteria in searching for contradictions, that is, the hypothesis is excluded when one or more contradictions arise.
Four models of deductive reasoning (L1 Type, L2 Type, S Type, and R Type) were found—the first two belonging to the approach driven by the search for “who lied”, the third to the approach centered on finding “who spilled the popcorn”, and the fourth based on reformulating the structure of the problem by previously working on relations between the premises. The different models were found in the two bodies of solutions examined, although with different frequencies in the two groups. This result is interesting for several reasons.
On the one hand, it demonstrates that in the two scenarios, namely with and without help, young students generated models of solutions that fit the four types, suggesting that the mental models perspective is useful to conceptualize and understand the possibilities of deductive reasoning within the reach of children. In a nutshell, children build mental models that represent the truth of the premises in the problem situation. Furthermore, it reveals that the different settings are not irrelevant in the children’s choice of models. Indeed, our results show that a majority of participants (59%) in the beyond-school scenario used the testing of hypotheses for the dimension “who lied”, apparently taking the most arduous approach for representing and checking all the possibilities against the premises. Even more clearly in the case of the L1 Type solutions, the students did not try to reduce the relational complexity and, as such, the reasoning required meticulous analysis of the hypotheses. This result is consistent with the conclusions of English [24], according to which solvers tend to avoid the complexity of relational assumptions by directing their effort to the exhaustive logical analysis of the series of premises. If the students are working on the problem with an extended time to deliver the solution, this seems a rather significant factor. On the contrary, many of the students who solved the problem in the classroom may have struggled with the reduced time to engage in this form of resolution. Thus, this model, which is underrepresented in the second body of solutions (9%), may have been the option of several students who were unable to take it forward.
Moreover, the solutions from both groups where students focused on the dimension “who spilled the popcorn” showed a more direct, expeditious, and clear process of achieving necessary conclusions, but such clear-cut approaches are also known to be less common [24,25]. Hence, it seems that the models L1, L2, and S progress in the increasing control capacity that they offer for hypothesis testing. In particular, in the L1 Type, at the start of the inferential reasoning, students do not keep track of those who told the truth or those who did not spill popcorn; in the L2 Type, they keep track of those who spoke the truth from the beginning; and, in the S Type, they keep track of those who did not spill popcorn and get the number of lies (as in the examples shown).
Finally, the R Type of reasoning is rather dissimilar, and looks like compelling evidence of the theory of mental models [12,24,25,28] in that it suggests the development of a more complete and refined model of the given situation, showing the understanding that some of the premises in the problem may be replaced by other equivalents, thus creating a new “version” of it. In other words, the students who used the R Type of deductive reasoning worked on the premises before moving to the systematic and exhaustive checking of hypotheses. This means that they dealt with the complexity of the relationships expressed in the problem and, in particular, with the indeterminacy involved in the premises [15], which is also related to the semantics of the problem. In fact, it was interesting to find that the frequency of this model was actually higher in the students from the classroom setting. This means they were able to realize that some of the propositions were mutually exclusive. One possible interpretation for this result is related to the contextual nature of the problem and to its semantic richness, one characteristic that is seen as relevant in triggering counterexamples [12,15,29].
5.2. Analytical Reasoning Problems as Deductive Reasoning Problems
Given that all the students were attending the fifth and sixth grades, their learning of formal logic in school is inexistent, and logical reasoning is very limited in their mathematics lessons, as it is delayed to more advanced school levels in the Portuguese curriculum. However, over several years of implementation of the mathematical problem-solving competition, it was observed that analytical reasoning problems, compared with several other non-routine problems proposed, were among the competitors’ favorites, apparently because they incite their curiosity and appeal to their cleverness [9]. This suggests that such problems deserve new attention from school mathematics concerning the development of deductive reasoning. The importance of knowing how children reason deductively on such contextual logical problems is thus justified. Moreover, since young children do not yet master the language of formal logic, it is also important to understand how they express their deductive reasoning with their language and representational resources.
The view that analytical reasoning problems are substantially deductive reasoning problems [17,25] is clearly conveyed by the analysis of the participants’ resolutions to the problem of the spilled popcorn. The children’s solutions revealed the strong presence of logical inferences expressed in the process used to solve the problem. With regard to the set of deductive reasoning skills involved in analytical reasoning problems, it seems clear that in the problem of the spilled popcorn, the students reached an understanding of the basic structure of the relations involved in the premises and rules of the problem, made extensive use of inferential reasoning to produce true and necessary inferences based on option elimination, drew additional or substitute rules from some of the initially given conditions, and identified equivalent propositions in the context of the problem situation. As in other studies with older students [11,23,25,30], young students reasoned deductively, using similar processes and language, although adjusted to their level of knowledge and development. Likewise, the results of the study corroborate findings of experiments with younger children, namely with regard to principles that most influence the success of solvers in analytical reasoning problems: (1) Selecting a premise that most readily yields an explicit problem-situation model and (2) integrating premises where appropriate in the existing model [24].
In light of the results, analytical reasoning problems represent a potential kind of challenging task for the development of deductive reasoning. Not only do they seem to encourage the use of logical structures of high complexity, they have been shown to be within reach of the students’ ability to reason deductively. The results also lead to the conclusion that this is a valuable resource for the integration of logical and deductive reasoning in the school setting, especially if one embraces the view that logic can and should be driven by the curriculum in order to make it meaningful, and as a way of establishing bridges with deductive reasoning in mathematics topics and in proofs [4,16,17,18,19,22].
As underlined by Newstead et al. [25], analytical reasoning problems differ from those tasks more typically used in the psychology of deductive reasoning. Firstly, they offer contextualized situations; secondly, they put deductive reasoning into action while solving a challenge rather than focusing on determining the truth of an abstract rule. This is in line with claims by several researchers who have studied productive ways of integrating deductive reasoning and logical principles in school mathematics [4,8,16,17,19]. Thus, from the standpoint of supporting students’ deductive reasoning and as potential tools for the development of logical competence in school mathematics, analytical reasoning problems are a still-underexplored resource.
5.3. Language and Resources in Expressing Deductive Reasoning
The children’s linguistic expression of their solutions to the problem seems to simultaneously reflect logical thinking in everyday contexts and deductive reasoning in formal logic problems.
A number of textual formulations were identified, such as: “If this… therefore that”, “suppose this… then that”, “if this, then that…; hence…”. In addition, relevant was the use of the word “however” in expressing the presence of some contradiction that led to the rejection of some hypothesis. That was perceptible within the logical scheme of identifying conflicting inferences, expressed in words like: “However, it cannot be”, “however, there is a contradiction”, and so forth. Moreover, in the case of the R Type of reasoning, students noticed the presence of mutually exclusive propositions, which they often conveyed through the words: “Either–or”, “either this or that”, “either this is true or that is true”, or “only one of the two can be true”. This shows that students efficiently dealt with the “exclusive or” in some of the solutions obtained.
Contrary to what is common in analytical reasoning problems, the use of tables was not the most frequent, although it was a representational resource used by some children in both contexts. The use of tables appears to have proven more effective and also easier in cases where the approach was focused on the dimension of “who spilled the popcorn”. In fact, in the approach focused on “who lied”, the participants who used the tabular representation had to build a succession of different tables, while in the other approach, a single table proved to be sufficient for the development of the entire reasoning.
To some extent, we may conclude that even young children have the linguistic resources to express their logical reasoning on a contextual problem in meaningful and strongly referential ways, which resonates with the perspective that mental models are not expressed by the rules and much less by the syntax of formal logic, as argued by Markovits and Barrouillet: “We consider it unlikely that reasoning problems are easily represented in even a semiabstract way, particularly among children” [28] (p. 32). This also indicates that analytical reasoning problems are a fruitful resource for the progressive development of logical reasoning, as they represent contextual problems that are, at the same time, intuitive, semi-abstract, and “pre-symbolic”; they are therefore interesting as catalysts in exploring deductive reasoning in mathematics education. The results furthermore corroborate the evidence that some studies have obtained with even younger children [31], namely that they are able to construct mathematical and deductive reasoning in solving non-routine problems and to use more or less conventional forms of representation in expressing their reasoning. One of the crucial functions of the use of expressive resources by young children is to unpack the structure of the problem [31].
6. Conclusions
In this study, we examined children’s solutions to a moderate mathematical challenge involving analytical reasoning, produced in two different contexts: The classroom and a web-based mathematics competition.
Our study found that children aged 10–12 years are capable of reasoning deductively in solving an analytical reasoning problem and that the deductive reasoning models revealed by their solutions are of four types, each with its own logical structure and corresponding to the dimensions of the problem (“who lied” and “who spilled the popcorn”) or a relationship between them. The four types of deductive reasoning appeared in the two settings in which the solutions were created, though with different frequencies.
Children can express deductive reasoning through language and representational resources while testing hypotheses systematically, looking for contradictions, and eliminating options. The textual formulations in their solutions show features of deductive reasoning typical of formal logic, as well as traits of everyday logical thinking. Although less frequent, other forms of representations were used, such as tables, ordered lists, or diagrams. The use of a single table was a powerful resource in implementing the S Type of deductive reasoning, while several tables had to be used for the L Type of approach.
The lowest success rate in the problem of the spilled popcorn was obtained with the students who solved the problem individually, without help, in limited time, and with basic resources. Despite the reduced success, those who successfully completed the task showed deductive reasoning models identical to those built by other students in a beyond-school environment. This leads to the assertion that deductive reasoning should be cultivated and reinforced in the school context, even with young children. Among several factors to consider, students should be given enough time to create their mental models of the situation; the use of resources may be important, namely representational resources, such as tables, ordered text, diagrams, notations, symbols, and registers that help to deal with relational complexity; good contextualized problems and purely mathematical problems with a relational character are desirable (the attractive factor of solving puzzles or enigmas is important in students’ engagement); the use of analytical reasoning problems with a slight degree of indeterminacy seems to be useful, as it brings up different types of deductive reasoning that may be beneficially shared in the class; and, finally, solving analytical reasoning problems involves a very significant expression of reasoning and, therefore, it constitutes an opportunity to foster the linguistic and representational abilities of students in expressing logical thinking, namely chains of deductive arguments.
Author Contributions
Conceptualization, S.C.; methodology, S.C.; formal analysis, S.C., N.A., and H.J.; writing—Original draft preparation, S.C.; writing—Review and editing, S.C., N.A., and H.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- NCTM. Principles and Standards for School Mathematics; National Council of Teachers of Mathematics: Reston, VA, USA, 2000. [Google Scholar]
- MOE. Mathematics syllabus—Primary One to Six; Ministry of Education—Curriculum Planning and Developmental Division: Singapore, 2012. [Google Scholar]
- Dreyfus, T. Why Johnny can’t prove. Educ. Stud. Math. 1999, 38, 85–109. [Google Scholar] [CrossRef]
- Lee, K. Students’ Logical Reasoning and Mathematical Proving of Implications. Ph.D. Thesis, Michigan State University, East Lansing, MI, USA, 2011. Available online: https://d.lib.msu.edu/etd/1959 (accessed on 7 January 2019).
- Inglis, M.; Simpson, A. Mathematicians and the Selection Task. In Proceedings of the 28th Conference of the International Group for the Psychology of Mathematics Education, Bergen, Norway, 14–18 July 2004; Høines, M.J., Fuglestad, A.B., Eds.; Bergen University College & PME: Bergen, Norway, 2004; Volume 3, pp. 89–96. [Google Scholar]
- Durand-Guerrier, V. Which notion of implication is the right one? From logical considerations to a didactic perspective. Educ. Stud. Math. 2003, 53, 5–34. [Google Scholar] [CrossRef]
- Stylianides, G.J.; Stylianides, A.J. Proof in school mathematics: Insights from psychological research into students’ ability for deductive reasoning. Math. Think. Learn. 2008, 10, 103–133. [Google Scholar] [CrossRef]
- Stylianides, A.J. Introducing young children to the role of assumptions in proving. Math. Think. Learn. 2007, 9, 361–385. [Google Scholar] [CrossRef]
- Carreira, S.; Jones, K.; Amado, N.; Jacinto, H.; Nobre, S. Youngsters Solving Mathematical Problems with Technology; Springer: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Kaufman, S.B.; Ross, H.J.; Silk, E.M. A Cognitive Model of Analytical Reasoning Using GRE Problems; Carnegie Mellon University: Pittsburgh, PA, USA, 2001. Available online: https://scottbarrykaufman.com/wp-content/uploads/2013/01/Kaufman-Etal-2001-GRE-Problems.pdf (accessed on 17 February 2019).
- Cox, R. Analytical Reasoning with Multiple External Representations. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 1996. Available online: https://www.era.lib.ed.ac.uk/bitstream/handle/1842/10550/Cox1996.pdf (accessed on 12 March 2019).
- Schroyens, W.; Schaeken, W.; D’Ydewalle, G. The processing of negations in conditional reasoning: A meta-analytic case study in mental model and/or mental logic theory. Think. Reas. 2001, 7, 121–172. [Google Scholar] [CrossRef]
- Johnson-Laird, P.N. Deductive reasoning. Annu. Rev. Psychol. 1999, 50, 109–135. [Google Scholar] [CrossRef] [PubMed]
- Johnson-Laird, P.N.; Byrne, R. A model point of view. Think. Reas. 1995, 1, 339–350. [Google Scholar] [CrossRef]
- Van der Henst, J.-B. Mental model theory versus the inference rule approach in relational reasoning. Think. Reas. 2002, 8, 193–203. [Google Scholar] [CrossRef]
- Nunes, T.; Bryant, P.; Evans, D.; Bell, D.; Gardner, S.; Gardner, A.; Carraher, J. The contribution of logical reasoning to the learning of mathematics in primary school. Br. J. Dev. Psychol. 2007, 25, 147–166. [Google Scholar] [CrossRef]
- Epp, S. The role of logic in teaching proof. Am. Math. Mon. 2003, 110, 886–899. [Google Scholar] [CrossRef]
- Bakó, M. Why we need to teach logic and how we can teach it. Int. J. Math. Teach. Learn. 2002. Available online: http://www.cimt.plymouth.ac.uk/journal/bakom.pdf (accessed on 12 March 2019).
- Hoyles, C.; Küchemann, D. Students’ understandings of logical implication. Educ. Stud. Math. 2002, 51, 193–223. [Google Scholar] [CrossRef]
- Ayalon, M.; Even, R. Deductive reasoning: In the eye of the beholder. Educ. Stud. Math. 2008, 69, 235–247. [Google Scholar] [CrossRef]
- Morsanyi, K.; McCormack, T.; O’Mahony, E. The link between deductive reasoning and mathematics. Think. Reas. 2018, 24, 234–257. [Google Scholar] [CrossRef]
- Lommatsch, C.W. Learning Logic: A mixed methods study to examine the effects of context ordering on reasoning about conditionals. Ph.D. Thesis, Utah State University, Logan, UT, USA, 2018. Available online: https://digitalcommons.usu.edu/etd/7011 (accessed on 10 February 2020).
- Cox, R.; Brna, P. Supporting the use of external representations in problem solving: The need for flexible learning environments. Int. J. Artif. Intell. Educ. 1995, 6, 239–302. [Google Scholar]
- English, L. Children’s reasoning in solving relational problems of deduction. Think. Reas. 1998, 4, 249–281. [Google Scholar] [CrossRef]
- Newstead, S.; Bradon, P.; Handley, S.; Dennis, I.; Evans, J. Predicting the difficulty of complex logical reasoning problems. Think. Reas. 2006, 12, 62–90. [Google Scholar] [CrossRef]
- Krippendorff, K. Content Analysis: An Introduction to its Methodology, 2nd ed.; Sage Publications: London, UK, 2004. [Google Scholar]
- Schreier, M. Qualitative Content Analysis in Practice; Sage Publications: London, UK, 2012. [Google Scholar]
- Markovits, H.; Barrouillet, P. The development of conditional reasoning: A mental model account. Dev. Rev. 2002, 22, 5–36. [Google Scholar] [CrossRef]
- Van der Henst, J.-B. Mental model theory and pragmatics. Behav. Brain Sci. 2000, 23, 283–284. [Google Scholar] [CrossRef]
- Yang, Y.; Johnson-Laird, P.N. Mental models and logical reasoning problems in the GRE. J. Exp. Psychol. Appl. 2001, 7, 308–316. [Google Scholar] [CrossRef] [PubMed]
- Canavarro, A.P.; Pinto, M.E. O raciocínio matemático aos seis anos: Características e funções das representações dos alunos (Mathematical reasoning at age six: Characteristics and functions of students’ representations). Quadrante 2012, 21, 51–79. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).