New Evidence about Skill-Biased Technological Change and Gender Wage Inequality
Abstract
1. Introduction
2. Literature Review
3. Data, Variables, Statistics, and Correlations
4. Empirical Analysis, Model Specification, and Estimation Methods
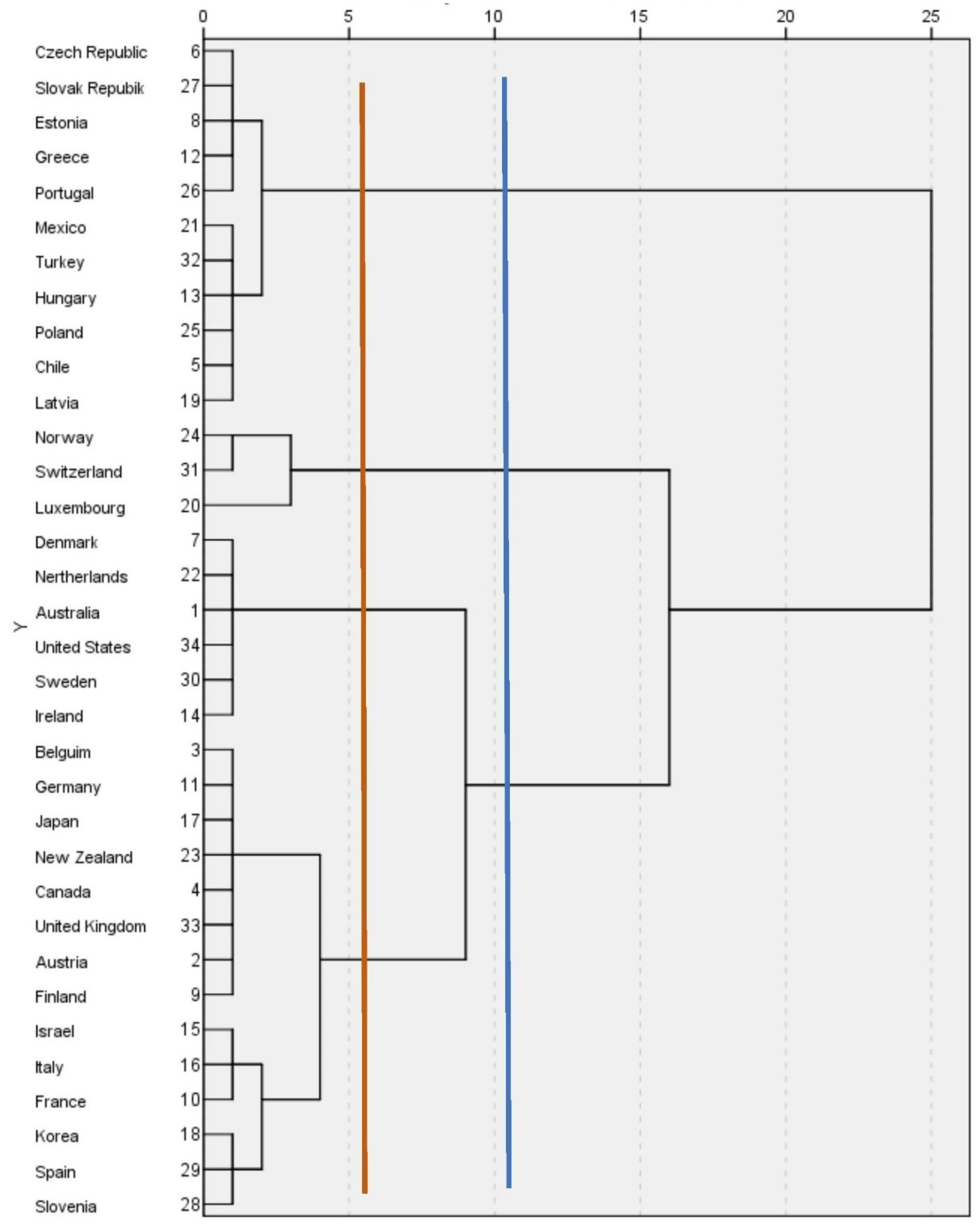
Exploratory Multivariate Analysis Technique
- -
- Cluster 1 consists only of Norway and Switzerland. The three most prominent characteristics of this cluster are the high environmental performance index, the highest expenditure on education as a percentage of GDP, and the lowest average CO2 emissions per capita.
- -
- Cluster 2 includes Australia, Denmark, Ireland, the Netherlands, Sweden, and the United States. This cluster has the highest CO2 emissions per capita and the lowest wage gap for all education levels, between most workers and women.
- -
- Cluster 3 consists only of Luxembourg. This country has the highest GDP per capita and the lowest education expenditure as a percentage of GDP.
- -
- Cluster 4 includes Austria, Belgium, Canada, Finland, France, Germany, Israel, Italy, Japan, Korea, New Zealand, Spain, and the United Kingdom. This cluster is the one with the highest average R&D as a percentage of GDP.
- -
- Cluster 5 consists of Chile, the Czech Republic, Estonia, Greece, Hungary, Latvia, Mexico, Poland, Portugal, the Slovak Republic, Slovenia, and Turkey. This group of countries has the lowest GDP per capita, the lowest environmental performance index, and the highest percentage of trade union membership.
5. Discussion of the Results
6. Conclusions and Policy Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Acemoglu, Daron. 2002. Technical change, inequality and labour market. Journal of Economic Literature 10: 7–72. [Google Scholar] [CrossRef]
- Acemoglu, Daron, and David Autor. 2011. Skills, tasks and technologies: Implications for employment and earnings. Handbook of Labour Economics 4: 1043–171. [Google Scholar] [CrossRef]
- Acemoglu, Daron, and Pascual Restrepo. 2018. The race between man and machine: Implications of the technology for growth, factor shares and employment. American Economic Review 108: 1488–542. [Google Scholar] [CrossRef]
- Acemoglu, Daron, and Pascual Restrepo. 2021. Tasks, Automation, and the Rise in US Wage Inequality. Working Paper 28920. Cambridge, MA: NBER—National Bureau Economic Research. [Google Scholar]
- Ahmed, Zahor, Bin Zhang, and Michael Cary. 2021. Linking economic globalization, economic growth, financial development, and ecological footprint: Evidence from symmetric and asymmetric ARDL. Ecological Indicators 121: 107060. [Google Scholar] [CrossRef]
- Antonczyk, Dirk, Thomas DeLeire, and Bernd Fitzenberger. 2018. Polarization and rising wage inequality: Comparing the US and Germany. Econometrics 6: 20. [Google Scholar] [CrossRef]
- Autor, David H., Lawrence F. Katz, and Melissa S. Kearney. 2008. Trends in US wage inequality: Revising the revisionists. The Review of Economics and Statistics 90: 300–23. Available online: https://www.jstor.org/stable/40043148 (accessed on 27 January 2023).
- Bashir, Muhammad Farhan, Benjiang Ma, Muhammad Adnan Bashir, Bilal, and Luqman Shzad. 2021. Scientific data-driven evaluation of academic publications on environmental Kuznets curve. Environmental Science and Pollution Research 28: 16982–99. [Google Scholar] [CrossRef]
- Benabou, Roland. 2000. Unequal societies: Income distribution and the social contract. American Economic Review 90: 96–129. [Google Scholar] [CrossRef]
- Berman, Eli, John Bound, and Stephen Machin. 1998. Implications of Skill-Biased Technological Change: International Evidence. National Bureau of Economic Research Working Paper 6166. Cambridge, MA: NBER. [Google Scholar] [CrossRef]
- Biewen, Martin, and Matthias Seckler. 2019. Unions, internationalization, tasks, firms, and worker characteristics: A detailed decomposition analysis of rising wage inequality in Germany. The Journal of Economic Inequality 17: 461–98. [Google Scholar] [CrossRef]
- Borjas, George J., Richard B. Freeman, and Lawrence F. Katz. 1997. How much do immigration and trade affect labor market outcomes? Brookings Papers on Economic Activity 1997: 1–90. [Google Scholar] [CrossRef]
- Broecke, Stijn, Glenda Quintini, and Marieke Vandeweyer. 2015. Why Is Wage Inequality so High in the United States? Pitching Cognitive Skills against Institutions (Once Again). Discussion Paper Series DPS 15.18; Leuven: Ku Leuven Center for Economic Studies. [Google Scholar]
- Buera, Francisco, Joseph Kaboski, Richard Rogerson, and Juan Vizcaino. 2022. Skill-biased structural change. The Review of Economic Studies 89: 592–625. [Google Scholar] [CrossRef]
- Bunderson, Stuart, and Anjan V. Thakor. 2020. Personal and Organizational Higher Purpose, Corporate Governance and Shareholder Value: Survey Results. St. Louis: Olin School of Business—Washington University in St. Louis. [Google Scholar] [CrossRef]
- Caliński, Tadeusz, and J. A. Harabasz. 1974. A Dendrite Method for Cluster Analysis. Communications in Statistics 3: 1–27. [Google Scholar] [CrossRef]
- Card, David, and Thomas Lemieux. 2001. Can falling supply explain the rising return to college for younger men? A cohort-based analysis. The Quarterly Journal of Economics 116: 705–46. [Google Scholar] [CrossRef]
- Card, David, Jorg Heining, and Patrick Kline. 2013. Workplace heterogeneity and the rise of west German wage inequality. The Quarterly Journal of Economics 128: 967–1015. [Google Scholar] [CrossRef]
- Çaliskan, Hulia Kesici. 2015. Technological change and economic growth. Procedia—Social and Behavioral Sciences 195: 649–54. [Google Scholar] [CrossRef]
- Craney, Trevor, and James Surles. 2002. Mode-Dependent Variance Inflation Factor Cutoff Values. Quality Engineering 14: 391–403. [Google Scholar] [CrossRef]
- Damelang, Andreas, and Michael Otto. 2023. Who is Replaced by Robots? Robotization and the Risk of Unemployment for Different Types of Workers. Work and Occupations, 1–26. [Google Scholar] [CrossRef]
- Everitt, Brian S. 1993. Cluster Analysis, 3rd ed. London: Hodder & Stoughton. [Google Scholar]
- Garson, D. David. 2008. Path Analysis: Topics in Multivariate Analysis. Raleigh: North Carolina State University. Administration Program. [Google Scholar]
- Grossman, Gene M., and Elhanan Helpman. 2018. Growth, trade and inequality. Econometrica 86: 37–83. [Google Scholar] [CrossRef]
- Gujarati, Damodar N., and Dawn C. Porter. 2008. Basic Econometrics, 5th ed. New York: McGraw-Hil Education. [Google Scholar]
- Henningsen, Arne, and Jeff D. Hamann. 2007. Systemfit: A Package for Estimating Systems of Simultaneous Software. Journal of Statistical Software 23: 1–40. [Google Scholar] [CrossRef]
- Hsu, Angel, and Alisa Zomer. 2016. Environmental Performance Index (EPI). New Haven: Yale University. [Google Scholar] [CrossRef]
- Hutter, Christian, and Enzo Weber. 2022. Labour market effects of wage inequality and Skill-biased technical change. Applied Economics 55: 3063–84. [Google Scholar] [CrossRef]
- Jacobs, Bas, and Uwe Thuemmel. 2022. Optimal linear income taxes and education subsidies under skill-biased technical change. International Tax and Public Finance. [Google Scholar] [CrossRef]
- Jestl, Stefan, Sandra M. Leitner, and Sebatian Leitner. 2022. The relative impact of different forces of globalization on wage inequality: A fresh look at the EU experience. Review of International Economics 30: 1003–37. [Google Scholar] [CrossRef]
- Katz, Lawrence F., and Kevin M. Murphy. 1992. Changes in relative wages, 1963–1987: Supply and demand factors. The Quarterly Journal of Economics 107: 35–78. [Google Scholar] [CrossRef]
- Khan, Yasir, Taimoor Hassan, Muhammad Tufail, Mohamed Marie, Muhammad Imran, and Xiqin Zhang. 2022. The nexus between CO2 emissions, human capital, technology transfer, and renewable energy: Evidence from Belt and Road countries. Environmental Science and Pollution Research 29: 59816–834. [Google Scholar] [CrossRef]
- Kiley, Michael T. 1999. The Supply of Skilled Labour and Skill-Biased Technological Progress. The Economic Journal 109: 708–24. [Google Scholar] [CrossRef]
- Kovalenko, Tim, and Marina Töpfer. 2021. Cyclical dynamics and the gender pay gap: A structural VAR approach. Economic Modelling 99: 105488. [Google Scholar] [CrossRef]
- Kristal, Tali, and Yinon Cohen. 2017. The causes of rising wage inequality: The race between institutions and technology. Socio-Economic Review 15: 187–212. [Google Scholar] [CrossRef]
- Krueger, Philipp, Daniel Metzger, and Jiaxin Wu. 2021. The Sustainability Wage Gap. ECGI Working Papers Series in Finance. Working Paper nº 718/2020; Geneva: ECGI. [Google Scholar]
- Kuznets, Simon. 1955. Economic growth and income inequality. American Economic Review 45: 1–28. [Google Scholar]
- Lemieux, Thomas. 2007. The Changing Nature of Wage Inequality. NBER Working Paper Series nº 13523; Cambridge, MA: NBER. [Google Scholar]
- Li, Xiaoyan, and Sana Ullah. 2022. Caring for the environment: How CO2 emissions respond to human capital in BRICS economies? Environmental Science & Pollution Research 29: 18036–46. [Google Scholar] [CrossRef]
- Machin, Stephen, and John Van Reenen. 1998. Technology and changes in skill structure: Evidence from seven OECD countries. The Quarterly Journal of Economics 113: 1215–44. [Google Scholar] [CrossRef]
- Madanipour, Ali, and Michael F. Thompson. 2020. Is a globalization linked to low corruption in OECD countries? Crime, Law and Social Change 73: 443–55. [Google Scholar] [CrossRef]
- Majerova, Ingrid, and Jan Nevima. 2017. The measurement of human development using the Ward method of cluster analysis. Journal of International Studies 10: 239–57. [Google Scholar] [CrossRef]
- Marsiglio, Simone, and Fabio Privileggi. 2021. On the economic growth and environmental trade-off: A multi-objective analysis. Annals of Operations Research 296: 263–89. [Google Scholar] [CrossRef]
- Meschi, Elena, Erol Taymaz, and Marco Vivarelli. 2016. Globalization, technological change and labor demand: A firm-level analysis for Turkey. Review of World Economy 152: 655–80. [Google Scholar] [CrossRef]
- Messina, Julian, and Joana Silva. 2019. Twenty Years of Wage Inequality in Latin America. The World Bank Economic Review 35: 117–47. [Google Scholar] [CrossRef]
- Michaelsen, Maren M. 2011. The Hidden-Increase in Wage Inequality: Skill-Biased and Ability-Biased Technological Change. Ruhr Economic papers nº 262. Bochum: Ruhr-Universität Bochum (RUB). [Google Scholar]
- Michaels, Guy, Ashwini Natraj, and John Van Reenen. 2014. Has ICT polarized skill demand? Evidence from eleven countries over 25 years. Review of Economics and Statistics 96: 60–77. [Google Scholar] [CrossRef]
- Moore, Thomas S. 2018. Occupational career change and gender wage inequality. Work and Occupations 45: 82–121. [Google Scholar] [CrossRef]
- Muinelo-Gallo, Leonel, and Oriol Roca-Sagalés. 2011. Economic growth and inequality: The role of fiscal policies. Australian Economic Papers 50: 74–97. [Google Scholar] [CrossRef]
- Murphy, Kevin M., and Robert H. Topel. 2016. Human Capital Investment, Inequality and Economic Growth. NBER Working Paper 21841. Available online: https://www.nber.org/papers/w21841 (accessed on 12 April 2023).
- Murtagh, Fionn, and Pierre Legendre. 2014. Ward’s Hierarchical Agglomerative Clustering Method: Wich Algorithms Implement Ward’s Criterion. Journal of Classification 31: 274–95. [Google Scholar] [CrossRef]
- Nogueira, Manuel Carlos, and Mara Madaleno. 2021. Are international indices good predictors of economic growth? Panel data and cluster analysis for European Union countries. Sustainability 13: 6003. [Google Scholar] [CrossRef]
- Nogueira, Manuel Carlos, and Mara Madaleno. 2023. Skill-Biased Tecnhological Change and Gender Inequality across OECD Countries—A Simultaneous Approach. Economies 11: 115. [Google Scholar] [CrossRef]
- Nogueira, Manuel Carlos, and Óscar Afonso. 2018. Intra-country wage inequality in the OECD countries. Panoeconomicus 65: 339–62. [Google Scholar] [CrossRef]
- Oostendorp, Remco. 2009. Globalization and the Gender Wage Gap. The World Bank Economic Review 23: 141–61. [Google Scholar] [CrossRef]
- Parnastuti, Losina, Paul W. Miller, and Ruhul Salim. 2013. Declining rates of return to education: Evidence from Indonesia. Bulletin of Indonesian Economic Studies 49: 213–36. [Google Scholar] [CrossRef]
- Pavcnik, Nina. 2017. The Impact of Trade on Inequality in Developing Countries. Working Paper nº 23878. Cambridge, MA: NBER—National Bureau of Economic Research. [Google Scholar]
- Picatoste, Xose, Anabela Mesquita, and Fernando González-Laxe. 2023. Gender wage gap, quality of earnings and gender digital divide in the European context. Empirica 50: 301–21. [Google Scholar] [CrossRef]
- Porter, Michael E. 1990. The Competitive Advantage of Nations. New York: Free Press. [Google Scholar]
- Porter, Michael E. 1991. America’s green strategy. Scientific American 4: 168. [Google Scholar] [CrossRef]
- Shen, Jing. 2014. Recent trends in gender wage inequality in the United States. Journal of Sociological Research 5: 32–49. [Google Scholar] [CrossRef]
- Strauss, Trudie, and Michael Johan Von Maltitz. 2017. Generalising Ward’s method for use with manhattan distances. PLoS ONE 1: e0168288. [Google Scholar] [CrossRef]
- Tang, Juan, Shihu Zhong, and Guocheng Xiang. 2019. Environmental regulation, directed technical change, and economic growth: Theoretic model and evidence from China. International Regional Science Review 42: 519–49. [Google Scholar] [CrossRef]
- Taniguchi, Hiroya, and Ken Yamada. 2022. ICT capital-skill complementary and wage inequality: Evidence from OECD countries. Labour Economics 76: 102151. [Google Scholar] [CrossRef]
- Topuz, Seher Gülşah. 2022. The Relationship Between Income Inequality and Economic Growth: Are Transmission Channels Effective? Social Indicators Research 162: 1177–231. [Google Scholar] [CrossRef]
- Tyron, Robert C. 1939. Cluster Analysis. Ann Arbor: Edwards Brothers. [Google Scholar]
- Tyrowicz, Joanna, and Magsalena Smyk. 2019. Wage inequality and structural change. Social Indicators Research 141: 503–38. [Google Scholar] [CrossRef]
- Violante, Giovanni L. 2008. Skill-biased technical change. In The New Palgrave Dictionary of Economics, 2nd ed. Edited by Steven N. Durlauf and Lawrence E. Blume. New York: Palgrave Macmillan. [Google Scholar]
- Vita, Giuseppe, Raffaele Zanchini, Giacomo Falcone, Mario D’Amico, Filippo Brun, and Giovanni Gulisano. 2021. Local, organic or protected? Detecting the role of different quality signals among Italian olive oil consumers through a hierarchical cluster analysis. Journal of Cleaner Production 290: 125795. [Google Scholar] [CrossRef]
- Wahiba, Nasfi Fkili Wahiba, and Dina Mahmoudi. 2023. Technological change, growth and income inequality. International Journal of Economics and Financial Issues 13: 121–31. [Google Scholar] [CrossRef]
- Wang, Li-Min, Xiang-Li Wu, and Nan-Cheng Chu. 2023. Financial development, technological innovation and urban-rural income gap: Time series evidence from China. PLoS ONE 18: e0279246. [Google Scholar] [CrossRef]
- Ward, Joe H., Jr. 1963. Hierarchical grouping to optimize an objective function. Journal of the American Statistical Association 58: 236–44. [Google Scholar] [CrossRef]
- Wendling, Zachary A., John W. Emerson, Daniel C. Esty, Marc A. Levy, and Alex de Sherbini. 2018. Environmental Performace Index. New Haven: Yale University Press. Available online: https://epi.yale.edu/downloads/epi2018reportv06191901.pdf (accessed on 12 April 2023).
- Western, Bruce, and Jake Rosenfeld. 2011. Unions, norms, and the rise in US wage inequality. American Sociological Review 76: 513–37. [Google Scholar] [CrossRef]
- Wood, Adrian. 1998. Globalization and the rise in labour market inequalities. The Economic Journal 108: 1463–82. [Google Scholar] [CrossRef]
| Variable | Definition | Unit | Source |
|---|---|---|---|
| WGHi,t/WGMi,t | Gap between wage rates of university graduates and high school graduates in country i and year t, in real terms | Index | OECD Education at a Glance—Kovalenko and Töpfer (2021); Acemoglu and Restrepo (2018, 2021) |
| WGMi,t/WGLi,t | Gap between wage rates of high school graduates and bellow high school graduates in country i and year t, in real terms. | Index | OECD Education at a Glance—Kovalenko and Töpfer (2021); Acemoglu and Restrepo (2018, 2021) |
| WGWHi,t/WGWMi,t | Gap between women’s wage rates of university graduates and high school graduates in country i and year t, in real terms, as a percentage of the wage rates of all workers. | Index | OECD Education at a Glance—Kovalenko and Töpfer (2021); Acemoglu and Restrepo (2018, 2021) |
| WGWMi,t/WGWLi,t | Gap between women’s wage rates of high school graduates and below high school in country i and year t, in real terms, as a percentage of the wage rates of all workers. | Index | OECD Education at a Glance—Kovalenko and Töpfer (2021); Acemoglu and Restrepo (2018, 2021) |
| SBTCi,t | Research and Development spending as a percentage of GDP in country i and year t | Percentage | OECD—Acemoglu and Restrepo (2018, 2021); Kristal and Cohen (2017) |
| Unioni,t | Share of unionized workers in country i and year t | Percentage | OECD—Kristal and Cohen (2017) |
| EPIi,t | Environmental Performance Index, in the country i and year t | Index | Environmental Law & Policy—Hsu and Zomer (2016); Wendling et al. (2018) |
| Educ.Expendi,t | Education expenditure as a percentage of GDP in country i and year t | Percentage | OECD Education at a Glance—Nogueira and Afonso (2018) |
| CO2 | CO2 emissions per capita in country i and year t | Tons | World Bank—Nogueira and Madaleno (2021) |
| KOFi,t | Globalization Economic Index in country i and year t | Index | KOF Swiss Economic Institute |
| GDP pci,t | Gross domestic product per capita in country i and year t, US dollar constant prices, 2015 PPPs | Value in dollars | OECD World Bank—Nogueira and Afonso (2018) |
| WGH | WGM | WGL | WGWH | WGWM | WGWL | SBTC | Union | EPI | Educ. Expend. | CO2 | KOF | GDPpc | Average | Standard Deviation | Max | Min | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| WGH | - | 0.06 | −0.48 | −0.13 | 0.11 | 0.02 | −0.36 | −0.41 | −0.24 | −0.29 | −0.23 | −0.25 | −0.40 | 154.63 | 23.361 | 260 | 115 |
| WGM | - | −0.18 | 0.09 | 0.06 | 0.10 | 0.18 | 0.16 | 0.21 | 0.04 | 0.11 | 0.18 | 0.29 | 107.72 | 12.360 | 146 | 61 | |
| WGL | - | 0.11 | 0.03 | 0.06 | 0.18 | 0.37 | 0.23 | 0.12 | 0.11 | 0.33 | 0.15 | 78.221 | 8.1625 | 101 | 54 | ||
| WGWH | - | 0.38 | 0.23 | −0.03 | 0.23 | 0.16 | −0.02 | −0.06 | 0.07 | 0.14 | 75.525 | 7.1177 | 148 | 61 | |||
| WGWM | - | 0.64 | 0.08 | 0.25 | 0.08 | −0.21 | −0.32 | 0.26 | 0.13 | 77.080 | 6.6743 | 98 | 54 | ||||
| WGWL | - | 0.13 | 0.44 | 0.19 | −0.07 | −0.15 | 0.40 | 0.38 | 76.154 | 6.6814 | 92 | 49 | |||||
| SBTC | - | 0.41 | 0.18 | 0.29 | 0.18 | 0.35 | 0.36 | 1.9327 | 1.0352 | 4.93 | 0.28 | ||||||
| Union | - | 0.39 | 0.35 | 0.06 | 0.47 | 0.46 | 24.813 | 17.418 | 72.5 | 4.53 | |||||||
| EPI | - | 0.22 | 0.22 | 0.44 | 0.41 | 79.770 | 8.3420 | 90.8 | 42.6 | ||||||||
| Educ. Expend. | - | 0.05 | −0.13 | 0.07 | 5.4694 | 1.0424 | 8.42 | 3.25 | |||||||||
| CO2 | - | 0.13 | 0.45 | 8.6885 | 4.0938 | 23.8 | 2.77 | ||||||||||
| KOF | - | 0.54 | 82.021 | 5.8417 | 90.9 | 61.8 | |||||||||||
| GDPpc | - | 38,045 | 23,153 | 116,597 | 8002 |
| Country | WGH | WGM | WGL | WGWH | WGWM | WGWL | SBTC (%) | Union (%) | EPI | Educ. Exp. | CO2 | KOF | GDPpc |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Australia | 132.85 | 97.35 | 83.5 | 77.72 | 75.81 | 80.01 | 2.01 | 16.26 | 83.78 | 5.67 | 17.42 | 80.54 | 55,856 |
| Austrium | 153.57 | 118.28 | 69.14 | 73.54 | 79.54 | 76.81 | 2.93 | 28.09 | 83.07 | 5.28 | 7.92 | 86.94 | 44,460 |
| Belgium | 133.71 | 99.35 | 88.78 | 81.36 | 82.63 | 80.82 | 2.54 | 52.46 | 77.80 | 6.11 | 9.31 | 89.51 | 40,622 |
| Canada | 140.42 | 113.71 | 81.71 | 72.63 | 70.54 | 66.81 | 1.75 | 26.76 | 81.22 | 6.21 | 16.08 | 82.87 | 42,771 |
| Chile | 246.51 | - | 67.25 | 66.25 | 72.00 | 78.00 | 0.36 | 14.68 | 72.12 | 6.28 | 4.41 | 76.33 | 12,826 |
| Czech Republic | 175.92 | - | 72.57 | 71.63 | 79.83 | 79.91 | 1.67 | 13.92 | 79.53 | 4.32 | 10.37 | 83.09 | 17,674 |
| Denmark | 127.14 | 102.57 | 82.42 | 77.01 | 80.54 | 81.91 | 2.93 | 68.20 | 86.55 | 7.09 | 7.19 | 87.72 | 53,587 |
| Estonia | 132.63 | 89.66 | 89.91 | 70.27 | 61.54 | 61.18 | 1.53 | 6.12 | 81.01 | 5.21 | 12.92 | 80.93 | 17,320 |
| Finland | 143.85 | 119.14 | 95.35 | 77.54 | 78.18 | 79.72 | 3.17 | 67.22 | 87.25 | 5.91 | 9.43 | 86.58 | 44,329 |
| France | 149.50 | 89.66 | 83.42 | 74.45 | 80.18 | 74.63 | 2.19 | 10.78 | 85.27 | 5.70 | 5.42 | 86.50 | 36,620 |
| Germany | 164.28 | 112.01 | 82.78 | 73.90 | 82.27 | 76.63 | 2.88 | 17.93 | 81.68 | 4.65 | 9.67 | 87.37 | 40,276 |
| Greece | 146.91 | 102.09 | 75.27 | 74.72 | 78.54 | 68.82 | 0.88 | 21.72 | 79.85 | 3.71 | 7.85 | 80.32 | 19,654 |
| Hungary | 204.01 | 109.92 | 74.42 | 72.91 | 87.72 | 83.18 | 1.24 | 11.06 | 76.38 | 4.50 | 5.03 | 84.27 | 12,575 |
| Ireland | 167.42 | 96.92 | 85.71 | 75.36 | 77.15 | 80.45 | 1.37 | 27.97 | 84.13 | 4.94 | 8.61 | 85.46 | 56,989 |
| Israel | 154.02 | 111.87 | 76.28 | 69.90 | 75.27 | 72.72 | 4.39 | 26.03 | 75.98 | 6.51 | 8.25 | 76.82 | 35,040 |
| Italy | 147.85 | - | 78.14 | 72.90 | 76.72 | 77.45 | 1.30 | 34.05 | 80.62 | 4.35 | 6.49 | 81.51 | 34,981 |
| Japan | 150.27 | - | 78.72 | - | - | - | 3.21 | 17.82 | 78.85 | 4.58 | 9.46 | 75.07 | 40,898 |
| Korea | 143.21 | - | 70.85 | 67.36 | 65.18 | 66.72 | 3.78 | 10.29 | 69.02 | 6.66 | 12.17 | 75.82 | 27,218 |
| Latvia | 145.20 | 98.40 | 88.80 | 77.40 | 71.80 | 69.60 | 0.59 | 13.49 | 78.76 | 4.42 | 4.72 | 75.03 | 14,981 |
| Luxembourg | 153.28 | 125.12 | 71.71 | 79.45 | 79.45 | 81.72 | 1.35 | 34.39 | 84.66 | 3.73 | 19.44 | 85.48 | 110,257 |
| Mexico | 192.33 | 120.35 | 62.16 | 69.16 | 77.40 | 72.66 | 0.40 | 13.90 | 67.92 | 5.59 | 3.93 | 67.07 | 9618 |
| Netherlands | 152.57 | 114.35 | 83.35 | 77.36 | 81.27 | 81.09 | 1.97 | 18.29 | 79.25 | 5.55 | 9.73 | 89.07 | 51,446 |
| New Zealand | 127.71 | 110.07 | 83.64 | 77.45 | 77.27 | 79.27 | 1.24 | 19.42 | 84.02 | 6.64 | 8.59 | 76.71 | 38,626 |
| Norway | 126.38 | 114.85 | 79.07 | 75.36 | 77.37 | 80.82 | 1.82 | 50.03 | 84.42 | 6.87 | 9.75 | 84.81 | 85,543 |
| Poland | 167.50 | 104.57 | 83.28 | 76.81 | 77.45 | 71.72 | 0.87 | 15.53 | 68.29 | 5.18 | 8.51 | 78.77 | 12,205 |
| Portugal | 166.35 | 101.14 | 70.14 | 73.54 | 74.00 | 71.74 | 1.37 | 17.60 | 74.39 | 5.53 | 4.98 | 82.39 | 19,728 |
| Slovak Republic | 171.72 | 131.47 | 68.18 | 70.27 | 73.91 | 73.36 | 0.75 | 14.05 | 79.11 | 4.12 | 6.67 | 81.48 | 17,781 |
| Slovenia | 181.71 | - | 76.85 | 86.09 | 86.18 | 84.36 | 2.07 | 30.69 | 81.02 | 5.03 | 7.38 | 79.32 | 24,177 |
| Spain | 142.64 | 109.0 | 79.35 | 84.18 | 76.58 | 76.08 | 1.27 | 15.85 | 84.29 | 4.71 | 5.97 | 83.59 | 29,731 |
| Sweden | 123.78 | 114.85 | 83.28 | 81.18 | 81.81 | 85.03 | 3.28 | 67.40 | 86.32 | 6.02 | 4.57 | 88.78 | 54,692 |
| Switzerland | 153.50 | 109.12 | 76.35 | 78.66 | 83.83 | 78.83 | 3.11 | 16.36 | 85.64 | 5.19 | 4.98 | 89.34 | 82,481 |
| Turkey | 160.92 | - | 69.57 | 83.57 | 80.43 | 69.00 | 0.86 | 7.75 | 59.38 | 4.60 | 4.71 | 68.36 | 10,583 |
| United Kingdom | 154.53 | - | 71.21 | 76.63 | 72.36 | 74.90 | 1.65 | 25.43 | 85.66 | 6.14 | 6.92 | 88.58 | 43,096 |
| United States | 174.46 | 108.5 | 67.64 | 69.90 | 71.00 | 70.72 | 2.82 | 10.84 | 79.62 | 6.72 | 17.22 | 81.13 | 54,888 |
| SBTC | 1.353 |
| Union | 1.624 |
| EPI | 1.353 |
| Educ. Expend | 1.267 |
| CO2 | 1.391 |
| KOF | 1.723 |
| GDPpc | 1.921 |
| Cluster | WGH | WGM | WGL | WGWH | WGWM | WGWL | SBTC (%) | Union (%) | EPI | Educ. Exp. | CO2 | KOF | GDPpc |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cluster 1 | 140.60 | 112.77 | 77.71 | 76.52 | 79.58 | 80.11 | 1.514 | 21.51 | 85.03 | 6.031 | 5.955 | 87.07 | 84,012 |
| Cluster 2 | 146.38 | 105.18 | 81.17 | 76.42 | 77.90 | 79.87 | 1.504 | 22.84 | 83.27 | 6.001 | 10.26 | 85.44 | 54,576 |
| Cluster 3 | 153.28 | 125.12 | 71.71 | 79.45 | 78.27 | 81.72 | 1.981 | 18.29 | 84.66 | 3.714 | 9.730 | 85.48 | 110,257 |
| Cluster 4 | 146.40 | 110.11 | 79.97 | 75.14 | 76.38 | 75.22 | 2.141 | 19.85 | 81.07 | 5.634 | 8.314 | 82.99 | 38.359 |
| Cluster 5 | 173.59 | 149.75 | 74.83 | 74.90 | 76.91 | 73.92 | 1.823 | 32.09 | 75.31 | 4.978 | 8.720 | 79.00 | 15,760 |
| Number of Countries | Number of Countries | |
|---|---|---|
| Cluster 1 | 1 | 2 |
| Cluster 2 | 17 | 6 |
| Cluster 3 | 2 | 1 |
| Cluster 4 | 14 | 13 |
| Cluster 5 | 12 | |
| Valid | 34 | 34 |
| Missing | 0 | 0 |
| Equation Number | K − k | m − 1 | K − k ≥ m − 1 | Identification |
|---|---|---|---|---|
| (1) | 9 − 8 | 1 | 1 ≥ 1 | Exactly identified |
| (2) | 9 − 8 | 1 | 1 ≥ 1 | Exactly identified |
| (3) | 9 − 8 | 1 | 1 ≥ 1 | Exactly identified |
| (4) | 9 − 8 | 1 | 1 ≥ 1 | Exactly identified |
| Variables | Coefficients | Variables | Coefficients |
|---|---|---|---|
| LnWGH/LnWGM | LnWGWH/LnWGWM | ||
| LnWGM/LnWGL | 0.28753 *** | LnWGWM/LnWGWL | 0.29931 *** |
| LnSBTC | 0.08913 ** | LnSBTC | 0.09153 ** |
| LnUnion | 0.00154 | LnUnion | 0.00348 |
| LnEPI | −0.07512 | LnEPI | −0.03283 |
| LnEduc.Expend. | 0.10543 *** | LnEduc.Expend. | 0.12325 *** |
| LnCO2 | 0.03714 ** | LnCO2 | 0.03118 * |
| LnGDPpc | 0.01573 ** | LnGDPpc | 0.01731 *** |
| Constant | 1.18325 *** | Constant | 1.32751 *** |
| LnWGM/LnWGL | LnWGWM/LnWGWL | ||
| LnSBTC | 0.07143 *** | LnSBTC | 0.08315 *** |
| LnUnion | −0.00254 ** | LnUnion | −0.00208 * |
| LnEPI | −0.10322 | LnEPI | −0.08371 |
| LnEduc.Expend. | 0.09163 ** | LnEduc.Expend. | 0.10351 * |
| LnCO2 | 0.01573 | LnCO2 | 0.02167 * |
| LnKOF | 0.06811 ** | LnKOF | 0.07363 ** |
| LnGDPpc | 0.01352 ** | LnGDPpc | 0.0184 ** |
| Constant | 0.95321 *** | Constant | 0.83151 *** |
| Variables | Coefficients | Variables | Coefficients |
|---|---|---|---|
| LnWGH/LnWGM | LnWGWH/LnWGWM | ||
| LnWGM/LnWGL | 0.31728 *** | LnWGWM/LnWGWL | 0.34176 *** |
| LnSBTC | 0.14325 *** | LnSBTC | 0.16032 *** |
| LnUnion | −0.09325 | LnUnion | −0.11327 |
| LnEPI | 0.00477 * | LnEPI | −0.00328 |
| LnEduc.Expend. | 0.10743 ** | LnEduc.Expend. | 0.11128 *** |
| LnCO2 | 0.01871 * | LnCO2 | 0.02174 * |
| LnGDPpc | −0.06122 ** | LnGDPpc | −0.07312 *** |
| Constant | 1.38751 *** | Constant | 1.07112 *** |
| LnWGM/LnWGL | LnWGWM/LnWGWL | ||
| LnSBTC | 0.06740 *** | LnSBTC | 0.07312 *** |
| LnUnion | −0.08212 | LnUnion | −0.09157 * |
| LnEPI | −0.11723 | LnEPI | −0.10124 |
| LnEduc.Expend. | 0.06188 *** | LnEduc.Expend. | 0.07774 *** |
| LnCO2 | 0.00216 ** | LnCO2 | 0.02767 ** |
| LnKOF | 0.03754 | LnKOF | 0.03284 |
| LnGDPpc | −0.02774 *** | LnGDPpc | −0.03861 ** |
| Constant | 0.83114 *** | Constant | 0.91718 *** |
| Variables | Coefficients | Variables | Coefficients |
|---|---|---|---|
| LnWGH/LnWGM | LnWGWH/LnWGWM | ||
| LnWGM/LnWGL | 0.41126 *** | LnWGWM/LnWGWL | 0.38651 *** |
| LnSBTC | 0.05138 ** | LnSBTC | 0.06274 *** |
| LnUnion | −0.03251 | LnUnion | −0.04715 |
| LnEPI | −0.07680 | LnEPI | −0.05317 |
| LnEduc.Expend. | 0.15712 *** | LnEduc.Expend. | 0.16321 ** |
| LnCO2 | 0.03711 ** | LnCO2 | 0.03255 *** |
| LnGDPpc | −0.05893 *** | LnGDPpc | −0.06925 *** |
| Constant | 0.79883 *** | Constant | 1.12630 *** |
| LnWGM/LnWGL | LnWGWM/LnWGWL | ||
| LnSBTC | 0.06122 *** | LnSBTC | 0.07312 *** |
| LnUnion | −0.10377 | LnUnion | −0.1186 *** |
| LnEPI | −0.02614 | LnEPI | −0.03744 |
| LnEduc.Expend. | 0.09683 *** | LnEduc.Expend. | 0.10328 *** |
| LnCO2 | 0.02194 ** | LnCO2 | 0.03741 ** |
| LnKOF | 0.06654 | LnKOF | 0.07142 * |
| LnGDPpc | −0.02167 ** | LnGDPpc | −0.03611 ** |
| Constant | 1.14748 *** | Constant | 0.93257 *** |
| Equation | Obs | Parms | RMSE | “R-sq” | Chi | p-Value |
|---|---|---|---|---|---|---|
| Cluster 2 | ||||||
| LnWGH/LnWGM | 64 | 7 | 0.0153 | 0.9716 | 47.17 | 0 |
| LnWGM/LnWGL | 64 | 7 | 0.0184 | 0.9742 | 44.91 | 0 |
| LnWGWH/LnWGWM | 50 | 7 | 0.0231 | 0.9814 | 36.14 | 0 |
| LnWGWH/LnWGWL | 50 | 7 | 0.0247 | 0.9831 | 48.99 | 0 |
| Cluster 4 | ||||||
| LnWGH/LnWGM | 83 | 7 | 0.0124 | 0.9712 | 36.19 | 0 |
| LnWGM/LnWGL | 83 | 7 | 0.0148 | 0.9732 | 47.31 | 0 |
| LnWGWH/LnWGWM | 104 | 7 | 0.0193 | 0.9766 | 51.19 | 0 |
| LnWGWM/LnWGWL | 104 | 7 | 0.0187 | 0.9751 | 50.38 | 0 |
| Cluster 5 | ||||||
| LnWGH/LnWGM | 48 | 7 | 0.0138 | 0.9737 | 31.11 | 0 |
| LnWGM/LnWGL | 48 | 7 | 0.0261 | 0.9851 | 37.21 | 0 |
| LnWGWH/LnWGWM | 37 | 7 | 0.0134 | 0.9736 | 42.18 | 0 |
| LnWGWM/LnWGWL | 37 | 7 | 0.0257 | 0.9834 | 48.39 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nogueira, M.C.; Madaleno, M. New Evidence about Skill-Biased Technological Change and Gender Wage Inequality. Economies 2023, 11, 193. https://doi.org/10.3390/economies11070193
Nogueira MC, Madaleno M. New Evidence about Skill-Biased Technological Change and Gender Wage Inequality. Economies. 2023; 11(7):193. https://doi.org/10.3390/economies11070193
Chicago/Turabian StyleNogueira, Manuel Carlos, and Mara Madaleno. 2023. "New Evidence about Skill-Biased Technological Change and Gender Wage Inequality" Economies 11, no. 7: 193. https://doi.org/10.3390/economies11070193
APA StyleNogueira, M. C., & Madaleno, M. (2023). New Evidence about Skill-Biased Technological Change and Gender Wage Inequality. Economies, 11(7), 193. https://doi.org/10.3390/economies11070193







