Deep Learning Based Fall Detection Algorithms for Embedded Systems, Smartwatches, and IoT Devices Using Accelerometers
Abstract
1. Introduction
- to present existing public datasets of fall detection,
- to describe the harmonization process for these datasets,
- to state the current accuracy of fall detection for tiny, mobile and embedded systems using deep learning algorithms,
- to invite and motivate researchers to compete and contribute in fall detection by using the existing databases and to provide various achievements for the future life of the elderly.
2. Related Work
2.1. Datasets
2.2. Position of Sensors
Wrist vs. Waist
2.3. Fall Detection Algorithms
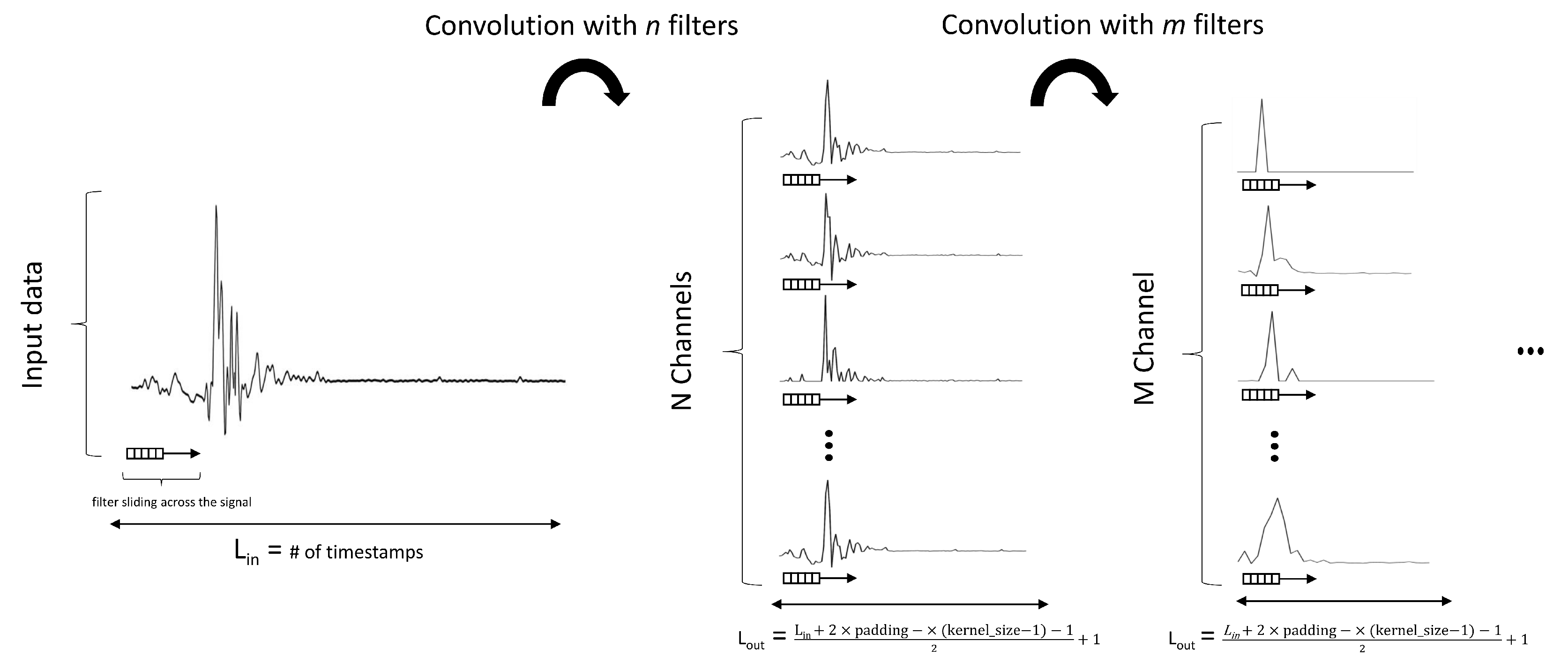
2.4. 1D Convolutional Neural Networks
2.5. Recurrent Neural Networks
Long Short-Term Memory
3. Experimental Setup
3.1. Data Preparation
3.1.1. Down and Upsampling Technique
3.1.2. SmartFall, Smartwatch, and Notch
- Cluster timestamps containing a fall to create separated 10 s segments.
- Each segment is upsampled from 310 (31 Hz) to 500 timestamps (50 Hz)
3.1.3. MUMA, UP Fall, and Sim Fall
3.2. Harmonized Dataset
3.3. Problem Formulation
3.4. Preprocessing
Signal Magnitude Vector (SMV)
3.5. Data Augmentation
- Shifting with a probability of and random shift value of in samples along the time axis (only used during signal magnitude vector training)
- Rotation with a probability of around x, y, and z-acceleration axes with a random angle between (only used during three-axis training)
3.6. Model Architectures
3.6.1. Classic 1D CNN
3.6.2. 1D ResNet
3.6.3. LSTM
3.7. Proposed Model Architecture
3.7.1. Maxpooling vs. Strided Convolutions
3.7.2. Global Average Pooling Layer
3.7.3. Learnable Parameters
3.7.4. Quantization
4. Evaluation
4.1. Evaluation Method
Evaluation Metric
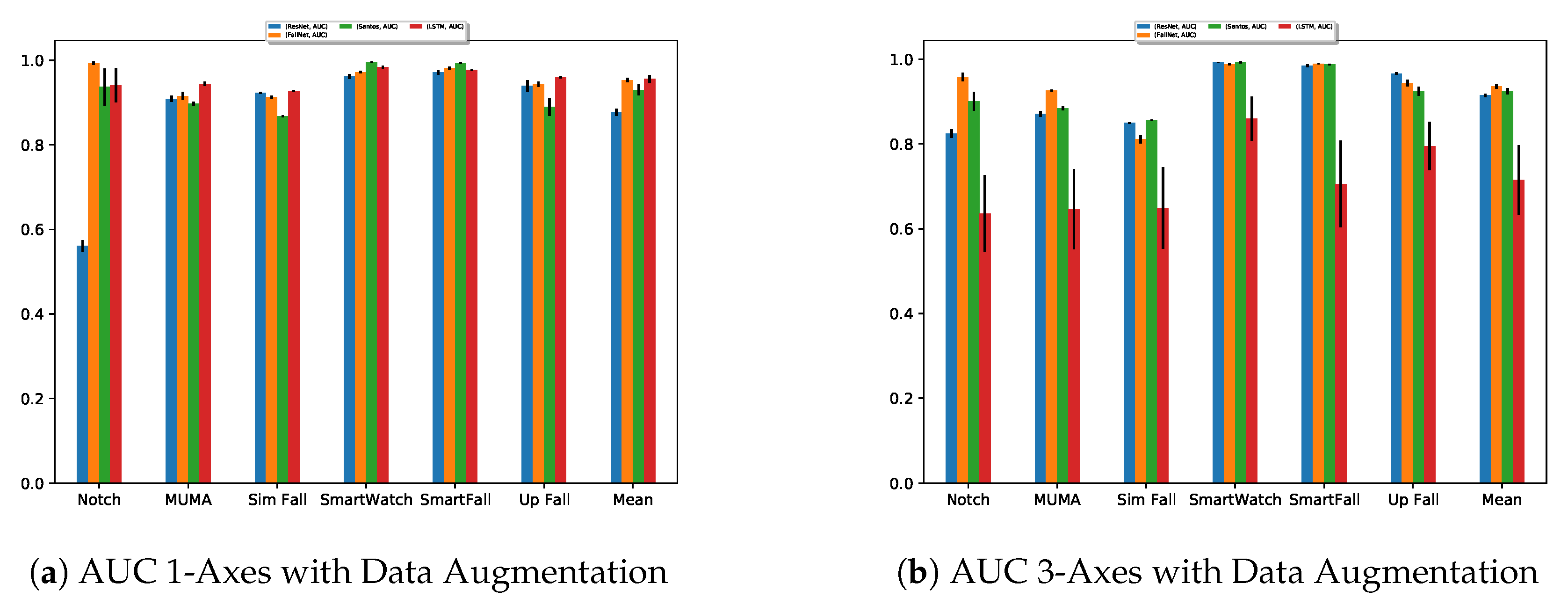
4.2. Effect of Augmentation
4.3. Learned Filters
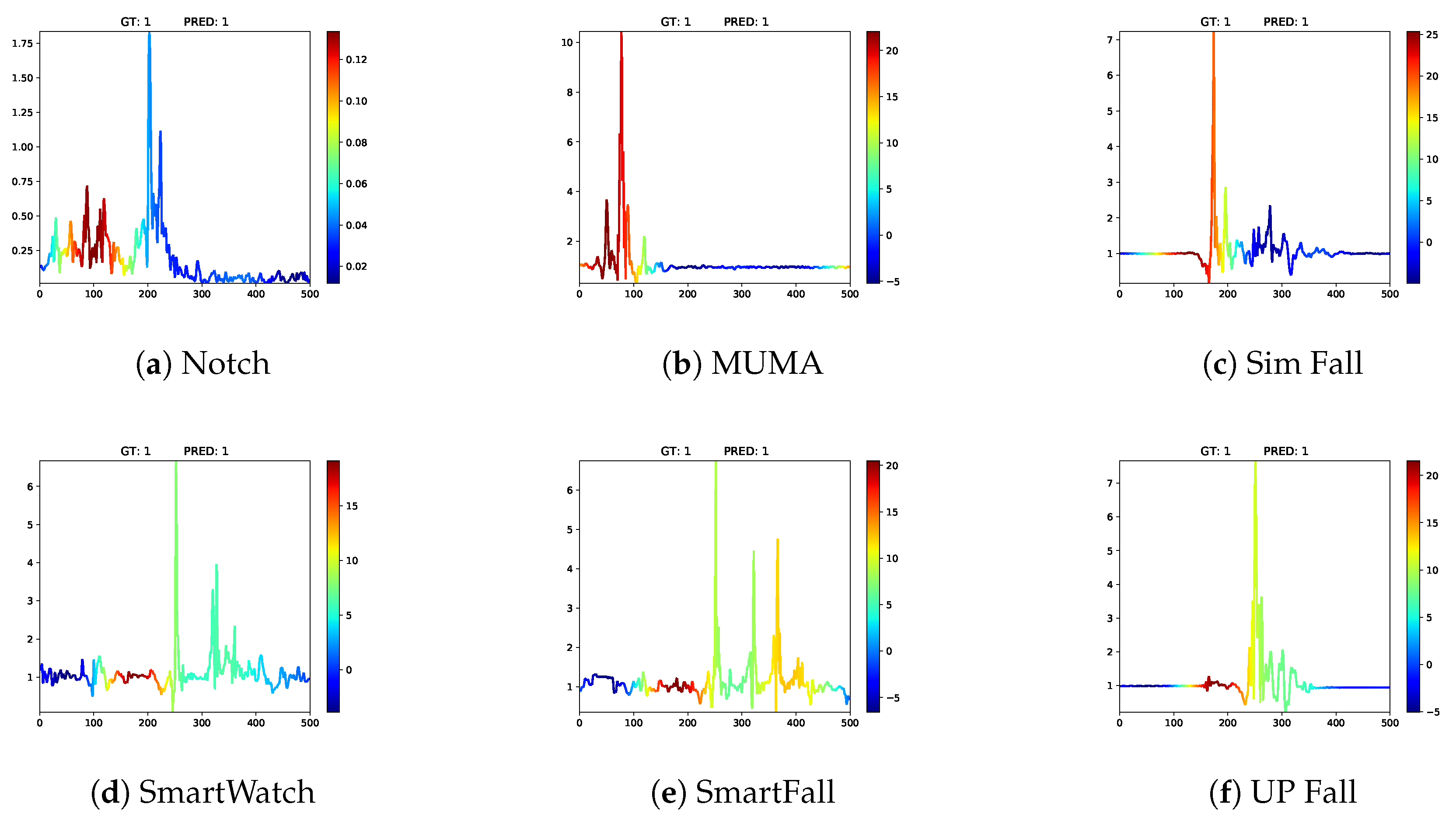
4.4. Class Activation Maps
4.5. Results
5. Discussion
6. Outlook and Application
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Stevens, J.A.; Corso, P.S.; Finkelstein, E.A.; Miller, T.R. The costs of fatal and non-fatal falls among older adults. Inj. Prev. 2006, 12, 290–295. [Google Scholar] [CrossRef]
- Chaudhuri, S.; Thompson, H.; Demiris, G. Fall detection devices and their use with older adults: A systematic review. J. Geriatr. Phys. Ther. 2014, 37, 178–196. [Google Scholar] [CrossRef]
- Boyle, J.; Karunanithi, M. Simulated fall detection via accelerometers. In Proceedings of the 2008 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 20–25 August 2008; pp. 1274–1277. [Google Scholar]
- Nunez-Marcos, A.; Azkune, G.; Arganda-Carreras, I. Vision-based fall detection with convolutional neural networks. Wirel. Commun. Mob. Comput. 2017, 2017, 9474806. [Google Scholar] [CrossRef]
- Alwan, M.; Rajendran, P.J.; Kell, S.; Mack, D.; Dalal, S.; Wolfe, M.; Felder, R. A smart and passive floor-vibration based fall detector for elderly. In Proceedings of the 2006 2nd International Conference on Information & Communication Technologies, Damascus, Syria, 24–28 April 2006; Volume 1, pp. 1003–1007. [Google Scholar]
- Daher, M.; Diab, A.; El Najjar, M.E.B.; Khalil, M.A.; Charpillet, F. Elder tracking and fall detection system using smart tiles. IEEE Sens. J. 2016, 17, 469–479. [Google Scholar] [CrossRef]
- Casilari, E.; Santoyo-Ramón, J.A.; Cano-García, J.M. UMAFall: A Multisensor Dataset for the Research on Automatic Fall Detection. Procedia Comput. Sci. 2017, 110, 32–39. [Google Scholar] [CrossRef]
- Frank, K.; Vera Nadales, M.J.; Robertson, P.; Pfeifer, T. Bayesian recognition of motion related activities with inertial sensors. In Proceedings of the 12th ACM International Conference Adjunct Papers on Ubiquitous Computing—Adjunct, Copenhagen, Denmark, 26–29 September 2010; Bardram, J.E., Ed.; ACM: New York, NY, USA, 2010; p. 445. [Google Scholar] [CrossRef]
- Vavoulas, G.; Pediaditis, M.; Spanakis, E.G.; Tsiknakis, M. The MobiFall dataset: An initial evaluation of fall detection algorithms using smartphones. In Proceedings of the IEEE 13th International Conference on Bioinformatics and Bioengineering (BIBE), Chania, Greece, 10–13 November 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Gasparrini, S.; Cippitelli, E.; Gambi, E.; Spinsante, S.; Wåhslén, J.; Orhan, I.; Lindh, T. Proposal and Experimental Evaluation of Fall Detection Solution Based on Wearable and Depth Data Fusion. In ICT Innovations 2015; Advances in Intelligent Systems and Computing; Loshkovska, S., Koceski, S., Eds.; Springer: Cham, Switzerland, 2016; Volume 399, pp. 99–108. [Google Scholar] [CrossRef]
- Medrano, C.; Igual, R.; Plaza, I.; Castro, M. Detecting falls as novelties in acceleration patterns acquired with smartphones. PLoS ONE 2014, 9, e94811. [Google Scholar] [CrossRef]
- Kwolek, B.; Kepski, M. Human fall detection on embedded platform using depth maps and wireless accelerometer. Comput. Methods Programs Biomed. 2014, 117, 489–501. [Google Scholar] [CrossRef]
- Özdemir, A.T.; Barshan, B. Detecting falls with wearable sensors using machine learning techniques. Sensors 2014, 14, 10691–10708. [Google Scholar] [CrossRef]
- Ojetola, O.; Gaura, E.; Brusey, J. Data set for fall events and daily activities from inertial sensors. In Proceedings of the 6th ACM Multimedia Systems Conference, Portland, OR, USA, 18–20 March 2015; Ooi, W.T., Feng, W., Liu, F., Eds.; ACM: New York, NY, USA, 2015; pp. 243–248. [Google Scholar] [CrossRef]
- Vilarinho, T.; Farshchian, B.; Bajer, D.G.; Dahl, O.H.; Egge, I.; Hegdal, S.S.; Lones, A.; Slettevold, J.N.; Weggersen, S.M. A Combined Smartphone and Smartwatch Fall Detection System. In Proceedings of the CIT/IUCC/DASC/PICom 2015, Liverpool, UK, 26–28 October 2015; pp. 1443–1448. [Google Scholar] [CrossRef]
- Wertner, A.; Czech, P.; Pammer-Schindler, V. An Open Labelled Dataset for Mobile Phone Sensing Based Fall Detection. In Proceedings of the 12th EAI International Conference on Mobile and Ubiquitous Systems: Computing, Networking and Services, Coimbra, Portugal, 22–24 July 2015; Zhang, P., Silva, J.S., Lane, N., Boavida, F., Rodrigues, A., Eds.; MobiQuitous: Coimbra, Portugal, 2015. [Google Scholar] [CrossRef]
- Aziz, O.; Musngi, M.; Park, E.J.; Mori, G.; Robinovitch, S.N. A comparison of accuracy of fall detection algorithms (threshold-based vs. machine learning) using waist-mounted tri-axial accelerometer signals from a comprehensive set of falls and non-fall trials. Med. Biol. Eng. Comput. 2017, 55, 45–55. [Google Scholar] [CrossRef]
- Sucerquia, A.; López, J.D.; Vargas-Bonilla, J.F. SisFall: A Fall and Movement Dataset. Sensors 2017, 17, 198. [Google Scholar] [CrossRef]
- Micucci, D.; Mobilio, M.; Napoletano, P. UniMiB SHAR: A Dataset for Human Activity Recognition Using Acceleration Data from Smartphones. Appl. Sci. 2017, 7, 1101. [Google Scholar] [CrossRef]
- Mauldin, T.R.; Canby, M.E.; Metsis, V.; Ngu, A.H.H.; Rivera, C.C. SmartFall: A Smartwatch-Based Fall Detection System Using Deep Learning. Sensors 2018, 18, 3363. [Google Scholar] [CrossRef]
- Chan, H.L. CGU-BES Dataset for Fall and Activity of Daily Life. Figshare 2018. [Google Scholar] [CrossRef]
- Martínez-Villaseñor, L.; Ponce, H.; Brieva, J.; Moya-Albor, E.; Núñez-Martínez, J.; Peñafort-Asturiano, C. UP-Fall Detection Dataset: A Multimodal Approach. Sensors 2019, 19, 1988. [Google Scholar] [CrossRef]
- Cotechini, V.; Belli, A.; Palma, L.; Morettini, M.; Burattini, L.; Pierleoni, P. A dataset for the development and optimization of fall detection algorithms based on wearable sensors. Data Brief 2019, 23, 103839. [Google Scholar] [CrossRef]
- Mauldin, T.; Ngu, A.H.; Metsis, V.; Canby, M.E.; Tesic, J. Experimentation and analysis of ensemble deep learning in iot applications. Open J. Internet Things 2019, 5, 133–149. [Google Scholar]
- Pannurat, N.; Thiemjarus, S.; Nantajeewarawat, E. Automatic Fall Monitoring: A Review. Sensors 2014, 14, 12900–12936. [Google Scholar] [CrossRef]
- Krupitzer, C.; Sztyler, T.; Edinger, J.; Breitbach, M.; Stuckenschmidt, H.; Becker, C. Hips Do Lie! A Position-Aware Mobile Fall Detection System. In Proceedings of the 2018 IEEE International Conference on Pervasive Computing and Communications (PerCom); Communications, Athens, Greece, 19–23 March 2018; pp. 1–10. [Google Scholar] [CrossRef]
- Liao, M.; Guo, Y.; Qin, Y.; Wang, Y. The application of EMD in activity recognition based on a single triaxial accelerometer. Bio-Med. Mater. Eng. 2015, 26 (Suppl. 1), S1533–S1539. [Google Scholar] [CrossRef]
- Bourke, A.K.; O’Brien, J.V.; Lyons, G.M. Evaluation of a threshold-based tri-axial accelerometer fall detection algorithm. Gait Posture 2007, 26, 194–199. [Google Scholar] [CrossRef]
- Kangas, M.; Konttila, A.; Winblad, I.; Jämsä, T. Determination of simple thresholds for accelerometry-based parameters for fall detection. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; pp. 1367–1370. [Google Scholar] [CrossRef]
- Salomon, R.; Lueder, M.; Bieber, G. iFall—A New Embedded System for the Detection of Unexpected Falls. In Proceedings of the Eighth Annual IEEE International Conference on Pervasive Computing and Communications Workshops (PerCom Workshops), Mannheim, Germany, 29 March–2 April 2010. [Google Scholar] [CrossRef]
- Vallabh, P.; Malekian, R.; Ye, N.; Bogatinoska, D.C. Fall detection using machine learning algorithms. In Proceedings of the 2016 24th International Conference on Software, Telecommunications and Computer Networks (SoftCOM), Split, Croatia, 22–24 September 2016; pp. 1–9. [Google Scholar] [CrossRef]
- Santos, G.L.; Endo, P.T.; Monteiro, K.H.C.; Rocha, E.S.; Silva, I.; Lynn, T. Accelerometer-Based Human Fall Detection Using Convolutional Neural Networks. Sensors 2019, 19, 1644. [Google Scholar] [CrossRef]
- Wang, G.; Li, Q.; Wang, L.; Zhang, Y.; Liu, Z. Elderly Fall Detection with an Accelerometer Using Lightweight Neural Networks. Electronics 2019, 8, 1354. [Google Scholar] [CrossRef]
- Jahanjoo, A.; Tahan, M.N.; Rashti, M.J. Accurate fall detection using three-axis accelerometer sensor and MLF algorithm. In Proceedings of the 2017 3rd International Conference on Pattern Recognition and Image Analysis (IPRIA), Shahrekord, Iran, 19–20 April 2017; pp. 90–95. [Google Scholar] [CrossRef]
- Ramachandran, A.; Adarsh, R.; Pahwa, P.; Anupama, K.R. Machine Learning-based Fall Detection in Geriatric Healthcare Systems. In Proceedings of the 2018 IEEE International Conference on Advanced Networks and Telecommunications Systems (ANTS), Indore, India, 16–19 December 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Wisesa, I.W.W.; Mahardika, G. Fall detection algorithm based on accelerometer and gyroscope sensor data using Recurrent Neural Networks. IOP Conf. Ser. Earth Environ. Sci. 2019, 258, 012035. [Google Scholar] [CrossRef]
- Hussain, F.; Hussain, F.; Ehatisham-ul Haq, M.; Azam, M.A. Activity-Aware Fall Detection and Recognition Based on Wearable Sensors. IEEE Sens. J. 2019, 19, 4528–4536. [Google Scholar] [CrossRef]
- Musci, M.; De Martini, D.; Blago, N.; Facchinetti, T.; Piastra, M. Online fall detection using recurrent neural networks. arXiv 2018, arXiv:1804.04976. [Google Scholar]
- Liu, K.C.; Hsieh, C.Y.; Hsu, S.J.P.; Chan, C.T. Impact of Sampling Rate on Wearable-Based Fall Detection Systems Based on Machine Learning Models. IEEE Sens. J. 2018, 18, 9882–9890. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Advances in Neural Information Processing Systems; AcM: New York, NY, USA, 2012; pp. 1097–1105. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. ImageNet: A Large-Scale Hierarchical Image Database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Chengdu, China, 15–17 December 2017; pp. 770–778. [Google Scholar]
- Wang, Z.; Yan, W.; Oates, T. Time Series Classification from Scratch with Deep Neural Networks: A Strong Baseline. CoRR 2016, abs/1611.06455. Available online: https://arxiv.org/abs/1611.06455 (accessed on 30 October 2020).
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Sztyler, T.; Stuckenschmidt, H. On-body Localization of Wearable Devices: An Investigation of Position-Aware Activity Recognition. In Proceedings of the 2016 IEEE International Conference on Pervasive Computing and Communications (PerCom), IEEE Computer Society, Sydney, Australia, 14–19 March 2016; pp. 1–9. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Um, T.T.; Pfister, F.M.J.; Pichler, D.; Endo, S.; Lang, M.; Hirche, S.; Fietzek, U.; Kulić, D. Data augmentation of wearable sensor data for parkinson’s disease monitoring using convolutional neural networks. In Proceedings of the 19th ACM International Conference on Multimodal Interaction, Glasgow, Scotland, 13–17 November, 2017; Lank, E., Ed.; ACM: New York, NY, 2017; pp. 216–220. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in PyTorch. In Proceedings of the NIPS 2017 Workshop Autodiff Submission, Long Beach, CA, USA, 9 December 2017. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Springenberg, J.T.; Dosovitskiy, A.; Brox, T.; Riedmiller, M. Striving for simplicity: The all convolutional net. arXiv 2014, arXiv:1412.6806. [Google Scholar]
- Fawaz, H.I.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P. Deep learning for time series classification: A review. CoRR 2018, abs/1809.04356. Available online: https://arxiv.org/abs/1809.04356 (accessed on 30 October 2020).
- Wu, J.; Leng, C.; Wang, Y.; Hu, Q.; Cheng, J. Quantized convolutional neural networks for mobile devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4820–4828. [Google Scholar]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning deep features for discriminative localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2921–2929. [Google Scholar]
- Aadahl, M.; Andreasen, A.H.; Hammer-Helmich, L.; Buhelt, L.; Jørgensen, T.; Glümer, C. Recent temporal trends in sleep duration, domain-specific sedentary behaviour and physical activity. A survey among 25–79-year-old Danish adults. Scand. J. Public Health 2013, 41, 706–711. [Google Scholar] [CrossRef]



| Dataset | Reference | Sensors | Sensor Location | Sampling Rate | Year |
|---|---|---|---|---|---|
| DLR | [8] | A, G, M | Waist | 100 Hz | 2010 |
| MobiFall | [9] | A, G, O | Thigh | 87 Hz (A) 100 Hz (G, O) | 2013 |
| TST Fall Detection | [10] | A | Waist Right Wrist | 100 Hz | 2014 |
| tFall | [11] | A | Thigh Hand bag | 45 Hz | 2014 |
| UR Fall Detection | [12] | A | Waist | 256 Hz | 2014 |
| Simulated Falls and ADL | [13] | A, G, M, O | Head, Chest, Waist, Right Ankle, Right Wrist, Right Thigh | 25 Hz | 2014 |
| Cogent Labs | [14] | A, G | Chest, Thigh | 100 Hz | 2015 |
| Project Gravity | [15] | A | Thigh, Wrist * | 50 Hz | 2015 |
| Graz | [16] | A, O | Waist | 5 Hz | 2015 |
| MUMAFall | [7] | A, G, M | Ankle, Chest, Thigh, Waist, Wrist | 100 Hz / 20 Hz * | 2016 |
| SFU Fall Detection | [17] | A | Right Ankles, Left Ankles, Right Thighs, Left Thighs, Waist, Sternum, Head | 128 Hz | 2016 |
| SisFall | [18] | , , G | Waist | 200 Hz | 2017 |
| UniMiB SHAR | [19] | A | Thigh | 200 Hz | 2017 |
| SmartWatch | [20] | A | Right Wrist, Left Wrist | 31.25 Hz | 2018 |
| Notch | [20] | A | Right Wrist, Left Wrist | 31.25 Hz | 2018 |
| CGU-BES | [21] | A | Chest | 200 Hz | 2018 |
| UP Fall Detection | [22] | A, G | Waist, Wrist, Neck, Thigh, Ankle | 18 Hz | 2019 |
| MARG | [23] | A | Waist | 50 Hz | 2019 |
| SmartFall | [24] | A | Right Wrist, Left Wrist | 31.25 Hz | 2019 |
| Data-Set | # Types of ADLS/Falls | # Samples of ADL/Falls | Duration of Samples (s) | ||
|---|---|---|---|---|---|
| Min-Max | Mean | Median | |||
| DLR | 15/1 | 1017 (961/56) | [0.27–864.33] s | 18.40 s | 9.46 s |
| MobiFall | 9/4 | 630 (342/288) | [0.27–864.33] s | 18.40 s | 9.46 s |
| MobiAct | 9/4 | 2526 (1879/647) | [4.89–300.01] s | 22.35 s | 9.85 s |
| TST Fall Detection | 4/4 | 264 (132/132) | [3.84–18.34] s | 8.6 s | 8.02 s |
| tFall | not typified/8 | 10909 (9883/1026) | 6 s | 6 s | 6 s |
| UR Fall Detection | 5/4 | 70 (40/30) | [2.11–13.57] s | 5.95 s | 5.27 s |
| Sim Fall and ADLS | 16/20 | 3184 ( 1120/1400) | [8.44–35.24] s | 20.15 s | 19.2 s |
| Cogent Labs | 8/6 | 1968 (1520/448 ) | [0.53–55.73] s | 13.15 s | 12.79 s |
| Graz | 8/6 | 1968 (1520/448 ) | [0.53–55.73] s | 13.15 s | 12.79 s |
| MUMAFall | 8/3 | 531 (322/209) | 15 s | 15 s | 15 s |
| SisFall | 19/15 | 4505 (2707/1798) | [9.99–179.99] s | 17.6 s | 14.99 s |
| UniMiB SHAR | 9/8 | 7013 (5314/1699) | 1 s | 1 s | 1 s |
| SmartFall | 4/4 | 2331 (1804/527) | N/A | N/A | N/A |
| SmartWatch | 4/4 | 181 (90/91) | N/A | N/A | N/A |
| Notch | 7/4 | 2563 (2456/107) | N/A | N/A | N/A |
| UP Fall Detection | 6/5 | 578 (306/272) | [10–60] s | 30 s | 10 s |
| SFU Fall Detection | 12/5 | 600 (240/360) | 15 s | 15 s | 15 s |
| CGU-BES | 8/4 | 180 (120/60) | 16.5 s | 16.5 s | 16.5 s |
| MARG | 5/13 | 432 (120/312) | [1.3–11.5] s | 5.3 s | 5.58 s |
| Source | Dataset | Falls/ ADLS [n/n] | Features | Classifier | Validation Method | Performance |
|---|---|---|---|---|---|---|
| [31] | MobiFall | 342/ 288 | Time domain | Naive Bayes, LS, ANN, SVM | 75–25 split, mixed user | 87.5% accuracy |
| [34] | MobiFall | 346/ 11080 | Time and frequency domain | MLP, SVM, KNN | 346 test samples | 97.29% sensitivity |
| [35] | MUMA | 198/ 400 | Biological risk factor | KNN | 80–20 split, mixed user | 84.1% accuracy |
| [36] | MUMA | 198/ 400 | Raw time series window | LSTM | 80–20 split, mixed user | 92% accuracy |
| [20] | SmartFall, Notch, Farseeing | 221/ 30000 | Time domain | SVM | 66–33 split, mixed user, LOO CV | 85% accuracy, 93% accuracy, 99% accuracy |
| [32] | SmartFall, Notch | 221/ 30000 | Raw time series window | CNN | 80–20 split, mixed user | 99.7% accuracy |
| [37] | SisFall | 1798/ 2707 | Time domain | SVM | 10 Fold CV, mixed user | 99.75% accuracy |
| [38] | SisFall | Not specified | Raw time series window | LSTM | Not specified | 97.16% accuracy |
| [39] | SisFall | 1575 Falls/ not specified | Time domain | SVM with RBF | 5 Fold CV, mixed user | 98% accuracy |
| [33] | SisFall | 1780 Falls/ 76926 ADL | Raw time series window | CNN and various other | 2 Fold CV, separated user | 99.94% accuracy |
| Dataset | Falls | ADL | Subjects | Age of Subjects |
|---|---|---|---|---|
| MUMA | 189 | 428 | 17 | 18–55 |
| Notch | 198 | 500 | 7 | 20–35 |
| Sim Fall | 286 | 258 | 17 | 19–27 |
| Smartwatch | 271 | 500 | 7 | 21–55 |
| SmartFall | 527 | 500 | 14 | 21–60 |
| UP Fall | 245 | 1381 | 17 | 18–24 |
| Total | 1716 | 3567 | 79 | 18–60 |
| Dataset | Our | LSTM | Santos | ResNet | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SMV | 3 Axis | SMV | 3 Axis | SMV | 3 Axis | SMV | 3 Axis | |||||||||
| Notch | 0.98 | 0.01 | 0.97 | 0.03 | 1.00 | 0.00 | 0.95 | 0.01 | 0.92 | 0.04 | 0.94 | 0.01 | 0.77 | 0.14 | 0.91 | 0.05 |
| MUMA | 0.92 | 0.00 | 0.80 | 0.04 | 0.92 | 0.01 | 0.75 | 0.04 | 0.91 | 0.01 | 0.91 | 0.01 | 0.90 | 0.01 | 0.89 | 0.02 |
| Sim Fall | 0.89 | 0.00 | 0.83 | 0.04 | 0.88 | 0.02 | 0.80 | 0.12 | 0.88 | 0.01 | 0.89 | 0.00 | 0.90 | 0.01 | 0.89 | 0.01 |
| SmartWatch | 0.99 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 0.95 | 0.04 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 |
| SmartFall | 0.99 | 0.00 | 1.00 | 0.00 | 0.99 | 0.00 | 0.92 | 0.02 | 1.00 | 0.00 | 1.00 | 0.00 | 0.99 | 0.00 | 1.00 | 0.00 |
| UP Fall | 0.98 | 0.00 | 0.90 | 0.02 | 0.98 | 0.00 | 0.78 | 0.07 | 0.99 | 0.00 | 0.97 | 0.00 | 0.99 | 0.00 | 0.96 | 0.02 |
| Average | 0.96 | 0.00 | 0.91 | 0.02 | 0.96 | 0.01 | 0.86 | 0.05 | 0.95 | 0.01 | 0.95 | 0.00 | 0.93 | 0.03 | 0.94 | 0.02 |
| Dataset | Our | LSTM | Santos | ResNet | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SMV | 3 Axis | SMV | 3 Axis | SMV | 3 Axis | SMV | 3 Axis | |||||||||
| Notch | 0.97 | 0.01 | 0.95 | 0.03 | 1.00 | 0.00 | 0.93 | 0.04 | 1.00 | 0.00 | 0.96 | 0.01 | 0.97 | 0.03 | 0.93 | 0.01 |
| MUMA | 0.93 | 0.01 | 0.94 | 0.01 | 0.91 | 0.01 | 0.84 | 0.06 | 0.92 | 0.00 | 0.92 | 0.00 | 0.92 | 0.01 | 0.94 | 0.01 |
| Sim Fall | 0.93 | 0.00 | 0.90 | 0.01 | 0.93 | 0.01 | 0.81 | 0.10 | 0.89 | 0.00 | 0.90 | 0.00 | 0.94 | 0.00 | 0.90 | 0.01 |
| SmartWatch | 0.99 | 0.00 | 1.00 | 0.00 | 0.99 | 0.00 | 0.95 | 0.03 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 |
| SmartFall | 0.99 | 0.00 | 1.00 | 0.00 | 0.98 | 0.00 | 0.92 | 0.03 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 |
| UP Fall | 0.98 | 0.00 | 0.99 | 0.00 | 0.97 | 0.00 | 0.91 | 0.05 | 0.98 | 0.00 | 0.99 | 0.00 | 0.98 | 0.00 | 0.99 | 0.00 |
| Average | 0.97 | 0.00 | 0.96 | 0.01 | 0.96 | 0.01 | 0.89 | 0.05 | 0.97 | 0.00 | 0.96 | 0.00 | 0.97 | 0.01 | 0.96 | 0.01 |
| Dataset | Our | |||||
|---|---|---|---|---|---|---|
| SMV | ||||||
| Precision | Recall | F1 | ||||
| Notch | 0.854 | 0.092 | 0.853 | 0.078 | 0.826 | 0.110 |
| MUMA | 0.926 | 0.017 | 0.910 | 0.024 | 0.912 | 0.023 |
| Sim Fall | 0.908 | 0.016 | 0.902 | 0.023 | 0.902 | 0.023 |
| SmartWatch | 0.982 | 0.004 | 0.982 | 0.004 | 0.982 | 0.004 |
| SmartFall | 0.976 | 0.009 | 0.975 | 0.010 | 0.975 | 0.010 |
| UP Fall | 0.952 | 0.013 | 0.940 | 0.035 | 0.942 | 0.029 |
| Average | 0.933 | 0.025 | 0.927 | 0.029 | 0.923 | 0.033 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kraft, D.; Srinivasan, K.; Bieber, G. Deep Learning Based Fall Detection Algorithms for Embedded Systems, Smartwatches, and IoT Devices Using Accelerometers. Technologies 2020, 8, 72. https://doi.org/10.3390/technologies8040072
Kraft D, Srinivasan K, Bieber G. Deep Learning Based Fall Detection Algorithms for Embedded Systems, Smartwatches, and IoT Devices Using Accelerometers. Technologies. 2020; 8(4):72. https://doi.org/10.3390/technologies8040072
Chicago/Turabian StyleKraft, Dimitri, Karthik Srinivasan, and Gerald Bieber. 2020. "Deep Learning Based Fall Detection Algorithms for Embedded Systems, Smartwatches, and IoT Devices Using Accelerometers" Technologies 8, no. 4: 72. https://doi.org/10.3390/technologies8040072
APA StyleKraft, D., Srinivasan, K., & Bieber, G. (2020). Deep Learning Based Fall Detection Algorithms for Embedded Systems, Smartwatches, and IoT Devices Using Accelerometers. Technologies, 8(4), 72. https://doi.org/10.3390/technologies8040072





