Application of Modeling and Control Approaches of Piezoelectric Actuators: A Review
Abstract
1. Introduction
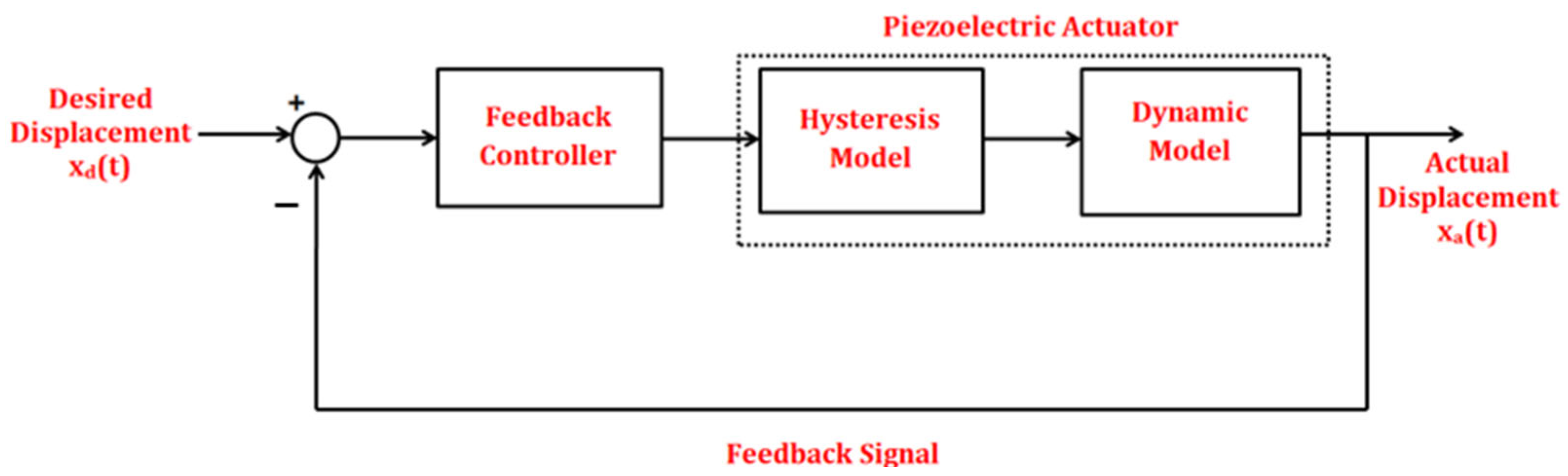
2. Overview of the Piezoelectric Actuation System
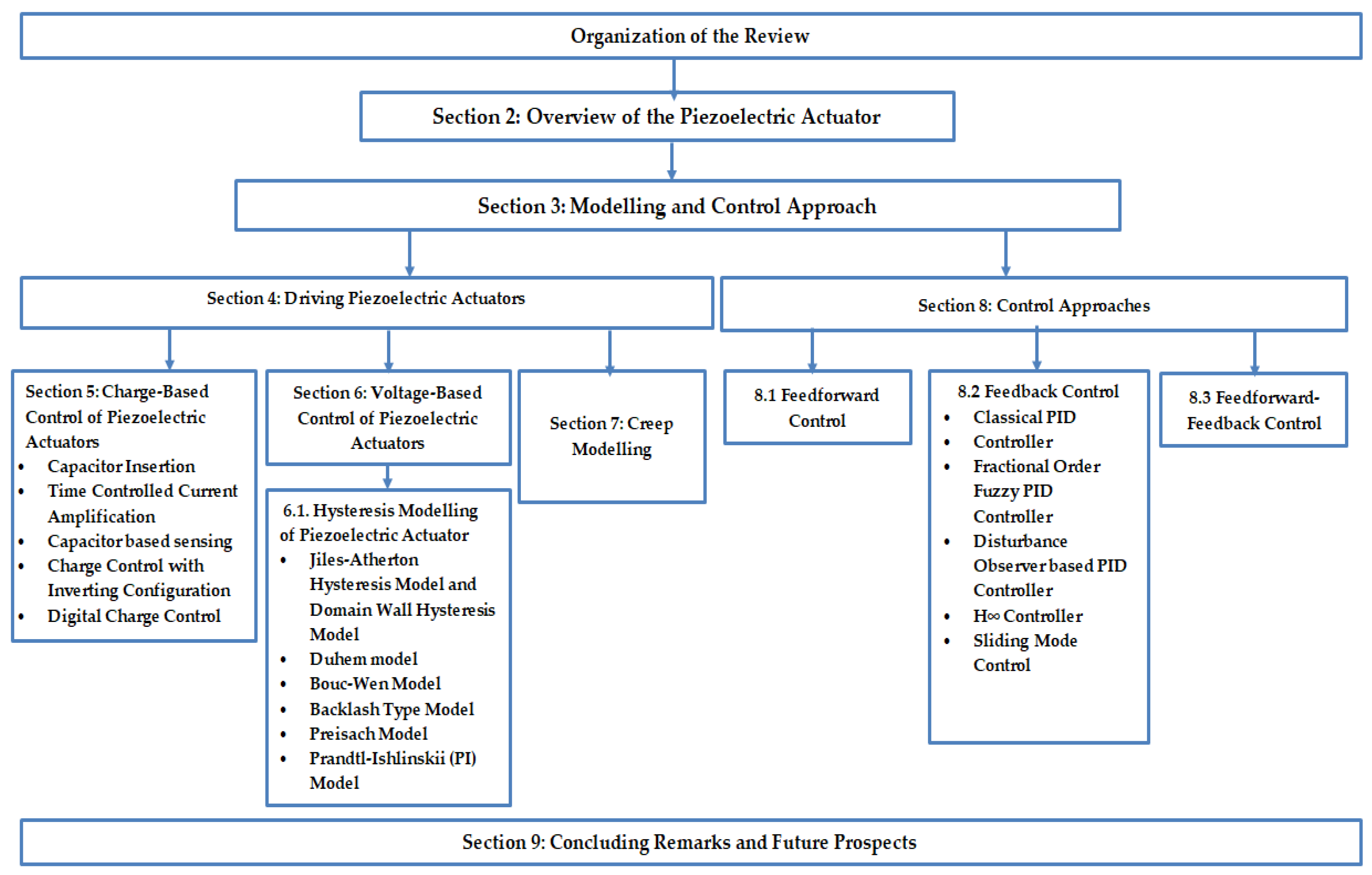
3. Comprehensive Dynamic System Model and Modeling/Control Issues of the Piezoelectric Actuator
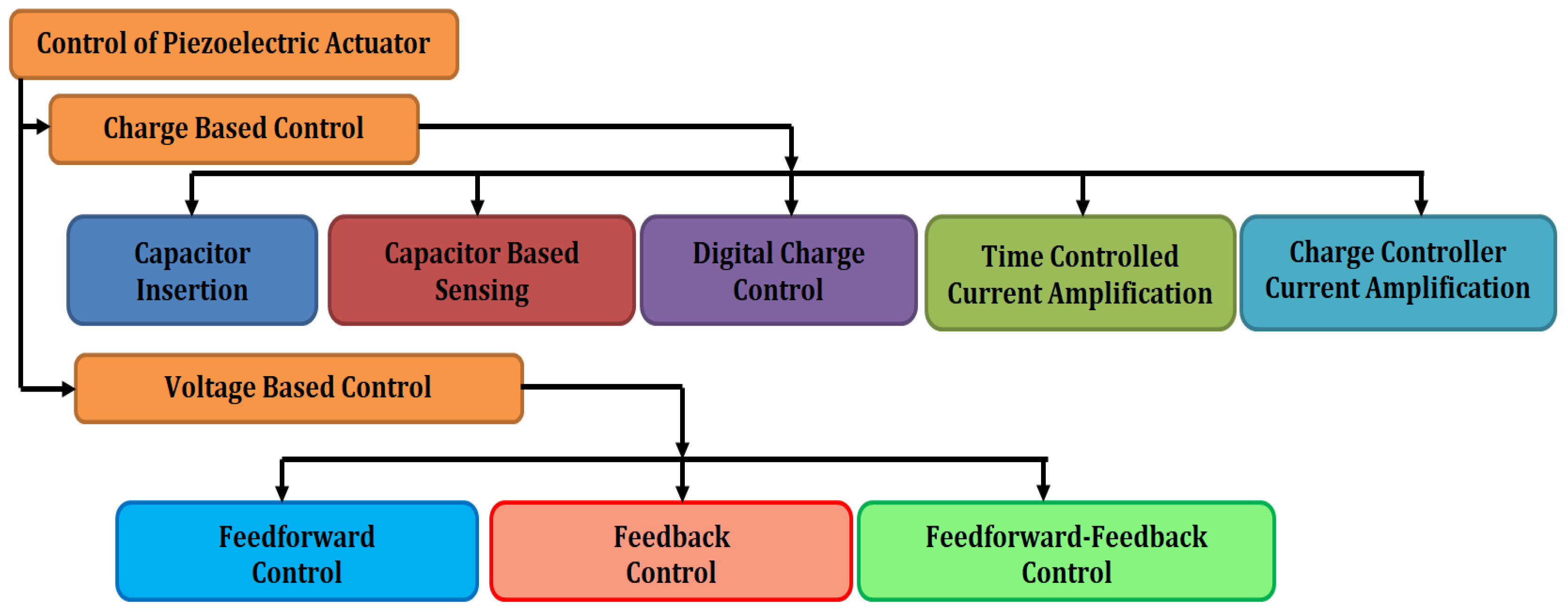
4. Driving and Control Methods of Piezoelectric Actuators
5. Charge-Based Control of Piezoelectric Actuators
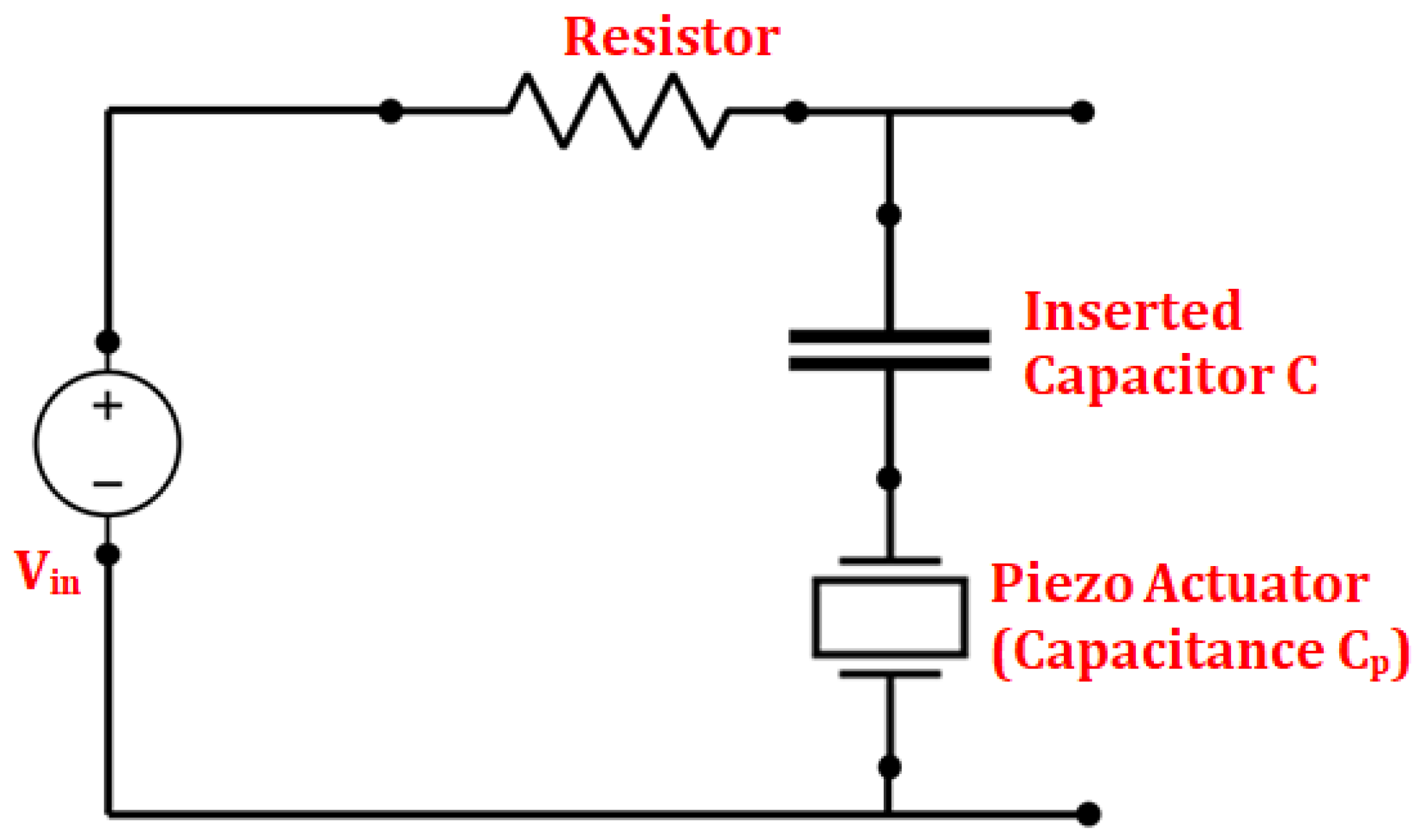
5.1. Capacitor Insertion
5.2. Time Controlled Current Amplification
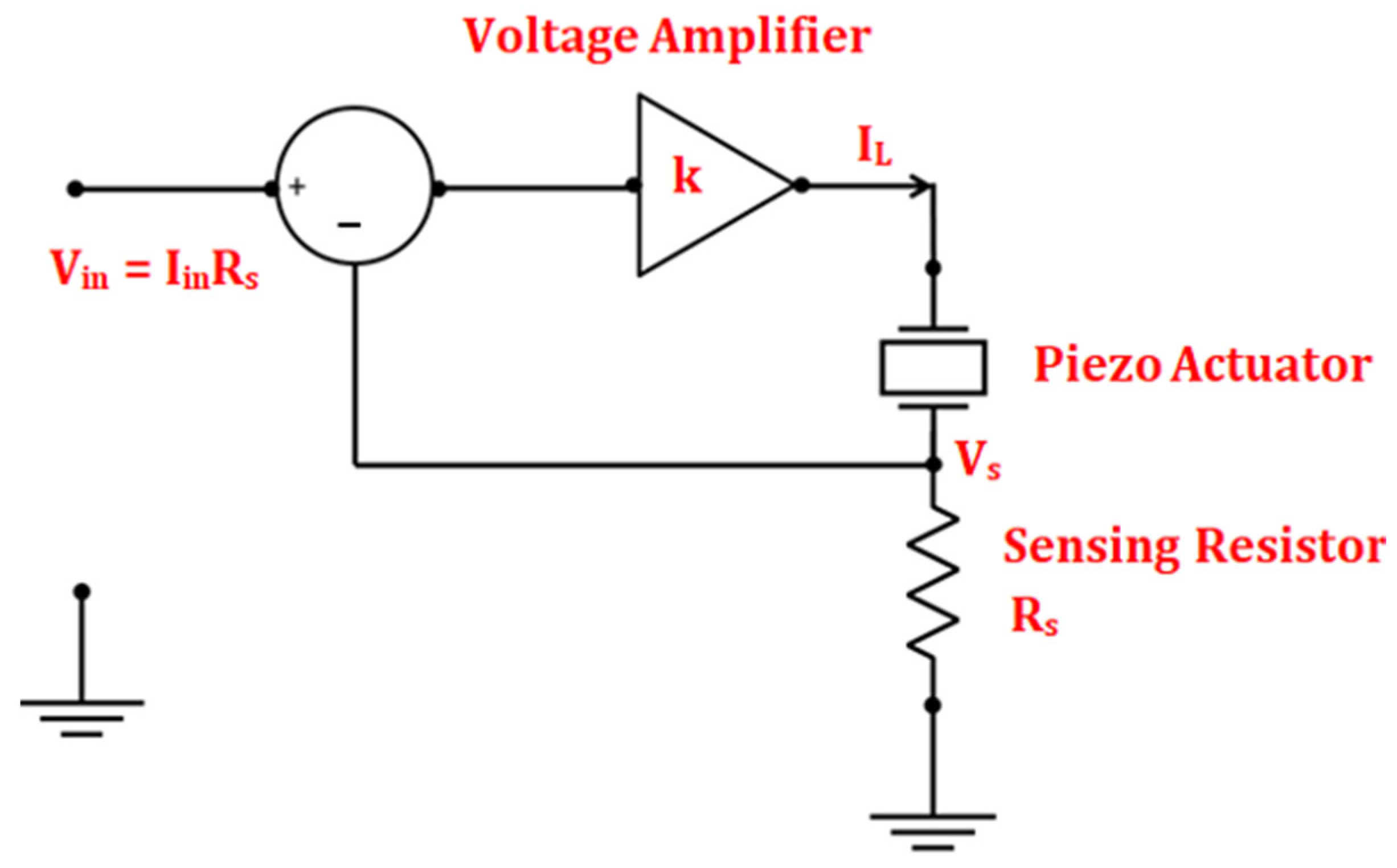
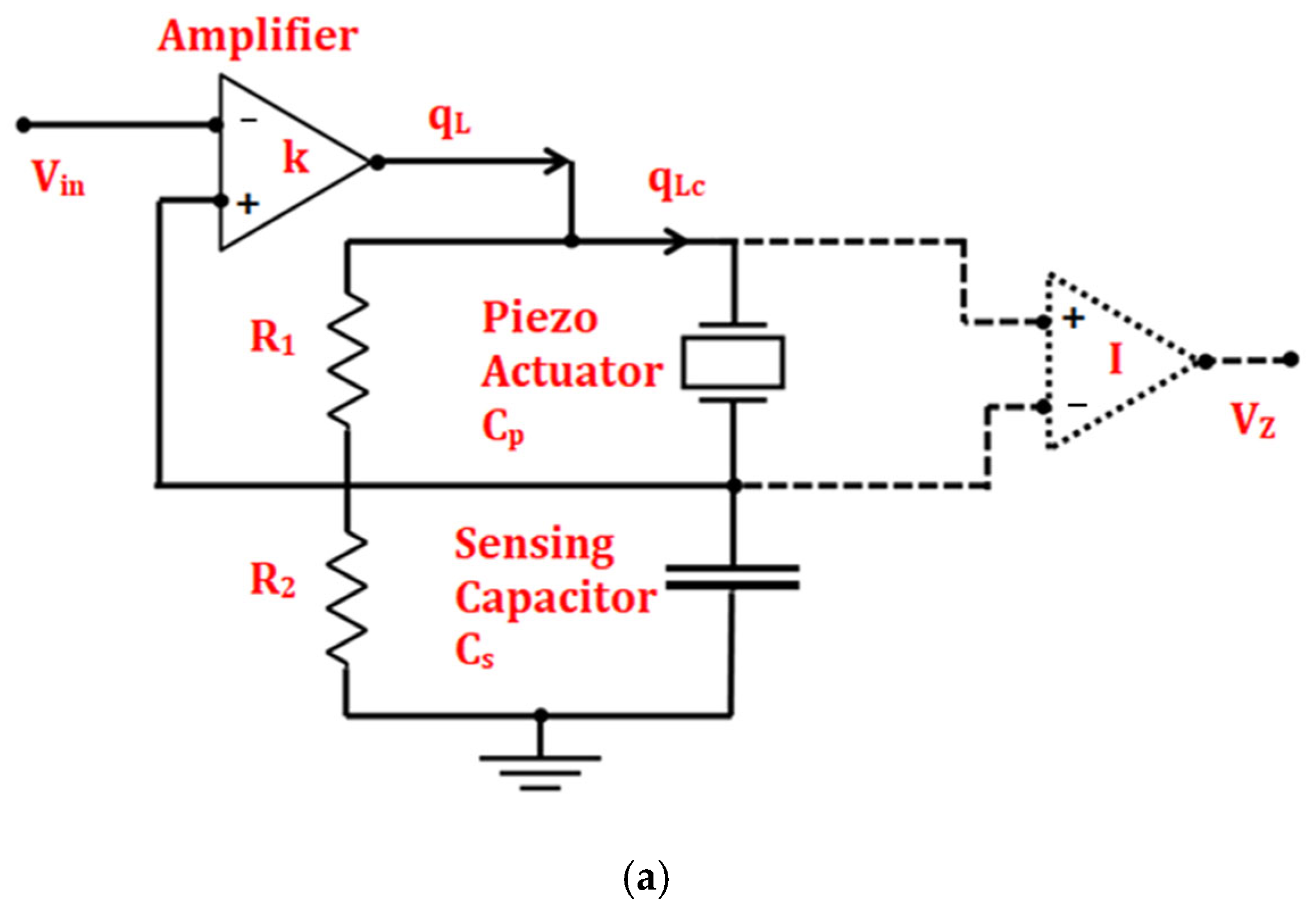
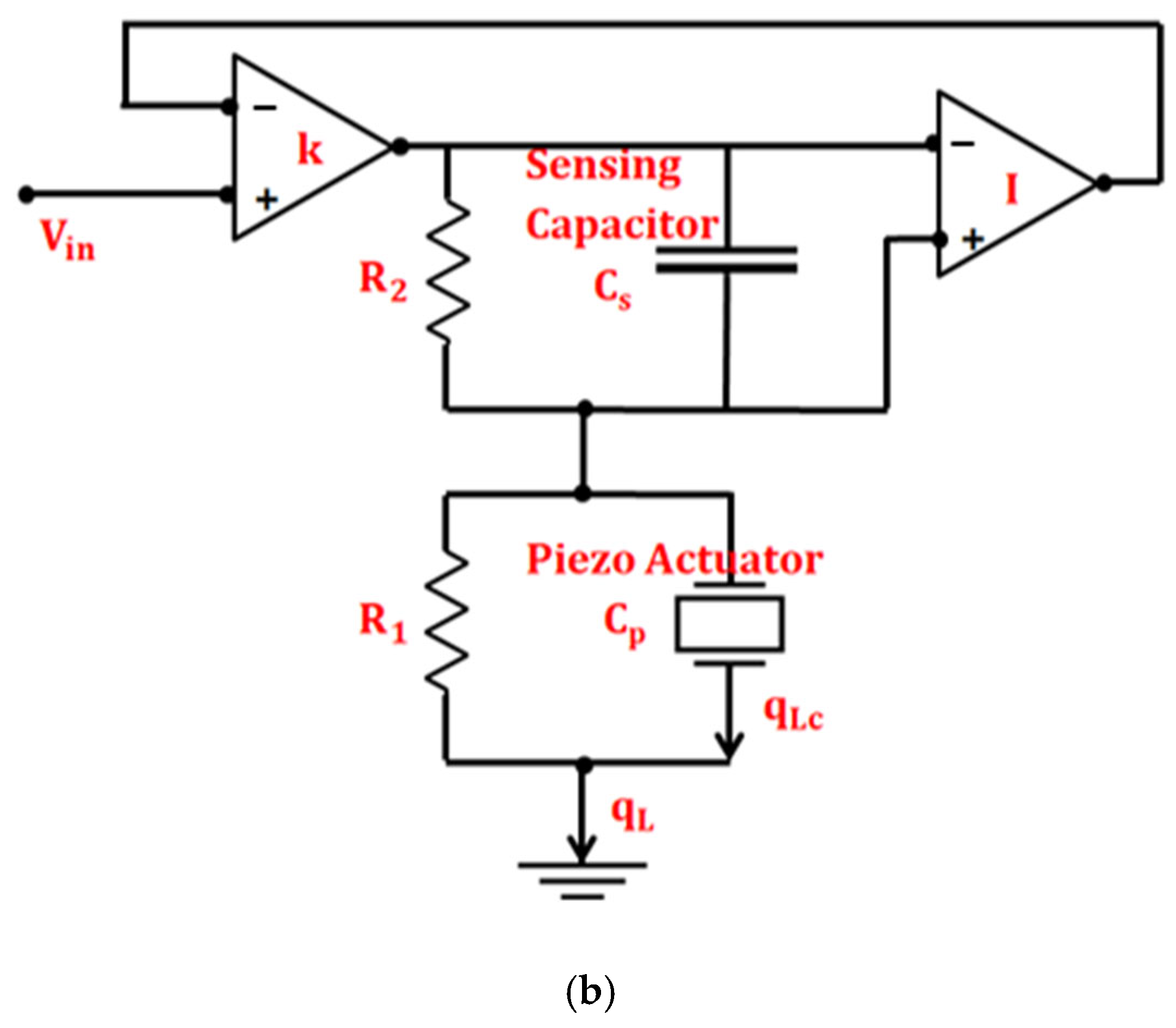
5.3. Capacitor Based Sensing
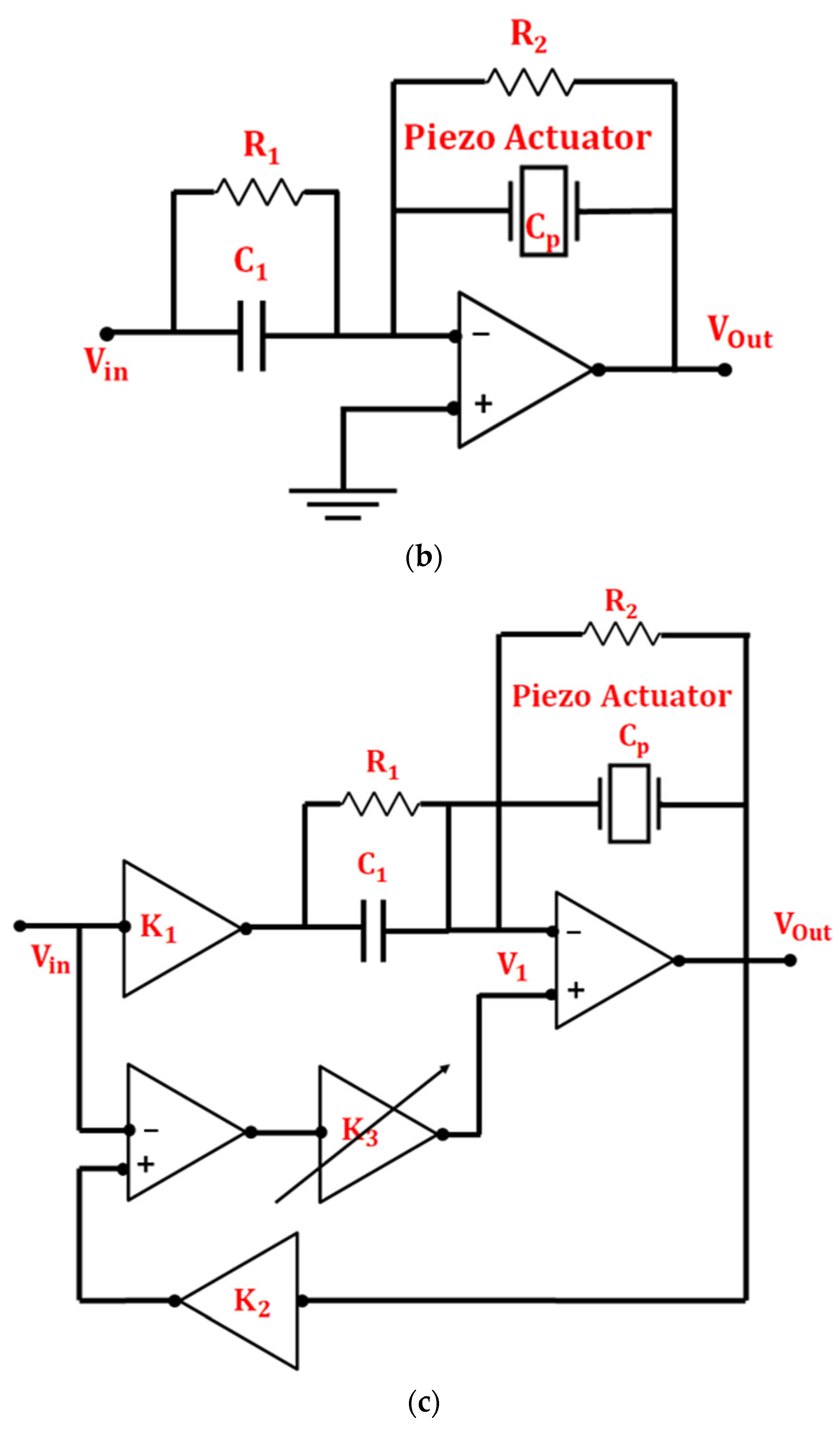
5.4. Charge Control with Inverting Configuration
5.5. Digital Charge Control
5.6. Comparison and Applications of the Charge-Based Control of the Piezoelectric Actuators
6. Voltage-Based Control of Piezoelectric Actuators
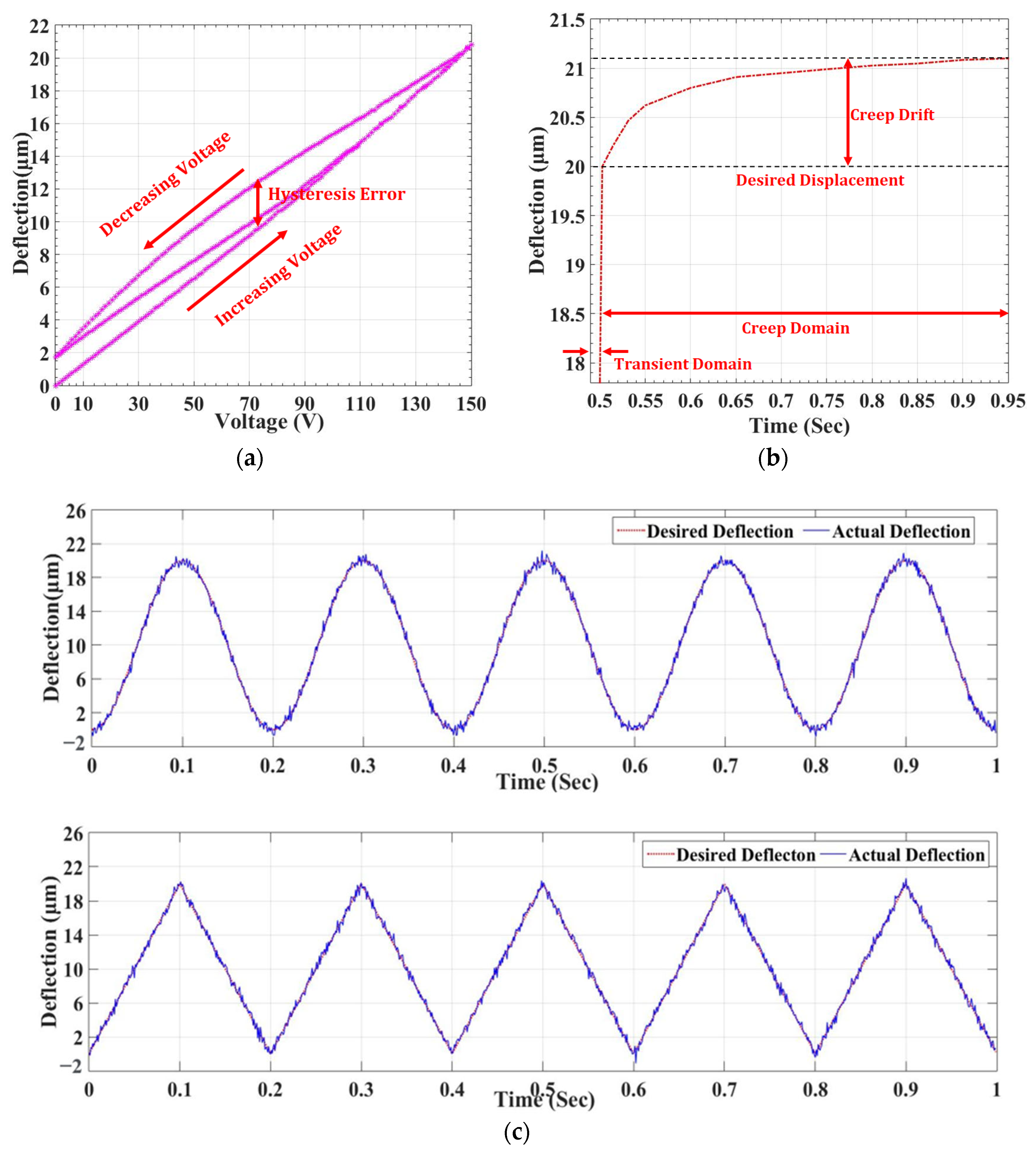
6.1. Hysteresis Modeling of Piezoelectric Actuator
6.1.1. Jiles–Atherton Hysteresis Model and Domain Wall Hysteresis Model
6.1.2. Duhem Model
6.1.3. Bouc–Wen Model
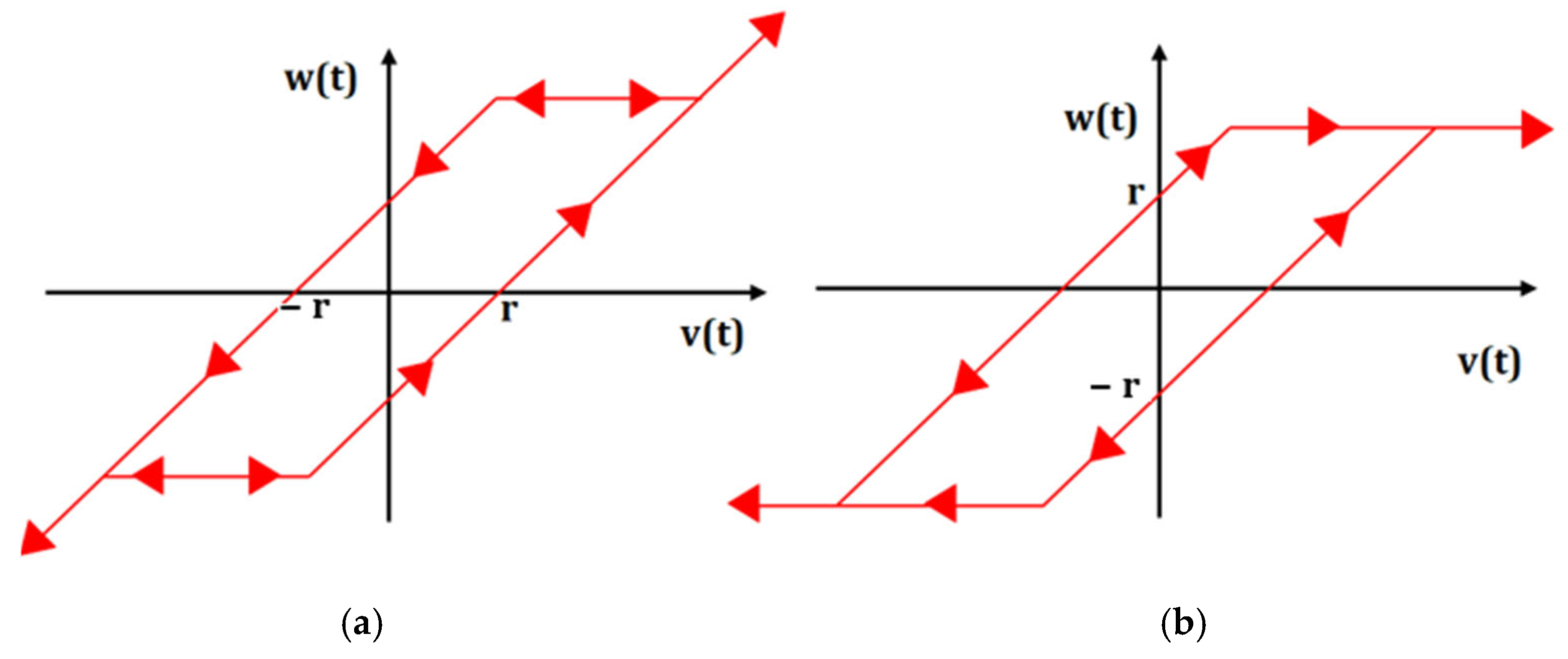
6.1.4. Backlash Type Model
6.1.5. Preisach Model
6.1.6. Prandtl–Ishlinskii (PI) Model
6.1.7. Krasnoselskii–Pokrovskii Model
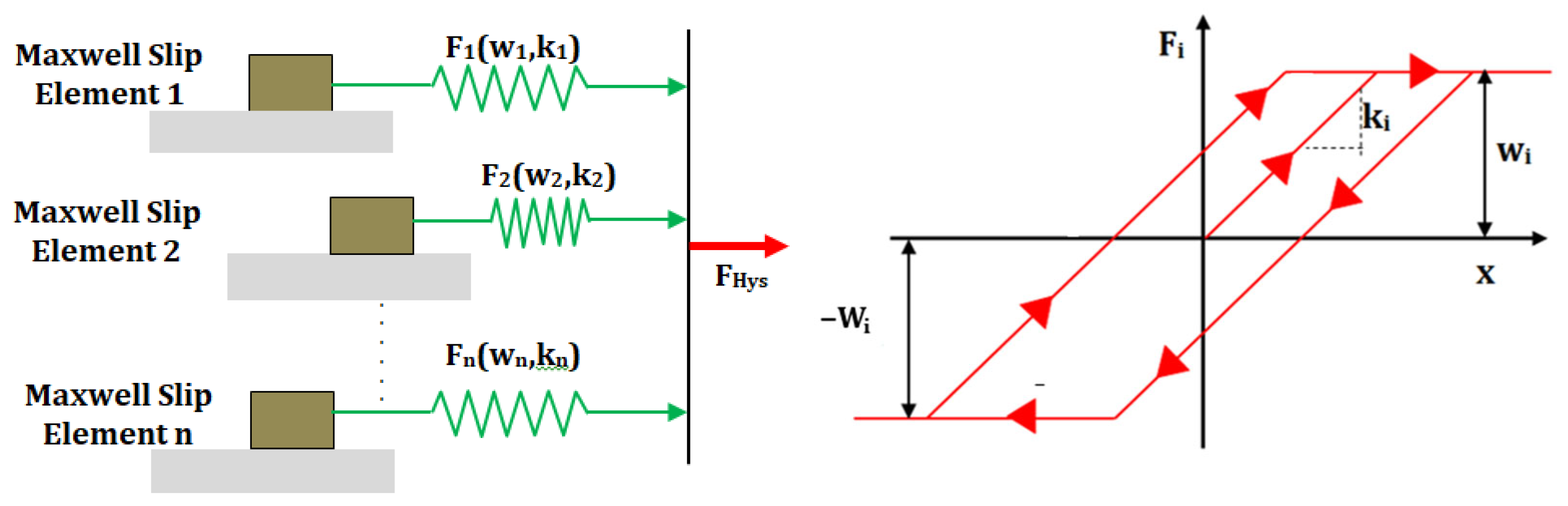
6.1.8. Maxwell–Slip Model
6.2. Applications and Comparison of the Hysteresis Model
| Author | Year | Ref. No. | Type of Actuator | Hysteresis Model | Observation |
|---|---|---|---|---|---|
| C. Zhou | 2021 | [144] | Piezo Stack | Modified Prandtl–Ishlinskii |
|
| X. Shan | 2021 | [145] | Pizeo Stack | Prandtl–Ishlinskii |
|
| K. Ahmed | 2021 | [146] | Piezoelectric nano-stage | Duhem |
|
| C. Zhou | 2022 | [147] | Piezo Stack | Prandtl–Ishlinskii |
|
| W. Wang | 2022 | [148] | Piezoelectric Positioning Stage | Prandtl–Ishlinskii |
|
| A. G. Baziyad | 2023 | [149] | Piezoelectric-driven nanopositioning Stage | Preisach |
|
| J. Lu | 2023 | [150] | Fast piezo-driven scanner | Bouc–Wen |
|
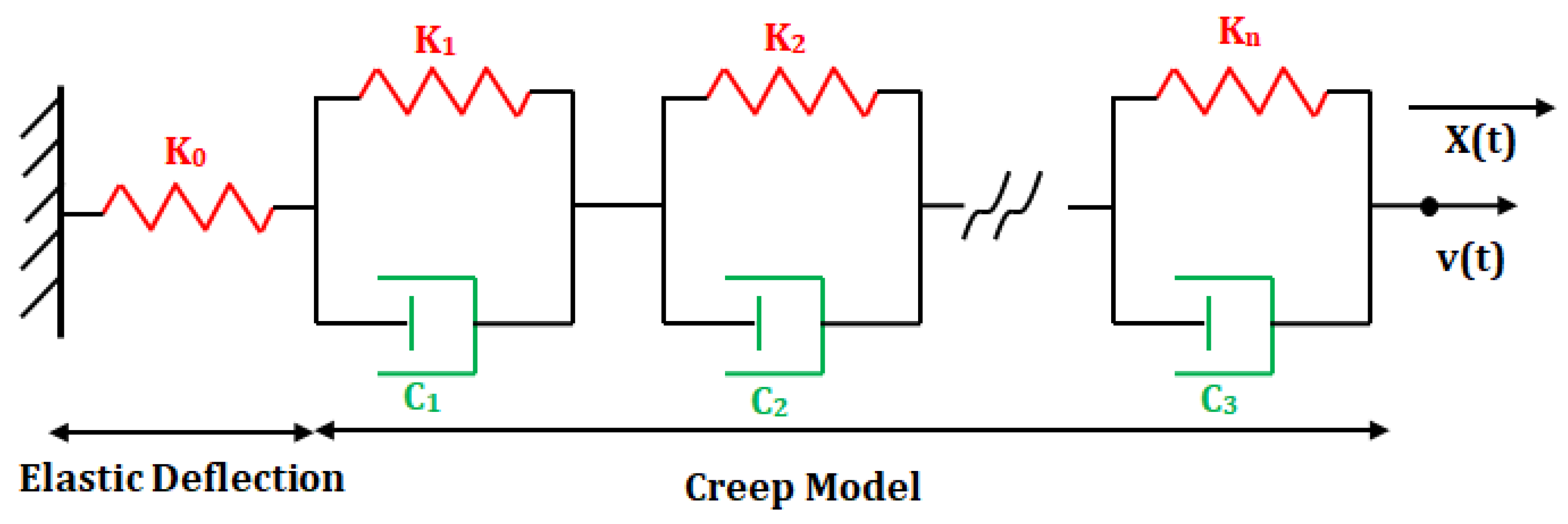
7. Modeling of Creep Behavior of the Piezoelectric Actuators
8. Control Approaches for Piezoelectric Actuator
8.1. Feedforward Control of Piezoelectric Actuators
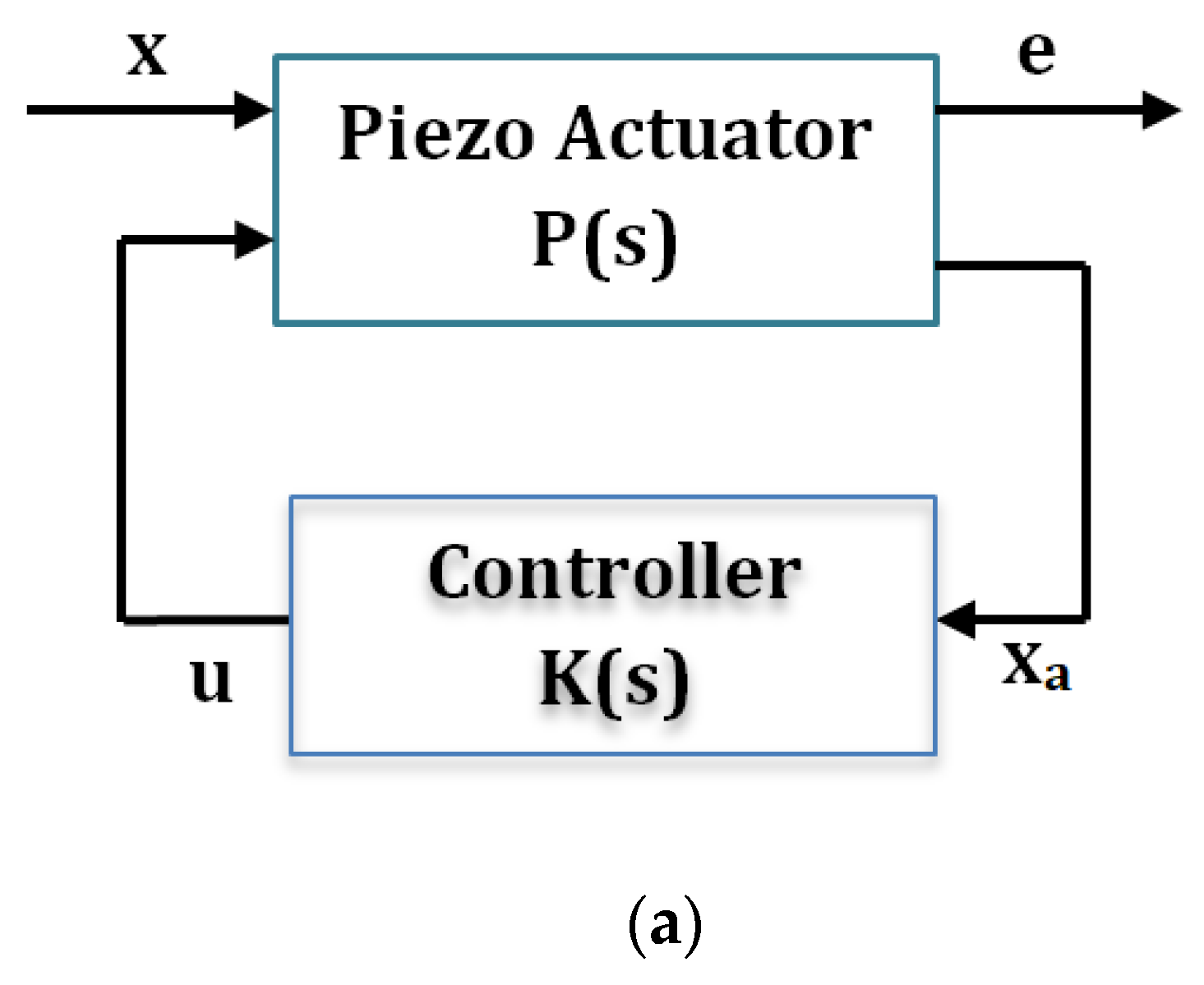
8.2. Feedback Control of Piezoelectric Actuators
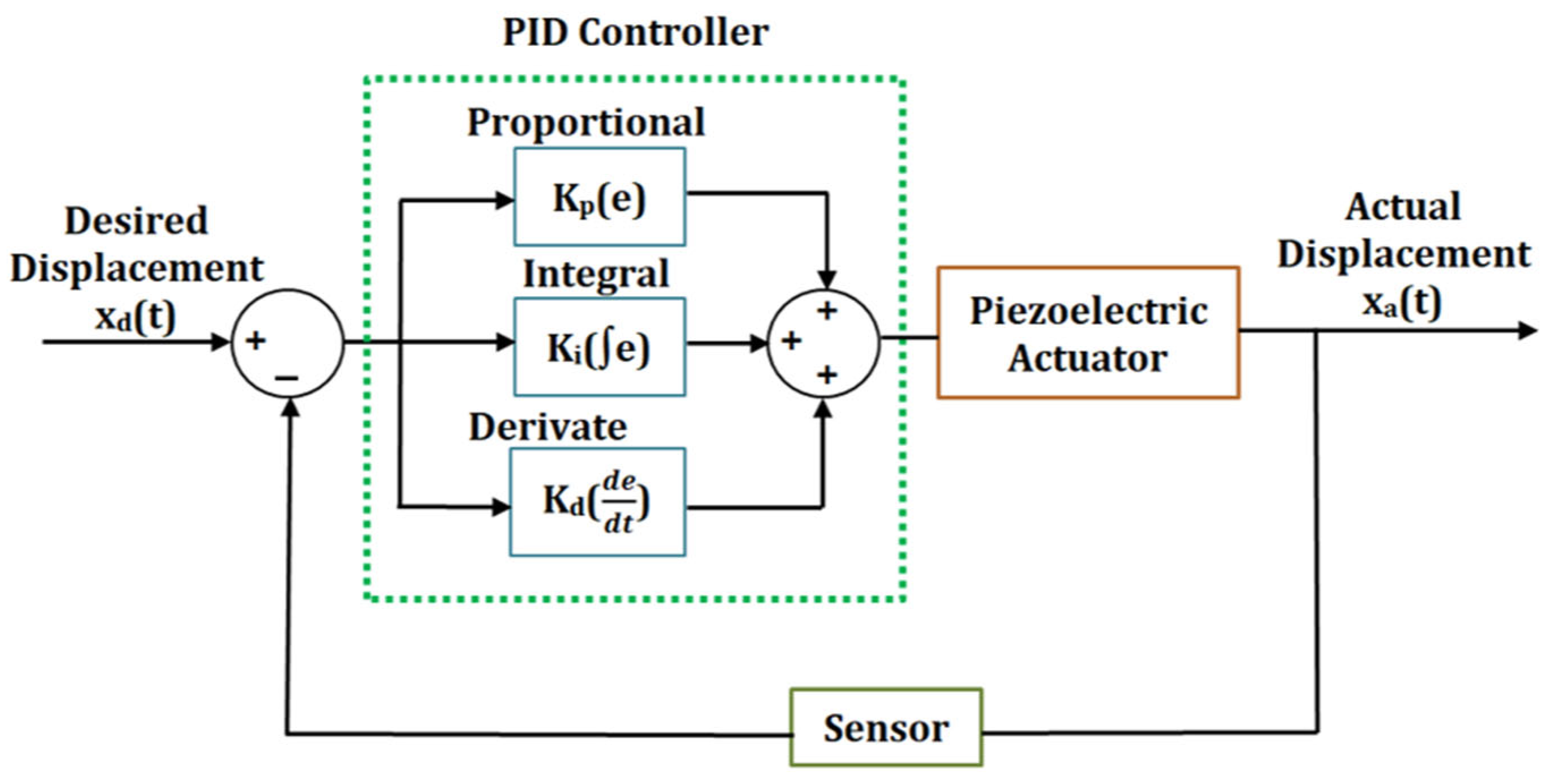
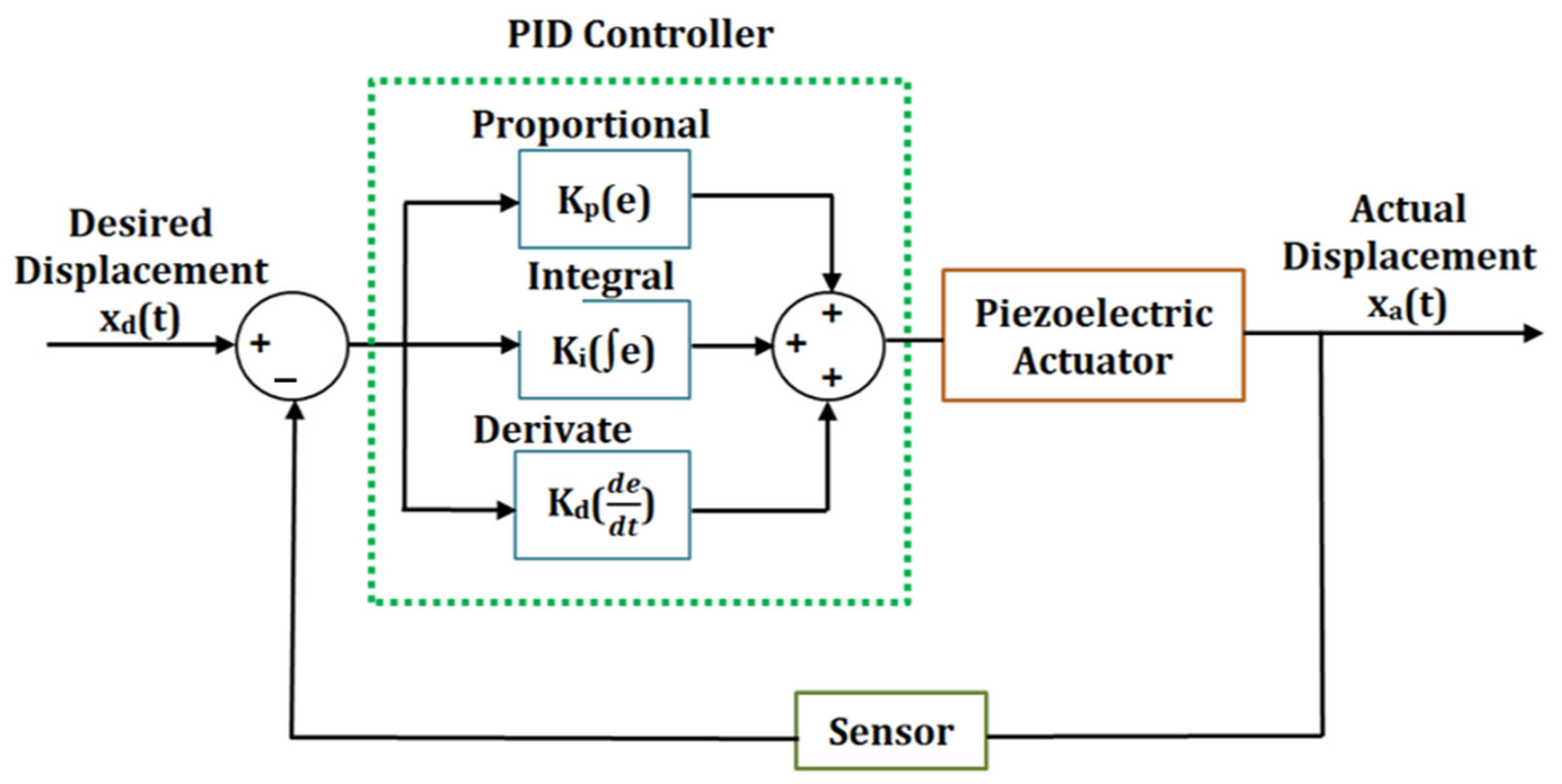
8.2.1. Classical PID Controller
8.2.2. Self-Tuning Fuzzy PID Controller
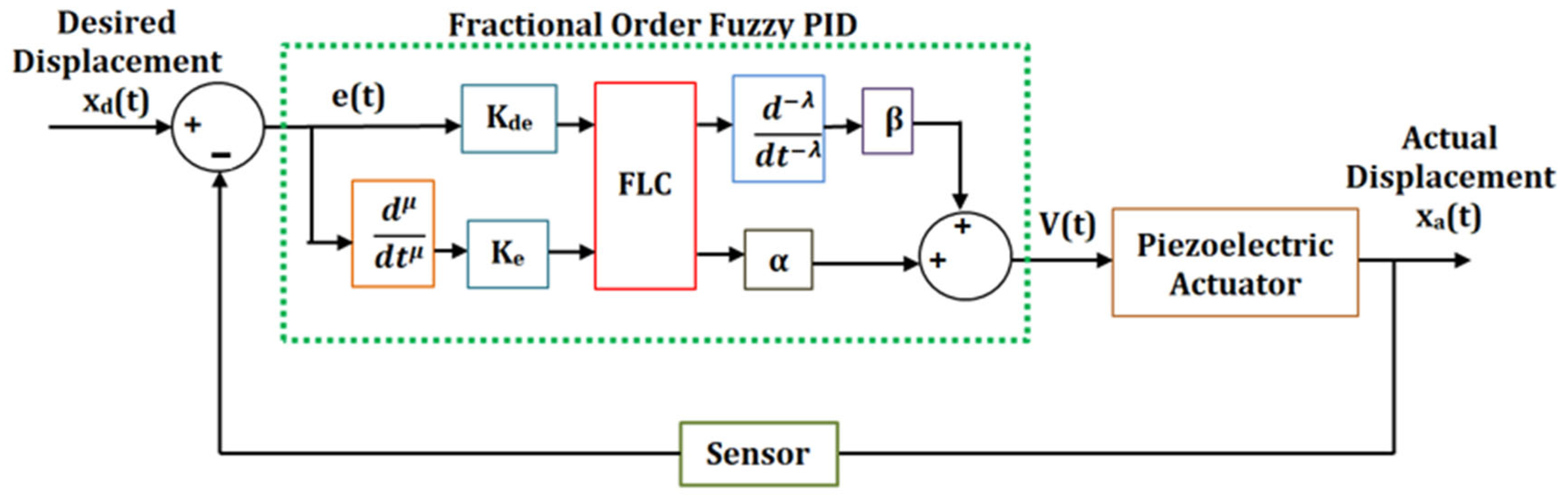
8.2.3. Fractional Order Fuzzy PID Controller
8.2.4. Disturbance Observer-Based PID Controller
8.2.5. H∞ Controller
8.2.6. Sliding Mode Control
8.3. Feedforward–Feedback Control of Piezoelectric Actuators
8.4. Applications of Control Strategies in Piezoelectric Actuators
9. Concluding Remarks and Future Prospects
- Development and enhancement of unique charge-based control method applicable to all types of piezoelectric actuators
- Development of realistic rate-dependent hysteresis models and inverse constructions to model the hysteresis behavior of the piezoelectric actuator at a very high-frequency range.
- Implementation of rate-dependent hysteresis models for multi-degree freedom actuators involving multiple piezoelectric actuators
- Development of an active vibration isolation approach to overcome the issues of dynamic vibration.
- Design, develop, and implement a novel control strategy to better control multi-degree freedom piezoelectric actuators and eliminate system nonlinearities to minimize errors.
Author Contributions
Funding
Conflicts of Interest
References
- Jia, Z.-Y.; Ma, J.-W.; Song, D.-N.; Wang, F.-J.; Liu, W. A review of contouring-error reduction method in multi-axis CNC machining. Int. J. Mach. Tools Manuf. 2018, 125, 34–54. [Google Scholar] [CrossRef]
- Wang, H.; Li, Y.; Wang, X.; Liu, Z.; Ahmed, M.F.; Zeng, C. Preparation and characterization of piezoelectric foams based on cyclic olefin copolymer. Eng. Sci. 2021, 16, 203–210. [Google Scholar] [CrossRef]
- Su, Y.-F.; Han, G.; Kong, Z.; Nantung, T.; Lu, N. Embeddable piezoelectric sensors for strength gain monitoring of cementitious materials: The influence of Coating Materials. Eng. Sci. 2020, 11, 66–75. [Google Scholar] [CrossRef]
- Muralidhara; Rao, R. Displacement characteristics of a piezo actuator-based prototype microactuator with a hydraulic displacement amplification system. J. Mech. Sci. Technol. 2015, 29, 4817–4822. [Google Scholar] [CrossRef]
- Mohith, S.; Navin Karanth, P.; Kulkarni, S.M. Performance analysis of valveless micropump with disposable chamber actuated through Amplified Piezo Actuator (APA) for biomedical application. Mechatronics 2020, 67, 102347. [Google Scholar] [CrossRef]
- Ling, M.; Cao, J.; Zeng, M.; Lin, J.; Inman, D.J. Enhanced mathematical modeling of the displacement amplification ratio for piezoelectric compliant mechanisms. Smart Mater. Struct. 2016, 25, 075022. [Google Scholar] [CrossRef]
- Naik, N.; Suresh, P.; Yadav, S.; Nisha, M.P.; Arias-Gonzáles, J.L.; Cotrina-Aliaga, J.C.; Bhat, R.; Jalageri, M.D.; Kaushik, Y.; Kunjibettu, A.B. A review on composite materials for energy harvesting in electric vehicles. Energies 2023, 16, 3348. [Google Scholar] [CrossRef]
- Mohith, S.; Karanth, P.N.; Kulkarni, S.M. Experimental investigation on performance of disposable micropump with retrofit piezo stack actuator for biomedical application. Microsyst. Technol. 2019, 25, 4741–4752. [Google Scholar] [CrossRef]
- El-Sayed, A.M.; Abo-Ismail, A.; El-Melegy, M.T.; Hamzaid, N.A.; Osman, N.A.A. Development of a Micro-Gripper Using Piezoelectric Bimorphs. Sensors 2013, 13, 5826–5840. [Google Scholar] [CrossRef]
- Abondance, T.; Jayaram, K.; Jafferis, N.T.; Shum, J.; Wood, R.J. Piezoelectric Grippers for Mobile Micromanipulation. IEEE Robot. Autom. Lett. 2020, 5, 4407–4414. [Google Scholar] [CrossRef]
- Jeon, J.; Han, C.; Han, Y.-M.; Choi, S.-B. A new type of a direct-drive valve system driven by a piezostack actuator and sliding spool. Smart Mater. Struct. 2014, 23, 075002. [Google Scholar] [CrossRef]
- Sohn, J.W.; Choi, S.-B. Identification of Operating Parameters Most Strongly Influencing the Jetting Performance in a Piezoelectric Actuator-Driven Dispenser. Appl. Sci. 2018, 8, 243. [Google Scholar] [CrossRef]
- Deng, G.; Cui, W.; Zhou, C.; Li, J. A piezoelectric jetting dispenser with a pin joint. Optik 2018, 175, 163–171. [Google Scholar] [CrossRef]
- Cai, K.; Tian, Y.; Wang, F.; Zhang, D.; Shirinzadeh, B. Development of a piezo-driven 3-DOF stage with T-shape flexible hinge mechanism. Robot. Comput. Manuf. 2016, 37, 125–138. [Google Scholar] [CrossRef]
- Eslami, B.; Solares, S.D. Experimental approach for selecting the excitation frequency for maximum compositional contrast in viscous environments for piezo-driven bimodal atomic force microscopy. J. Appl. Phys. 2016, 119, 084901. [Google Scholar] [CrossRef]
- Muralidhara; Vasa, N.J.; Makaram, S. Investigations on a directly coupled piezoactuated tool feed system for micro-electro-discharge machine. Int. J. Mach. Tools Manuf. 2009, 49, 1197–1203. [Google Scholar] [CrossRef]
- Tian, X.; Zhang, B.; Liu, Y.; Chen, S.; Yu, H. A novel U-shaped stepping linear piezoelectric actuator with two driving feet and low motion coupling: Design, modeling and experiments. Mech. Syst. Signal Process. 2019, 124, 679–695. [Google Scholar] [CrossRef]
- Lu, Z.-Q.; Shao, D.; Fang, Z.-W.; Ding, H.; Chen, L.-Q. Integrated vibration isolation and energy harvesting via a bistable piezo-composite plate. J. Vib. Control 2020, 26, 779–789. [Google Scholar] [CrossRef]
- Rodriguez-Fortun, J.M.; Orus, J.; Alfonso, J.; Gimeno, F.B.; Castellanos, J.A. Flatness-Based Active Vibration Control for Piezoelectric Actuators. IEEE/ASME Trans. Mechatron. 2013, 18, 221–229. [Google Scholar] [CrossRef]
- Tavakolpour, A.R.; Mailah, M.; Mat Darus, I.Z.; Tokhi, O. Self-learning active vibration control of a flexible plate structure with piezoelectric actuator. Simul. Model. Pract. Theory 2010, 18, 516–532. [Google Scholar] [CrossRef]
- Mohith, S.; Upadhya, A.R.; Navin, K.P.; Kulkarni, S.M.; Rao, M. Recent trends in piezoelectric actuators for precision motion and their applications: A review. Smart Mater. Struct. 2021, 30, 013002. [Google Scholar] [CrossRef]
- Boukari, A.-F.; Carmona, J.-C.; Moraru, G.; Malburet, F.; Chaaba, A.; Douimi, M. Piezo-actuators modeling for smart applications. Mechatronics 2011, 21, 339–349. [Google Scholar] [CrossRef]
- Xue, D.; Zhou, Y.; Bao, H.; Gao, J.; Zhou, C.; Ren, X. Large piezoelectric effect in Pb-free Ba(Ti, Sn)O3-x(Ba, Ca)TiO3 ceramics. Appl. Phys. Lett. 2011, 99, 122901. [Google Scholar] [CrossRef]
- Su, X.; Jia, Y.; Han, C.; Hu, Y.; Fu, Z.; Liu, K.; Yu, Y.; Yan, X.; Wang, Y. Flash sintering of lead zirconate titanate ceramics under an alternating current electrical field. Ceram. Int. 2019, 45, 5168–5173. [Google Scholar] [CrossRef]
- Kholodkova, A.A.; Danchevskaya, M.N.; Ivakin, Y.D.; Muravieva, G.P.; Smirnov, A.D.; Tarasovskii, V.P.; Ponomarev, S.G.; Fionov, A.S.; Kolesov, V.V. Properties of barium titanate ceramics based on powder synthesized in supercritical water. Ceram. Int. 2018, 44, 13129–13138. [Google Scholar] [CrossRef]
- Naik, R.; Mohit, S.; Chavan, S. Piezoelectric property investigation on PVDF/ZrO2/ZnO nanocomposite for energy harvesting application. Eng. Res. Express 2021, 3, 025003. [Google Scholar] [CrossRef]
- Colorado, S.A.; Colorado, H.A. Manufacturing of zinc oxide structures by thermal oxidation processes as scalable methods towards inexpensive electric generators. Ceram. Int. 2017, 43, 15846–15855. [Google Scholar] [CrossRef]
- Bakhtiari-Shahri, M.; Moeenfard, H. Energy harvesting from unimorph piezoelectric circular plates under random acoustic and base acceleration excitations. Mech. Syst. Signal Process. 2019, 130, 502–523. [Google Scholar] [CrossRef]
- Rios, S.A.; Fleming, A.J. A new electrical configuration for improving the range of piezoelectric bimorph benders. Sens. Actuators A Phys. 2015, 224, 106–110. [Google Scholar] [CrossRef]
- Ozaki, T.; Hamaguchi, K. Performance of direct-driven flapping-wing actuator with piezoelectric single-crystal PIN-PMN-PT. J. Micromech. Microeng. 2018, 28, 025007. [Google Scholar] [CrossRef]
- Almeida, A.; Andrews, G.; Jaiswal, D.; Hoshino, K. The Actuation Mechanism of 3D Printed Flexure-Based Robotic Microtweezers. Micromachines 2019, 10, 470. [Google Scholar] [CrossRef] [PubMed]
- Habineza, D.; Rakotondrabe, M.; Le Gorrec, Y. Bouc–Wen Modeling and Feedforward Control of Multivariable Hysteresis in Piezoelectric Systems: Application to a 3-DoF Piezotube Scanner. IEEE Trans. Control Syst. Technol. 2015, 23, 1797–1806. [Google Scholar] [CrossRef]
- Habineza, D.; Rakotondrabe, M.; Le Gorrec, Y. Simultaneous suppression of badly damped vibrations and cross-couplings in a 2-DoF piezoelectric actuator by using feedforward standard H∞ approach. In Next-Generation Robotics II; and Machine Intelligence and Bio-Inspired Computation: Theory and Applications IX; SPIE: Baltimore, MD, USA, 2015; p. 94940L. [Google Scholar] [CrossRef]
- Bu, Z.; Lin, S.; Huang, X.; Li, A.; Wu, D.; Zhao, Y.; Luo, Z.; Wang, L. A novel piezostack-driven jetting dispenser with corner-filleted flexure hinge and high-frequency performance. J. Micromech. Microeng. 2018, 28, 075001. [Google Scholar] [CrossRef]
- Hwang, H.S.; Nasser, J.; Sodano, H.A. Piezoelectric Stack Actuator for Measurement of Interfacial Shear Strength at High Strain Rates. Exp. Mech. 2019, 59, 979–990. [Google Scholar] [CrossRef]
- Santhya, M.; Upadhya, A.R.; Panambur, N.K.; Kulkarni, S.M. Performance analysis of a novel piezo actuated valveless micropump for biomedical application. AIP Conf. Proc. 2020, 2236, 070002. [Google Scholar] [CrossRef]
- Dsouza, R.D.; Navin, K.P.; Theodoridis, T.; Sharma, P. Design, fabrication and testing of a 2 DOF compliant flexural microgripper. Microsyst. Technol. 2018, 24, 3867–3883. [Google Scholar] [CrossRef]
- Dong, W.; Chen, F.; Yang, M.; Du, Z.-J.; Tang, J.; Zhang, D. Development of a highly efficient bridge-type mechanism based on negative stiffness. Smart Mater. Struct. 2017, 26, 095053. [Google Scholar] [CrossRef]
- Chen, F.; Du, Z.-J.; Yang, M.; Gao, F.; Dong, W.; Zhang, D. Design and analysis of a three-dimensional bridge-type mechanism based on the stiffness distribution. Precis. Eng. 2018, 51, 48–58. [Google Scholar] [CrossRef]
- Dong, W.; Chen, F.; Gao, F.; Yang, M.; Sun, L.; Du, Z.; Tang, J.; Zhang, D. Development and analysis of a bridge-lever-type displacement amplifier based on hybrid flexure hinges. Precis. Eng. 2018, 54, 171–181. [Google Scholar] [CrossRef]
- Chen, F.; Gao, Y.; Dong, W.; Du, Z. Design and Control of a Passive Compliant Piezo-Actuated Micro-Gripper With Hybrid Flexure Hinges. IEEE Trans. Ind. Electron. 2020, 68, 11168–11177. [Google Scholar] [CrossRef]
- Tian, X.; Liu, Y.; Chen, W.; Deng, J.; Liu, J. Development and experiment evaluation of an H-shape linear piezoelectric actuator operated in stepping mode. Ceram. Int. 2018, 44, S246–S249. [Google Scholar] [CrossRef]
- Wang, Y.-J.; Yang, C.; Sue, C.-Y.; Wang, Y.-T. Analysis of a 0.1-μm stepping bi-axis piezoelectric stage using a 2-DOF lumped model. Microsyst. Technol. 2020, 26, 425–436. [Google Scholar] [CrossRef]
- Li, J.; Zhao, H.; Shao, M.; Zhou, X.; Huang, H.; Fan, Z. Design and experiment performances of an inchworm type rotary actuator. Rev. Sci. Instrum. 2014, 85, 085004. [Google Scholar] [CrossRef]
- Shao, S.; Song, S.; Liu, K.; Xu, M. A piezo-driven rotary inchworm actuator featured with simple structure and high output torque. Int. J. Appl. Electromagn. Mech. 2019, 59, 317–325. [Google Scholar] [CrossRef]
- Zhong, B.; Zhu, J.; Jin, Z.; He, H.; Sun, L.; Wang, Z. Improved inertial stick-slip movement performance via driving waveform optimization. Precis. Eng. 2019, 55, 260–267. [Google Scholar] [CrossRef]
- Gao, Q.; He, M.; Lu, X.; Zhang, C.; Cheng, T. Simple and high-performance stick-slip piezoelectric actuator based on an asymmetrical flexure hinge driving mechanism. J. Intell. Mater. Syst. Struct. 2019, 30, 2125–2134. [Google Scholar] [CrossRef]
- Grybas, I.; Bansevicius, R.; Jurenas, V.; Bubulis, A.; Janutenaite, J.; Kulvietis, G. Ultrasonic standing waves-driven high resolution rotary table. Precis. Eng. 2016, 45, 396–402. [Google Scholar] [CrossRef]
- Wang, L.; Shu, C.; Zhang, Q.; Jin, J. A novel sandwich-type traveling wave piezoelectric tracked mobile system. Ultrasonics 2017, 75, 28–35. [Google Scholar] [CrossRef]
- Liao, C.; Xu, M.; Xiao, R.; Han, W. Integrated design of piezo-actuated 2-DOF submillimeter-range super-resolution platform with self-sensing unit. Mech. Syst. Signal Process. 2020, 139, 106569. [Google Scholar] [CrossRef]
- Chen, F.; Dong, W.; Yang, M.; Sun, L.; Du, Z. A PZT Actuated 6-DOF Positioning System for Space Optics Alignment. IEEE/ASME Trans. Mechatron. 2019, 24, 2827–2838. [Google Scholar] [CrossRef]
- Li, J.; Huang, H.; Morita, T. Stepping piezoelectric actuators with large working stroke for nano-positioning systems: A review. Sens. Actuators A Phys. 2019, 292, 39–51. [Google Scholar] [CrossRef]
- Wang, L.; Chen, W.; Liu, J.; Deng, J.; Liu, Y. A review of recent studies on non-resonant piezoelectric actuators. Mech. Syst. Signal Process. 2019, 133, 106254. [Google Scholar] [CrossRef]
- Wang, S.; Rong, W.; Wang, L.; Xie, H.; Sun, L.; Mills, J.K. A survey of piezoelectric actuators with long working stroke in recent years: Classifications, principles, connections and distinctions. Mech. Syst. Signal Process. 2019, 123, 591–605. [Google Scholar] [CrossRef]
- Gu, G.-Y.; Zhu, L.-M.; Su, C.-Y.; Ding, H.; Fatikow, S. Modeling and control of piezo-actuated nanopositioning stages: A survey. IEEE Trans. Autom. Sci. Eng. 2016, 13, 313–332. [Google Scholar] [CrossRef]
- Rakotondrabe, M. Multivariable classical Prandtl–Ishlinskii hysteresis modeling and compensation and sensorless control of a nonlinear 2-dof piezoactuator. Nonlinear Dyn. 2017, 89, 481–499. [Google Scholar] [CrossRef]
- Sabarianand, D.V.; Karthikeyan, P.; Muthuramalingam, T. A review on control strategies for compensation of hysteresis and creep on piezoelectric actuators based micro systems. Mech. Syst. Signal Process. 2020, 140, 106634. [Google Scholar] [CrossRef]
- Gan, J.; Zhang, X. A review of nonlinear hysteresis modeling and control of piezoelectric actuators. AIP Adv. 2019, 9, 040702. [Google Scholar] [CrossRef]
- Chen, J.; Peng, G.; Hu, H.; Ning, J. Dynamic Hysteresis Model and Control Methodology for Force Output Using Piezoelectric Actuator Driving. IEEE Access 2020, 8, 205136–205147. [Google Scholar] [CrossRef]
- Chi, Z.; Xu, Q. Recent Advances in the Control of Piezoelectric Actuators. Int. J. Adv. Robot. Syst. 2014, 11, 182. [Google Scholar] [CrossRef]
- Yang, Y. Piezoelectric Actuators Application and Hysteresis Modelling: A Brief Survey. Open Access Libr. J. 2023, 10, e10482. [Google Scholar] [CrossRef]
- Hassani, V.; Tjahjowidodo, T.; Do, T.N. A survey on hysteresis modeling, identification and control. Mech. Syst. Signal Process. 2014, 49, 209–233. [Google Scholar] [CrossRef]
- Goldfarb, M.; Celanovic, N. Modeling piezoelectric stack actuators for control of micromanipulation. IEEE Control Syst. 1997, 17, 69–79. [Google Scholar] [CrossRef]
- Adriaens, H.J.M.T.S.; De Koning, W.L.; Banning, R. Modeling piezoelectric actuators. IEEE/ASME Trans. Mechatron. 2000, 5, 331–341. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, D.; Yu, C.W. Dynamic modeling of a novel workpiece table for active surface grinding control. Int. J. Mach. Tools Manuf. 2001, 41, 609–624. [Google Scholar] [CrossRef]
- Bazghaleh, M.; Grainger, S.; Mohammadzaheri, M. A review of charge methods for driving piezoelectric actuators. J. Intell. Mater. Syst. Struct. 2018, 29, 2096–2104. [Google Scholar] [CrossRef]
- Moheimani, S.O.R. Invited Review Article: Accurate and fast nanopositioning with piezoelectric tube scanners: Emerging trends and future challenges. Rev. Sci. Instrum. 2008, 79, 071101. [Google Scholar] [CrossRef]
- Minase, J.; Lu, T.-F.; Cazzolato, B.; Grainger, S. A review, supported by experimental results, of voltage, charge and capacitor insertion method for driving piezoelectric actuators. Precis. Eng. 2010, 34, 692–700. [Google Scholar] [CrossRef]
- Ma, Y.T.; Huang, L.; Shao, W.W. New Open Loop Control Improves Linearity of Piezoelectric Actuators. Adv. Mater. Res. 2011, 211–212, 520–524. [Google Scholar] [CrossRef]
- Ru, C.; Chen, L.; Shao, B.; Rong, W.; Sun, L. A new amplifier for improving piezoelectric actuator linearity based on current switching in precision positioning. Meas. Sci. Technol. 2008, 19, 015203. [Google Scholar] [CrossRef]
- Špiller, M.; Hurák, Z. Hybrid charge control for stick–slip piezoelectric actuators. Mechatronics 2011, 21, 100–108. [Google Scholar] [CrossRef]
- Moheimani, S.O.R.; Vautier, B.J.G. Resonant control of structural vibration using charge-driven piezoelectric actuators. IEEE Trans. Control Syst. Technol. 2005, 13, 1021–1035. [Google Scholar] [CrossRef]
- Fleming, A.J.; Moheimani, S.O.R. A grounded-load charge amplifier for reducing hysteresis in piezoelectric tube scanners. Rev. Sci. Instrum. 2005, 76, 073707. [Google Scholar] [CrossRef]
- Fleming, A.J. Quantitative scanning probe microscope topographies by charge linearization of the vertical actuator. Rev. Sci. Instrum. 2010, 81, 103701. [Google Scholar] [CrossRef]
- Rios, S.A.; Fleming, A.J. Design of a Charge Drive for Reducing Hysteresis in a Piezoelectric Bimorph Actuator. IEEE/ASME Trans. Mechatron. 2016, 21, 51–54. [Google Scholar] [CrossRef]
- Yi, K.A.; Veillette, R.J. A charge controller for linear operation of a piezoelectric stack actuator. IEEE Trans. Control Syst. Technol. 2005, 13, 517–526. [Google Scholar] [CrossRef]
- Yang, C.; Li, C.; Zhao, J. A Nonlinear Charge Controller With Tunable Precision for Highly Linear Operation of Piezoelectric Stack Actuators. IEEE Trans. Ind. Electron. 2017, 64, 8618–8625. [Google Scholar] [CrossRef]
- Yang, C.; Li, C.; Xia, F.; Zhu, Y.; Zhao, J.; Youcef-Toumi, K. Charge Controller With Decoupled and Self-Compensating Configurations for Linear Operation of Piezoelectric Actuators in a Wide Bandwidth. IEEE Trans. Ind. Electron. 2019, 66, 5392–5402. [Google Scholar] [CrossRef]
- Jin, T.; Peng, Y.; Xing, Z.; Lei, L. A Charge Controller for Synchronous Linear Operation of Multiple Piezoelectric Actuators. IEEE Access 2019, 7, 90741–90749. [Google Scholar] [CrossRef]
- Bazghaleh, M.; Grainger, S.; Mohammadzaheri, M.; Cazzolato, B.; Lu, T.-F. A digital charge amplifier for hysteresis elimination in piezoelectric actuators. Smart Mater. Struct. 2013, 22, 075016. [Google Scholar] [CrossRef]
- Bazghaleh, M.; Grainger, S.; Cazzolato, B.; Lu, T.-F.; Oskouei, R. Implementation and analysis of an innovative digital charge amplifier for hysteresis reduction in piezoelectric stack actuators. Rev. Sci. Instrum. 2014, 85, 045005. [Google Scholar] [CrossRef]
- Zhong, J.; Nishida, R.; Shinshi, T. A digital charge control strategy for reducing the hysteresis in piezoelectric actuators: Analysis, design, and implementation. Precis. Eng. 2021, 67, 370–382. [Google Scholar] [CrossRef]
- Yang, C.; Xia, F.; Wang, Y.; Youcef-Toumi, K. Comprehensive study of charge-based motion control for piezoelectric nanopositioners: Modeling, instrumentation and controller design. Mech. Syst. Signal Process. 2022, 166, 108477. [Google Scholar] [CrossRef]
- Gu, G.-Y.; Zhu, L.-M.; Su, C.-Y.; Ding, H. Motion Control of Piezoelectric Positioning Stages: Modeling, Controller Design, and Experimental Evaluation. IEEE/ASME Trans. Mechatron. 2013, 18, 1459–1471. [Google Scholar] [CrossRef]
- Takács, J. A phenomenological mathematical model of hysteresis. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2001, 20, 1002–1015. [Google Scholar] [CrossRef]
- Mielke, A.; Theil, F. On rate-independent hysteresis models. Nonlinear Differ. Equ. Appl. 2004, 11, 151–189. [Google Scholar] [CrossRef]
- Al Janaideh, M.; Rakheja, S.; Su, C.-Y. Experimental characterization and modeling of rate-dependent hysteresis of a piezoceramic actuator. Mechatronics 2009, 19, 656–670. [Google Scholar] [CrossRef]
- Ma, F.; Zhang, H.; Bockstedte, A.; Foliente, G.C.; Paevere, P. Parameter Analysis of the Differential Model of Hysteresis. J. Appl. Mech. 2004, 71, 342–349. [Google Scholar] [CrossRef]
- Jiang, C.; Deng, M.; Hayakawa, Y. Operator-based parallel compensation control for hysteresis using ELM-based stop-type PI model. In Proceedings of the 2012 IEEE International Conference on Mechatronics and Automation, Chengdu, China, 5–8 August 2012; pp. 2054–2058. [Google Scholar] [CrossRef]
- Jiles, D.C.; Atherton, D.L. Theory of ferromagnetic hysteresis. J. Magn. Magn. Mater. 1986, 61, 48–60. [Google Scholar] [CrossRef]
- Cao, S.; Wang, B.; Yan, R.; Huang, W.; Yang, Q. Optimization of Hysteresis Parameters for the Jiles-Atherton Model Using a Genetic Algorithm. IEEE Trans. Appl. Supercond. 2004, 14, 1157–1160. [Google Scholar] [CrossRef]
- Smith, R.C.; Ounaies, Z. A Domain Wall Model for Hysteresis in Piezoelectric Materials. J. Intell. Mater. Syst. Struct. 2000, 11, 62–79. [Google Scholar] [CrossRef]
- Massad, J.E.; Smith, R.C. A Domain Wall Model for Hysteresis in Ferroelastic Materials. J. Intell. Mater. Syst. Struct. 2003, 14, 455–471. [Google Scholar] [CrossRef]
- Oh, J.H.; Bernstein, D.S. Semilinear Duhem model for rate-independent and rate-dependent hysteresis. IEEE Trans. Autom. Control 2005, 50, 631–645. [Google Scholar] [CrossRef]
- Lin, C.-J.; Lin, P.-T. Tracking control of a biaxial piezo-actuated positioning stage using generalized Duhem model. Comput. Math. Appl. 2012, 64, 766–787. [Google Scholar] [CrossRef]
- Xie, W.-F.; Fu, J.; Yao, H.; Su, C.-Y. Observer based control of piezoelectric actuators with classical Duhem modeled hysteresis. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 4221–4226. [Google Scholar] [CrossRef]
- D’souza, R.D.; Benny, B.; Sequeira, A.; Karanth, N. Hysteresis Modeling of Amplified Piezoelectric Stack Actuator for the Control of the Microgripper. Am. Sci. Res. J. Eng. Technol. Sci. (ASRJETS) 2016, 15, 265–281. [Google Scholar]
- Xuehui, G.; Bo, S. Identification for Bouc-Wen hysteresis system with hopfield neural network. In Proceedings of the 2017 9th International Conference on Modelling, Identification and Control (ICMIC), Kunming, China, 10–12 July 2017; pp. 248–253. [Google Scholar] [CrossRef]
- Mohith, S.; Rao, M.; Navin Karanth, P.; Kulkarni, S.M.; Upadhya, A.R. Development and assessment of large stroke piezo-hydraulic actuator for micro positioning applications. Precis. Eng. 2021, 67, 324–338. [Google Scholar] [CrossRef]
- Ren, B.; San, P.P.; Ge, S.S.; Lee, T.H. Adaptive dynamic surface control for a class of strict-feedback nonlinear systems with unknown backlash-like hysteresis. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 4482–4487. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, C.; Zhang, Y. Adaptive Backstepping Control of a Class of Uncertain Nonlinear Systems With Unknown Backlash-Like Hysteresis. IEEE Trans. Autom. Control 2004, 49, 1751–1757. [Google Scholar] [CrossRef]
- Song, G.; Zhao, J.; Zhou, X.; de Abreu-Garcia, J. Tracking Control of a Piezoceramic Actuator With Hysteresis Compensation Using Inverse Preisach Model. IEEE/ASME Trans. Mechatron. 2005, 10, 198–209. [Google Scholar] [CrossRef]
- Viswamurthy, S.; Ganguli, R. Modeling and compensation of piezoceramic actuator hysteresis for helicopter vibration control. Sens. Actuators A Phys. 2007, 135, 801–810. [Google Scholar] [CrossRef]
- Iyer, R.V.; Tan, X. Control of hysteretic systems through inverse compensation: Algorithms, adaptation, and embedded implementation. IEEE Control Syst. 2009, 29, 83–99. [Google Scholar] [CrossRef]
- Nguyen, P.-B.; Choi, S.-B.; Song, B.-K. A new approach to hysteresis modelling for a piezoelectric actuator using Preisach model and recursive method with an application to open-loop position tracking control. Sens. Actuators A Phys. 2018, 270, 136–152. [Google Scholar] [CrossRef]
- Al Janaideh, M.; Rakheja, S.; Su, C.-Y. A generalized Prandtl–Ishlinskii model for characterizing the hysteresis and saturation nonlinearities of smart actuators. Smart Mater. Struct. 2009, 18, 045001. [Google Scholar] [CrossRef]
- Chen, Y.; Qiu, J.; Palacios, J.; Smith, E.C. Tracking control of piezoelectric stack actuator using modified Prandtl–Ishlinskii model. J. Intell. Mater. Syst. Struct. 2013, 24, 753–760. [Google Scholar] [CrossRef]
- Gu, G.-Y.; Zhu, L.-M.; Su, C.-Y. Modeling and Compensation of Asymmetric Hysteresis Nonlinearity for Piezoceramic Actuators With a Modified Prandtl–Ishlinskii Model. IEEE Trans. Ind. Electron. 2014, 61, 1583–1595. [Google Scholar] [CrossRef]
- Al Janaideh, M.; Su, C.-Y.; Rakheja, S. Development of the rate-dependent Prandtl–Ishlinskii model for smart actuators. Smart Mater. Struct. 2008, 17, 035026. [Google Scholar] [CrossRef]
- Banks, H.T.; Kurdila, A.J.; Webb, G. Identification of hysteretic control influence operators representing smart actuators part I: Formulation. Math. Probl. Eng. 1997, 3, 287–328. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, X. Model order reduction for the Krasnoselskii–Pokrovskii (KP) model. Smart Mater. Struct. 2019, 28, 095001. [Google Scholar] [CrossRef]
- Vo-Minh, T.; Tjahjowidodo, T.; Ramon, H.; Van Brussel, H. A New Approach to Modeling Hysteresis in a Pneumatic Artificial Muscle Using The Maxwell-Slip Model. IEEE/ASME Trans. Mechatron. 2011, 16, 177–186. [Google Scholar] [CrossRef]
- Miri, N.; Mohammadzaheri, M.; Chen, L. A comparative study of different physics-based approaches to modelling of piezoelectric actuators. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Wollongong, NSW, Australia, 9–12 July 2013; pp. 1211–1216. [Google Scholar] [CrossRef]
- Liu, Y.; Du, D.; Qi, N.; Zhao, J. A Distributed Parameter Maxwell-Slip Model for the Hysteresis in Piezoelectric Actuators. IEEE Trans. Ind. Electron. 2019, 66, 7150–7158. [Google Scholar] [CrossRef]
- Yeh, T.-J.; Lu, S.-W.; Wu, T.-Y. Modeling and Identification of Hysteresis in Piezoelectric Actuators. J. Dyn. Syst. Meas. Control 2006, 128, 189–196. [Google Scholar] [CrossRef]
- Hegewald, T.; Kaltenbacher, B.; Kaltenbacher, M.; Lerch, R. Efficient Modeling of Ferroelectric Behavior for the Analysis of Piezoceramic Actuators. J. Intell. Mater. Syst. Struct. 2008, 19, 1117–1129. [Google Scholar] [CrossRef]
- Deng, L.; Tan, Y. Diagonal recurrent neural network with modified backlash operators for modeling of rate-dependent hysteresis in piezoelectric actuators. Sens. Actuators A Phys. 2008, 148, 259–270. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, J. Research on Hysteresis of Piezoceramic Actuator Based on the Duhem Model. Sci. World J. 2013, 2013, 814919. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Shan, J.; Gabbert, U.; Qi, N. Hysteresis and creep modeling and compensation for a piezoelectric actuator using a fractional-order Maxwell resistive capacitor approach. Smart Mater. Struct. 2013, 22, 115020. [Google Scholar] [CrossRef]
- Zsurzsan, T.-G.; Andersen, M.A.; Zhang, Z.; Andersen, N.A. Preisach model of hysteresis for the Piezoelectric Actuator Drive. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 002788–002793. [Google Scholar] [CrossRef]
- Gan, J.; Zhang, X.; Wu, H. A generalized Prandtl-Ishlinskii model for characterizing the rate-independent and rate-dependent hysteresis of piezoelectric actuators. Rev. Sci. Instrum. 2016, 87, 035002. [Google Scholar] [CrossRef]
- Wang, G.; Chen, G. Identification of piezoelectric hysteresis by a novel Duhem model based neural network. Sens. Actuators A Phys. 2017, 264, 282–288. [Google Scholar] [CrossRef]
- Qin, Y.; Zhao, X.; Zhou, L. Modeling and Identification of the Rate-Dependent Hysteresis of Piezoelectric Actuator Using a Modified Prandtl-Ishlinskii Model. Micromachines 2017, 8, 114. [Google Scholar] [CrossRef]
- Gan, J.; Zhang, X. An enhanced Bouc-Wen model for characterizing rate-dependent hysteresis of piezoelectric actuators. Rev. Sci. Instrum. 2018, 89, 115002. [Google Scholar] [CrossRef]
- Luo, Y.; Qu, Y.; Zhang, Y.; Xu, M.; Xie, S.; Zhang, X. Hysteretic modeling and simulation of a bilateral piezoelectric stack actuator based on Preisach model. Int. J. Appl. Electromagn. Mech. 2019, 59, 271–280. [Google Scholar] [CrossRef]
- Li, Z.; Shan, J.; Gabbert, U. Inverse Compensation of Hysteresis Using Krasnoselskii-Pokrovskii Model. IEEE/ASME Trans. Mechatron. 2018, 23, 966–971. [Google Scholar] [CrossRef]
- Gan, J.; Mei, Z.; Chen, X.; Zhou, Y.; Ge, M.-F. A Modified Duhem Model for Rate-Dependent Hysteresis Behaviors. Micromachines 2019, 10, 680. [Google Scholar] [CrossRef]
- Gan, J.; Zhang, X. Nonlinear Hysteresis Modeling of Piezoelectric Actuators Using a Generalized Bouc–Wen Model. Micromachines 2019, 10, 183. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Huang, Q.; Wang, H.; Qiu, J. Hysteresis modeling and tracking control for piezoelectric stack actuators using neural-Preisach model. Int. J. Appl. Electromagn. Mech. 2019, 61, 445–459. [Google Scholar] [CrossRef]
- Li, Y.; Feng, Y.; Feng, J.; Liu, Y. Parameter Identification Based on PSO Algorithm for Piezoelectric Actuating System with Rate-dependent Prandtl-Ishlinskii Hysteresis Modeling Method. In Proceedings of the 2019 IEEE 4th International Conference on Advanced Robotics and Mechatronics (ICARM), Toyonaka, Japan, 3–5 July 2019; pp. 36–41. [Google Scholar] [CrossRef]
- Pan, W.; Xu, R.; Zhou, M. Modeling of Hysteresis for Piezo-driven Stages using a Rate-dependent Krasnosel’skii-Pokrovskii Model. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 1604–1609. [Google Scholar] [CrossRef]
- Liu, D.; Fang, Y.; Wang, H. Intelligent Rate-Dependent Hysteresis Control Compensator Design With Bouc-Wen Model Based on RMSO for Piezoelectric Actuator. IEEE Access 2020, 8, 63993–64001. [Google Scholar] [CrossRef]
- Liu, L.; Yun, H.; Li, Q.; Ma, X.; Chen, S.-L.; Shen, J. Fractional Order Based Modeling and Identification of Coupled Creep and Hysteresis Effects in Piezoelectric Actuators. IEEE/ASME Trans. Mechatron. 2020, 25, 1036–1044. [Google Scholar] [CrossRef]
- Dong, R.; Tan, Y. A modified Prandtl–Ishlinskii modeling method for hysteresis. Phys. B Condens. Matter 2009, 404, 1336–1342. [Google Scholar] [CrossRef]
- Jiang, H.; Ji, H.; Qiu, J.; Chen, Y. A modified prandtl-ishlinskii model for modeling asymmetric hysteresis of piezoelectric actuators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 1200–1210. [Google Scholar] [CrossRef]
- Wang, X.; Pommier-Budinger, V.; Gourinat, Y.; Reysset, A. A modified Preisach model for hysteresis in piezoelectric actuators. In Proceedings of the 2013 IEEE 11th International Workshop of Electronics, Control, Measurement, Signals and their application to Mechatronics, Toulouse, France, 24–26 June 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Song, X.; Duggen, L.; Lassen, B.; Mangeot, C. Modeling and identification of hysteresis with modified Preisach model in piezoelectric actuator. In Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017; pp. 1538–1543. [Google Scholar] [CrossRef]
- Lin, F.-J.; Shieh, H.-J.; Huang, P.-K. Adaptive Wavelet Neural Network Control With Hysteresis Estimation for Piezo-Positioning Mechanism. IEEE Trans. Neural Netw. 2006, 17, 432–444. [Google Scholar] [CrossRef]
- Zhao, X.; Tan, Y. Neural network based identification of Preisach-type hysteresis in piezoelectric actuator using hysteretic operator. Sens. Actuators A Phys. 2006, 126, 306–311. [Google Scholar] [CrossRef]
- Li, P.; Yan, F.; Ge, C.; Zhang, M. Ultra-precise tracking control of piezoelectric actuators via a fuzzy hysteresis model. Rev. Sci. Instrum. 2012, 83, 085114. [Google Scholar] [CrossRef]
- Li, P.; Yan, F.; Ge, C.; Wang, X.; Xu, L.; Guo, J.; Li, P. A simple fuzzy system for modelling of both rate-independent and rate-dependent hysteresis in piezoelectric actuators. Mech. Syst. Signal Process. 2013, 36, 182–192. [Google Scholar] [CrossRef]
- Xu, Q.; Wong, P.-K. Hysteresis modeling and compensation of a piezostage using least squares support vector machines. Mechatronics 2011, 21, 1239–1251. [Google Scholar] [CrossRef]
- Wong, P.-K.; Xu, Q.; Vong, C.-M.; Wong, H.-C. Rate-Dependent Hysteresis Modeling and Control of a Piezostage Using Online Support Vector Machine and Relevance Vector Machine. IEEE Trans. Ind. Electron. 2012, 59, 1988–2001. [Google Scholar] [CrossRef]
- Zhou, C.; Feng, C.; Aye, Y.N.; Ang, W.T. A Digitized Representation of the Modified Prandtl–Ishlinskii Hysteresis Model for Modeling and Compensating Piezoelectric Actuator Hysteresis. Micromachines 2021, 12, 942. [Google Scholar] [CrossRef] [PubMed]
- Shan, X.; Song, H.; Cao, H.; Zhang, L.; Zhao, X.; Fan, J. A Dynamic Hysteresis Model and Nonlinear Control System for a Structure-Integrated Piezoelectric Sensor-Actuator. Sensors 2021, 21, 269. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, K.; Yan, P.; Li, S. Duhem Model-Based Hysteresis Identification in Piezo-Actuated Nano-Stage Using Modified Particle Swarm Optimization. Micromachines 2021, 12, 315. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.; Yuan, M.; Feng, C.; Ang, W.T. A Modified Prandtl–Ishlinskii Hysteresis Model for Modeling and Compensating Asymmetric Hysteresis of Piezo-Actuated Flexure-Based Systems. Sensors 2022, 22, 8763. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, J.; Xu, M.; Chen, G. Hysteresis Characteristics and MPI Compensation of Two-Dimensional Piezoelectric Positioning Stage. Micromachines 2022, 13, 321. [Google Scholar] [CrossRef]
- Baziyad, A.G.; Ahmad, I.; Bin Salamah, Y. Precision Motion Control of a Piezoelectric Actuator via a Modified Preisach Hysteresis Model and Two-Degree-of-Freedom H-Infinity Robust Control. Micromachines 2023, 14, 1208. [Google Scholar] [CrossRef]
- Lu, J.; Wang, J.; Bo, Y.; Zhang, X. Hysteresis Modeling and Compensation for a Fast Piezo-Driven Scanner in the UAV Image Stabilization System. Drones 2023, 7, 392. [Google Scholar] [CrossRef]
- Rakotondrabe, M.; Clévy, C.; Lutz, P. Complete Open Loop Control of Hysteretic, Creeped, and Oscillating Piezoelectric Cantilevers. IEEE Trans. Autom. Sci. Eng. 2010, 7, 440–450. [Google Scholar] [CrossRef]
- Islam, M.S.; Beamish, J. Piezoelectric creep in LiNbO3, PMN-PT and PZT-5A at low temperatures. J. Appl. Phys. 2019, 126, 204101. [Google Scholar] [CrossRef]
- Jung, H.; Gweon, D.-G. Creep characteristics of piezoelectric actuators. Rev. Sci. Instrum. 2000, 71, 1896–1900. [Google Scholar] [CrossRef]
- Georgiou, H.M.S.; Ben Mrad, R. Dynamic electromechanical drift model for PZT. Mechatronics 2008, 18, 81–89. [Google Scholar] [CrossRef]
- Rakotondrabe, M. Modeling and compensation of multivariable creep in multi-DOF piezoelectric actuators. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 4577–4581. [Google Scholar] [CrossRef]
- He, X.; Wang, D.; Wang, L.; Melnik, R. Modelling of creep hysteresis in ferroelectrics. Philos. Mag. 2018, 98, 1256–1271. [Google Scholar] [CrossRef]
- Croft, D.; Shed, G.; Devasia, S. Creep, Hysteresis, and Vibration Compensation for Piezoactuators: Atomic Force Microscopy Application. J. Dyn. Syst. Meas. Control 2001, 123, 35–43. [Google Scholar] [CrossRef]
- Wang, X.; Budinger, V.; Gourinat, Y. A Specific Methodology of Creep Compensation for Piezoelectric Actuators by Open-Loop Control. Appl. Mech. Mater. 2013, 281, 141–145. [Google Scholar] [CrossRef]
- Liu, Y.; Shan, J.; Qi, N. Creep modeling and identification for piezoelectric actuators based on fractional-order system. Mechatronics 2013, 23, 840–847. [Google Scholar] [CrossRef]
- Changhai, R.; Lining, S. Hysteresis and creep compensation for piezoelectric actuator in open-loop operation. Sens. Actuators A Phys. 2005, 122, 124–130. [Google Scholar] [CrossRef]
- Devasia, S.; Eleftheriou, E.; Moheimani, S.O.R. A Survey of Control Issues in Nanopositioning. IEEE Trans. Control Syst. Technol. 2007, 15, 802–823. [Google Scholar] [CrossRef]
- Gharieb, W. Creep compensation in piezoelectric actuators for nanopositioning technology. Int. J. Nanomanuf. 2009, 4, 267–273. [Google Scholar] [CrossRef]
- Liu, Y.F.; Li, J.; Hu, X.H.; Zhang, Z.M.; Cheng, L.; Lin, Y.; Zhang, W.J. Modeling and control of piezoelectric inertia–friction actuators: Review and future research directions. Mech. Sci. 2015, 6, 95–107. [Google Scholar] [CrossRef]
- Ang, W.T.; Khosla, P.K.; Riviere, C.N. Feedforward Controller With Inverse Rate-Dependent Model for Piezoelectric Actuators in Trajectory-Tracking Applications. IEEE/ASME Trans. Mechatron. 2007, 12, 134–142. [Google Scholar] [CrossRef]
- Lin, C.J.; Chen, S.Y. Evolutionary algorithm based feedforward control for contouring of a biaxial piezo-actuated stage. Mechatronics 2009, 19, 829–839. [Google Scholar] [CrossRef]
- Leang, K.K.; Zou, Q.; Devasia, S. Feedforward control of piezoactuators in atomic force microscope systems: Inversion-based compensation for dynamics and hysteresis. IEEE Control Syst. 2009, 29, 70–82. [Google Scholar] [CrossRef]
- Xiao, S.; Li, Y. Modeling and High Dynamic Compensating the Rate-Dependent Hysteresis of Piezoelectric Actuators via a Novel Modified Inverse Preisach Model. IEEE Trans. Control Syst. Technol. 2013, 21, 1549–1557. [Google Scholar] [CrossRef]
- Rakotondrabe, M. Bouc–Wen Modeling and Inverse Multiplicative Structure to Compensate Hysteresis Nonlinearity in Piezoelectric Actuators. IEEE Trans. Autom. Sci. Eng. 2011, 8, 428–431. [Google Scholar] [CrossRef]
- Feng, Y.; Rabbath, C.A.; Su, C.-Y. Inverse Duhem Model Based Robust Adaptive Control for Flap Positioning System with SMA actuators. IFAC Proc. Vol. 2011, 44, 8126–8131. [Google Scholar] [CrossRef]
- Gu, G.-Y.; Zhu, L.-M. Motion control of piezoceramic actuators with creep, hysteresis and vibration compensation. Sens. Actuators A Phys. 2013, 197, 76–87. [Google Scholar] [CrossRef]
- Gu, G.-Y.; Yang, M.-J.; Zhu, L.-M. Real-time inverse hysteresis compensation of piezoelectric actuators with a modified Prandtl-Ishlinskii model. Rev. Sci. Instrum. 2012, 83, 065106. [Google Scholar] [CrossRef]
- Rahman, M.A.; Al Mamun, A.; Yao, K. Rate dependent direct inverse hysteresis compensation of piezoelectric micro-actuator used in dual-stage hard disk drive head positioning system. Rev. Sci. Instrum. 2015, 86, 085002. [Google Scholar] [CrossRef]
- Wang, D.; Yu, P.; Wang, F.; Chan, H.-Y.; Zhou, L.; Dong, Z.; Liu, L.; Li, W.J. Improving Atomic Force Microscopy Imaging by a Direct Inverse Asymmetric PI Hysteresis Model. Sensors 2015, 15, 3409–3425. [Google Scholar] [CrossRef]
- Yu, G.-R.; You, C.-S.; Hong, R.-J. Self-Tuning Fuzzy Control of a Piezoelectric Actuator System. In Proceedings of the 2006 IEEE International Conference on Systems, Man and Cybernetics, Taipei, Taiwan, 8–11 October 2006; pp. 1108–1113. [Google Scholar] [CrossRef]
- Lin, C.-J.; Yang, S.-R. Precise positioning of piezo-actuated stages using hysteresis-observer based control. Mechatronics 2006, 16, 417–426. [Google Scholar] [CrossRef]
- Sun, F.; Qi, S.; Bao, J.; Xu, F.; Zhao, W. Design and PID Control of Piezoelectric Micro-motion Stage. In Proceedings of the 2018 IEEE International Conference on Intelligence and Safety for Robotics (ISR), Shenyang, China, 24–27 August 2018; pp. 110–115. [Google Scholar] [CrossRef]
- Bruno, N.; Zhu, Y.; Liu, C.; Gao, Q.; Li, Y. Development of a piezoelectric high speed on/off valve and its application to pneumatic closed-loop position control system. J. Mech. Sci. Technol. 2019, 33, 2747–2759. [Google Scholar] [CrossRef]
- Alexandrov, A.G.; Palenov, M.V. Adaptive PID controllers: State of the art and development prospects. Autom. Remote Control 2014, 75, 188–199. [Google Scholar] [CrossRef]
- Sharkawy, A.B. Genetic fuzzy self-tuning PID controllers for antilock braking systems. Eng. Appl. Artif. Intell. 2010, 23, 1041–1052. [Google Scholar] [CrossRef]
- Huba, M. Comparing 2DOF PI and predictive disturbance observer based filtered PI control. J. Process Control 2013, 23, 1379–1400. [Google Scholar] [CrossRef]
- Zheng, Q.; Goforth, F.J. A disturbance rejection based control approach for hysteretic systems. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 3748–3753. [Google Scholar] [CrossRef]
- Liang, Y.; Xu, S.; Hong, K.; Wang, G.; Zeng, T. Neural network modeling and single-neuron proportional–integral–derivative control for hysteresis in piezoelectric actuators. Meas. Control. 2019, 52, 1362–1370. [Google Scholar] [CrossRef]
- Chuang, N.; Petersen, I.R. Robust H∞ control of hysteresis in a piezoelectric stack actuator. IFAC Proc. Vol. 2008, 41, 1996–2001. [Google Scholar] [CrossRef]
- Soleymanzadeh, D.; Ghafarirad, H.; Zareinejad, M. Sensorless adaptive sliding mode position control for piezoelectric actuators with charge leakage. J. Intell. Mater. Syst. Struct. 2020, 31, 40–52. [Google Scholar] [CrossRef]
- Medhat, A.; Youssef, M. Optimized PID tracking controller for piezoelectric hysteretic actuator model. World J. Model. Simul. 2013, 9, 223–234. [Google Scholar]
- Wu, H.; Su, W.; Liu, Z. PID controllers: Design and tuning methods. In Proceedings of the 2014 9th IEEE Conference on Industrial Electronics and Applications, Hangzhou, China, 9–11 June 2014; pp. 808–813. [Google Scholar] [CrossRef]
- Rahman, N.U.; Alam, M.N. Active vibration control of a piezoelectric beam using PID controller: Experimental study. Lat. Am. J. Solids Struct. 2012, 9, 657–673. [Google Scholar] [CrossRef]
- Ding, B.; Li, Y.; Xiao, X.; Tang, Y. Optimized PID tracking control for piezoelectric actuators based on the Bouc-Wen model. In Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, 3–7 December 2016; pp. 1576–1581. [Google Scholar] [CrossRef]
- Wahid, N.; Hassan, N. Self-Tuning Fuzzy PID Controller Design for Aircraft Pitch Control. In Proceedings of the 2012 Third International Conference on Intelligent Systems Modelling and Simulation, Kota Kinabalu, Malaysia, 8–10 February 2012; pp. 19–24. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, G. Intelligent Vibration Control for High-Speed Spinning Beam Based on Fuzzy Self-Tuning PID Controller. Shock Vib. 2015, 2015, 617038. [Google Scholar] [CrossRef][Green Version]
- Bing, S.; Weibin, R.; Bin, G.; Changhai, R.; Lining, S. Modeling and control of a novel piezoelectric actuated precision fast positioning system. Smart Mater. Struct. 2008, 17, 025032. [Google Scholar] [CrossRef]
- Li, D.; Fu, Y.; Yang, L. Coupling dynamic modeling and simulation of three-degree-of-freedom micromanipulator based on piezoelectric ceramic of fuzzy PID. Mod. Phys. Lett. B 2017, 31, 1750140. [Google Scholar] [CrossRef]
- Rebai, A.; Guesmi, K.; Gozim, D.; Hemici, B. Design of an optimized fractional order fuzzy PID controller for a piezoelectric actuator. In Proceedings of the 2014 15th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Hammamet, Tunisia, 21–23 December 2014; pp. 456–461. [Google Scholar] [CrossRef]
- Haji, V.H.; Monje, C.A. Fractional order fuzzy-PID control of a combined cycle power plant using Particle Swarm Optimization algorithm with an improved dynamic parameters selection. Appl. Soft Comput. 2017, 58, 256–264. [Google Scholar] [CrossRef]
- Zamani, A.-A.; Tavakoli, S.; Etedali, S.; Sadeghi, J. Online tuning of fractional order fuzzy PID controller in smart seismic isolated structures. Bull. Earthq. Eng. 2018, 16, 3153–3170. [Google Scholar] [CrossRef]
- Birs, I.R.; Folea, S.; Muresan, C.I. An optimal fractional order controller for vibration attenuation. In Proceedings of the 2017 25th Mediterranean Conference on Control and Automation (MED), Valletta, Malta, 3–6 July 2017; pp. 828–832. [Google Scholar] [CrossRef]
- Yi, J.; Chang, S.; Shen, Y. Disturbance-Observer-Based Hysteresis Compensation for Piezoelectric Actuators. IEEE/ASME Trans. Mechatron. 2009, 14, 456–464. [Google Scholar] [CrossRef]
- Ishigami, Y.; Takahashi, S.; Kawajiri, T.; Ishimaru, I. Disturbance Feedback System with PID Control and Disturbance Observer for Spectroscopic Measurement Device. IFAC Proc. Vol. 2011, 44, 2448–2451. [Google Scholar] [CrossRef]
- Basha, S.M.; Swarup, A. Disturbance observer based fuzzy PID and robust PID autopilot design for bank-to-turn missile. In Proceedings of the 2017 8th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Delhi, India, 3–5 July 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Helfrich, B.E.; Lee, C.; Bristow, D.A.; Xiao, X.H.; Dong, J.; Alleyne, A.G.; Salapaka, S.M.; Ferreira, P.M. Combined H∞-feedback and eterative learning control design with application to nanopositioning systems. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 3893–3900. [Google Scholar] [CrossRef]
- Lee, G.; You, K.; Kang, T.; Yoon, K.J.; Lee, J.O.; Park, J.K. Modeling and Design of H-Infinity Controller for Piezoelectric Actuator LIPCA. J. Bionic Eng. 2010, 7, 168–174. [Google Scholar] [CrossRef]
- Chuang, N.; Petersen, I.R. Robust H∞ Control of Hysteresis in a Piezoelectric Stack Actuator1. J. Dyn. Syst. Meas. Control 2013, 135, 064501. [Google Scholar] [CrossRef]
- Xiao, S.; Li, Y. Dynamic compensation and H∞ control for piezoelectric actuators based on the inverse Bouc–Wen model. Robot. Comput. Manuf. 2014, 30, 47–54. [Google Scholar] [CrossRef]
- Jiaqiang, E.; Qian, C.; Liu, H.; Liu, G. Design of the H∞ robust control for the piezoelectric actuator based on chaos optimization algorithm. Aerosp. Sci. Technol. 2015, 47, 238–246. [Google Scholar] [CrossRef]
- Brahim, M.; Bahri, I.; Bernard, Y. Modeling and robust closed loop position controllers of Piezoelectric Actuator Drive (PAD). In Proceedings of the 2017 14th International Multi-Conference on Systems, Signals & Devices (SSD), Marrakech, Morocco, 28–31 March 2017; pp. 560–565. [Google Scholar] [CrossRef]
- Brahim, M.; Bernard, Y.; Bahri, I. Modelling, design, and real time implementation of robust H-infinity position control of piezoelectric actuator drive. Int. J. Mechatron. Autom. 2018, 6, 151. [Google Scholar] [CrossRef]
- Lan, X.; Liang, D.; Mao, C.; Li, A.; Wang, J. Design of Two-degree-of-freedom H∞ Controller for Three-dimensional Piezo-positioning System. In Proceedings of the 2019 IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 March 2019; pp. 1078–1082. [Google Scholar] [CrossRef]
- Shen, J.-C.; Jywe, W.-Y.; Chiang, H.-K.; Shu, Y.-L. Precision tracking control of a piezoelectric-actuated system. Precis. Eng. 2008, 32, 71–78. [Google Scholar] [CrossRef]
- Huang, S.; Tan, K.K.; Lee, T.H. Adaptive Sliding-Mode Control of Piezoelectric Actuators. IEEE Trans. Ind. Electron. 2009, 56, 3514–3522. [Google Scholar] [CrossRef]
- Wehr, M.; Stockert, S.; Ionescu, C.; Abel, D.; Hirt, G. Sliding Mode Control of Piezoelectric Stack Actuators for Roll Gap Adjustment in a Cold Rolling Mill. In Proceedings of the 2019 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Hong Kong, China, 8–12 July 2019; pp. 1207–1214. [Google Scholar] [CrossRef]
- Yu, Z.; Wu, Y.; Fang, Z.; Sun, H. Modeling and compensation of hysteresis in piezoelectric actuators. Heliyon 2020, 6, e03999. [Google Scholar] [CrossRef] [PubMed]
- Rakotondrabe, M.; Agnus, J.; Lutz, P. Feedforward and IMC-feedback control of a nonlinear 2-DOF piezoactuator dedicated to automated micropositioning tasks. In Proceedings of the 2011 IEEE International Conference on Automation Science and Engineering, Trieste, Italy, 24–27 August 2011; pp. 393–398. [Google Scholar] [CrossRef]
- Liu, Y.; Shan, J.; Gabbert, U. Feedback/feedforward control of hysteresis-compensated piezoelectric actuators for high-speed scanning applications. Smart Mater. Struct. 2015, 24, 015012. [Google Scholar] [CrossRef]
- Ko, P.-J.; Wang, Y.-P.; Tien, S.-C. Inverse-feedforward and robust-feedback control for high-speed operation on piezo-stages. Int. J. Control 2013, 86, 197–209. [Google Scholar] [CrossRef]
- Zhou, M.; Zhang, Q.; Wang, J. Feedforward-Feedback Hybrid Control for Magnetic Shape Memory Alloy Actuators Based on the Krasnosel’skii-Pokrovskii Model. PLoS ONE 2014, 9, e97086. [Google Scholar] [CrossRef]
- Chen, H.-Y.; Liang, J.-W. Hysteresis compensation of a piezoelectric-stack-actuator-driven (PSA-driven) system using inversion-based models and feedback control. J. Intell. Fuzzy Syst. 2018, 35, 3243–3253. [Google Scholar] [CrossRef]
- Li, Z.; Huang, N.; Zhong, Y.; Ma, G.; Liu, G.; Zhu, D. Feedback Feed-Forward Control of Piezoelectric Positioning Stages and Experimental Evaluation. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018; pp. 3758–3762. [Google Scholar] [CrossRef]
- Saleem, A.; Al Hattali, M.; Shafiq, M.; Bahadur, I. Tracking Control of Piezoelectric Actuators using Feedforward/Feedback Learning-based Controller. In Proceedings of the 2019 6th International Conference on Control, Decision and Information Technologies (CoDIT), Paris, France, 23–26 April 2019; pp. 1981–1985. [Google Scholar] [CrossRef]
- Chi, Z.; Jia, M.; Xu, Q. Fuzzy PID Feedback Control of Piezoelectric Actuator with Feedforward Compensation. Math. Probl. Eng. 2014, 2014, 107184. [Google Scholar] [CrossRef]
- Sousa, F.M.M.; Amarante, V.M.B.; Fonseca, R.R. Adaptive Fuzzy Feedforward-Feedback Controller Applied to Level Control in an Experimental Prototype. IFAC-PapersOnLine 2019, 52, 219–224. [Google Scholar] [CrossRef]
- Beijen, M.A.; Heertjes, M.F.; Butler, H.; Steinbuch, M. H ∞ feedback and feedforward controller design for active vibration isolators. IFAC-PapersOnLine 2017, 50, 13384–13389. [Google Scholar] [CrossRef]
- Ahamd, I.; Abdurraqeeb, A.M. H∞ control design with feed-forward compensator for hysteresis compensation in piezoelectric actuators. Automatika 2017, 57, 691–702. [Google Scholar] [CrossRef]
- Velasco, J.; Barambones, O.; Calvo, I.; Zubia, J.; de Ocariz, I.S.; Chouza, A. Sliding Mode Control with Dynamical Correction for Time-Delay Piezoelectric Actuator Systems. Materials 2020, 13, 132. [Google Scholar] [CrossRef] [PubMed]
- Leang, K.K.; Devasia, S. Feedback-Linearized Inverse Feedforward for Creep, Hysteresis, and Vibration Compensation in AFM Piezoactuators. IEEE Trans. Control Syst. Technol. 2007, 15, 927–935. [Google Scholar] [CrossRef]
- Napole, C.; Barambones, O.; Derbeli, M.; Calvo, I. Advanced Trajectory Control for Piezoelectric Actuators Based on Robust Control Combined with Artificial Neural Networks. Appl. Sci. 2021, 11, 7390. [Google Scholar] [CrossRef]
- Yu, S.; Feng, Y.; Yang, X. Extended state observer–based fractional order sliding-mode control of piezoelectric actuators. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2021, 235, 39–51. [Google Scholar] [CrossRef]
- Li, D.; Cao, H.; Chen, X. Fuzzy control of milling chatter with piezoelectric actuators embedded to the tool holder. Mech. Syst. Signal Process. 2021, 148, 107190. [Google Scholar] [CrossRef]
- Yu, S.; Xie, M.; Wu, H.; Ma, J.; Li, Y.; Gu, H. Composite proportional-integral sliding mode control with feedforward control for cell puncture mechanism with piezoelectric actuation. ISA Trans. 2022, 124, 427–435. [Google Scholar] [CrossRef]
- Shi, B.; Shi, R.; Wang, F. Design of an adaptive feedforward/feedback combined control for piezoelectric actuated micro positioning stage. Precis. Eng. 2022, 78, 199–205. [Google Scholar] [CrossRef]
- Xiong, Y.; Jia, W.; Zhang, L.; Zhao, Y.; Zheng, L. Feedforward Control of Piezoelectric Ceramic Actuators Based on PEA-RNN. Sensors 2022, 22, 5387. [Google Scholar] [CrossRef]
- Cheng, L.; Chen, W.; Tian, L.; Xie, Y. A Finite-Time Sliding-Mode Controller Based on the Disturbance Observer and Neural Network for Hysteretic Systems with Application in Piezoelectric Actuators. Sensors 2023, 23, 6246. [Google Scholar] [CrossRef] [PubMed]
- Napole, C.; Barambones, O.; Derbeli, M.; Calvo, I. Design and experimental validation of a piezoelectric actuator tracking control based on fuzzy logic and neural compensation. Fuzzy Sets Syst. 2023, 464, 108449. [Google Scholar] [CrossRef]









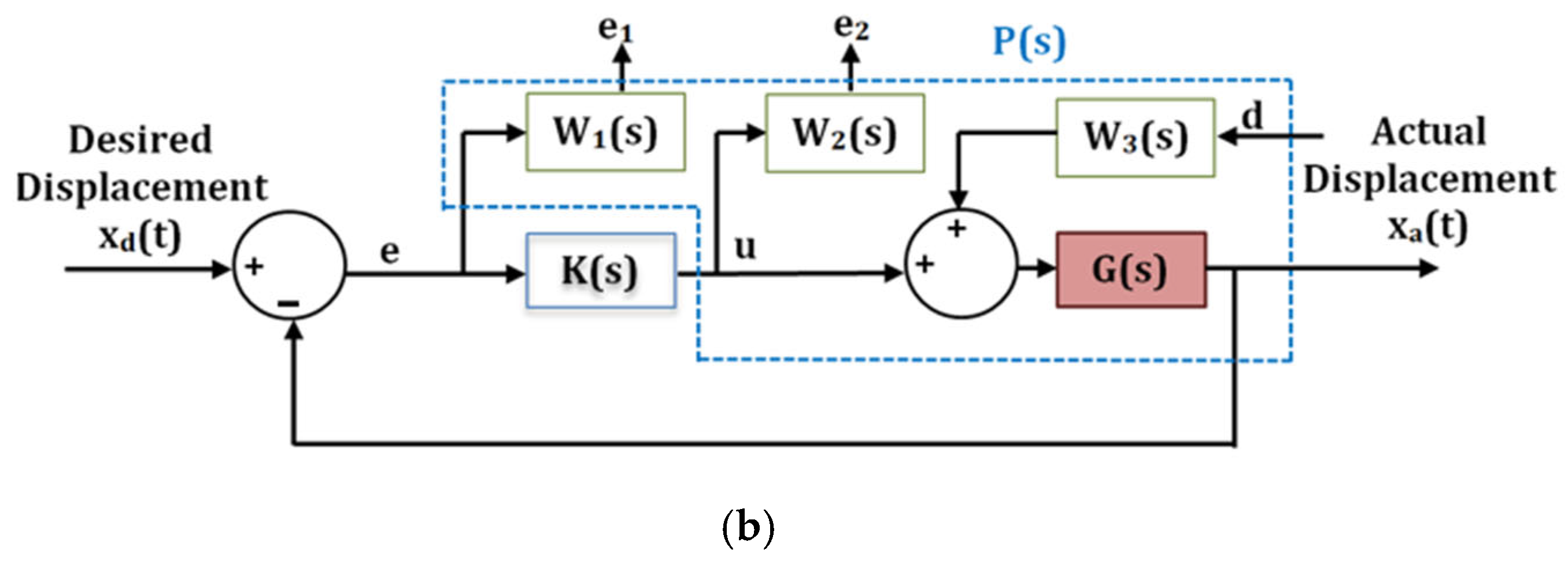

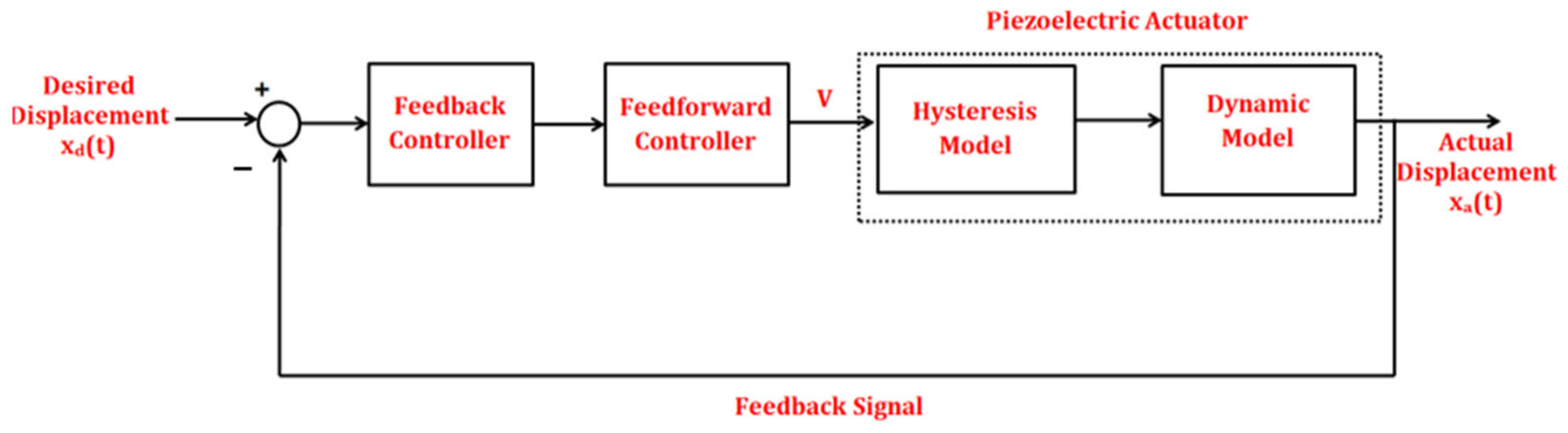
| Author | Year | Ref. No. | Type of Actuator | Method of Charge Control | Voltage (V) | Frequency (Hz) | Range of Motion (μm) | Approximate % Reduction in Hysteresis | Approximate % Reduction in Creep |
|---|---|---|---|---|---|---|---|---|---|
| J. Minase | 2010 | [68] | Piezo Stack | Capacitor Insertion | 100 | 10 | 2.25 | 99.59 | 99.87 |
| Y. T. Ma | 2011 | [69] | Piezo Stack | Capacitor Insertion | 5 | 5 | 5 | 94.36 | 77.00 |
| A. J. Fleming | 2005 | [73] | Piezo Tube | Capacitor based sensing | ±6 | 10 | ±3.00 | 89.00 | ---- |
| A. J. Fleming | 2010 | [74] | Piezo Stack | Capacitor based sensing | 150 | 100 | 7.8 | 95.35 | ---- |
| Shannon A. | 2015 | [75] | Bimorph | Capacitor based sensing | −50 to +200 | 15 | ±1250 | 92.00 | ---- |
| C. Yang | 2017 | [77] | Piezo Stack | Nonlinear Charge Controller | 100 | 2 | 6.50–7.00 | 88.00 | ---- |
| T. Jin | 2019 | [79] | Piezo Stack | Linear Charge Controller | 4.5 | 2 | 2.50–3.00 | 71.33 | ---- |
| T. Jin | 2019 | [79] | Piezo Stack | Nonlinear Charge Controller | 4.5 | 2 | 2.50–3.00 | 91.29 | ---- |
| M. Bazghaleh | 2014 | [81] | Piezo Stack | Digital Charge Amplification | 40 | 10 | 11.54 | 91.00 | ---- |
| J. Zhong | 2021 | [82] | Piezo Stack | Digital ChargeConrol | 120 | 1–1000 | ±2.00 | 99 | |
| Chen Yang | 2022 | [83] | Piezo Stack | Nonlinear Charge Controller | 50 | 10–400 | 3.3 | 97 |
| Author | Year | Ref. No. | Type of Actuator | Hysteresis Model | Observation |
|---|---|---|---|---|---|
| T. Hegewald | 2008 | [116] | Piezo Stack | Jiles–Atherton |
|
| L. Deng | 2008 | [117] | Piezo Positioning Stage | Backlash |
|
| M. Zhou | 2013 | [118] | Piezo Stack | Duhem |
|
| Y. Liu | 2013 | [119] | Piezo Positioning Stage | Maxwell–Slip |
|
| T.-G. Zsurzsan | 2015 | [120] | Piezo Motor | Preisach |
|
| J. Gan | 2016 | [121] | Preloaded Piezo Stack | Prandtl–Ishlinskii |
|
| G. Wang | 2017 | [122] | Amplified Piezo Stack | Duhem |
|
| Y. Qin | 2017 | [123] | Compliant Piezo Stage | Prandtl–Ishlinskii |
|
| J. Gan | 2018 | [124] | Compliant Piezo Stage | Bouc–Wen |
|
| Y. Luo | 2018 | [125] | Piezo Stack | Preisach |
|
| Z. Li | 2018 | [126] | Piezo Positioning Stage | Krasnoselskii–Pokrovskii |
|
| D. Gan | 2019 | [127] | Compliant Piezo Stage | Duhem |
|
| J. Gan | 2019 | [128] | Compliant Piezo Stage | Bouc–Wen |
|
| Y. Chen | 2019 | [129] | Piezo Stack | Preisach |
|
| Y. Li | 2019 | [130] | Piezo Stack | Prandtl–Ishlinskii |
|
| W. Pan | 2019 | [131] | Piezo Positioning Stage | Krasnoselskii–Pokrovskii |
|
| D. Liu | 2020 | [132] | Piezo Bimorph | Bouc–Wen |
|
| L. Liu | 2020 | [133] | Amplified Piezo Stack | Bouc–Wen |
|
| Hysteresis Model | Jiles–Atherton | Domain Wall | Duhem | Bouc–Wen | Backlash Type | Preisach | Prandtl–Ishlinskii | Krasnoselskii–Pokrovskii | Maxwell–Slip |
|---|---|---|---|---|---|---|---|---|---|
| Parameter | |||||||||
| Inverse Model | Easy | Easy | Difficult | Easy | Easy | Difficult | Easy | Difficult | Difficult |
| Rate-Independent | Yes | Yes | No | No | No | Yes | Yes | Yes | Yes |
| Rate-Dependent | No | No | Yes | Yes | Yes | No | No | No | No |
| Parameter Identification | Easy | Easy | Difficult | Easy | Easy | Difficult | Easy | Easy | Easy |
| Author | Year | Ref. No. | Control Method | Type of Actuator | Sensor Used in Control | Observation |
|---|---|---|---|---|---|---|
| W. T. Ang | 2007 | [164] | Feedforward | Piezo Stack | N/A |
|
| K. K. Leang | 2009 | [166] | Feedforward | Piezo Tube | N/A |
|
| G. Y. Gu | 2012 | [171] | Feedforward | Piezo Stack | N/A |
|
| D. Wang | 2015 | [173] | Feedforward | Piezo Tube | N/A |
|
| N. U. Rahman | 2012 | [187] | Feedback Classical PID | Piezo Cantilever | Piezo Strain Sensor |
|
| B. Ding | 2016 | [188] | Feedback Classical PID | Piezo Stack | Capacitive Sensor |
|
| S. Bing | 2008 | [191] | Feedback Self-Tuning Fuzzy PID | Piezo Positioning Stage | Laser Vibrometer |
|
| Dongjie Li | 2017 | [192] | Feedback Self-Tuning Fuzzy PID | Piezo Positioning Stage | - |
|
| I. R. Birs | 2017 | [196] | Feedback Fractional Order Fuzzy PID | Piezo Cantilever | Piezo Strain Sensor |
|
| J. Yi | 2009 | [197] | Feedback Disturbance Observer PID | Piezo Cantilever | Fiber Optic Sensor |
|
| N. Chuang | 2010 | [202] | Feedback H Infinity | Piezo Stack | Differential Probe |
|
| S. Xiao | 2014 | [203] | Feedback H Infinity | Piezo Stack | Capacitive Sensor |
|
| M. Brahim | 2018 | [206] | Feedback H Infinity | Rotary Piezo Motor | Torque Sensor |
|
| S. Huang | 2009 | [209] | Feedback Sliding Mode | Piezo Stack | LVDT |
|
| M. Wehr | 2019 | [210] | Feedforward Sliding Mode | Piezo Stack | N/A |
|
| Z. Yu | 2020 | [211] | Feedback Sliding Mode | Piezo Positioning Stage | Laser Sensor |
|
| H. Y. Chen | 2018 | [216] | Feedforward- Feedback | Piezo Stack | Load Cell |
|
| A. Saleem | 2019 | [218] | Feedforward- Feedback | Amplified Piezo Stack | Laser Sensor |
|
| I. Ahmad | 2016 | [222] | Feedforward- Feedback | Piezo Positioning Stage | N/A |
|
| C. Napole | 2021 | [225] | Feedforward With ANN | Piezo Stack | N/A |
|
| S. Yu | 2021 | [226] | Feedback Sliding-Mode Control | Piezo Positioning Platform | - |
|
| D. Li | 2021 | [227] | Feedback Fuzzy Controller | Piezo Stack | Laser Sensor |
|
| S. Yu | 2022 | [228] | Feedforward Control With Composite Proportional–Integral Sliding Mode Control | Piezo Stack | Laser Sensor |
|
| B. Shi | 2022 | [229] | Feedforward /Feedback | Amplified Piezo Stack | Capacitive Sensor |
|
| Y. Xiong | 2022 | [230] | Feedforward Control | Piezo Positioning Platform | N/A |
|
| L. Cheng | 2023 | [231] | Feedback Sliding Mode | Piezo Stack | Strain Gauge Sensor |
|
| C. Napole | 2023 | [232] | Feedforward /Feedback With Fuzzy Logic | Piezo Stack | Wheatstone Bridge |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanchan, M.; Santhya, M.; Bhat, R.; Naik, N. Application of Modeling and Control Approaches of Piezoelectric Actuators: A Review. Technologies 2023, 11, 155. https://doi.org/10.3390/technologies11060155
Kanchan M, Santhya M, Bhat R, Naik N. Application of Modeling and Control Approaches of Piezoelectric Actuators: A Review. Technologies. 2023; 11(6):155. https://doi.org/10.3390/technologies11060155
Chicago/Turabian StyleKanchan, Mithun, Mohith Santhya, Ritesh Bhat, and Nithesh Naik. 2023. "Application of Modeling and Control Approaches of Piezoelectric Actuators: A Review" Technologies 11, no. 6: 155. https://doi.org/10.3390/technologies11060155
APA StyleKanchan, M., Santhya, M., Bhat, R., & Naik, N. (2023). Application of Modeling and Control Approaches of Piezoelectric Actuators: A Review. Technologies, 11(6), 155. https://doi.org/10.3390/technologies11060155








