Assembly Strategy for Modular Components Using a Dual-Arm Space Robot with Flexible Appendages
Abstract
1. Introduction
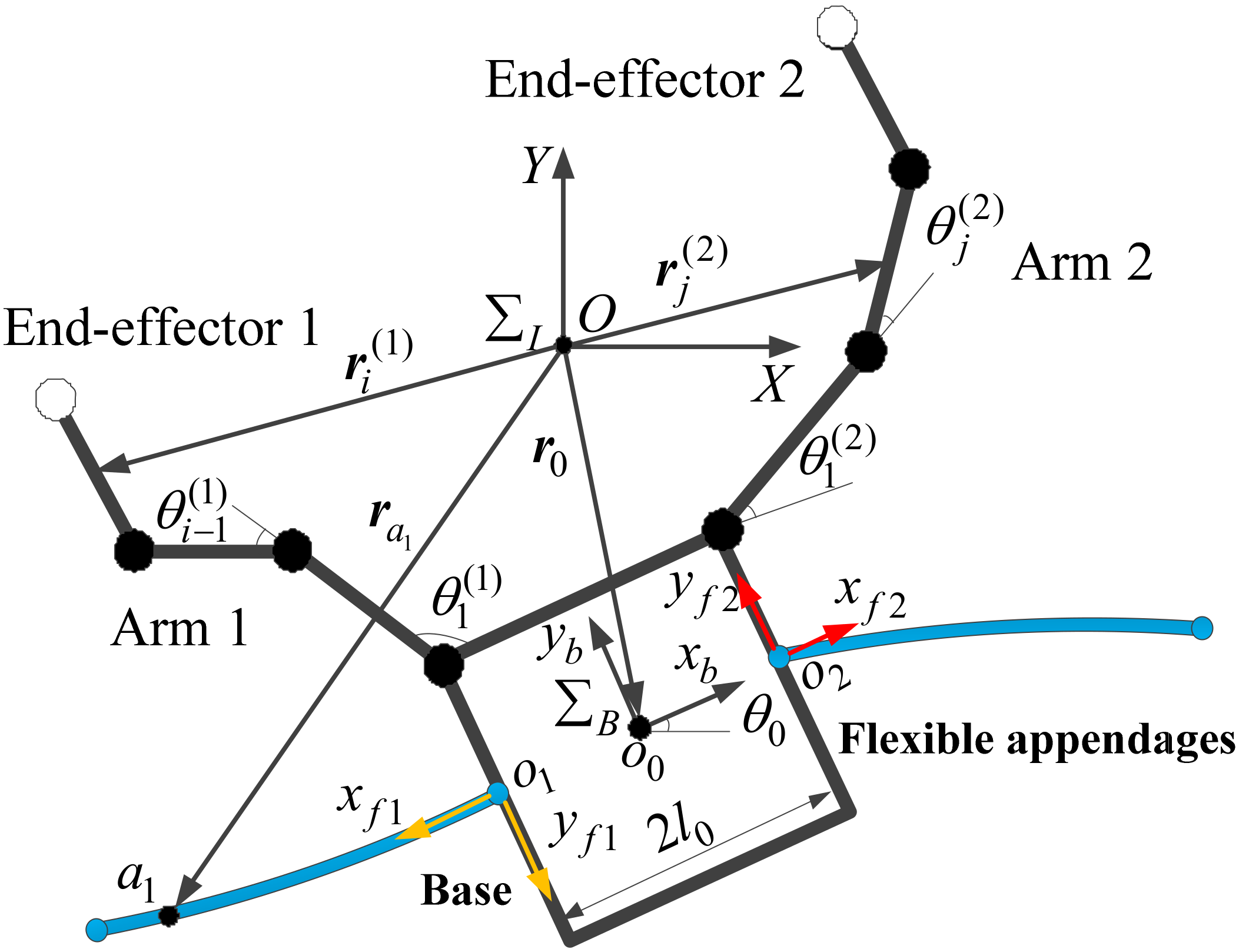
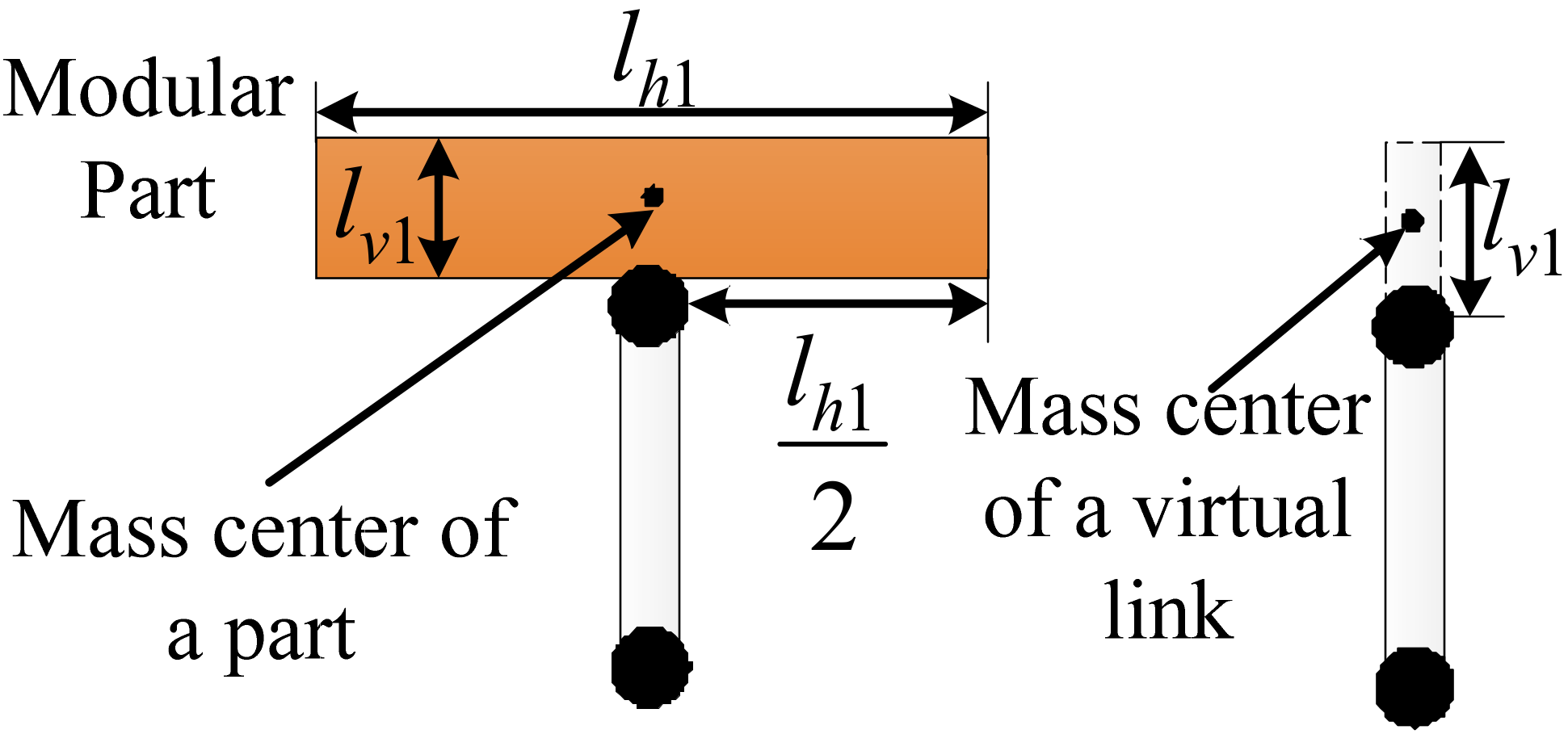
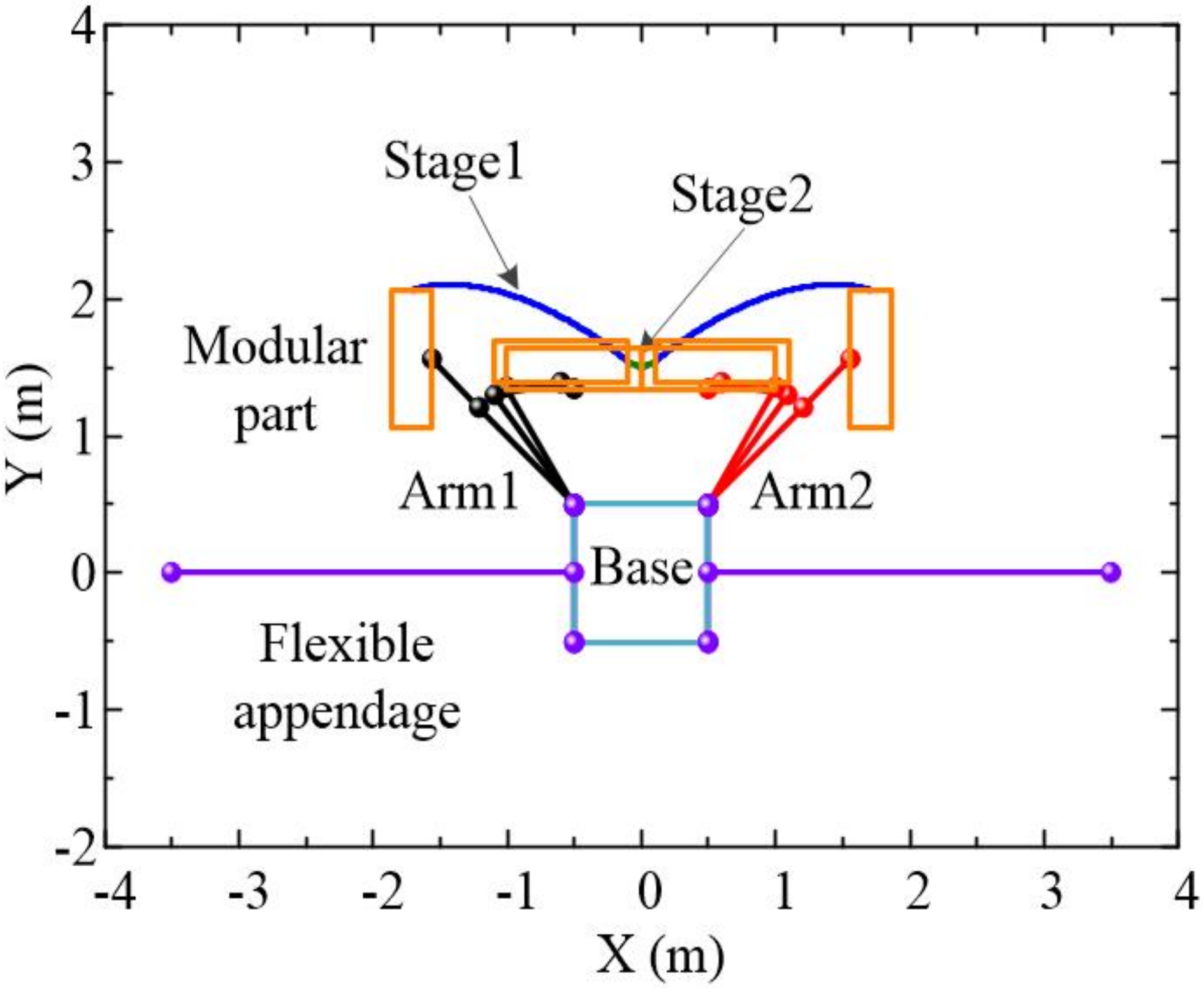
2. Dynamics of a Dual-Arm Space Robot with Flexible Appendages
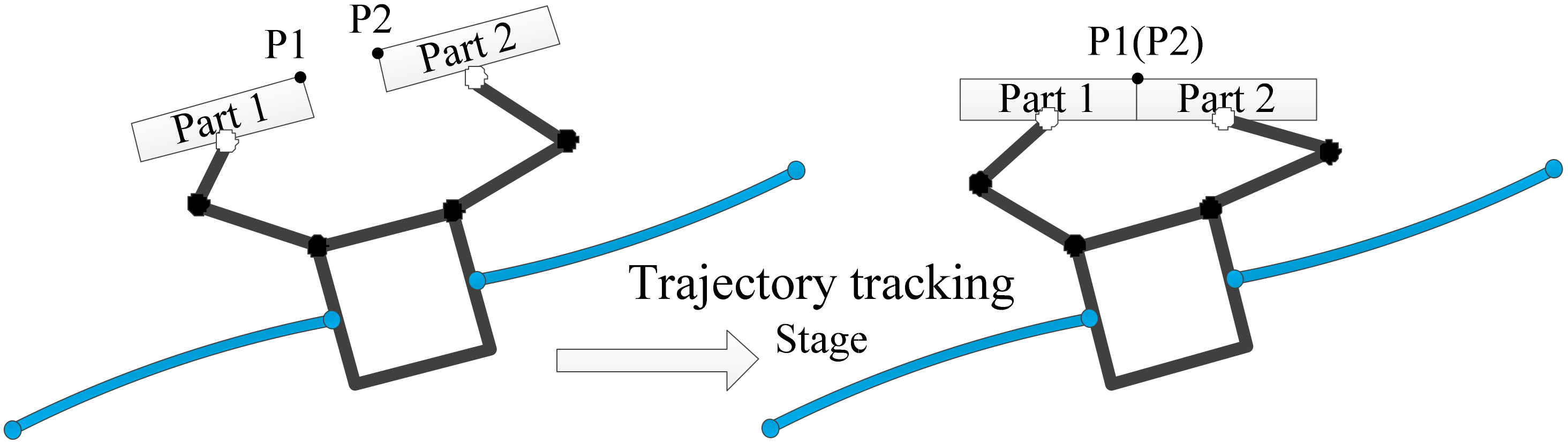
3. Two-Stage Control Scheme for Assembly
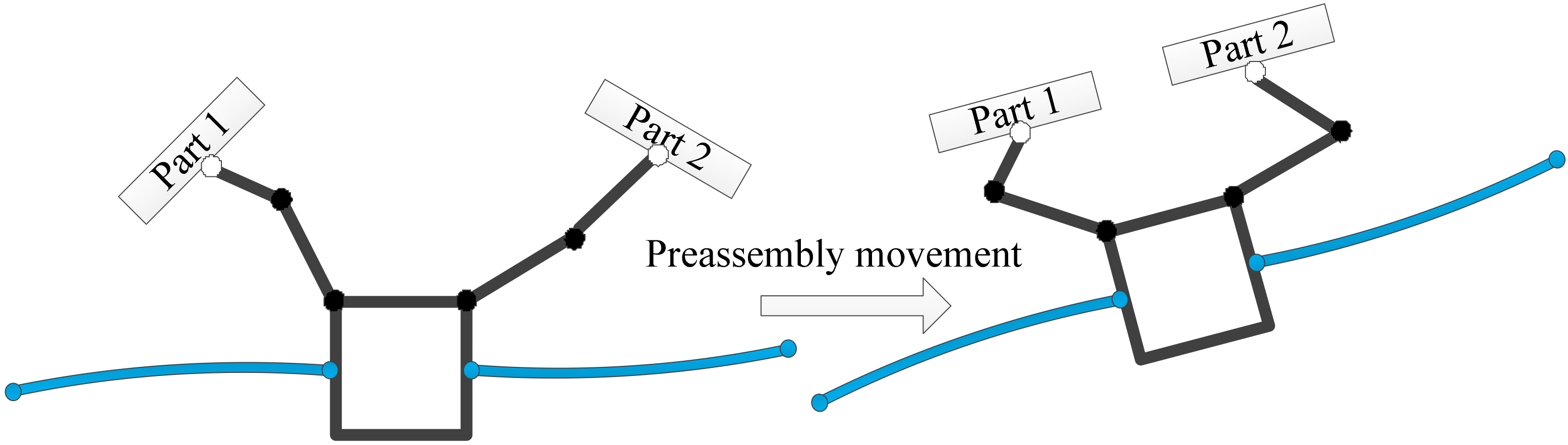
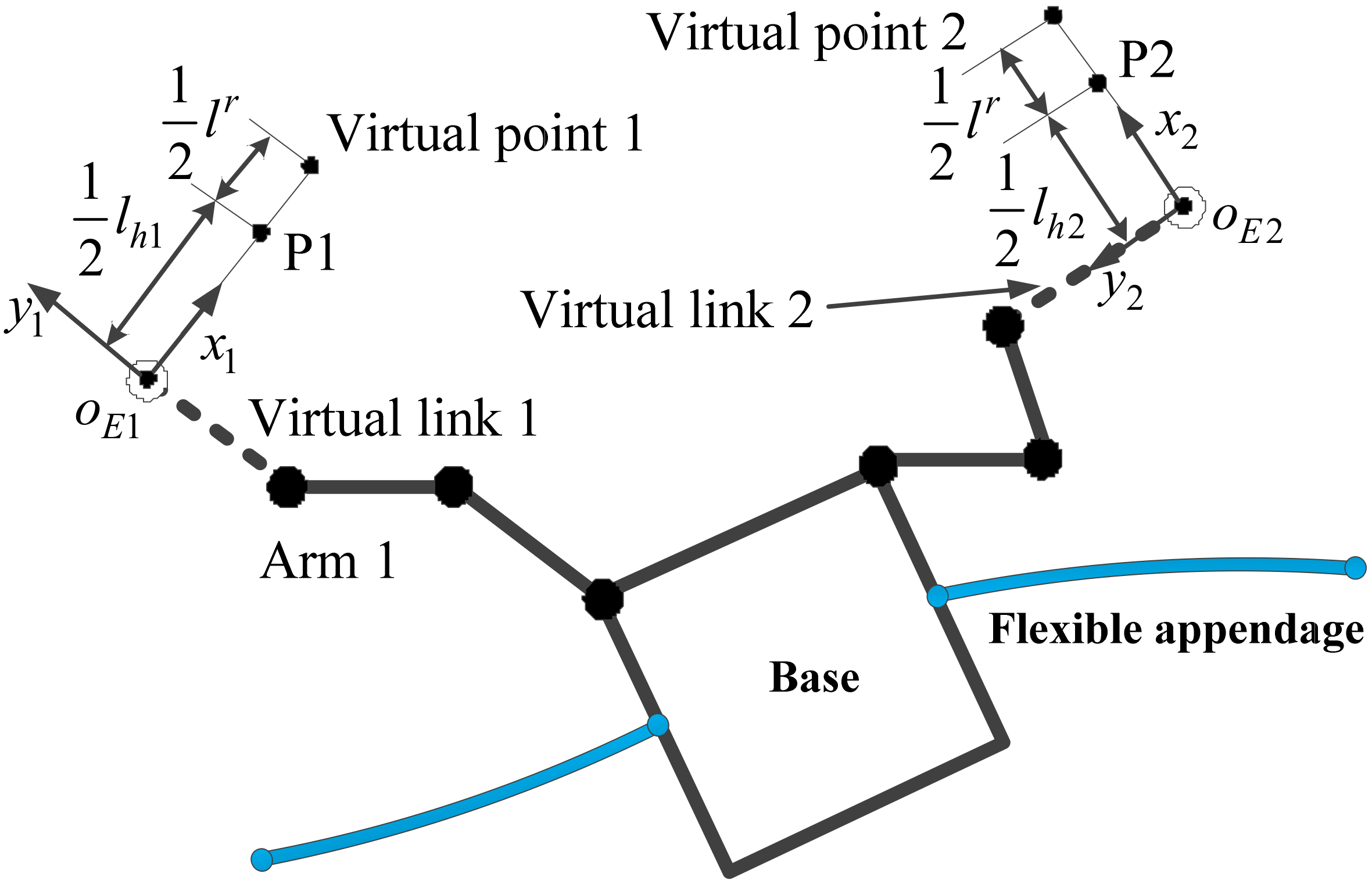
3.1. Controller Design for the Preassembly Stage
3.2. Controller Design for the Trajectory Tracking Stage
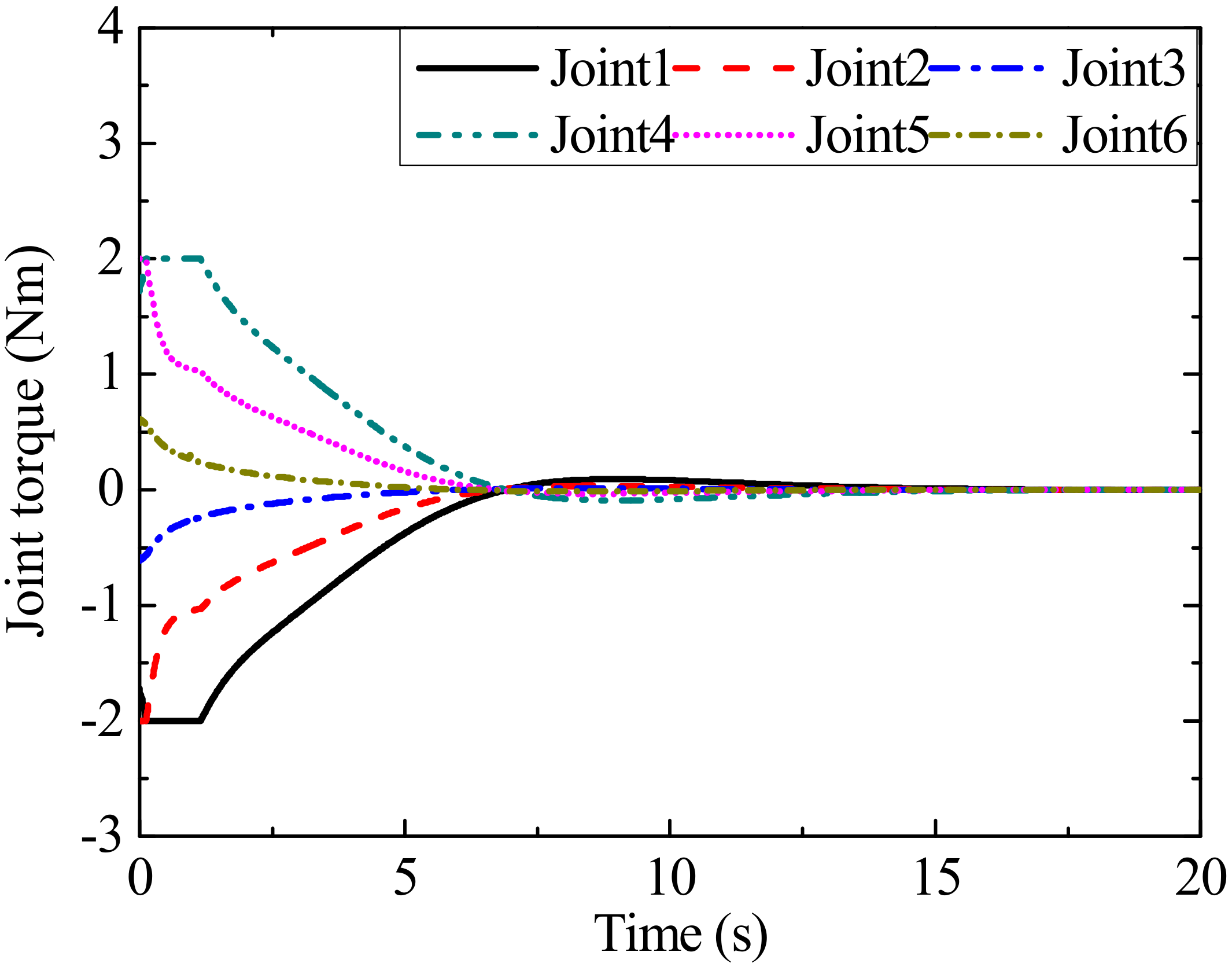
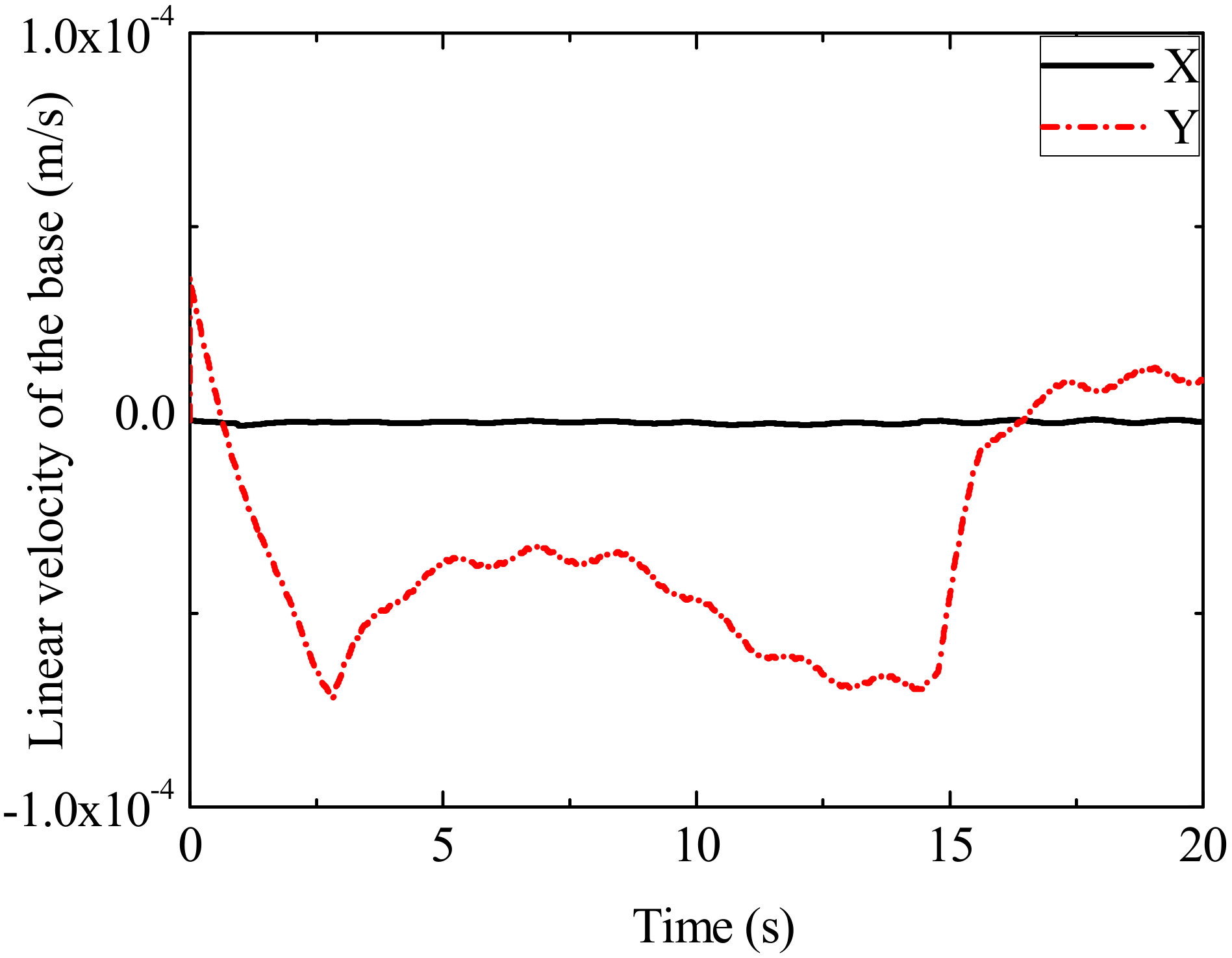
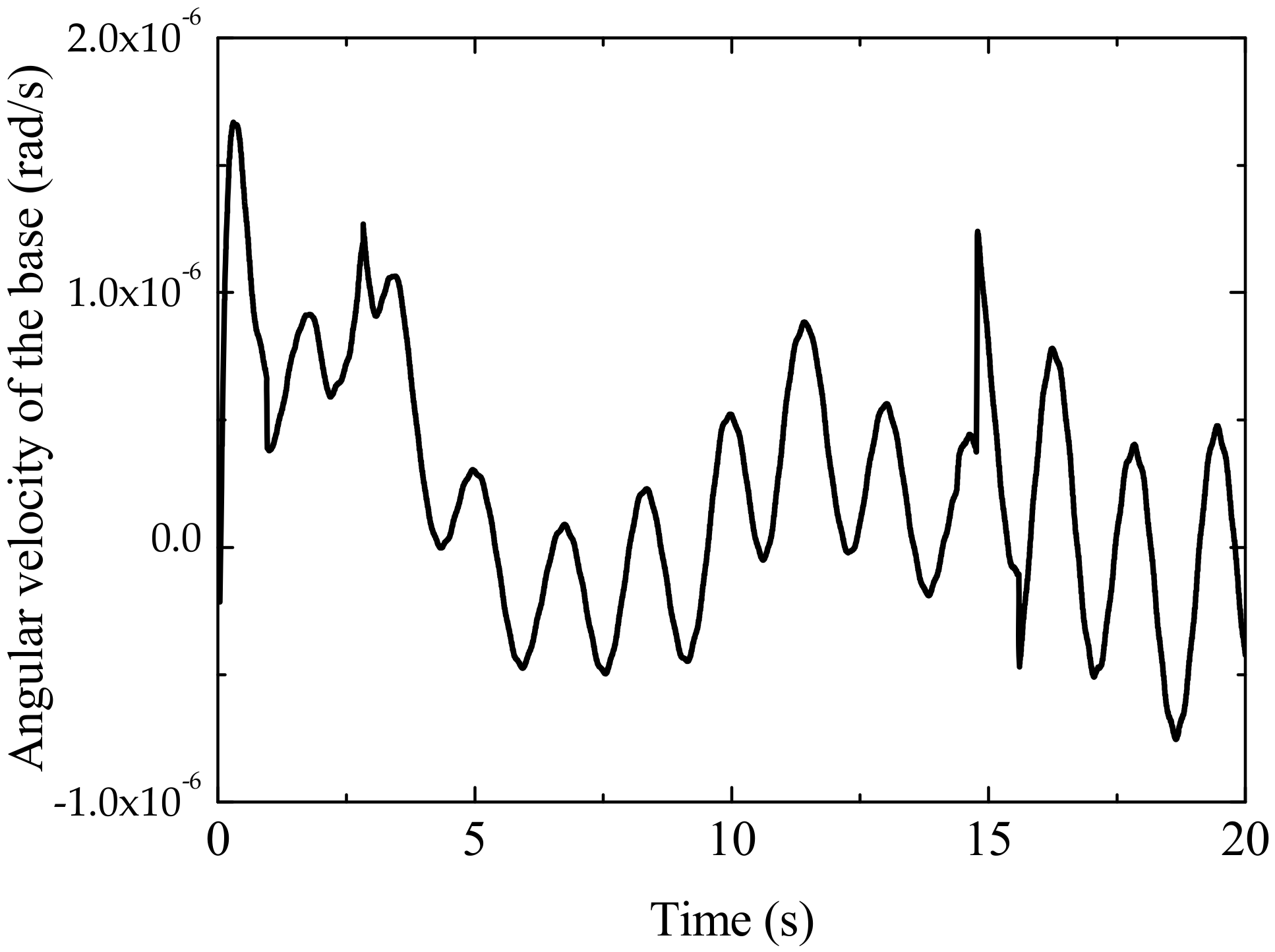
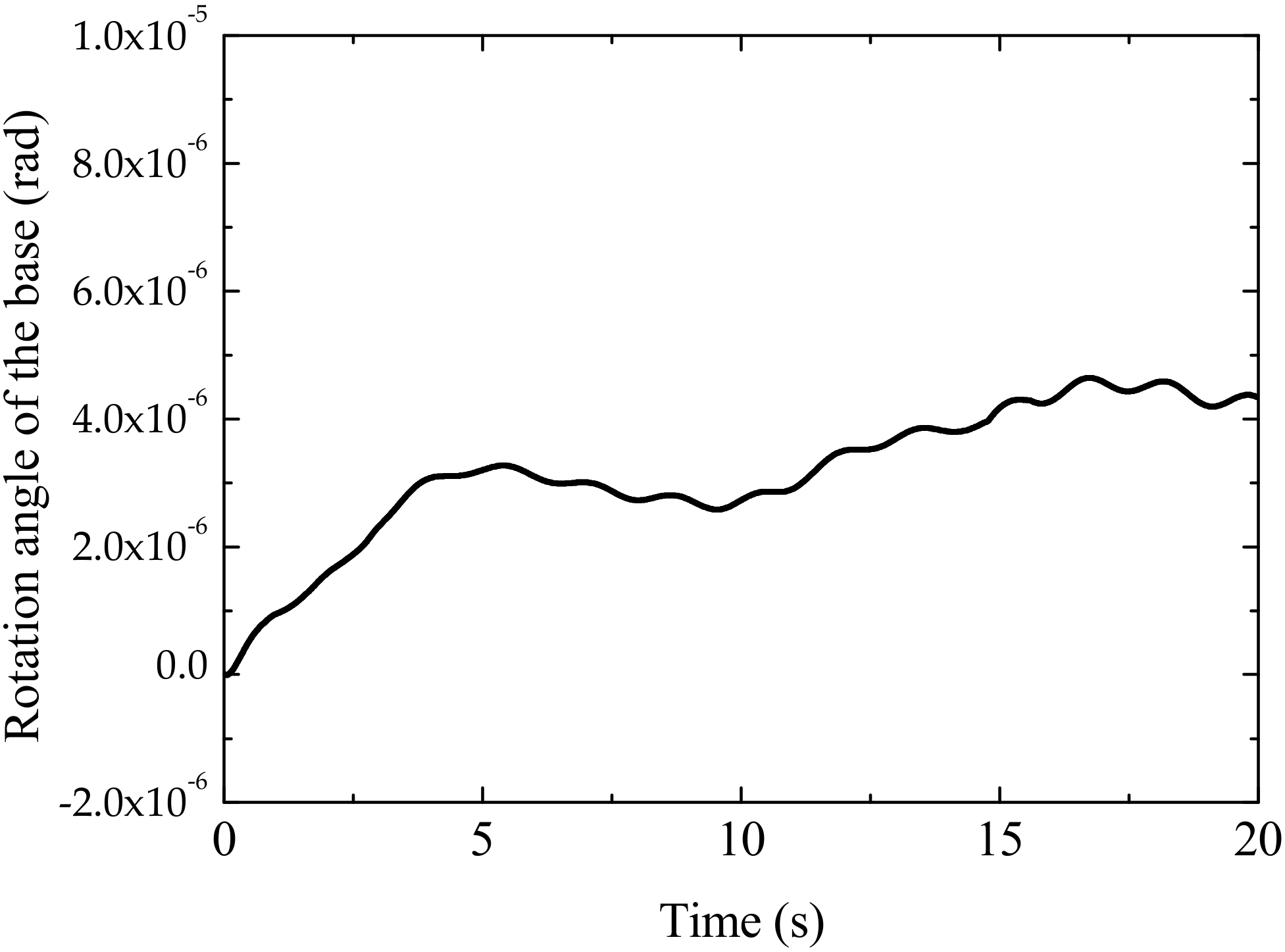
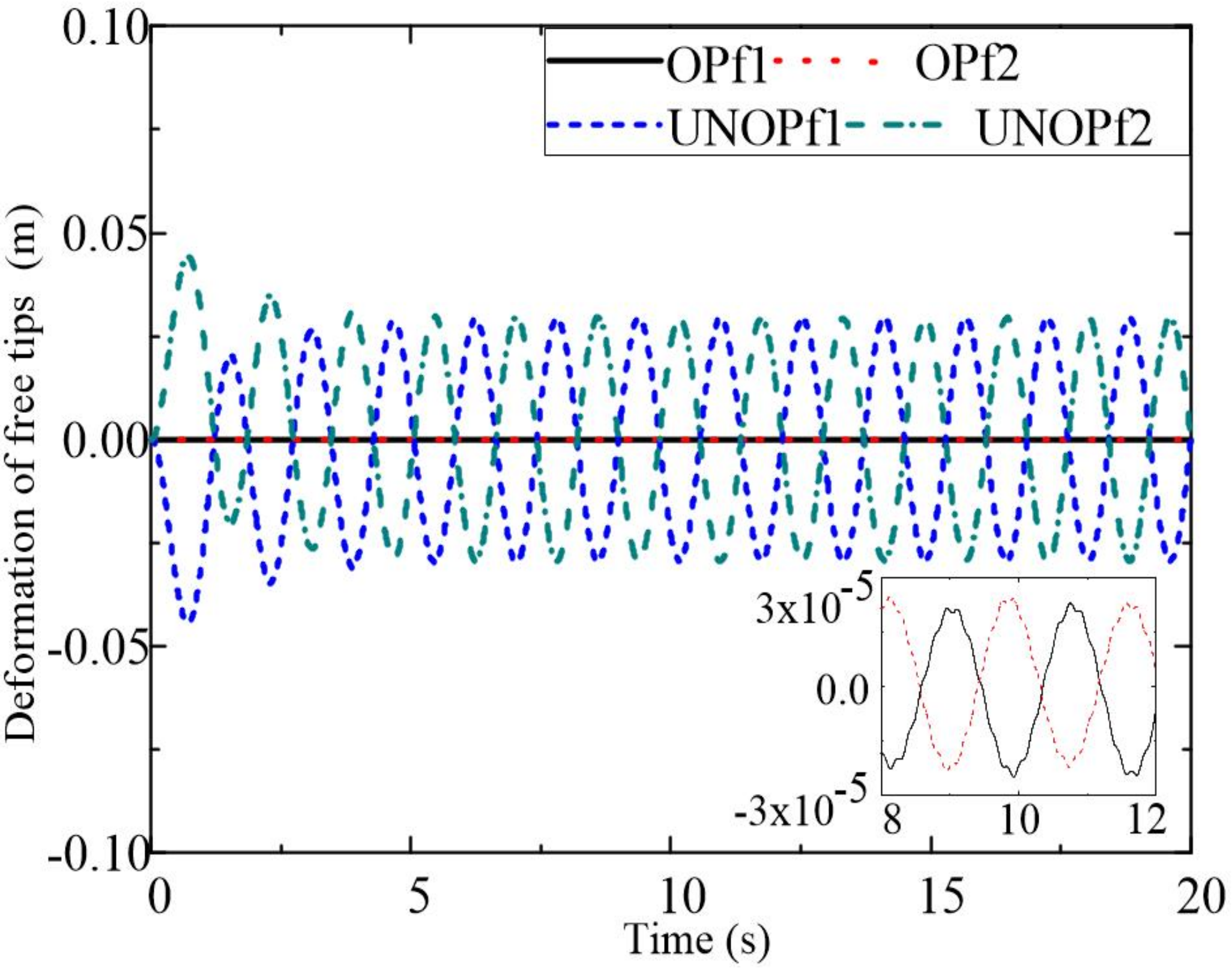
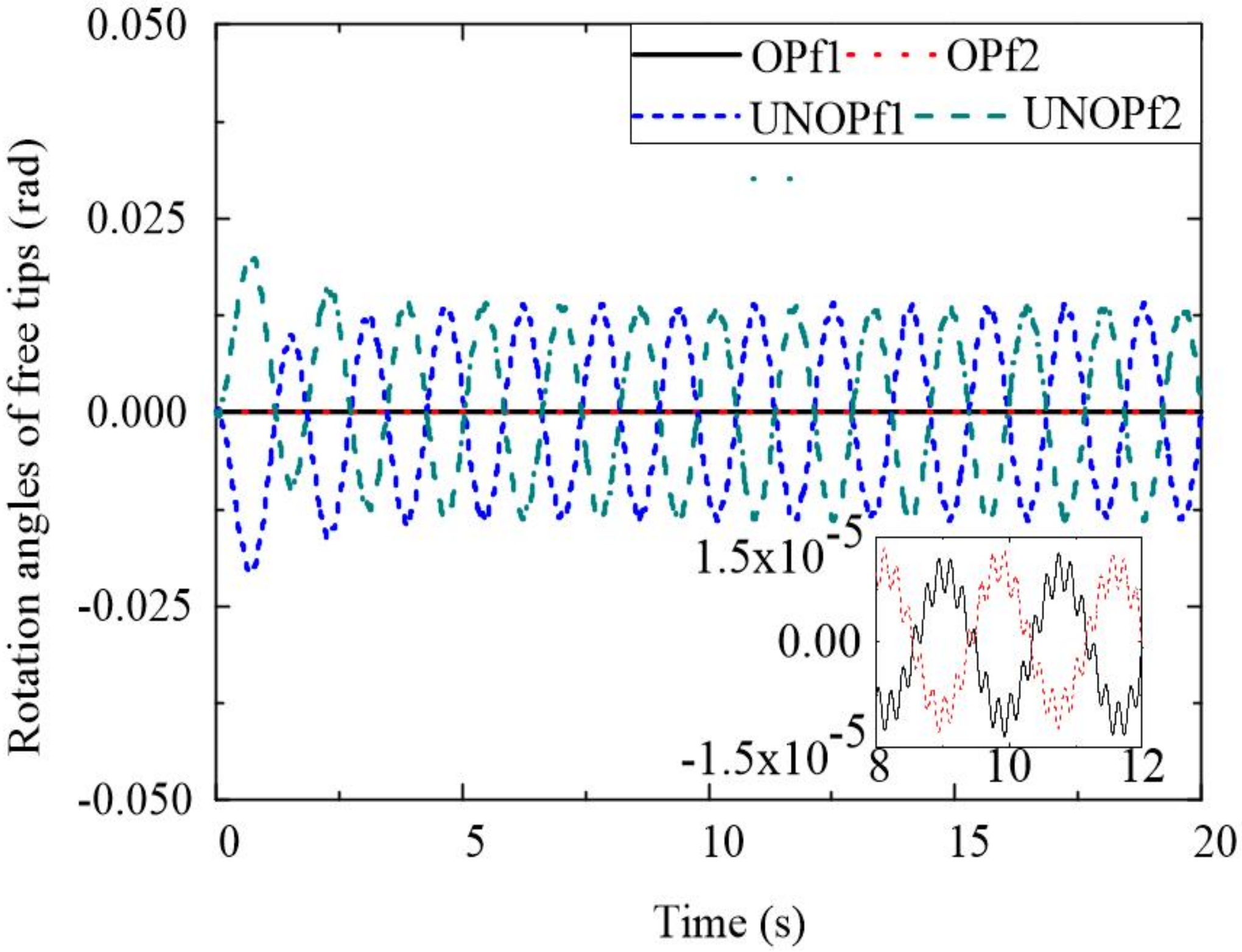
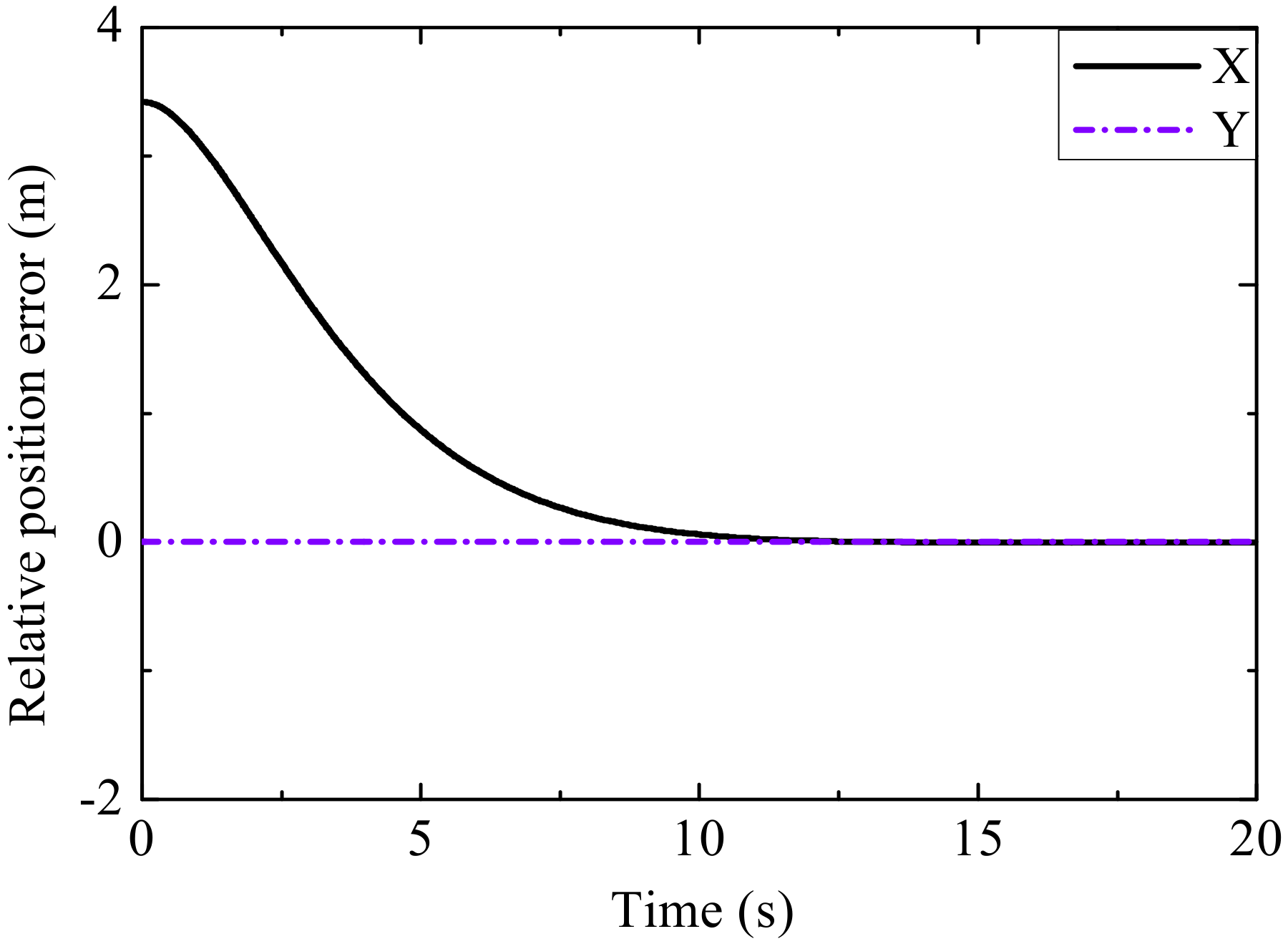
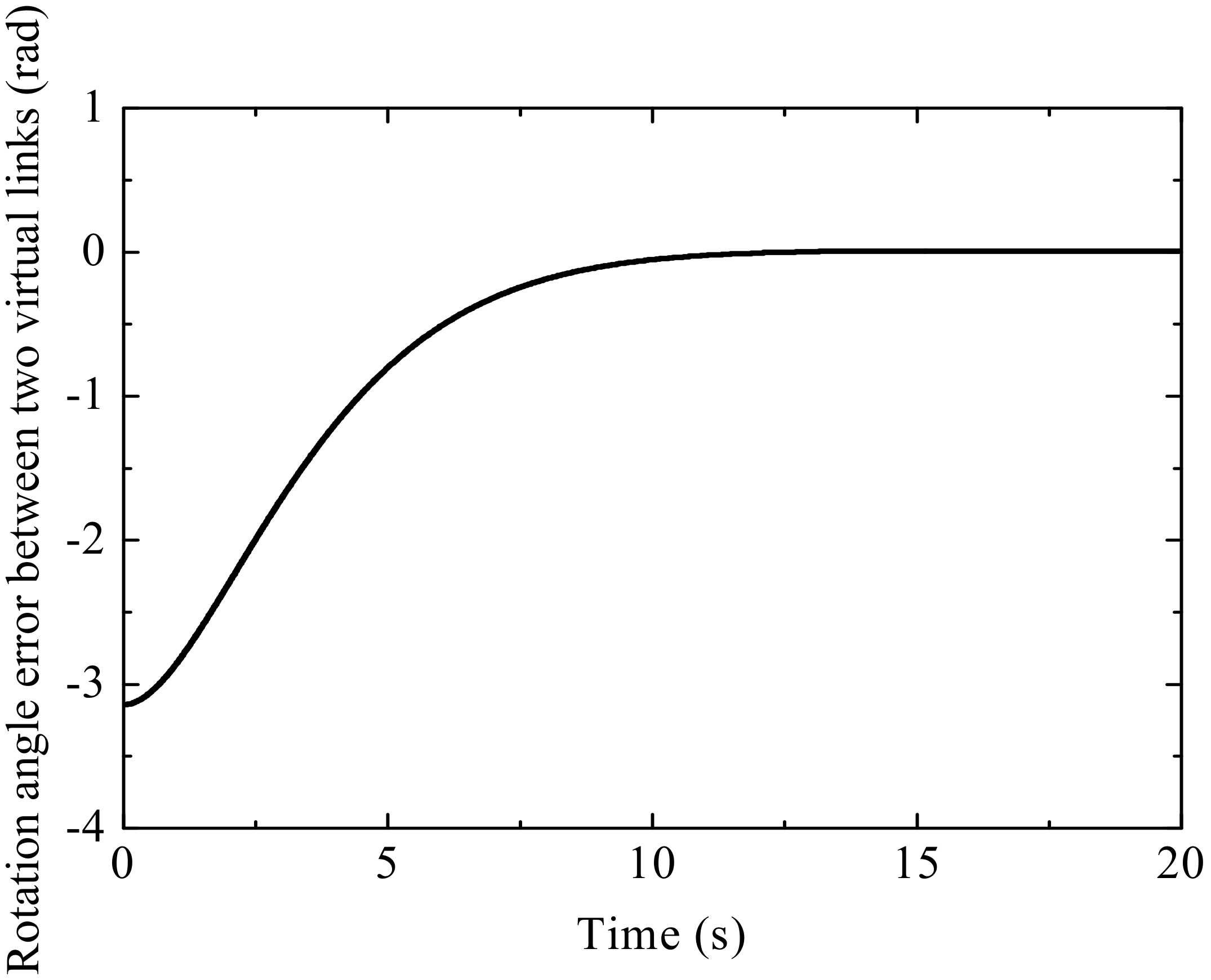
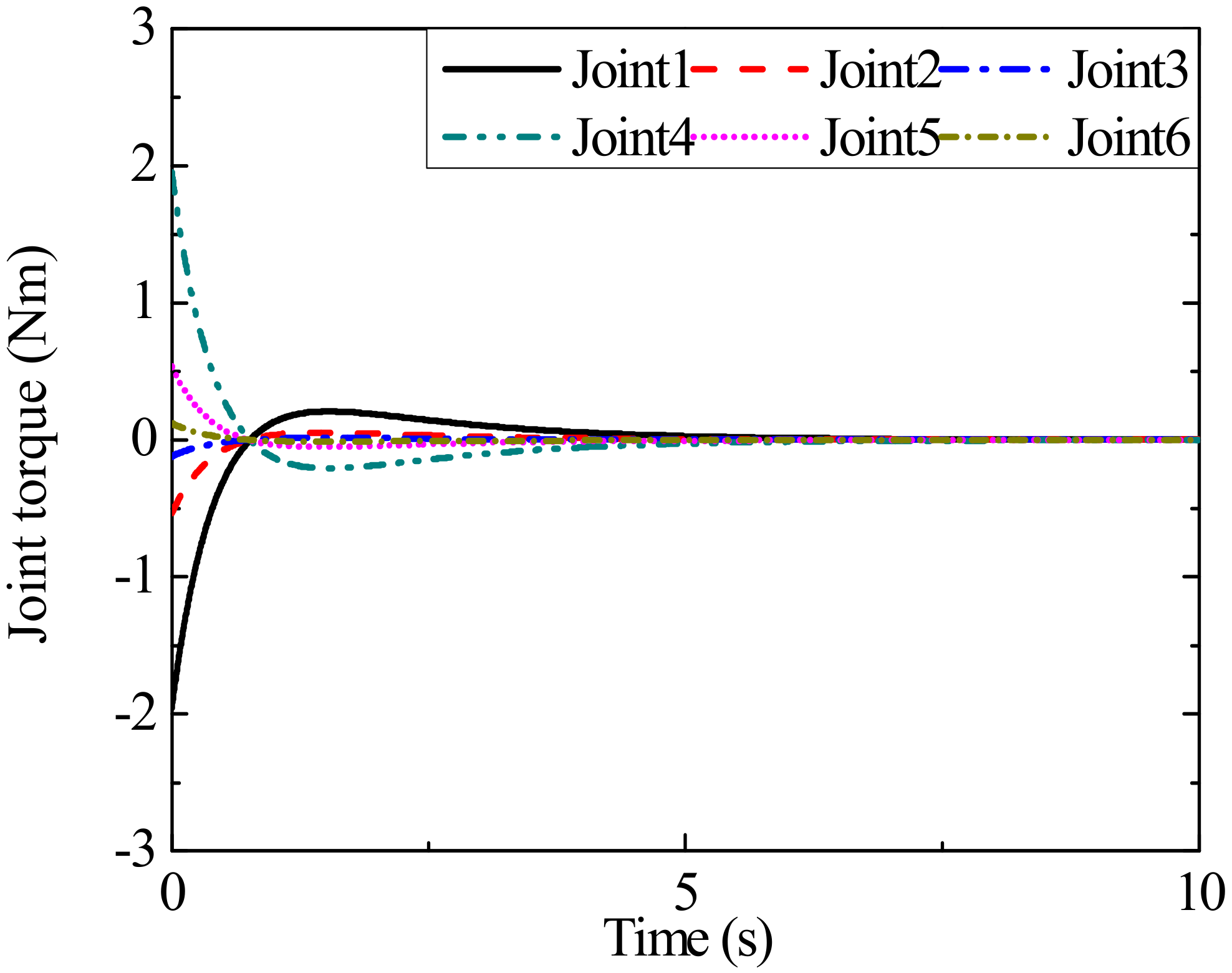
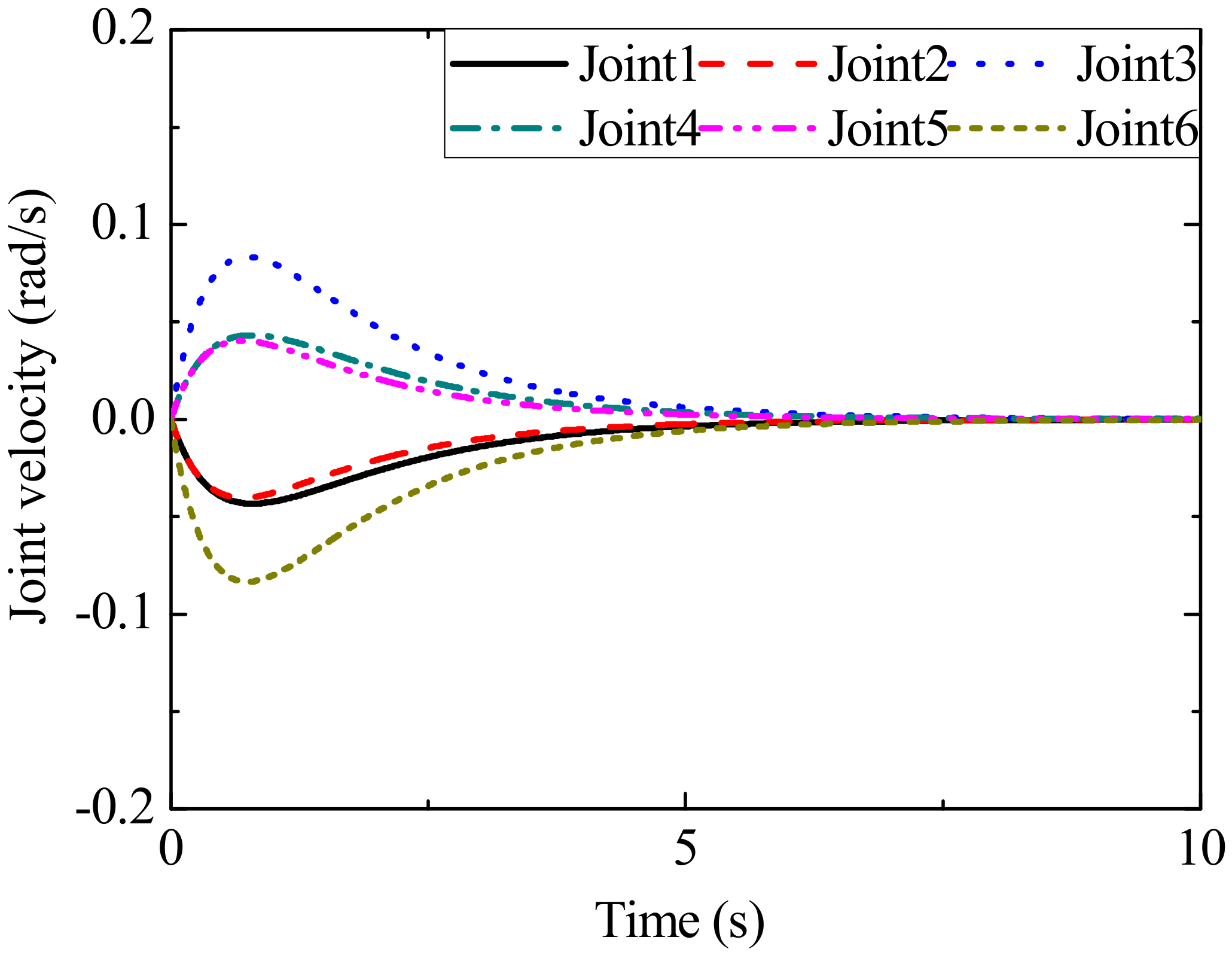
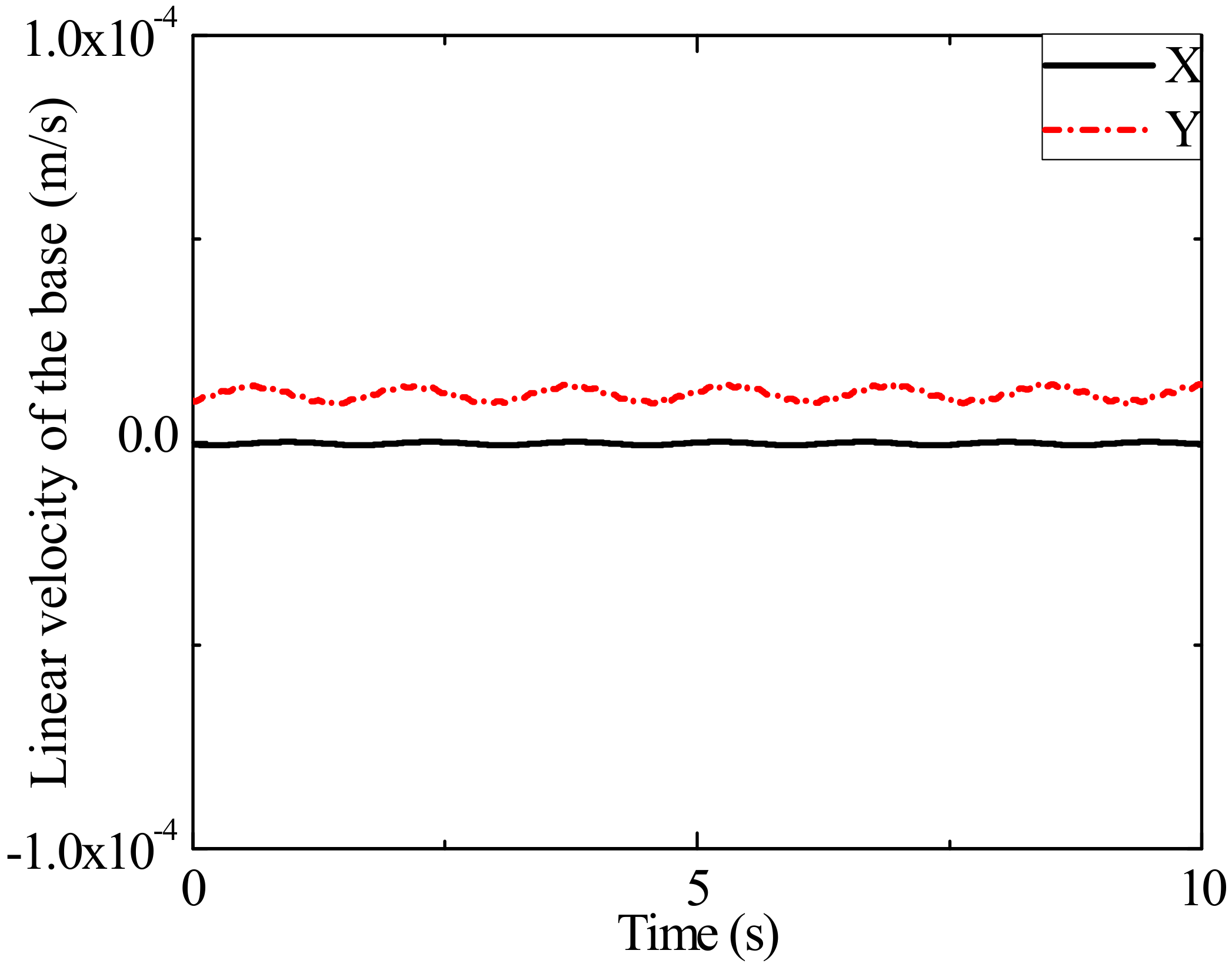
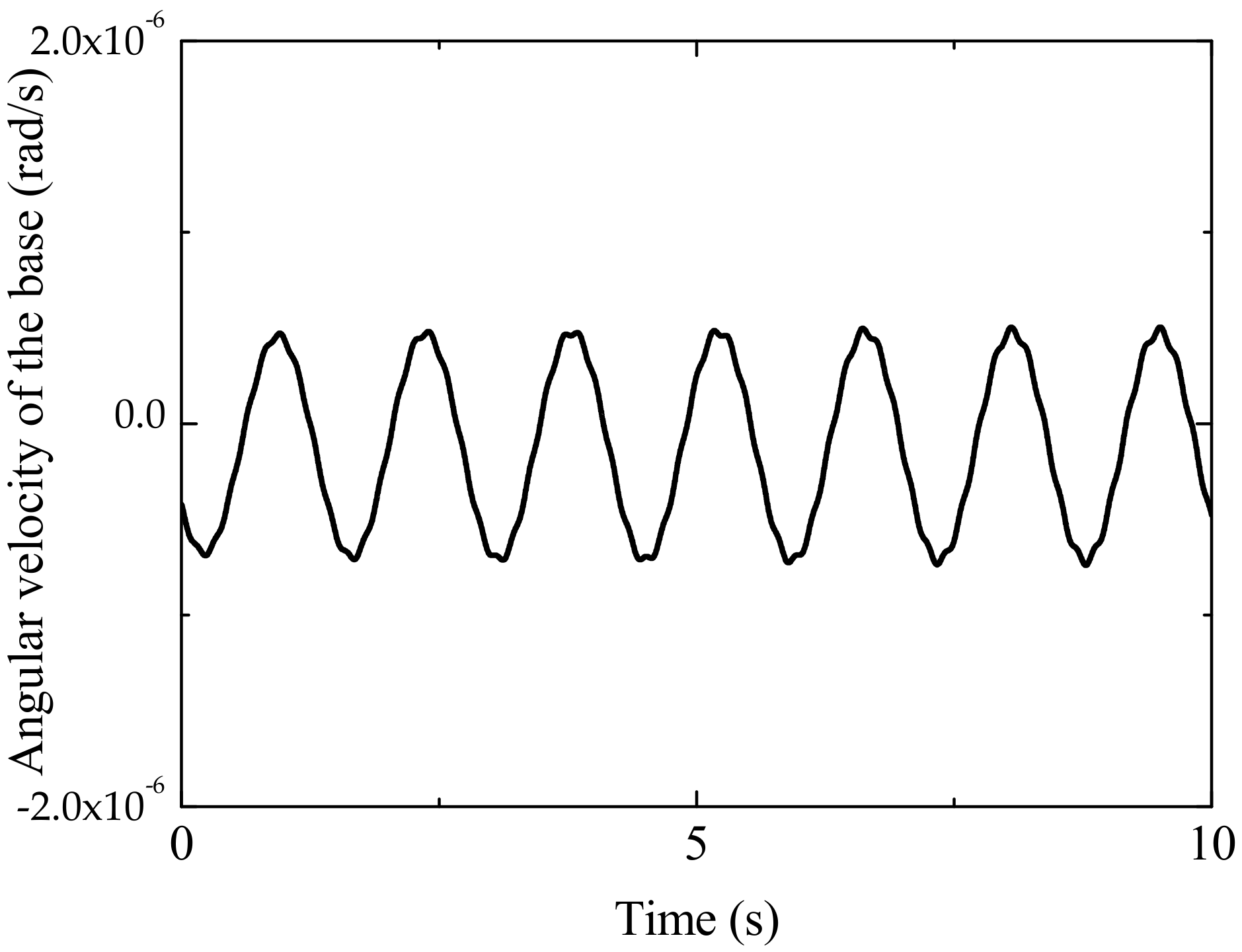
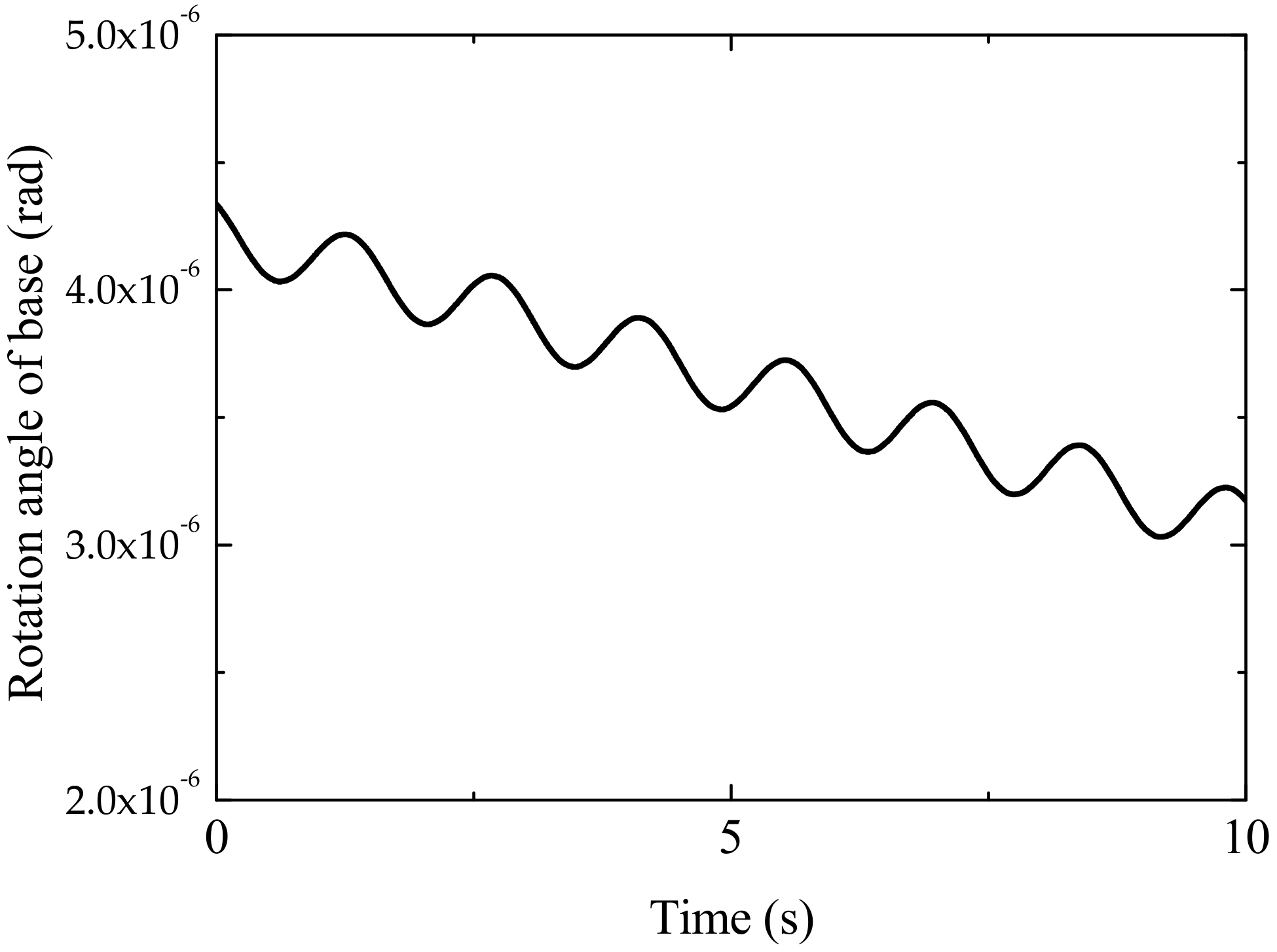
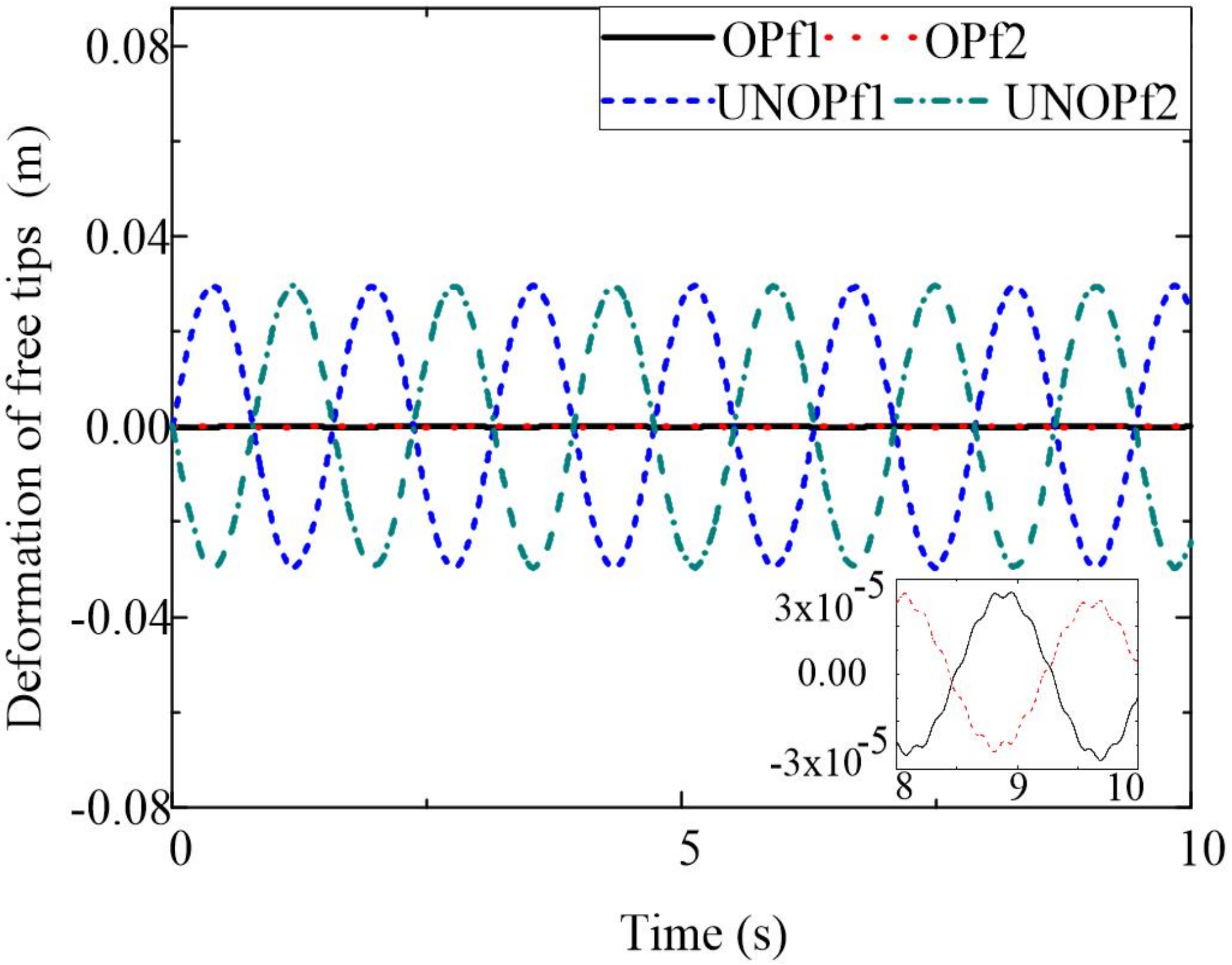
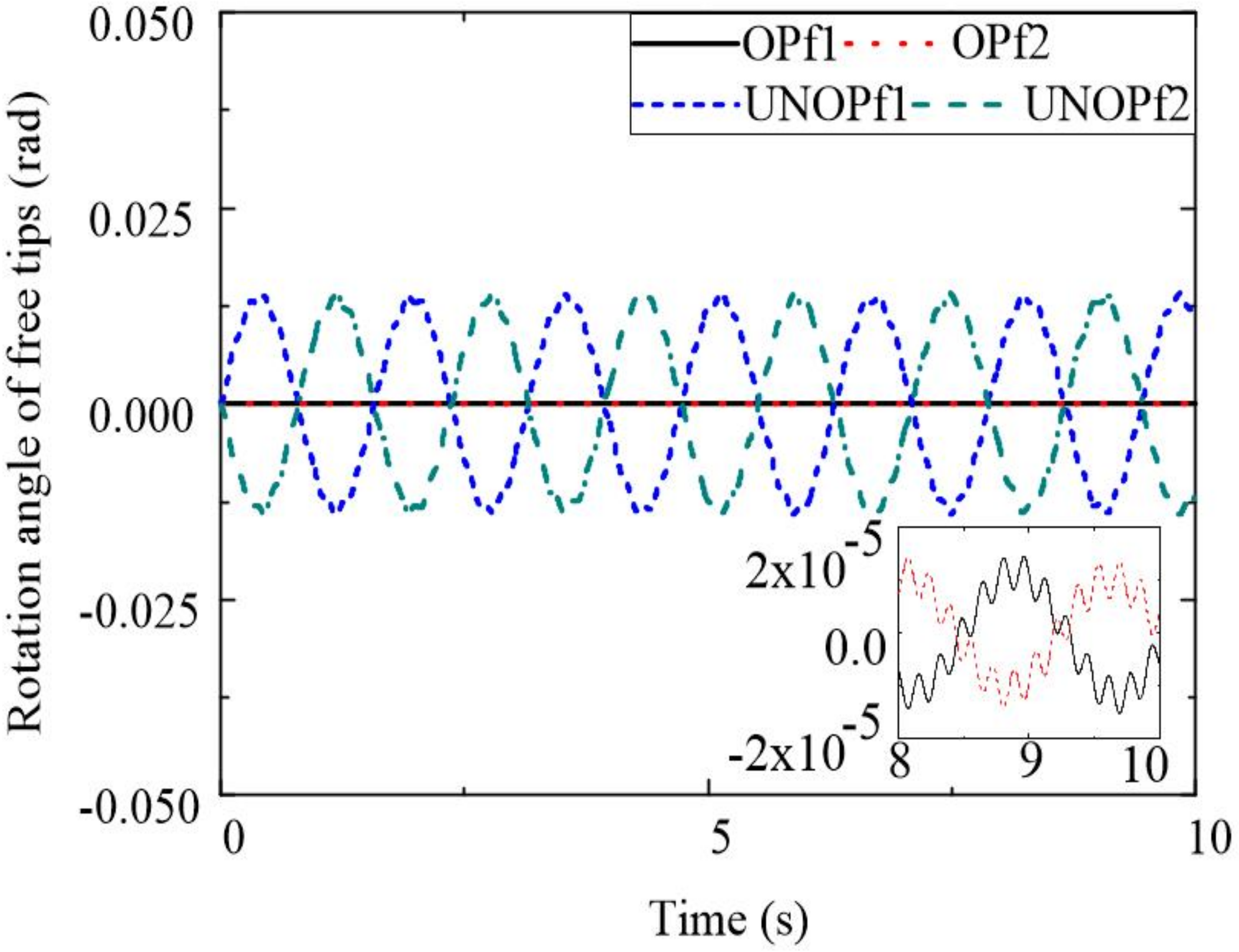
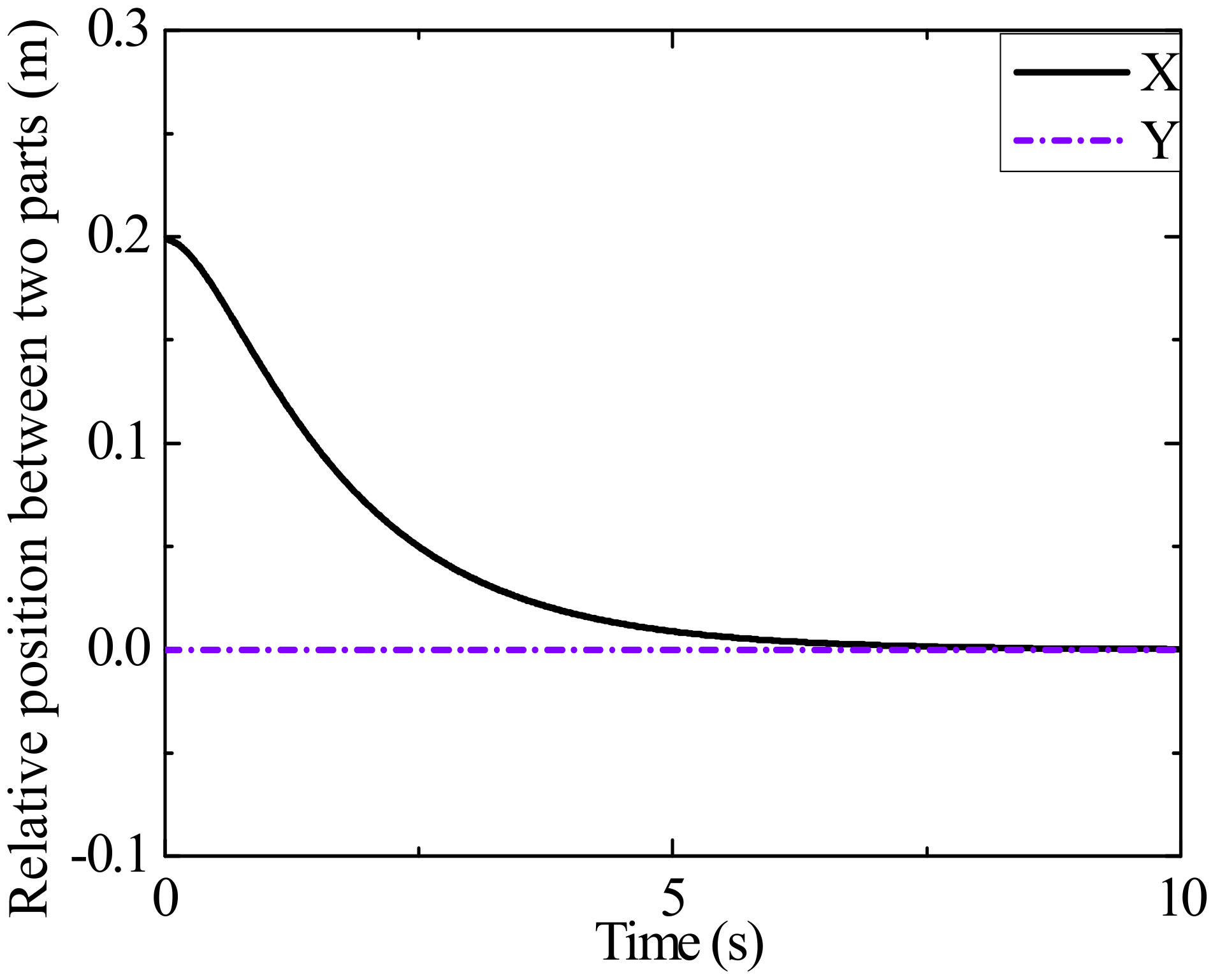
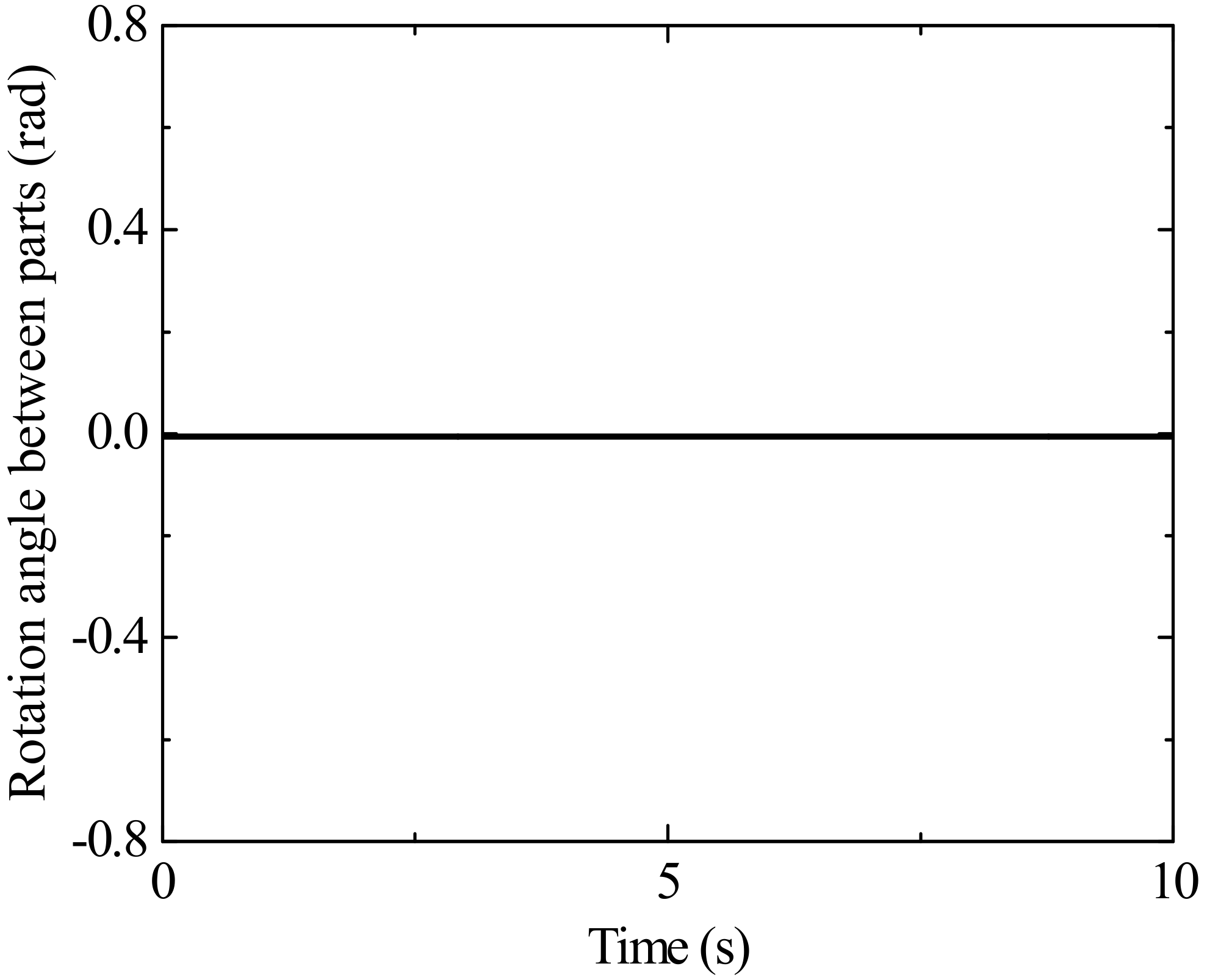
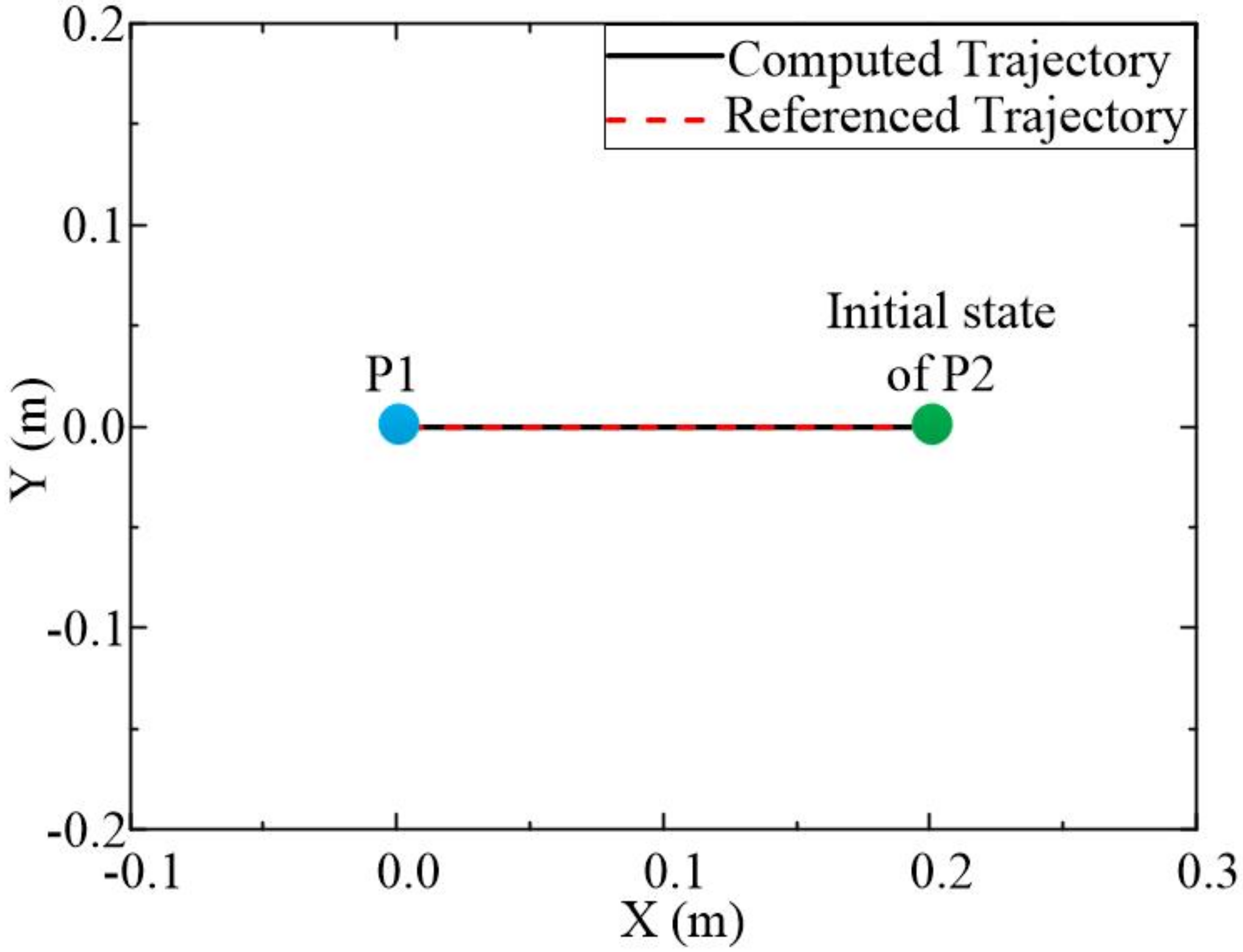
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Moghaddam, B.M.; Chhabra, R. On the guidance, navigation and control of in-orbit space robotic missions: A survey and prospective vision. Acta Astronaut. 2021, 184, 70–100. [Google Scholar] [CrossRef]
- Flores-Abad, A.; Ma, O.; Pham, K.; Ulrich, S. A review of space robotics technologies for on-orbit servicing. Prog. Aerosp. Sci. 2014, 68, 1–26. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Impact dynamic modelling and adaptive target capturing control for tethered space robots with uncertainties. IEEE ASME Trans. Mechatron. 2016, 21, 2260–2271. [Google Scholar] [CrossRef]
- Mohan, S.; Miller, D.W. Dynamic Control Model Calculation: A Model Generation Architecture for Autonomous On-Orbit Assembly. J. Spacecr. Rockets 2014, 51, 1430–1453. [Google Scholar] [CrossRef]
- Basmadji, F.L.; Seweryn, K.; Sasiadek, J.Z. Space robot motion planning in the presence of nonconserved linear and angular momenta. Multibody Syst. Dyn. 2020, 50, 71–96. [Google Scholar] [CrossRef]
- Oegerle, W.R.; Purves, L.R.; Budinoff, J.G.; Moe, R.V.; Carnahan, T.M.; Evans, D.C.; Kim, C.K. Concept for a large scalable space telescope: In-space assembly. In Proceedings of the SPIE 6265, Space Telescopes and Instrumentation I: Optical, Infrared, and Millimeter, Orlando, FL, USA, 14 June 2006. [Google Scholar] [CrossRef]
- Torisaka, A.; Hasegawa, S.; Miura, S.; Parque, V.; Miyashita, T.; Yamakawa, H.; Natori, M.C. Electromagnet-Based Three-Dimensional Self-Assembly System for Hierarchical Modular Space Structures. J. Spacecr. Rockets 2021, 58, 472–485. [Google Scholar] [CrossRef]
- Pirat, C.; Ribes-Pleguezuelo, P.; Keller, F.; Marchi, A.Z.; Walker, R. Toward the Autonomous Assembly of Large Telescopes Using CubeSat Rendezvous and Docking. J. Spacecr. Rockets 2022, 59, 375–388. [Google Scholar] [CrossRef]
- Gardner, J.P.; Mather, J.C.; Clampin, M.; Doyon, R.; Greenhouse, M.A.; Hammel, H.B.; Hutchings, J.B.; Jakobsen, P.; Lilly, S.J.; Long, K.S.; et al. The james webb space telescope. Sp. Sci. Rev. 2006, 123, 485–606. [Google Scholar] [CrossRef]
- Holub, V. Orb2: Spherical Space Station Designed for Single Launch and On-Orbit Assembly. J. Spacecr. Rockets 2021, 58, 708–714. [Google Scholar] [CrossRef]
- Zappulla, R.; Virgili-Llop, J.; Zagaris, C.; Park, H.; Romano, M. Dynamic air-bearing hardware-in-the-loop testbed to experimentally evaluate autonomous spacecraft proximity maneuvers. J. Spacecr. Rockets 2017, 54, 825–839. [Google Scholar] [CrossRef]
- Cao, K.; Li, S.; She, Y.; Biggs, J.D.; Liu, Y.; Bian, L. Dynamics and on-orbit assembly strategies for an orb-shaped solar array. Acta Astronaut. 2021, 178, 881–893. [Google Scholar] [CrossRef]
- Yang, S.J.; Wen, H.; Hu, Y.H.; Jin, D.P. Coordinated motion control of a dual-arm space robot for assembling modular parts. Acta Astronaut. 2020, 177, 627–638. [Google Scholar] [CrossRef]
- Staritz, P.J.; Skaff, S.; Urmson, C.; Whittaker, W. Skyworker: A robot for assembly, inspection and maintenance of large scale orbital facilities. In Proceedings of the 2001 ICRA, IEEE International Conference on Robotics and Automation (Cat. No.01CH37164), Seoul, Republic of Korea, 21–26 May 2001; pp. 4180–4185. [Google Scholar] [CrossRef]
- Hu, Q.; Zhang, Y.; Zhang, J.; Hu, H. Formation control of multi-robots for on-orbit assembly of large solar sails. Acta Astronaut. 2016, 123, 446–454. [Google Scholar] [CrossRef]
- Yang, S.J.; Wen, H.; Jin, D.P. Trajectory planning of dual-arm space robots for target capturing and base manoeuvring. Acta Astronaut. 2019, 164, 142–151. [Google Scholar] [CrossRef]
- Dong, G.; Zhu, Z.H. Position-based visual servo control of autonomous robotic manipulators. Acta Astronaut. 2015, 115, 291–302. [Google Scholar] [CrossRef]
- Huang, P.F.; Xu, Y.; Liang, B. Dynamic balance control of multi-arm free-floating space robots. Int. J. Adv. Robot. Syst. 2005, 2, 117–124. [Google Scholar] [CrossRef]
- Senda, K.; Murotsu, Y.; Mitsuya, A.; Adachi, H.; Ito, S.; Shitakubo, J.; Matsumoto, T. Hardware experiments of a truss assembly by an autonomous space learning robot. J. Spacecr. Rockets 2002, 39, 267–273. [Google Scholar] [CrossRef]
- Dubowsky, S.; Boning, P. Coordinated control of space robot teams for the on-orbit construction of large flexible space structures. Adv. Robot. 2010, 24, 303–323. [Google Scholar] [CrossRef]
- Karumanchi, S.; Edelberg, K.; Nash, J.; Bergh, C.; Smith, R.; Emanuel, B.; Carlton, J.; Koehler, J.; Kim, J.; Mukherjee, R.; et al. Payload-centric autonomy for in-space robotic assembly of modular space structures. J. Field Robot. 2018, 35, 1005–1021. [Google Scholar] [CrossRef]
- Lu, Y.; Huang, Z.; Zhang, W.; Wen, H.; Jin, D. Experimental investigation on automated assembly of space structure from cooperative modular components. Acta Astronaut. 2020, 171, 378–387. [Google Scholar] [CrossRef]
- Yu, Z.; Liu, X.; Cai, G. Dynamics modeling and control of a 6-DOF space robot with flexible panels for capturing a free floating target. Acta Astronaut. 2016, 128, 560–572. [Google Scholar] [CrossRef]
- Gasbarri, P.; Pisculli, A. Dynamic/control interactions between flexible orbiting space-robot during grasping, docking and post-docking manoeuvres. Acta Astronaut. 2015, 110, 225–238. [Google Scholar] [CrossRef]
- Xu, W.; Meng, D.; Chen, Y.; Qian, H.; Xu, Y. Dynamics modeling and analysis of a flexible-base space robot for capturing large flexible spacecraft. Multibody Syst. Dyn. 2014, 32, 357–401. [Google Scholar] [CrossRef]
- Meng, D.; Liu, H.; Li, Y.; Xu, W.; Liang, B. Vibration suppression of a large flexible spacecraft for on-orbit operation. Sci. China Inform. Sci. 2017, 60, 050203. [Google Scholar] [CrossRef]
- Meng, D.; Lu, W.; Xu, W.; She, Y.; Wang, X.; Liang, B.; Yuan, B. Vibration suppression control of free-floating space robots with flexible appendages for autonomous target capturing. Acta Astronaut. 2018, 151, 904–918. [Google Scholar] [CrossRef]
- Grant, M.; Sp, B. CVX: Matlab Software for Disciplined Convex Programming, Version 2.0 Beta. Available online: http://cvxr.com/cvx (accessed on 5 September 2013).




| Mass (kg) | Dimension (m) | ||
|---|---|---|---|
| Base | 20 | 3.33 | 1 × 1 |
| Links 1, 3 | 5 | 0.833 | 1 |
| Links 2, 4 | 5 | 0.533 | 0.5 |
| Modular parts 1, 2 | 5 | 0.454 | 1 × 0.3 |
| Symbols (Unit) | Initial Conditions (t = 0) | |
|---|---|---|
| Position of the base | (m) | |
| Attitude of the base | Identity matrix | |
| Joint angles of arm 1 | (rad) | |
| Joint angles of arm 2 | (rad) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Zhang, Y.; Chen, T.; Wen, H.; Jin, D. Assembly Strategy for Modular Components Using a Dual-Arm Space Robot with Flexible Appendages. Aerospace 2022, 9, 819. https://doi.org/10.3390/aerospace9120819
Yang S, Zhang Y, Chen T, Wen H, Jin D. Assembly Strategy for Modular Components Using a Dual-Arm Space Robot with Flexible Appendages. Aerospace. 2022; 9(12):819. https://doi.org/10.3390/aerospace9120819
Chicago/Turabian StyleYang, Shuji, Yonglei Zhang, Ti Chen, Hao Wen, and Dongping Jin. 2022. "Assembly Strategy for Modular Components Using a Dual-Arm Space Robot with Flexible Appendages" Aerospace 9, no. 12: 819. https://doi.org/10.3390/aerospace9120819
APA StyleYang, S., Zhang, Y., Chen, T., Wen, H., & Jin, D. (2022). Assembly Strategy for Modular Components Using a Dual-Arm Space Robot with Flexible Appendages. Aerospace, 9(12), 819. https://doi.org/10.3390/aerospace9120819






