Effect of Installation Error on Rotary Seal of Aero Engine
Abstract
1. Introduction
2. Theoretical Analysis of Seal Flow Field
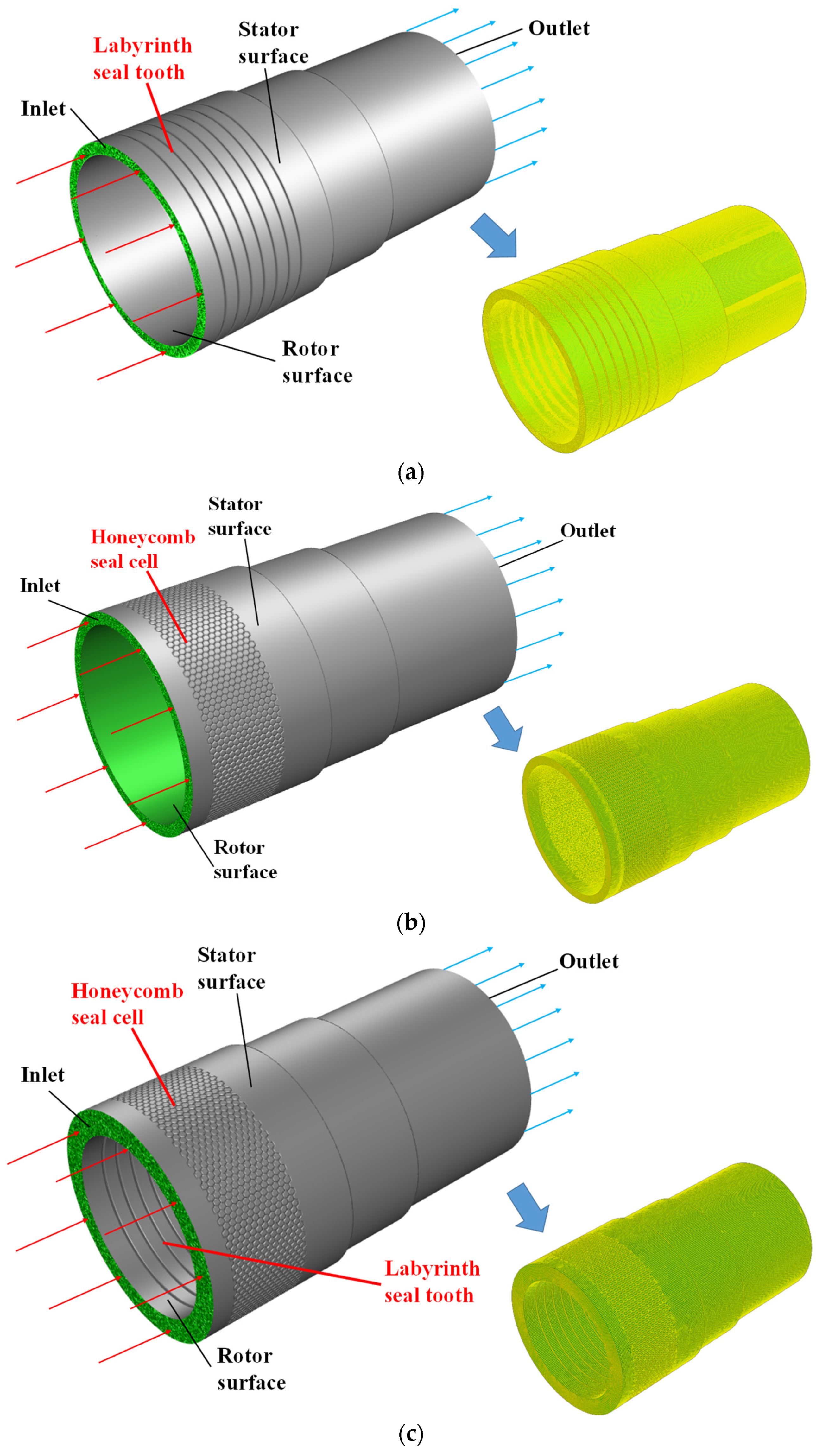
2.1. Seal Flow Field Numerical Model
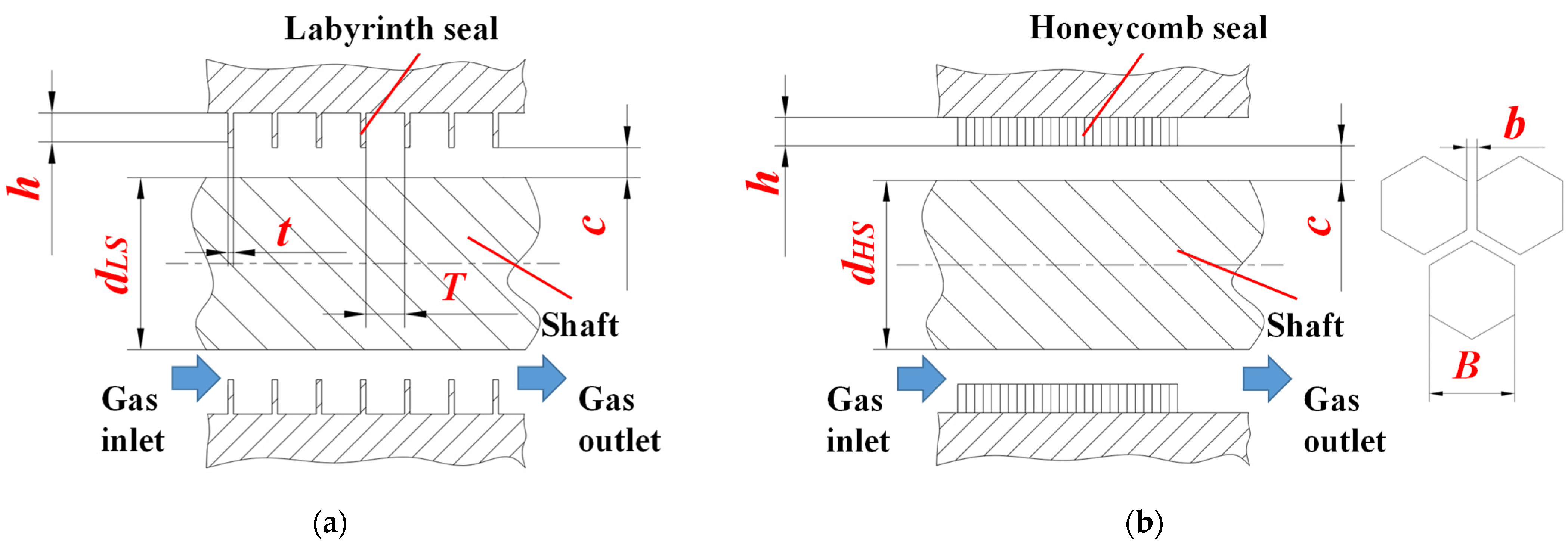
2.1.1. Structure Parameters of Numerical Model
2.1.2. Mesh Division and Boundary Conditions of Numerical Model
2.2. Analysis of Seal Flow Field without Eccentricity
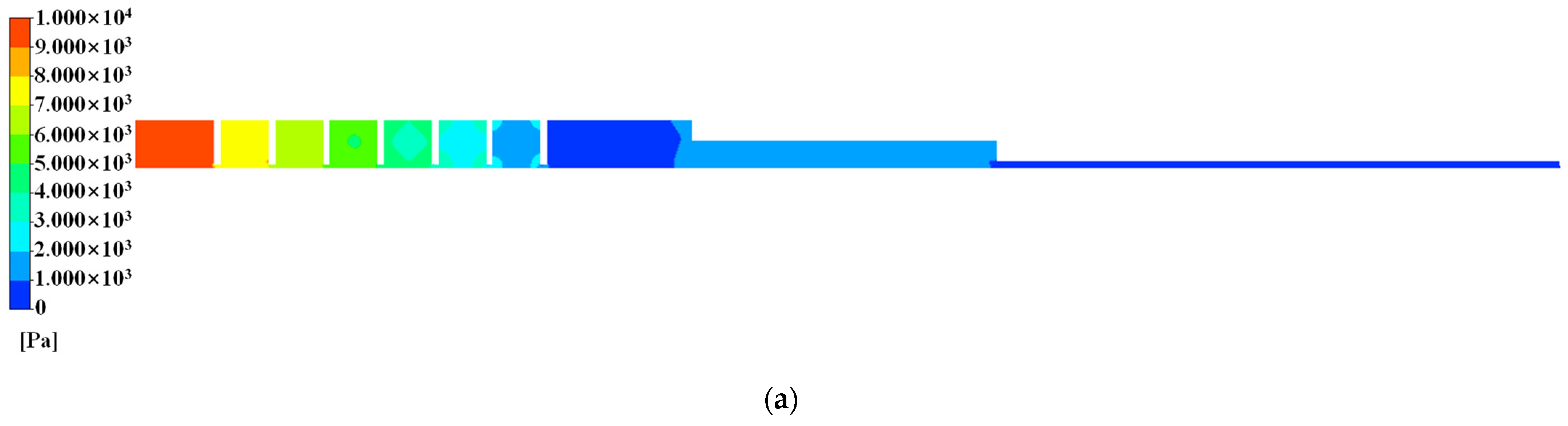
2.2.1. Analysis of Seal Leakage Characteristics without Eccentricity
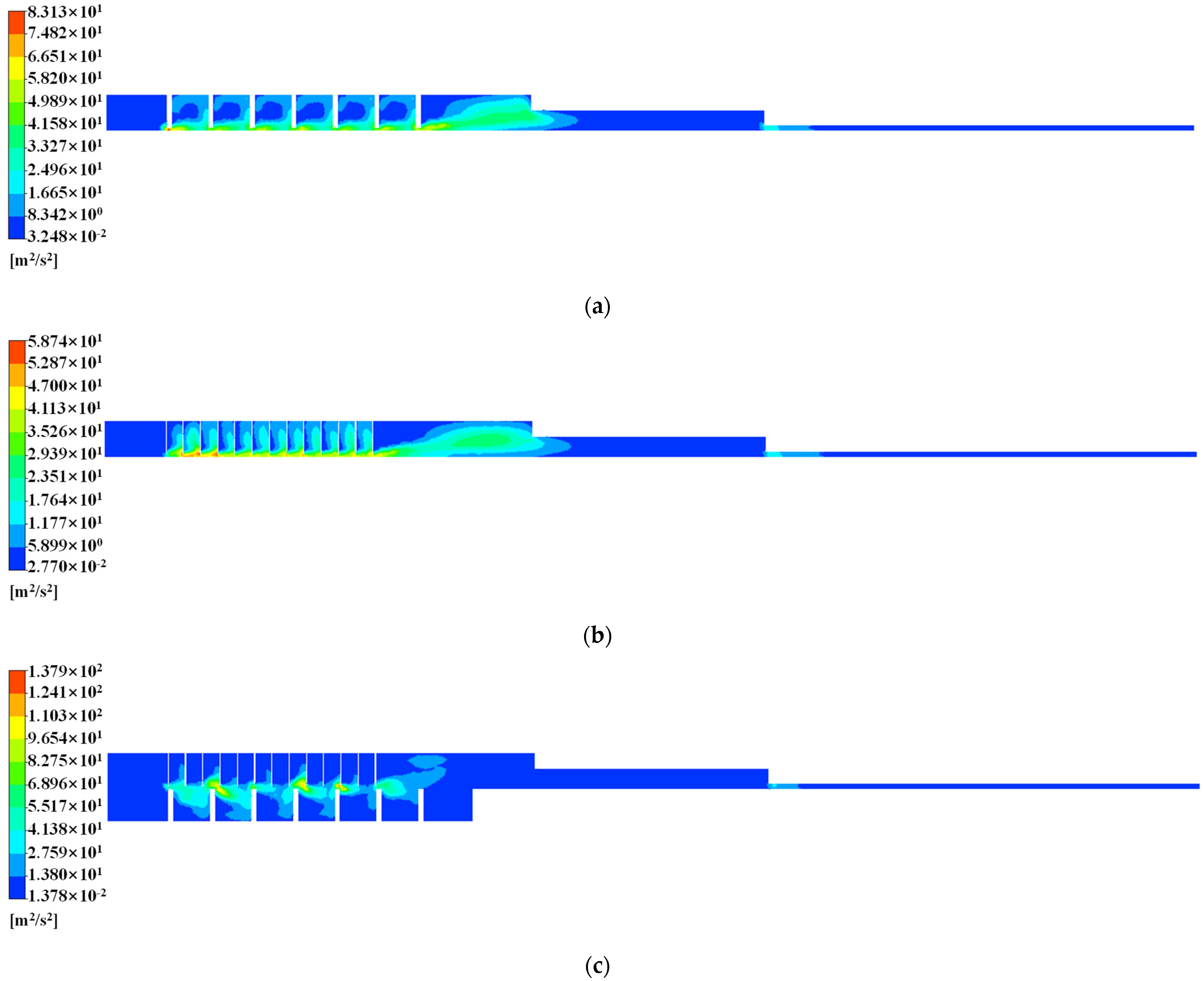
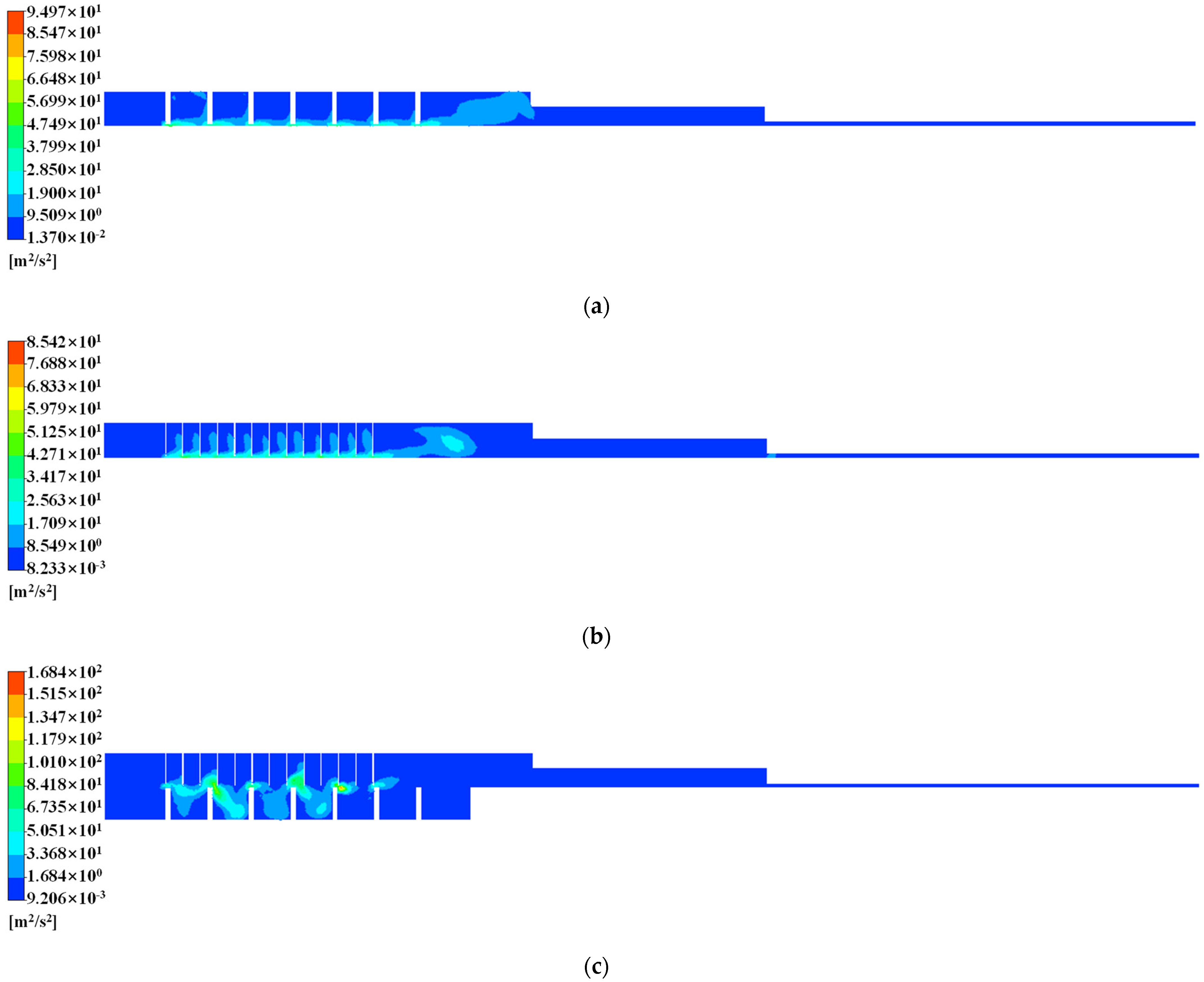
2.2.2. Analysis of Seal Flow Field Characteristics without Eccentricity
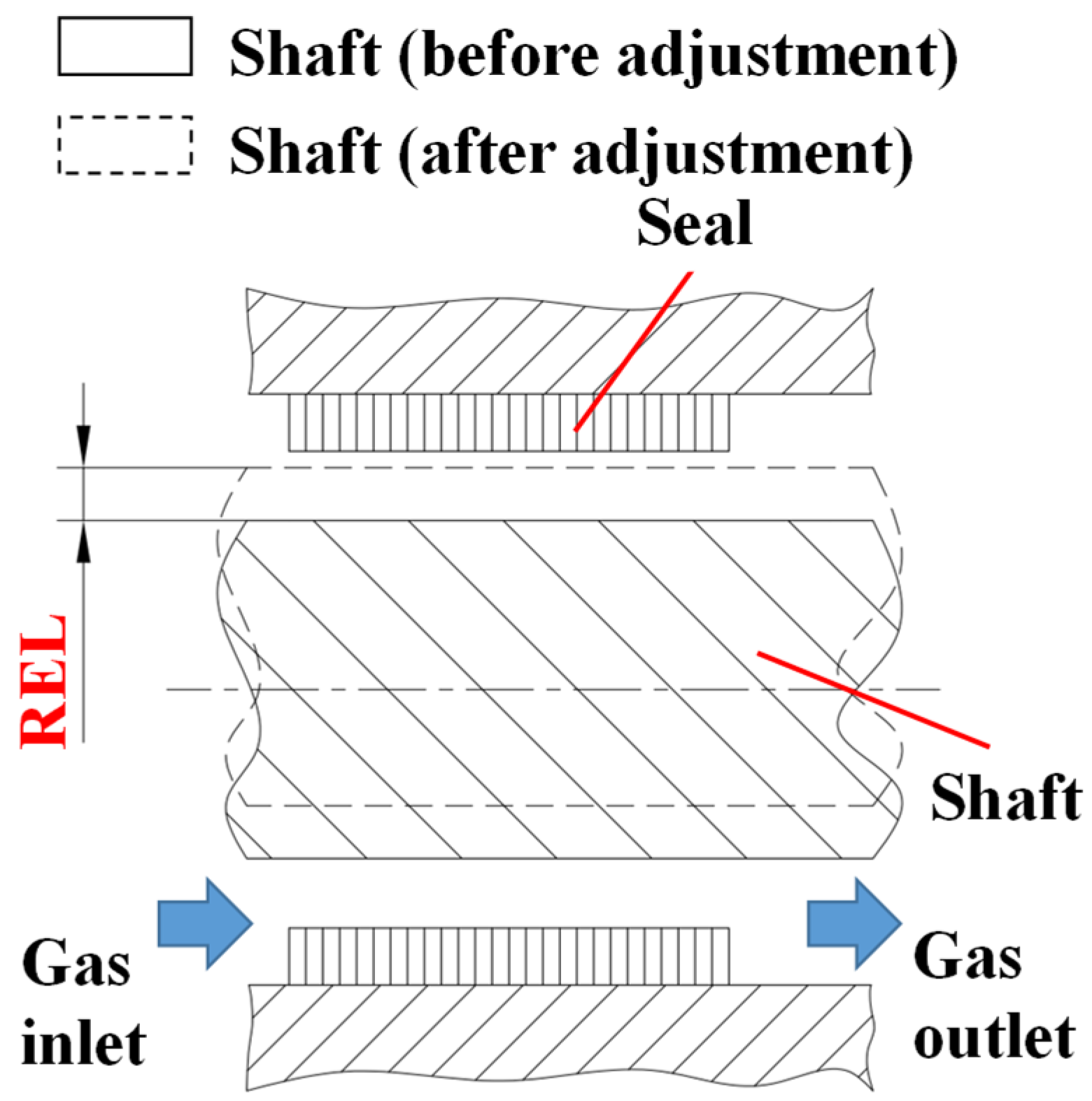
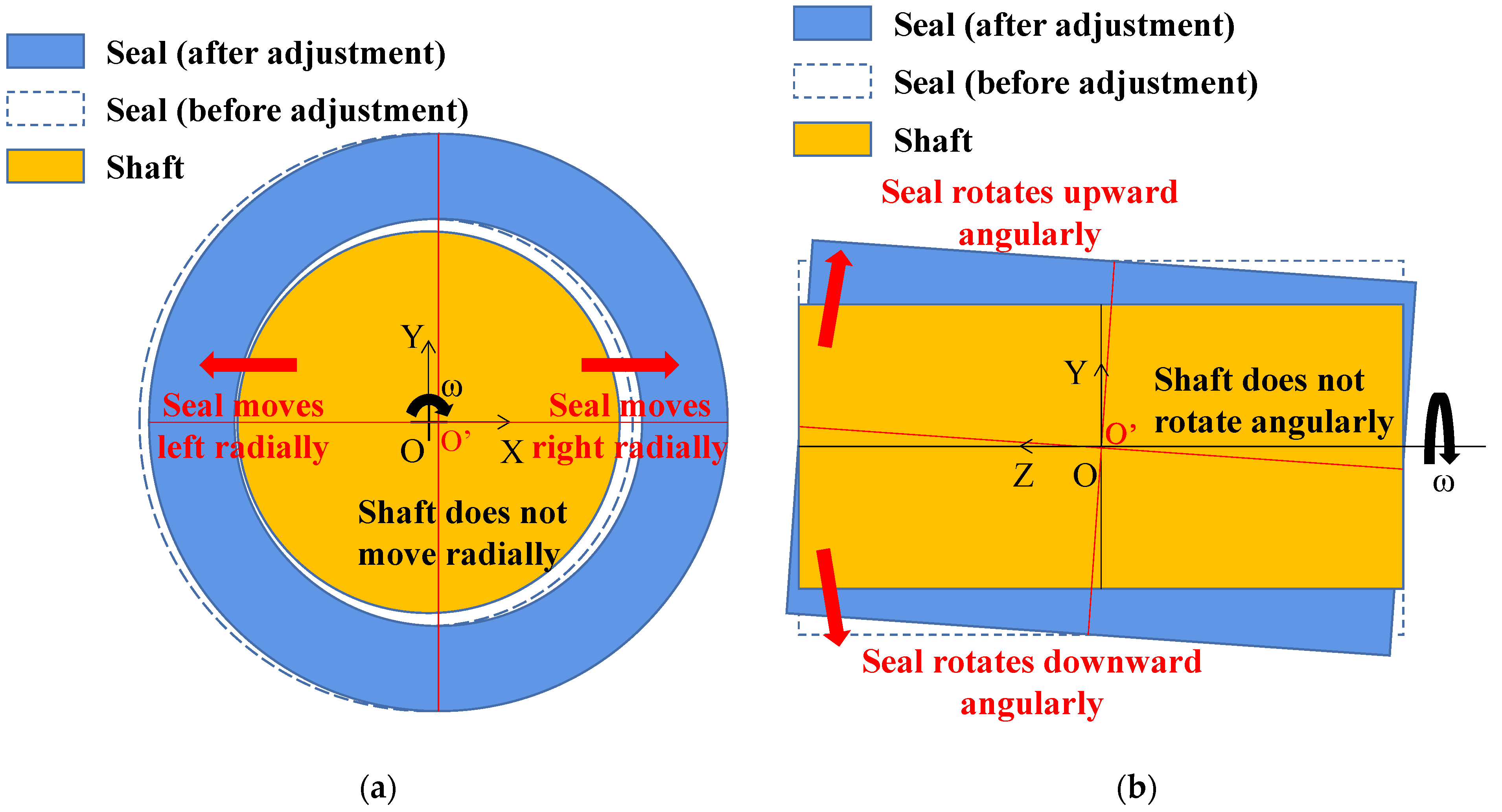
2.3. Analysis of the Effect of Radial Eccentricity on Seal Flow Field
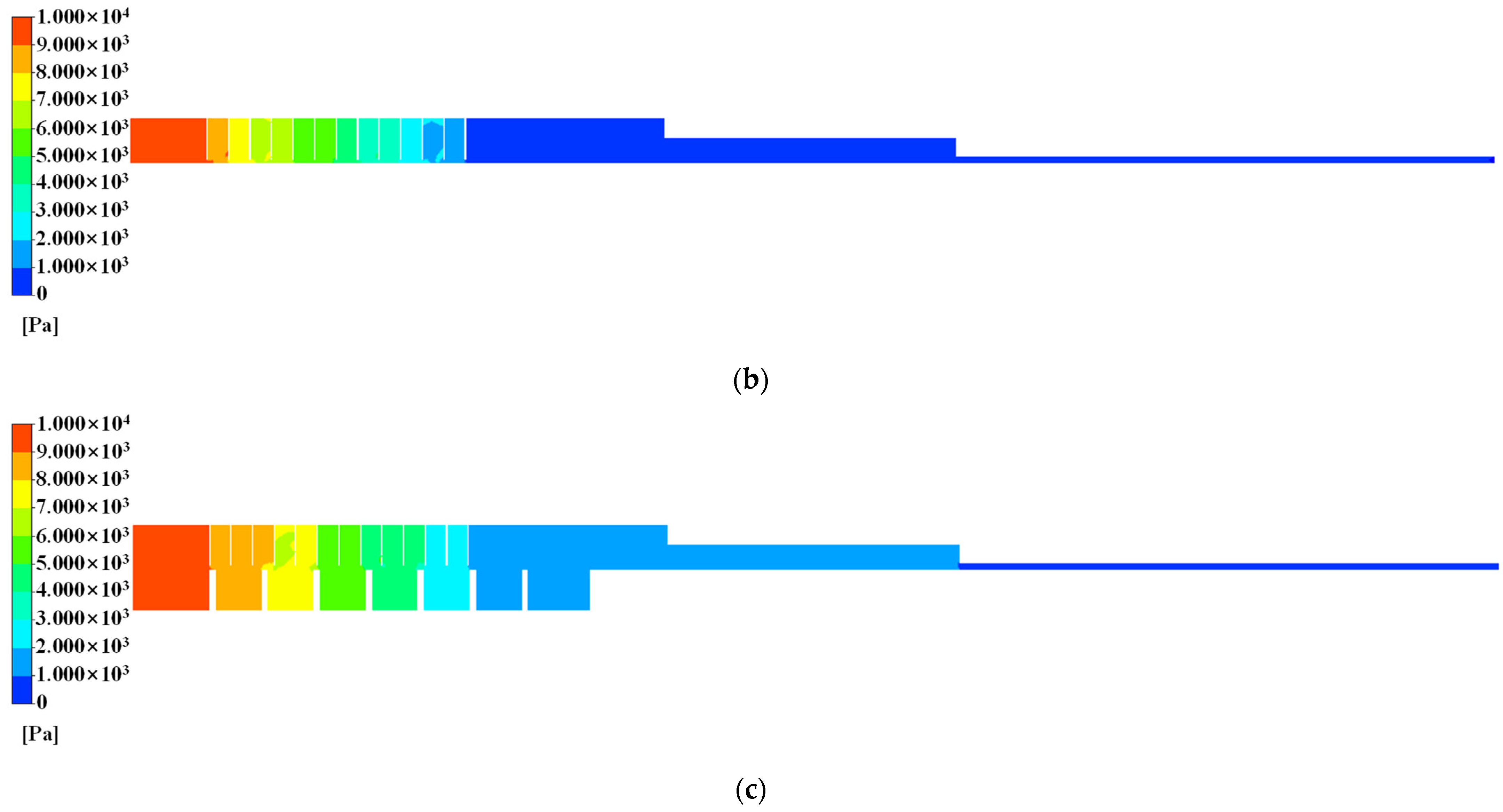
2.3.1. Analysis of Seal Leakage Characteristics under Radial Eccentricity
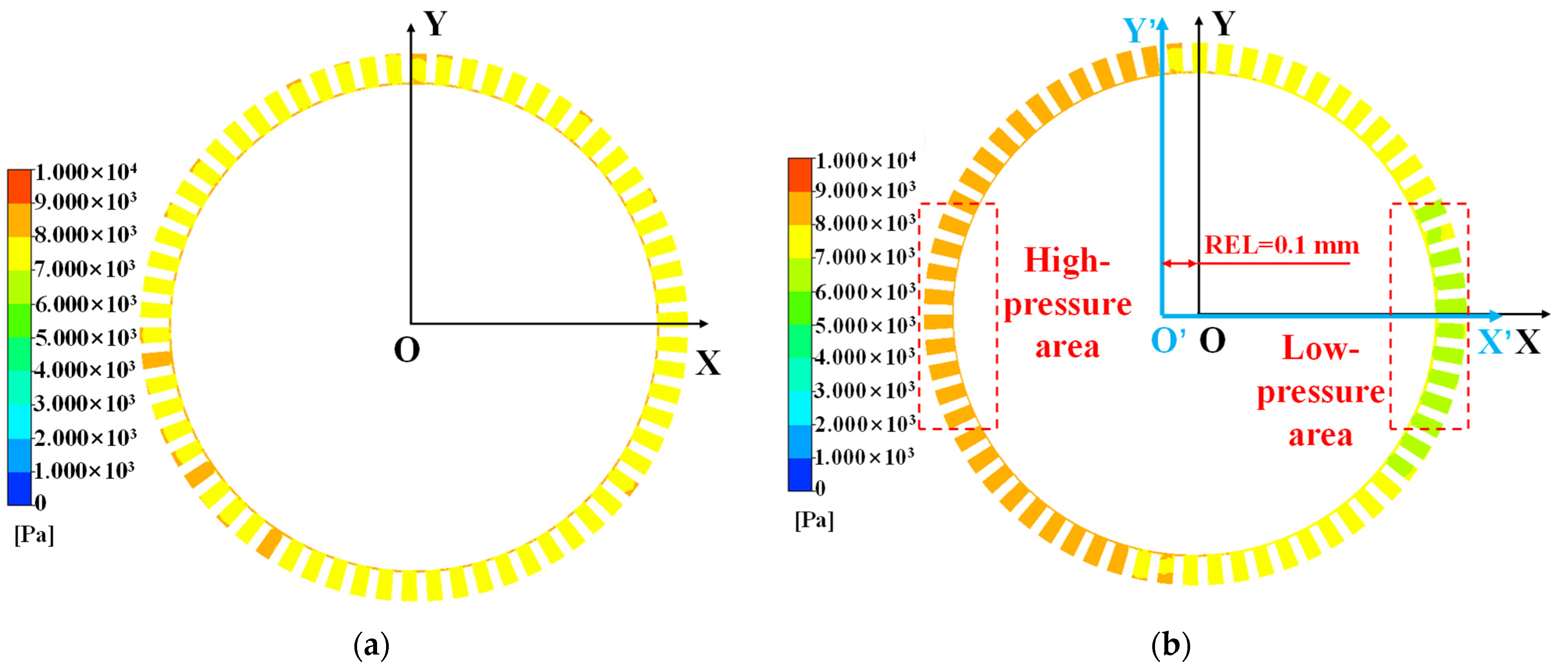
2.3.2. Analysis of Seal Flow Field Characteristics under Radial Eccentricity
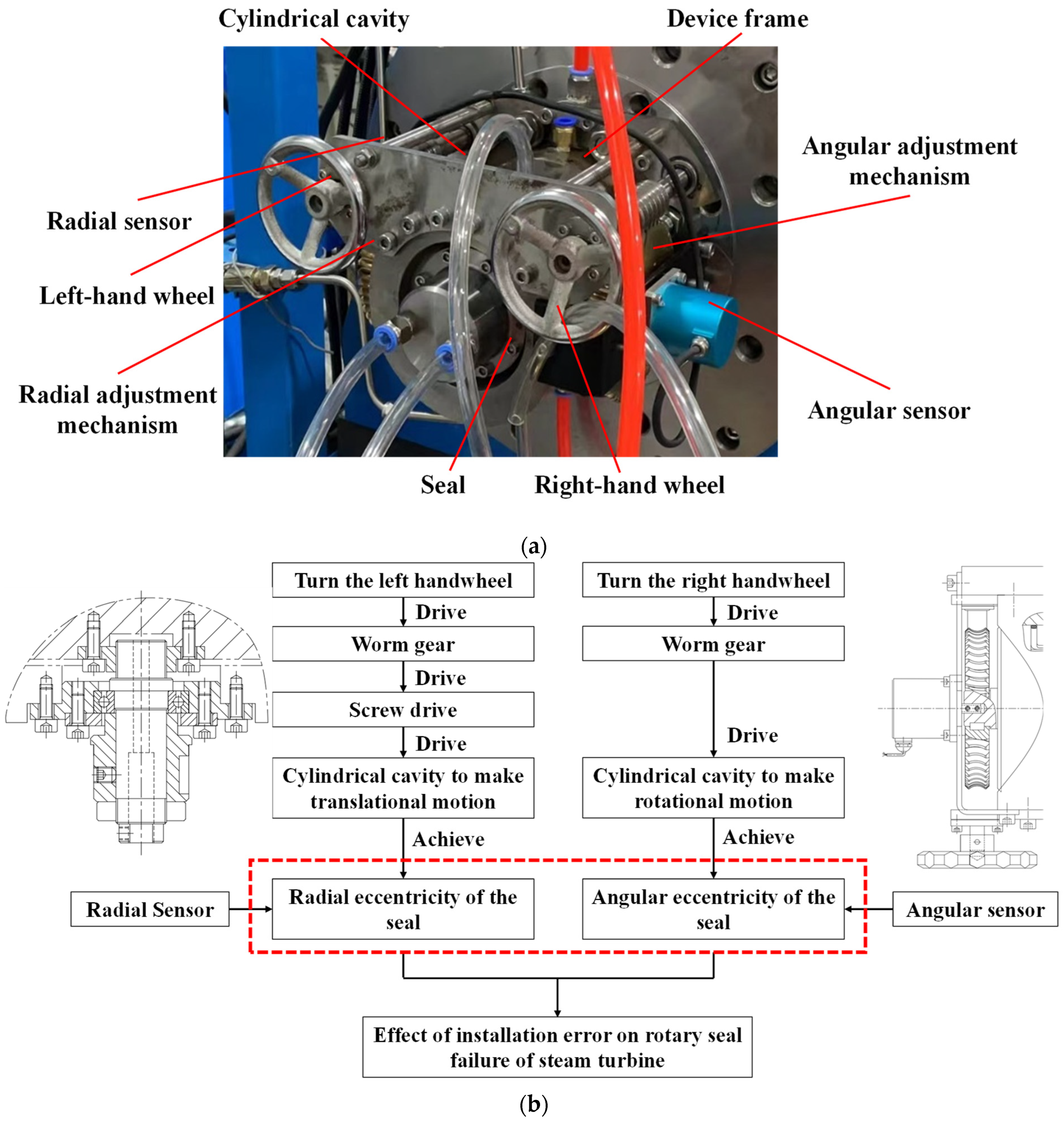
3. Introduction of the Experiment System
3.1. Introduction of Experiment Device
3.2. Introduction of Experiment Seals
3.3. Introduction of Experiment Plan
4. Experimental Analysis of Seal Leakage Characteristics
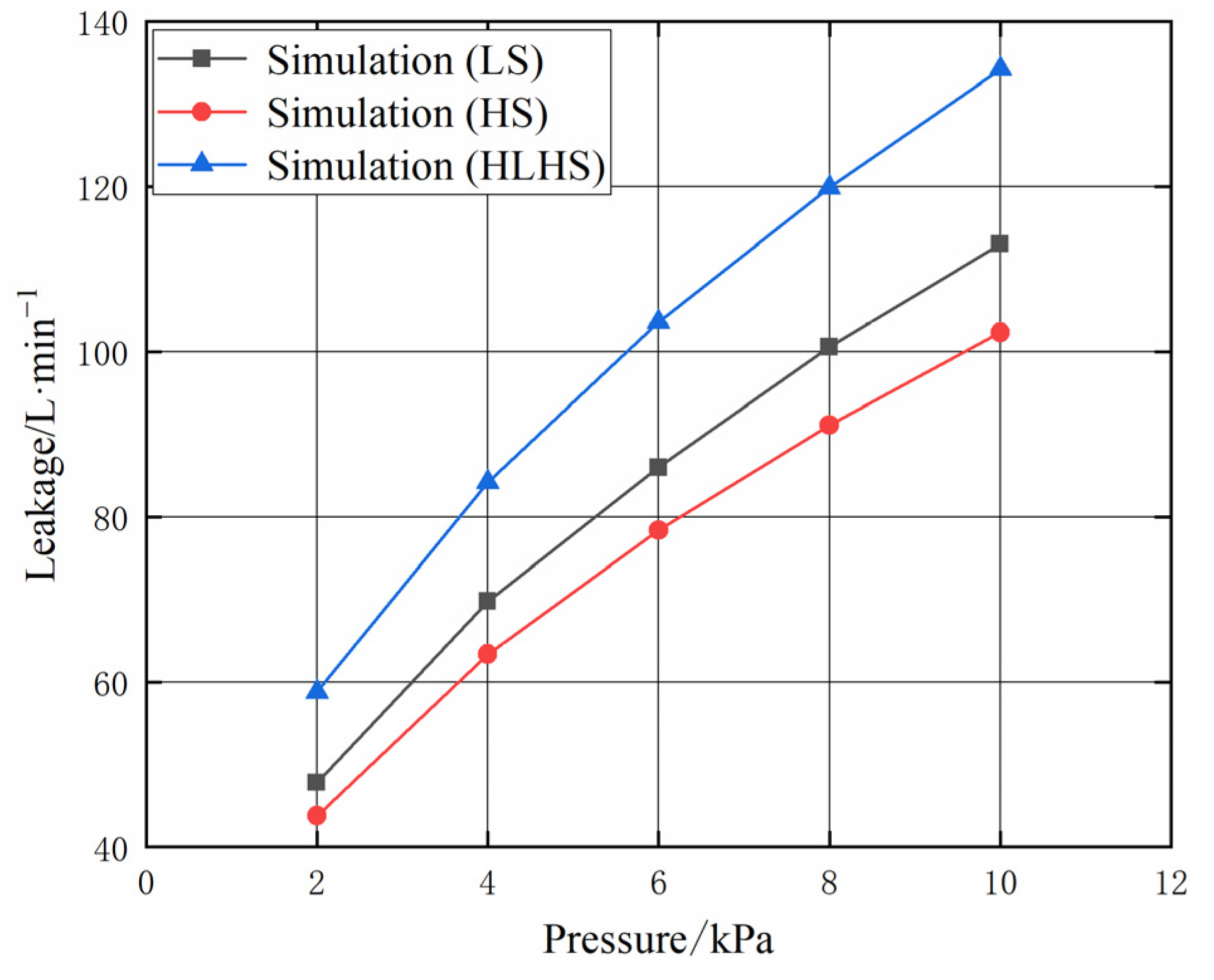
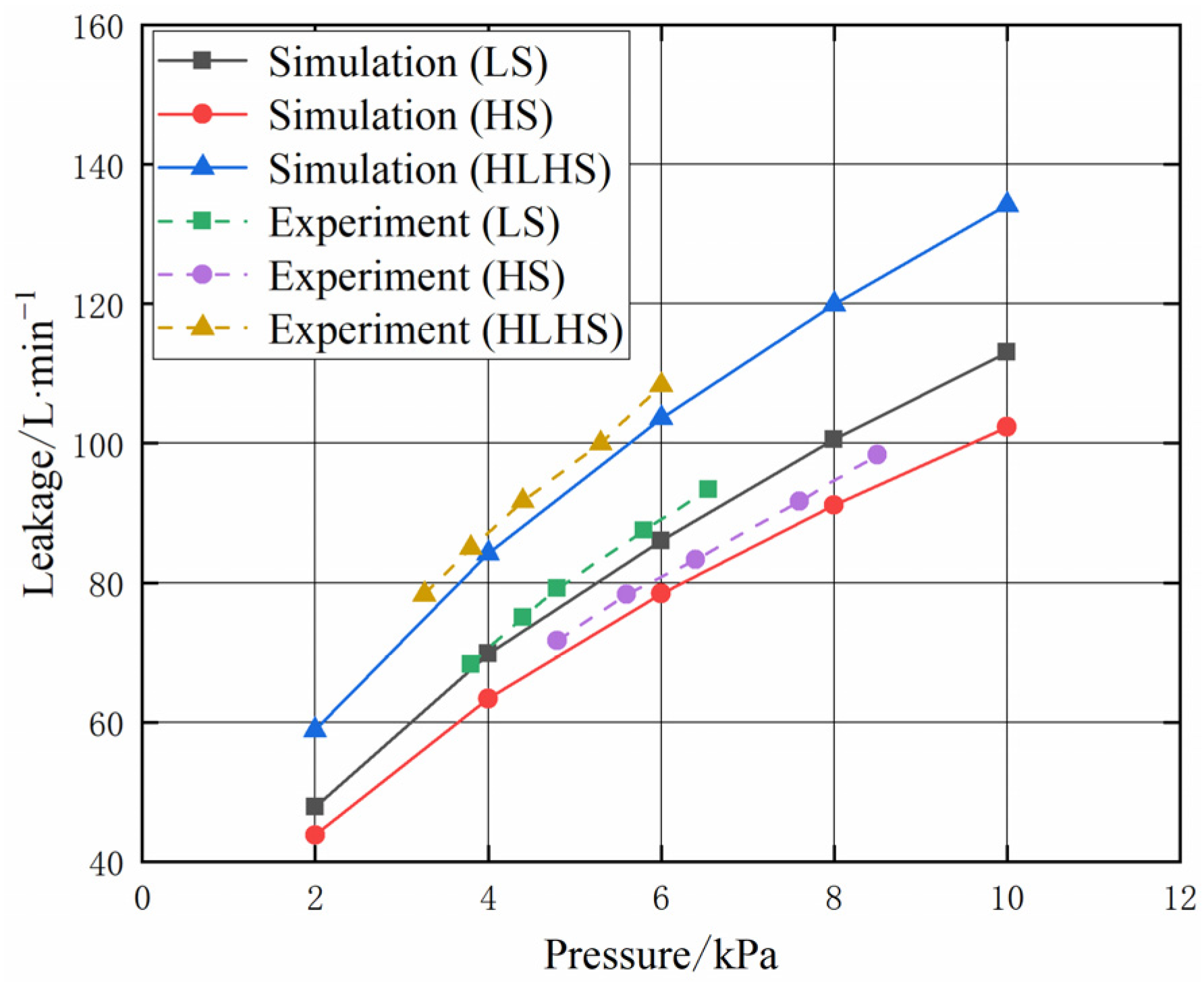
4.1. Verification of Theoretical Analysis Results of Seal Flow Field
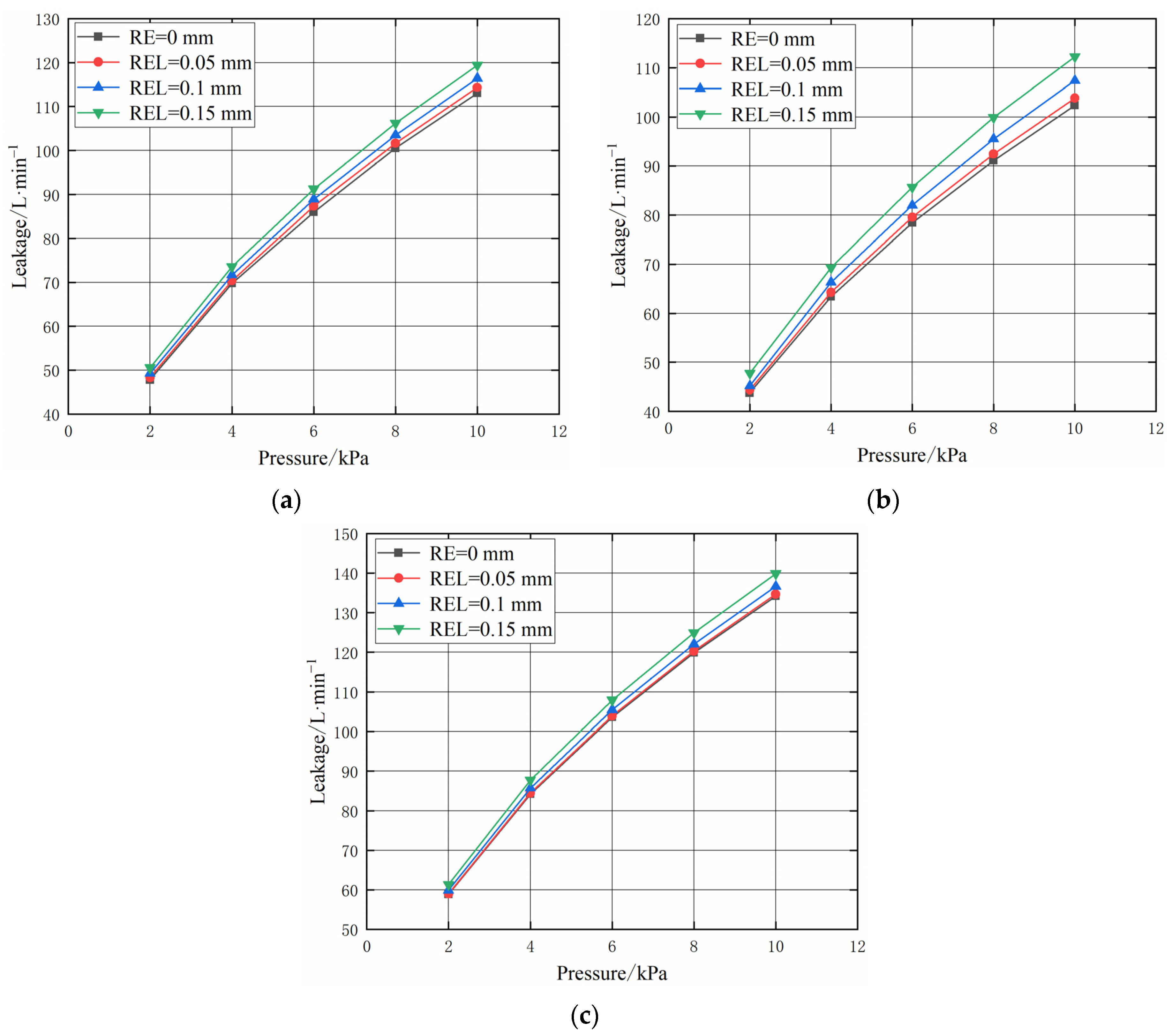
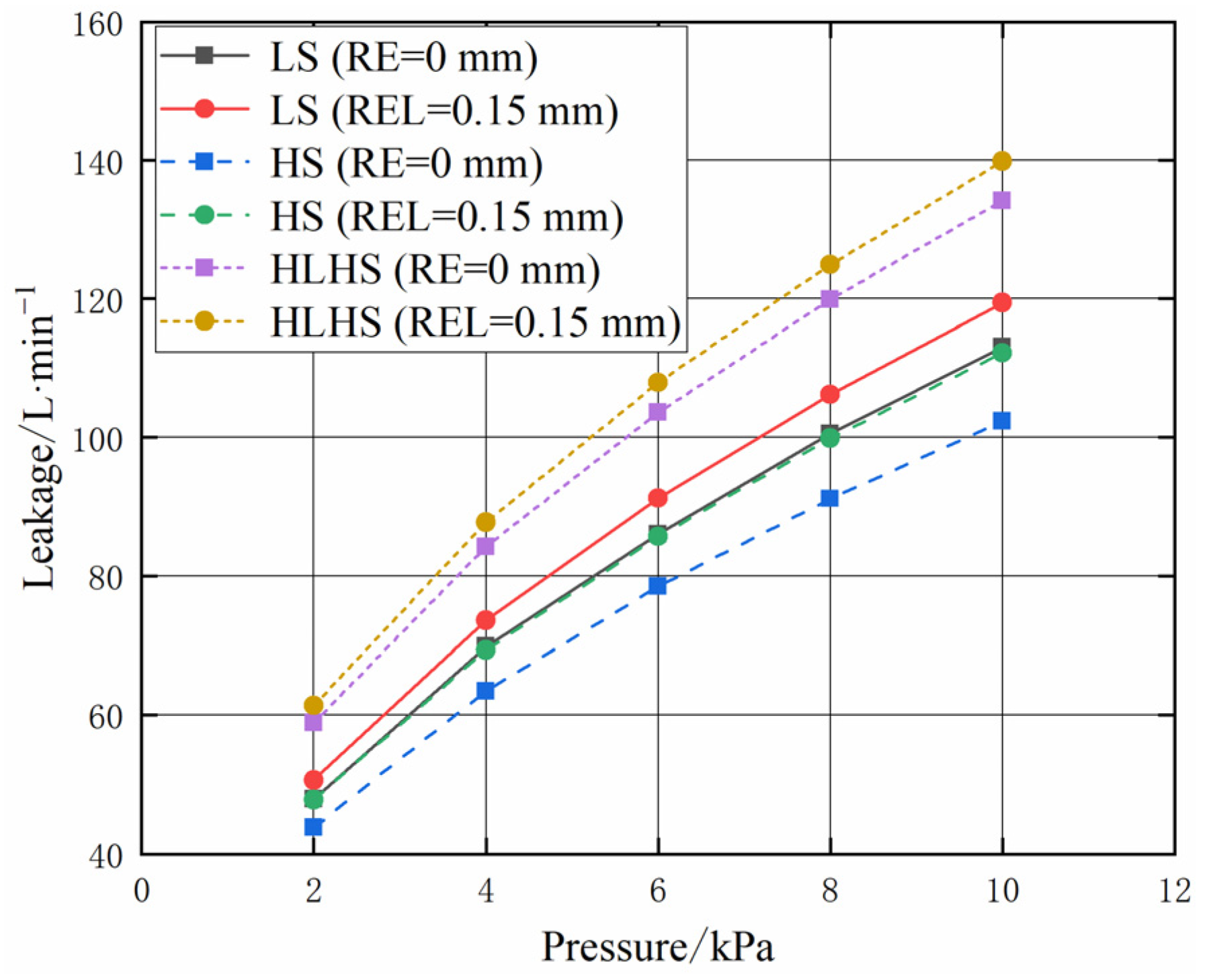
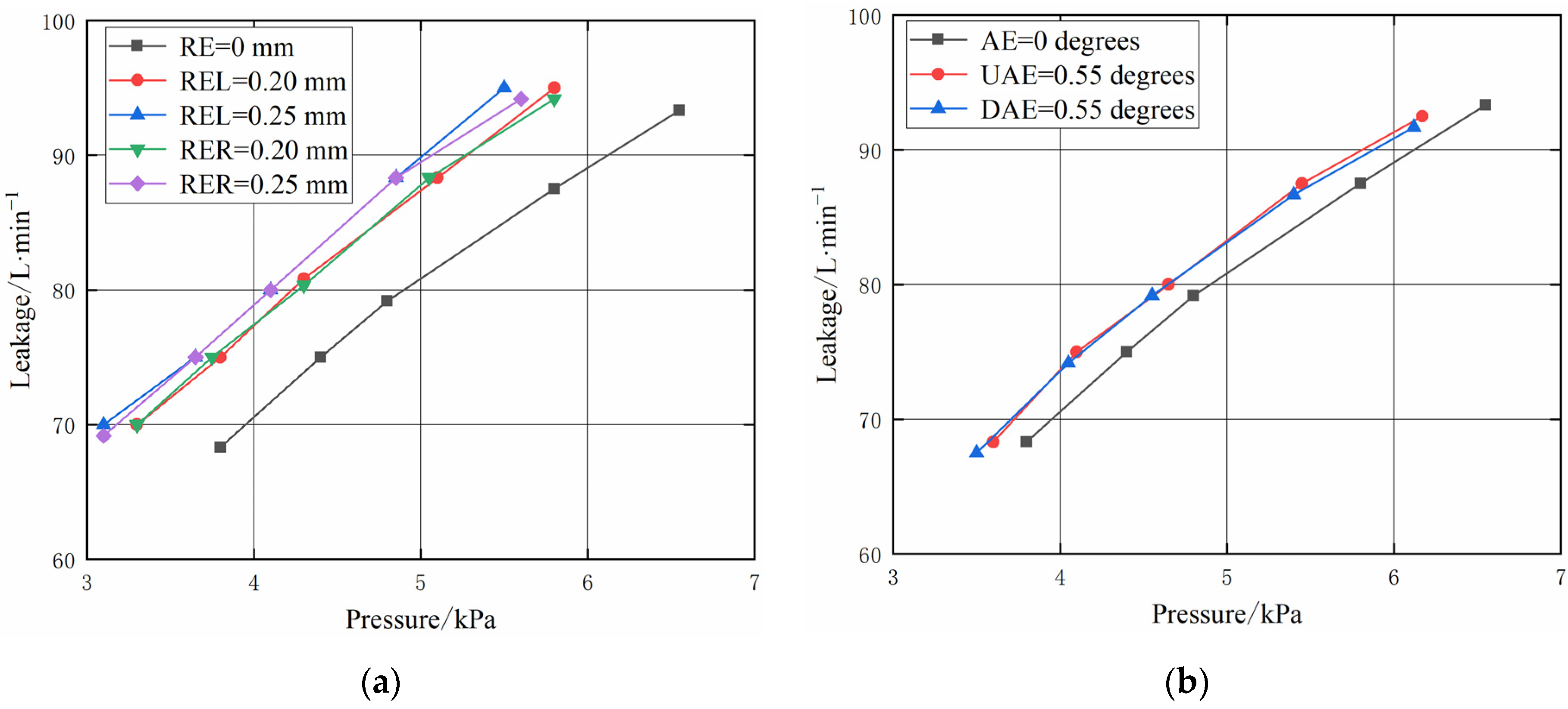
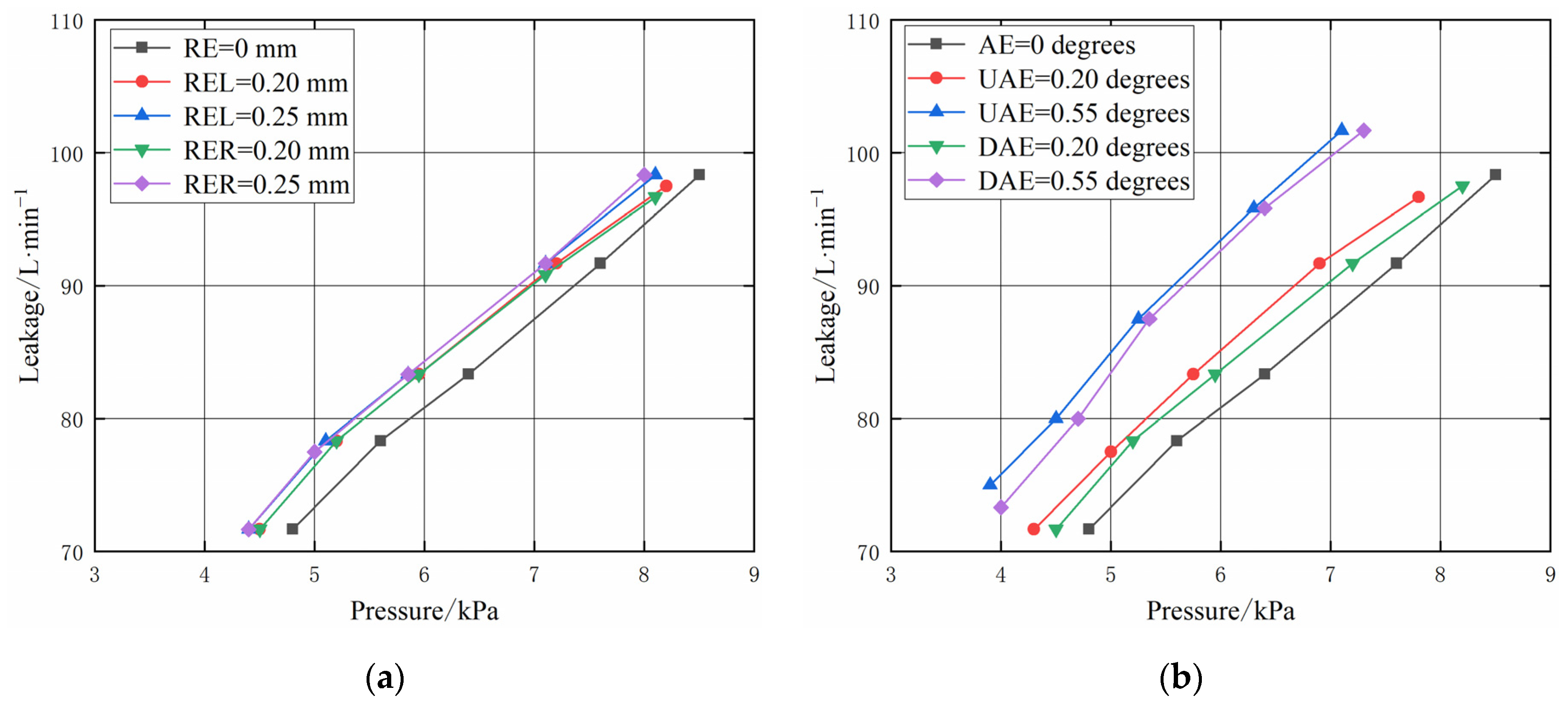
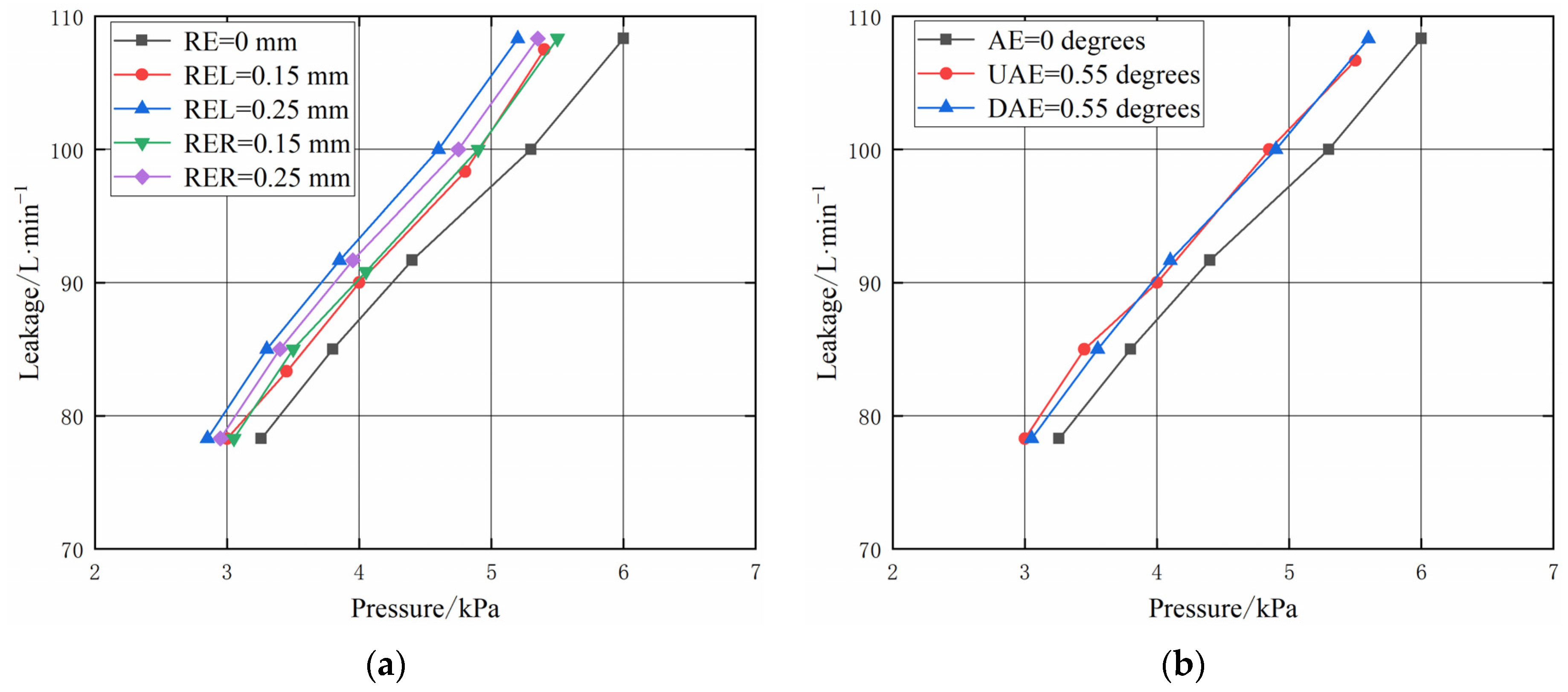
4.2. Analysis of Seal Leakage Characteristics under Eccentricity
4.3. Comparison of Seal Leakage Characteristics of Three Types of Seals
5. Conclusions
- (1)
- The numerical simulation results show that the turbulent kinetic energy of the gas in the honeycomb seal is the smallest, the turbulent kinetic energy of the gas in the labyrinth seal is the second, and the turbulent kinetic energy of the gas in the hybrid labyrinth–honeycomb seal is the largest. It shows that under the same working conditions, the kinetic energy of the gas in the honeycomb seal is converted into the most internal energy and the most fully dissipated. The kinetic energy of the gas in the hybrid labyrinth–honeycomb seal is converted into the least internal energy and the worst energy dissipation effect. Therefore, the seal performance of the honeycomb seal is better than that of the labyrinth seal, and the seal performance of the labyrinth seal is better than that of the hybrid labyrinth–honeycomb seal;
- (2)
- The experiment results show that when the radial installation error (radial eccentricity) is maximum, the leakage of the labyrinth seal increases by about 12.2% compared with that without radial installation error, the leakage of the honeycomb seal increases by about 5.3% compared with that without radial installation error, and the leakage of the hybrid labyrinth–honeycomb seal increases by about 7.8% compared with that without radial installation error;
- (3)
- The experiment results show that when the angular installation error (angular eccentricity) is maximum, the leakage of the labyrinth seal increases by 3.9% compared with that without angular installation error, the leakage of the honeycomb seal increases by 15.8% compared with that without angular installation error, and the leakage of the hybrid labyrinth–honeycomb seal increases by 5.0% compared with that without angular installation error;
- (4)
- The numerical simulation and experimental results show that, when there is installation error (eccentricity), the leakage relationship among the three types of seals is as follows: the leakage of the hybrid labyrinth–honeycomb seal is the largest, followed by the labyrinth seal, and the honeycomb seal is the smallest. Therefore, the honeycomb seal can better adapt to eccentricity. In the presence of eccentricity, a honeycomb seal should be preferred.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| B | The honeycomb cell diameter, mm |
| b | The honeycomb cell wall thickness, mm |
| c | The seal radius clearance, unit: mm |
| dLS | The diameter of shaft of labyrinth seal, mm |
| dHS | The diameter of shaft of honeycomb seal, mm |
| dHLHS | The diameter of shaft of hybrid labyrinth–honeycomb seal, mm |
| h | The seal depth, mm |
| T | The tooth spacing, mm |
| t | The tooth thickness, mm |
| Abbreviation | |
| AE | Angular eccentricity, degree |
| DAE | Downward angular eccentricity, degree |
| HLHS | Hybrid labyrinth–honeycomb seal |
| HS | Honeycomb seal |
| LS | Labyrinth seal |
| RE | Radial eccentricity, mm |
| REL | Radial eccentricity to the left, mm |
| RER | Radial eccentricity to the right, mm |
| UAE | Upward angular eccentricity, unit: degree |
References
- Yang, Y.C.; Mi, Z.G.; Zhang, W.C.; Chang, J.Q.; Liu, Y.J.; Zhong, B.T.; Yang, W.H. Experimental Study on the Effect of Rubbing Mode on Radial Crack Initiation in Labyrinth Seal Fins of Shrouded Turbine Blade. Aerospace 2022, 9, 441. [Google Scholar] [CrossRef]
- Munz, O.; Pychynski, T.; Schwitzke, C.; Bauer, H. Continued Experimental Study on the Friction Contact between a Labyrinth Seal Fin and a Honeycomb Stator: Slanted Position. Aerospace 2018, 5, 82. [Google Scholar] [CrossRef]
- Song, X.L.; Liu, M.H.; Hu, X.P.; Wang, X.L.; Liao, T.H.; Sun, J.F. Numerical Analysis of Flow across Brush Elements Based on a 2-D Staggered Tube Banks Model. Aerospace 2021, 8, 19. [Google Scholar] [CrossRef]
- Wang, W.Z.; Liu, Y.Z. Analysis of the sealing performance and creep behavior of the inner casing of a 1000 MW supercritical steam turbine under bolt relaxation. Eng. Fail. Anal. 2015, 57, 363–376. [Google Scholar] [CrossRef]
- Wang, W.B.; Pang, X.L.; Zheng, C.Z.; Volinsky, A.A. Failure analysis of high nickel alloy steel seal ring used in turbomachinery. Eng. Fail. Anal. 2017, 80, 49–56. [Google Scholar] [CrossRef]
- Nayak, K.C. Effect of rotation on leakage and windage heating in labyrinth seals with honeycomb lands. J. Eng. Gas Turbines Power 2020, 142, 081001. [Google Scholar] [CrossRef]
- Childs, D.W.; Moyer, D.S. Vibration characteristics of the HPOTP (high-pressure oxygen turbopump) of the SSME (space shuttle main engine). J. Eng. Gas Turbines Power 1985, 107, 152–159. [Google Scholar] [CrossRef]
- Gu, C.J.; Zhang, W.F.; Yang, X.C.; Cao, H.; Li, C. Effect of inlet preswirl and hole arrangement patterns on the dynamic characteristics of honeycomb seals. Chin. Soc. Electr. Eng. 2021, 41, 4208–4217. [Google Scholar]
- Qin, B.P.; Zhang, W.F.; Cao, H.; Yin, L.; Wang, Y.F.; Li, C. Static and dynamic characteristics of eccentric labyrinth seals. Tribology 2020, 40, 735–745. [Google Scholar]
- Kamouni, M. Prediction of leakage flow and rotordynamic characteristics for an eccentric labyrinth gas seal. J. Eng. Sci. Technol. 2017, 12, 2922–2938. [Google Scholar]
- Pugachev, A.O.; Kleinhans, U.; Gaszner, M. Prediction of rotordynamic coefficients for short labyrinth gas seals using computational fluid dynamics. J. Eng. Gas Turbines Power 2012, 134, 062501. [Google Scholar] [CrossRef]
- Untaroiu, A.; Morgan, N.; Hayrapetian, V.; Schiavello, B. Dynamic response analysis of balance drum labyrinth seal groove geometries optimized for minimum leakage. J. Vib. Acoust. 2017, 139, 021014. [Google Scholar] [CrossRef]
- Yahyai, M.A.; Mba, D. Rotor dynamic response of a centrifugal compressor due to liquid carry over: A case study. Eng. Fail. Anal. 2014, 45, 436–448. [Google Scholar] [CrossRef]
- Teran, L.A.; Roa, C.V.; Muñoz-Cubillos, J.; Aponte, R.D.; Valdes, J.; Larrahondo, F.; Rodríguez, S.A.; Coronado, J.J. Failure analysis of a run-of-the-river hydroelectric power plant. Eng. Fail. Anal. 2016, 68, 87–100. [Google Scholar] [CrossRef]
- Li, W.; Wang, X.; Zhang, X.H.; Zhang, X.J.; Zhu, Y.L.; Chen, H.S. Experimental and numerical investigations of closed radial inflow turbine with labyrinth seals. J. Eng. Gas Turbines Power 2018, 140, 102502. [Google Scholar] [CrossRef]
- Jia, X.Y.; Zheng, Q.; Jiang, Y.T.; Zhang, H. Leakage and rotordynamic performance of T type labyrinth seal. Aerosp. Sci. Technol. 2019, 88, 22–31. [Google Scholar] [CrossRef]
- Flouros, M.; Cottier, F.; Hirschmann, M.; Salpingidou, C. Numerical Investigation on Windback Seals Used in Aero Engines. Aerospace 2018, 5, 12. [Google Scholar] [CrossRef]
- Kong, X.Z.; Liu, G.W.; Liu, Y.X.; Zheng, L.X. Experimental testing for the influences of rotation and tip clearance on the labyrinth seal in a compressor stator well. Aerosp. Sci. Technol. 2017, 71, 556–567. [Google Scholar] [CrossRef]
- Zhao, Y.Z.; Wang, C.H. Shape Optimization of Labyrinth Seals to Improve Sealing Performance. Aerospace 2021, 8, 92. [Google Scholar] [CrossRef]
- Yang, X.C.; Zhang, W.F.; Gu, C.J.; Zhang, X.B.; Li, C. Leakage performance and static stability of hybrid labyrinth-honeycomb seals. Tribology 2021, 41, 738–748. [Google Scholar]
- Childs, D.; Elrod, D.; Hale, K. Annular honeycomb seals: Test results for leakage and rotordynamic coefficients; comparisons to labyrinth and smooth configurations. J. Eng. Gas Turbines Power 1989, 111, 293–300. [Google Scholar] [CrossRef]
- Soulas, T.; Andres, L.S. A bulk flow model for off-centered honeycomb gas seals. J. Eng. Gas Turbines Power 2007, 129, 185–194. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, R.; Sun, D.; Zhou, M. Influence Factors of Honeycomb Seal Performance and Stability Analysis of Rotor System. J. Aerosp. Eng. 2022, 35, 04022042. [Google Scholar] [CrossRef]
- Liu, C.R.; Yan, Z.; Wang, X.Z.; He, L.D.; Jia, X.Y.; Wang, W.H. Research on the influence of honeycomb cell blockage on the seal leakage characteristics. Int. J. Turbo Jet Eng. 2022. [Google Scholar] [CrossRef]
- Li, J.; Kong, S.R.; Yan, X.; Obi, S.; Feng, Z.P. Numerical investigations on leakage performance of the rotating labyrinth honeycomb seal. J. Eng. Gas Turbines Power 2010, 132, 062501. [Google Scholar] [CrossRef]
- Yan, X.; Li, J.; Feng, Z.P. Effects of inlet preswirl and cell diameter and depth on honeycomb seal characteristics. J. Eng. Gas Turbines Power 2010, 132, 122506. [Google Scholar] [CrossRef]
- Li, Z.G.; Li, J.; Feng, Z.P. Numerical investigations on the leakage and rotordynamic characteristics of pocket damper seals-part I: Effects of pressure ratio, rotational speed, and inlet preswirl. J. Eng. Gas Turbines Power 2015, 137, 032503. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; He, L.; Jia, X.; Zhu, H.; Chen, T.; Wang, W. Effect of Installation Error on Rotary Seal of Aero Engine. Aerospace 2022, 9, 820. https://doi.org/10.3390/aerospace9120820
Liu C, He L, Jia X, Zhu H, Chen T, Wang W. Effect of Installation Error on Rotary Seal of Aero Engine. Aerospace. 2022; 9(12):820. https://doi.org/10.3390/aerospace9120820
Chicago/Turabian StyleLiu, Chunrui, Lidong He, Xingyun Jia, Haozhe Zhu, Tao Chen, and Wenhao Wang. 2022. "Effect of Installation Error on Rotary Seal of Aero Engine" Aerospace 9, no. 12: 820. https://doi.org/10.3390/aerospace9120820
APA StyleLiu, C., He, L., Jia, X., Zhu, H., Chen, T., & Wang, W. (2022). Effect of Installation Error on Rotary Seal of Aero Engine. Aerospace, 9(12), 820. https://doi.org/10.3390/aerospace9120820





