Abstract
Active fault-tolerant control systems perform fault diagnosis and reconfigurable control. There is a bidirectional uncertainty between them, and an integrated scheme is proposed here to account for that. The system considers both actuator and sensor faults, as well as the external disturbance. The diagnostic module is designed using an unknown input observer, and the controller is constructed on the basis of an adaptive method. The integrated strategy is presented, and the stability of the overall system is analyzed. Moreover, different kinds of anti-windup techniques are utilized to modify the original controllers, because of the different controller structures. A simulation of the integrated anti-windup fault-tolerant control method is demonstrated using a numerical model of Boeing 747. The results show that it can guarantee the stability of the post-fault aircraft and increase the control performance for the overall faulty system.
1. Introduction
The electrical flight control system (EFCS) is the industrial standard for commercial aircraft and has been widely used in the aviation sector, because it can improve the safety and performance of aircraft [1]. Following the development of commercial aircraft, EFCSs are becoming more complex than before and the performance requirements (such as safety, reliability, maintainability, etc.) have increased [2]. In response to this, fault-tolerant control (FTC) has gained importance because it can deal with system faults automatically, make the system stable, and regain the performance of faulty aircraft. Furthermore, fault signal monitoring has improved so that the integration of estimation and reconfiguration has attracted particular interest during the last decade [3].
FTC consists of passive fault-tolerant control (PFTC) and active fault-tolerant control (AFTC) [4]. In PFTC, a class of presumed faults are tackled by the designed controller, so that it is a special kind of robust control. The structure of the controller is simple because there is no need to add a diagnostic module, but the fault-tolerant capability is limited [5,6]. Thus, recently the focus has been on AFTC because of its outstanding fault handling capability [7,8,9,10,11,12,13]. The main feature of AFTC is that it contains both estimation and reconfiguration. In most of the literature works, these two modules are designed independently in the FTC system, and the estimation is only used for monitoring or diagnosis. Moreover, the capability of it is often overrated, and very few articles concentrate on the integrated scheme of fault-tolerant controller design.
To design an active fault-tolerant controller capable of addressing the mentioned difficulties, it is necessary to develop an integrated design method, with no need for a prior knowledge of faults. There are few papers about the integration of estimator and controller. In [14], a robust observer was presented to obtain system states and actuator faults. The linear matrix inequality (LMI) technique was utilized to reconfigure the controller. A disturbance observer was proposed to obtain fault signals in [15]. Based on the designed estimator, a controller is reconfigured using a modified fuzzy dynamic output feedback method to address faults (actuator or sensor) and mismatched input disturbances. The authors of [16] presented an integrated strategy of AFTC where the PD extended state observer was designed to estimate system states and actuator/sensor faults, and the control law was designed using a modified LMI-based robustness procedure. A reduced-order observer was to deal with the problem of fault estimation and a reconfigurable controller was built for nonlinear discrete-time systems in [17]. In the existing integrated strategy, adaptive control and robust control were used, and the theorems are mathematically correct. However, there are several weaknesses when applying this in EFCSs, because of the many assumptions about the rank of the system matrices.
Furthermore, the phenomenon of actuator saturation is important in the integrated reconfigurable strategy, because aircraft actuators are physically limited and faults will decrease their capability. Many works have focused on the combination of anti-windup and FTC [18,19,20,21,22,23,24]. The common design process is designing an original reconfigurable controller and modifying it using different anti-windup methods. In the cited literature, the magnitude saturation has been well addressed, however the rate limiting (another important constraint) has been ignored. Moreover, the integrated design strategies which can tackle the pairing between the estimation and reconfiguration have not been used, so that the real-time reconfigurable performance can not be guaranteed.
With respect to the mentioned problems, the contributions of this paper mainly include the following two points. First, different from the works in [7,8,9,10,11,12,13], an integrated reconfigurable control strategy is presented to cancel the pairing between estimator and controller, and to improve the performance of the controller. Moreover, compared with the works in [14,15,16,17], both actuator and sensor faults are considered in the design of integrated fault-tolerant control. Second, two common actuator constraints (magnitude and rate) are considered to design the anti-windup FTC scheme using different techniques. In contrast with the proposed anti-windup reconfigurable controller, most of the existing anti-windup schemes can just address the magnitude saturation [18,19,20,21,22,23,24].
The rest of this paper is organized as follows. Section 2 gives the normal/post-fault aircraft modeling. In Section 3, the integrated strategy and their anti-windup modifications are given. In Section 4, the simulation results and analyses are presented, and Section 5 reports conclusions of this paper.
The following notations will be used throughout the paper: I signifies an identity matrix, signifies the diagonal matrix, and signifies the pseudo-inverse.
2. System Modeling
It is necessary to construct an appropriate aircraft model for the integrated design. The model of an aircraft during normal operation (without faults and actuator constraints) is described as
where denotes the system state, in which is the forward velocity, is the vertical velocity, q is the pitch angle rate, is the pitch angle, and denotes the system output, and denotes the system input, in which is the perturbation from trim in the ith elevator. A, B, and C are the system matrix, the input matrix, and the output matrix, respectively. The detailed expressions are shown in Appendix A.
If the aircraft operates in the presence of actuator and sensor faults, system (1) can be rewritten under the fictitious multiplicative fault formulation as
where denotes the controller outputs, denotes the fictitious multiplicative actuator fault value, is an indication matrix, is the effectiveness factor, denotes the additive actuator fault value, d denotes the external disturbance, denotes the measured output, and denotes the sensor fault value. The detailed modeling and analysis for faults can be found in reference [25].
Assumption 1
([5]). All of the faults and disturbance in (2) are norm-bounded, and the first time derivatives of faults are norm-bounded, too.
Considering Assumption 1, we can augment the faulty system (2) into
where , , , , .
3. Integrated Strategy and Anti-Windup Modification
In the AFTC strategy, there is a pairing between the estimation and reconfiguration, that is, the controller needs fault information provided by the estimator, and the estimator needs to know which strategy is available for reconfiguration [5]. Moreover, the actuator saturation is the most common nonlinearity in a control system and affects its stability [26]. Thus, the integrated fault-tolerant control scheme and its anti-windup modification are important for EFCS because they guarantee the aircraft to track the command signal in the presence of actuator faults and saturations. Inspired by this problem, a novel integrated anti-windup method for linear systems is presented.
3.1. Integrated Reconfigurable Controller Design
An integrated scheme is utilized to design the reconfigurable controller in this subsection. In the augmented faulty model (3), the unknown fault values , , and are contained in and are obtained by using the diagnostic module. The design procedure of the integrated strategy contains three steps: (1) Design a reconfigurable controller to control the aircraft to track the desired command, (2) design a fault estimator to estimate the states of the augment faulty system, and (3) calculate the undecided parameters of the controller and estimator by analyzing the stability of the overall system.
Augment the healthy system (1) into
where , , , .
The reference control law is chosen as
where is the controller state vector, r is the command signal, and and are control gains.
Thus, the reference model (as a command generator) represented by the augmented system (4) and the reference controller (5) is obtained as
where , , , , .
The system dynamics is completely controllable by calculating the controllability matrix, and the detailed data are given in the Appendix A. An optimal control technique (such as LQR) is used here to adjust the reference controller gains. The detailed design procedure can be found in [7], and thus it is omitted here.
Moreover, the system dynamics can be derived from (3) by introducing a new control variable as
where , , , , , .
Defining the error between the reference model state and the system state as , a reconfigurable control law is chosen as
Substituting the reference model (6), the system (7), and the control law (8) into the error expression yields
where .
and are control gains, and are designed by analyzing the stability of the post-fault aircraft model, that is, ensuring where is a Hurwitz matrix. The term represents the errors between the faulty aircraft and the reference model, and it affects the control performance. Furthermore, the control gains are calculated by an adaptive integrated strategy to address the unknown external disturbance and system parameter errors.
In the design procedure of the fault estimator, an observer is described as
where is the observer state vector and is the estimate of . The remaining undefined matrices are designed observer gain matrices.
The design objective is to make sure that the error between the faulty system state and its estimate converges to zero. Substituting (3) and (10) into yields
where , .
Remark 1.
The observer matrices are designed by analyzing the stability of the system, that is, ensuring , where M is Hurwitz. The term represents a coupling between estimator and controller, and it affects the estimation performance. The integrated scheme is shown in Figure 1. The following theorem is proposed to guarantee the stability of the overall system and to calculate the corresponding adaptive adjustment laws.
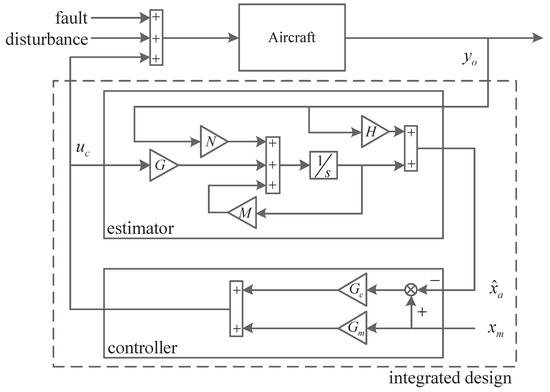
Figure 1.
Block diagram of the integration.
Theorem 1.
Proof.
Rewrite the controller error dynamic system as
where is a Hurwitz matrix, , and .
A Lyapunov candidate function is chosen as
where , .
Setting and so that and , the first and second items of (12) are obtained. Moreover, setting yields . Thus, the rest of (15) is transformed into
where .
As is Hurwitz, it can be concluded that is the unique solution of the following Lyapunov matrix equation:
where is any symmetric positive-definite matrix.
Remark 2.
The errors and are always nonzero in the application so that it is necessary to integrate the estimator and the controller. The adaptive laws cancel the adverse effect of the coupling and improve the capability of the reconfigurable control.
3.2. Anti-Windup Mechanisms
Actuator constraints consist of rate and magnitude saturation. In this paper, a modified software rate limiter () is utilized to address the rate constraint problem. As shown in Figure 2, the plants “” and “” consist of actual aircraft models, “” represents the ultimate reference controller (the original controller with/without a compensator), “” represents the ultimate reconfigurable controller, “M” is the reference model, and the actuator “A” is position-controlled and is subject to saturation of physical systems (i.e., they only provide a certain amount of force or moment). In this scheme, the reference controller is modified by , and a signal has taken the place of the limiter in its quasilinear part. The reconfigurable controller can also be modified by , and another signal has taken the place of the limiter in the post-fault model. If the physical limitations of the actuators are not considered in the design procedure, the control performance will not be satisfactory and could possibly even lead to disastrous consequences. It is difficult to design integrated anti-windup controllers because of the different controller structures. The type of (the Laplace transform of ) and (the Laplace transform of ) are denoted as and , respectively [29].
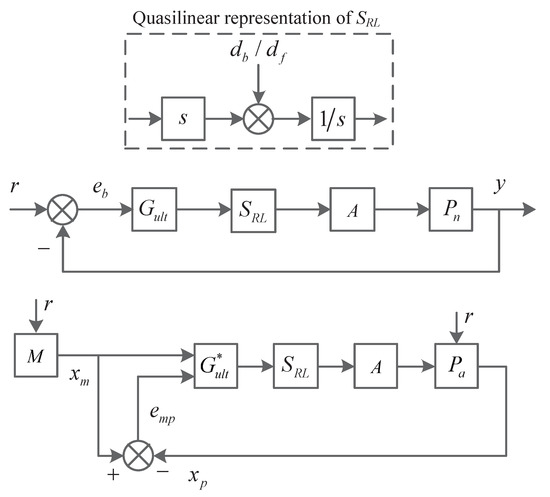
Figure 2.
The reference controller with module.
Assumption 2
([30]). Whether actuators work in saturation or not, the normal and post-fault aircraft with are stable, and two feasible conditions are and .
Theorem 2.
The stable system with rate limiters will exhibit asymptotic stability in response to the injected signals and , if the types of ultimate controllers are more than zero.
Proof.
The block diagram algebra for the normal system can be got from Figure 2 as
where is the error, R is the command signal, and Y is the system output. The majuscules denote the Laplace transform of their corresponding time functions. The actuator “A” is ignored in this algorithm, because the linear part of “A” is insignificant and the rate constraint in it can be canceled by . The detailed actuator model is shown in Appendix A.
Applying the final value theorem, it can be obtained that
As , the type of the first item is and the type of the second item is . The stable normal system with rate limiters is going to achieve asymptotic stability if and , i.e., . Considering Assumption 2, should hold.
Furthermore, the block diagram algebra for the faulty model is shown as follows:
where , , and denote the plant elements, respectively, and is the ultimate expression of . Other majuscules are the Laplace transforms of their corresponding signals.
Applying the final value theorem, it can be obtained from (20) that
In a similar way, all the types of terms on the right-hand side of (21) should be less than zero. Thus, should hold. This completes the proof of Theorem 2. □
Remark 3.
In this paper, satisfies , so that it is not necessary to add a compensator to the original controller; however, does not satisfy , so that in this case the ultimate controller can be defined with a compensator as .
Remark 4.
Based on the work in [30], the software rate limiters can provide enough stability margins for the linear design. Assumption of closed-loop stability is just the first step to analyze Theorem 2, so that the final value theorem can be utilized. We can use the asymptotic stability to derive a condition about the type of the injected signals and the type of controllers. The designed rate limiters and compensators may decrease the performance of the unconstrained system, but the performance of the constrained system is improved.
For the magnitude saturation problem, as the reference controller and reconfigurable controller have different block diagram architectures, different schemes should be used to modify these two controllers. An observer-based scheme is utilized to modify the reference controller to mitigate windup, as shown in Figure 3. The control signal will not reflect the plant if there is a mismatch between and , which is the reason causing windup. The modified reference controller is given as
where is the designed gain matrix. The design task is choosing such that is Hurwitz. An effective design procedure is to analyze the difference between a system with actuator constraint and a system without it. The unconstrained normal system with state vector is shown as
and the constrained normal system with state vector is shown as
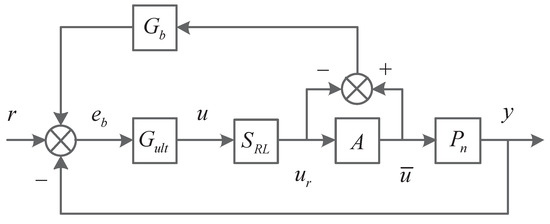
Figure 3.
The reference controller with anti-windup module.
Finally, the mismatch between the two systems is shown as . Subtracting (23) from (24), the mismatch system is shown as
Assuming can be decomposed as and choosing , the gain is designed as
where is the last columns of , and is the remaining column of . The closed-loop system exhibits asymptotic stability.
Remark 5.
The observer-based approach is intuitively appealing as the concept of the observer is widely used [26]. Amplitude constraint is addressed by feeding back the error between and to the reference controller, and it will not be modified when .
As shown in Figure 4, the anti-windup problem in the reconfigurable controller is tackled by using a modified conditioning technique. “O” represents the estimator, and “” represents the reconfigurable controller consisting of a compensator and a software rate limiter. is chosen as the reference signal and the controller is described as
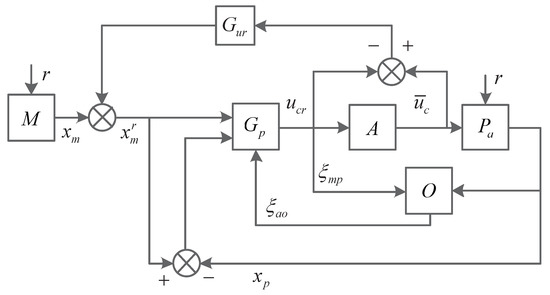
Figure 4.
The reconfigurable controller with anti-windup module.
In the conditioning technique, an auxiliary input , which is called realizable reference, is chosen as a new reference signal to make sure that there is no difference between and . The new controller is
Note that the actual reference signal does not appear in (28), so that an assumption on the present realizability () of the control is held as
Remark 6.
In the modified conditioning technique case, the realizable reference removes the effect of the nonlinearity on the system input, so that the reconfigurable controller is “conditioned” back to the unconstrained mode as soon as it can.
4. Application Example
The integrated anti-windup scheme is simulated on a numerical model of Boeing 747, which is trimmed at straight and level flight. The external disturbance is defined as a uniform “1-cosine” vertical gust [31]. Two flight conditions are shown in Table 1 and Table 2, respectively. The detailed data for this aircraft are obtained solely from a Boeing 747 simulator description (Boeing D6-30643) and are provided in the NASA report [32].

Table 1.
Flight condition 1.

Table 2.
Flight condition 2.
4.1. Anti-Windup FTC in Condition 1 at 0.5 Ma and 20,000 ft
In this condition, the reference command is a step signal given at 2 s, the elevator is locked in , the surface deflection loses effectiveness, the bias of the sensor is , and all faults are given at the same time (0 s), that is, , , , and . The limits of magnitude and rate are and /s, respectively.
Figure 5a shows the necessity of the FTC strategy because there is a significant decrease for control performance in the post-fault aircraft with LQR (red) than in the healthy aircraft with LQR (blue). In Figure 5b, however, the control performance of FTC in the post-fault aircraft (red) is nearly the same as the one of the LQR in the normal aircraft (blue). When there are magnitude and rate saturation modules in the actuators, as shown in Figure 6, the FTC method without anti-windup (red) will reduce the control performance or even make the system unstable. The anti-windup reconfigurable method is designed using a compensator (blue) to deal with the windup phenomenon and regains the performance of the post-fault aircraft. Figure 7 shows the estimates of actuator and sensor fault values. They are estimated accurately using the proposed estimator at about 5 s after occurrence. The faulty aircraft model with actuator saturation modules (magnitude and rate) is used in Figure 8. It compares the actuator deflections (, , , ) and rates (, , , ) between the original FTC method and the FTC with capability of anti-windup. The actuators with FTC meet their constraints so that the aircraft is unstable; on the contrary, the proposed anti-windup modifications mitigate the effects of saturation and guarantee the stability of the aircraft.
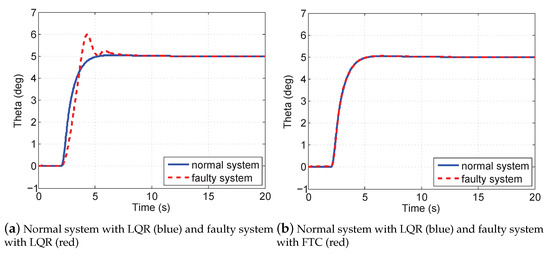
Figure 5.
Effect of the integrated fault-tolerant strategy.
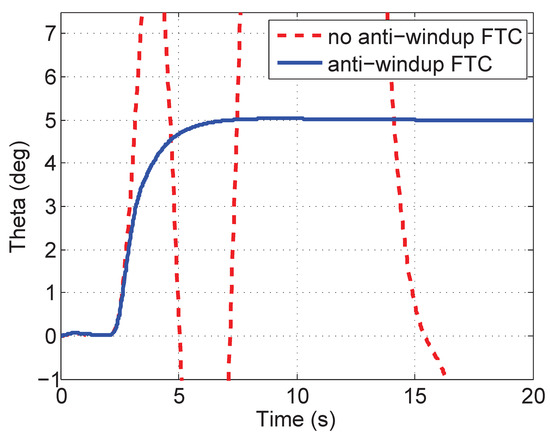
Figure 6.
Comparison between FTC without constraints (red) and anti-windup FTC with constraints (blue).
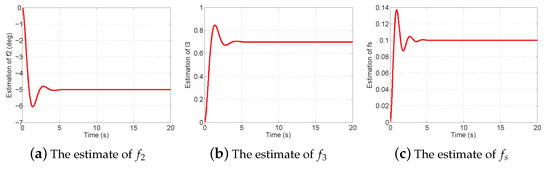
Figure 7.
Estimates of fault values.
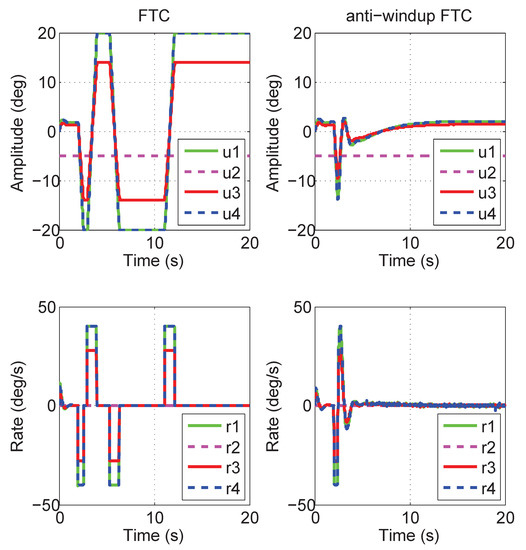
Figure 8.
Actuator deflections and rates.
4.2. Anti-Windup FTC in Condition 2 at 0.8 Ma and 40,000 ft
A higher altitude and faster condition than before is considered to verify the effectiveness of the presented method, where is a step signal given at 2 s, is locked in , loses effectiveness, and the bias of the sensor is . That is, , , , and . The limits of magnitude and rate are and /s, respectively.
Figure 9 shows the pitch angles of the normal and faulty aircraft. From Figure 9a, it can be seen that the reduction of the control performance for the faulty aircraft with LQR (red) is more serious than the one in Figure 5a. However, FTC in the faulty system in Figure 9b (red) can also recover the control performance of the healthy system with LQR (blue). In Figure 10, we can get the same results as in Figure 6. Figure 11 shows the estimates of fault values. Figure 12 shows the actuator outputs of FTC and anti-windup FTC in the faulty aircraft with two kinds of saturation modules. As actuator 1 is locked in , actuators 2 and 3 meet their constraints so that FTC cannot guarantee the post-fault aircraft stability. On the contrary, the anti-windup FTC can cancel out the nonlinear windup phenomenon in the actuators and make the faulty aircraft stable.
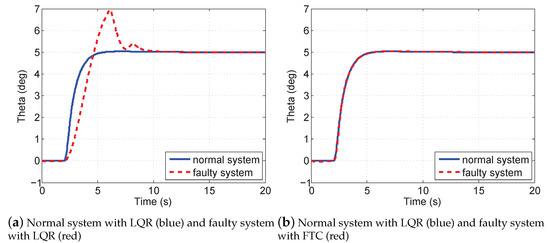
Figure 9.
Effect of the integrated fault-tolerant strategy.
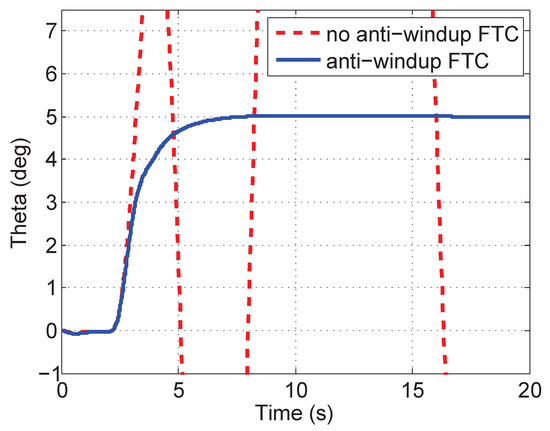
Figure 10.
Comparison between FTC without constraints (red) and anti-windup FTC with constraints (blue).
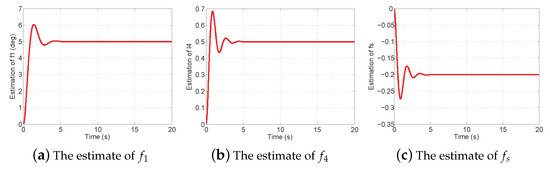
Figure 11.
Estimates of fault values.
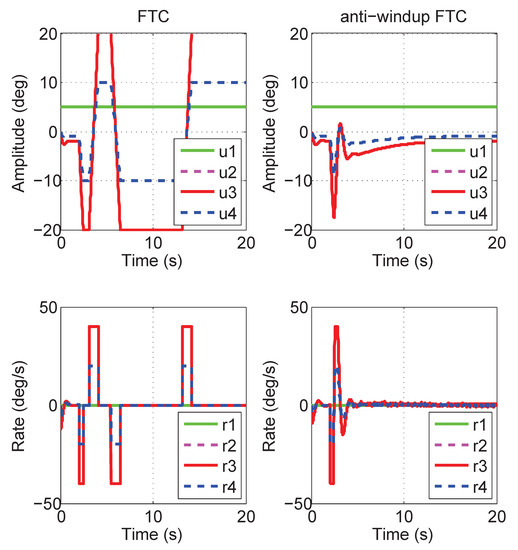
Figure 12.
Actuator deflections and rates.
5. Conclusions
In this paper, we proposed a novel anti-windup integrated reconfigurable control approach for a rigid aircraft experiencing faults and actuator saturation. A reference controller using an optimal control scheme and a reconfigurable controller using an adaptive scheme are designed without actuator constraints. To obtain accurate fault signals, an estimation module using an observer-based method is presented. For the overall faulty system, an integrated strategy is utilized to calculate the adaptive adjustment control and estimate gains by analyzing the system stability. Three anti-windup schemes are utilized to modify the original designed controllers. Actuator and sensor faults are discussed and analyzed to verify the effectiveness of the proposed reconfigurable control method. The simulation results of the case study show that the presented method can decrease the effects of faults and actuator constraints in different flight conditions.
Author Contributions
Conceptualization, Y.L. and S.H.; methodology, Y.L.; software, Y.L.; validation, S.H.; formal analysis, J.L.; investigation, J.L.; resources, Y.L.; data curation, S.H.; writing—original draft preparation, Y.L.; writing—review and editing, E.Z.; visualization, Y.L.; supervision, E.Z.; project administration, S.H.; funding acquisition, S.H. All authors have read and agreed to the published version of the manuscript.
Funding
The work reported in this paper is supported by the National Key Research and Development Plan of China under Grant No. 2019YFB1706001, the Industrial Internet Innovation and Development Project of China under Grant TC190H46B, the National Natural Science Foundation of China under Grant No. 61773001, and the Beijing Nature Foundation under Grant No. 4153059.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
See reference [32].
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following symbols and acronyms are used in this manuscript:
| A, B, C | System Matrices |
| d | External Disturbance |
| e | Error |
| Additive Fault | |
| Fictitious Multiplicative Fault | |
| Sensor Fault | |
| H, G, M, N | Estimator Gains |
| h | Flight Altitude |
| L | Indication Matrix |
| Gust Wavelength | |
| q | Pitch Angle Rate |
| r | Reference Command |
| u | System Input |
| Forward Velocity | |
| Lyapunov Function | |
| Aircraft Velocity | |
| Vertical Velocity | |
| Gust Velocity | |
| x | System State |
| y | System Output |
| Elevator Deflection | |
| Pitch Angle | |
| EFCS | Electrical Flight Control System |
| FTC | Fault-Tolerant Control |
| PFTC | Passive Fault-Tolerant Control |
| AFTC | Active Fault-Tolerant Control |
| LMI | Linear Matrix Inequality |
Appendix A
In this part, the detailed models for the aircraft and actuator are provided. A schematic for Boeing 747 is shown in Figure A1, and the main control inputs for the longitudinal control are elevators. There are four independent elevators, and they can achieve the longitudinal output angle (the pitch angle). The longitudinal flight control objective is to control elevators so that the pitch angle for aircraft can track the command signal. The expressions of the matrices in (1) can be got using the following small-disturbance equations for longitudinal motions:
whose the details can be found in [33].
Combining with the expression of state x, A, B, and C can be got as
Figure A1.
The schematic for Boeing 747.
Moreover, the block diagram of the actuator for elevator is shown in Figure A2. It consists of an actuator gain (), a saturation module for rate limiting, an integrator, and another saturation module for level constraint.
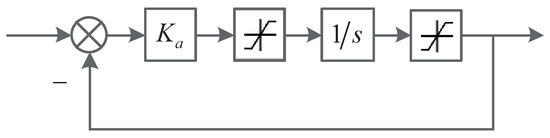
Figure A2.
The block diagram for actuator.
References
- Liu, Y.S.; Ren, Z.; Cooper, J.E. Integrated strategy for commercial aircraft fault-tolerant control. J. Guid. Control. Dyn. 2018, 41, 1419–1430. [Google Scholar] [CrossRef]
- Liu, Y.S.; Dong, X.W.; Ren, Z.; Cooper, J.E. Fault-tolerant control for commercial aircraft with actuator faults and constraints. J. Frankl. Inst. 2019, 356, 3849–3868. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Jiang, J. Bibliographical review on reconfigurable fault-tolerant control systems. Annu. Rev. Control. 2008, 32, 229–252. [Google Scholar] [CrossRef]
- Habibi, H.; Howard, I.; Simani, S. Reliability improvement of wind turbine power generation using model-based fault detection and fault tolerant control: A review. Renew. Energy 2019, 135, 877–896. [Google Scholar] [CrossRef]
- Lan, J.L.; Patton, R.J. A new strategy for integration of fault estimation within fault-tolerant control. Automatica 2016, 69, 48–59. [Google Scholar] [CrossRef]
- Lan, J.L.; Patton, R.J. Integrated fault estimation and fault-tolerant control for uncertain Lipschitz nonlinear systems. Int. J. Robust Nonlinear Control. 2017, 27, 761–780. [Google Scholar] [CrossRef]
- Wang, J.; Wang, S.P.; Wang, X.J.; Shi, C.; Mileta, M.T. Active fault tolerant control for vertical tail damaged aircraft with dissimilar redundant actuation system. Chin. J. Aeronaut. 2016, 29, 1313–1325. [Google Scholar] [CrossRef]
- Wang, X.J.; Wang, S.P.; Yang, Z.W.; Zhang, C. Active fault-tolerant control strategy of large civil aircraft under elevator failures. Chin. J. Aeronaut. 2015, 28, 1658–1666. [Google Scholar] [CrossRef][Green Version]
- Chakravarty, A.; Mahanta, C. Actuator fault-tolerant control (FTC) design with post-fault transient improvement for application to aircraft control. Int. J. Robust Nonlinear Control. 2016, 26, 2049–2074. [Google Scholar] [CrossRef]
- Song, X.Q.; Liu, C.S.; Zhang, S.J. Adaptive active fault tolerant control for discrete-time systems with uncertainties. Asian J. Control. 2016, 18, 1417–1426. [Google Scholar] [CrossRef]
- Lu, P.; Kampen, E.J.; Visser, C.; Chu, Q.P. Aircraft fault-tolerant trajectory control using incremental nonlinear dynamic inversion. Control. Eng. Pract. 2016, 57, 126–141. [Google Scholar] [CrossRef]
- Ma, Y.J.; Tao, G.; Jiang, B.; Cheng, Y.H. Multiple-model adaptive control for spacecraft under sign errors in actuator response. J. Guid. Control. Dyn. 2016, 39, 628–641. [Google Scholar] [CrossRef]
- Boskovic, J.D.; Jackson, J.A.; Mehra, R.K.; Nguyen, N.T. Multiple-model adaptive fault-tolerant control of a planetary lander. J. Guid. Control. Dyn. 2009, 32, 1812–1826. [Google Scholar] [CrossRef]
- Gao, Z.W.; Ding, S.X. Actuator fault robust estimation and fault-tolerant control for a class of nonlinear descriptor systems. Automatica 2007, 43, 912–920. [Google Scholar] [CrossRef]
- Han, J.; Zhang, H.G.; Wang, Y.C.; Liu, Y. Disturbance observer based fault estimation and dynamic output feedback fault tolerant control for fuzzy systems with local nonlinear models. ISA Trans. 2015, 59, 114–124. [Google Scholar] [CrossRef]
- Shi, F.M.; Patton, R.J. Fault estimation and active fault tolerant control for linear parameter varying descriptor systems. Int. J. Robust Nonlinear Control. 2015, 25, 689–706. [Google Scholar] [CrossRef]
- Qian, H.M.; Peng, Y.; Yang, G.Y. Reduced-order observer-based fault estimation and fault-tolerant control for a class of discrete Lipschitz nonlinear systems. Optim. Control. Appl. Methods 2016, 37, 1236–1262. [Google Scholar] [CrossRef]
- Jeyasenthil, R.; Choi, S.B. A new anti-windup compensator based on quantitative feedback theory for an uncertain linear system with input saturation. Appl. Sci. 2019, 9, 2958. [Google Scholar] [CrossRef]
- Lu, Y.B.; Huang, P.F.; Meng, Z.J. Adaptive anti-windup control of post-capture combination via tethered space robot. Adv. Space Res. 2019, 64, 847–860. [Google Scholar] [CrossRef]
- An, H.; Wu, Q.Q. Anti-windup disturbance suppression control of feedback linearizable systems with application to hypersonic flight vehicles. J. Aerosp. Eng. 2019, 233, 3952–3967. [Google Scholar] [CrossRef]
- Fan, J.H.; Zheng, Z.Q.; Zhang, Y.M. Fault-tolerant control for output tracking systems subject to actuator saturation and constant disturbances: An LMI approach. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Portland, OR, USA, 8–11 August 2011. [Google Scholar]
- Fan, J.H.; Zhang, Y.M.; Zheng, Z.Q. Hybrid fault-tolerant flight control against actuator faults and input saturation: A set-invariance approach. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Minneapolis, MN, USA, 13–16 August 2012. [Google Scholar]
- Fan, J.H.; Zheng, Z.Q.; Zhang, Y.M. Control allocation-based fault-tolerant control for overactuated systems with saturation and imperfect fault information. In Proceedings of the Infotech@Aerospace 2011, St. Louis, MO, USA, 29–31 March 2011. [Google Scholar]
- Zhang, S.J.; Meng, Q.K. An anti-windup INDI fault-tolerant control scheme for flying wing aircraft with actuator faults. ISA Trans. 2019, 93, 172–179. [Google Scholar] [CrossRef] [PubMed]
- Habibi, H.; Nohooji, H.R.; Howard, I. Backstepping Nussbaum gain dynamic surface control for a class of input and state constrained systems with actuator faults. Inf. Sci. 2019, 21, 31–48. [Google Scholar] [CrossRef]
- Kappor, N.; Tell, A.R.; Daoutidis, P. An anti-windup design for linear systems with input saturation. Automatica 1998, 34, 559–574. [Google Scholar] [CrossRef]
- Wang, D.; Lum, K.Y. Adaptive unknown input observer approach for aircraft actuator fault detection and isolation. Int. J. Adapt. Control. Signal Process. 2007, 482, 27–46. [Google Scholar] [CrossRef]
- Chen, J.; Patton, R.J.; Zhang, H.Y. Design of unknown input observers and robust fault detection filters. Int. J. Control. 1996, 63, 85–105. [Google Scholar] [CrossRef]
- Nise, N.S. Control Systems Engineering, 6th ed.; John Wiley & Sons: Chichester, UK, 2007. [Google Scholar]
- Hess, R.A.; Snell, S.A. Flight control system design with rate saturating actuators. J. Guid. Control. Dyn. 1997, 20, 90–96. [Google Scholar] [CrossRef]
- Wright, J.R.; Cooper, J.E. Introduction to Aircraft Aeroelasticity and Loads, 2nd ed.; John Wiley & Sons: Chichester, UK, 2014. [Google Scholar]
- Heffley, R.K.; Jewell, W.F. Aircraft Handling Qualities Data; NASA: Washington, DC, USA, 1972.
- Caughey, D.A. Introduction to Aircraft and Control Course Notes for M&AE 5070; Cornell University: Ithaca, NY, USA, 2011. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).