Deep Neural Network Feature Selection Approaches for Data-Driven Prognostic Model of Aircraft Engines
Abstract
1. Introduction
- Extract meaningful features for neural network-based and deep learning data-driven models from the C-MAPSS dataset.
- Suggest the novel neural network-based feature selection method for aircraft gas turbine engines RUL prediction.
- Develop deep neural network models from selected features.
- Show how the developed methodology can improve the RUL prediction model by comparing its performance/error and complexity to the model derived from original features.
1.1. Neural Network for RUL Prediction
1.2. Related Works
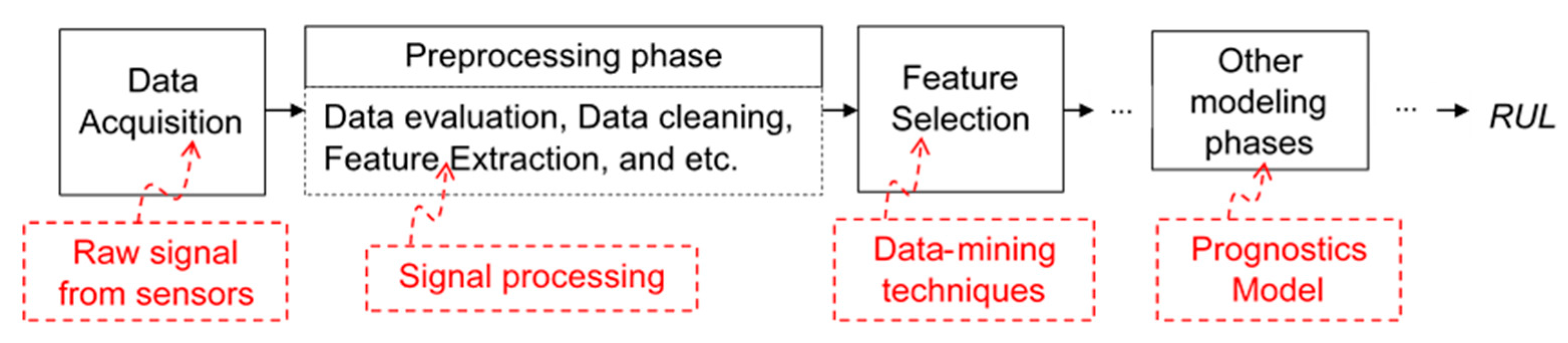
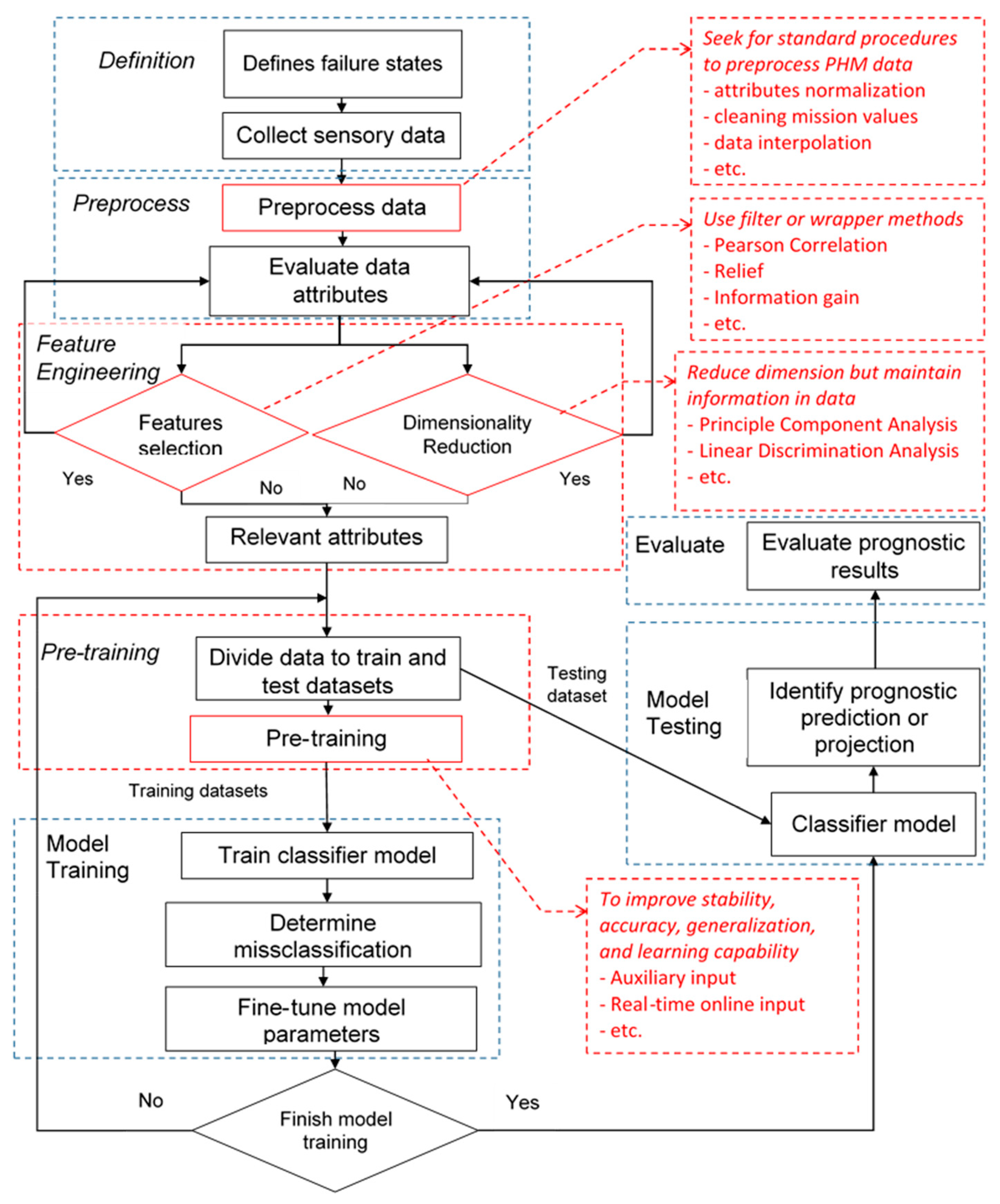
2. Methodology
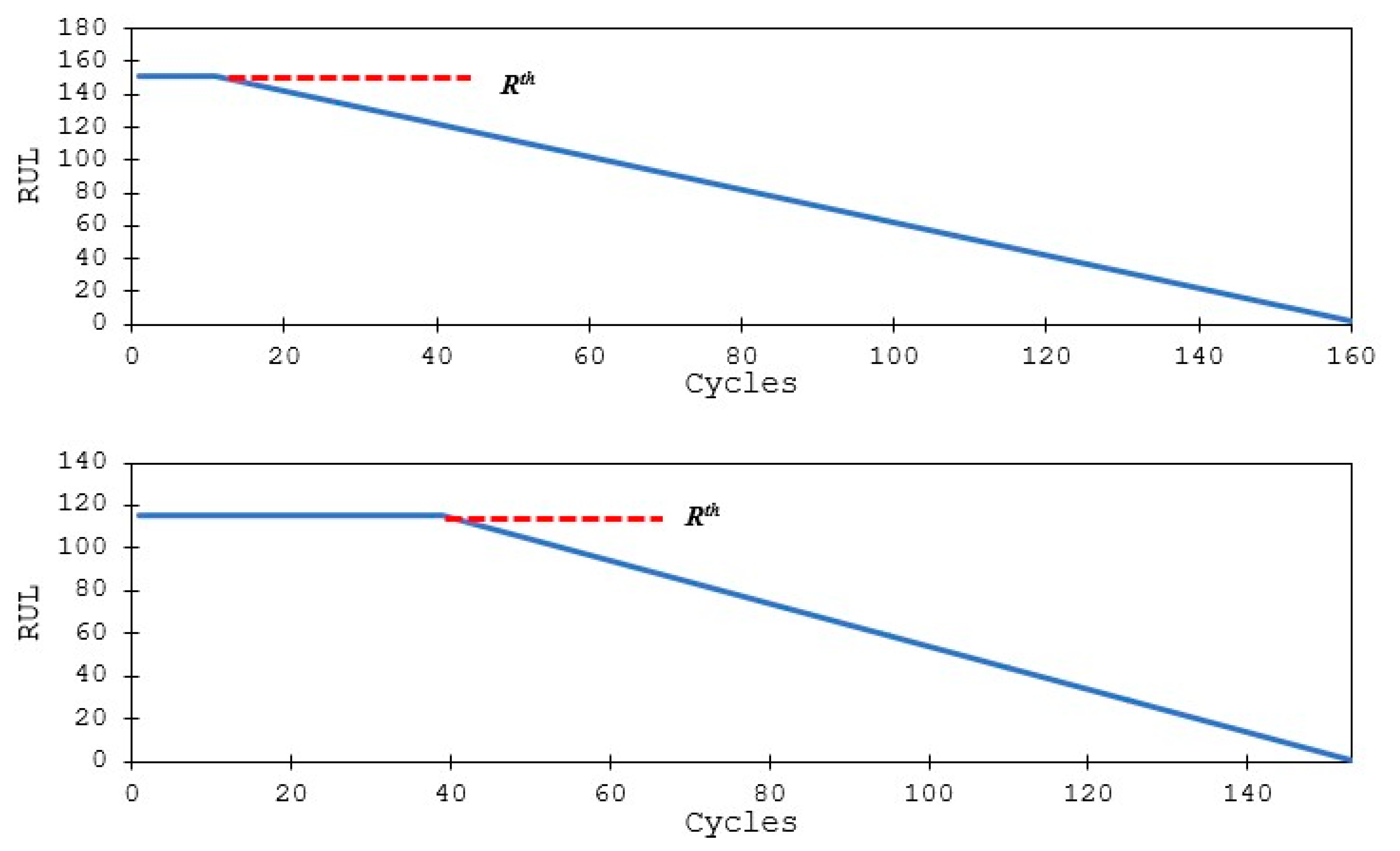
2.1. Problem Definition
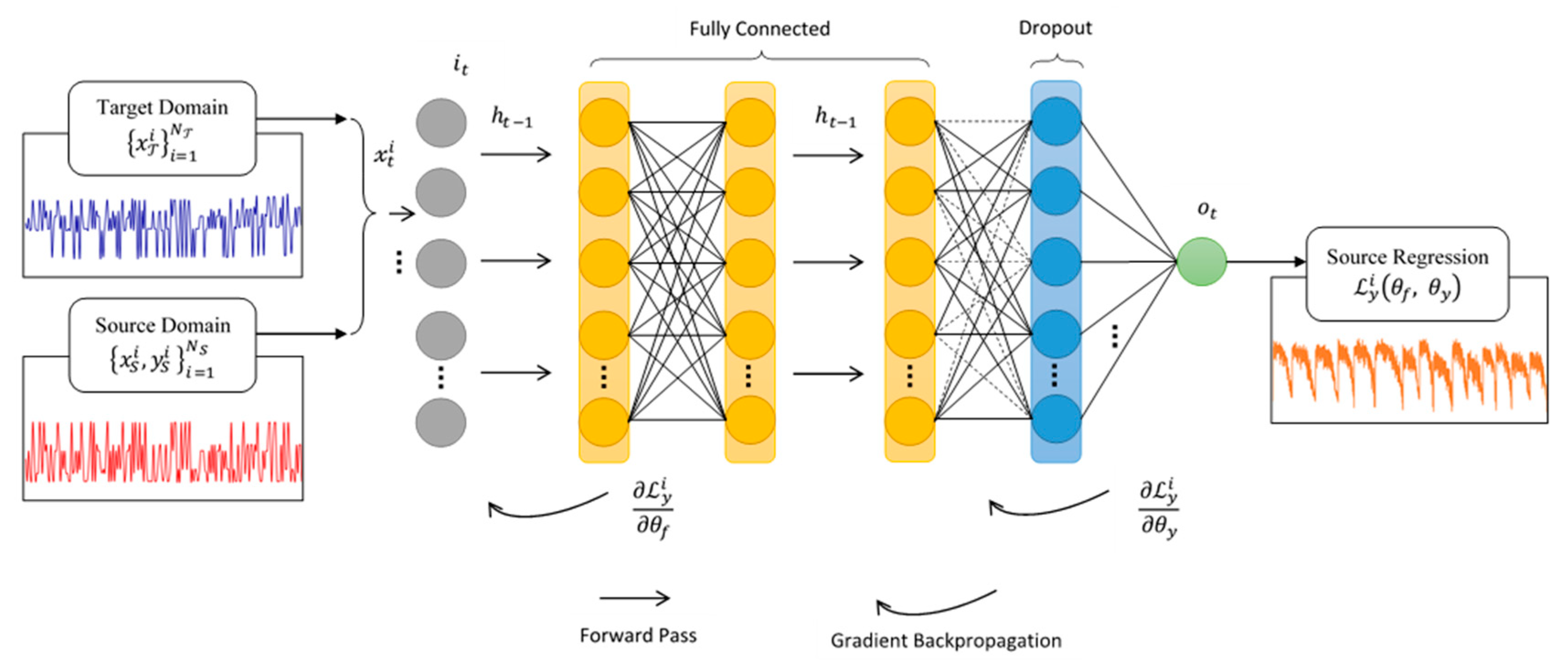
2.2. Deep Neural Network Architecture
- Supervised training protocol for regression tasks
- A multi-threaded and distributed parallel computation that can be run on a single or a multi-node cluster
- Automatic, per-neuron, adaptive learning rate for fast convergence
- Optional specification of the learning rate, annealing, and momentum options
- Regularization options to prevent model overfitting
- Elegant and intuitive web interface (Flow)
- Grid search for hyperparameter optimization and model selection
- Automatic early stopping based on the convergence of user-specified metric to a user-specified tolerance
- Model check-pointing for reduced run times and model tuning
- Automatic pre- and post-processing for categorical numerical data
- Additional expert parameters for model tuning
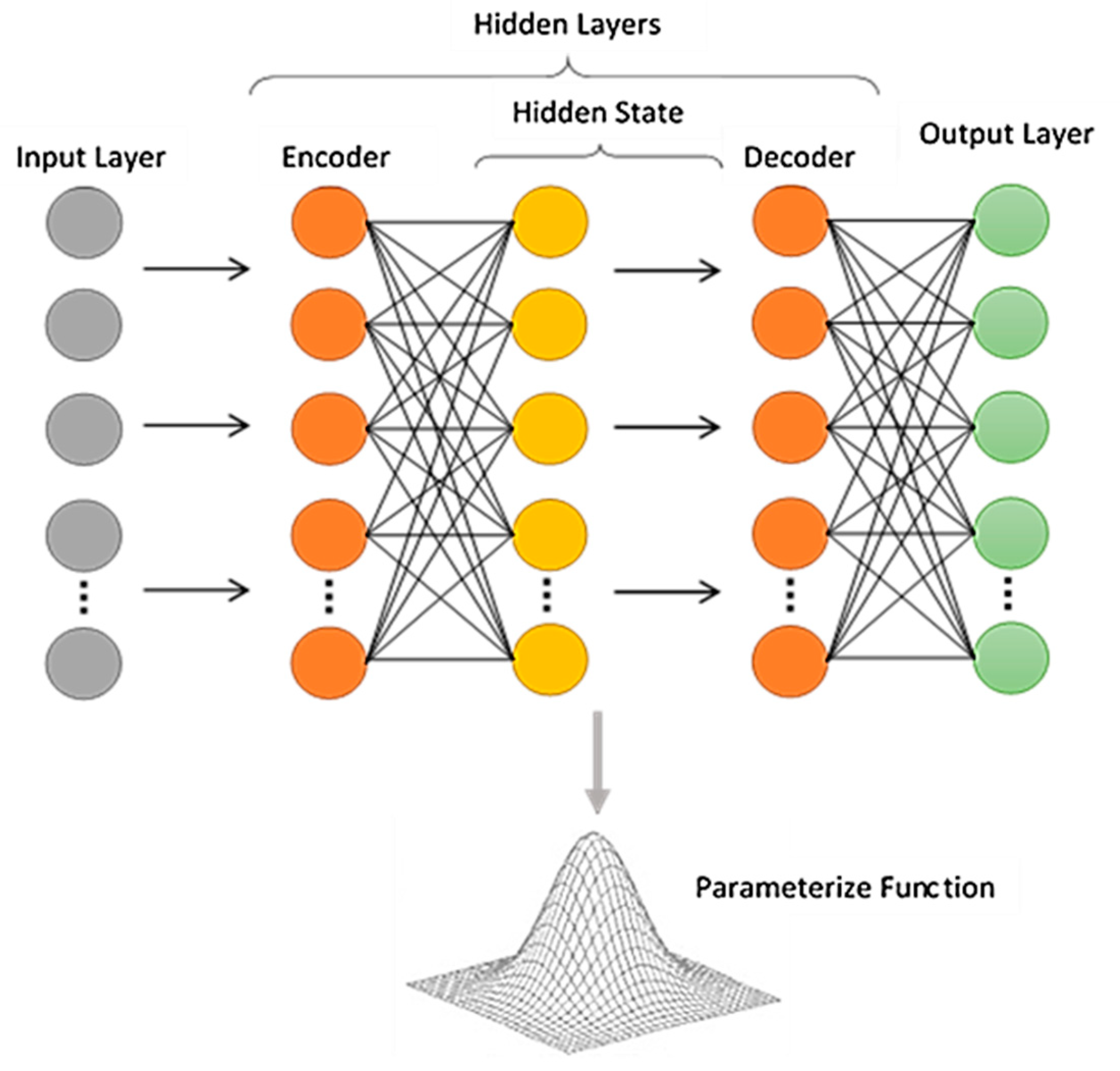
- Deep auto-encoders for unsupervised feature learning.
2.3. Feature Selection Methods for Neural Network Architectures
2.4. Neural Network Data-Driven Modeling Framework
3. Experimental Setup and Results
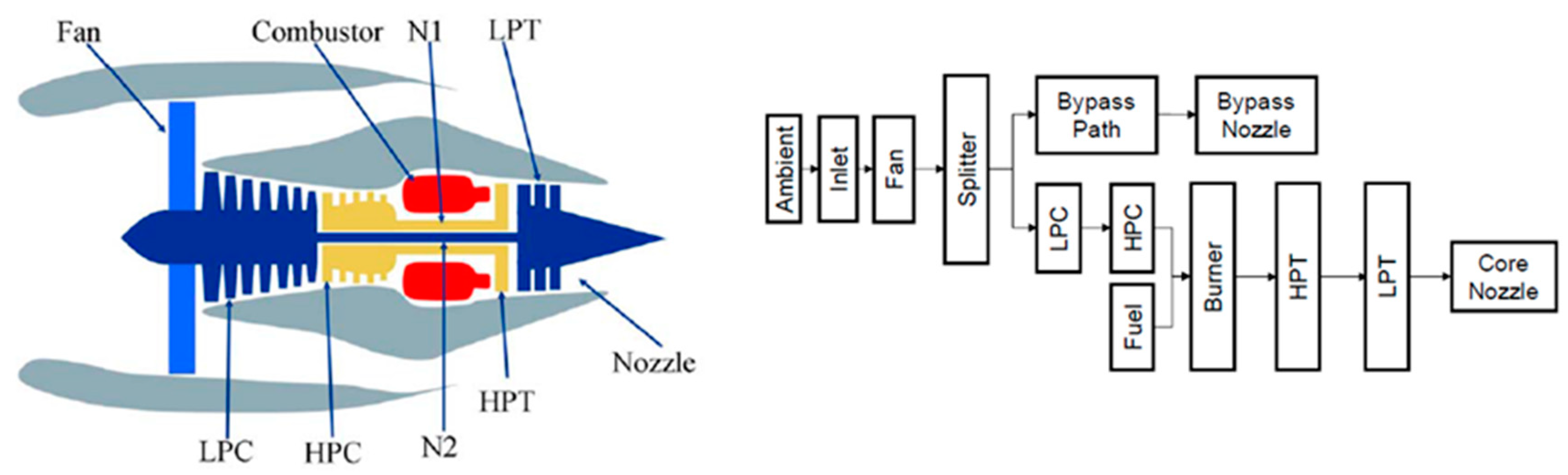
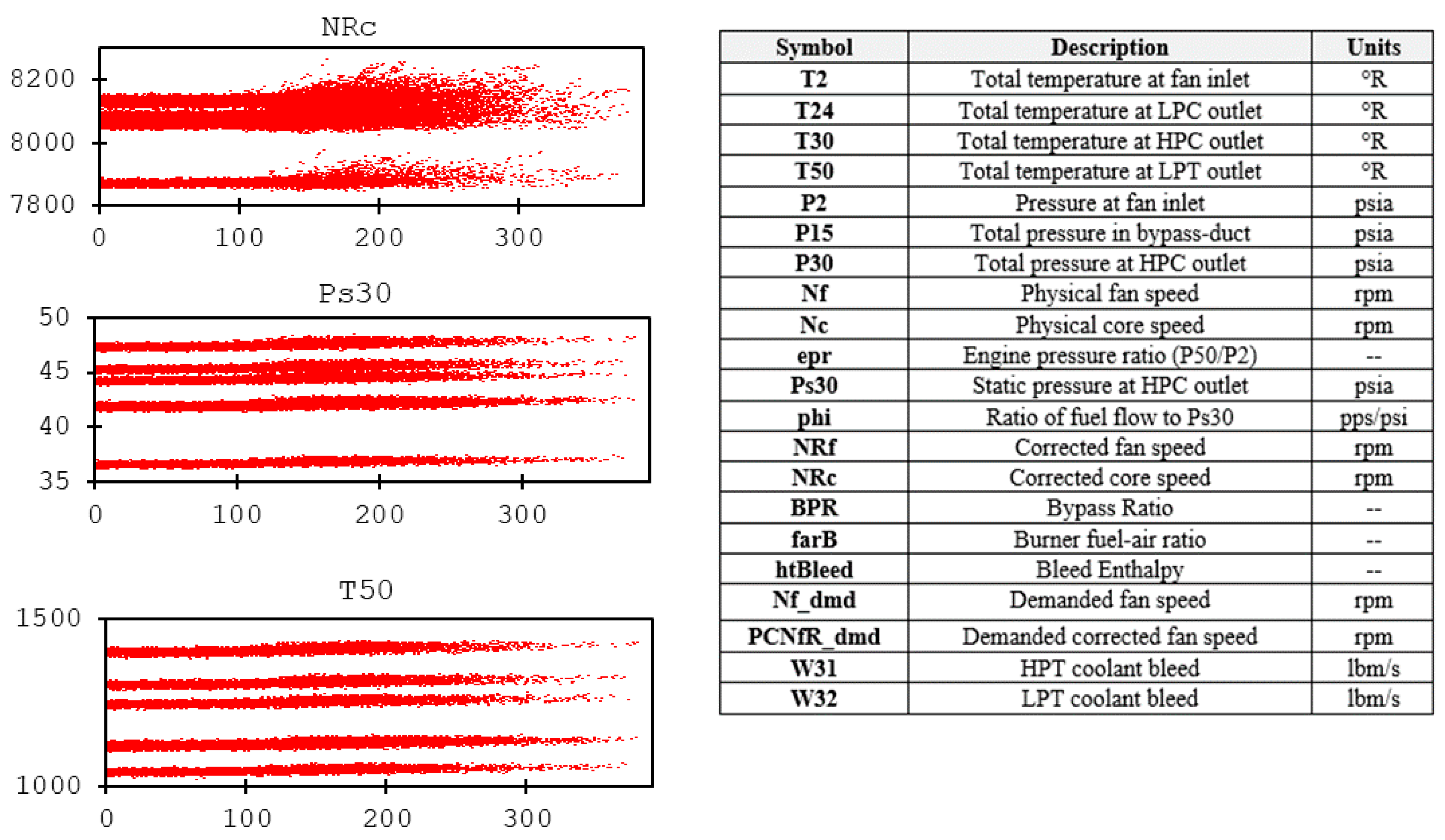
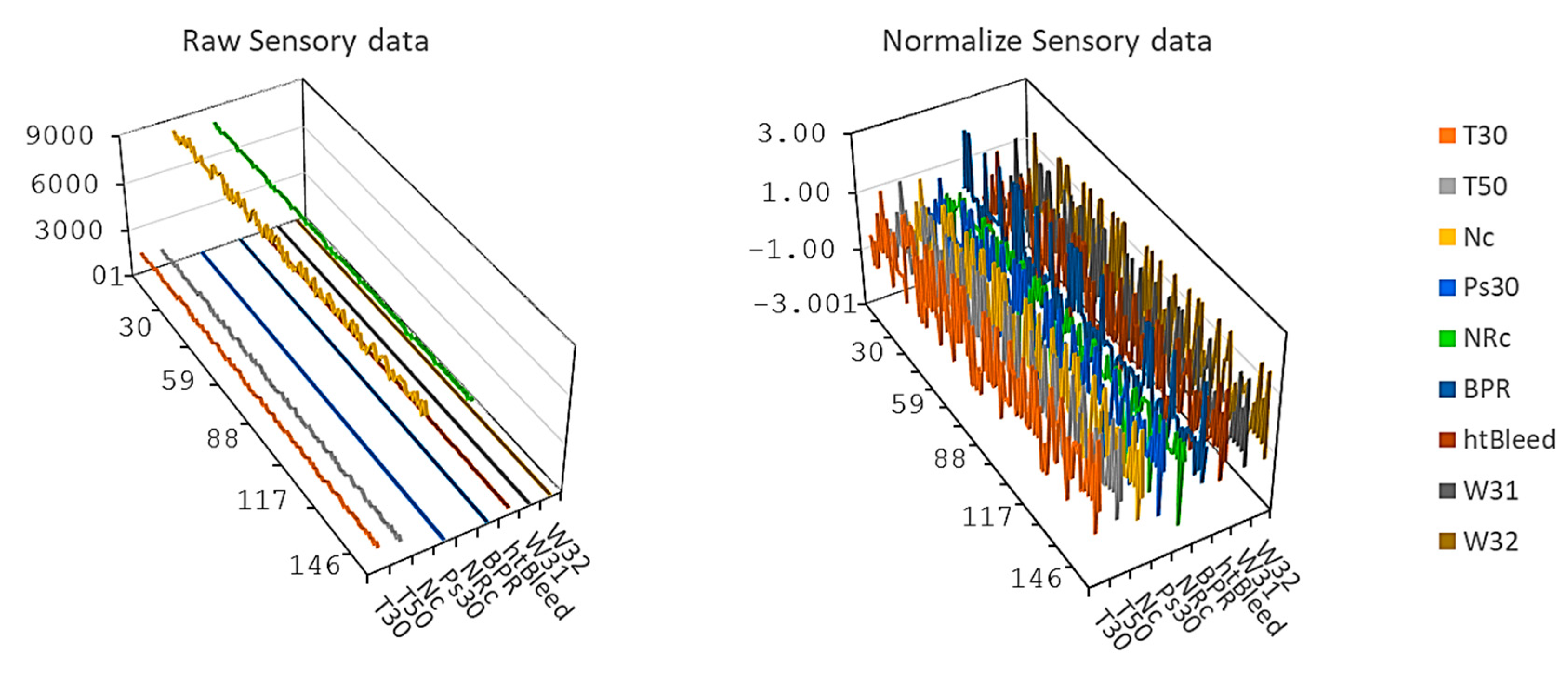
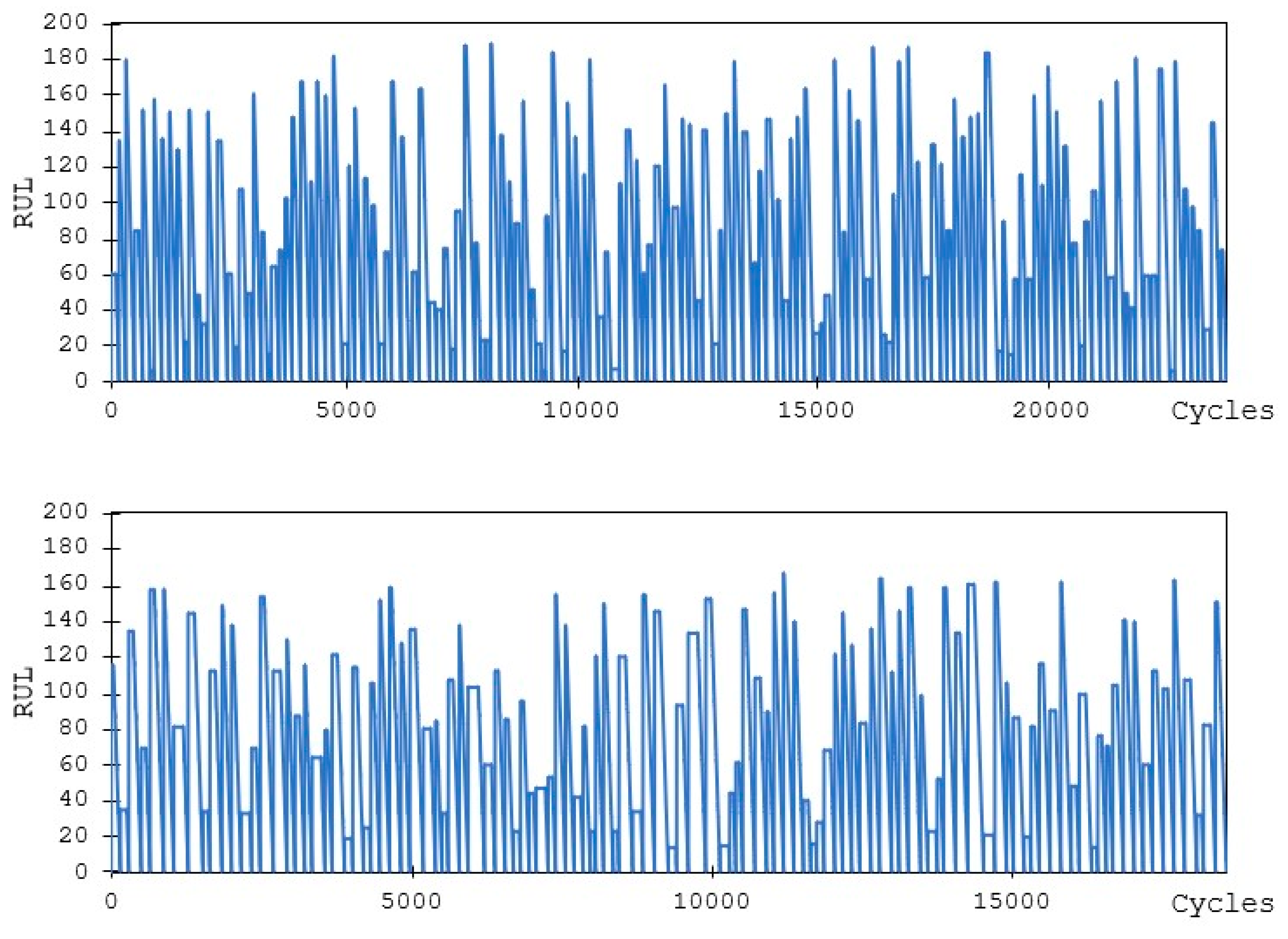
3.1. C-MAPSS Aircraft Engines Data
3.2. Training Procedure and Hyperparameters Selection
- 5 Folds Cross-Validation
- 1000 Training cycles
- 0.001 Learning rate
- 0.9 Momentum
- Linear sampling.
3.3. Experimental Setup and Results
3.3.1. Feature Selection for Aircraft Engine Dataset
- Pearson correlation; 8 attributes: T30, T50, Ne, Ps30, NRc, BPR, farB, and htBleed.
- Relief algorithm; 2 attributes: P15 and Nf_dmd.
- SVM selection; 11 attributes: T2, T24, P30, Nf, epr, phi, NRF, Nf_dmd, PCNfR_dmd, W31, and W32.
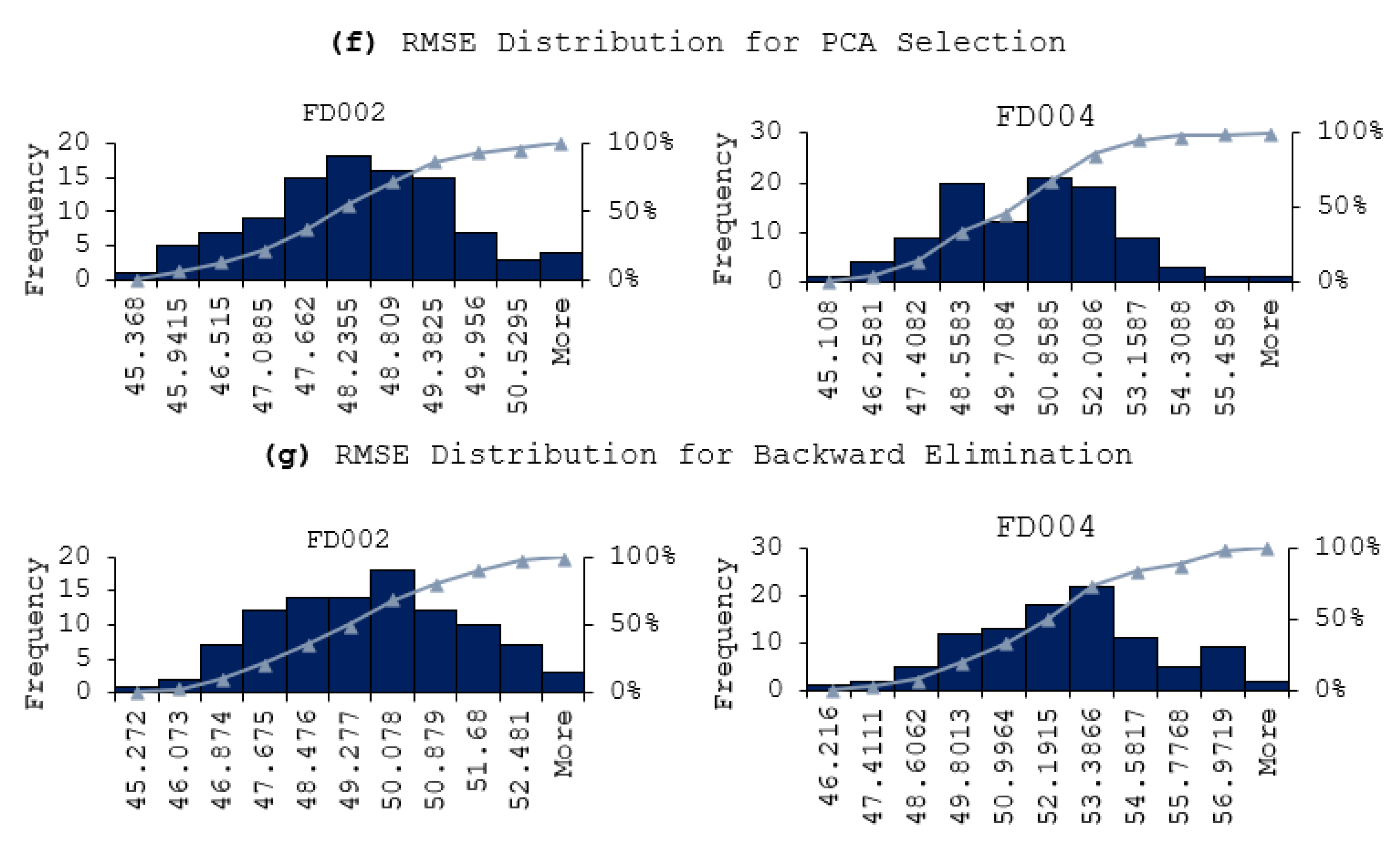
- PCA selection; 17 attributes: T2, T24, T30, T50, P2, P15, P30, Nf, Ne, epr, Ps30, phi, farB, htBleed, Nf_dmd, W31, and W32.
- Deviation selection; 11 attributes: T2, T24, T50, P2, P15, Ne, epr, Ps30, farB, PCNfR_dmd, and W32.
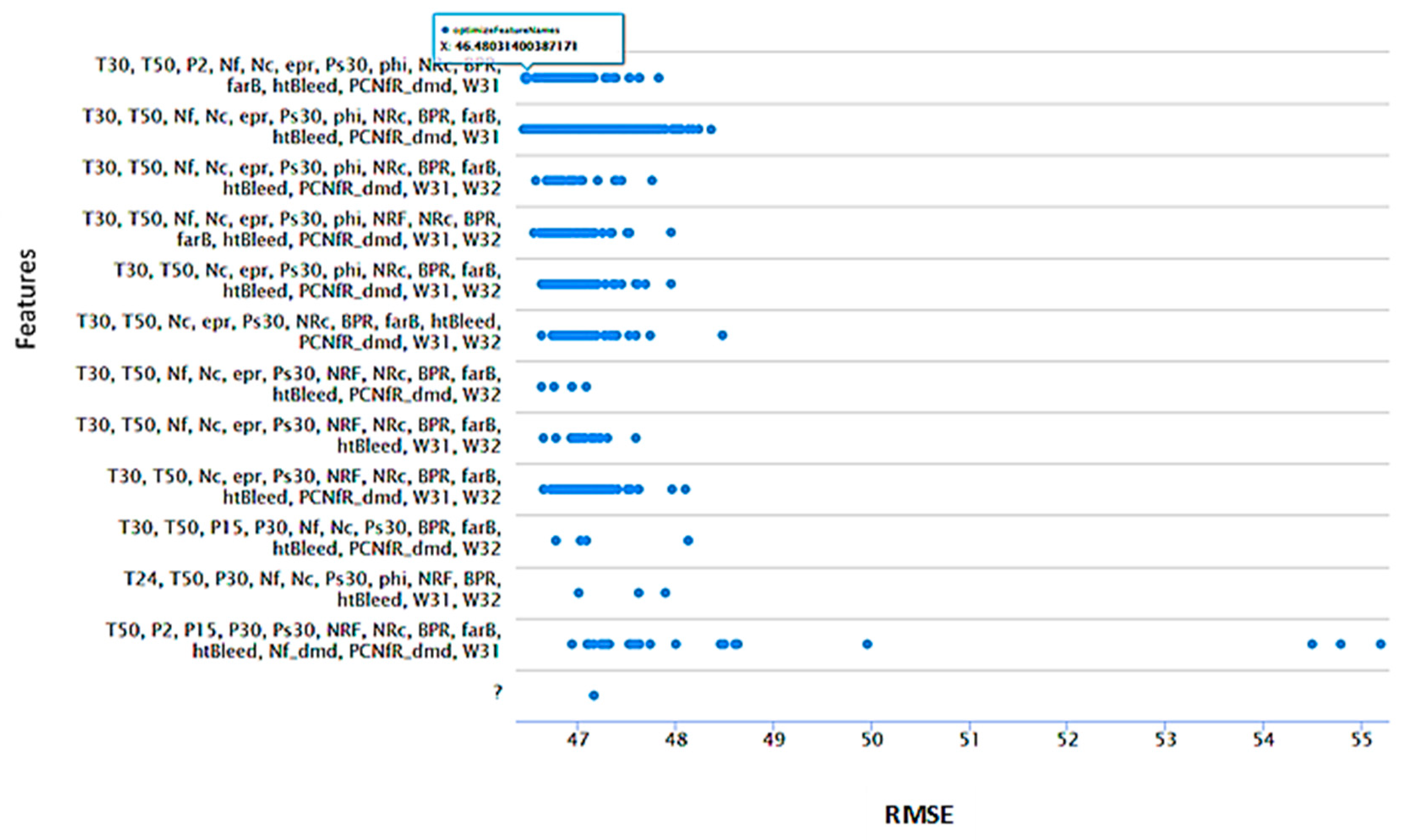
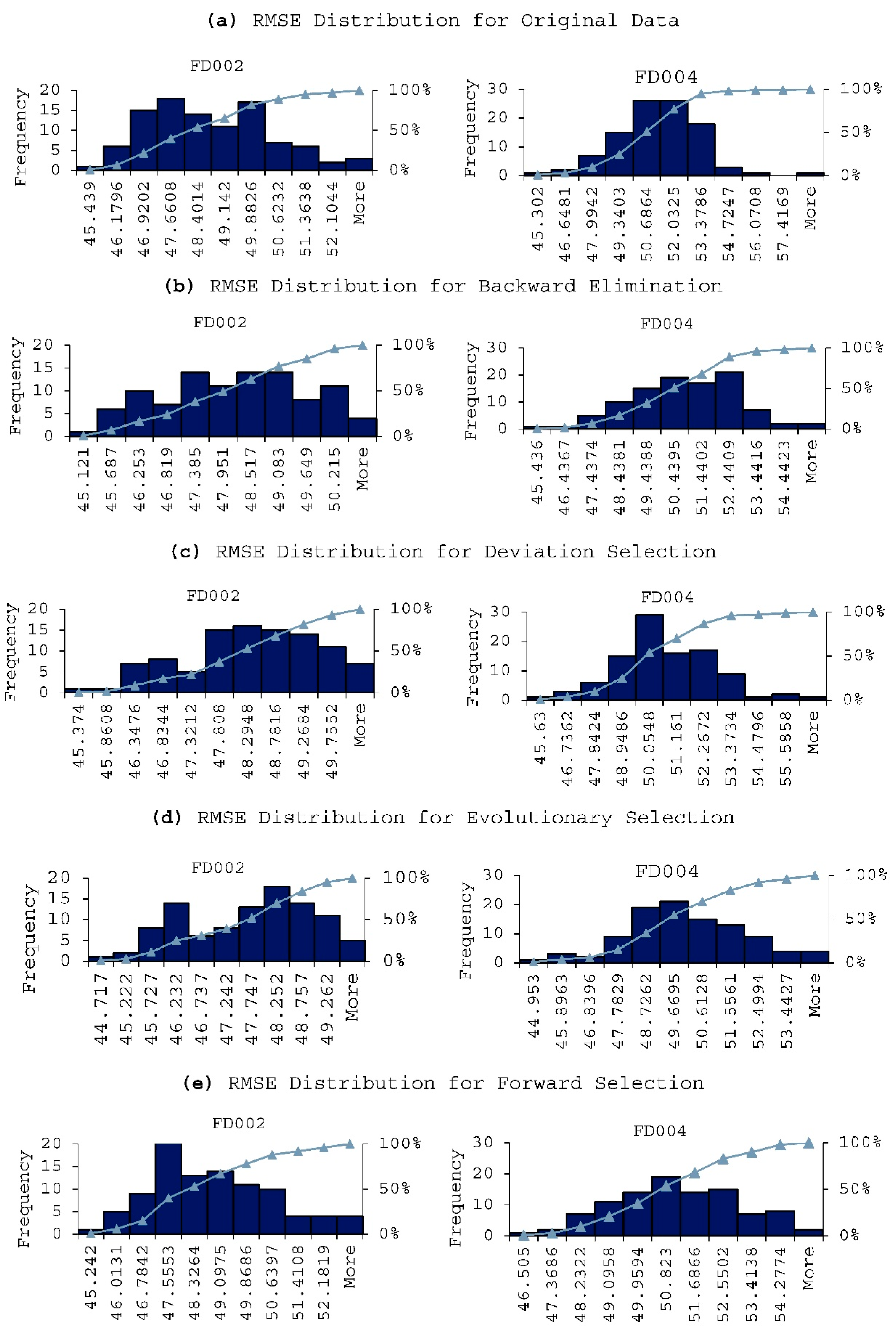
- Backward elimination; validate RMSE 46.429 from 19 attributes; T2, T30, P2, P15, P30, Nf, epr, Ps30, phi, NRF, NRc, BPR, farB, htBleed, Nf_dmd, PNCfR_dmd, W31, and W32.
- Evolutionary selection; validate RMSE 46.451 from 14 attributes; T2, T30, T50, P2, Nf, Ne, epr, Ps30, NRc, BPR, farB, htBleed, W31, and W32.
- Forward selection methods; validate RMSE 46.480 from 11 attributes; T2, T30, T50, P2, P15, Ps30, NRc, BPR, farB, htBleed, and Nf_dmd.
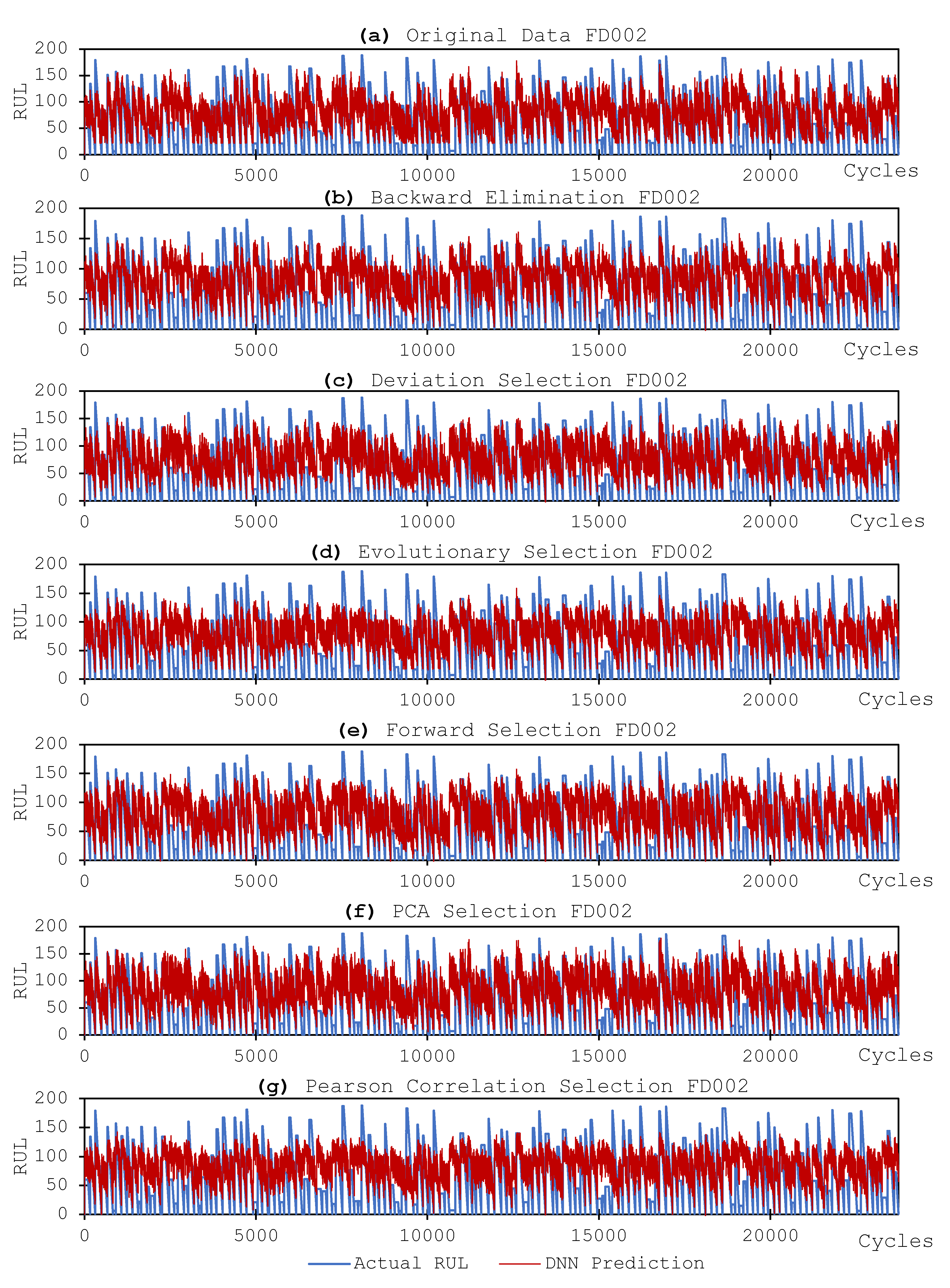
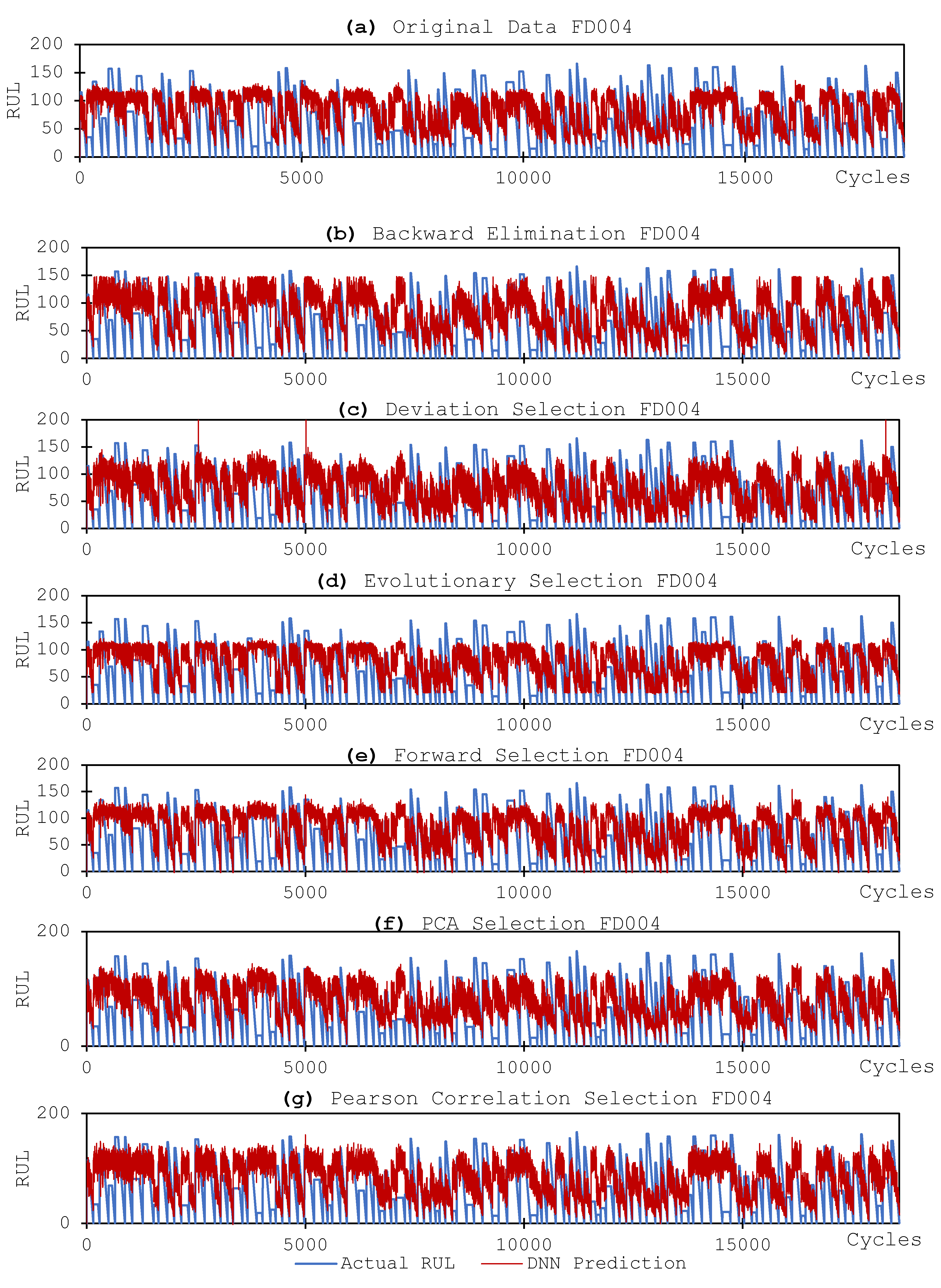
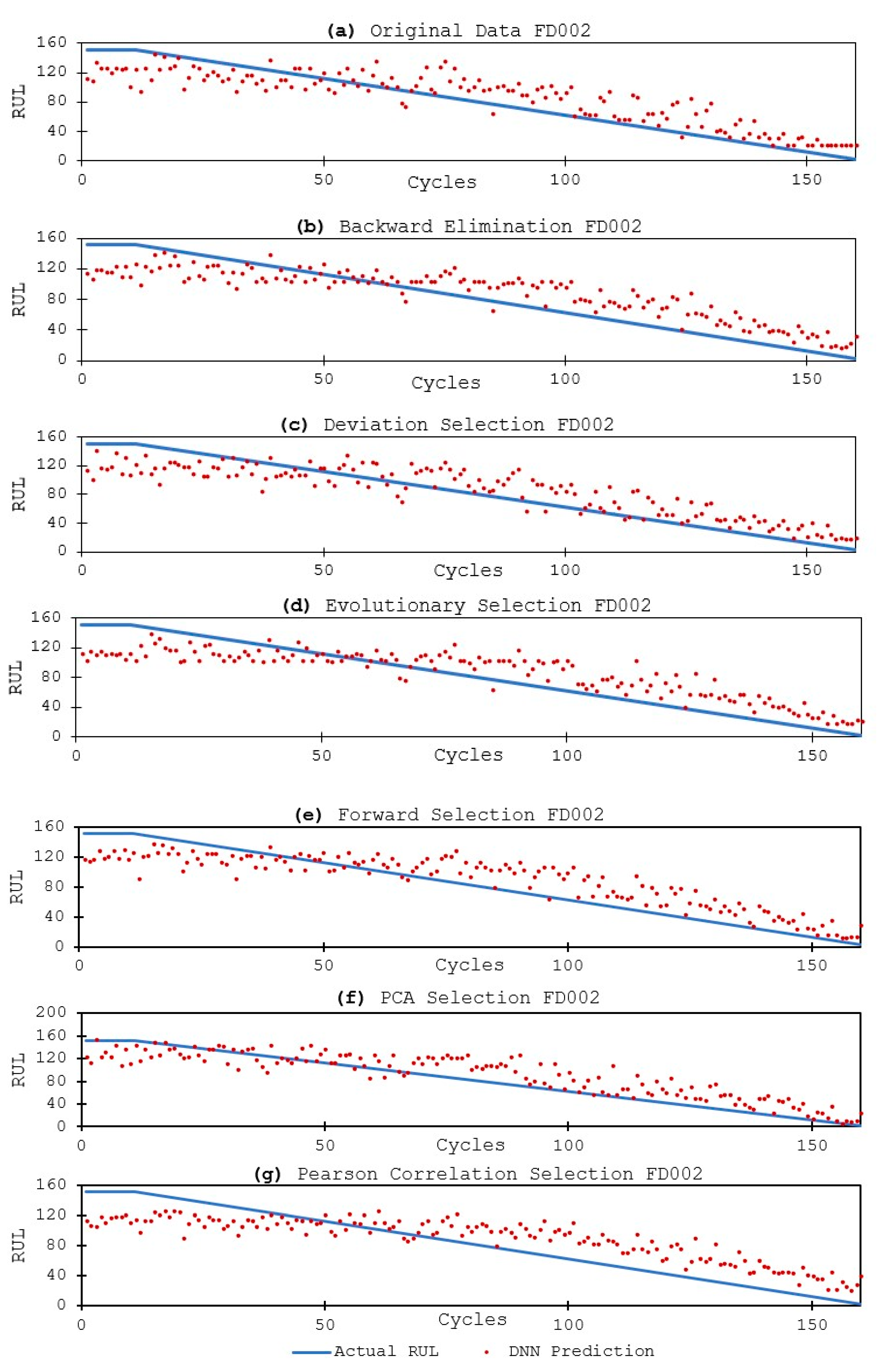
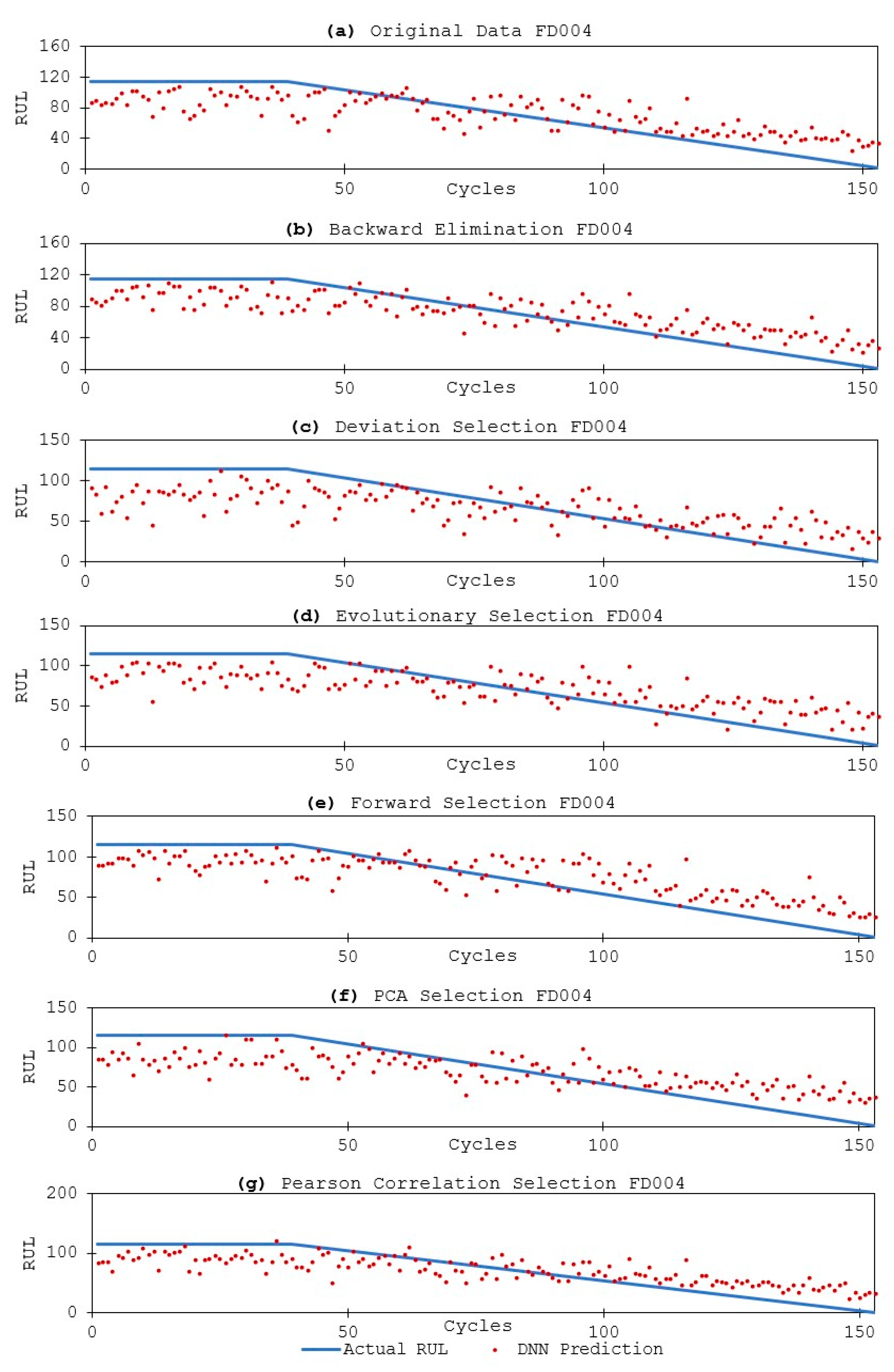
3.3.2. DNN Models and Results
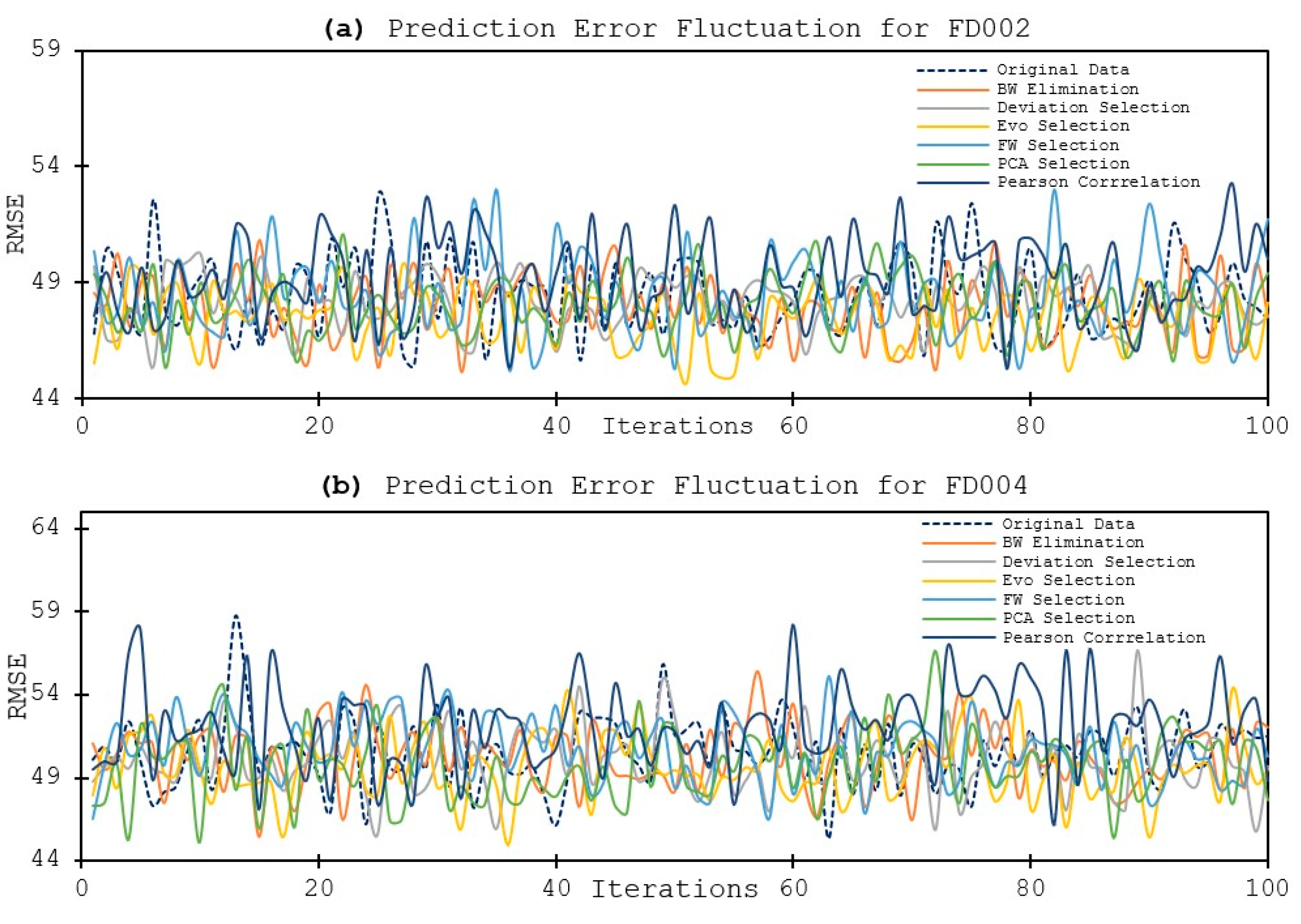
4. Discussion
- (1)
- Utilizing fewer features to train the model has shown to lower the error distribution range, compared to using more features. This is due to that the initial random weights assigned to the hidden nodes are smaller when using less feature in model training. In other words, the models are more robust and reliable when using less features. Same observation is also applied for the fluctuation of the prediction errors, in that the prediction results are more stable when using less features in model training.
- (2)
- In terms of model performance and accuracy, although using selected features does not always guarantee better results, the feature selection methods still help in terms of reducing a computational burden while offering better prediction performance. In our experiment, the Evolutionary selection can achieve both better performance and complexity reduction.
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Attributes | T2 | T24 | T30 | T50 | P2 | P15 | P30 | Nf | Nc | epr | Ps30 | phi | NRF | NRc | BPR | farB | htBleed | Nf_dmd | PCNfR_dmd | W31 | W32 | RUL |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T2 | 1.0000 | 0.9441 | 0.8709 | 0.8979 | 0.9864 | 0.9864 | 0.9731 | 0.5725 | 0.8618 | 0.8266 | 0.7060 | 0.9729 | 0.1643 | 0.3528 | −0.5426 | 0.7936 | 0.8732 | 0.5720 | 0.1642 | 0.9777 | 0.9777 | −0.0023 |
| T24 | 0.9441 | 1.0000 | 0.9822 | 0.9810 | 0.9158 | 0.9441 | 0.9686 | 0.8106 | 0.9785 | 0.9051 | 0.8957 | 0.9688 | 0.4801 | 0.6241 | −0.7779 | 0.8050 | 0.9830 | 0.8103 | 0.4800 | 0.9624 | 0.9624 | −0.0064 |
| T30 | 0.8709 | 0.9822 | 1.0000 | 0.9896 | 0.8429 | 0.8848 | 0.9290 | 0.8957 | 0.9978 | 0.9290 | 0.9607 | 0.9295 | 0.6209 | 0.7520 | −0.8759 | 0.8047 | 0.9987 | 0.8954 | 0.6208 | 0.9171 | 0.9171 | −0.0253 |
| T50 | 0.8979 | 0.9810 | 0.9896 | 1.0000 | 0.8841 | 0.9196 | 0.9567 | 0.8439 | 0.9873 | 0.9616 | 0.9368 | 0.9571 | 0.5447 | 0.7156 | −0.8467 | 0.8591 | 0.9902 | 0.8436 | 0.5446 | 0.9464 | 0.9464 | −0.0378 |
| P2 | 0.9864 | 0.9158 | 0.8429 | 0.8841 | 1.0000 | 0.9963 | 0.9798 | 0.5242 | 0.8329 | 0.8438 | 0.6736 | 0.9795 | 0.1136 | 0.3305 | −0.5253 | 0.8241 | 0.8455 | 0.5237 | 0.1135 | 0.9857 | 0.9857 | −0.0031 |
| P15 | 0.9864 | 0.9441 | 0.8848 | 0.9196 | 0.9963 | 1.0000 | 0.9933 | 0.5944 | 0.8762 | 0.8782 | 0.7339 | 0.9931 | 0.1981 | 0.4075 | −0.5955 | 0.8403 | 0.8871 | 0.5940 | 0.1980 | 0.9964 | 0.9964 | −0.0029 |
| P30 | 0.9731 | 0.9686 | 0.9290 | 0.9567 | 0.9798 | 0.9933 | 1.0000 | 0.6791 | 0.9226 | 0.9187 | 0.8054 | 1.0000 | 0.3070 | 0.5081 | −0.6842 | 0.8577 | 0.9309 | 0.6787 | 0.3069 | 0.9991 | 0.9991 | −0.0003 |
| Nf | 0.5725 | 0.8106 | 0.8957 | 0.8439 | 0.5242 | 0.5944 | 0.6791 | 1.0000 | 0.9033 | 0.7829 | 0.9726 | 0.6801 | 0.9028 | 0.9245 | −0.9712 | 0.5913 | 0.8937 | 1.0000 | 0.9028 | 0.6559 | 0.6558 | 0.0027 |
| Nc | 0.8618 | 0.9785 | 0.9978 | 0.9873 | 0.8329 | 0.8762 | 0.9226 | 0.9033 | 1.0000 | 0.9291 | 0.9643 | 0.9231 | 0.6349 | 0.7711 | −0.8855 | 0.7996 | 0.9979 | 0.9030 | 0.6347 | 0.9100 | 0.9100 | −0.0134 |
| epr | 0.8266 | 0.9051 | 0.9290 | 0.9616 | 0.8438 | 0.8782 | 0.9187 | 0.7829 | 0.9291 | 1.0000 | 0.8924 | 0.9192 | 0.5087 | 0.7271 | −0.8475 | 0.9141 | 0.9297 | 0.7827 | 0.5086 | 0.9092 | 0.9091 | 0.0014 |
| Ps30 | 0.7060 | 0.8957 | 0.9607 | 0.9368 | 0.6736 | 0.7339 | 0.8054 | 0.9726 | 0.9643 | 0.8924 | 1.0000 | 0.8062 | 0.8001 | 0.8931 | −0.9654 | 0.7326 | 0.9597 | 0.9724 | 0.8000 | 0.7848 | 0.7847 | −0.0426 |
| phi | 0.9729 | 0.9688 | 0.9295 | 0.9571 | 0.9795 | 0.9931 | 1.0000 | 0.6801 | 0.9231 | 0.9192 | 0.8062 | 1.0000 | 0.3084 | 0.5094 | −0.6853 | 0.8579 | 0.9314 | 0.6797 | 0.3083 | 0.9991 | 0.9991 | −0.0005 |
| NRF | 0.1643 | 0.4801 | 0.6209 | 0.5447 | 0.1136 | 0.1981 | 0.3070 | 0.9028 | 0.6349 | 0.5087 | 0.8001 | 0.3084 | 1.0000 | 0.9277 | −0.8842 | 0.2952 | 0.6173 | 0.9031 | 1.0000 | 0.2766 | 0.2765 | 0.0044 |
| NRc | 0.3528 | 0.6241 | 0.7520 | 0.7156 | 0.3305 | 0.4075 | 0.5081 | 0.9245 | 0.7711 | 0.7271 | 0.8931 | 0.5094 | 0.9277 | 1.0000 | −0.9574 | 0.5425 | 0.7496 | 0.9245 | 0.9275 | 0.4792 | 0.4792 | −0.0309 |
| BPR | −0.5426 | −0.7779 | −0.8759 | −0.8467 | −0.5253 | −0.5955 | −0.6842 | −0.9712 | −0.8855 | −0.8475 | −0.9654 | −0.6853 | −0.8842 | −0.9574 | 1.0000 | −0.6644 | −0.8742 | −0.9712 | −0.8842 | −0.6601 | −0.6601 | −0.0320 |
| farB | 0.7936 | 0.8050 | 0.8047 | 0.8591 | 0.8241 | 0.8403 | 0.8577 | 0.5913 | 0.7996 | 0.9141 | 0.7326 | 0.8579 | 0.2952 | 0.5425 | −0.6644 | 1.0000 | 0.8060 | 0.5910 | 0.2950 | 0.8554 | 0.8553 | −0.0649 |
| htBleed | 0.8732 | 0.9830 | 0.9987 | 0.9902 | 0.8455 | 0.8871 | 0.9309 | 0.8937 | 0.9979 | 0.9297 | 0.9597 | 0.9314 | 0.6173 | 0.7496 | −0.8742 | 0.8060 | 1.0000 | 0.8934 | 0.6172 | 0.9191 | 0.9190 | −0.0254 |
| Nf_dmd | 0.5720 | 0.8103 | 0.8954 | 0.8436 | 0.5237 | 0.5940 | 0.6787 | 1.0000 | 0.9030 | 0.7827 | 0.9724 | 0.6797 | 0.9031 | 0.9245 | −0.9712 | 0.5910 | 0.8934 | 1.0000 | 0.9030 | 0.6554 | 0.6554 | 0.0030 |
| PCNfR_dmd | 0.1642 | 0.4800 | 0.6208 | 0.5446 | 0.1135 | 0.1980 | 0.3069 | 0.9028 | 0.6347 | 0.5086 | 0.8000 | 0.3083 | 1.0000 | 0.9275 | −0.8842 | 0.2950 | 0.6172 | 0.9030 | 1.0000 | 0.2765 | 0.2764 | 0.0048 |
| W31 | 0.9777 | 0.9624 | 0.9171 | 0.9464 | 0.9857 | 0.9964 | 0.9991 | 0.6559 | 0.9100 | 0.9092 | 0.7848 | 0.9991 | 0.2766 | 0.4792 | −0.6601 | 0.8554 | 0.9191 | 0.6554 | 0.2765 | 1.0000 | 0.9999 | 0.0031 |
| W32 | 0.9777 | 0.9624 | 0.9171 | 0.9464 | 0.9857 | 0.9964 | 0.9991 | 0.6558 | 0.9100 | 0.9091 | 0.7847 | 0.9991 | 0.2765 | 0.4792 | −0.6601 | 0.8553 | 0.9190 | 0.6554 | 0.2764 | 0.9999 | 1.0000 | 0.0030 |
| RUL | −0.0023 | −0.0064 | −0.0253 | −0.0378 | −0.0031 | −0.0029 | −0.0003 | 0.0027 | −0.0134 | 0.0014 | −0.0426 | −0.0005 | 0.0044 | −0.0309 | −0.0320 | −0.0649 | −0.0254 | 0.0030 | 0.0048 | 0.0031 | 0.0030 | 1.0000 |
Appendix B
| Eignvector | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Component | Standard Deviation | Proportion Of Variance | Cumulative Variance | T2 | T24 | T30 | T50 | P2 | P15 | P30 | Nf | Nc | epr | Ps30 | phi | NRF | NRc | BPR | farB | htBleed | Nf_dmd | PCNfR_dmd | W31 | W32 |
| PC 1 | 4.1098 | 0.8043 | 0.8043 | 0.2125 | 0.2380 | 0.2422 | 0.2421 | 0.2088 | 0.2187 | 0.2293 | 0.2143 | 0.2421 | 0.2325 | 0.2325 | 0.2294 | 0.1464 | 0.1835 | −0.2143 | 0.2047 | 0.2423 | 0.2142 | 0.1463 | 0.2265 | 0.2265 |
| PC 2 | 1.8911 | 0.1703 | 0.9746 | 0.2432 | 0.0759 | −0.0129 | 0.0338 | 0.2694 | 0.2294 | 0.1739 | −0.2437 | −0.0234 | 0.0343 | −0.1505 | 0.1731 | −0.4207 | −0.3244 | 0.2381 | 0.1294 | −0.0105 | −0.2440 | −0.4208 | 0.1900 | 0.1900 |
| PC 3 | 0.6210 | 0.0184 | 0.9930 | −0.2203 | −0.2194 | −0.1148 | 0.0276 | −0.0668 | −0.0637 | −0.0351 | −0.1583 | −0.1055 | 0.4065 | −0.0113 | −0.0345 | −0.0745 | 0.2675 | −0.1636 | 0.7255 | −0.1142 | −0.1582 | −0.0747 | −0.0391 | −0.0391 |
| PC 4 | 0.2765 | 0.0036 | 0.9966 | −0.1973 | −0.1956 | −0.1354 | −0.0125 | 0.1133 | 0.1197 | 0.1552 | −0.1492 | −0.0729 | 0.3738 | −0.0685 | 0.1558 | −0.0679 | 0.3512 | −0.2851 | −0.6037 | −0.1303 | −0.1498 | −0.0681 | 0.1400 | 0.1399 |
| PC 5 | 0.1898 | 0.0017 | 0.9983 | 0.2407 | 0.1279 | 0.1338 | 0.2365 | −0.1105 | −0.1263 | −0.1444 | −0.1089 | 0.2504 | 0.0171 | 0.1765 | −0.1436 | −0.2556 | 0.5771 | 0.3024 | −0.1262 | 0.1371 | −0.1126 | −0.2598 | −0.1894 | −0.1890 |
| PC 6 | 0.1429 | 0.0010 | 0.9993 | −0.1080 | −0.0508 | −0.1018 | −0.2787 | 0.1666 | 0.1661 | 0.1402 | −0.0006 | 0.0850 | −0.5969 | −0.2325 | 0.1398 | 0.0629 | 0.5242 | 0.1348 | 0.1816 | −0.0949 | −0.0067 | 0.0564 | 0.1473 | 0.1473 |
| PC 7 | 0.0912 | 0.0004 | 0.9997 | 0.3962 | 0.2324 | −0.0820 | −0.3642 | −0.0725 | −0.1049 | −0.1372 | 0.1574 | 0.2384 | 0.2671 | −0.5964 | −0.1412 | −0.0471 | 0.0686 | −0.2038 | 0.0105 | −0.0991 | 0.1585 | −0.0485 | 0.0028 | 0.0024 |
| PC 8 | 0.0467 | 0.0001 | 0.9998 | 0.2674 | 0.1477 | −0.3715 | 0.0978 | −0.0681 | −0.0160 | 0.1226 | −0.0583 | 0.0358 | −0.3458 | 0.2701 | 0.1267 | −0.1464 | −0.0277 | −0.6182 | 0.0391 | −0.1879 | −0.0548 | −0.1362 | −0.1777 | −0.1775 |
| PC 9 | 0.0363 | 0.0001 | 0.9999 | 0.0132 | −0.0133 | 0.7894 | −0.0969 | −0.0175 | −0.0065 | 0.0249 | −0.0527 | −0.0336 | −0.0869 | 0.0295 | 0.0252 | −0.0552 | 0.0009 | −0.1860 | 0.0047 | −0.5529 | −0.0523 | −0.0533 | −0.0472 | −0.0457 |
| PC 10 | 0.0328 | 0.0001 | 0.9999 | 0.0008 | −0.0389 | 0.1788 | −0.7296 | −0.0113 | −0.0056 | 0.0201 | −0.0967 | −0.0508 | 0.0283 | 0.3284 | 0.0208 | −0.1045 | 0.0016 | −0.1610 | 0.0012 | 0.5025 | −0.0962 | −0.1026 | −0.0400 | −0.0441 |
| PC 11 | 0.0311 | 0.0000 | 1.0000 | 0.1051 | 0.1076 | −0.2848 | −0.3377 | 0.0413 | 0.0245 | −0.0107 | 0.1014 | 0.1245 | 0.2238 | 0.5163 | −0.0125 | 0.0465 | 0.0011 | 0.3575 | −0.0016 | −0.5287 | 0.1028 | 0.0463 | 0.0864 | 0.0873 |
| PC 12 | 0.0138 | 0.0000 | 1.0000 | −0.2578 | −0.2810 | −0.0020 | 0.0108 | 0.0167 | −0.0099 | −0.0864 | −0.1056 | 0.8618 | −0.0568 | 0.0304 | −0.0848 | −0.0164 | −0.2225 | −0.1099 | −0.0024 | −0.0025 | −0.1110 | −0.0253 | 0.0644 | 0.0496 |
| PC 13 | 0.0118 | 0.0000 | 1.0000 | 0.0477 | −0.0185 | 0.0025 | 0.0839 | −0.0086 | −0.1363 | −0.4283 | 0.0260 | −0.1718 | −0.1710 | 0.1638 | −0.4312 | −0.1047 | 0.0539 | −0.2109 | −0.0039 | 0.0099 | 0.0176 | −0.1249 | 0.4655 | 0.4744 |
| PC 14 | 0.0101 | 0.0000 | 1.0000 | −0.0021 | −0.0067 | −0.0005 | −0.0023 | 0.0098 | 0.0070 | −0.0020 | 0.0012 | 0.0090 | 0.0009 | 0.0001 | −0.0028 | 0.0001 | −0.0025 | −0.0016 | 0.0000 | 0.0020 | 0.0007 | −0.0008 | −0.7132 | 0.7008 |
| PC 15 | 0.0071 | 0.0000 | 1.0000 | 0.5000 | −0.7791 | 0.0160 | 0.0235 | −0.1718 | −0.1149 | 0.1418 | 0.1483 | −0.0349 | −0.0279 | 0.0250 | 0.1270 | −0.0272 | 0.0099 | 0.0680 | 0.0015 | 0.0178 | 0.1666 | −0.0003 | 0.0504 | 0.0501 |
| PC 16 | 0.0058 | 0.0000 | 1.0000 | 0.0583 | −0.2380 | −0.0142 | 0.0054 | 0.6356 | 0.4221 | −0.2979 | 0.1703 | −0.0600 | 0.0165 | 0.0288 | −0.2753 | −0.0146 | 0.0194 | −0.0802 | −0.0018 | −0.0146 | 0.1399 | −0.0673 | −0.2421 | −0.2634 |
| PC 17 | 0.0025 | 0.0000 | 1.0000 | 0.0239 | −0.0042 | 0.0006 | −0.0014 | −0.0321 | 0.0275 | −0.7104 | −0.0225 | 0.0000 | 0.0017 | −0.0024 | 0.7009 | 0.0127 | −0.0002 | 0.0038 | 0.0001 | −0.0002 | −0.0181 | 0.0232 | 0.0068 | 0.0081 |
| PC 18 | 0.0011 | 0.0000 | 1.0000 | −0.0506 | 0.0059 | 0.0006 | 0.0011 | 0.0861 | −0.0696 | −0.0029 | −0.4001 | 0.0033 | −0.0050 | 0.0004 | −0.0007 | −0.5777 | 0.0057 | −0.0026 | 0.0000 | 0.0008 | 0.4897 | 0.5014 | −0.0056 | −0.0055 |
| PC 19 | 0.0008 | 0.0000 | 1.0000 | −0.2540 | 0.0089 | 0.0007 | 0.0033 | 0.4119 | −0.6623 | 0.1074 | 0.3333 | −0.0010 | −0.0155 | 0.0051 | 0.1922 | −0.1498 | −0.0006 | −0.0017 | −0.0002 | 0.0011 | 0.2199 | −0.3095 | −0.0178 | −0.0180 |
| PC 20 | 0.0004 | 0.0000 | 1.0000 | 0.3279 | −0.0012 | 0.0002 | 0.0002 | 0.4451 | −0.4099 | −0.0213 | −0.4508 | 0.0004 | 0.0104 | 0.0000 | −0.0349 | 0.3864 | 0.0000 | −0.0001 | 0.0002 | 0.0002 | −0.3040 | 0.2821 | 0.0029 | 0.0029 |
| PC 21 | 0.0002 | 0.0000 | 1.0000 | 0.0385 | −0.0005 | 0.0000 | 0.0000 | 0.0661 | −0.0567 | −0.0051 | 0.4972 | 0.0001 | 0.0022 | −0.0001 | −0.0091 | −0.4057 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | −0.5855 | 0.4860 | 0.0009 | 0.0010 |
Appendix C
References
- Saxena, A.; Goebel, K. Turbofan Engine Degradation Simulation Data Set. NASA Ames Prognostics Data Repository, NASA Ames Research Center, Moffett Field. 2008. Available online: http://ti.arc.nasa.gov/project/prognostic-data-repository (accessed on 10 May 2019).
- Atamuradov, V.; Medjaher, K.; Dersin, P.; Lamoureux, B.; Zerhouni, N. Prognostics and health management for maintenance practitioners-review, implementation and tools evaluation. Int. J. Progn. Health Manag. 2017, 8, 1–31. [Google Scholar]
- Papakostas, N.; Papachatzakis, P.; Xanthakis, V.; Mourtzis, D.; Chryssolouris, G. An approach to operational aircraft maintenance planning. Decis. Support Syst. 2010, 48, 604–612. [Google Scholar] [CrossRef]
- Cubillo, A.; Perinpanayagam, S.; Esperon-Miguez, M. A review of physics-based models in prognostics: Application to gears and bearings of rotating machinery. Adv. Mech. Eng. 2016, 8, 1687814016664660. [Google Scholar] [CrossRef]
- Si, X.-S.; Wang, W.; Hu, C.-H.; Zhou, D.-H. Remaining useful life estimation—A review on the statistical data driven approaches. Eur. J. Oper. Res. 2011, 213, 1–14. [Google Scholar] [CrossRef]
- Lei, Y.; Li, N.; Guo, L.; Li, N.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal Process. 2018, 104, 799–834. [Google Scholar] [CrossRef]
- Faghih-Roohi, S.; Hajizadeh, S.; Nunez, A.; Babuška, R.; De Schutter, B. Deep Convolutional Neural Networks for Detection of Rail Surface Defects. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 2584–2589. [Google Scholar]
- Mehrotra, K.; Mohan, C.K.; Ranka, S. Elements of Artificial Neural Networks; MIT Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Zhao, G.; Zhang, G.; Ge, Q.; Liu, X. Research Advances in Fault Diagnosis and Prognostic Based on Deep Learning. In Proceedings of the 2016 Prognostics and System Health Management Conference (PHM-Chengdu), Chengdu, China, 19–21 October 2016; pp. 1–6. [Google Scholar]
- Xiongzi, C.; Jinsong, Y.; Diyin, T.; Yingxun, W. Remaining Useful Life Prognostic Estimation for Aircraft Subsystems or Components: A Review. In Proceedings of the 2011 10th International Conference on Electronic Measurement & Instruments, Chengdu, China, 16–19 August 2011; Volume 2, pp. 94–98. [Google Scholar]
- Yuan, M.; Wu, Y.-T.; Lin, L. Fault Diagnosis and Remaining Useful Life Estimation of Aero Engine Using LSTM Neural Network. In Proceedings of the 2016 IEEE International Conference on Aircraft Utility Systems (AUS), Beijing, China, 10–12 October 2016; pp. 135–140. [Google Scholar]
- Khan, F.; Eker, O.F.; Khan, A.; Orfali, W. Adaptive Degradation Prognostic Reasoning by Particle Filter with a Neural Network Degradation Model for Turbofan Jet Engine. Data 2018, 3, 49. [Google Scholar] [CrossRef]
- Li, X.; Ding, Q.; Sun, J.-Q. Remaining useful life estimation in prognostics using deep convolution neural networks. Reliab. Eng. Syst. Saf. 2018, 172, 1–11. [Google Scholar] [CrossRef]
- Zhang, A.; Wang, H.; Li, S.; Cui, Y.; Liu, Z.; Yang, G.; Hu, J. Transfer Learning with Deep Recurrent Neural Networks for Remaining Useful Life Estimation. Appl. Sci. 2018, 8, 2416. [Google Scholar] [CrossRef]
- Kong, Z.; Cui, Y.; Xia, Z.; Lv, H. Convolution and Long Short-Term Memory Hybrid Deep Neural Networks for Remaining Useful Life Prognostics. Appl. Sci. 2019, 9, 4156. [Google Scholar] [CrossRef]
- Zheng, S.; Ristovski, K.; Farahat, A.; Gupta, C. Long Short-Term Memory Network for Remaining Useful Life estimation. In Proceedings of the 2017 IEEE International Conference on Prognostics and Health Management (ICPHM), Dallas, TX, USA, 19–21 June 2017; pp. 88–95. [Google Scholar]
- Wu, Y.-T.; Yuan, M.; Dong, S.; Lin, L.; Liu, Y. Remaining useful life estimation of engineered systems using vanilla LSTM neural networks. Neurocomputing 2018, 275, 167–179. [Google Scholar] [CrossRef]
- Ellefsen, A.L.; Bjoerlykhaug, E.; Æsøy, V.; Ushakov, S.; Zhang, H. Remaining useful life predictions for turbofan engine degradation using semi-supervised deep architecture. Reliab. Eng. Syst. Saf. 2019, 183, 240–251. [Google Scholar] [CrossRef]
- Candel, A.; Parmar, V.; LeDell, E.; Arora, A. Deep Learning with H2O; H2O. ai Inc.: Mountain View, CA, USA, 2016. [Google Scholar]
- Bengio, Y. Learning Deep Architectures for AI. Found. Trends Mach. Learn. 2009, 2, 1–127. [Google Scholar] [CrossRef]
- Goodfellow, I.; Warde-Farley, D.; Mirza, M.; Courville, A.; Bengio, Y. Maxout networks. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16−21 June 2013; pp. 1319–1327. [Google Scholar]
- Ben-David, S.; Blitzer, J.; Crammer, K.; Kulesza, A.; Pereira, F.C.N.; Vaughan, J.W. A theory of learning from different domains. Mach. Learn. 2010, 79, 151–175. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; LaRochelle, H.; LaViolette, F.; Marchand, M.; Lempitsky, V. Domain-Adversarial Training of Neural Networks. J. Mach. Learn. Res. 2016, 17, 189–209. [Google Scholar] [CrossRef]
- Guyon, I.; Gunn, S.; Nikravesh, M.; Zadeh, L.A. (Eds.) Feature Extraction: Foundations and Applications. Springer: New York, NY, USA, 2008. [Google Scholar]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Sarwate, D. Mean-square correlation of shift-register sequences. IEEE Proc. F Commun. Radar Signal Process. 1984, 131, 101. [Google Scholar] [CrossRef]
- Sun, Y. Iterative RELIEF for Feature Weighting: Algorithms, Theories, and Applications. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1035–1051. [Google Scholar] [CrossRef]
- Derksen, S.; Keselman, H.J. Backward, forward and stepwise automated subset selection algorithms: Frequency of obtaining authentic and noise variables. Br. J. Math. Stat. Psychol. 1992, 45, 265–282. [Google Scholar] [CrossRef]
- Vafaie, H.; Imam, I.F. Feature Selection Methods: Genetic Algorithms vs. Greedy-Like Search. In Proceedings of the International Conference on Fuzzy and Intelligent Control Systems, LoUIsville, KY, USA, 26 June−2 July 1994; Volume 51, p. 28. [Google Scholar]
- Javed, K.; Gouriveau, R.; Zemouri, R.; Zerhouni, N. Features Selection Procedure for Prognostics: An Approach Based on Predictability. IFAC Proc. Vol. 2012, 45, 25–30. [Google Scholar] [CrossRef]
- Wirth, R.; Hipp, J. CRISP-DM: Towards a Standard Process Model for Data Mining. In Proceedings of the 4th International Conference on the Practical Applications of Knowledge Discovery and Data Mining; Springer: London, UK, 2000; pp. 29–39. [Google Scholar]
- Khumprom, P.; Yodo, N. A Data-Driven Predictive Prognostic Model for Lithium-Ion Batteries based on a Deep Learning Algorithm. Energies 2019, 12, 660. [Google Scholar] [CrossRef]
- Erhan, D.; Manzagol, P.A.; Bengio, Y.; Bengio, S.; Vincent, P. The difficulty of training deep architectures and the effect of unsupervised pre-training. AISTATS 2009, 5, 153–160. [Google Scholar]
- Saxena, A.; Goebel, K.; Simon, D.; Eklund, N. Damage Propagation Modeling for Aircraft Engine Run-to-Failure Simulation. In Proceedings of the 2008 International Conference on Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008; pp. 1–9. [Google Scholar]
- Frederick, D.K.; DeCastro, J.A.; Litt, J.S. User’s Guide for the Commercial Modular Aero-Propulsion System Simulation (C-MAPSS); NASA/TM-2007-215026; NASA: Washington, DC, USA, 1 October 2007.
- Van der Drift, A. Evolutionary selection, a principle governing growth orientation in vapour-deposited layers. Philips Res. Rep. 1967, 22, 267–288. [Google Scholar]
| Description | C-MAPSS | |||
|---|---|---|---|---|
| FD001 | FD002 | FD003 | FD004 | |
| Number of training engines | 100 | 260 | 100 | 248 |
| Number of testing engines | 100 | 259 | 100 | 248 |
| Operational conditions | 1 | 6 | 1 | 6 |
| Fault modes | 1 | 1 | 2 | 2 |
| Hyperparameters | Range |
|---|---|
| Epoch | {100, 1000, 5000, 7000, 10,000} |
| Training sample per iteration | AUTO |
| Batch size | 1 |
| Leaning rate annealing | {10−10, 10−8, 10−5, 10−1} |
| Momentum | {0.1, 0.2, 0.3, 0.5, 0.6, 0.8, 0.99} |
| L1: Regularization that constraint the absolute value | {10−20, 10−15, 10−10, 10−5, 10−1, 0} |
| L2: Regularization that constraint the sum of square weights | {10−20, 10−15, 10−10, 10−5, 10−1, 0} |
| Max w2: Maximum sum of square of incoming weight into the neuron | {0, 10, 100, 10,000, ∞} |
| Pearson Correlation | Relief Algorithm | SVM | PCA | Deviation | |||||
|---|---|---|---|---|---|---|---|---|---|
| Attributes | Weight | Attribute | Weight | Attribute | Weight | Attribute | Weight | Attribute | Weight |
| farB | −0.0648807 | P15 | 2.55555 × 10−5 | epr | 28.062965 | htBleed | 0.24226001 | PCNfR_dmd | 1.00002156 |
| Ps30 | −0.0426395 | Nf_dmd | 4.29878 × 10−13 | T2 | 24.031467 | T30 | 0.24219398 | farB | 1.00000884 |
| T50 | −0.0377657 | farB | −1.76803 × 10−13 | Nf_dmd | 15.921074 | Ne | 0.24213648 | P15 | 1.00000751 |
| BPR | −0.0320325 | T2 | −3.5083 × 10−13 | Nf | 15.293535 | T50 | 0.24212279 | epr | 1.00000215 |
| NRc | −0.0308729 | P2 | −1.41209 × 10−12 | T24 | 11.169562 | T24 | 0.23799320 | P2 | 1.00000079 |
| htBleed | −0.0254014 | PCNfR_dmd | −3.58802 × 10−12 | W31 | 9.070028 | epr | 0.23251894 | T2 | 1.00000049 |
| T30 | −0.0253007 | phi | −8.18383 × 10−7 | W32 | 8.806654 | Ps30 | 0.23247642 | Ne | 1.00000022 |
| Ne | −0.0133643 | Nf | −1.94057 × 10−6 | PCNfR_dmd | 6.597514 | phi | 0.22942893 | T50 | 1.00000016 |
| T24 | −0.0063673 | NRF | −2.22812 × 10−6 | NRF | 5.849870 | P30 | 0.22931342 | Ps30 | 1.00000013 |
| P2 | −0.0031016 | P30 | −3.43389 × 10−6 | P30 | 5.529144 | W31 | 0.22654883 | W32 | 1.00000013 |
| P15 | −0.0028634 | T24 | −3.2525 × 10−5 | phi | 5.262733 | W32 | 0.22654313 | T24 | 1.00000011 |
| T2 | −0.0023212 | W31 | −6.1066 × 10−5 | Ne | 0.026252 | P15 | 0.21870245 | T30 | 1.00000000 |
| phi | −0.0004811 | W32 | −6.76249 × 10−5 | P15 | −0.151776 | Nf | 0.21427293 | P30 | 0.99999998 |
| P30 | −0.0003329 | epr | −9.125 × 10−5 | P2 | −0.726430 | Nf_dmd | 0.21420247 | NRF | 0.99999993 |
| epr | 0.0013847 | Ne | −0.00017538 | farB | −16.274719 | T2 | 0.21253812 | BPR | 0.99999985 |
| Nf | 0.0026742 | BPR | −0.000324083 | T30 | −24.291950 | P2 | 0.20884536 | NRc | 0.99999984 |
| W32 | 0.0029798 | NRc | −0.000344686 | htBleed | −24.530502 | farB | 0.20473956 | phi | 0.99999978 |
| Nf_dmd | 0.0030117 | Ps30 | −0.000364589 | NRc | −32.369914 | NRc | 0.18353047 | Nf | 0.99999973 |
| W31 | 0.0030517 | T50 | −0.000397835 | T50 | −40.853420 | NRF | 0.14637480 | W31 | 0.99999957 |
| NRF | 0.0044269 | T30 | −0.000422547 | Ps30 | −53.894591 | PCNfR_dmd | 0.14634719 | htBleed | 0.99999829 |
| PCNfR_dmd | 0.0048232 | htBleed | −0.000613424 | BPR | −65.865476 | BPR | −0.21428742 | Nf_dmd | 0.99998466 |
| Methods | RMSE | Score | |||
|---|---|---|---|---|---|
| FD002 | FD004 | FD002 | FD004 | ||
| Original data | 45.439 | 45.302 | 645,121 | 427,968 | |
| SVM | Unusable | ||||
| Relief algorithm | |||||
| Backward elimination | 45.121 | 45.436 | 645,132 | 211,129 | |
| Deviation | 45.374 | 45.630 | 740,936 | 256,776 | |
| Evolutionary Selection | 44.717 | 44.953 | 518,025 | 355,458 | Best Overall |
| Forward selection | 45.242 | 46.505 | 1,353,749 | 423,997 | |
| PCA | 45.368 | 45.108 | 1,450,397 | 406,872 | |
| Pearson correlation | 45.272 | 46.216 | 502,579 | 338,400 | |
| Feature Selection Method | Model | Output Weights | Errors | ||
|---|---|---|---|---|---|
| Original (All 21 Attributes) | Layer ----- | Unit ---- | Type ----------- | Layer 2: −0.389707 Layer 3: −0.954436 Layer 4: −0.798112 Layer 5: 1.135641 | root_mean_squared_error: 45.439 +/− 0.000 absolute_error: 37.062 +/− 26.289 relative_error: 285.29% +/− 1071.56% relative_error_lenient: 40.87% +/− 26.92% relative_error_strict: 290.30% +/− 1070.51% normalized_absolute_error: 0.933 root_relative_squared_error: 0.963 squared_error: 2064.669 +/− 2549.829 correlation: 0.426 squared_correlation: 0.182 prediction_average: 68.095 +/− 47.177 spearman_rho: 0.406 kendall_tau: 0.28 |
| 1 2 3 4 5 | 21 12 12 12 1 | Input Rectifier Rectifier Rectifier 0.4 Dropout Linear | |||
| Backward Elimination | Layer ----- | Unit ---- | Type ----------- | Layer 2: −0.383010 Layer 3: −0.791862 Layer 4: −0.706631 Layer 5: 1.064392 | root_mean_squared_error: 45.121 +/− 0.000 absolute_error: 36.707 +/− 26.240 relative_error: 275.51% +/− 1043.67% relative_error_lenient: 40.75% +/− 26.64% relative_error_strict: 281.59% +/− 1042.46% normalized_absolute_error: 0.924 root_relative_squared_error: 0.956 squared_error: 2035.929 +/− 2509.247 correlation: 0.417 squared_correlation: 0.174 prediction_average: 68.095 +/− 47.177 spearman_rho: 0.399 kendall_tau: 0.278 |
| 1 2 3 4 5 | 19 11 11 11 1 | Input Rectifier Rectifier Rectifier 0.4 Dropout Linear | |||
| Deviation Selection | Layer ----- | Unit ---- | Type ----------- | Layer 2: −0.274669 Layer 3: −0.962801 Layer 4: −0.156934 Layer 5: 0.528834 | root_mean_squared_error: 45.374 +/− 0.000 absolute_error: 37.420 +/− 25.662 relative_error: 283.25% +/− 1026.67% relative_error_lenient: 41.82% +/− 26.69% relative_error_strict: 290.19% +/− 1025.24% normalized_absolute_error: 0.942 root_relative_squared_error: 0.962 squared_error: 2058.794 +/− 2489.328 correlation: 0.383 squared_correlation: 0.147 prediction_average: 68.095 +/− 47.177 spearman_rho: 0.375 kendall_tau: 0.261 |
| 1 2 3 4 5 | 11 7 7 7 1 | Input Rectifier Rectifier Rectifier 0.4 Dropout Linear | |||
| Evolutionary Selection* | Layer ----- | Unit ---- | Type ----------- | Layer 2: −0.820539 Layer 3: −0.729643 Layer 4: −1.375567 Layer 5: 1.658891 | root_mean_squared_error: 44.717 +/− 0.000 absolute_error: 36.402 +/− 25.971 relative_error: 271.60% +/− 1022.51% relative_error_lenient: 40.89% +/− 26.50% relative_error_strict: 278.38% +/− 1021.18% normalized_absolute_error: 0.917 root_relative_squared_error: 0.948 squared_error: 1999.604 +/− 2499.212 correlation: 0.415 squared_correlation: 0.172 prediction_average: 68.095 +/− 47.177 spearman_rho: 0.401 kendall_tau: 0.280 |
| 1 2 3 4 5 | 14 9 9 9 1 | Input Rectifier Rectifier Rectifier 0.4 Dropout Linear | |||
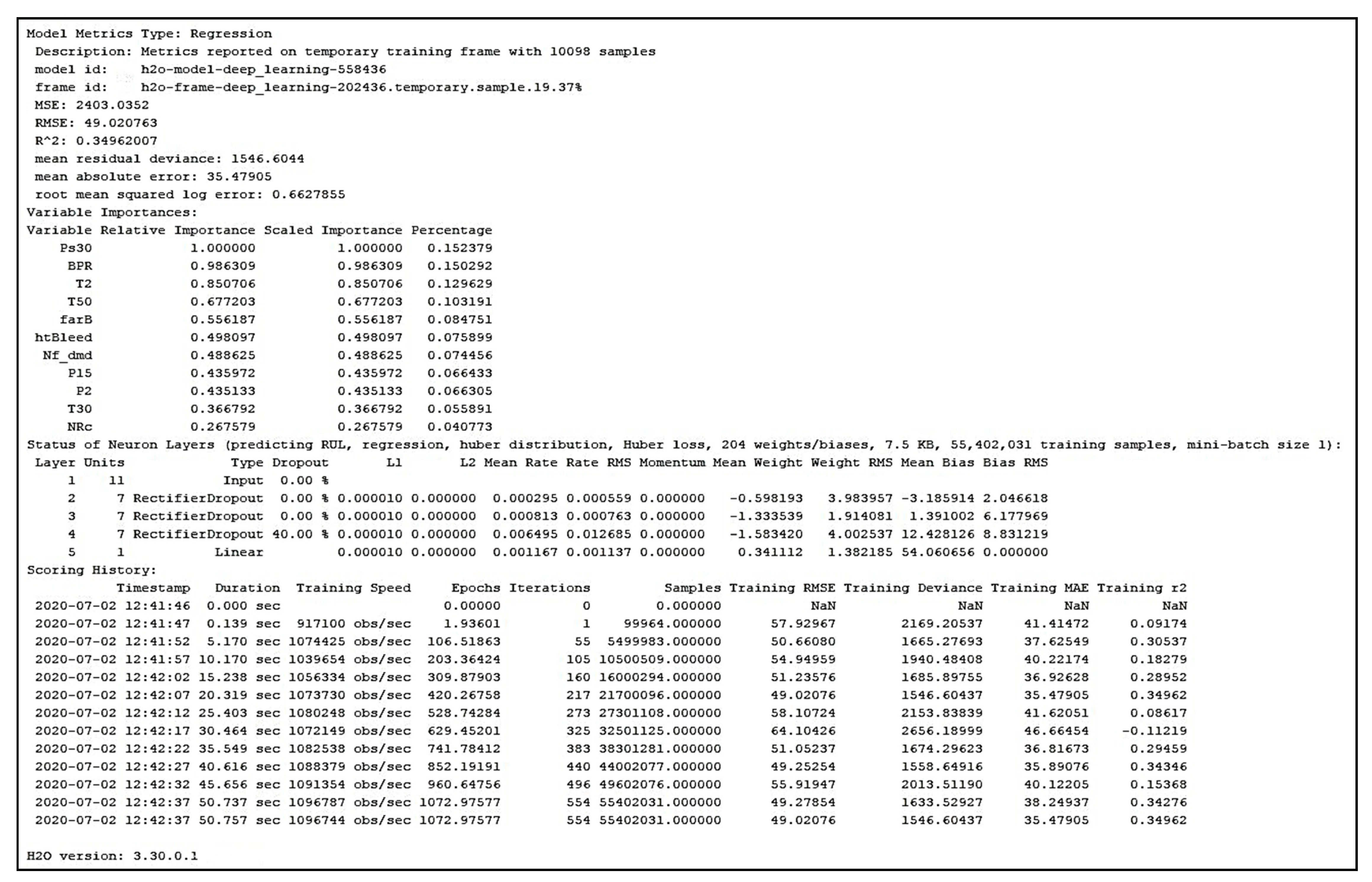
| Forward Selection | Layer ----- | Unit ---- | Type ----------- | Layer 2: −0.598193 Layer 3: −1.333539 Layer 4: −1.583420 Layer 5: 0.341112 | root_mean_squared_error: 45.242 +/− 0.000 absolute_error: 36.817 +/− 26.294 relative_error: 275.71% +/− 1038.01% relative_error_lenient: 41.12% +/− 26.56% relative_error_strict: 282.81% +/− 1036.64% normalized_absolute_error: 0.927 root_relative_squared_error: 0.959 squared_error: 2046.830 +/− 2564.139 correlation: 0.403 squared_correlation: 0.163 prediction_average: 68.095 +/− 47.177 spearman_rho: 0.390 kendall_tau: 0.272 |
| 1 2 3 4 5 | 11 7 7 7 1 | Input Rectifier Rectifier Rectifier 0.4 Dropout Linear | |||
| PCA Selection | Layer ----- | Unit ---- | Type ----------- | Layer 2: −0.022651 Layer 3: −1.327223 Layer 4: −1.541491 Layer 5: 1.298059 | root_mean_squared_error: 45.368 +/− 0.000 absolute_error: 36.694 +/− 26.680 relative_error: 264.95% +/− 1016.32% relative_error_lenient: 41.31% +/− 26.37% relative_error_strict: 275.07% +/− 1014.64% normalized_absolute_error: 0.924 root_relative_squared_error: 0.962 squared_error: 2058.300 +/− 2623.562 correlation: 0.390 squared_correlation: 0.152 prediction_average: 68.095 +/− 47.177 spearman_rho: 0.382 kendall_tau: 0.266 |
| 1 2 3 4 5 | 17 10 10 10 1 | Input Rectifier Rectifier Rectifier 0.4 Dropout Linear | |||
| Backward Elimination | Layer ----- | Unit ---- | Type ----------- | Layer 2: −0.853966 Layer 3: −1.340343 Layer 4: −0.972141 Layer 5: 0.786599 | root_mean_squared_error: 45.272 +/− 0.000 absolute_error: 37.002 +/− 26.084 relative_error: 269.63% +/− 1010.61% relative_error_lenient: 41.23% +/− 26.36% relative_error_strict: 277.67% +/− 1009.11% normalized_absolute_error: 0.932 root_relative_squared_error: 0.960 squared_error: 2049.533 +/− 2474.691 correlation: 0.382 squared_correlation: 0.146 prediction_average: 68.095 +/− 47.177 spearman_rho: 0.364 kendall_tau: 0.253 |
| 1 2 3 4 5 | 8 6 6 6 1 | Input Rectifier Rectifier Rectifier 0.4 Dropout Linear | |||
| Average RMSE | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Original Data | BW Elimination | Deviation | Evo Selection | FW Selection | PCA | Pearson | |||||||
| FD002 | FD004 | FD002 | FD004 | FD002 | FD004 | FD002 | FD004 | FD002 | FD004 | FD002 | FD004 | FD002 | FD004 |
| 48.398 | 50.541 | 47.907 | 50.331 | 48.160 | 50.081 | 47.452 | 49.650 | 48.434 | 50.708 | 48.072 | 49.737 | 49.203 | 52.111 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khumprom, P.; Grewell, D.; Yodo, N. Deep Neural Network Feature Selection Approaches for Data-Driven Prognostic Model of Aircraft Engines. Aerospace 2020, 7, 132. https://doi.org/10.3390/aerospace7090132
Khumprom P, Grewell D, Yodo N. Deep Neural Network Feature Selection Approaches for Data-Driven Prognostic Model of Aircraft Engines. Aerospace. 2020; 7(9):132. https://doi.org/10.3390/aerospace7090132
Chicago/Turabian StyleKhumprom, Phattara, David Grewell, and Nita Yodo. 2020. "Deep Neural Network Feature Selection Approaches for Data-Driven Prognostic Model of Aircraft Engines" Aerospace 7, no. 9: 132. https://doi.org/10.3390/aerospace7090132
APA StyleKhumprom, P., Grewell, D., & Yodo, N. (2020). Deep Neural Network Feature Selection Approaches for Data-Driven Prognostic Model of Aircraft Engines. Aerospace, 7(9), 132. https://doi.org/10.3390/aerospace7090132





