1. Introduction
Flow visualization is crucial for understanding the fluid dynamics of engineering systems. However, a technology gap persists in the area of flow visualizations of optically inaccessible flow fields, such as flows in fully integrated systems. A technique known as positron emission tomography (PET) is gaining popularity in addressing this technology gap. It is currently heavily utilized in the medical field to non-invasively visualize physiological processes in humans and small animals. Its use in the medical field involves introducing radioisotopes that emit positrons in a region of interest (ROI) within the subject. An individual positron annihilates with a nearby electron to create two gamma-rays with equal 511 keV energy. These coincident gamma rays are emitted at nearly 180 degrees from each other, and are subsequently detected by two separate detectors within a detector array. The arrays are typically arranged in a ring configuration. Each pair of coincident detections describes a path, or line of response (LOR), between the two triggered detectors along which the radioisotope is presumed to have been located at the time of the positron emission. As the radioisotopes continue to decay, multiple LORs are acquired and processed with image reconstruction algorithms in order to map the radioisotope distribution within the subject.
The use of PET in the engineering field for flow field visualizations is anticipated to be fundamentally similar to its use in the medical field. However, restrictions on the utilized types and quantities of radioisotopes would be reduced as no biological tissue would be present.
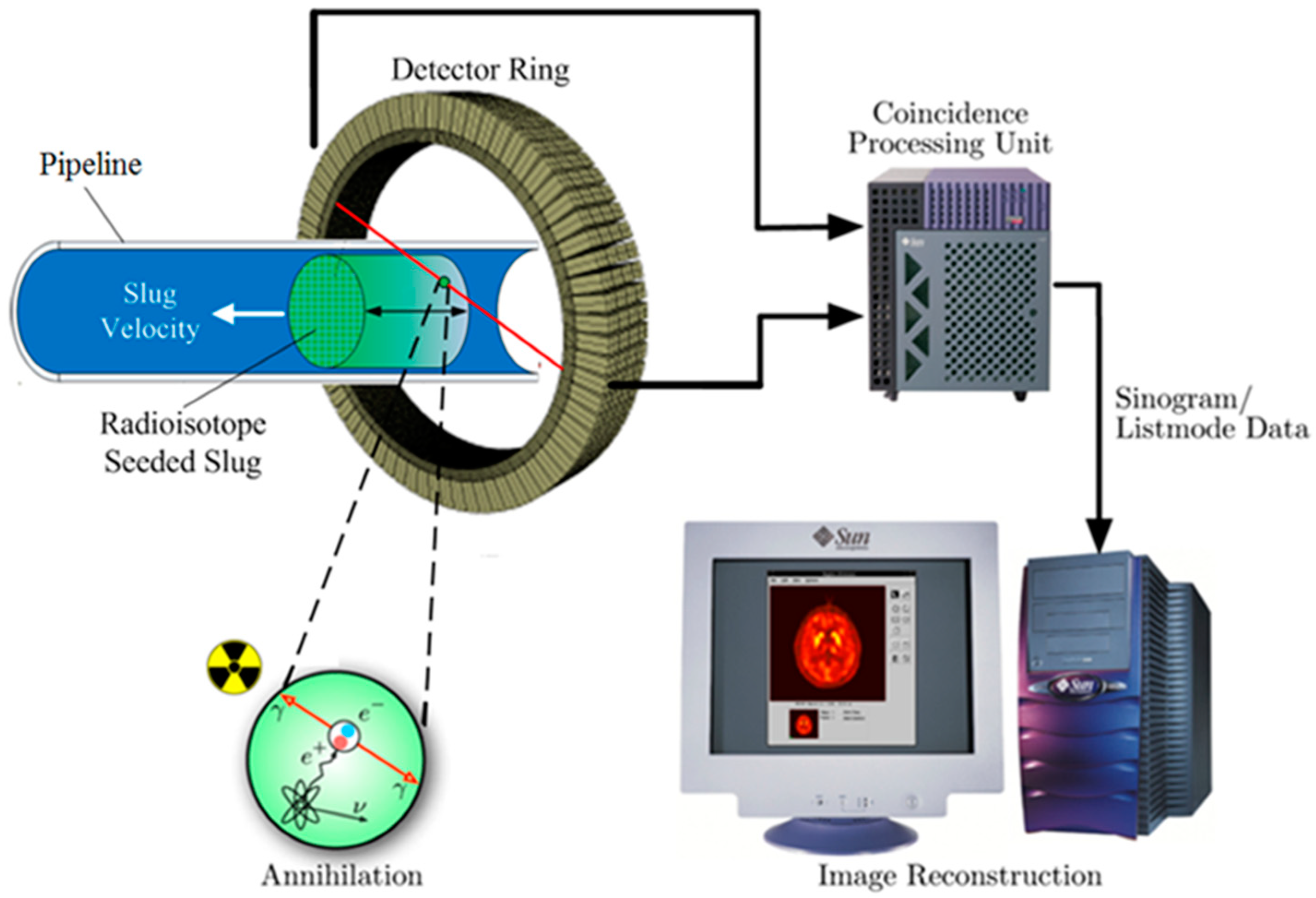
Figure 1 depicts a conceptual schematic of how the technique can be applied to visualize the flow in a metal pipeline. The schematic conveys the process in which a slug of the flowing media containing radioisotopes of the bulk media (the green slug of liquid) is injected into the flow. The radioisotopes decay and the resulting coincident gamma rays are detected as the slug of liquid traverses the flow field within the detector’s field of view. The LORs are then processed to reconstruct the radioisotope distribution in the flow path. As in the medical field, regions with high coincidence detection rates are a result of high radioisotope concentrations in the flow field. These regions of high concentration can be mapped spatially and, under the correct conditions, temporally, thus revealing various attributes of the flow field.
The benefits of this technique are anticipated to be as follows:
The technique is considered non-intrusive as it is possible to utilize radioisotopes of the bulk media; for example, the radioisotope oxygen-15 can be used in systems containing oxygen carrying media, such as liquid oxidizer propellant systems, and carbon-11 in systems with carbon based media, such as liquid methane. Utilizing the radioisotope of the bulk media is anticipated to preserve the thermochemical properties of the working media as it traverses the engineering system and undergoes thermochemical processes. Compared to other flow visualization techniques such as particle image velocimetry (PIV) or laser Doppler velocimetry (LDV) which require seed particles, the chemical composition of the mixture can remain unchanged.
The relatively high energy photons (511 keV) emitted after the decay of the radioisotopes are capable of penetrating the containment walls of metallic vessels and containment structures, rendering this technique to be an effective tool for characterizing fluid flows inside engineering systems that are subject to high temperatures and/or pressures. This is seen as one of the main advantages of PET compared to PIV or LDV which require optically transparent structures.
The proposed radioisotopes have relatively short half-lives, on the order of minutes. This attribute results in the mitigation of radiological hazards associated with the implementation process, which contributes to the technology’s accepted widespread use in the medical field.
Visualization of flows within engineering systems is an effective tool in troubleshooting anomalous performance and identifying inefficiencies in the fluid flow inside developmental and/or fully integrated systems.
The concept of flow field visualization using PET was first reported in 1987 through a collaborative effort by Rolls Royce, the University of Birmingham Physics Department, and Rutherford Appleton Laboratory [
2]. Through this collaborative partnership, the group was able to explore the use of the state-of-the-art in PET technology at that time to visualize the flow field in annular oil volumes in a rotating power turbine shaft and in a small helicopter engine. In the study an oil film attached to the inner wall of a spinning shaft was simulated by a positron line source of sodium-22 with a diameter of 1.5 mm and a total activity 125 µCi. PET cameras built by Rolls Royce were used to detect emitted gamma rays. Results showed that the simulated film inside a rotating power turbine locking shaft was resolvable to within 6.6 mm. Follow-on testing performed by these organizations involved the use of the same PET system to visualize the flow of oil as it was fed into a bearing rig [
3]. Results from this experimentation demonstrated the successful visualization of the steady state oil flow through three different injection paths. This was accomplished through scanning durations over 10 min resulting in a spatial resolution of 2.5 mm in X and Y planes parallel to the detectors and a 15 mm resolution in the Z direction, normal to the detector planes. Although results were promising for these efforts, these particular demonstrations were, for steady state flows with mapping, achieved over prolonged scanning durations using a multi-wire proportional counter (MWPC). Although MWPCs were known for their high-energy resolution they are also known to have a low detection efficiency [
4]. It is anticipated that less scanning time will be required with current detection technology which will be necessary for the flow regimes that are of interest for this particular study.
An alternate application was explored by Khalili et al. (1998) to visualize and quantitatively characterize the time-dependent scalar transport through natural opaque permeable sediments [
5]. These experiments were successfully carried out over test durations of 180 min for various sandy sediments, most importantly, sands of very fine grain size, and packings of spherical glass beads. The results presented demonstrated that “PET can provide a novel way of visualizing three-dimensional, transient flows inside natural as well as artificial sediments.” However, the temporal resolution of the PET measurements for this study was not reported.
Each of these previous applications have been constrained to the investigation of long timescale flow phenomena due to the limited temporal resolution of previous detector technologies. However, recent improvements in PET technology promise enhanced temporal resolution and, therefore, increased applicability in the engineering field to capture flow features on shorter time scales as compared to e.g., the sediment transport problem. The detector arrays have transitioned from the use of traditional photo multiplier tubes (PMTs) to the use of silicon photomultipliers (SiPMs), also known as an avalanche photo diodes (APDs). Additionally, lutetium-yttrium oxyorthoscilicate (LYSO) scintillation crystals have been shown to have superior detection capability over the traditional gadolinium oxyorthosilicate (GSO) and bismuth germanate (BGO) scintillating crystals. With a scintillation decay constant of 40 ns the maximum theoretical allowable count rate with LYSO is 25 Mcps. This is approximately 8 times larger than that of a BGO crystal with a decay constant of 300 ns [
6]. The implications of these advances are a primary driver for the present investigation aimed at documenting the potential of these novel detection technologies for mapping out features of flows, and objects of engineering interest with the goal of eventually measuring transient fluid flow phenomena in constrained visually obstructed geometries.
This paper reports on progress made in characterizing a modern PET system’s ability to visualize two categories of flow features in a visually inaccessible pipe flow with a circular orifice. The first category refers to flow features that are steady in nature, however are constrained to detection acquisitions over a short time scale due to the transient, laminar diffusion and/or turbulent mixing of the radioisotopes throughout the flow field. Preliminary estimates suggested that the time-scales associated with such diffusion-driven processes could likely facilitate 3D flow structure mapping with modern PET systems. For the chosen example problem, after the radioisotope has been introduced at the pipe inflow, its concentration in the recirculating (or secondary) flow regions ahead and downstream of the orifice is initially low. The resulting identifiable large radioisotope concentration gradients would, therefore, reveal such recirculating flow regions. The second category refers to flow features that are anticipated to be more readily resolved on a long time scale when the radioisotope concentration in the core flow and secondary flow are approaching a steady-state limit. For the chosen problem, these features include the axial location and diameter of the orifice plate. From an application point of view the interest would be for example on the detection of deposits that build up over time and cause a stenosis and thus total pressure loss in pipe flow. As already discussed, previous work has already conveyed the technology’s ability to resolve stationary, or steady state radioisotope distributions given a sufficiently long acquisition window. With regard to category two, the present investigation is novel as it identifies the minimum required acquisition times associated with modern PET systems with emphasis on their utility in resolving geometrical features that may be present in practical fluid system applications, such as flow obstructions.
The primary objective of this study was to identify the required acquisition durations necessary for a modern PET system to adequately resolve the stated flow features given a fixed specific activity level and flow Reynolds number. This paper discusses details regarding the methodology undertaken to develop the study to meet this objective. In particular, details are provided regarding the use of a continuum-based computational fluid dynamics (CFD) technique combined with Monte Carlo-based probabilistic models to simulate the passage of a water/radioisotope solution through an orifice pipe flow, as well as the resulting photon emission and propagation through the fluid and containment material. The simulation input parameters are discussed followed by the simulation approach and its validation by way of comparison with data from the literature.
The results obtained from the various simulations are then discussed and conclusions are drawn with respect to proposed follow-up experiments. Particular focus is paid to predicting the capability of the selected PET system to resolve the short and long time-scale features as previously indicated. The paper concludes with a brief discussion of further work related to expanding the use of the present analysis process to varying specific activity levels and Reynolds numbers. The intent of this study and future studies is to ascertain a correlation amongst these pertinent parameters, and the use of such correlations as a basis for follow-up experiments to be performed utilizing the modelled PET system.
2. Methodology
To achieve the stated objective it was decided to consider a canonical flow problem, the separated flow behind an orifice plate in a pipe. The parameters (pipe diameter, velocity, orifice diameter) were chosen such that the characteristic time-scales associated with the diffusion of the radioisotope species into the recirculating flow region was on the order of seconds. A time-scale of seconds was anticipated to be accessible to PET flow field mapping techniques that utilize existing scanning configurations and image reconstruction protocols. Besides being canonical, this geometry also has practical relevance for many industrial applications where orifices are used as a passive means to control and measure flow rates.
The diffusion process will cause a gradual increase of the radioisotope in the recirculating flow region. As a result the concentration gradient across the shear layer that delineates the core flow from the recirculating flow will decrease and the ability of the PET system to differentiate between the core flow and the recirculating flow will diminish.
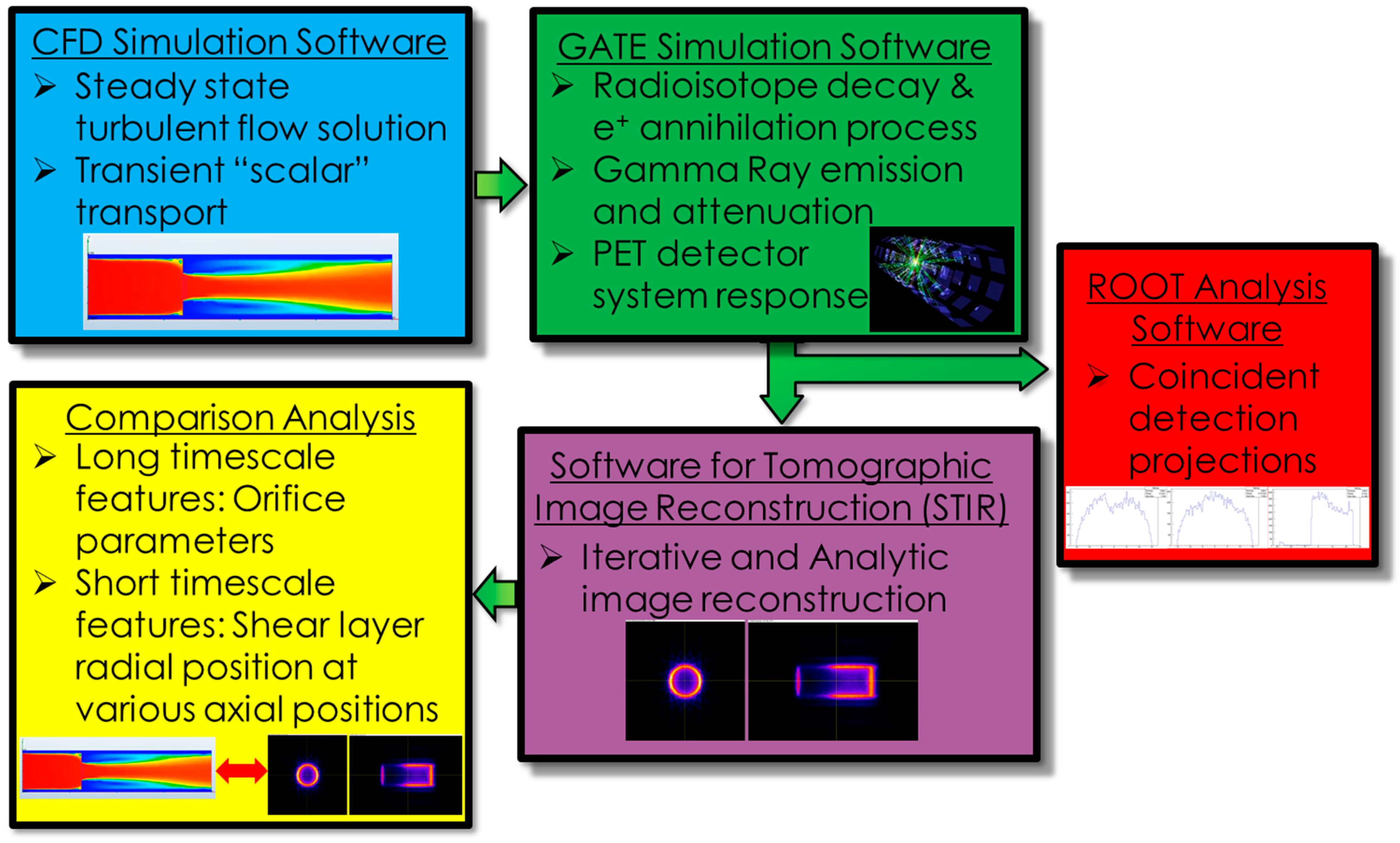
With this canonical application in mind, a process was developed to evaluate the PET systems response to the simulated transient transport of the radioisotope species through the orifice, and its subsequent diffusion into the recirculating flow region. The process began with an initial CFD simulation which was conducted to determine the steady state flow of the bulk media through an orifice. Once a steady state solution was obtained, the resulting flow field solution was used as an input to the subsequent transient simulation of the radioisotope transport through the flow field. The resulting transient mapping of the radioisotope concentration was then used to generate source maps for each time step. An attenuation map consisting of the orifice and pipe material as well as the liquid bulk media was also generated using the computational domain defined for the CFD simulation. These source and attenuation maps were then used as inputs for the simulation of the response of a PET detector. The coincidence detection rates were computed with an open source Monte Carlo simulation software package known as GEANT4 Applications for Tomographic Emission (GATE) produced by the OpenGATE collaboration [
7]. The primary data obtained from the GATE simulations were projection data consisting of the LORs and their associated time stamps. This data set was then passed to the Software for Tomographic Image Reconstruction (STIR) toolkit where an iterative, ordered subset expectation maximization (OSEM) algorithm was used to reconstruct the radioisotope distribution for each acquisition [
8]. These various elements and their relative position in the data flow sequence are depicted at a high level in the diagram shown in
Figure 2. Details regarding each of these elements are discussed in the following subsections.
2.1. Steady State Flow Field Simulation
The pipe and orifice geometry were chosen to emulate a proposed experimental setup with an ANSI 2 inch schedule 40 stainless steel (SS304) pipe. A British Standard, square edge circular orifice plate was used with a 30 degrees downstream bevel and an aspect ratio (β = d
orifice/D
pipe) of 0.5. The computational domain encompassed the entire three-dimensional volume. A cross section of the axisymmetric geometry is shown in
Figure 3.
The CFD simulations were carried out with a Reynolds-averaged Navier–Stokes solver provided by the Autodesk CFD software (2019 Version, Autodesk Inc., San Rafael, CA, USA). Water was chosen as the bulk media. A Reynolds number of 67,000, with respect to the orifice diameter and the centerline maximum flow velocity, was targeted which corresponded to an inlet velocity condition of 0.4 m/s. A fully developed velocity profile was prescribed at the inflow boundary. A constant pressure of 0 Pa with respect to an atmospheric gauge pressure was assumed at the outflow boundary. The global temperature was set to 21 °C (70 °F) with the heat transfer solver disabled. No-slip and no-penetration boundary conditions were enforced on the wetted surfaces of the pipe and orifice plate.
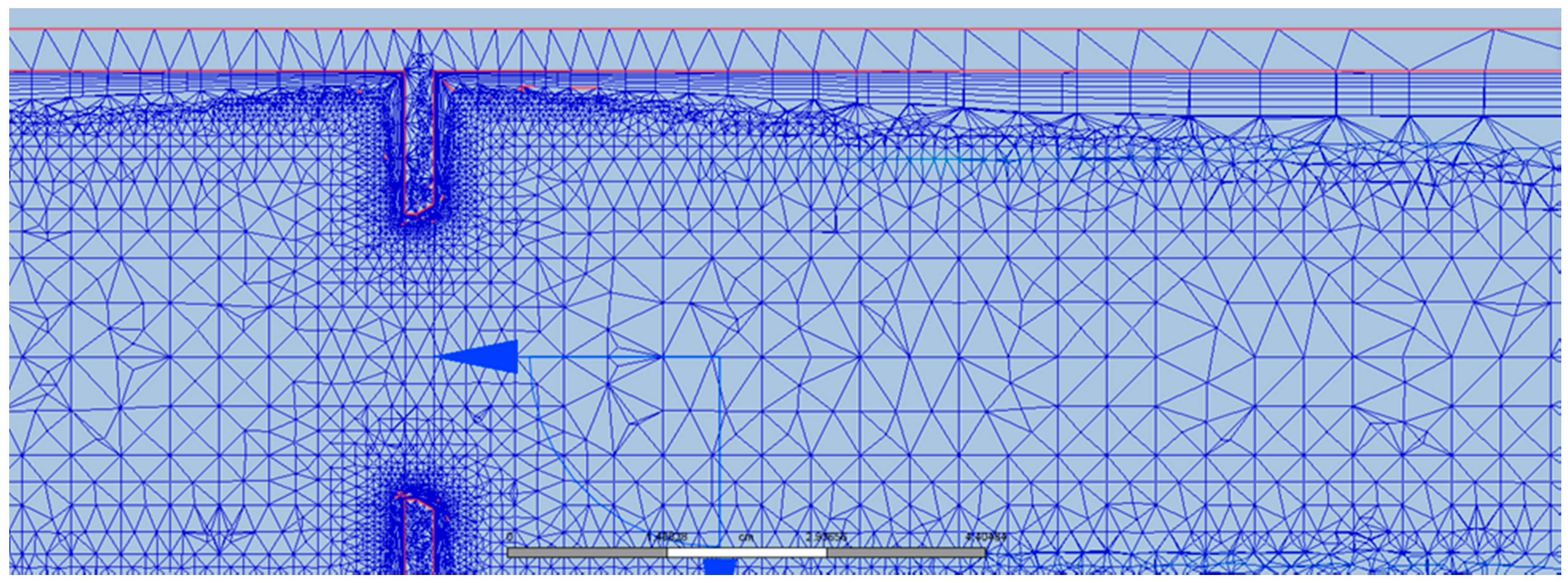
Two unstructured tetrahedral meshes were generated. The fine mesh had 20.1 × 10
6 fluid elements and 4.5 × 10
6 nodes. The coarse mesh was based on the fine mesh solution and optimized for concurrent runs of the CFD and GATE software and consisted of 1.4 × 10
6 elements (including solid elements) and 2.6 × 10
6 nodes. The two different meshes are shown in
Figure 4 and
Figure 5. For both meshes, the pipe material was included in the model in order for it to be present, and accurately aligned in the follow-on Monte Carlo physics simulations. Accurately accounting for the solid material in the GATE simulations is critical for obtaining the correct wall material attenuation and detector response.
The SST k-ω turbulence model was selected for the CFD simulations. This turbulence model employs the k-ω model near walls and the k-ε turbulence model in the freestream. Standard, published, values were used for each of the model parameters [
9].
In Autodesk CFD the governing partial differential equations (PDEs) are discretized with a finite element method. The finite element method uses polynomial shape functions to represent the dependent variables over each element [
10]. When 3D tetrahedral elements are chosen to construct the mesh, as was the case for this study, the polynomial shape functions are assigned a linear form by the Autodesk CFD software. These representations are substituted into the governing PDEs and then the weighted integral of these equations is taken over each element. The result is a set of algebraic equations for the dependent variables at each node of every element. These equations are solved iteratively until convergence criteria for the dependent variables at each node have been met.
This finite element method is applied directly to the diffusion and source terms of the governing PDEs, where the weight functions are chosen to be the same form as the shape functions. However, to increase numerical stability a modified Petrov–Galerkin upwind scheme was employed to discretize the convective term. The modified scheme utilizes a different weight function for the convective terms, as opposed to the standard Petrov–Galerkin scheme which assigns the same weight function to all temporal and spatial terms. The time derivatives were discretized utilizing an implicit, backward differencing scheme.
2.2. Radioisotope Species Transport Transient Simulation
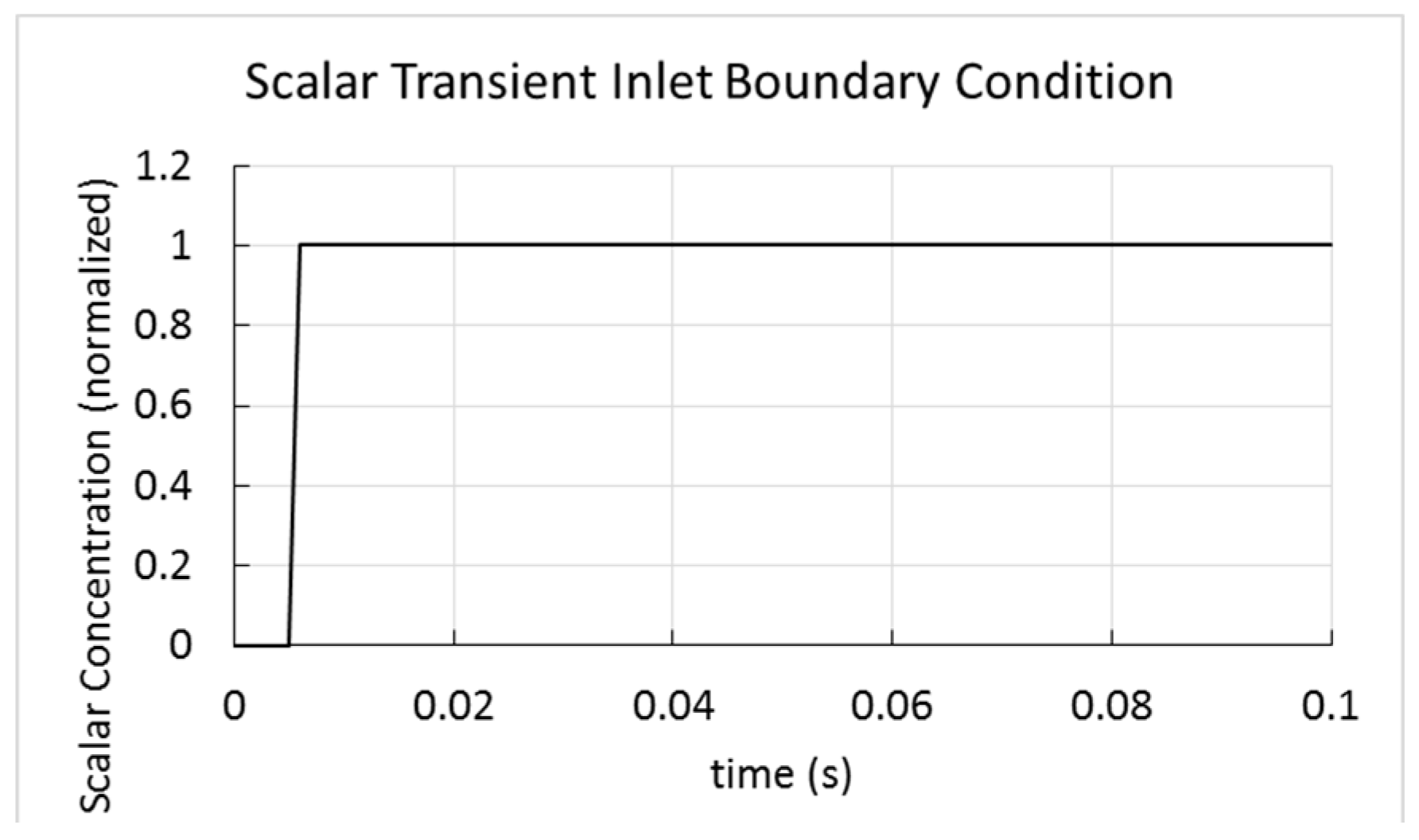
A passive scalar transport equation was solved to model the evolution of the F-18/water solution in the pipe after its impulsive injection. A ramp function at the inlet boundary was set to simulate the injection process. The ramp function is shown in
Figure 6 where the scalar (radioisotope) concentration value was normalized by the respective maximum specific activities specified for the individual test cases.
The transient transport simulation was only run on the coarse mesh described in the previous section. A constant time step of 0.001 s was used for the full length of the simulation. Three iterations were performed for each time step.
The commonly used fluorine-18 (F-18) radioisotope was chosen for this study due to its relatively long half-life (109.728 min) as compared to other radioisotopes of interest, i.e., oxygen-15 (O-15) with a half-life of ~2 min. The relatively long half-life of F-18 facilitates the assumption that the concentration of the radioisotope can remain constant over the time scale of the simulation (on the order of 10 s). A value of 1 × 10
−5 cm
2⁄s was used for the diffusivity of stable fluorine to account for the diffusion transport mechanism. This value was conservative with respect to the range of values published in literature [
11].
The output from the CFD simulations served as input to generate voxelized radioisotope distributions, or source mappings, for the PET system response simulations.
2.3. Positron Emission Tomography System Response Simulation
In order to characterize the response of a PET system to the radioisotope distribution through the flow field, simulations were performed using the GATE software. The GATE software utilized the voxelized radioisotope distribution to simulate the multiple facets of the PET detection process. This includes the initial decay process within each voxel containing the F-18 radioisotopes, the attenuation of the resulting gamma ray emissions through the flowing media and containment wall material; the interaction of the gamma rays with the detectors; and the processing electronics where coincidence events are flagged and corresponding event times and spatial coordinates are recorded. Critical parameters that govern the performance of a PET system, such as detector energy resolution, detector block configuration, and coincidence processing electronics dead times, are used as inputs into the GATE simulation. These parameter values were selected to be representative of a commercially available modern PET system and held constant over all test cases.
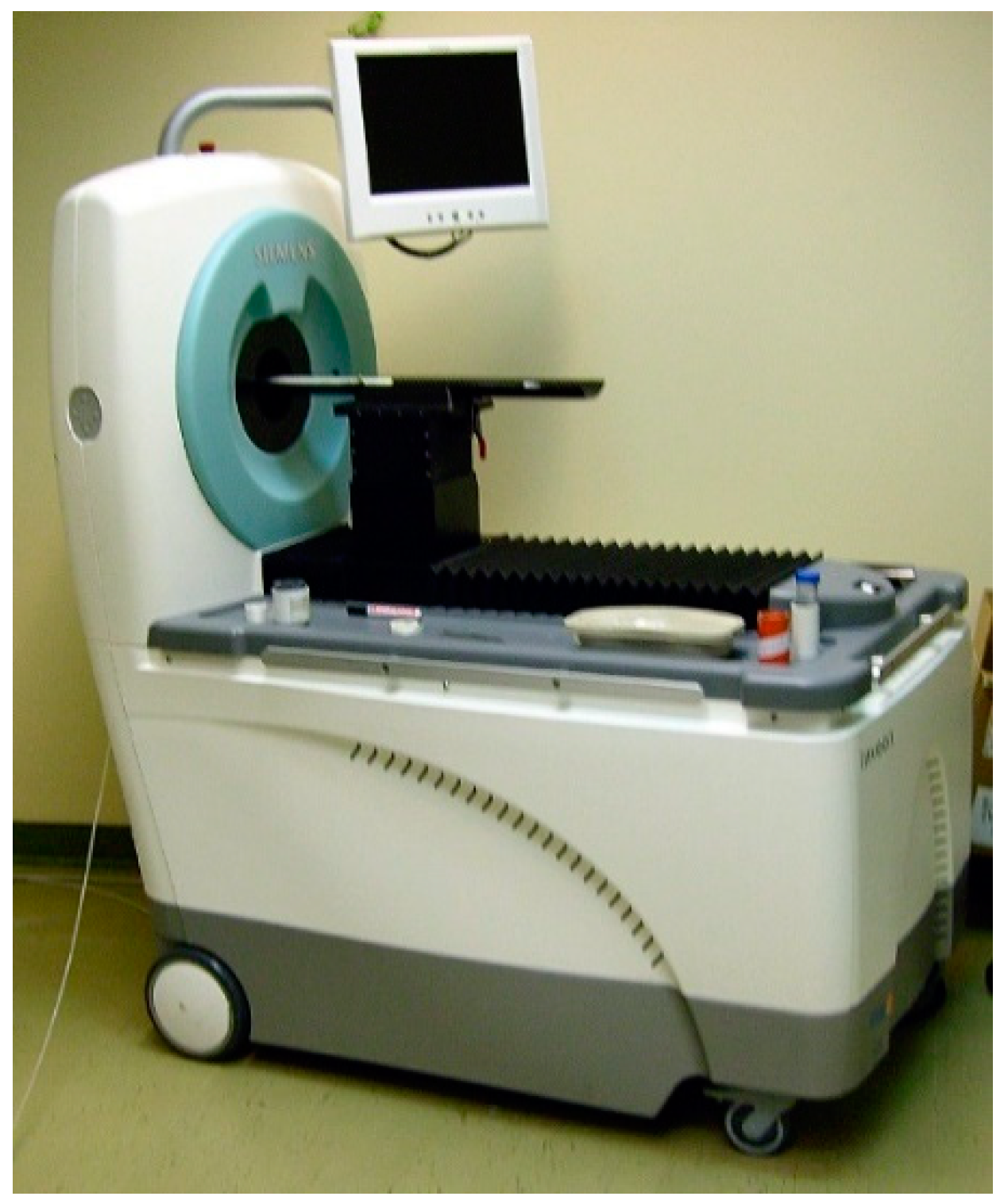
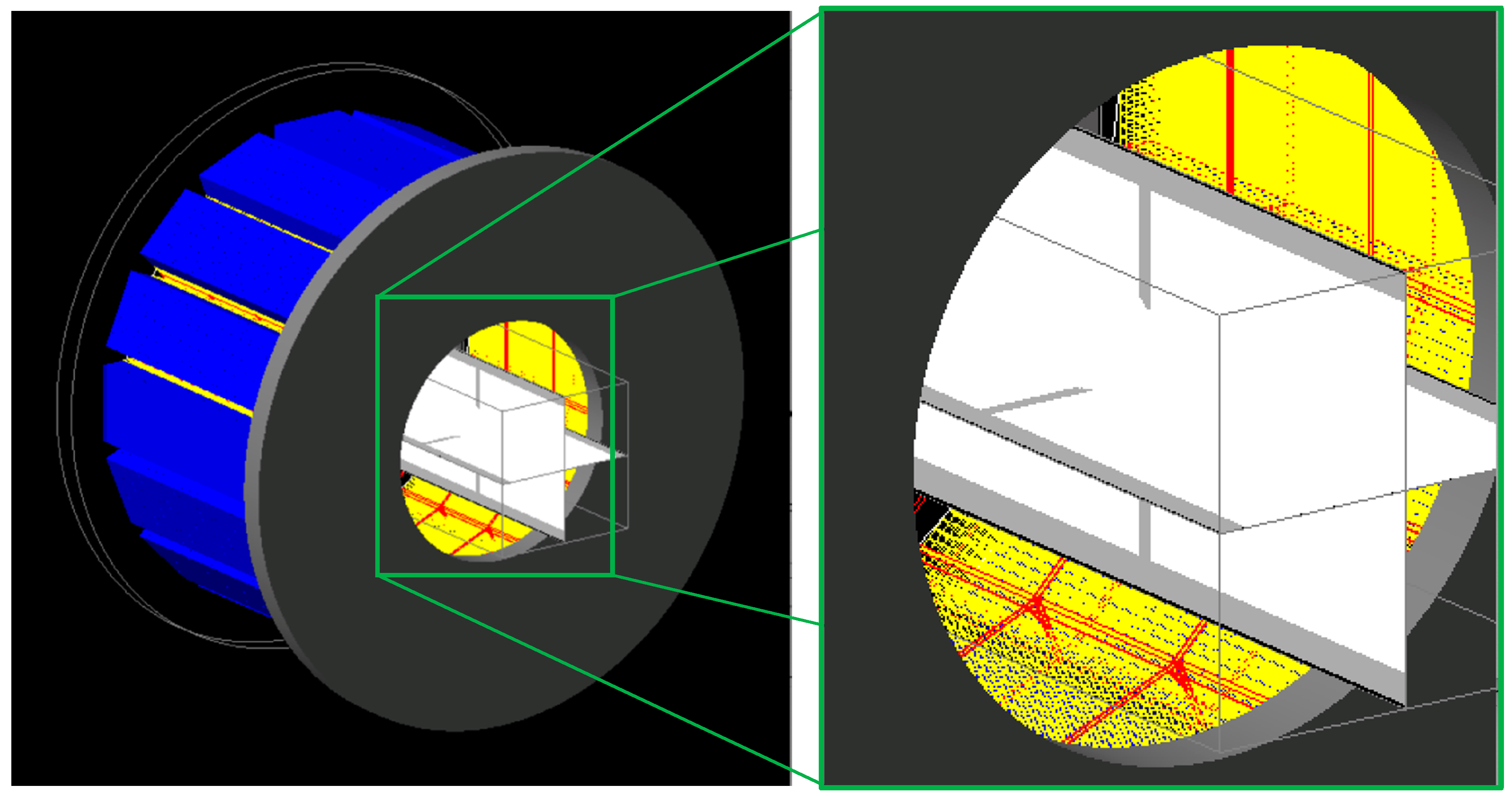
The PET system chosen for the present study is the Siemens Inveon PET system (Siemens Medical Solutions USA, Inc., Malvern, PA, USA), shown in
Figure 7. The GATE model for this system was developed using geometrical and performance parameters identified in previous studies [
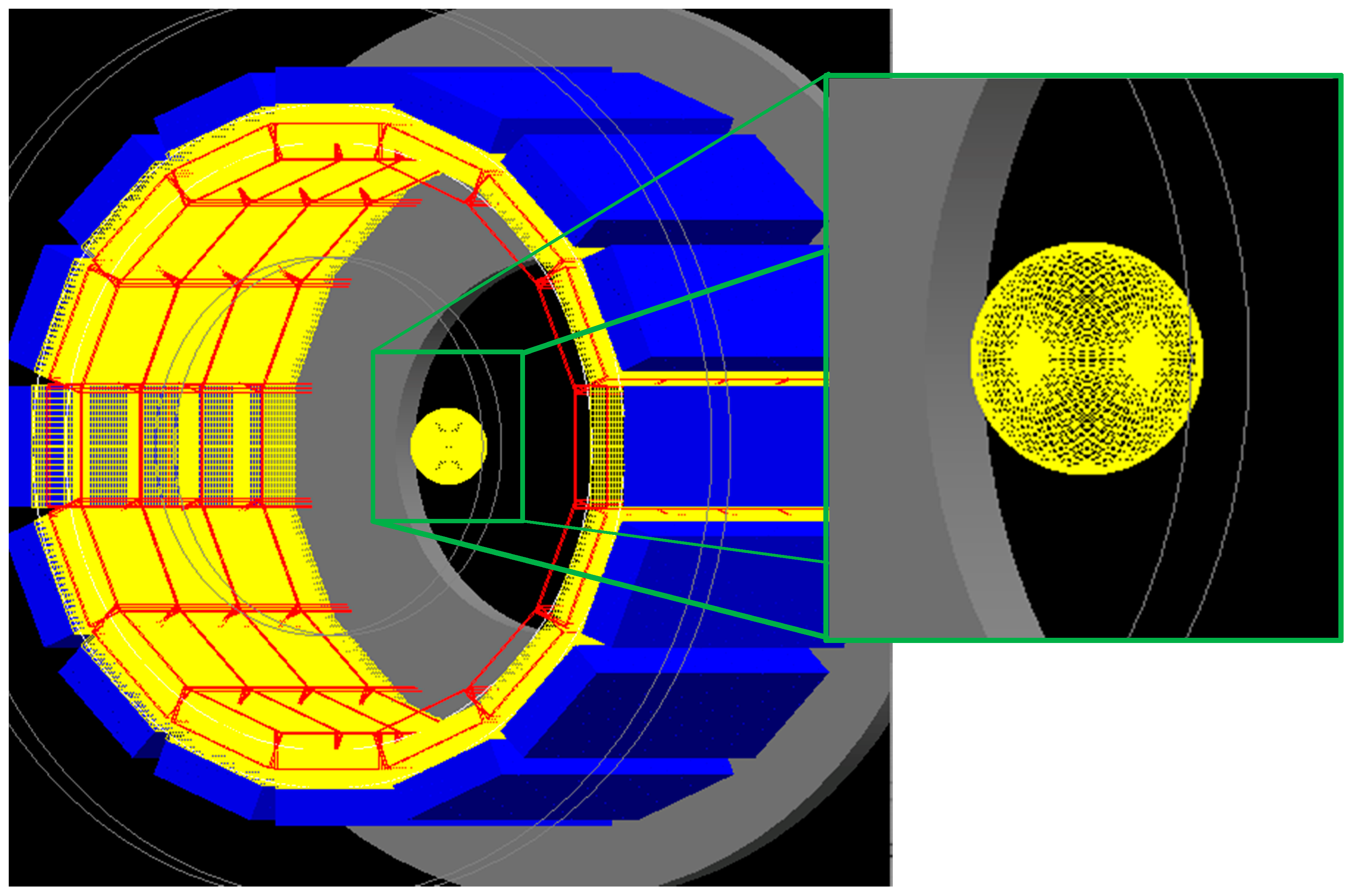
12]. The model geometry consists of 16 detector modules in a 16.1 cm diameter ring configuration with a 12.7 cm axial field of view (FOV) and a 10.0 cm transverse FOV. Each module contains a one by four array of detector blocks, with the four blocks oriented axially. Each detector block consists of a 20 by 20 array of lutetium oxyorthosilicate (LSO) scintillating crystals. The dimensions for each crystal are 1.59 mm × 1.59 mm × 10.00 mm. The model also includes other photon scattering materials that are in the physical system, such as the light guides that direct scintillation photons to position-sensitive photomultiplier tubes (PSPMT), the electronics packs containing the signal-processing electronics, and the lead shields at the axial ends of the detector ring.
Detector performance and signal processing parameters were incorporated into a digitizer module. Some of the key features included a 350 keV to 650 keV energy acceptance window to mitigate scattered photon detection, a 3.432 ns coincidence timing window, and 14.6% energy resolution determined through empirical measurements and a comparison with publicly accessible manufacturer data. Signal processing deadtime was incorporated by including a deadtime feature set in paralyzable mode which results in single detections within the deadtime specified window being eliminated from coincidence processing.
The GATE model for the Siemens Inveon system was extensively validated in previous work [
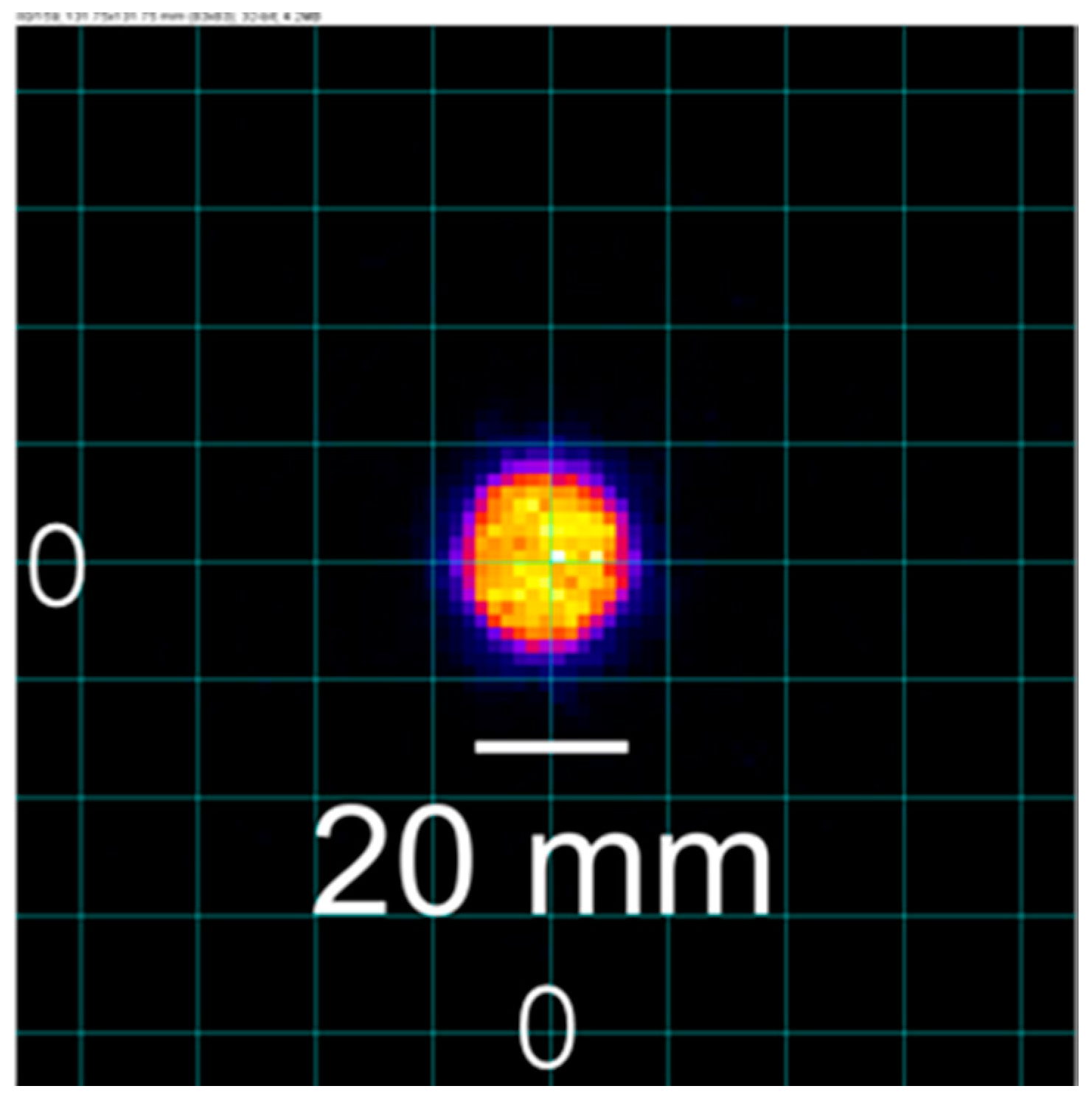
12]. However, to ensure the input parameters were accurate for the current study, a truncated validation process was performed. This process consisted of simulating the system response and image reconstruction algorithm output for a 20 mm diameter spherical source of F-18 in solution with water, without a containment structure. The source is depicted within the field of view (FOV) of the detector in
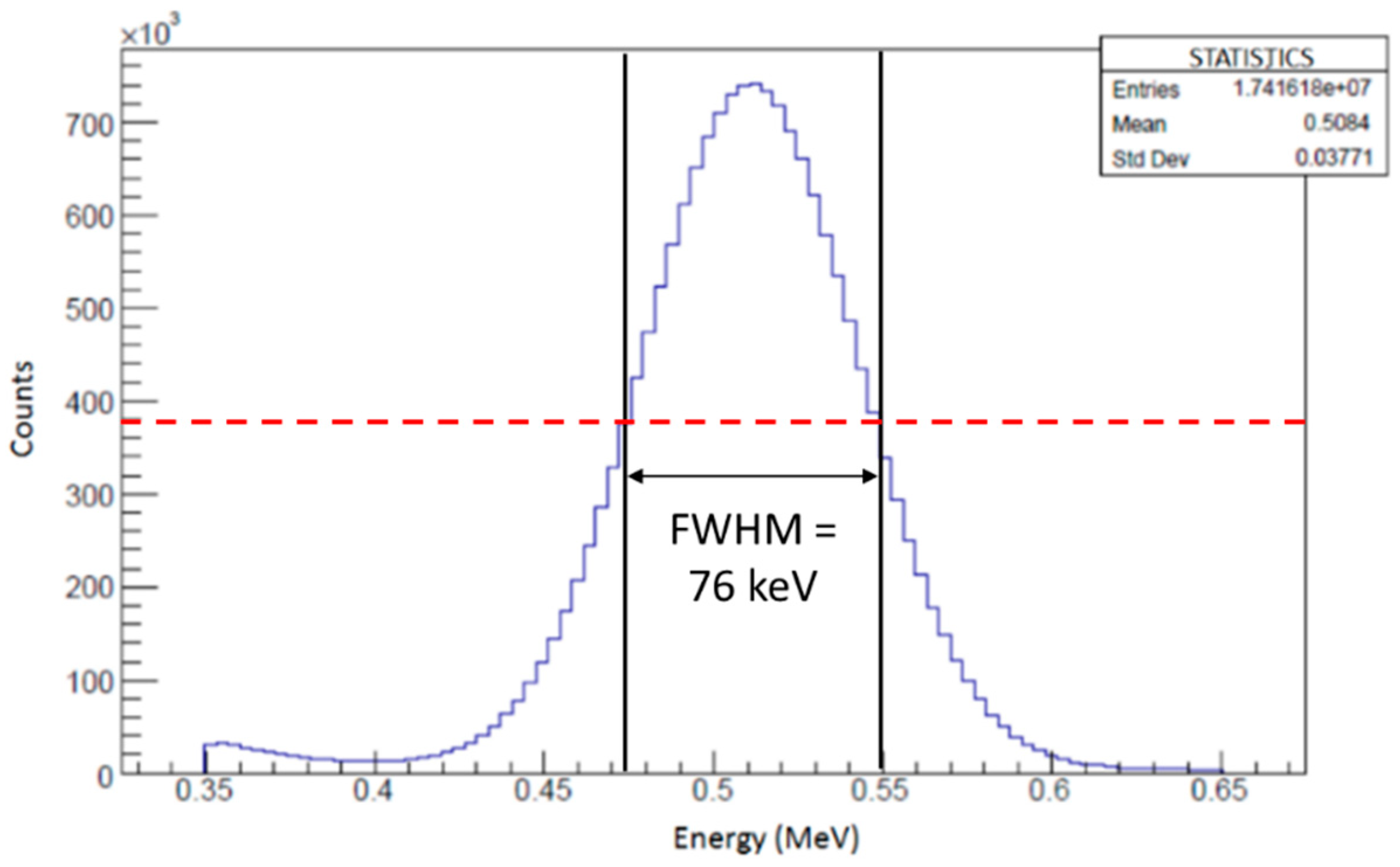
Figure 8. The resulting energy spectrum is shown in
Figure 9 with a full width at half maximum (FWHM) of 76 keV, corresponding to a 14.9% energy resolution. This is in good agreement with the 14.6% energy resolution prescribed above, in addition to published F-18 spectra using LSO scintillating crystal-based systems [
12,
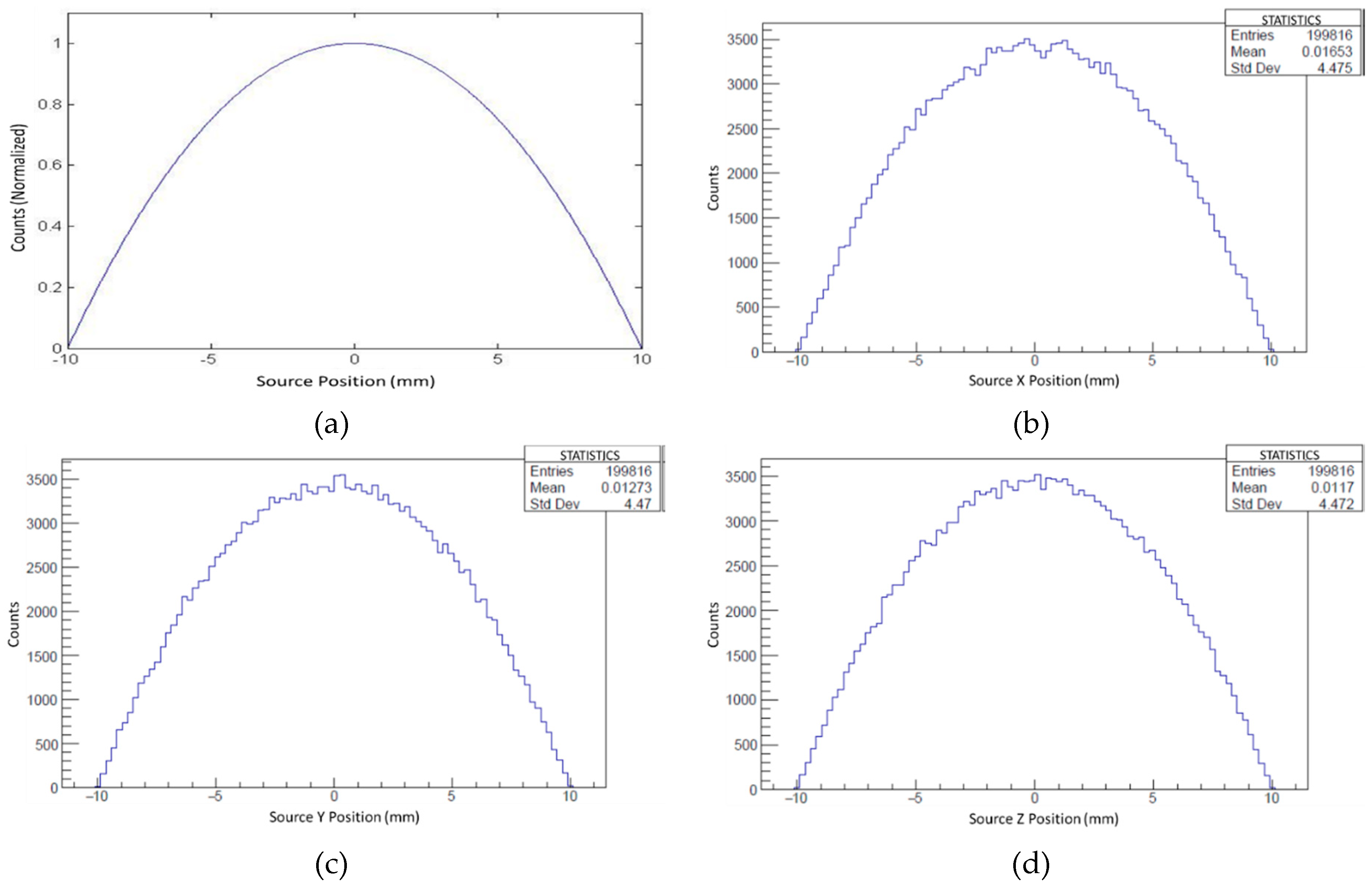
13]. The simulation of the systems response is conveyed with the histograms shown in
Figure 10b–d, which represent projections of all coincident detections onto the x, y, and z axes, respectively. These projections are in good agreement with the normalized, theoretical source distribution generated assuming an infinite number of detections. This reference distribution is shown in
Figure 10a.
Once validated, the “voxelized source” tool provided by the GATE software was used to generate source input files from the radioisotope concentration maps obtained from the CFD. Although it was possible to generate concentration maps for each incremental time step, a time-average of the flow field over the duration of each GATE data acquisition was used as source input for the GATE simulations in order to reduce the computational demand.
A maximum specific activity of 155 Bq/voxel (91.2 Bq/mm
3) was set, resulting in a total activity of 32.3 MBq within the detectors FOV. The chosen activity level was sufficiently below the total activity level of 100 MBq, which corresponds to the activity level associated with the systems reported peak noise equivalent count rate (NECR) [
12]. Activity levels above 100 MBq would result in oversaturation of the detector, and, therefore, a reduction of the coincidence detection rate.
Additionally, an attenuation map was generated using the simulation geometry in order to spatially correlate the source with the physical material of the pipe and flowing media. This was done to accurately account for scattering and attenuation of emitted gamma-rays. The resulting flow geometry shown within the field of view of the modeled detector system is depicted in
Figure 11. Although the figure only shows the orthogonal planes of the geometry, the Monte Carlo simulation accounts for the full three-dimensional effects of the flow geometry.
All GATE simulations were run on a Macbook Pro with an i5 processor with 4 cores, as well as on the Discovery high-performance computing cluster located at New Mexico State University.
2.4. Image Reconstruction
The final element of the simulation process utilizes the coincidence detection data generated by the GATE simulations to reconstruct the radioisotope distribution within the flow field being analyzed. This was accomplished by using an image reconstruction software package known as Software for Tomographic Image Reconstruction (STIR). The STIR package contains a range of analytical and numerical, or iterative, image reconstruction algorithms. For the present study, an iterative ordered subset expectation maximization (OSEM) algorithm was used. The specific implementation of this type of algorithm in STIR is referred to as the ordered subset maximization a posteriori one step late (OSMAPOSL) algorithm. The number of subsets for each simulation was set to 16 with four sub-iterations. It is common to use an estimated prior distribution, referred to as a “prior”, to assist in increasing image quality. Although no priors were used for this initial scope of work, implementation of priors based on CFD results are of interest for future studies. Noise corrections for random and scattered coincidence detections as well as attenuation corrections were applied. Random corrections were applied using random detection projection data, which was obtained from a delayed coincidence detection window, as is the typical practice in the medical field. The coincidence window was 3.432 ns with a delay of 100 ns.
Scatter correction was deemed necessary after identifying a scatter fraction of 29.1% during initial simulation runs. The scatter correction process utilized the single scatter simulation algorithm available in the STIR package. The iterative process outlined in Reference [
8] was used with 2 iterations proving to provide improved scatter correction results. Attenuation correction was accomplished using an attenuation map of the pipe, water, and air material within the detector FOV. The attenuation map consisted of attenuation coefficient values assigned to each voxel depending on their respective materials. Values of 0.666 cm
−1, 0.097 cm
−1, and 1.050 × 10
−4 cm
−1 were used for SS304, water, and air respectively [
8,
14,
15]. Corrections were applied as additive sinograms according to,
where
is the additive sinogram,
is a set of sinograms with random detections,
is a set of sinograms with bin normalization values (all set to 1 for this study),
is the scatter sinograms as estimated using STIR, and
is a set of sinograms containing attenuation correction factors which were computed using the attenuation map and Beer’s Law.
Validation of the OSMAPOSL algorithm was accomplished using the coincidence detection data from the 20 mm diameter F-18/water spherical source. The resulting reconstructed image is shown in
Figure 12. As can be seen, the reconstructed sphere is in the expected location and the diametrical edge of the sphere is discernable to within an approximate 1 mm uncertainty.
3. Results and Discussion
This section provides a description of the simulation results, their interpretation, and the conclusions that can be drawn.
3.1. Steady State Flow Field Simulation Results
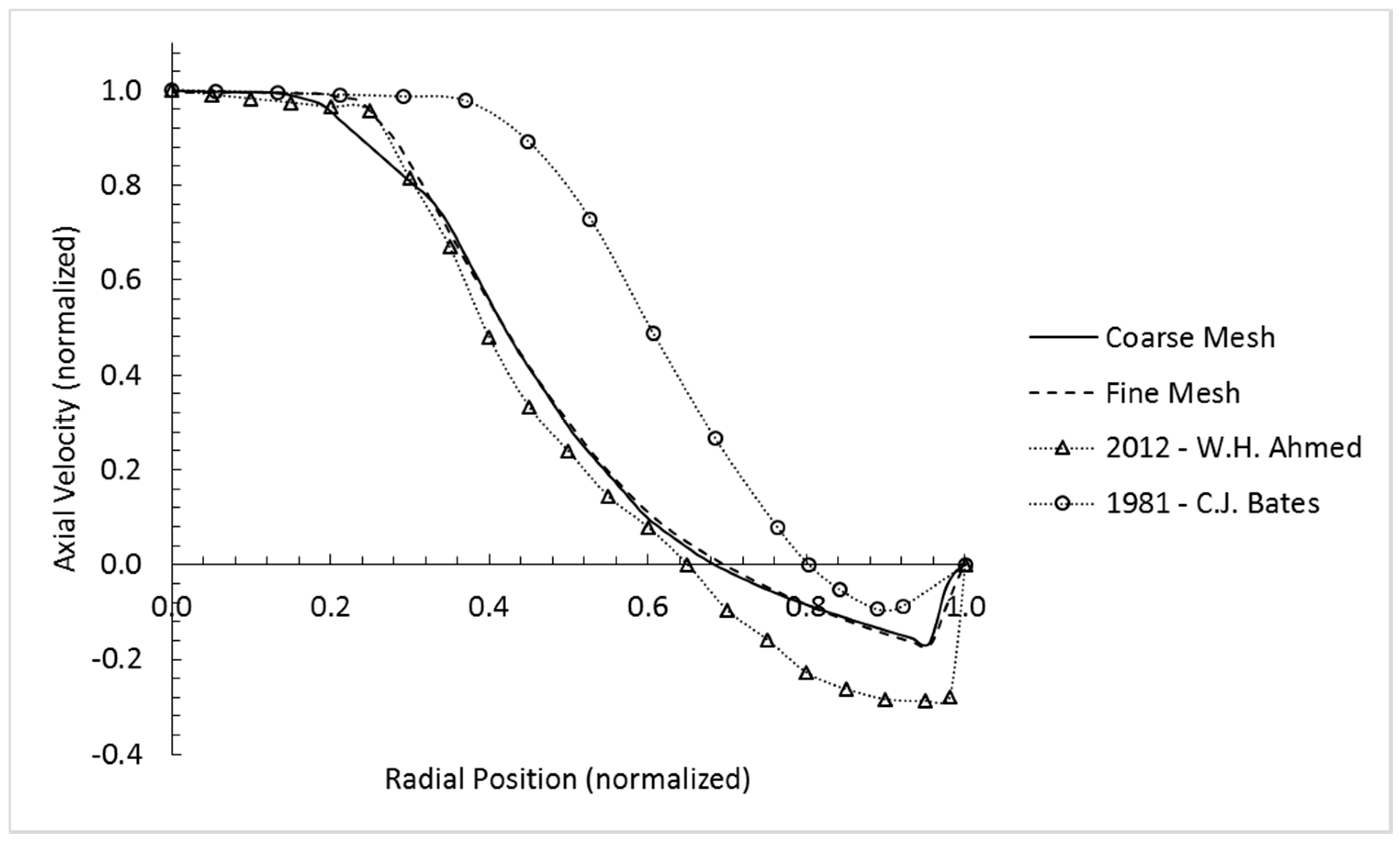
Radial profiles of the normalized axial velocity at the axial position of z/D = 1.0 obtained from the steady state flow field in
Figure 13 indicate grid convergence of the results. The profiles are similar to those obtained by Ahmed for the same problem (2012) [
16]. Ahmed employed the k-ε renormalization group (RNG) turbulence model to account for low-Reynolds-number effects. Compared to the simulation performed by Ahmed, the present profiles indicate a weaker reverse flow inside the recirculation region. Outside the recirculation region the agreement with the Ahmed profile is good. Also included in
Figure 13 is a measured profile by Bates (1981) [
17]. Interestingly, in the experiment the recirculation is also weaker than in the Ahmed simulation.
Contour plots of the turbulent intensity (TI) for a radial plane are shown in
Figure 14.
Radial profiles of the turbulence kinetic energy (TKE) from the centerline (r = 0) to the outer wall for an axial position of z/D = 1.0 are provided in
Figure 15. The experimental profile by Bates was taken at z/D = 0.9. The TKE was normalized by the square of the freestream velocity (
). It can be seen that the radial position of the peak TKE values for all simulation results, including those reported by Ahmed, are slightly shifted inward, towards the centerline, relative to the experimental data. The TKE peak value for the fine mesh is close to the experimental peak value. Larger peak values were obtained for the fine mesh simulation and the RNG simulation by Ahmed.
Although the coarse mesh results were not in perfect agreement with the published data, they were deemed acceptable for the purpose of the present investigation. The rationale for this decision was twofold: (1) With the TKE values being higher and more broadly distributed the turbulent diffusion rate of radioisotopes into the secondary flow would be greater. This is a conservative estimate with actual experimental results expected to take more time, providing more time with favorable radioisotope concentration gradients, and therefore permitting more detections to be acquired to enable visualization of the short timescale flow features, i.e., the radial position of the shear layer. (2) The nature of the study relies more heavily on the relative differences between the input flow field and the PET visualized flow field. So long as the flow conditions represented reasonably accurate time scales, the deviations are conjectured to be inconsequential with regard to meeting the objectives of the present study.
3.2. Radioisotope Species Transport Simulation Results
Concentration maps of the F-18 radioisotope species are shown in
Figure 16a–c at 1.0, 2.5, and 7.5 s, respectively, after injection of the radioisotope. The leading edge of the labeled slug of fluid propagates to the orifice in ~0.2 s, which is the anticipated time based on the mean flow velocity and distance traveled. The F-18 media then traverses through the orifice and passes over the large recirculating flow regions downstream of the orifice. For t = 1.0, small separated flow regions can be discerned upstream of the orifice and the isotope is seen to be transported backward in the recirculating flow regions downstream of the orifice. The downstream shear-layer is clearly identifiable for several seconds with the F-18 concentration starting to diffuse into the recirculating region and beginning to approach a uniform distribution. Although F-18 concentration gradients are still present at 7.5 s post-injection, they have drastically diminished with the recirculating and core flow regions being difficult to discern from each other.
The present study used
Figure 16c, corresponding to a radioisotope distribution at 7.5 s post-injection, to generate the activity maps for the GATE simulation’s voxelized source input files. For the current study this single frame was used as a representation of the average distribution over the full acquisition duration.
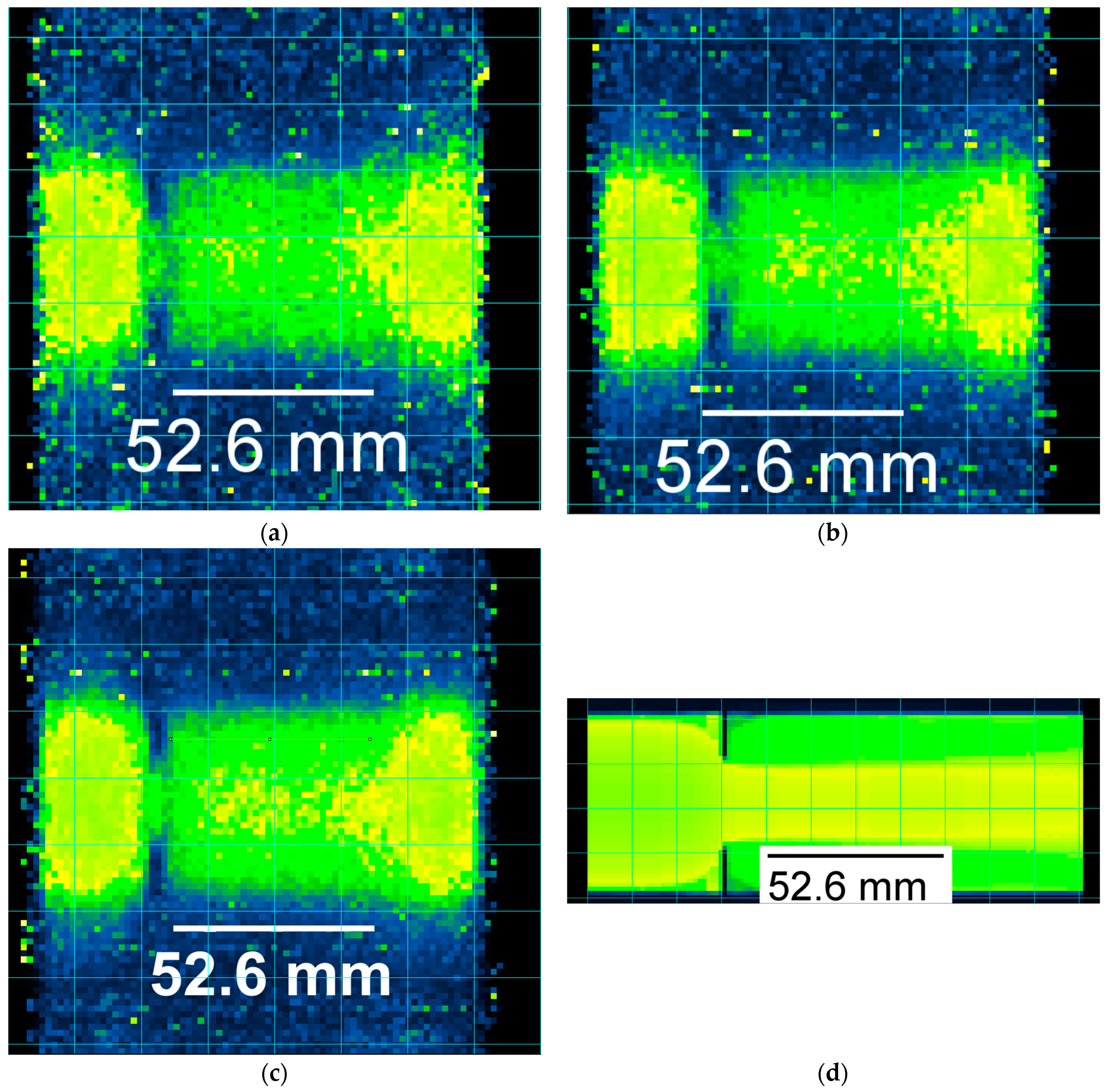
3.3. GATE Simulation Results
Figure 17a through 17c depict transverse views of the 3D reconstruction of the F-18/water solution distribution at 7.5 s post-injection. Reconstructions are of test cases consisting of the previously specified maximum specific activity level of 155 Bq/voxel (91.2 Bq/mm
3), and acquisition windows of 15, 30, and 45 s. A reference for the expected visualization is provided by the CFD simulation results, and is shown in
Figure 17d. The 30 s and 45 s test cases were included as GATE simulation results began to convey the need for additional detections to adequately resolve flow features of interest. At this point the assumption that the instantaneous flow field at 7.5 s post-injection would accurately represent the average flow field is no longer accurate for a continuous acquisition. However, its continued use was rationalized based on an approach where a sequence of separate pulses with corresponding 15 s acquisitions could be used to accurately reconstruct the data sets for the longer acquisition windows.
The qualitative comparison between these images conveys, in general, the ability of the PET system to generate a 3D reconstruction of the radioisotope distribution as the acquisition time increases, with adequate resolution of key geometric and flow features achieved with acquisition times as low as 15 s. This statement is justified by the readily identifiable orifice plate features, diametrical edge of the pipe, as well as discernable differences between detection levels in the primary flow and the secondary, recirculating flow.
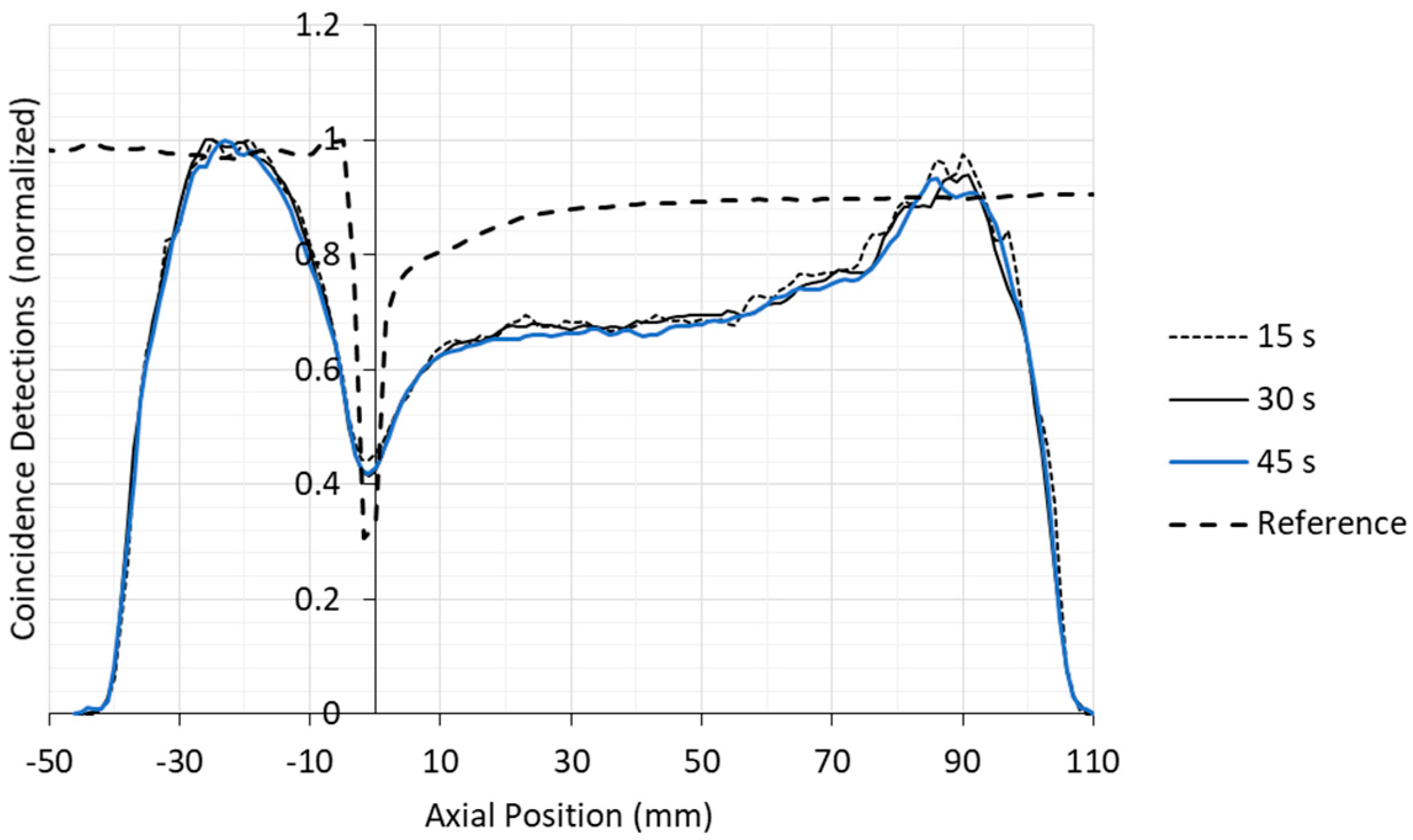
An axial projection of all detections on the pipe centerline was taken for each image reconstruction shown in
Figure 17a through 17d; these axial profiles are shown in
Figure 18. Each profile was normalized with its maximum value. These values are in the region upstream of the orifice due to the uniformly distributed concentration of radioisotopes across the flow. Smoothing of the profiles is exhibited as the acquisition time, and therefore number of detections, is increased, as is expected due to the Poisson-based probabilistic process of the photon detection. The projections of the emission data show a deviation from the reference projection starting just upstream of the orifice plate (~0.3 pipe diameters, ~−15.8 mm), up to approximately 1.5 diameters (78.9 mm) downstream of the orifice plate. Deviations from the reference profile resume to minor magnitudes further downstream, however only for a short axial distance before the edge of the scanners FOV is reached, where the number of detections drop off dramatically. This deviation is suspected to be attributed to an effective shadow being cast from the attenuation of emissions in the orifice plate material. The effects of this “shadow” are anticipated to be improved with a higher-resolution attenuation map utilized during the scatter correction process. The resolution of the attenuation map used for scatter correction was reduced to the extent that the orifice plate was no longer apparent. This was done to reduce the computational expense as the scatter correction process with the full resolution map resulted in prohibitively long computational times. An intermediate resolution level is anticipated to be an adequate compromise to reduce the attenuation effects on the image reconstruction process.
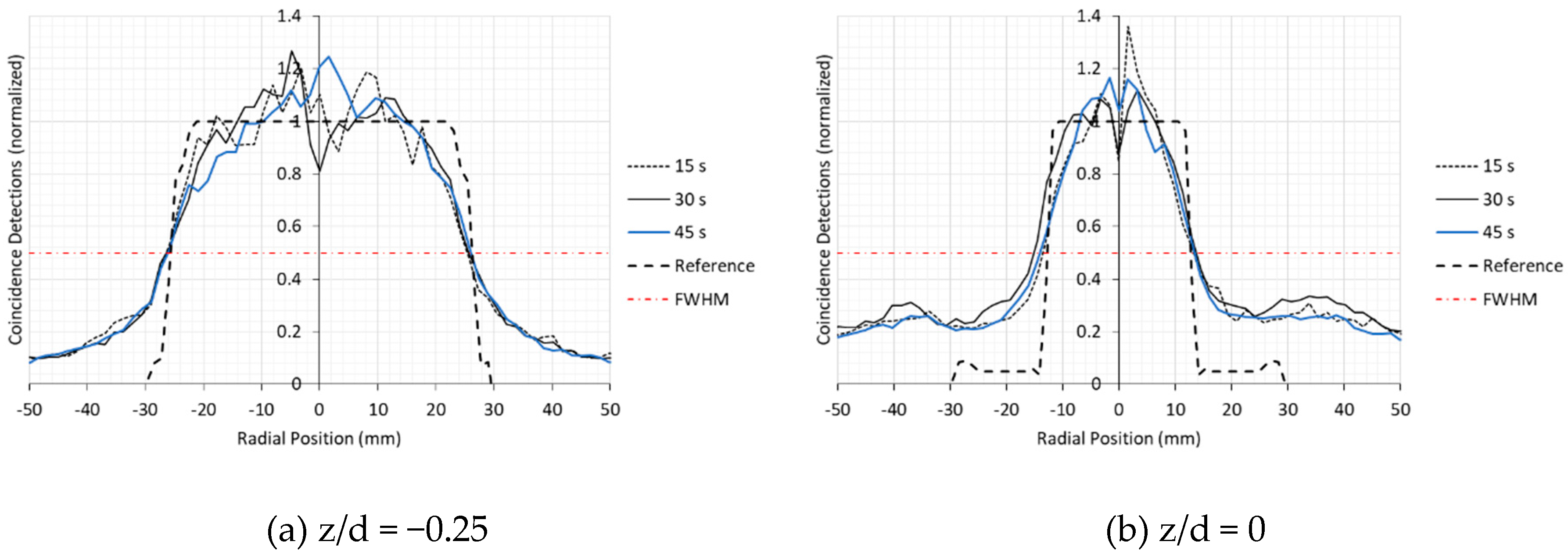
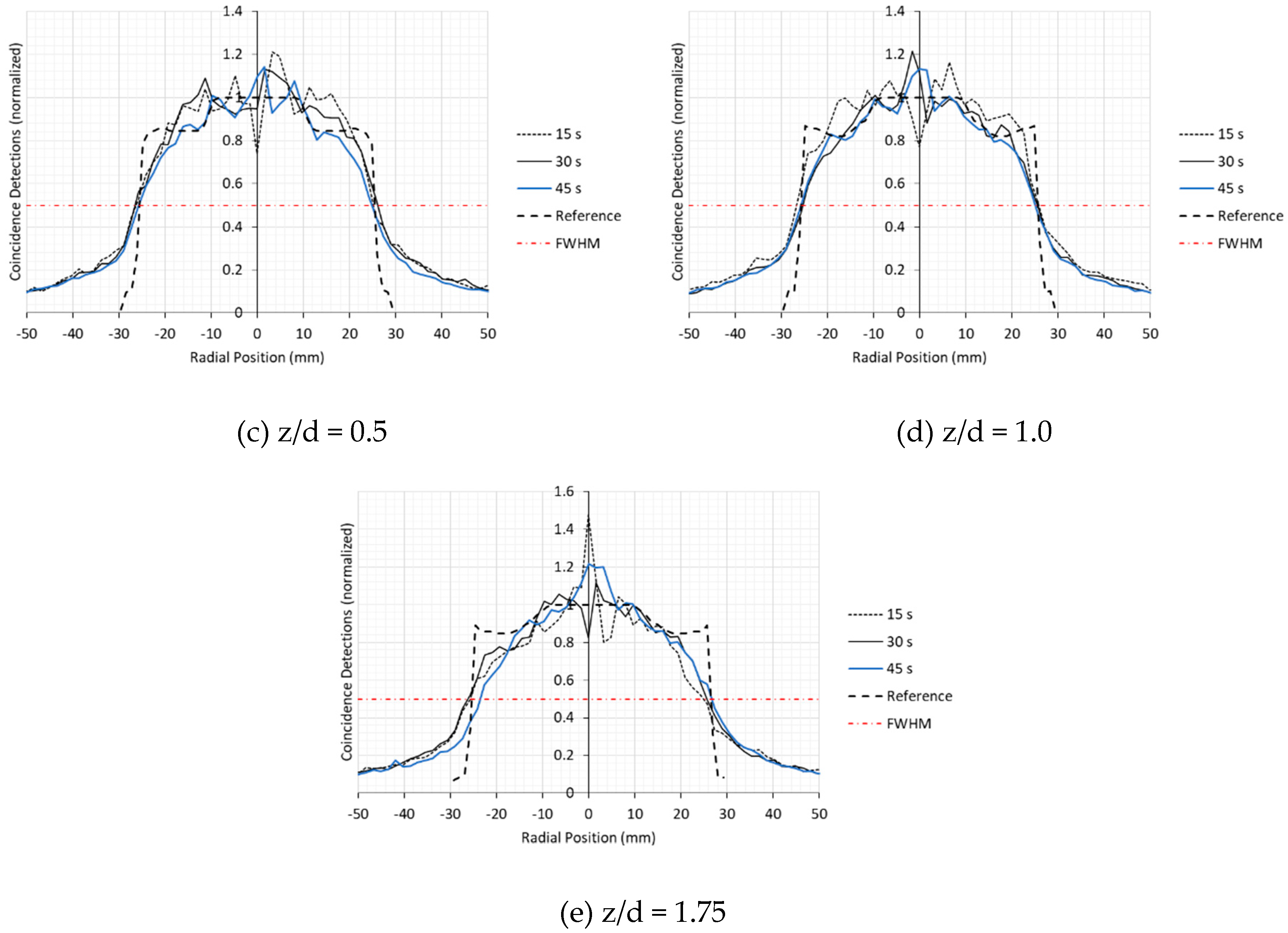
Transverse tomographic slices were taken at axial positions of z/d = −0.25, 0, 0.5, 1.0, and 1.75 (z = −13.2, 0, 26.3, 52.6, and 92.1 mm) for each test case. Radial profile plots were generated crossing through the pipe centerline for each of these slices. These profiles represent the root mean square averages taken over radial profiles from 0° to 180° at 5° increments. Coincidence detection values are normalized to the average detection values within the primary flow region for each respective profile. The profiles are shown in
Figure 19a–e.
It is customary to use a profile’s full width at half maximum (FWHM) as a quantitative criterion for resolving a feature of interest. In particular, the National Electrical Manufacturers Association (NEMA) NU-2 PET Performance Standard defines the spatial resolution of a PET system based on the accuracy in which the FWHM of the detection profile of a small spherical source within the detectors FOV matches the sources physical diameter [
18]. Building on this criterion, a quantitative analysis of the radial profiles shown indicates that, even with the effects of the shadow region and for relatively low acquisition times employed here, the diameter of the pipe is resolvable to within a few millimeters at all axial locations. The highest levels of deviation of ~3 mm are at the z/d = 0, and z/d = 1.75 axial locations. At z/d = 0 the higher level of inaccuracy can be attributed to the increased attenuation of the orifice material, while reduced sensitivity near the edge of the detectors FOV can be a cause for the reduced accuracy at z/d = 1.75.
A high degree of non-uniformity can be seen across all test cases with profile amplitudes within the primary flow regions deviating as much as 43% from the reference profiles for 15 s acquisition test cases. However, at 45 s the amplitudes of the deviations drop sufficiently low to identify overall trends of the profile. This is particularly the case at the z/d = 0.5 and z/d = 1.0 axial positions, which is closer to the mid-plane of the detector system where the sensitivity is expected to be higher. For these axial locations, the profiles general trends seem to follow the reference profile with relative accuracy, except at the outer diameter of the pipe where, again, the sensitivity is expected to be reduced. Such results suggest that the shear-layer of the flow may become resolvable to within 5 mm for a 45 s acquisition time. Performing a statistically significant number of these test cases may be warranted for definitive conclusions to be drawn.
In addition to repeated simulations for the present test cases to establish statistical significance, simulations will also be performed with elevated activity levels closer to that which corresponds to the Inveon system’s peak NECR. This will be done to ascertain an optimal specific activity for the flow field discussed herein. Once this is established, flows with other Reynolds numbers will be simulated with the goal of generating a correlation between the Reynolds number and required activity levels and acquisition times to resolve the flow features of interest. It is anticipated that increased turbulence intensities and, therefore, stronger turbulent diffusion, at higher Reynolds numbers will result in increased rates of mixing of isotopes into the recirculating region. This is anticipated to reduce the amount of time that is available to acquire coincidence detections, thereby diminishing the ability to visualize the radial extent of the shear layer. As previously indicated, the overarching objective is to utilize these simulation results as a basis for experiments whereby the correlation may be validated with empirical data.