Investigation of the Trailing Edge Modification Effect on Compressor Blade Aerodynamics Using SST k-ω Turbulence Model
Abstract
1. Introduction
2. Methodology
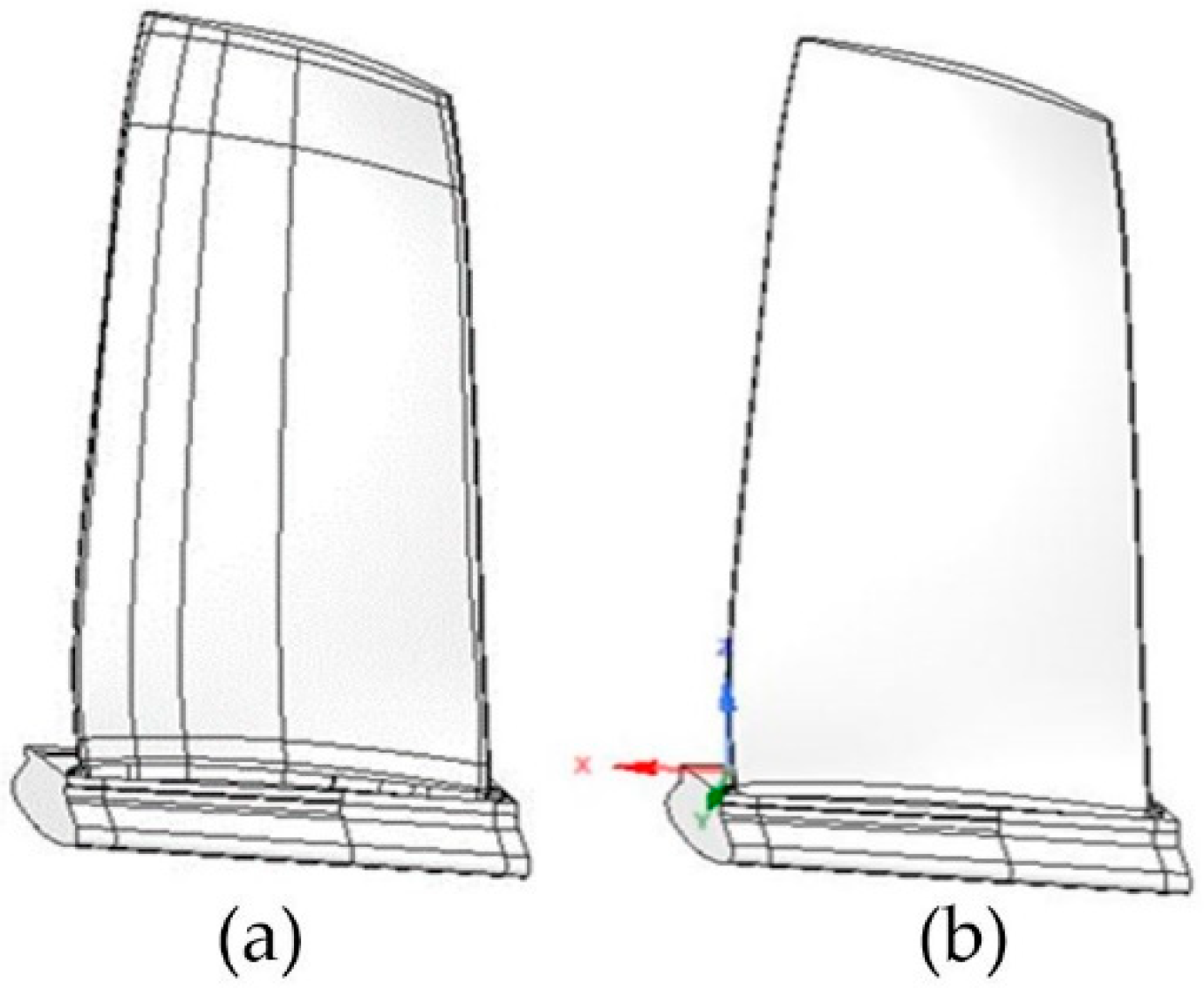
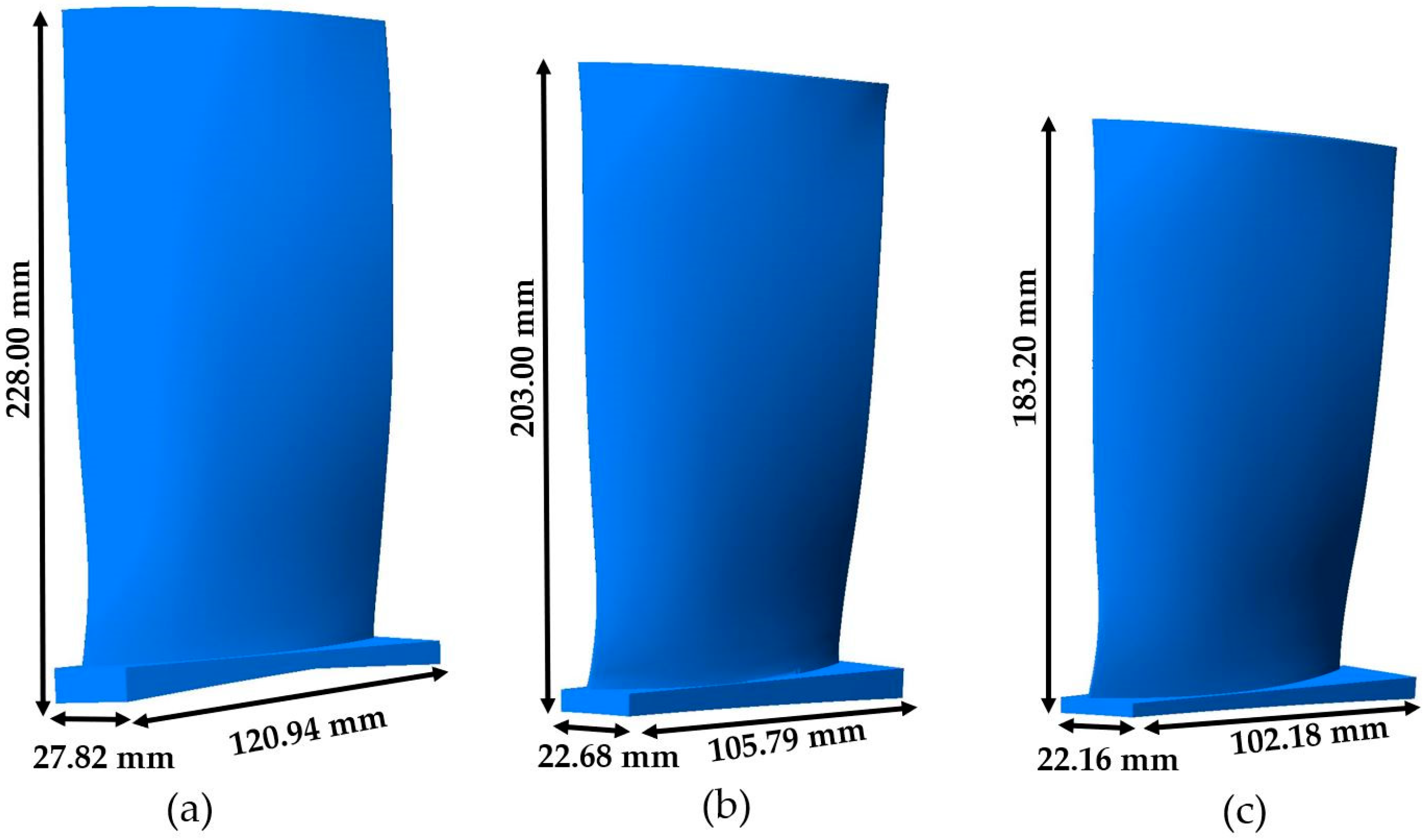
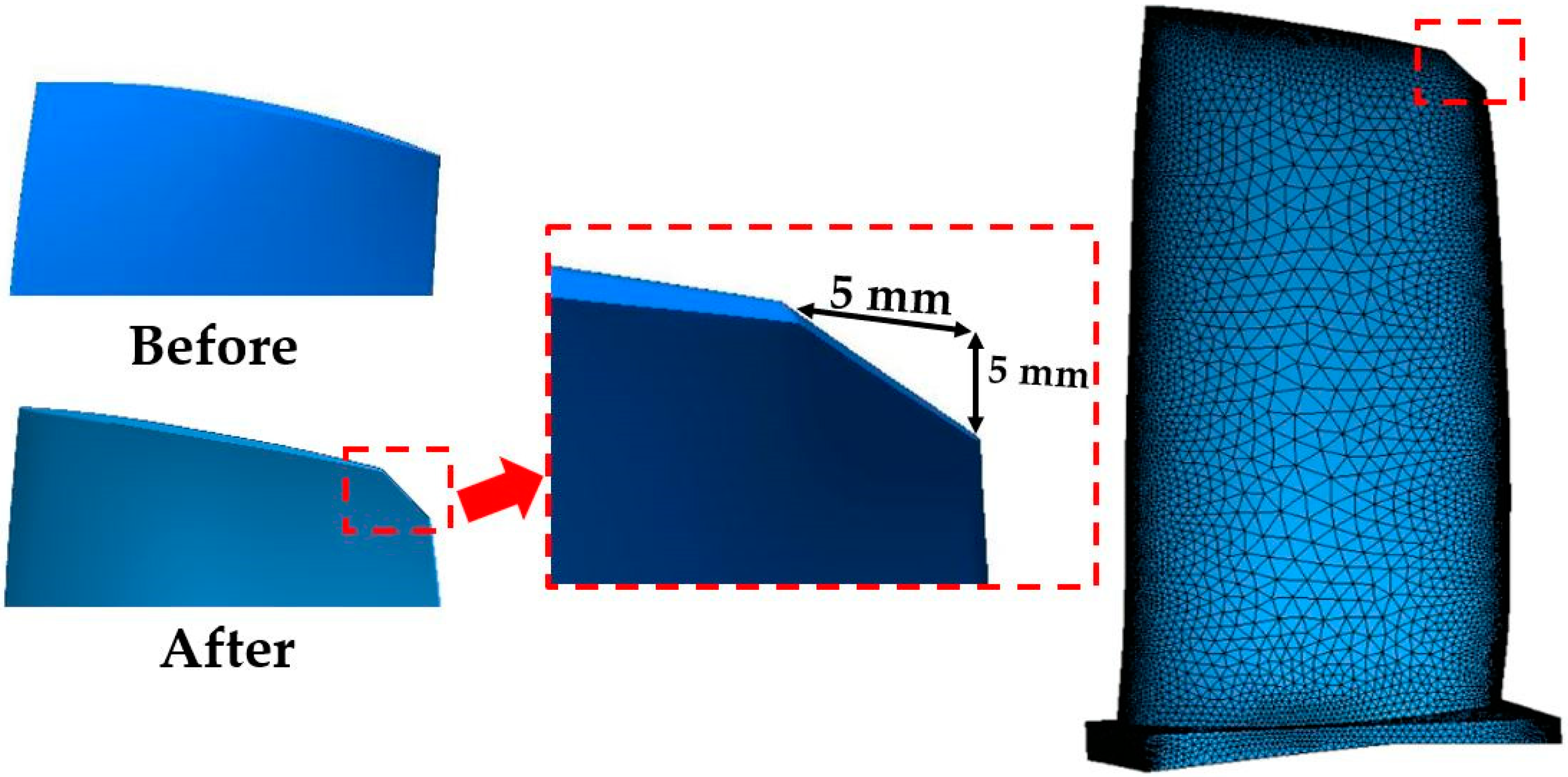
2.1. Geometry and Mesh Details
2.2. Mathematical Model
2.3. Turbulence Flow of Compressible Fluid
- Wilcox STD k-ω
- Transformed k-ε,
2.4. Initial and Boundary Conditions
2.5. Numerical Investigation
3. Results and Discussion
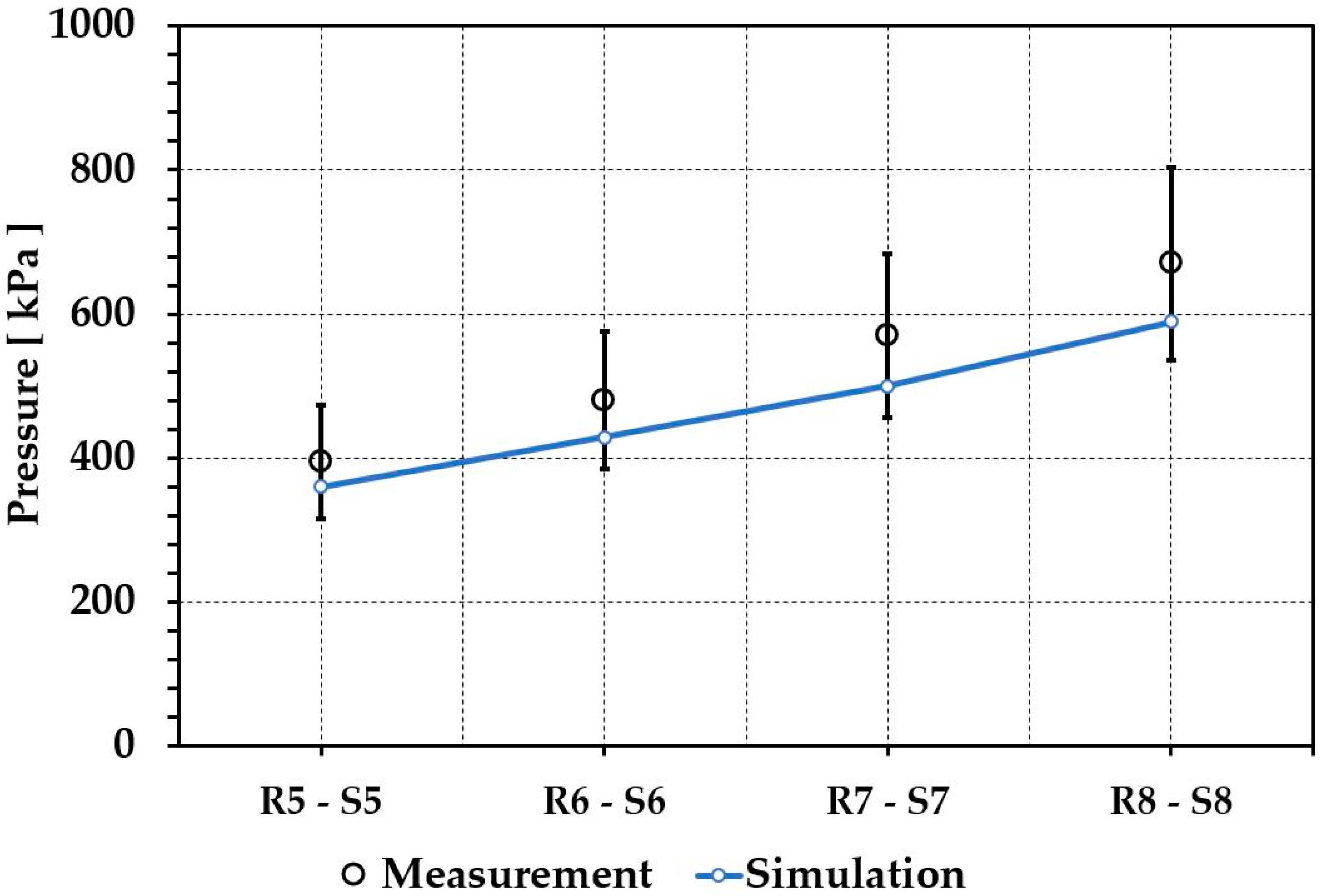
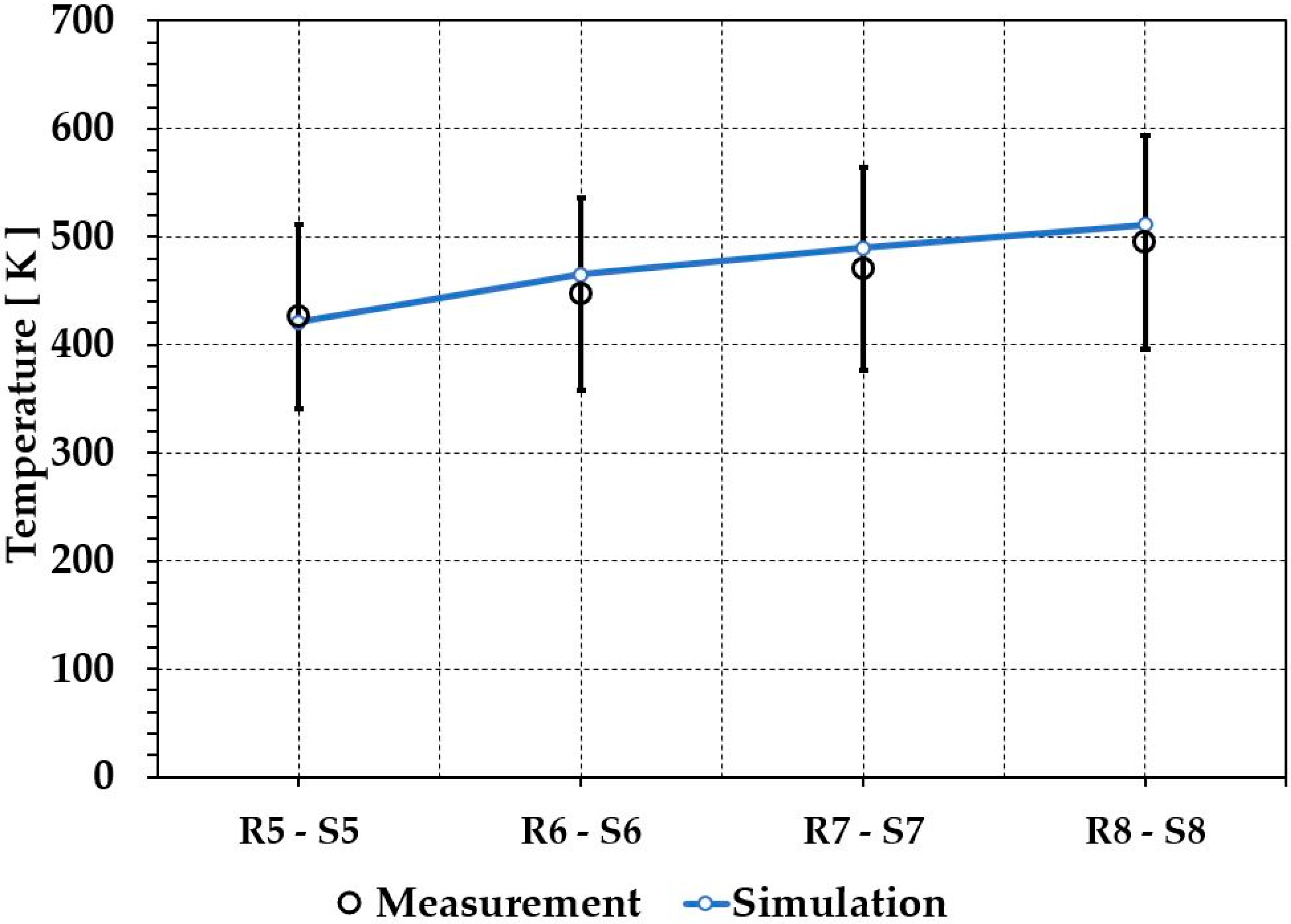
3.1. Validation Study
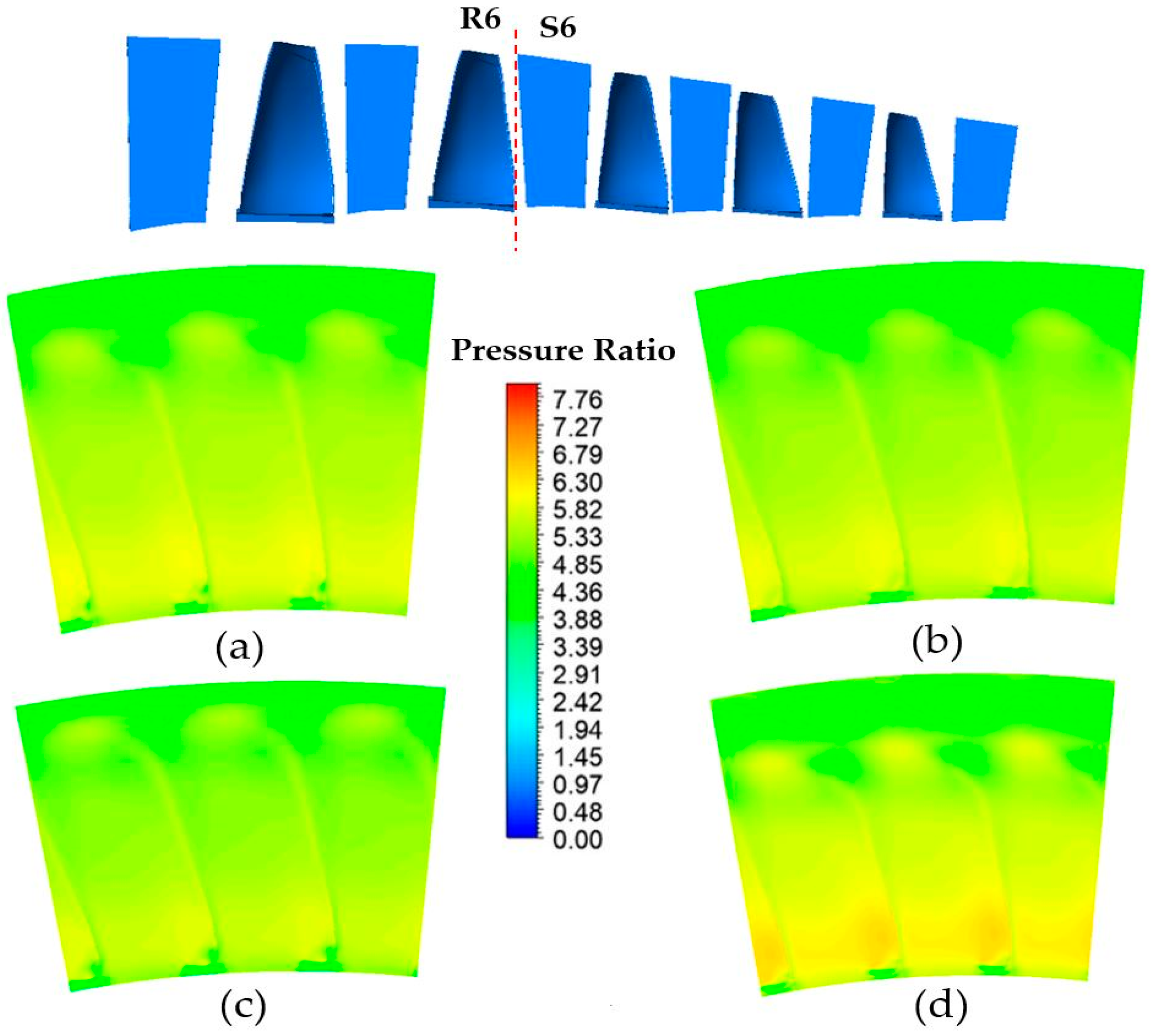
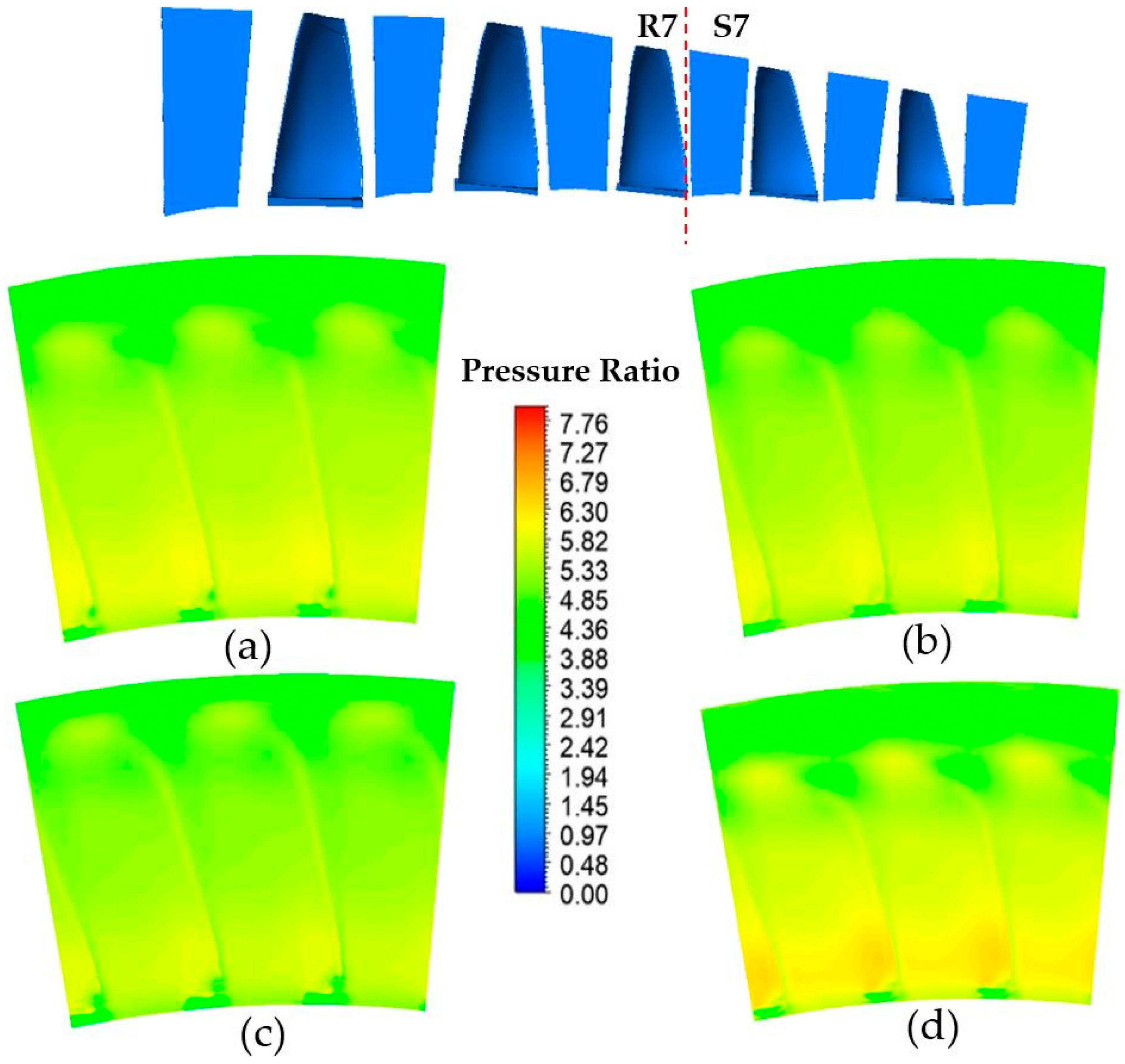
3.2. Fluid Flow in Rotational Domain
4. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| fr1 | production multiplier term |
| k | turbulent kinetic energy (m2/s2) |
| Pk | production of turbulent kinetic energy (kg/m·s3) |
| argument in the determination of production multiplier | |
| r * | ratio of the strain rate and rotation rate tensor magnitudes |
| S | strain rate magnitude (s−1) |
| Sij | strain rate tensor (s−1) |
| ui | fluctuation velocity component in the ith direction (m/s) |
| Fi | force in the ith direction (m/s) |
| Ui | mean velocity component in the ith direction (m/s) |
| xi | Cartesian coordinate in the ith direction (m) |
| y | minimum distance to a no-slip wall (m) |
| y+ | dimensionless wall distance |
| ε | turbulence dissipation rate (m2/s3) |
| δijk | permutation tensor |
| μ | molecular dynamics viscosity (kg/m·s) |
| μt | eddy viscosity (kg/m·s) |
| μeff | effective viscosity accounting for turbulence (kg/m·s) |
| pa | atmospheric pressure (Pa) |
| p | pressure (Pa) |
| Ω | rotation rate magnitude (s−1) |
| Ωij | rotation rate tensor (s−1) |
| Ωijrot | rotation rate of the system (rad/s) |
| ω | specific dissipation rate (s−1) |
References
- Ning, T.; Gu, C.W.; Ni, W.D.; Li, X.T.; Liu, T.Q. Aerodynamics analysis and three-dimensional redesign of a multi-stage axial flow compressor. Energies 2016, 9, 296. [Google Scholar] [CrossRef]
- Bian, T.; Han, Q.; Sayar, S.; Feng, J.; Böhle, M. Flow loss and structure of circular arc blades with different leading edges. Adv. Mech. Eng. 2018, 10, 1–12. [Google Scholar] [CrossRef]
- Wei, Z.J.; Qiao, W.Y.; Liu, J.; Duan, W.H. Reduction of end wall secondary flow losses with leading-edge fillet in a highly loaded low-pressure turbine. Proc. Inst. Mech. Eng. Part A. J. Power Energy 2016, 230, 184–195. [Google Scholar] [CrossRef]
- Gao, J.; Fu, W.; Wang, F.; Zheng, Q.; Yue, G.; Dong, P. Experimental and numerical investigations of tip clearance flow and loss in a variable geometry turbine cascade. Proc. Inst. Mech. Eng. Part A. J. Power Energy 2018, 232, 157–169. [Google Scholar] [CrossRef]
- Bakhtiari, F.; Wartzek, F.; Leichtfuß, S.; Schiffer, H.P.; Goinis, G.; Nicke, E. Design and optimization of a new stator for the Transonic Compressor Rig at TU Darmstadt. In Proceedings of the Deutscher Luft- und Raumfahrtkongress, Rostock, Sweden, 22–24 September 2015. [Google Scholar]
- Liu, B.; Tao, Y.; Yu, X. Application of MCST method to design the blade leading edge in axial compressors. In Proceedings of the 6th International Symposium on Fluid Machinery and Fluids Engineering (ISFMFE), Wuhan, China, 22–25 October 2014. [Google Scholar] [CrossRef]
- Razavi, S.R.; Sammak, S.; Boroomand, M. Multidisciplinary design and optimizations of swept and leaned transonic rotor. J. Eng. Gas Turbines Power 2017, 139, GTP-17-1155. [Google Scholar] [CrossRef]
- Neshat, M.A.; Akhlaghi, M.; Fathi, A.; Khaledi, H. Investigating the effect of blade sweep and lean in one stage of an industrial gas turbine’s transonic compressor. Propul. Power Res. 2015, 4, 221–229. [Google Scholar] [CrossRef]
- Wu, D.; Yan, P.; Chen, X.; Wu, P.; Yang, S. Effect of trailing-edge modification of a mixed-flow pump. ASME. J. Fluids Eng. 2015, 137, 101205. [Google Scholar] [CrossRef]
- Castegnaro, S. Effects of NACA 65-blade’s Trailing edge modifications on the performance of a low-speed tube-axial fan. Energy Procedia 2015, 82, 965–970. [Google Scholar] [CrossRef][Green Version]
- Arbabi, A.; Ghaly, W.; Medd, A. Aerodynamic inverse blade design of axial compressors in three-dimensional flow using a commercial CFD program. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar]
- Liu, Y.; Sun, J.; Tang, Y.; Lu, L. Effect of slot at blade root on compressor cascade performance under different aerodynamic parameters. Appl. Sci. 2016, 6, 421. [Google Scholar] [CrossRef]
- Dhanya, C.S.; Sarath, R.S. Numerical analysis of turbine tip modifications in a linear turbine cascade. In IOP Conference Series: Materials Science and Engineering; IOP Publishing Ltd.: Bristol, UK, 2018; Volume 377, p. 012051. [Google Scholar] [CrossRef]
- Lu, H.W.; Yang, Y.; Guo, S.; Huang, Y.X.; Wang, H.; Zhong, J.J. Flow control in linear compressor cascades by inclusion of suction side dimples at varying locations. Proc. Inst. Mech. Eng. Part A. J. Power Energy 2018, 232, 706–721. [Google Scholar] [CrossRef]
- Choi, M.G.; Ryu, J. Numerical study of the axial gap and hot streak effects on thermal and flow characteristics in two-stage high pressure gas turbine. Energies 2018, 11, 2654. [Google Scholar] [CrossRef]
- Tao, R.; Xiao, R.; Wang, Z. Influence of blade leading-edge shape on cavitation in a centrifugal pump impeller. Energies 2018, 11, 2588. [Google Scholar] [CrossRef]
- Barth, T.J.; Jespersen, D.C. The design and application of upwind schemes on unstructured meshes. In Proceedings of the 27th Aerospace Sciences Meeting, Reno, NV, USA, 9–12 January 1989. [Google Scholar]
- Ali, S.; Elliott, K.J.; Savory, E.; Zhang, C.; Martinuzzi, R.J.; Lin, W.E. Investigation of the performance of turbulence models with respect to high flow curvature in centrifugal compressors. J. Fluids Eng. 2015, 138, 051101. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 2007, 32, 1598–1605. [Google Scholar] [CrossRef]
- Menter, F.R. Zonal two-equation k-ω turbulence models for aerodynamic flows. In Proceedings of the 24th Fluid Dynamics Conference, Moffett Field, CA, USA, 6–9 July 1993. [Google Scholar]
- ANSYS, Inc. Chapter 2. Turbulence and wall function theory. In CFX-Solver Theory Guide R19.2; Ansys Inc.: Canonsburg, PA, USA, 2019; pp. 31–44. [Google Scholar]
- ANSYS, Inc. Chapter 1. Basic Solver Capability Theory. In CFX-Solver Theory Guide R19.2; Ansys Inc.: Canonsburg, PA, USA, 2019; pp. 65–70. [Google Scholar]
- Simões, M.R.; Montojos, B.G.; Moura, N.R.; Su, J. Validation of turbulence models for simulation of axial flow compressor. In Proceedings of the 20th International Congress of Mechanical Engineering (COBEM), Gramado, RS, Brazil, 15–20 November 2009. [Google Scholar]
- Yin, S.; Jin, D.; Gui, X.; Zhu, F. Application and comparison of SST model in numerical simulation of the axial compressor. J. Therm. Sci. 2010, 19, 300–309. [Google Scholar] [CrossRef]
- Boretti, A. Experimental and computational analysis of a transonic compressor rotor. In Proceedings of the 17th Australasian Fluid Mechanics Conference, Auckland, New Zealand, 5–9 December 2010. [Google Scholar]
- Sonoda, T.; Arima, T.; Endicott, G.; Olhofer, M.; Sendhoff, B. The effect of Reynolds number on a transonic swept fan OGV in a small turbofan engine. In Proceedings of the ASME Turbo Expo 2012, Copenhagen, Denmark, 11–15 June 2012. [Google Scholar]
- Halder, P.; Rhee, S.H.; Samad, A. Numerical optimization of wells turbine for wave energy extraction. Int. J. Nav. Archit. Ocean Eng. 2017, 9, 11–24. [Google Scholar] [CrossRef]
- McMullan, W.A.; Page, G.J. Towards Large Eddy Simulation of gas turbine compressors. Prog. Aerosp. Sci. 2012, 52, 30–47. [Google Scholar] [CrossRef]
- Duchaine, F.; Maheu, N.; Moureau, V.; Balarac, G.; Moreau, S. Large-Eddy Simulation and conjugate heat transfer around a low-Mach turbine blade. J. Turbomach. 2013, 136, 051015. [Google Scholar] [CrossRef]

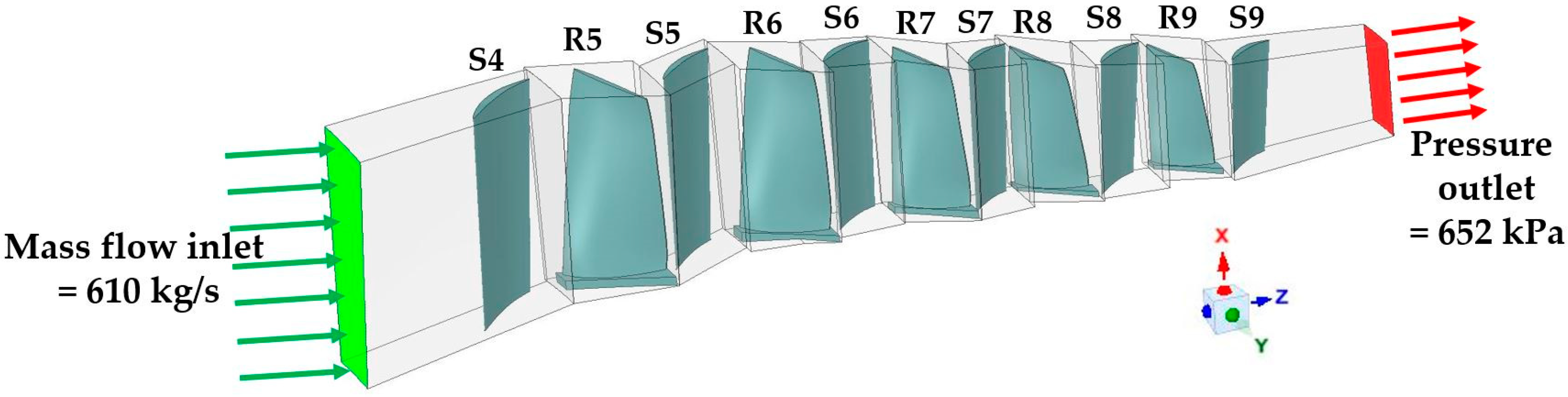
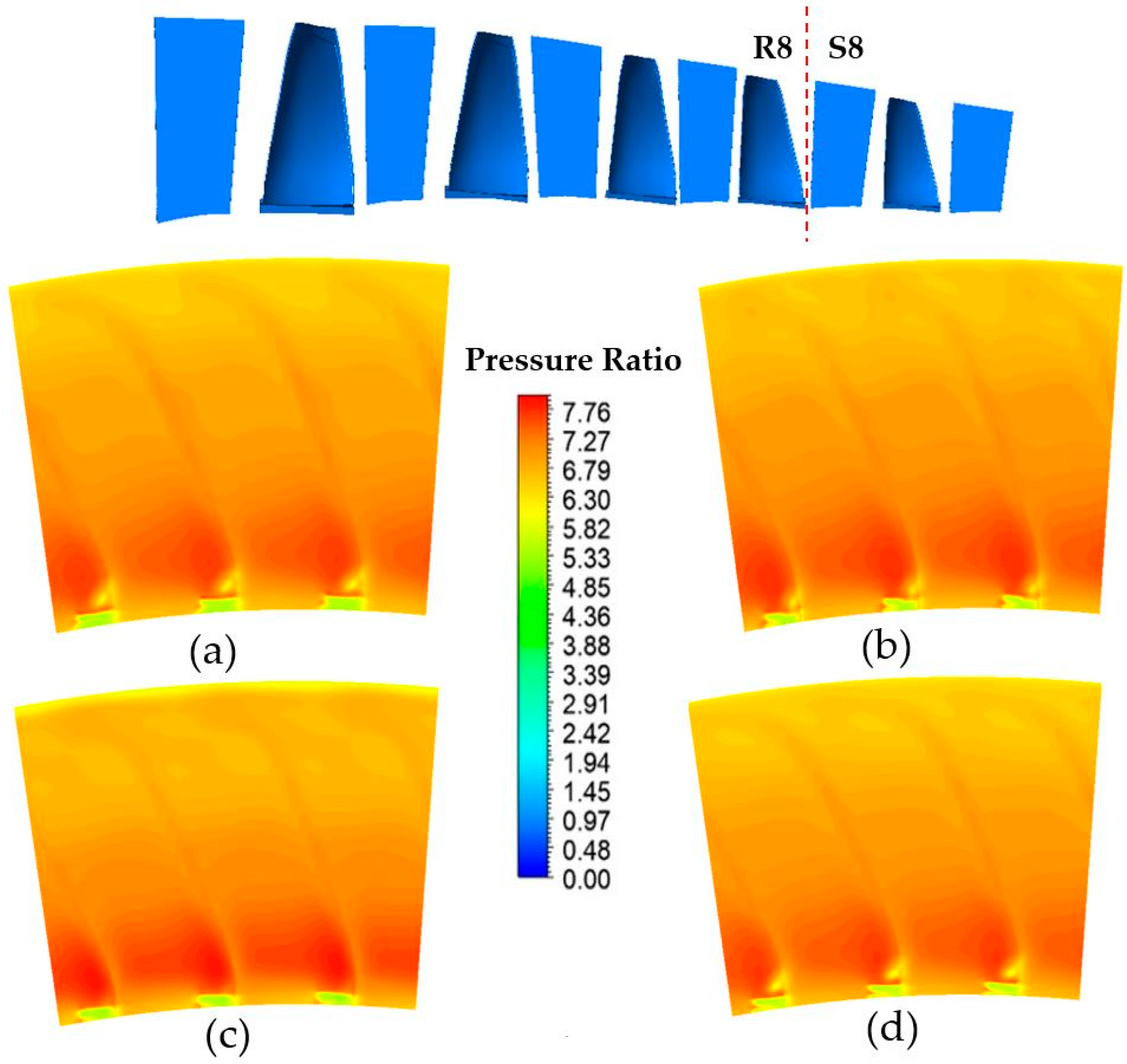
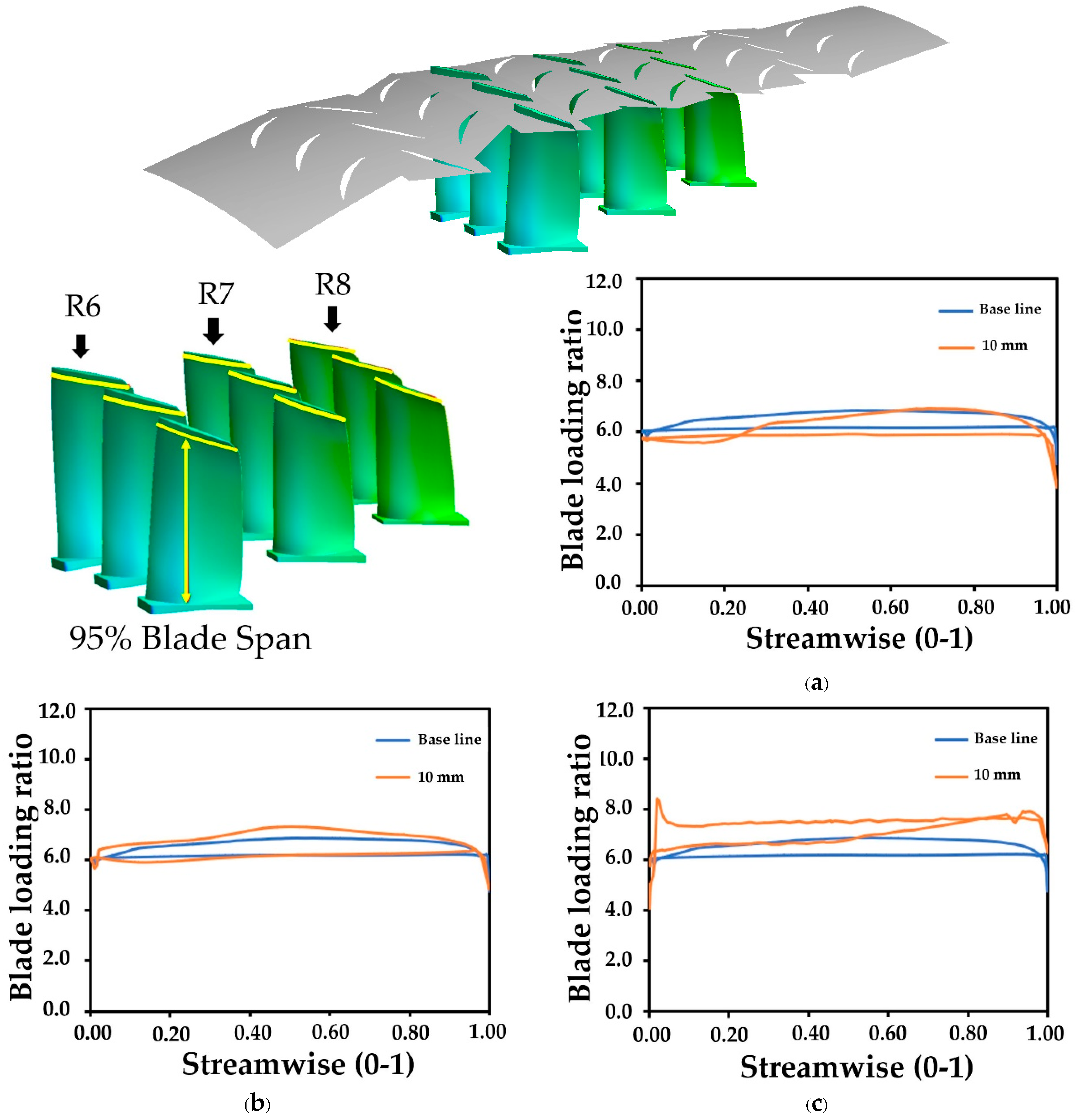
| Domain | Nodes | Elements | No. of Blades |
|---|---|---|---|
| S4 | 434,398 | 1,880,465 | 63 |
| R5 | 644,654 | 2,689,547 | 58 |
| S5 | 413,149 | 1,797,943 | 71 |
| R6 | 558,787 | 2,320,838 | 66 |
| S6 | 358,677 | 1,520,767 | 73 |
| R7 | 468,637 | 1,932,659 | 75 |
| S7 | 307,316 | 1,261,484 | 75 |
| R8 | 403,899 | 1,663,696 | 77 |
| S8 | 285,277 | 1,214,127 | 79 |
| R9 | 325,074 | 1,366,770 | 82 |
| S9 | 237,098 | 1,002,103 | 81 |
| All Domain | 4,436,966 | 18,650,399 | - |
| Numerical Parameters | Setting |
|---|---|
| Solver | Pressure-based |
| Special discretization | High resolution scheme for advection term |
| High resolution scheme for turbulence quantities | |
| Convergence control | Max. Iteration 1000 |
| Convergence criteria | 1.0 × 10−4 |
| Time scale control | Auto Timescale |
| Length scale option | Conservative |
| Time scale factor | Auto Timescale |
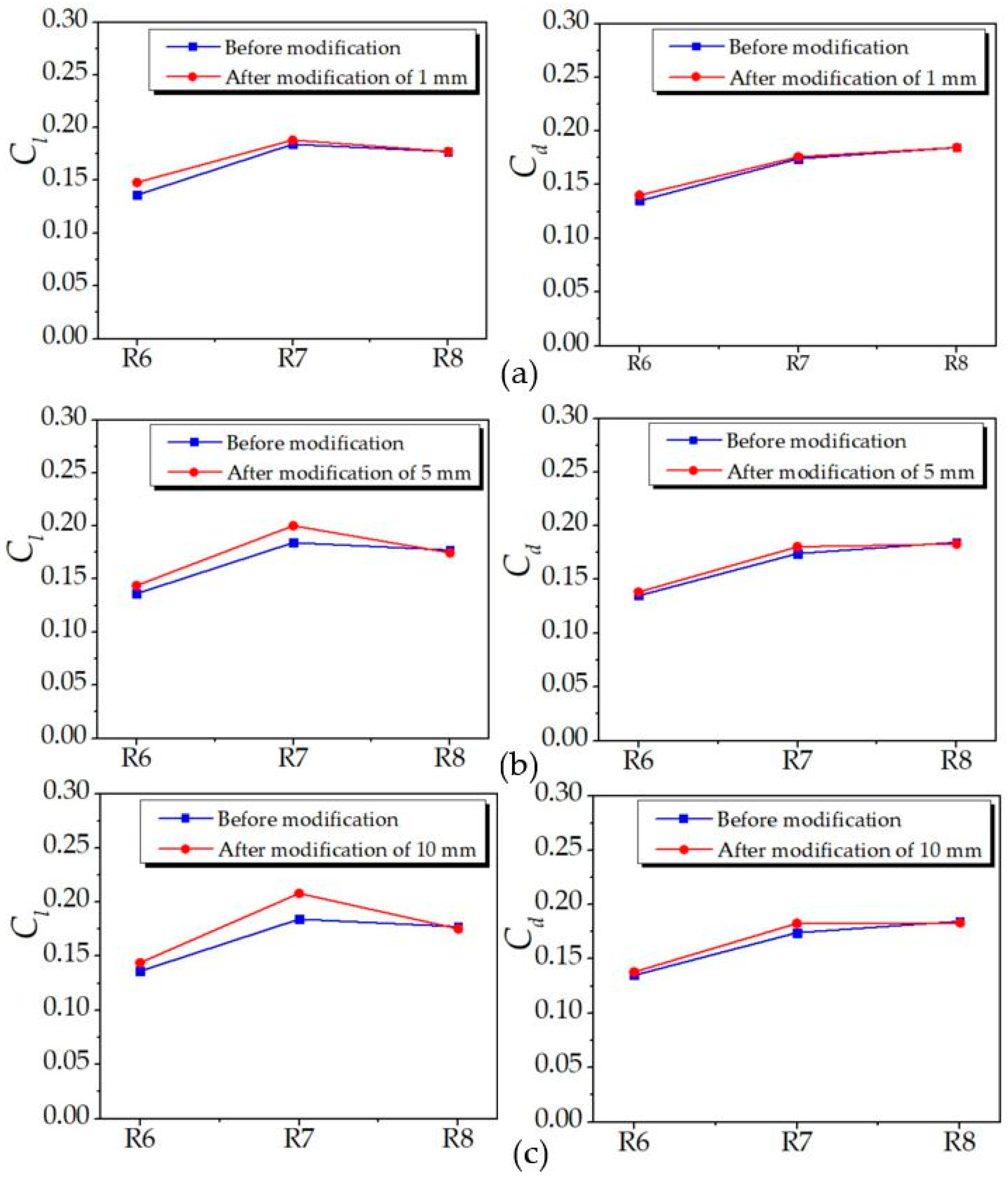
| Stages | Fz (N) | Fy (N) | Area (m2) | Cl | Cd |
|---|---|---|---|---|---|
| Before modification | |||||
| R6 | 866.173 | 857.821 | 0.05542 | 0.1362 | 0.1349 |
| R7 | 877.440 | 829.332 | 0.04150 | 0.1842 | 0.1741 |
| R8 | 725.145 | 755.115 | 0.03564 | 0.1773 | 0.1846 |
| After modification of 1 mm | |||||
| R6 | 941.792 | 891.838 | 0.05537 | 0.1481 (+8.74%) | 0.1402 (+3.93%) |
| R7 | 896.533 | 837.688 | 0.04152 | 0.1882 (+2.17%) | 0.1759 (+1.03%) |
| R8 | 725.115 | 755.148 | 0.03566 | 0.1773 (0.00%) | 0.1846 (0.00%) |
| After modification of 5 mm | |||||
| R6 | 913.889 | 879.026 | 0.05534 | 0.1438 (+5.58%) | 0.1383 (+2.52%) |
| R7 | 953.400 | 858.918 | 0.04149 | 0.2003 (+8.74%) | 0.1805 (−3.68%) |
| R8 | 714.005 | 748.08 | 0.03563 | 0.1747 (−1.47%) | 0.1830 (−0.87%) |
| After modification of 10 mm | |||||
| R6 | 915.914 | 877.969 | 0.05530 | 0.1440 (+5.73%) | 0.1380 (+2.30%) |
| R7 | 991.220 | 870.310 | 0.04141 | 0.2081 (+12.97%) | 0.1827 (+4.94%) |
| R8 | 717.413 | 749.50 | 0.03555 | 0.1754 (−1.07%) | 0.1832 (−0.76%) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaewbumrung, M.; Tangsopa, W.; Thongsri, J. Investigation of the Trailing Edge Modification Effect on Compressor Blade Aerodynamics Using SST k-ω Turbulence Model. Aerospace 2019, 6, 48. https://doi.org/10.3390/aerospace6040048
Kaewbumrung M, Tangsopa W, Thongsri J. Investigation of the Trailing Edge Modification Effect on Compressor Blade Aerodynamics Using SST k-ω Turbulence Model. Aerospace. 2019; 6(4):48. https://doi.org/10.3390/aerospace6040048
Chicago/Turabian StyleKaewbumrung, Mongkol, Worapol Tangsopa, and Jatuporn Thongsri. 2019. "Investigation of the Trailing Edge Modification Effect on Compressor Blade Aerodynamics Using SST k-ω Turbulence Model" Aerospace 6, no. 4: 48. https://doi.org/10.3390/aerospace6040048
APA StyleKaewbumrung, M., Tangsopa, W., & Thongsri, J. (2019). Investigation of the Trailing Edge Modification Effect on Compressor Blade Aerodynamics Using SST k-ω Turbulence Model. Aerospace, 6(4), 48. https://doi.org/10.3390/aerospace6040048







