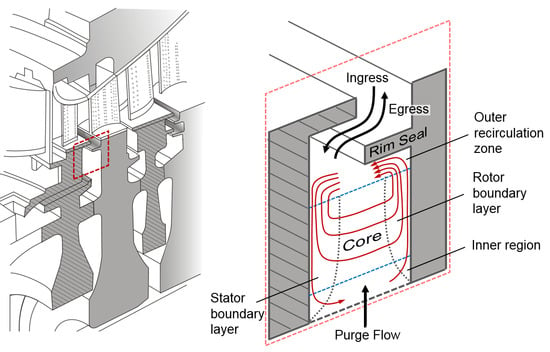
Effect of Ingress on Flow and Heat Transfer Upstream and Downstream of a Rotating Turbine Disc
Abstract
1. Introduction
2. Brief Review of Relevant Research
3. Experimental Rig and Instrumentation
4. Theoretical Models and Data Analysis
4.1. Adiabatic Effectiveness of the Rotor
4.2. Sealing Effectiveness of the Stator
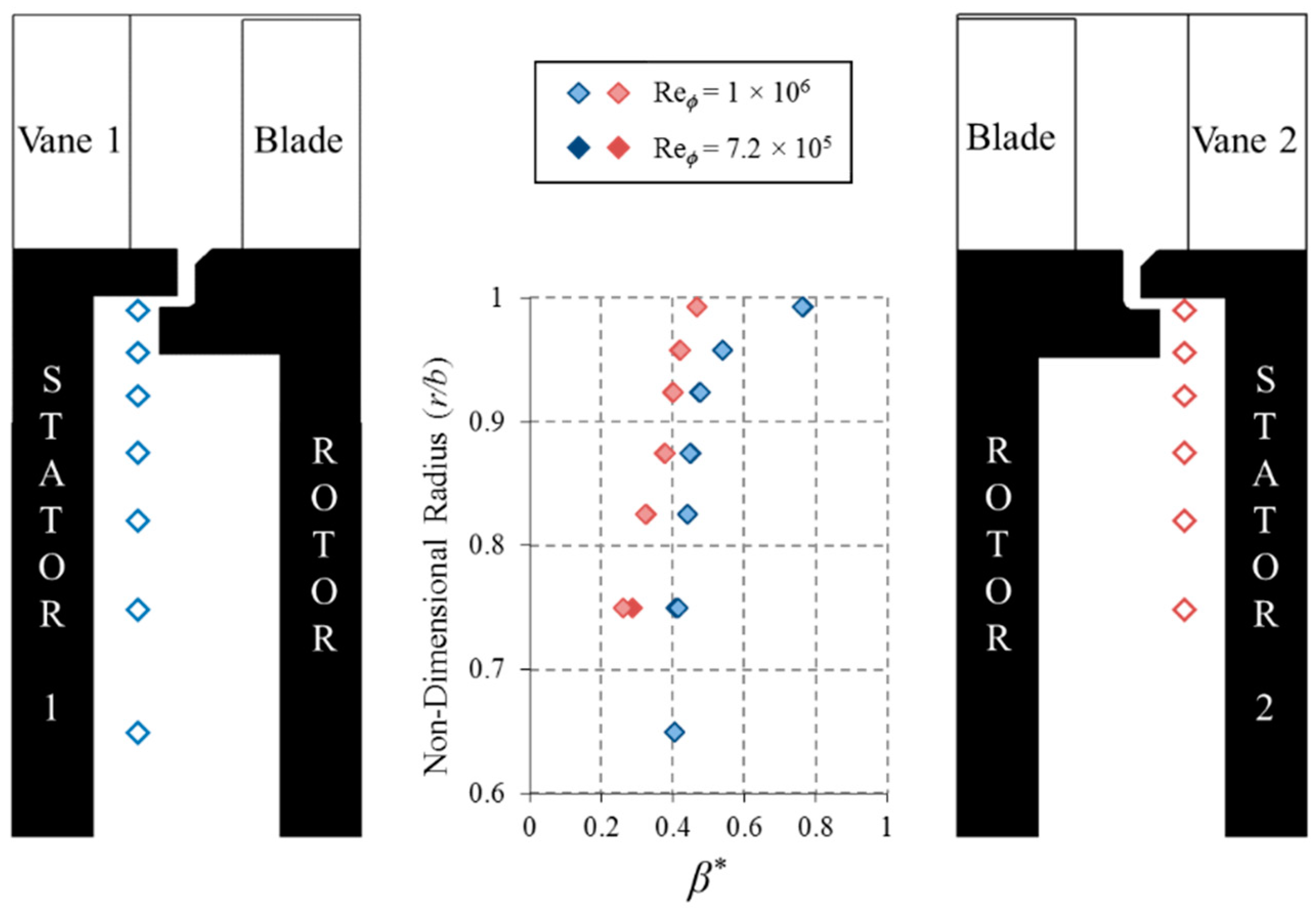
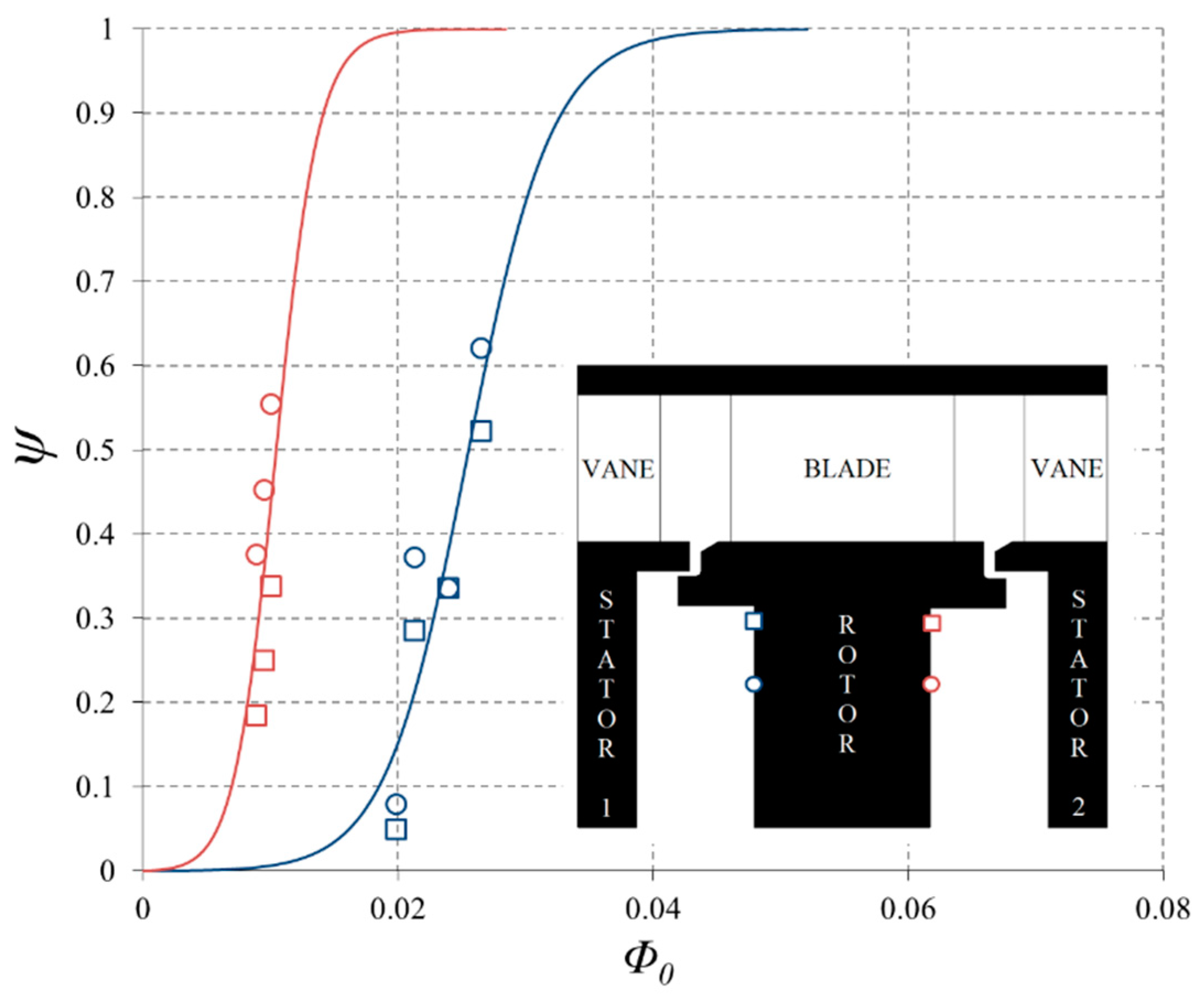
4.3. Calculation of Buffer Parameter Ψ
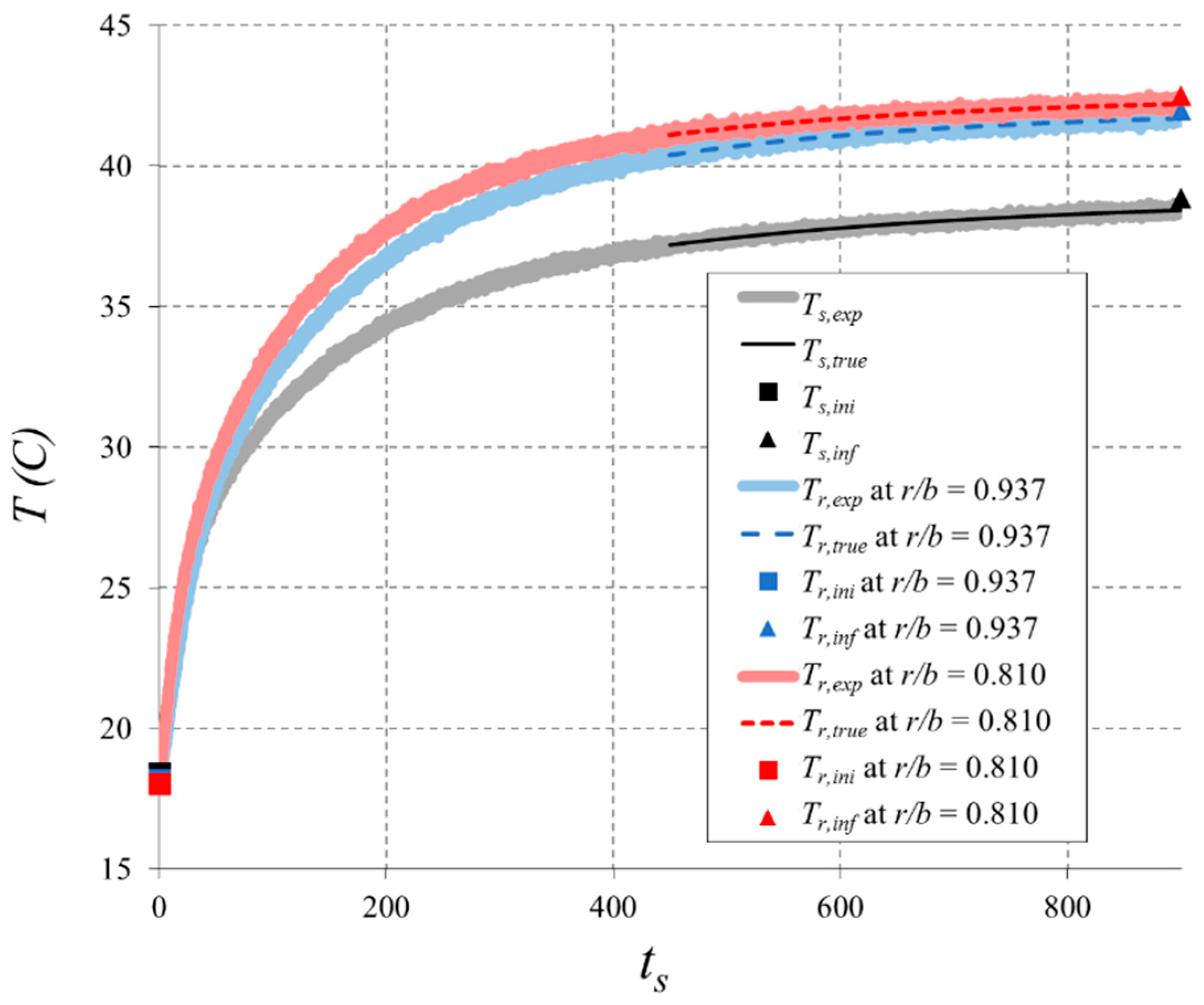
4.4. Maximum Likelihood Estimation (MLE) Analysis of Transient Temperature Measurements
5. Discussion of Experimental Results
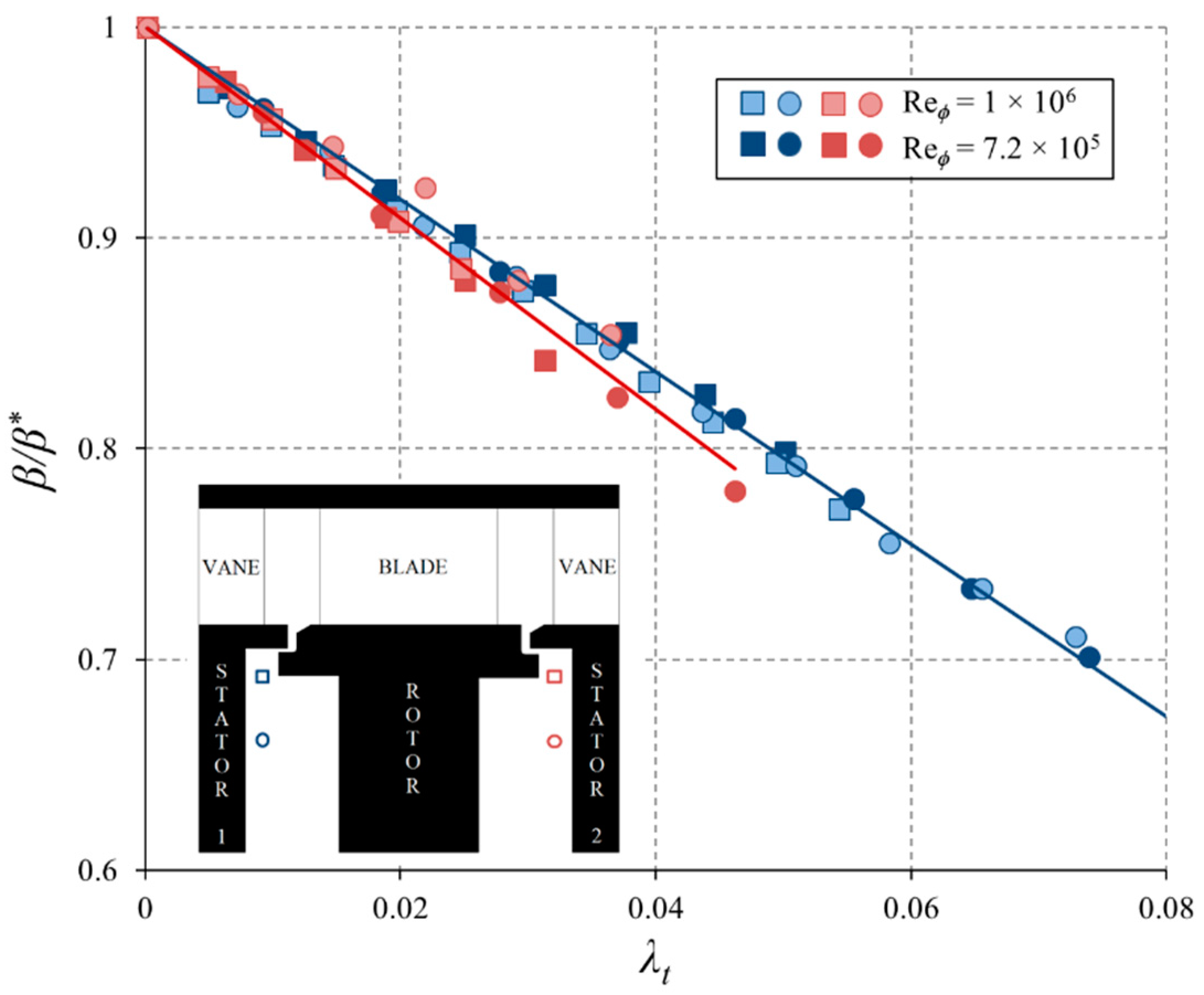
5.1. Swirl Ratios in the Core
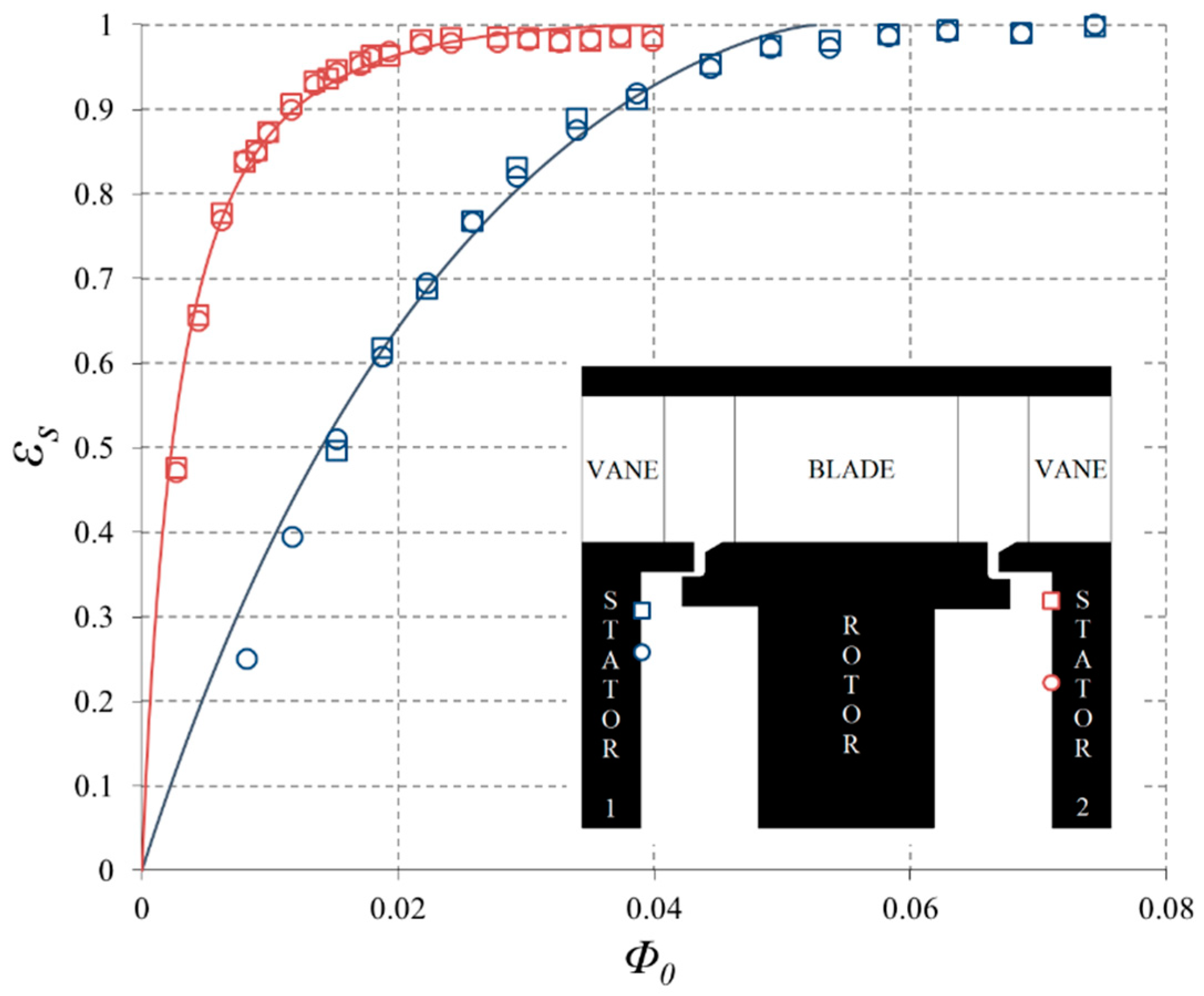
5.2. Sealing Effectiveness
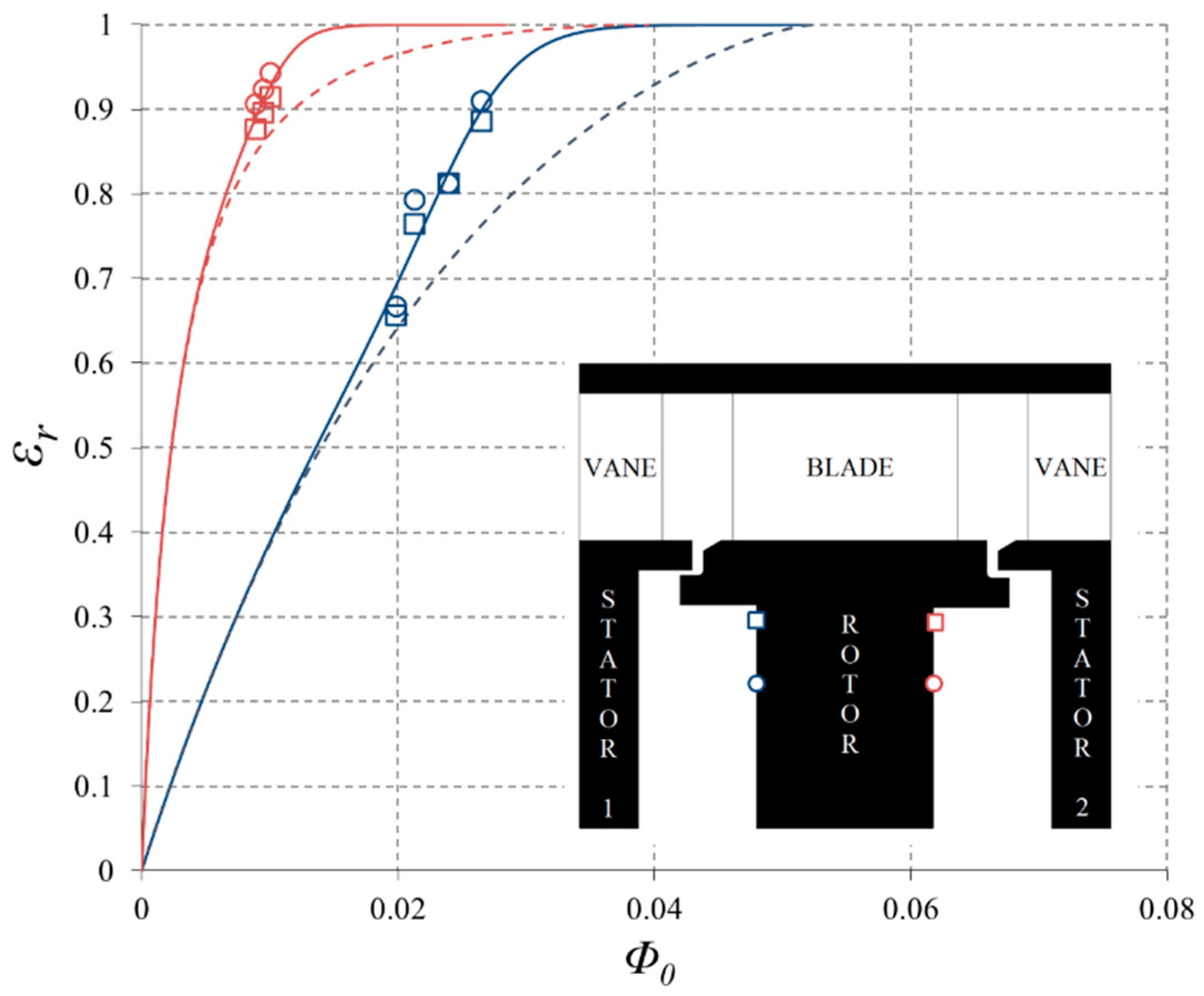
5.3. Adiabatic Effectiveness of the Rotor
6. Conclusions
- The sealing effectiveness for the downstream wheel-space was larger than for the upstream one; this was attributed to the fact that the circumferential variation of pressure (which is the driver of externally-induced ingress) in the annulus downstream of the blades was much smaller than that upstream.
- In the core of both wheel-spaces, the swirl ratio, which increased with increasing radius and with decreasing purge flow rate, could be correlated with the local turbulent flow parameter, λt. However, the swirl ratio in the downstream wheel-space was smaller than that in the upstream one; this was attributed to the fact that the swirl in the annulus downstream of the blades was much smaller than that upstream.
- A maximum likelihood estimation analysis was applied successfully to extrapolate transient temperature measurements in the core and rotor surfaces to determine the buffer parameter, Ψ, in both upstream and downstream wheel-spaces.
- Using the calculated values of Ψ for both wheel-spaces, there was mainly good qualitative agreement between the experimental and theoretical variations of rotor effectiveness with non-dimensional purge.
- It was shown that the buffer effect, Δε, of the purge flow was larger for the upstream seal than for the downstream one; this was attributed to the fact that the sealing effectiveness for the upstream wheel-space was lower than the downstream one.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| a | inner radius of rotor |
| A,B | constants |
| b | outer radius of rotor |
| c | concentration |
| cp | specific heat at constant pressure |
| C,D,E | constants |
| Cw,o | nondimensional flow rate (= o/μb) |
| f | function relationship between β and β* |
| f’ | empirical constant |
| G | gap ratio (= S/b) |
| Gc | seal-clearance ratio (= sc,ax/b) |
| H | total enthalpy |
| H’ | total enthalpy of rotor when frictional effects are neglected |
| ks | thermal conductivity of solid |
| l | negative logarithm of likelihood function |
| mass flow rate | |
| n | number of data points |
| P | likelihood function |
| r | radius |
| R | recovery factor |
| Reϕ | rotational Reynolds number (= ρΩb2/μ) |
| sc,ax | axial clearance of seals |
| sc,rad | radial clearance of seals |
| soverlap | axial overlap of seals |
| S | axial space between rotor and stator |
| t | time |
| T | temperature |
| U | bulk-mean velocity through rim-seal clearance (= o/2πρbsc,ax) |
| Vϕ | tangential velocity in wheel-spaces |
| Wr | work done by the rotor from r = a to r = b |
| β | swirl ratio in wheel-space (= Vϕ/Ωr) |
| β* | swirl ratio when λt = 0 |
| Γc | ratio of discharge coefficients |
| ΔT | difference between initial and extrapolated steady-state temperatures |
| Δε | buffer effect (= εr − εs) |
| εr | adiabatic effectiveness of rotor (= (H’ − Hi)/(Ho − Hi)) |
| εs | concentration effectiveness of stator (= (cs − ci)/(co − ci)) |
| Θo | ratio of flow parameters (= Φo/Φmin) |
| λT,o | turbulent flow parameter (= Cw,o Reϕ−0.8) |
| λt | local turbulent flow parameter (= λT,o(r/b)−13/5) |
| μ | dynamic viscosity |
| ρ | density |
| σ | standard deviation from maximum likelihood estimation |
| Φo | nondimensional flow parameter (= U/ |
| Φmin | value of Φo when there is no ingress |
| Ψ | buffer parameter (= f’(o/r)) |
| Ω | angular velocity of rotor |
| Subscripts | |
| ad | adiabatic |
| exp | experimental measurements |
| i | ingress |
| inf | extrapolated steady-state temperature |
| ini | initial steady-state temperature |
| true | “true” values from maximum likelihood estimation |
| o | purge flow |
| r | rotor |
| s | stator |
| t | total values |
References
- Scobie, J.A.; Sangan, C.M.; Owen, J.M.; Lock, G.D. Review of Ingress in Gas Turbines. ASME J. Eng. Gas Turbines Power 2016, 138, 120801. [Google Scholar] [CrossRef]
- Chew, J.W.; Gao, F.; Palermo, D.M. Flow Mechanisms in Axial Turbine Rim Sealing. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 6, 0954406218784612. [Google Scholar] [CrossRef]
- Chew, J.W.; Green, T.; Turner, A.B. Rim Sealing of Rotor-Stator Wheelspaces in the Presence of External Flow. In ASME 1994 Turbo Expo Volume 1: Turbomachinery, Paper 94-GT-126; American Society of Mechanical Engineers: New York, NY, USA, 1994. [Google Scholar]
- Pountney, O.J.; Sangan, C.M.; Lock, G.D.; Owen, J.M. Effect of Ingestion on Temperature of Turbine Disks. ASME J. Turbomach. 2013, 135, 051010. [Google Scholar] [CrossRef]
- Cho, G.; Sangan, C.M.; Owen, J.M.; Lock, G.D. Effect of Ingress on Turbine Discs. ASME J. Eng. Gas Turbines Power 2016, 138, 042502. [Google Scholar] [CrossRef]
- Mear, L.I.; Owen, J.M.; Lock, G.D. Theoretical Model to Determine Effect of Ingress on Turbine Disks. ASME J. Eng. Gas Turbines Power 2016, 138, 032502. [Google Scholar] [CrossRef]
- Owen, J.M.; Tang, H.; Lock, G.D. Model of Effect of Hot Gas Ingress on Temperatures of Turbine Disks. ASME J. Eng. Gas Turbines Power 2019, 141, 012501. [Google Scholar] [CrossRef]
- Patinios, M.; Scobie, J.A.; Sangan, C.M.; Lock, G.D. Performance of Rim-Seals in Upstream and Downstream Cavities over a Range of Flow Coefficients. Int. J. Turbomach. Propuls. Power 2017, 2, 21. [Google Scholar] [CrossRef]
- Cho, G.; Tang, H.; Owen, J.M.; Lock, G.D. On the Measurement and Analysis of Data from Transient Heat Transfer. Int. J. Heat Mass Transf. 2016, 98, 268–276. [Google Scholar] [CrossRef]
- Owen, J.M. Prediction of Ingestion Through Turbine Rim Seals. Part II: Externally Induced and Combined Ingress. ASME J. Turbomach. 2011, 133, 031006. [Google Scholar] [CrossRef]
- Sangan, C.M.; Pountney, O.J.; Zhou, K.; Wilson, M.; Owen, J.M.; Lock, G.D. Experimental Measurements of Ingestion Through Turbine Rim Seals. Part 1: Externally-Induced Ingress. ASME J. Turbomach. 2013, 135, 021012. [Google Scholar] [CrossRef]
- Davison, A.C. Statistical Models; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Silvey, S.D. Statistical Inference; Chapman and Hall: London, UK, 1975. [Google Scholar]
- Owen, J.M.; Rogers, R.H. Flow and Heat Transfer in Rotating-Disc. Systems, Volume 1: Rotor-Stator Systems; Research Studies Press: Taunton, UK; John Wiley: New York, NY, USA, 1989. [Google Scholar]
- Mear, L.I. Theoretical Modelling of Flow in Rotor-Stator Systems. Ph.D. Thesis, University of Bath, Bath, UK, 2015. [Google Scholar]
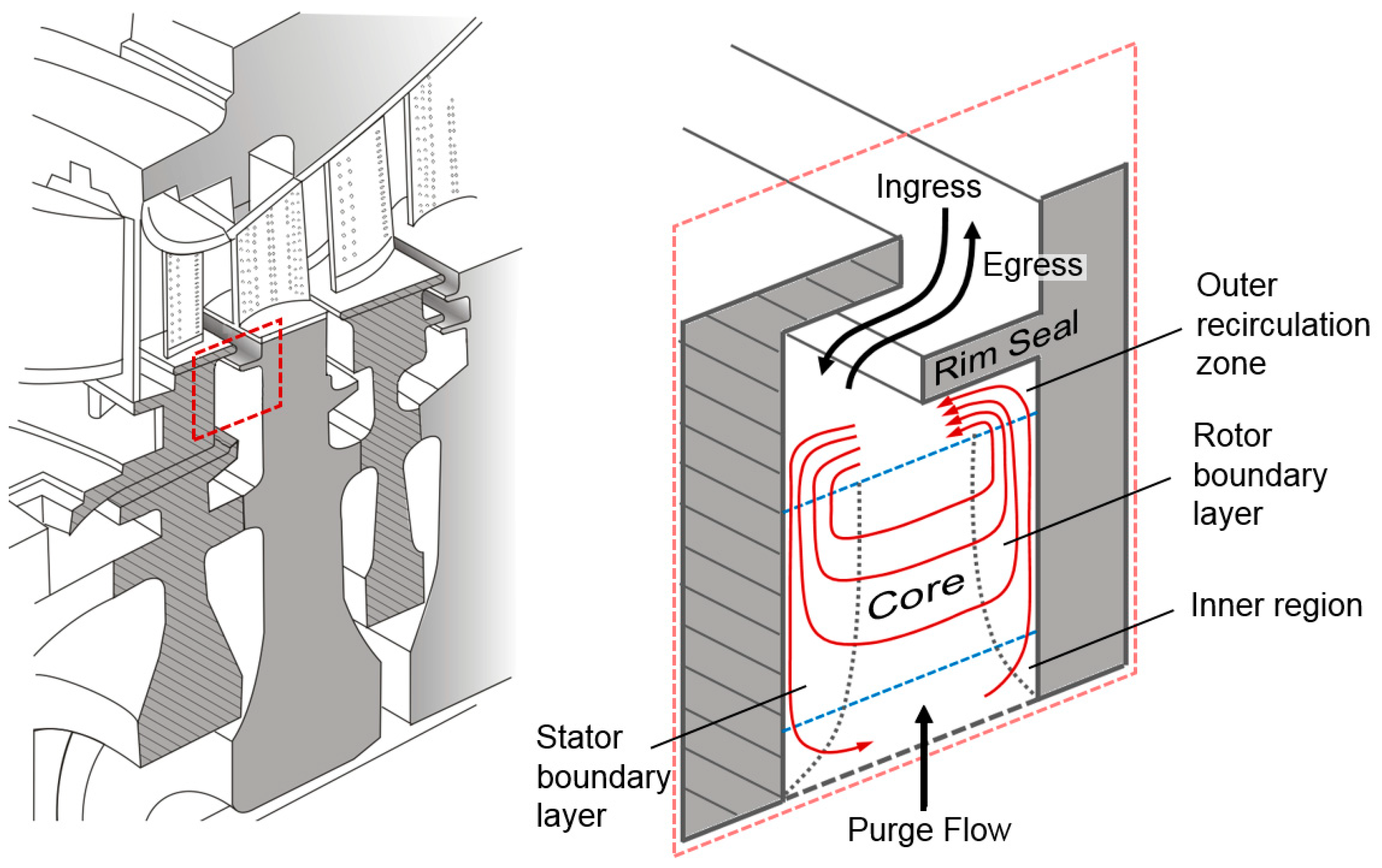
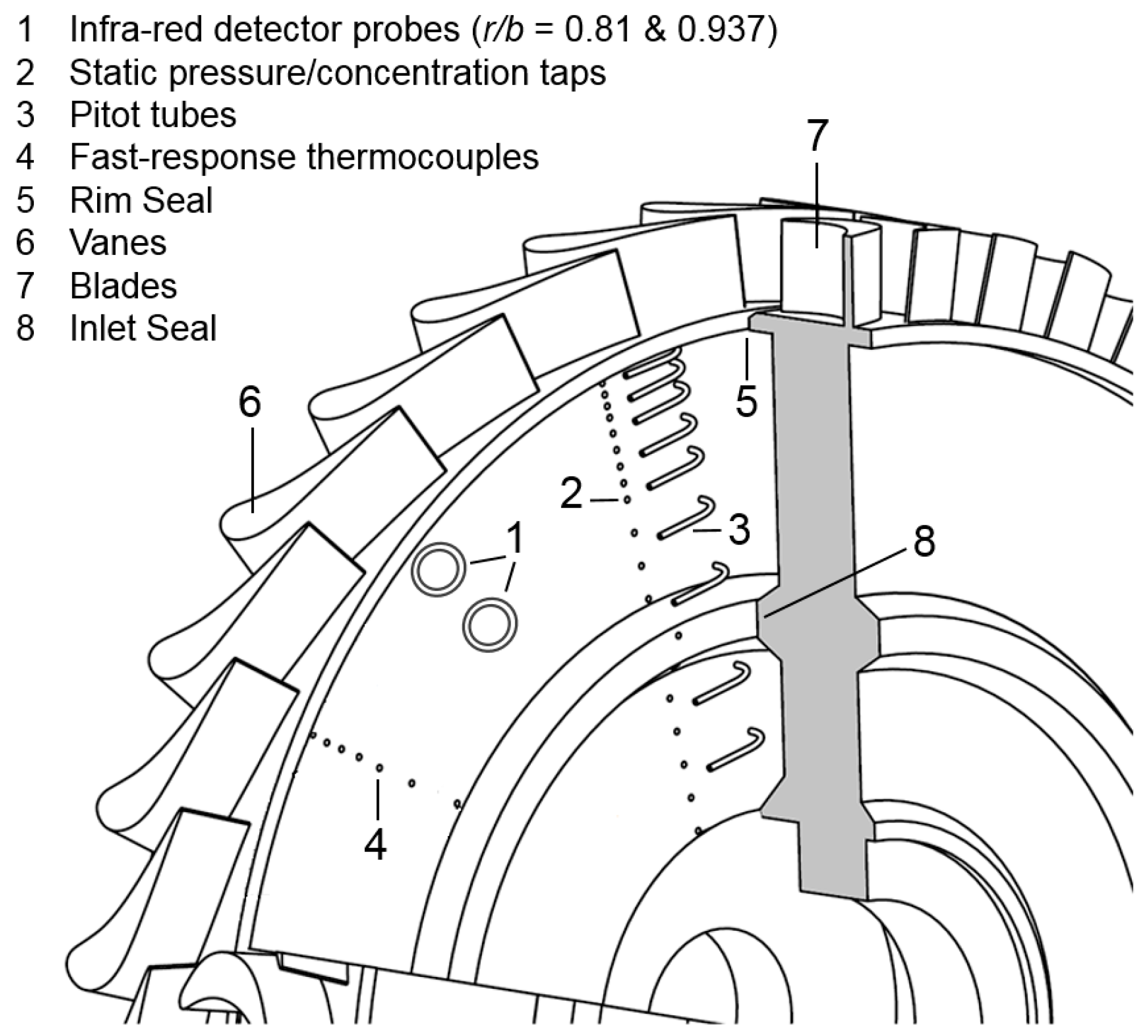
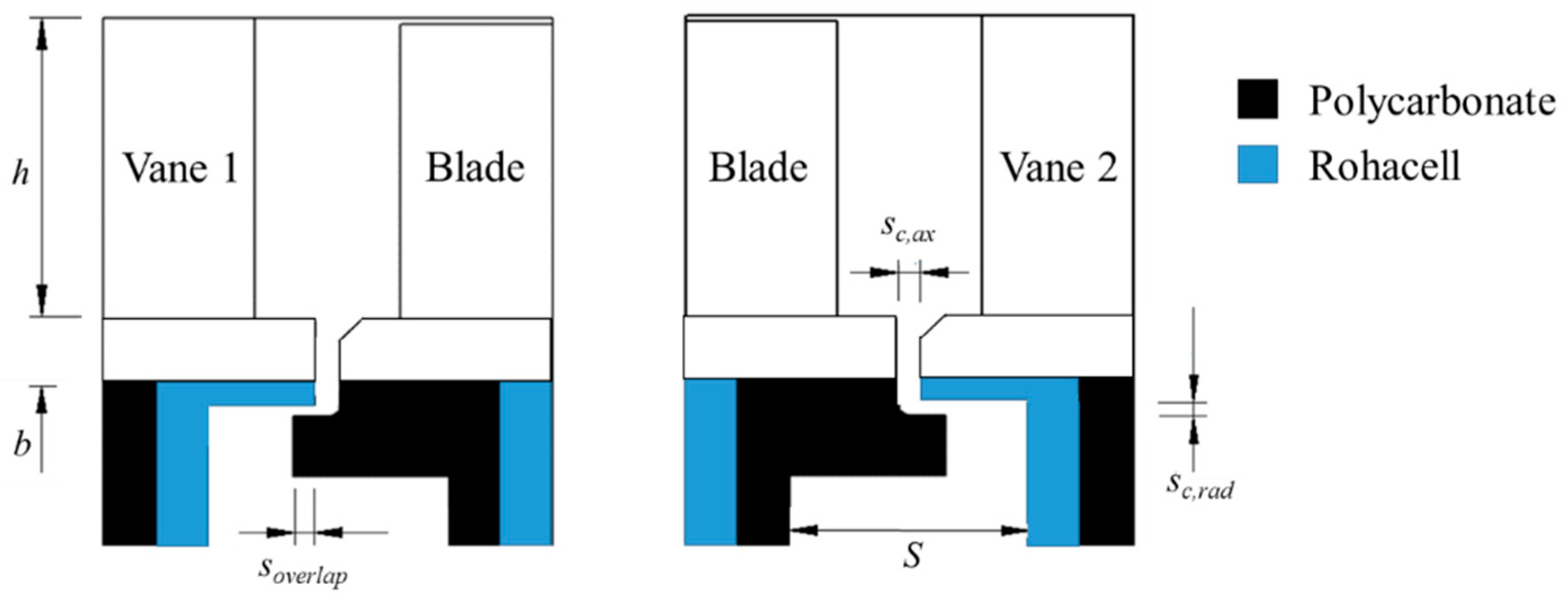
| Parameters | Values |
|---|---|
| b (outer radius of the disc) | 190 mm |
| S (axial width of both wheel-spaces) | 10 mm |
| sc,ax (axial clearance) | 2 mm |
| sc,rad (radial clearance) | 1.28 mm |
| soverlap (axial overlap) | 1.86 mm |
| Gc (seal-clearance ratio, = sc,ax/b) | 0.0105 |
| G (gap ratio, = S/b) | 0.0526 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, H.; Cho, G.; Patinios, M.; Scobie, J.A.; Sangan, C.M.; Owen, J.M.; Lock, G.D. Effect of Ingress on Flow and Heat Transfer Upstream and Downstream of a Rotating Turbine Disc. Aerospace 2019, 6, 49. https://doi.org/10.3390/aerospace6050049
Tang H, Cho G, Patinios M, Scobie JA, Sangan CM, Owen JM, Lock GD. Effect of Ingress on Flow and Heat Transfer Upstream and Downstream of a Rotating Turbine Disc. Aerospace. 2019; 6(5):49. https://doi.org/10.3390/aerospace6050049
Chicago/Turabian StyleTang, Hui, GeonHwan Cho, Mario Patinios, James A. Scobie, Carl M. Sangan, J. Michael Owen, and Gary D. Lock. 2019. "Effect of Ingress on Flow and Heat Transfer Upstream and Downstream of a Rotating Turbine Disc" Aerospace 6, no. 5: 49. https://doi.org/10.3390/aerospace6050049
APA StyleTang, H., Cho, G., Patinios, M., Scobie, J. A., Sangan, C. M., Owen, J. M., & Lock, G. D. (2019). Effect of Ingress on Flow and Heat Transfer Upstream and Downstream of a Rotating Turbine Disc. Aerospace, 6(5), 49. https://doi.org/10.3390/aerospace6050049