Practical Approach for Absolute Density Field Measurement Using Background-Oriented Schlieren
Abstract
:1. Introduction
2. Methodologies
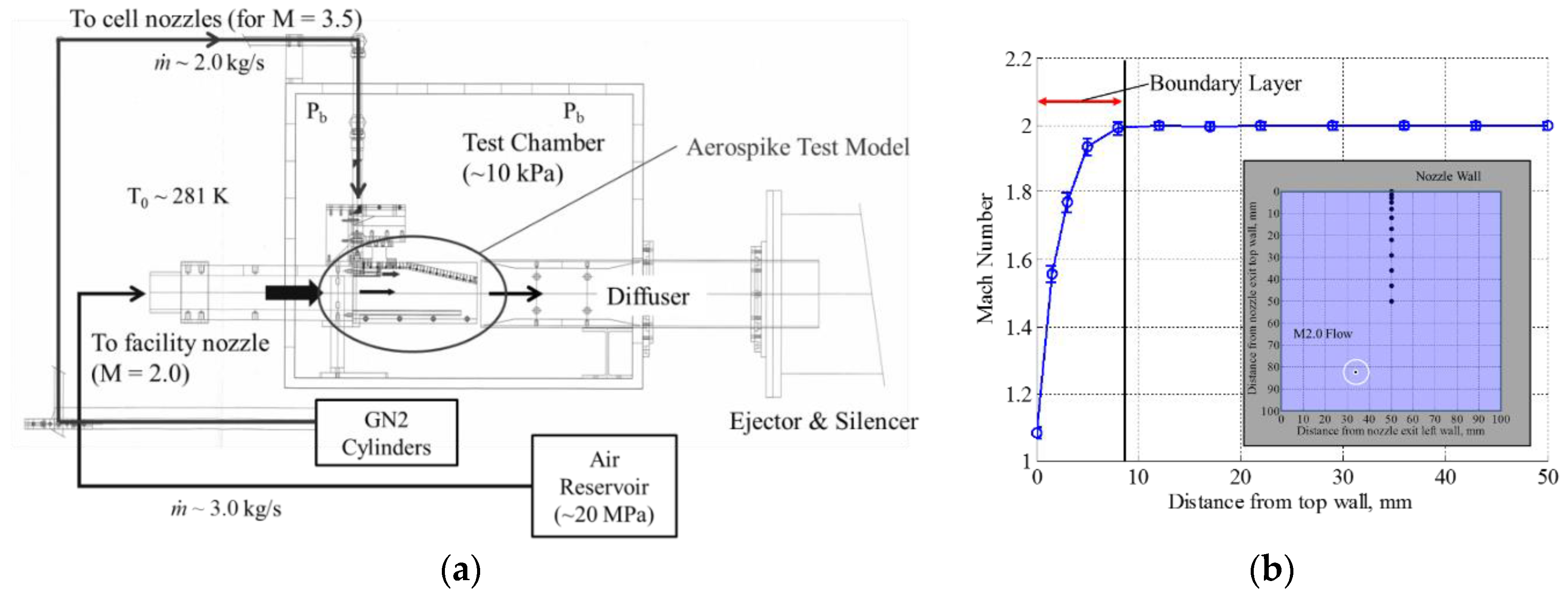
2.1. Wind Tunnel Facility and Flow Conditions
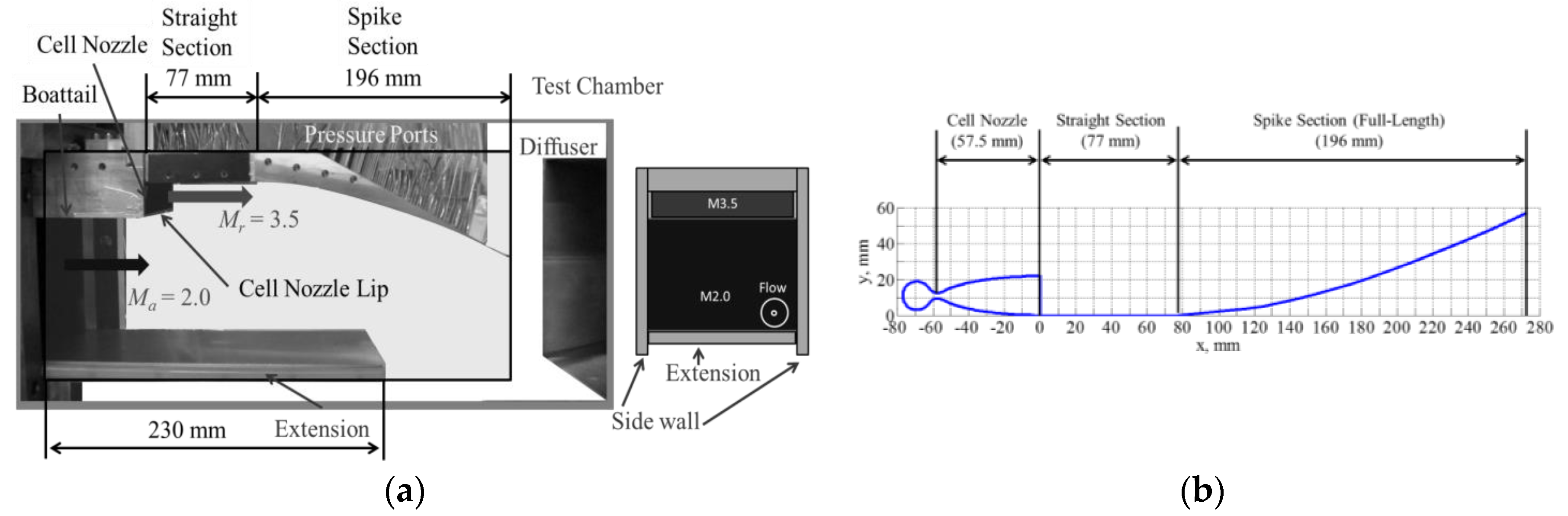
2.2. Aerospike Nozzle
2.3. BOS Measurement System
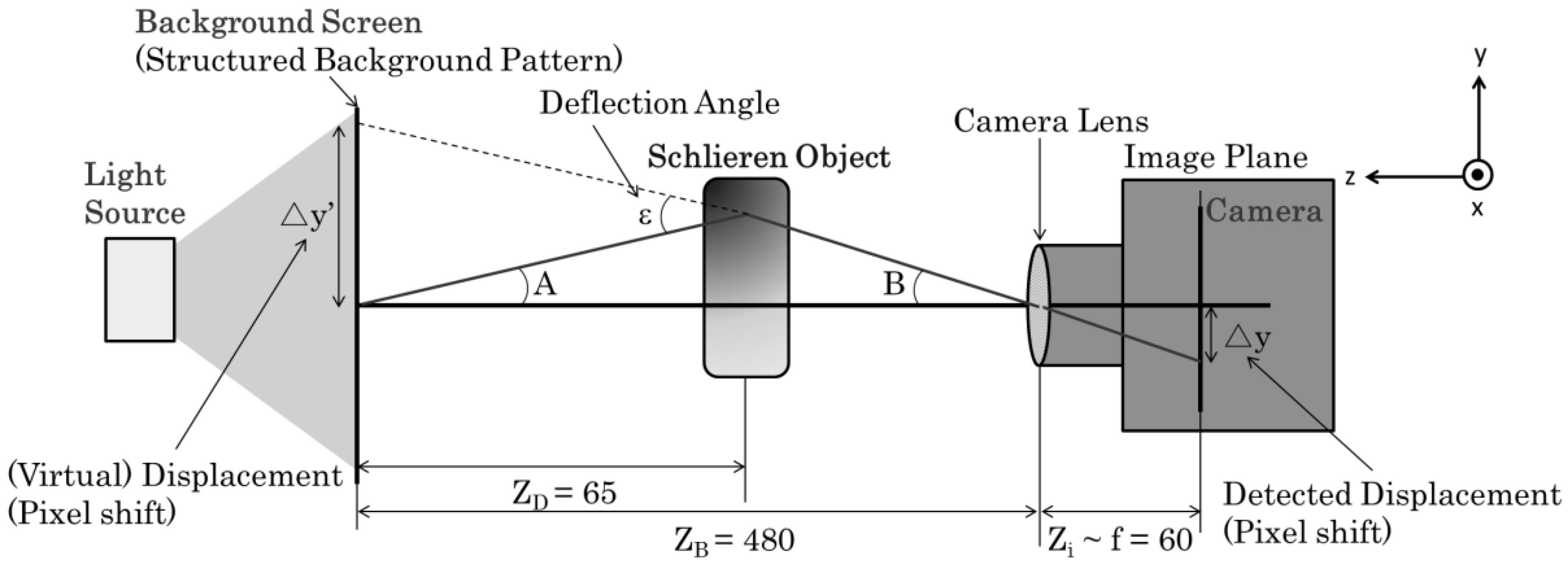
2.3.1. Basic Concept of BOS
2.3.2. BOS Setup
2.4. BOS Post-Processing
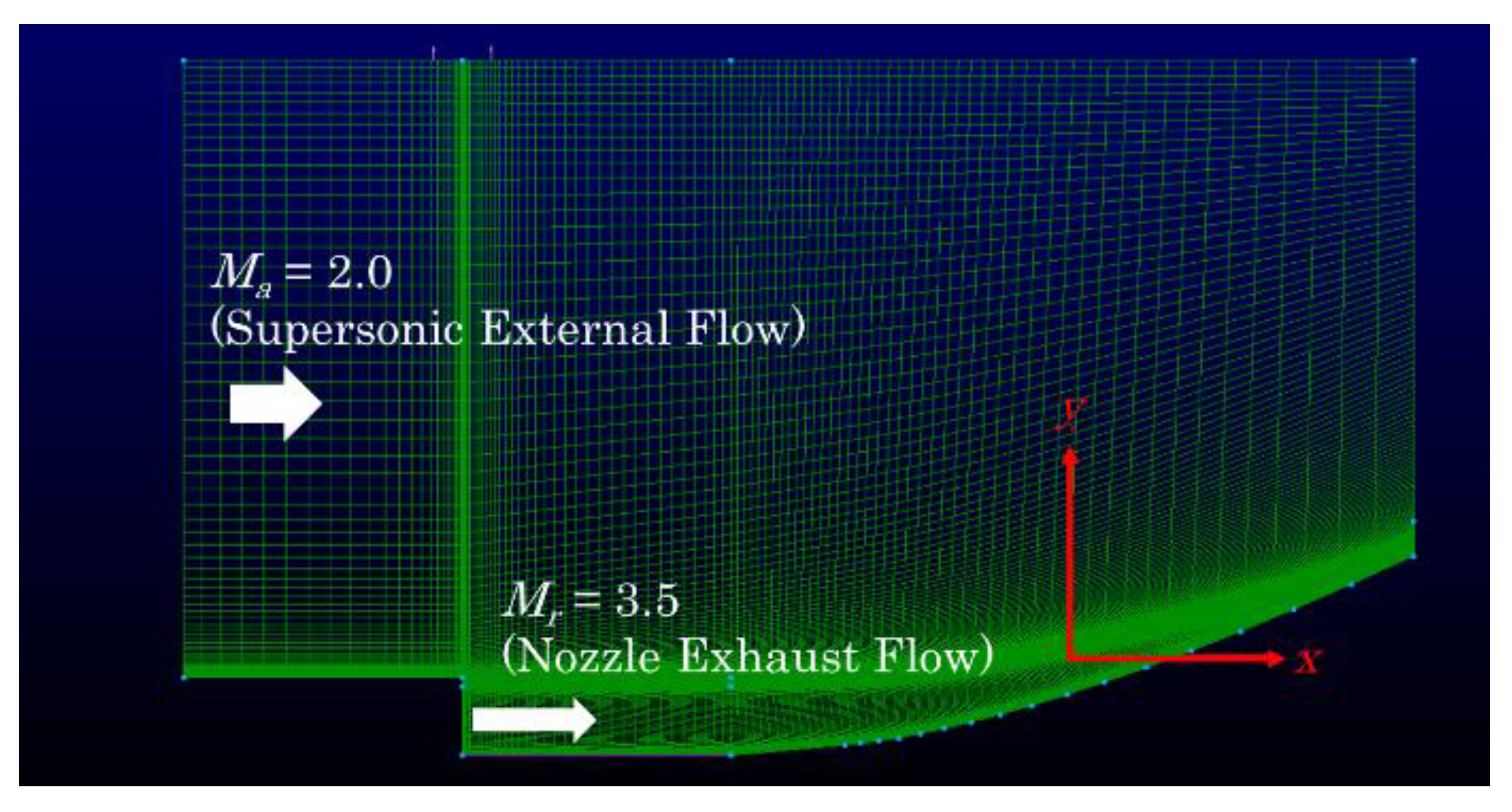
2.5. Computational Fluid Dynamics and Code Validation
3. Results and Discussion
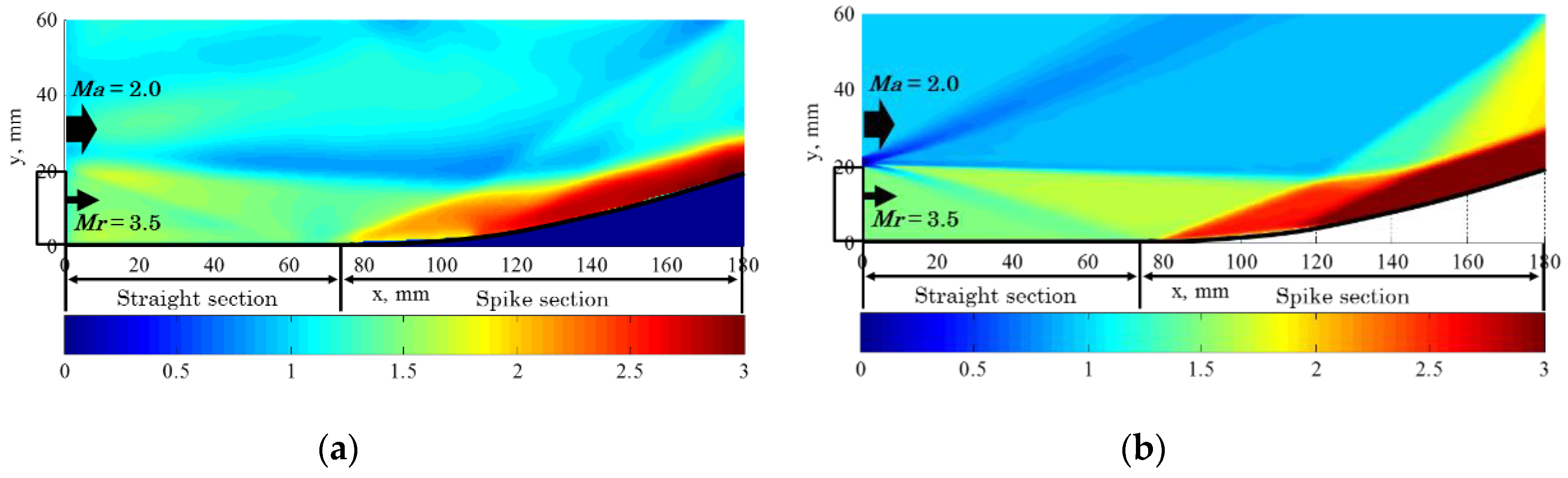
3.1. Qualitative Evaluation of the Flowfield
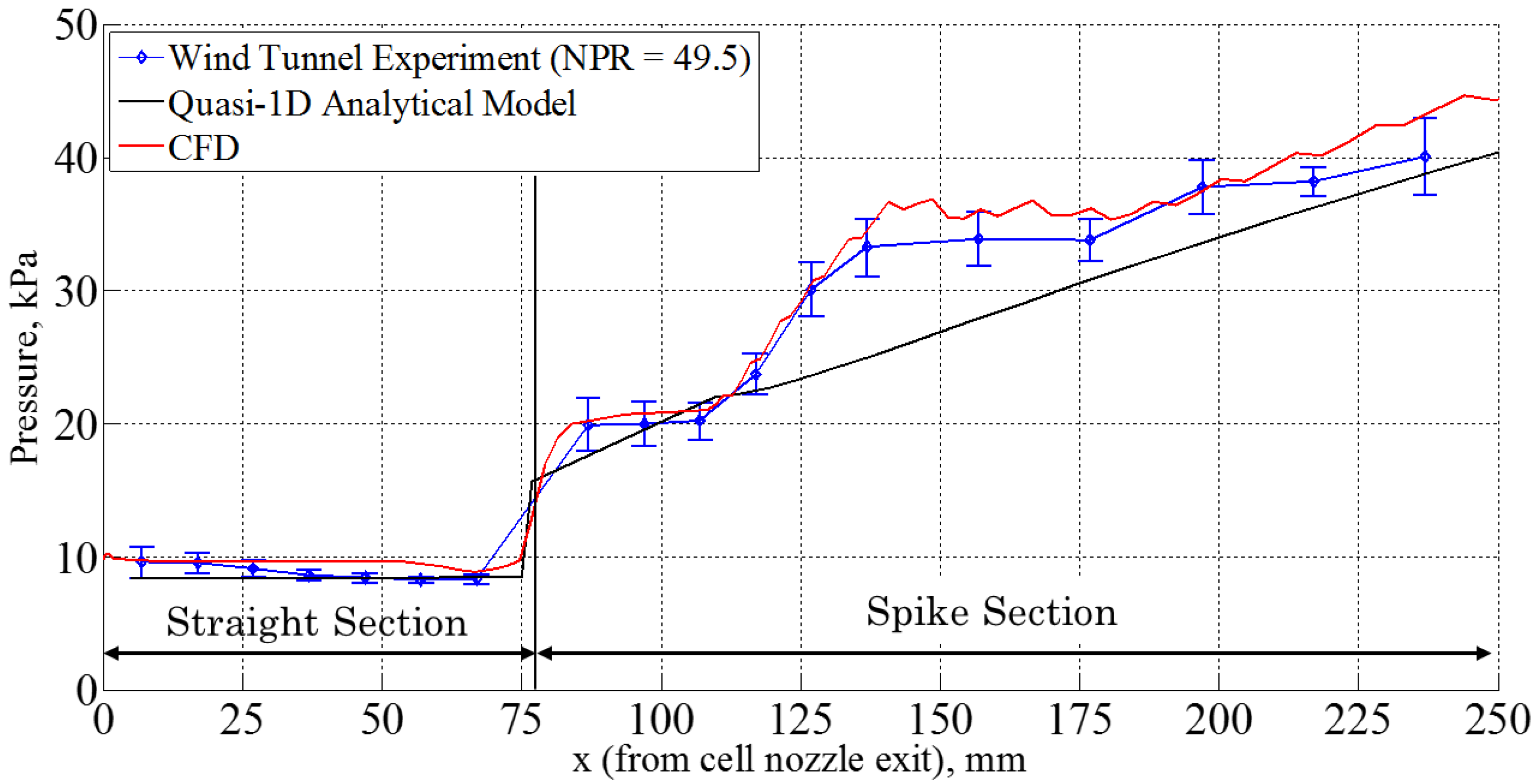
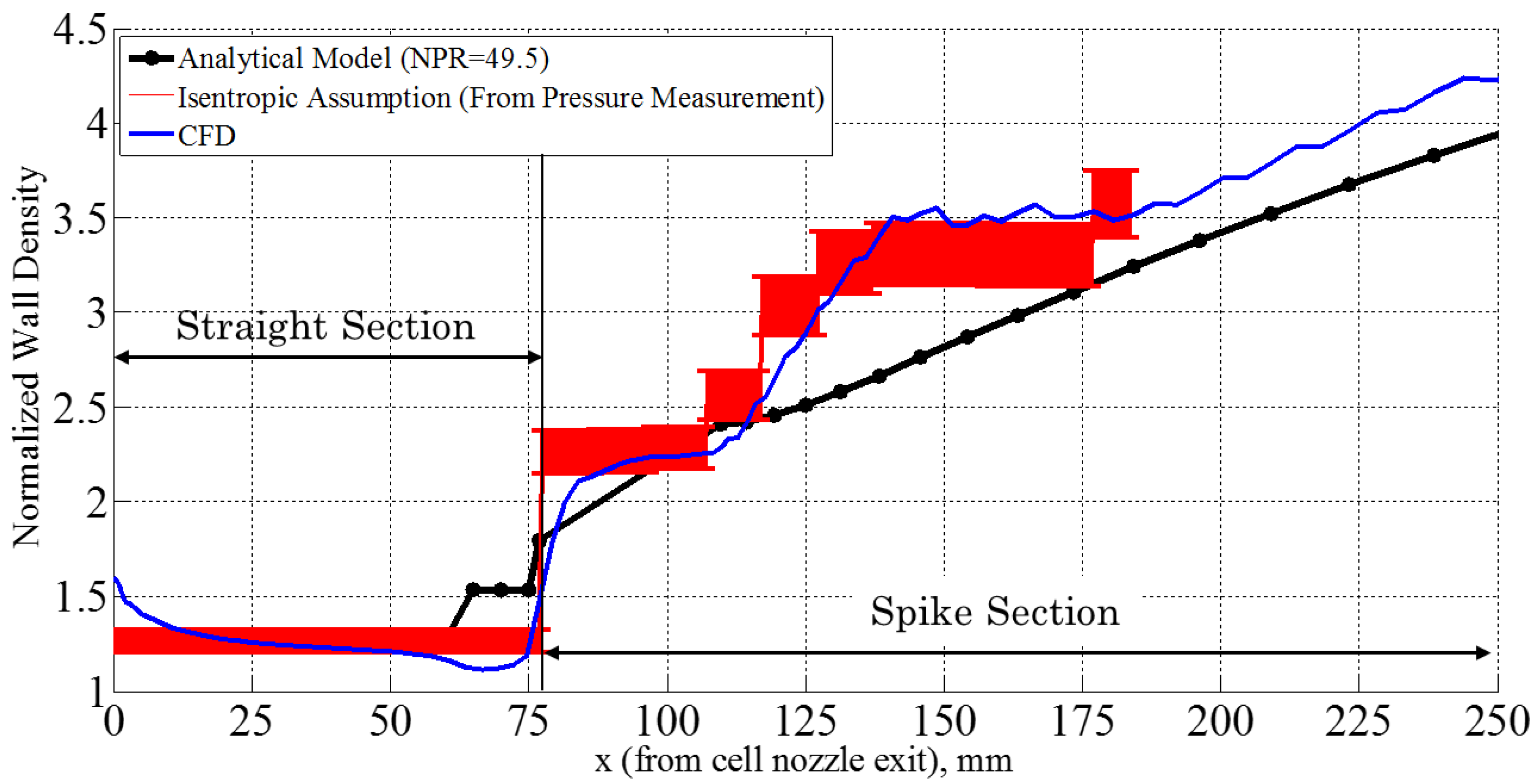
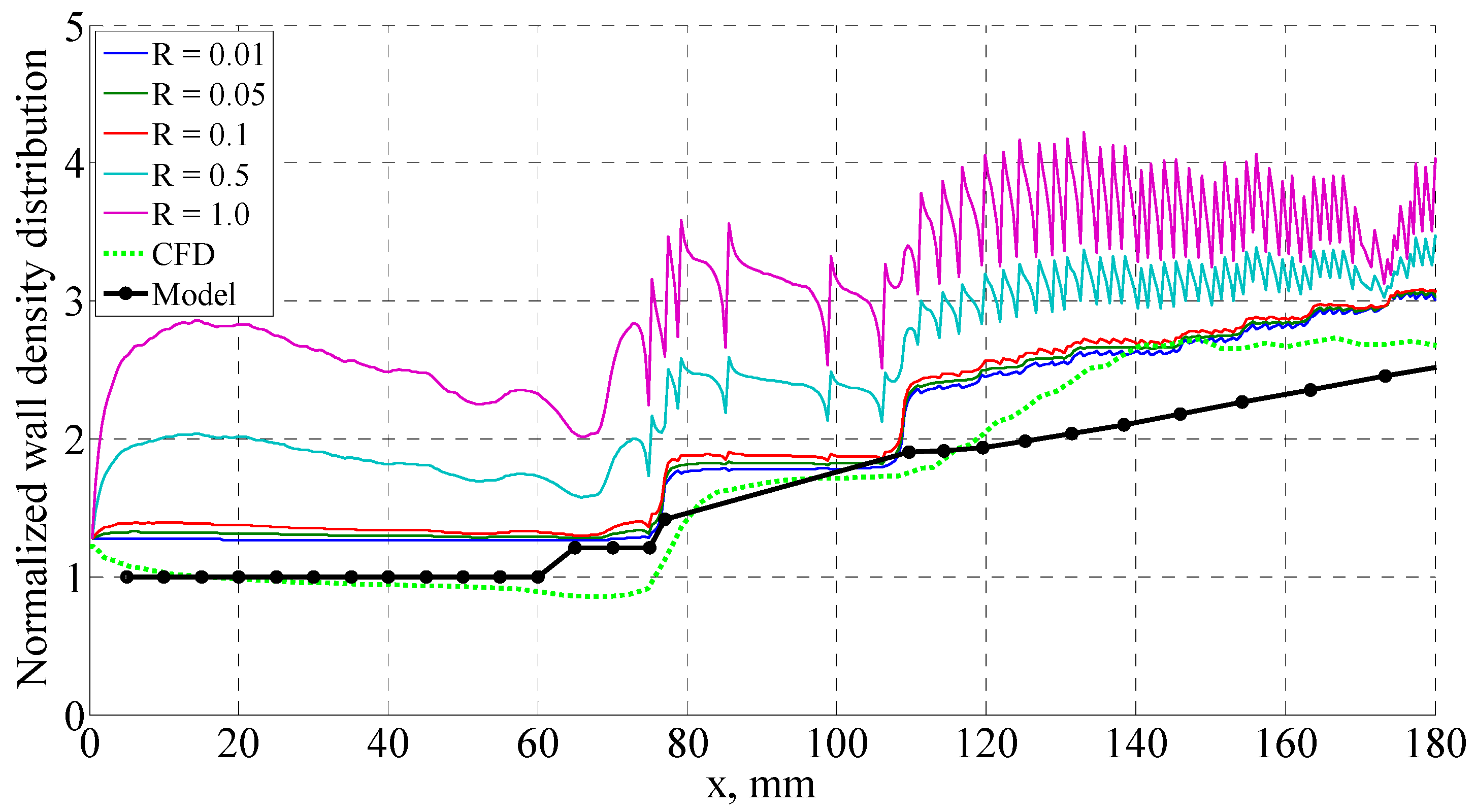
3.2. Modeling of Spike Wall Pressure and Density Distributions
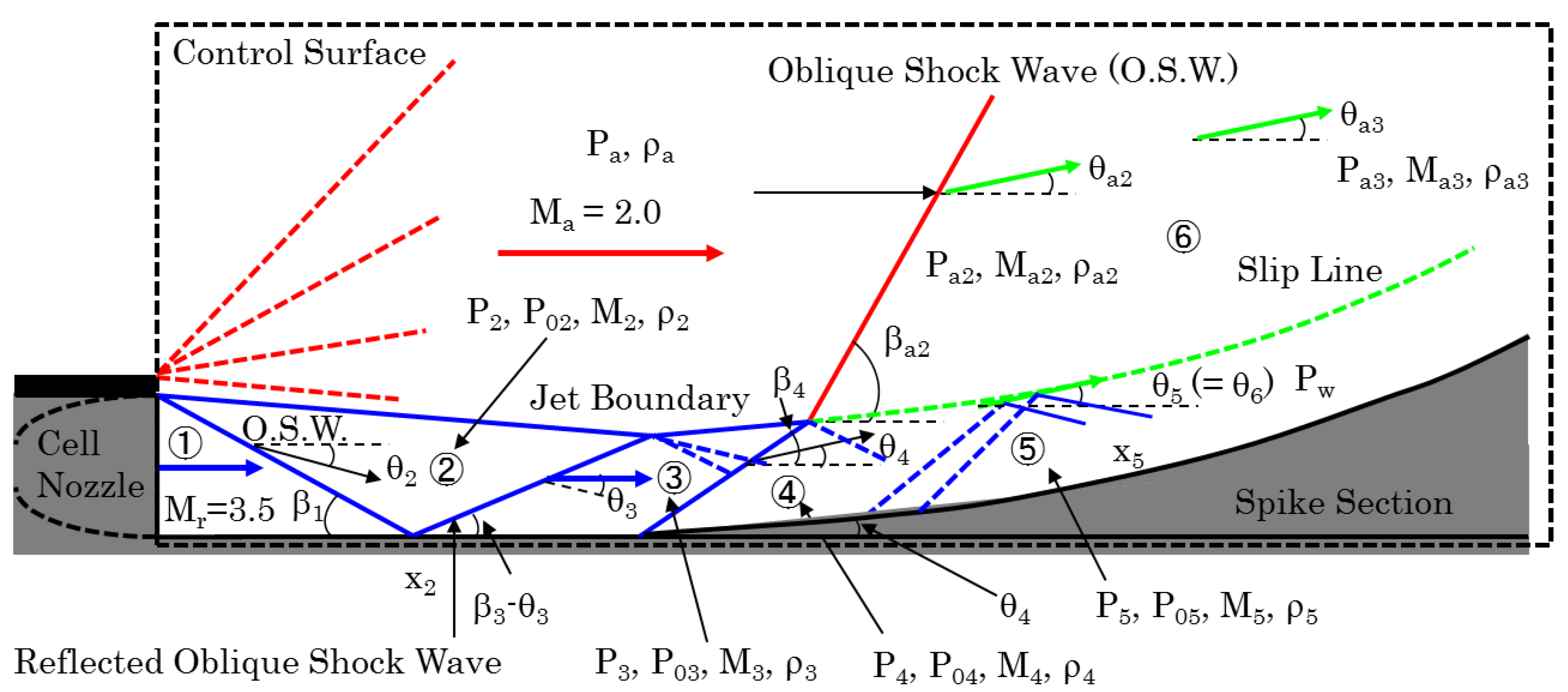
3.2.1. Analytical Model
- (1)
- The Mach number of the external flow entering the spike nozzle surface is 2.0.
- (2)
- The Mach number of the cell nozzle jet at its exit is 3.5.
- (3)
- The specific heat ratio γ is constant at a value of 1.4 throughout this study because all the flows are non-reactive.
- (4)
- The entire flowfield is two-dimensional.
- (5)
- The flow properties change isentropically except in the region of a shock wave.
- (6)
- No energy loss occurs due to either skin friction or passing through of oblique shock waves on the wall surface.
- (7)
- The static pressures and flow angles of the cell jet and external flows are the same across the slip surface.
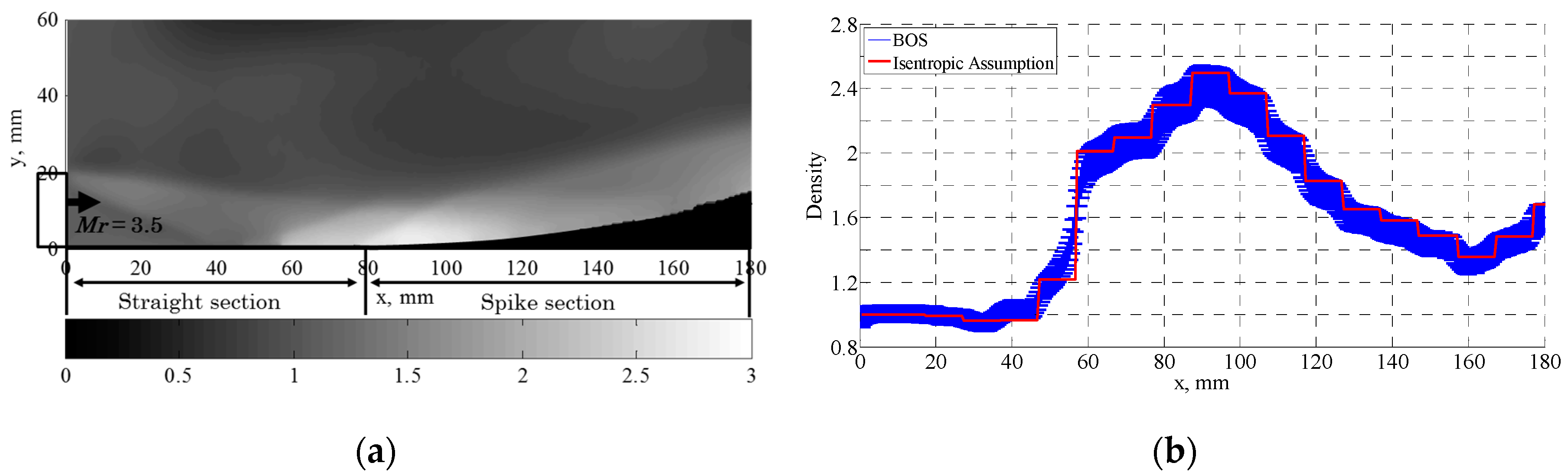
3.2.2. Simplified Isentropic Assumption
3.3. Quantitative Evaluation
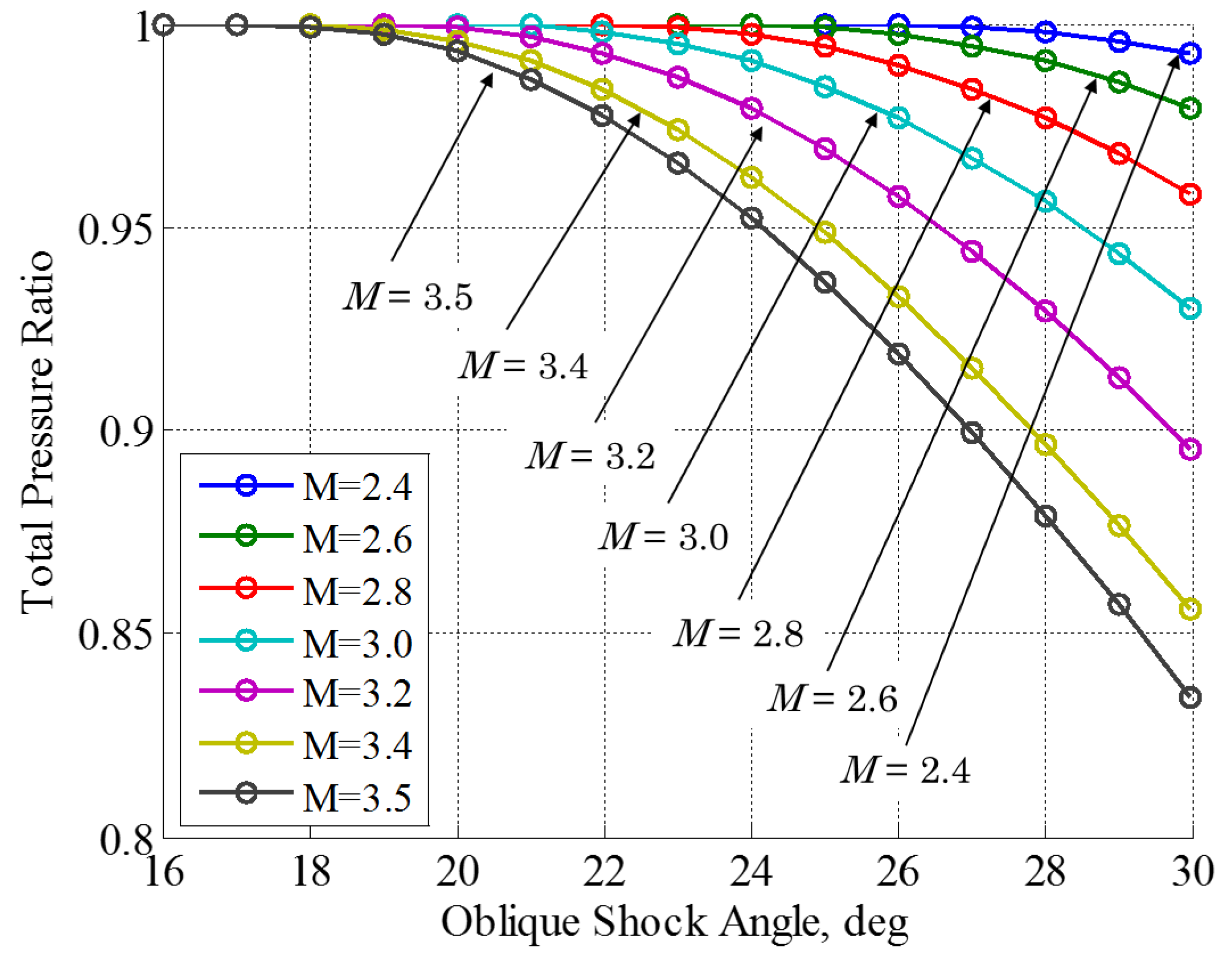
3.4. Application to other Conditions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| f | focal length, mm |
| M | Mach number |
| NPR | nozzle pressure ratio defined as P0r/Pb |
| n | refractive index |
| Pa | static pressure of freestream, kPa |
| Pb | static pressure in the test chamber, kPa |
| P0r | total pressure of the cell nozzle flow, kPa |
| Pr | static pressure at the cell nozzle exit, kPa |
| Pw | static pressure on nozzle surface, kPa |
| T | temperature, K |
| W | width of schlieren object, mm |
| x | coordinate axis in streamwise direction |
| y | coordinate axis in perpendicular to flow direction |
| z | coordinate axis in line-of-sight direction |
| β | oblique shock wave angle, rad |
| ε | image deflection |
| γ | specific heat ratio (=1.4) |
| ρ | density, kg/m3 |
| θ | angle, rad |
| Subscripts | |
| 0 | stagnation or reference condition |
| a | ambient or freestream condition |
| b | environmental condition |
| r | cell nozzle flow condition |
References
- Settles, G.S.; Hargather, M.J. A Review of Recent Developments in Schlieren and Shadowgraph Techniques. Meas. Sci. Technol. Top. Rev. 2017, 28, 042001. [Google Scholar] [CrossRef]
- Hargather, M.J.; Settles, G.S. Natural-Background-Oriented Schlieren Imaging. Exp. Fluids 2010, 48, 59–68. [Google Scholar] [CrossRef]
- Raffel, M. Background-Oriented Schlieren (BOS) Technique. Exp. Fluids 2015, 56, 145–160. [Google Scholar] [CrossRef]
- Hargather, M.J.; Settles, G.S. A Comparison of Three Quantitative Schlieren Techniques. Opt. Lasers Eng. 2012, 50, 8–17. [Google Scholar] [CrossRef]
- Meyer, G.E.A. Computerized Background-Oriented Schlieren. Exp. Fluids 2002, 33, 181–187. [Google Scholar] [CrossRef]
- Venkatakrishnan, L. Density Measurements in an Axisymmetric Underexpanded Jet by Background-Oriented Schlieren Technique. AIAA J. 2005, 43, 1574–1579. [Google Scholar] [CrossRef]
- Venkatakrishnan, L.; Meier, G.E.A. Density Measurements Using the Background Oriented Schlieren Technique. Exp. Fluids 2004, 37, 237–247. [Google Scholar] [CrossRef]
- Hartmann, U.; Adamczuk, R.; Seume, J. Tomographic Background Oriented Schlieren Applications for Turbomachinery. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. AIAA-2015-1690. [Google Scholar]
- Goldhahn, E.; Seume, J. Background Oriented Schlieren Technique: Sensitivity, Accuracy, Resolution and Application to a Three-Dimensional Density Field. Exp. Fluids 2007, 43, 241–249. [Google Scholar] [CrossRef]
- Bichal, A.; Thurow, B.S. On the Application of Background Oriented Schlieren for Wavefront Sensing. Meas. Sci. Technol. 2014, 25, 015001. [Google Scholar] [CrossRef]
- Takahashi, H.; Tomioka, S.; Sakuranaka, N.; Tomita, T.; Kuwamori, K.; Masuya, G. Influence of External Flow on Plume Physics of Clustered Linear Aerospike Nozzles. J. Propuls. Power 2014, 30, 1199–1212. [Google Scholar] [CrossRef]
- Takahashi, H.; Tomioka, S.; Tomita, T.; Sakuranaka, N. Aerodynamic Characterization of Linear Aerospike Nozzles in Off-Design Flight Conditions. J. Propuls. Power 2015, 31, 204–218. [Google Scholar] [CrossRef]
- Geers, J.S.; Yu, K.H. Systematic Application of Background-Oriented Schlieren for Isolator Shock Train Visualization. AIAA J. 2017, 55, 1105–1117. [Google Scholar] [CrossRef]
- Heineck, J.T.; Banks, D.W.; Schairer, E.T.; Haering, E.A., Jr.; Bean, P.S. Background Oriented Schlieren (BOS) of a Supersonic Aircraft in Flight. In Proceedings of the AIAA Flight Testing Conference, Washington, DC, USA, 13–17 June 2016. AIAA-2016-3356. [Google Scholar]
- Smith, N.T.; Heineck, J.T.; Schairer, E.T. Optical Flow for Flight and Wind Tunnel Background Oriented Schlieren Imaging. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017. AIAA-2017-0472. [Google Scholar]
- Bonelli, F.; Viggiano, A.; Magi, V. A numerical analysis of hydrogen underexpanded jets. In Proceedings of the Spring Technical Conference of the ASME Internal Combustion Engine Division 2012, ASME 2012 Internal Combustion Engine Division Spring Technical Conference (ICES 2012), Torino, Italy, 6–9 May 2012; pp. 681–690. [Google Scholar]
- Bonelli, F.; Viggiano, A.; Magi, V. A Numerical Analysis of Hydrogen Underexpanded Jets Under Real Gas Assumption. J. Fluids Eng. 2013, 135, 121101. [Google Scholar] [CrossRef]
- Gui, L.; Merzkirch, W. A Comparative Study of the MQD Method and Several Correlation-Based PIV Evaluation Algorithms. Exp. Fluids 2000, 28, 36–44. [Google Scholar]
- Takahashi, H.; Munakata, T.; Sato, S. Thrust Augmentation by Airframe-Integrated Linear-Spike Nozzle Concept for High-Speed Aircraft. Aerospace 2018, 5, 19. [Google Scholar] [CrossRef]
- Agon, A.; Abeynayake, D.; Smart, M. Applicability of Viscous and Inviscid Flow Solvers to the Hypersonic REST Inlet. In Proceedings of the 18th Australian Fluid Mechanics Conference, Launceston, Australia, 3–7 December 2012; pp. 3–6. [Google Scholar]
- Ward, A.D.T.; Smart, M.K.; Gollan, R.J. Development of a Rapid Inviscid-Boundary Layer Aerodynamic Tool. In Proceedings of the 22nd AIAA International Space Planes and Hypersonics Systems and Technologies Conference, Moscow, Russia, 21–24 September 2018. AIAA-2018-5270. [Google Scholar]



| Component | Parameter | Setup Used in This Study |
|---|---|---|
| Camera (Nikon D700) | Shutter speed Aperture (f-number) ISO sensitivity Spatial resolution of camera Focal length (f) | 1/4000 s F4 200 4256 × 2832 (12 M) 60 mm |
| Background pattern | Spatial resolution of background pattern (random noise) Pattern contrast | 2000 × 2000 pixels Black and white (binary) |
| Overall setup | Distance between lens and density object (ZB − ZD) Distance between object and background pattern (ZD) | 365 mm 115 mm |
| Noise Source | Note | Value |
|---|---|---|
| Freestream | Static pressure variation for test window duration | 1.2% |
| Measurement and deriving displacement field | Background noise from calculated displacement field using two images containing only external flows and depth of field information; maximum displacement in the background image is approximately 1.0 pixel due to the existence of external flow; this image will be subtracted for later post-processing. Spatial variation of the displacement was found to be approximately 0.1 pixel. | 1 pixel ~ 1% |
| Line-of-sight integration | Inherent in calculated displacement field especially caused by the boundary layer profile (assuming line-of-sight distribution of the flowfield to be a tabletop profile) | 2.1% |
| Absolute density | From the wall boundary condition and error due to the Gibbs phenomenon | 3.0% |
| Boundary | Type | Details | Normalized Value | Note |
|---|---|---|---|---|
| Left boundary | Dirichlet | (x, y) = (0, M2.0 region) (x, y) = (0, M3.5 region) | 1.0 (=ρ/ρa) 1.27 (=ρr/ρa) | Assuming an isentropic nozzle exit condition. |
| Top boundary | Neumann | First-order derivative of density across the boundary is assumed to be zero. | ||
| Right boundary | Neumann | Same as above | ||
| Wall boundary | Dirichlet | Wall density distribution | Derived wall density distribution from isentropic assumption based on measured wall pressure distribution or other models. |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takahashi, H. Practical Approach for Absolute Density Field Measurement Using Background-Oriented Schlieren. Aerospace 2018, 5, 129. https://doi.org/10.3390/aerospace5040129
Takahashi H. Practical Approach for Absolute Density Field Measurement Using Background-Oriented Schlieren. Aerospace. 2018; 5(4):129. https://doi.org/10.3390/aerospace5040129
Chicago/Turabian StyleTakahashi, Hidemi. 2018. "Practical Approach for Absolute Density Field Measurement Using Background-Oriented Schlieren" Aerospace 5, no. 4: 129. https://doi.org/10.3390/aerospace5040129
APA StyleTakahashi, H. (2018). Practical Approach for Absolute Density Field Measurement Using Background-Oriented Schlieren. Aerospace, 5(4), 129. https://doi.org/10.3390/aerospace5040129





