Effect of Piezo-Embedded Inverted Flag in Free Shear Layer Wake
Abstract
1. Introduction
- Harvest energy to increase battery life.
- Sense changes in the wing wake for gust alleviation.
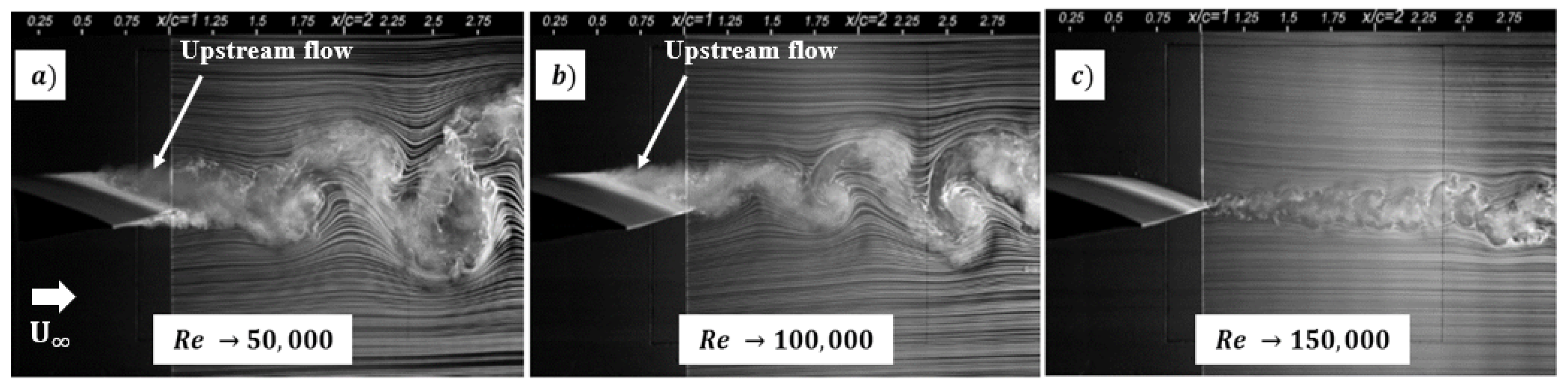
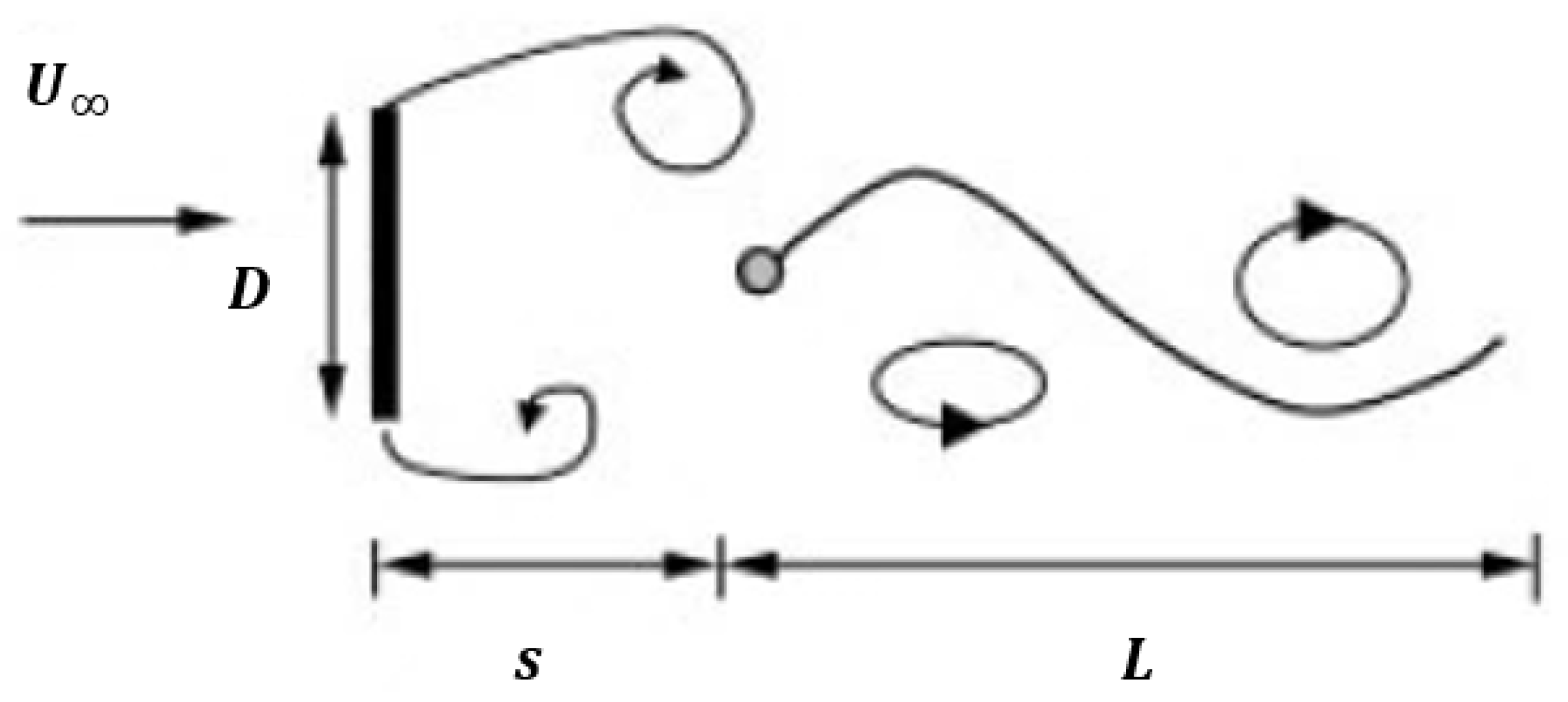
1.1. Wing Wake
1.2. Flexible Smart Materials
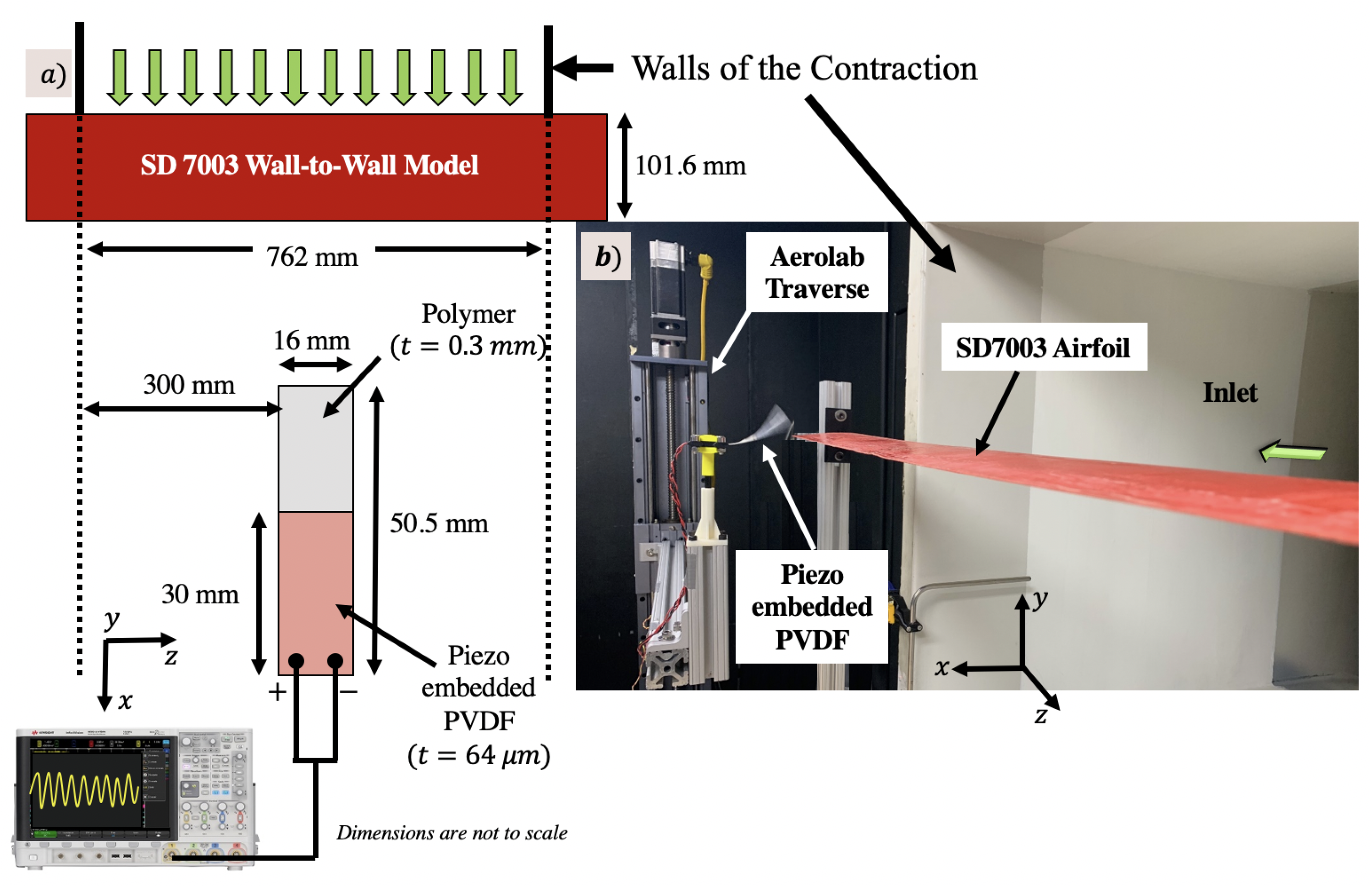
2. Experimental Setup
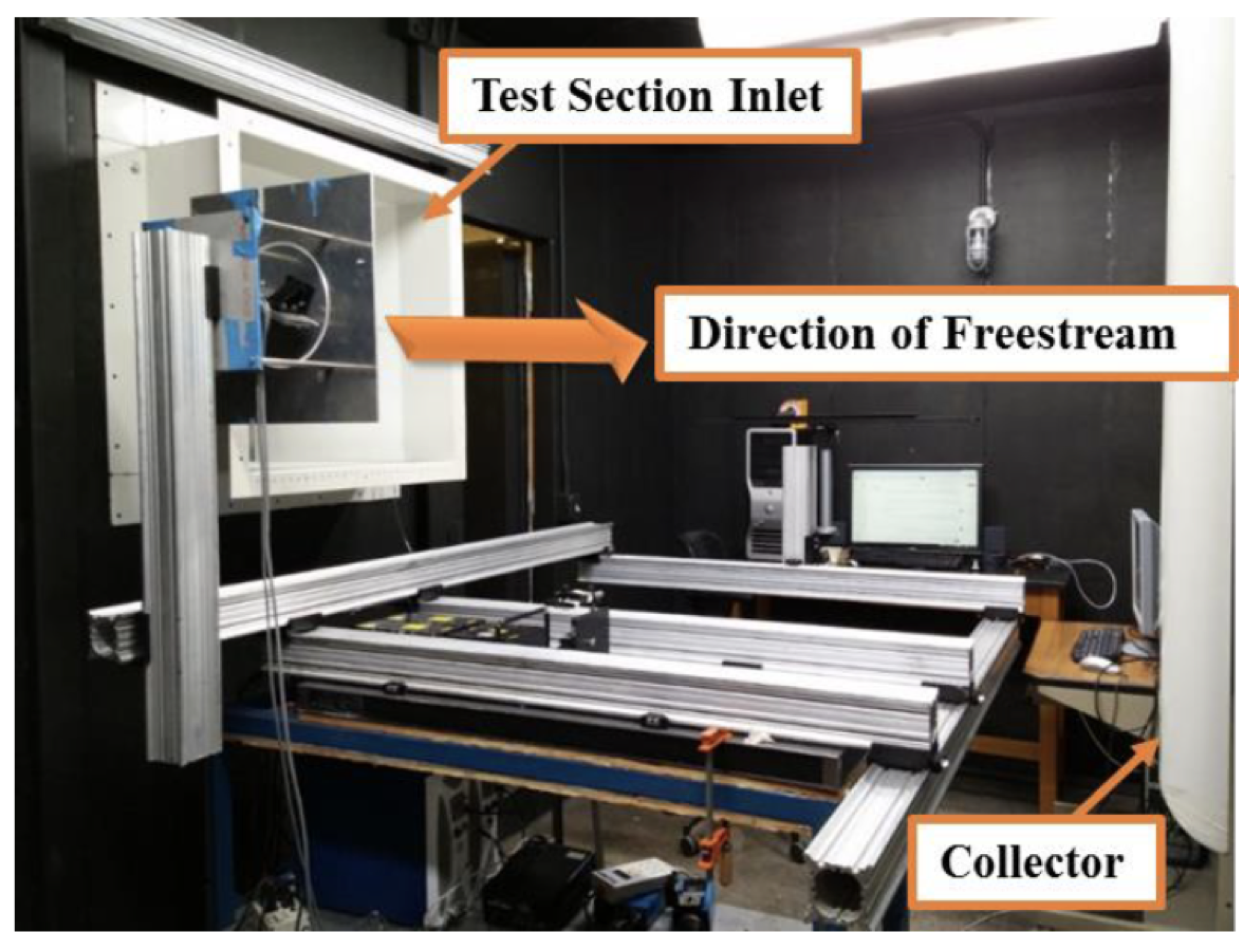
2.1. Wind Tunnel
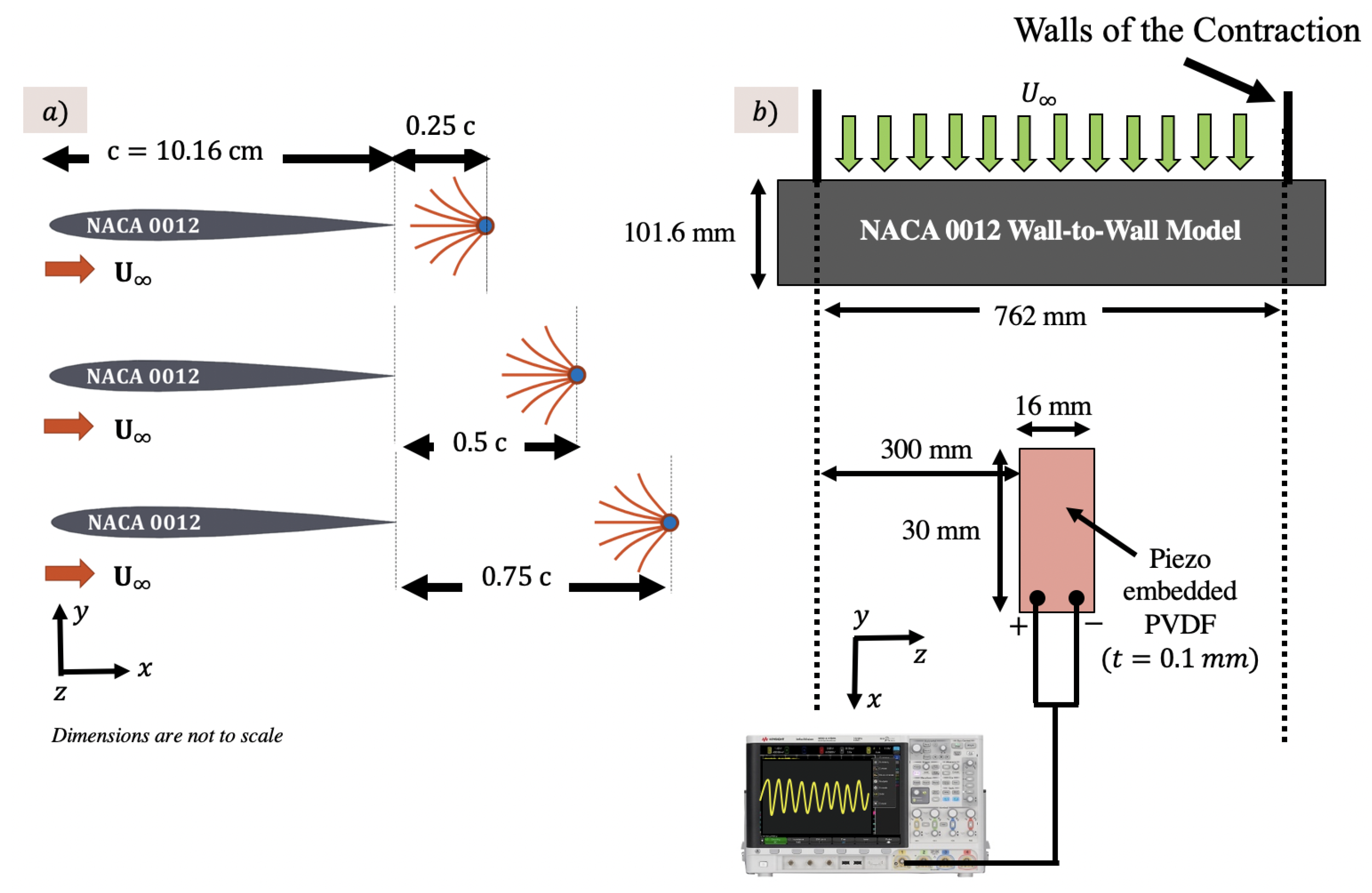
2.2. Wing Models
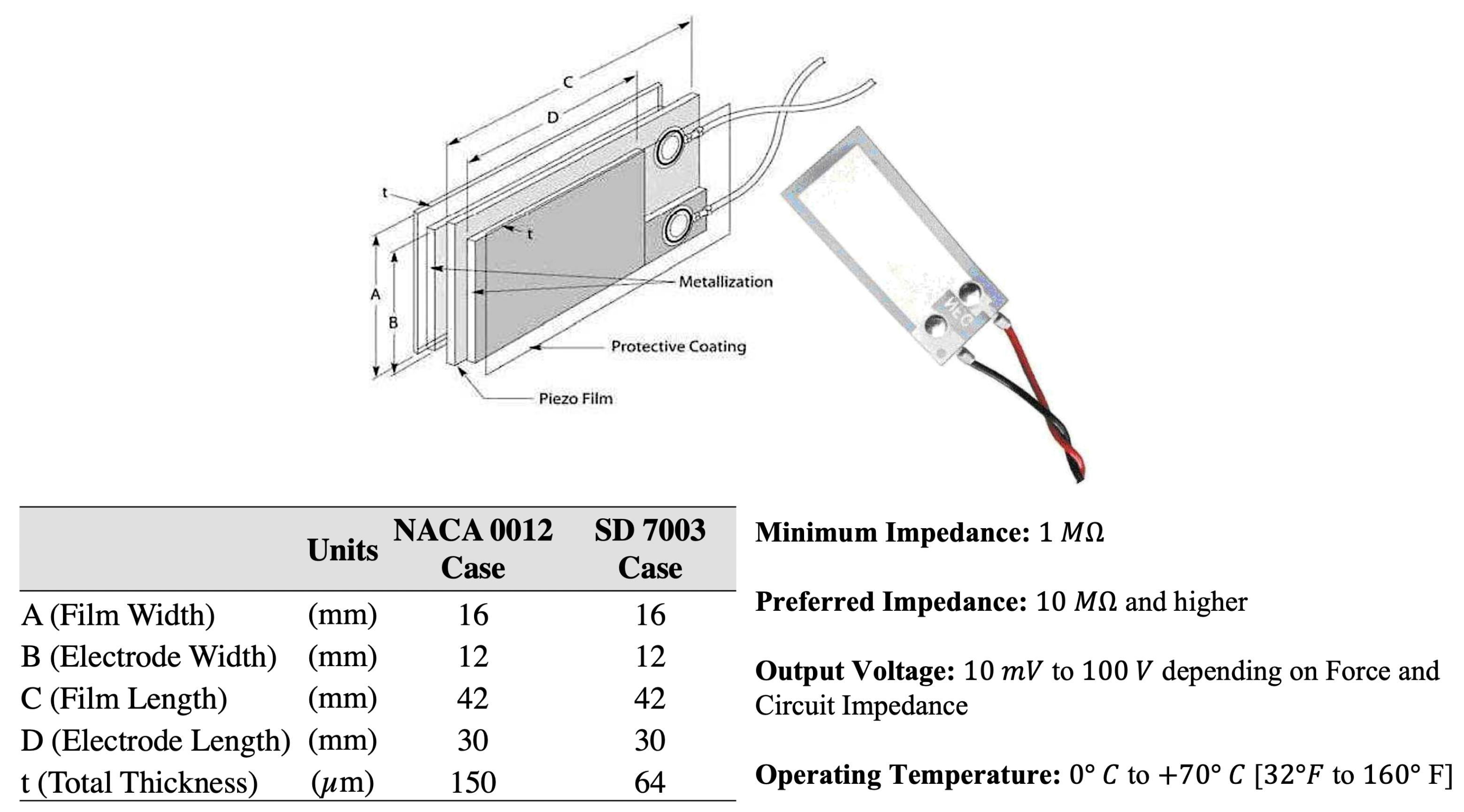
2.3. Piezo Embedded PVDF Material
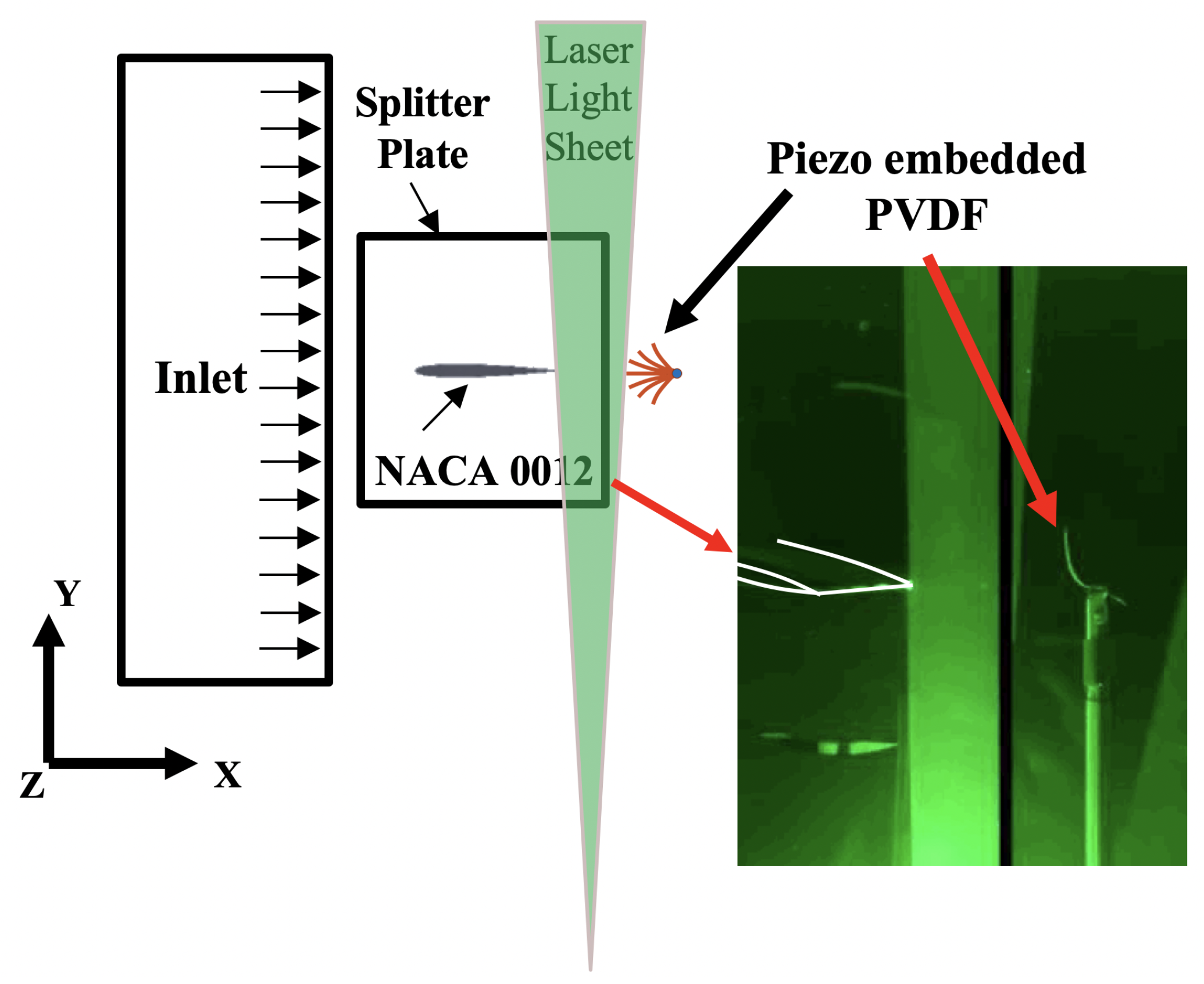
2.4. Test Setup
2.5. Particle Image Velocimetry (PIV) Setup
2.6. Tensile Testing
3. Results
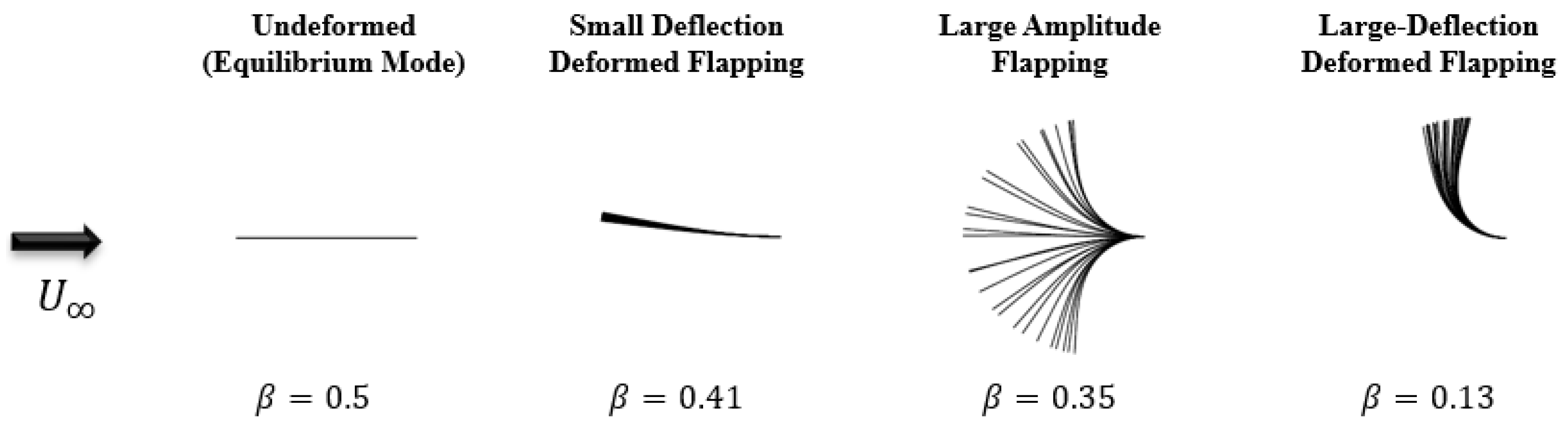
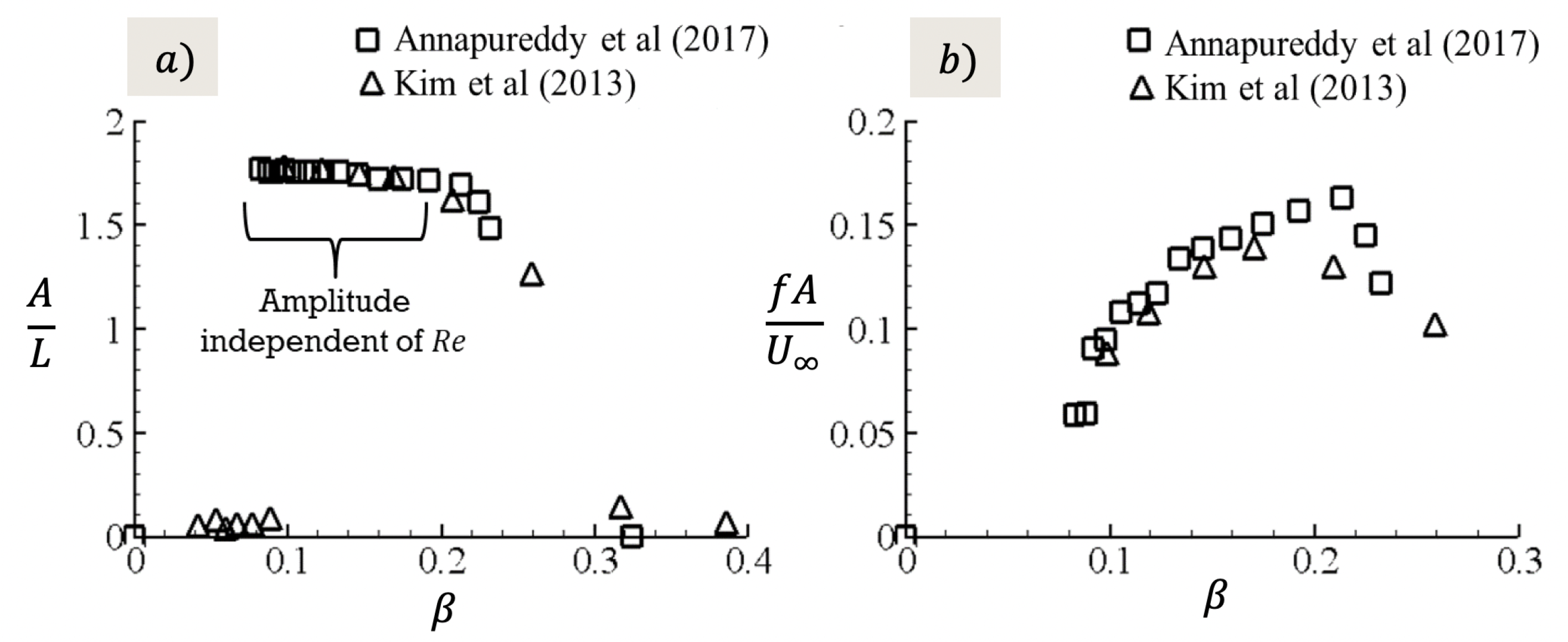
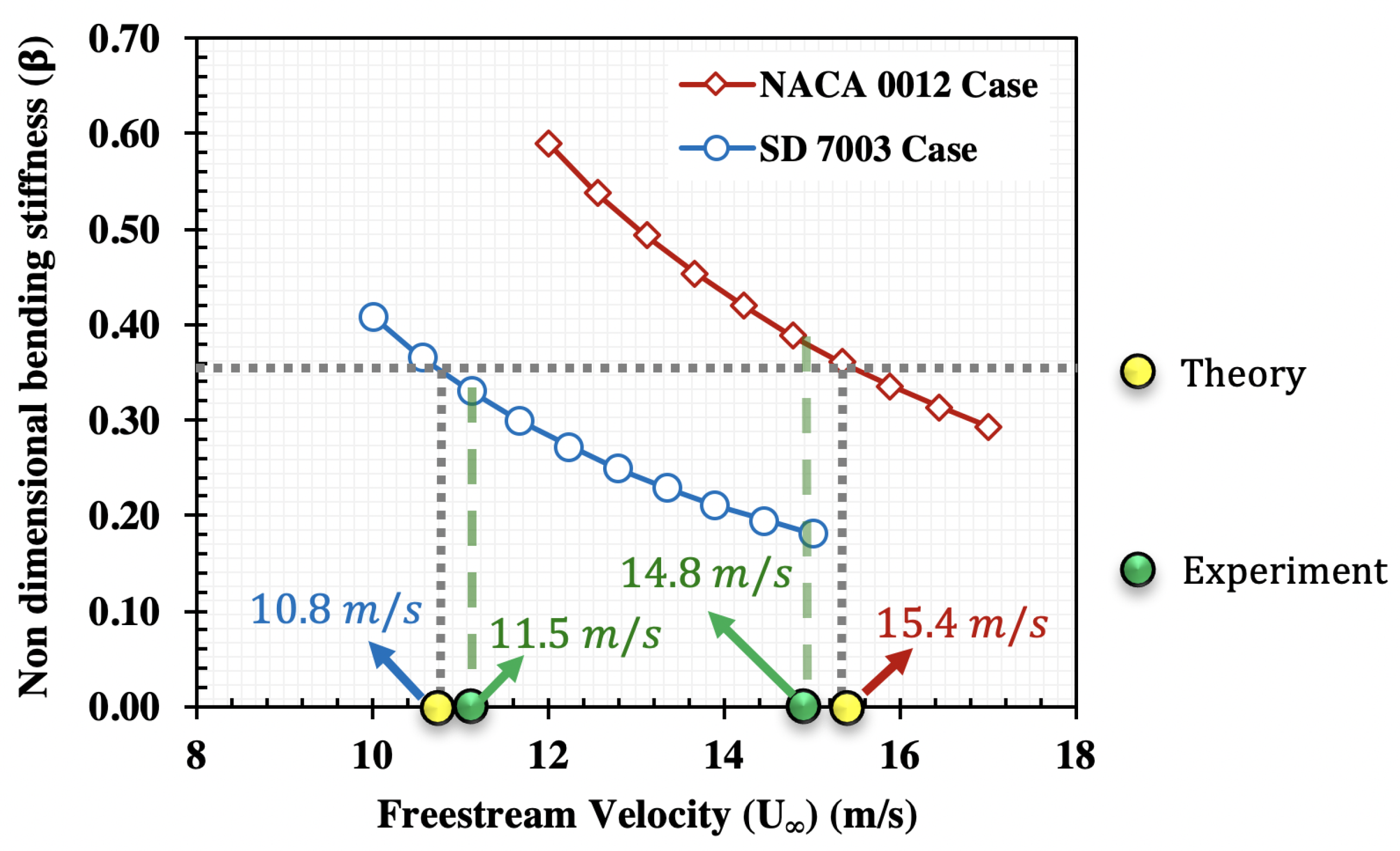
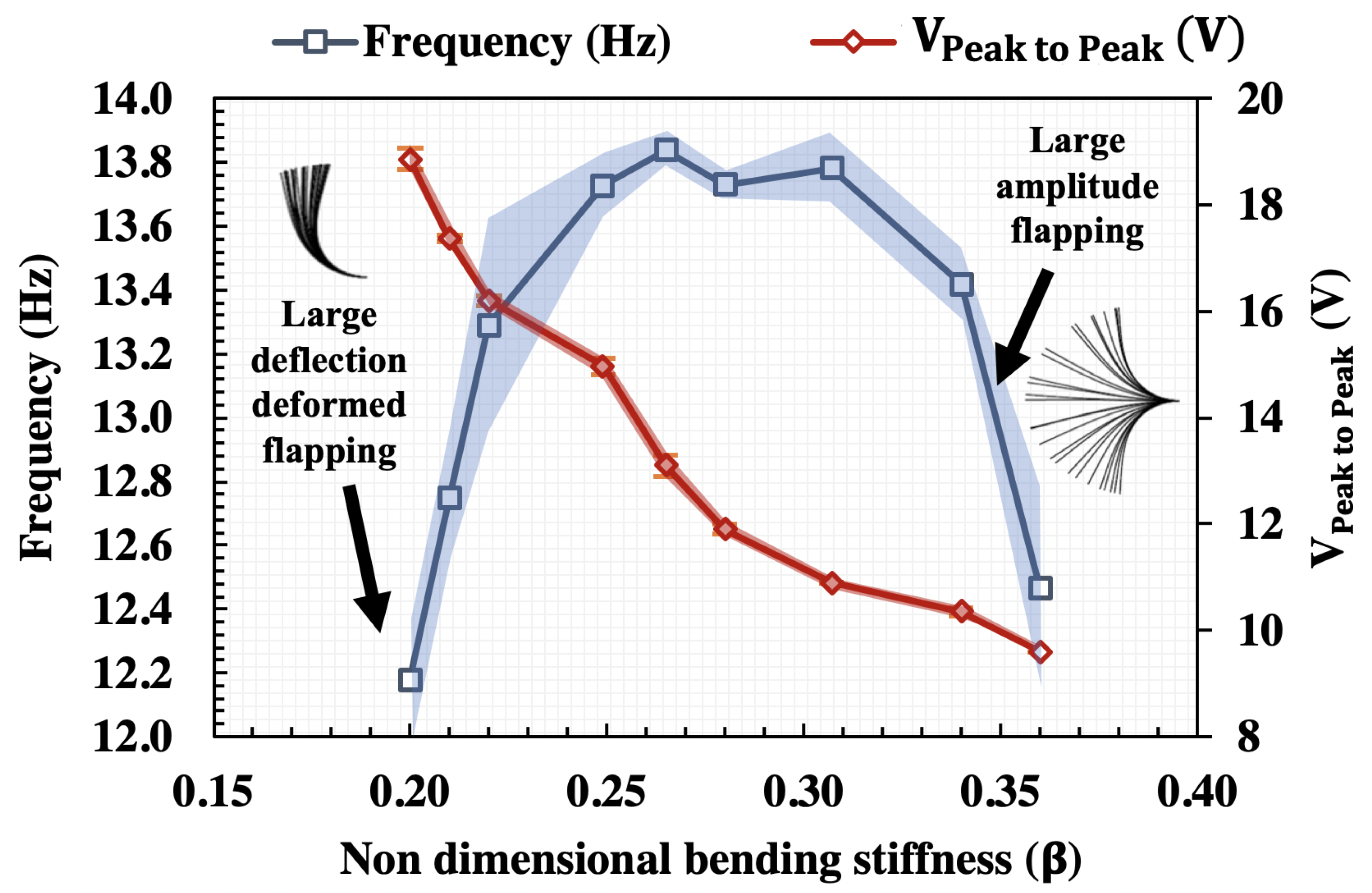
3.1. Non-Dimensional Bending Stiffness
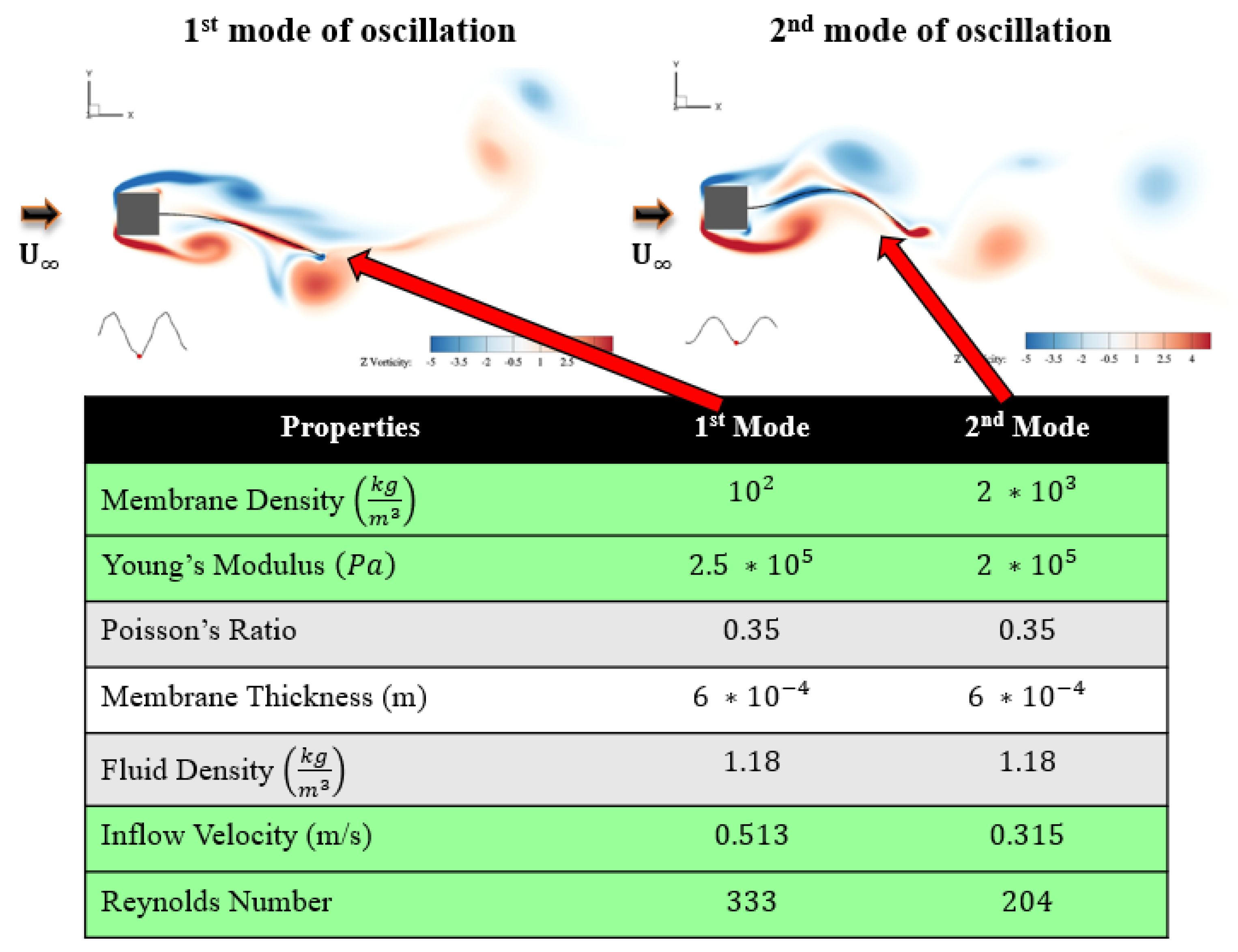
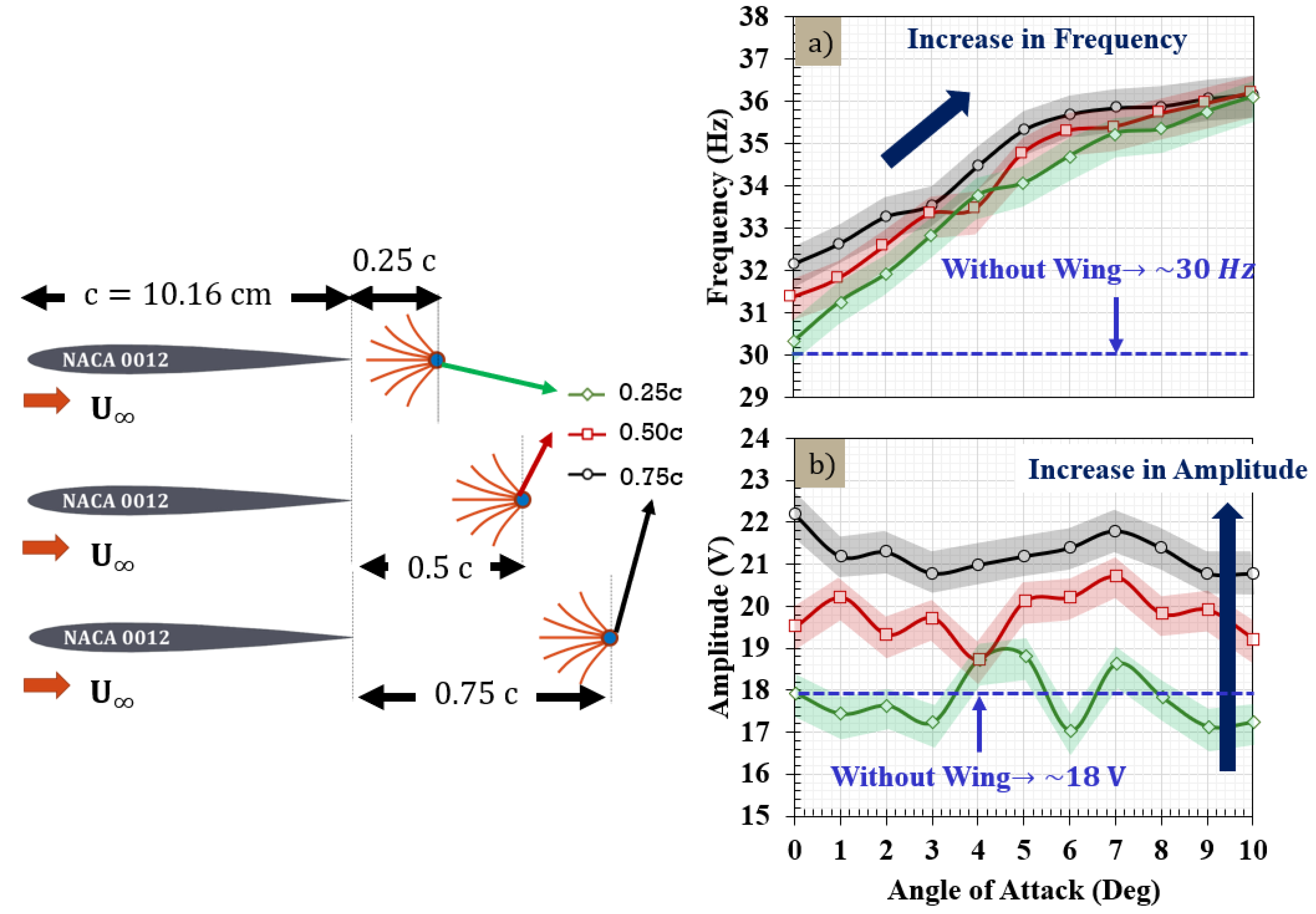
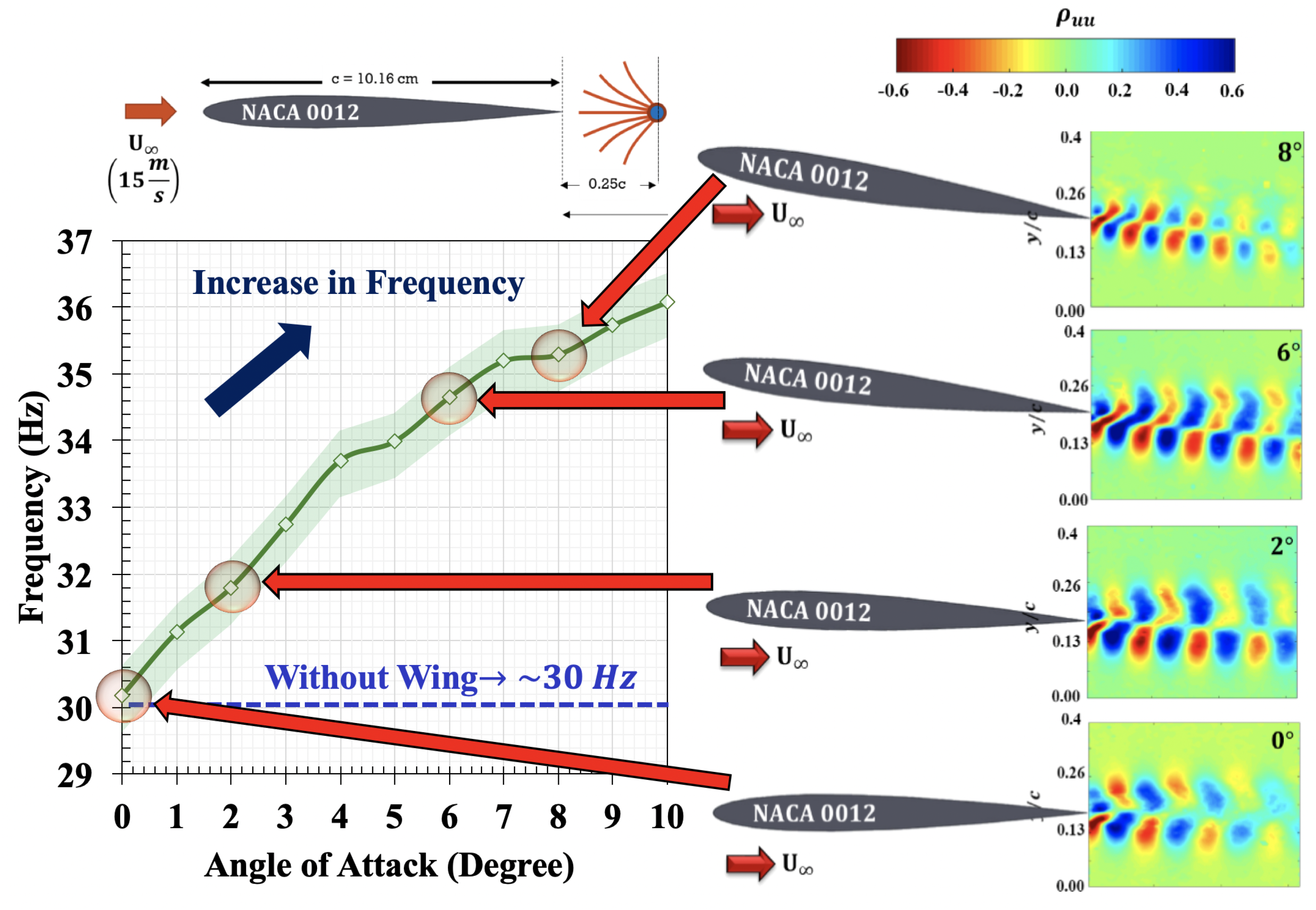
3.2. PVDF Oscillations in NACA 0012 Wake
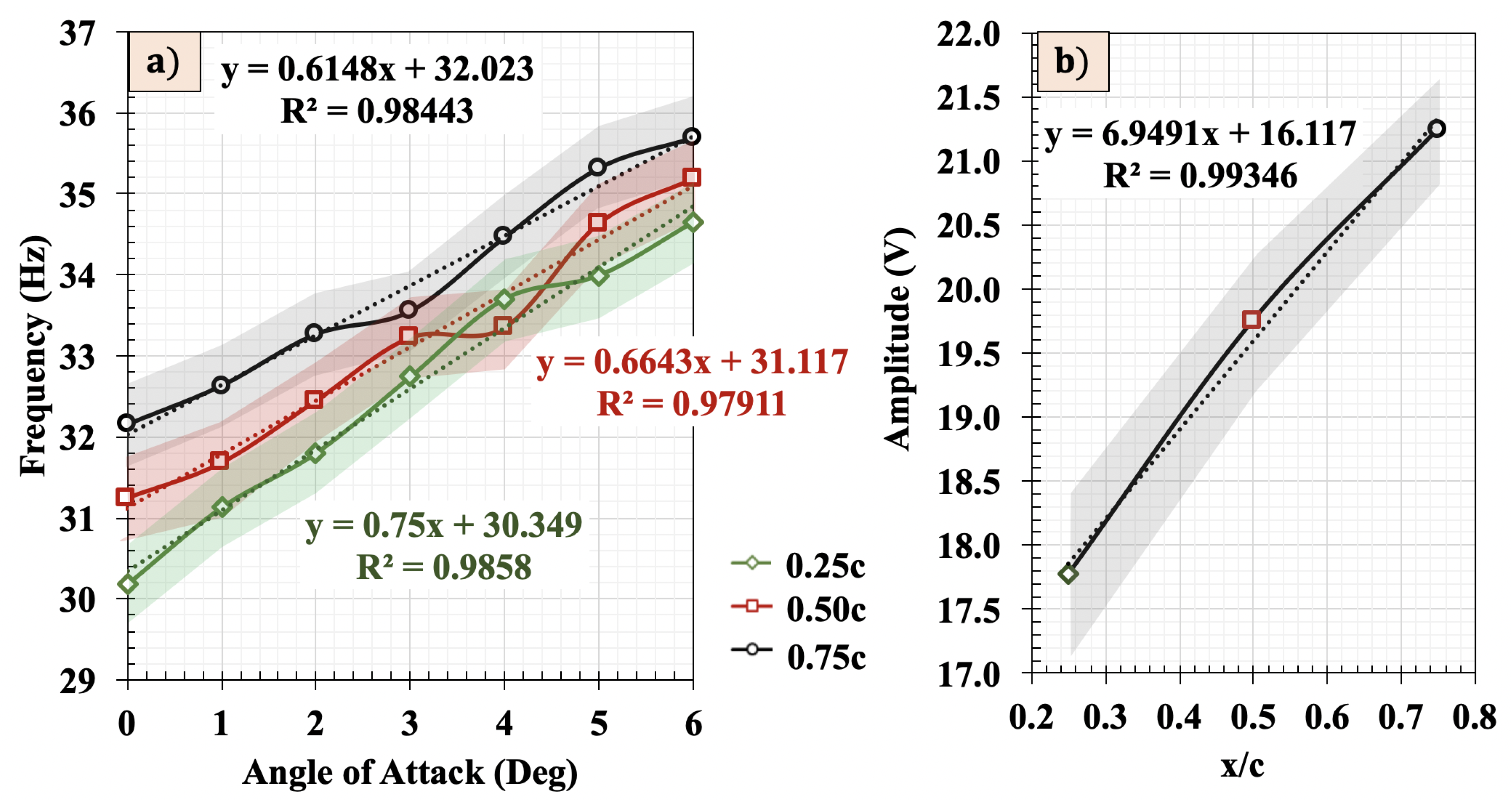
3.3. Relationship between Oscillation Frequency and Coherent Structures
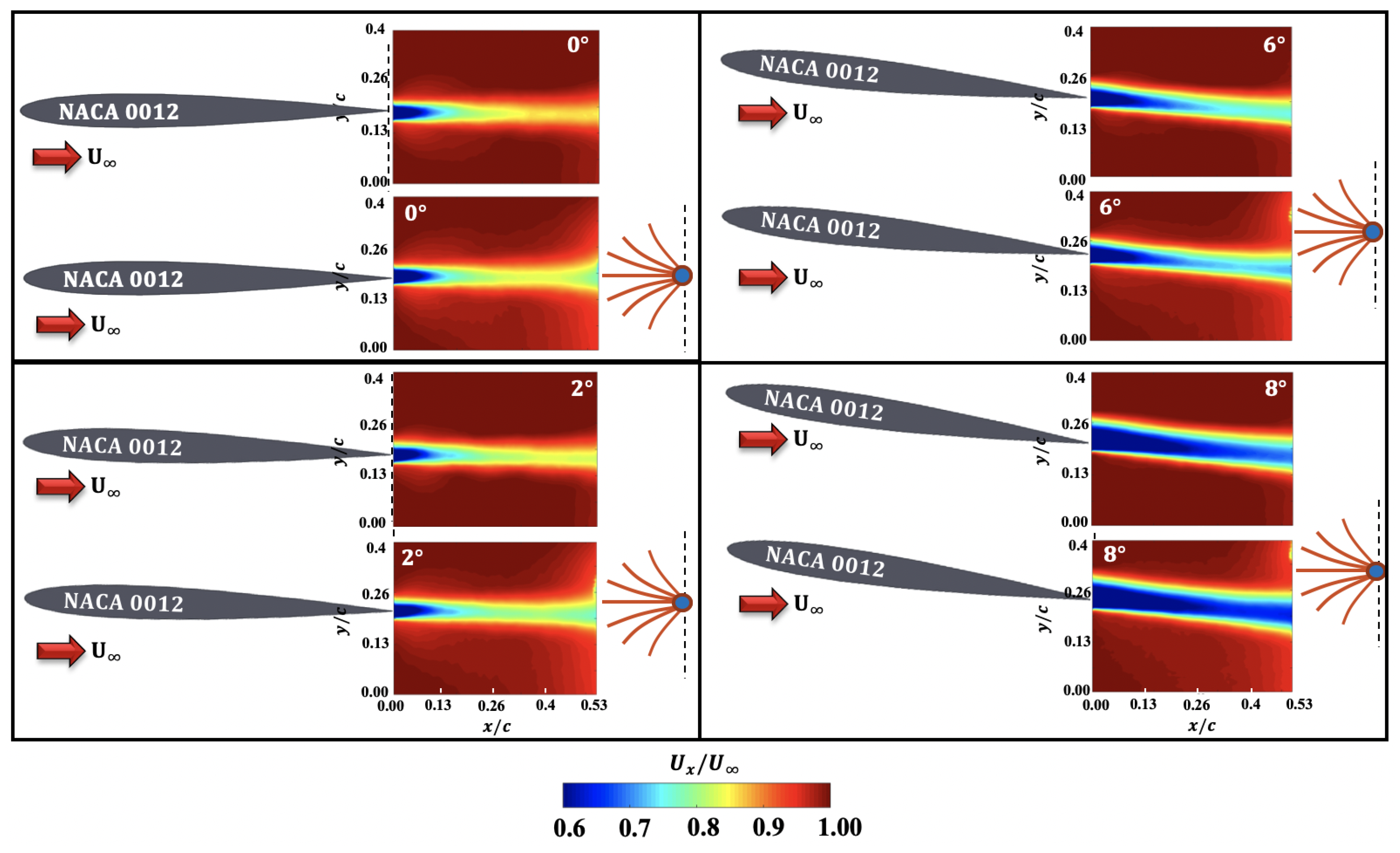
3.4. Influence of PVDF on the Wake Structure—PIV Results
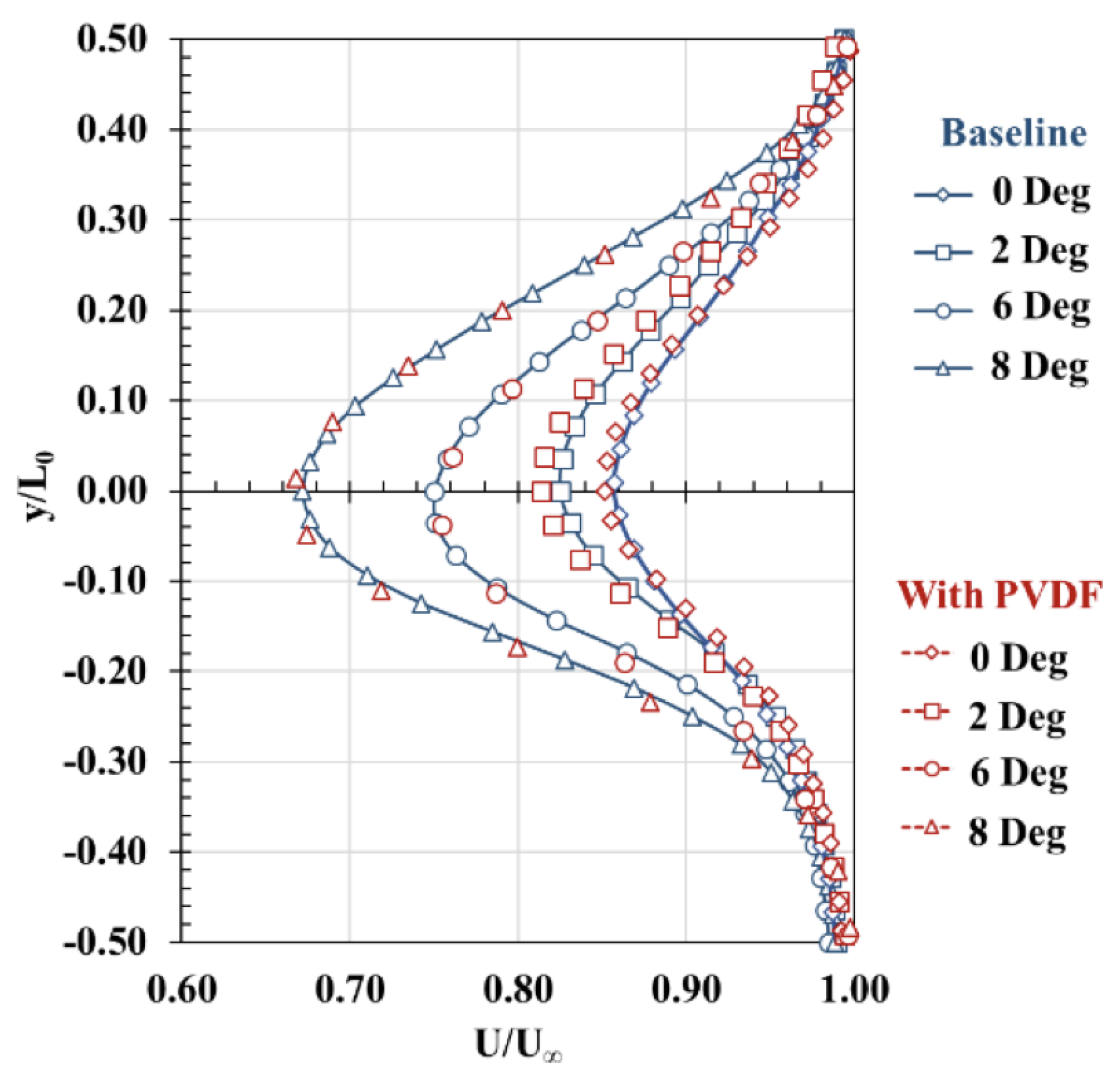
3.4.1. U-Velocity Contours
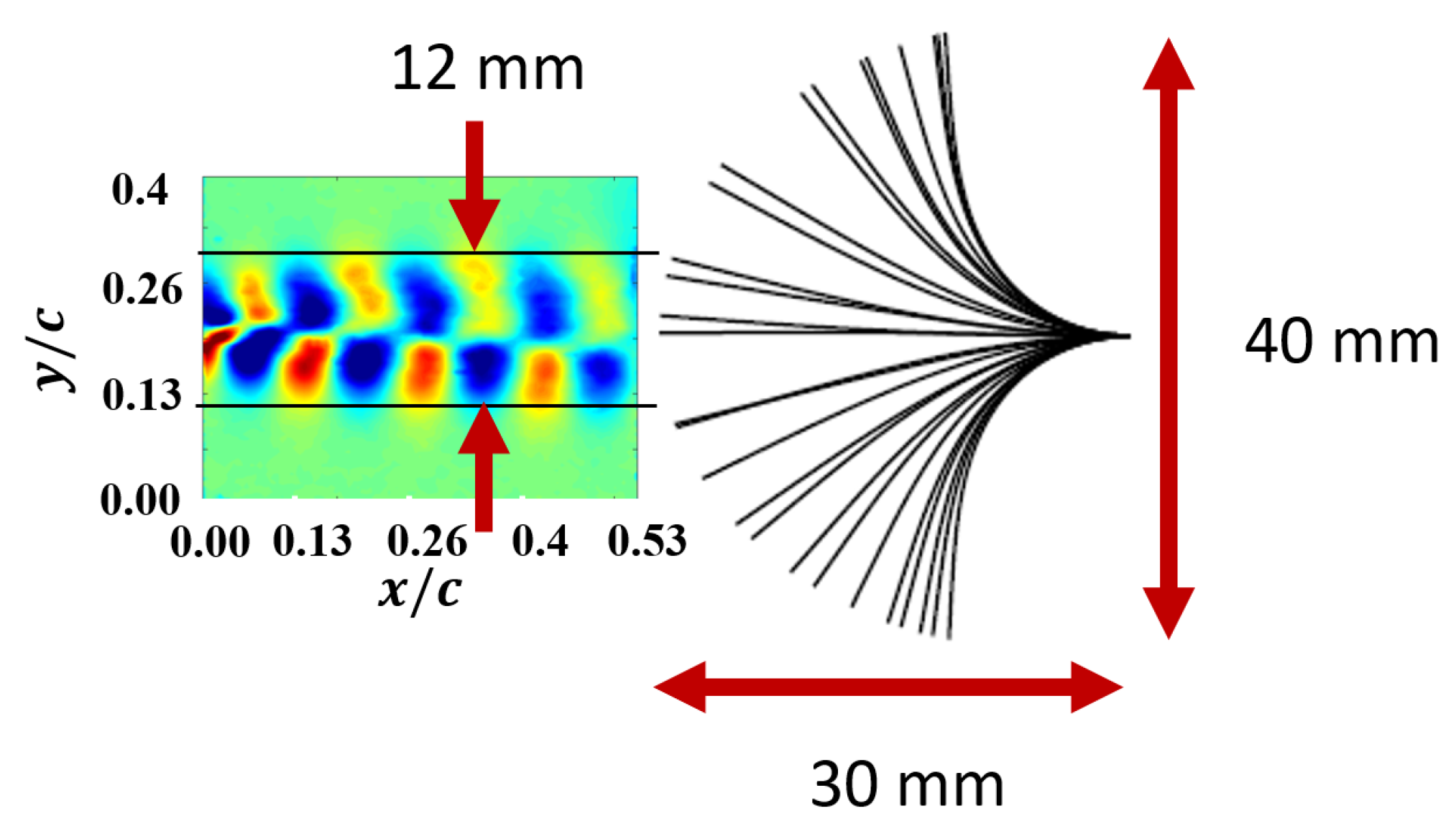
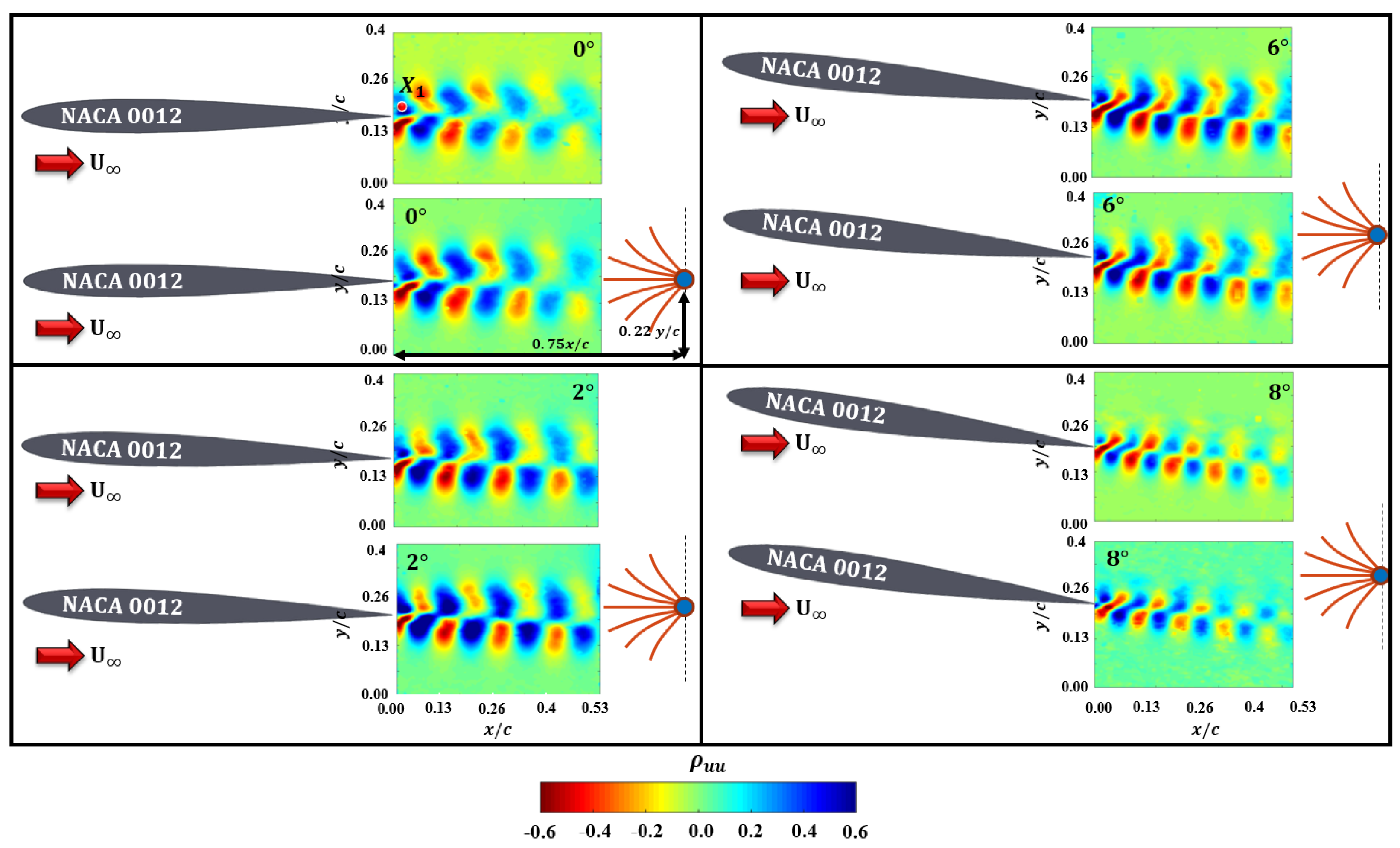
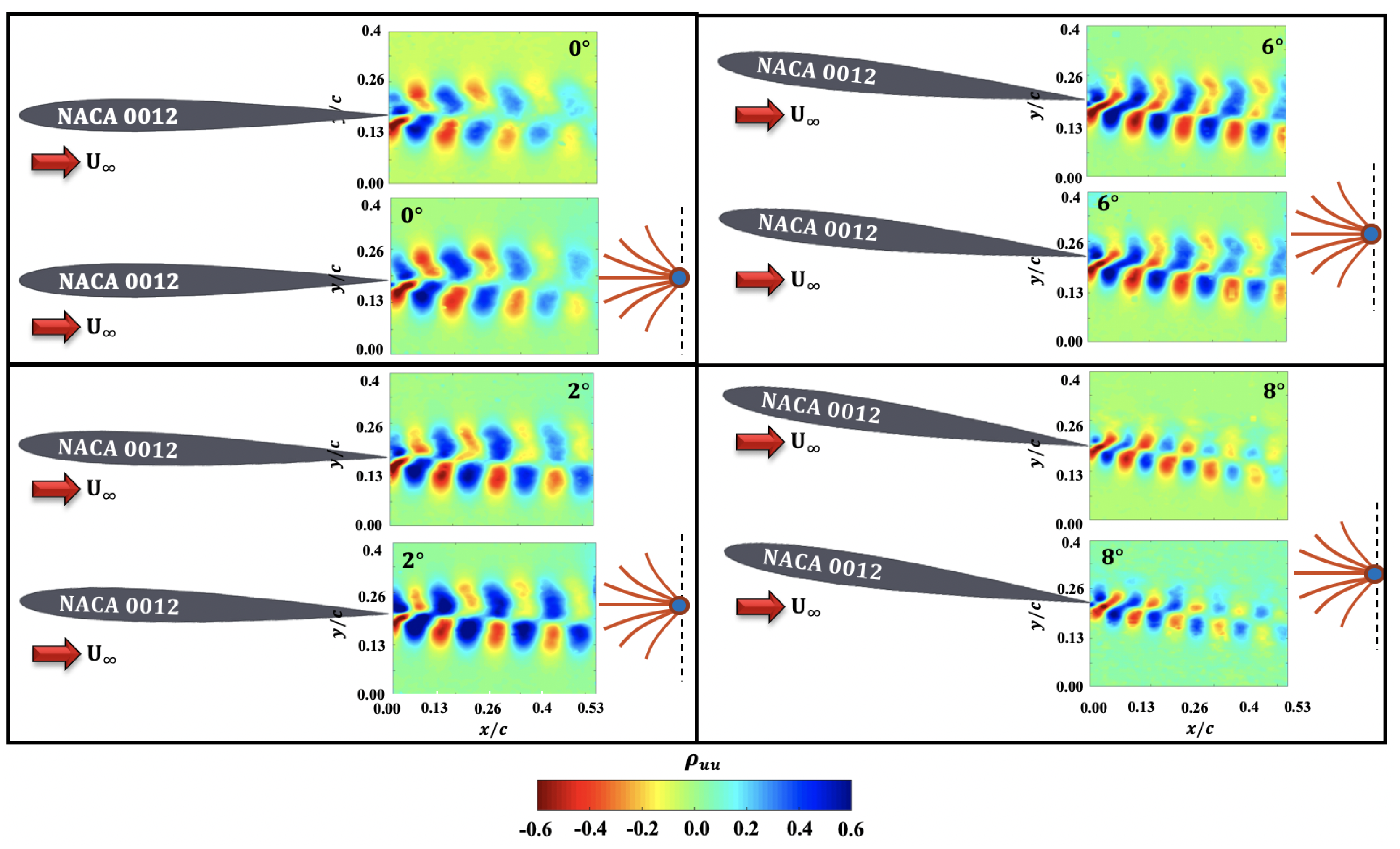
3.4.2. Two-Point Correlations
3.5. Performance of Piezo Embedded PVDF-Polymer Sensor in Freestream
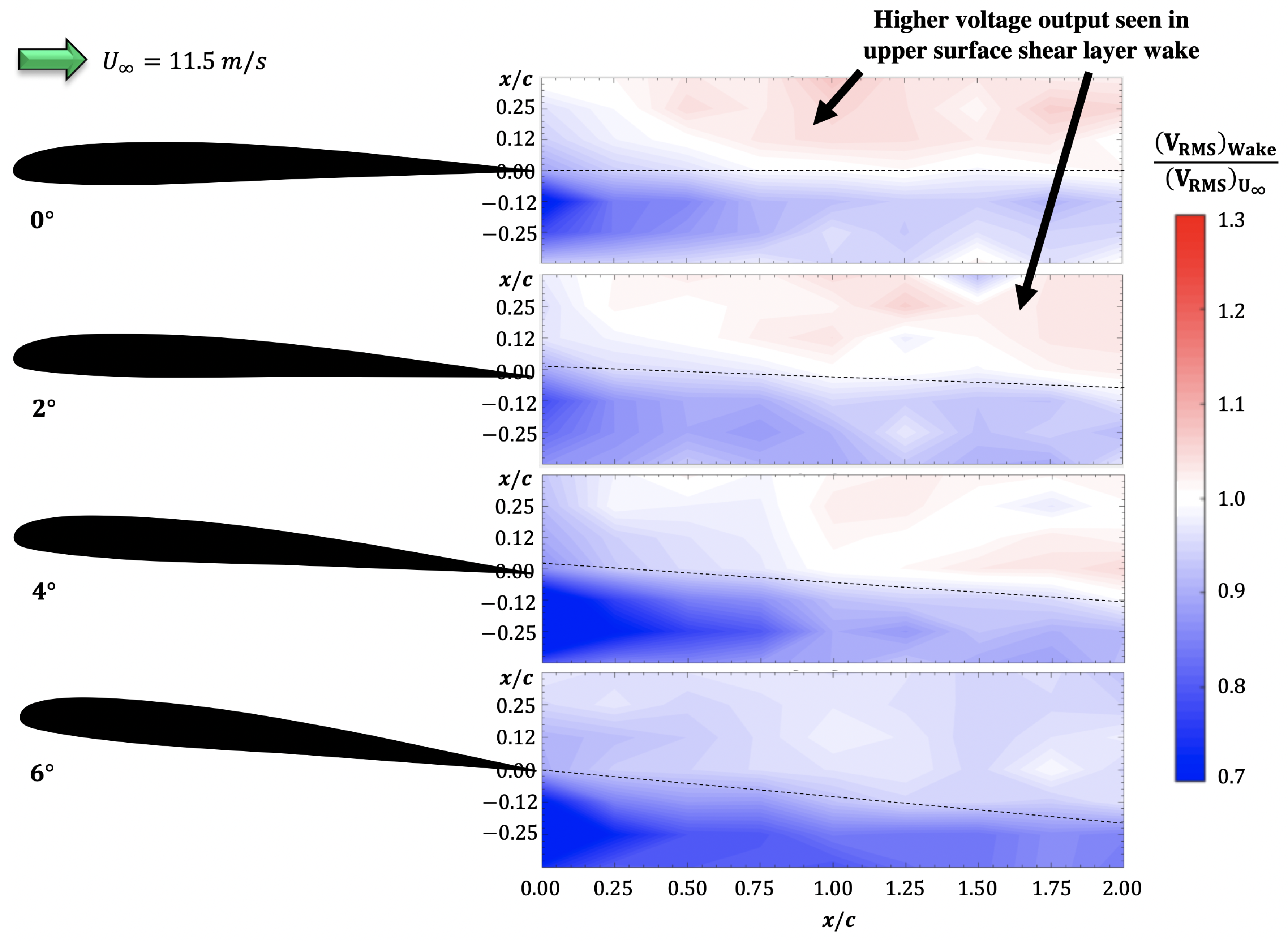
3.6. Voltage Root Mean Square () in the Wake of SD7003 Wake
4. Conclusions
- The inverted flag configuration is sensitive to unsteady flows. This dependency is shown by the increase in oscillation frequency and amplitude as a function of angle of attack and the downstream distance from the trailing edge of the airfoil. The oscillation frequency increased linearly with an increase in angle of attack similar to the linear trend of lift coefficient with angle of attack. The peak to peak voltage output was increased with an increase in downstream distances from the trailing edge of the wing.
- The increase in sensor frequency with angle of attack could be due to the increase in coherent structures in the wake of the wing confirmed by the two-point correlations of fluctuating and velocity components.
- Even with high unsteady wake, the presence of piezo embedded PVDF did not affect the upstream wake signature as evidenced by the momentum deficit contours and profiles as well as the two-point correlations of the fluctuating velocity components.
- Higher peak-to-peak voltage output was seen when the PVDF-polymer configuration experienced large deflection deformed flapping mode at non-dimensional bending stiffness value of 0.21.
- It is highly surprising that the voltage RMS contour in the wake of SD7003 airfoil shows distinct wake characteristics such as upper and lower surface shear layers and downwash angle. Higher voltage RMS values were observed in the upper surface shear layer wake when compared to the lower surface shear layer wake.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PVDF | Polyvinylidene Difluoride |
| RMS | Root Mean Square |
| c | Chord Length (m) |
| Coordinate System (m) | |
| Density (kg/m) | |
| Freestream Velocity (m/s) | |
| L | Membrane Length (m) |
| t | Membrane Thickness (m) |
| Non-dimensional Bending Stiffness | |
| A | Oscillation Amplitude (m) |
| f | Oscillation Frequency (Hz) |
| Poisson’s Ratio | |
| Streamwise Fluctuating Velocity (m/s) | |
| Streamwise Velocity (m/s) | |
| Transverse Velocity Fluctuating (m/s) | |
| V | Voltage (V) |
| Wake Half Width (m) | |
| E | Young’s Modulus (Pa) |
References
- Joshi, D. Exploring the latest drone technology for commercial, industrial and military drone uses. Tech Insider, 13 July 2017. [Google Scholar]
- Flyntl, J. How Long Can a Drone Fly? 3D Insider, 28 August 2017. [Google Scholar]
- Schmidt, D.K. Stability augmentation and active flutter suppression of a flexible flying-wing drone. J. Guid. Control Dyn. 2016, 39, 409–422. [Google Scholar] [CrossRef]
- Yarusevych, S.; Sullivan, P.E.; Kawall, J.G. On vortex shedding from an airfoil in low-Reynolds-number flows. J. Fluid Mech. 2009, 632, 245–271. [Google Scholar] [CrossRef]
- Huang, R.F.; Lin, C.L. Vortex shedding and shear-layer instability of wing at low-Reynolds numbers. AIAA J. 1995, 33, 1398–1403. [Google Scholar] [CrossRef]
- Huang, R.F.; Lee, H.W. Turbulence effect on frequency characteristics of unsteady motions in wake of wing. AIAA J. 2000, 38, 87–94. [Google Scholar] [CrossRef]
- Guan, Y.; Pröbsting, S.; Stephens, D.; Gupta, A.; Morris, S.C. On the wake flow of asymmetrically beveled trailing edges. Exp. Fluids 2016, 57, 78. [Google Scholar] [CrossRef]
- Allen, J.; Smits, A. Energy harvesting eel. J. Fluids Struct. 2001, 15, 629–640. [Google Scholar] [CrossRef]
- Gilmanov, A.; Le, T.B.; Sotiropoulos, F. A numerical approach for simulating fluid structure interaction of flexible thin shells undergoing arbitrarily large deformations in complex domains. J. Comput. Phys. 2015, 300, 814–843. [Google Scholar] [CrossRef]
- Liou, W.; Pantula, S.; Liu, T.; Montefort, J.; Ludens, D. Flow past a cylinder with a flapping element attached to its end. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007; p. 1309. [Google Scholar]
- Stanewsky, E. Adaptive wing and flow control technology. Prog. Aerosp. Sci. 2001, 37, 583–667. [Google Scholar] [CrossRef]
- Neuhart, D.H.; Pendergraft, O.C., Jr. A Water Tunnel Study of Gurney Flaps; NASA Technical Report NASA-TM-4071; NASA: Washington, DC, USA, 1988.
- Jang, C.S.; Ross, J.C.; Cummings, R.M. Numerical investigation of an airfoil with a Gurney flap. Aircr. Des. 1998, 1, 75. [Google Scholar] [CrossRef]
- Storms, B.L.; Jang, C.S. Lift enhancement of an airfoil using a Gurney flap and vortex generators. J. Aircr. 1994, 31, 542–547. [Google Scholar] [CrossRef]
- Traub, L.W. Examination of Gurney Flap Pressure and Shedding Characteristics. J. Aircr. 2017, 54, 1990–1995. [Google Scholar] [CrossRef]
- Lee, H.T.; Kroo, I.; Bieniawski, S. Flutter suppression for high aspect ratio flexible wings using microflaps. In Proceedings of the 43rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Denver, CO, USA, 22–25 April 2002; p. 1717. [Google Scholar]
- Goza, A.; Colonius, T. A strongly-coupled immersed-boundary formulation for thin elastic structures. J. Comput. Phys. 2017, 336, 401–411. [Google Scholar] [CrossRef]
- Kim, D.; Cossé, J.; Cerdeira, C.H.; Gharib, M. Flapping dynamics of an inverted flag. J. Fluid Mech. 2013, 736. [Google Scholar] [CrossRef]
- Akcabay, D.T.; Young, Y.L. Hydroelastic response and energy harvesting potential of flexible piezoelectric beams in viscous flow. Phys. Fluids 2012, 24, 054106. [Google Scholar] [CrossRef]
- Gurugubelli, P.; Jaiman, R. Self-induced flapping dynamics of a flexible inverted foil in a uniform flow. J. Fluid Mech. 2015, 781, 657–694. [Google Scholar] [CrossRef]
- Annapureddy, S.; Acharya, S.; Gilmanov, A.; Stolarski, H. Experimental and Numerical Investigation of the Oscillation of an Inverted Flag; Tsfp Digital Library Online; Begel House Inc.: Danbury, CT, USA, 2017. [Google Scholar]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gunasekaran, S.; Ross, G. Effect of Piezo-Embedded Inverted Flag in Free Shear Layer Wake. Aerospace 2019, 6, 33. https://doi.org/10.3390/aerospace6030033
Gunasekaran S, Ross G. Effect of Piezo-Embedded Inverted Flag in Free Shear Layer Wake. Aerospace. 2019; 6(3):33. https://doi.org/10.3390/aerospace6030033
Chicago/Turabian StyleGunasekaran, Sidaard, and Grant Ross. 2019. "Effect of Piezo-Embedded Inverted Flag in Free Shear Layer Wake" Aerospace 6, no. 3: 33. https://doi.org/10.3390/aerospace6030033
APA StyleGunasekaran, S., & Ross, G. (2019). Effect of Piezo-Embedded Inverted Flag in Free Shear Layer Wake. Aerospace, 6(3), 33. https://doi.org/10.3390/aerospace6030033



