Comparative Study of Aircraft Boarding Strategies Using Cellular Discrete Event Simulation
Abstract
1. Introduction
2. Background
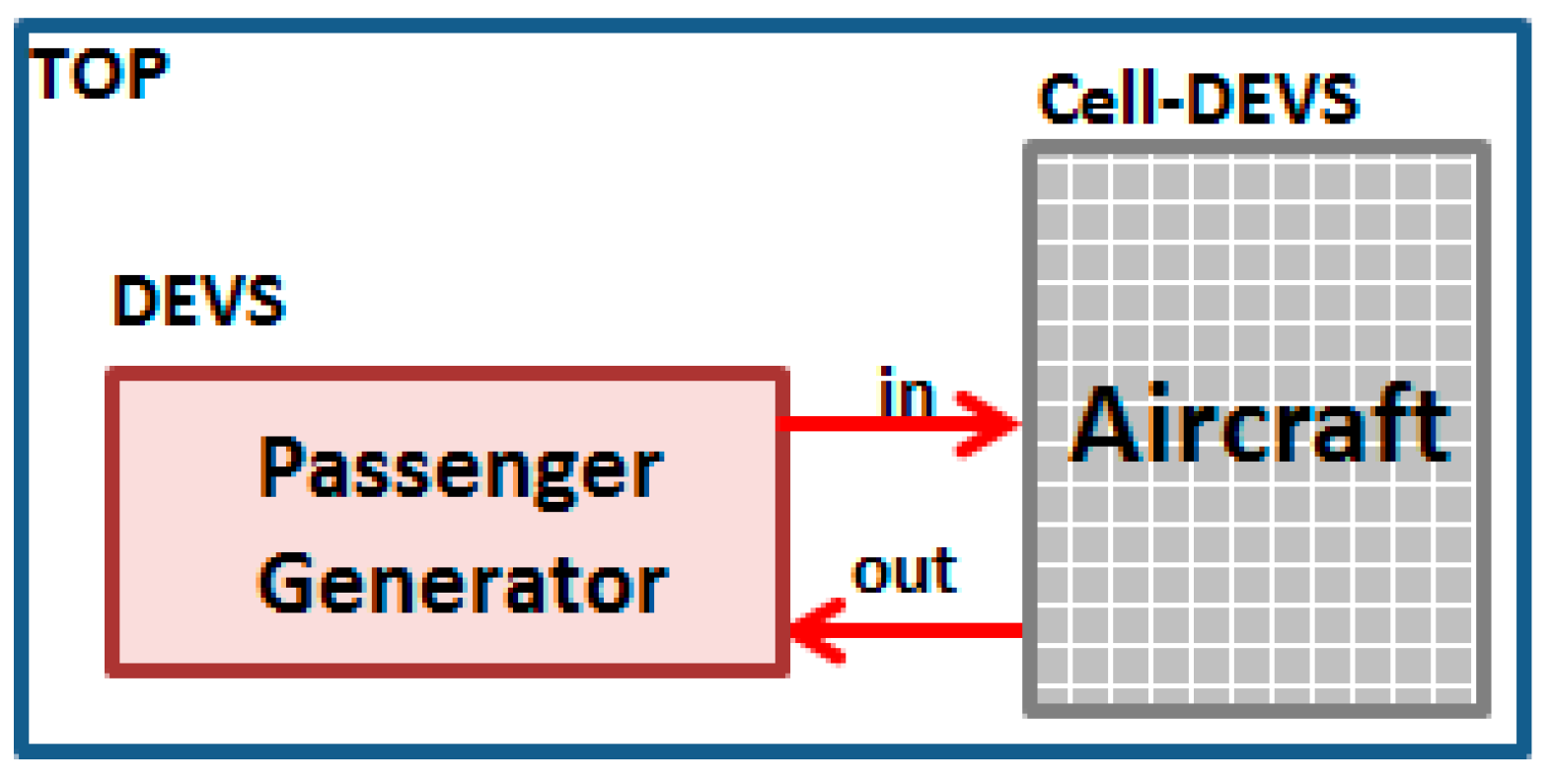
Cellular Discrete Event Approach
3. Modeling Assumptions
- Walking Speed: the speed range at which passenger walks from the moment he/she enters the aircraft till reaching the target seat (unit: meter per second).
- Clearing Time: the time range passengers spend on storing their luggage in the overhead compartment or underneath the seat in the front (unit: seconds).
- Getting out of Seat: the time range a passenger takes to get up from their seat, allowing other passengers to sit within that row (unit: seconds).
- Passenger Flow Rate: the range number of passengers that enter the aircraft at a certain amount of time (unit: passenger per second).
- Walking Delay: the average time it takes a passenger to pass a row (unit: milliseconds).
- Luggage Delay: the average time spent by individual passengers to store their luggage in the overhead compartment (unit: milliseconds).
- Middle Seat Delay: the delay time a window passenger should wait at the row until middle/aisle passengers who are already seated within that row get up (unit milliseconds).
- Aisle Seat Delay: the delay time a window or middle passenger should wait at the row until aisle passenger who is already seated within that row gets up (unit milliseconds).
4. System Design
- type: cell
- width: 10
- height: 43
- neighbors: aircraft(−1,−1) aircraft(−1,0) aircraft(−1,1) aircraft(0,−4)
- neighbors: aircraft(0,−3) aircraft(0,−2) aircraft(0,−1) aircraft(0,0)
- neighbors: aircraft(0,1) aircraft(0,2) aircraft(0,3)
- neighbors: aircraft(1,−1) aircraft(1,0) aircraft(1,1)
5. Implementation Details
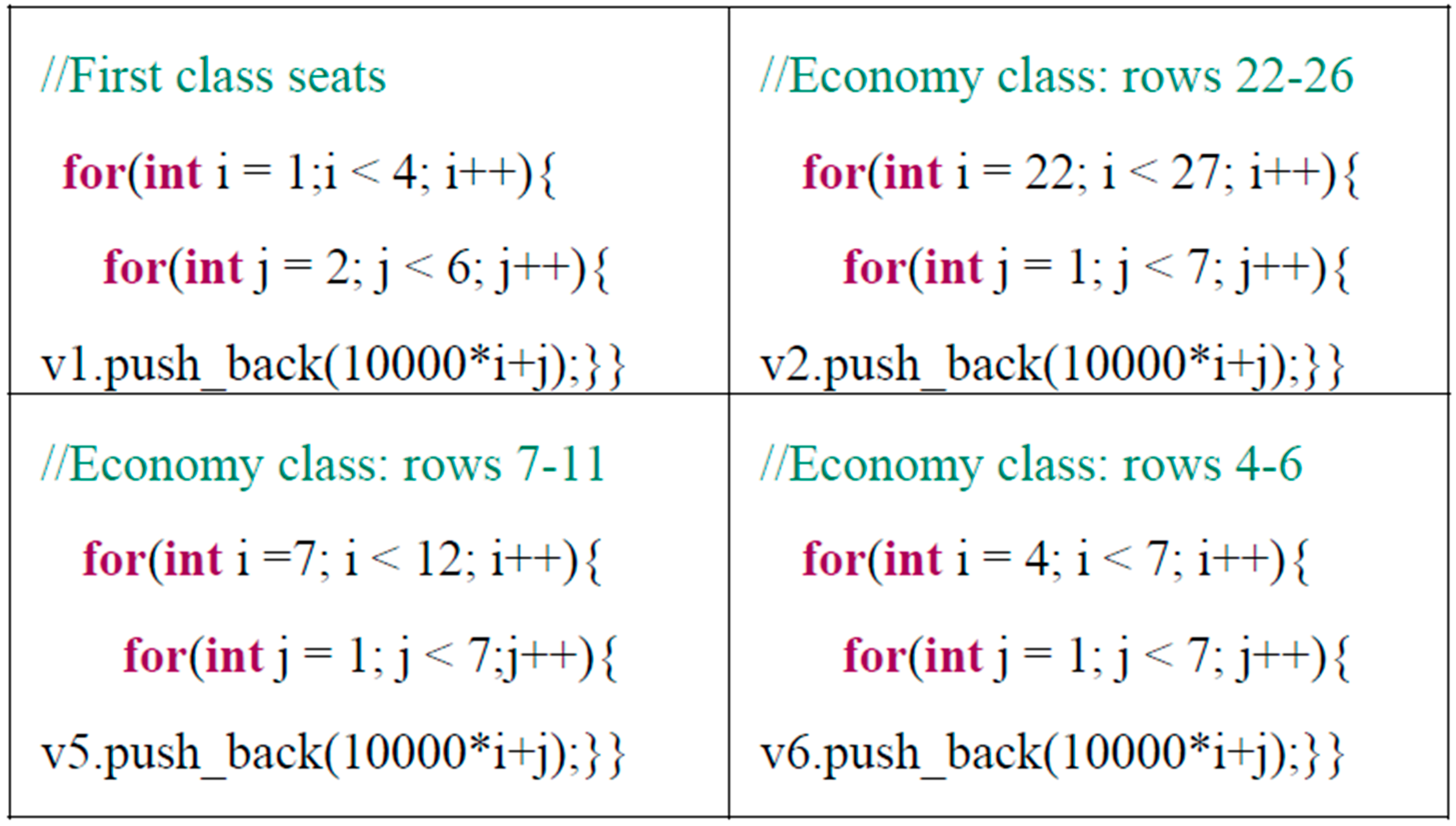
5.1. Seat Generation in Back-to-Front Strategy
5.2. Seat Generation in Random Strategy
5.3. Seat Generation in Window Middle Aisle (WMA) Strategy
5.4. Seat Generation in Zone Rotate Strategy
5.5. Seat Generation in Reverse Pyramid (RP) Strategy
5.6. Seat Generation in Optimal Strategy
5.7. Seat Generation in Optimal Practical Strategy
5.8. Seat Generation in Efficient Strategy
5.9. Aircraft Rules Specification and Implementation
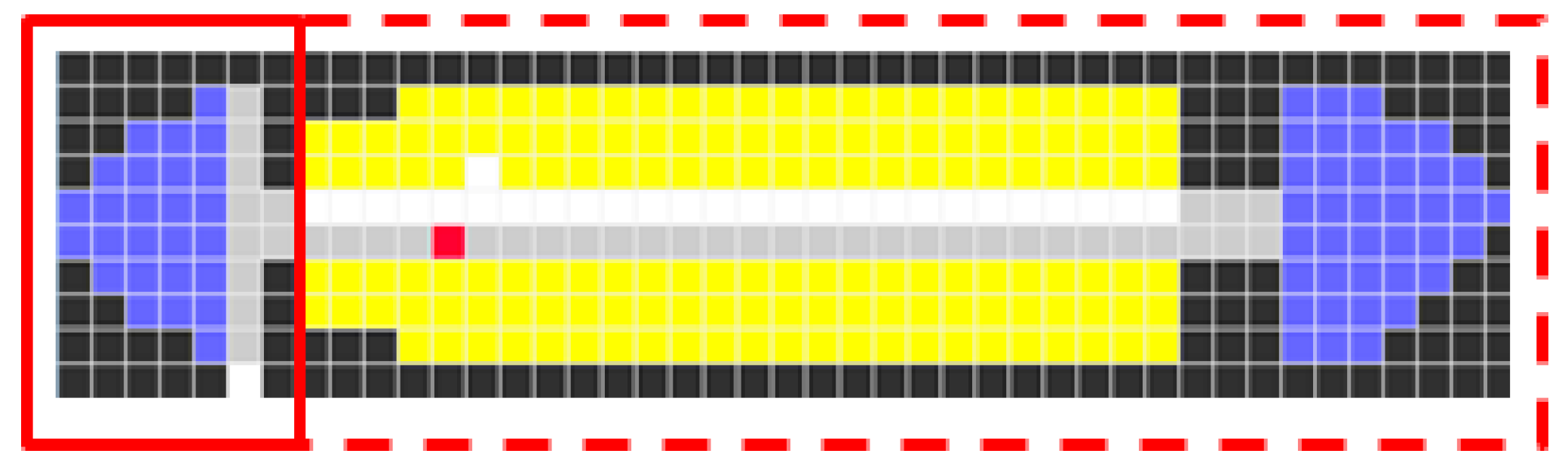
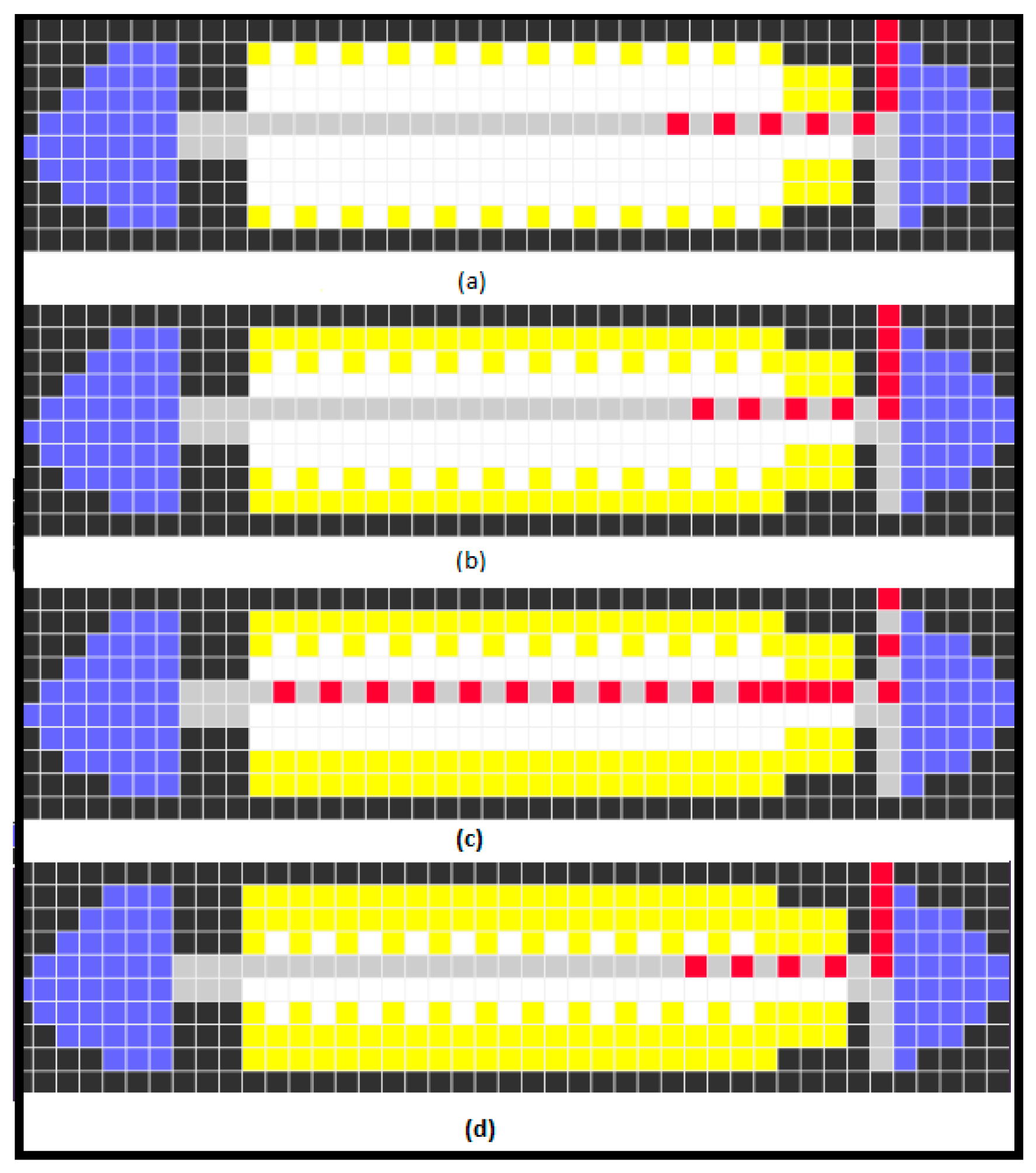
- pre-seat rules: a set of nine rules with responsibilities to send requests to the Passenger Generator model to release passengers and guide passengers at the aircraft door to walk to the beginning of the seats aisle. The area that pre-seat rules apply to is from cell (0, 0) to cell (6, 0) where cell (y, x) defines the y and x coordinates of the cell on the grid. The affected area by pre-seat rules is highlighted in a surrounding solid box in Figure 17.
- seating rules: a set of 33 rules handling passengers’ forward movement within the aisle and occupation of seats. These rules only apply to the cells that represent the seats (both first-class and economy) and the aisle, as well as passengers on these cells. This area is highlighted in Figure 17 with a surrounding dashed box.
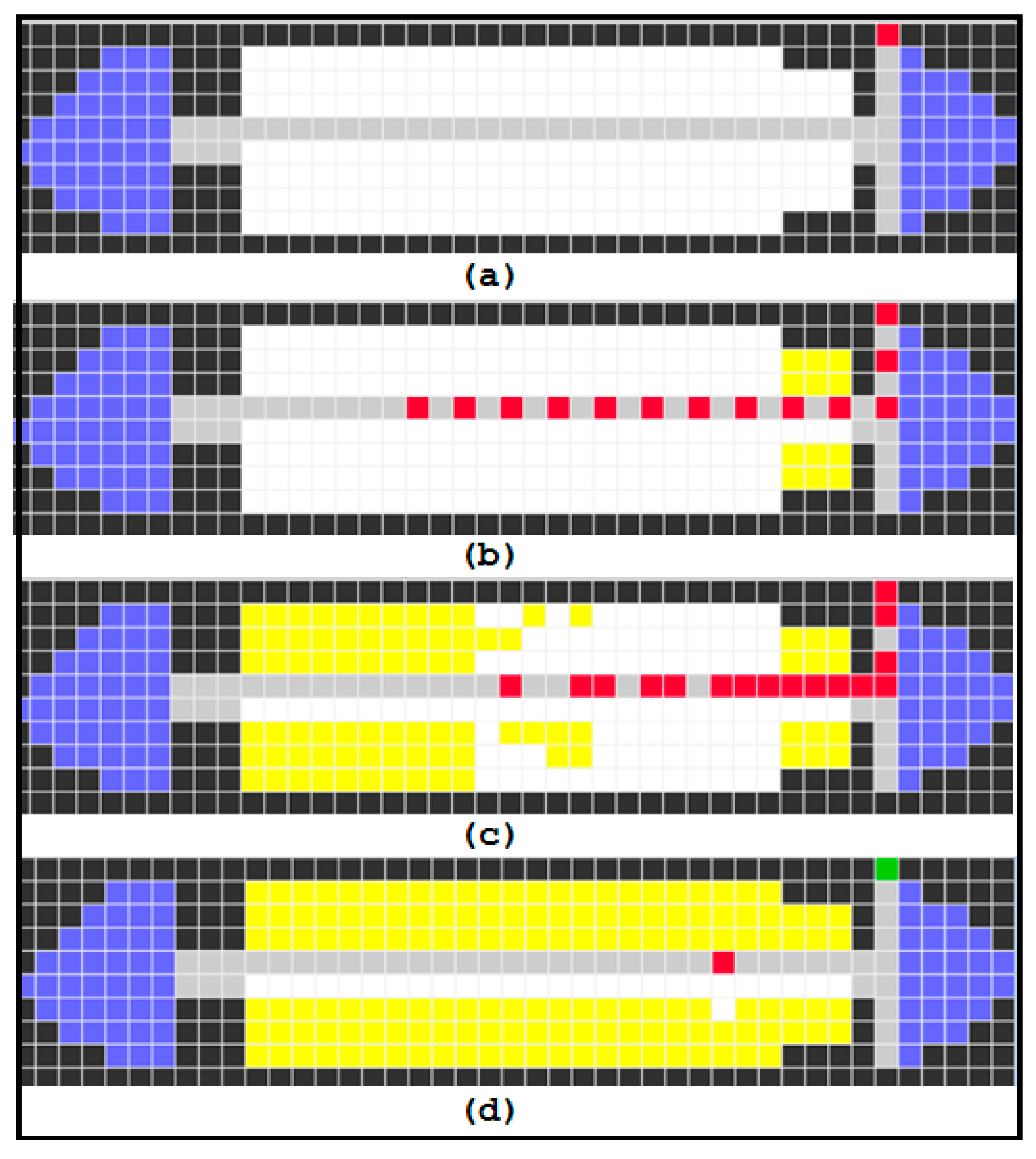
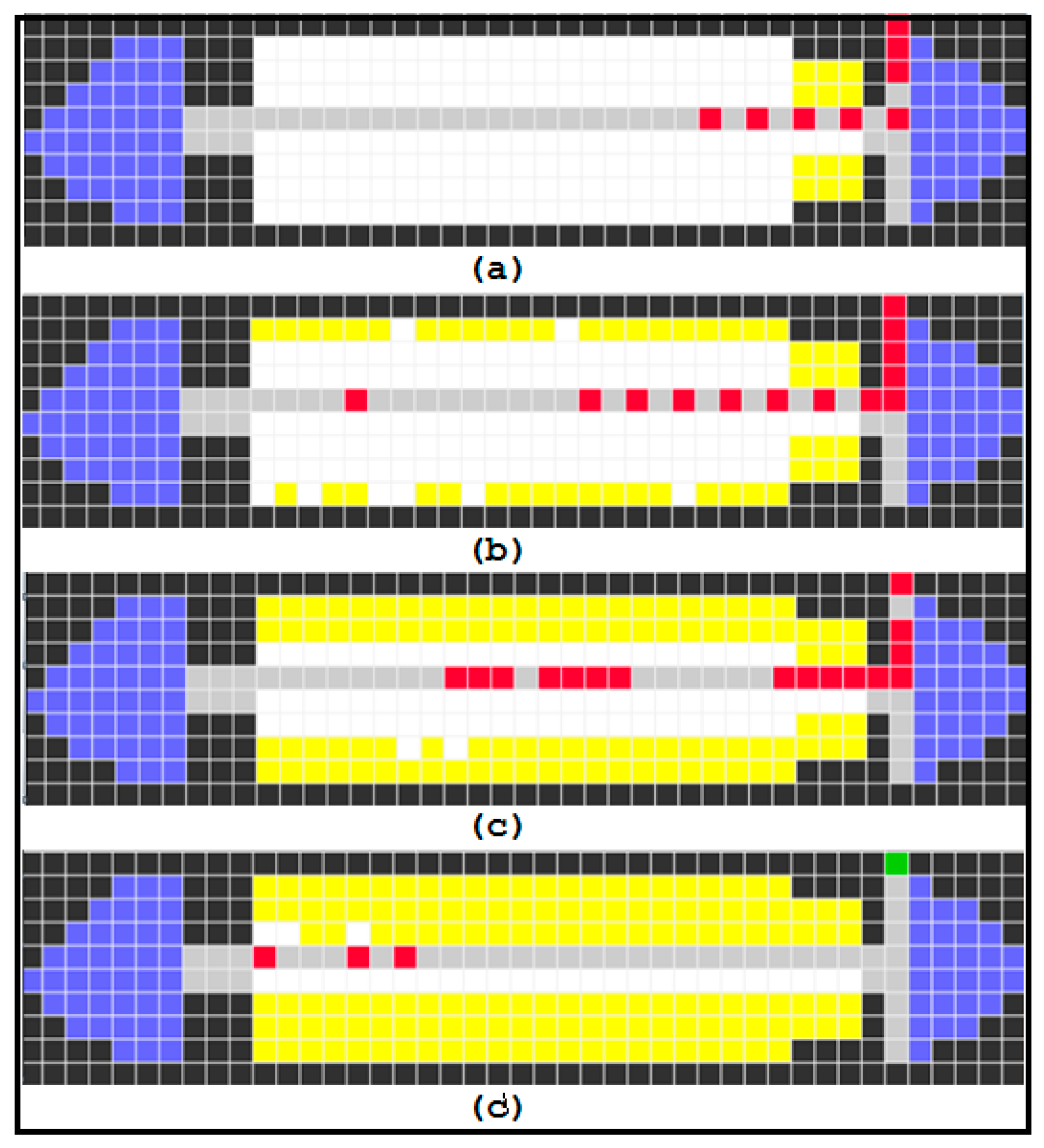
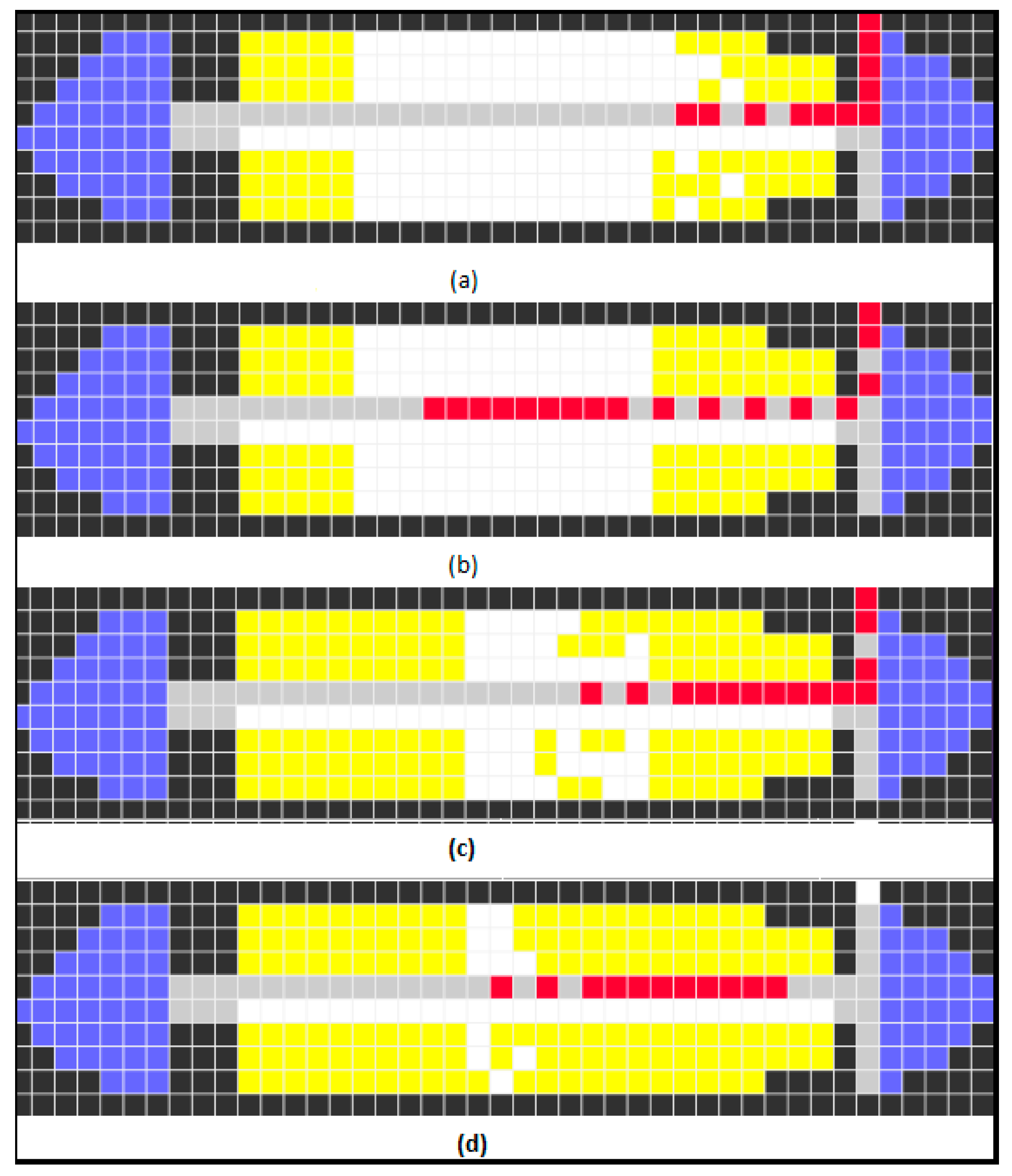
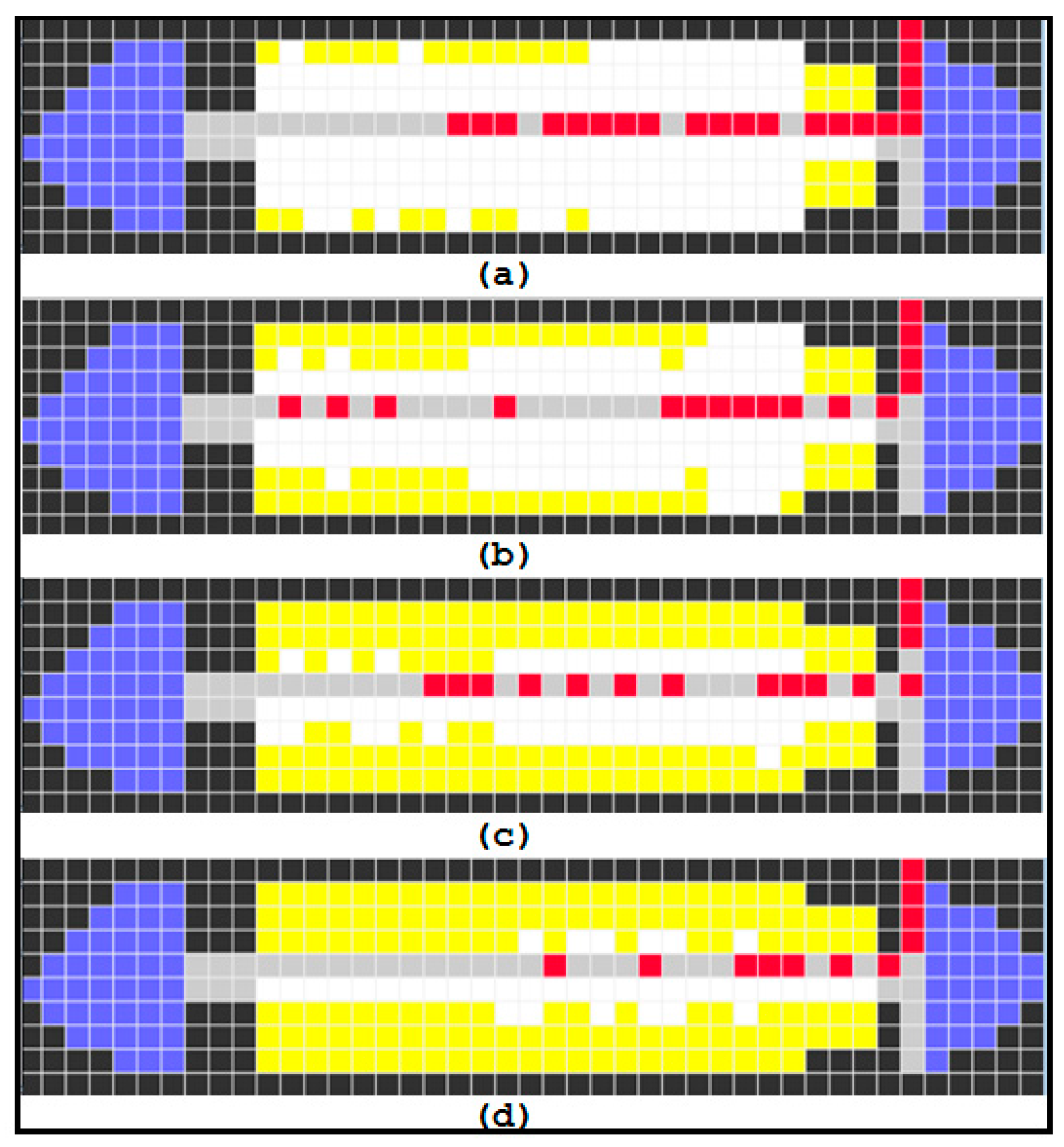
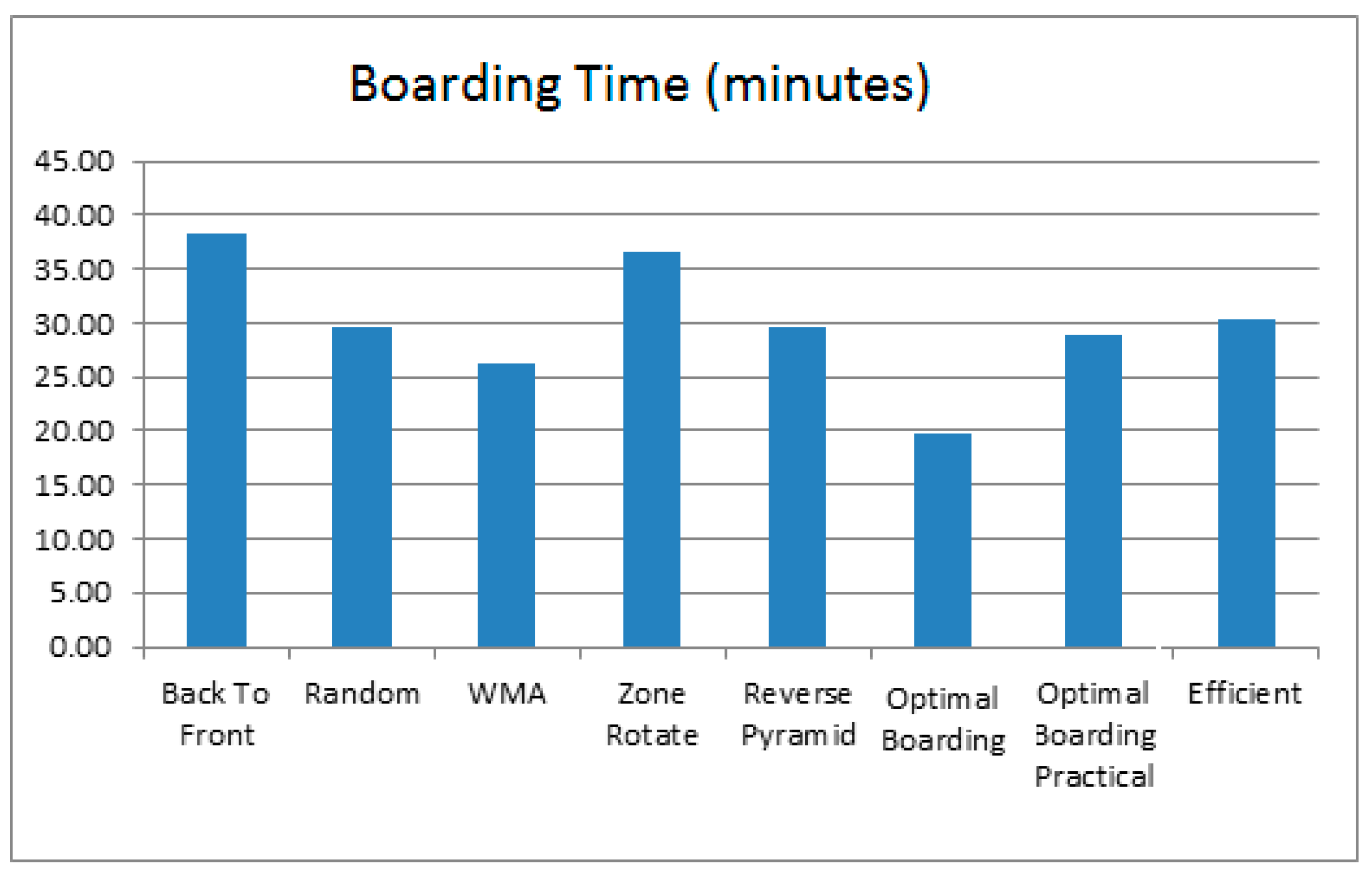
6. Simulation Results
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Van den Briel, M.; Villalobos, J.; Hogg, G. The aircraft boarding problem. In Proceedings of the 12th Industrial Engineering Research Conference (IERC), Portland, OR, USA, 18–20 May 2003. [CD ROM]; Paper No. 2153. [Google Scholar]
- Van Den Briel, M.H.L.; Villalobos, J.R.; Hogg, G.L.; Lindemann, T.; Mulé, A.V. America west airlines develops efficient boarding strategies. Interfaces 2005, 35, 191–201. [Google Scholar] [CrossRef]
- Ferrari, P.; Nagel, K. Robustness of efficient passenger boarding strategies for airplanes. Transp. Res. Rec. J. Transp. Res. Board 2005, 1915, 44–54. [Google Scholar] [CrossRef][Green Version]
- Nyquist, D.C.; McFadden, K.L. A study of the airline boarding problem. J. Air Transp. Manag. 2008, 14, 197–204. [Google Scholar] [CrossRef]
- Van Landeghem, H.; Beuselinck, A. Reducing passenger boarding time in airplanes: A simulation based approach. Eur. J. Oper. Res. 2002, 142, 294–308. [Google Scholar] [CrossRef]
- Marelli, S.; Mattocks, G.; Merry, R. The role of computer simulation in reducing airplane turn time. Aero Mag. 1998, 1, 10. [Google Scholar]
- Steffen, J.H. Optimal boarding method for airline passengers. J. Air Transp. Manag. 2008, 14, 146–150. [Google Scholar] [CrossRef]
- Bazargan, M. A linear programming approach for aircraft boarding strategy. Eur. J. Oper. Res. 2007, 183, 394–411. [Google Scholar] [CrossRef]
- Zeigler, B.P.; Praehofer, H.; Kim, T.G. Theory of Modeling and Simulation: Integrating Discrete Event and Continuous Complex Dynamic Systems; Academic press: Cambridge, MA, USA, 2000. [Google Scholar]
- Wainer, G.A. Discrete-Event Modeling and Simulation: A Practitioner’s Approach; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Jafer, S.; Mi, W. Simulation of aircraft boarding strategies with discrete-event cellular DEVS. In Proceedings of the Symposium on Theory of Modeling & Simulation-DEVS Integrative, Tampa, FL, USA, 13–16 April 2014; Society for Computer Simulation International: San Diego, CA, USA, 2014; p. 32. [Google Scholar]
- Schultz, M.; Christian, S.; Hartmut, F. Efficiency of Aircraft Boarding Procedures. In Proceedings of the ICRAT 2008, Fairfax, VA, USA, 1–4 June 2008. [Google Scholar]
- Audenaert, J.; Verbeeck, K.; Berghe, G.V. Multi-agent based simulation for boarding. In Proceedings of the 21st Belgian-Netherlands Conference on Artificial Intelligence, Eindhoven, The Netherlands, 29–30 October 2009; pp. 3–10. [Google Scholar]
- Jaehn, F.; Neumann, S. Airplane boarding. Eur. J. Oper. Res. 2015, 244, 339–359. [Google Scholar] [CrossRef]
- Schultz, M. The Seat Interference Potential as an Indicator for the Aircraft Boarding Progress; No. 2017-01-2113; SAE Technical Paper; SAE: Warrendale, PA, USA, 2017. [Google Scholar]
- Mas, S.; Juan, A.A.; Arias, P.; Fonseca, P. A simulation study regarding different aircraft boarding strategies. In Modeling and Simulation in Engineering, Economics, and Management; Springer: Berlin/Heidelberg, Germany, 2013; pp. 145–152. [Google Scholar]
- Steiner, A.; Philipp, M. Speeding up the airplane boarding process by using pre-boarding areas. In Proceedings of the 9th Swiss Transport Research Conference, Monte Verità, Switzerland, 9–11 September 2009; pp. 1–30. [Google Scholar]
- Bauer, M.; Bhawalkar, K.; Edwards, M. Boarding at the Speed of Flight. UMAP J. 2007, 28, 237. [Google Scholar]
- Ciarallo, F.W.; Ward, K.K.; Hill, R.R. Modeling Airline Boarding for Improved Efficiency and Passenger Experience. In Proceedings of the IIE Annual Conference, Pittsburgh, PA, USA, 20–23 May 2017; Institute of Industrial and Systems Engineers (IISE): Norcross, GA, USA, 2017; pp. 1900–1905. [Google Scholar]
- Schultz, M.; Kunze, T.; Fricke, H. Boarding on the critical path of the turnaround. In Proceedings of the 10th USA/Europe air Traffic Management Research and Development Seminar (ATM2013), Chicago, IL, USA, 10–13 June 2013. [Google Scholar]
- Wainer, G. CD++: A toolkit to develop DEVS models. Softw. Pract. Exp. 2002, 32, 1261–1306. [Google Scholar] [CrossRef]
- Muller, J. Optimal Boarding Methods for Airline Passengers; Hamburg University Internal Report; Hamburg University: Hamburg, Germany, August 2009. [Google Scholar]
- Schultz, M. Aircraft Boarding-Data, Validation, Analysis. In Proceedings of the 12th USA/Europe Air Traffic Management Research and Development Seminar, Seattle, WA, USA, 26–30 June 2017. [Google Scholar]
- Schultz, M. Reliable Aircraft Boarding for Fast Turnarounds. In Proceedings of the ENRI International Workshop on ATM/CNS (EIWAC 2017), Tokyo, Japan, 14–16 November 2017. [Google Scholar]
- Cell-DEVS Boarding Strategies. Available online: https://youtu.be/sodyh4e5yyE?list=PLRvCUnTmrqJCyZNDGAgJmXSu0N1i8GMzv (accessed on 26 November 2017).
- Steffen, J.H.; Hotchkiss, J. Experimental test of airplane boarding methods. J. Air Transp. Manag. 2012, 18, 64–67. [Google Scholar] [CrossRef]





















| Parameter | Range | Unit |
|---|---|---|
| Walking Speed | 0.27–0.44 | [m/s] |
| Clearing Time | 6–30 | [s] |
| Getting out of seat | 3–4.2 | [s] |
| Passenger flow rate | 0.2–1 | [pax/s] |
| Parameter | Time | Unit |
|---|---|---|
| Walking delay | 2270 | ms |
| Luggage Delay | 18,000 | ms |
| Two passengers get out of seats | 4200 | ms |
| Middle passenger gets out of seat | 3600 | ms |
| Aisle passenger gets out of seat | 3000 | ms |
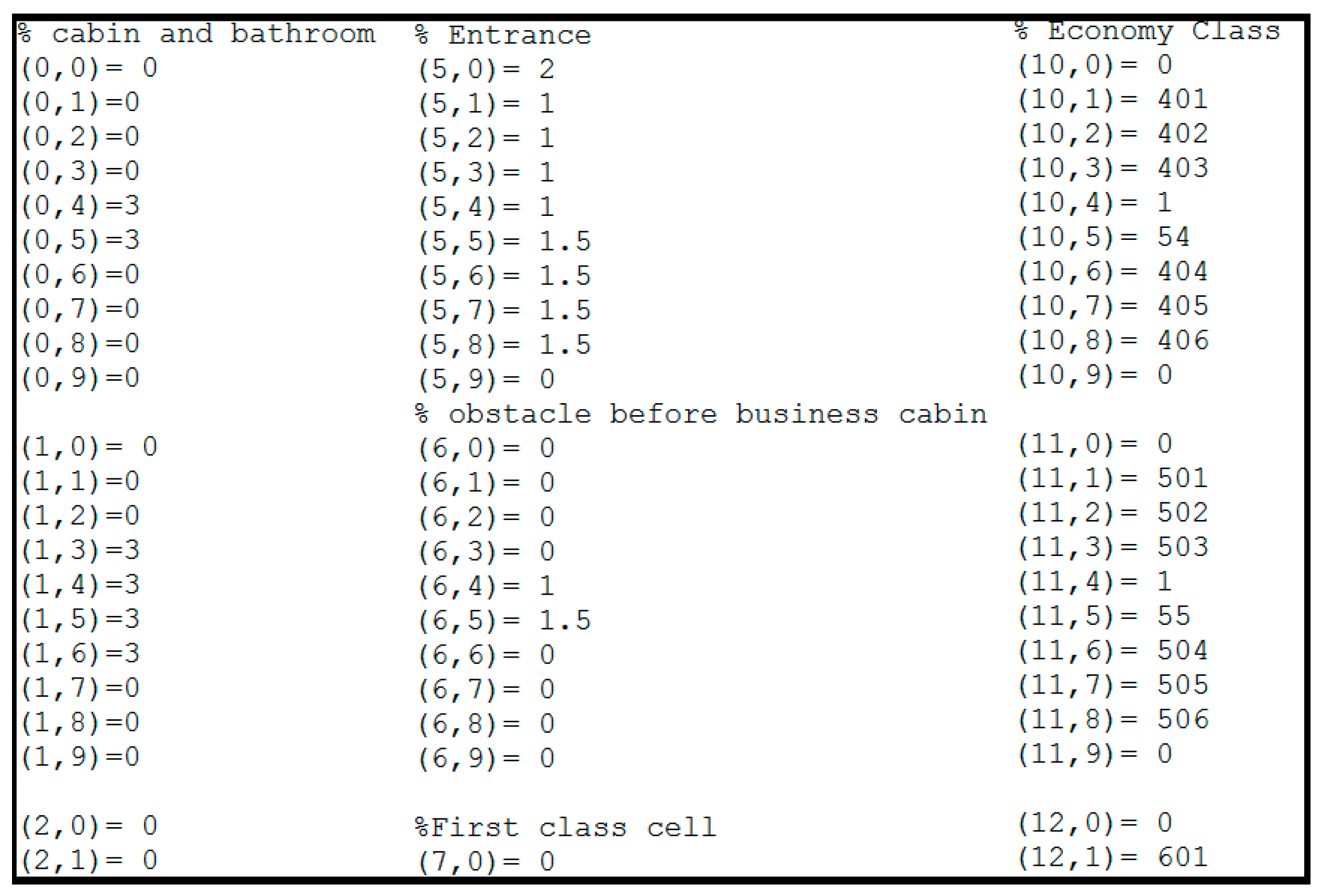
| State Name | State Value | Color | Description |
|---|---|---|---|
| Wall | 0 | Black | Wall or obstacle |
| Aisle | 1, 51–76 | Gray | Aisle |
| Door Open | 2 | Green | Boarding door is open |
| Cabin | 3 | Blue | Cabin or bathroom or cafe |
| Empty Passenger Seat | 100–3000 | white | Passenger seat |
| Walking Passenger | 10,000–300,000 | Red | Walking Passenger |
| Seats with passenger | 4 | Yellow | Seat is occupied with passenger |
| Door Closed | 9 | Green | All the passengers have been boarded |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jafer, S.; Mi, W. Comparative Study of Aircraft Boarding Strategies Using Cellular Discrete Event Simulation. Aerospace 2017, 4, 57. https://doi.org/10.3390/aerospace4040057
Jafer S, Mi W. Comparative Study of Aircraft Boarding Strategies Using Cellular Discrete Event Simulation. Aerospace. 2017; 4(4):57. https://doi.org/10.3390/aerospace4040057
Chicago/Turabian StyleJafer, Shafagh, and Wei Mi. 2017. "Comparative Study of Aircraft Boarding Strategies Using Cellular Discrete Event Simulation" Aerospace 4, no. 4: 57. https://doi.org/10.3390/aerospace4040057
APA StyleJafer, S., & Mi, W. (2017). Comparative Study of Aircraft Boarding Strategies Using Cellular Discrete Event Simulation. Aerospace, 4(4), 57. https://doi.org/10.3390/aerospace4040057




