A New Gaskinetic Model to Analyze Background Flow Effects on Weak Gaseous Jet Flows from Electric Propulsion Devices
Abstract
:1. Introduction
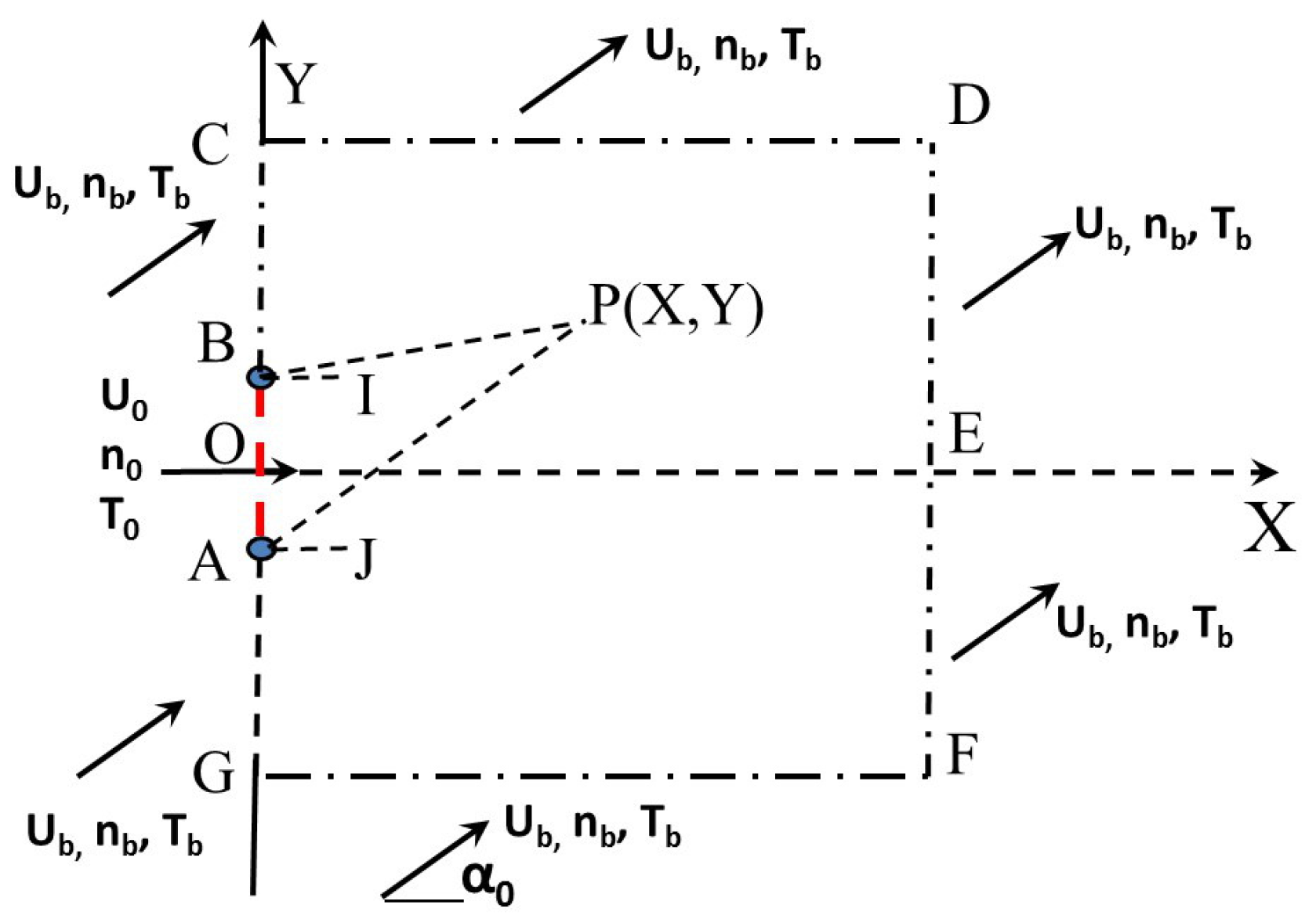
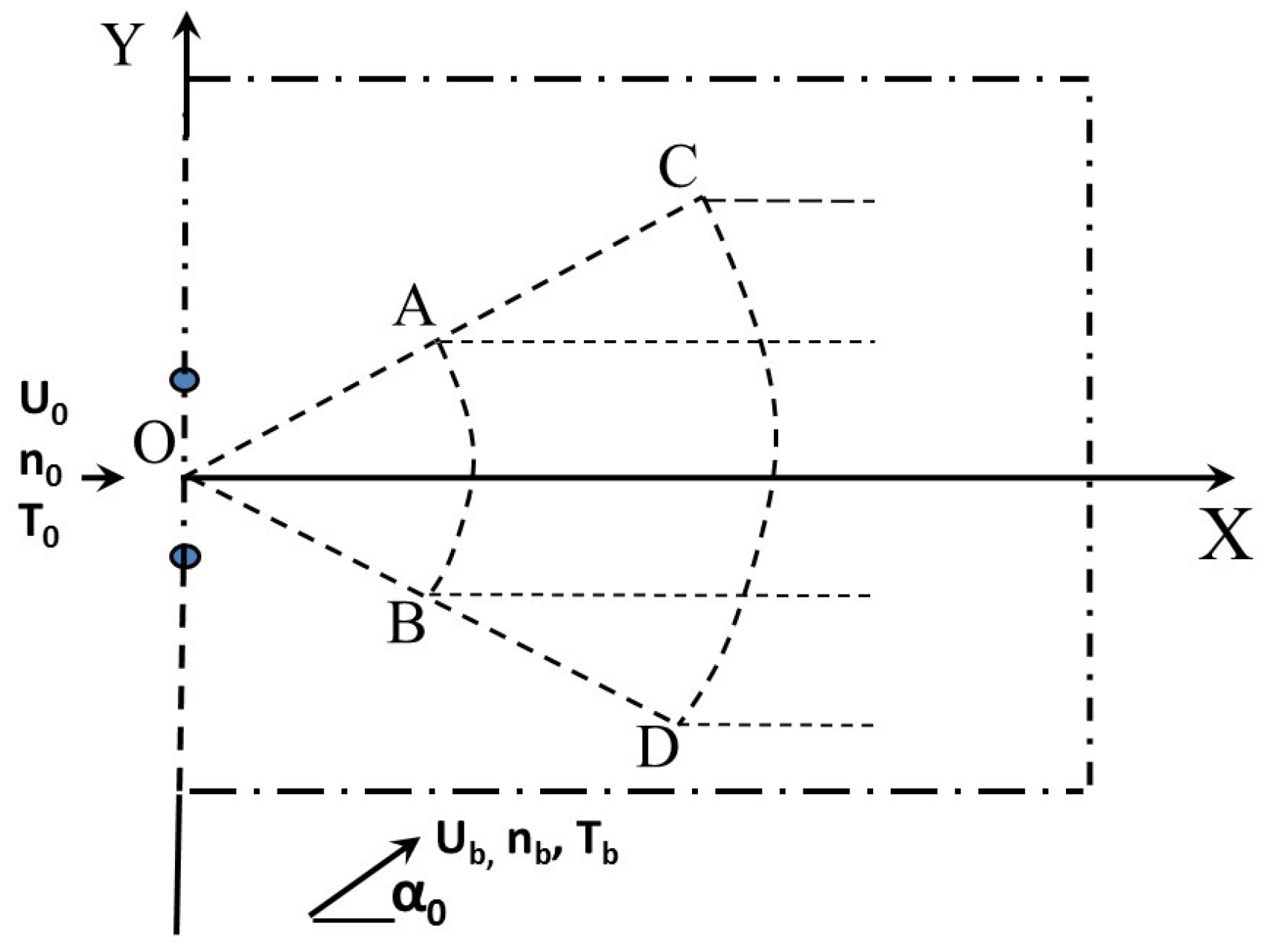
2. Collisionless Jet Expanding into a Uniform Dilute Background Flow
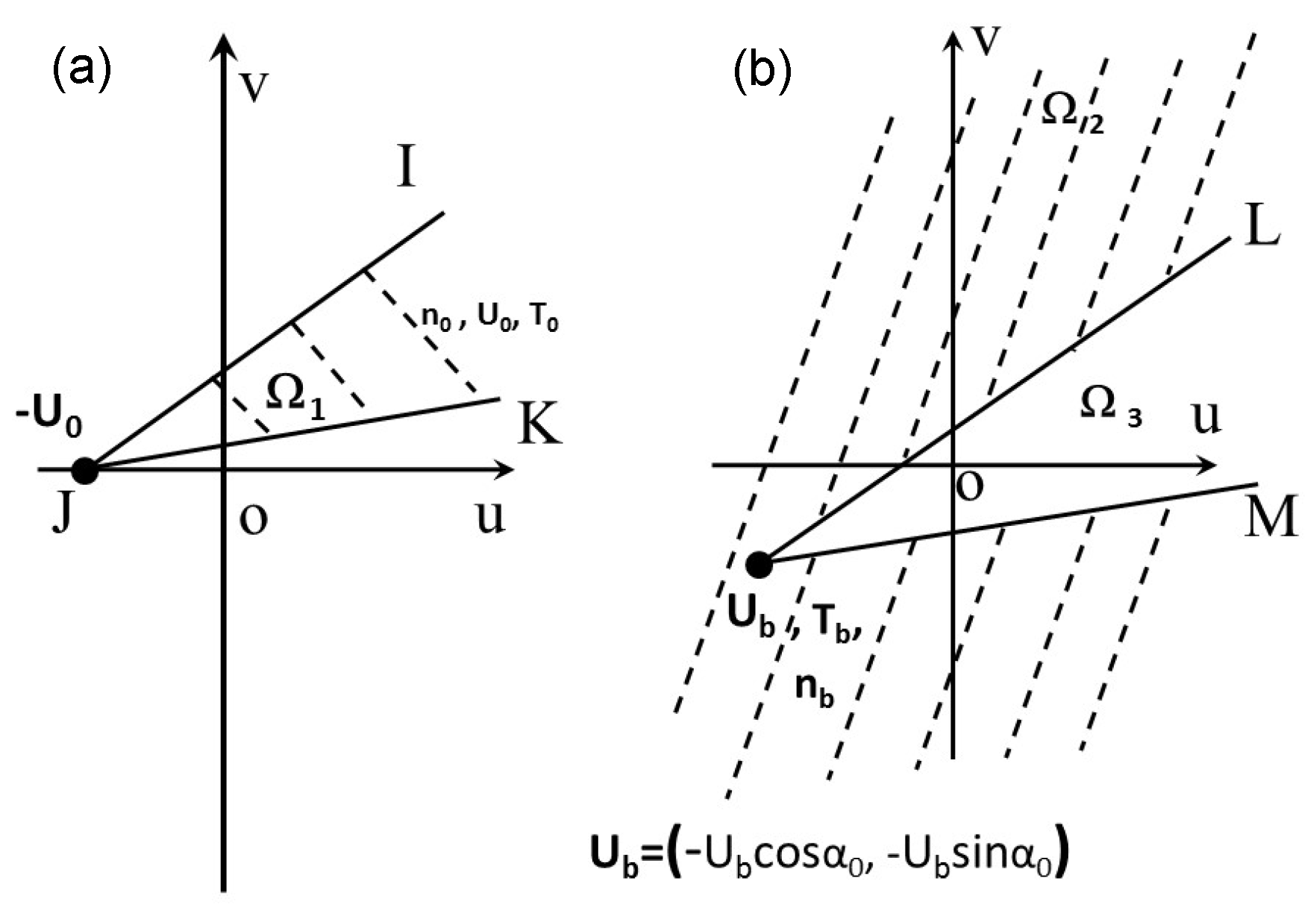
2.1. Derivations for the Mixture Density, Velocities, Temperature, and Pressure
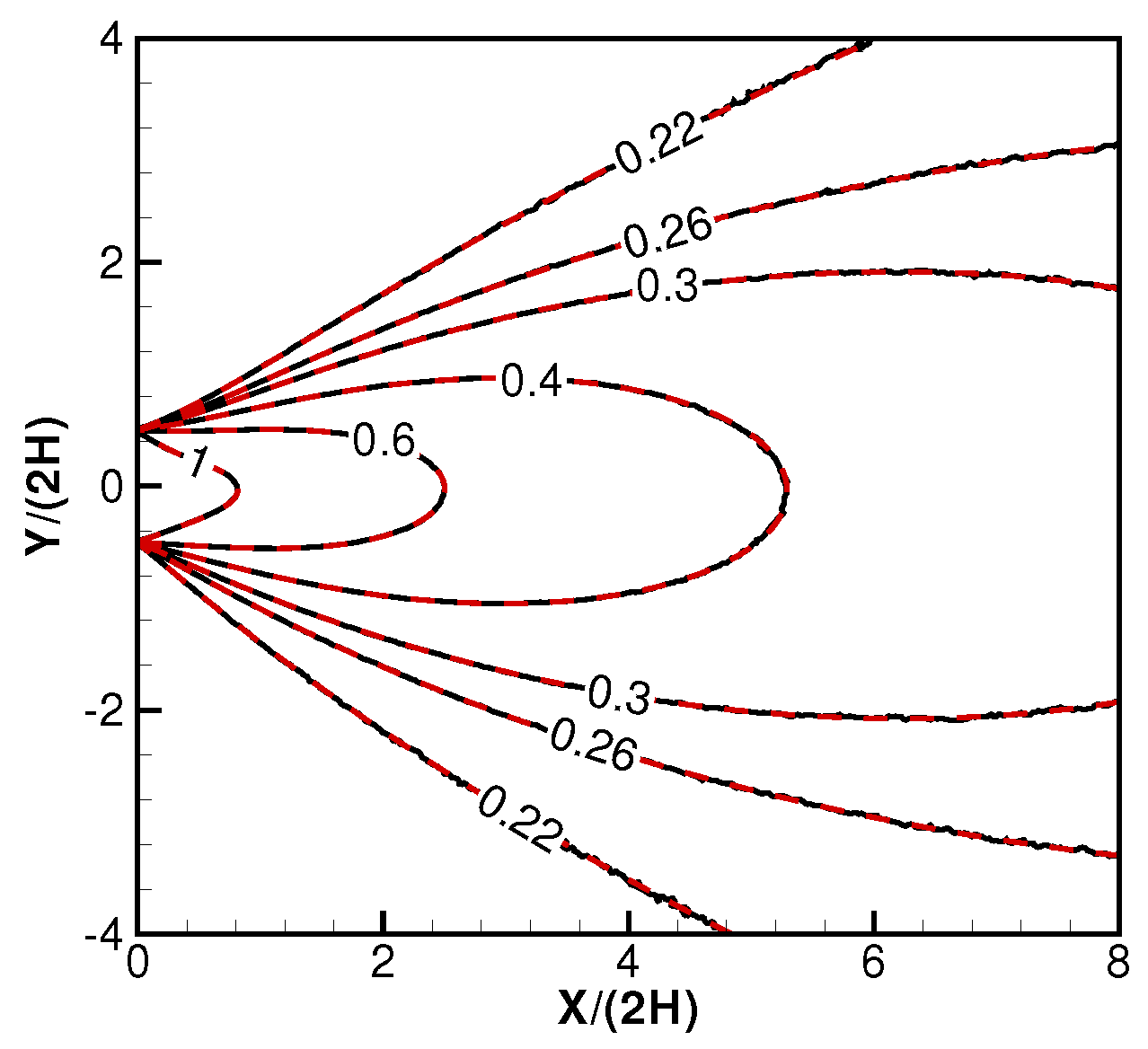
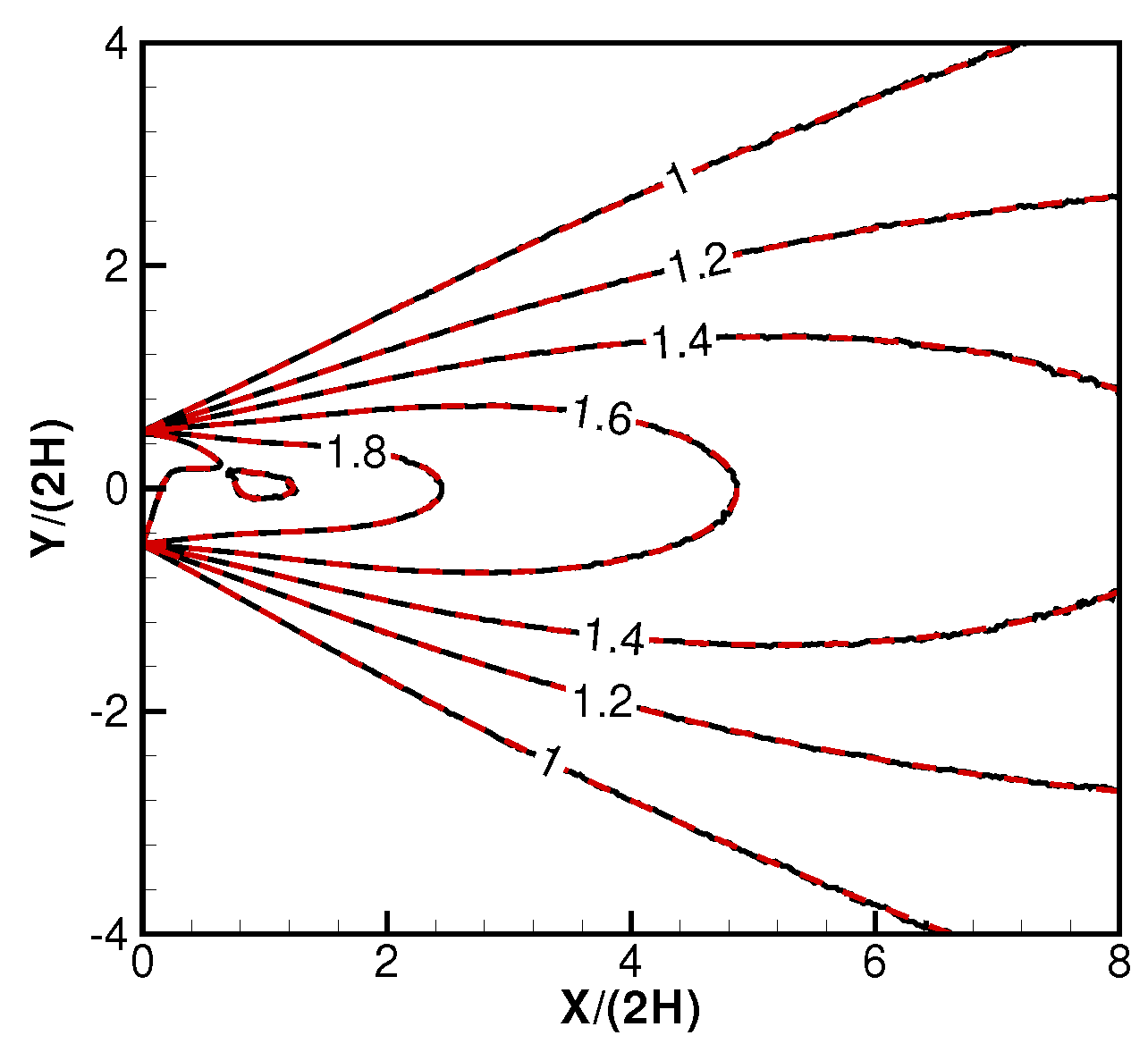
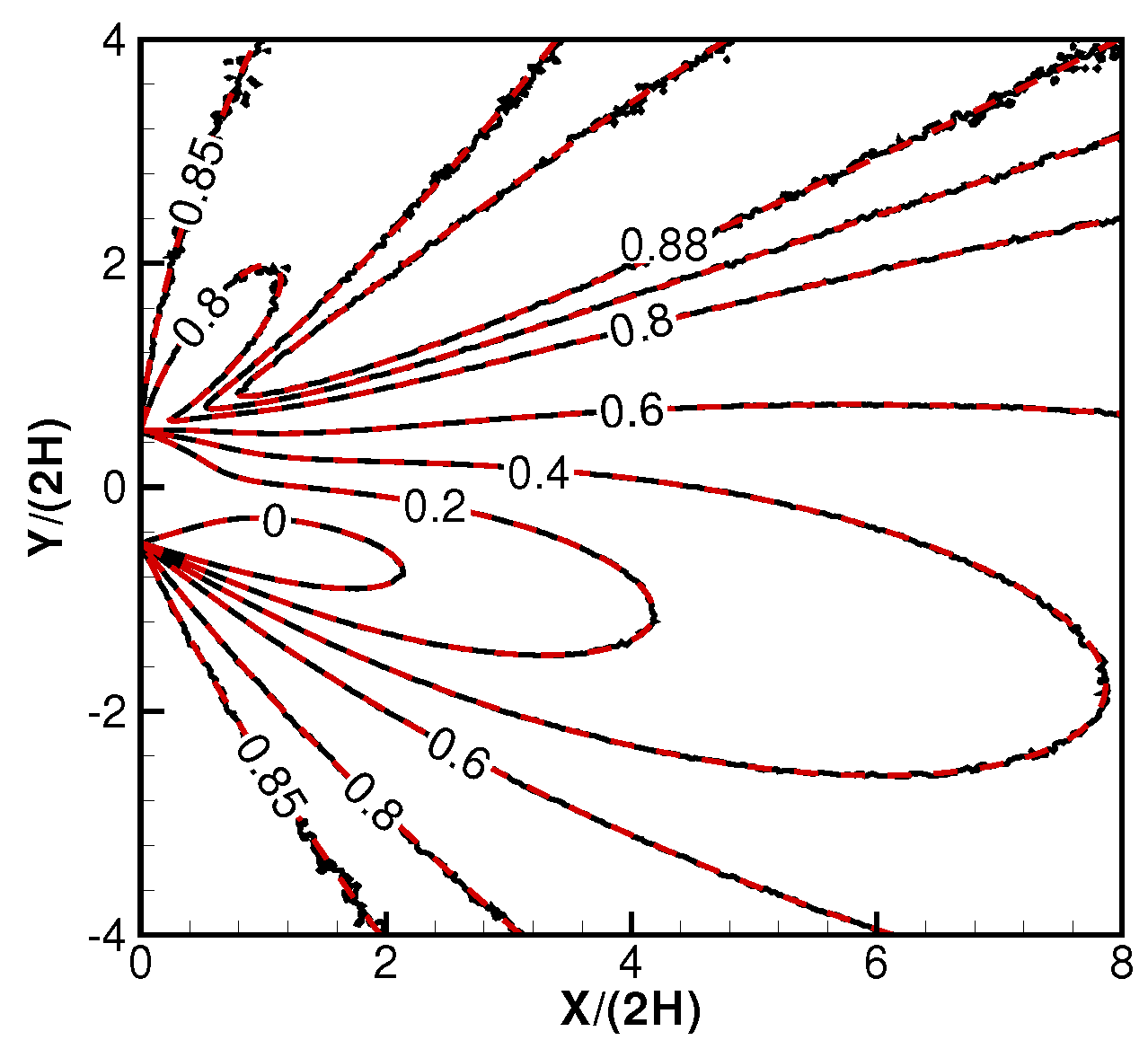
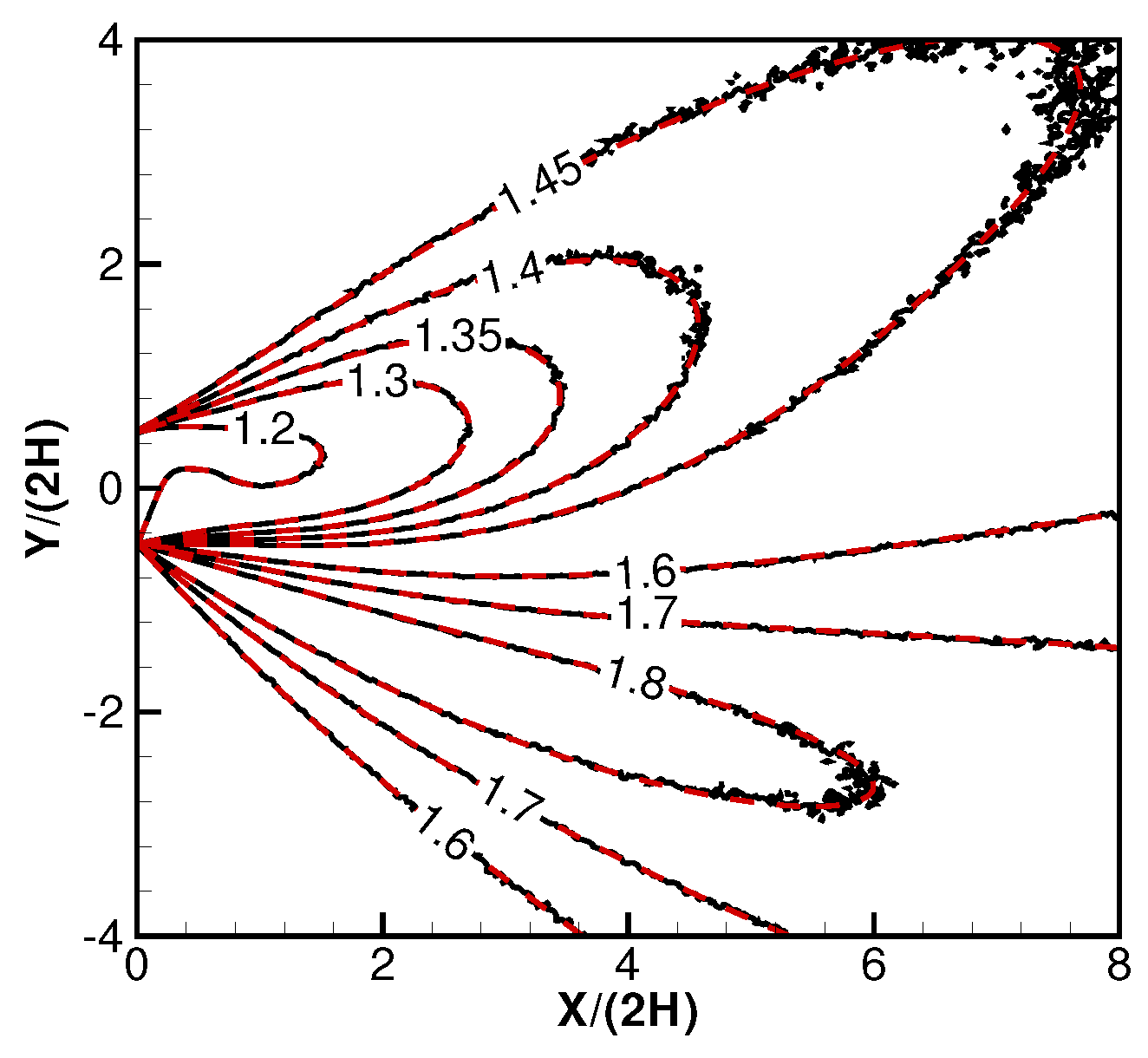
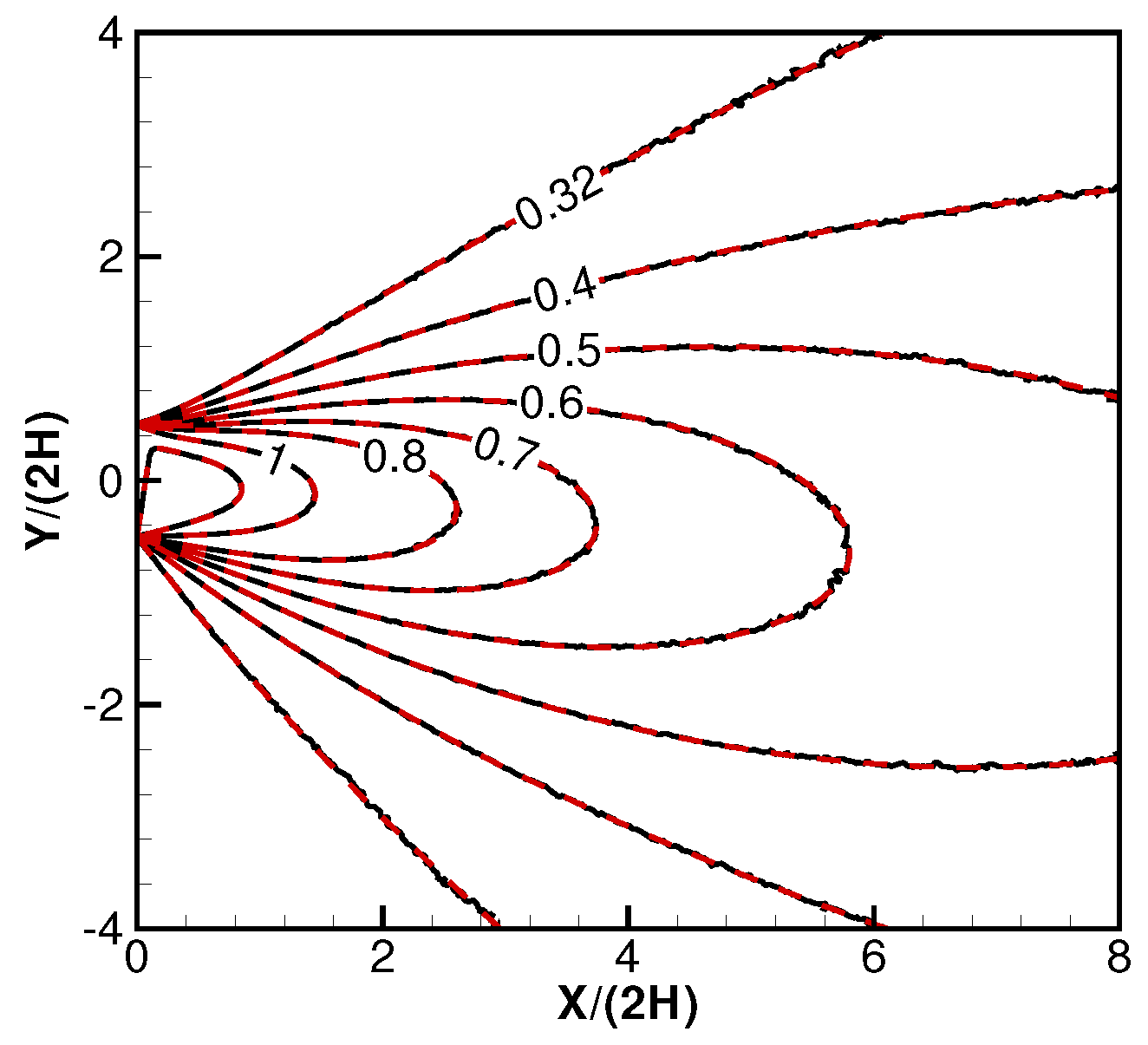
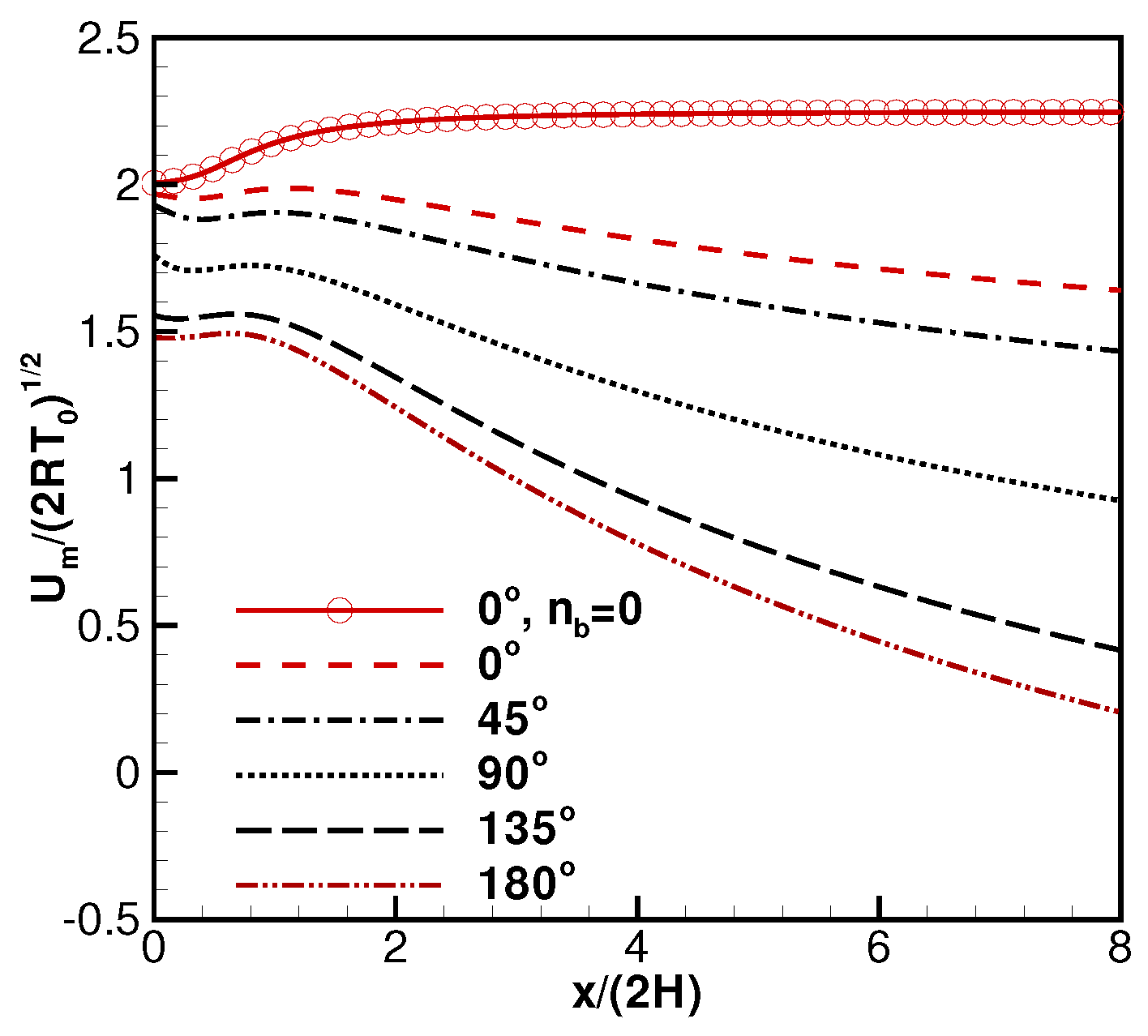
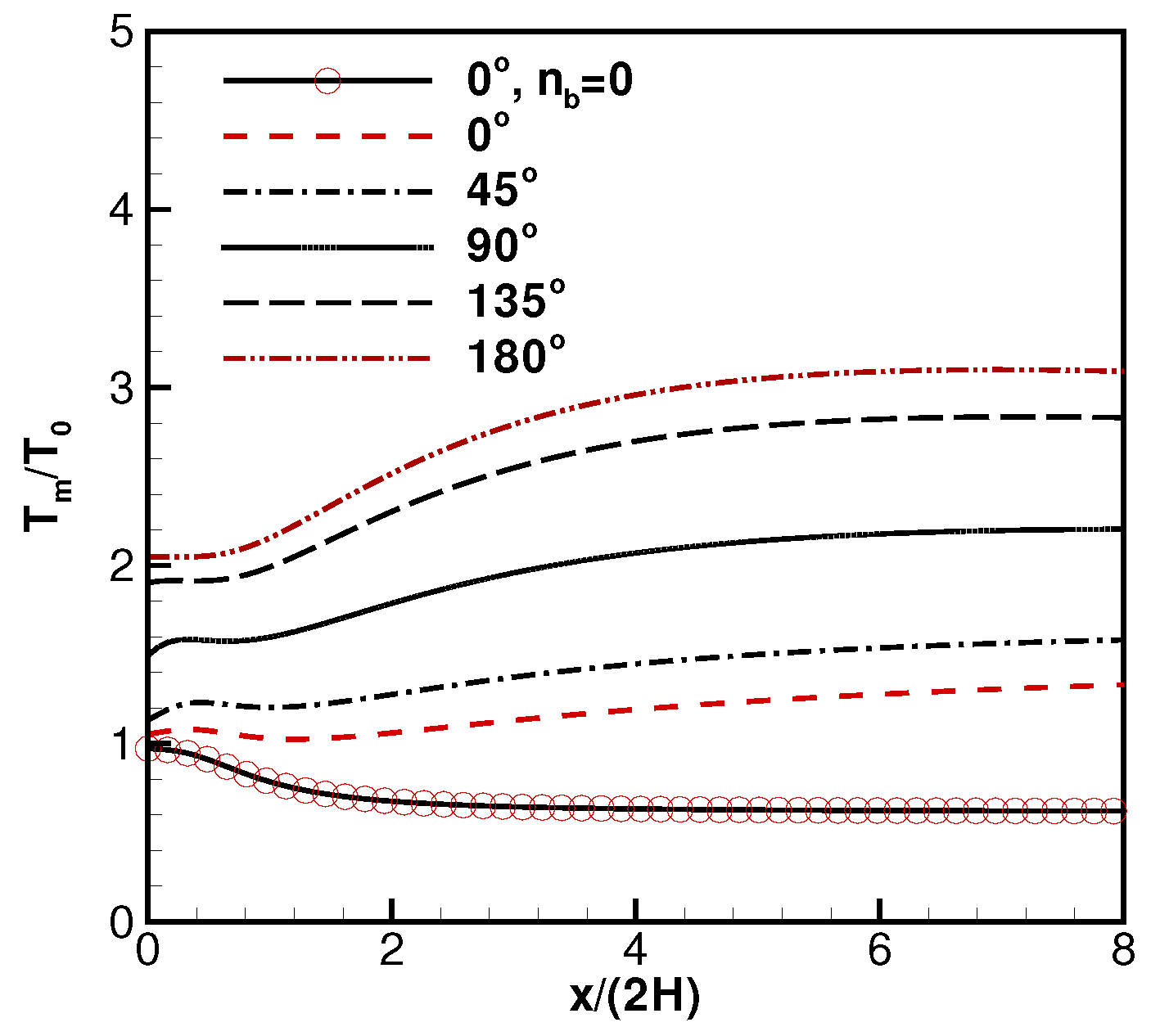
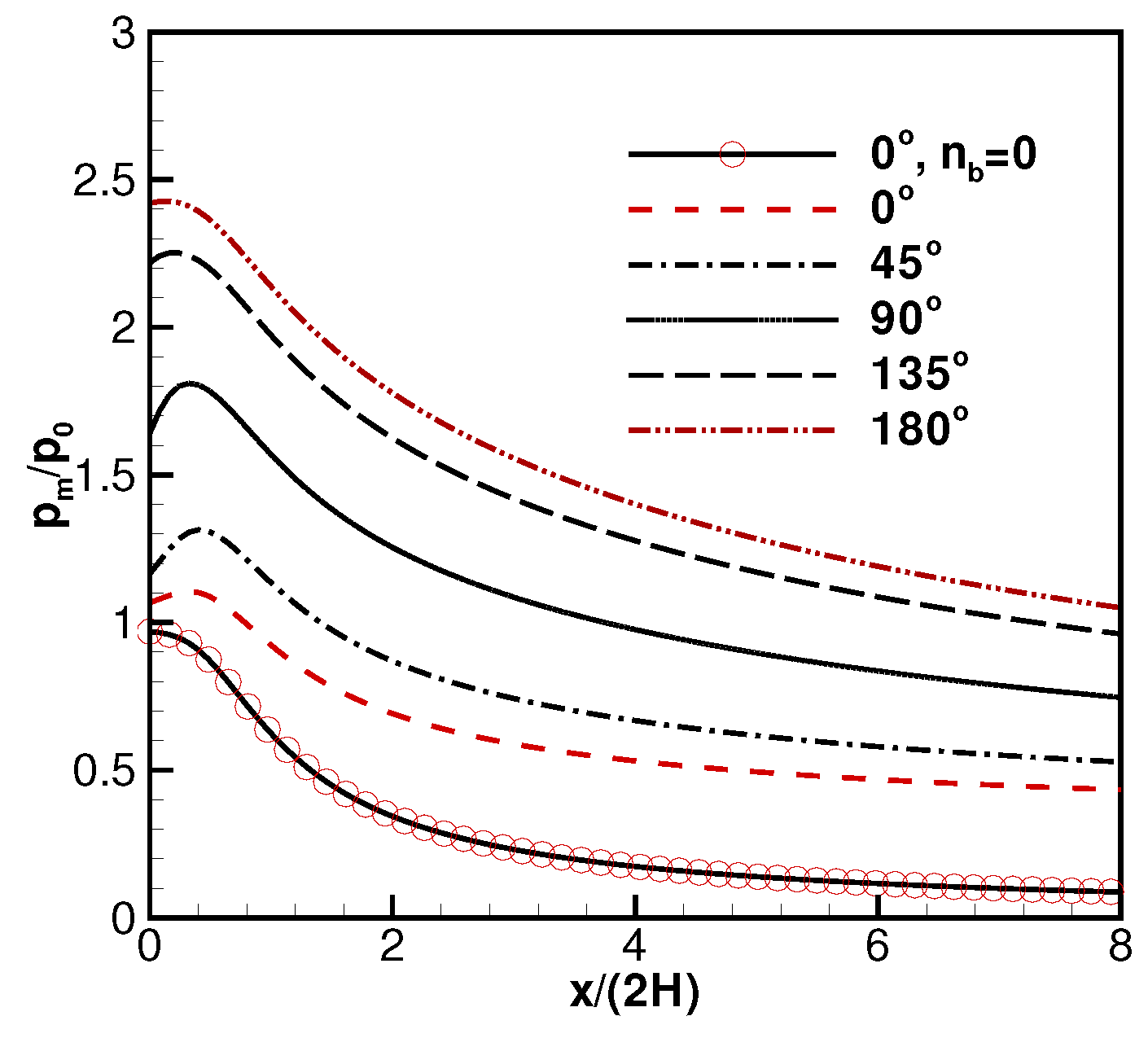
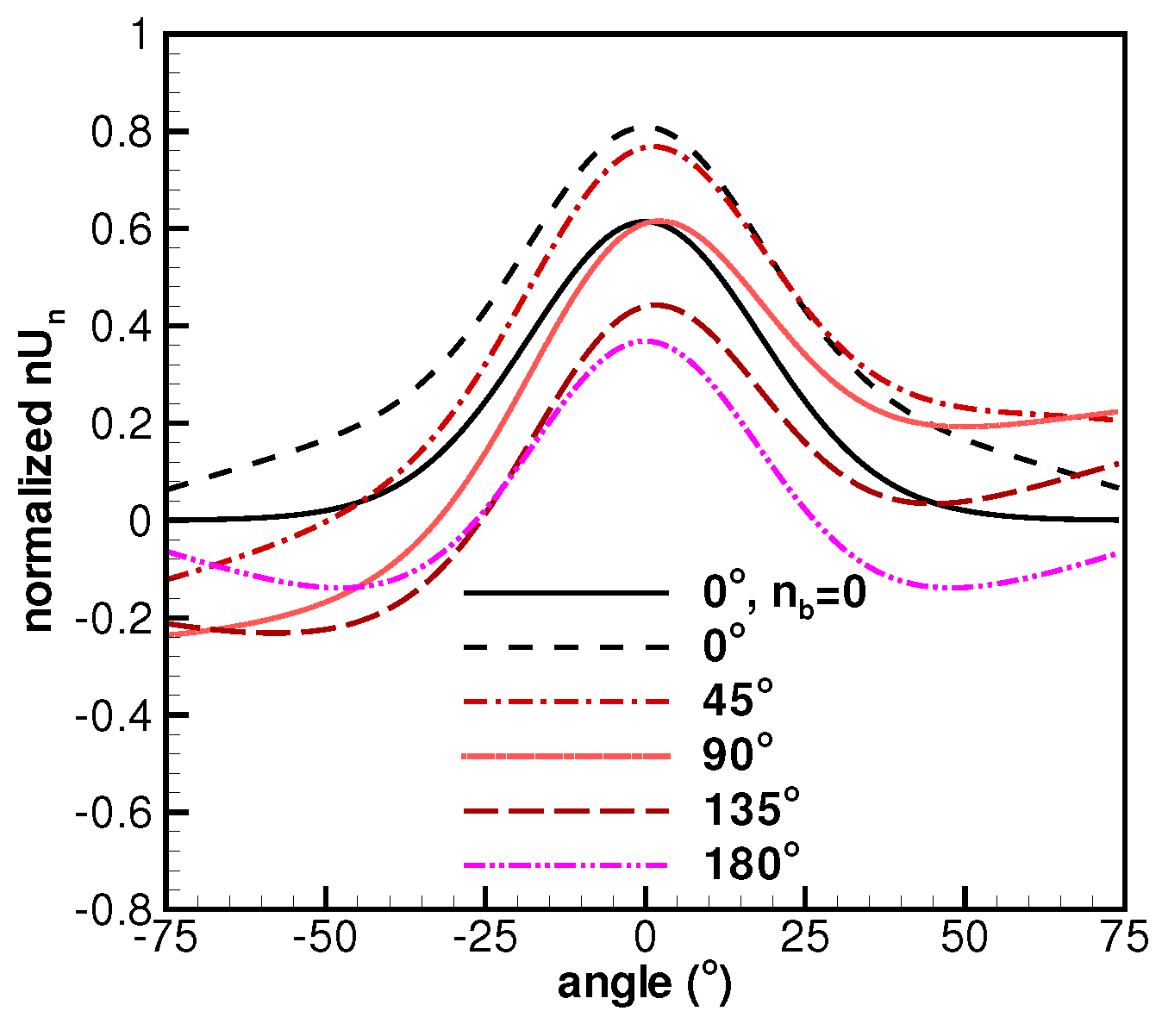
2.2. Validations and Discussions on the Derived Formulas
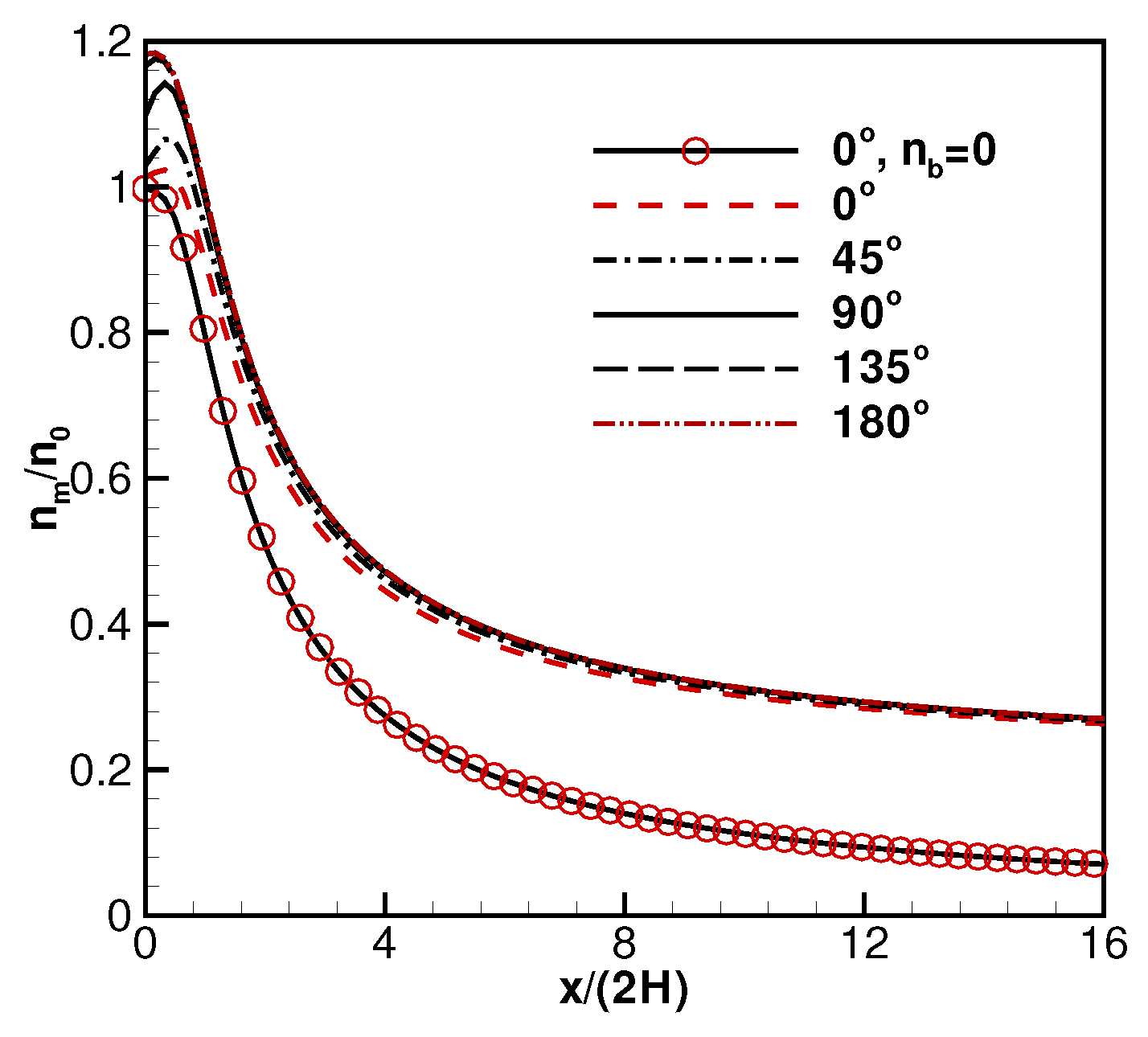
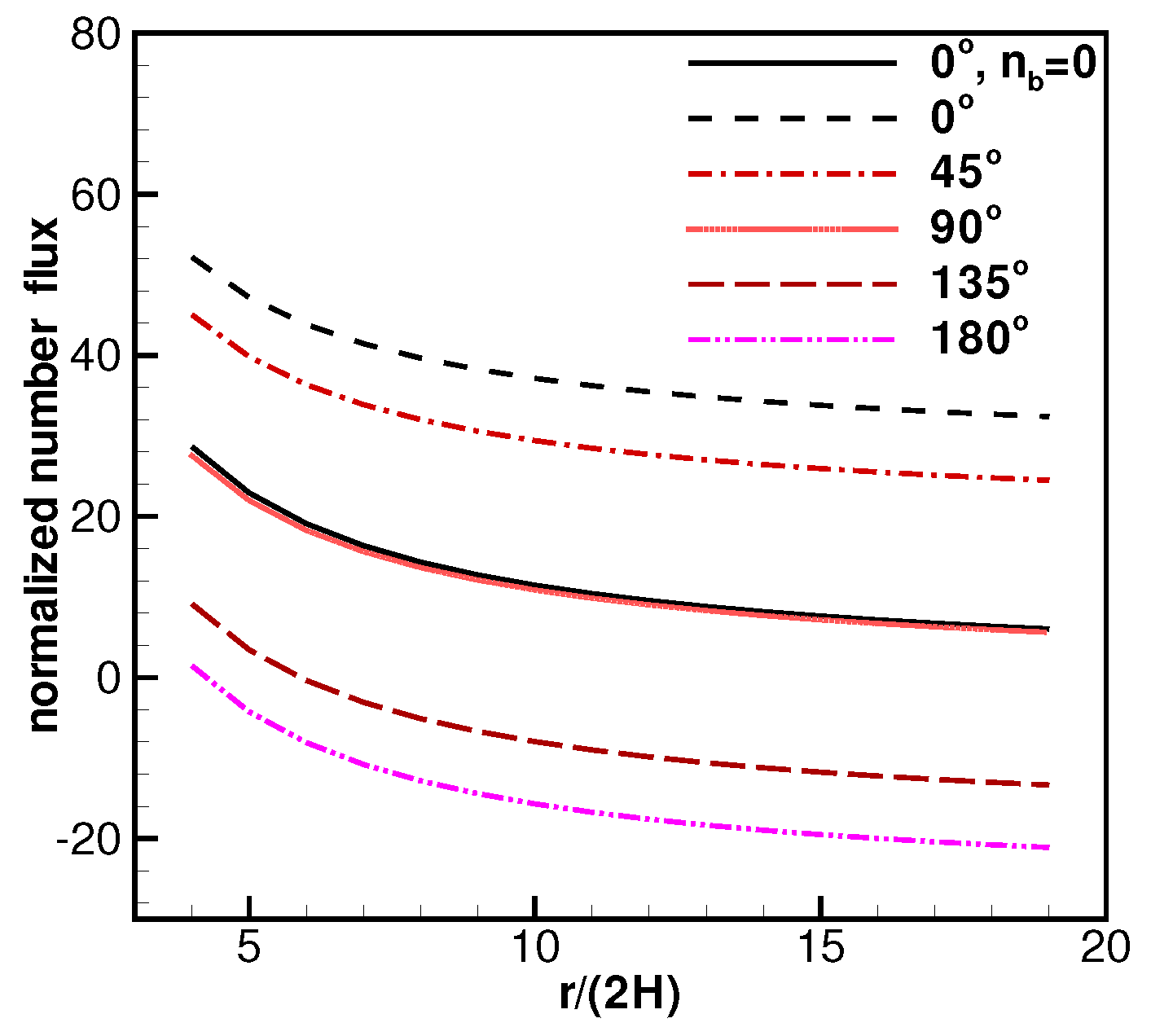
2.3. Background Flow Effects on Electric Propulsion (EP) Devices’ Performance
3. New Methods to Recover the Flow Parameters with Limited Measurements
3.1. Linearized Governing Equations for the Density and Number Fluxes
- Step 1:
- perform initial estimations on the seven parameters: , , , , , and ;
- Step 2:
- select a total of measured densities at different points, ;
- Step 3:
- select a total of measured number fluxes along the X-direction, , ;
- Step 4:
- select a total of measured number fluxes along the Y-direction, , ;Here . The properties can be from the same or different points, e.g., measured number density and fluxes at one point offer three relations.
- Step 5:
- for each selected point, compute the corresponding and ;
- Step 6:
- for each of the measured densities, use and , and the five guessed parameters, , , , , and , to compute the corresponding –, and a total of guessed jet number number density can be computed by using Equation (2). With the measured densities, , a total of linear algebraic equations about –, are properly constructed;
- Step 7:
- for each of the measured number fluxes along the X-direction, , by using the and for each point, and the seven guessed parameters, , , , , , and , a set of coefficients – can be computed, and a guessed jet number flux can also be computed by using Equation (3). A total of linear algebraic equations about – are properly constructed;
- Step 8:
- for each of the measured number fluxes along the Y-direction, , by using the and , and the seven guessed parameters, , , , , , and , seven coefficients – can be computed. A guessed jet number fluxes along the Y-direction, can also be computed by using Equation (4). Together with the measured data , a total of linear algebraic equations about – are properly constructed;
- Step 9:
- solve the above seven linear algebraic equations, e.g., by using a Gaussian elimination method, and obtain –;
- Step 10:
- if these seven small perturbation parameters are sufficiently small, then stop the iterations; the seven true parameters characterizing the whole flowfield are recovered;
- Step 11:
- if these seven small perturbation numbers are not small, then update the guessed values by multiplying with , , , , , and ; go to Step 5, and repeat the above steps.
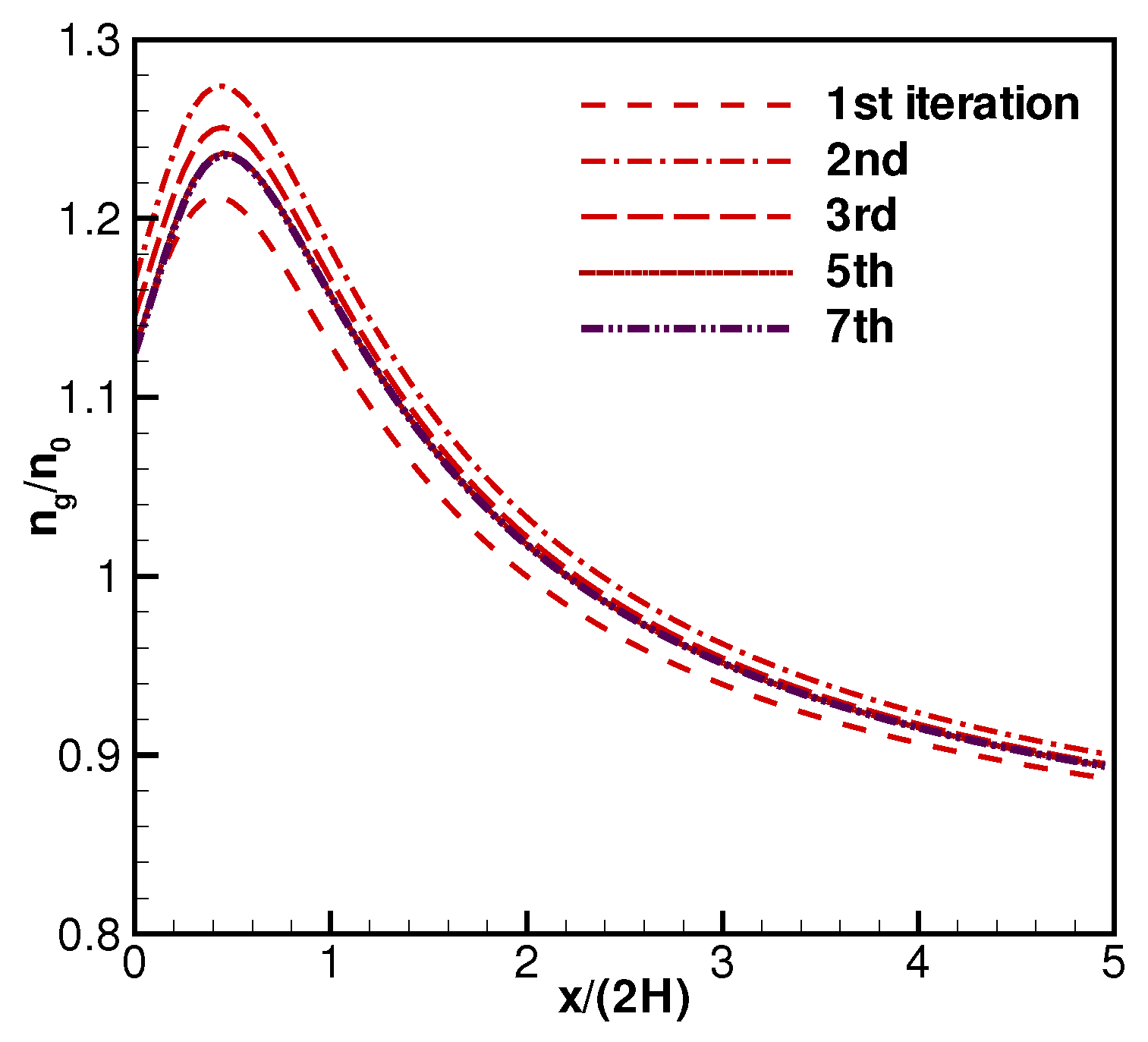
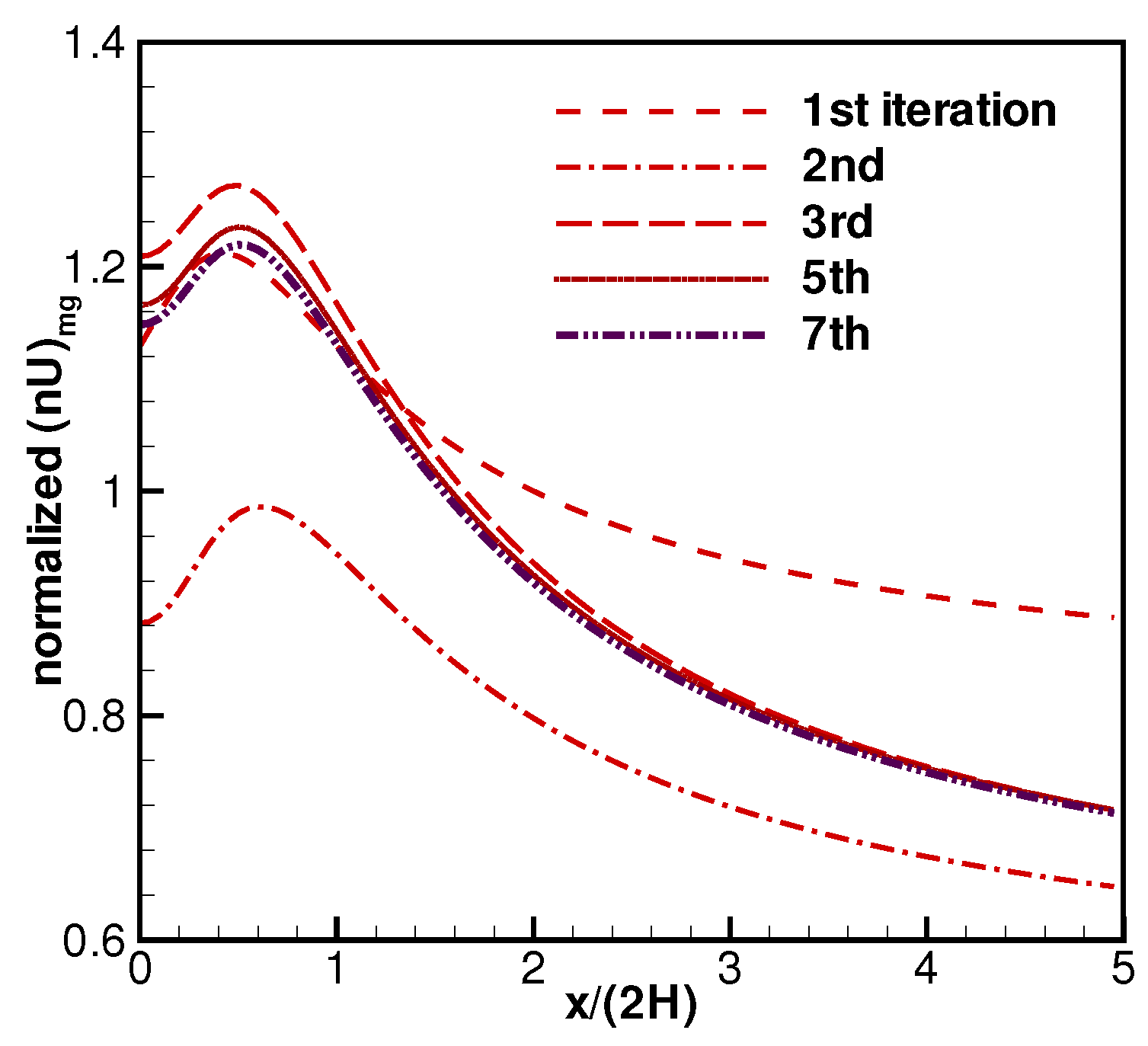
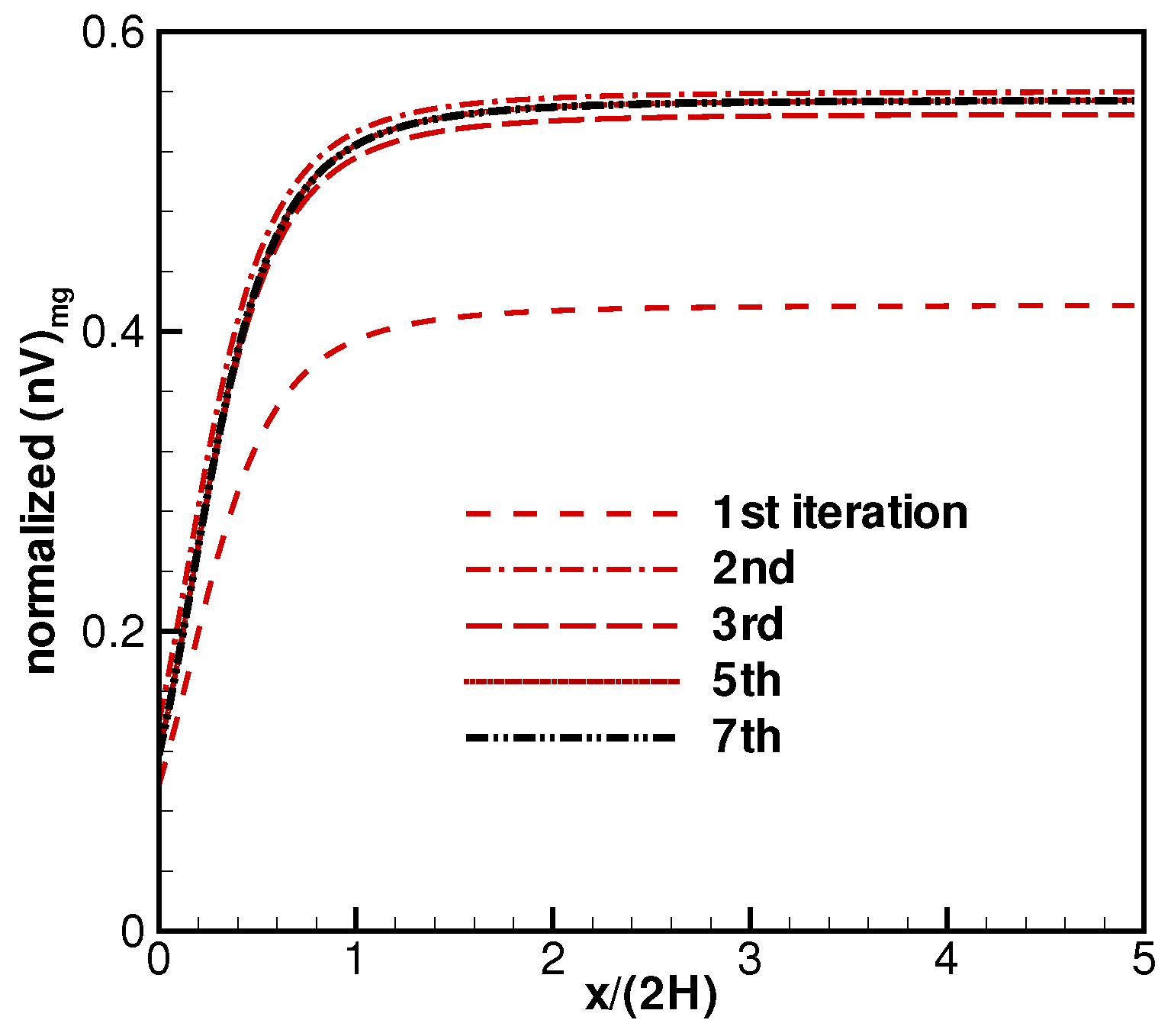
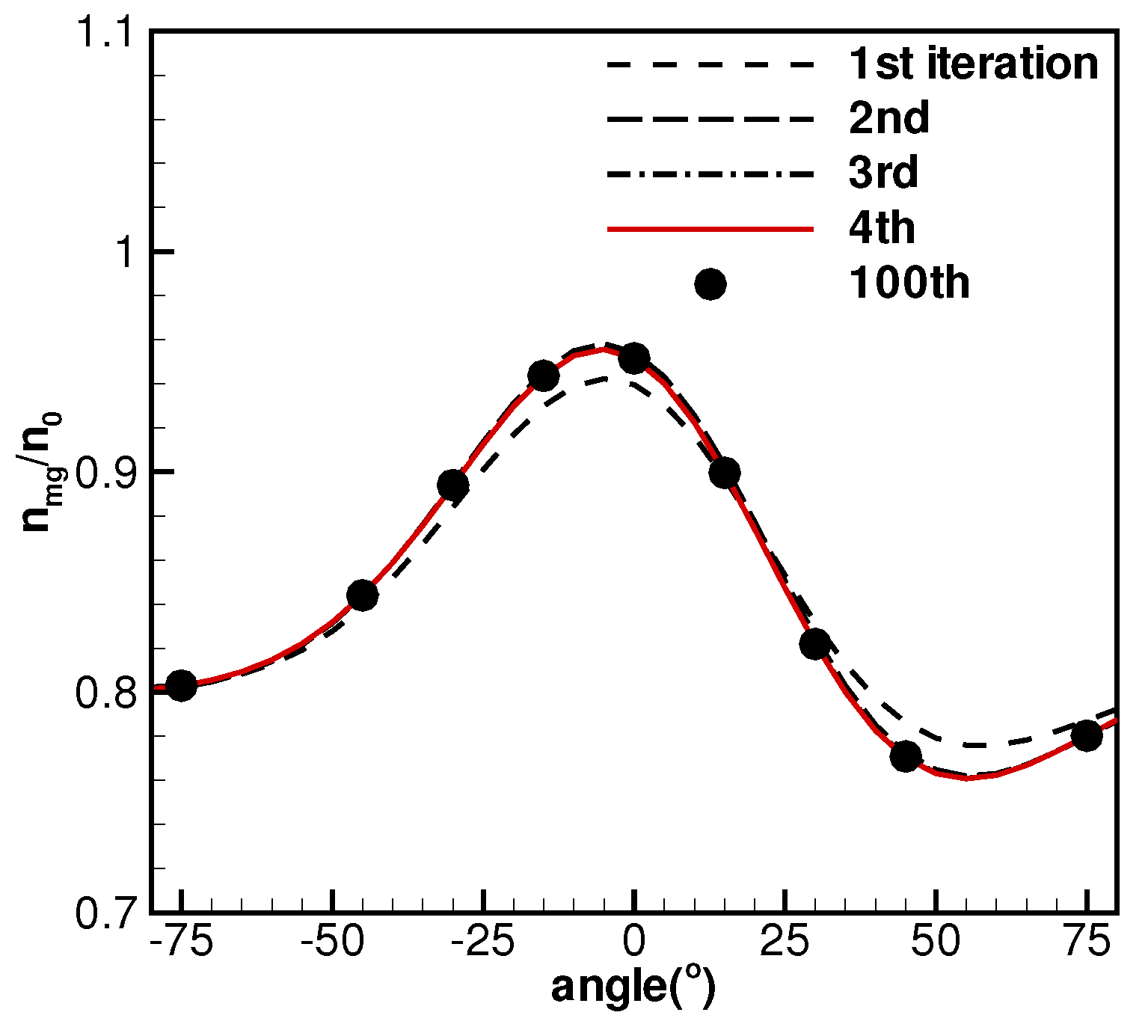
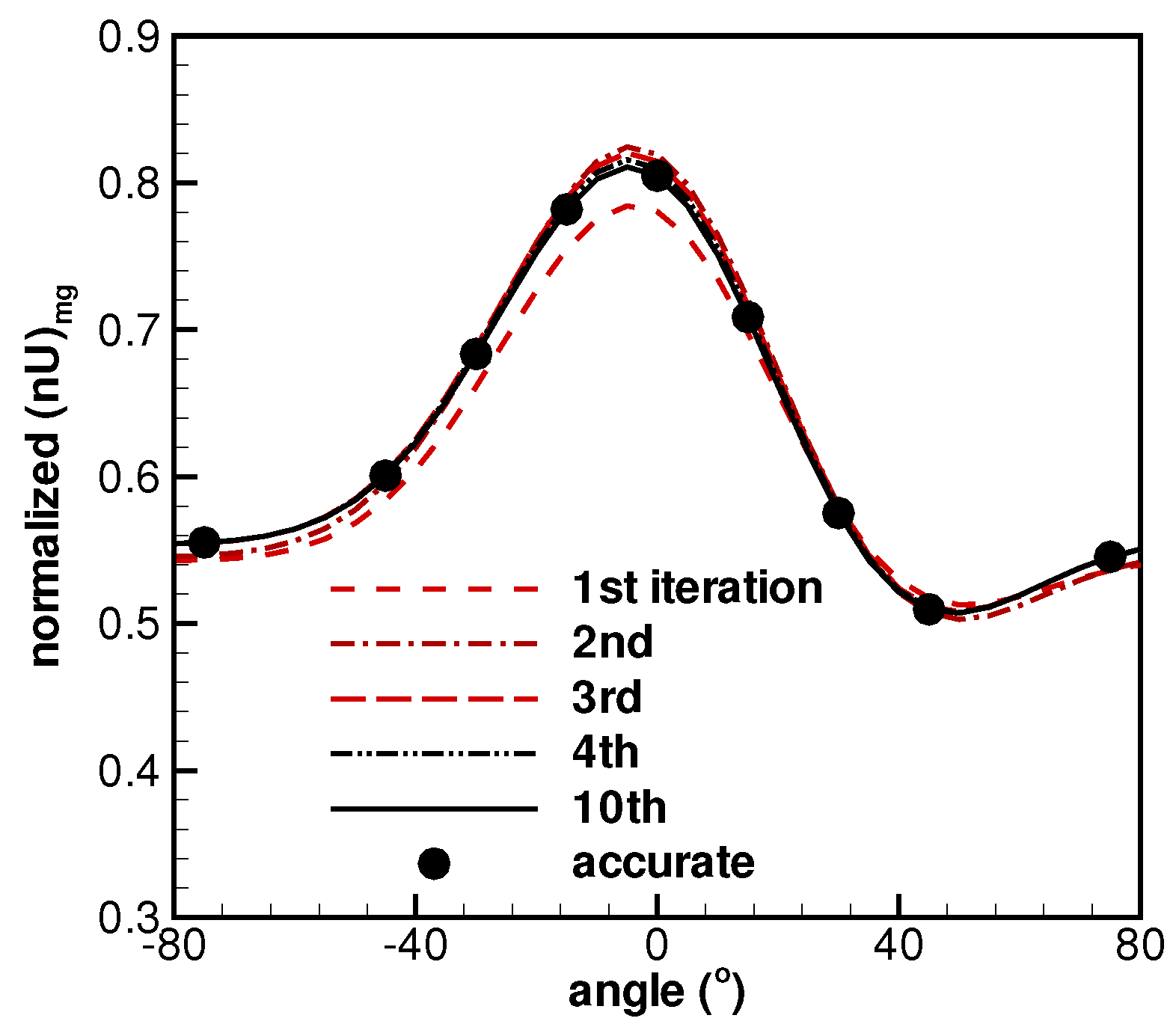
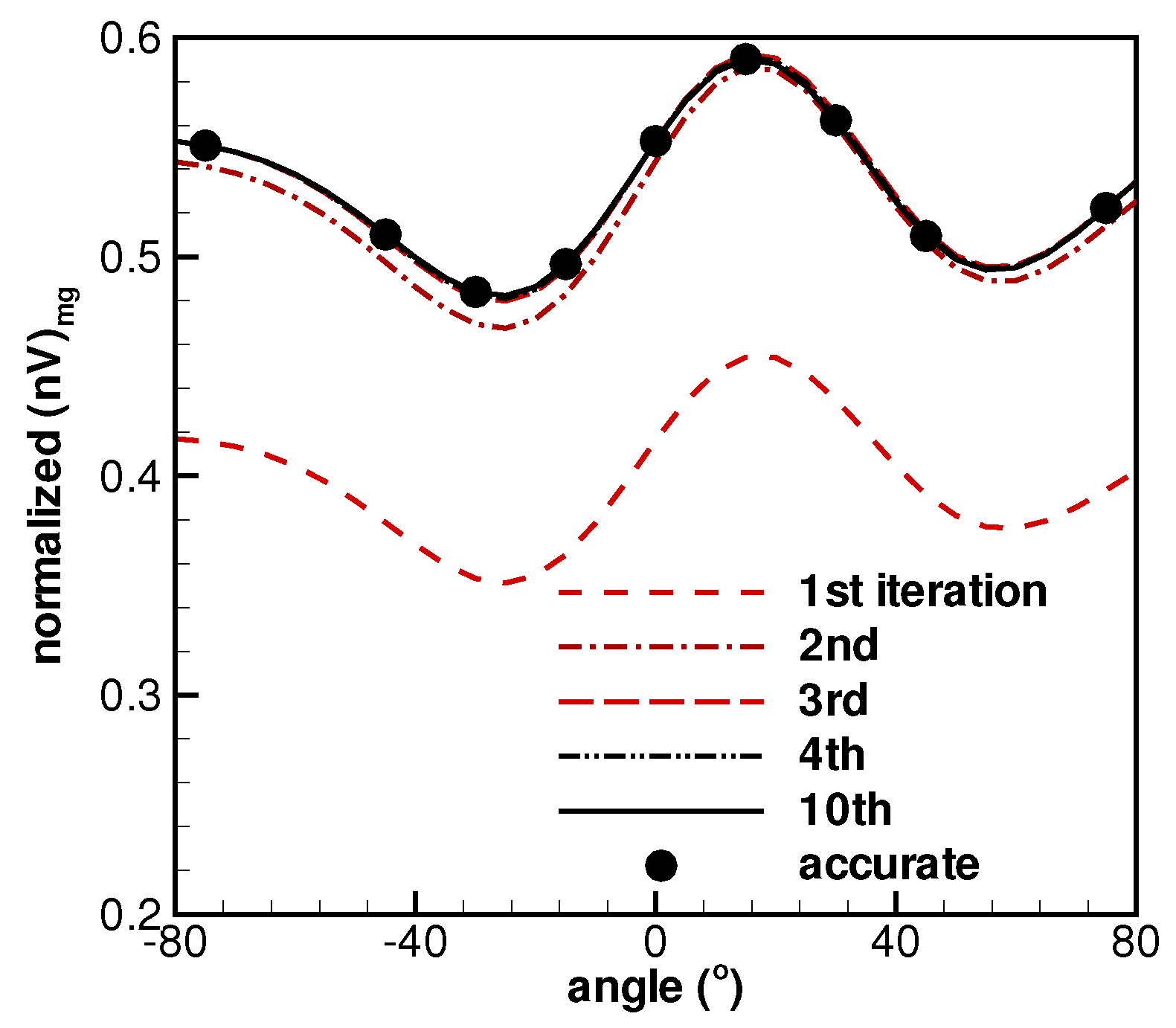
3.2. Test Cases and Discussions
4. Conclusions
Acknowledgments
Conflicts of Interest
Appendix A. Expressions for Coefficients Ai, Bi, and Ci
References
- Sanna, G.; Tomassetti, G. Introduction to Molecular Beams Gas Dynamics; Imperial College Press: London, UK, 2005. [Google Scholar]
- Maev, R.; Leshchynsky, V. Introduction to Low Pressure Gas Dynamic Spray; Wiley-Vch: Weinheim, Germany, 2008. [Google Scholar]
- Hastings, D.; Garrett, H. Spacecraft-Environment Interactions; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Simons, G.A. Effects of nozzle boundary layers on rocket exhaust plumes. AIAA J. 1972, 10, 1534–1535. [Google Scholar] [CrossRef]
- Jian, H.; Chu, Y.; Cao, H.; Cao, Y.; He, X.; Xia, G. Three-dimensional IFE-PIC numerical simulation of background pressure’s effect on accelerator grid impingement current for ion optics. Vacuum 2015, 116, 130–138. [Google Scholar] [CrossRef]
- Byers, C.C.; Dankanich, J.W. A review of facility effects on Hall effect thrusters. In Proceedings of the 31st International Electric Propulsion Conference, Ann Arbor, MI, USA, 20–24 September 2009. IEPC-2009-076.
- Gildea, S.R.; Sanchez, M.M.; Nakles, M.R.; Hargus, W.A. Experimentally characterizing the plume of a divergent cusped field thruster. In Proceedings of the 31st International Electric Propulsion Conference, Ann Arbor, MI, USA, 20–24 September 2009. AFRL-RZ-ED-TP-2009-316.
- Dankanich, J.W.; Swiatek, M.W.; Yim, T. A step towards electric propulsion testing standards: Pressure measurements and effective pumping speeds. In Proceedings of the48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Altanta, GA, USA, 30 July–1 August 2012. AIAA paper 2012-3737.
- Jones, M.L. Results of large vacuum facility tests of an MPD arc thruster. AIAA J. 1966, 4, 1455–1456. [Google Scholar] [CrossRef]
- Sovey, J.S.; Mantenieks, M.A. Performance and lifetime assessment of MPD arc thruster technology. In Proceedings of the 24th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Boston, MA, USA, 11–13 July 1988. AIAA Paper 88-3211.
- Nakles, M.R.; Hargus, W.A. Background pressure effects on ion velocity distribution within a medium-power Hall thruster. J. Propuls. Power 2011, 27, 737–743. [Google Scholar] [CrossRef]
- Randolph, T.; Kim, V.; Kozubsky, K.; Zhurin, V.; Day, M. Facility effects on stationary plasma thruster testing. In Proceedings of the 23rd International Electric Propulsion Conference, Seattle, WA, USA, 13–16 September 1993. IEPC-93-93 844.
- Hofer, R.R.; Peterson, P.Y.; Gallimore, A.D. Characterizing vacuum facility back pressure effects on the performance of a Hall thruster. In Proceedings of the 27th International Electric Propulsion Conference, Pasadena, CA, USA, 15–19 October 2001. IEPC-01-045.
- Walker, M.L.R.; Gallimore, A.D.; Boyd, I.D.; Cai, C. Vacuum chamber pressure maps of a Hall thruster cold-flow expansion. J. Propuls. Power 2004, 20, 1127–1132. [Google Scholar] [CrossRef]
- Rovey, J.L.; Walker, M.L.R.; Gallimore, A. Magnetically filtered Faraday probe for measuring the ion current density profile of a Hall thruster. Rev. Sci. Instrum. 2006, 77, 013503. [Google Scholar] [CrossRef]
- Kamhawi, H.; Huang, W.; Haag, T.; Spektor, R. Investigation of the effects of facility background pressure on the performance and voltage-current characteristics of the high voltage Hall accelerator. In Proceedings of the 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference 2014, Cleveland, OH, USA, 28–30 July 2014. AIAA Paper 2014-17063.
- Huang, W.; Kamhawi, H.; Hagg, W. Facility effect characterization test of NASA’s HERMes Hall thruster. In Proceedings of the 52nd AIAA/SAE/ASEE Jointed Propulsion Conference, Salt Lake City, UT, USA, 25–27 July 2016. AIAA paper 2016-4842.
- Li, X.; Zhang, T.; Jia, Y.; Chen, J. Numerical simulations of space background pressure effects on stability parameters for ion thruster grids. Vac. Cryog. 2012, 18, 71–76. Available online: http://www.cqvip.com/qk/95890x/201202/43092185.html (accessed on 1 December 2016). (In Chinese)[Google Scholar]
- Yim, J.; Burt, J. Characterization of vacuum facility background gas through simulation and considerations for electric propulsion ground testing chambers. In Proceedings of the 51st AIAA/SAE/ASEE Joint Propulsion Conference, Orlando, FL, USA, 27–29 July 2015. AIAA paper 2015-3825.
- Bird, G. Molecular Gas Dynamics and the Direct Simulation of Gas Flows, 2nd ed.; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Narasimha, R. Collisionless expansion of gases into vacuum. J. Fluid Mech. 1962, 12, 294–308. [Google Scholar] [CrossRef]
- Liepmann, H.W. Gas kinetics and gasdynamics of orifice flow. J. Fluid Mech. 1961, 10, 65–79. [Google Scholar] [CrossRef]
- Cai, C.; Zou, C. Gaskinetic solutions for high Knudsen number planar jet impingement flows. Commun. Comput. Phys. 2013, 14, 960–978. [Google Scholar] [CrossRef]
- Cai, C.; Huang, X. High speed rarefied round jet impingement flows. AIAA J. 2012, 50, 2908–2911. [Google Scholar] [CrossRef]
- Cai, C.; Khasawneh, K. Collisionless gas flows over a flat cryogenic pump plate. J. Vac. Sci. Technol. A 2009, 27, 601–610. [Google Scholar] [CrossRef]
- Cai, C.; Boyd, I.D.; Sun, Q. Free molecular background flow in a vacuum chamber equipped with two-sided pumps. J. Vac. Sci. Technol. A 2006, 24, 9–19. [Google Scholar] [CrossRef]
- Cai, C.; Boyd, I.D.; Sun, Q. Free molecular flows between two plates equipped with pumps. J. Thermophys. Heat Transf. 2007, 21, 95–104. [Google Scholar] [CrossRef]
- Noller, H.G. Approximate calculation of expansion of gas from nozzles into high vacuum. J. Vac. Sci. Technol. 1966, 6, 202. [Google Scholar] [CrossRef]
- Liu, H.; Cai, C.; Zou, C. An object-oriented implementation of the DSMC method. Comput. Fluids 2012, 57, 65–75. [Google Scholar] [CrossRef]
| Point | Angle () | x (m) | y (m) | |||
|---|---|---|---|---|---|---|
| A | −75 | 0.776 | −2.898 | 0.803 | 0.542 | 0.538 |
| B | −45 | 2.122 | −2.121 | 0.844 | 0.586 | 0.498 |
| C | −30 | 2.598 | −1.500 | 0.894 | 0.667 | 0.472 |
| D | −15 | 2.898 | −0.776 | 0.944 | 0.763 | 0.485 |
| E | 0.000 | 3.000 | 0.000 | 0.952 | 0.785 | 0.539 |
| F | 15 | 2.898 | 0.776 | 0.899 | 0.691 | 0.576 |
| G | 30 | 2.598 | 1.500 | 0.822 | 0.561 | 0.549 |
| H | 45 | 2.122 | 2.121 | 0.771 | 0.497 | 0.497 |
| I | 75 | 0.776 | 2.898 | 0.780 | 0.532 | 0.509 |
| Parameter Names | Initial Values | 1st Iteration | 2nd | 3rd | 4th | 8th | 15th |
|---|---|---|---|---|---|---|---|
| 0.60 | 0.989 | 1.007 | 1.018 | 1.002 | 0.999 | 1.000 | |
| 1.0 | 1.175 | 1.232 | 1.197 | 1.205 | 1.201 | 1.199 | |
| 1.2 | 0.802 | 0.801 | 0.799 | 0.799 | 0.800 | 0.799 | |
| 1.0 | 0.649 | 0.697 | 0.779 | 0.794 | 0.800 | 0.799 | |
| 25.0 | 37.57 | 46.59 | 44.99 | 44.99 | 44.99 | 45.00 | |
| 250.0 | 220.8 | 127.1 | 221.5 | 178.9 | 195.3 | 200.4 | |
| 250.0 | 346.7 | 381.5 | 306.2 | 303.9 | 299.9 | 300.0 |
| Relative Errors | Initial Values | 1st Iteration | 2nd | 3rd | 4th | 8th | 15th |
|---|---|---|---|---|---|---|---|
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, C. A New Gaskinetic Model to Analyze Background Flow Effects on Weak Gaseous Jet Flows from Electric Propulsion Devices. Aerospace 2017, 4, 5. https://doi.org/10.3390/aerospace4010005
Cai C. A New Gaskinetic Model to Analyze Background Flow Effects on Weak Gaseous Jet Flows from Electric Propulsion Devices. Aerospace. 2017; 4(1):5. https://doi.org/10.3390/aerospace4010005
Chicago/Turabian StyleCai, Chunpei. 2017. "A New Gaskinetic Model to Analyze Background Flow Effects on Weak Gaseous Jet Flows from Electric Propulsion Devices" Aerospace 4, no. 1: 5. https://doi.org/10.3390/aerospace4010005
APA StyleCai, C. (2017). A New Gaskinetic Model to Analyze Background Flow Effects on Weak Gaseous Jet Flows from Electric Propulsion Devices. Aerospace, 4(1), 5. https://doi.org/10.3390/aerospace4010005




