Momentum- and Energy-Based Analyses of the Aerodynamic Effects of Boundary Layer Ingestion and Propulsion–Airframe Integration on a Blended Wing Body–Turbofan Configuration
Abstract
1. Introduction
2. Methodology
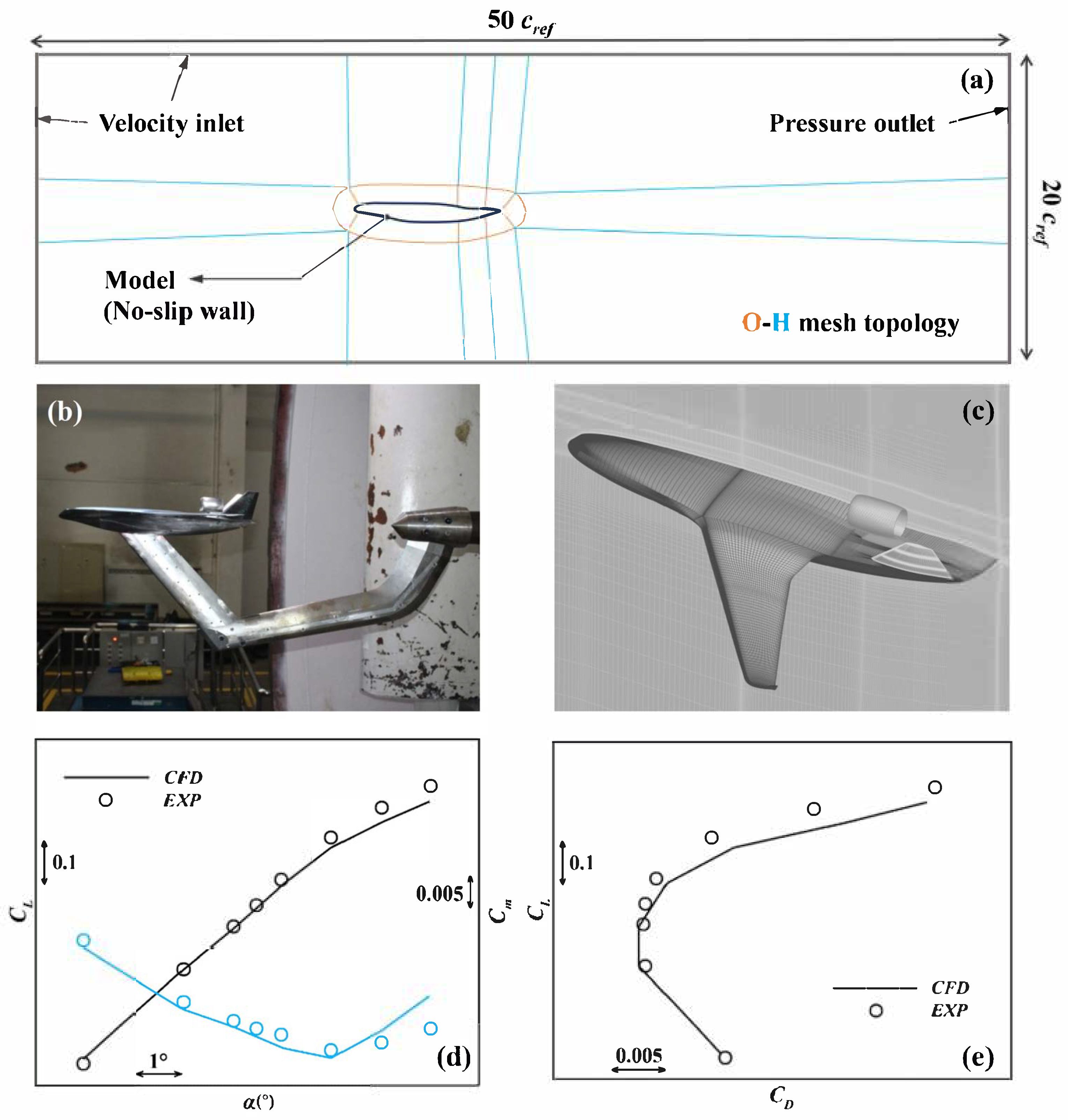
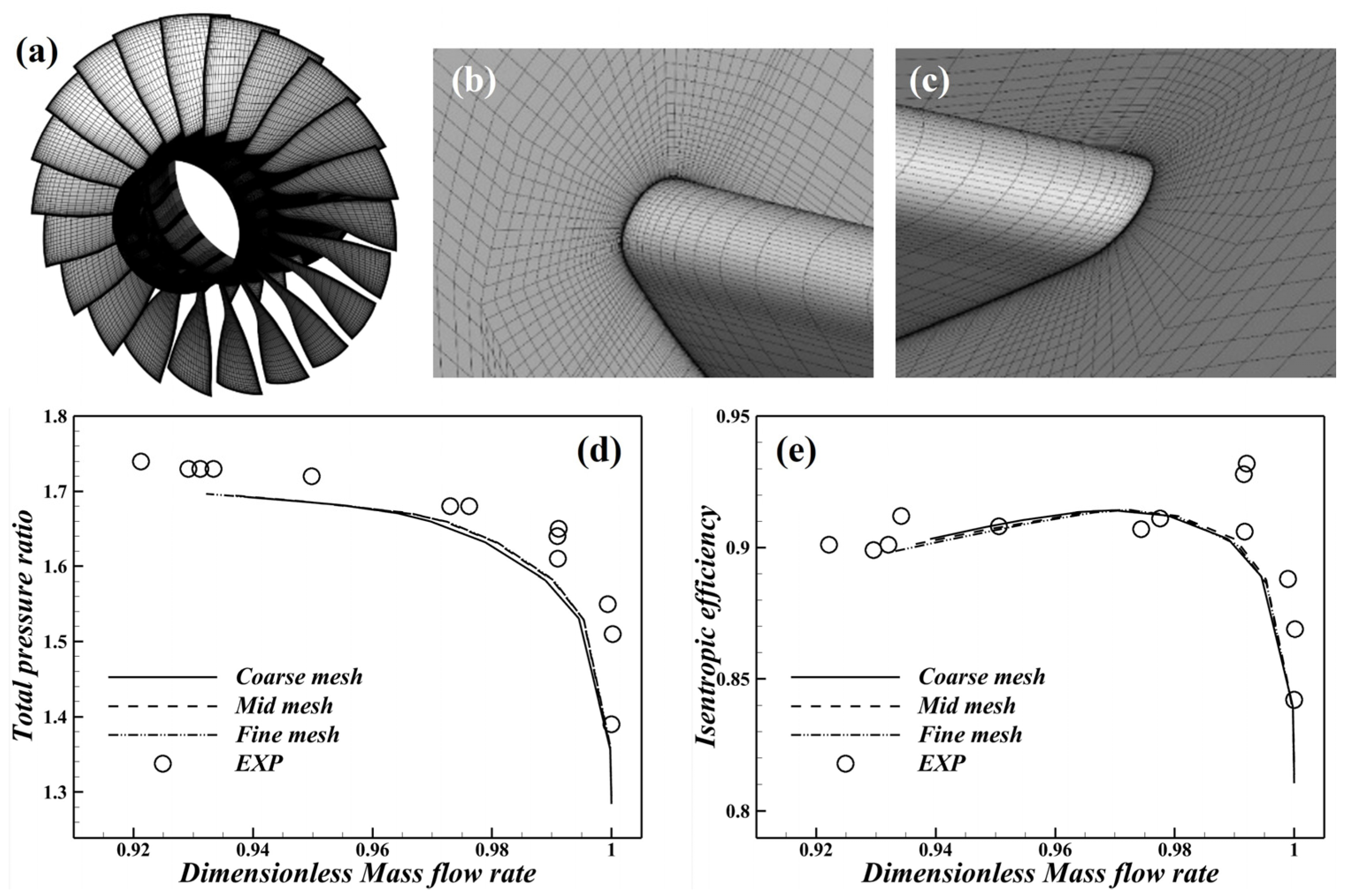
2.1. Numerical Methods and Validation
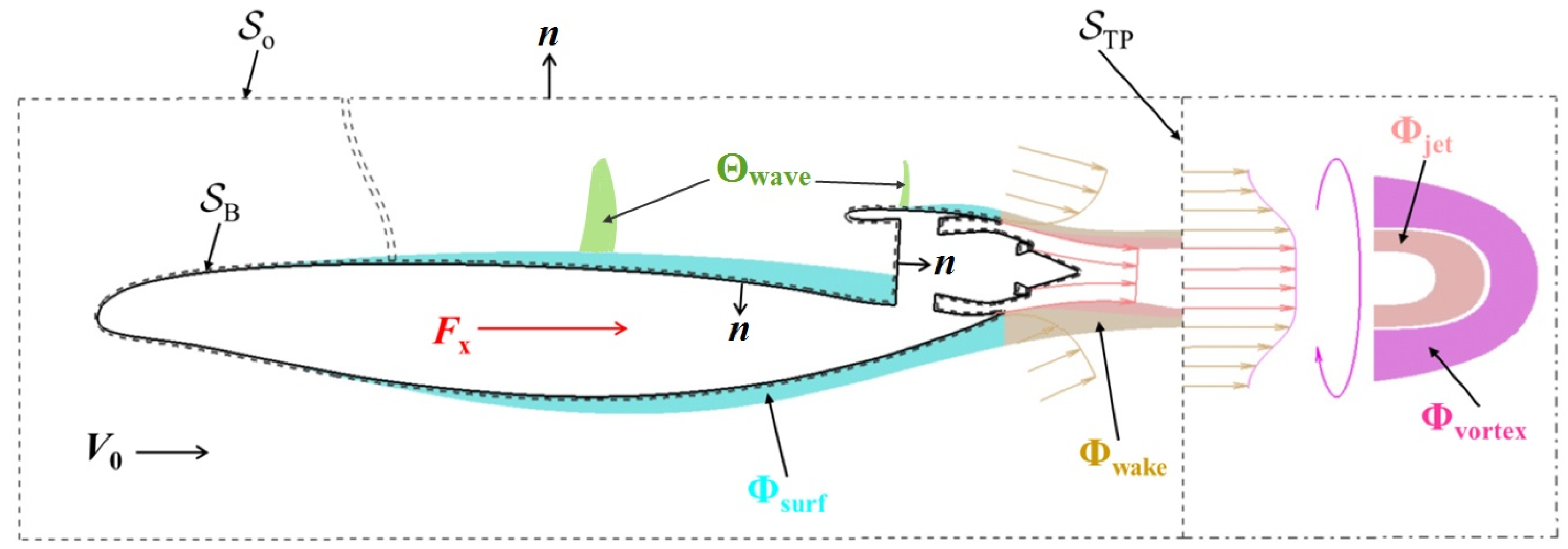
2.2. Aerodynamic Performance Accounting Methods for BLI Layout
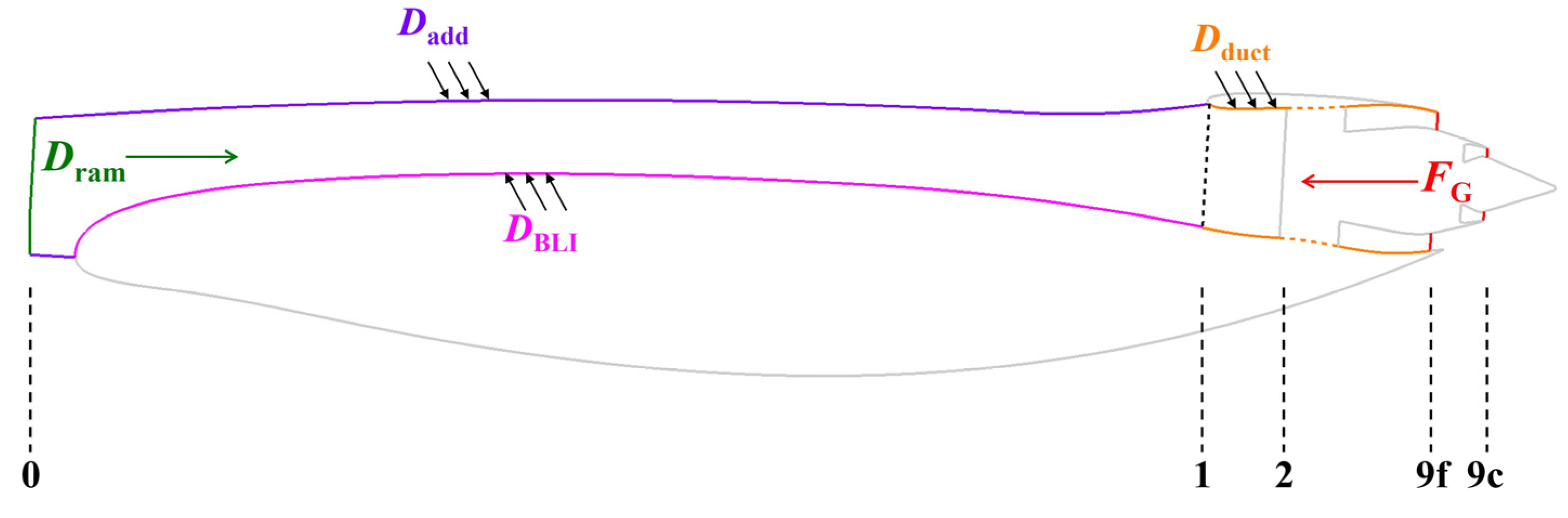
2.2.1. Drag Calculation Method
2.2.2. Power Balance Analysis Method
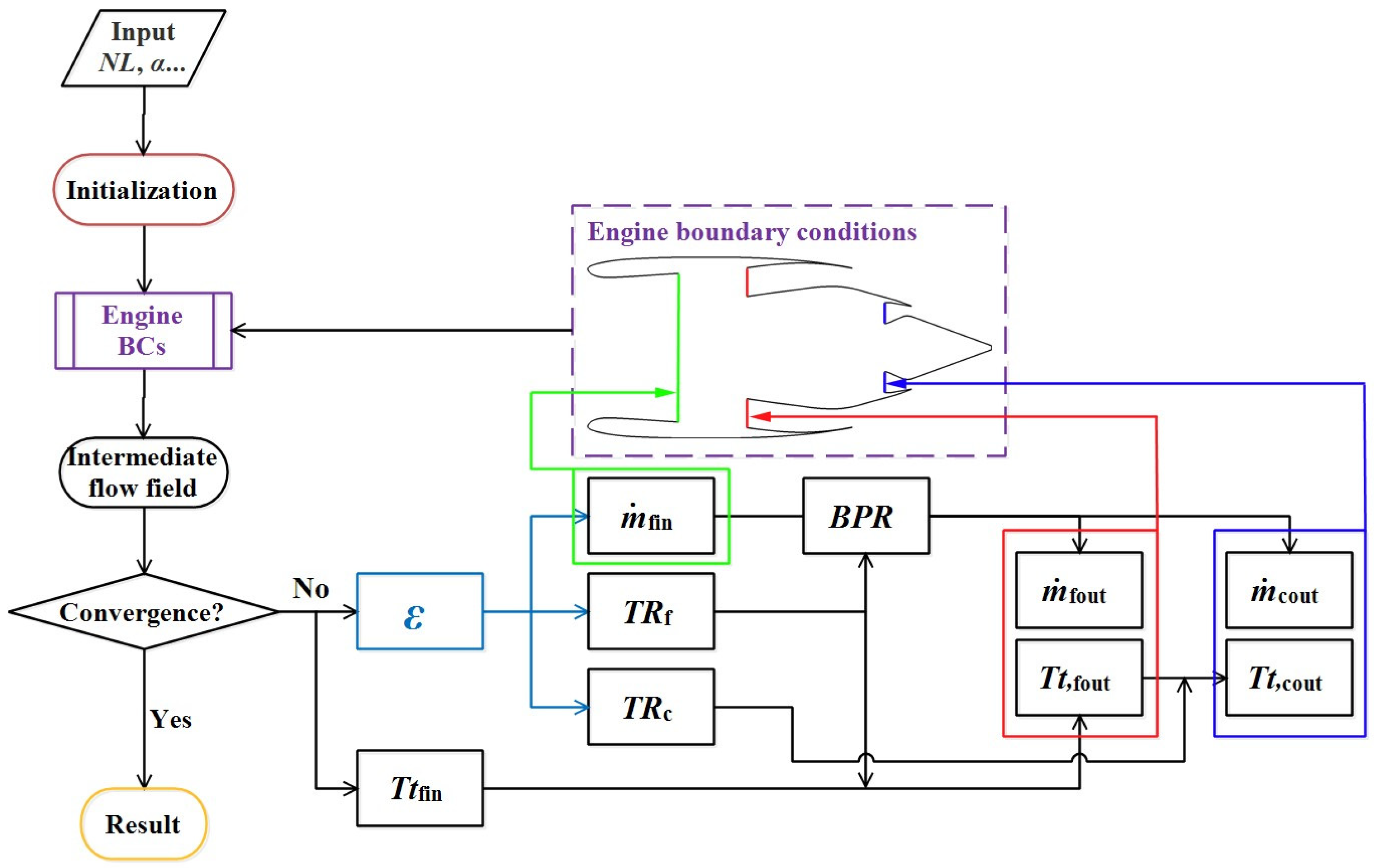
2.3. Engine Boundary Conditions for BLI Layout
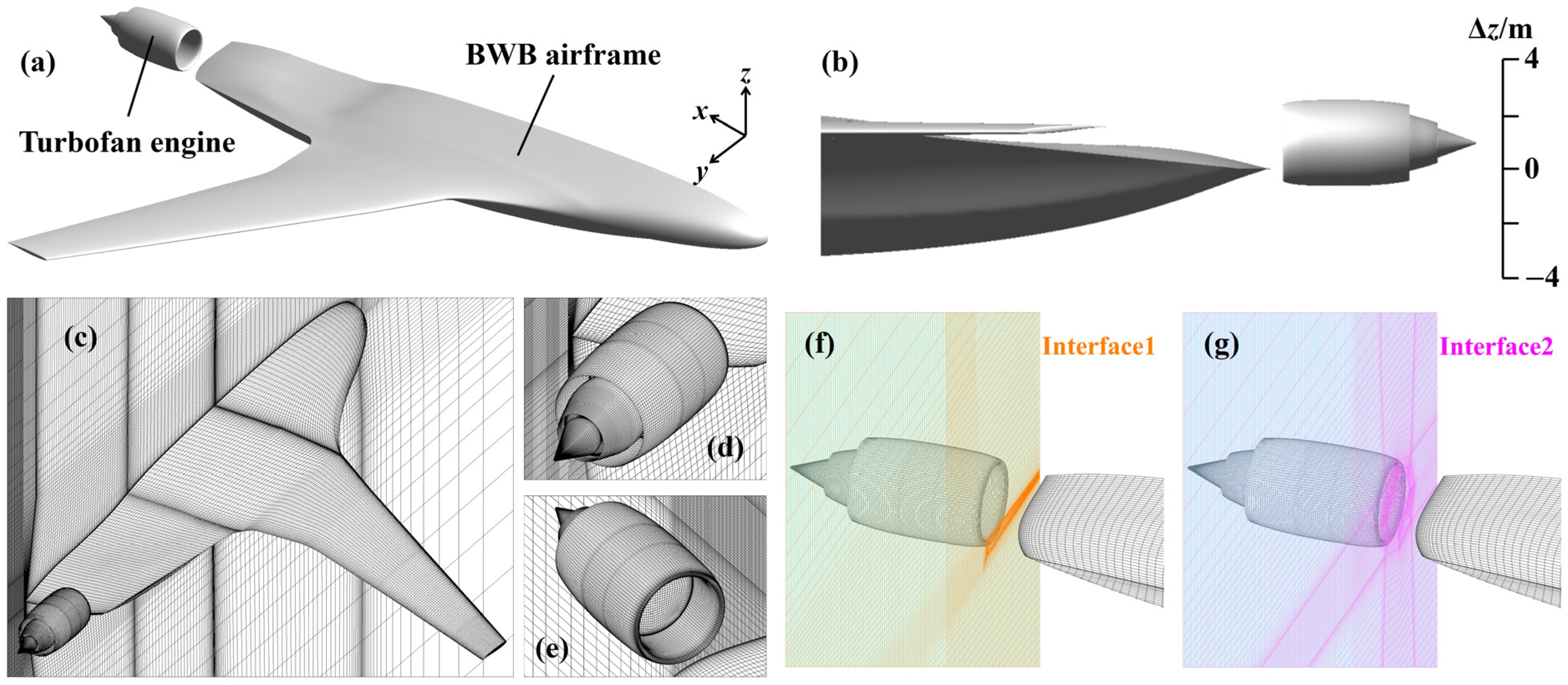
3. Geometric Model and Operating Conditions
- (a)
- The total wetted area is kept constant throughout the transition, thereby avoiding the friction drag reduction typically associated with highly integrated BLI layouts. This approach allows partial separation of BLI benefits from PAI effects.
- (b)
- The engine position is varied continuously, facilitating not only a direct comparison between BLI and non-BLI conditions, but also an investigation of different levels of the ingested boundary layer.
4. Results
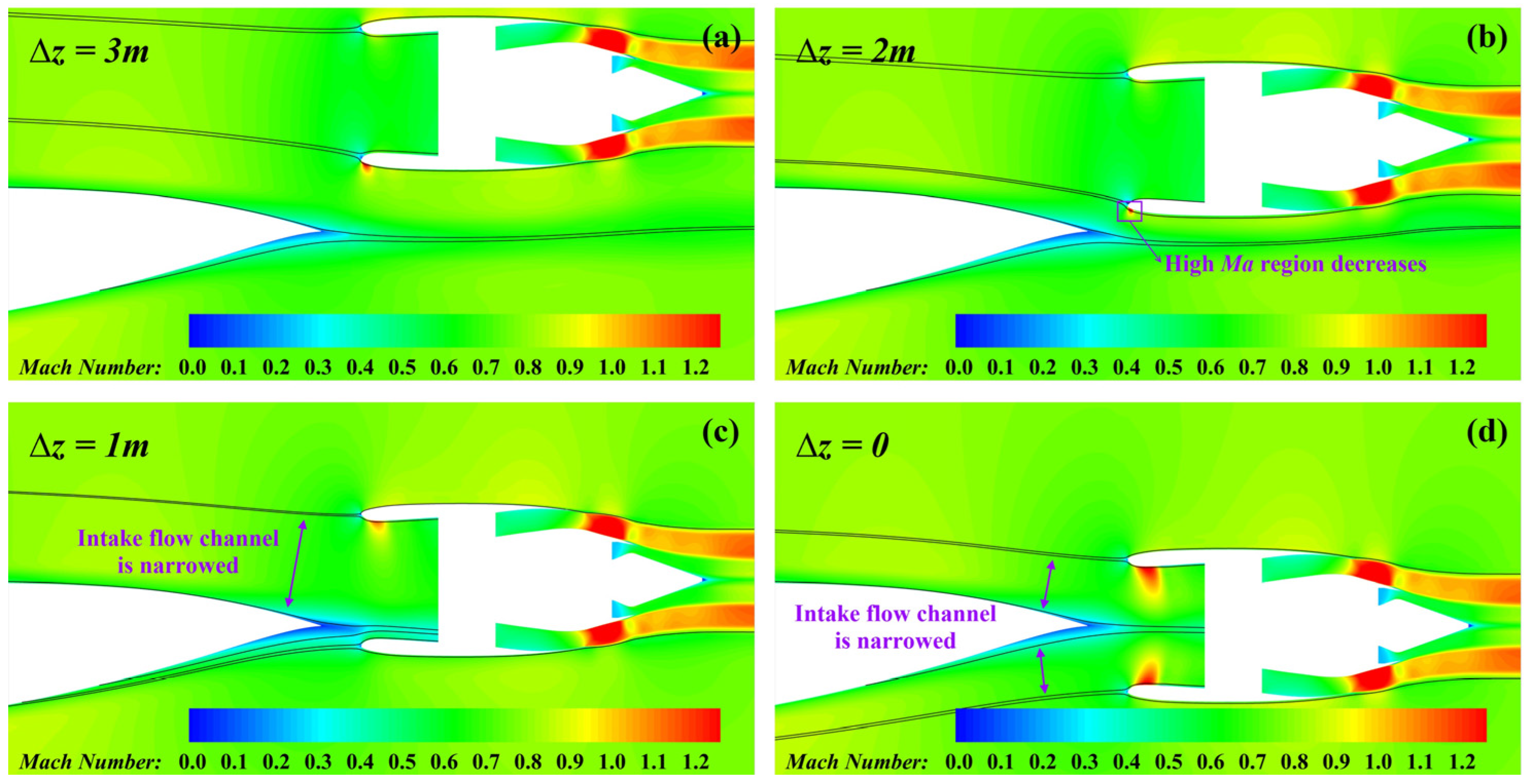
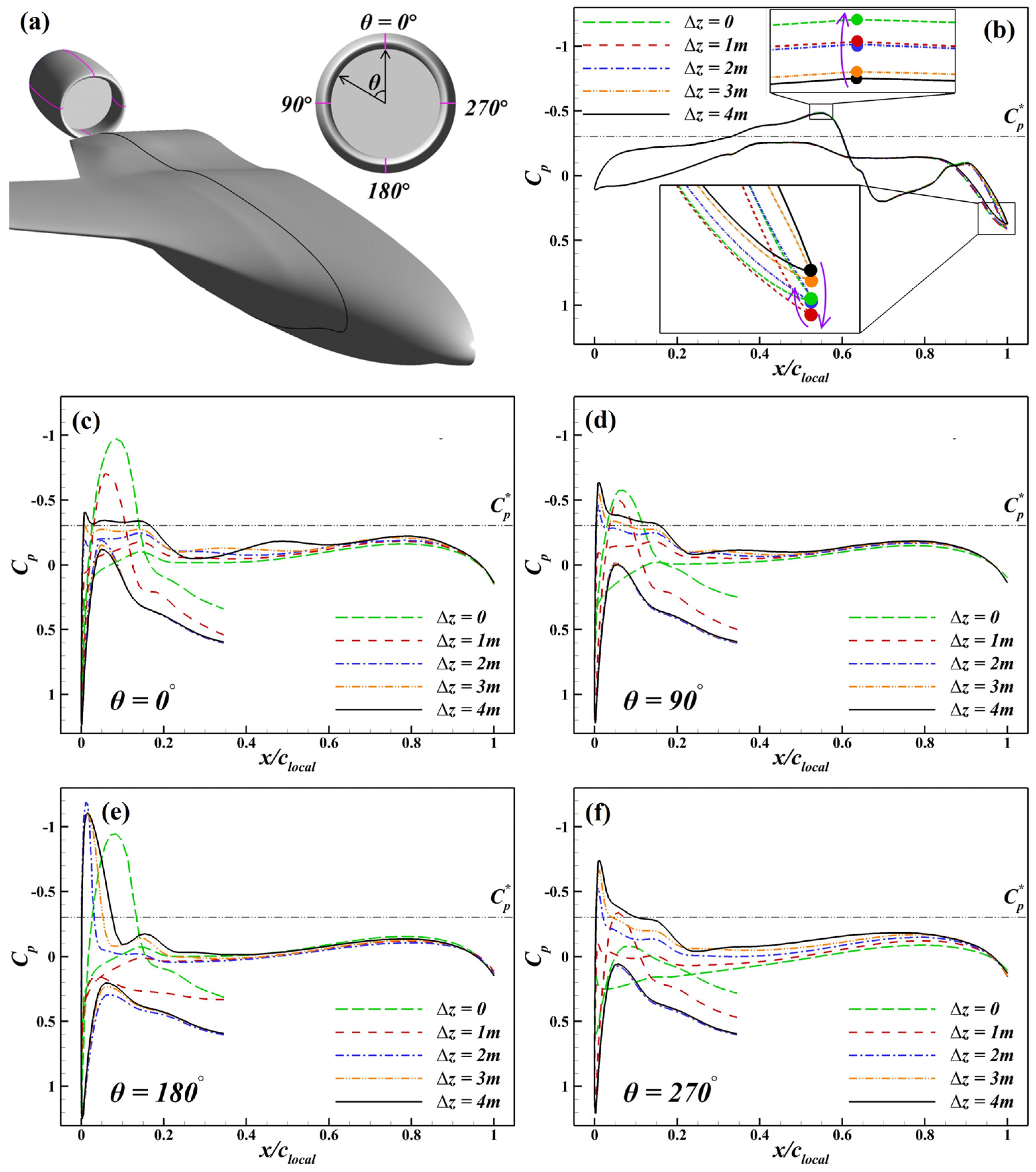
4.1. Overview of Airframe–Engine Flow Interaction
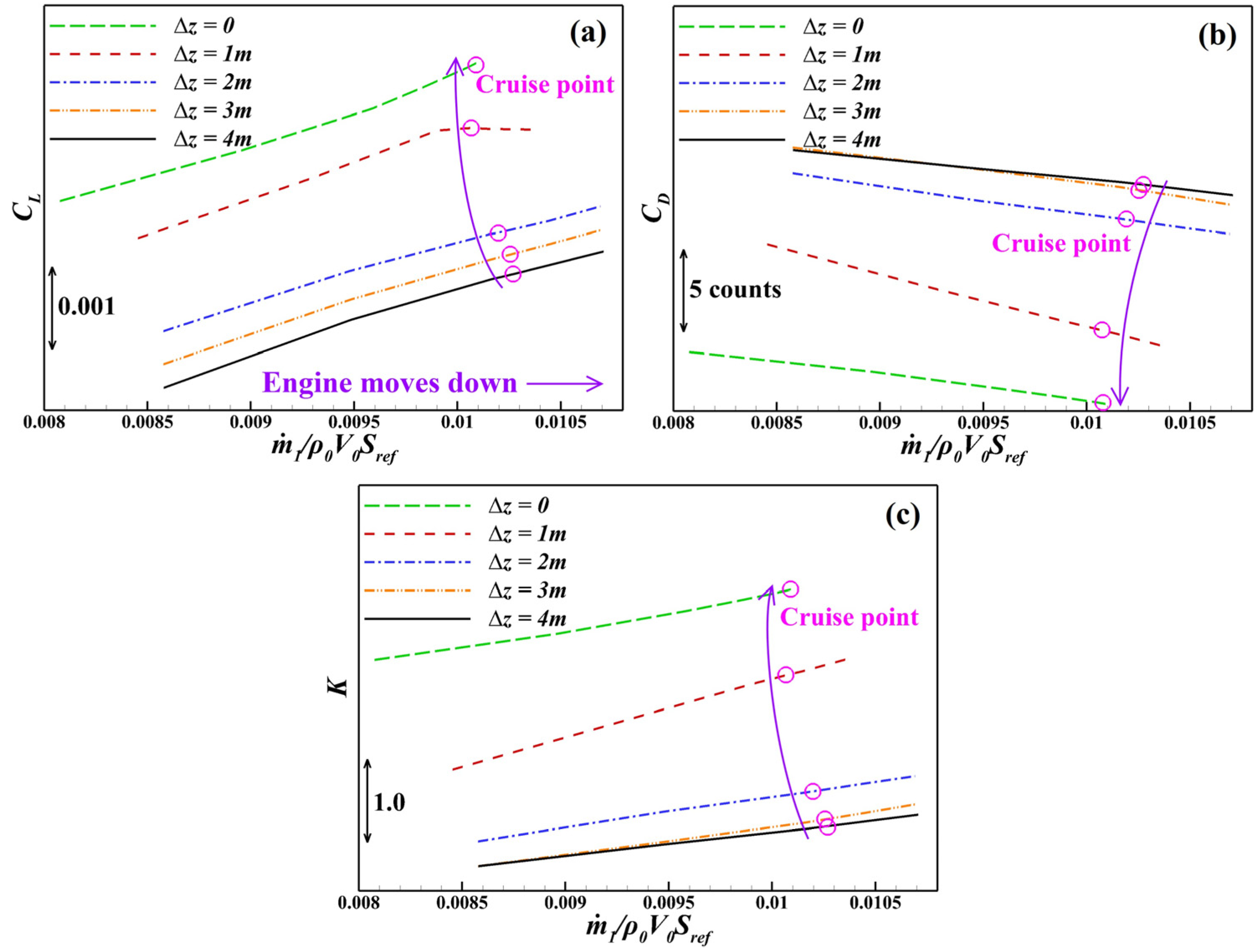
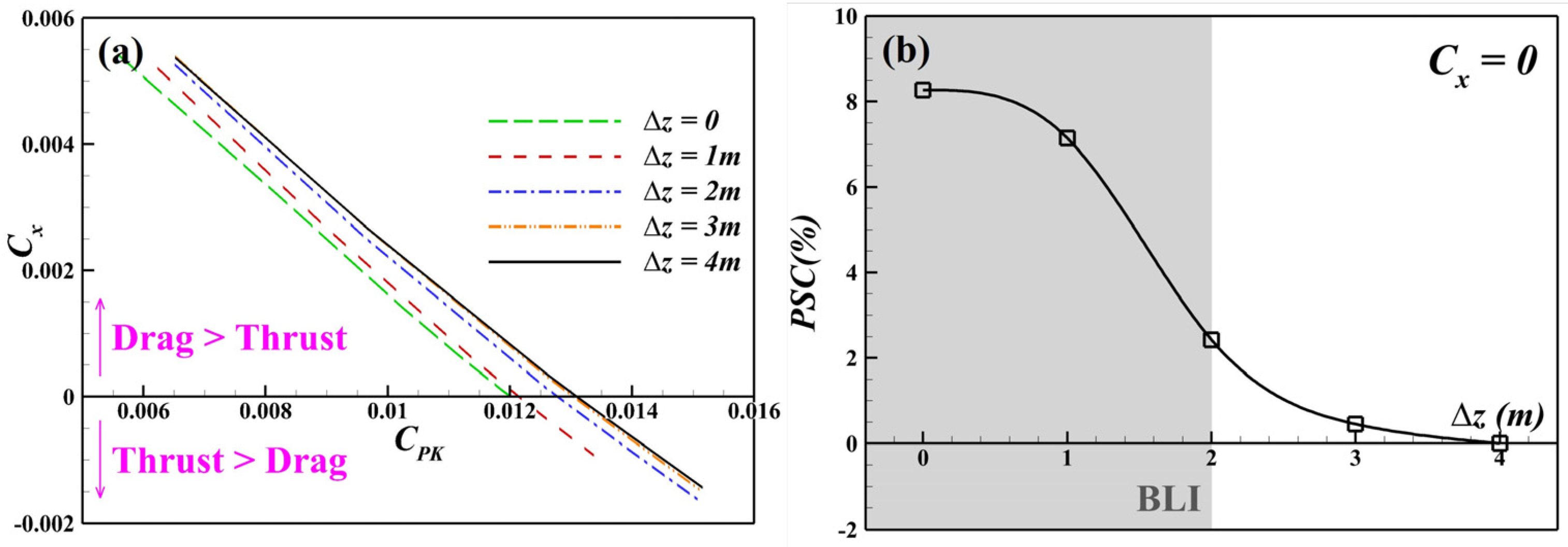
4.2. Momentum-Based Analysis
4.3. Energy-Based Analysis
4.3.1. Engine Mechanical Power and PSC Benefit
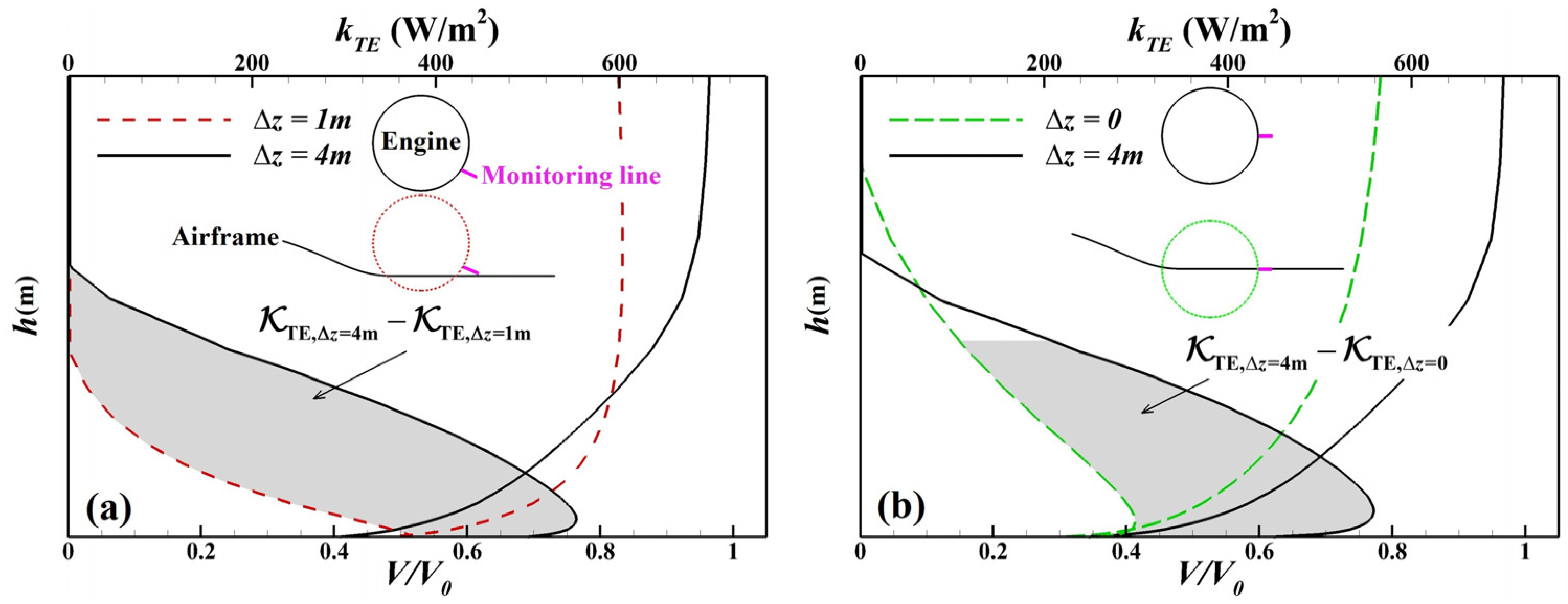
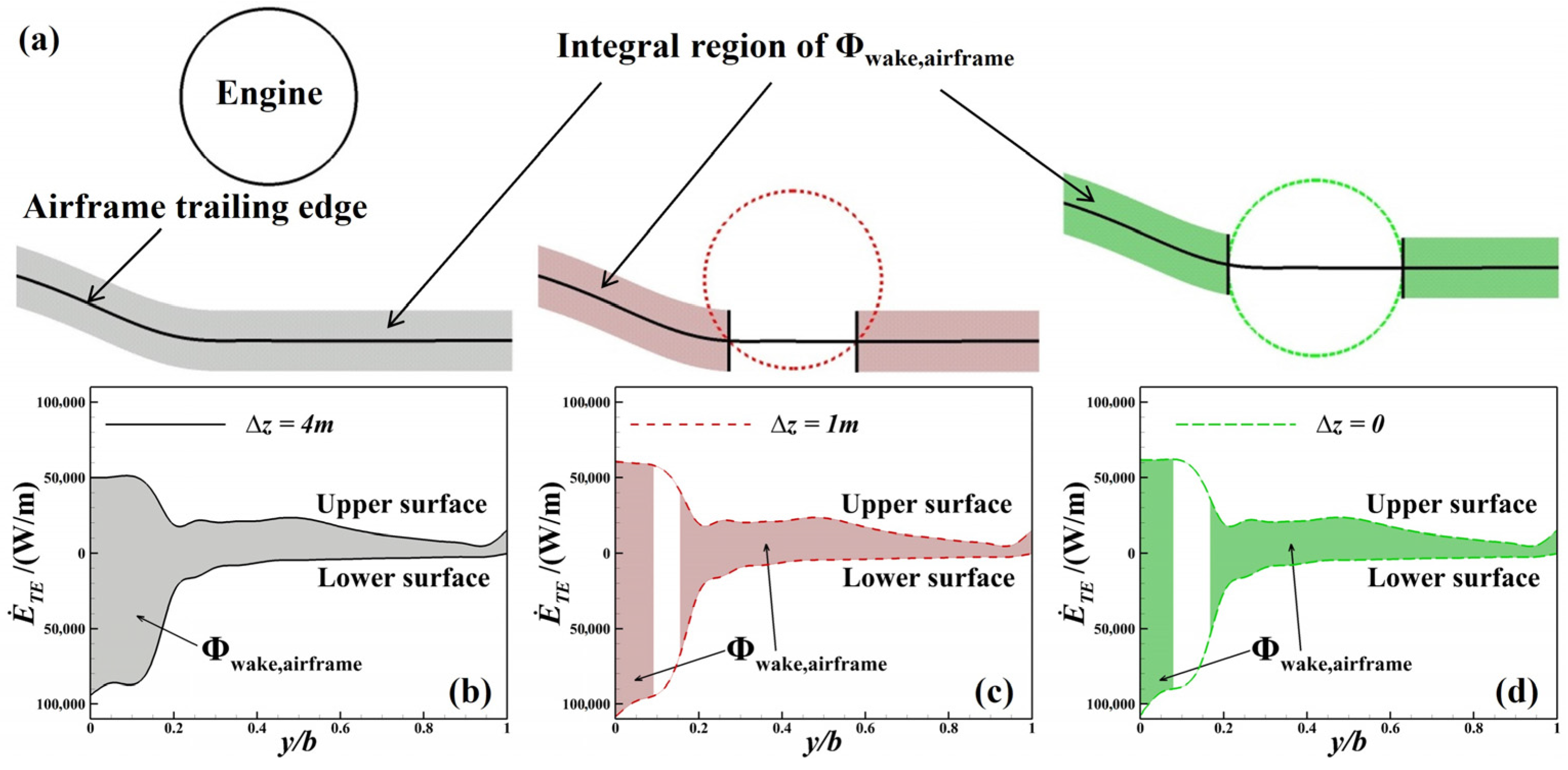
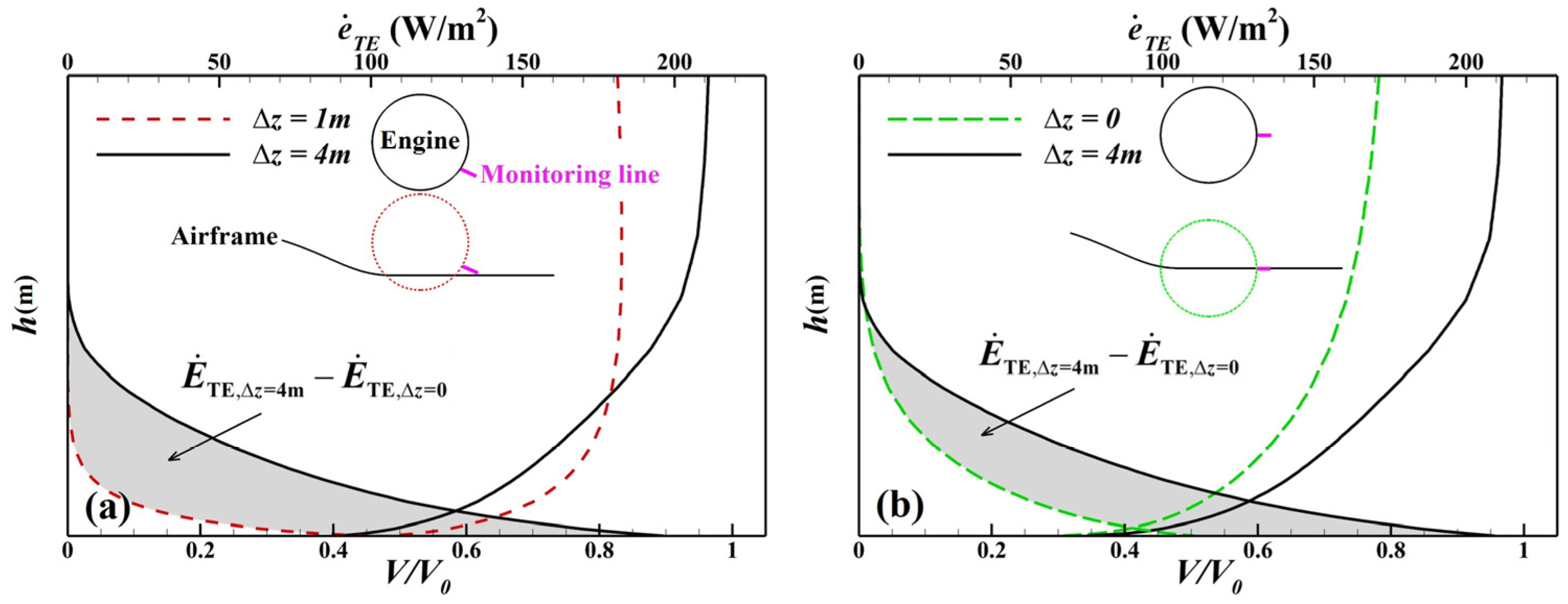
4.3.2. Boundary Layer Dissipation
4.3.3. Wake Dissipation
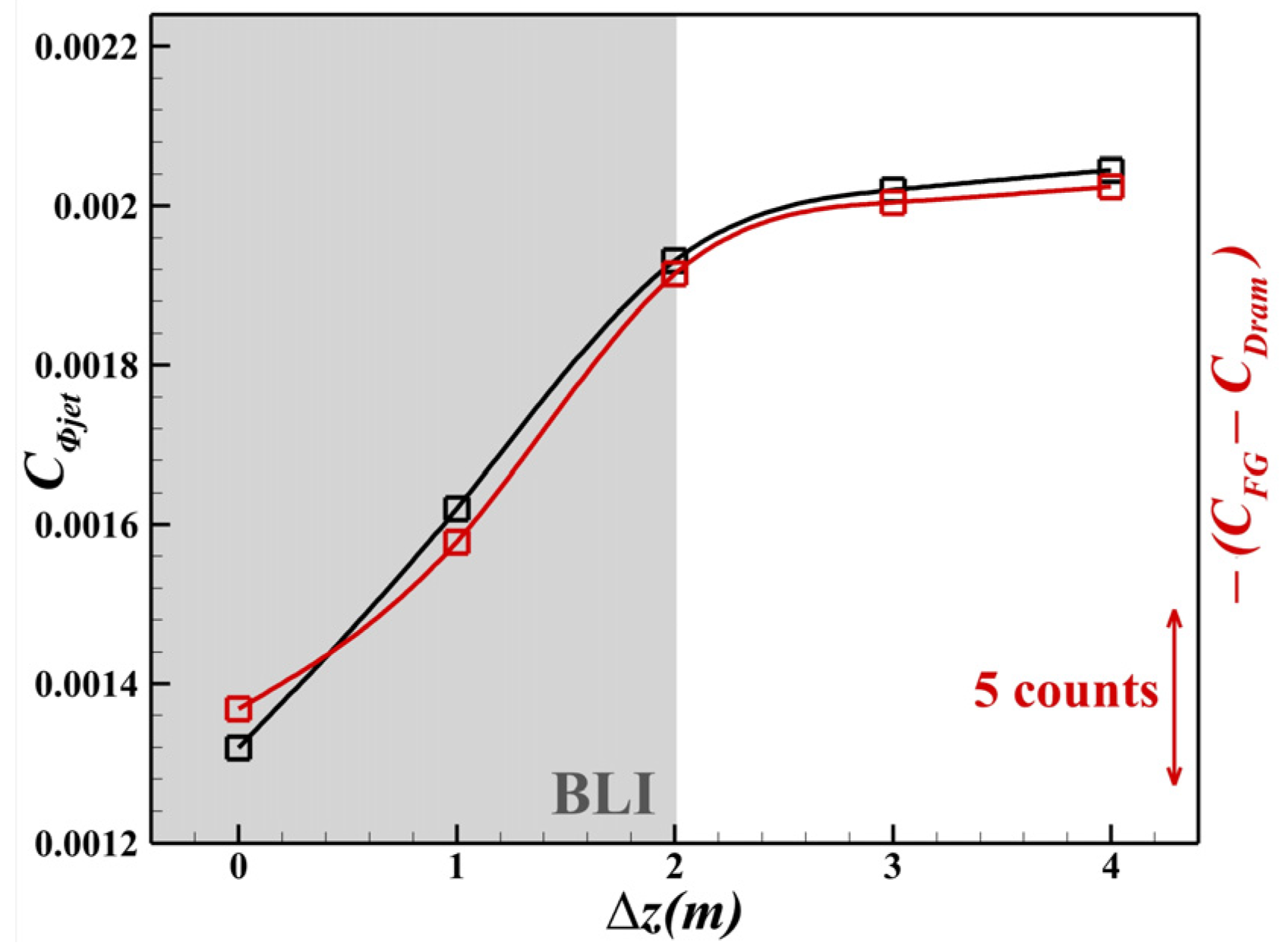
4.3.4. Jet Dissipation
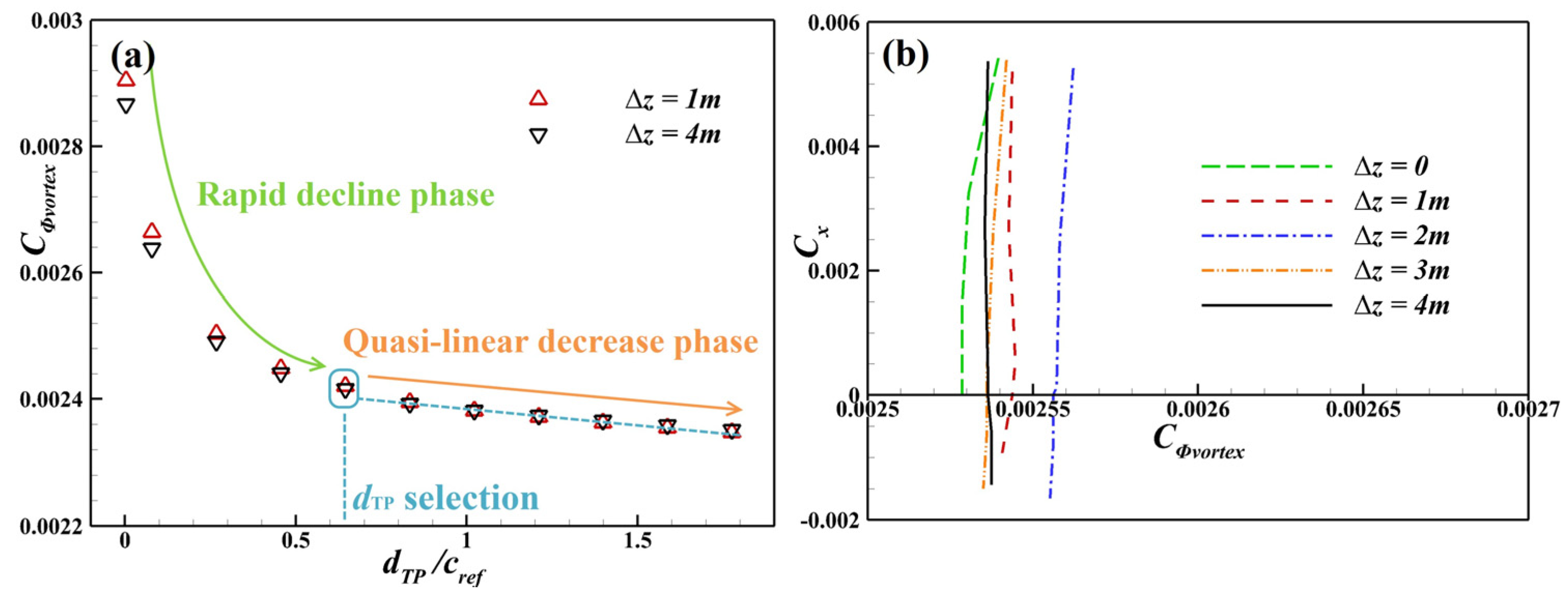
4.3.5. Vortex Dissipation
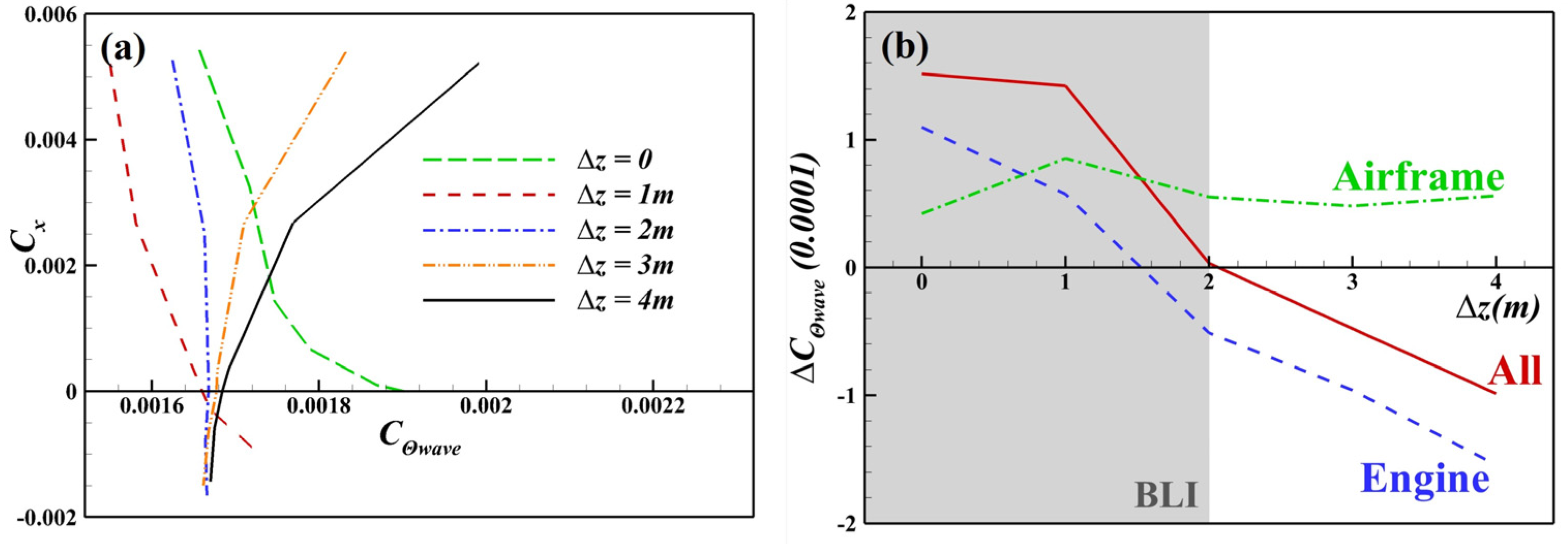
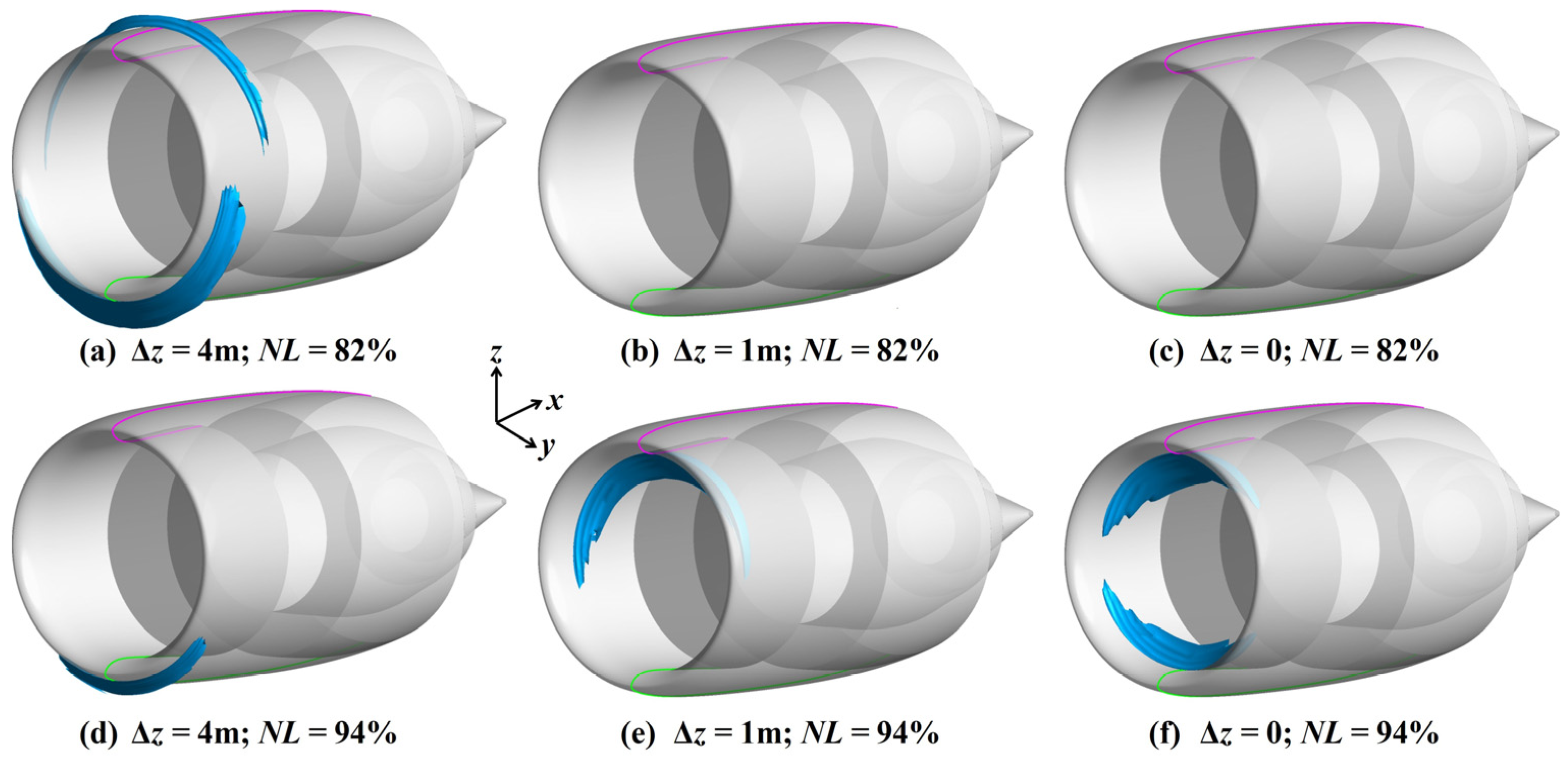
4.3.6. Shock Wave Dissipation
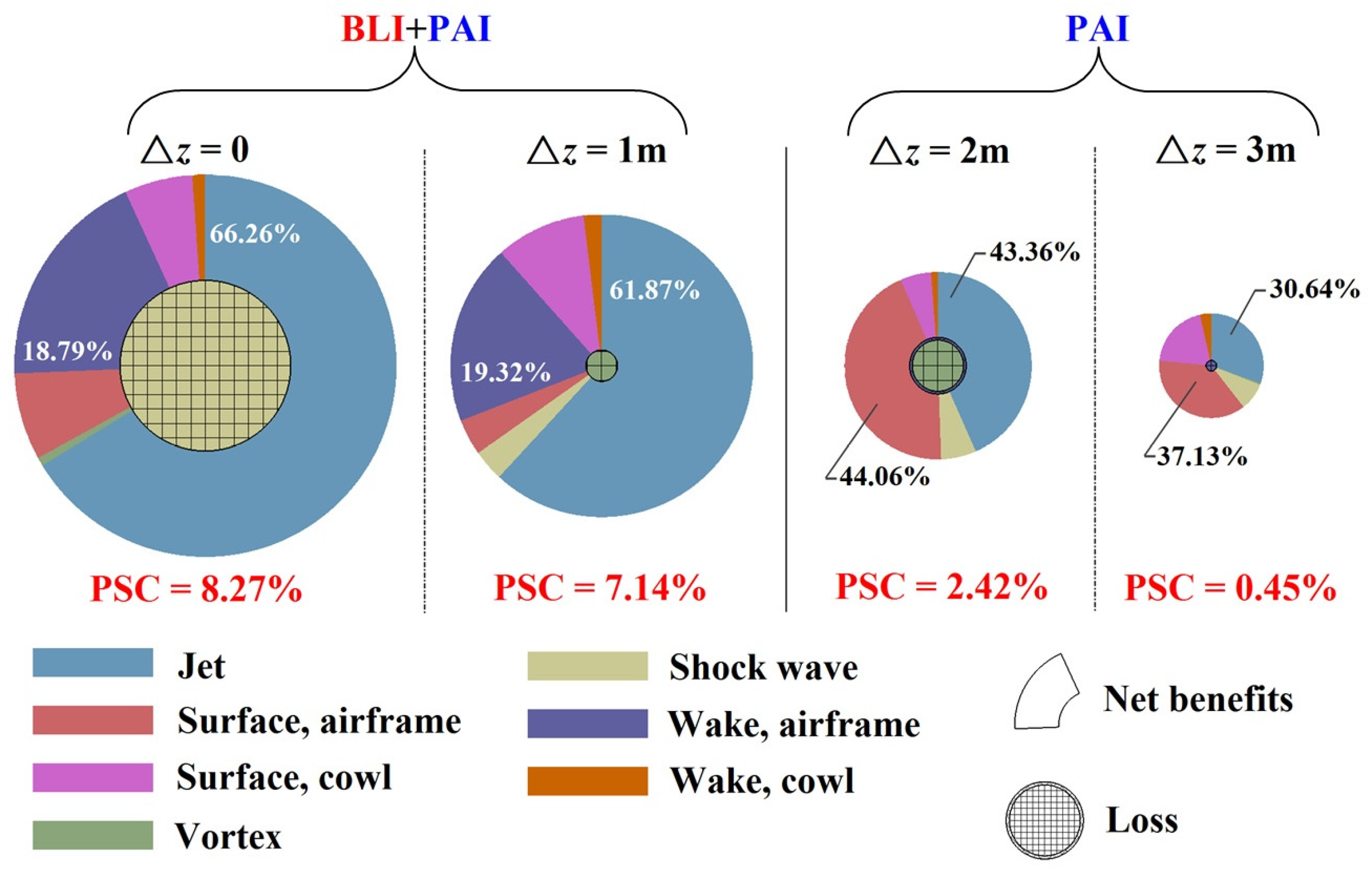
4.3.7. Benefit Compositions
5. Discussion
5.1. Comparison with Prior Works
5.2. Limitations and Design Relevance
6. Conclusions
- (a)
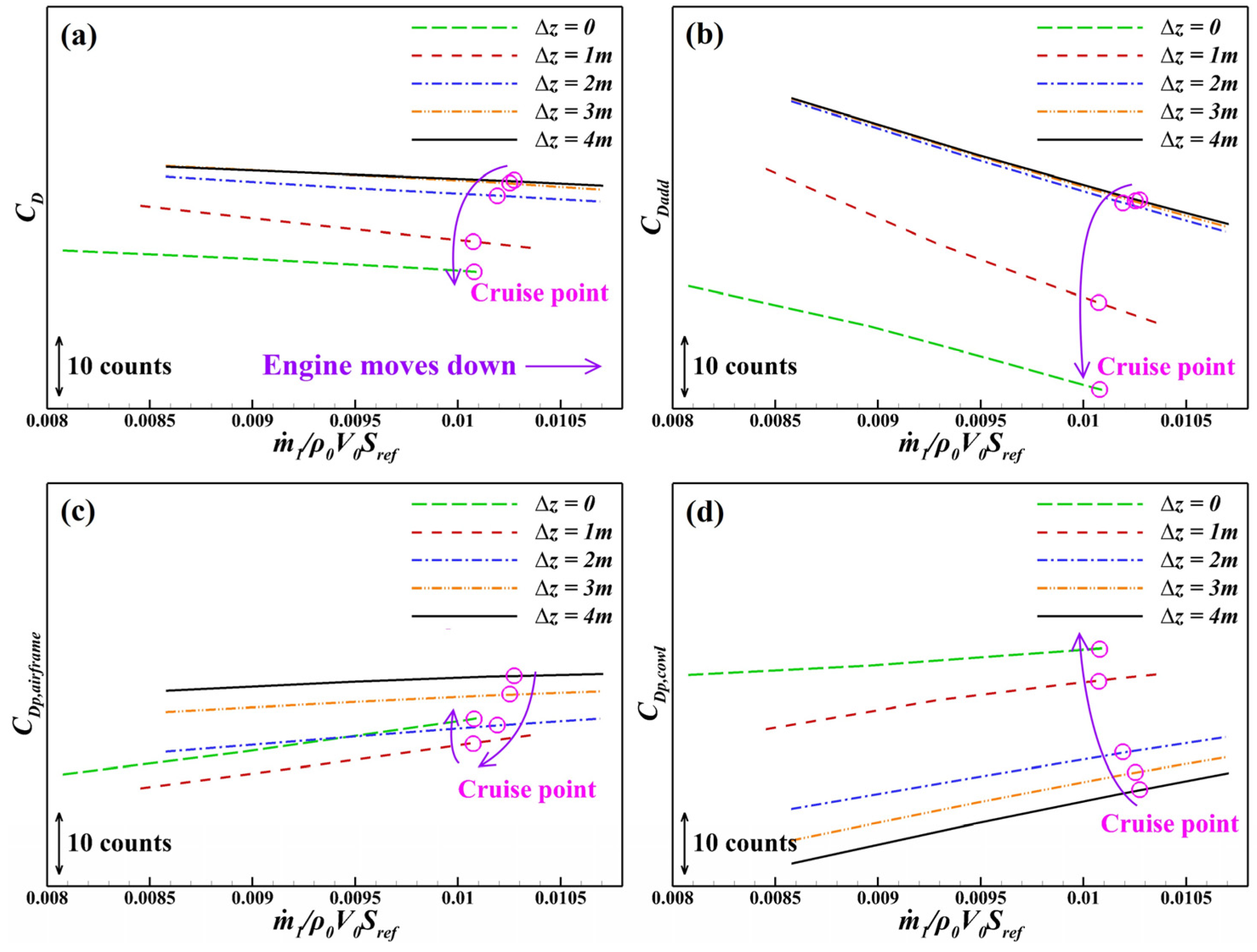
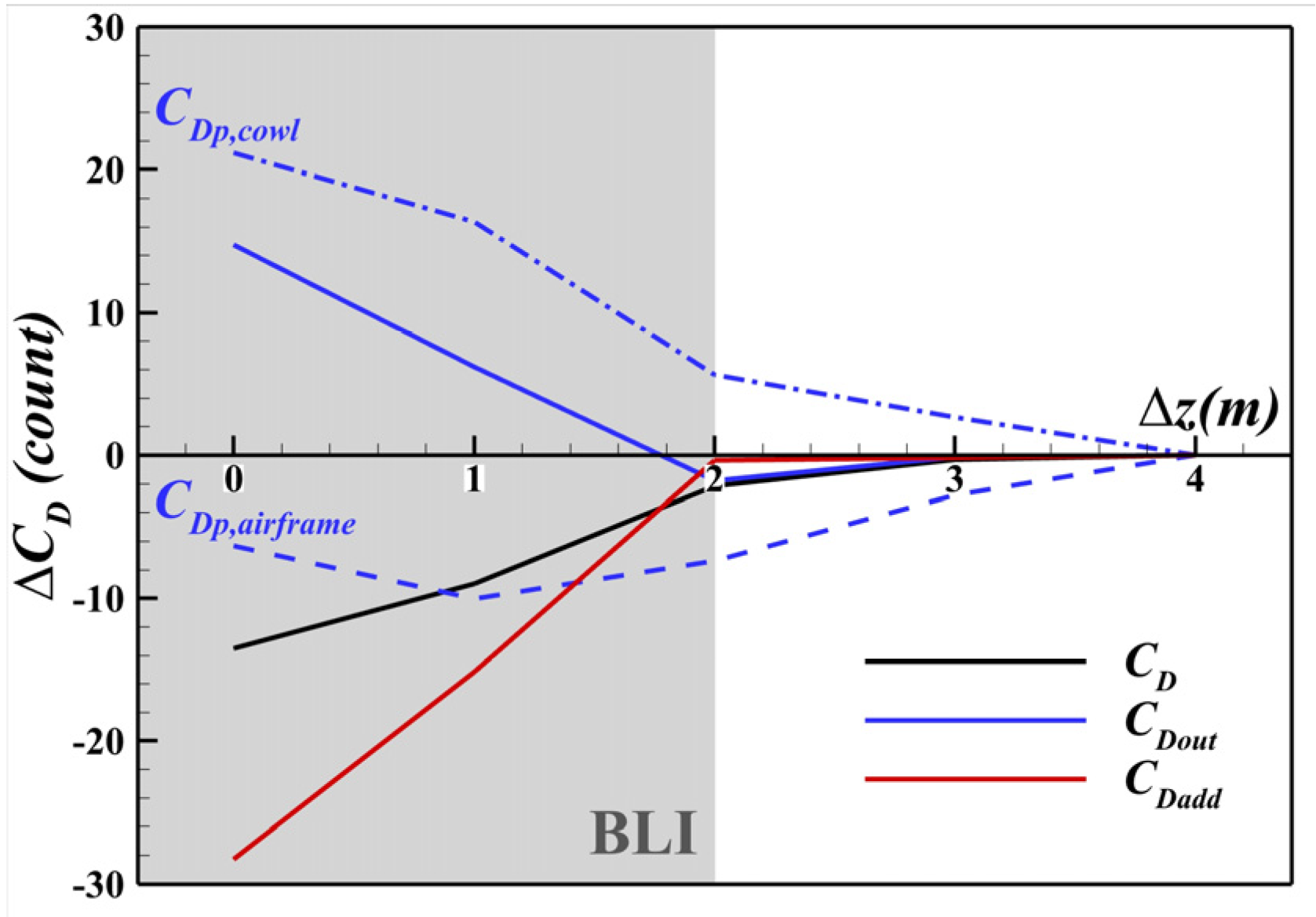
- Transitioning from the non-BLI to the BLI intake yields a 9.0–13.5 counts drag reduction with a negligible change in lift, resulting in a 1.7–2.6 improvement in the lift-to-drag ratio. In the BLI stage, competition emerges between the BLI-induced benefits and the PAI-induced penalties. The additional drag decreases by up to 28 counts, which is attributed primarily to the inlet total pressure reduction. In contrast, the external drag increases by up to 14.5 counts, primarily because the PAI alters the cowl pressure gradient direction via the expansion of the capture streamtube and the outward shift in the inlet stagnation point.
- (b)
- During cruising, the PSC benefits in the BLI stage reach 7.14–8.27%, with the jet dissipation contributing more than 60% and the wake dissipation nearly 20%. As the engine moves closer to the airframe, the PAI has a favourable impact on boundary layer dissipation, while the BLI itself exerts little direct influence. For the portion of the cowl immersed in the airframe wake, both the boundary layer and wake dissipation are significantly suppressed, owing to the reduced edge velocity in the local boundary layer. The reduction in jet dissipation is attributed ultimately to the lower required thrust under the BLI, both of which are governed by the same nozzle flow parameters. The shock wave dissipation exhibits a nonlinear trend with the engine position, as the PAI causes the shock waves to alternately appear on the cowl and within the inlet. The vortex dissipation, dominated by the lift-induced vortices, remains nearly constant across all cases.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | |
| A | Area [m2] |
| a | speed of sound [m/s] |
| CD, CL | Drag and lift coefficients [-] |
| CDadd, CDp | Additional drag and pressure drag coefficients [-] |
| CF | Thrust coefficient [-] |
| Cp, Cp* | Pressure coefficient and critical pressure coefficient [-] |
| CPK | Mechanical power coefficient [-] |
| CX | Axial force coefficient [-] |
| CΦ, CΘ | Viscosity and volume dissipation coefficients [-] |
| cref | Reference chord [m] |
| D | (Total) drag [N] |
| Dadd, DBLI, Dduct, Dram | Additional drag, idealized BLI drag, internal drag, and ram drag on the streamtube control volume [N] |
| Dairframe, Dcowl, Dscrub | Drag on airframe, nacelle cowl, and nozzle fairing cone [N] |
| Dairframe_BLI, Dairframe_rest | Force on airframe due to capture streamtube interaction and on airframe excluding capture streamtube region [N] |
| Dadd_BLI, Dout_BLI | BLI additional drag and BLI external drag [N] |
| Dout | External drag, including cowl and airframe drag [N] |
| dTP | Streamwise distance from engine to Trefftz plane [m] |
| Kinetic energy deposited of a certain line [kg m/s3] and per unit length [kg/s3] | |
| F | Thrust [N] |
| FG, Fduct, Fnet | Total thrust, internal thrust, and installed net thrust [N] |
| Fx | Net axial force [N] |
| fd | Dynamic distortion correction factor [-] |
| H | Altitude [m] |
| h | Wall distance or height [m] |
| hL | Height of the low–total-pressure zone [m] |
| K | Lift-to-drag ratio [-] |
| , k | Kinetic energy defect of a certain line [kg m/s3] and per unit length [kg/s3] |
| M | Mach number [-] |
| Mass flow rate [kg/s] | |
| NL | Engine rotational speed [%] |
| n | Unit normal vector to the wall [-] |
| PK | Mechanical power [W] |
| p, pt | Static pressure and total pressure [Pa] |
| PRmin | Minimum total-pressure ratio within the low-pressure zone [-] |
| R | Specific gas constant [J/(kg K)] |
| RA1, RF | Radius of inlet face and fan face [m] |
| Sref | Reference area [m2] |
| Boundary surface [m2] | |
| T, Tt | Static temperature and total temperature [K] |
| TRf, TRc | Fan and core temperature ratio [-] |
| TRf,ηmax | Fan temperature ratio at peak efficiency [-] |
| u, v, w | Velocities along x-, y- and z-axis [m/s] |
| V, V | velocity vector and scalar [m/s] |
| Shock wave region [m3] | |
| x0 | Freestream direction [-] |
| Greek Symbols | |
| α | Angle of attack [°] |
| γ | Isentropic exponent [-] |
| ΔCD | Changes in drag coefficient [-] |
| ΔCΘwave | Change in shock-wave dissipation coefficient from NL = 82% to 94% [-] |
| ΔTRf | Loss in the fan temperature ratio at peak efficiency [-] |
| ΔV | Velocity deficit [m/s] |
| Δy, Δy+ | Wall-normal height [m] and nondimensional wall-normal height [-] of the first-layer mesh |
| Δz | Vertical offset between the airframe trailing edge and the engine axis [m] |
| ε | Average total pressure loss [-] |
| ζ | Shock wave sensor [-] |
| ηP | Propulsion efficiency [-] |
| θ | Circumferential angle [°] |
| Θwave | Shock wave dissipation [W] |
| ν | Kinematic viscosity [m2/s] |
| ρ | Density [kg/m3] |
| τc, τf | Core and fan temperature ratio loss factor [-] |
| τw | Wall stress [Pa] |
| τ | Viscous stress tensor [Pa] |
| Φjet, Φsurf, Φvortex, Φwake | Jet dissipation, boundary layer dissipation, vortex dissipation, and wake dissipation [W] |
| Subscripts and Superscripts | |
| airframe | Airframe |
| B | Body surface |
| c | Engine core |
| clean | Clean inlet condition |
| cout | Boundary condition at core exit |
| cowl | Cowl |
| dis | Distorted inlet condition |
| ed | Edge of the boundary layer |
| f | Fan |
| fin | Boundary condition at fan face |
| fout | Boundary condition at bypass fan exit |
| o | Outer boundary |
| out | Quasi-one-dimensional nozzle |
| ref | Reference distortion condition |
| TE | Trailing edge |
| TP | Trefftz plane |
| 0 | Undisturbed freestream |
| 1 | Inlet |
| 2 | Fan face |
| 9f | Bypass nozzle exit |
| 9c | Core nozzle exit |
| ‘ | Baseline condition |
| Abbreviations | |
| AVIC | Aviation industry corporation of China |
| BC | Boundary condition |
| BLI | Boundary layer ingestion |
| BPR | Bypass ratio [-] |
| BWB | Blended wing body |
| CFD | Computational fluid dynamics |
| PAI | Propulsion–airframe integration |
| PR | Total pressure ratio [-] |
| PSC | Power saving coefficient [-] |
| RANS | Reynolds-averaged Navier–Stokes |
| SST | Shear–stress transport |
| TR | Total temperature ratio [-] |
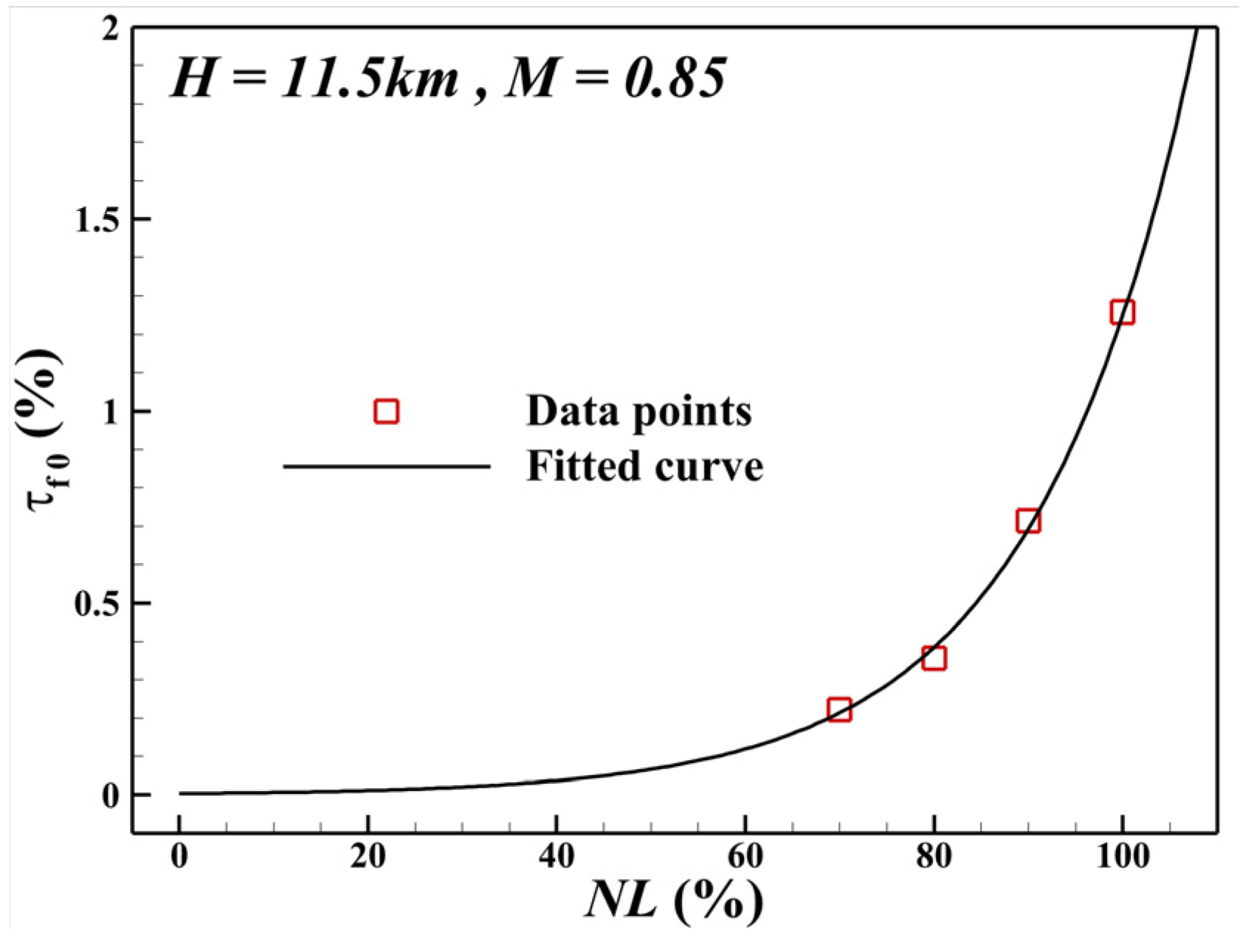
Appendix A. Reference Distortion State and Effect on Fan Performance

| NL (%) | ΔTRf | TRf,ηmax | τf,ref (%) |
|---|---|---|---|
| 100 | 0.01467 | 1.16554 | 1.258 |
| 90 | 0.00798 | 1.11859 | 0.713 |
| 80 | 0.00388 | 1.08656 | 0.357 |
| 70 | 0.00237 | 1.06666 | 0.222 |

References
- Liebeck, R.H. Design of the blended wing body subsonic transport. J. Aircr. 2004, 41, 10–25. [Google Scholar] [CrossRef]
- Qin, N.; Vavalle, A.; Le Moigne, A.; Laban, M.; Hackett, K.; Weinerfelt, P. Aerodynamic considerations of blended wing body aircraft. Prog. Aerosp. Sci. 2004, 40, 321–343. [Google Scholar] [CrossRef]
- Okonkwo, P.; Smith, H. Review of evolving trends in blended wing body aircraft design. Prog. Aerosp. Sci. 2016, 82, 1–23. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, M.; Chen, Y.; Sang, W.; Tan, Z.; Li, D.; Zhang, B. Assessment on critical technologies for conceptual design of blended-wing-body civil aircraft. Chin. J. Aeronaut. 2019, 32, 1797–1827. [Google Scholar] [CrossRef]
- Xin, Z.; Chen, Z.; Gu, W.; Wang, G.; Tan, Z.; Li, D.; Zhang, B. Nacelle-airframe integration design method for blended-wing-body transport with podded engines. Chin. J. Aeronaut. 2019, 32, 1860–1868. [Google Scholar] [CrossRef]
- Diamantidou, D.E.; Hosain, M.L.; Kyprianidis, K.G. Recent advances in boundary layer ingestion technology of evolving powertrain systems. Sustainability 2022, 14, 1731. [Google Scholar] [CrossRef]
- Moirou, N.G.M.; Sanders, D.S.; Laskaridis, P. Advancements and prospects of boundary layer ingestion propulsion concepts. Prog. Aerosp. Sci. 2023, 138, 100897. [Google Scholar] [CrossRef]
- Smith, L.H. Wake ingestion propulsion benefit. J. Propuls. Power 1993, 9, 74–82. [Google Scholar] [CrossRef]
- Drela, M. Power balance in aerodynamic flows. AIAA J. 2009, 47, 1761–1771. [Google Scholar] [CrossRef]
- Arntz, A.; Atinault, O.; Merlen, A. Exergy-based formulation for aircraft aeropropulsive performance assessment: Theoretical development. AIAA J. 2015, 53, 1627–1639. [Google Scholar] [CrossRef]
- Lv, P.; Rao, A.G.; Ragni, D.; Veldhuis, L. Performance analysis of wake and boundary-layer ingestion for aircraft design. J. Aircr. 2016, 53, 1517–1526. [Google Scholar] [CrossRef]
- Lv, P.; Zhang, M.; Cao, F.; Lin, D.; Mo, L. 2D numerical study on the flow mechanisms of boundary layer ingestion through power-based analysis. Aerospace 2022, 9, 184. [Google Scholar] [CrossRef]
- Mutangara, N.E.; Smith, L.; Craig, K.J.; Sanders, D.S. Potential for energy recovery from boundary-layer ingesting actuator disk propulsion. J. Aircr. 2024, 61, 611–624. [Google Scholar] [CrossRef]
- Kim, H.; Felder, J. Control volume analysis of boundary layer ingesting propulsion systems with or without shock wave ahead of the inlet. In Proceedings of the 49th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011; p. 222. [Google Scholar]
- Habermann, A.L.; Bijewitz, J.; Seitz, A.; Hornung, M. Performance bookkeeping for aircraft configurations with fuselage wake-filling propulsion integration. CEAS Aeronaut. J. 2019, 11, 529–551. [Google Scholar] [CrossRef]
- Hendricks, E.S. A Review of Boundary Layer Ingestion Modeling Approaches for Use in Conceptual Design. NASA/TM—2018-219926; NASA Glenn Research Center: Cleveland, OH, USA, 2018. [Google Scholar]
- Menegozzo, L.; Benini, E. Boundary layer ingestion propulsion: A review on numerical modeling. J. Eng. Gas Turbines Power 2020, 142, 120801. [Google Scholar] [CrossRef]
- Budziszewski, N.; Friedrichs, J. Modelling of a boundary layer ingesting propulsor. Energies 2018, 11, 708. [Google Scholar] [CrossRef]
- Goldberg, C.; Nalianda, D.; MacManus, D.; Pilidis, P.; Felder, J. Method for simulating the performance of a boundary layer ingesting propulsion system at design and off-design. Aerosp. Sci. Technol. 2018, 78, 312–319. [Google Scholar] [CrossRef]
- de Vega, L.L.; Dufour, G.; Rosa, N.G. Fully coupled body force–engine performance methodology for boundary layer ingestion. J. Propuls. Power 2021, 37, 192–201. [Google Scholar] [CrossRef]
- Hall, D.K.; Lieu, M. Propulsor models for computational analysis of aircraft aerodynamic performance with boundary layer ingestion. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–15 & 19–21 January 2021; American Institute of Aeronautics and Astronautics: Orlando, FL, USA, 2021; p. 0991. [Google Scholar]
- Blumenthal, B.T.; Elmiligui, A.A.; Geiselhart, K.A.; Campbell, R.L.; Maughmer, M.D.; Schmitz, S. Computational investigation of a boundary-layer-ingestion propulsion system. J. Aircr. 2018, 55, 1141–1153. [Google Scholar] [CrossRef]
- Tse, T.; Hall, C. Aerodynamics and power balance of a distributed aft-fuselage boundary layer ingesting aircraft. Aerospace 2023, 10, 122. [Google Scholar] [CrossRef]
- Chen, Z.; Galbraith, M.C.; Spakovszky, Z.S.; Greitzer, E.M.; Sabnis, J.S. Tail-integrated boundary layer ingesting propulsion systems for turbo-electric aircraft. J. Turbomach. 2023, 146, 021004. [Google Scholar] [CrossRef]
- Fernández, A.M.; Smith, H. Effect of a fuselage boundary layer ingesting propulsor on airframe forces and moments. Aerosp. Sci. Technol. 2020, 100, 105808. [Google Scholar] [CrossRef]
- Machado, L.M.; Chau, T.; Duensing, J. Toward the development of an underwing boundary layer ingesting distributed propulsion system for the SUSAN electrofan. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024; p. 1327. [Google Scholar]
- Seitz, A.; Habermann, A.L.; Peter, F.; Troeltsch, F.; Pardo, A.C.; Corte, B.D.; van Sluis, M.; Goraj, Z.; Kowalski, M.; Zhao, X.; et al. Proof of concept study for fuselage boundary layer ingesting propulsion. Aerospace 2021, 8, 16. [Google Scholar] [CrossRef]
- Zhao, X.; Van Hoorn, P.; Yao, H.-D.; Alderman, J. Parameter sensitivity study on inflow distortion of boundary layer ingested turbofans. Aerospace 2022, 9, 426. [Google Scholar] [CrossRef]
- Battiston, A.; Magrini, A.; Ponza, R.; Benini, E. Design optimization of rear-fuselage boundary-layer ingestion shrouded propulsor. J. Aircr. 2024, 62, 602–612. [Google Scholar] [CrossRef]
- Chau, T.; Anibal, J.L.; Lowe, B.M.; Machado, L.M.; Duensing, J.C. High-fidelity aeropropulsive assessment of distributed electric propulsion and boundary layer ingestion for the SUSAN electrofan. In Proceedings of the AIAA SCITECH 2025 Forum, Orlando, FL, USA, 12–16 January 2025; p. 1275. [Google Scholar]
- Chan, D.T.; Jones, G.S.; Langston, S.L.; Kwok, A.K. Experimental investigation of a boundary layer ingesting tailcone thruster configuration at the national transonic facility. In Proceedings of the AIAA Aviation Forum and ASCEND 2024, Orlando, FL, USA, 29 July–2 August 2024; p. 3515. [Google Scholar]
- Lengyel-Kampmann, T.; Karboujian, J.; Koc, K.; Schnell, R.; Winkelmann, P. Experimental investigation on a lightweight, efficient, counter-rotating fan with and without boundary layer ingestion. CEAS Aeronaut. J. 2024, 15, 207–226. [Google Scholar] [CrossRef]
- Uranga, A.; Drela, M.; Greitzer, E.M.; Hall, D.K.; Titchener, N.A.; Lieu, M.K.; Siu, N.M.; Casses, C.; Huang, A.C.; Gatlin, G.M.; et al. Boundary layer ingestion benefit of the D8 transport aircraft. AIAA J. 2017, 55, 3693–3708. [Google Scholar] [CrossRef]
- Uranga, A.; Drela, M.; Hall, D.K.; Greitzer, E.M. Analysis of the aerodynamic benefit from boundary layer ingestion for transport aircraft. AIAA J. 2018, 56, 4271–4281. [Google Scholar] [CrossRef]
- Hall, D.K.; Huang, A.C.; Uranga, A.; Greitzer, E.M.; Drela, M.; Sato, S. Boundary layer ingestion propulsion benefit for transport aircraft. J. Propuls. Power 2017, 33, 1118–1129. [Google Scholar] [CrossRef]
- Gray, J.S.; Mader, C.A.; Kenway, G.K.W.; Martins, J.R.R.A. Modeling boundary layer ingestion using a coupled aeropropulsive analysis. J. Aircr. 2018, 55, 1191–1199. [Google Scholar] [CrossRef]
- Yildirim, A.; Gray, J.S.; Mader, C.A.; Martins, J.R.R.A. Boundary-layer ingestion benefit for the STARC-ABL concept. J. Aircr. 2022, 59, 896–911. [Google Scholar] [CrossRef]
- Leifsson, L.; Ko, A.; Mason, W.H.; Schetz, J.A.; Grossman, B.; Haftka, R.T. Multidisciplinary design optimization of blended-wing-body transport aircraft with distributed propulsion. Aerosp. Sci. Technol. 2013, 25, 16–28. [Google Scholar] [CrossRef]
- Kim, H.; Liou, M.-S. Flow simulation and optimal shape design of N3-X hybrid wing body configuration using a body force method. Aerosp. Sci. Technol. 2017, 71, 661–674. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Y.; Wu, J. Energy-based aerodynamic analysis on the blended-wing-body aircraft with boundary layer ingestion. Int. J. Aerosp. Eng. 2022, 2022, 6452099. [Google Scholar] [CrossRef]
- Ochs, S.S.; Tillman, G.; Joo, J.; Voytovych, D.M. Computational fluid dynamics-based analysis of boundary layer ingesting propulsion. J. Propuls. Power 2017, 33, 522–530. [Google Scholar] [CrossRef]
- Hardin, L.; Tillman, G.; Sharma, O.; Berton, J.; Arend, D. Aircraft system study of boundary layer ingesting propulsion. In Proceedings of the 48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Orlando, FL, USA, 30 July–1 August 2012; p. 3993. [Google Scholar]
- Li, Z.; Lu, Y.; Pan, T. Conceptual design of layered distributed propulsion system to improve power-saving benefit of boundary-layer ingestion. Aerospace 2024, 11, 141. [Google Scholar] [CrossRef]
- Sabo, K.M.; Drela, M. Benefits of boundary layer ingestion propulsion. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Orlando, FL, USA, 5–9 January 2015; p. 1667. [Google Scholar]
- Carrier, G.; Atinault, O.; Grenon, R.; Verbecke, C. Numerical and experimental aerodynamic investigations of boundary layer ingestion for improving propulsion efficiency of future air transport. In Proceedings of the 31st AIAA Applied Aerodynamics Conference, Orlando, FL, USA, 5–9 January 2013; p. 2406. [Google Scholar]
- Bilyaz, I.S.; Percin, Ö.B. Aerodynamic measurements and benefit quantification of a boundary layer ingested propulsion system. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024; p. 1199. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, M.; Tao, Y.; Li, J.; Li, D.; Zhang, Y.; Yuan, C.; Sang, W.; Zhang, B. Research on analytical scaling method and scale effects for subscale flight test of blended wing body civil aircraft. Aerosp. Sci. Technol. 2020, 106, 106114. [Google Scholar] [CrossRef]
- Niu, X.; Li, J.; Zhang, H.; Yang, Z. Investigation of improvement design on aileron surface flow state of high lift configuration in BWB. Aerospace 2022, 9, 842. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, J.; Shi, L.; Cui, B. Design optimization for the entire aircraft structure of civil aircraft with blended-wing-body layout. Struct. Multidiscip. Optim. 2024, 67, 106. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H. Crashworthiness analysis of PRSEUS-based blended-wing-body civil aircraft. Aerosp. Sci. Technol. 2024, 146, 108927. [Google Scholar] [CrossRef]
- Strazisar, A.J.; Wood, J.R.; Hathaway, M.D.; Suder, K.L. Laser Anemometer Measurements in a Transonic Axial-Flow Fan Rotor (No. NAS 1.60: 2879); NASA: Washington, DC, USA, 1989. [Google Scholar]
- Adjei, R.A.; Fan, C. Multi-objective design optimization of a transonic axial fan stage using sparse active subspaces. Eng. Appl. Comput. Fluid Mech. 2024, 18, 2325488. [Google Scholar] [CrossRef]
- Da, L.; Hanan, L.; Zhe, Y.; Tianyu, P.; Hai, D.; Qiushi, L. Optimization of a transonic axial-flow compressor under inlet total pressure distortion to enhance aerodynamic performance. Eng. Appl. Comput. Fluid Mech. 2020, 14, 1002–1022. [Google Scholar] [CrossRef]
- Farokhi, S. Aircraft Propulsion, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Sanders, D.S.; Laskaridis, P. Full-aircraft energy-based force decomposition applied to boundary-layer ingestion. AIAA J. 2020, 58, 4357–4373. [Google Scholar] [CrossRef]
- Lovely, D.; Haimes, R. Shock detection from computational fluid dynamics results. In Proceedings of the 14th Computational Fluid Dynamics Conference, Norfolk, VA, USA, 1–5 November 1999; p. 3285. [Google Scholar]
- Debogdan, C.E.; Dicus, J.H.; Evans, D.G.; Soeder, R.H. Effect of a 180 Deg-Extent Inlet Pressure Distortion on the Internal Flow Conditions of a TF30-P-3 (No. E-8206); NASA: Washington, DC, USA, 1975. [Google Scholar]
- Cheng, B.Q.; Tao, Z.Y.; Li, J. Aerodynamic stability analysis of inlet total pressure distortion for turbofan. J. Propuls. Technol. 2003, 24, 22. [Google Scholar]
- Wang, Z.; Shen, X.; Hu, J. Prediction and evaluation of aerodynamic stability of high bypass ratio turbofan engine deployed with thrust reverser. Acta Aeronaut. Astronaut. Sin. 2017, 38, 120192. [Google Scholar]






| Work | Focus | Key Findings |
|---|---|---|
| Smith [8] | Theoretical analysis using the energy-based method | 20% gains under idealized conditions (high propulsor loading, high wake form factor, flattened wake profiles) |
| Sabo & Drela [44] | Experiment with blunt body and downstream fan | >26% fan power saving, validating the theoretical benefit by Smith [8] |
| Uranga et al. [33,34] | Experimental and numerical analysis on D8 | 8.2% PSC gain with >60% from jet and >30% from boundary layer dissipation due to reduced wetted area |
| Yildirim et al. [37] | Optimization of aft-mounted BLI layout | >10% PSC gain by ingesting a large portion of the fuselage boundary layer |
| Zhao et al. [40] | Energy-based analysis on BWB with integrated BLI engine | 5% power saving under current design; >18% theoretical PSC with full fuselage boundary layer ingestion |
| Present study | Momentum- and energy-based analyses of non-integrated BWB–turbofan configuration | 1.7–2.6 lift-to-drag gain; 7.1–8.3% PSC with >60% from jet and ~20% from wake dissipation. Despite nonnegligible PAI and BLI trade-offs, PAI contributes >2% PSC for non-BLI states |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Li, D.; Li, P.; Zhang, B. Momentum- and Energy-Based Analyses of the Aerodynamic Effects of Boundary Layer Ingestion and Propulsion–Airframe Integration on a Blended Wing Body–Turbofan Configuration. Aerospace 2025, 12, 846. https://doi.org/10.3390/aerospace12090846
Wang G, Li D, Li P, Zhang B. Momentum- and Energy-Based Analyses of the Aerodynamic Effects of Boundary Layer Ingestion and Propulsion–Airframe Integration on a Blended Wing Body–Turbofan Configuration. Aerospace. 2025; 12(9):846. https://doi.org/10.3390/aerospace12090846
Chicago/Turabian StyleWang, Gang, Dong Li, Peifeng Li, and Binqian Zhang. 2025. "Momentum- and Energy-Based Analyses of the Aerodynamic Effects of Boundary Layer Ingestion and Propulsion–Airframe Integration on a Blended Wing Body–Turbofan Configuration" Aerospace 12, no. 9: 846. https://doi.org/10.3390/aerospace12090846
APA StyleWang, G., Li, D., Li, P., & Zhang, B. (2025). Momentum- and Energy-Based Analyses of the Aerodynamic Effects of Boundary Layer Ingestion and Propulsion–Airframe Integration on a Blended Wing Body–Turbofan Configuration. Aerospace, 12(9), 846. https://doi.org/10.3390/aerospace12090846





