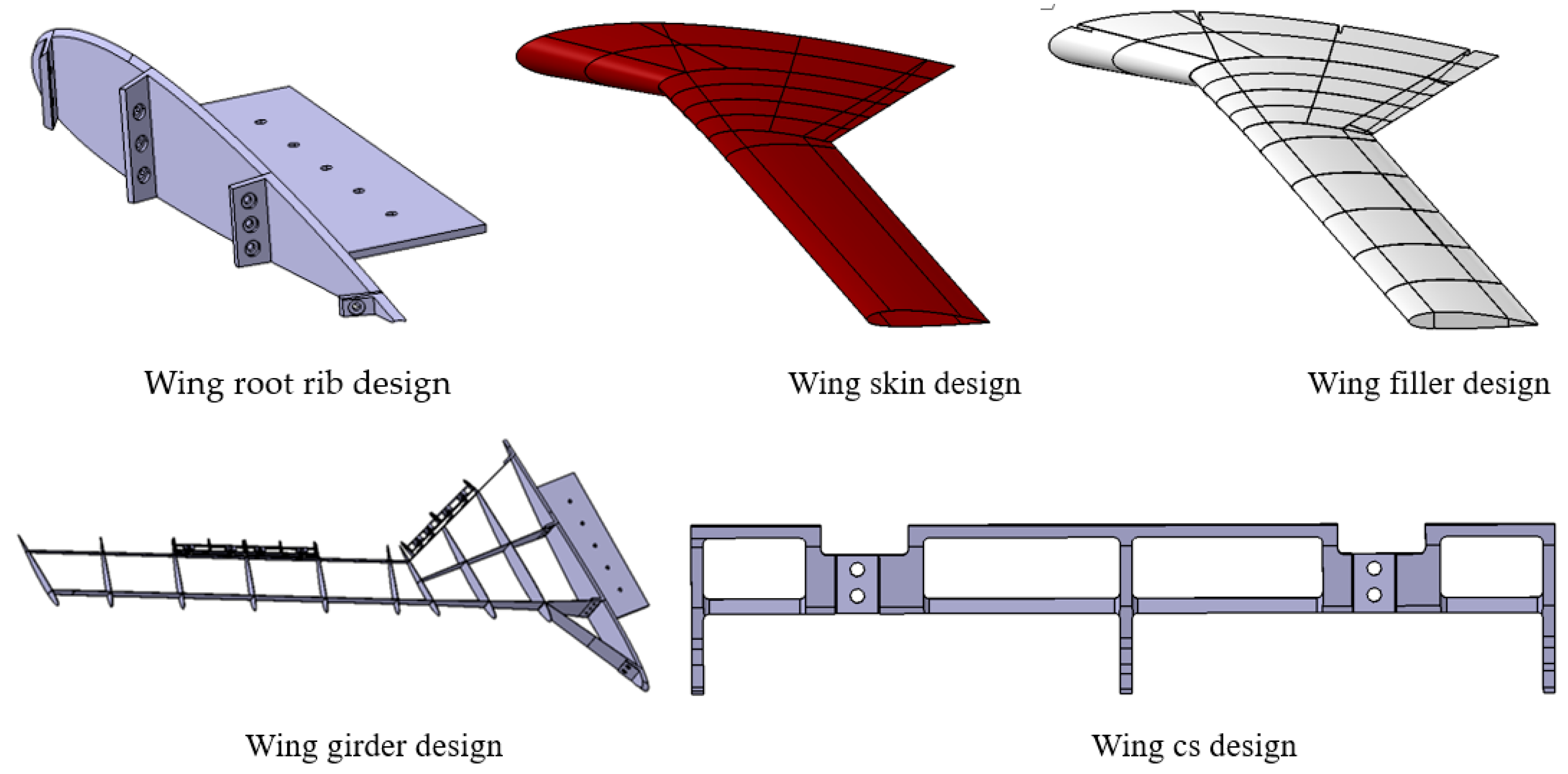
Figure 1.
Geometry design of the present wing model (i.e., there are four wing cs in the present wing).
Figure 1.
Geometry design of the present wing model (i.e., there are four wing cs in the present wing).
Figure 2.
High-aspect-ratio wing model.
Figure 2.
High-aspect-ratio wing model.
Figure 3.
Physical drawing of wing girder and rib structure.
Figure 3.
Physical drawing of wing girder and rib structure.
Figure 4.
Physical drawing of wing interior filled with EPS foam.
Figure 4.
Physical drawing of wing interior filled with EPS foam.
Figure 5.
Photograph of the assembled high-aspect-ratio aircraft wing.
Figure 5.
Photograph of the assembled high-aspect-ratio aircraft wing.
Figure 6.
Finite element model of the high-aspect-ratio aircraft wing. (i.e., different colors mean different skin partitions).
Figure 6.
Finite element model of the high-aspect-ratio aircraft wing. (i.e., different colors mean different skin partitions).
Figure 7.
Schematic diagram of the impact hammer modal testing principle.
Figure 7.
Schematic diagram of the impact hammer modal testing principle.
Figure 8.
Layout of model measurement points.
Figure 8.
Layout of model measurement points.
Figure 9.
Layout of measurement points on site and installation of the LMS system.
Figure 9.
Layout of measurement points on site and installation of the LMS system.
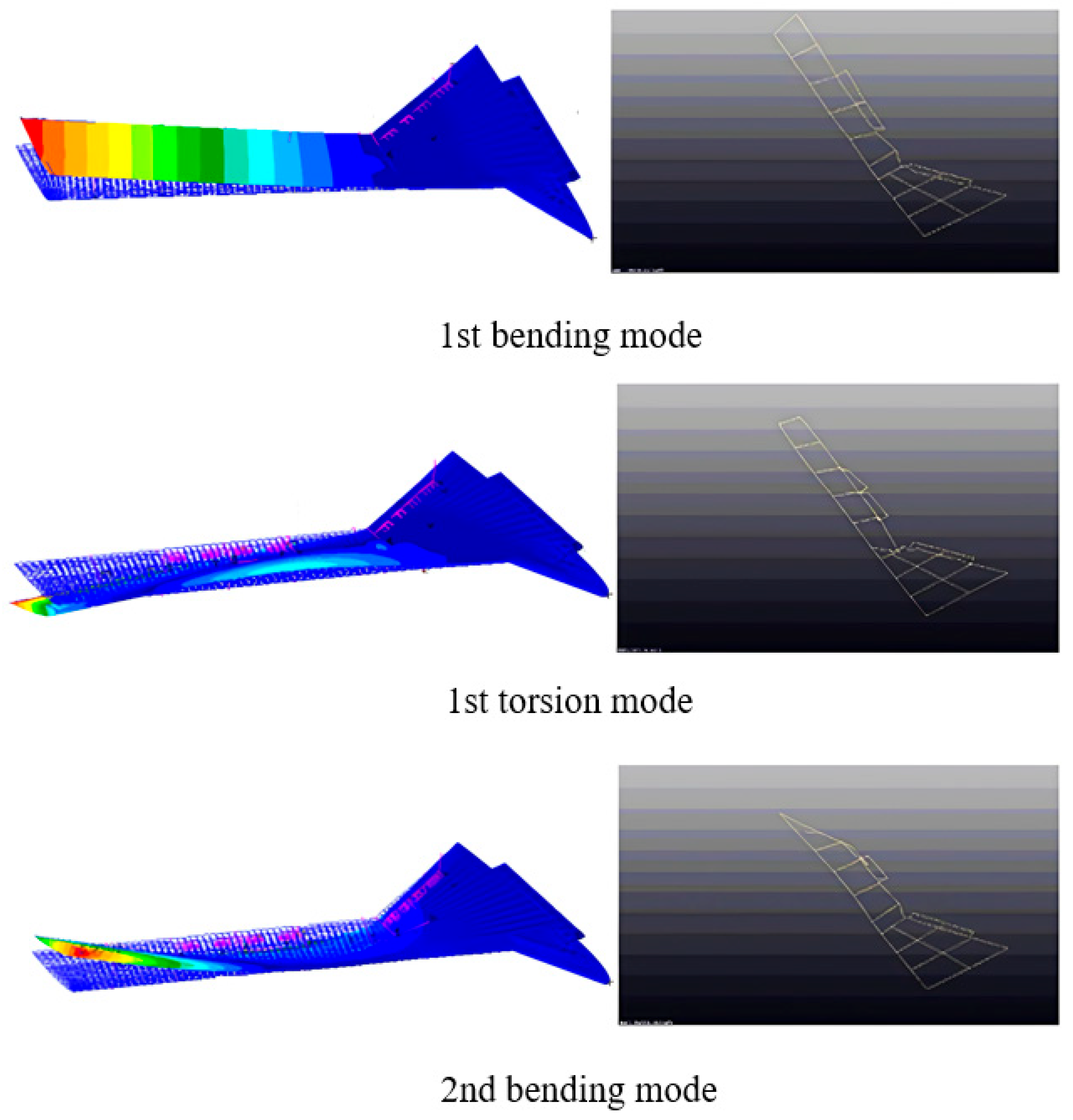
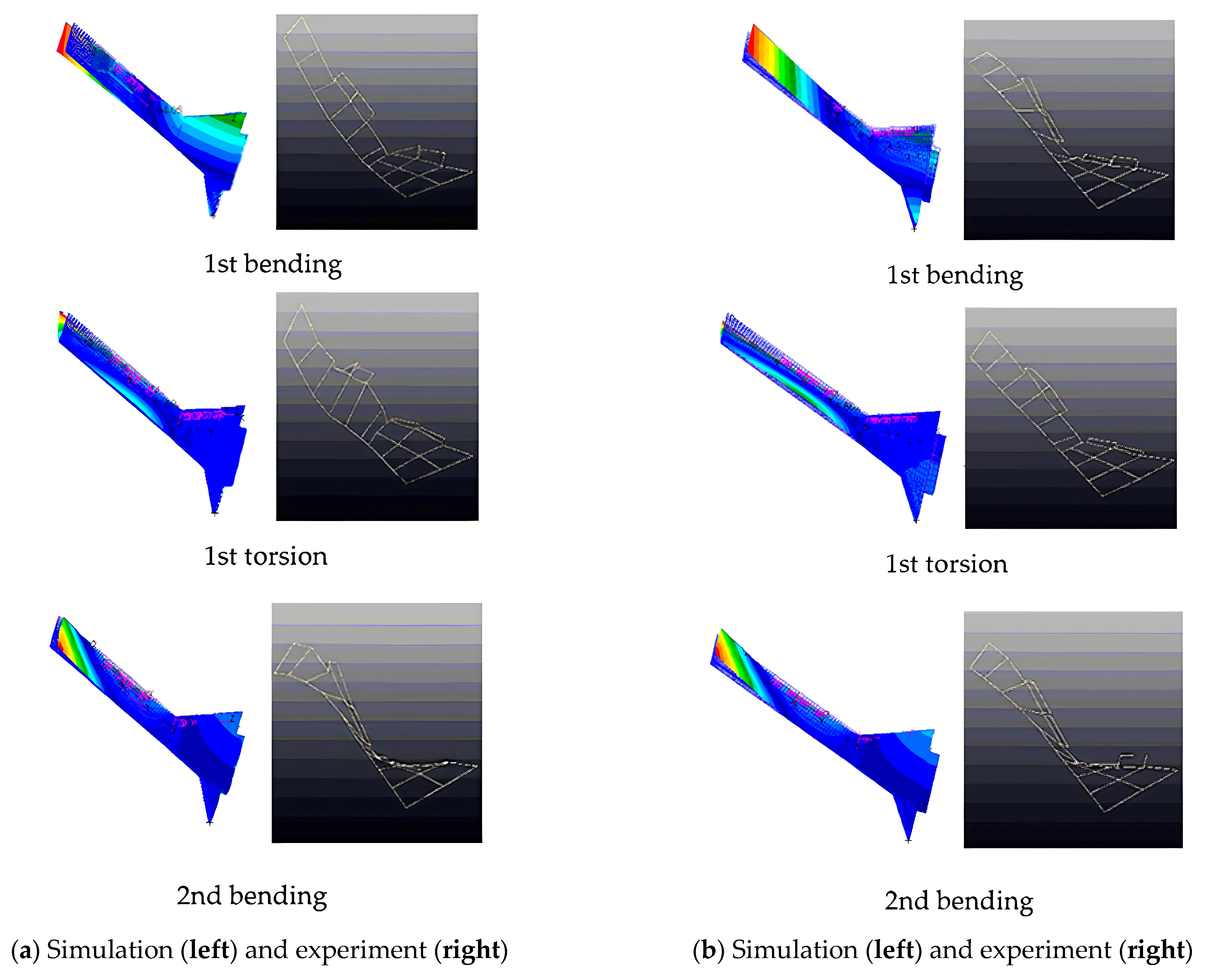
Figure 10.
Comparison of the modes under the fixed boundary condition obtained by numerical simulation (left) and experiment (right).
Figure 10.
Comparison of the modes under the fixed boundary condition obtained by numerical simulation (left) and experiment (right).
Figure 11.
Ground-mounted mechanism for the release of two degrees of freedom.
Figure 11.
Ground-mounted mechanism for the release of two degrees of freedom.
Figure 12.
Sensor mounting and measurement point layout.
Figure 12.
Sensor mounting and measurement point layout.
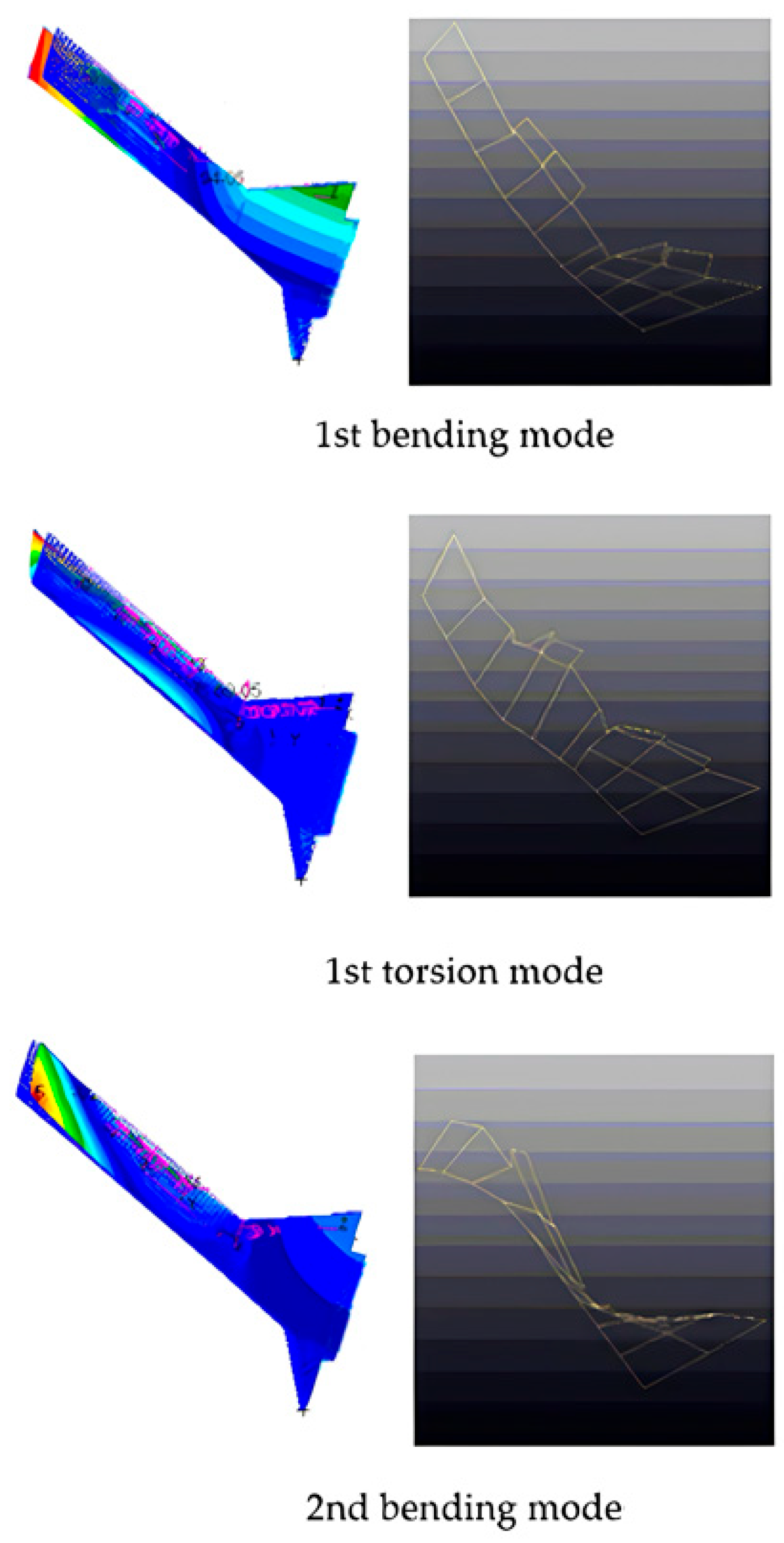
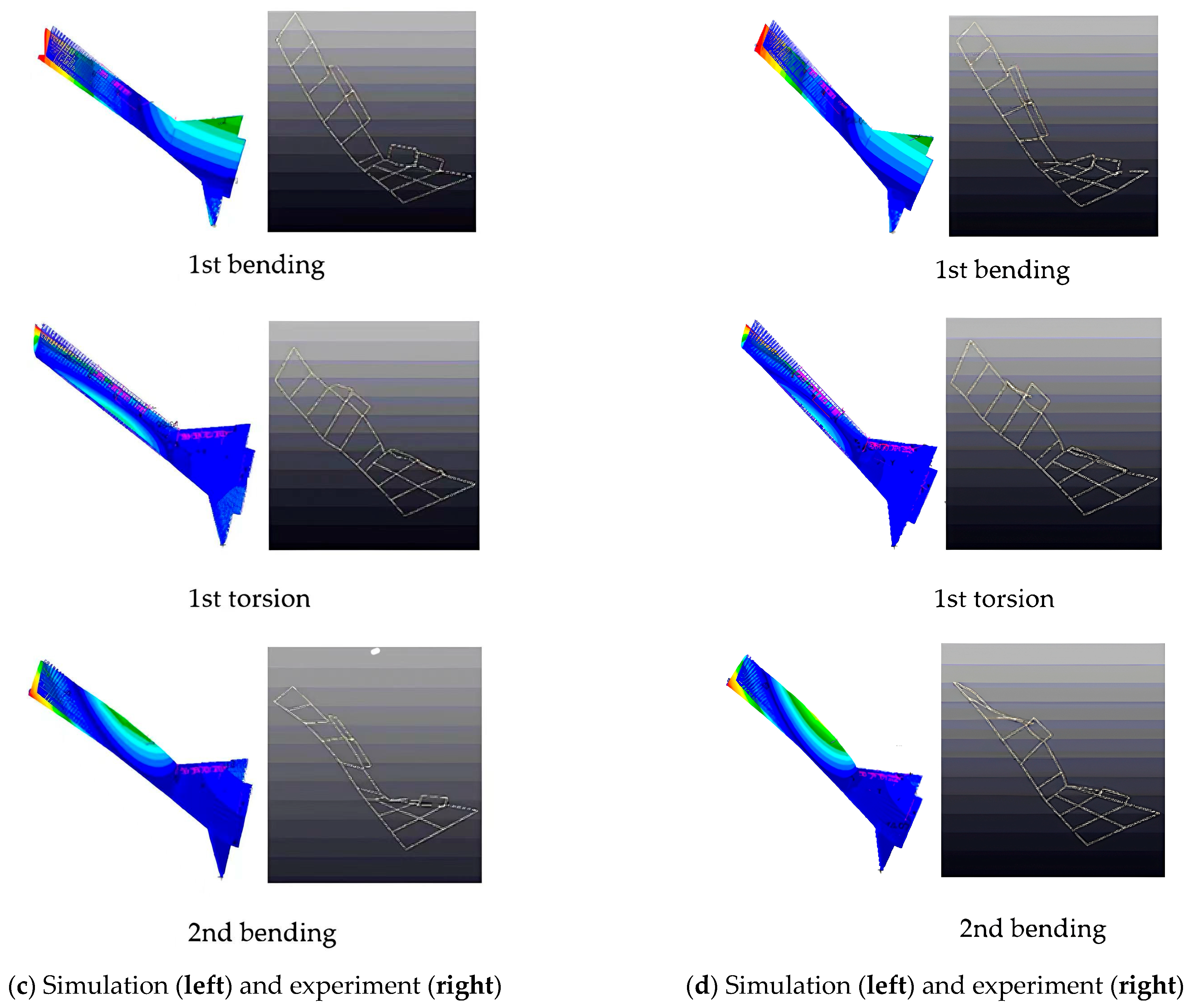
Figure 13.
Comparison of the modes under the boundary with two-degrees-of-freedom release, as obtained by numerical simulation (left) and experiment (right).
Figure 13.
Comparison of the modes under the boundary with two-degrees-of-freedom release, as obtained by numerical simulation (left) and experiment (right).
Figure 14.
CS distribution.
Figure 14.
CS distribution.
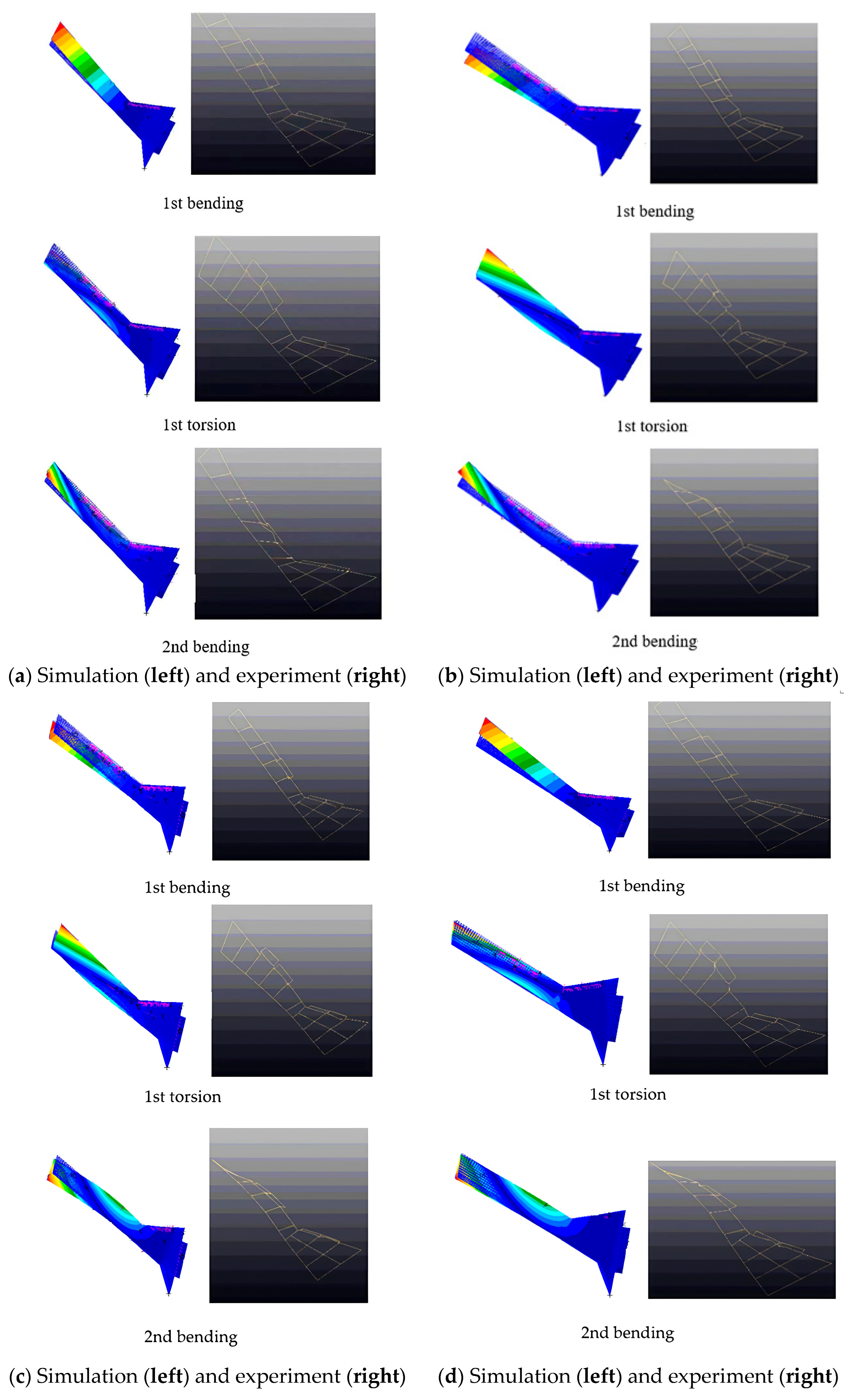
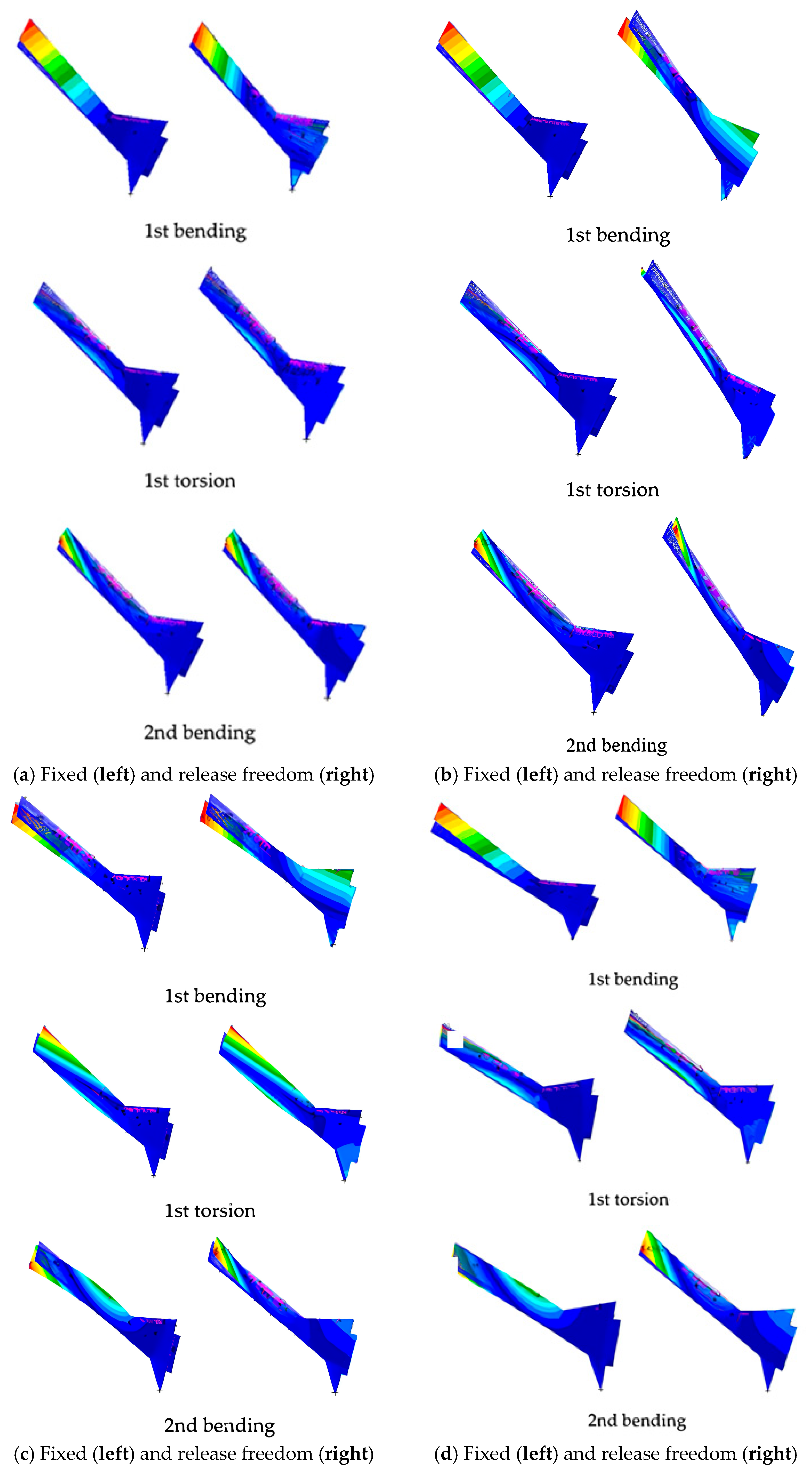
Figure 15.
Comparison of the modes of different CS mass states under fixed boundary conditions: (a) State 1, (b) State 2, (c) State 3, (d) State 4, (e) State 5, (f) State 6, and (g) State 7.
Figure 15.
Comparison of the modes of different CS mass states under fixed boundary conditions: (a) State 1, (b) State 2, (c) State 3, (d) State 4, (e) State 5, (f) State 6, and (g) State 7.
Figure 16.
Comparison of the modes of different CS mass states under the boundary condition with two-degrees-of-freedom release: (a) State 1, (b) State 2, (c) State 3, and (d) State 4.
Figure 16.
Comparison of the modes of different CS mass states under the boundary condition with two-degrees-of-freedom release: (a) State 1, (b) State 2, (c) State 3, and (d) State 4.
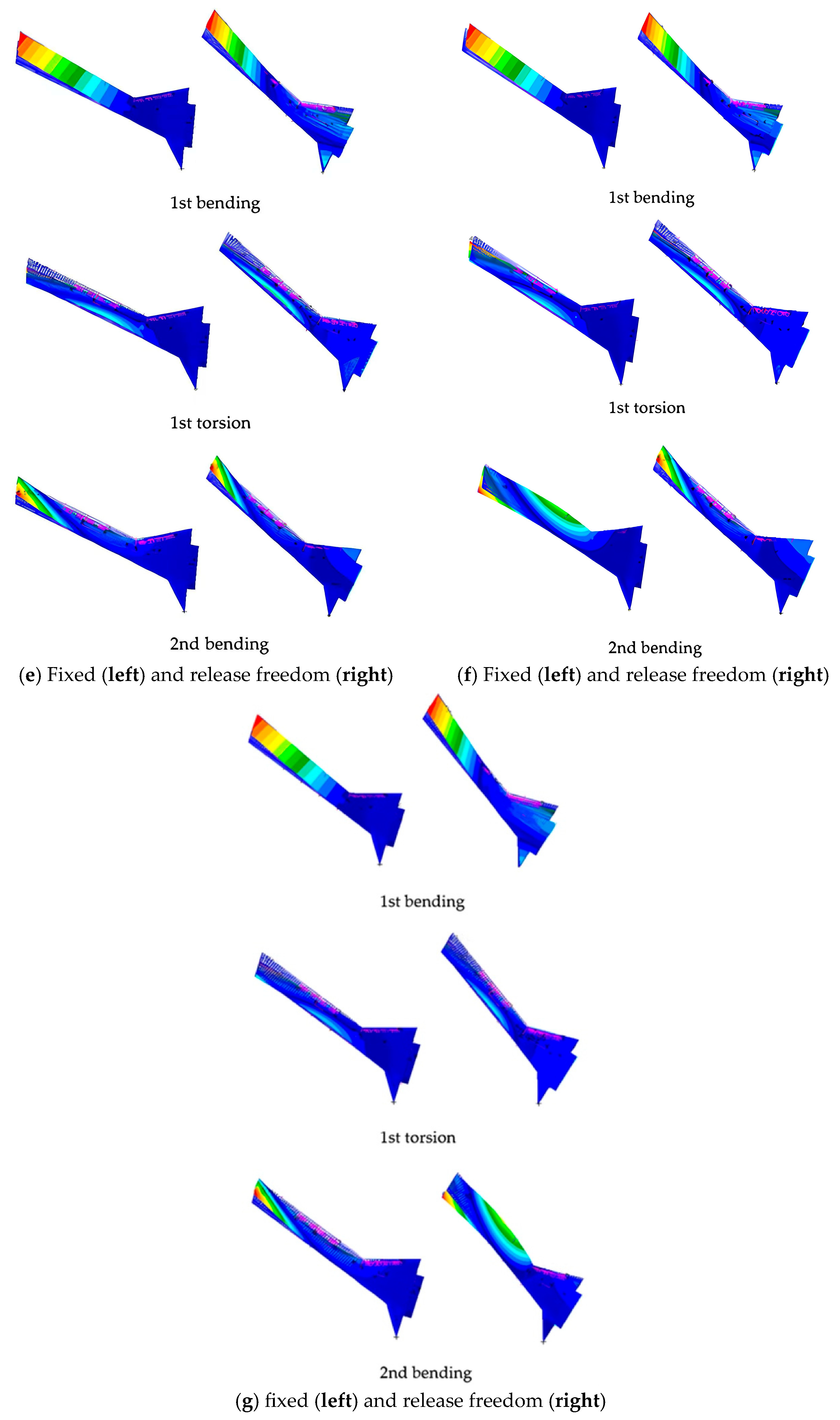
Figure 17.
Comparison of the modes under different boundary conditions of different mass states: (a) State 1, (b) State 2, (c) State 3, (d) State 4, (e) State 5, (f) State 6, and (g) State 7.
Figure 17.
Comparison of the modes under different boundary conditions of different mass states: (a) State 1, (b) State 2, (c) State 3, (d) State 4, (e) State 5, (f) State 6, and (g) State 7.
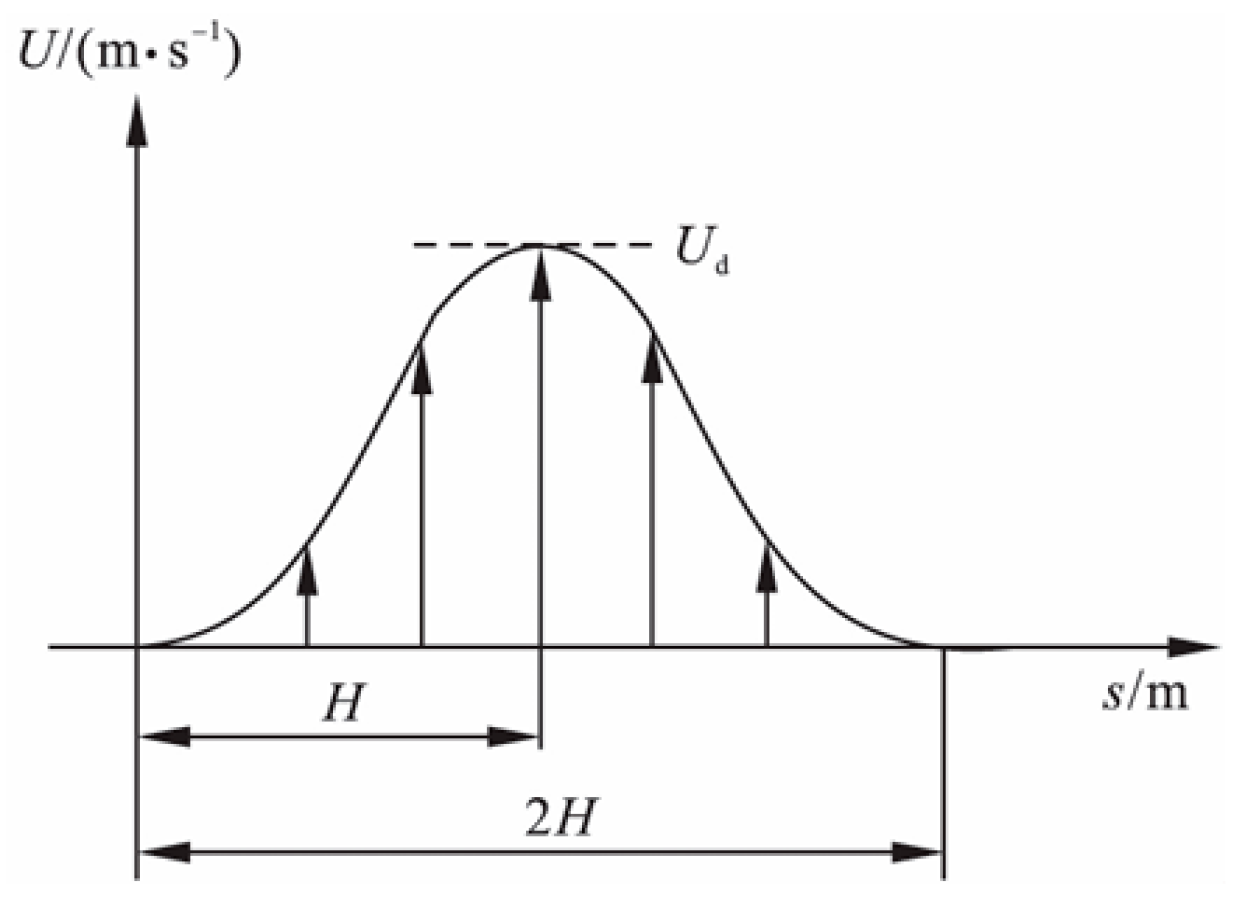
Figure 18.
1-cos discrete gust velocity profile.
Figure 18.
1-cos discrete gust velocity profile.
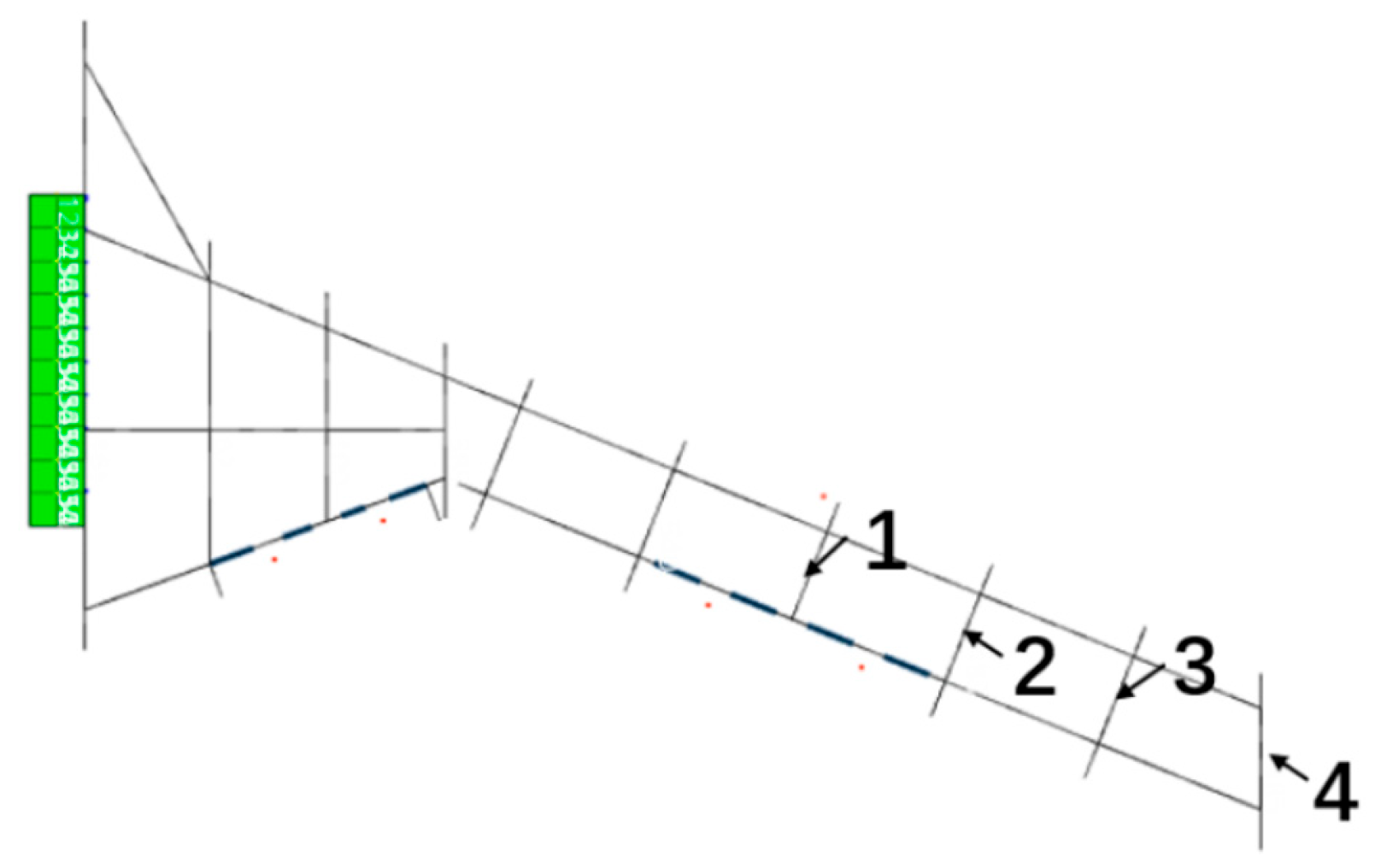
Figure 19.
Acceleration response measurement points.
Figure 19.
Acceleration response measurement points.
Figure 20.
Acceleration response of point 1.
Figure 20.
Acceleration response of point 1.
Figure 21.
Acceleration response of point 2.
Figure 21.
Acceleration response of point 2.
Figure 22.
Acceleration response of point 3.
Figure 22.
Acceleration response of point 3.
Figure 23.
Acceleration response of point 4.
Figure 23.
Acceleration response of point 4.
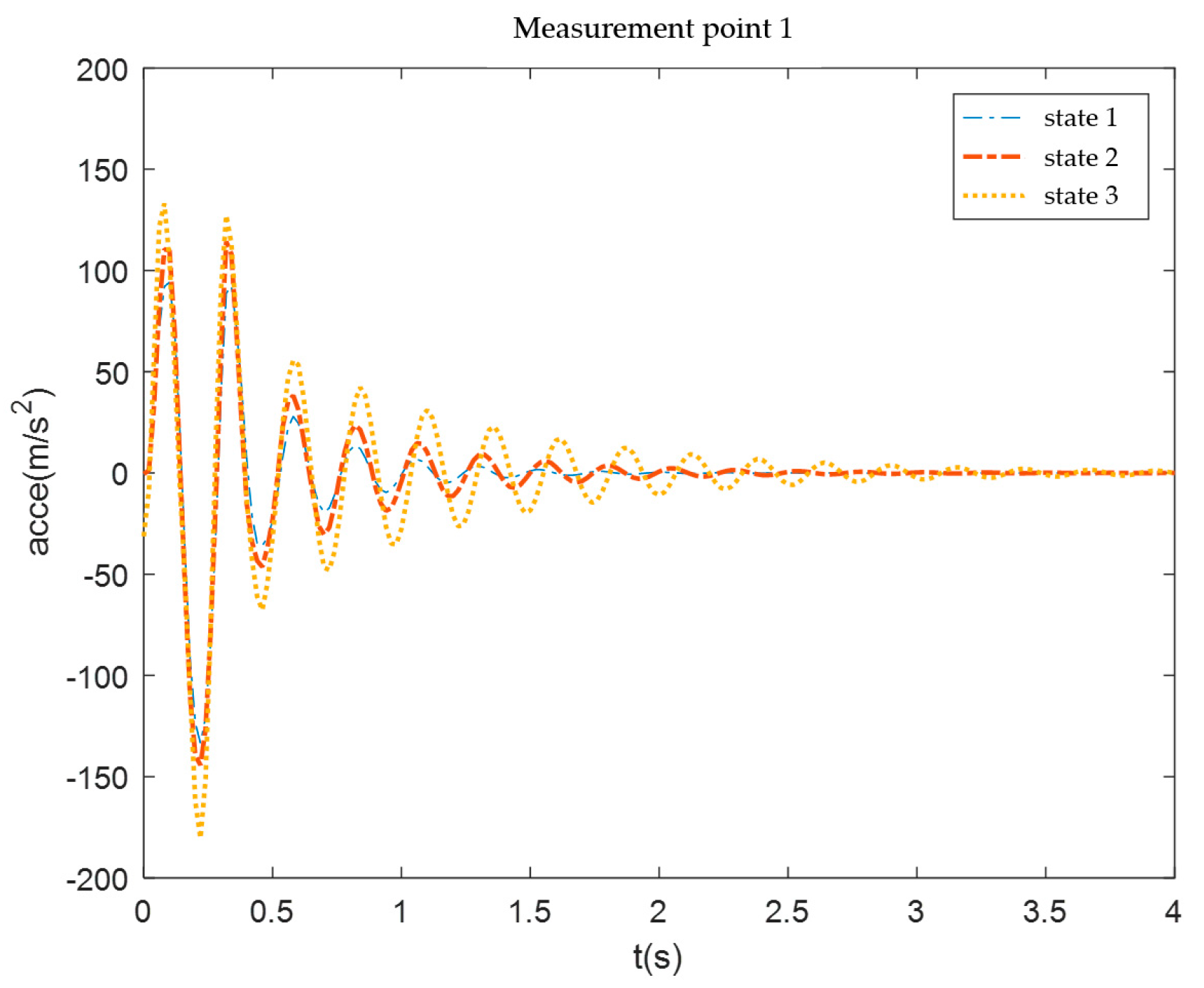
Figure 24.
Measurement point 1 acceleration response.
Figure 24.
Measurement point 1 acceleration response.
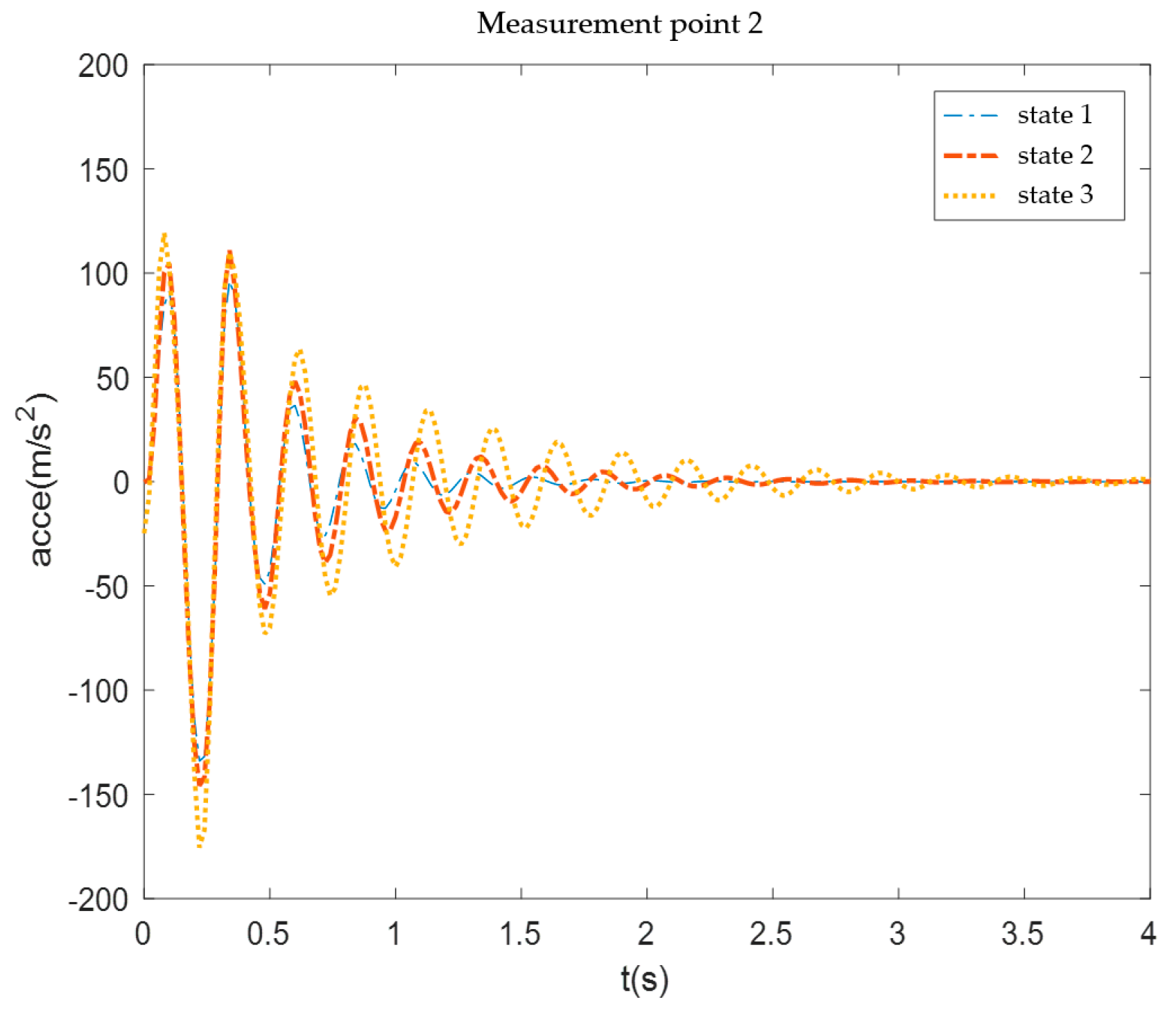
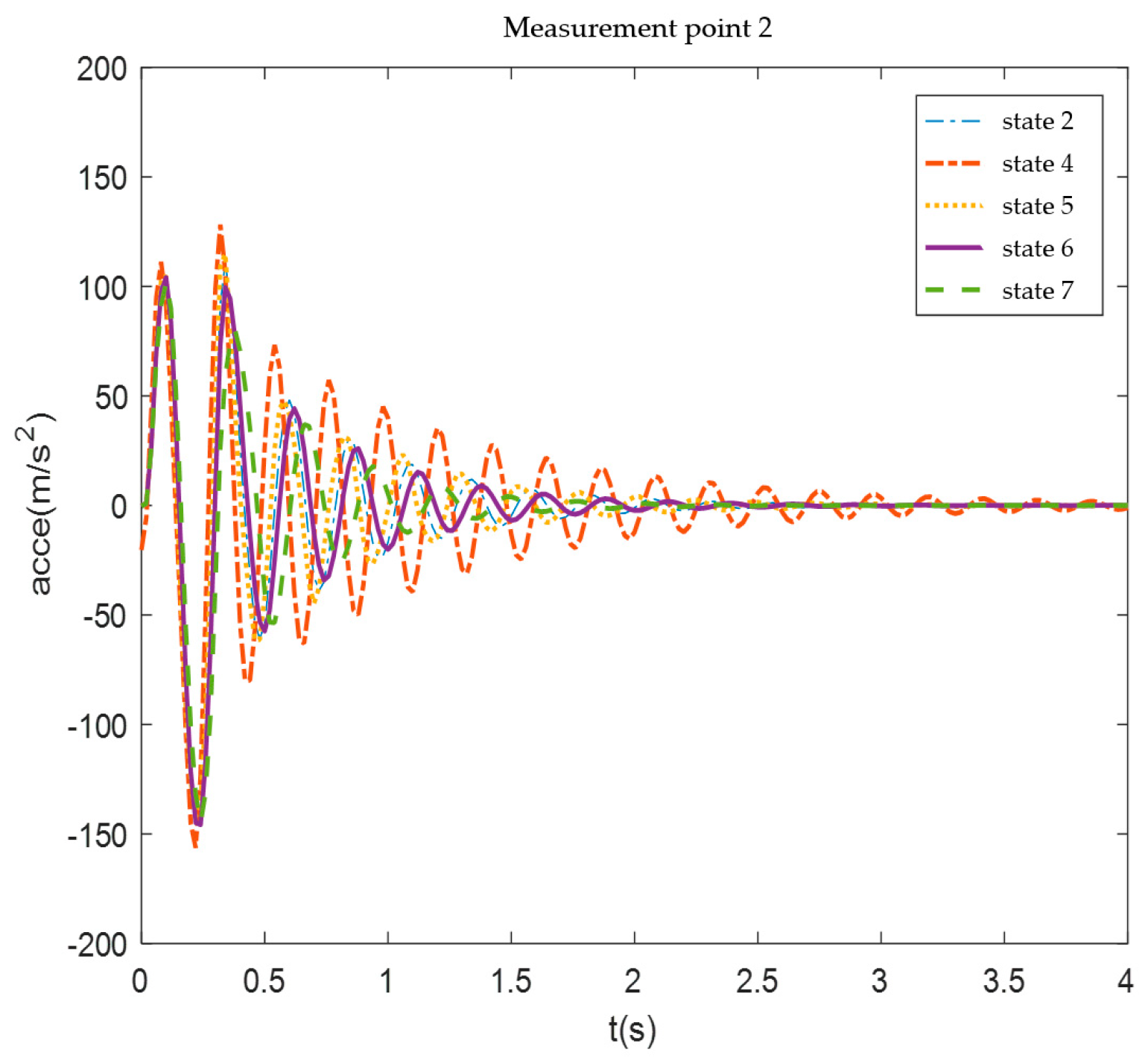
Figure 25.
Measurement point 2 acceleration response.
Figure 25.
Measurement point 2 acceleration response.
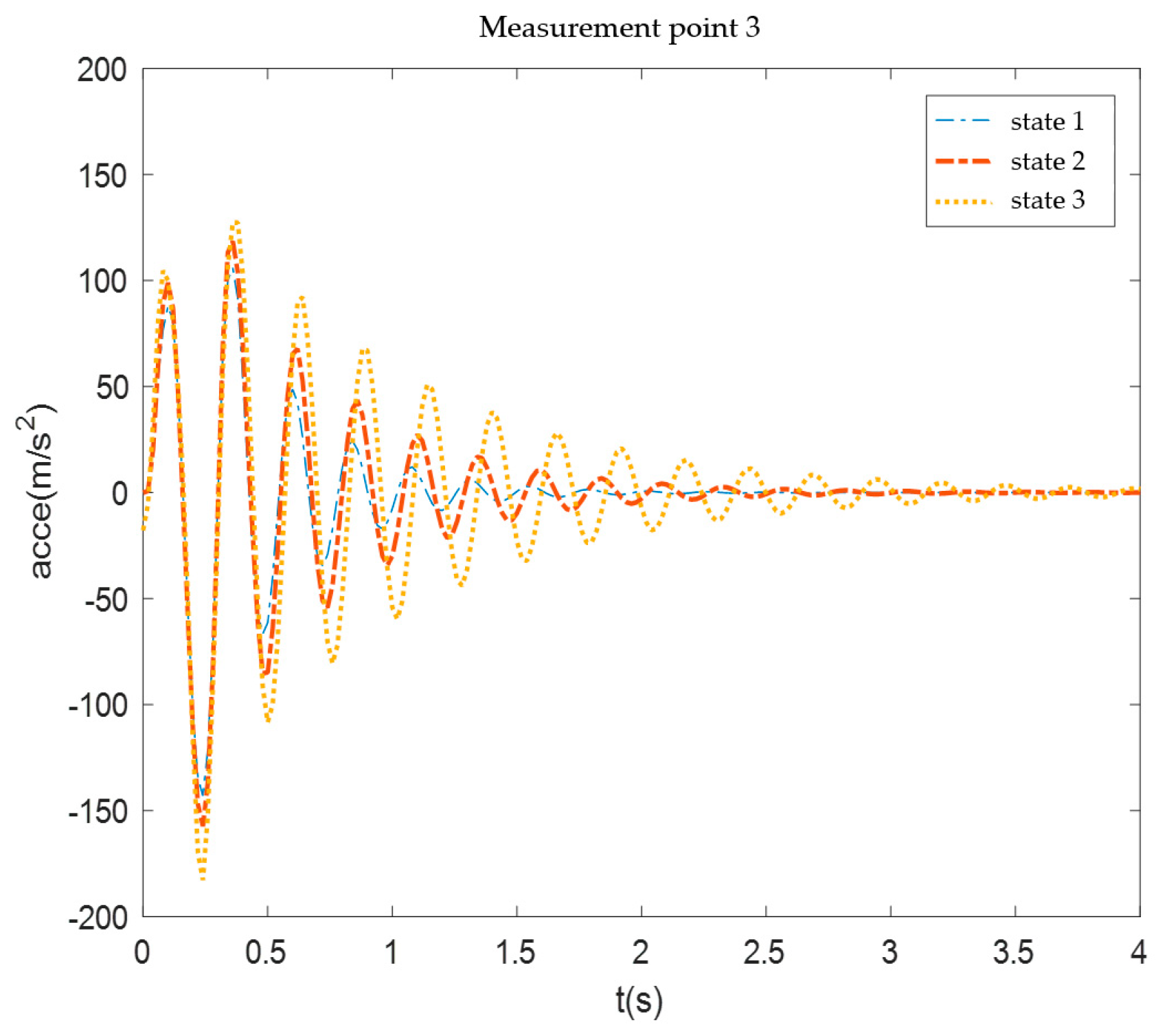
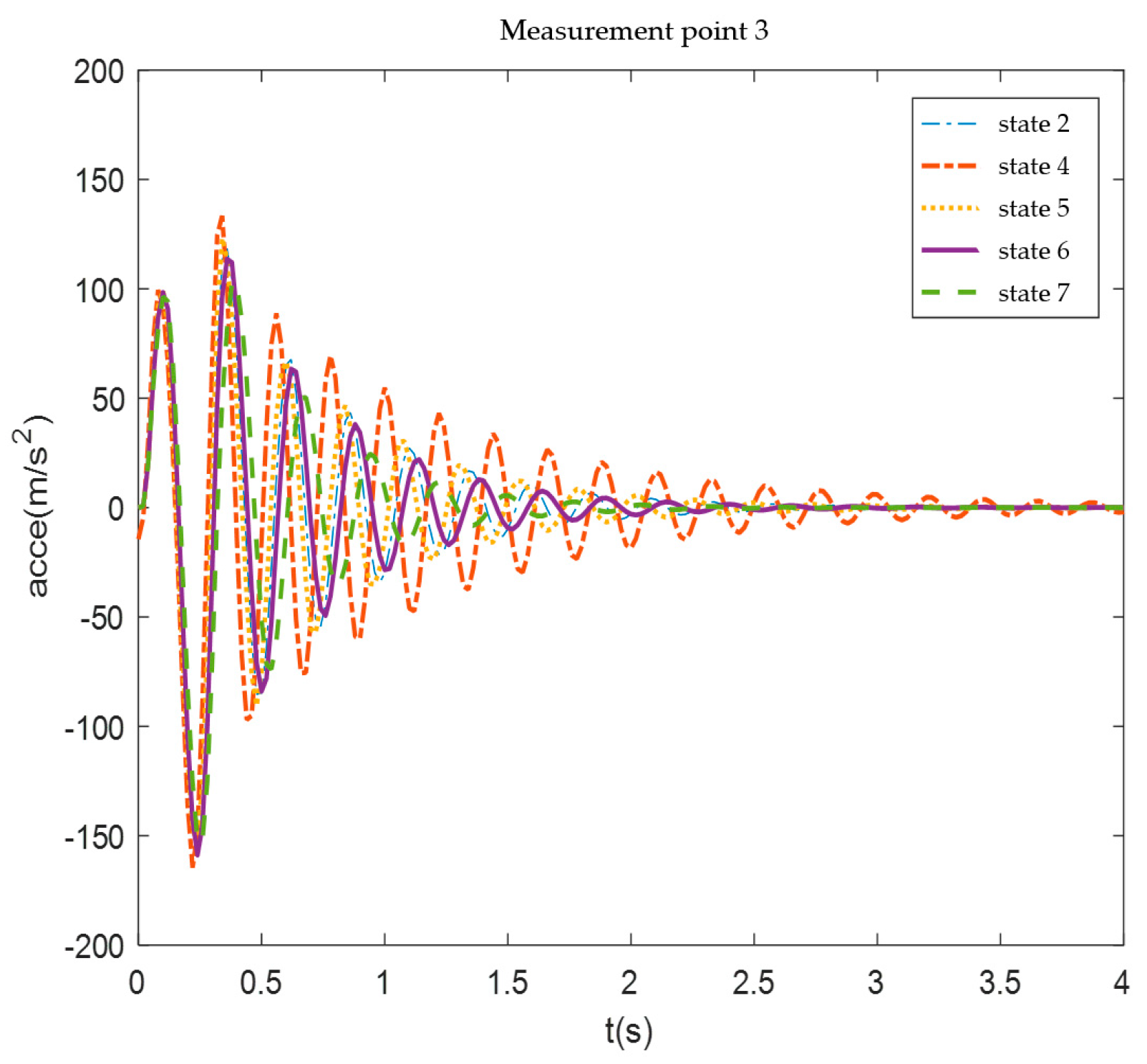
Figure 26.
Measurement point 3 acceleration response.
Figure 26.
Measurement point 3 acceleration response.
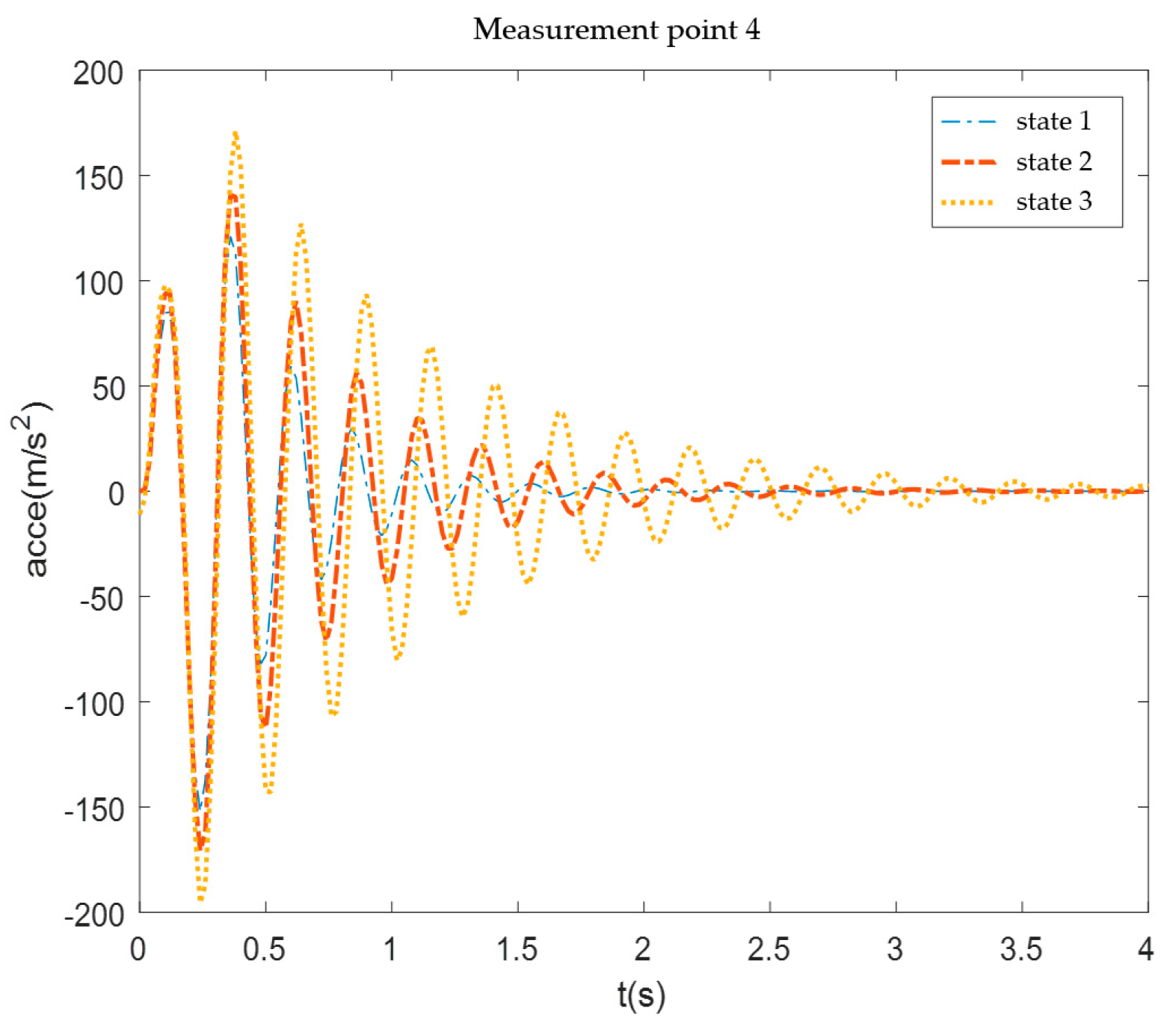
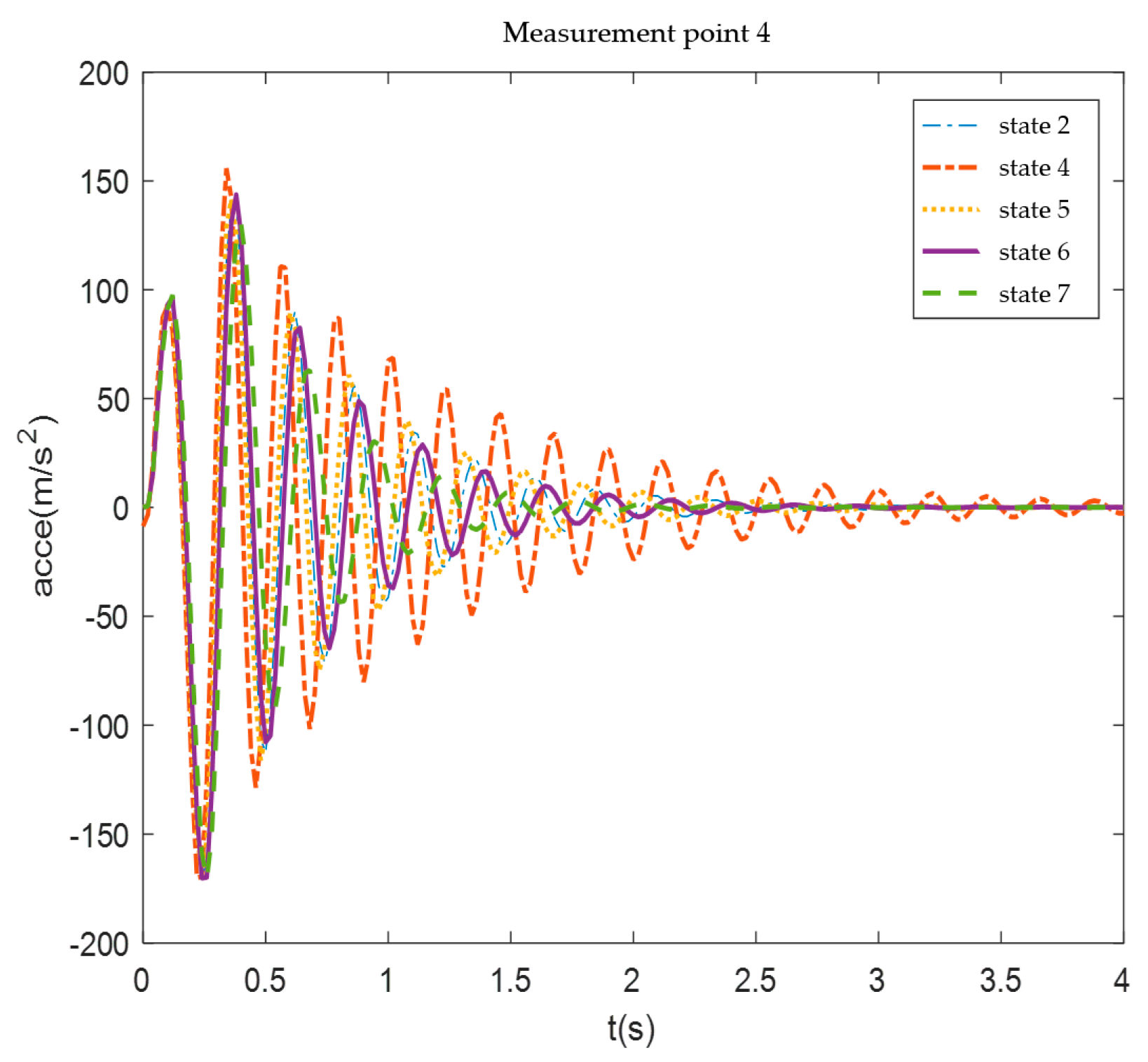
Figure 27.
Measurement point 4 acceleration response.
Figure 27.
Measurement point 4 acceleration response.
Table 1.
Main parameters of the high-aspect-ratio wing model.
Table 1.
Main parameters of the high-aspect-ratio wing model.
| Assemblies | Mass | Material |
|---|
| CS | 0.6 kg | 7075 Al |
| Girder | 10.4 kg | 7075 Al |
| Skin | 0.184 kg | Carbon Fiber-Reinforced Epoxy |
| Filler | 0.47 kg | EPS |
| Total mass | 11.654 kg |
Table 2.
Types and numbers of mesh in each section.
Table 2.
Types and numbers of mesh in each section.
| Components | Type | Number of Mesh |
|---|
| Skin | Four-node shell element | 2196 |
| Girder and rib | Four-node shell element | 577 |
| Filler | Solid hexahedral element | 1887 |
| CS | Four-node shell element | 298 |
Table 3.
Comparison of the natural frequencies obtained by numerical simulation and experiment under the fixed boundary condition.
Table 3.
Comparison of the natural frequencies obtained by numerical simulation and experiment under the fixed boundary condition.
| Mode | Simulated Frequency (Hz) | Experimental Frequency (Hz) | Description | Relative Error |
|---|
| 1 | 3.61 | 3.52 | First bending | 2.8% |
| 2 | 9.91 | 9.77 | First torsion | 1.5% |
| 3 | 17.95 | 19.28 | Second bending | 6.8% |
Table 4.
Comparison of the frequencies under the boundary with two-degrees-of-freedom release obtained by numerical simulation and experiment.
Table 4.
Comparison of the frequencies under the boundary with two-degrees-of-freedom release obtained by numerical simulation and experiment.
| Mode | Simulated Frequency (Hz) | Experimental Frequency (Hz) | Descriptions |
|---|
| 1 | 3.76 | 3.54 | First bending |
| 2 | 10.22 | 9.93 | First torsion |
| 3 | 20.49 | 19.82 | Second bending |
Table 5.
CS mass adding state.
Table 5.
CS mass adding state.
| State | CS 1 | CS 2 | CS 3 | CS 4 |
|---|
| State 1 | −150 g | −150 g | −150 g | −150 g |
| State 2 (base state) | 0 g | 0 g | 0 g | 0 g |
| State 3 | 150 g | 150 g | 150 g | 150 g |
| State 4 | 150 g | 150 g | −150 g | −150 g |
| State 5 | 150 g | −150 g | 150 g | −150 g |
| State 6 | −150 g | 150 g | −150 g | 150 g |
| State 7 | −150 g | −150 g | 150 g | 150 g |
Table 6.
Comparison of the frequencies of different CS mass states obtained by simulation and experiment frequency under fixed boundary conditions.
Table 6.
Comparison of the frequencies of different CS mass states obtained by simulation and experiment frequency under fixed boundary conditions.
| State | First Bending (Hz) | First Torsion (Hz) | Second Bending (Hz) |
|---|
| Simulated | Experimental | Simulated | Experimental | Simulated | Experimental |
|---|
| State 1 | 3.76 | 3.54 | 10.22 | 9.93 | 20.49 | 19.82 |
| State 2 | 3.61 | 3.52 | 9.91 | 9.77 | 17.95 | 19.28 |
| State 3 | 3.49 | 3.34 | 9.66 | 9.59 | 18.52 | 18.43 |
| State 4 | 3.50 | 3.28 | 9.67 | 8.55 | 18.65 | 18.39 |
| State 5 | 3.56 | 3.39 | 9.81 | 9.18 | 18.12 | 18.95 |
| State 6 | 3.68 | 3.51 | 10.07 | 9.37 | 18.63 | 18.40 |
| State 7 | 3.75 | 3.62 | 10.22 | 10.41 | 19.22 | 19.12 |
Table 7.
Variable parameter GVT test conditions.
Table 7.
Variable parameter GVT test conditions.
| State | CS 1 | CS 2 | CS 3 | CS 4 |
|---|
| State 2+ | 0 g | 0 g | 0 g | 0 g |
| State 4+ | 150 g | 150 g | −150 g | −150 g |
| State 5+ | 150 g | −150 g | 150 g | −150 g |
| State 7+ | −150 g | −150 g | 150 g | 150 g |
Table 8.
Comparison of the frequencies obtained by simulation and experiment under the boundary condition with two-degrees-of-freedom release.
Table 8.
Comparison of the frequencies obtained by simulation and experiment under the boundary condition with two-degrees-of-freedom release.
| State | First Bending (Hz) | First Torsion (Hz) | Second Bending (Hz) |
|---|
| Simulated | Experimental | Simulated | Experimental | Simulated | Experimental |
|---|
| State 2+ | 3.76 | 3.54 | 10.22 | 9.93 | 20.49 | 19.82 |
| State 4+ | 3.61 | 3.52 | 9.91 | 9.77 | 17.95 | 19.28 |
| State 5+ | 3.49 | 3.34 | 9.66 | 9.59 | 16.52 | 18.43 |
| State 7+ | 3.50 | 3.28 | 8.67 | 8.55 | 17.65 | 18.39 |
Table 9.
Comparison of the frequency of different states under fixed and released two-degrees-of-freedom conditions.
Table 9.
Comparison of the frequency of different states under fixed and released two-degrees-of-freedom conditions.
| State | First Bending (Hz) | First Torsion (Hz) | Second Bending (Hz) |
|---|
| Fixed | Release Two Degrees of Freedom | Fixed | Release Two Degrees of Freedom | Fixed | Release Two Degrees of Freedom |
|---|
| State 1 | 3.76 | 6.05 | 10.22 | 11.19 | 20.49 | 17.26 |
| State 2 | 3.61 | 5.85 | 9.91 | 10.78 | 17.95 | 19.62 |
| State 3 | 3.49 | 5.66 | 9.66 | 10.45 | 16.52 | 18.43 |
| State 4 | 3.50 | 5.99 | 9.67 | 10.48 | 16.65 | 18.39 |
| State 5 | 3.56 | 5.85 | 9.81 | 10.69 | 18.12 | 19.81 |
| State 6 | 3.68 | 5.86 | 10.07 | 10.92 | 17.63 | 19.32 |
| State 7 | 3.75 | 5.74 | 10.22 | 11.15 | 20.22 | 17.25 |
Table 10.
Computational conditions for gust response.
Table 10.
Computational conditions for gust response.
| Calculated Variables | Value |
|---|
| Altitude | 0 km |
| Mach | 0.2 |
| Gust speed | 16.46 m/s |
| Gust size | 10.0 m |