Performance and Stall Margin Evaluation of Axial Slot Casing Treatment in a Transonic Multistage Compressor

Abstract

Adverse pressure gradients are intrinsic to compressor flow behavior and are further intensified by secondary effects associated with rotor tip clearance flow interactions. Tip clearance generates leakage flow, which leads to the formation of tip leakage vortices, a major contributor to aerodynamic losses in axial compressors. These vortices significantly influence both compressor performance and operational stability. Extensive prior research has demonstrated that passive casing treatments, particularly axial slots, can substantially improve the stall margin in axial compressors. In this work, the performance of a new casing treatment geometry is investigated using the concept of recirculating flow within semi-circular axial slots. The proposed casing treatment geometry builds upon recent experimental findings involving single-rotor configurations. It was applied to the first rotor row of a three-and-a-half-stage (3.5-stage) axial compressor comprising an inlet guide vane followed by three rotor–stator stages. The numerical model incorporates axial slots with a novel periodic interface approach implemented in a multistage compressor simulation. Three-dimensional steady-state RANS (Reynolds Average Navier-Stokes) simulations were performed to investigate the aerodynamic effects of the casing treatment across various rotational speeds. The results for the casing treatment configuration were compared with those of a baseline smooth casing. The introduction of the new casing treatment produced noticeable modifications to the internal flow structure, particularly in the tip region, resulting in improved overall compressor stability within the operating range of 85 to 100% of design speed.

1. Introduction

Compressor designers must address a wide range of performance requirements, among which two primary aerodynamic objectives are paramount: achieving high efficiency and ensuring sufficient stall margin throughout the turbomachine’s operational life. In high-performance compressors, the internal flow frequently encounters strong adverse pressure gradients due to the elevated pressure loading across each blade row. These gradients can trigger boundary-layer separation on the suction side of the blades at various spanwise locations, leading to unsteady flow phenomena.

Despite decades of research, the current understanding of flow instabilities and stall mechanisms in axial compressors remains incomplete. Even state-of-the-art numerical tools often fail to accurately predict stall onset. As highlighted by Day [1], after more than 75 years of focused investigation, a comprehensive understanding of compressor stall has yet to be achieved, underscoring the complexity of the phenomenon.

Berdanier [2] emphasizes that the latest generation of high-bypass-ratio turbofan engines, characterized by smaller core diameters in axial compressors, presents additional design challenges. These include maintaining high efficiency and aerodynamic stability in multistage axial compressors operating with reduced tip clearances and elevated rotational speeds.

Furthermore, tip clearances do not scale proportionally with blade miniaturization due to manufacturing tolerances, design constraints, and allowances required for transient operation and thermal expansion. Tip clearance strongly influences turbomachinery performance and is recognized as a dominant source of aerodynamic loss in axial compressors. Excessive tip clearance reduces efficiency and diminishes the operational range of the machine [2,3].

In the tip clearance region, the pressure differential between the suction and pressure sides of the blade drives a cross-flow known as tip leakage flow (TLF) [4,5]. This flow interacts with the primary passage flow, generating complex vortical structures referred to as tip leakage vortices (TLVs). Studies by Zhong et al. [4] and Ha [6] have shown that TLVs are critical contributors to stall inception in axial compressors.

The adverse pressure gradients intrinsic to compressor operation are further amplified by the effects of TLVs, which are commonly observed in various types of turbomachinery, as described by Leitner et al. [7]. These vortical structures introduce unsteady flow behavior and localized loss mechanisms that degrade overall compressor performance.

A thorough understanding of tip leakage flow physics, particularly in multistage environments, is therefore essential for optimizing compressor design. Improving off-design performance and achieving effective stage matching become increasingly challenging as pressure ratios rise. This issue is especially critical in the preliminary design phase of multistage axial compressors, as emphasized by Day [1].

The interaction between the TLF, the main flow, and other vortical structures contributes to the formation and intensification of the TLV, which plays a central role in stall and surge phenomena [8]. Stall is characterized by large-scale flow separation on the compressor blades, which constrains the machine’s operational range and reduces efficiency.

Two primary approaches have been developed to enhance stall margin in axial compressors. The first involves active flow control technologies, which typically inject momentum into low-energy regions or extract weak flows to reduce aerodynamic blockages. In some cases, both injection and extraction are applied simultaneously, as described by Gutiérrez et al. [9]. Another strategy involves the use of active bleed valves, as demonstrated by Sheng et al. [10], to extend the stable operating range of compressors.

The second approach involves passive flow control using casing treatments (CTs). Unlike active systems, passive CTs have no moving parts and are comparatively simpler to design, install, and manufacture. Examples include circumferential grooves and axial slots. These methods were extensively investigated in the 1970s and have recently regained attention due to their demonstrated ability to significantly improve stall margin with minimal efficiency penalties.

Numerous CT configurations have been proposed in the literature to enhance stall margin while minimizing performance degradation. For example, Alone et al. [11] examined several bent skewed slot geometries at different rotational speeds. The most successful configuration achieved a 24.83% improvement in stall margin at 80% design speed, but with a substantial efficiency penalty of 4.27%. In contrast, Kuang et al. [9] investigated the effect of axial slot CTs on the NASA Rotor 67 compressor and found that the best configuration improved stall margin by 26.85% with negligible efficiency loss.

Table 1. Comparison of axial slots performance of works found in the literature.

Authors	Year	Number of Compressor Stages	ΔSM	Δηis,peak
Kuang et al. [8]	2013	Isolated Rotor	+26.85%	±0%
Alone et al. [11]	2017	1	+24.89%	−4.27%
Ba et al. [12]	2020	1	+15.81%	−0.97%
Zhang et al. [13]	2021	1	+26.6%	−0.83%

summarizes selected studies on axial slot casing treatments and their impact on compressor performance.

Passive casing treatments (CTs) operate by obstructing leakage flow within the tip gap region, thereby modifying the local flow field to delay the onset of stall. However, each compressor design requires a customized CT configuration to maximize stall margin improvements.

The availability of advanced Computational Fluid Dynamics (CFD) tools now enables detailed investigations of three-dimensional flow structures in turbomachinery. Numerical simulations have been extensively employed to support engineering decision-making, particularly for evaluating geometric modifications to compressor CTs. These tools have facilitated major advancements in turbomachinery design, fostering the development of innovative concepts aimed at reducing internal losses associated with complex flow phenomena.

It is important to emphasize that the installation of CTs does not universally result in improved stall margins. Consequently, the selection and configuration of CTs should be guided by insights from recent studies, with CFD simulations serving as a key instrument for evaluating expected improvements in operational stability while minimizing efficiency penalties. As a result, substantial research efforts have been devoted to developing effective solutions for this engineering challenge [14].

In recent years, growing attention has been directed toward the influence of CTs on stall margin enhancement in multistage axial compressors. Experimental investigations have been conducted on multistage configurations, such as the two-stage axial compressor studied by Wei et al. [15] and the four-stage DLR research compressor analyzed by Goinis et al. [16]. This research has been significantly accelerated by advances in CFD capabilities. Wei et al. [15] employed a single-passage, steady-state numerical analysis of the first rotor to assess the effect of CTs on overall compressor performance, while Goinis et al. [16] used a computational domain including the inlet guide vane (IGV) as well as the first rotor and stator to analyze CT effects in a four-stage configuration.

The DLR study was carried out on an existing laboratory compressor to determine whether the rotor exhibited tip-limited compressor behavior, characterized by spike-type or wall-initiated stall mechanisms in the rotor tip region. The presence of tip-limited stall behavior in the first stage is highly advantageous for CT application, as it typically yields the greatest benefit.

Diaz et al. [17] conducted numerical investigations on a four-stage high-performance axial compressor, applying passive wall treatments in the form of axisymmetric circumferential grooves. They observed that implementing groove-type CTs in the second stage did not produce significant benefits at rotational speeds above 60% of design speed (N60). This finding is consistent with the earlier conclusion of Rabe and Ha [18], who noted that the flow field of the first rotor largely dictates stall characteristics in two-stage compressors.

In the present study, an axial slot-type passive wall treatment was implemented on the casing of the well-documented 3.5-stage axial compressor “74A”, as described by Steinke [19]. Three-dimensional CFD simulations based on the Reynolds-Averaged Navier–Stokes (RANS) equations were conducted. These simulations were used to validate the smooth-casing baseline against experimental performance data and to assess the aerodynamic impact of the casing treatment.

Among several tested variable-geometry configurations of the IGV and stators, the most effective setup was identified from laboratory testing at 100% design speed, with setting angles of 15° for the IGV and 10° for stators 1, 2, and 3. Experimental data for this configuration indicated a rapid deterioration in compressor efficiency when operating below 85% of design speed. In this off-design regime, the flow is dominated by separation, recirculation, reattachment, and strong unsteadiness.

As a result, RANS numerical simulations are not reliable below 85% of design speed. In this operating range, predictions of surge margin, efficiency, and mass flow rate become increasingly inaccurate, and simulations often fail to converge.

Nevertheless, the enhancement of stall margin within the high-efficiency operating range of high-performance, transonic, multistage axial compressors remains a topic of significant interest in both academic and industrial research. Accordingly, in the present study, only operating points at or above 85% of design speed were analyzed to evaluate the influence of axial slots on stall margin performance.

2. Description of the CT and Methodology

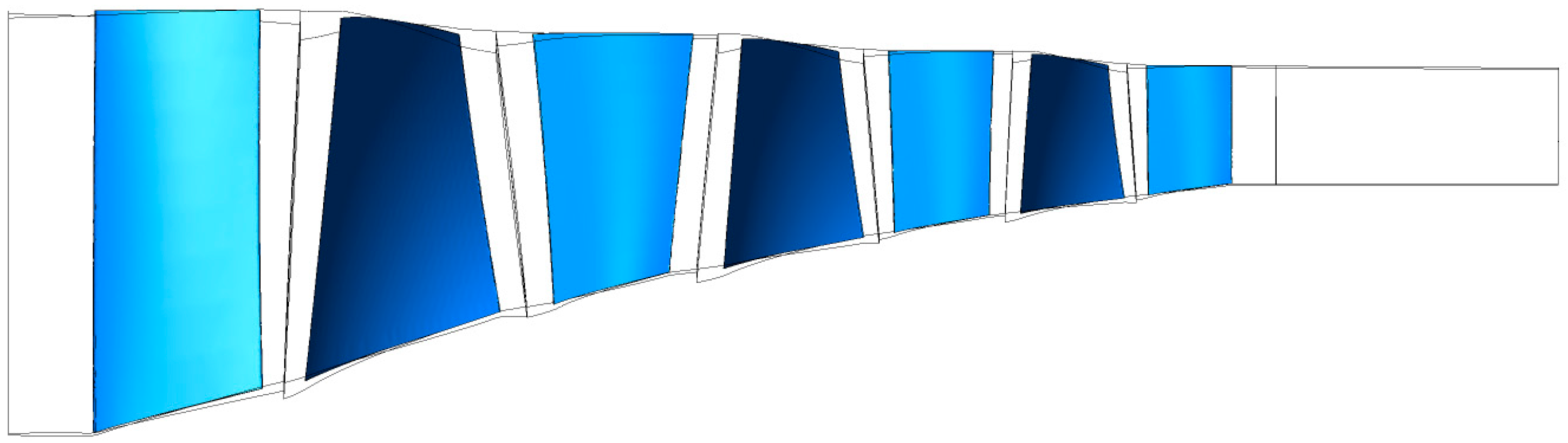
In the present study, an axial slot casing treatment (ASCT) was implemented in the casing above the first rotor row of a multistage axial compressor. The compressor under investigation is a turbomachine operating in the transonic flow regime. Figure 1 presents the meridional view of the compressor analyzed in this work. Additional details regarding the compressor characteristics can be found in the studies of Steinke and Veres [19,20].

Table 2. Geometrical parameters for 3.5 stages axial compressor from Steinke [19].

Design Parameters	Value
Number of the IGV Blade	26
Blade Count R1	28
Blade Count S1	34
Blade Count R2	32
Blade Count S2	46
Blade Count R3	39
Blade Count S3	54
Estimated Efficiency	79.9%
Tip diameter of Rotor 1	0.505 m
Rotor 1 hub to tip ratio	0.54
Rotor 1 tip gap (% of span)	<1.0%

(adapted from Steinke [19]) presents the geometric parameters of the 3.5-stage axial compressor. The design speed is 16,042.3 rpm under standard ambient conditions (288.2 K and 1 atm), and the blade tip speed at Rotor 1 reaches 431 m/s.

The solidity of Rotor 1 varies between 1.3 and 2.5, with an average value of 1.7. The solidity of Rotor 2 ranges from 1.2 to 1.8, with an average of 1.4, while Rotor 3 exhibits values between 1.2 and 1.5, with an average of 1.3. According to the experimentally validated findings of Greitzer et al. [21], passive casing treatments (CTs) tend to be more effective when rotor solidity exceeds 1.5. Under such conditions, blade loading is higher, and the stall initiation mechanism shifts from blade stall to wall stall. Greitzer’s research was pivotal in advancing the understanding of stall initiation mechanisms in axial compressors, demonstrating that systematic variation in rotor solidity enables the transition between blade stall and wall stall.

In the present study, the passive wall treatment is applied exclusively to Rotor 1, following the justification provided by Rabe and Ha [18] and Greitzer et al. [21]. Given the relatively low solidity values of Rotors 2 and 3, substantial improvements in stall margin are not anticipated in the downstream stages.

The primary objective is to stabilize the flow near the tip region of Rotor 1 by energizing the boundary layer and reducing tip leakage flow (TLF). This approach aims to suppress the formation of the tip leakage vortex (TLV), thereby delaying flow separation and limiting the propagation of flow disturbances to subsequent rotor stages.

The proposed configuration is a modified version of the standard CT described by Lu et al. [22] and Brignole et al. [23]. It consists of 84 slots, corresponding to three axial slots per blade passage, as illustrated in Figure 2. The slot width remains consistent with the standard CT configuration. The number of slots was increased from 64 (in the standard configuration) to 84 to preserve proportionality with the increased tip diameter of Rotor 1, which was scaled from 0.380 m (standard CT) to 0.505 m (present CT), thereby maintaining three axial slots per passage.

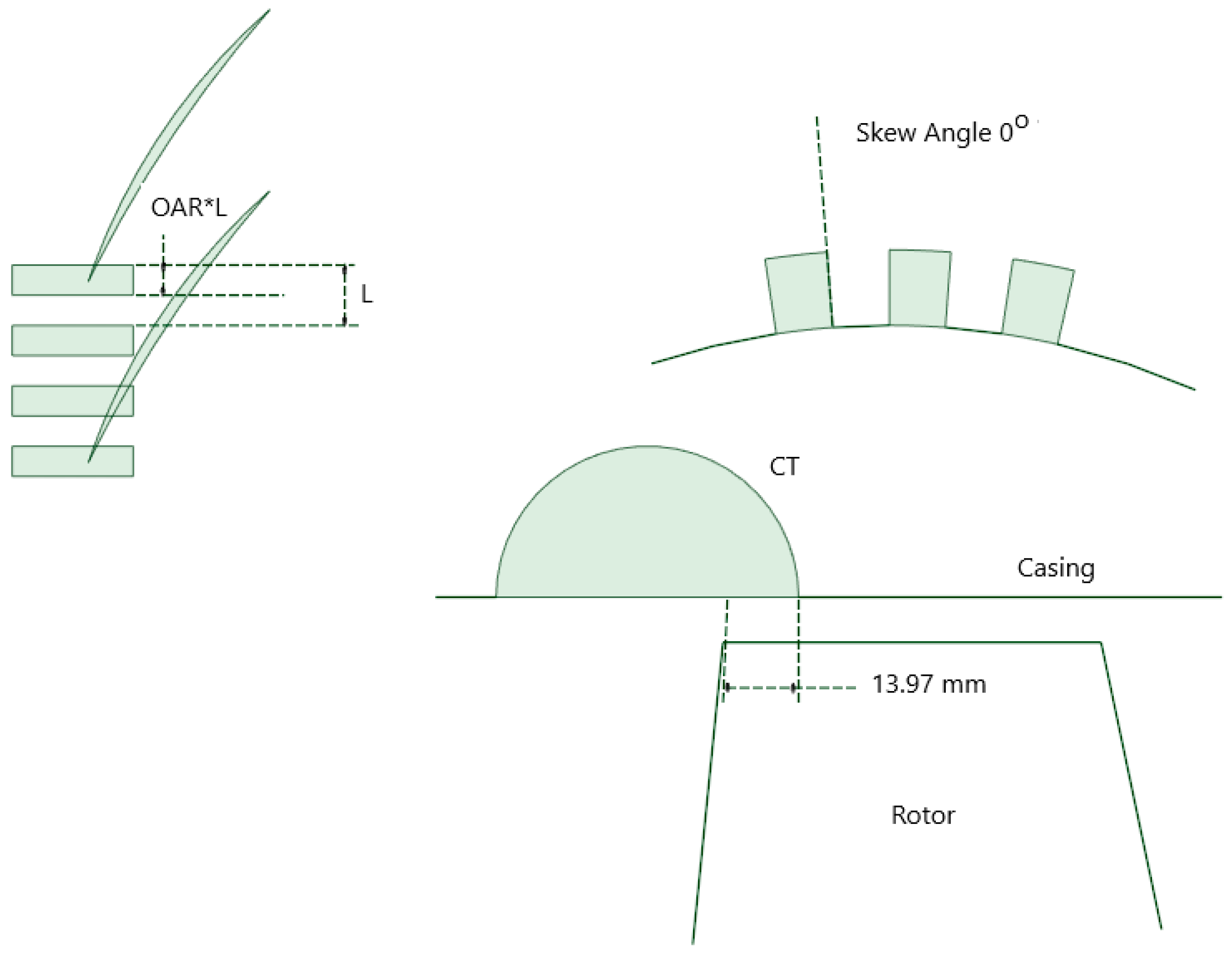
The geometry of a single cavity consists of a semi-circular slot with a rectangular opening surface. The axial length corresponds to approximately 66% of the Rotor 1 tip axial chord. The axial overlap ratio (Lex) is defined as the ratio between the distance from the blade leading edge (LE) to the treatment trailing edge (TE) and the rotor tip chord. This parameter determines the axial positioning of the slots, which in the present configuration corresponds to 33% of the blade tip chord, i.e., 13.97 mm. The open area ratio (OAR) is defined as the ratio of the slot opening surface area to the casing surface area within a single passage. The skew angle (SA) is defined as the deviation of the axial slot from the casing normal. For the proposed CT configuration, Lex, OAR, and SA are 33% (13.97 mm), 0.5, and 0°, respectively.

The choice of a skew angle of 0° is supported by the findings of Engels et al. [24], who proposed simplified axial slot models for the first rotor of the TP-400 engine. The validity of this simplification was demonstrated through comparison with rig data. Similarly, the selection of an axial slot CT with 33% chord exposure is based on the study by Lu et al. [25], which reported the highest stall margin improvement among the configurations analyzed. Specifically, a stall margin improvement of nearly 21.43% (in terms of corrected mass flow rate) was achieved with 33.3% rotor tip axial chord exposure, without any efficiency penalty.

The CT configuration employed in the present study consists of three identical semi-circular cavities per blade passage, positioned directly above the leading edge of the Rotor 1 blades and oriented axially, with a circumferential lean angle of 0° relative to the direction of rotation. Owing to their semi-circular geometry, the slot depth was implicitly defined by the axial length. The Rotor 1 tip chord measures approximately 42.3 mm, comparable to the tip chord length of the Darmstadt Transonic Compressor (DTC). However, the axial slot length used in this work is shorter than that of the standard CT applied to the DTC, corresponding to approximately 66% of the Rotor 1 tip chord, i.e., about 28.3 mm.

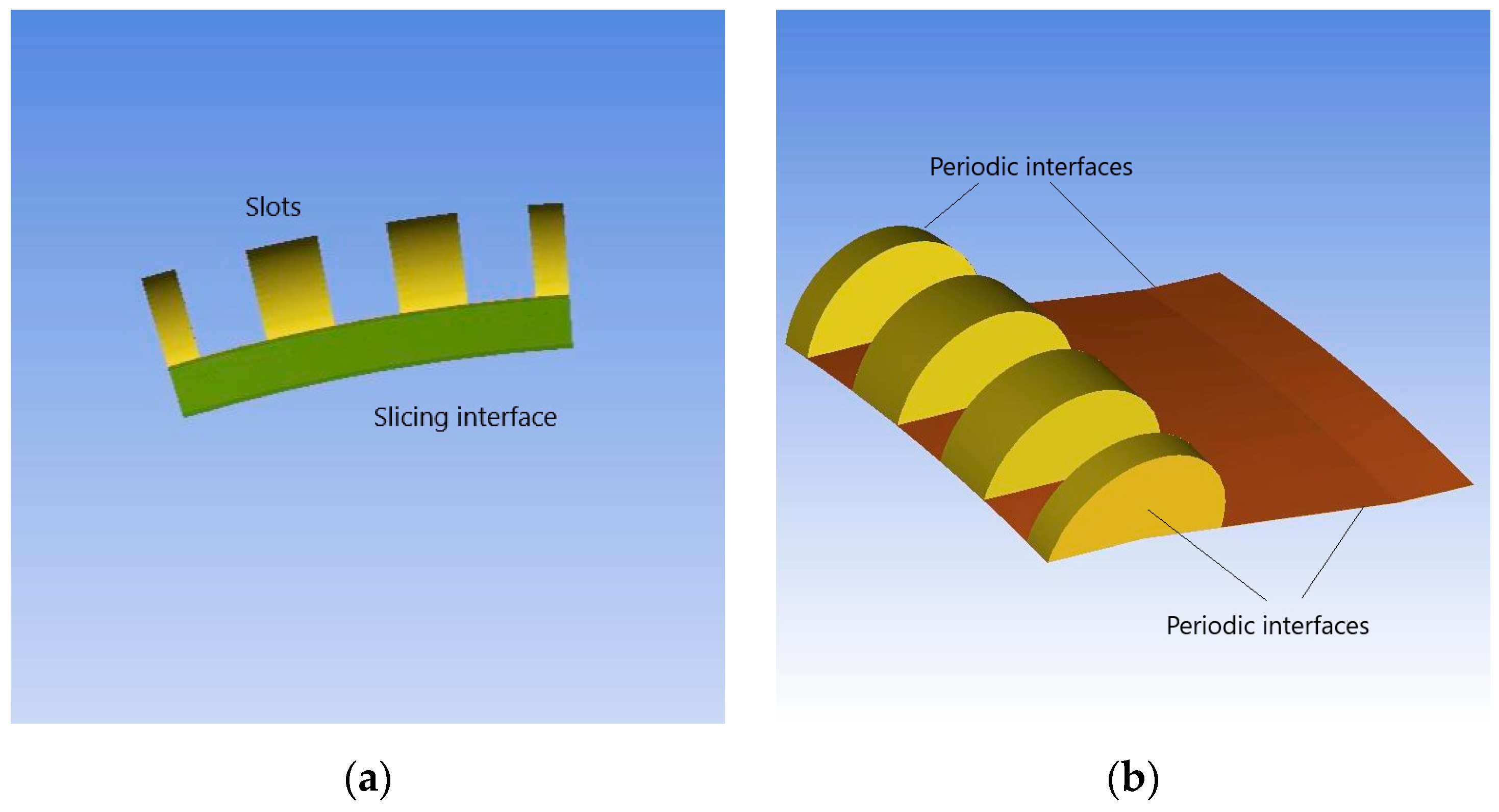
The axial slots were modeled using a slicing interface approach to generate novel semi-circular and thin slicing periodic interfaces. Figure 3 illustrates the detailed construction of the axial slots with slicing interfaces. This slicing interface method was employed to connect the rotor passage section with the casing axial slots, thereby eliminating non-axisymmetric boundary conditions and enabling steady-state simulations.

The larger periodic interface area of the present CT allows for a more effective radial exchange of momentum and energy. This approach differs from that proposed by Lu et al. [22], which relied on a thin periodic interface corresponding to 3% of the tip clearance height to exchange information with neighboring passages.

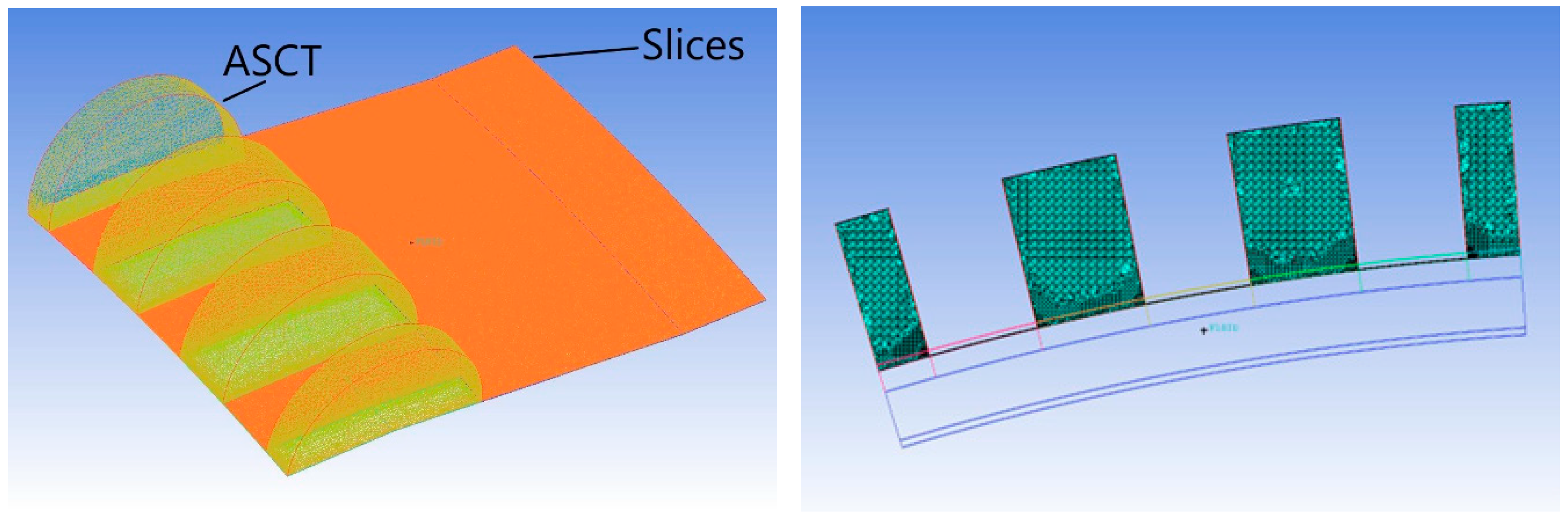
Figure 4 presents the meridional view of the axial compressor with CT and slicing interface above the Rotor 1 passage.

It is anticipated that the flow within the axial slots will exhibit time-independent recirculation patterns. Consequently, meaningful improvements in compressor stall margin can be predicted using steady RANS simulations, even though circumferential averaging between rotors and stators may not fully capture the inherently unsteady nature of the underlying flow structures.

A three-dimensional CFD solver will be employed to characterize the flow field through a numerically approximated solution. From these simulations, a compressor performance map will be generated and compared against experimental data. Subsequently, CFD simulations with the casing treatment (CT) applied to Rotor 1 will be conducted to evaluate performance differences between the smooth-casing and treated-casing configurations. Stall margin improvements will be assessed under various operating conditions, specifically along the N = 100%, N = 95%, and N = 85% speed lines.

3. Numerical Scheme Used for 3D Flow Calculations

The ANSYS^® CFX version 19.2 solver was employed to perform numerical simulations based on the discretized three-dimensional RANS equations. The solver utilizes the finite volume method to discretize the governing equations. It was used to compute the flow field characteristics and subsequently evaluate the influence of the passive wall treatment on the axial compressor’s stall margin.

Steady-state simulations were performed by solving the Reynolds-Averaged Navier–Stokes (RANS) equations. The Rhie and Chow interpolation scheme [26] was employed for the discretization of mass terms to prevent pressure–velocity decoupling. A high-resolution, second-order scheme was adopted for the discretization of the momentum equations. This scheme utilizes the Monotonic Upstream-centered Scheme for Conservation Laws (MUSCL) approach with limiter functions, which dynamically adjust the discretization order in the presence of flow discontinuities. For turbulence closure, the two-equation k–ω Shear Stress Transport (SST) model developed by Menter [27] was selected, owing to its demonstrated ability to accurately capture both near-wall and free-stream turbulence characteristics.

At the compressor inlet, boundary conditions specified the total pressure, total temperature, turbulence intensity, and axial flow direction. The IGV inlet conditions were set to a constant total pressure of 101,325 Pa and a total temperature of 288.15 K. Advection terms were discretized using the high-resolution scheme described above. Solid walls were modeled as adiabatic with a no-slip boundary condition.

Mixing-plane interfaces were implemented between blade rows to account for the interaction between rotating and stationary components. Rotational periodicity was enforced in the circumferential direction to reduce computational cost, enabling the simulation of a single passage per blade row rather than the full annulus. This modeling strategy is widely accepted and has been shown to yield accurate results in the vicinity of the design point, as reported by Liu, Ju, and Zhang [28].

For simulations incorporating casing treatment (CT), a frozen-rotor interface was defined between Rotor 1 and the axial slot region to account for relative motion between these zones. At the outlet boundary, the spanwise static pressure distribution was prescribed according to the radial equilibrium equation.

The compressor performance map was constructed using results from steady-state simulations. For each rotational speed, a speed line was generated by progressively increasing the static back pressure at the outlet, beginning from a low value (near choke conditions) [29] and continuing until the numerical solution failed to converge. Non-convergence was interpreted as an indication of stall onset, consistent with prior studies [30,31], which have recognized that stall corresponds to highly unsteady flow behavior incompatible with steady-state boundary conditions.

Steady convergence of simulations with CT may thus, indicate an extended operational range and improved stall margin. The same stall detection criteria applied to the smooth casing configuration were used for the treated cases. Numerical stall was identified by diverging mass flow, a monotonic decrease in total pressure ratio and efficiency, or failure to converge within a static back pressure variation of 1%, consistent with the methodologies of Wilke and Kau [32] and Engels et al. [24].

Convergence of the RANS equations was assessed by monitoring the decay and stabilization of Root Mean Square (RMS) residuals. Convergence was deemed acceptable when RMS residuals for continuity fell below 10⁻⁴ and when those for momentum fell below 10⁻³. Furthermore, global imbalances in continuity, momentum, and energy across the computational domain were required to remain below 0.01 (<1%).

The RANS methodology consists of averaging the conservation equations over a sufficiently long period to eliminate turbulent fluctuations while retaining the time dependence of the averaged quantities. The RANS equations (Equations (1)–(3)) are expressed as follows [33]:

Mass conservation equation:

$${\displaystyle \frac{\partial \rho }{\partial t}}+{\displaystyle \frac{\partial }{\partial x_j}}\left(\rho u_j\right)=0$$

(1)

Momentum conservation equation:

$${\displaystyle \frac{\partial \left(\rho u_i\right)}{\partial t}}+{\displaystyle \frac{\partial }{\partial x_j}}\left(\rho u_i{u}_j\right)=-{\displaystyle \frac{\partial p}{\partial x_i}}+{\displaystyle \frac{\partial }{\partial x_j}}\left[\mu \left({\displaystyle \frac{\partial u_i}{\partial x_j}}+{\displaystyle \frac{\partial u_j}{\partial x_i}}-{\displaystyle \frac{2}{3}}{\delta }_{ij}{\displaystyle \frac{\partial u_l}{\partial x_l}}\right)\right]+{\displaystyle \frac{\partial }{\partial x_j}}(-\rho \overline{{\mathsf{ú}}_i{\mathsf{ú}}_j})$$

(2)

Energy conservation equation:

$${\displaystyle \frac{\partial e}{\partial t}}+{\displaystyle \frac{\partial }{\partial x_j}}\left[u_j\left(e+p\right)-u_i{\tau }_{ij}-q_j\right]=0$$

(3)

The RANS approach to turbulence modeling requires the appropriate representation of the Reynolds stresses. To compute the eddy viscosity of the flow, the two-equation k–ω Shear Stress Transport (SST) turbulence model developed by Menter [27] was employed. This choice follows the work of Tomita et al. [34], in which the authors conducted an extensive comparison and performed several tests using both structured and unstructured mesh types under different turbulence modeling approaches.

The k–ω SST model is well-suited for application in turbomachinery flow fields and has been widely adopted by researchers, as discussed by Tomita et al. [34]. The model combines the advantages of the Wilcox k–ω formulation and the k–ε model. The turbulent (or eddy) viscosity, μ_t, is defined as a function of the turbulent kinetic energy (k) and the specific dissipation rate (ω). The governing equations of the turbulence model are expressed as follows:

$${\displaystyle \frac{\partial \left(\rho k\right)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho u_{j}k\right)}{\partial x_j}}=P-{\beta }^{\prime }\rho \omega k+{\displaystyle \frac{\partial }{\partial x_j}}\left[\left(\mu +{{\sigma }_k\mu }_t\right){\displaystyle \frac{\partial k}{\partial x_j}}\right]$$

(4)

$${\displaystyle \frac{\partial \left(\rho \omega \right)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho u_j\omega \right)}{\partial x_j}}={\displaystyle \frac{\gamma }{{\nu }_t}}P-\beta \rho {\omega }^2{\displaystyle \frac{\partial }{\partial x_j}}\left[\left(\mu +{{\sigma }_{\omega }\mu }_t\right){\displaystyle \frac{\partial \omega }{\partial x_j}}\right]+2\left(1-F_1\right){\displaystyle \frac{\rho {\sigma }_{\omega 2}}{\omega }}{\displaystyle \frac{\partial k}{\partial x_j}}{\displaystyle \frac{\partial \omega }{\partial x_j}}$$

(5)

With:

$$P={\tau }_{ij}{\displaystyle \frac{\partial u_i}{\partial x_j}}$$

(6)

$${\tau }_{ij}={\mu }_t\left(2S_{ij}-{\displaystyle \frac{2}{3}}{\displaystyle \frac{\partial u_k}{\partial x_k}}{\delta }_{ij}\right)-{\displaystyle \frac{2}{3}}\rho k{\delta }_{ij}$$

(7)

$$S_{ij}={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{\partial u_i}{\partial x_j}}+{\displaystyle \frac{\partial u_j}{\partial x_i}}\right)$$

(8)

The turbulence eddy viscosity is defined as:

$${\mu }_t={\displaystyle \frac{\rho a_{1}k}{max(a_1\omega ,\Omega F_2)}}$$

(9)

An interpolation between constants (${\mathrm{\varnothing }}_1$) from the original k–ω model and constants (${\mathrm{\varnothing }}_2$) from the k–ε is made in Equation (10).

$$\varnothing =F_1{\varnothing }_1+(1-F_1){\varnothing }_2$$

(10)

Additional functions are determined by the following equations:

$$F_1=\mathit{tanh}\left({arg}_1^4\right)$$

(11)

$${\mathit{arg}}_1=\mathit{min}\left(max\left({\displaystyle \frac{\sqrt{k}}{{\beta }^{\prime }\omega d}},{\displaystyle \frac{500\nu }{d^2\omega }}\right),{\displaystyle \frac{4\rho {\sigma }_{\omega 2}k}{C{D}_{k\omega }{d}^2}}\right)$$

(12)

$$C{D}_{k\omega }=max\left(2\rho {\sigma }_{\omega 2}{\displaystyle \frac{1}{\omega }}{\displaystyle \frac{\partial k}{\partial x_j}}{\displaystyle \frac{\partial \omega }{\partial x_j}},1{\times 10}^{-20}\right)$$

(13)

$$F_2=\mathit{tanh}\left({arg}_2^2\right)$$

(14)

$${\mathit{arg}}_2=\mathit{max}\left({\displaystyle \frac{2\sqrt{k}}{{\beta }^{\prime }\omega d}},{\displaystyle \frac{500\nu }{d^2\omega }}\right)$$

(15)

The constants values are:

$${\gamma }_1={\displaystyle \frac{{\beta }_1}{{\beta }^{\prime }}}-{\displaystyle \frac{{\sigma }_{\omega 1}{\kappa }^2}{\sqrt{{\beta }^{\prime }}}}$$

$${\gamma }_2={\displaystyle \frac{{\beta }_2}{{\beta }^{\prime }}}-{\displaystyle \frac{{\sigma }_{\omega 2}{\kappa }^2}{\sqrt{{\beta }^{\prime }}}}$$

σ_k1 = 0.85; σ_k2 = 1.0; σ_ω1 = 0.5; σ_ω2 = 0.856;

β₁ = 0.075; β₂ = 0.0828; β′ = 0.09; κ = 0.41; a₁ = 0.31

4. Mesh Generation and Its Evaluation

Unstructured meshes composed of tetrahedral elements were generated using the commercial software ICEM CFD (version 19.2, ANSYS^®) to discretize the fluid domain of the compressor, including both the physical wall domains and the computational domains bounded by periodic and rotor–stator interfaces. To accurately resolve the near-wall flow and capture the viscous effects within the boundary layer, prism layers were applied to all solid surfaces. Figure 5 presents a cross-sectional view of the axial slot mesh, highlighting the unstructured tetrahedral elements and the prism layers adjacent to the walls, which improve boundary-layer resolution—a critical requirement for the numerical treatment of convective terms in the momentum equations. A transitional slice meshing (shown in orange) was used to interface the ASCT region with the rotating domain.

Each blade row, including rotors, stators, and the ASCT, was meshed independently to ensure mesh quality and to allow for localized refinements.

Independent meshing of each component offers several advantages, including greater flexibility in local refinement, improved control over key meshing parameters, and simplified mesh modification and treatment implementation. This modular approach also facilitates the application and integration of the axial slot CT mesh onto the Rotor 1 domain. Figure 6a shows the unstructured mesh of Rotor 1, while Figure 6b presents the unstructured mesh of the axial slots superimposed above the Rotor 1 mesh.

A single-passage fluid domain was simulated for each blade row to reduce computational cost. Periodic boundary conditions were imposed in the circumferential (blade-to-blade) direction, a widely adopted practice in turbomachinery CFD that provides computational efficiency while maintaining acceptable accuracy. In addition, the lateral boundaries of the slice and the slots were modeled using periodic boundary conditions.

To adequately resolve the boundary layer and capture near-wall flow phenomena, grid refinement was applied in the vicinity of solid surfaces. The first grid point off the wall was positioned at 1.0 × 10⁻⁷ m from the blade and endwall surfaces, yielding a dimensionless wall distance of y⁺ < 1.1. This resolution ensures that the viscous sublayer is fully captured without relying on wall-function approximations, thereby improving the accuracy of turbulence modeling near walls. Figure 7 shows an isometric view of the axial compressor with CT generated in CFX (version 19.2, ANSYS^®).

The computational domain outlet was positioned 0.11681 m downstream of the Stator 3 trailing edge (TE), consistent with the extension used in the experimental facility. In this region, a progressively coarsened grid was applied to reduce computational cost while preserving flow accuracy. A non-reflective boundary condition was imposed at the outlet to suppress artificial wave reflections and ensure physically consistent outflow behavior.

The frozen-rotor approach was adopted at the Rotor 1/slice interface to model the interaction between the rotating and stationary components, while mixing-plane interfaces were applied at all other rotor–stator interfaces to enable steady-state simulations. This methodology facilitates the circumferential averaging of flow properties across adjacent blade rows, providing efficient yet reliable predictions of time-averaged flow fields.

To verify the mesh independence of the numerical results for smooth casing (SC) configurations, four distinct unstructured grids were generated. The main characteristics of these meshes are summarized in

Table 3. Main parameters of axial compressor with SC wall grid refinement study.

	Number of Elements (Millions)	Number of Prism Layers	Initial Height (m)	y+
Mesh 1 (coarse)	8.2	27	1.00 × 10−7	<1.1
Mesh 2 (medium)	14.3	27	1.00 × 10−7	<1.1
Mesh 3 (fine)	25.2	27	1.00 × 10−7	<1.1
Mesh 4 (high fine)	33.9	27	1.00 × 10−7	<1.1

. In all cases, the dimensionless wall distance (y⁺) was maintained below 1.1, ensuring sufficient resolution of the near-wall viscous sublayer.

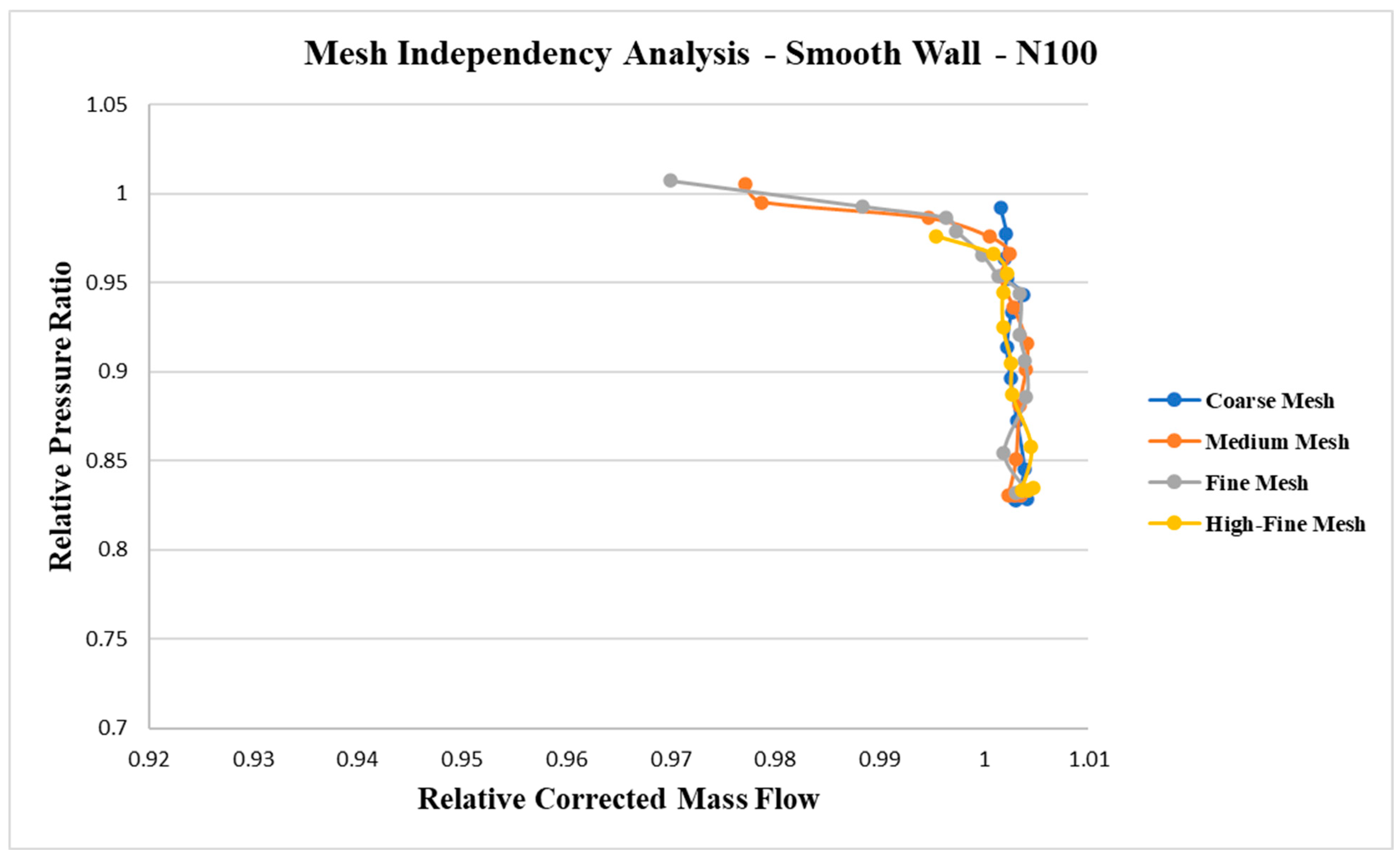
The smooth casing (SC) compressor performance map at the design-point rotational speed (N = 100%) was obtained through numerical simulations using four different mesh configurations, as shown in Figure 8. The pressure ratio (PR) and mass airflow are presented in normalized form in Figure 8, with reference values of PR = 4.0 and mass airflow = 29.71 kg/s.

The overall trends and predicted values of the SC performance curves showed close agreement across all four meshes, indicating mesh-independent results up to an outlet static pressure of 320 kPa.

The grid refinement study was conducted following the procedure described by Celik et al. [35], which assesses the numerical convergence of CFD simulations using the Grid Convergence Index (GCI) as an estimate of discretization error. In this approach, simulations are performed on at least three successively refined grids.

The GCI methodology was applied to the SC compressor performance curves presented in Figure 8. The results indicate that the discretization error is within 5%, and the overall numerical uncertainty is estimated at approximately 5%. These values fall within the generally accepted range for grid-converged CFD simulations using three distinct mesh levels.

The adopted procedure involved generating the compressor performance map using a fine grid and verifying the results against reference data. Two additional maps were obtained with coarser grids by systematically reducing the number of grid lines in each segment of the model. The initial set of distinct meshes (Mesh 1, Mesh 2, and Mesh 3) resulted in discretization errors (GCI) greater than 5%, necessitating the generation of a finer mesh model.

A subsequent refinement study was conducted using three new distinct meshes (Mesh 2, Mesh 3, and Mesh 4). The results of this study are summarized in

Table 4. SC axial compressor calculations of discretization error for meshes 2, 3, and 4.

Psout	Compressor outlet static pressure (kPa)	325	320
N4 (millions)	No of nodes grid 4	10.73	10.73
N3 (millions)	No of nodes grid 3	8.20	8.20
N2 (millions)	No of nodes grid 2	4.85	4.85
r34	Grid refinement ratio 34	1.094	1.094
r23	Grid refinement ratio 23	1.191	1.191
Variable φ4	PR (Pressure Ratio) grid 4	3.905	3.864
Variable φ3	PR (Pressure Ratio) grid 3	3.916	3.863
Variable φ2	PR (Pressure Ratio) grid 2	3.903	3.865
e34	Relative error 34	0.011	−0.001
e23	Relative error 23	−0.013	0.002
p	Local order of accuracy p	1.33	2.68
φ34ext	PR 34 Extrapolated value	3.818	3.868
ea34 (%)	Approximate relative error 34	0.284	0.028
e34ext (%)	Extrapolated relative error 34	2.290	0.104
GCI34h_fine (%)	High Fine Grid Convergence Index 34	2.80	0.13

, with GCI calculations performed at two outlet static pressure conditions, 320 kPa and 325 kPa, within the stable operating region of the compressor, prior to stall onset in the simulations.

The variable nomenclature used in Table 4 follows the methodology presented by Celik et al. [35]: N represents the number of nodes in each simulation model; r is the refinement ratio, defined as the cubic root of the node-count ratio; φ denotes the variable of interest, in this case, the compressor pressure ratio (PR); p is the local order of accuracy; e is the relative error of φ (PR); and GCI is the estimated discretization error of the fine grid (Mesh 3) relative to the very fine grid (Mesh 4).

Using Mesh 3 as the reference grid and comparing it to the finer Mesh 4, the maximum discretization error was found to be 2.79% at an outlet static pressure (Ps,out) of 325 kPa. Based on this assessment, Mesh 3 (fine mesh) was selected as the reference grid for subsequent simulations, providing an appropriate balance between computational cost, mesh refinement verification, and solution accuracy, which was later validated against experimental data in Section 5 of this paper.

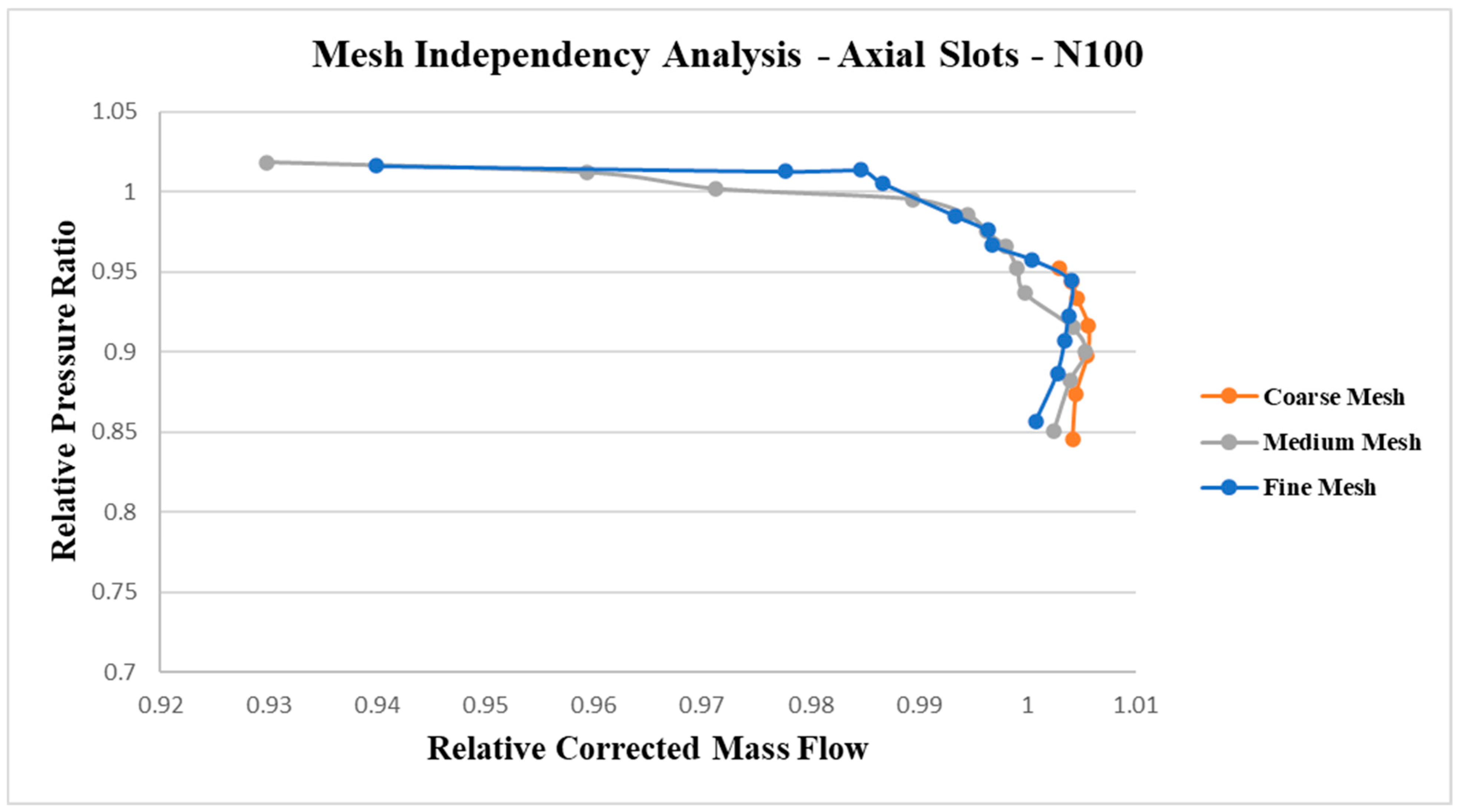
The compressor performance map for the axial slot casing treatment (CT) at the design-point rotational speed (N = 100%) was then obtained through numerical simulations using the three distinct mesh configurations, as illustrated in Figure 9.

The pressure ratio (PR) and mass airflow shown in Figure 9 are presented in normalized form, with reference values of PR = 4.0 and mass airflow = 29.71 kg/s. The overall trends and predicted values of the axial slot CT performance curves exhibited close agreement across all three meshes, indicating mesh-independent results up to an outlet static pressure of 320 kPa.

The grid refinement study methodology proposed by Celik et al. [35] was also applied to verify the mesh independence of the numerical results for the axial slot compressor CT configuration. The mesh independence study was conducted using three distinct unstructured grids to determine the appropriate refinement level and to select the optimal mesh, ensuring numerical accuracy while minimizing computational cost.

The main characteristics of these meshes are summarized in

Table 5. Main parameters of axial compressor with CT grid refinement study.

	Number of Elements (Millions)	Number of Prism Layers	Initial Height (m)	y+
Mesh 5 (coarse)	10.4	27	1.00 × 10−7	<1.1
Mesh 6 (medium)	17.9	27	1.00 × 10−7	<1.1
Mesh 7 (fine)	31.3	27	1.00 × 10−7	<1.1

. In all cases, the dimensionless wall distance (y⁺) was maintained below 1.1, ensuring sufficient resolution of the near-wall viscous sublayer.

The Grid Convergence Index (GCI) methodology provides an estimated numerical uncertainty of approximately 5%, with discretization errors (GCI) maintained within 5% for the grid selections (Meshes 2, 3, and 4).

The grid refinement study for the CT configuration, based on three distinct meshes (Meshes 5, 6, and 7), is summarized in

Table 6. Axial slots calculations of discretization error for meshes 5, 6, and 7.

Psout	Compressor outlet static pressure (kPa)	315	250
N7 (millions)	No of nodes grid 7	11.02	11.02
N6 (millions)	No of nodes grid 6	6.51	6.51
N5 (millions)	No of nodes grid 5	3.9	3.9
r67	Grid refinement ratio 67	1.192	1.192
r56	Grid refinement ratio 56	1.186	1.186
Variable φ7	PR (Pressure Ratio) grid 7	3.832	3.425
Variable φ6	PR (Pressure Ratio) grid 6	3.809	3.402
Variable φ5	PR (Pressure Ratio) grid 5	3.775	3.383
e67	Relative error 67	−0.022	−0.024
e56	Relative error 56	−0.034	−0.019
p	Local order accuracy p	2.73	1.20
φ67ext	PR67 Extrapolated value	3.868	3.527
ea67 (%)	Approximate relative error 67	0.577	0.692
e67ext (%)	Extrapolated relative error 67	0.931	2.870
GCI67fine (%)	Fine Grid Convergence Index 67	1.17	3.69

.

Using the medium grid (Mesh 6) as the reference compared to the fine grid (Mesh 7), the discretization error was found to be 3.69% at an outlet static pressure of 250 kPa. For other outlet static pressure conditions, the discretization error in the predicted pressure ratios remained below 1.2% up to an outlet static pressure of 320 kPa.

The GCI study for the axial compressor with the axial slot CT configuration led to the selection of Mesh 7 (fine mesh) as the reference for subsequent simulations, as it provided an appropriate balance between computational effort and acceptable discretization error for CFD analysis.

Mesh 7 (fine grid) was derived from Mesh 3 (fine grid) of the smooth casing (SC) axial compressor model, with the addition of the axial slot casing model at the same fine-grid level of refinement.

5. Validation of CFD Simulations with Experimental Data of Multi-Stage Axial Compressor (SC at 100% Speed Line)

Following the 3D flow simulations used to generate the compressor map for the SC configuration, the numerically predicted results were compared with the available experimental data for the same configuration [19]. The comparisons between experimental and predicted compressor performance are presented in the figures below.

For the SC wall casing, the stall point was overpredicted by the simulation. At higher mass flow rates, the predicted total pressure ratios were consistently lower than the experimental values. This discrepancy is primarily attributed to the overprediction of blade boundary-layer and endwall losses by the CFD model. While the overall trends of the predicted total pressure ratio curves, both with and without the axial slot CT, generally follow the experimental data at higher mass flow rates, notable deviations occur near the stall point. Specifically, the experimental pressure ratio curve tends to plateau and then slightly decrease near stall, whereas the numerical predictions exhibit a similar profile but with an overall lower pressure ratio.

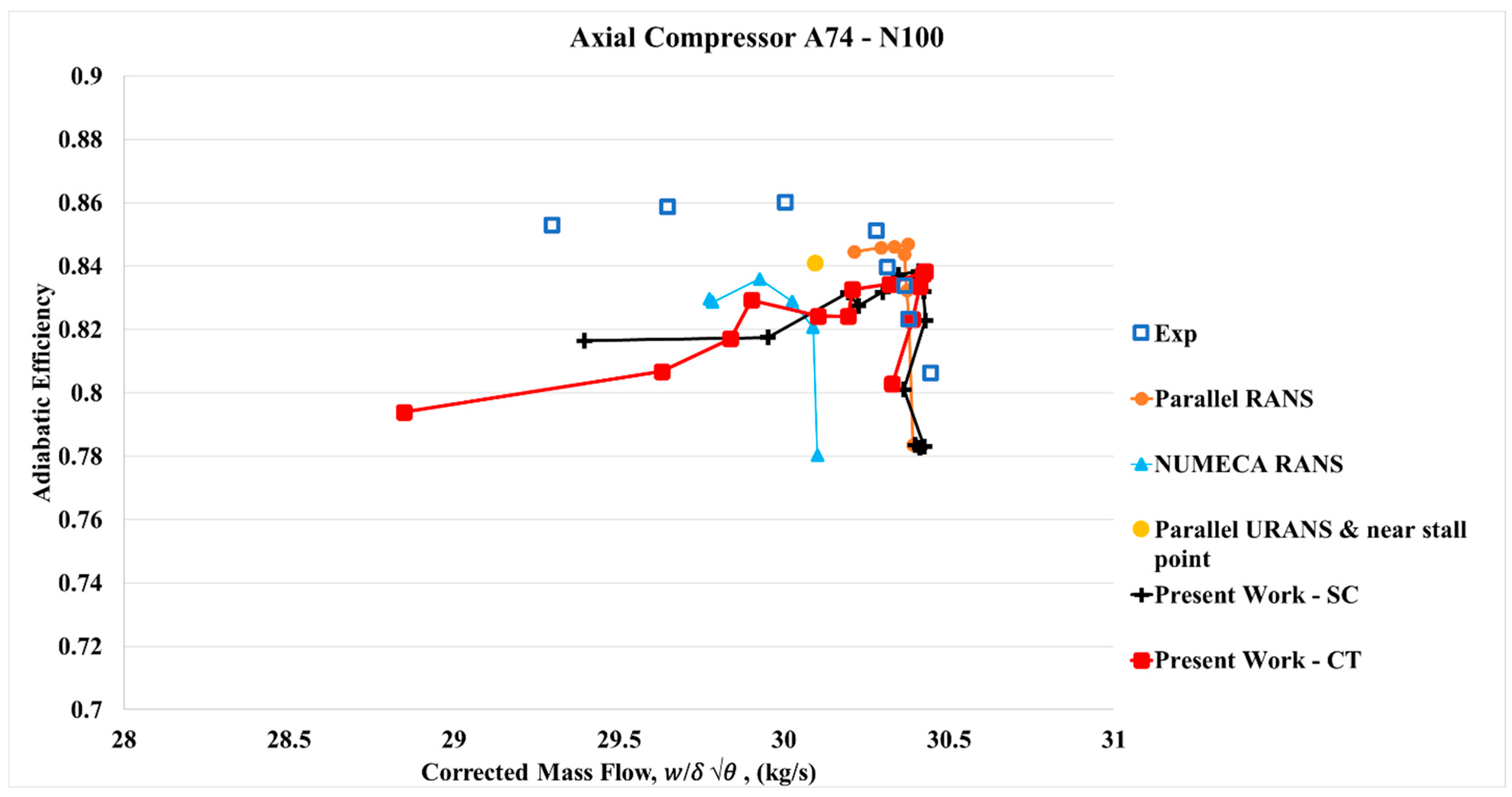
With respect to isentropic efficiency, only minor discrepancies were observed between simulation and experiment. These differences may be attributed to limitations in the turbulence model and/or experimental uncertainties, particularly those associated with measuring small temperature rises. The maximum efficiency predicted by the CFD simulations was approximately 83.8% at design speed, exceeding the original design calculation of 79.9% reported by Steinke [19]. In laboratory experiments, a peak isentropic efficiency of approximately 86% was recorded at design speed with IGV and stator setting angles adjusted for maximum efficiency—the same configuration used in the CFD model.

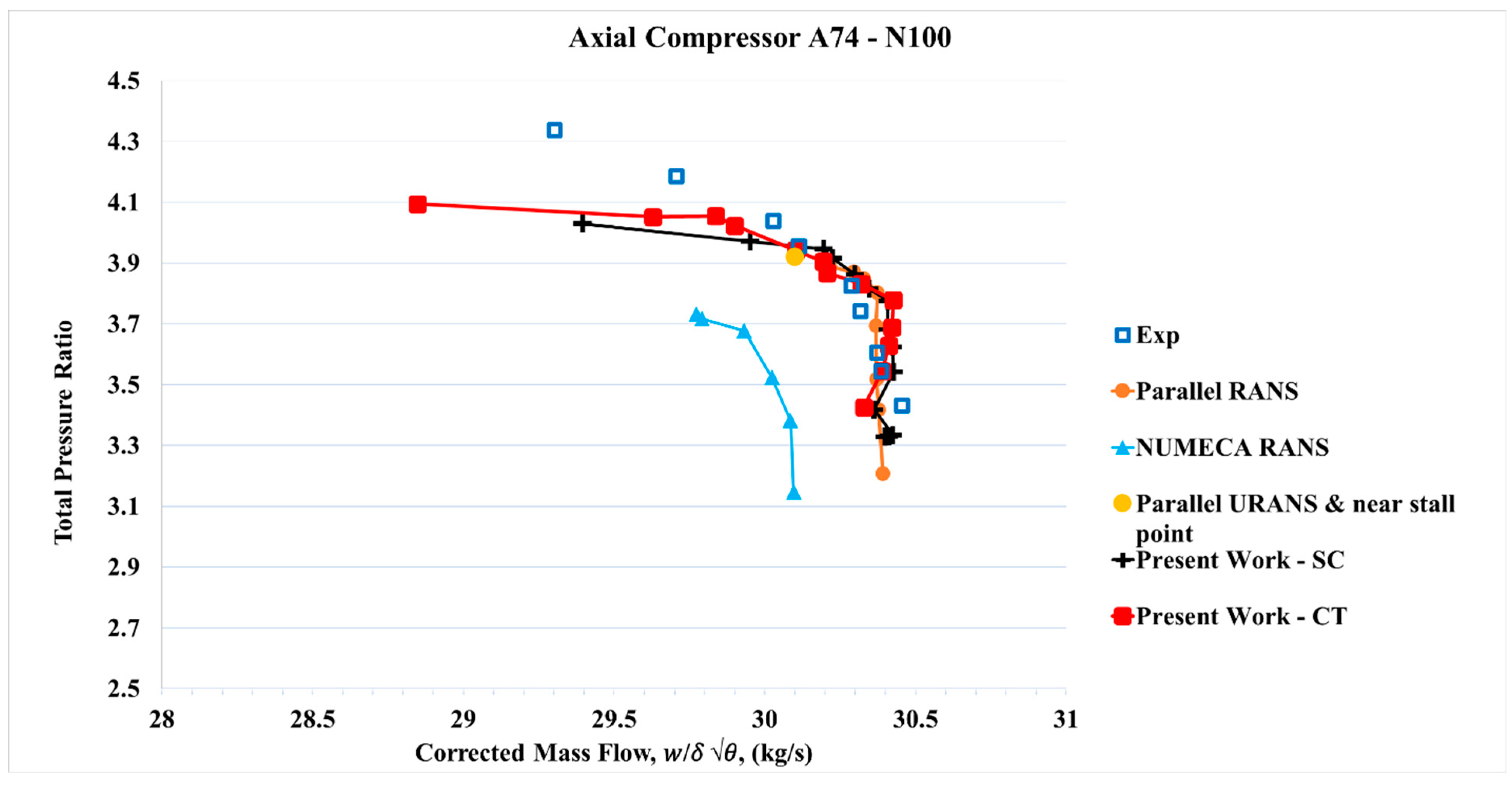
A relevant study by Liu et al. [28] performed 3D CFD simulations of the NASA 3.5-stage axial compressor 74 using both in-house parallel RANS and URANS solvers, as well as the commercial software NUMECA Autogrid5, under identical meshing conditions. Their results were benchmarked against the experimental dataset provided by Steinke [19]. In the present work, CFD simulations using ANSYS^® CFX version 19.2 for the smooth casing at the design speed line (N = 100%) were compared against the same experimental reference. The resulting compressor maps, total pressure ratio vs. corrected mass flow rate and isentropic efficiency vs. corrected mass flow rate, are shown in Figure 10 and Figure 11.

The corrected mass flow rate is (${\displaystyle \frac{w}{\delta }}$ $\sqrt{\theta })$ where $\theta$ is the ratio of total temperature to the standard reference temperature of 288.2 K, and δ is the ratio of total pressure to the standard reference pressure of 1 atm.

Overall, good agreement is observed across most of the operating range. However, deviations become more pronounced under highly throttled conditions near the compressor outlet, where the static pressure is elevated.

Another possible explanation for the deviation from experimental data in the high-pressure ratio region lies in the modeling of the stators within the numerical simulations. In the laboratory-tested axial compressor, the stators are mounted using a cantilevered construction, with the vanes attached to the compressor casing and a clearance present at the hub. The magnitude of this stator hub clearance is comparable to that of the rotor tip clearance.

In the present simulations, however, ideal stators without hub clearance were modeled, which may have contributed to the observed discrepancy. A hub vortex originating from the stator region was identified in the simulations, and a similar phenomenon was also reported by Liu et al. [28] for stators 2 and 3.

Interestingly, the presence of hub clearance in stators may have a beneficial effect on compressor performance. According to Lee et al. [36] and Zhang et al. [37], hub leakage can suppress hub vortex development, thereby improving overall compressor efficiency. This contrasts with the detrimental effect of rotor tip leakage, which promotes the formation of tip leakage vortices and degrades flow near the rotor tip region.

6. Results

To compare the performance of the passive wall treatment against the reference SC case across different speed lines, the following equation was employed to quantify the variation in compressor stall margin [38]:

$$\mathsf{\Delta }\mathrm{S}\mathrm{M}=\left({\displaystyle \frac{{\dot{m}}_{stall,SW}}{{\dot{m}}_{stall,CT}}}\times {\displaystyle \frac{{PR}_{stall,CT}}{{PR}_{stall,SW}}}\right)-1$$

(16)

The compressor map for the SC configuration was obtained through 3D CFD flow simulations, extended up to the last convergence point prior to numerical divergence, which represents the physical stall condition. Subsequently, the axial slot casing treatment applied to the first rotor row was simulated, and compressor maps with CT were generated up to stall. The variation in stall margin was then calculated using Equation (16), based on the mass flow rate and the corresponding pressure ratio at the compressor outlet at the last convergence point, comparing both SC and CT configurations.

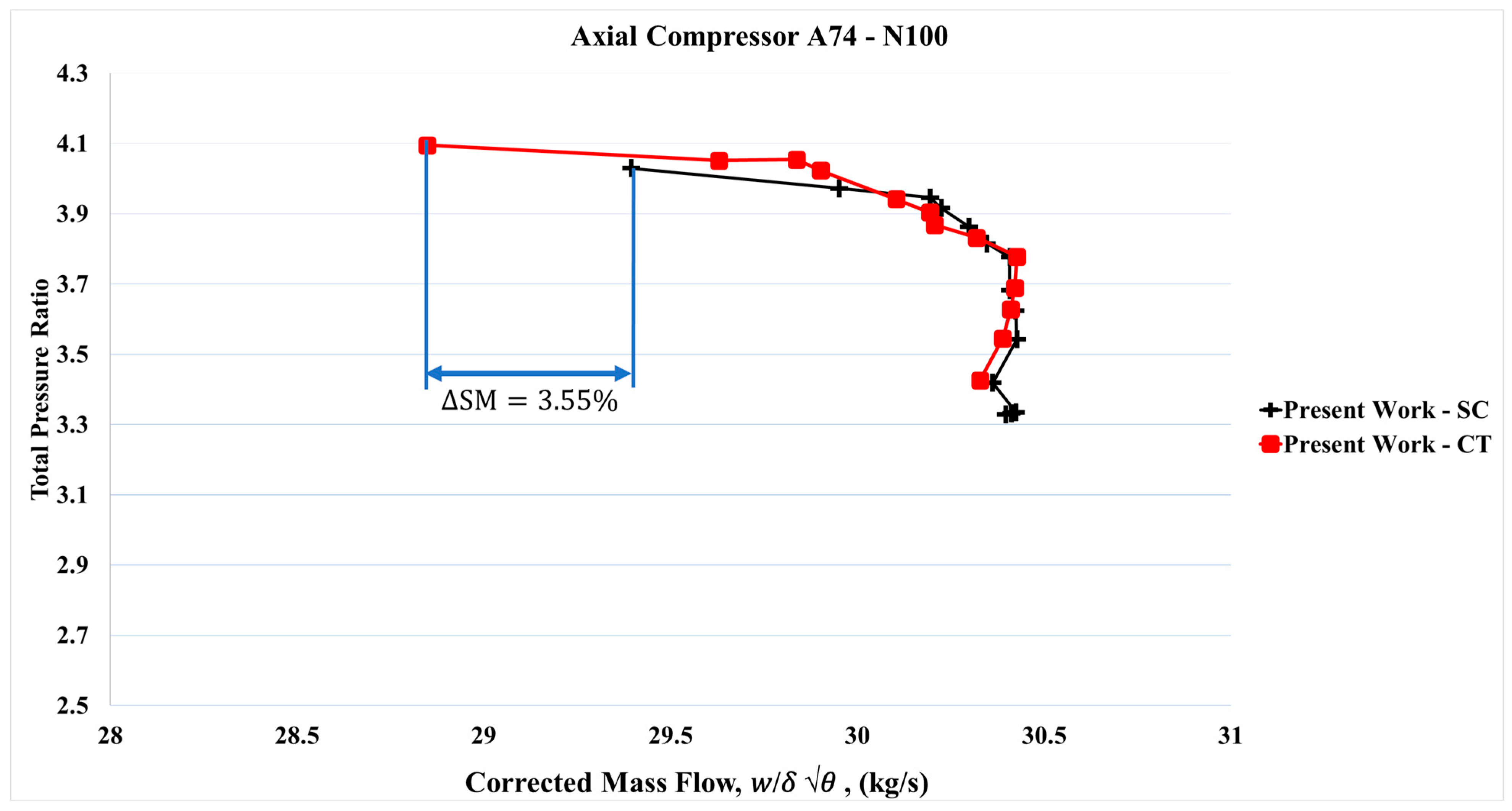
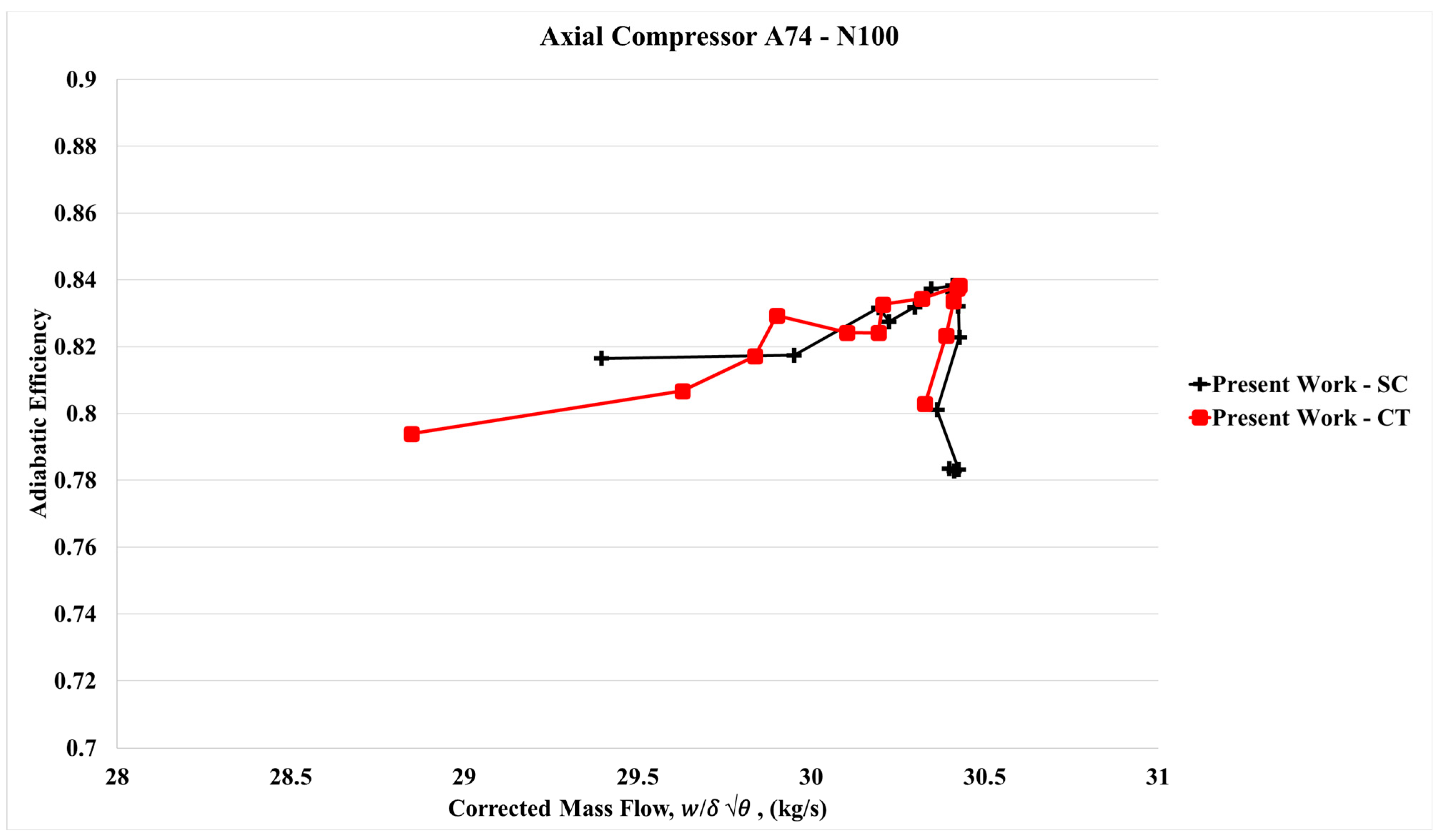
6.1. Performance Map at Speed Line 100%N (N100)—With Axial Slots

The performance maps with axial slots demonstrated an extension of the compressor’s operating range, as shown in Figure 12 and Figure 13. The rotor blade design of the axial compressor 74A remains representative of modern practice, with Rotor 1 blades featuring a multiple circular arc (MCA) profile to mitigate shock wave losses. Even at design speed, the axial compressor exhibited an increased operational range when equipped with axial slot casing treatment (CT). The improvement in stall margin was quantified at 3.55%.

The CT functions by extracting low-momentum fluid from above the Rotor 1 tip, recirculating it within the slots, and reintroducing it upstream of the Rotor 1 leading edge. This mechanism reduces the formation of tip leakage vortices downstream in the Rotor 1 flow passage, thereby enhancing overall compressor stability.

This recirculating flow was observed across the operating speeds analyzed in the present study, ranging from 85 to 100% of the design speed. The proposed CT is more compact than the standard CT studied by Liu et al. [22], which employed axial semi-circular slots 33% longer, of equal width, and with a more complex manufacturing requirement due to a skew angle of 45°. Both designs feature approximately the same Rotor 1 tip length and Rotor 1 tip speeds.

The stall margin improvement obtained with the standard CT was 7.38%, but with a 1% efficiency penalty. In contrast, one of the key objectives of the present study was achieved: the newly proposed CT (ASCT) preserved compressor efficiency. The ASCT successfully met the target of avoiding performance and efficiency degradation when operating at design speed.

Another important objective is to investigate the potential benefits of CT application under off-design operating conditions, where compressors often experience reduced performance and increased susceptibility to instability.

6.2. Performance Map at Speed Line 95%N (N95)—With Axial Slots

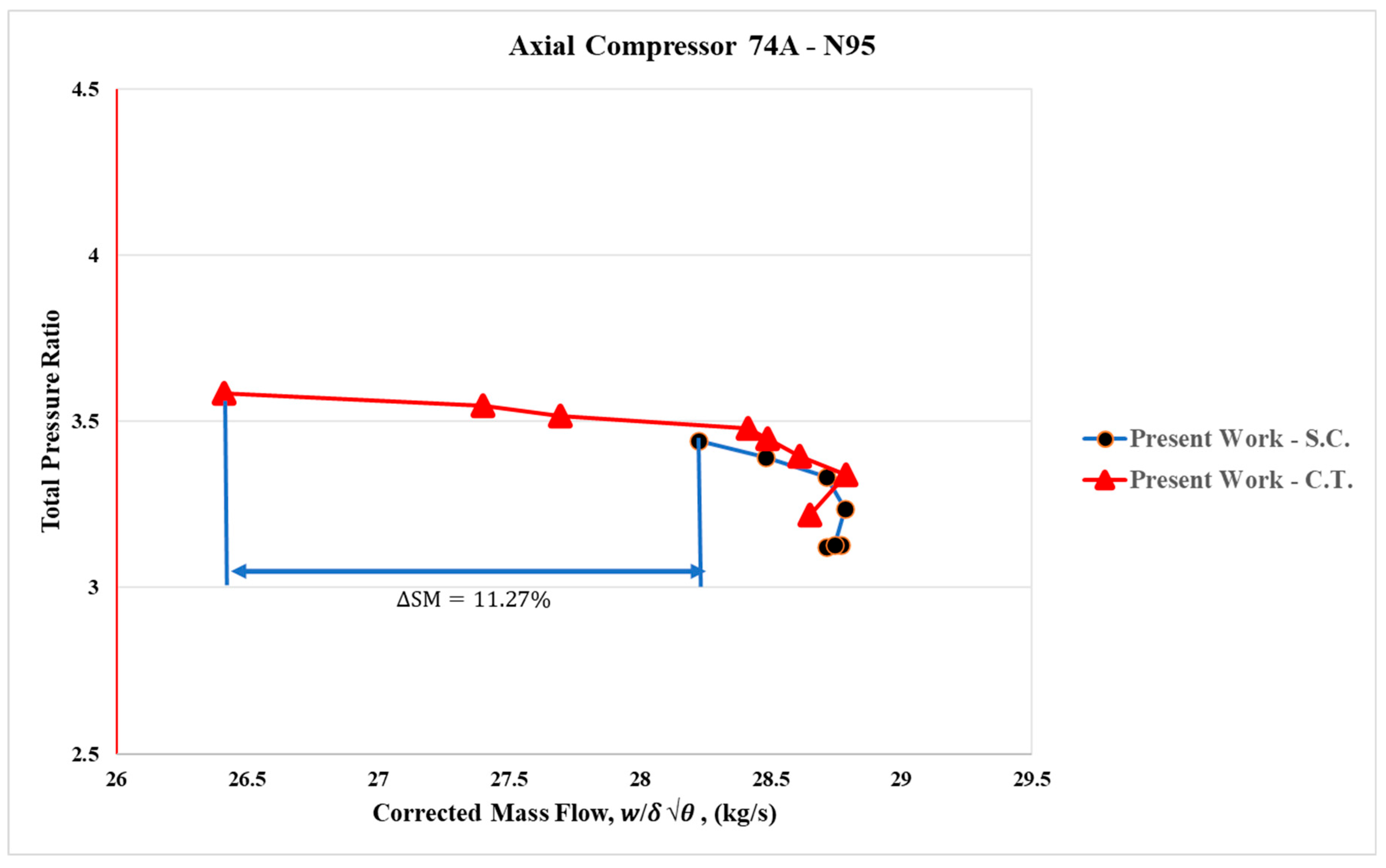
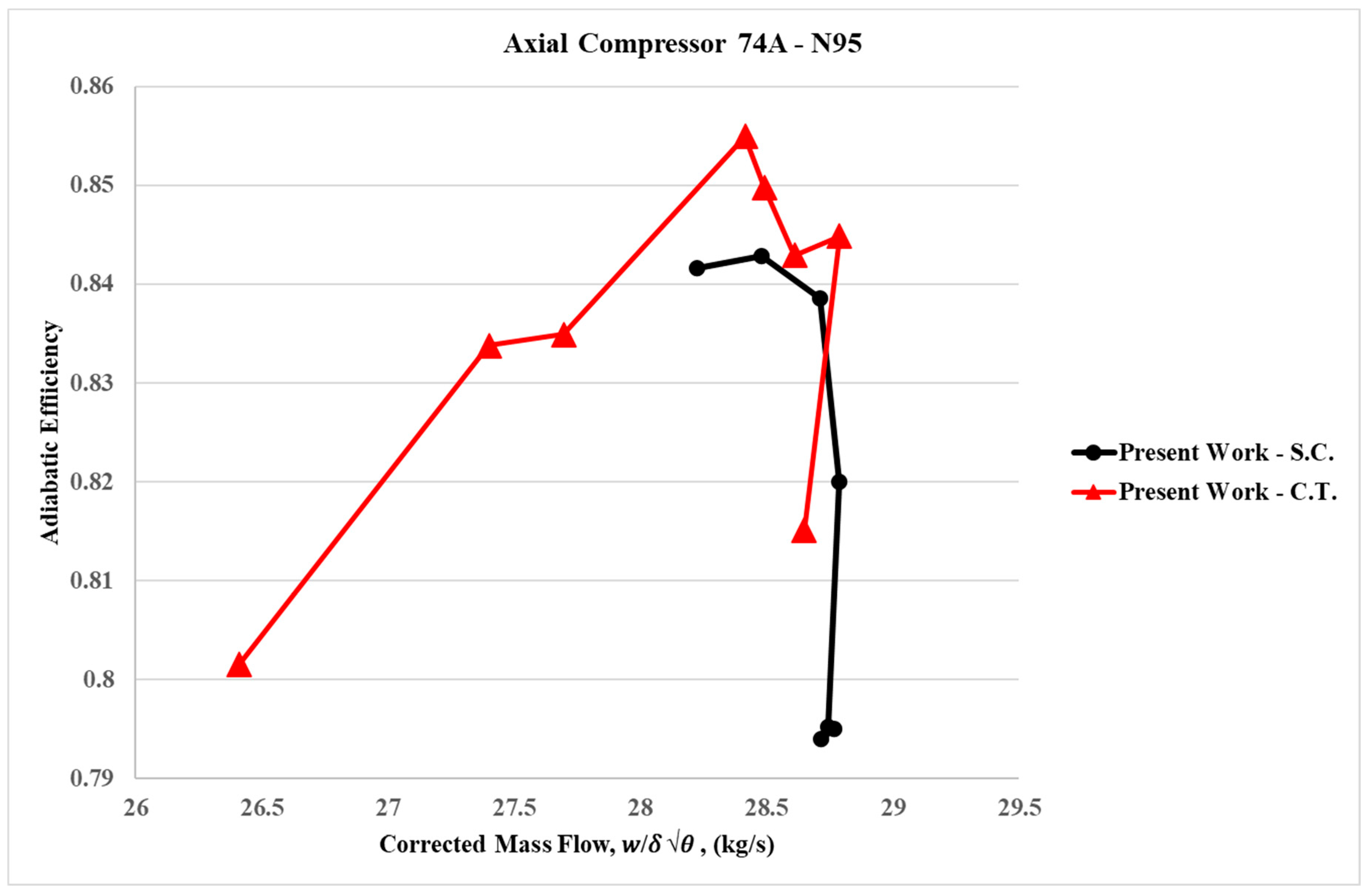
The stall margin was significantly improved, reaching +11.27% with axial slots at 95% of the design speed N (16,042.3 rpm). The compressor map with characteristic curves at 95% design speed is presented in Figure 14 and Figure 15. The primary objective of achieving a positive stall margin was successfully met, accompanied by a notable increase in compressor efficiency.

At 95% design speed, the expected circulation flow is clearly established within the slots. This recirculating flow effectively suppressed the development of the tip leakage vortex (TLV), mitigated flow unsteadiness, and reduced the overall tip leakage flow (TLF). The influence of the casing treatment (CT) at 95% design speed can therefore be considered successful.

The intensity of the shock wave in the Rotor 1 blade tip region was reduced. A 5% reduction in rotor speed also decreased shock wave intensity, thereby contributing to reduced flow separation within the rotor passage. In addition, the suppression of the tip leakage vortex, due to the blockage of tip leakage flow, enhanced flow stability in the Stator 1 passage and delayed the onset of compressor stall. Section 6.6 further illustrates the reduction in shock wave intensity both at Rotor 1 blade tip region and at 30% blade span from the hub in Stator 1, when compared to the SC cases.

6.3. Performance Map at Speed Line 85%N (N85)—With Axial Slots

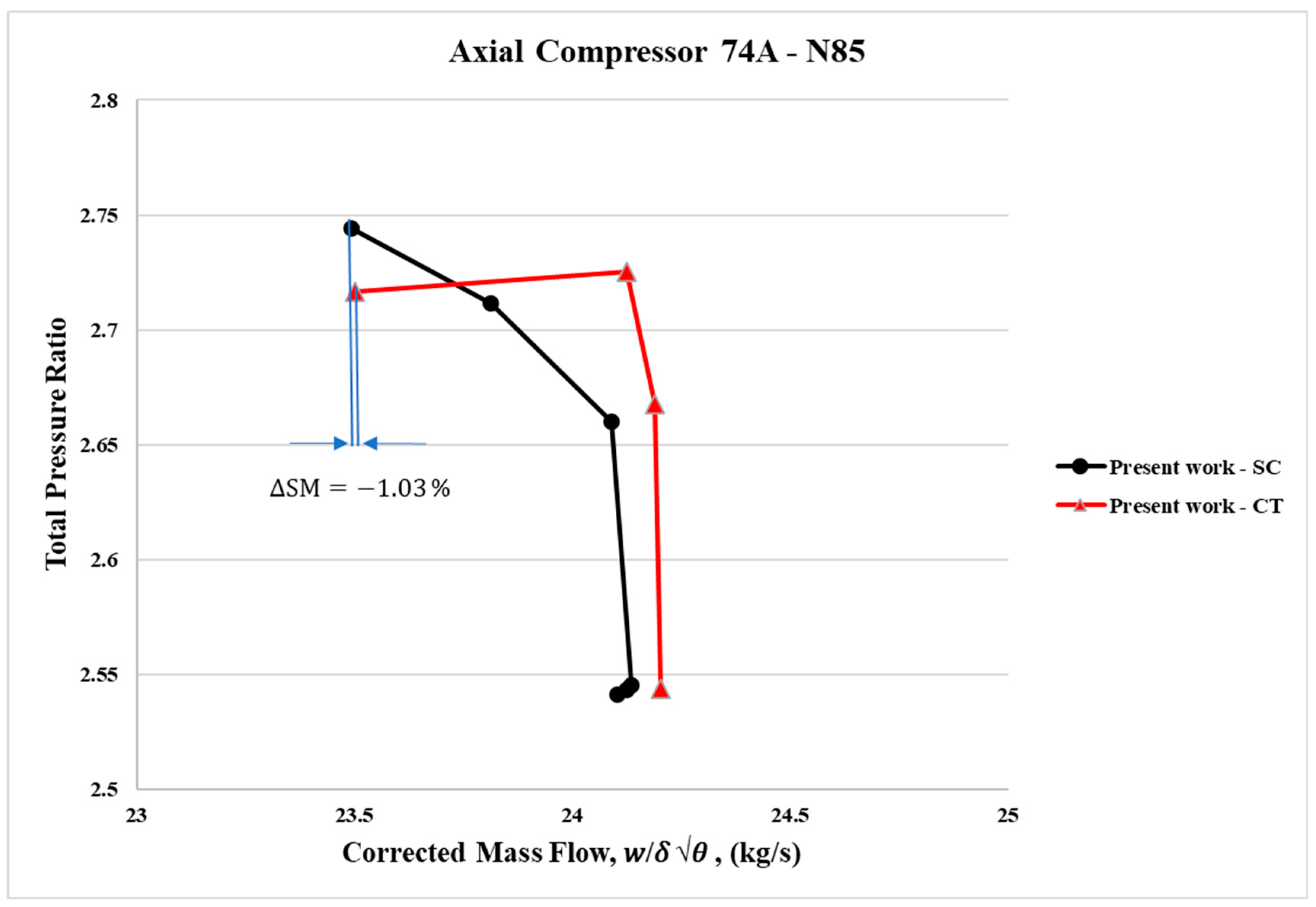
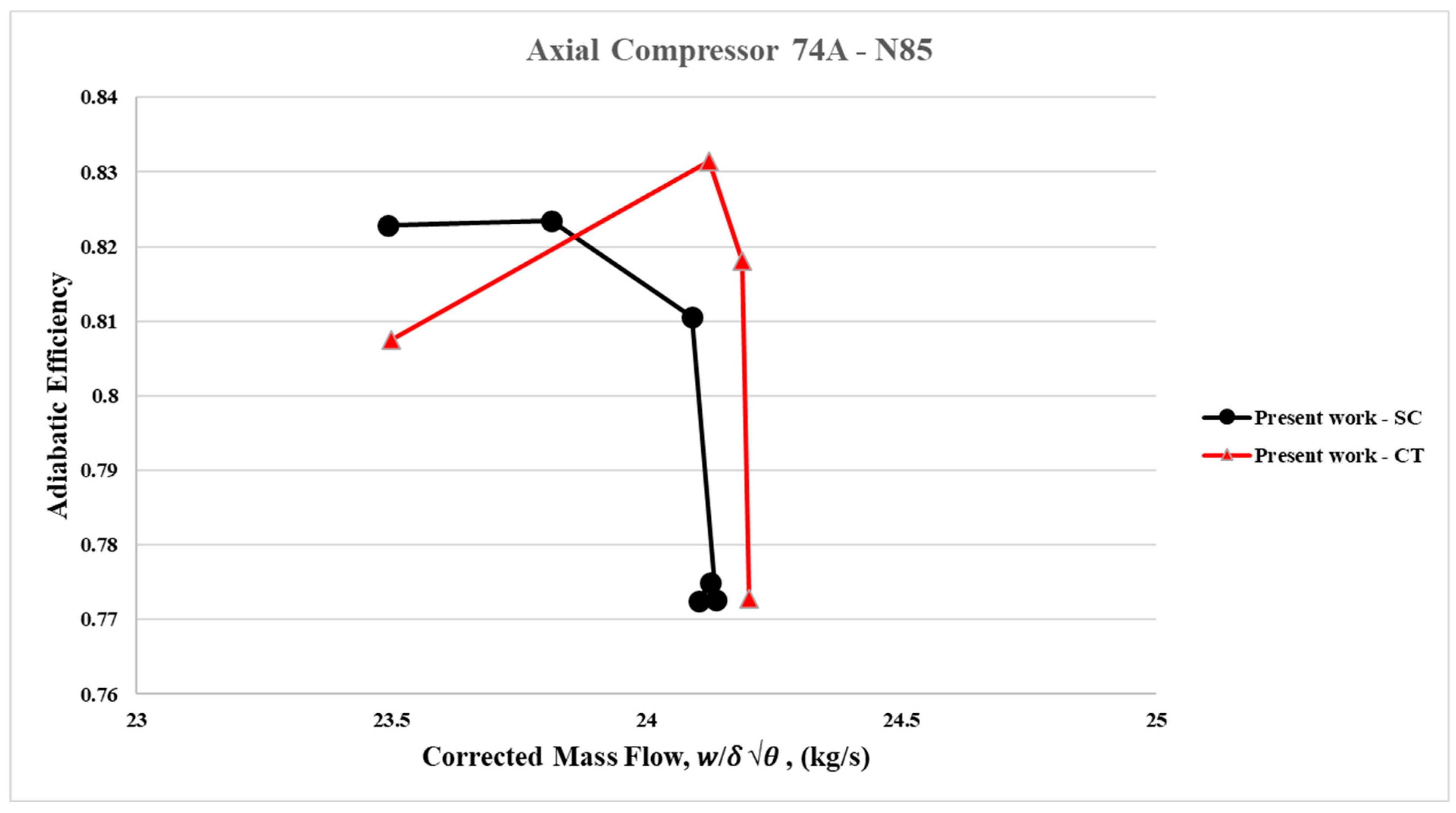
No improvement in stall margins was observed with axial slots compared to simulations without axial slots at the speed line of 85% N (16,042.3 rpm) as presented in Figure 16 and Figure 17.

Only a limited number of CFD simulation points were successfully obtained at 85% of the design speed (N), for both the smooth casing and the CT configurations, due to the strong unsteady effects generated under these off-design operating conditions. In this regime, the stall margin gain was not improved; instead, it bordered the negative side with axial slots. Specifically, the stall margin variation was –1.03%, while the efficiency improvement was marginal, at +0.79% with axial slots. In this case, the recirculation effect within the axial slots appears to negatively impact stability. The stall mechanism is no longer dominated by vortex breakdown but by blade stall. Consequently, improvements to rotor tip flow were insufficient to delay stall inception. Furthermore, the radial redistribution of blade loading induced by the ASCT instead triggered stall at a slightly higher corrected mass flow rate. These findings are consistent with the conclusions of Guinet et al. [3], who investigated CT performance at 0.5% tip clearance.

The CFD steady-state RANS simulations were able to capture the flow behavior at 85% of the design speed up to the final point of numerical convergence. Beyond this limit, the solution diverged, and the growth of unsteady flow phenomena could not be resolved with the mixing-plane interface employed in the model. At operating conditions far from the design point, as observed both experimentally and numerically at or below 85% of design speed, misalignments between the flow and the blades arise, leading to a significant deterioration in compressor efficiency and performance. As expected, this flow mismatch increases entropy generation and enhances losses associated with blade surfaces and tip clearances.

There is also evidence that under these conditions, instability originates in the blade region rather than through tip stall mechanisms. Although steady RANS simulations have limitations in fully capturing the evolution of unsteady flow at low rotational speeds, they were able to detect oscillatory behavior associated with the growth of unsteadiness, leading to numerical divergence. This outcome indicates that CTs are ineffective for axial compressors operating at low rotational speeds. For the compressor investigated in this study, performance and efficiency degrade rapidly at or below 85% of design speed, and the application of CT does not provide meaningful benefits under these operating conditions. Nevertheless, steady RANS simulations with unstructured meshes still yield valuable insights for designers.

6.4. Stall Margins Calculations of Axial Compressor with Axial Slots CT

Table 7. Variation in $\dot{m_{\mathit{s}}}$, PR, η_{is, peak}, and SM with axial slots at different speeds.

N (%)	$\dot{{\mathit{m}}_{\mathit{s}}}$	PR	ηisen,peak	ΔSM
100	−1.86%	+1.62%	−0.01%	+3.55%
95	-6.42%	+4.13%	+1.21%	+11.27%
85	+0.03%	−0.70%	+0.79%	−1.03%

shows the variation in $\dot{m_s}$ (airflow close to stall), PR (pressure ratio), η_isen,peak (isentropic efficiency peak), and ΔSM or SMI (stall margin improvement) relative to the SC case at different corrected rotational speeds for the axial slots applied to the casing of the first rotor blade row. Significant improvements in stall margin with the axial slots were observed at 95% N (16,042.3 rpm), accompanied by an increase in efficiency. However, as discussed previously, at 85% N, no improvement in stall margin was observed, and only marginal or negligible gains in efficiency were obtained with the axial slots.

6.5. Meridional Pressure Distributions of Axial Compressor with and Without Axial Slots CT

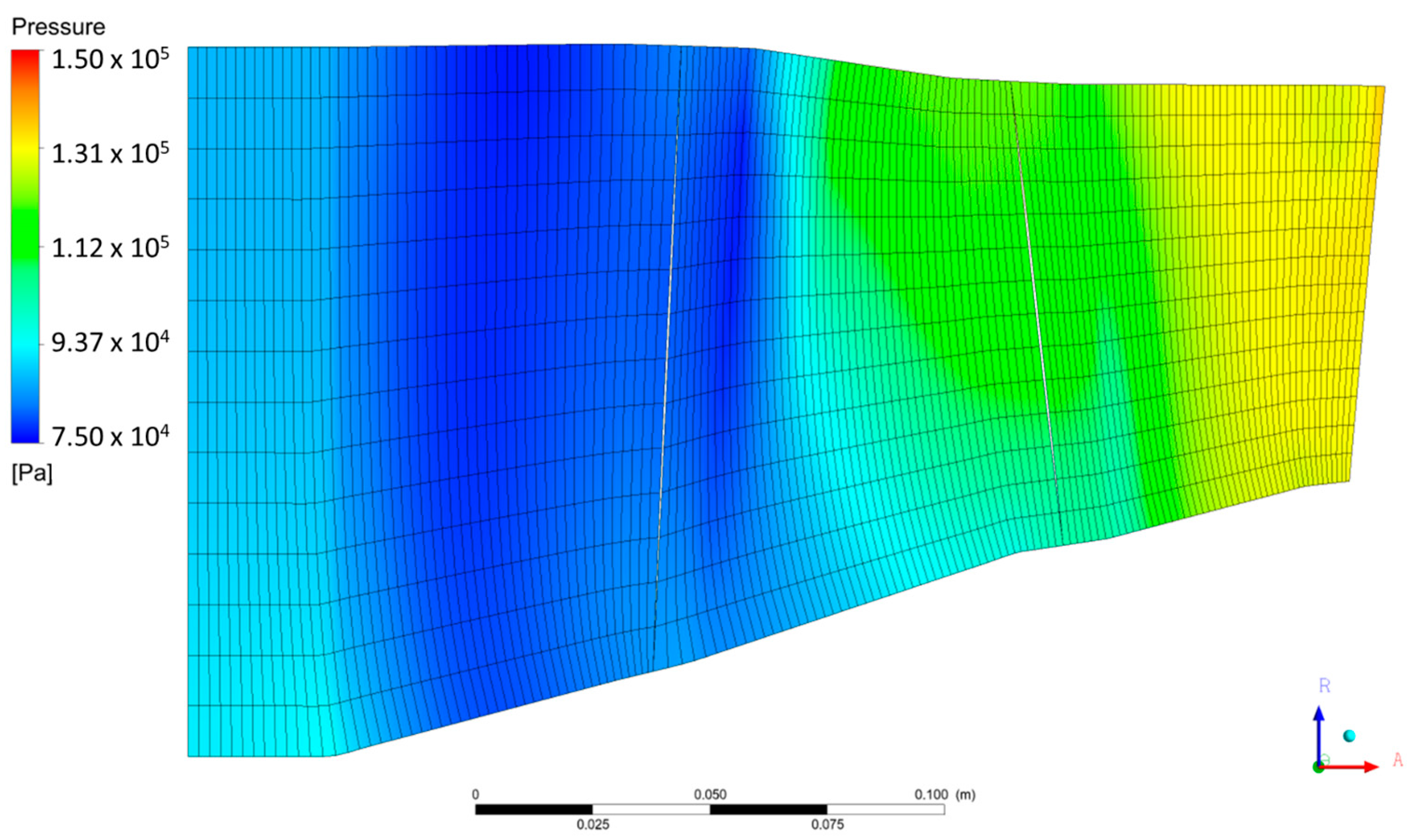
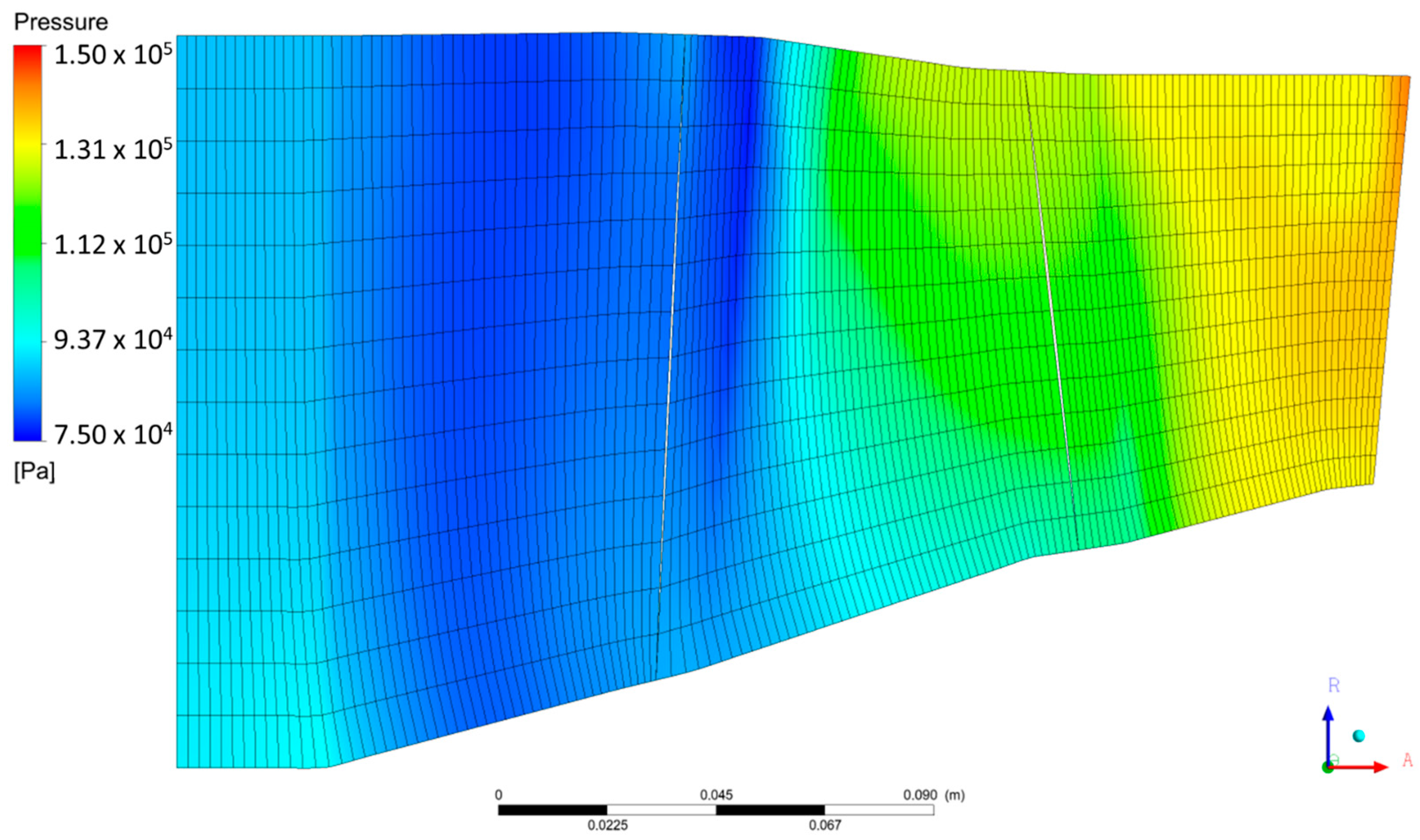
Figure 18 shows the meridional pressure distribution of the axial compressor (without CT) at 95% N, with an outlet static pressure of 285 kPa (near stall).

Figure 19 presents the meridional pressure distribution of the axial compressor with axial slots implemented in the Rotor 1 casing at 95% N and an outlet static pressure of 295 kPa (near stall). No significant differences in pressure distribution are observed in the meridional plane within the Rotor 1 region. However, greater pressure recovery is evident at the Stator 1 outlet for the ASCT configuration.

6.6. Mach Number Distributions of Multi-Stage Axial Compressor with and Without Axial Slots CT

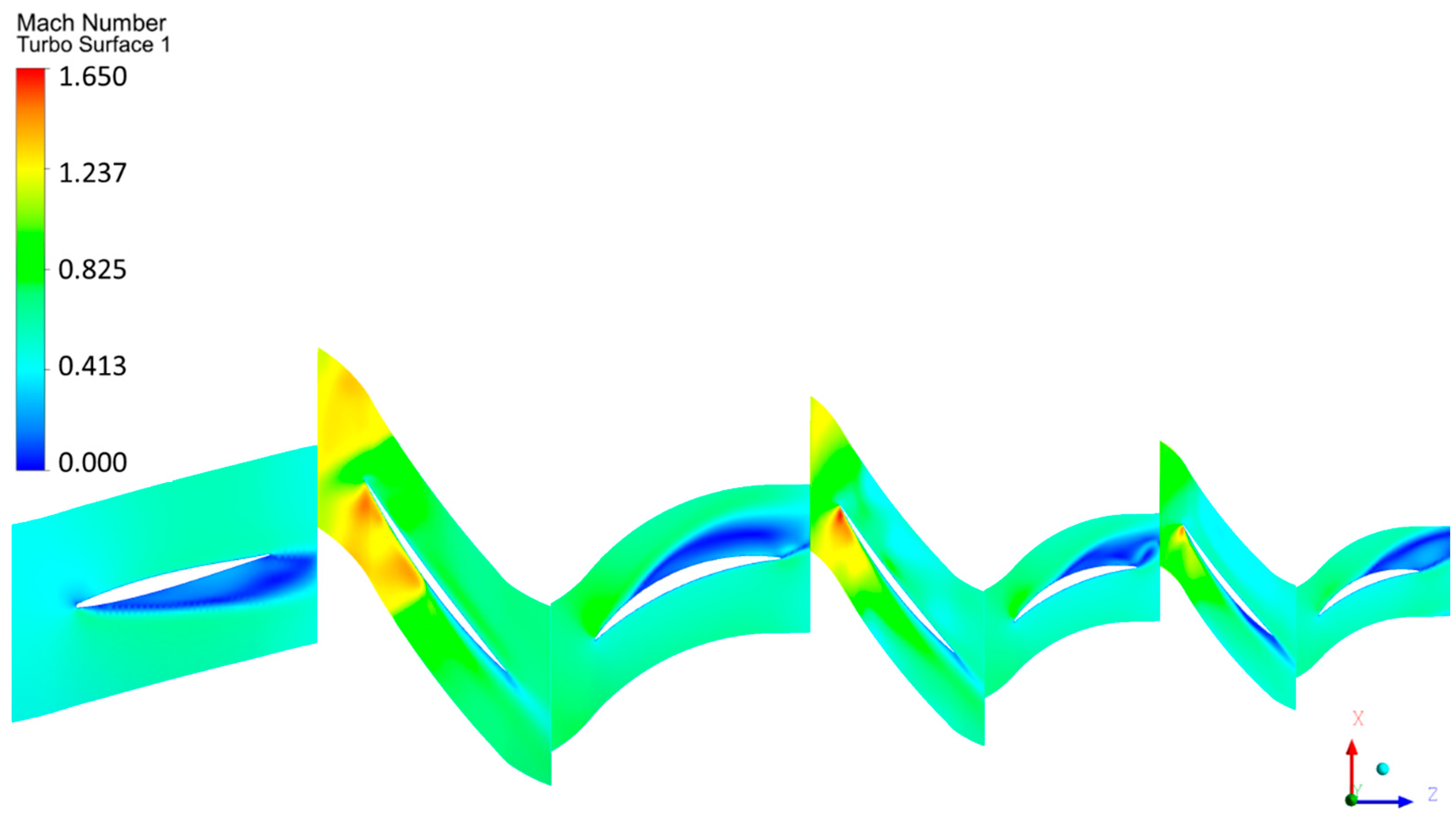
Figure 20 and Figure 21 compare the Mach number contours at 95% N for the SC configuration and the ASCT. The results show that shock waves are weaker with the CT than with the smooth casing. The ASCT improves compressor stability by reducing the intensity of shock wave interactions. Furthermore, the introduction of axial slots decreases the penetration of the tip leakage vortex into the blade passage, thereby mitigating its adverse effects. The suppression of the tip leakage vortex enhances flow stability in the blade tip region, effectively delaying the onset of compressor stall.

Figure 22 and Figure 23 compare the Mach number contours at 95% N for the SC configuration and the ASCT at 30% span from the hub. Shock wave interactions are observed from 30% span up to the Rotor 1 shroud. In addition, shocks are evident at approximately 30% span from the hub in Stator 1 and in subsequent stages, which may be associated with boundary-layer thickness effects in the stator hub region. However, the shock waves are consistently weaker with the CT compared to the smooth casing, even at 30% span.

It is concluded that the ASCT improved compressor stability by reducing the severity of shock wave interactions in Stator 1. Furthermore, the introduction of axial slots mitigated the penetration of the tip leakage vortex into the blade passage. The suppression of the tip leakage vortex enhanced flow stability in the Stator 1 passage, thereby delaying the onset of compressor stall.

6.7. Relative Pressure Distributions over Passage Rotor 1 of Multi-Stage Axial Compressor (Smooth Casing and with Axial Slots)

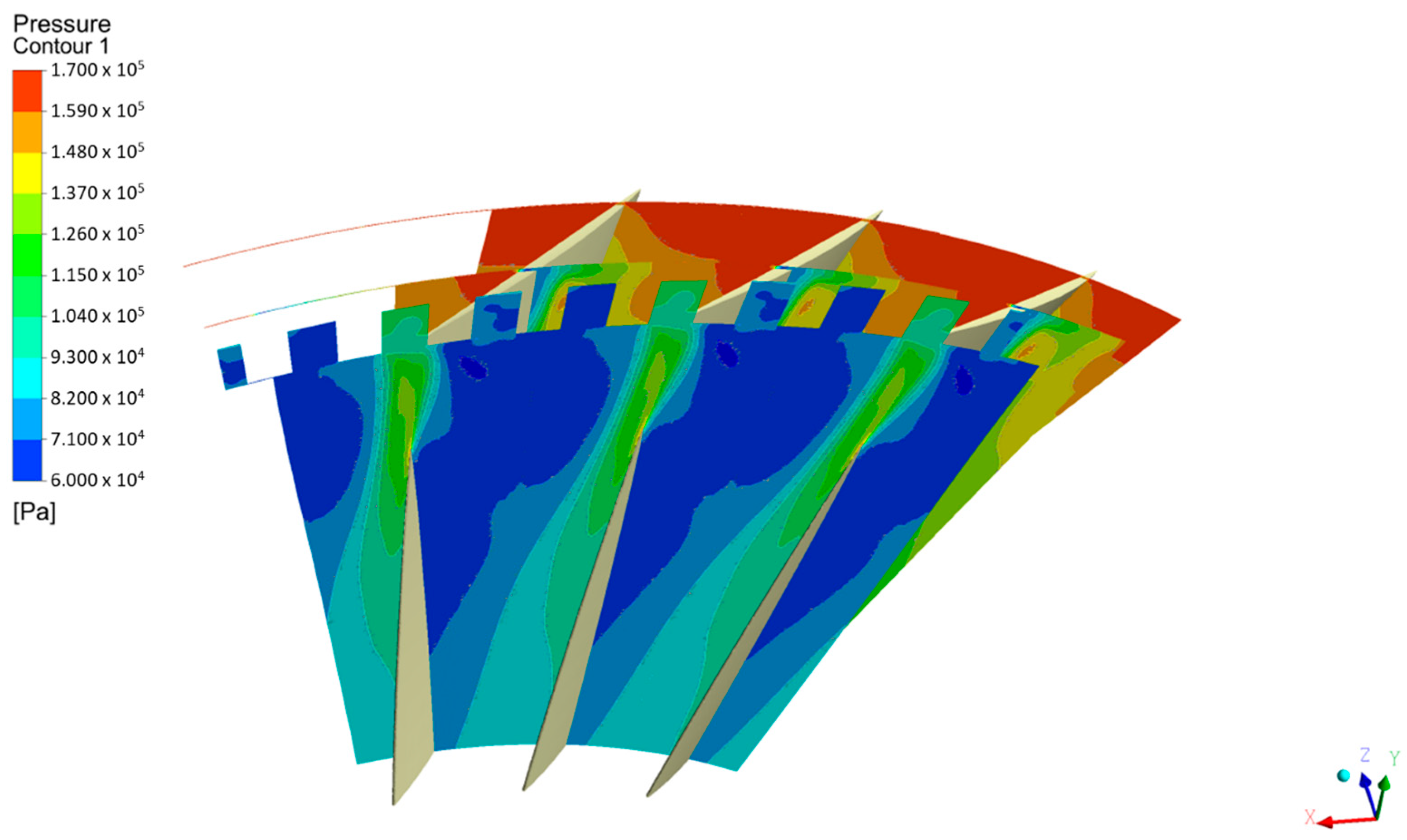
At 95% N, Figure 24 presents the pressure contours in blade-to-blade planes under near-stall conditions. With the incorporation of axial slots, the low-pressure region associated with the TLV is noticeably reduced. The flow enters the slots, where vortices are generated, thereby mitigating the leakage effect between blade surfaces. The recirculating flow within the slots re-enters the mainstream at a more forward axial position, where it interacts with the TLV, as illustrated in Figure 25. This interaction weakens the TLV, delays stall onset, and consequently, extends the compressor stall margin.

6.8. Streamlines Inside Axial Slots over Rotor 1 Multi-Stage Axial Compressor

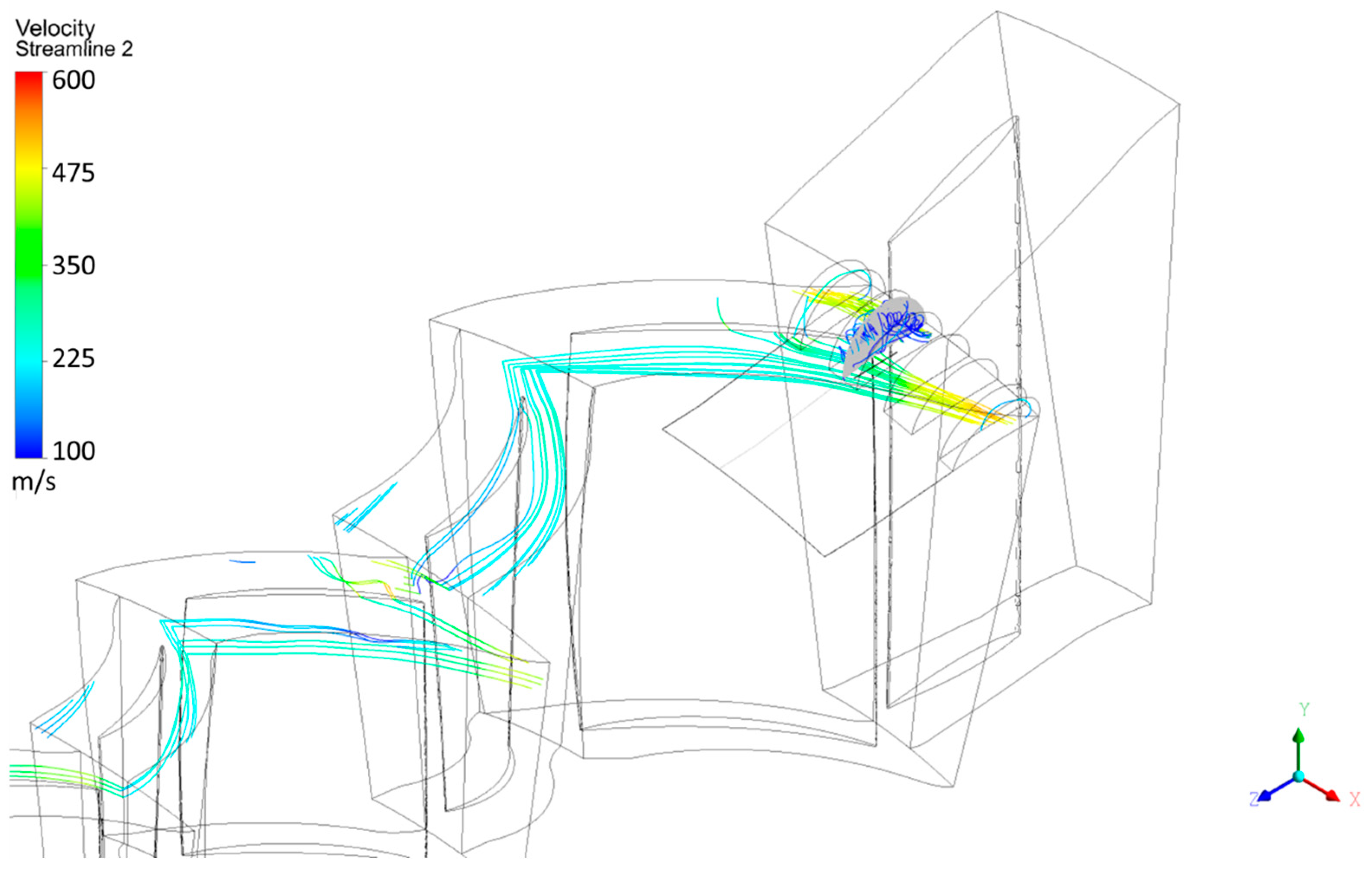
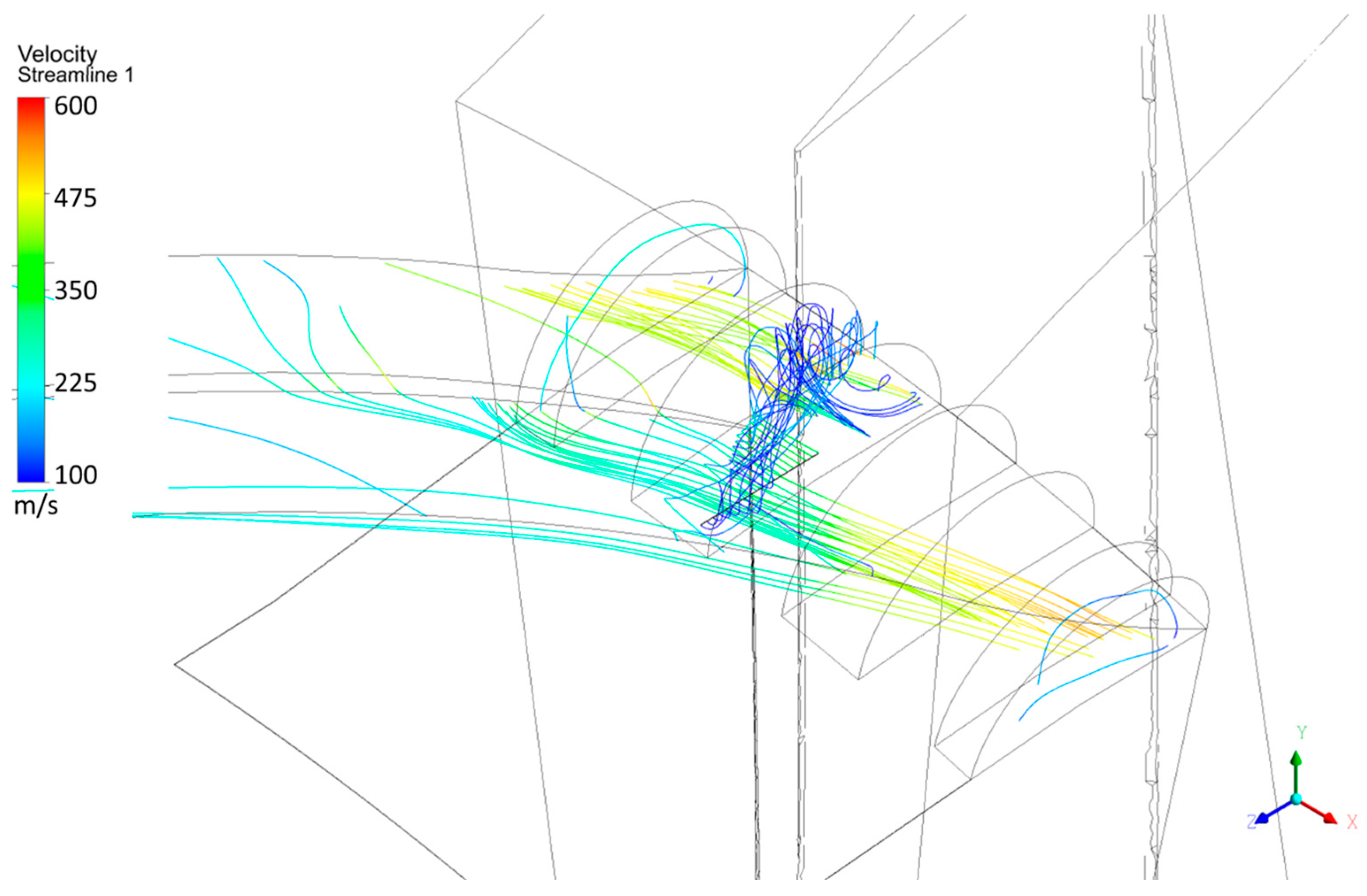
The recirculation effect within the ASCT, as observed in the experimental validation presented by Brignole, Danner, and Kau [23], was confirmed in the present multi-stage axial compressor configuration with the CT applied to the Rotor 1 casing, as illustrated in Figure 26.

The streamline visualization feature of the post-processing software was employed to generate the streamlines shown in Figure 26. The initial flow seeding was defined as a semi-circular area located within the second axial slot, represented in gray. Figure 27 presents an alternative seeding strategy, where the initial flow seed was defined as a line segment placed inside the second axial slot, represented in black.

Streamlines originating from these seed regions display low-velocity colors while circulating within the slots, and they exit through the leading edge of the slots as indicated by the yellow streamlines, corresponding to higher velocities. Owing to periodic symmetry, these streamlines re-enter the computational domain and continue downstream toward the subsequent compressor stages.

7. Conclusions and Future Work

Improvements in the design margins of a multistage, high-performance axial-flow compressor were achieved, even within the context of highly optimized transonic blade designs. The results presented in this study demonstrate a modest enhancement in stall margin at 100% design speed and a significant improvement at 95% N. However, no improvement in stall margin was observed at 85% N.

At 95% design speed, the ASCT improved compressor stability by reducing the severity of shock wave interactions, including those in Stator 1. The introduction of axial slots mitigated the penetration of the tip leakage vortex (TLV) into the blade passage, thereby enhancing flow stability in the tip region and delaying the onset of stall.

Despite these gains in stall margin, compressor efficiency did not show significant improvement. This finding is consistent with the work of Goinis, Voss, and Nicke [39], and Goinis, Voss, and Aulich [40], who demonstrated that CTs are effective for improving stall margins but are less effective in increasing overall efficiency when blade designs are already highly optimized. This highlights the trade-off between stall margin improvement and efficiency retention in axial compressor design. The limited or negligible gains in efficiency observed in this study may be attributed to a balance between energizing the tip flow region through axial slots and the additional entropy generation associated with recirculating flow inside the slots. Consequently, the focus of CT design should remain on stall margin improvements. This study contributes by providing insights into the flow mechanisms in the rotor tip region that facilitate stall margin enhancement in high-performance compressors. The central challenge in such designs remains the enhancement of both pressure ratio and stall margin while maintaining overall machine efficiency—an objective that the present work achieved.

The implementation of a novel periodic interface modeling approach for the ASCT in a multistage axial compressor simulation proved robust and may be applied to future CT investigations. Furthermore, the RANS methodology, using unstructured meshes to generate compressor performance maps with and without CT, continues to provide valuable guidance for designers by offering a practical compromise between computational cost and predictive capability in early stage compressor development. While the rotor–stator mixing-plane interfaces used in this study cannot capture the full unsteady flow transfer to downstream stages at off-design conditions, the present methodology enables a reasonably accurate evaluation of performance maps and assessment of CT effectiveness on stall margin and efficiency.

The findings of this work are limited to compressor operation not far from the design rotational speed. For operation below 85% N, accurate prediction requires full-annulus unsteady simulations to capture rotating stall or surge phenomena. Although steady RANS simulations cannot resolve these unsteady behaviors in detail, they can detect oscillations leading to divergence and thus, provide an indication of instability onset. For the compressor investigated, performance and efficiency degraded rapidly at or below 85% N, confirming that CT application is not effective under such conditions.

For future work, it is recommended to extend the present study by performing full 3D CFD simulations of the 74A compressor with ASCT under varied stator clocking conditions to better assess the influence of stator angular positioning on stall margin improvement.