Effect of Quasi-Static Door Operation on Shear Layer Bifurcations in Supersonic Cavities †
Abstract
1. Introduction
2. Methodology
2.1. Configurations
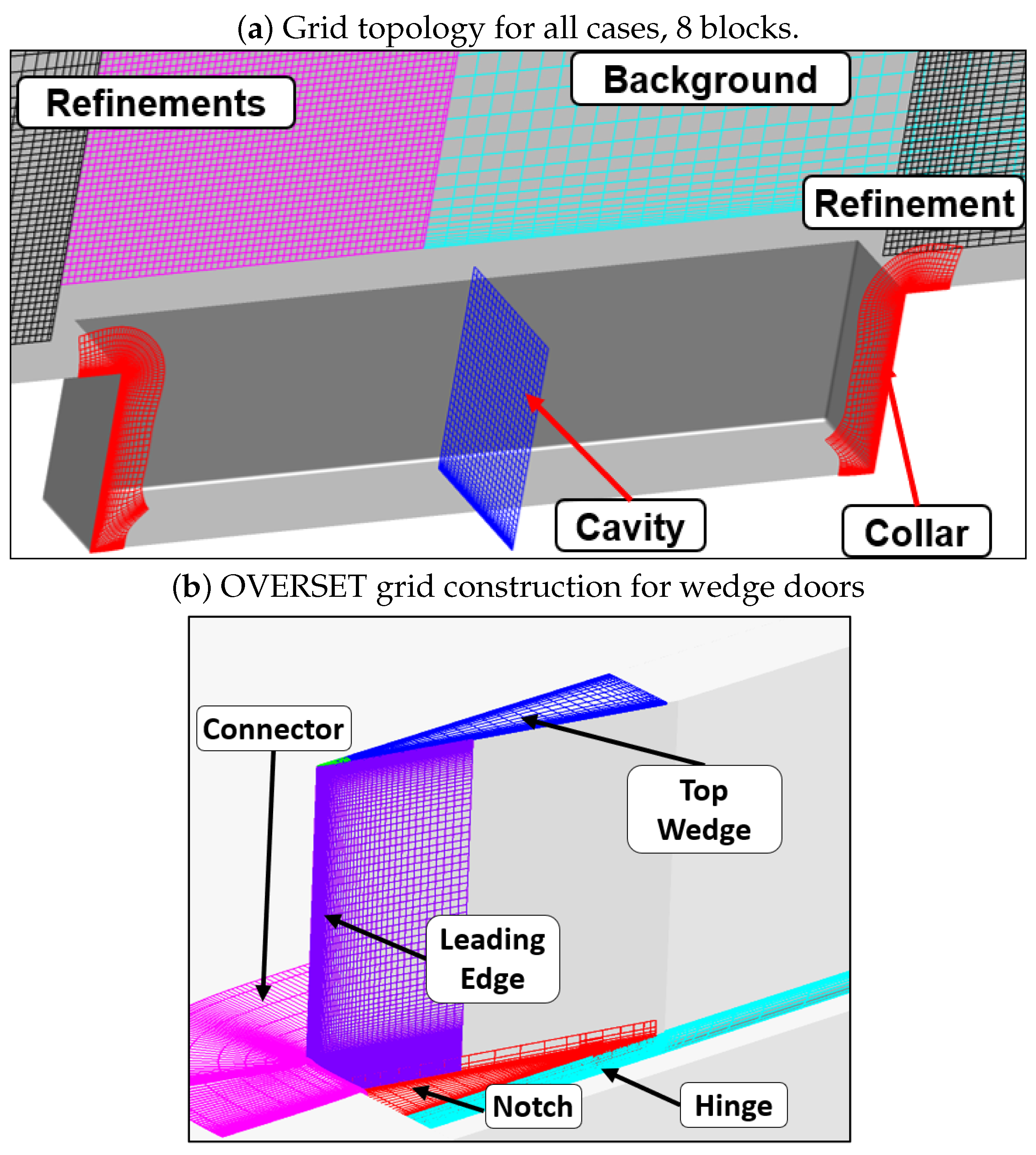
2.2. Computational Methodology
3. Results
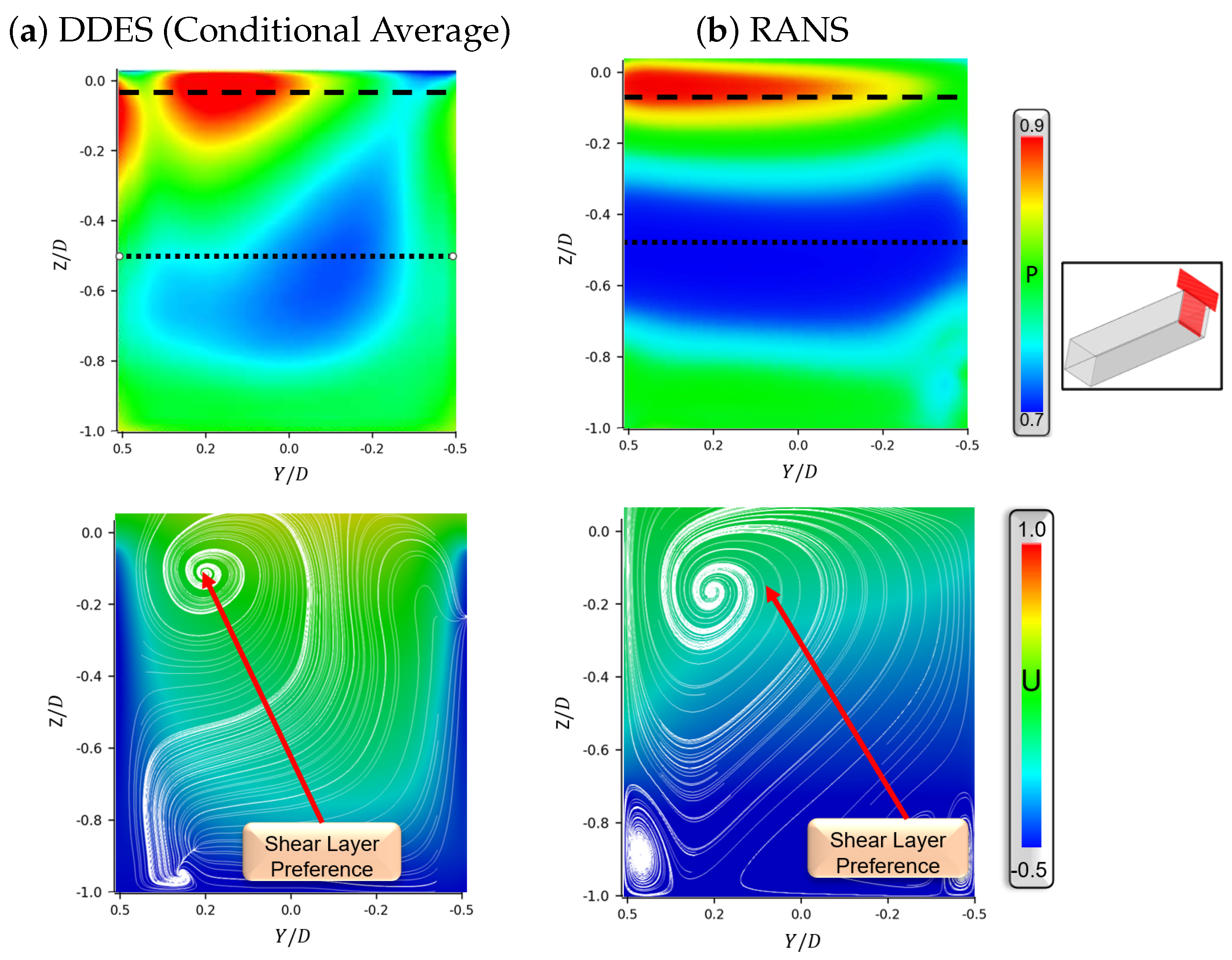
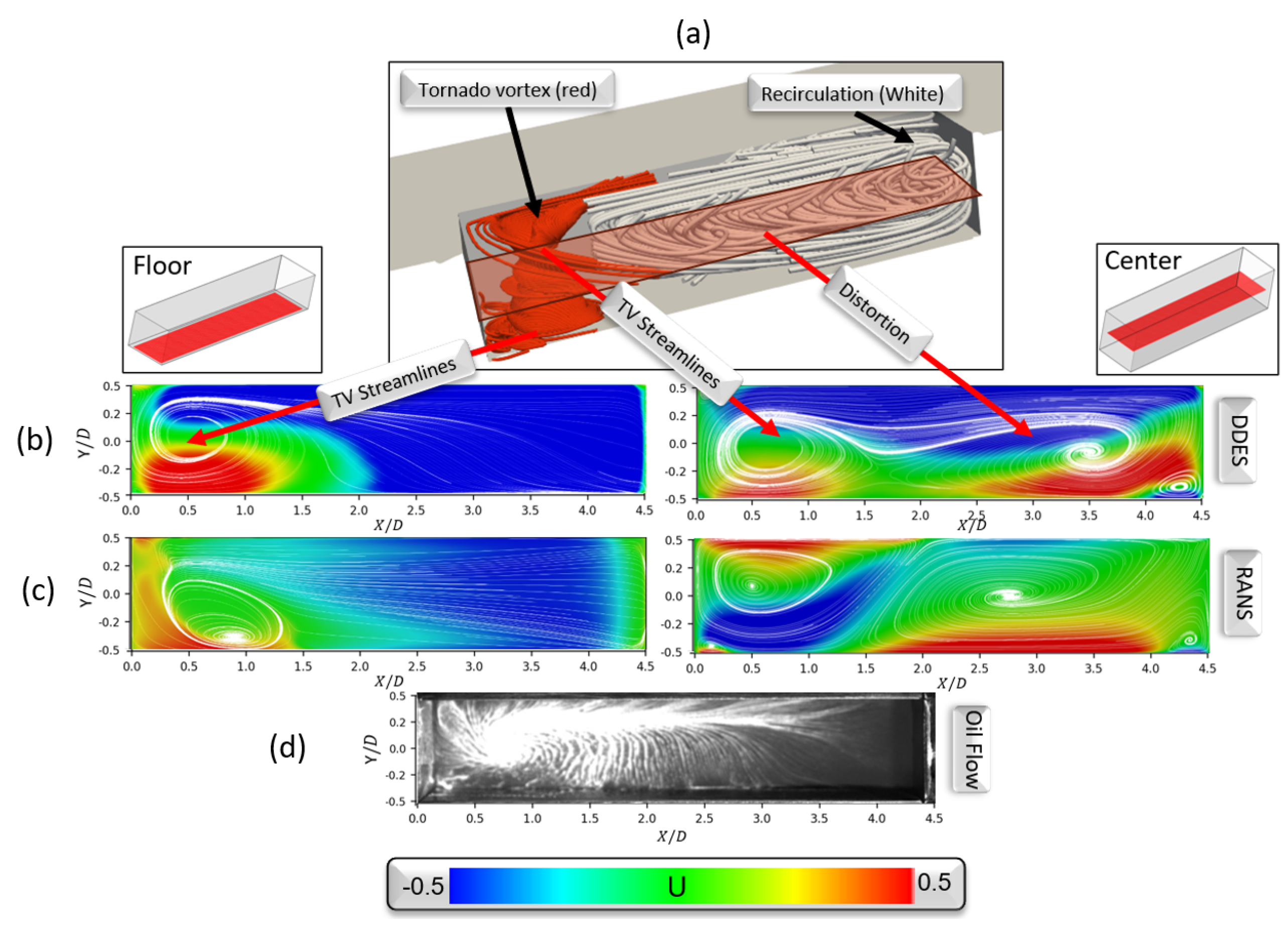
3.1. Cavity Dynamics Without Doors
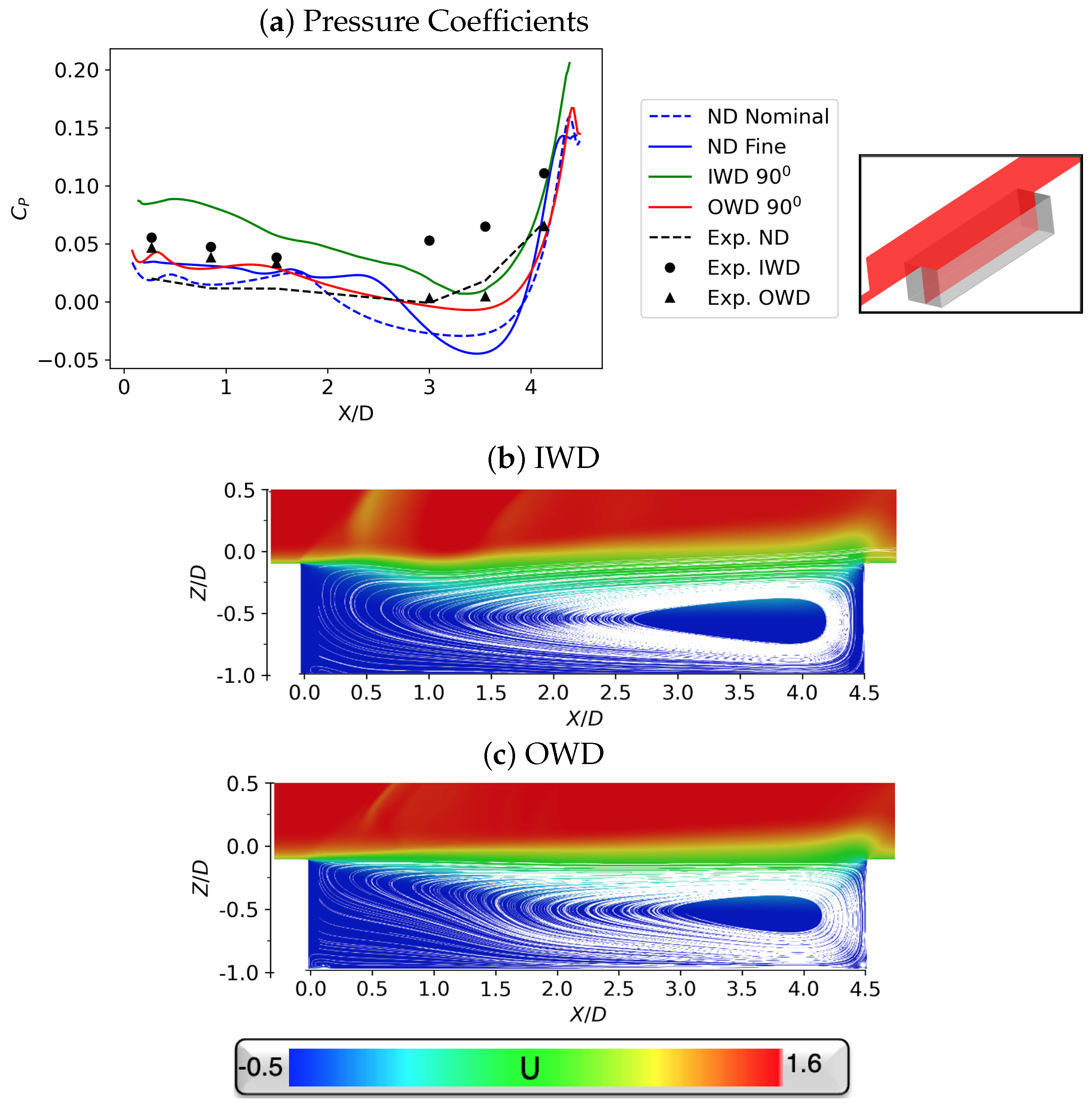
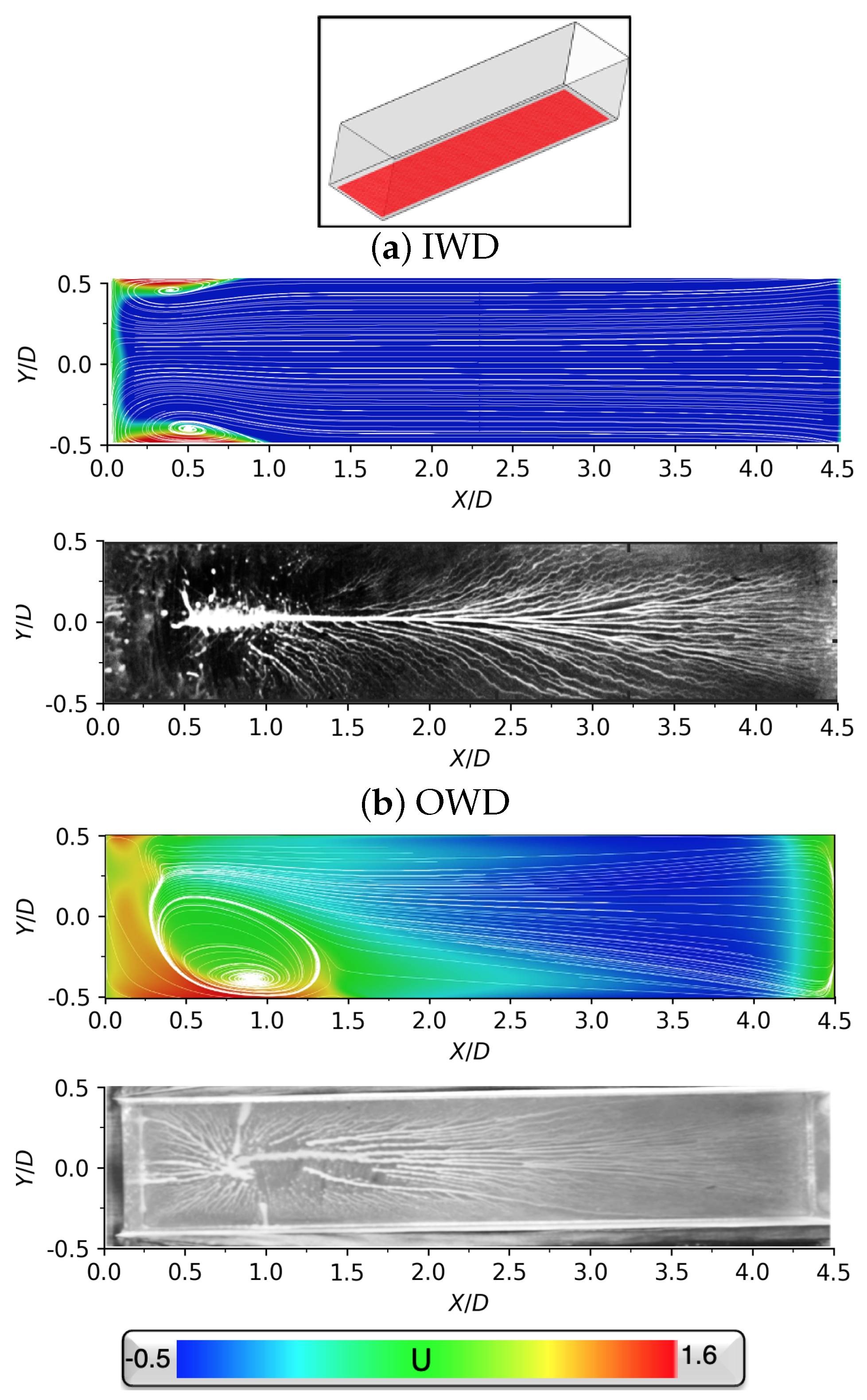
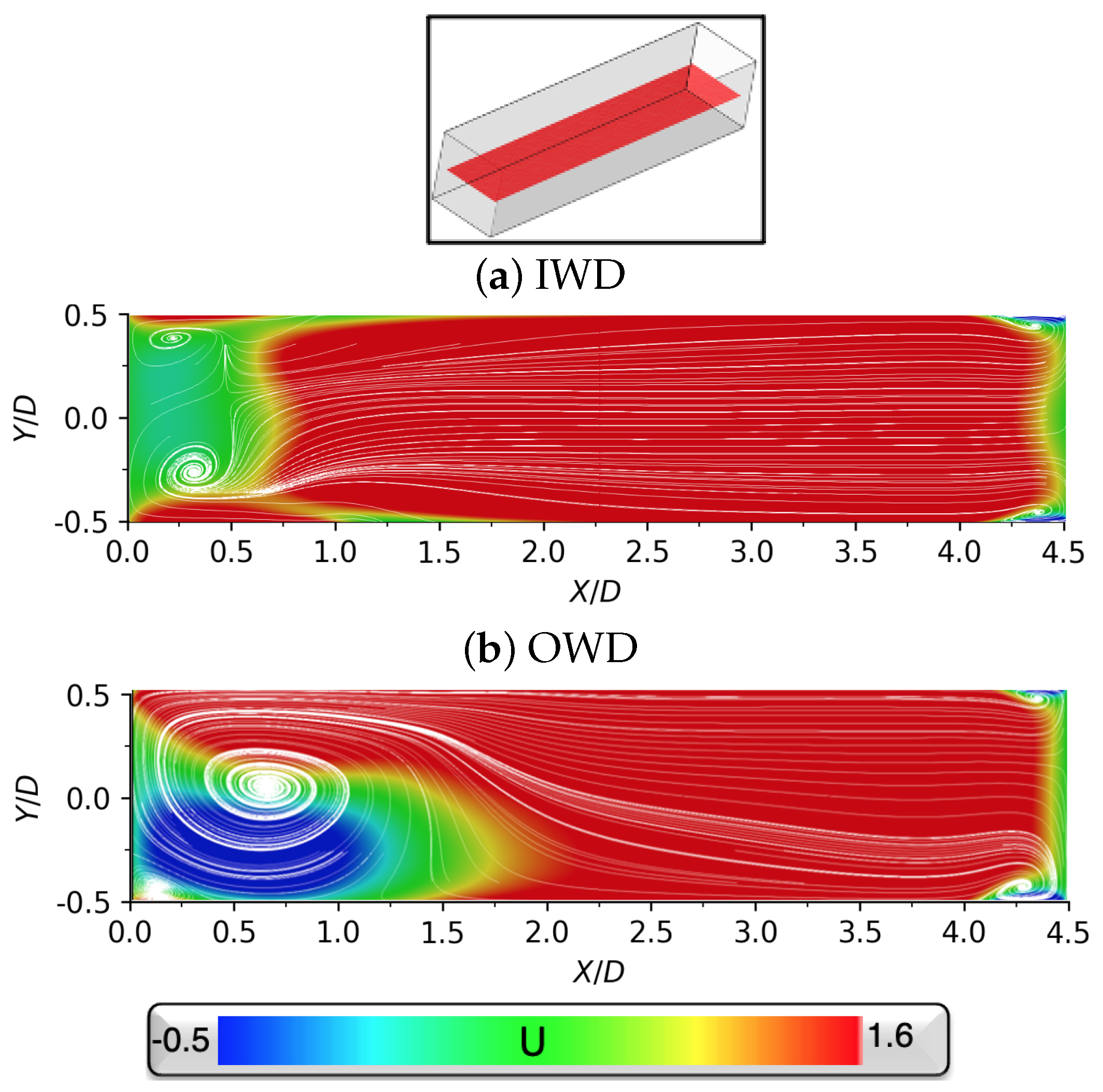
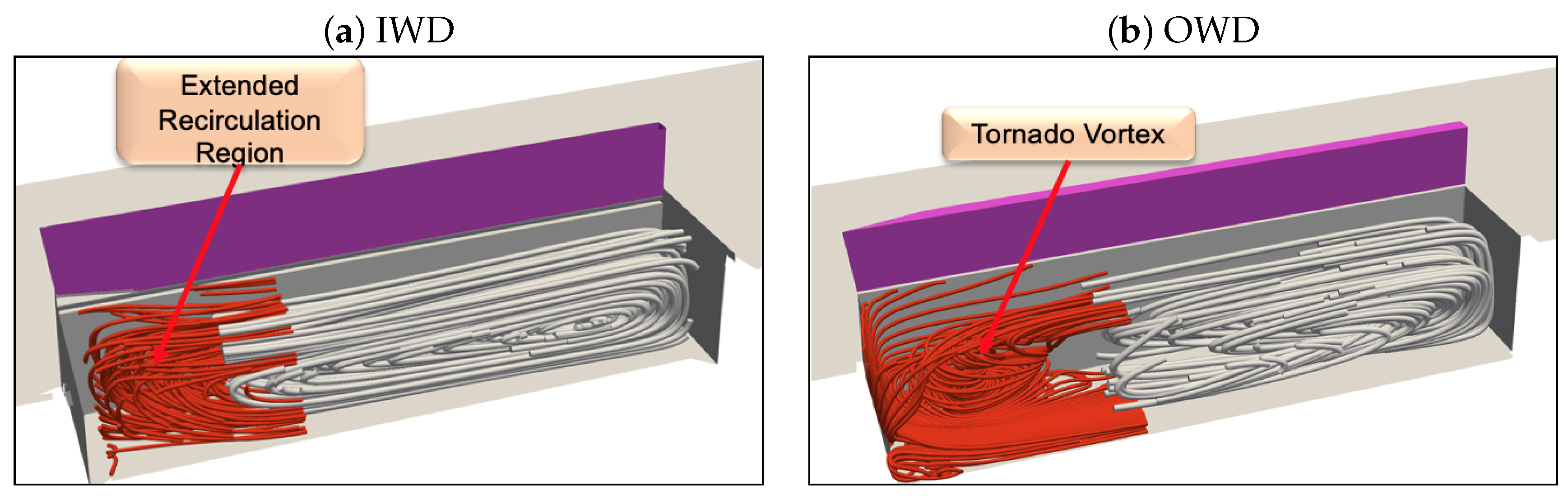
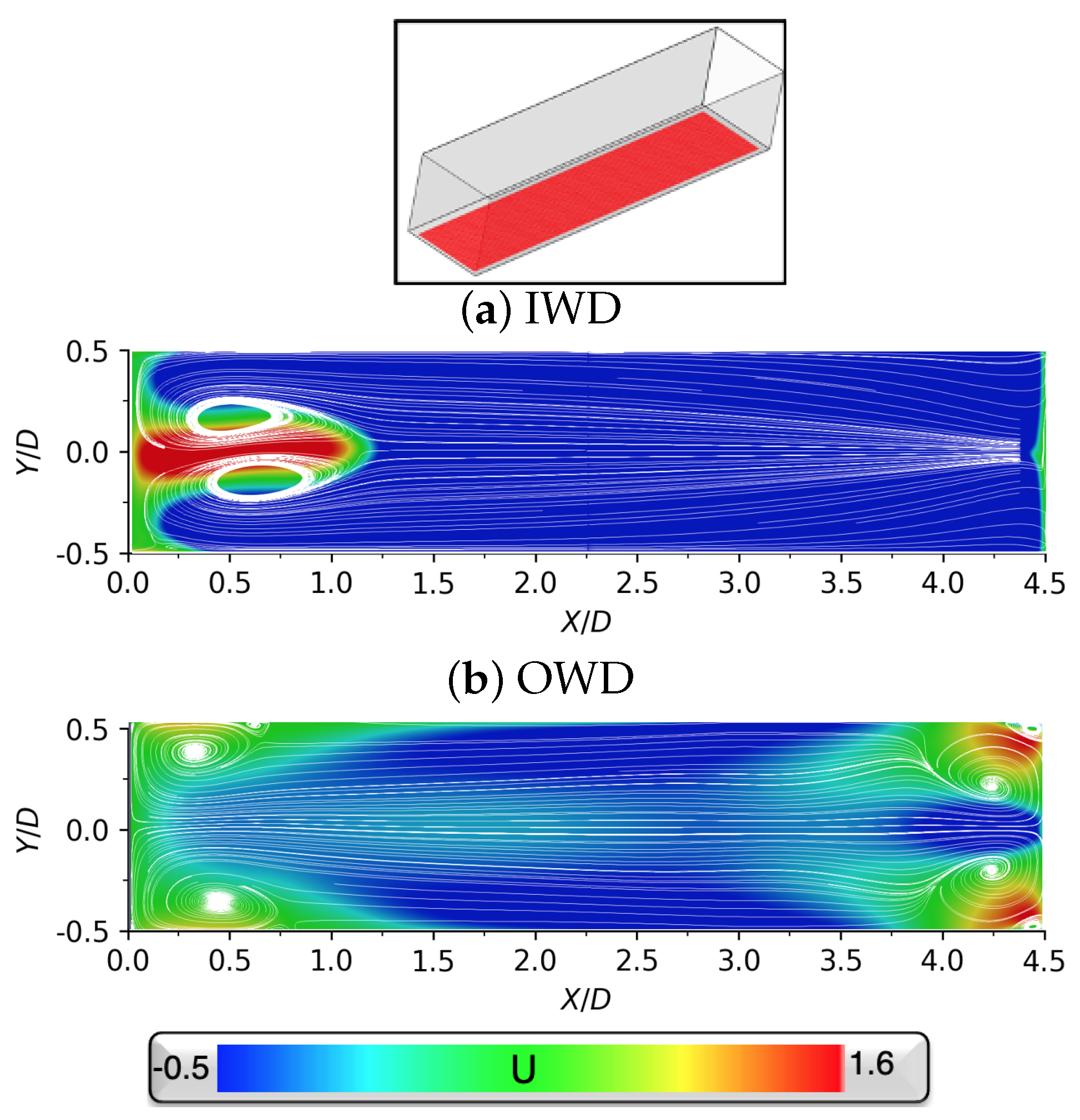
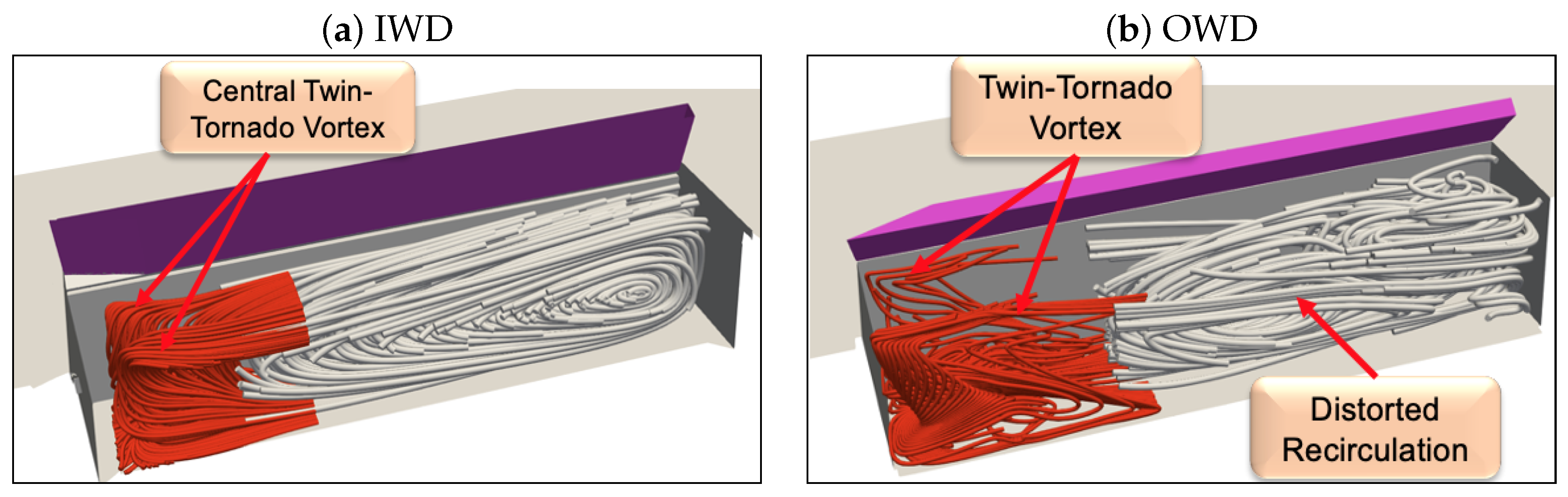
3.2. Fully Open Doors
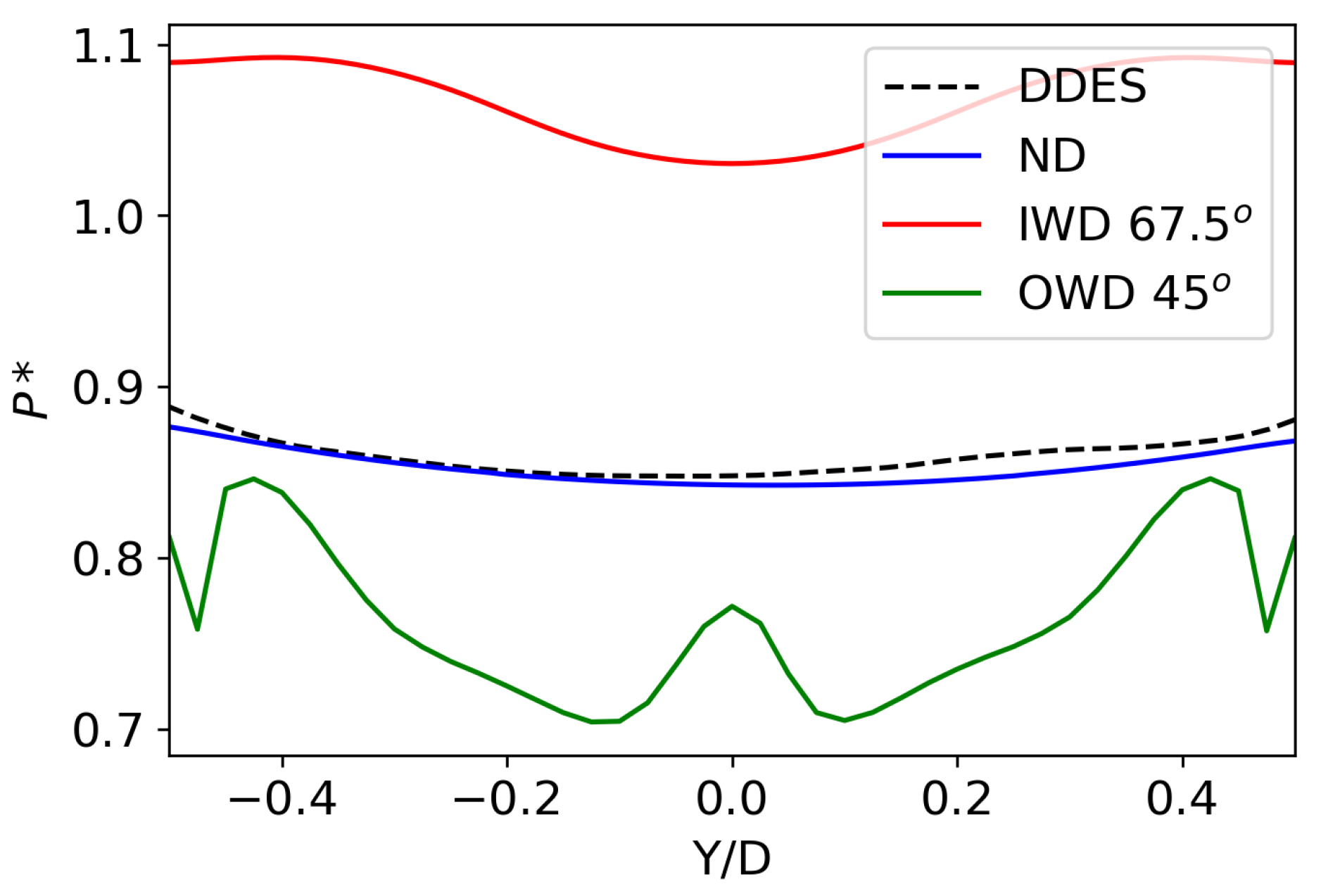
3.3. Critical Door Angle
4. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| pressure coefficient | |
| Computer Aided Design | |
| Detached Eddy Simulation | |
| Delayed DES | |
| Direct Numerical Simulation | |
| Decibel | |
| f | frequency |
| Inner Wedge Doors | |
| shear layer convective speed | |
| Large Eddy Simulation | |
| L::D | cavity length, width, and depth ratio |
| M | Mach number |
| Outer Wedge Doors | |
| n | integer, frequency interval |
| No Doors | |
| P | pressure |
| r | recovery factor |
| Reynolds Averaged Navier–Stokes | |
| Reynolds number based on cavity depth | |
| Reynolds number per meter | |
| strain rate tensor | |
| length based Strouhal number | |
| T | temperature |
| tornado vortex | |
| streamwise, spanwise and wall normal velocities | |
| streamwise, spanwise and wall normal directions | |
| phase lag | |
| boundary layer thickness | |
| correction factor | |
| density | |
| ratio of specific heats | |
| vorticity | |
| door angle | |
| critical door angle | |
| modeled shear stress tensor | |
| freestream value | |
| non-dimensionalized quantity | |
| stagnation value | |
| fluctuating quantity | |
| vector quantity | |
| transposed vector or matrix |
References
- Rockwell, D. Review—Self-Sustaining Oscillations of Flow Past Cavities. AIAA J. 1978, 100, 152–165. [Google Scholar] [CrossRef]
- Lin, J.C.; Rockwell, D. Organized Oscillations of Initially Turbulent Flow past a Cavity. AIAA J. 2001, 39, 1139–1151. [Google Scholar] [CrossRef][Green Version]
- Cattafesta, L.N.; Williams, D.R.; Rowley, C.W.; Alvi, F.S. Review of active control of flow-induced cavity resonance. In Proceedings of the 33rd AIAA Fluid Dynamics Conference and Exhibit, Orlando, FL, USA, 23–26 June 2003. [Google Scholar]
- Rossiter, J. Wind Tunnel Experiments on the Flow over Rectangular Cavities at Subsonic and Transonic Speeds. Ministry of Aviation, Aeronautical Research Council, Reports and Memoranda. 1964, Volume 1. Available online: https://reports.aerade.cranfield.ac.uk/handle/1826.2/4020 (accessed on 17 March 2023).
- Cattafesta, L.N.; Song, Q.; Williams, D.R.; Rowley, C.W.; Alvi, F.S. Active control of flow-induced cavity oscillations. Prog. Aerosp. Sci. 2008, 44, 479–502. [Google Scholar] [CrossRef]
- Saddington, A.; Thangamani, V.; Knowles, K. A comparison of passive control methods for a cavity in transonic flow. J. Aircr. 2016, 53, 1439–1447. [Google Scholar] [CrossRef]
- Ukeiley, L.S.; Ponton, M.K.; Seiner, J.M.; Jansen, B. Suppression of Pressure Loads in Cavity Flows. AIAA J. 2004, 42, 70–79. [Google Scholar] [CrossRef]
- Vakili, A.D.; Gauthier, C. Control of cavity flow by upstream mass-injection. J. Aircr. 1994, 31, 169–174. [Google Scholar] [CrossRef]
- Rizzetta, D.P.; Visbal, M.R. Large-eddy simulation of supersonic cavity flowfields including flow control. In Proceedings of the 32nd AIAA Fluid Dynamics Conference and Exhibit, St. Louis, MI, USA, 24–26 June 2002; Volume 41. [Google Scholar] [CrossRef]
- Sun, Y.; Taira, K.; Cattafesta, L.N.; Ukeiley, L.S. Spanwise effects on instabilities of compressible flow over a long rectangular cavity. Theor. Comput. Fluid Dyn. 2017, 31, 555–565. [Google Scholar] [CrossRef]
- Lawson, S.J.; Barakos, G.N. Review of numerical simulations for high-speed, turbulent cavity flows. Prog. Aerosp. Sci. 2011, 47, 186–216. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Q.; Cattafesta, L.N.; Ukeiley, L.S.; Taira, K. Effects of side-walls and leading-edge blowing on flows over long rectangular cavities. AIAA J. 2019, 57, 106–119. [Google Scholar] [CrossRef]
- Larcheveque, L.; Sagaut, P.; Labbe, O. Large-eddy simulation of a subsonic cavity flow including asymmetric three-dimensional effects. J. Fluid Mech. 2007, 577, 105–126. [Google Scholar] [CrossRef]
- Heller, H.; Bliss, D. The physical mechanism of flow-induced pressure fluctuations in cavities and concepts for their suppression. In Proceedings of the 2nd Aeroacoustics Conference, Hampton, VA, USA, 24–26 March 1975; pp. 75–491. [Google Scholar] [CrossRef]
- Powell, A. The sound-producing oscillations of round underexpanded jets impinging on normal plates. J. Acoust. Soc. Am. 1988, 83, 515–533. [Google Scholar] [CrossRef]
- Wagner, J.L.; Beresh, S.J.; Casper, K.M.; DeMauro, E.P.; Arunajatesan, S. Resonance Dynamics in Compressible Cavity Flows using Time-Resolved Particle Image Velocimetry and Pressure Sensitive Paint. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2015. [Google Scholar] [CrossRef]
- Basley, J.; Pastur, R.L.; Lusseyran, F.; Soria, J.; Delprat, N. On the modulating effect of three-dimensional instabilities in open cavity flow. J. Fluid Mech. 2014, 759, 546–578. [Google Scholar] [CrossRef]
- Knisley, C.; Rockwell, D. Self-sustained low-frequency components in an impinging shear layer. J. Fluid Mech. 1982, 116, 157–186. [Google Scholar] [CrossRef]
- Delprat, N. Rossiter’s formula: A simple spectral model for a complex amplitude modulation process? Phys. Fluids 2006, 18, 071703. [Google Scholar] [CrossRef]
- Gai, S.L.; Kleine, H.; Andrew, J.N. Supersonic Flow over a Shallow Open Rectangular Cavity. J. Aircr. 2015, 52, 609–616. [Google Scholar] [CrossRef]
- Doshi, P.S.; Ranjan, R.; Gaitonde, D.V. 2D and 3D stability of cavity flows in high Mach number regimes. In Proceedings of the ASME 2019 International Mechanical Engineering Congress and Exposition, Salt Lake City, UT, USA, 11–19 November 2019; Volume 7, pp. 1–10. [Google Scholar] [CrossRef]
- Bourquard, C.; Faure-Beaulieu, A.; Noiray, N. Whistling of deep cavities subject to turbulent grazing flow: Intermittently unstable aeroacoustic feedback. J. Fluid Mech. 2020, 909, 1–29. [Google Scholar] [CrossRef]
- Beresh, S.J.; Wagner, J.L.; Casper, K.M. Supersonic flow over a finite-width rectangular cavity. AIAA J. 2015, 53, 296–310. [Google Scholar] [CrossRef]
- Wagner, J.; Beresh, S.; Casper, K.; DeMauro, E.; Lynch, K.; Spillers, R.; Henfling, J.; Spitzer, S. Effects of cavity width on resonance dynamics using planform time-resolved particle image velocimetry. AIAA J. 2018, 2018-0359, 660–675. [Google Scholar]
- Bres, G.A.; Colonius, T. Direct numerical simulations of three-dimensionl cavity flows. In Proceedings of the 13th AIAA/CEAS Aeroacoustics Conference (28th AIAA) Aeroacoustics Conference), Southamptonm, UK, 14–17 June 2007; pp. 1–16. [Google Scholar] [CrossRef]
- Basley, J.; Pastur, L.R.; Delprat, N.; Lusseyran, F. Space-time aspects of a three-dimensional multi-modulated open cavity flow. Phys. Fluids 2013, 25, 064105. [Google Scholar] [CrossRef]
- Casper, K.M.; Wagner, J.L.; Beresh, S.J.; Spillers, R.W.; Henfling, F.J.; Dechant, L.J. Spatial distribution of pressure resonance in compressible cavity flow. J. Fluid Mech. 2018, 848, 660–675. [Google Scholar] [CrossRef]
- Chin, D.; Granlund, K.; Maatz, I.; Schmit, R.F.; Reeder, M.F. Stochastic store trajectory of ice models from a cavity into supersonic flow. J. Aircr. 2019, 56, 1313–1319. [Google Scholar] [CrossRef]
- Chin, D.; Turpin, A.; Granlund, K. Time-dependent aerodynamic loads on single and tandem stores in a supersonic cavity. J. Aircr. 2020, 57, 702–714. [Google Scholar] [CrossRef]
- Wagner, J.L.; Casper, K.M.; Beresh, S.J.; Hunter, P.S.; Spillers, R.W.; Henfling, J.F. Response of a store with tunable natural frequencies in compressible cavity flow. J. Aircr. 2016, 53, 2351–2360. [Google Scholar] [CrossRef]
- Crook, D.; Lao, T.C.W.; Kelso, R.M. Three-dimensional flow within shallow, narrow cavities. J. Fluid Mech. 2013, 735, 587–612. [Google Scholar] [CrossRef]
- Turpin, A.M.; Speth, R.L.; Sherer, S.E.; Granlund, K.O. Low-frequency, spanwise oscillation in a finite-width cavity at Mach 1.5. Phys. Fluids 2021, 33, 076102. [Google Scholar] [CrossRef]
- Williams, O.J.; Smits, A.J. Asymmetries in Nominally Symmetric Flows. Annu. Rev. Fluid Mech. 2025, 57, 35–60. [Google Scholar] [CrossRef]
- Mallat, B.; Pastur, L.R. Experimental study and passive control of the bistable dynamics of the three-dimensional air-wake flow of a finite-width double backward-facing step. J. Wind. Eng. Ind. Aerodyn. 2021, 215, 104702. [Google Scholar] [CrossRef]
- Herry, B.; Keirsbulck, L.; Labraga, L.; Paquet, J.-B. Flow Bistability Downstream of Three-Dimensional Double Backward Facing Steps at Zero-Degree Sideslip. J. Fluids Eng. 2011, 133, 054501. [Google Scholar] [CrossRef]
- He, K.; Minelli, G.; Su, X.; Gao, G.; Krajnović, S. On state instability of the bi-stable flow past a notchback bluff body. J. Fluid Mech. 2022, 931, R6. [Google Scholar] [CrossRef]
- Zeng, R.; Li, S. Bistability of turbulent flow in open-channel expansion: Characterization and suppression. Phys. Fluids 2022, 34, 065106. [Google Scholar] [CrossRef]
- Pavia, G.; Passmore, M.; Varney, M.; Hodgson, G. Salient three-dimensional features of the turbulent wake of a simplified square-back vehicle. J. Fluid Mech. 2020, 888, A33. [Google Scholar] [CrossRef]
- Luo, Y.; Luo, Y.; Tian, H.; Wu, C.; Li, H.; Wang, Y. Open the ORCID record for Yimin Wang [Opens in a new window] and Shuhai Zhang Open the ORCID record for Shuhai Zhang Evolution of tornado-like vortices in three-dimensional compressible rectangular cavity flows. J. Fluid Mech. 2022, 955, A9. [Google Scholar] [CrossRef]
- Ashton, R.; Refan, M.; Iungo, G.V.; Hangan, H. Wandering corrections from PIV measurements of tornado-like vortices. J. Wind. Eng. Ind. Aerodyn. 2019, 189, 163–172. [Google Scholar] [CrossRef]
- Douay, C.L.; Lusseyran, F.; Pastur, L.R. The onset of centrifugal instability in an open cavity flow. Fluid Dyn. Res. 2016, 48, 061410. [Google Scholar] [CrossRef]
- Douay, C.L.; Pastur, L.R.; Lusseyran, F. Centrifugal instabilities in an experimental open cavity flow. J. Fluid Mech. 2016, 788, 670–694. [Google Scholar] [CrossRef]
- Picella, F.; Loiseau, J.-C.; Lusseyran, F.; Robinet, J.-C.; Cherubini, S.; Pastur, L. Successive bifurcations in a fully three-dimensional open cavity flow. J. Fluid Mech. 2018, 844, 855–877. [Google Scholar] [CrossRef]
- Unalmis, O.; Clemens, N.T.; Dolling, D.S. Cavity oscillation mechanisms in high-speed flows. AIAA J. 2004, 42, 2035–2041. [Google Scholar] [CrossRef]
- Turpin, A.M.; Chin, D.; Granlund, K. Supersonic cavity flow subjected to continuous and transient leading-edge blowing. AIAA J. 2020, 58, 4415–4425. [Google Scholar] [CrossRef]
- Outten, B.; Sheehan, M.; Mehta, Y.; Kumar, R. Effect of Doors on Cavity Acoustics at Supersonic Speeds. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar] [CrossRef]
- Sheta, E.F.; Harris, R.E.; George, B.; Ukeiley, L.; Luke, E. Loads and Acoustics Prediction on Deployed Weapons Bay Doors. J. Vib. Acoust. 2017, 139, 031007. [Google Scholar] [CrossRef]
- Casper, K.M.; Wagner, J.L.; Beresh, S.J.; Henfling, J.F.; Spillers, R.W.; Pruett, B.O. Complex geometry effects on cavity resonance. AIAA J. 2016, 54, 320–330. [Google Scholar] [CrossRef]
- Barakos, G.; Lawson, S.; Steijl, R. Numerical Simulations of High-Speed Turbulent Cavity Flows. Flow Turbul. Combust. 2009, 83, 569–585. [Google Scholar] [CrossRef]
- Baugher, S.K.; Outten, B.; Gaitonde, D.V.; Kumar, R. 3D Effects of Quasi-Static Door Opening on Supersonic Cavity Flows. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024; pp. 2024–2729. [Google Scholar]
- Spalart, P.; Allmaras, S. A one-equation turbulence model for aerodynamic flows. AIAA J. 1994, 439, 5–21. [Google Scholar] [CrossRef]
- Outten, B.S.; Sheehan, M.; Kumar, R.; Baugher, S.; Gaitonde, D.V. Effect of Dynamic Door Motion on Cavity Acoustics at Supersonic Speeds. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024. [Google Scholar]
- Jespersen, D.; Pulliam, T.H.; Childs, M. OVERFLOW Turbulence Modeling Resource Validation Results. Technical Report, NAS Technical Report: NAS-2016-01. 2016. Available online: https://turbmodels.larc.nasa.gov/Papers/NAS_Technical_Report_NAS-2016-01.pdf (accessed on 7 July 2019).
- NASA. Overflow Resource. Available online: https://overflow.larc.nasa.gov/ (accessed on 12 October 2019).
- Anderson, J.D. Computational Fluid Dynamics: An Introduction; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Titarev, V.A.; Toro, E.F. Finite-volume WENO schemes for three-dimensional conservation laws. J. Comput. Phys. 2004, 201, 238–260. [Google Scholar] [CrossRef]
- Tramel, R.; Nichols, R.; Buning, P. Addition of Improved Shock-Capturing Schemes to OVERFLOW 2.1. In Proceedings of the 19th AIAA Computational Fluid Dynamics, San Antonio, TX, USA, 22–25 June 2009. [Google Scholar] [CrossRef]
- NASA. Chimera Grid Tools Resource. Available online: https://www.nas.nasa.gov/software/chimera.html (accessed on 9 June 2022).
- Grace, S.M.; Dewar, W.G.; Wroblewski, D.E. Experimental investigation of the flow characteristics within a shallow wall cavity for both laminar and turbulent upstream boundary layers. Exp. Fluids 2004, 36, 791–804. [Google Scholar] [CrossRef]
- Baugher, S.K.; Prasad, C.; Gaitonde, D.V. Large Eddy Simulation and Modal Analysis of Cavity Bays with Different Door Configurations. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar] [CrossRef]
- Baugher, S.K.; Speth, R.; Sherer, S.; Gaitonde, D.V. 3D Cavity Bay Dynamics with Effect of Doors. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024. [Google Scholar] [CrossRef]








| Parameter | Polysonic Wind Tunnel (FSU) |
|---|---|
| Mach | 1.6 |
| 292 K | |
| 20.6 kPa | |
| 11.1 mm | |
| D | 50.1 mm |
| 4.5 |
| Grid | Baseline | IWD/OWD |
| Nominal | ||
| Fine |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baugher, S.; Gaitonde, D.; Outten, B.; Kumar, R.; Speth, R.; Sherer, S. Effect of Quasi-Static Door Operation on Shear Layer Bifurcations in Supersonic Cavities. Aerospace 2025, 12, 668. https://doi.org/10.3390/aerospace12080668
Baugher S, Gaitonde D, Outten B, Kumar R, Speth R, Sherer S. Effect of Quasi-Static Door Operation on Shear Layer Bifurcations in Supersonic Cavities. Aerospace. 2025; 12(8):668. https://doi.org/10.3390/aerospace12080668
Chicago/Turabian StyleBaugher, Skyler, Datta Gaitonde, Bryce Outten, Rajan Kumar, Rachelle Speth, and Scott Sherer. 2025. "Effect of Quasi-Static Door Operation on Shear Layer Bifurcations in Supersonic Cavities" Aerospace 12, no. 8: 668. https://doi.org/10.3390/aerospace12080668
APA StyleBaugher, S., Gaitonde, D., Outten, B., Kumar, R., Speth, R., & Sherer, S. (2025). Effect of Quasi-Static Door Operation on Shear Layer Bifurcations in Supersonic Cavities. Aerospace, 12(8), 668. https://doi.org/10.3390/aerospace12080668






