Koopman Predictor-Based Integrated Guidance and Control Under Multi-Force Compound Control System
Abstract
1. Introduction
- (1)
- The mathematical model of the strapdown interceptor under the multi-force compound control is established, taking into account the physical limitations, working principles, and dynamic characteristics of the aerodynamic rudder, attitude control engine, and orbit control engine.
- (2)
- The high-order, strongly coupled, and strongly nonlinear interceptor kinematics/dynamics model under multi-force compound control is transformed into a linear IGC model using the Koopman predictor on the premise of satisfying the accuracy.
- (3)
- Based on the linear IGC model, the extended disturbance observer (EDO) and adaptive weight-based control allocation scheme are combined with the Koopman predictor-based sliding mode control (KPSMC) to form the IGC law for the interceptor under the multi-force compound control. The proposed Koopman predictor-based IGC method simplifies the complex model while retaining the dynamic characteristics, balancing the difficulty of the controller design and the control performance.
2. Problem Formulation
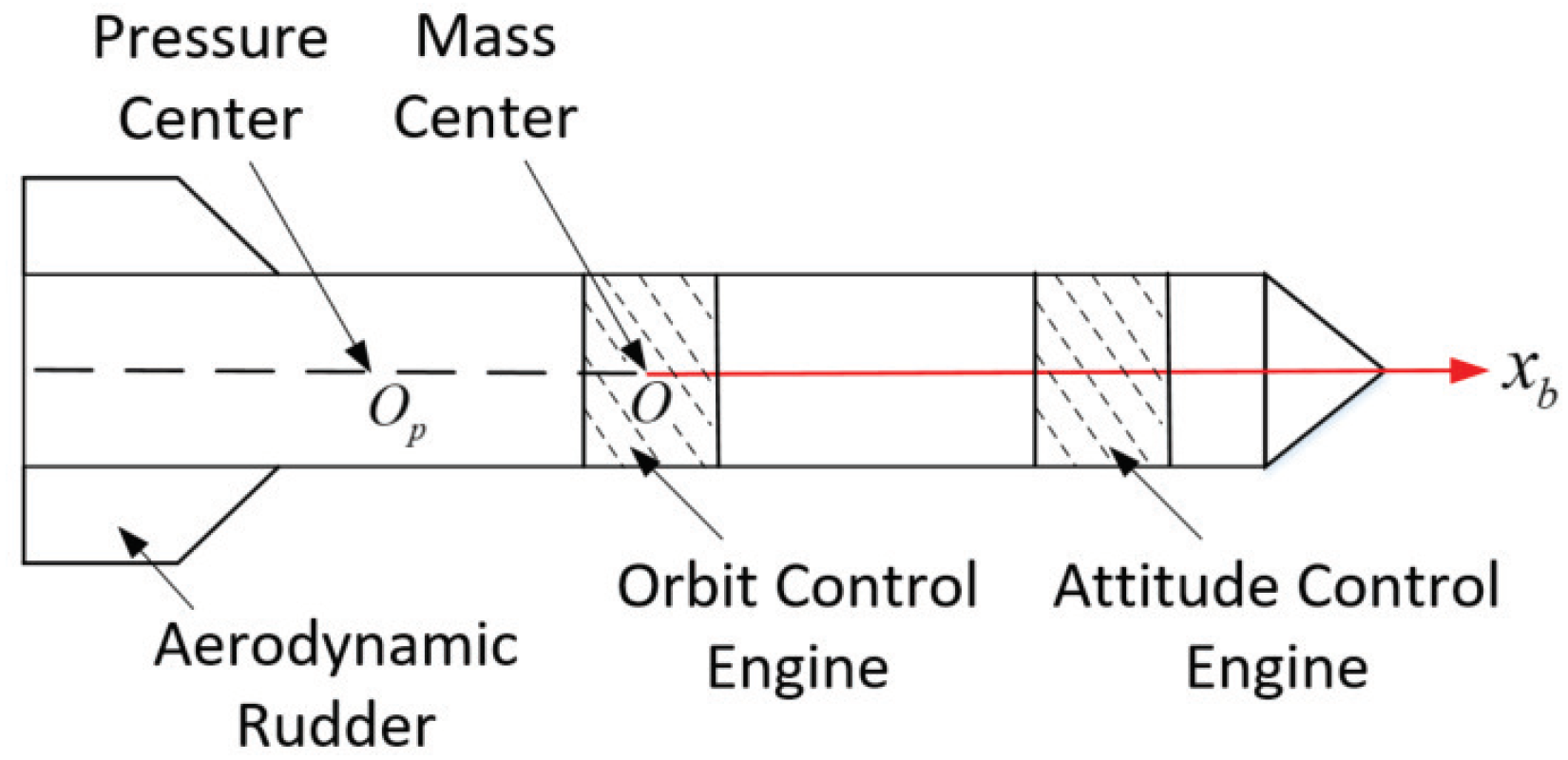
2.1. Multi-Force Compound Control System
- (1)
- The aerodynamic rudder and attitude control engine inevitably generate the force increments while generating the moment increments that affect the trajectory. Among them, the additional acceleration increment generated by the attitude control engine is particularly significant.
- (2)
- Due to the drift of the mass center caused by installation error and fuel consumption, the action point of the divert thrust is unavoidably deviated from the mass center, resulting in additional moment disturbance to the attitude.
- (3)
- The thrusts provided by the engines are fixedly connected to the interceptor.
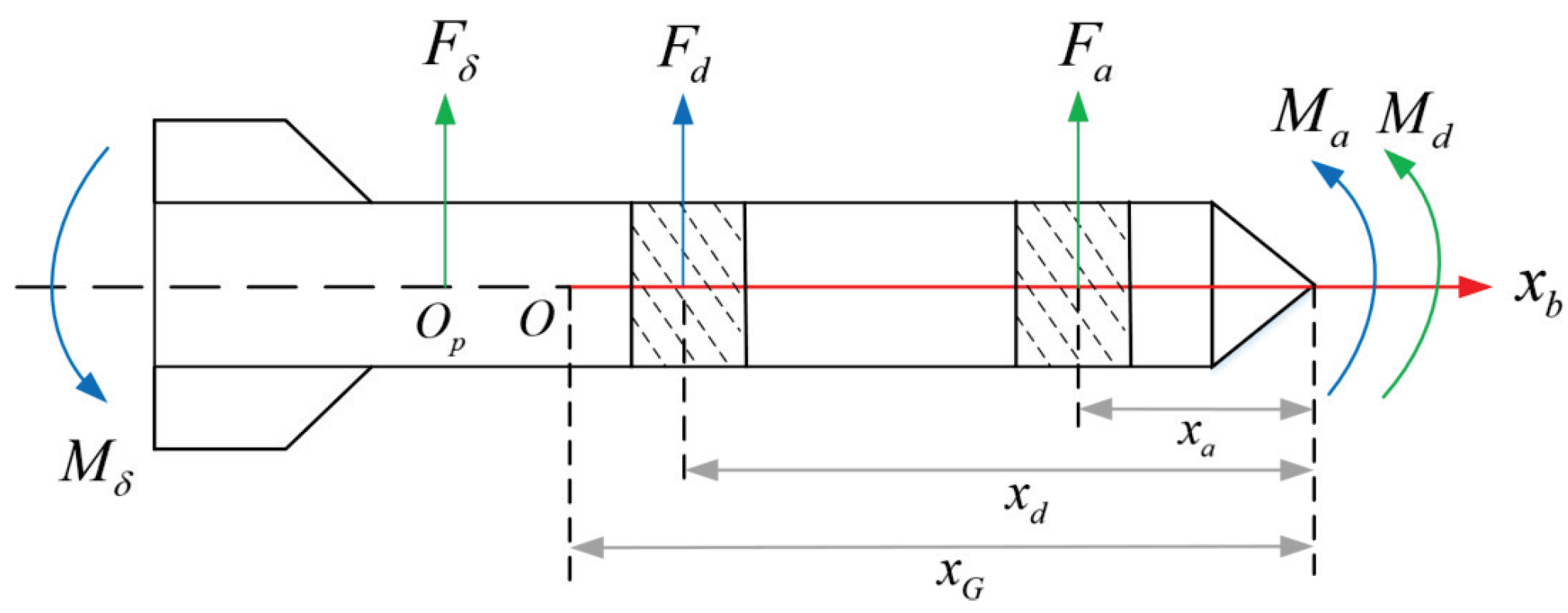
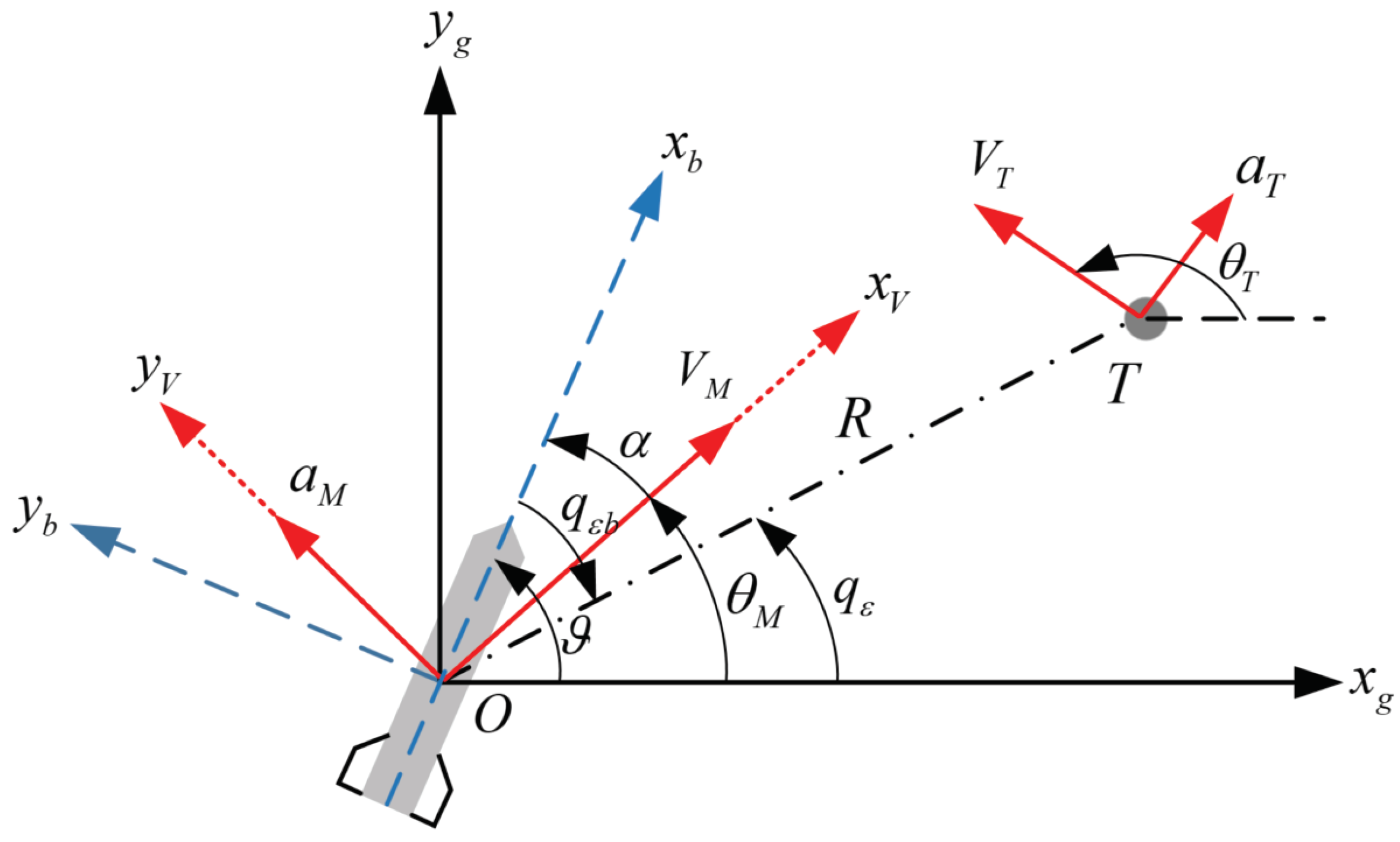
2.2. Mathematical Model for Strapdown Interceptor Under Multi-Force Compound Control
2.3. Problem Analysis
- (1)
- Strong couplings. The effects of multiple control inputs are coupled, and the trajectory/attitude control systems are coupled.
- (2)
- High-order and strong nonlinearity. The relative order between the controlled outputs and the control inputs is high, and there are complex nonlinear relationships between states.
- (3)
- Overdriven control. The guidance and control system under the multi-force compound control is an overdriven control system, in which the number of control inputs exceeds the number of controlled outputs.
- (4)
- Dissimilar actuators compound control. Each actuator in the multi-force compound control system has different limitations and dynamic characteristics.
- (5)
- Unknown mismatched uncertainties. There are multiple disturbances in the controlled system that cannot be directly compensated for by the control inputs.
- (1)
- Reflecting the strongly coupled and nonlinear characteristics of the controlled system in the control law to improve the control performance.
- (2)
- Including the control allocation scheme that can simultaneously satisfy input constraints, save fuel and implement control commands.
- (3)
- Ensuring the stability and robustness of the control system.
3. IGC Model Under Multi-Force Compound Control Based on Koopman Operator
3.1. Koopman Operator-Based Linear Predictor
3.2. Linear IGC Model for Interceptor Under Multi-Force Compound Control
3.2.1. Data Collection
3.2.2. Determine Lifted States
3.2.3. Construct Linear IGC Model
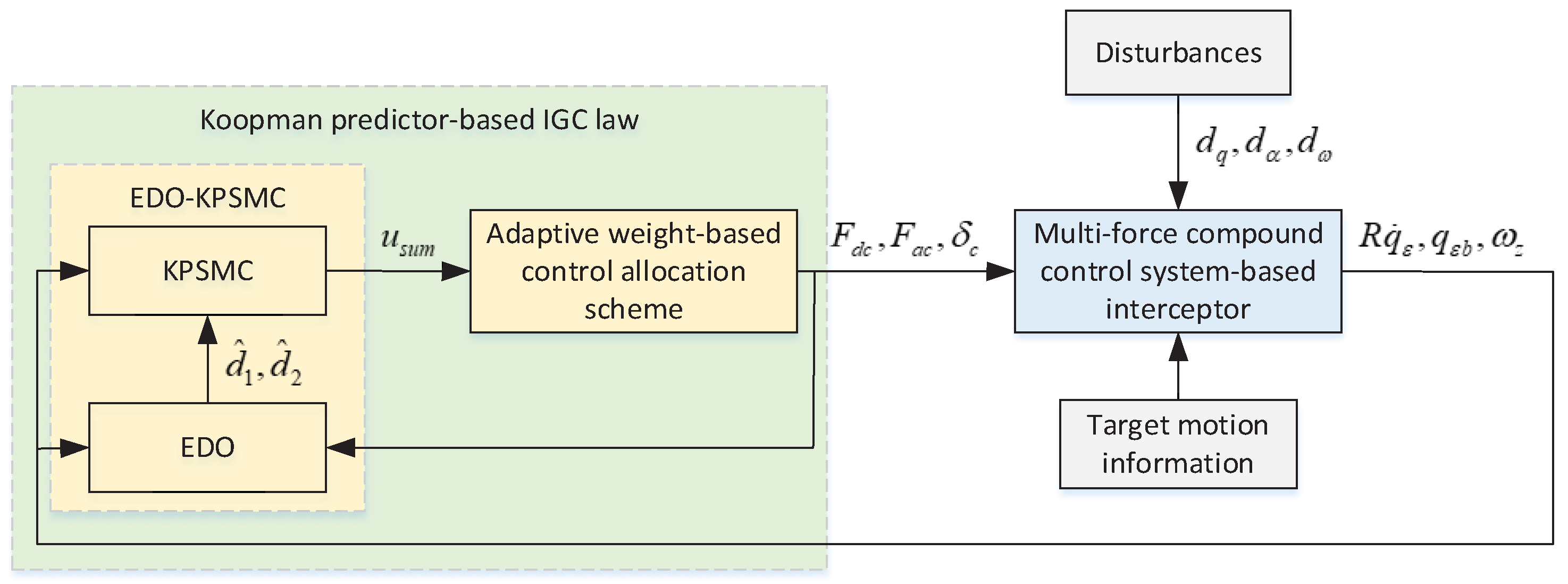
4. Koopman Predictor-Based IGC Law
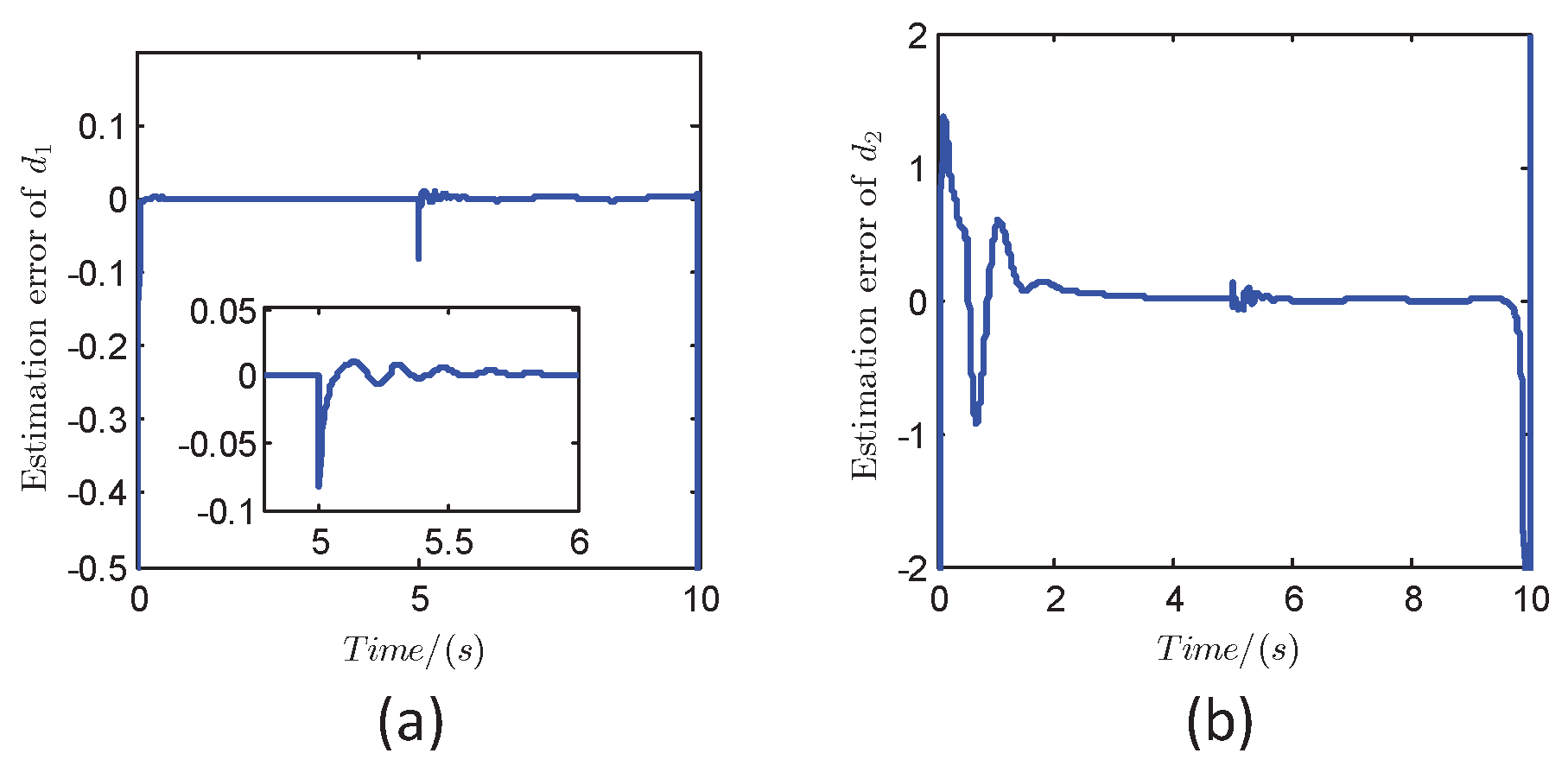
4.1. EDO for Koopman Predictor-Based IGC System
4.2. KPSMC-Based IGC Law Under Multi-Force Compound Control
4.3. Adaptive Weight-Based Control Allocation Scheme
- (1)
- Normalize the input range of actuators. Describing the control inputs in terms of a uniform standard, the control inputs are subjected to the following normalization transformation:where is the normalized control input. is the maximum control input, , representing the , , and in the multi-force compound control, respectively.Equation (33) transforms the absolute control input into the relative control input. Introducing the normalized control inputs into the adaptive weights is helpful for improving the fairness of the control allocation.
- (2)
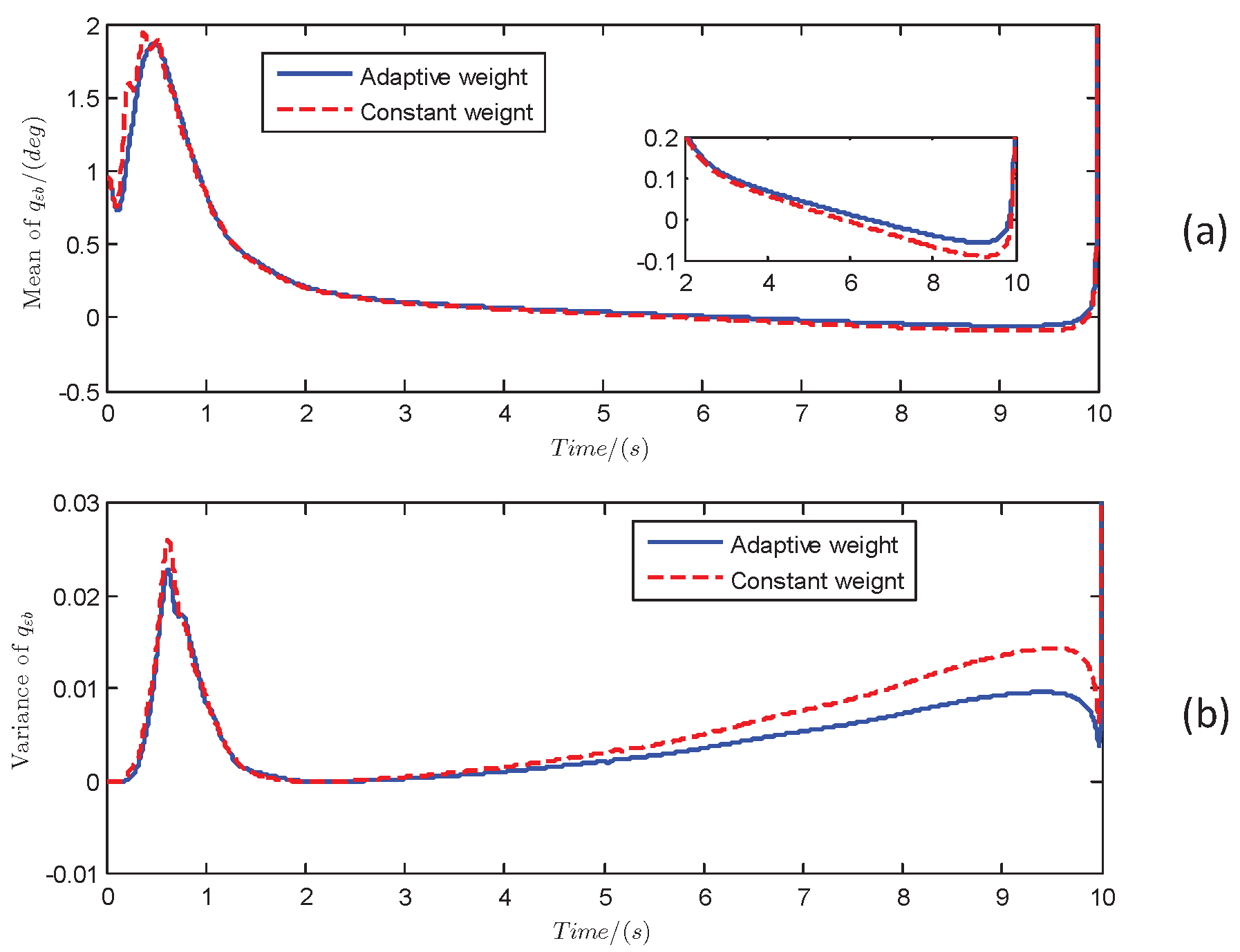
- Coordinate the residual control capability. The control allocation scheme needs to avoid input saturation as much as possible. Additionally, considering that the fuel-consuming and non-fuel-consuming actuators simultaneously exist in the multi-force compound control system, the fuel margin should be considered in the control allocation scheme to avoid premature fuel exhaustion.Based on the above requirements, an adaptive weight based on a quadratic function with real-time control input as the benchmark is proposed as follows:where , and the initial of it is . The meanings of and are shown in Figure 6. is a positive constant used as the base weight to avoid the weight being zero. is a function determined by the consumed fuel as follows:where is a positive adjustment parameter. , , , and are defined in Equation (5).
5. Simulation Studies
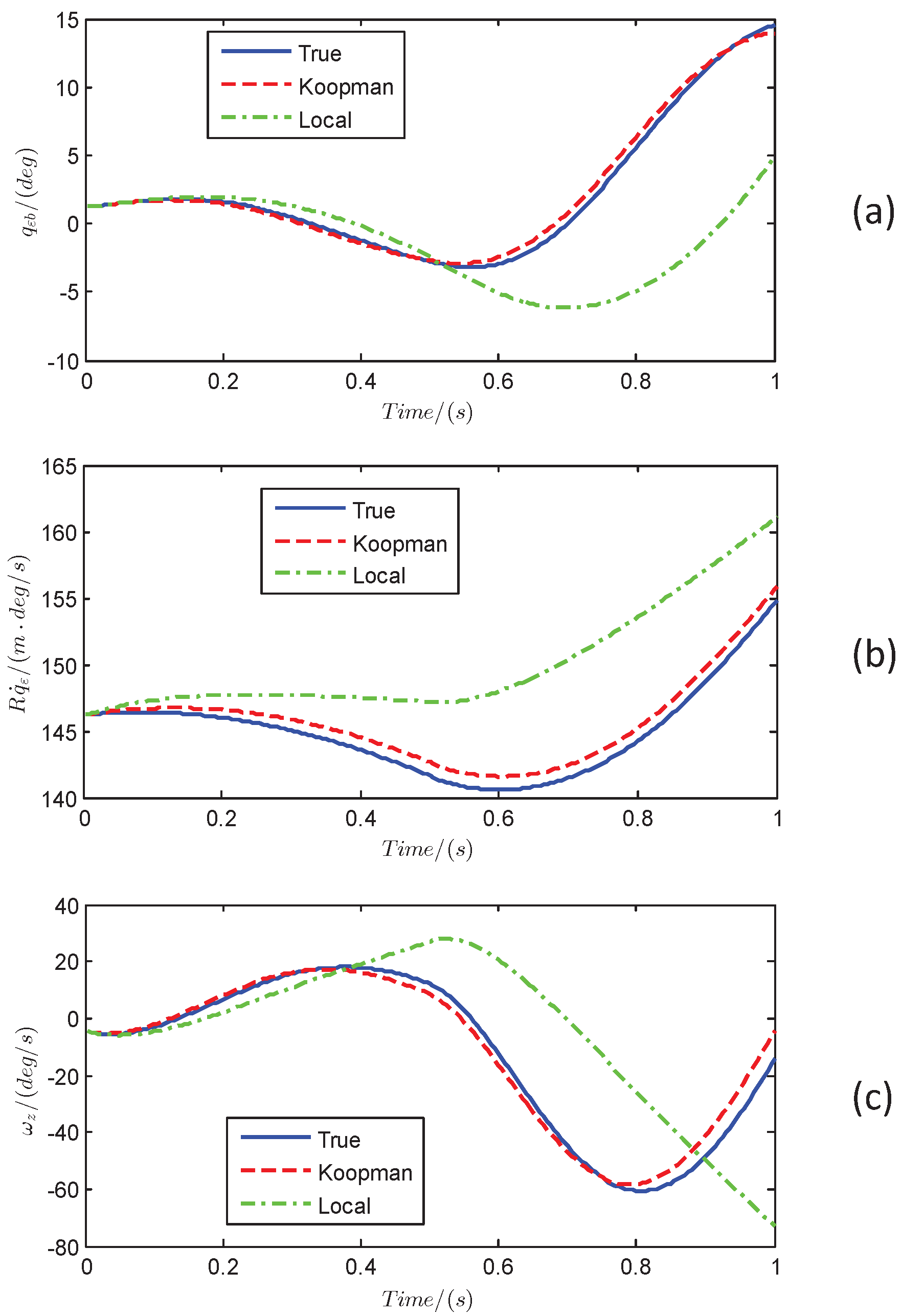
5.1. Accuracy of Koopman Predictor
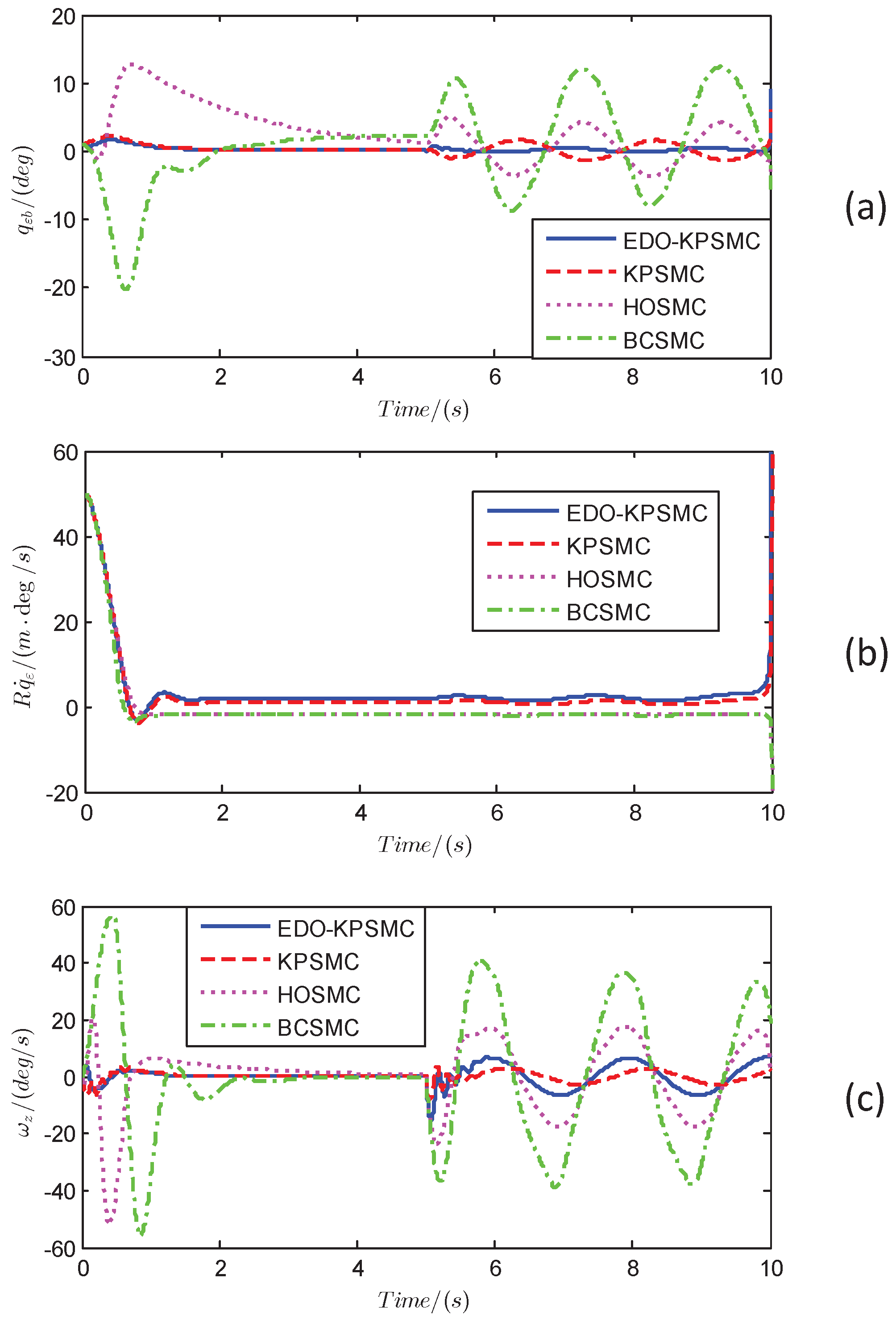
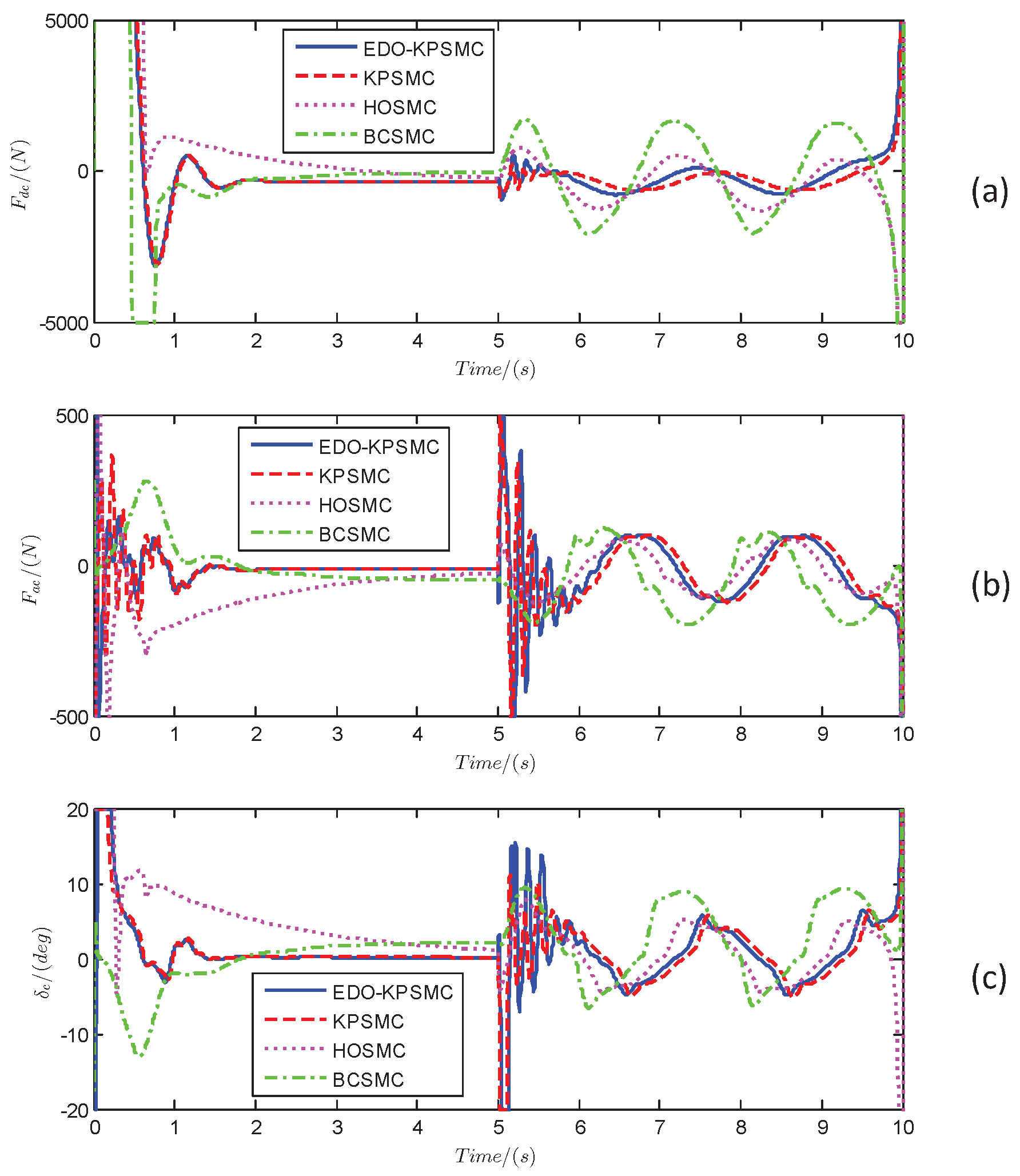
5.2. Effectiveness of EDP-KPSMC
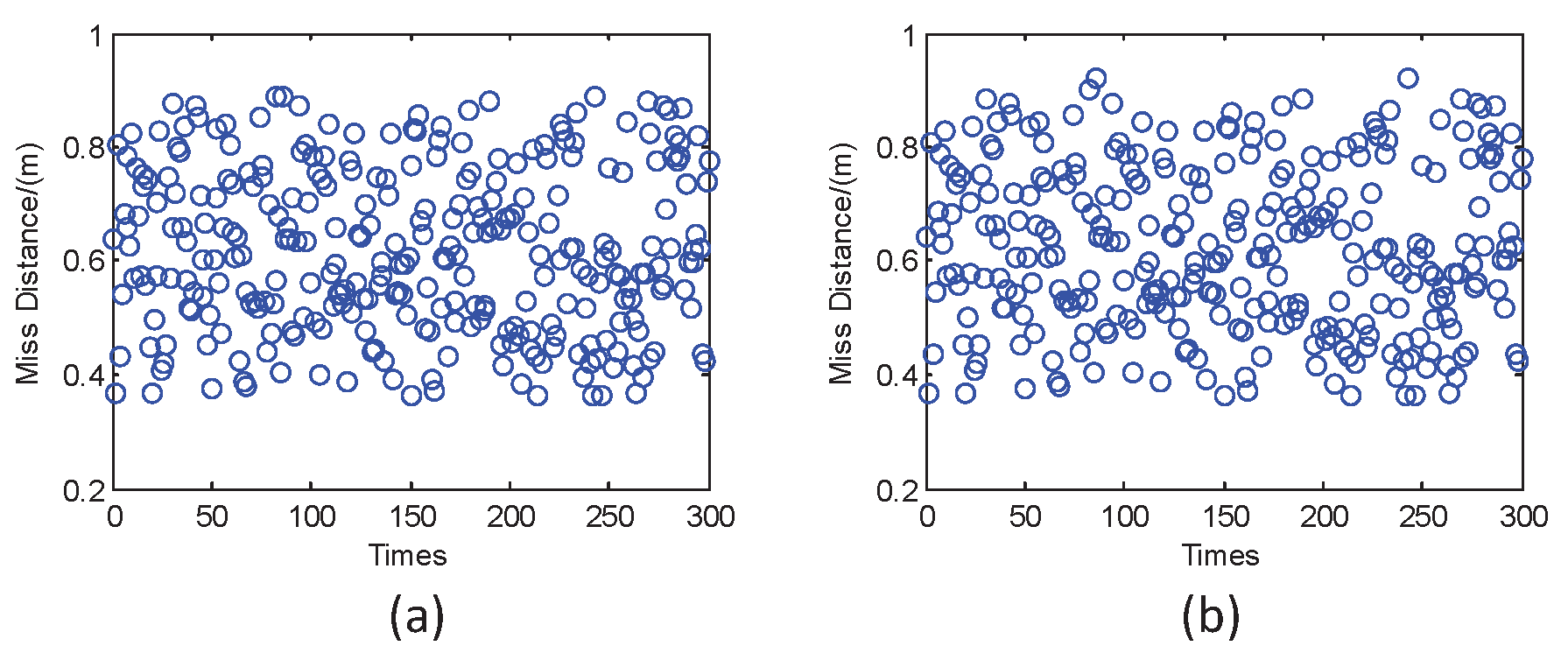
5.3. Effectiveness of Adaptive Weight-Based Control Allocation Scheme
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Ding, Y.; Yue, X.; Chen, G.S.; Si, J.S. Review of control and guidance technology on hypersonic vehicle. Chinese J. Aeronaut. 2022, 35, 1–18. [Google Scholar] [CrossRef]
- Peng, Q.; Chen, G.; Guo, J.G.; Guo, Z.Y. Finite-time convergent sliding mode guidance Law-based capture region with multiple constraints. IEEE Trans. Aerosp. Electron. Syst. 2025. Early Access. [Google Scholar] [CrossRef]
- Kim, S.; Cho, D.; Kim, H.J. Force and moment blending control for fast response of agile dual missiles. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 938–947. [Google Scholar] [CrossRef]
- Zhang, Y.A.; Wu, H.L.; Liu, J.M.; Sun, Y.M. A blended control strategy for intercepting high-speed target in high altitude. Proc. Inst. Mech. Eng. Part J. Aerosp. Eng. 2018, 232, 2263–2285. [Google Scholar] [CrossRef]
- Guo, Y.; Guo, J.H.; Liu, X.; Li, A.J.; Wang, C.Q. Finite-time blended control for air-to-air missile with lateral thrusters and aerodynamic surfaces. Aerosp. Sci. Technol. 2020, 97, 105638. [Google Scholar] [CrossRef]
- Ashrafiuon, H. Guidance and attitude control of unstable rigid bodies with single-use thrusters. IEEE Trans. Control Syst. Technol. 2017, 25, 401–413. [Google Scholar] [CrossRef]
- Shtessel, Y.B.; Tournes, C.H. Integrated higher-order sliding mode guidance and autopilot for dual-control missiles. J. Guid. Control Dyn. 2009, 32, 79–94. [Google Scholar] [CrossRef]
- Lee, H.; Bang, H. Efficient thrust management algorithm for variable thrust solid propulsion system with multi-nozzles. J. Spacecr. Rockets 2020, 57, 328–345. [Google Scholar] [CrossRef]
- Li, Z.B.; Dong, Q.L.; Zhang, X.Y.; Zhang, H.R.; Zhang, F. Field-to-view constrained integrated guidance and control for hypersonic homing missiles intercepting supersonic maneuvering targets. Aerospace 2022, 9, 640. [Google Scholar] [CrossRef]
- Yu, X.J.; Luo, S.B.; Liu, G.Q. Integrated design of multi-constrained snake maneuver surge guidance control for hypersonic vehicles in the dive segment. Aerospace 2023, 10, 765. [Google Scholar] [CrossRef]
- Li, Z.B.; Dong, Q.L.; Zhang, X.Y.; Gao, Y.F. Impact angle constrained integrated guidance and control for supersonic skid-toturn missiles using backstepping with global fast terminal sliding mode control. Aerosp. Sci. and Technol. 2022, 122, 107386. [Google Scholar] [CrossRef]
- Zhao, B.; Xu, S.; Guo, J.; Jiang, R.; Zhou, J. Integrated strapdown missile guidance and control based on neural network disturbance observer. Aerosp. Sci. Technol. 2019, 84, 170–181. [Google Scholar] [CrossRef]
- Luo, X.Y.; Song, J.; Zhao, M.F.; Li, W.L.; Wei, M.J. Integrated guidance and control for a hypersonic vehicle with disturbance and measurement noise suppression. IEEE Trans.Control Syst. Technol. 2024, 60, 7172–7184. [Google Scholar] [CrossRef]
- Lu, N.B.; Guo, J.G.; Guo, Z.Y.; Wang, G.Q. Asymmetric BLOS constraint-involved intelligent integrated guidance and control approach for flight vehicle equipped with strapdown seeker. Adv. Space. Res. 2023, 72, 4461–4473. [Google Scholar] [CrossRef]
- Guo, J.G.; Peng, Q.; Guo, Z.Y. SMC-Based Integrated Guidance and Control for Beam Riding Missiles with Limited LBPU. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2969–2978. [Google Scholar] [CrossRef]
- Zhao, B.; Feng, Z.X.; Guo, J.G. Integral barrier Lyapunov functions-based integrated guidance and control design for strap-down missile with field-of-view constraint. Trans. Inst. Meas. Control. 2021, 43, 1464–1477. [Google Scholar] [CrossRef]
- Guo, J.G.; Zhou, Y.H.; Zhou, M. Adaptive control law based integrated guidance and control design for missile with the radome error compensation. Proc. Inst. Mech. Eng. 2024, 238, 361–371. [Google Scholar] [CrossRef]
- Kim, H.G.; Beck, D. Integrated guidance and control for collision course stabilization of dual-controlled interceptors. Aerospace 2024, 11, 9. [Google Scholar] [CrossRef]
- Peng, Q.; Chen, G.; Guo, J.G.; Guo, Z.Y. Attitude/orbit engine compound control for hypersonic target interceptor with discrete-time inputs and state constraints. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 4939–4951. [Google Scholar] [CrossRef]
- Koopman, B.O. Hamiltonian systems and transformation in Hilbert space. Proc. Natl. Acad. Sci. USA 1931, 17, 315–318. [Google Scholar] [CrossRef]
- Bevanda, P.; Sosnowski, S.; Hirche, S. Koopman operator dynamical models: Learning, analysis and control. Annu. Rev. Control 2021, 52, 197–212. [Google Scholar] [CrossRef]
- Pan, S.W.; Duraisamy, K. On the lifting and reconstruction of nonlinear systems with multiple invariant sets. Nonlinear Dyn. 2024, 112, 10157–10165. [Google Scholar] [CrossRef]
- Korda, M.; Mezic, I. Linear predictors for nonlinear dynamical systems: Koopman operator meets model predictive control. Automatica 2018, 93, 149–160. [Google Scholar] [CrossRef]
- Uchida, D.; Yamashita, A.; Asama, H. Data-driven koopman controller synthesis based on the extended H2 norm characterization. IEEE Control. Syst. Lett. 2021, 5, 1795–1800. [Google Scholar] [CrossRef]
- Zhang, X.L.; Pan, W.; Scattolini, R.; Yu, S.Y.; Xu, X. Robust tube-based model predictive control with Koopman operators. Automatica 2022, 137, 110114. [Google Scholar] [CrossRef]
- Zhou, M.; Liu, M.F.; Hu, G.J.; Guo, Z.Y.; Guo, J.G. Koopman operator-based integrated guidance and control for strap-down high-speed missiles. IEEE Trans.Control Syst. Technol. 2024, 32, 2436–2443. [Google Scholar] [CrossRef]
- Li, S.P.; Guo, J.G. An angle error extraction algorithm based on JADE for three-channel radar seeker system with the existence of deception jamming. Digit. Signal Process. 2022, 131, 103754. [Google Scholar] [CrossRef]
- Han, T.; Hu, Q.L.; Wang, Q.Y.; Xin, M.; Shin, H.S. Constrained 3-D trajectory planning for aerial vehicles without range measurement. IEEE Trans. Syst. Man, Cybern. Syst. 2024, 54, 6001–6013. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, Z.Q.; Guo, J.G.; Guo, Z.Y. Three-dimensional piecewise guidance strategy for multi-UAVs guaranteeing simultaneous arrival and field-of-view constraint. Trans. Inst. Meas. Control. 2022, 44, 2248–2263. [Google Scholar]
- Williams, M.O.; Kevrekidis, I.G.; Rowley, C.W. A data–driven approximation of the Koopman operator: Extending dynamic mode decomposition. J. Nonlinear Sci. 2015, 25, 1307–1346. [Google Scholar] [CrossRef]
- Korda, M.; Mezic, I. On convergence of extended dynamic mode decomposition to the Koopman operator. J. Nonlinear Sci. 2018, 28, 687–710. [Google Scholar] [CrossRef]
- Ginoya, D.; Shendge, P.D.; Phadke, S.B. Sliding mode control for mismatched uncertain systems using an extended disturbance observer. IEEE Trans. Ind. Electron. 2014, 61, 1983–1992. [Google Scholar] [CrossRef]
- Peng, Q.; Guo, J.G.; Zhou, J. Integrated guidance and control system design for laser beam riding missiles with relative position constraint. Aerosp. Sci. Technol. 2020, 98, 105693. [Google Scholar] [CrossRef]


| EDO-KPSMC | KPSMC | HOSMC | BCSMC | |
|---|---|---|---|---|
| Miss distance (m) | 0.37 | 0.25 | 0.12 | 0.10 |
| Divert thrust impulse () | 5.87 | 5.83 | 7.54 | 8.99 |
| Attitude thrust impulse () | 0.47 | 0.50 | 0.78 | 0.79 |
| Adaptive Weight | Constant Weight | |
|---|---|---|
| Miss distance (m) | 0.62 | 0.62 |
| Divert thrust impulse () | 8.31 | 8.47 |
| Attitude thrust impulse () | 0.62 | 0.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Q.; Chen, G.; Guo, J.; Guo, Z. Koopman Predictor-Based Integrated Guidance and Control Under Multi-Force Compound Control System. Aerospace 2025, 12, 213. https://doi.org/10.3390/aerospace12030213
Peng Q, Chen G, Guo J, Guo Z. Koopman Predictor-Based Integrated Guidance and Control Under Multi-Force Compound Control System. Aerospace. 2025; 12(3):213. https://doi.org/10.3390/aerospace12030213
Chicago/Turabian StylePeng, Qian, Gang Chen, Jianguo Guo, and Zongyi Guo. 2025. "Koopman Predictor-Based Integrated Guidance and Control Under Multi-Force Compound Control System" Aerospace 12, no. 3: 213. https://doi.org/10.3390/aerospace12030213
APA StylePeng, Q., Chen, G., Guo, J., & Guo, Z. (2025). Koopman Predictor-Based Integrated Guidance and Control Under Multi-Force Compound Control System. Aerospace, 12(3), 213. https://doi.org/10.3390/aerospace12030213







