Simulation of Shock-to-Detonation Transition by OpenFOAM
Abstract
1. Introduction
2. Governing Equations
3. Results
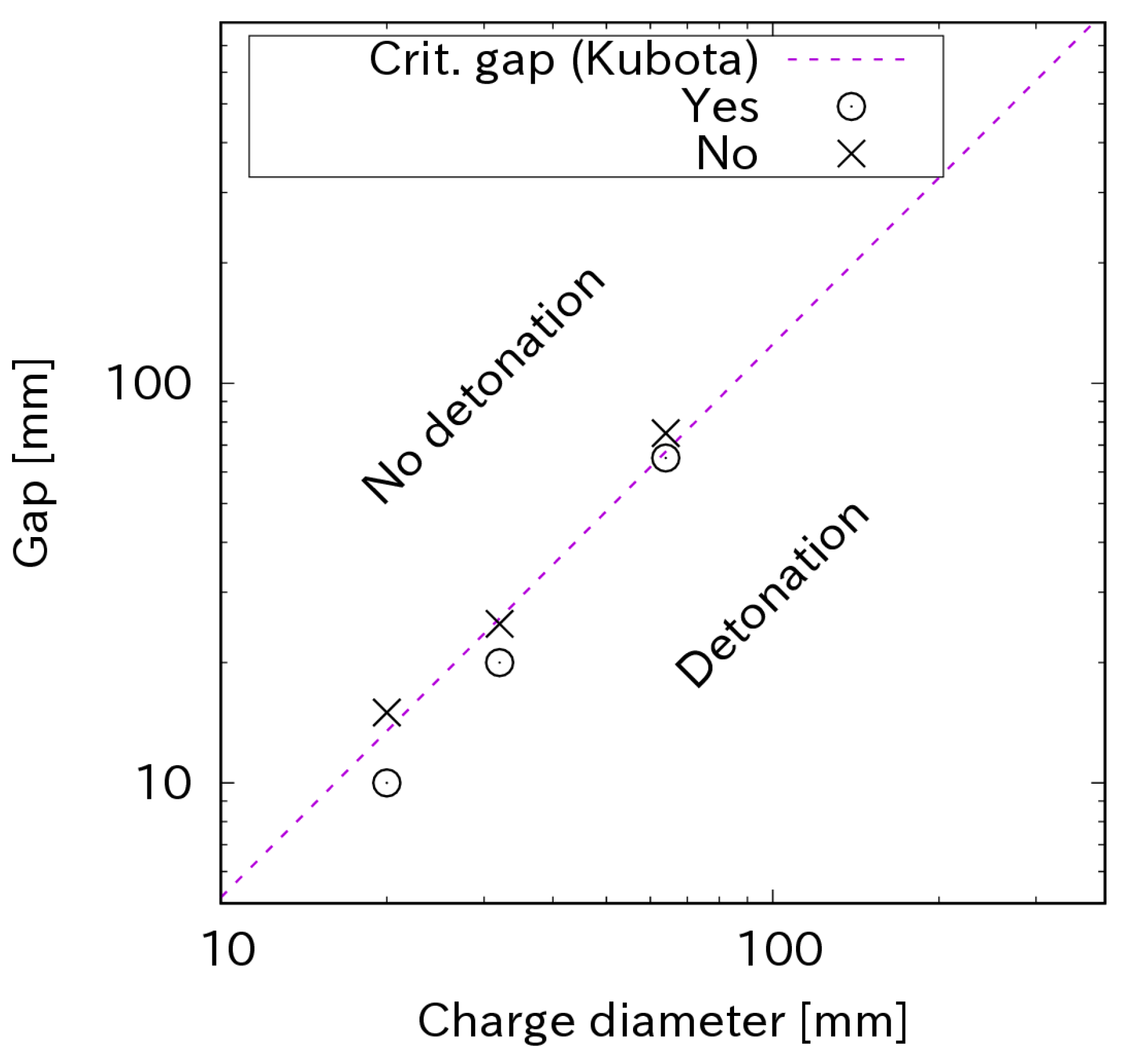
3.1. Pop Plot Calculation
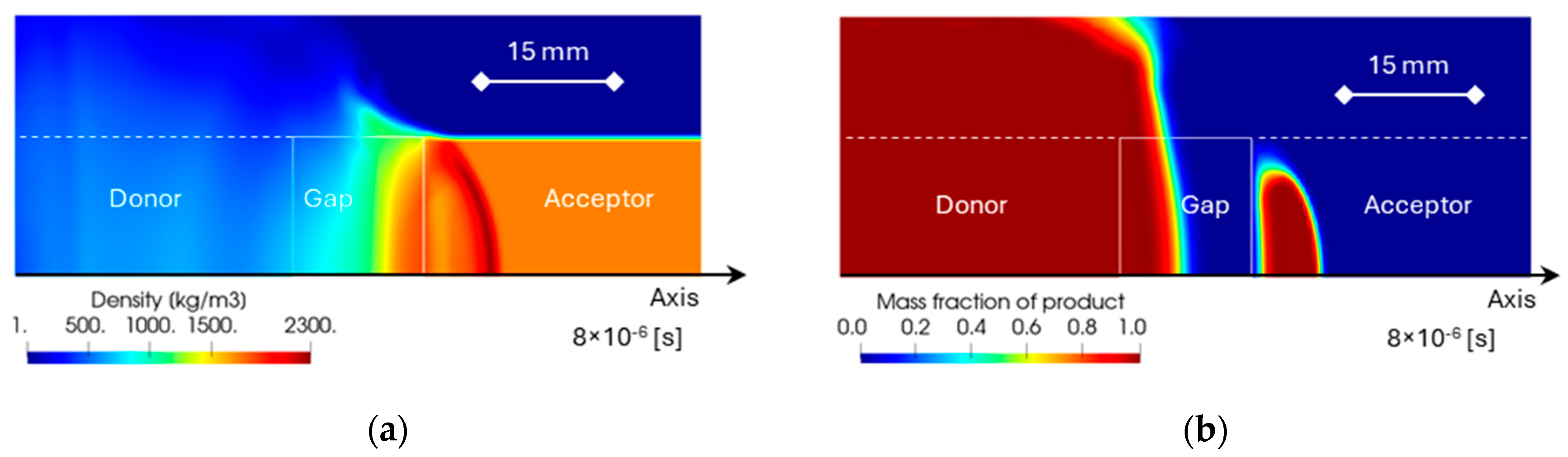
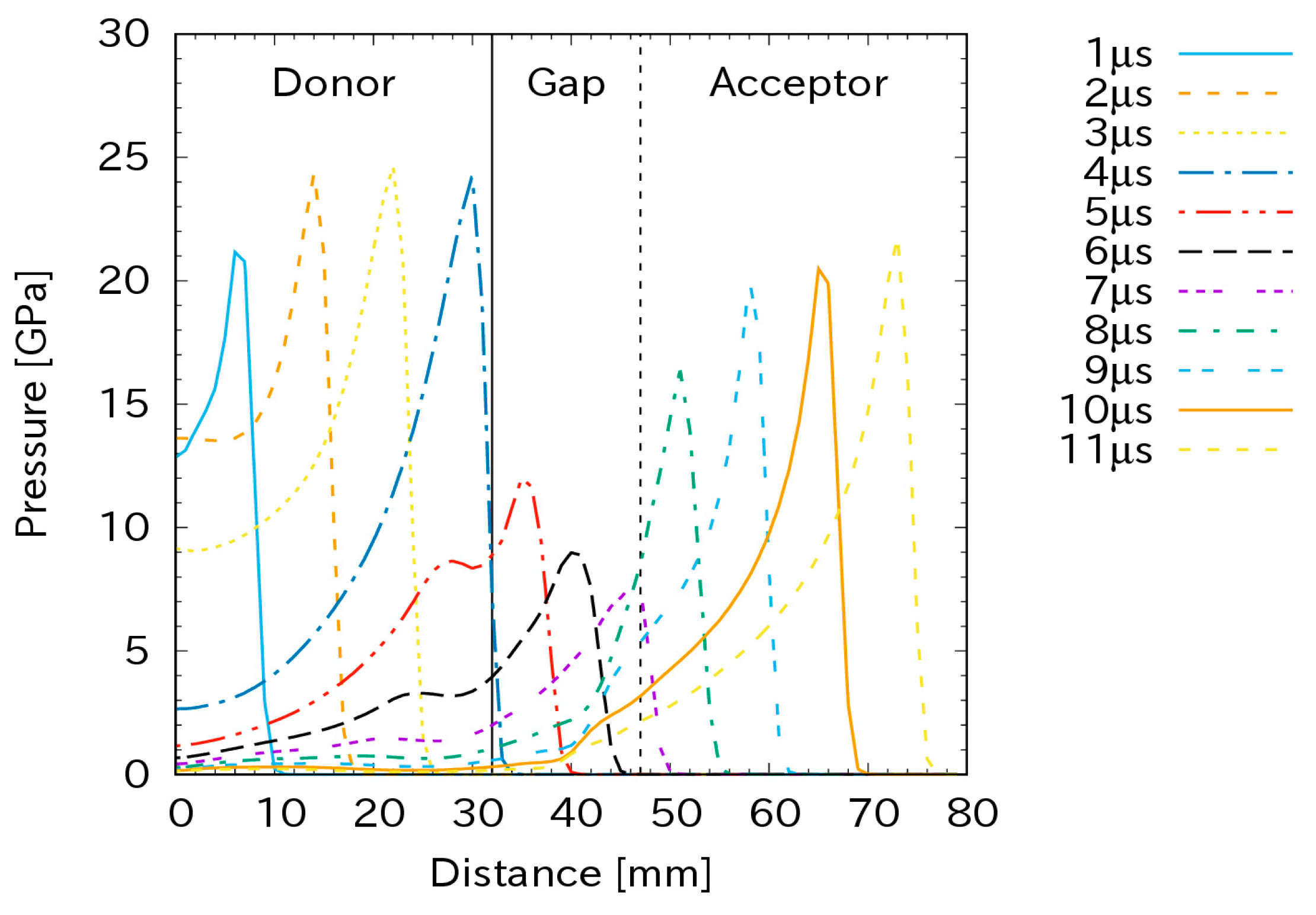
3.2. Sympathetic Detonation Simulation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, L.; Wang, C.; Feng, C.; Lu, F.; Lu, J.; Wang, X.; Guo, X. Study on random initiation phenomenon for sympathetic detonation of explosive. Def. Technol. 2013, 9, 224–228. [Google Scholar] [CrossRef]
- Saburi, T.; Kobota, S.; Wada, Y.; Yoshida, M. Development of numerical code for physical hazard analysis of high-energy materials. Sci. Tech. Energetic Mater. 2013, 74, 124–131. [Google Scholar]
- Kim, K.H.; Yoh, J.J. A particle level-set based Eulerian method for multi-material detonation simulation of high explosive and metal confinements. Proc. Combust. Inst. 2013, 34, 2025–2033. [Google Scholar] [CrossRef]
- Yang, G.; Fu, Y.; Hu, D.; Han, X. Feasibility analysis of SPH method in the simulation of condensed explosives detonation with ignition and growth model. Comput. Fluids 2013, 88, 51–59. [Google Scholar] [CrossRef]
- Ansys Inc. Ansys LS-DYNA. Multiphysics Solver. Available online: https://www.ansys.com/products/structures/ansys-ls-dyna (accessed on 9 January 2020).
- Ansys Inc. Ansys Autodyn. Short Duration, Severe Loading Simulations. Available online: https://www.ansys.com/products/structures/ansys-autodyn (accessed on 9 January 2020).
- Yuan, P.; Zhao, Y. Numerical simulation of damage to ship structure by underwater contact explosion shock wave. Chem. Eng. Trans. 2017, 62, 673–678. [Google Scholar]
- Chen, J.K.; Ching, H.K.; Allahdadi, F.A. Shock-induced detonation of high explosives by high velocity impact. J. Mech. Mater. Struct. 2007, 2, 1701–1721. [Google Scholar] [CrossRef]
- Openfoam. Available online: https://openfoam.org/ (accessed on 9 January 2020).
- Menikoff, R. JWL Equation of State; Technical Report 2017, LA-UR-15-29536; Los Alamos National Laboratory (LANL): Los Alamos, NM, USA, 2015. [Google Scholar]
- Segletes, S.B. An Analysis on the Stability of the Mie-Gruneisen Equation of State for Describing the Behavior of Shock-Loaded Materials; Technical Report 1991, BRL-TR-3214; U.S. Army Laboratory Command: Adelphi, ML, USA, 1991. [Google Scholar]
- Tarver, C.T. Modeling detonation experiments on Triaminotrinitrobenzene (TATB)-based explosives LX-17, PBX 9502, and ultrafine TATB. Energetic Mater. 2012, 30, 220–251. [Google Scholar] [CrossRef]
- Lorenzo, M.D.; Pelanti, M.P.; Lafon, P. HLLC-type and path-conservative schemes for a single-velocity six-equation two-phase flow model: A comparative study. Appl. Math. Comput. 2018, 333, 95–117. [Google Scholar] [CrossRef]
- Shima, E.; Kitamura, K. Parameter-free simple low-dissipation AUSM-family scheme for all speeds. AIAA 2011, 49, 1693–1709. [Google Scholar] [CrossRef]
- Urtiew, P.A.; Vandersall, K.S.; Tarver, C.M.; Gacia, F.; Forbes, J.W. Shock initiation of composition B and C-4 explosives: Experiments and modeling. In Proceedings of the International Conference of Shock Waves in Condensed Matter, Saint Petersburg, Russia, 3–8 September 2006. [Google Scholar]
- Gibbs, T.R.; Popolato, A. LASL Explosive Property Data; University of California Press: Berkeley, CA, USA, 1980; p. 19. [Google Scholar]
- Kubota, S.; Liu, Z.; Otsuki, S.; Nakayama, Y.; Ogata, Y.; Yoshida, M. A numerical study of sympathetic detonation in gap test. Mater. Sci. Forum 2004, 465–466, 163–168. [Google Scholar] [CrossRef]
- Kim, B.; Kim, M.; Yoh, J.J. Shock to detonation transition analysis using experiments and models. Proc. Combust. Inst. 2017, 36, 2699–2707. [Google Scholar] [CrossRef]




| Parameter | Reactant | Product | Unit |
|---|---|---|---|
| A | 778.1 | 5.242 | [Mbar] |
| B | −0.05301 | 0.07678 | (Mbar] |
| R1 | 11.3 | 4.2 | [-] |
| R2 | 1.13 | 1.1 | [-] |
| ω | 0.8938 | 0.5 | [-] |
| E0 | - | 4.9505 | [MJ/kg] |
| ρ0 | 1717.0 | - | [kgm−3] |
| Parameter | Reactant | Unit |
|---|---|---|
| I | 4.0 × 1012 | [s−1] |
| a | 0.0367 | [-] |
| b | 0.667 | [-] |
| x | 7.0 | [-] |
| G1 | 140.0 × 106 | [Mbar−2s−1] |
| c | 0.667 | [-] |
| d | 1.0 | [-] |
| y | 2.0 | [-] |
| G2 | 1000.0 × 106 | Mbar−3s−1 |
| e | 0.222 | [-] |
| g | 1.0 | [-] |
| z | 3.0 | [-] |
| λImax | 0.022 | [-] |
| λG1max | 0.7 | [-] |
| λG2min | 0.0 | [-] |
| Parameter | Value | Unit |
|---|---|---|
| c0 | 5240.0 | (ms−1) |
| a | 0.48 | (-) |
| s | 1.4 | (-) |
| Γ0 | 1.97 | (-) |
| ρ0 | 2703.0 | (kgm−3) |
| Parameter | Value | Unit |
|---|---|---|
| c0 | 2180.0 | (ms−1) |
| a | 0.0 | (-) |
| s | 1.41 | (-) |
| Γ0 | 0.85 | (-) |
| ρ0 | 1182.0 | (kgm−3) |
| c0 | 2180.0 | (ms−1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dinh, T.X.; Yoshida, M.; Ishikura, S. Simulation of Shock-to-Detonation Transition by OpenFOAM. Aerospace 2025, 12, 214. https://doi.org/10.3390/aerospace12030214
Dinh TX, Yoshida M, Ishikura S. Simulation of Shock-to-Detonation Transition by OpenFOAM. Aerospace. 2025; 12(3):214. https://doi.org/10.3390/aerospace12030214
Chicago/Turabian StyleDinh, Thien Xuan, Masatake Yoshida, and Shuichi Ishikura. 2025. "Simulation of Shock-to-Detonation Transition by OpenFOAM" Aerospace 12, no. 3: 214. https://doi.org/10.3390/aerospace12030214
APA StyleDinh, T. X., Yoshida, M., & Ishikura, S. (2025). Simulation of Shock-to-Detonation Transition by OpenFOAM. Aerospace, 12(3), 214. https://doi.org/10.3390/aerospace12030214





