Inverse Design of Additive Manufactured Rocket Propellant Grains with Non-Uniform Properties
Abstract
1. Introduction
2. Physical Model and Numerical Schemes
2.1. Chamber Model and Time Integration
2.2. Level Set Method
3. Automatic Optimizer Description
3.1. Design Space
3.2. Sampling Plan and Dataset Creation
3.3. Surrogate Modeling
3.4. Design Problem and Optimizer
4. Test Applications
5. Further Applications
5.1. Flexibility Enhancements
5.2. Launcher Test Case
6. Evaluation of Surrogate Applicability
7. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| First coefficient for ballistic distribution | |
| Grain burning surface | |
| Nozzle throat area | |
| b | Second coefficient for ballistic distribution |
| Characteristic velocity | |
| Multiplicative factor for characteristic velocity | |
| Total impulse estimated by optimizer | |
| Total impulse required | |
| L | Required length of the grain |
| Maximum allowed length of the grain | |
| Mass flow of gas produced through solid propellant combustion | |
| Mass flow of gas expelled through nozzle | |
| n | Pressure exponent for burning rate |
| N | Total number of snapshots |
| Gas pressure in combustion chamber | |
| Pressure value estimated by optimizer at i-th time snapshot | |
| Pressure value from target curve at i-th time snapshot | |
| r | Burning rate of the propellant |
| Casing radius | |
| Radial coordinate | |
| Perfect gas constant | |
| Gas temperature in combustion chamber | |
| Burning time estimated by optimizer | |
| Burning time required | |
| Velocity field of the level set Equation | |
| Gas volume in combustion chamber | |
| Parameters vector | |
| Specific heat ratio of gas | |
| Mach function for mass flow | |
| Nozzle area expansion ratio | |
| Implicit function for level set definition | |
| Solid propellant density | |
| Gas density in combustion chamber | |
| Pseudo-time for level set reinitialization |
Appendix A
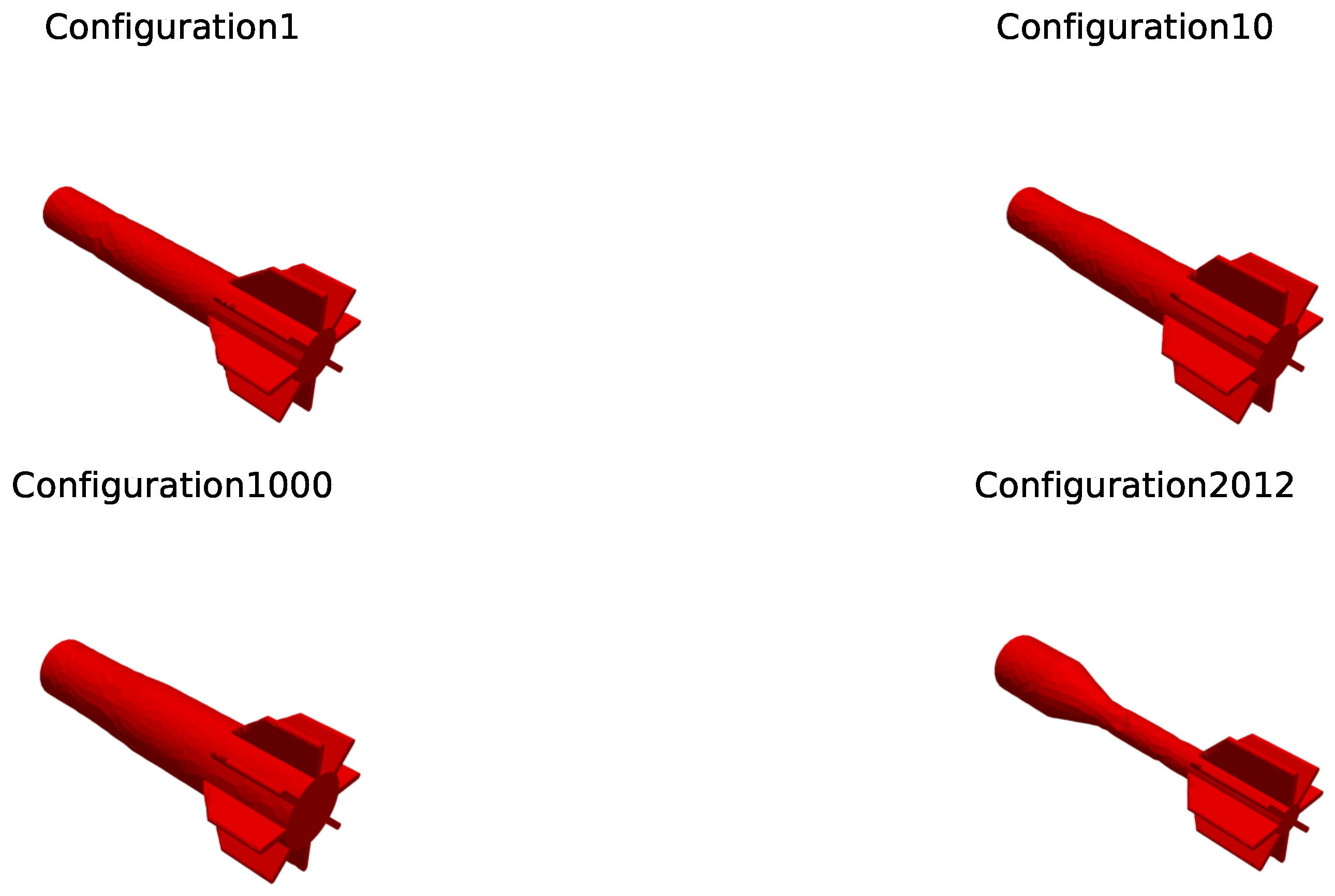






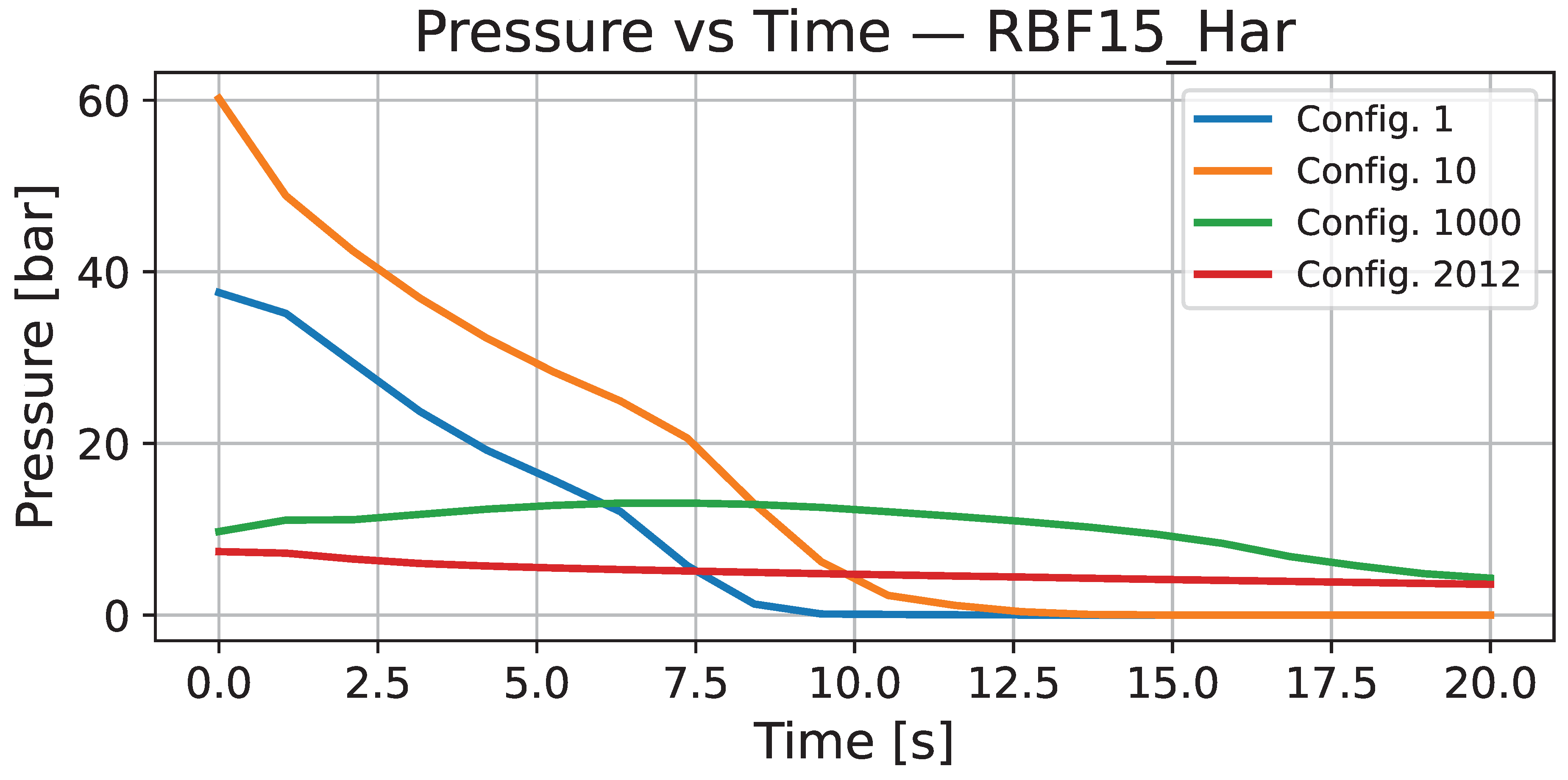

References
- Lysien, K.; Stolarczyk, A.; Jarosz, T. Solid Propellant Formulations: A Review of Recent Progress and Utilized Components. Materials 2021, 14, 6657. [Google Scholar] [CrossRef]
- Sutton, G.P.; Biblarz, O. Rocket Propulsion Elements, 9th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Heister, S.D.; Anderson, W.E.; Pourpoint, T.L.; Cassady, R.J. Rocket Propulsion; Cambridge University Press: Cambridge, UK, 2019; Volume 47. [Google Scholar]
- Muravyev, N.V.; Monogarov, K.A.; Schaller, U.; Fomenkov, I.V.; Pivkina, A.N. Progress in additive manufacturing of energetic materials: Creating the reactive microstructures with high potential of applications. Propellants Explos. Pyrotech. 2019, 44, 941–969. [Google Scholar] [CrossRef]
- Straathof, M.H.; van Driel, C.A.; van Lingen, J.N.; Ingenhut, B.L.; ten Cate, A.T.; Maalderink, H.H. Development of propellant compositions for vat photopolymerization additive manufacturing. Propellants Explos. Pyrotech. 2020, 45, 36–52. [Google Scholar] [CrossRef]
- Zhou, X.; Mao, Y.; Zheng, D.; Zhong, L.; Wang, R.; Gao, B.; Wang, D. 3D printing of RDX-based aluminized high explosives with gradient structure, significantly altering the critical dimensions. J. Mater. Sci. 2021, 56, 9171–9182. [Google Scholar] [CrossRef]
- Kirby, L.; Udaykumar, H.; Song, X. Pressure-assisted binder jetting for additive manufacturing of mock energetic composites. Propellants Explos. Pyrotech. 2024, 49, e202300175. [Google Scholar] [CrossRef]
- Wejsa, J. ARDEC Report. Presentation at the NDIA Armament Systems Forum. Available online: https://ndia.dtic.mil/wp-content/uploads/2014/armaments/Wed16567_Wejsa.pdf (accessed on 31 October 2025).
- Tillinghast, R.; Zunino, J. Additive Manufacturing Methods, Techniques, Procedures, and Applications. Enabling Technologies for Military Applications. Presentation at the NDIA Armament Systems Forum. Available online: https://ndia.dtic.mil/wp-content/uploads/2015/armament/wed17417_Tillinghast.pdf (accessed on 31 October 2025).
- Pastrone, D.; Sangermano, M.; Garino, S.; Maggi, F. Composite Propellant Manufacturing Process Based on Deposition and Light-Activated Polymerization for Solid Rocket Motors. WO2020212785A1, 22 October 2020. [Google Scholar]
- Garino, S.; Antonaci, P.; Pastrone, D.; Sangermano, M.; Maggi, F. Photo-Polymerization for Additive Manufacturing of Composite Solid Propellants. Acta Astronaut. 2021, 182, 58–65. [Google Scholar] [CrossRef]
- Galavotti, A.; Noè, C.; Polizzi, G.; Antonaci, P.; Maggi, F.; Masseni, F.; Pastrone, D. Solid Rocket Propellant Photo-Polymerization with an In-House LED-UV Prototype. Polymers 2023, 15, 1633. [Google Scholar] [CrossRef]
- Zumbo, A.; Stumpo, L.; Antonaci, P.; Ferrero, A.; Masseni, F.; Polizzi, G.; Tetti, G.; Pastrone, D. Rheological and Mechanical Characterization of 3D-Printable Solid Propellant Slurry. Polymers 2024, 16, 576. [Google Scholar] [CrossRef] [PubMed]
- Masseni, F.; Zumbo, A.; Stumpo, L.; Polizzi, G.; Tetti, G.; Lusetti, T.; Noé, C.; Antonaci, P.; Ferrero, A.; Pastrone, D.; et al. Advancements in Photocurable Solid Propellants for Additive Manufacturing. In Proceedings of the AIAA SCITECH 2025 Forum, Orlando, FL, USA, 6–10 January 2025; AIAA Paper 2025-2330. [Google Scholar] [CrossRef]
- McClain, M.; Gunduz, I.; Son, S. Additive Manufacturing of Ammonium Perchlorate Composite Propellant with High Solids Loadings. Proc. Combust. Inst. 2019, 37, 3135–3142. [Google Scholar] [CrossRef]
- McClain, M.; Afriat, A.; Montano, B.J.; Ray, S.; Rhoads, J.; Gunduz, I.E.; Son, S.F. Investigation of Additively Manufactured Layered Composite Solid Propellant. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; AIAA Paper 2020-1427. [Google Scholar] [CrossRef]
- McClain, M.S.; Afriat, A.; Montano, B.J.; Rhoads, J.F.; Gunduz, I.E.; Son, S.F. Dynamic Combustion of Functionally Graded Additively Manufactured Composite Solid Propellant. J. Propuls. Power 2021, 37, 725–732. [Google Scholar] [CrossRef]
- Chen, N.; He, C.; Pang, S. Additive Manufacturing of Energetic Materials: Tailoring Energetic Performance via Printing. J. Mater. Sci. Technol. 2022, 127, 29–47. [Google Scholar] [CrossRef]
- Scheithauer, U.; Schwarzer, E.; Richter, H.J.; Moritz, T. Thermoplastic 3D Printing—an Additive Manufacturing Method for Producing Dense Ceramics. Int. J. Appl. Ceram. Technol. 2015, 12, 26–31. [Google Scholar] [CrossRef]
- Chandru, R.A.; Balasubramanian, N.; Oommen, C.; Raghunandan, B.N. Additive Manufacturing of Solid Rocket Propellant Grains. J. Propuls. Power 2018, 34, 1090–1093. [Google Scholar] [CrossRef]
- Li, M.; Yang, W.; Xu, M.; Hu, R.; Zheng, L. Study of Photocurable Energetic Resin Based Propellants Fabricated by 3D Printing. Mater. Des. 2021, 207, 109891. [Google Scholar] [CrossRef]
- Poppe, G.; Koch, P.; Bozic, O.; Lancelle, D. Optimization of Finocyl Grain Geometries of Solid Rocket Boosters. In Proceedings of the European Conference for Aerospace Sciences, Krakow, Poland, 29 June–3 July 2015. [Google Scholar]
- Kamran, A.; Guozhu, L. An Integrated Approach for Optimization of Solid Rocket Motor. Aerosp. Sci. Technol. 2012, 17, 50–64. [Google Scholar] [CrossRef]
- Zeping, W.; Donghui, W.; Weihua, Z.; Okolo, P.N.; Yang, F. Solid-Rocket-Motor Performance-Matching Design Framework. J. Spacecr. Rocket. 2017, 54, 698–707. [Google Scholar] [CrossRef]
- Albarado, K.; Hartfield, R.; Hurston, W.; Jenkins, R. Solid rocket motor design using hybrid optimization. Int. J. Aerosp. Eng. 2012, 2012, 987402. [Google Scholar] [CrossRef]
- Tola, C.; Nikbay, M. Solid rocket motor propellant optimization with coupled internal ballistic–structural interaction approach. J. Spacecr. Rocket. 2018, 55, 936–947. [Google Scholar] [CrossRef]
- Mitchell, I.M. The Flexible, Extensible and Efficient Toolbox of Level Set Methods. J. Sci. Comput. 2008, 35, 300–329. [Google Scholar] [CrossRef]
- Polizzi, G.; Ferrero, A.; Masseni, F.; Pastrone, D. A Numerical Method for Burnback Analysis of UV-cured Solid Rocket Propellant Grains. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024; p. 0635, AIAA Paper 2024-0635. [Google Scholar] [CrossRef]
- Osher, S.; Fedkiw, R. Level Set Methods and Dynamic Implicit Surfaces; Applied Mathematical Sciences; Springer: New York, NY, USA, 2003. [Google Scholar]
- Barrère, M.; Jaumotte, A.; Fraeijs de Veubeke, B.; Vandenkerckhove, J. Rocket Propulsion; Elsevier: Amsterdam, The Netherlands, 1960. [Google Scholar] [CrossRef]
- Püskülcü, G.; Ulas, A. 3-D grain burnback analysis of solid propellant rocket motors: Part 1–ballistic motor tests. Aerosp. Sci. Technol. 2008, 12, 579–584. [Google Scholar] [CrossRef]
- Göçmez, A.; Erişken, C.; Yilmazer, Ü.; Pekel, F.; Özkar, S. Mechanical and Burning Properties of Highly Loaded Composite Propellants. J. Appl. Polym. Sci. 1998, 67, 1457–1464. [Google Scholar] [CrossRef]
- Forrester, A.; Sobester, A.; Keane, A. Engineering Design via Surrogate Modelling: A Practical Guide; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar] [CrossRef]
- Sheils, T.M. Tapered Grain Geometry and Statistical Learning for Solid Rocket Motor Simulation. Ph.D. Thesis, Auburn University, Auburn, AL, USA, 2023. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, 2015. Available online: https://www.tensorflow.org/ (accessed on 31 October 2025).
- Jekabsons, G.; Zhang, Y. Adaptive Basis Function Construction: An Approach for Adaptive Building of Sparse Polynomial Regression Models. Mach. Learn. 2010, 1, 127–155. [Google Scholar] [CrossRef]
- Demo, N.; Tezzele, M.; Rozza, G. EZyRB: Easy Reduced Basis method. J. Open Source Softw. 2018, 3, 661. [Google Scholar] [CrossRef]
- Brooks, W.T. Solid Propellant Grain Design and Internal Ballistics; NASA Special Publication NASA-SP-8076; National Aeronautics and Space Administration: Washington, DC, USA, 1972. [Google Scholar]
- Blank, J.; Deb, K. Pymoo: Multi-Objective Optimization in Python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]
- Federici, L.; Zavoli, A.; Colasurdo, G.; Mancini, L.; Neri, A. Integrated Optimization of First-Stage SRM and Ascent Trajectory of Multistage Launch Vehicles. J. Spacecr. Rocket. 2021, 58, 786–797. [Google Scholar] [CrossRef]
- Cavallini, E.; Favini, B.; Di Giacinto, M.; Serraglia, F. Analysis of VEGA Solid Stages Static Firing Tests Towards the Maiden Flight. In Proceedings of the 48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Atlanta, GA, USA, 30 July–1 August 2012; p. 4211, AIAA Paper 2012-4211. [Google Scholar] [CrossRef]






















| Parameters | Values and Limits | |
|---|---|---|
| Geometric | D1 | [3, 8] cm |
| L1 | [4, 8] cm | |
| L2 | [4, 8] cm | |
| D2 | [3, 8] cm | |
| L3 | [10, 20] cm | |
| L4 | [3, 5] cm | |
| L5 | [3, 8] cm | |
| Fin Height | [3, 5] cm | |
| Fin Radius | [0.2, 0.4] cm | |
| Fixed/Ballistic | Casing Radius | 11 cm |
| Throat Area | 6.75 cm2 | |
| Propellant Density | 1740 kg/m3 | |
| Ballistic | [] | |
| Ballistic b | [0.6, 3.1] |
| Parameters | Values and Limits | |
|---|---|---|
| Geometric | D1 | [3, 8] cm |
| L1 | 0.2 L cm | |
| L2 | 0.2 L cm | |
| D2 | [3, 8] cm | |
| L3 | 0.2 L cm | |
| L4 | 0.2 L cm | |
| L5 | 0.2 L cm | |
| Fin Height | [3, 5] cm | |
| Fin Radius | [0.2, 0.4] cm | |
| Fixed/Ballistic | Casing Radius | 11 cm |
| Throat Area | 6.75 cm2 | |
| Propellant Density | 1740 kg/m3 | |
| Grain Length, L | 30 cm | |
| Ballistic | [] | |
| Ballistic b | [0.6, 3.1] |
| Model | Free-Length RMSE | Fixed-Length RMSE |
|---|---|---|
| Neural Network | 0.0636 | 0.0399 |
| ABFC | 5.2181 | 2.2299 |
| POD-RBF | 3.8951 | 1.3095 |
| Booster | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Booster 1 | 96,980.62 | 16.84 | 6.75 | 1.26 | 0.01 | 0.22 | 0.3 | 0.49 | 90.0 | 101,325 |
| Booster 2 | 68,665.10 | 15.78 | 6.75 | 1.26 | 0.01 | 0.22 | 0.3 | 0.49 | 63.0 | 101,325 |
| Booster 3 | 64,094.46 | 15.79 | 6.75 | 1.26 | 0.01 | 0.22 | 0.3 | 0.49 | 63.0 | 101,325 |
| Booster 4 | 54,221.99 | 15.79 | 6.75 | 1.26 | 0.01 | 0.22 | 0.3 | 0.49 | 53.0 | 101,325 |
| Booster 5 | 41,192.75 | 15.79 | 6.75 | 1.26 | 0.01 | 0.22 | 0.3 | 0.49 | 42.4 | 101,325 |
| Booster 6 | 37,765.58 | 14.73 | 6.75 | 1.26 | 0.01 | 0.22 | 0.3 | 0.49 | 42.4 | 101,325 |
| Booster 7 | 67,205.49 | 17.89 | 6.75 | 1.26 | 0.01 | 0.22 | 0.3 | 0.49 | 50.0 | 101,325 |
| Booster 8 | 34,748.21 | 17.89 | 6.75 | 1.26 | 0.01 | 0.22 | 0.3 | 0.49 | 30.0 | 101,325 |
| Booster | Free-Length 3000-Sample Database | Fixed-Length 4096-Sample Database |
|---|---|---|
| Booster 1 | Performance: ; ; = 780,33.68* Ns | Performance: ; ; = 36,253.28* Ns |
| Booster 2 | Performance: ; ; = 67,779.71 | Performance: ; ; = 36,253.28* Ns |
| Booster 3 | Performance: ; ; = 61,572.43 | Performance: ; ; = 36,253.28* Ns |
| Booster 4 | Performance: ; ; = 53,510.23 | Performance: ; ; = 36,253.28* Ns |
| Booster 5 | Performance: ; ; = 41,453.50 | Performance: ; ; = 36,253.28* Ns |
| Booster 6 | Performance: ; ; = 37,416.69 | Performance: ; ; = 34,716.67 |
| Booster 7 | Performance: ; ; = 63,964.19 | Performance: ; ; = 36,253.28* Ns |
| Booster 8 | Performance: ; ; = 34,602.36 | Performance: ; ; = 31,676.27 |
| Parameters | Values and Limits | |
|---|---|---|
| Geometric () | (One for each k-th port) | [3, 10] |
| 0.5 | ||
| 0.5 | ||
| (One for all k ports) | [1, 3] | |
| 0.5 | ||
| 0.2 | ||
| 50 cm | ||
| m | ||
| Fixed/Ballistic | Casing Radius | 15 cm |
| Throat Area | [12, 28] cm2 | |
| Grain Length, L | 40 cm | |
| [] | ||
| [] | ||
| [] | ||
| [1, 2.5] cm | ||
| [3, 8] cm | ||
| [8.5, 10] cm | ||
| [2, 7.5] | ||
| [0.2, 0.58] | ||
| Booster | RBF-Harmonic (* Constraint Violation) | RBF-Fin (* Constraint Violation) |
|---|---|---|
| Booster 1 | Performance: ; ; = 67,658.30 | Performance: ; ; = 65,937.25 |
| Booster 2 | Performance: ; ; = 71,965.33* Ns | Performance: ; ; = 79,868.90* Ns |
| Booster 3 | Performance: ; ; = 65,965.10 | Performance: ; ; = 74,942.46 |
| Booster 4 | Performance: ; ; = 69,125.67* Ns | Performance: ; ; = 75,741.14* Ns |
| Booster 5 | Performance: ; ; = 66,680.28* Ns | Performance: ; ; = 75,514.79* Ns |
| Booster 6 | Performance: ; ; = 61,158.74* Ns | Performance: ; ; = 75,572.99* Ns |
| Booster 7 | Performance: ; ; = 87,374.70 | Performance: ; ; = 87,162.99 |
| Booster 8 | Performance: ; ; = 68,605.84 | Performance: ; ; = 76,901.13 |
| Booster | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Zefiro23 | 79,589.26 | 20.0 | 13.49 | 1.26 | 0.01 | 0.3 | 0.4 | 0.4 | 33.0 | 101,325 |
| Parameters | Values and Limits | |
|---|---|---|
| Geometric | ||
| Fixed/Ballistic | Casing Radius | 15 cm |
| Throat Area | [12, 28] cm2 | |
| Grain Length, L | 40 cm | |
| [] | ||
| [] | ||
| [] | ||
| 0 cm | ||
| [3, 8] cm | ||
| 15 cm | ||
| [2, 7.5] |
| Configuration | Optimum Vector and Performance for Zefiro23 |
|---|---|
| RBF-Harmonic | Performance: ; ; |
| RBF-Fin | Performance: ; ; |
| RBF-Cylinder | Performance: ; ; |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polizzi, G.; Ferrero, A.; Masseni, F.; Pastrone, D. Inverse Design of Additive Manufactured Rocket Propellant Grains with Non-Uniform Properties. Aerospace 2025, 12, 996. https://doi.org/10.3390/aerospace12110996
Polizzi G, Ferrero A, Masseni F, Pastrone D. Inverse Design of Additive Manufactured Rocket Propellant Grains with Non-Uniform Properties. Aerospace. 2025; 12(11):996. https://doi.org/10.3390/aerospace12110996
Chicago/Turabian StylePolizzi, Giovanni, Andrea Ferrero, Filippo Masseni, and Dario Pastrone. 2025. "Inverse Design of Additive Manufactured Rocket Propellant Grains with Non-Uniform Properties" Aerospace 12, no. 11: 996. https://doi.org/10.3390/aerospace12110996
APA StylePolizzi, G., Ferrero, A., Masseni, F., & Pastrone, D. (2025). Inverse Design of Additive Manufactured Rocket Propellant Grains with Non-Uniform Properties. Aerospace, 12(11), 996. https://doi.org/10.3390/aerospace12110996







