Trajectory Approximation of a Low-Performance E-Sail with Fixed Orientation

Abstract

The Electric Solar Wind Sail (E-sail) is a propellantless propulsion system that converts solar wind dynamic pressure into a deep-space thrust through a grid of long conducting tethers. The first flight test, needed to experience the true potential of the E-sail concept, is likely to be carried out using a single spinning cable deployed from a small satellite, such as a CubeSat. This specific configuration poses severe limitations to both the performance and the maneuverability of the spacecraft used to analyze the actual in situ thruster capabilities. In fact, the direction of the spin axis in a single-tether configuration can be considered fixed in an inertial reference frame, so that the classic sail pitch angle is no longer a control variable during the interplanetary flight. This paper aims to determine the polar form of the propelled trajectory and the characteristics of the osculating orbit of a spacecraft propelled by a low-performance spinning E-sail with an inertially fixed axis of rotation. Assuming that the spacecraft starts the trajectory from a parking orbit that coincides with the Earth’s heliocentric orbit and that its spin axis belongs to the plane of the ecliptic, a procedure is illustrated to solve the problem accurately with a set of simple analytical relations.

1. Introduction

Twenty years after the first publication regarding the Electric Solar Wind Sail (E-sail) concept [1,2], the attention of the scientific community is currently focused on the possibility of flight testing [3] this advanced propellantless propulsion system, which is known to use the charged particles in solar wind to generate thrust through a grid of long, thin, and electrically conducting tethers [4,5,6]. During the development of this propulsion concept, different geometric arrangements of the conducting cable assembly were proposed, to achieve a deployable, lightweight, and maneuverable space structure, capable of intercepting and reflecting the charged particles that populate the solar wind stream.

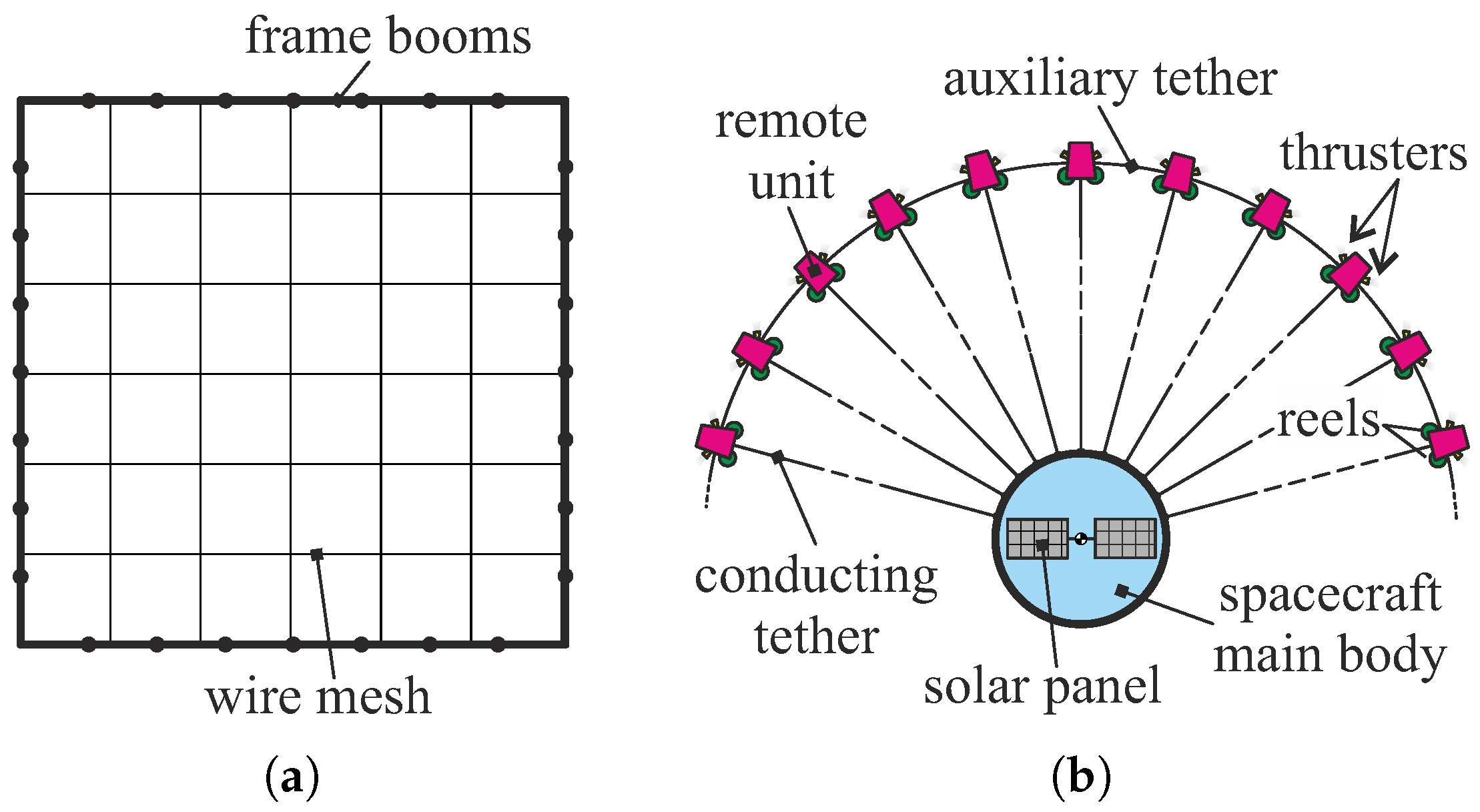
Over the years, the geometric shape of the E-sail has evolved from the grid structure sketched in Figure 1a, originally proposed by inventor Pekka Janhunen in the early 2000s [1], to a more refined and more complex spinning configuration consisting of a series of long conducting tethers that are deployed from the main body of the spacecraft [3]. The latter configuration is shown in Figure 1b, which also illustrates the main elements of the E-sail-based spacecraft, such as, for example, the auxiliary tether, with the function of keeping the conducting tethers separated from each other, the remote unit that contains the thrusters used to control the spin rate and maneuver the sail nominal plane, and the solar panels that provide the electric power needed to operate the electron gun, which maintains the high electric potential (usually positive) of the tethers. The generic conducting tether is stretched by the centrifugal force obtained through the rotation of the entire spacecraft about the spin axis perpendicular to the nominal plane of the sail at an appropriate angular velocity. A detailed analysis of the propulsive characteristics of the E-sail and a thorough discussion of the history of the development of this propulsion system can be found in the review paper by Bassetto et al. [7], while a recent special issue of Aerospace [8] brings together a set of papers outlining the latest advances in technology related to E-sail and plasma brake [9,10,11] concepts. In this regard, for example, refs. [12,13,14] analyze a number of rather exotic mission scenarios that can be achieved using a high-performance E-sail, in which the spacecraft moves around a displaced non-Keplerian orbit [12], maintains a stationary position relative to the Sun [13], or achieves an inversion of the direction of the angular momentum vector with a two-dimensional heliocentric trajectory [14]. The performance of an E-sail propulsion system has also been studied in a more conventional heliocentric scenario, such as transfer between Keplerian orbits [15,16] and phasing maneuvers along a circular orbit on the ecliptic plane [17].

In an initial in-orbit experiment to test the thruster capabilities, the technological challenges associated with building, assembling, and deploying such a large structure in orbit prompted the designers to consider a simplified E-sail model consisting of a single tether placed in rotation around an axis with a fixed direction relative to an inertial reference frame [18,19]. The single tether is supposed to be mounted on a small satellite, possibly a CubeSat [20]. This particular and rather simple E-sail configuration was adopted in the designs of the Estonian ESTCube-1 (1U CubeSat) student satellite [21,22,23,24] and of the Finnish Aalto-1 (3U CubeSat) student satellite [25,26,27], which attempted in 2013 and 2017, respectively, to obtain the first in situ test of E-sail-related technology (more specifically, the plasma brake) through the deployment of a single conducting tether in a low-Earth orbit; see Figure 2.

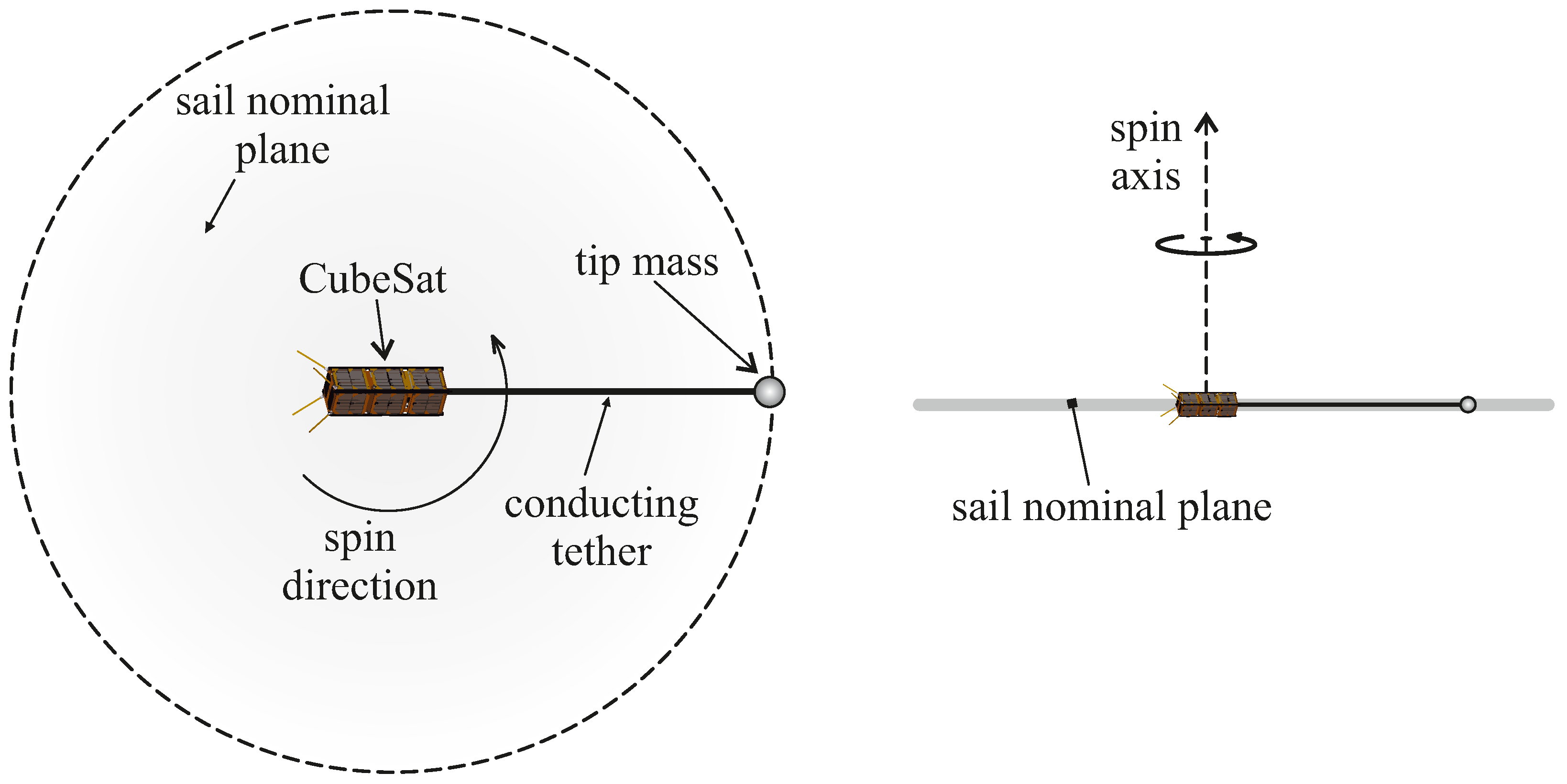
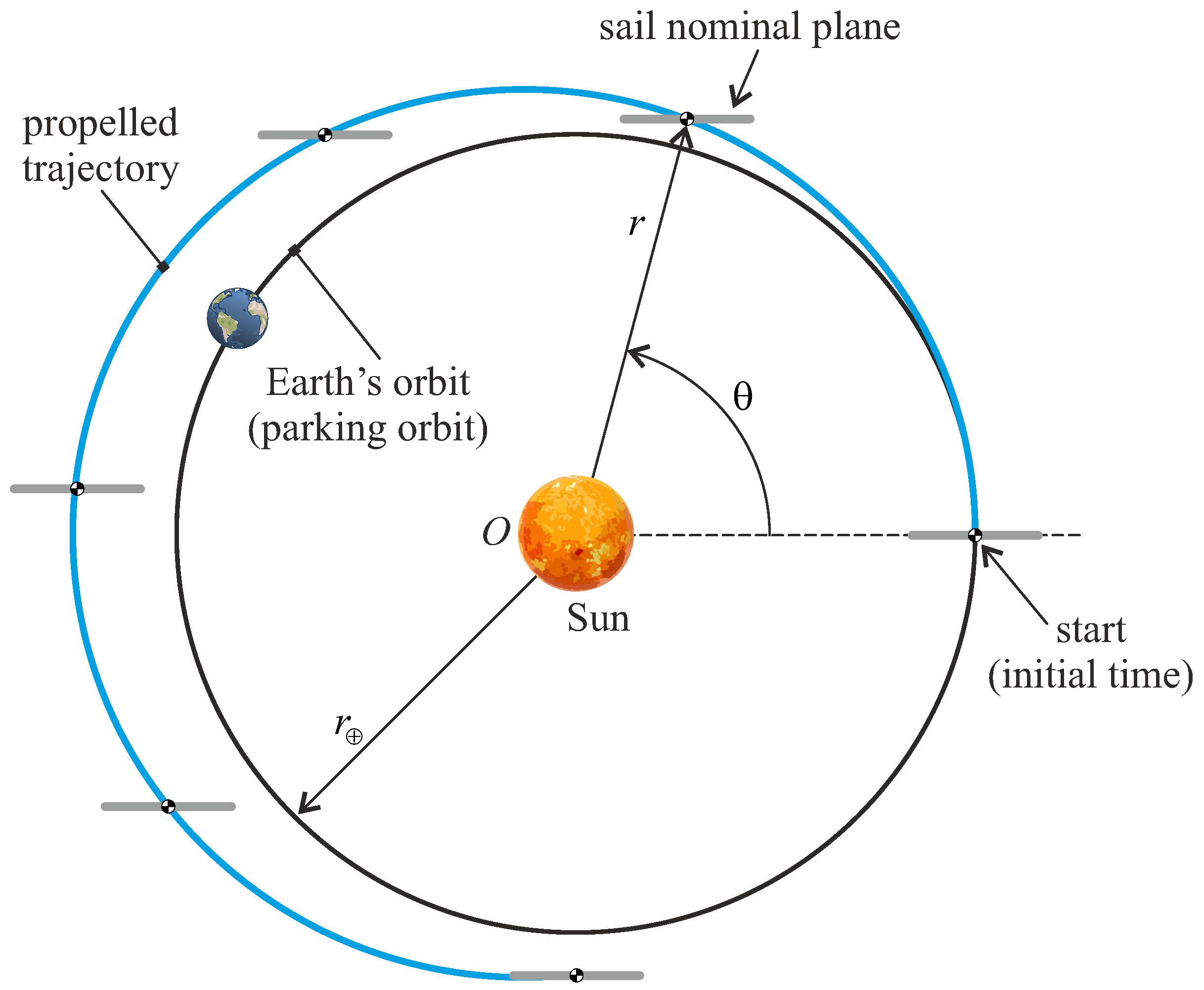
Unfortunately, in both missions, the tether deployment did not take place for technical reasons, so a true in situ test of the E-sail concept (or related plasma brake technology) is currently still lacking. In general, the use of a single conducting tether, the length of which is obviously constrained by the small payload capacity of a CubeSat, places severe limitations on both the thrust performance and maneuverability of the spacecraft used to analyze the propulsive capabilities of the E-sail. The conceptual configuration scheme is shown in Figure 3, where the tether is stretched by the centrifugal force obtained by spinning the small spacecraft around an axis perpendicular to the nominal direction of the tether, at the end of which is a tip mass to increase the inertia of the system.

However, it is very difficult, if not impossible, to equip the CubeSat with a remote unit to house the thrusters necessary to vary the direction of the spin axis (and thus the orientation of the nominal sail plane) following a desired control strategy. In practice, the direction of the spin axis can therefore be considered fixed in an inertial reference frame, and the only control variable is the binary state of the electron gun (either on or off), which indicates the on/off condition of the propulsion system, as discussed in Bassetto et al. [19]. In this regard, the authors’ recent paper [28] analyzes in detail the optimal heliocentric (i.e., minimum time) transfer of a single-tether E-sail taking into account the control term related to the state of the electron gun.

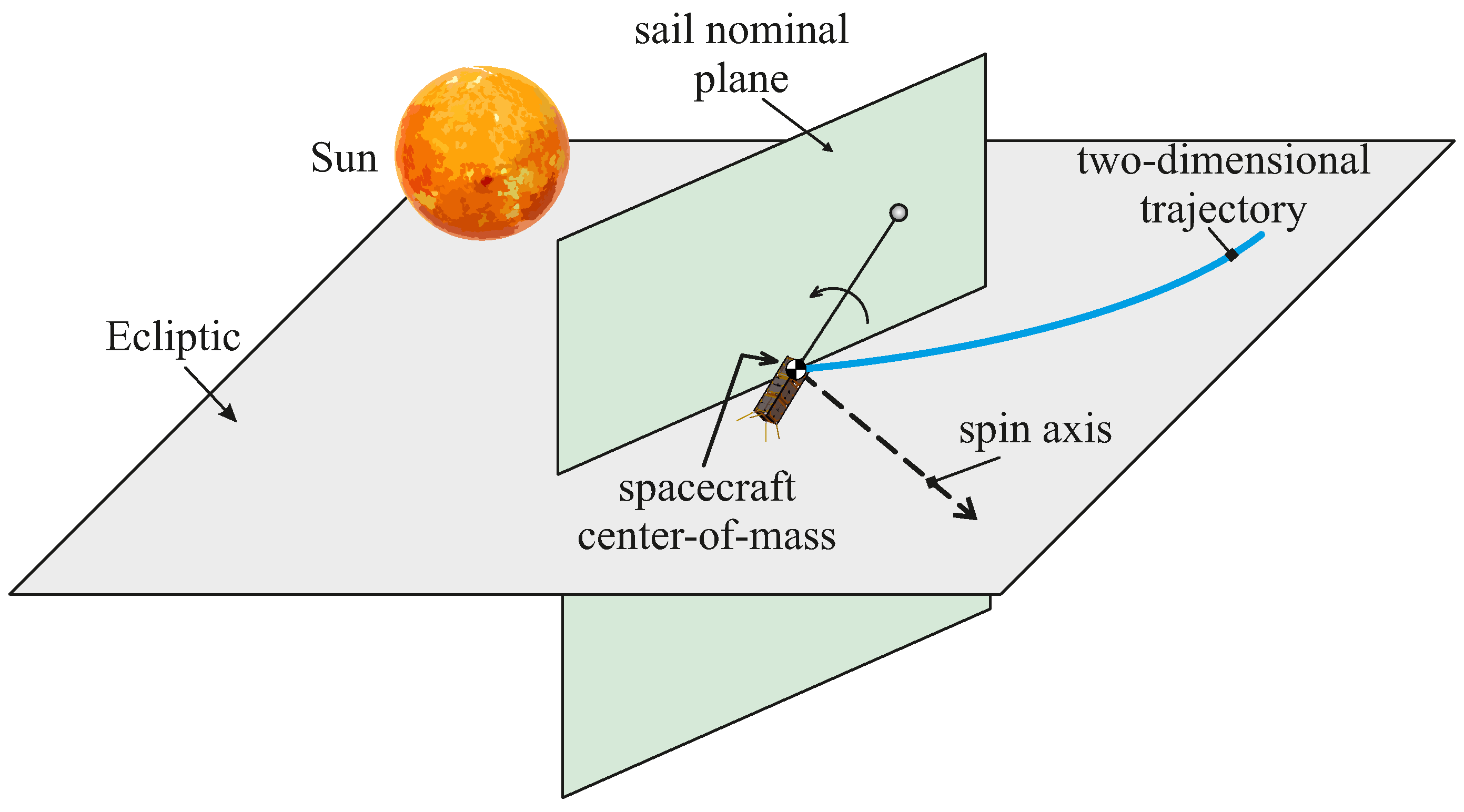
An E-sail with a single tether is clearly capable of providing a propulsive acceleration of small magnitude that, because of the reduced vehicle maneuverability due to the fixed direction of the spacecraft spin axis, can allow the satellite to travel along propelled trajectories placed close to the initial parking orbit. Within the framework of these assumptions, this paper describes an analytical procedure to determine, accurately and with simple relationships, the polar form of the propelled trajectory and the characteristics of the osculating orbit in a heliocentric scenario in which the spacecraft starts from a parking orbit coincident with that of the Earth. The latter is approximated, as usual in a preliminary design, by a circular trajectory of radius equal to one astronomical unit, which belongs to the ecliptic. It is also assumed that the spacecraft spin axis also belongs to the plane of the ecliptic, which is therefore always perpendicular to the sail nominal plane, as shown in Figure 4. The spacecraft dynamics analysis is performed by assuming that the E-sail is always on during flight, so that the spacecraft trajectory does not contain coasting arcs during transfer. The latter assumption greatly simplifies the design of the trajectory, since the orbit of the spacecraft depends only on the orientation of the sail nominal plane relative to the Sun–spacecraft line at the beginning of the transfer. The proposed methodology is also particularly effective for low-to-medium flight times and allows for the rapid study of some interesting mission scenarios, such as, for example, phasing maneuvers along the parking orbit, without the need for numerical simulations.

This paper is organized as follows. With the help of an appropriate approximation of spacecraft dynamics, the next section describes the procedure used to determine the set of analytical relations describing the spacecraft trajectory, while in Section 3, the approximate equations are used to analyze the flight of a low-performance, single-tether E-sail in some typical mission scenarios. Finally, the last section summarizes the main results of this work.

2. Spacecraft Dynamics and Approximations

As mentioned earlier, in this paper, we consider an E-sail-based spacecraft whose distance from the Sun is, during the entire propelled flight, approximately equal to one astronomical unit. This is the case of a low-performance E-sail that leaves the Earth’s sphere of influence with zero hyperbolic excess velocity relative to the planet, which is assumed to trace a circular heliocentric orbit on the ecliptic. The orbital period of the spacecraft osculating orbit is of the order of one year (which corresponds to the value of the orbital period of the starting planet). This period is several orders of magnitude longer than the period of rotation of the spacecraft around its spin axis, which is on the order of a few tens of minutes, as discussed by Janhunen et al. [29,30].

Taking into account that the total mass of the spacecraft is a constant of motion, in agreement with Bassetto et al. [19], the propulsive acceleration vector $\mathit{a}$ induced by the rotating E-sail can be determined by evaluating the average value of the thrust vector during an entire period of rotation of the spacecraft about its spin axis. Recalling that the E-sail is always switched on during the flight, the expression of $\mathit{a}$ is given by Equation (16) of ref. [19], which coincides with the result obtained from a geometric approach by Huo et al. [31], viz.

$$\mathit{a}=\frac{a_c}{2}\left(\frac{r_{\oplus }}{r}\right)\left[\widehat{\mathit{r}}+\left(\widehat{\mathit{r}}·\widehat{\mathit{n}}\right)\widehat{\mathit{n}}\right]$$

(1)

where r is the Sun–spacecraft distance, $r_{\oplus }\triangleq 1\mathrm{AU}$ is a reference distance, $\widehat{\mathit{r}}$ is the Sun–spacecraft (radial) unit vector, and $\widehat{\mathit{n}}$ is the unit vector normal to the sail nominal plane in direction opposite to the Sun. Note that $\widehat{\mathit{n}}$ is collinear to the unit vector $\widehat{\mathit{k}}$ of the spacecraft spin axis, but the two unit vectors are parallel or antiparallel depending on the spacecraft position along the trajectory. More precisely, $\widehat{\mathit{n}}·\widehat{\mathit{k}}=1$ and so $\widehat{\mathit{n}}\equiv \widehat{\mathit{k}}$ when $\widehat{\mathit{r}}·\widehat{\mathit{k}}\ge 0$, while $\widehat{\mathit{n}}·\widehat{\mathit{k}}=-1$ and so $\widehat{\mathit{n}}\equiv -\widehat{\mathit{k}}$ when $\widehat{\mathit{r}}·\widehat{\mathit{k}}<0$. In Equation (1), $a_c$ represents the characteristic acceleration, defined as the maximum value of the propulsive acceleration when the solar distance is equal to $r_{\oplus }$. The characteristic acceleration is the typical performance parameter of a spacecraft equipped with a propellantless propulsion system such as the E-sail. It depends both on the design characteristics of the E-sail (such as, for example, the number and length of the conducting tethers, the electrical voltage, etc.), and on the total mass of the spacecraft (the value of which is itself a function of the characteristics of the E-sail). A detailed mathematical model useful to estimate the characteristic acceleration is discussed in ref. [32]. In the case of a low-performance propulsion system, $a_c$ is small when compared to the Sun’s gravitational acceleration at one astronomical unit of distance. In other words, in the rest of this paper, we assume that

$$\frac{a_c}{{\mu }_{\odot }/r_{\oplus }^2}\ll 1$$

(2)

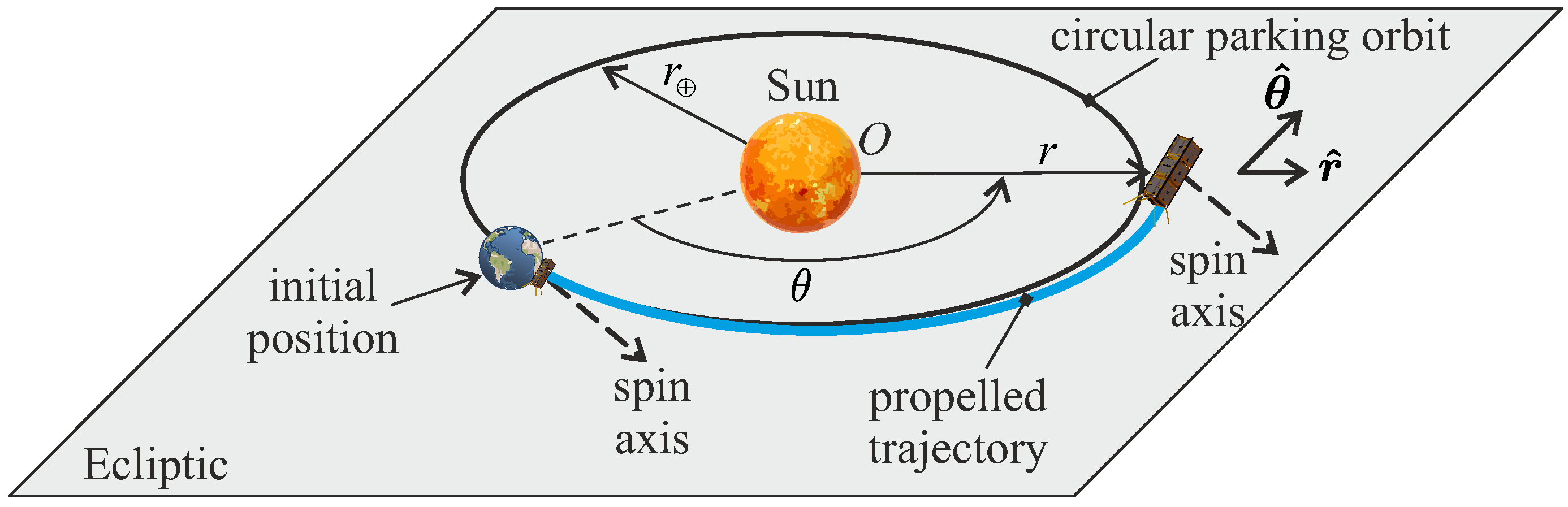
The propulsive acceleration vector in Equation (1) can be conveniently rewritten as the sum of two components in a polar reference frame $\mathcal{T}(O;r,\theta )$ with unit vectors $\widehat{\mathit{r}}$ and $\widehat{\mathit{\theta }}$, where O is the Sun’s center of mass, $\theta$ is the polar angle measured counterclockwise from the Sun–spacecraft line at the beginning of the flight (i.e., at time $t=t_0$), while $\widehat{\mathit{\theta }}$ indicates the transverse unit vector in the direction of the spacecraft inertial velocity. The polar reference frame is illustrated in Figure 5, which also shows that the direction of the spacecraft spin axis remains fixed during flight.

Introducing the sail pitch angle $\alpha \in [-90,90]\mathrm{deg}$ defined as the angle between the Sun–spacecraft line and the unit vector $\widehat{\mathit{n}}$, and using the approach described in ref. [19], the propulsive acceleration in Equation (1) can be rewritten as

$$\mathit{a}=\frac{a_c}{2}\left(\frac{r_{\oplus }}{r}\right)\left[\left(1+{cos}^2\left({\alpha }_0-\theta \right)\right)\widehat{\mathit{r}}+cos\left({\alpha }_0-\theta \right)sin\left({\alpha }_0-\theta \right)\widehat{\mathit{\theta }}\right]$$

(3)

where ${\alpha }_0\triangleq \alpha \left(t_0\right)\in [-90,90]\mathrm{deg}$ is the sail pitch angle at the initial time $t_0$. Note that ${\alpha }_0$ is a constant of motion and can be considered as a design parameter in the preliminary trajectory analysis. In particular, the value of ${\alpha }_0$ depends on the strategy used to deploy the E-sail at the beginning of the transfer [33,34,35]. Taking into account the expression of $\mathit{a}$ from Equation (3), the spacecraft dynamics is described in the polar reference frame $\mathcal{T}$ by the differential equations

$$\begin{array}{cc}\hfill \frac{\mathrm{d}r}{\mathrm{d}t}& =v_r\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}\theta }{\mathrm{d}t}& =\frac{h}{r^2}\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{v}_r}{\mathrm{d}t}& =-\frac{{\mu }_{\odot }}{r^2}+\frac{h^2}{r^3}+\frac{a_c}{2}\left(\frac{r_{\oplus }}{r}\right)\left[1+{cos}^2\left({\alpha }_0-\theta \right)\right]\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}h}{\mathrm{d}t}& =r\mathit{a}·\widehat{\mathit{\theta }}\equiv \frac{a_c{r}_{\oplus }}{2}cos\left({\alpha }_0-\theta \right)sin\left({\alpha }_0-\theta \right)\hfill \end{array}$$

(7)

where $v_r$ is the radial component of the spacecraft inertial velocity, h is the magnitude of the specific angular momentum vector, and ${\mu }_{\odot }$ is the Sun’s gravitational parameter. The equations of motion (4)–(7) are completed by the initial conditions that model the spacecraft on a circular orbit of radius $r_{\oplus }$, that is,

$$r\left(t_0\right)=r_{\oplus },\theta \left(t_0\right)=0,v_r\left(t_0\right)=0,h\left(t_0\right)=\sqrt{{\mu }_{\odot }{r}_{\oplus }}$$

(8)

Combining Equations (5) and (7), we obtain the differential equation that describes the $\theta$-variation of h, viz.

$$\frac{\mathrm{d}h}{\mathrm{d}\theta }=\frac{a_c{r}_{\oplus }{r}^2}{2h}cos\left({\alpha }_0-\theta \right)sin\left({\alpha }_0-\theta \right)$$

(9)

which can be rewritten in dimensionless form as

$$\frac{\mathrm{d}{\tilde{h}}^2}{\mathrm{d}\theta }={\tilde{a}}_c{\left(\frac{r}{r_{\oplus }}\right)}^{2}cos\left({\alpha }_0-\theta \right)sin\left({\alpha }_0-\theta \right)$$

(10)

where $\tilde{h}\triangleq h/\sqrt{{\mu }_{\odot }{r}_{\oplus }}$, and ${\tilde{a}}_c\triangleq a_c/({\mu }_{\odot }/r_{\oplus }^2)$. Note that $\sqrt{{\mu }_{\odot }{r}_{\oplus }}$ coincides with the value of h along the initial circular orbit of radius $r_{\oplus }$, while ${\tilde{a}}_c\ll 1$ according to the assumption of Equation (2). Equation (10) is the basis for the analytical procedure described in the next section, which allows us to obtain the approximate expression of the propelled trajectory (and the parameters of the osculating orbit) as a function of the E-sail propulsive characteristics.

2.1. Approximation of the Propelled Trajectory

During the heliocentric flight, due to the small value of the dimensionless characteristic acceleration ${\tilde{a}}_c$, the E-sail-based spacecraft remains close to the circular parking orbit, so that the approximation ${\left(r/r_{\oplus }\right)}^2\simeq 1$ can be used. Accordingly, the right-hand side of Equation (10) reduces to ${\tilde{a}}_{c}cos\left({\alpha }_0-\theta \right)sin\left({\alpha }_0-\theta \right)$, and the differential Equation (10) can be analytically solved using standard methods, with initial condition $\tilde{h}=1$ when $\theta =0$. The result is given by the following expression of ${\tilde{h}}^2$ as a function of the polar angle:

$${\tilde{h}}^2\simeq 1+\frac{{\tilde{a}}_c}{2}\left[{sin}^2{\alpha }_0-{sin}^2\left(\theta -{\alpha }_0\right)\right]$$

(11)

which is a simple relationship that allows the $\theta$-variation of the angular momentum h to be analytically estimated as

$$h\simeq \sqrt{{\mu }_{\odot }{r}_{\oplus }}\sqrt{1+\frac{{\tilde{a}}_c}{2}\left[{sin}^2{\alpha }_0-{sin}^2\left(\theta -{\alpha }_0\right)\right]}$$

(12)

Note that the latter equation is consistent with the results of ref. [19]. Moreover, Equation (12) can be further simplified using a first-order Taylor series expansion. In fact, recalling that ${\tilde{a}}_c\ll 1$, Equation (12) reduces to

$$h\simeq \sqrt{{\mu }_{\odot }{r}_{\oplus }}\left\{1+\frac{{\tilde{a}}_c}{4}\left[{sin}^2{\alpha }_0-{sin}^2\left(\theta -{\alpha }_0\right)\right]\right\}$$

(13)

which will be used later in this section to obtain an analytical approximation of the two components of the spacecraft velocity in the polar reference frame $\mathcal{T}$.

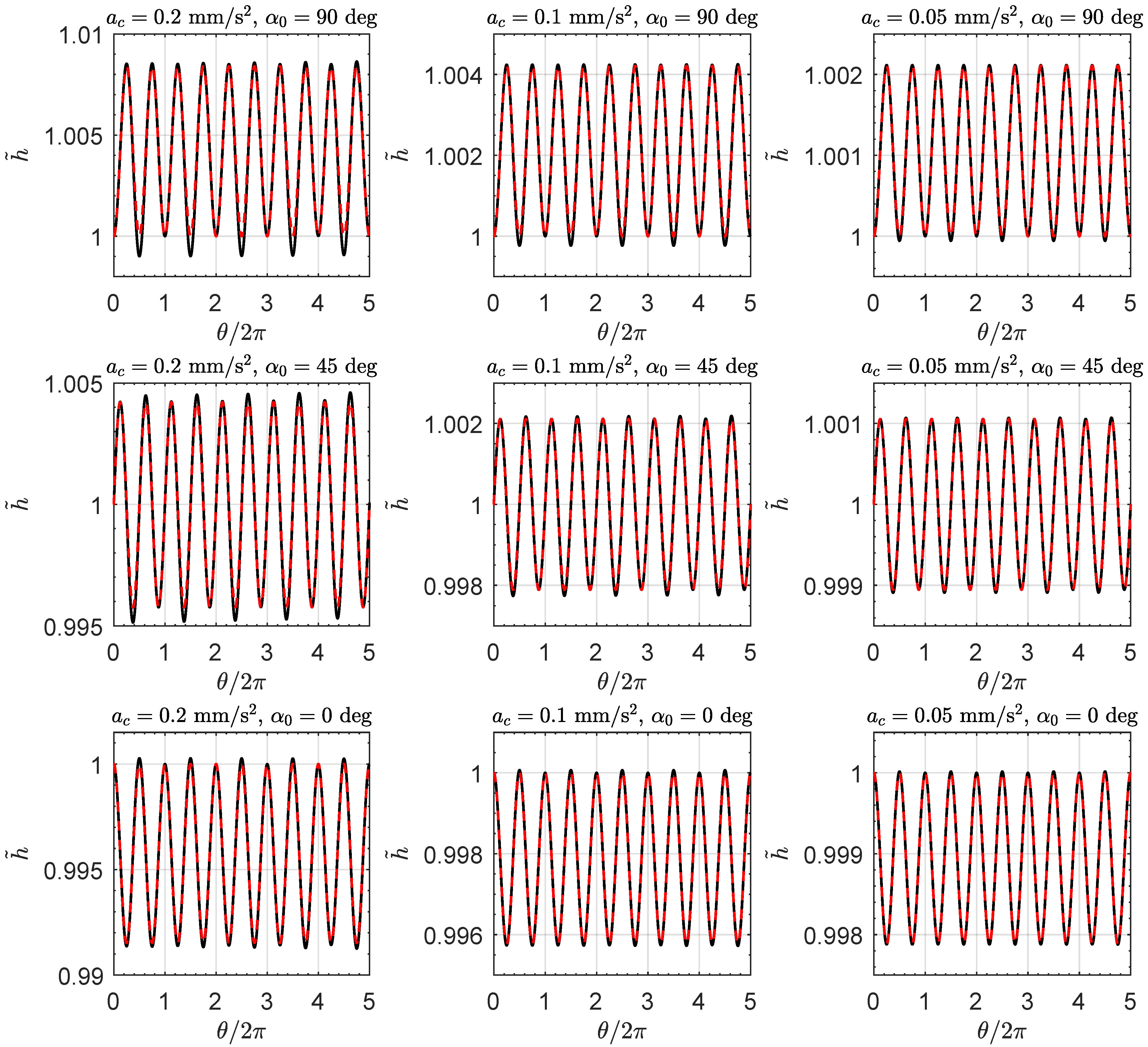
The function $\tilde{h}=\tilde{h}\left(\theta \right)$ obtained from Equation (13) is shown in Figure 6 (red dashed line) when $a_c\in \{0.2,0.1,0.05\}\mathrm{mm}/{\mathrm{s}}^2$ and ${\alpha }_0\in \{90,45,0\}\mathrm{deg}$. Note that the value of $a_c$ used in Figure 6 is consistent with the (even lower, actually) performance of a single-tether E-sail-based CubeSat [20], while the graphs relating to cases where ${\alpha }_0<0$ have been omitted here for the sake of conciseness. Figure 6 also shows in the black solid line the $\theta$-variation of $\tilde{h}$ obtained by numerical integration of the spacecraft equations of motion (4)–(7), using a procedure based on the Adams–Bashforth–Moulton PECE solver [36,37], with a relative and absolute tolerance of ${10}^{-12}$.

It is clear that the red dashed line is substantially superimposed on the black solid line. This interesting result indicates that the analytical approximation given by Equation (12) accurately describes the actual variation of the specific angular momentum with the polar angle, at least when the spacecraft makes fewer than five revolutions around the Sun, i.e., when $\theta \le 10\pi \mathrm{rad}$.

The approximate polar form expression of the propelled trajectory, on the other hand, was obtained by first evaluating the effective shape of the function $r=r\left(\theta \right)$ through numerical simulations for a set of values of the dimensionless pair $\{{\tilde{a}}_c,{\alpha }_0\}$ with $a_c\le 0.2\mathrm{mm}/{\mathrm{s}}^2$, and then using a curve-fitting procedure [37]. Using a set of about 50 pairs $\{{\tilde{a}}_c,{\alpha }_0\}$ and assuming $\theta \in [0,10\pi ]\mathrm{rad}$, the curve fitting procedure gives the following approximate polar form expression of the propelled trajectory:

$$\frac{r}{r_{\oplus }}\simeq 1+\frac{{\tilde{a}}_c\left(1+1.4{sin}^2{\alpha }_0\right)}{2}\left(1-cos\theta \right)$$

(14)

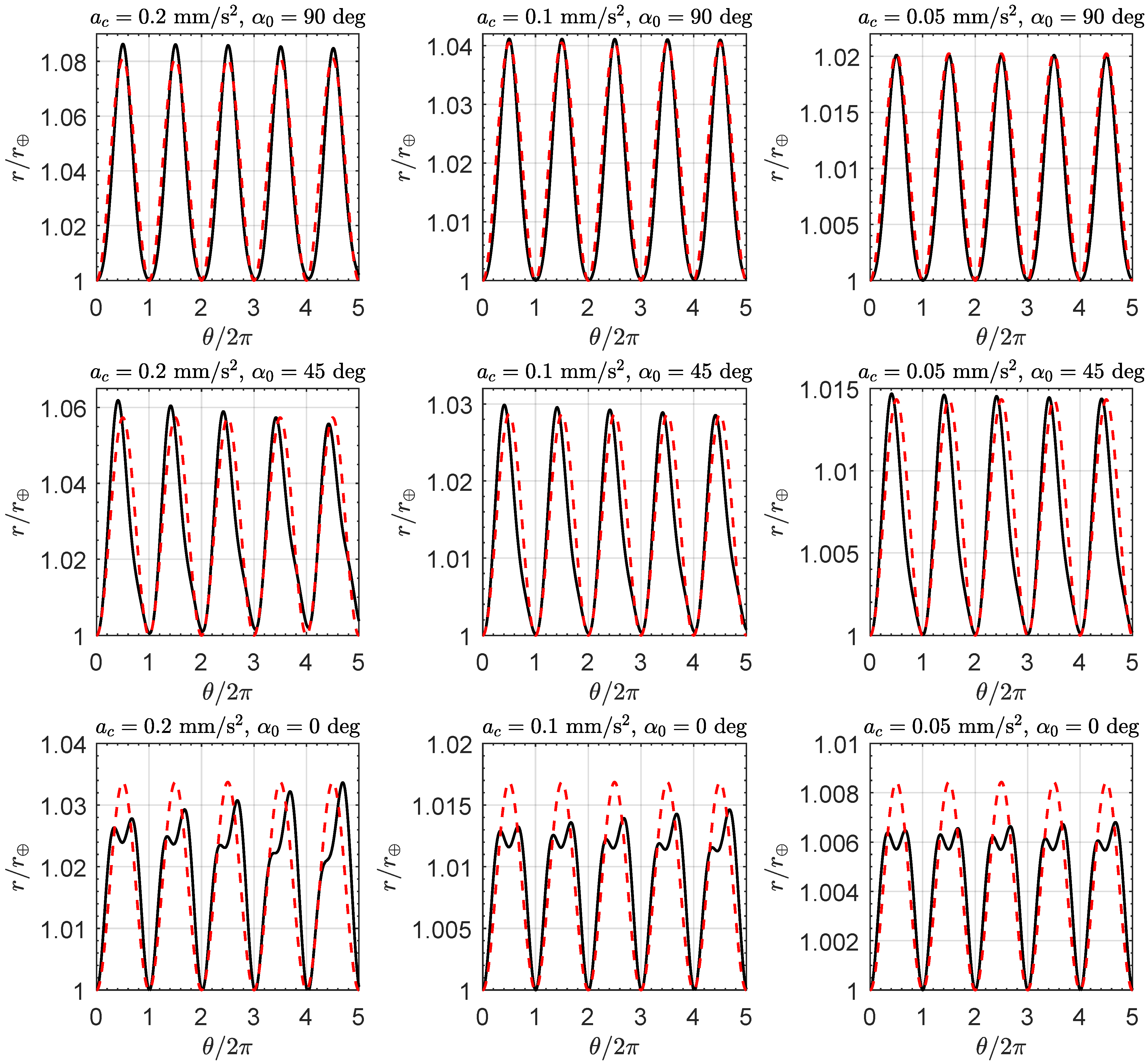
The accuracy of the previous equation was tested using the results obtained with an orbit simulator, and the results are summarized in Figure 7 for nine different pairs of $a_c$ and ${\alpha }_0$. The graphs in Figure 7 clearly indicate that, when $\theta \le 10\pi \mathrm{rad}$, the polar trajectory (14) approximates very well the actual variation of r with $\theta$ when the initial pitch angle $|{\alpha }_0|$ is sufficiently close to $90\mathrm{deg}$, that is, when the E-sail is deployed in a nearly edgewise configuration with respect to the Sun. Note that the polar angle of $10\pi \mathrm{rad}$ is reached with a flight time of about $5\mathrm{years}$, because the spacecraft (when the characteristic acceleration is sufficiently small) completes a revolution around the Sun in roughly $1\mathrm{year}$.

On the other hand, when the value of ${\alpha }_0$ approaches $0\mathrm{deg}$, that is, when the E-sail is deployed in a Sun-facing attitude, the approximate expression (14) is still able to capture the oscillatory behavior of the actual function $r=r\left(\theta \right)$, but the aphelion distance estimated with Equation (14) is slightly higher than the value returned by the orbit simulator. Nevertheless, the position of the perihelion is still accurately described by the analytical expression.

The combined use of Equations (13) and (14) makes it easy to calculate, in the analytical form, the approximate expressions of the radial ($v_r$) and transverse ($v_{\theta }$) components of the spacecraft inertial velocity vector. In fact, bearing in mind that $h=r{v}_{\theta }$, the $\theta$-variation of $v_{\theta }$ is

$$\frac{v_{\theta }}{\sqrt{{\mu }_{\odot }/r_{\oplus }}}=\frac{h}{r}\simeq {\displaystyle \frac{1+{\displaystyle \frac{{\tilde{a}}_c}{4}}\left[{sin}^2{\alpha }_0-{sin}^2\left(\theta -{\alpha }_0\right)\right]}{1+{\displaystyle \frac{{\tilde{a}}_c\left(1+1.4{sin}^2{\alpha }_0\right)}{2}}\left(1-cos\theta \right)}}$$

(15)

Finally, recalling Equation (5), the radial component of the spacecraft velocity $v_r$ can be written as

$$v_r=\frac{\mathrm{d}r}{\mathrm{d}\theta }\frac{\mathrm{d}\theta }{\mathrm{d}t}\equiv \frac{\mathrm{d}r}{\mathrm{d}\theta }\frac{h}{r^2}$$

(16)

which gives the approximate expression

$$\frac{v_r}{\sqrt{{\mu }_{\odot }/r_{\oplus }}}\simeq {\displaystyle \frac{{\tilde{a}}_c\left(1+1.4{sin}^2{\alpha }_0\right)sin\theta }{2}}{\displaystyle \frac{1+{\displaystyle \frac{{\tilde{a}}_c}{4}}\left[{sin}^2{\alpha }_0-{sin}^2\left(\theta -{\alpha }_0\right)\right]}{{\left[1+{\displaystyle \frac{{\tilde{a}}_c\left(1+1.4{sin}^2{\alpha }_0\right)}{2}}\left(1-cos\theta \right)\right]}^2}}$$

(17)

The accuracy of Equations (15) and (17) was tested through numerical simulations. In this regard, observations similar to those already expressed in the case of the function $r=r\left(\theta \right)$ apply, i.e., the approximate expressions of $v_{\theta }$ and $v_r$ are more accurate when the initial pitch angle is nearly $90\mathrm{deg}$. In this case, the figures showing the comparison between the approximate equations and the numerical results are omitted for the sake of brevity.

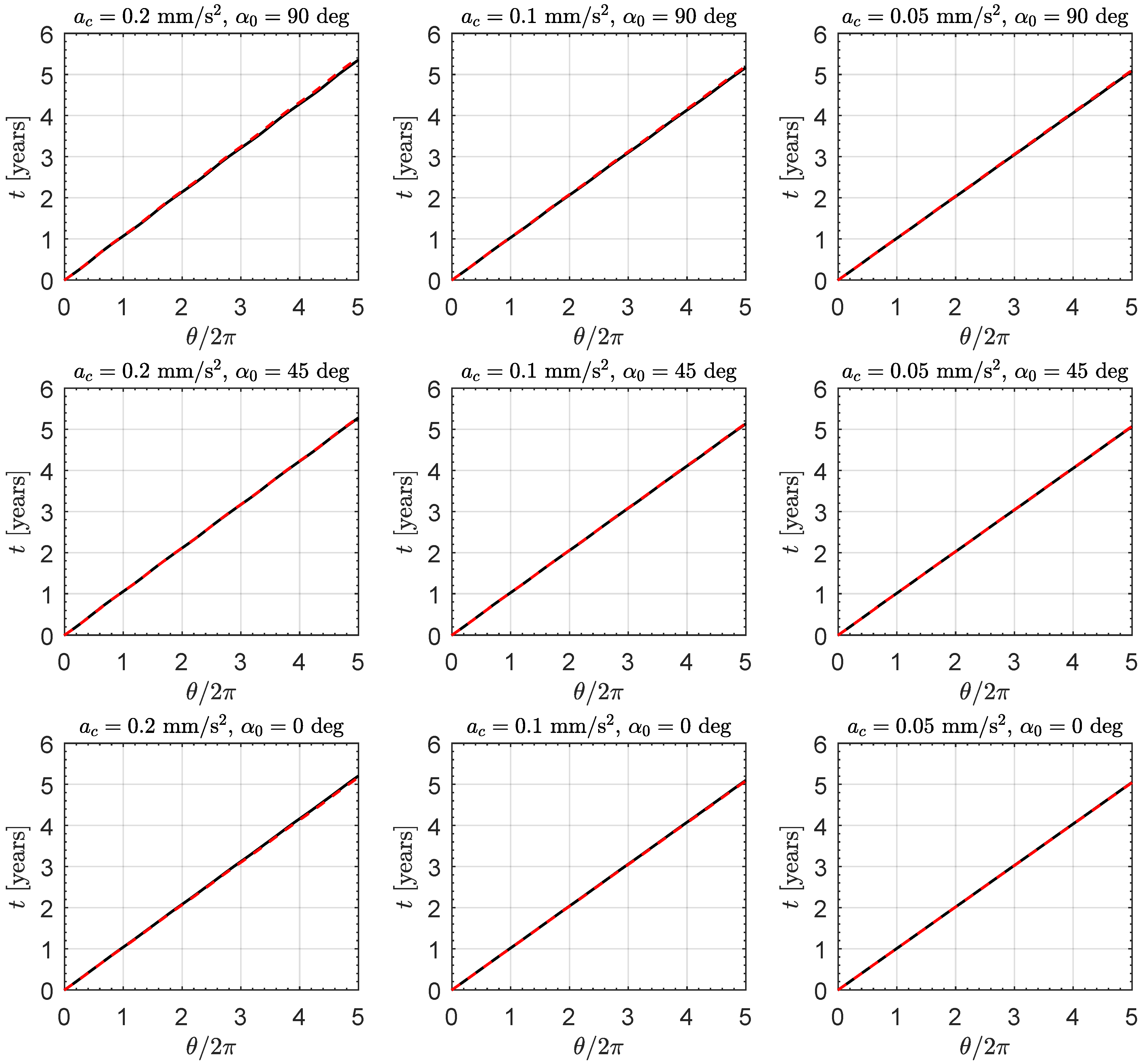
2.2. Approximate Expression of the Flight Time

An approximate expression of the spacecraft flight time t, as a function of the polar angle $\theta$ along the propelled trajectory, can be obtained using Equations (5) and (14). In fact, according to Figure 6, observe that $\tilde{h}\simeq 1$ for $\theta \le 10\pi \mathrm{rad}$ and $a_c\le 0.2\mathrm{mm}/{\mathrm{s}}^2$, so that the angular momentum magnitude during the propelled flight can be approximated by $h\simeq \sqrt{{\mu }_{\odot }{r}_{\oplus }}$. As a result, Equations (5) and (14) give

$$\mathrm{d}t\simeq \sqrt{\frac{r_{\oplus }^3}{{\mu }_{\odot }}}{\left[1+\frac{{\tilde{a}}_c\left(1+1.4{sin}^2{\alpha }_0\right)}{2}\left(1-cos\theta \right)\right]}^2\mathrm{d}\theta$$

(18)

which can be further simplified with a Taylor series expansion (recall that ${\tilde{a}}_c\ll 1$) as

$$\mathrm{d}t\simeq \sqrt{\frac{r_{\oplus }^3}{{\mu }_{\odot }}}\left[1+{\tilde{a}}_c\left(1+1.4{sin}^2{\alpha }_0\right)\left(1-cos\theta \right)\right]\mathrm{d}\theta$$

(19)

The latter can be easily integrated to derive the analytical approximation of the function $t=t\left(\theta \right)$, viz.

$${\displaystyle \frac{t}{\sqrt{r_{\oplus }^3/{\mu }_{\odot }}}}\simeq \theta +{\tilde{a}}_c\left(1+1.4{sin}^2{\alpha }_0\right)\left(\theta -sin\theta \right)$$

(20)

The accuracy of the above equation is confirmed by the graphs in Figure 8, where it can be observed that the results of numerical simulations are substantially superimposable on the curve obtained using the approximation given by Equation (20).

The set of analytical Equations (13), (14), (15), (17), and (20) are used in the next section to obtain a rapid estimate of the characteristics of the transfer trajectory in some exemplary mission scenarios.

3. Mission Applications

A possible application of the analytical model discussed in the previous section is now illustrated by considering the case in which the initial E-sail nominal plane contains the direction to the Sun. In other term, ${\alpha }_0=90\mathrm{deg}$ is considered in the approximate analytical model to further simplify the polar form expressions of the propelled trajectory and the osculating orbit characteristics. Recall that this particular initial condition allows for a more accurate approximation of the equation $r=r\left(\theta \right)$ and the two components of the spacecraft inertial velocity. Of course, the application discussed in this section can be generalized to a generic value (positive or negative) of ${\alpha }_0$.

The situation considered in this section is sketched in Figure 9, which explicitly states that, during the propelled flight, the sail nominal plane remains parallel to its initial (i.e., at the time of deployment) orientation.

From the viewpoint of the approximate mathematical model, when the condition ${\alpha }_0=90\mathrm{deg}$ is substituted into Equations (13), (14), (15), and (17), the expressions of h, r, $v_r$, and $v_{\theta }$ become

$$\begin{array}{cc}\hfill h& \simeq 0.25\sqrt{{\mu }_{\odot }{r}_{\oplus }}\left[4+{\tilde{a}}_c{sin}^2\theta \right]\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill r& \simeq r_{\oplus }\left[1+1.2{\tilde{a}}_c\left(1-cos\theta \right)\right]\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill v_{\theta }& \simeq 1.25\sqrt{\frac{{\mu }_{\odot }}{r_{\oplus }}}\frac{4+{\tilde{a}}_c{sin}^2\theta }{5+6{\tilde{a}}_c\left(1-cos\theta \right)}\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill v_r& \simeq 7.5\sqrt{\frac{{\mu }_{\odot }}{r_{\oplus }}}{\tilde{a}}_{c}sin\theta \frac{4+{\tilde{a}}_c{sin}^2\theta }{{\left[5+6{\tilde{a}}_c\left(1-cos\theta \right)\right]}^2}\hfill \end{array}$$

(24)

while the approximate relation for the time of flight in Equation (20) is simplified as

$$t\simeq \sqrt{\frac{r_{\oplus }^3}{{\mu }_{\odot }}}\left[\theta +2.4{\tilde{a}}_c\left(\theta -sin\theta \right)\right]$$

(25)

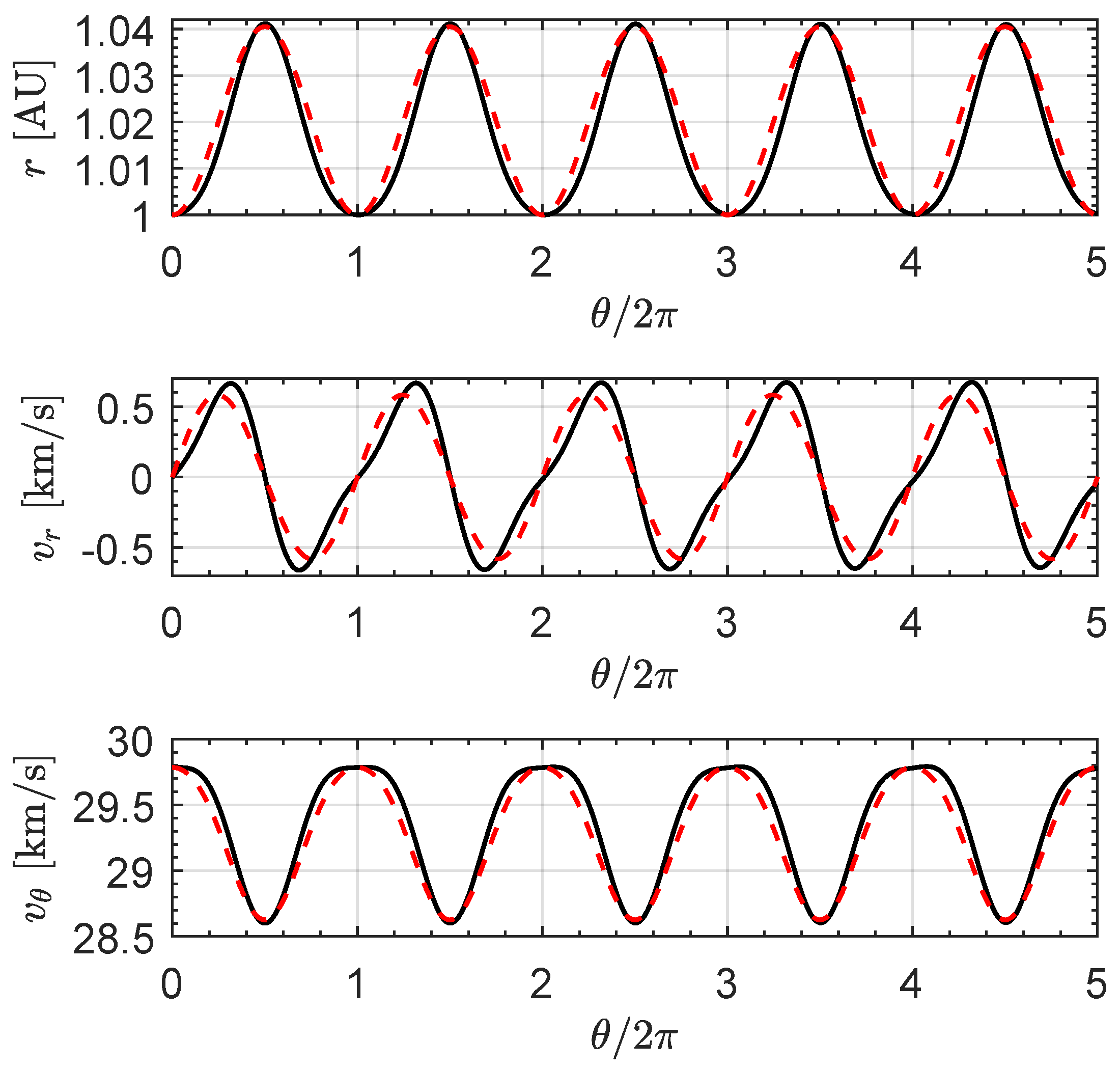
Consider now a characteristic acceleration $a_c=0.1\mathrm{mm}/{\mathrm{s}}^2$, which corresponds to a dimensionless value ${\tilde{a}}_c=a_c/({\mu }_{\odot }/r_{\oplus }^2)\simeq 0.0169$, being ${\mu }_{\odot }/r_{\oplus }^2\simeq 5.93\mathrm{mm}/{\mathrm{s}}^2$. In this case, the $\theta$-variations of the state variables $\{r,v_r,v_{\theta }\}$ obtained from Equations (22)–(24) are drawn in Figure 10 with a red dashed line. In the same figure, the black solid lines indicate the functions obtained by numerical integration of the spacecraft equations of motion.

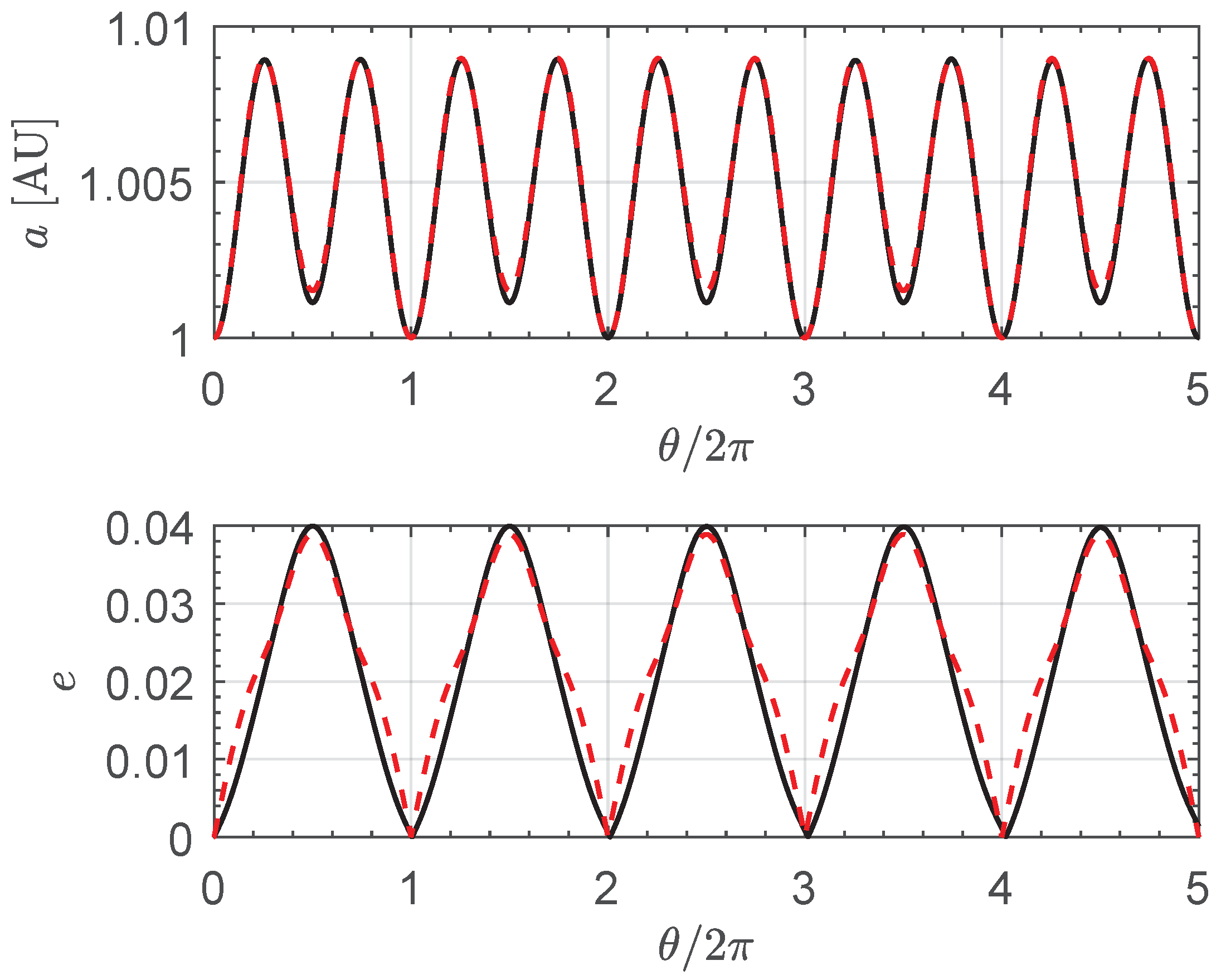
As expected, the analytical equations come close to the actual $\theta$-variation of the spacecraft state variables, and a similar comment applies to the $\theta$-variation of the semimajor axis a and the eccentricity e of the osculating orbit, which are shown in Figure 11. Note that the analytical approximation of a and e can be obtained by substituting Equations (21)–(24) in the well known expressions

$$a=-\frac{{\mu }_{\odot }}{\left(v_r^2+v_{\theta }^2\right)-2{\mu }_{\odot }/r},e=\sqrt{1-\frac{h^2}{{\mu }_{\odot }a}}$$

(26)

Consider, for example, a case in which the spacecraft is required to reach a radial distance $r=r_f=1.03\mathrm{AU}$, a value compatible with the maximum attainable distance of roughly $1.04\mathrm{AU}$; see Figure 10. Assuming the transfer is completed in less than one full revolution around the Sun (i.e., $\theta \le 2\pi \mathrm{rad}$), Equation (22) gives the value ${\theta }_f$ of the spacecraft polar angle at the end of the flight, when the condition $r=r_f$ is reached, that is,

$${\theta }_f=arccos\left(1-\frac{r_f/r_{\oplus }-1}{1.2{\tilde{a}}_c}\right)\simeq \{118.84,241.15\}\mathrm{deg}$$

(27)

The latter result is consistent with the graph in the upper part of Figure 10. Assuming, for example, a final polar angle ${\theta }_f=118.84\mathrm{deg}$, Equation (25) gives a flight time of about $123.5\mathrm{days}$, which is roughly $8\%$ smaller than the actual flight time (equal to $134\mathrm{days}$) obtained via numerical integration of the equations of motion.

A second application of the proposed mathematical model involves estimating the performance of the E-sail required to complete an assigned mission scenario. Assume again the condition ${\alpha }_0=90\mathrm{deg}$, and consider a transfer in which the spacecraft reaches a solar distance equal to $1.03\mathrm{AU}$, with $\theta \le 2\pi \mathrm{rad}$. The minimum value of the characteristic acceleration required to reach such a radial distance can be obtained by enforcing the condition $max\left(r\right)=r_f=1.03\mathrm{AU}$, i.e., by selecting the value of ${\tilde{a}}_c$ so that the aphelion of the propelled trajectory is located precisely at a distance from the Sun equal to $r_f$. According to Equation (22), the aphelion distance is approximated by the following expression:

$$max\left(r\right)\simeq r_{\oplus }\left(1+2.4{\tilde{a}}_c\right)$$

(28)

so that the condition $max\left(r\right)=r_f=1.03\mathrm{AU}$ gives the (minimum) required value of the dimensionless characteristic acceleration

$${\tilde{a}}_c\simeq \frac{r_f/r_{\oplus }-1}{2.4}=0.0125$$

(29)

which corresponds to a dimensional value of $a_c\simeq 0.0741\mathrm{mm}/{\mathrm{s}}^2$. This value is confirmed by numerical simulations.

4. Conclusions

In the context of interplanetary trajectories generated with an Electric Solar Wind Sail (E-sail), the present work presented an analytical approach to obtain an approximation of both the polar form of the propelled trajectory and some important features of its heliocentric osculating orbit, in the special case where the propellantless propulsion system is designed with a single conducting tether rotating around an inertially fixed direction with an assigned angular velocity.

This specific E-sail arrangement models the characteristics of the spacecraft configuration that will most likely be used to achieve the first flight test of the propulsion system invented by Pekka Janhunen in the early 2000s. The procedure proposed in this paper is designed to provide accurate results when the spin axis belongs to the ecliptic, the spacecraft starts from a circular parking orbit that describes the Earth’s heliocentric trajectory, and the magnitude of the propulsive acceleration has a small value compared to the solar (local) gravitational acceleration. This is, in fact, the case representing the performance of a single conducting tether of limited length (compared to the total tether length in a full-scale E-sail typically considered in the literature), which is deployed by a small spacecraft such as a CubeSat.

A suitable approximation of the spacecraft equations of motion and the thrust vector of the E-sail allowed obtaining a compact expression of the angular momentum vector, which, in turn, can be used to derive the approximate expression of the propelled trajectory in polar form. The set of analytical equations obtained is useful for quickly analyzing spacecraft performance in some typical heliocentric mission scenarios involving a first-generation E-sail. Although validation of the proposed method, carried out by direct comparison with the results of numerical integration of the equations of motion, indicates that the analytical expressions obtained in this work approximate well the actual dynamics of the system, the main limitation of the proposed approach lies in the important assumption of an almost constant Sun–spacecraft distance during flight. On the other hand, this assumption is valid only for a very low-performance E-sail with low-to-medium flight times (the case discussed in this paper considers a maximum number of complete revolutions around the Sun equal to 5), while the propulsive acceleration given by a medium-performance propulsion system is capable of significantly changing the radial distance of the spacecraft in a (relatively) small time interval. This is, for example, the case for an E-sail-based spacecraft, whose characteristic acceleration approaches the canonical value of about $1\mathrm{mm}/{\mathrm{s}}^2$, as reported in several papers by the authors. However, this inherent limitation of the method proposed in this paper does not apply to a first-generation E-sail, i.e., the propulsion system that is hoped to be used to obtain the first in situ evidence of the E-sail potential.

With this last important aspect in mind, a possible and interesting extension of this work is to consider the more general case in which the spin axis of the E-sail has a fixed inertial direction inclined with respect to the ecliptic. In such a case, the propulsive acceleration has a non-zero component perpendicular to the ecliptic and the resulting spacecraft trajectory is three-dimensional. This important feature makes it possible to study some interesting mission scenarios, such as a transfer to an inclined heliocentric orbit.