Modelling Rigid Body Potential of Small Celestial Bodies for Analyzing Orbit–Attitude Coupled Motions of Spacecraft
Abstract
1. Introduction
2. Background and Gravity Estimation Models
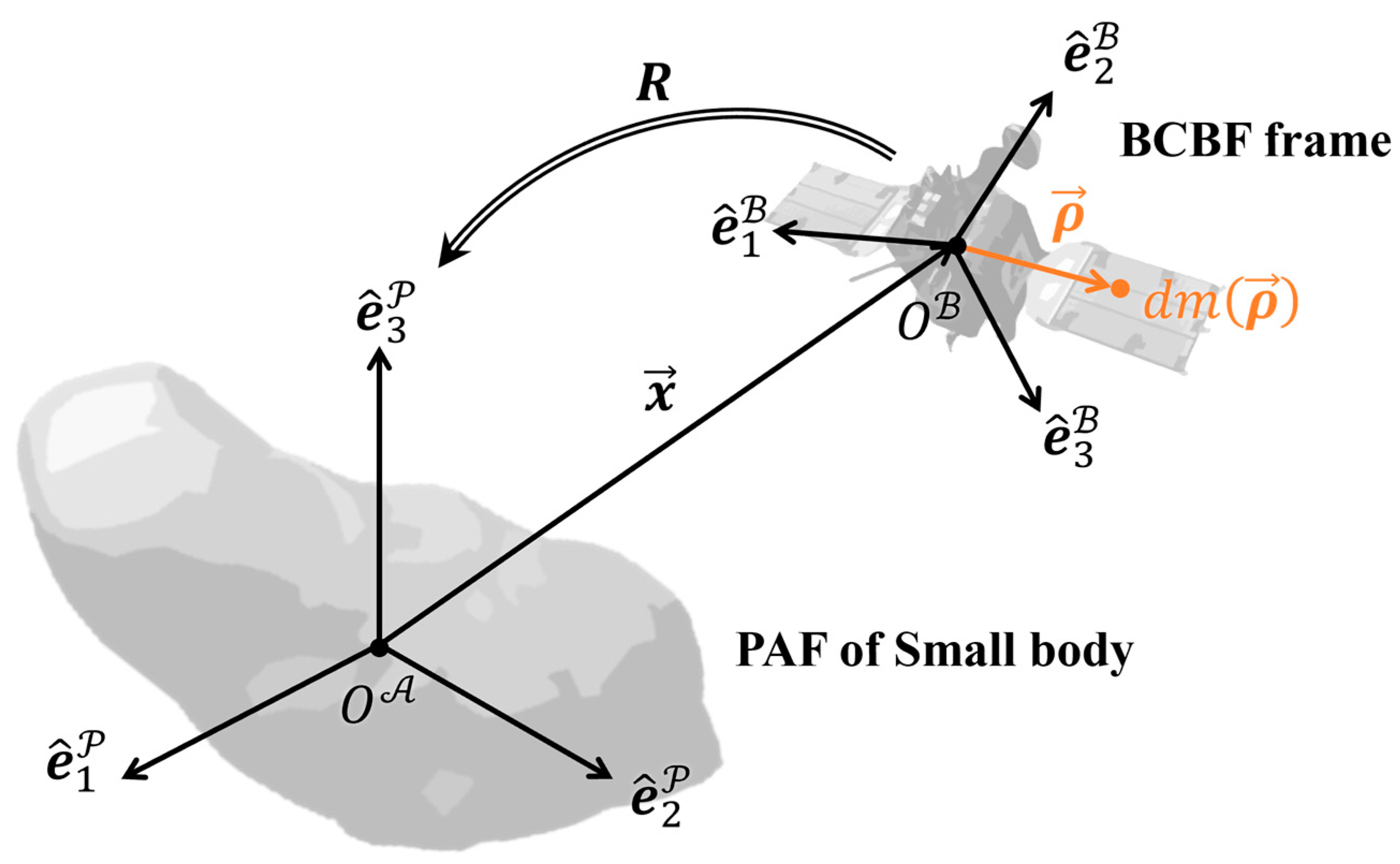
2.1. Background
2.2. Gravity Estimation Models
2.2.1. Point Mass Model
2.2.2. Extended Body Model
2.2.3. Triaxial Ellipsoid Model
3. Rigid Body Potential
4. Application of Rigid Body Potential
4.1. Point Mass Model
4.2. Extended Body Model
4.3. Triaxial Ellipsoidal Model
5. Numerical Simulations
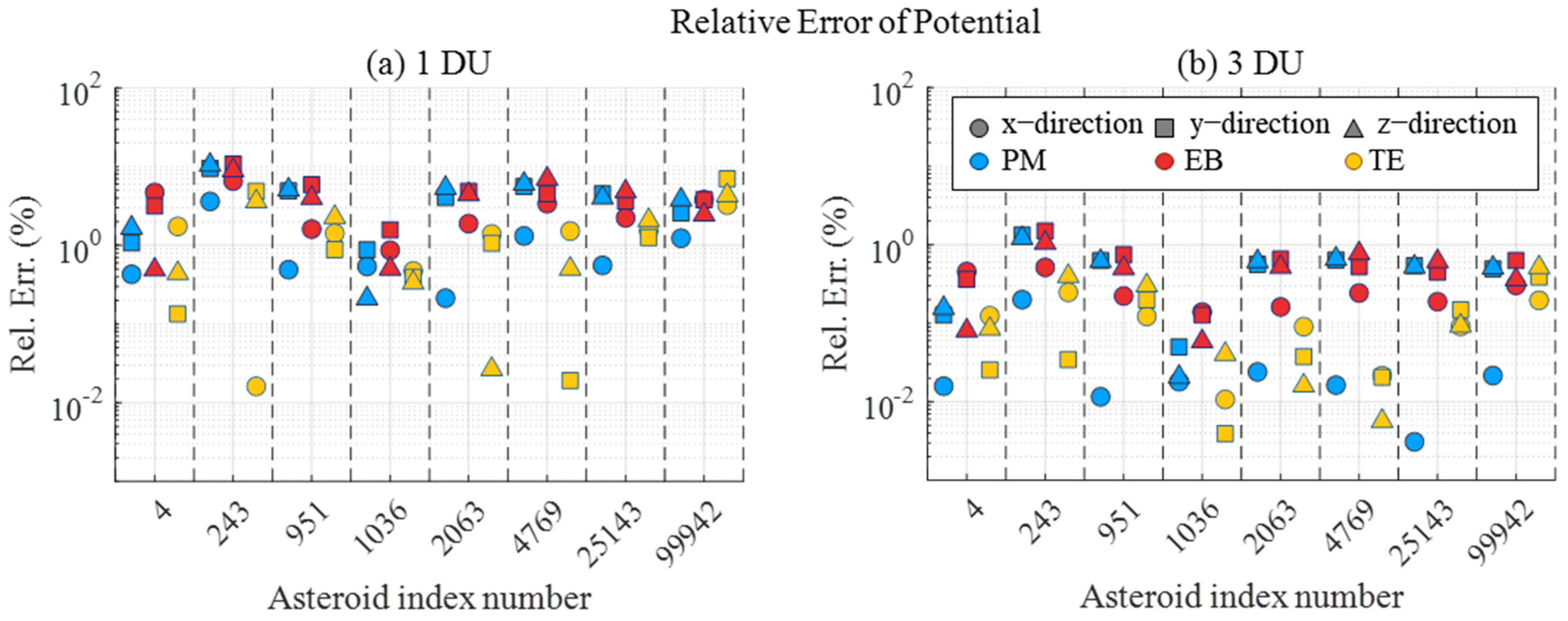
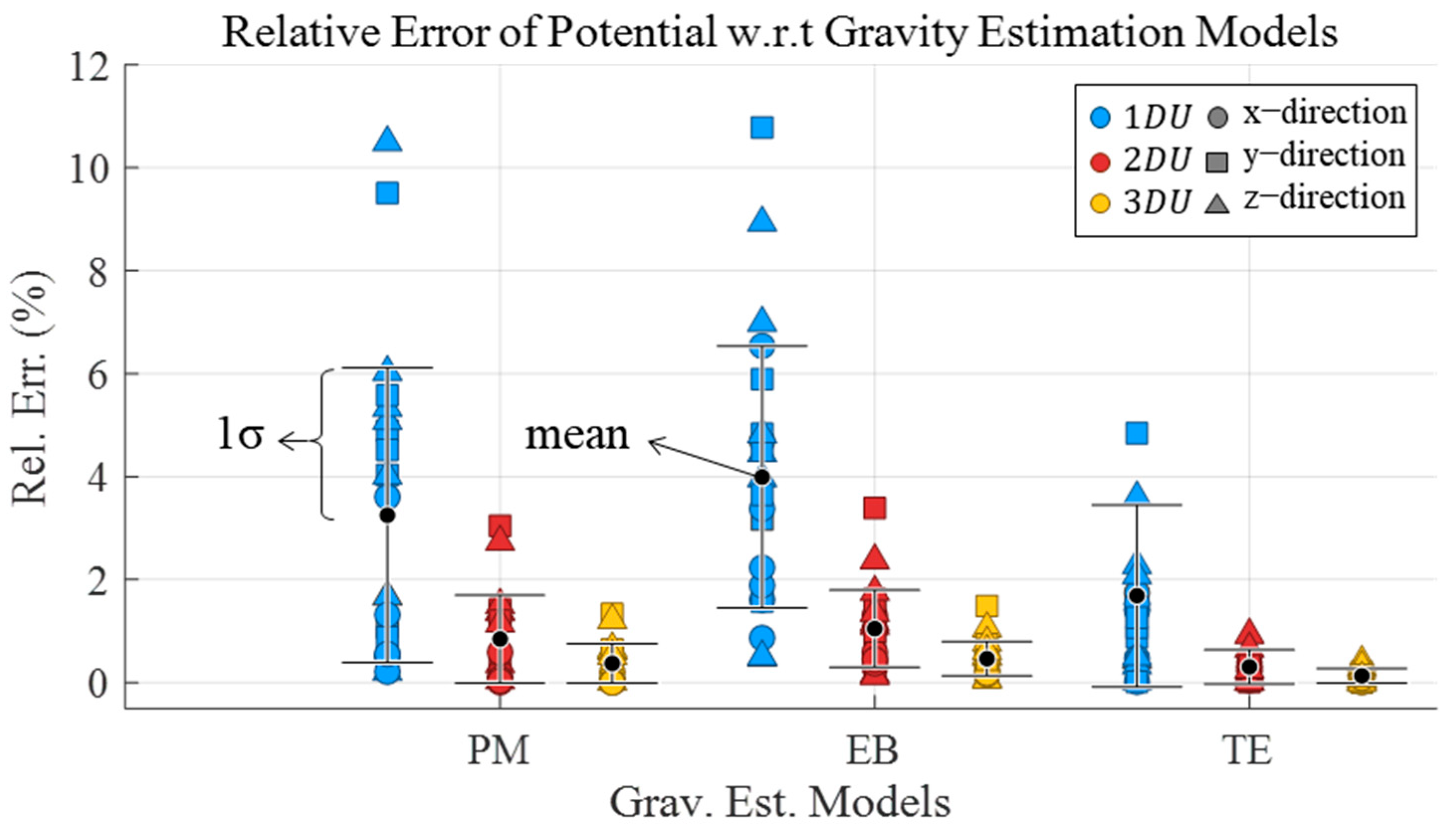
5.1. Analysis on Gravity Estimation Models
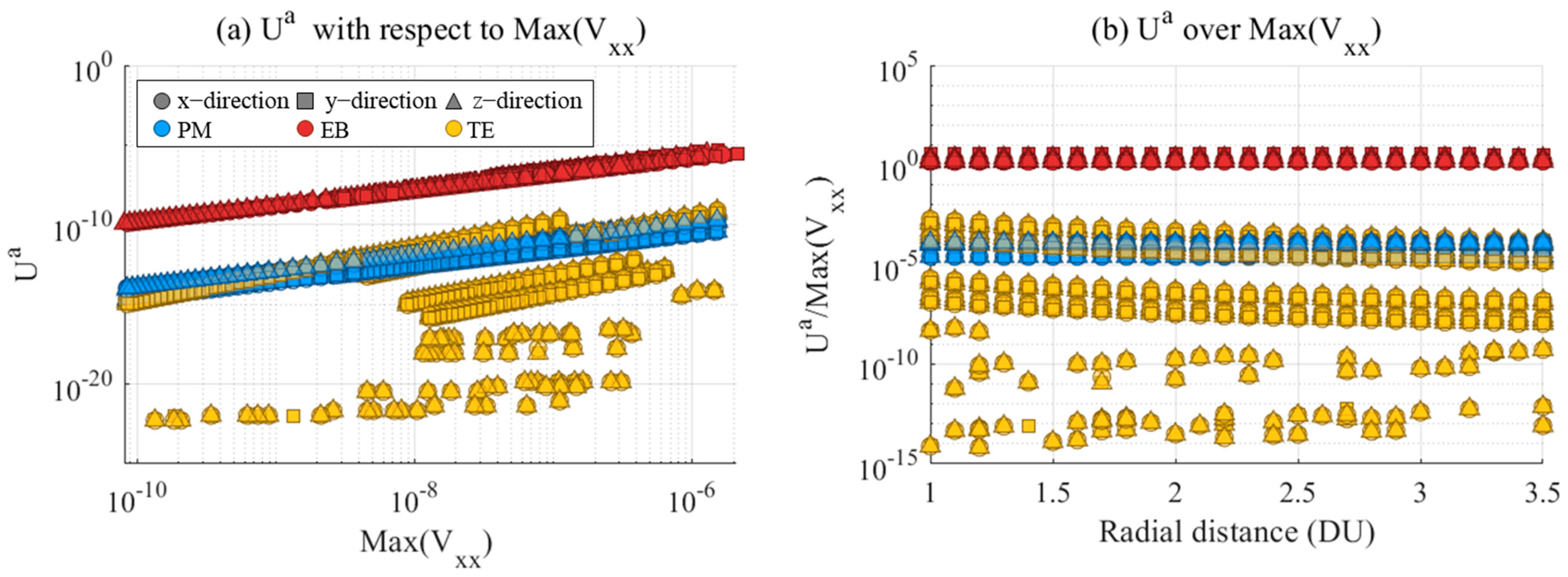
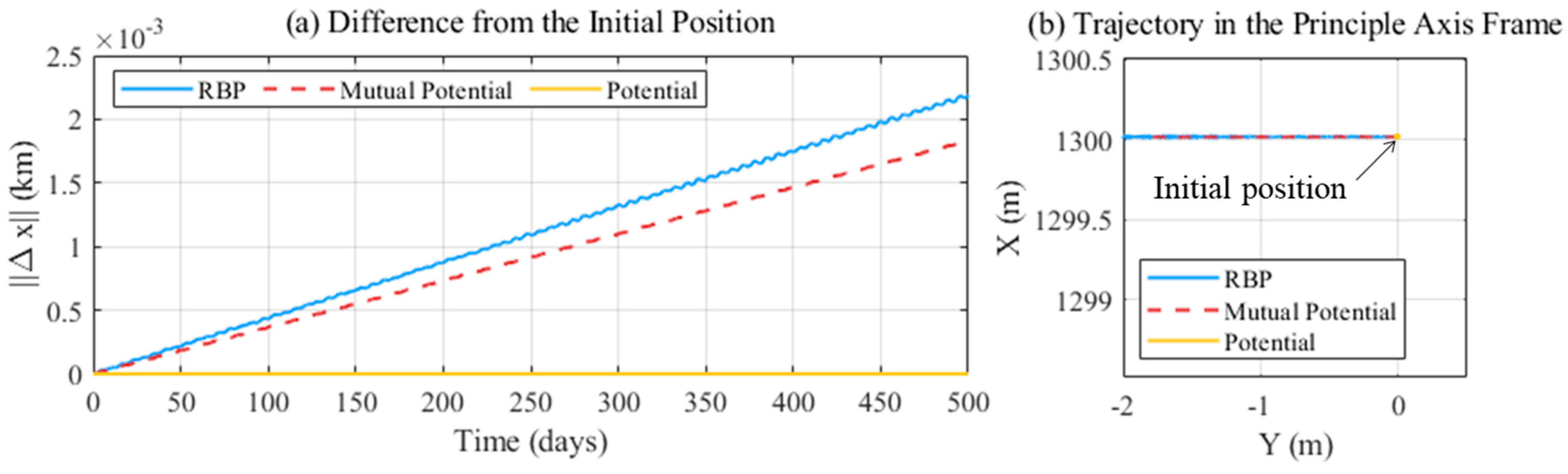
5.2. Analysis on Rigid Body Potential
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Corollary A1: General Framework of Rigid Body Potential
Appendix B. Derivation of Rigid Body Potential
Appendix B.1. Proof of Example 1 (Point Mass Model)
Appendix B.2. Proof of Example 2 (Extended Body Model)
Appendix B.3. Proof of Example 3 (Triaxial Ellipsoidal Model)
Appendix C. Direct Integration Model
References
- Kawaguchi, J.; Fujiwara, A.; Uesugi, T. Hayabusa-Its Technology and Science Accomplishment Summary and Hayabusa-2. Acta Astronaut. 2008, 62, 639–647. [Google Scholar] [CrossRef]
- Accomazzo, A.; Lodiot, S.; Companys, V. Rosetta Mission Operations for Landing. Acta Astronaut. 2016, 125, 30–40. [Google Scholar] [CrossRef]
- Rayman, M.D. Lessons from the Dawn Mission to Ceres and Vesta. Acta Astronaut. 2020, 176, 233–237. [Google Scholar] [CrossRef]
- Tsuda, Y.; Saiki, T.; Terui, F.; Nakazawa, S.; Yoshikawa, M.; Watanabe, S. ichiro Hayabusa2 Mission Status: Landing, Roving and Cratering on Asteroid Ryugu. Acta Astronaut. 2020, 171, 42–54. [Google Scholar] [CrossRef]
- Berry, K.; Getzandanner, K.; Moreau, M.; Antreasian, P.; Polit, A.; Nolan, M.; Enos, H.; Lauretta, D. Revisiting OSIRIS-REx Touch-And-Go (TAG) Performance Given the Realities of Asteroid Bennu. In Proceedings of the Annual AAS Guidance, Navigation and Control Conference, Breckenridge, CO, USA, 30 January–5 February 2020; American Astronautical Society (AAS): Springfield, VA, USA, 2020. [Google Scholar]
- Oh, D.Y.; Collins, S.; Drain, T.; Hart, W.; Imken, T.; Larson, K.; Marsh, D.; Muthulingam, D.; Steven Snyder, J.; Trofimov, D.; et al. Development of the Psyche Mission for NASA’s Discovery Program. In Proceedings of the 36th International Electric Propulsion Conference, Vienna, Austria, 15–20 September 2019; Electric Rocket Propulsion Society: Toulouse, France, 2019. [Google Scholar]
- Ozaki, N.; Yamamoto, T.; Gonzalez-Franquesa, F.; Gutierrez-Ramon, R.; Pushparaj, N.; Chikazawa, T.; Tos, D.A.D.; Çelik, O.; Marmo, N.; Kawakatsu, Y.; et al. Mission Design of DESTINY+: Toward Active Asteroid (3200) Phaethon and Multiple Small Bodies. Acta Astronaut. 2022, 196, 42–56. [Google Scholar] [CrossRef]
- Iwata, T.; Kitazato, K.; Abe, M.; Ohtake, M.; Arai, T.; Arai, T.; Hirata, N.; Hiroi, T.; Honda, C.; Imae, N.; et al. Investigation of the solar system disk structure during the cruising phase of the solar power sail mission. In Proceedings of the 49th Lunar and Planetary Science Conference, The Woodlands, TX, USA, 19–23 March 2018; Springer: Dordrecht, The Netherlands, 2018; Volume 208. [Google Scholar]
- Sincarsin, G.B.; Hughes, P.C. Gravitational Orbit-Attitude Coupling for Very Large Spacecraft. Celest. Mech. 1983, 31, 143–161. [Google Scholar] [CrossRef]
- Masiero, J.R.; Mainzer, A.K.; Bauer, J.M.; Cutri, R.M.; Grav, T.; Kramer, E.; Pittichová, J.; Wright, E.L. Asteroid Diameters and Albedos from Neowise Reactivation Mission Years Six and Seven. Planet. Sci. J. 2021, 2, 162. [Google Scholar] [CrossRef]
- Pravec, P.; Harris, A.W.; Kušnirák, P.; Galád, A.; Hornoch, K. Absolute Magnitudes of Asteroids and a Revision of Asteroid Albedo Estimates from WISE Thermal Observations. Icarus 2012, 221, 365–387. [Google Scholar] [CrossRef]
- Zhang, F.; Duan, G. Coupled Dynamics and Integrated Control for Position and Attitude Motions of Spacecraft: A Survey. IEEE/CAA J. Autom. Sin. 2023, 10, 2187–2208. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, S. Orbital Dynamics and Equilibrium Points around an Asteroid with Gravitational Orbit–Attitude Coupling Perturbation. Celest. Mech. Dyn. Astron. 2016, 125, 265–285. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, S. Non-Equatorial Equilibrium Points around an Asteroid with Gravitational Orbit-Attitude Coupling Perturbation. Astrodynamics 2020, 4, 1–16. [Google Scholar] [CrossRef]
- Werner, R.A.; Scheeres, D.J. Mutual Potential of Homogeneous Polyhedra. Celest. Mech. Dyn. Astron. 2005, 91, 337–349. [Google Scholar] [CrossRef]
- Chappaz, L.; Howell, K.C. Bounded Orbits near Binary Systems Comprised of Small Irregular Bodies. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, Reston, Virginia, 4 August 2014; American Institute of Aeronautics and Astronautics: Springfield, VA, USA, 2014. [Google Scholar]
- Hou, X.; Scheeres, D.J.; Xin, X. Mutual Potential between Two Rigid Bodies with Arbitrary Shapes and Mass Distributions. Celest. Mech. Dyn. Astron. 2017, 127, 369–395. [Google Scholar] [CrossRef]
- Bolatti, D.A.; De Ruiter, A.H.J. Galerkin Variational Integrators for Orbit Propagation with Applications to Small Bodies. J. Guid. Control. Dyn. 2019, 42, 347–363. [Google Scholar] [CrossRef]
- Wang, Y.; Zhong, R.; Xu, S. Orbital Perturbation Due to Orbit-Attitude Coupling near Asteroids. Aircr. Eng. Aerosp. Technol. 2018, 90, 104–113. [Google Scholar] [CrossRef]
- Carry, B. Density of Asteroids. Planet. Space Sci. 2012, 73, 98–118. [Google Scholar] [CrossRef]
- Gao, Y.; Li, H.-N.; He, S.-M. First-Round Design of the Flight Scenario for Chang’e-2′s Extended Mission: Takeoff from Lunar Orbit. Acta Mech. Sin. 2012, 28, 1466–1478. [Google Scholar] [CrossRef]
- Prockter, L.; Murchie, S.; Cheng, A.; Krimigis, S.; Farquhar, R.; Santo, A.; Trombka, J. The NEAR Shoemaker Mission to Asteroid 433 Eros. Acta Astronaut. 2002, 51, 491–500. [Google Scholar] [CrossRef]
- D’Amario, L.A.; Bright, L.E.; Wolf, A.A. Galileo Trajectory Design. Space Sci. Rev. 1992, 60, 23–78. [Google Scholar] [CrossRef]
- Beshore, E.; Sutter, B.; Mink, R.; Lauretta, D.; Moreau, M.; Boynton, W.; Dworkin, J.; Everett, D.; Shinohara, C.; Gal-Edd, J. The OSIRIS-REx Asteroid Sample Return Mission. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015; IEEE: New York, NY, USA, 2015; pp. 1–14. [Google Scholar]
- Russell, C.; Raymond, C. The Dawn Mission to Minor Planets 4 Vesta and 1 Ceres; Russell, C., Raymond, C., Eds.; Springer New York: New York, NY, USA, 2012; ISBN 978-1-4614-4902-7. [Google Scholar]
- Yoshikawa, M.; Kawaguchi, J.; Fujiwara, A.; Tsuchiyama, A. Sample Return Missions; Elsevier: Amsterdam, The Netherlands, 2021; ISBN 9780128183304. [Google Scholar]
- Guelman, M. Closed-Loop Control of Close Orbits around Asteroids. J. Guid. Control. Dyn. 2015, 38, 854–860. [Google Scholar] [CrossRef]
- Scheeres, D.J. Dynamics about Uniformly Rotating Triaxial Ellipsoids: Applications to Asteroids. Icarus 1994, 110, 225–238. [Google Scholar] [CrossRef]
- Smith, O.K. Eigenvalues of a Symmetric 3 × 3 Matrix. Commun. ACM 1961, 4, 168. [Google Scholar] [CrossRef]
- Werner, R.A.; Scheeres, D.J. Exterior Gravitation of a Polyhedron Derived and Compared with Harmonic and Mascon Gravitation Representations of Asteroid 4769 Castalia. Celest. Mech. Dyn. Astron. 1997, 65, 313–344. [Google Scholar] [CrossRef]
- Park, R.S.; Werner, R.A.; Bhaskaran, S. Estimating Small-Body Gravity Field from Shape Model and Navigation Data. J. Guid. Control. Dyn. 2010, 33, 212–221. [Google Scholar] [CrossRef]

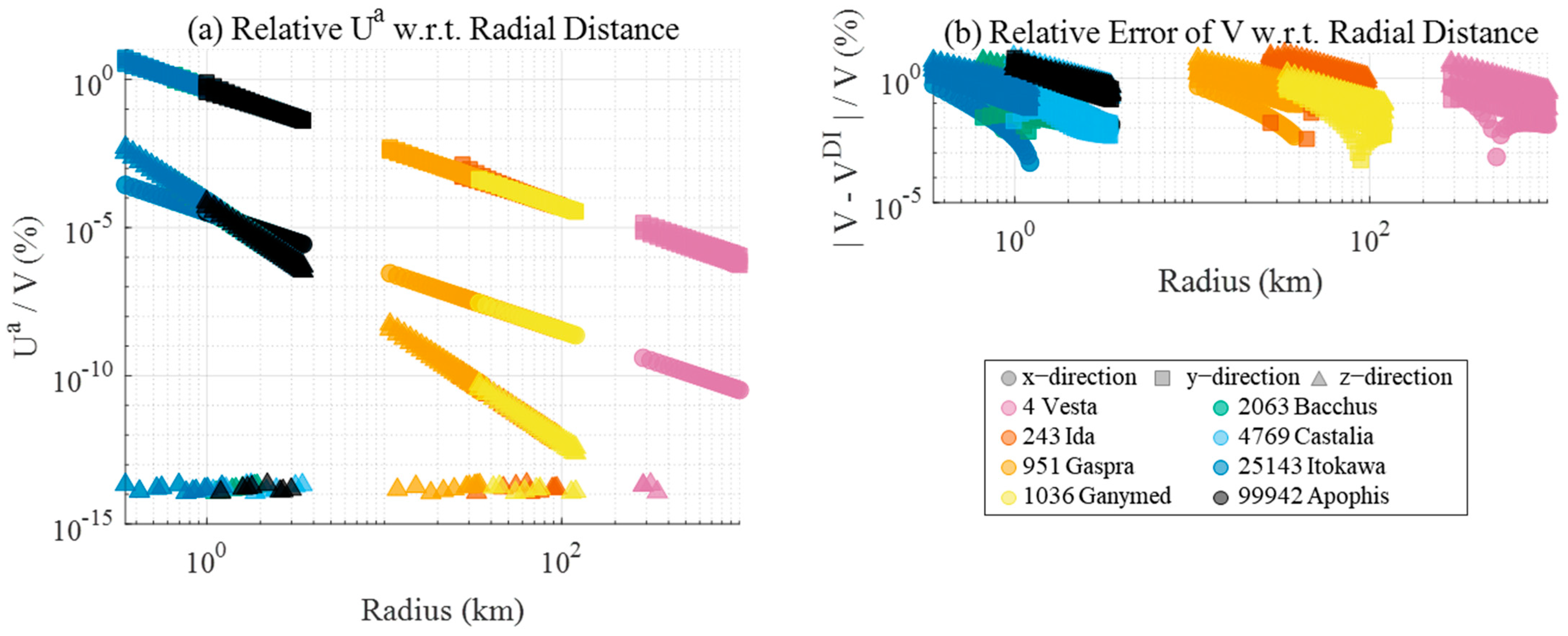
| Index # | Name | (AU) | (m) | (kg) | (m) | |||
|---|---|---|---|---|---|---|---|---|
| 4 | Vesta | |||||||
| 243 | Ida | |||||||
| 433 | Eros | |||||||
| 951 | Gaspra | |||||||
| 1036 | Ganymed | * | ||||||
| 1620 | Geographos | |||||||
| 4179 | Toutatis | |||||||
| 4769 | Castalia | |||||||
| 25143 | Itokawa | |||||||
| 99942 | Apophis |
| Small Body | ) | ) | Number of Faces |
|---|---|---|---|
| 4 Vesta | |||
| 243 Ida | |||
| 951 Gaspra | |||
| 1036 Ganymed | |||
| 2063 Bacchus | |||
| 4769 Castalia | |||
| 25143 Itokawa | |||
| 99942 Apophis |
| Case | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Park, C. Modelling Rigid Body Potential of Small Celestial Bodies for Analyzing Orbit–Attitude Coupled Motions of Spacecraft. Aerospace 2024, 11, 364. https://doi.org/10.3390/aerospace11050364
Lee J, Park C. Modelling Rigid Body Potential of Small Celestial Bodies for Analyzing Orbit–Attitude Coupled Motions of Spacecraft. Aerospace. 2024; 11(5):364. https://doi.org/10.3390/aerospace11050364
Chicago/Turabian StyleLee, Jinah, and Chandeok Park. 2024. "Modelling Rigid Body Potential of Small Celestial Bodies for Analyzing Orbit–Attitude Coupled Motions of Spacecraft" Aerospace 11, no. 5: 364. https://doi.org/10.3390/aerospace11050364
APA StyleLee, J., & Park, C. (2024). Modelling Rigid Body Potential of Small Celestial Bodies for Analyzing Orbit–Attitude Coupled Motions of Spacecraft. Aerospace, 11(5), 364. https://doi.org/10.3390/aerospace11050364








