Abstract
A novel station-keeping strategy leveraging periodic revolutions of homeomorphic orbits in the Elliptic Restricted Three-Body Problem within the pulsating frame is presented. A systemic approach founded on arc-length continuation is presented for the discovery, computation, and classification of periodic revolutions that morph from their traditional circular restricted three-body counterparts to build an a priori dataset. The dataset is comprehensive in covering all possible geometric architectures of the restricted problem. Shape similarity is quantified using Hausdorff distance and works as a filter for the station-keeping algorithm in relation to appropriate target conditions. Finally, an efficient scheme to quantify impulsive orbit maintenance maneuvers that minimize the total fuel cost is presented. The proposed approach is salient in its generic applicability across any elliptic three-body system and any periodic orbit family. Finally, average annual station-keeping costs using the described methodology are quantified for selected “orbits of interest” in the cis-lunar and the Sun–Earth systems. The robustness and efficacy of the approach instill confidence in its applicability for realistic mission design scenarios.
1. Introduction
The search for efficient, flexible, and robust orbit maintenance strategies has gained increased traction with the success of the Artemis 1 mission and the prospects for future crewed and robotic lunar exploration. Ever since the discovery of quasi-periodic orbits in the Sun–Earth–Moon system by Robert Farquhar and Ahmed Kamel, research exploring their use for future mission architectures has continued to be a growing interest in Lagrange Point Orbits (LPOs) [1]. For instance, several periodic orbits have been tested as candidates for the Lunar Gateway, and eventually, NASA earmarked an orbit from the Southern Near Rectilinear Halo family around the Earth–Moon with a 9:2 synodic resonance, as the orbit for establishing a sustained human presence in the cis-lunar space [2,3]. Additionally, to aid preliminary mission design and analysis, several periodic orbit initial conditions associated with the Circular Restricted Three-Body Problem (CR3BP) have been computed and stored for several three-body systems of interest [4]. However, metadata from the aforementioned database are associated with periodicity established in simplified dynamics which do not account for realistic multi-body perturbation effects, thereby limiting applicability for realistic mission design.
Previous studies have demonstrated that rather expectantly, LPOs in the CR3BP lose their periodicity when realistic perturbations are embedded into the dynamical system [1,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. Since unmodeled perturbations significantly affect nominal spacecraft trajectory, it has been demonstrated that autonomous trajectory re-planning, guidance, and station-keeping analyses are of utmost importance for the success of these missions [17,18,19,25,27,28,29,30]. Several methods have been used so far by researchers ranging from location-based Target Point Approach (TPA), shape-similar trajectories, to finite-time Lyapunov exponents (FTLEs) in the form of the Cauchy Green Tensor (CGT) [17,18,25,27,28]. Studies performed on the effects of the Sun’s gravity on the spacecraft as an additional perturbing force, through the Bi-Circular Restricted Four-Body Problem (BCR4BP) in the Sun–Earth–Moon system which presented significant positional deviation from a perfectly periodic halo orbit [6,7,8,9,10]. For Europa, due to the proximity to both Io and Ganymede, the Concentric Circular Restricted Four-Body Problem (CCR4BP) was a better approximation as all three moons are in resonance with each other [19,20]. Another paper that focuses on the Sun–Earth–Moon system also includes the effect of albedo on the celestial bodies themselves as an additional parameter [10]. Non-uniform gravitational fields have also been studied in the context of perturbations to the CR3BP whereas the primary and secondary were considered oblate spheroids with no obliquity [10,11,12,13,14,15,16,17,18]. Many of these studies focus on the Europa and Enceladus as the proximity to both the planet and moon affect the perceived gravity as a function of latitude [13,14,15,16]. These analyses provide important insights for potential future long-term scientific missions to observe the geological activity and discover life on these icy moons.
Many studies have also focused on characterizing LPOs and studying station keeping (SK) in a dynamical system of higher complexity. For instance, the restricted Ephemeris model has been used as a preliminary test for SK of halo orbits which has the effect of solar radiation pressure (SRP) embedded in the dynamical system [17,18]. Other studies have either focused on different three-body systems or solely analyzed the effects of non-circular orbits on the autonomous CR3BP dynamics. These studies determined the effects of eccentricity by analyzing the dynamical behavior in the Elliptic Restricted Three-Body Problem (ER3BP) [21,22,23,24,25,26]. It has been proved mathematically that the system dynamics become further chaotic and more unstable for any spacecraft in the ER3BP when compared to the original CR3BP [21]. The results are indicative of the fact that consideration of eccentricity leading to non-autonomous motion can have profound effects on the legacy dynamical structures from the more benign circular restricted case. Periodicity for halo orbit counterparts has been achieved via numerical continuation and shows significant dissimilarity from corresponding motions in the CR3BP family [22,23,24,25]. Therefore, the need to analyze systems of intermediate fidelity using advanced numerical methods to understand long-term dynamical behavior and motion structures has been established. There have been SK methods used within the ER3BP using multiple impulses per orbit-rev and a monodromy matrix analog [26]. The aforementioned station-keeping papers focused on keeping the CR3BP orbit as the nominal reference orbit without carrying out a robust and holistic search for novel periodic structures catering to an incremental addition of fidelity to the original autonomous dynamical system.
A significant operational challenge in the context of long-duration “orbiter-type” space missions is determining the appropriate cadence of the Orbit Determination (OD), SK, and Science Objective (SO) cycle. For instance, a spacecraft, initially placed in a Low Lunar Orbit (LLO) to perform high-resolution imaging of the lunar terrain requires constant SK maneuvers to maintain the orbit in the presence of anomalous lunar gravity [31]. On the other hand, SK maneuver quantification requires accurate navigation input from OD. Therefore, a significant fraction of a revolution is attributed to OD and SK, limiting imaging science opportunities. This hampers the overall efficiency of the mission and novel orbit maintenance strategies that can provide an efficient cadence such that the final goal is achieved, are of utmost importance.
In this paper, a novel, elegant, and robust methodology is proposed to generate orbits from the well-documented CR3BP periodic orbits in the presence of the ER3BP dynamical system. These orbits are periodic over the entire state space and bear a resemblance to their CR3BP counterparts in shape and period as derived from continuation. They are therefore termed “homeomorphic” to their CR3BP counterparts and the orbit revs termed as Homoemorphic Periodic Orbits (HPOs) for the rest of the paper. Enforcing shape similarity preserves the attractiveness of the discovered orbit rev (like eclipse conditions, periapse altitude, etc.) while equipping mission designers with more realistic dynamical behavior. The underlying algorithm employs an arc-length homotopy approach to achieve convergence using the CR3BP periodic conditions as the initial guess. The results demonstrate the robustness and generality of the algorithm as it could apply to different periodic orbit families in several systems and geometrical configurations.
Finally, an optimal orbit maintenance algorithm utilizing a single-impulse per-rev architecture is employed to quantify the fuel cost that leverages the pre-computed and tabulated periodic revs. In the optimization scheme, a “target condition” database of HPOs is built for the ER3BP dynamics based on the desired amount of revs by matching the position and velocity vectors although not requiring the initial and final true anomalies to match. The associated periodic conditions are saved as metadata with the initial true anomaly as a classifying parameter. Progression along the proposed SK architecture is achieved by drawing from the generated dataset to identify the target future state. A single-shooting algorithm is then used to solve for the correction maneuvers required to achieve the final state associated with the next HPO rev. Annual fuel costs are estimated for different “orbits of interest” in the cis-lunar and the Sun–Earth systems. Additional filtering of the database has been explored by using the shape-similarity metric to reduce the target state search space in the search for an optimal SK architecture. The rest of the paper is organized as follows: Section 1 and Section 2 deal with theoretical preliminaries which include succinct descriptions of the ER3BP, numerical continuation techniques, and shape similarity metrics. Section 3 formulates the problem of HPO searches and discusses the SK strategy in detail. Section 4 provides results achieved by implementing the algorithms in Section 3 in the context of selected “orbits of interests”. Section 5 concludes the paper and describes avenues for building on the current work in the future.
2. Preliminaries
2.1. Elliptic Restricted Three-Body Problem
The ER3BP is a non-autonomous dynamical system that defines the motion of a restricted mass in the presence of a primary-secondary pair that orbits their barycenter in an ellipse. The fixed rotation rate renders CR3BP as an autonomous Hamiltonian system, but unfortunately, when the circular assumption is relaxed, the system is no longer autonomous due to the changing rotation rate. Although non-autonomous, the system can still be written in Hamiltonian form but still requires careful alteration to the equations of motion [32]. In particular, an additional reference frame is required to derive the governing dynamical equations. The pulsating frame, shown in Figure 1, is defined for this purpose such that the perceived distance between the primary and secondary remains constant relative to the frame, thereby admitting equilibrium point analogs which could be explored for periodic conditions, akin to the Lagrange Point Orbits (LPOs) in the CR3BP.
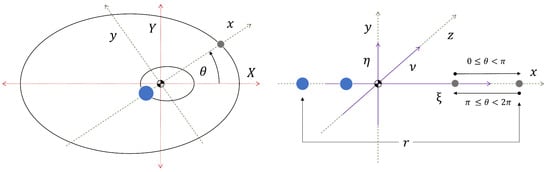
Figure 1.
(Left) Rotating and inertial reference frames in the ER3BP. (Right) Pulsating and rotating reference frames in the ER3BP.
The pulsating frame is constructed using the set of orthonormal basis vectors , relative to the primary-secondary distance, and analogous to the of the barycentric synodic frame, respectively. Figure 1 depicts the inertial, rotating, and pulsating frames schematically to better represent how they relate to one another. As a byproduct of the elliptical motion of the primary and secondary, the equilibrium points demonstrate pulsating motion, as depicted in Figure 2. Using Szebehely’s Equations [33] and implementing the modifications proposed by Broucke [21], the ER3BP is governed by the following system of equations:
Coupled with the following secondary parameter definitions,
where p denotes the semi-latus rectum of the ‘elliptical’ system and r denotes the normalized distance between the primary and secondary. Additionally, refers to the relative mass parameter, and indicate the distance from the spacecraft to the primary or secondary, respectively, as measured in the pulsating frame. Note that the primed/stroked quantities in Equation (1) denote derivatives and corresponding order with respect to the true anomaly, , rather than time.
Figure 2.
Drift in the equilibrium point analogs owing to the elliptic motion.
Altogether, equations in (1), in conjunction with the supplemental equations in (2), governs motion in the ER3BP. In this model, the Jacobi normalized units, also known as canonical units, are used such that the semi-major axis of the system is 1 Distance Unit (DU). Additionally, the period of the system is normalized by to become 1 Time Unit (TU), although the actual units are with respect to the true anomaly. Propagation with true anomaly as the free variable requires knowledge of the initial spacecraft position and velocity vectors along with the desired starting system dynamics, captured by , and computed according to the following:
For the remainder of this paper, the canonical conversions are in the context of the Earth–Moon system, , 1 DU = 389,703 km, and 1 TU = 382,981 s which consistent with the Three-Body Periodic Orbit Database [4]. The initial conditions for members of the CR3BP periodic orbit families were obtained and developed as a part of this work from this database and used as a warm-start for the algorithms. Figure 3 depicts the deviation from traditional periodic behavior in the presence of the ER3BP dynamics within the Earth–Moon system underscoring the loss of periodicity.
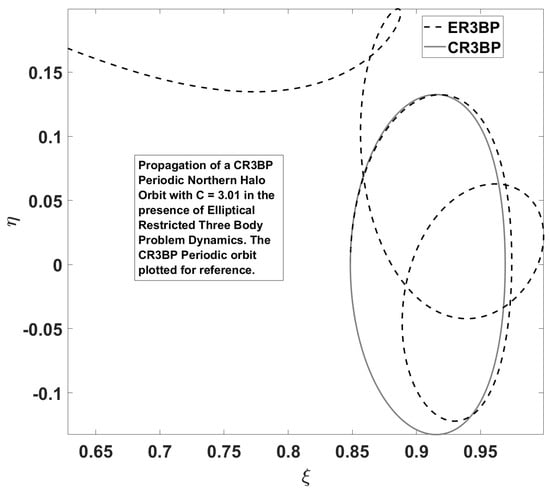
Figure 3.
Departure from periodic behavior in the ER3BP.
2.2. Numerical Continuation
As previously discussed, the CR3BP is an autonomous system, where members of the periodic orbit families exhibit periodicity in both position and velocity without any implicit time dependence. In contrast, the ER3BP is non-autonomous, thereby introducing a substantial increase in problem complexity and consequential dynamical system analysis, making the discovery of intriguing “orbits of interest” significantly more challenging.
Numerical continuation can be defined as the process of generating approximate solutions for a system of non-linear equations in a finite-dimensional space. In general, continuation techniques form a powerful class of numerical methods that can be utilized to analyze the dynamical behavior of mathematical models resembling complex systems. The underlying theme is to track the solution of a system of equations as the continuation parameter is varied and utilizes an iterative solution scheme to map the entire solution space. This approach enables a robust survey of the solution space and provides a methodology to identify interesting features like bifurcations and limit spaces. Continuation methods, often known as homotopy methods, are extremely efficient in achieving convergence for high-fidelity systems [6,7,8] and low-thrust spacecraft trajectory design applications [34,35]. In this work, two continuation methods, natural parameter and arc-length continuation, were leveraged.
2.2.1. Natural Parameter Continuation
The simplest of the two schemes, natural parameter continuation, is a type of predictor–corrector scheme that corrects the solutions of each step based on previous solutions without predicting an initial approximation. Generally, it follows the path generated by the dependent variables, which in this instance are the initial conditions of the spacecraft and system, with respect to fixed natural parameters, either the system eccentricity or true anomaly. By dividing the solution space into unit steps and predicting the next solution at a future step, the dynamical system morphs from the ideal CR3BP to the higher fidelity ER3BP. As the algorithm progresses, the positional deviation from the original periodic halo orbit is restricted as a soft constraint to maintaining shape similarity. Note that the solution must guarantee convergence to ensure periodicity at all intermediate steps. A converged solution refers to matching position and velocity conditions within the pulsating frame after one orbit for a fixed initial geometry. Natural parameter continuation has its limitations in certain dynamical regions: (1) bifurcations form multiple branching solutions and (2) failures near critical limit points where the solution path reverses direction. For these cases, arc-length continuation is far more robust.
2.2.2. Arc-Length Continuation
Arc-length continuation is a powerful numerical tool for studying the behavior of nonlinear systems. This method extends the traditional continuation approach by incorporating the arc-length parameter as an additional variable, allowing for a systematic exploration of the solution branches and their associated stability properties. By tracing the solutions along a continuous path in the parameter space, arc-length continuation provides valuable insights into the global system behavior, enabling the identification of critical points, limit cycles, and other important phenomena. Moreover, this technique facilitates the tracking of solutions through bifurcation points, offering a comprehensive understanding of system dynamics beyond the scope of classical continuation methods like natural parameter continuation.
The arc length of a function refers to the distance that a curvature traverses as the variables change in a system. Consider a nonlinear system governed by , where represents the state variable vector and denotes the parameter. Arc-length continuation involves introducing an additional equation that constrains the solution search space and is a function of the arc length. This constraint equation is differentiated with respect to the new arc-length parameter, s, resulting in an additional equation . Note that the dots above a variable denote derivatives with respect to the arc length. Therefore, the effective arc length is the norm of the infinitesimal change in the solution path. The algorithm to search for shape-similar periodic structures presented later is founded on arc-length continuation and follows the generic architecture presented as Algorithm 1. It facilitates a smooth and robust traversal of the solution space for periodic orbit revs in an iterative fashion considering eccentricity, e, as the continuation parameter while maintaining the initial system geometry. Careful considerations must therefore be imposed to ensure that the orbits do not diverge and preserve parent orbit geometry. For instance, a freely evolving continuation scheme may morph a CR3BP halo orbit into an ER3BP periodic planar orbit at the desired final eccentricity. This emphasizes the need for a metric that characterizes the degree of shape similarity.
| Algorithm 1: Generic Arc-Length Continuation Algorithm |
 |
2.3. Data Filtering Using Hausdorff Distance
The previously described continuation scheme leads to an unbounded traversal of the dense solution space. Additionally, if the orbital revs are geometrically dissimilar, the dataset is not immediately useful for tasks like designing an optimal orbit maintenance strategy. Therefore, a shape similarity metric was introduced to filter out orbit revs from the comprehensive dataset that geometrically resemble the parent orbit. Although studies on shape-similar orbits have been done, they have yet to quantify it [25]. The Hausdorff Distance (HD) is a topographic metric that determines the proximity of two sets by cataloging and comparing the largest deformation distance between members of the sets. Determining the supremum of all the infimum (see Figure 4) distances provides an approach whereby shape similarity can be effectively quantified.
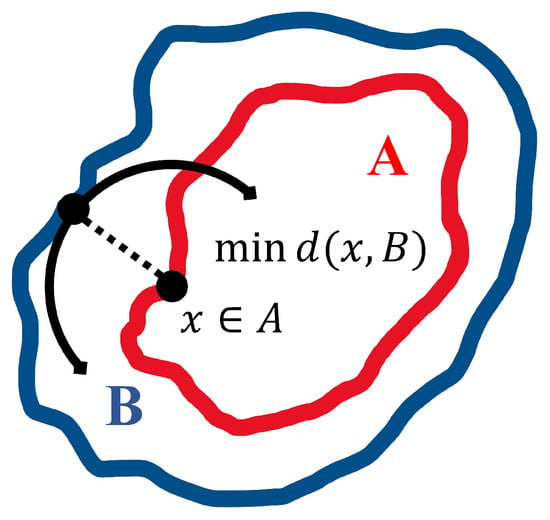
Figure 4.
Schematic depicting the infimum distance between set B and a selected point in A.
Computing HD for quantification of shape similarity between two continuous orbits is affected by the discretization or sampling density. Therefore, an optimal sampling density was identified by conducting a convergence analysis. It is hereby noted that, once discretization was performed, the infimum was calculated by employing a simple vector difference approach. Figure 5 shows the convergence of HD for two distinct orbits from the same parent counterpart—Halo Orbit from the Northern EML1 Family, for one rev and two revs. Figure 6 shows the same process applied to a Northern EML3 with for an identical initial geometry. For all four cases, the orbits were sampled at increasing densities up to 1000 with a parent orbit reference sampling density of 5000 points. It was observed that the HD magnitude converged for sampling density ≥200 as shown for the HPOs. Numerical identification of the optimal sampling density led to a more efficient algorithm workflow. Furthermore, HD effectively enables the filtering of orbit revs that are shape-similar or homeomorphic to their parent orbit from the unbounded dataset of possible periodic orbit revs spanning the entire solution space.
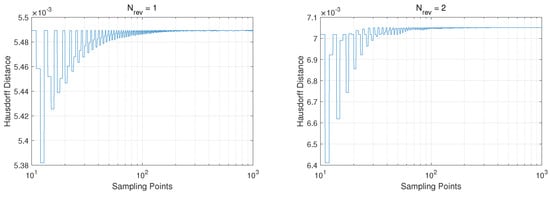
Figure 5.
Convergence test of estimated HD between the parent EML1 orbit and HPO for .
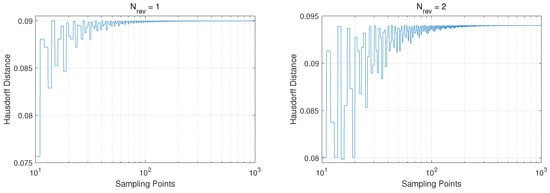
Figure 6.
Convergence test of estimated HD between the parent EML3 orbit and HPO for .
After a filtered dataset has been prepared, target conditions for a shooting scheme can be immediately ascertained by comparing the HD of the current orbit rev with the HD for the other revs in the dataset. Any maintenance algorithm can therefore be informed about possible “attractive” choices for future targeting. Essentially, the HD parameters can be embedded in the maintenance algorithm and make it substantially more efficient through an informed selection of boundary conditions.
3. Problem Formulation
In the context of the current work, the initial problem is the discovery of periodic orbit revs and the generation of a holistic dataset. Constraining the morphed shape and size of these orbits close to their CR3BP “parent orbits” while maintaining periodicity in a higher fidelity system is a particularly challenging endeavor. Although the solution space is also populated with multi-rev solutions, the unmodeled perturbing effects often significantly alter the shape of the converged revs and may compromise the mission requirements. After cataloging the converged HPOs at several initial true anomalies for a given primary-secondary system, target states for the SK shooting algorithm are extracted relative to the initial true anomaly. Although there are infinitely many impulsive SK configurations that can account for the deviations due to unmodeled system dynamics and navigation errors, in this study, the location is limited to the plane crossings made by the spacecraft. A detailed description of the methodology along with the underlying algorithm is presented in a subsequent section. Comparing the energy cost at each cycle and selecting the lowest combined value for insertion to the periodic orbits reveals an optimal single-pulse per-rev SK architecture. By alternating the cycles of observation and SK continuously, these orbits are expected to resemble their traditional periodic counterparts while also being maintained for the expected duration of the mission.
3.1. The HOPE Algorithm
The HOmeomorphic Periodic revs Evaluation (HOPE) algorithm utilizes an arc-length homotopy approach that converges to periodic initial conditions in the higher fidelity ER3BP system. The algorithm utilizes eccentricity as the continuation parameter for a fixed initial true anomaly. By segmenting the process, a sequential and iterative algorithm flow was achieved and presented in Algorithm 2. The calculations were performed on MATLAB R2023a using a mex version of MATLAB’s ode45 with absolute tolerances of and relative tolerances of . In fsolve, ‘MaxIteration’ was set at 10,000, whereas ‘MaxFunctionEvaluation’ was set at 1000 with both step and function tolerances of for the Earth–Moon system.
| Algorithm 2: Homeomorphic Periodic Revolutions Evaluation (HOPE) Algorithm |
 |
The algorithm was “warm-started” with the CR3BP “parent” orbit conditions and was differentially corrected to obtain new periodic conditions. Although the system could be “cold-started” with randomly generated initial conditions, convergence was invariably harder to achieve for such cases. Furthermore, even for the converged solutions, there is no guarantee that such a solution would be homeomorphic. Note that in Equation (3a) and (3b) for the circular assumptions, the r and parameters have values of 1 and 0, respectively. However, the pulsating frame used to analyze the ER3BP system leads to temporal variation in the r and ; the geometry is then continually defined under Keplerian assumptions. Next, continuation is performed starting with a constant initial true anomaly, , with the eccentricity continually modified in incremental steps until the desired eccentricity value is achieved and similar to the real dynamical system (e.g., for the Earth–Moon system [1,36]). This is unlike the real Earth–Moon which has a temporally evolving eccentricity that varies in the range of 0.0255 to 0.0775 but is restricted to allow preliminary analysis [36].
It is hereby noted that an initialization is necessary as the derivatives of the function with respect to the arc length are not explicitly known at the first iteration step. Natural parameter continuation is adept at estimating the derivatives and with two states and their derivatives known, the loop iterates to solve the arc length and dynamic constraints along with the derivatives of the future step computed as the Jacobian of the system. As previously mentioned, the algorithm is warm-started with the CR3BP periodic orbit condition and then continues to explore the solution space as the parameters are changed. Furthermore, note that the Jacobian may not always be full rank and for those cases, the path closest to the original state values may be selected instead so that the algorithm progresses as this is an indication of a bifurcation. Due to the chaotic nature of the dynamics and the densely populated solution space for periodic orbit revs, convergence is expected to be sensitive to numerical tolerances and must be constrained to ensure that the solutions do not diverge into other orbital families. The output is recorded for all converged orbits belonging to the current solution path, which displays periodic behavior over required revs. An “eccentricity continuation path” is traversed for all the initial geometry configurations every since system periapsis. Due to the arc-length step being decoupled from natural parameter values, a stop feature is implemented once the desired eccentricity is obtained.
Results from the aforementioned EML1 northern halo orbit with a period of 12 days has a state description as shown in Table 1 and has the corresponding dataset depicted in Figure 7, Figure 8, Figure 9 and Figure 10. The HOPE algorithm generated the depicted periodic revs using a constant arc-length step size of for all conditions.

Table 1.
EML1 halo orbit parameters in normalized units (DU,VU) [4].
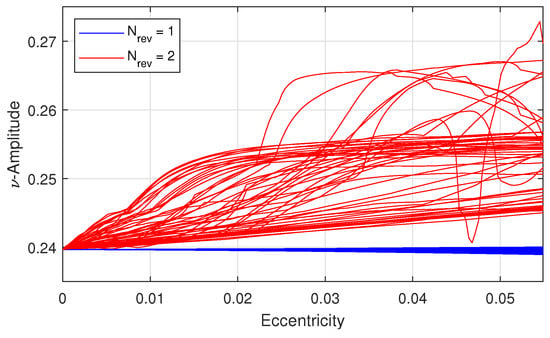
Figure 7.
Bounded -amplitudes for HPO families with different initial geometries.
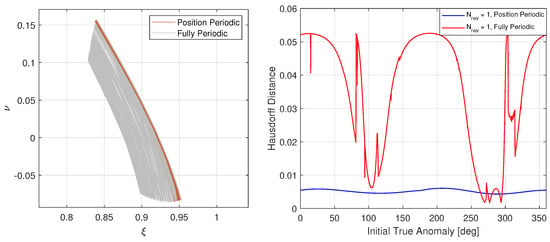
Figure 8.
Comprehensive set of HPO configurations for at different initial geometries. Unfiltered orbits shown on the left, with corresponding Hausdorff distances shown on the right.
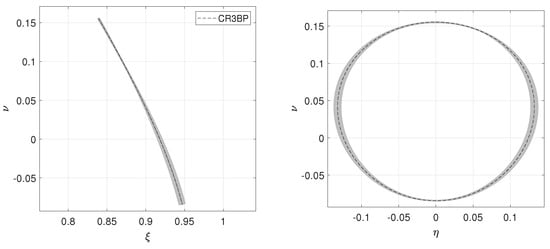
Figure 9.
Plot depicting the filtered dataset for at all initial geometry configurations. Reference halo orbit has = 93,400 km.
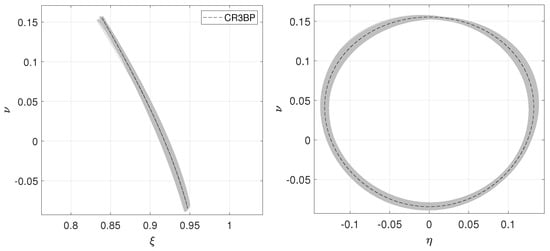
Figure 10.
Plot depicting the filtered dataset for at all initial geometry configurations. Reference halo orbit has = 93,400 km.
Since the motion is defined in the pulsating frame, it is important to note that the -axis projections can be treated as an effective Z-amplitude. For gaining heuristic insights into the nature of solutions, the -amplitudes were plotted vs. eccentricity for both HPOs (see Figure 7). Graphical comparisons elucidate the relative shape divergence due to eccentricity continuation. It is also hereby noted that due to the chaotic nature of the system, establishing convergence for solutions requires a substantially larger computational effort. However, a successful survey of the entire solution space leads to local solutions that satisfy the periodicity constraint given the initial conditions and a prescribed number of revolutions. The HOPE algorithm was tested and demonstrated to be robust in generating HPOs for for several orbit families and systems even though convergence was neither guaranteed nor shape similarity always possible. The combined set of initial state descriptors along with shape-similarity metrics were embedded into the dataset and then used to extract geometrically informed boundary conditions for the impulsive SK algorithm. Stitching together partially periodic revs maintains continuity in position and helps maintain the next revolutions for free. Small velocity discontinuities were permitted to provide flexibility and carefully balance the trade-off between shape similarity and periodicity to avoid over-constraining the system. For the aforementioned northern halo orbit, the maximum allowable HD was based on the one-rev position periodic orbit set. Given that the two-rev orbits, whether fully periodic or not, would require more leeway, filtering criteria were more relaxed with a maximum allowable HD that was twice as large as the respective one-rev case.
3.2. Station Keeping
Once the dataset of all the possible periodic orbits is generated, the station-keeping process in Algorithm 3 was implemented to quantify maintenance costs for sustaining presence in the neighborhood of any CR3BP periodic orbit of interest. To commence the process, the dynamical system and starting true anomaly must be selected, thus determining the starting periodic revolution which is natural to the respective celestial geometry. Mission duration will give the necessary amount of time the spacecraft must station-keep to satisfy the desired lifetime requirements. After the ith periodic rev is finished, the spacecraft is propagated across all the future plane crossings that are accessible to commence the maneuvers. With all the possible combinations of impulses based on Figure 11 and the number of periodic orbits within the generated dataset, the selection is restricted to minimize the impulse costs at each crossing by an estimated “ideal” transfer time. Note that this requires an underlying assumption that the respective periods of the orbits are relatively close. Although this may not always be true, the resulting correction leg is bound to be quasi-optimal given the other constraints.
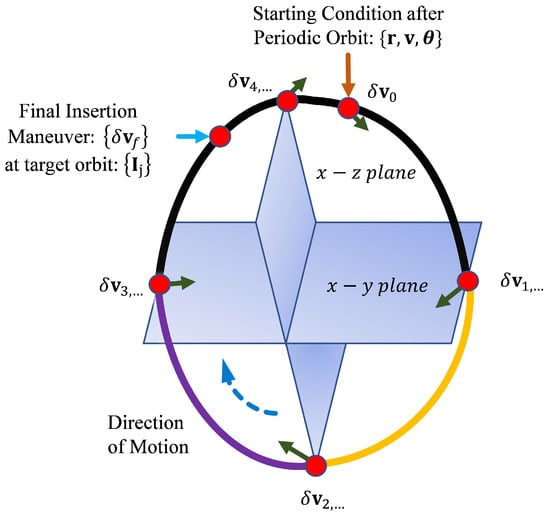
Figure 11.
Conceptualization of the optimal single-impulse per-rev SK architecture.
The equations of motion are in terms of the true anomaly within the pulsating frame and true estimates for the require multiple conversion steps. Exploring the kinematic derivatives with respect to time requires derivative change [21] as follows:
The inclusion of Equation (4) allows the true velocity values to be calculated given the current state. For the conversion of the velocity vectors in the pulsating frame to the rotating frame requires the product rule resulting in the following:
In terms of magnitude, the inertial and rotating frame vectors are the same with the only change being the direction which is rotated about the z-axis by the true anomaly and the origin which can be translated. For the spacecraft’s position, the conversion from the pulsating to rotating frames is via a simple scaling factor r as the frame pulsates.
| Algorithm 3: Station-Keeping Algorithm |
 |
Since this station-keeping mechanism solves the problem on a per-orbit basis, the costs per-orbit are non-uniform depending on the state of the system and the spacecraft. Furthermore, the solutions will invariably depend on the initial celestial geometry. Therefore, launch considerations and mission architecture must account for the interdependence between geometry and maintenance fuel consumption.
4. Results
Given the success of the Artemis I mission and the planned Lunar Gateway, studying the insertion and maintenance of periodic orbit analogs in the Earth–Moon system is crucial for the advanced mission design of future missions. Utilizing the dataset as seen in Figure 9 and Figure 10, the necessary station-keeping costs for 1 year of operations are shown. This process was repeated at intervals of for various initial system geometries.
As evident from Figure 12, although initial geometry can significantly alter the single-impulse station-keeping costs to maintain the orbit, the costs are still bounded across the entire domain for the = 93,400 km CR3BP parent halo orbit. To elaborate further, Figure 13 depicts the accumulated per-rev costs to maintain 32 revs over a period of a year for the most and least optimal scenarios.
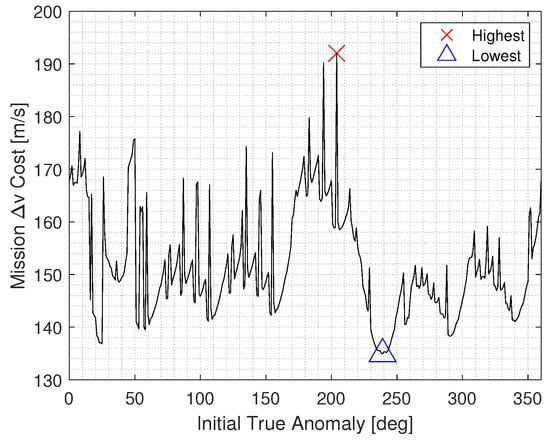
Figure 12.
Trend capturing the effect of initial geometry on station-keeping costs for sustaining a 1-year lifetime on the selected EML1 northern halo orbit.
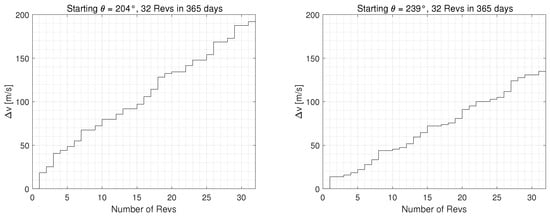
Figure 13.
Cumulative station-keeping costs for the EML1 northern halo orbit over a 1-year lifetime for (left) and (right).
Each impulse performed is represented as a discontinuous jump from one rev to another in Figure 13. For the trajectory with an initial true anomaly of , the total annual station-keeping cost with the single-impulse per-rev architecture is 192 m/s or about 6 m/s per-rev on average. Some solutions are used, but not often which then makes the particular maneuvers quite expensive. Furthermore, the cost per-rev is consistent throughout the path taken. Nevertheless, other initial states lead to improved results, as seen from the initial true anomaly of which has better stability. This characteristic can be seen from the repetitive maneuvers that appear to occur, especially those of solutions which decrease the costs significantly. The total annual station-keeping cost comes out as 135 m/s or about 4.2 m/s per-rev on average. This leads to a distribution of maneuvering costs since the SK costs vary from 1.71 m/s to 12.4 m/s per-rev. It should be noted that the costs would further decrease if more frequent maneuvers are implemented in far more unstable local regions, but this paper only characterizes strictly one impulse per-rev scenarios.
For a more intuitive representation, the paths were mapped onto the pulsating frame shown in Figure 14 where the red dot denotes the starting position state and the green dot denotes the final position state. Due to the orbital period being out of resonance with the lunar orbit, the spacecraft must continuously perform corrective maneuvers to maintain a shape-similar trajectory for an extended period of time. The magenta vectors show the impulses necessary to maintain the orbit which have a strong dependence on the starting conditions. The solid black lines indicate the HPO revs, whereas the dashed blue lines represent the intermediate trajectories denoting the post-maneuver path that transfers the spacecraft to the next selected rev. It is immediately evident based on a graphical analysis of the trajectories in Figure 14, that the hypothesis proposing a direct correlation between shape similarity of the orbital revs holds true. Unsurprisingly, with the single-impulse per-rev architecture, the “local” optimal location was at the apoapsis of the current rev. This leads to lower station-keeping costs which are seen in Figure 12 and Figure 13. Considering that this only shows the perspective from the pulsating frame with respect to the Lagrange points, the true path for the lowest cost trajectory was also plotted as observed in the Moon-Centered Rotating Frame.
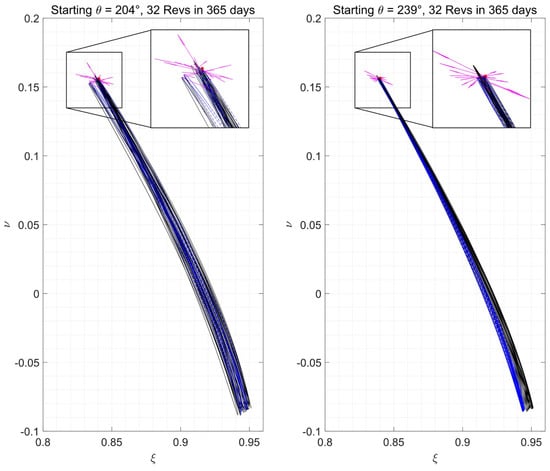
Figure 14.
Pulsating frame trajectories for the EML1 northern halo orbit. Magenta arrows denote the optimal impulsive maneuvers.
When viewing the trajectory from the Moon-Centered Rotating Frame in Figure 15, the distortion produced by the eccentricity can be further observed. The cumulative trajectory as observed in this frame forms a shape akin to a truncated cone as the pulsating frame expands and contracts. This leads to a variation in the Z-amplitude () of 0.0298 DU or 11,600 km due to the eccentricity. This variation is consistent throughout all the successive HPO revs and for every configuration due to an absence of resonance with the Moon’s motion. Typically, the periodic orbit revs were followed during the closest approaches of the Earth and Moon, but the intermediate transfer trajectories occurred as the overall system slowed down at a much farther distance, thus reducing the costs required to transfer arcs. At its closest approach, the Moon’s gravity is dominant, and therefore impulses are necessary to prevent ejection towards the Moon. Likewise, when the spacecraft is at its furthest, the Earth’s gravity is dominant; therefore, impulses are required to prevent the spacecraft from ejecting towards the Earth. The station-keeping trajectory tends to maneuver in a direction away from the dominant force to minimize opposing effects. Thus, optimal domains could be analyzed and this insight can be further refined to design a multi-impulse per-rev maintenance architecture.
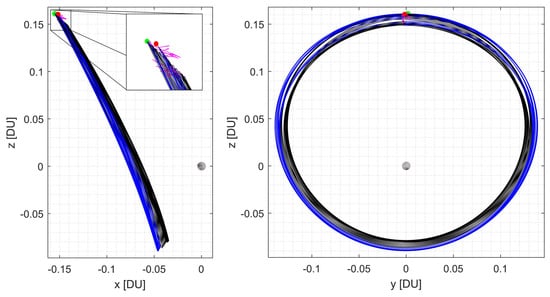
Figure 15.
x-z and y-z projections of the most optimal case plotted in the Moon-Centered Rotating Frame. Magenta arrows denote the optimal impulsive maneuvers.
A worthwhile consideration previously noted is the scalar change in lunar eccentricity. Although not incorporated in this work, this effect can be easily simulated by changing the primary-secondary distance in Equation (1) and initial conditions from Equation (3a) and (3b) to accurately model the effect of the non-linear eccentricity as a function of the true anomaly. Given that the periodicity of these orbits can be sensitive to minor changes, this would drastically alter the dataset and subsequent station-keeping costs.
Since the launch of the James Webb Space Telescope (JWST) on the 25th of December 2021, the telescope has provided a large amount of data and scientific information [37]. Due to the infrared nature of the telescope, it had to be stationed at a location that was relatively near the Earth but constantly facing away from the Sun. The nominal Southern Halo Orbit with = 984,000 km and C = 3.000747 was selected as an ideal location to perform observations, studying the selected orbit and quantifying the maintenance costs over a 20-year lifespan would help with budgeting during preliminary mission design. A lack of accurate orbit parameters means that a parent orbit based on the graphical representation was selected as an approximate analog orbit which has the initial states shown in Table 2. In this case , 1 DU = 149,597,871 km, and 1 TU = 5,022,635 s for the Sun–Earth system [4]. Furthermore, the step and function tolerances for fsolve were altered to for better convergence.

Table 2.
JWST Southern Halo Orbit parameters in normalized units (DU,VU) [4,38].
The nominal orbit in the Sun–Earth system has a period of 180 days, just under 6 months. Since the eccentricity is not constant, the value used was based on an averaged estimate near 2030 (e.g., [39]). The filtered database of shape-similar revs was utilized to perform station-keeping quantification for several initial geometries and Figure 16 provides a depiction similar to the previous case. The output was observed to show high sensitivity to the starting initial geometry. Even a small offset, close to a single degree, between sequential scenarios translates to drastic changes in the station-keeping costs. In Figure 17, two trajectories were presented to compare and contrast incurred costs.
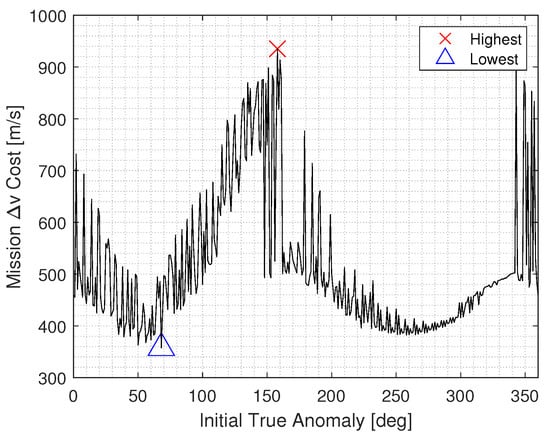
Figure 16.
Trend capturing the effect of initial geometry on station-keeping costs for sustaining a 20-year lifetime of the JWST.
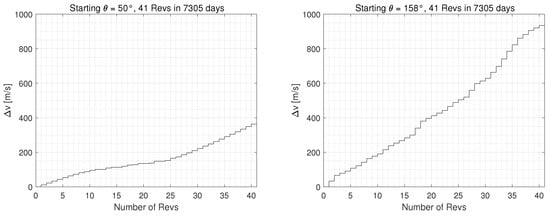
Figure 17.
Cumulative station-keeping costs for the JWST orbit over a 20-year lifetime for (left) and (right).
For the trajectory with an initial true anomaly of , Figure 17 shows that the total annual station-keeping cost comes out to be 363 m/s or about 8.86 m/s per-rev on average. Several solutions were used, but not very often due to the instability of the system, thus rendering the particular orbit rev maneuvers quite expensive. For the initial and final segments of the path, the single rev orbits are selected rather than the intermediate segment between orbits 10 and 25 where the costs can be as low as 2.16 m/s which more closely resembles costs to the real JWST. The least optimal condition starts at an initial true anomaly of , requiring large impulses to prevent escape from the system. This is visualized in Figure 18 within the pulsating frame.
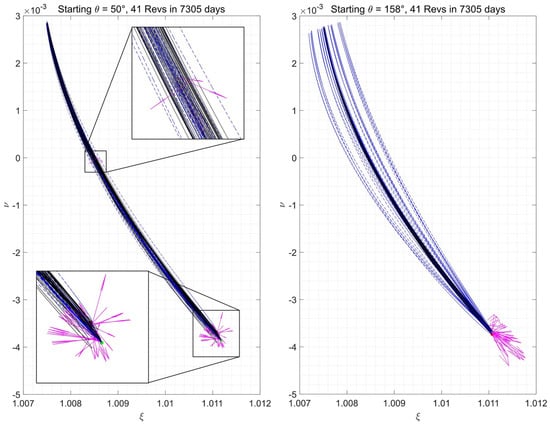
Figure 18.
Pulsating frame trajectories for the JWST orbit.
Considering that the orbital period for the nominal JWST orbit has 2:1 resonance with the Earth, most of the station-keeping maneuvers were performed under similar geometric conditions. Since the orbital period does not exactly match the resonance value, the spacecraft must continuously correct at the precessing true anomaly values. The magenta vector that indicates the impulses are much more significant for the latter case which is also reflected in the accumulated costs over the 20-year mission lifetime. For the more optimal case, a magnified sub-image is provided to show that most maneuvers tended to be perpendicular to the trajectory path. The shape similarity of the path once again shows that the proximity of the trajectory to the parent orbit lowered station-keeping costs. There is enough stability for certain HPOs that the optimal impulsive maneuver is shown to be at the x-y plane rather than at apoapse. For a more insightful visual representation, in Figure 19 the spacecraft path is plotted in the Earth-Centered Rotating Frame.
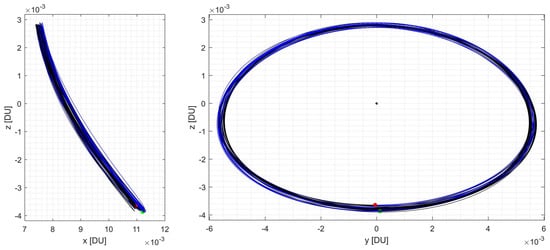
Figure 19.
x-z and y-z projections of an optimal JWST SK orbit bundle observed in the Earth-Centered Rotating Frame without a depiction of the impulsive maneuvers.
The trajectory in Figure 19 better resembles the true path taken by the spacecraft as it traversed the region. Even though the system’s eccentricity is smaller when compared to the Earth–Moon system, the overall orbit size is significantly larger. A Z-amplitude () variation of DU or 64,640 km was observed due to the eccentric secondary orbit, which is commensurate to the real orbit profile for the JWST mission. The presence of certain resonant orbit revs and initial geometric conditions where convergence was difficult due to instability leads to a complex and almost enigmatic correlation between and . Careful analysis could only reveal a weak correlation. It is therefore hypothesized that the stability index of the individual HPO revs is possibly a much more significant factor. In the front view within Figure 19, the positional deviation from the ideal CR3BP halo orbit is quite noticeable, as the Earth is provided there for scale. Since both the Earth and Sun were on the same side of the orbit, there was no preference as to when the station-keeping maneuvers were necessary. This path also stays completely out of the Earth–Moon system shadows as JWST was designed to be a solar-powered telescope. It is hereby noted that SRP is an important forcing function not considered a part of this work. A more accurate result and SK quantification would also consider this effect but such analysis is amenable to the described methodology.
Since the revs in the EML1 halo discussed earlier were very unstable and sensitive to perturbations, all the course corrections were performed immediately after one period of each rev. On the other hand, for the JWST there was enough stability for certain orbits to sustain multiple x-y plane crossings, resulting in lower average annual fuel consumption. Although this architecture limits the maximum impulse count to one per-rev, the real telescope performs such a maneuver on a monthly basis [38]. This is effectively six station-keeping maneuvers per-rev, which is not very far off from the design in this paper. Therefore, the conservative costs of the optimal trajectory using the single-impulse per-rev architecture is expected to be within an order of magnitude of the true values for a 20-year mission lifetime.
5. Conclusions
A novel methodology for the discovery of ER3BP periodic counterparts of the CR3BP parent orbit was presented. Additionally, total mission orbit maintenance costs were estimated using a single-impulse per-rev architecture. First, numerical continuation methods were implemented to generate an a priori dataset of quasi-periodic orbits in the ER3BP based on the initial true anomaly and eccentricity of the primary-secondary system. Evaluating these results for , in addition to striking a balance between the periodicity and homeomorphism, was used as an input for an orbital maintenance algorithm to evaluate the fuel requirements to maintain the spacecraft for a given mission lifetime and insertion conditions. The proposed method performs a maneuver at either the end of the periodic orbit or at one of the sequential plane crossings to get the spacecraft to insert into the next quasi-periodic orbits. If necessary, an additional impulse is used to match all the velocities and thereby the conditions necessary for periodicity. Two case studies were presented in the Earth–Moon and Sun–Earth systems to demonstrate the applicability and robustness of the described methodology.
An northern halo orbit was analyzed in the cis-lunar space with a period of 12 days for annual station-keeping costs, for a total average of 32 revs. The most- and least-optimal trajectories were studied in further detail, which came to an overall cost of 135 m/s and 192 m/s, respectively. It was observed that as the trajectory arc more closely resembled the original parent orbit, the lower the SK costs were. Generally, the impulses were to prevent the escaping of the spacecraft toward any of the two major bodies. Effects of the eccentricity led to larger variations in the orbital size but maintained the overall shape. Given that the JWST was recently launched and is currently providing positional information, the corresponding Southern Halo was analyzed using the same approach for a twenty-year life expectancy of the telescope. The 180-day period resulted in an average of 41 revs used for mission success. An optimal trajectory was studied in further detail with an overall cost of 363 m/s. Such a value is not very far off from the real mission specs as the SK architecture was only slightly more conservative in its estimate. The effectiveness of the proposed approach instills confidence in its applicability for preliminary mission design and quantification of orbit maintenance estimation.
Author Contributions
K.I.A. and S.K.S. were involved in conceptualization and problem formulation. K.I.A. and S.K.S. were involved in numerical analysis of results. K.I.A. was involved in writing and editing the manuscript and S.K.S. was responsible for internal manuscript review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
We are pleased to acknowledge the Rensselaer Polytechnic Institute for sponsorship of various aspects of this research. This work was completed at the Rensselaer Polytechnic Institute in the Advanced Space Concepts Lab (ASCLab).
Data Availability Statement
The data associated with this work is available on request. Much of the information can be found in the JPL Three-Body Periodic Orbit Catalog (https://ssd.jpl.nasa.gov/tools/periodic_orbits.html) for the periodic orbits. For information relating to JWST and the current trajectory, User Documentation (https://jwst-docs.stsci.edu/jwst-observatory-characteristics/jwst-orbit) was used by STScI.
Conflicts of Interest
The authors have no conflict of interest to disclose.
References
- Farquhar, R.; Kamel, A. Quasi-periodic orbits about the translunar libration point. Celest. Mech. Dyn. Astron. 1973, 7, 458–473. [Google Scholar] [CrossRef]
- NASA. Orion Reference Guide; NASA: Washington, DC, USA, 2022; pp. 51–65. [Google Scholar]
- European Space Agency. Angelic Halo Orbit Chosen for Humankind’s First Lunar Outpost; ESA: Paris, France, 2019. [Google Scholar]
- JPL Solar System Dynamics. Three-Body Periodic Orbits. 2023. Available online: https://ssd.jpl.nasa.gov/tools/periodic_orbits.html (accessed on 13 January 2023).
- Tselousova, A.; Trofimov, S.; Shirobokov, M. Station-keeping in high near-circular polar orbits around the Moon. Acta Astronaut. 2021, 188, 185–192. [Google Scholar] [CrossRef]
- Boudad, K.K.; Howell, K.C.; Davis, D.C. Dynamics of synodic resonant near rectilinear halo orbits in the bicircular four-body problem. Adv. Space Res. 2020, 66, 2194–2214. [Google Scholar] [CrossRef]
- McCarthy, B.; Howell, K. Quasi-Periodic Orbits in the Sun-Earth-Moon Bicircular Restricted Four-Body Problem. In Proceedings of the 31st AAS/AIAA Space Flight Mechanics Meeting, Virtual, 2 February 2021. [Google Scholar]
- Ming, W.; Yang, C.; Zhang, H. Family of resonant quasi-periodic distant retrograde orbits in cislunar space. In Proceedings of the 28th International Symposium on Space Flight Dynamics ISSFD, Beijing, China, 19–23 October 2022. [Google Scholar]
- de Almeida Junior, A.K.; de Almeida Prado, A.F.B. Comparisons between the circular restricted three-body and bi-circular four body problems for transfers between the two smaller primaries. Sci. Rep. 2022, 12, 4148. [Google Scholar] [CrossRef] [PubMed]
- Singh, J.; Omale, S.O. Effects of Albedo and Oblateness in the Bi-Circular Restricted Four-Body Problem. Partial Differ. Equ. Appl. Math. 2023, 7, 100464. [Google Scholar] [CrossRef]
- Zotos, E.E. How does the oblateness coefficient influence the nature of orbits in the restricted three-body problem? Astrophys. Space Sci. 2015, 358, 33. [Google Scholar] [CrossRef]
- Albidah, A.B.; Abdullah. Halo Orbits under Some Perturbations in cr3bp. Symmetry 2023, 15, 481. [Google Scholar] [CrossRef]
- Yousuf, S.; Kishor, R.; Kumar, M. Motion about equilibrium points in the Jupiter-Europa system with oblateness. Appl. Math. Nonlinear Sci. 2023, 8, 2075–2090. [Google Scholar] [CrossRef]
- Salazar, F.; Alkhaja, A.; Fantino, E.; Alessi, E.M. Science orbits in the Saturn–Enceladus circular restricted three-body problem with oblate primaries. Acta Astronaut. 2021, 180, 398–416. [Google Scholar] [CrossRef]
- Russell, R.P.; Lara, M. On the design of an Enceladus science orbit. Acta Astronaut. 2009, 65, 27–39. [Google Scholar] [CrossRef]
- Bury, L.; McMahon, J. The effect of zonal harmonics on dynamical structures in the circular restricted three-body problem near the secondary body. Celest. Mech. Dyn. Astron. 2020, 132, 45. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, Y.; Shi, Y.; Zhang, C.; Zhang, H. Performance analysis of impulsive station-keeping strategies for cis-lunar orbits with the ephemeris model. Acta Astronaut. 2022, 198, 152–160. [Google Scholar] [CrossRef]
- Guzzetti, D.; Zimovan, E.M.; Howell, K.C.; Davis, D.C. Stationkeeping analysis for spacecraft in lunar near rectilinear halo orbits. Adv. Astronaut. Sci. 2017, 160, 3199–3218. [Google Scholar]
- Feng, Z.; Xu, M.; Jian, K.; Li, J. Stationkeeping of halo orbits in Jupiter-Europa-Io system. Adv. Space Res. 2023, 71, 2629–2639. [Google Scholar] [CrossRef]
- Blazevski, D.; Ocampo, C. Periodic orbits in the concentric circular restricted four-body problem and their invariant manifolds. Phys. D Nonlinear Phenom. 2012, 241, 1158–1167. [Google Scholar] [CrossRef]
- Broucke, R. Stability of Periodic orbits in the Elliptic, Restricted Three-Body Problem. AIAA J. 1969, 7, 1003–1009. [Google Scholar] [CrossRef]
- Sheth, D.; Thomas, V.O. Halo orbits around L1, L2, and L3in the photogravitational Sun–Mars elliptical restricted three-body problem. Astrophys. Space Sci. 2022, 367, 99. [Google Scholar] [CrossRef]
- Peng, H.; Bai, X.; Xu, S. Continuation of periodic orbits in the Sun-Mercury elliptic restricted three-body problem. Commun. Nonlinear Sci. Numer. Simul. 2017, 47, 1–15. [Google Scholar] [CrossRef]
- Peng, H.; Xu, S. Transfer to a Multi-revolution Elliptic Halo orbit in Earth–Moon Elliptic Restricted Three-Body Problem using stable manifold. Adv. Space Res. 2015, 55, 1015–1027. [Google Scholar] [CrossRef]
- Alvarado, K.I.; Singh, S.K. Orbit maintenance via homeomorphic, periodic orbit revs in the Elliptic Restricted Three-Body Problem. In Proceedings of the 2023 AAS/AIAA Astrodynamics Specialist Conference, Big Sky, MT, USA, 13–17 August 2023. [Google Scholar]
- Gurfil, P.; Meltzer, D. Stationkeeping on unstable orbits: Generalization to the elliptic restricted three-body problem. J. Astronaut. Sci. 2006, 54, 29–51. [Google Scholar] [CrossRef]
- Howell, K.C.; Pernicka, H.J. Station-keeping method for libration point trajectories. J. Guid. Control. Dyn. 1993, 16, 151–159. [Google Scholar] [CrossRef]
- Fu, X.; Baresi, N.; Armellin, R. Stochastic optimization for stationkeeping of periodic orbits using a high-order Target Point Approach. Adv. Space Res. 2022, 70, 96–111. [Google Scholar] [CrossRef]
- Zhang, H.; Li, S. Station-keeping of libration point orbits by means of projecting to the manifolds. Acta Astronaut. 2019, 163, 38–44. [Google Scholar] [CrossRef]
- Singh, S.K.; Junkins, J.L. Stochastic learning and extremal-field map based autonomous guidance of low-thrust spacecraft. Sci. Rep. 2022, 12, 17774. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.K.; Woollands, R.; Taheri, E.; Junkins, J. Feasibility of quasi-frozen, near-polar and extremely low-altitude lunar orbits. Acta Astronaut. 2020, 166, 450–468. [Google Scholar] [CrossRef]
- Carletta, S.; Pontani, M.; Teofilatto, P. Characterization of Low-Energy Quasiperiodic Orbits in the Elliptic Restricted 4-Body Problem with Orbital Resonance. Aerospace 2022, 9, 175. [Google Scholar] [CrossRef]
- Szebehely, V. Theory of Orbits: The Restricted Problem of Three Bodies. In Theory of Orbit; Academic Press: Cambridge, MA, USA, 1967; pp. 556–652. [Google Scholar] [CrossRef]
- Singh, S.; Junkins, J.; Anderson, B.; Taheri, E. Eclipse-conscious transfer to lunar gateway using ephemeris-driven terminal coast arcs. J. Guid. Control Dyn. 2021, 44, 1972–1988. [Google Scholar] [CrossRef]
- Singh, S.K.; Taheri, E.; Woollands, R.; Junkins, J. Mission design for close-range lunar mapping by quasi-frozen orbits. In Proceedings of the 70th International Astronautical Congress, Washington, DC, USA, 21–25 October 2019. [Google Scholar]
- NASA. Eclipses and the Moon’s Orbit; NASA: Washington, DC, USA, 2012. Available online: https://eclipse.gsfc.nasa.gov/SEhelp/moonorbit.html (accessed on 23 May 2023).
- NASA Space Science Data Coordinated Archive. James Webb Space Telescope (JWST). 2022. Available online: https://nssdc.gsfc.nasa.gov/nmc/spacecraft/display.action?id=2021-130A (accessed on 16 June 2023).
- Space Telescope Science Institute. JWST Orbit; Space Telescope Science Institute: Baltimore, MD, USA, 2023; Available online: https://jwst-docs.stsci.edu/jwst-observatory-characteristics/jwst-orbit (accessed on 25 July 2023).
- Simon, J.L.; Bretagnon, P.; Chapront, J.; Chapront-Touze, M.; Francou, G.; Laskar, J. Numerical expressions for precession formulae and mean elements for the Moon and the planets. Astron. Astrophys. 1994, 282, 663. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).