An Autonomous Tow Truck Algorithm for Engineless Aircraft Taxiing
Abstract
1. Introduction
2. Literature Review
- In order to speed up the results, some studies permit solutions that may result in vehicle conflicts during the strategic planning phase.
- Many tow truck-based taxiing strategies prioritise identifying conflict-free routes and schedules, without considering the efficient allocation of tow trucks, such as minimising taxi delays or maximising fuel savings.
- Current performance metrics predominantly focus on taxi delays and the number of potential vehicle conflicts, neglecting the incorporation of fuel consumption and fuel saving metrics which could underscore the environmental advantages of utilising tow trucks.
- The proposed taxiing solutions are often only tested on one airport layout, leaving their effectiveness on airports of different sizes and layouts unverified.
- Performance evaluations of taxiing algorithms are frequently conducted using a single medium-level traffic scenario. This approach, while useful for initial testing, fails to assess the system’s robustness across different traffic levels.
- Such evaluations often employ a fixed number of tow trucks, discarding potential variations in the number of available tow trucks.
- The scheduling process frequently overlooks the state of charge of tow truck batteries, potentially distorting tow truck efficiency estimates, and underestimates the number of tow trucks for effective taxi operations.
- Several strategies do not continuously monitor for potential conflicts with other vehicles during the entire cycle of the operations, particularly for tow trucks when they are not actively towing. This leads to oversimplified solutions which, in reality, can be hazardous, failing to account for potential safety risks.
- The proposed algorithm is designed to prevent vehicle conflicts during the strategic phase for all simulated scenarios, ensuring safer and more efficient operations.
- A tow truck scheduling algorithm has been developed, which factors in the distance between the tow truck and the aircraft, battery charge level, potential route conflicts, and tow truck utilisation history during the simulated period.
- A more comprehensive set of performance metrics has been adopted, including fuel consumption, fuel savings, and tow truck utilisation.
- The algorithm underwent rigorous testing across four diverse airport layouts, encompassing a variety of sizes and geometries, to validate its broad applicability. These tests included simulations with a wide range of traffic levels and tow truck numbers.
- The simulations now consider the state of charge of the tow trucks, ensuring a more accurate depiction of tow truck availability and operational capabilities.
- The proposed system features continuous conflict checks for both aircraft and tow trucks, whether they are actively towing or not. This allows for the detection of potential conflicts with other vehicles throughout the entire cycle of operations, enhancing safety and system reliability.
3. Description of Algorithm
3.1. Airport Modelling and Assumptions
- is the total number of tow trucks;
- is the total number of depots in the airfield.
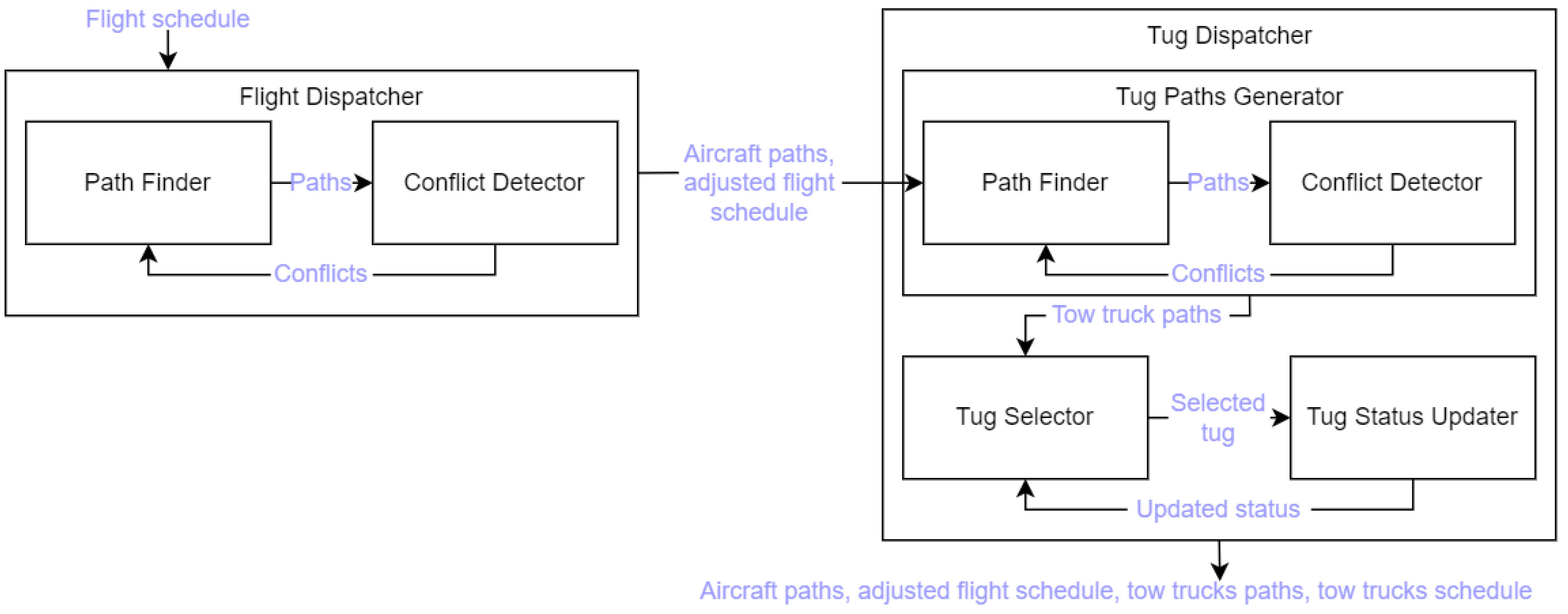
3.2. Flight Dispatcher
- and are input to the module Path Finder, which finds the ideal (i.e., shortest) path and the ideal (i.e., shortest) taxi distance. This distance is then divided by to find an ideal taxi time .
- The module attempts to find a conflict-free solution. First, the ideal path is forwarded to the Conflict Detector module. This module checks if the path is conflict-free; produces a Vehicle Occupation Table (VOT), which stores all the time windows during which the edges of the path are occupied by the vehicle; and, if potential conflicts are detected, stores them in the Edges in Conflict List (ECL), which contains a list of edges that need to be excluded from the next iteration of Path Finder.
- If potential conflicts are detected, Path Finder calculates a new path, excluding the edges listed in ECL, and the feasibility of the path—indicating whether the module found a feasible path (i.e., and are connected by a number of edges)—is checked. If the path is not feasible, the solution is discarded and the process restarts with an incremented (see point 5); otherwise, the feasible path is sent again to the Conflict Detector to check for the presence of conflicts. This process is repeated until a conflict-free path is identified or, as mentioned, until the path is flagged as not feasible. In case a conflict-free path is found, the module calculates and stores of the current iteration.
- is incremented by a time interval equal to 10 s (i.e., with the same duration of a time window) and the process is repeated from point 2 for a new iteration.
- New solutions are calculated until the of a new solution is greater than or equal to the of any solution, in which case the search for solutions is stopped for the analysed runway. The whole process is repeated for the next runway until all the LEPs (in case of an arrival) or all the ToPs (in case of a departure) are analysed.
- In case no conflict-free solutions are found (meaning that all of the solutions are discarded because the corresponding paths are considered to be unfeasible), the whole set of solutions is marked as unfeasible and the algorithm stops the calculations for the selected simulation.
- The solution with the lowest is selected, and the VOT of the selected solution is appended to the Global Occupation Table (GOT), which represents the combination of all the VOTs of the selected solutions of the previously analysed aircraft; therefore, when the first aircraft is analysed, the GOT is empty.
3.3. Tug Dispatcher
- Static and Dynamic Allocation of Tow Trucks
- 2.
- Tow Truck Allocation Criteria
- Availability of a conflict-free route from the tow truck’s location to the aircraft’s that permits the tow truck to reach the aircraft exactly at the of the aircraft;
- If multiple tow trucks meet the first criterion, the tow truck with the lowest associated Total Mission Cost (given by Equation (3)) is chosen;
- If more than one tow truck has the lowest associated cost as defined in the second criterion, the tow truck with the least utilisation time is selected to ensure a fair distribution of missions between the tow trucks.
- is the time that needs to complete the towing mission;
- is the maximum over all the tow trucks;
- is the maximum battery charge, equal to 100%;
- is the minimum allowed battery charge, equal to 20%;
- is the battery charge of .
- 3.
- Time-Wise and Fuel-Wise Approach
- Time-Wise Approach: In this approach, no tow trucks are assigned to the flight, and the aircraft is permitted to taxi with its own engines.
- Fuel-Wise Approach: Alternatively, if the Fuel-Wise Approach is chosen, the algorithm seeks to delay the of the aircraft by up to a maximum of 10 min. It then recalculates the aircraft schedule to determine if, under these adjusted conditions, (a) the aircraft route remains feasible (it should not be in conflict with the routes of the subsequent flights), and (b) at least one tow truck becomes available to satisfy the first criterion. If both conditions are met, the algorithm updates the aircraft schedule and assigns it a tow truck. However, if either condition is not met, the aircraft is instructed to taxi with its own engines.
- 4.
- Depot Allocation Criteria
- A conflict-free route exists from the final position of the assigned aircraft, , to the depot under consideration.
- The depot under consideration has at least one available parking slot at the time the tow truck is scheduled to arrive.
- The time required to return to the depot under consideration is shorter than the time needed to return to any other depot.
- 5.
- Battery Discharge Rates
- The Higher Battery Discharging Rate () is the battery discharge rate applied when the tow truck is in motion and loaded and is set equal to 2%/min.
- The Lower Battery Discharging Rate () is the battery discharge rate applied when the tow truck is in motion and unloaded and is set equal to 1%/min.
- The Battery Charging Rate () is the recharge rate applied when the tow truck is at a charging point in a depot and is set equal to 2%/min.
4. Testing and Results
- To assess the performance of engineless taxiing with tow trucks across various dispatch approaches;
- To analyse the size of the fleet of tow trucks that is necessary to cater for a certain level of airport traffic;
- To explore the impact of tow truck battery performance on the efficacy of the algorithm.
4.1. Performance Metrics
4.2. Airport Selection
- Malta International Airport (MLA): relatively small in size.
- Ben Gurion Airport (TLV): medium-sized, featuring a unique layout of the runways.
- Toulouse–Blagnac Airport (TLS): medium-sized, with a classic layout of runways.
- Dallas/Fort Worth International Airport (DFW): one of the busiest airports in the world [34].
4.3. Test Scenarios
4.4. Test Results
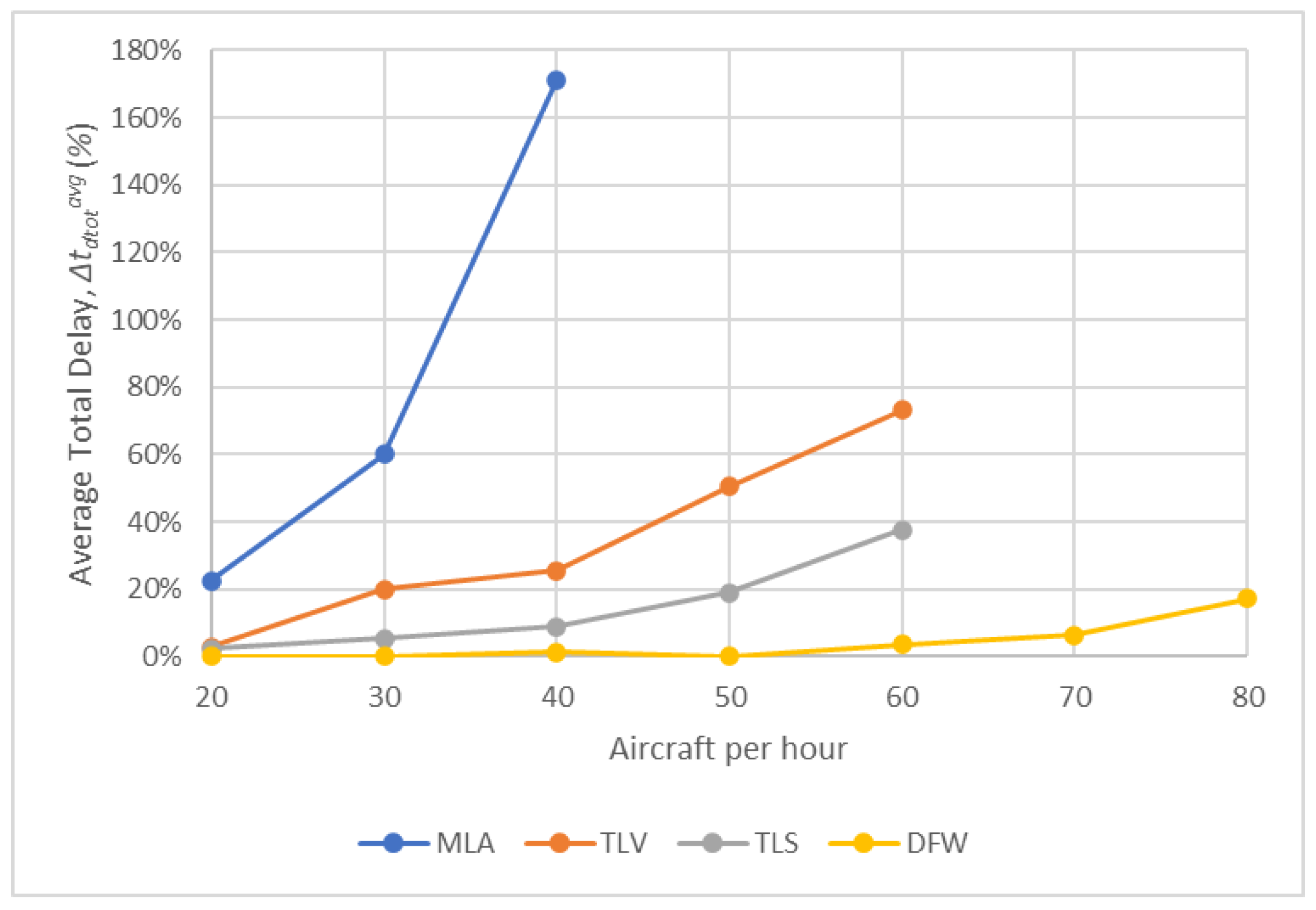
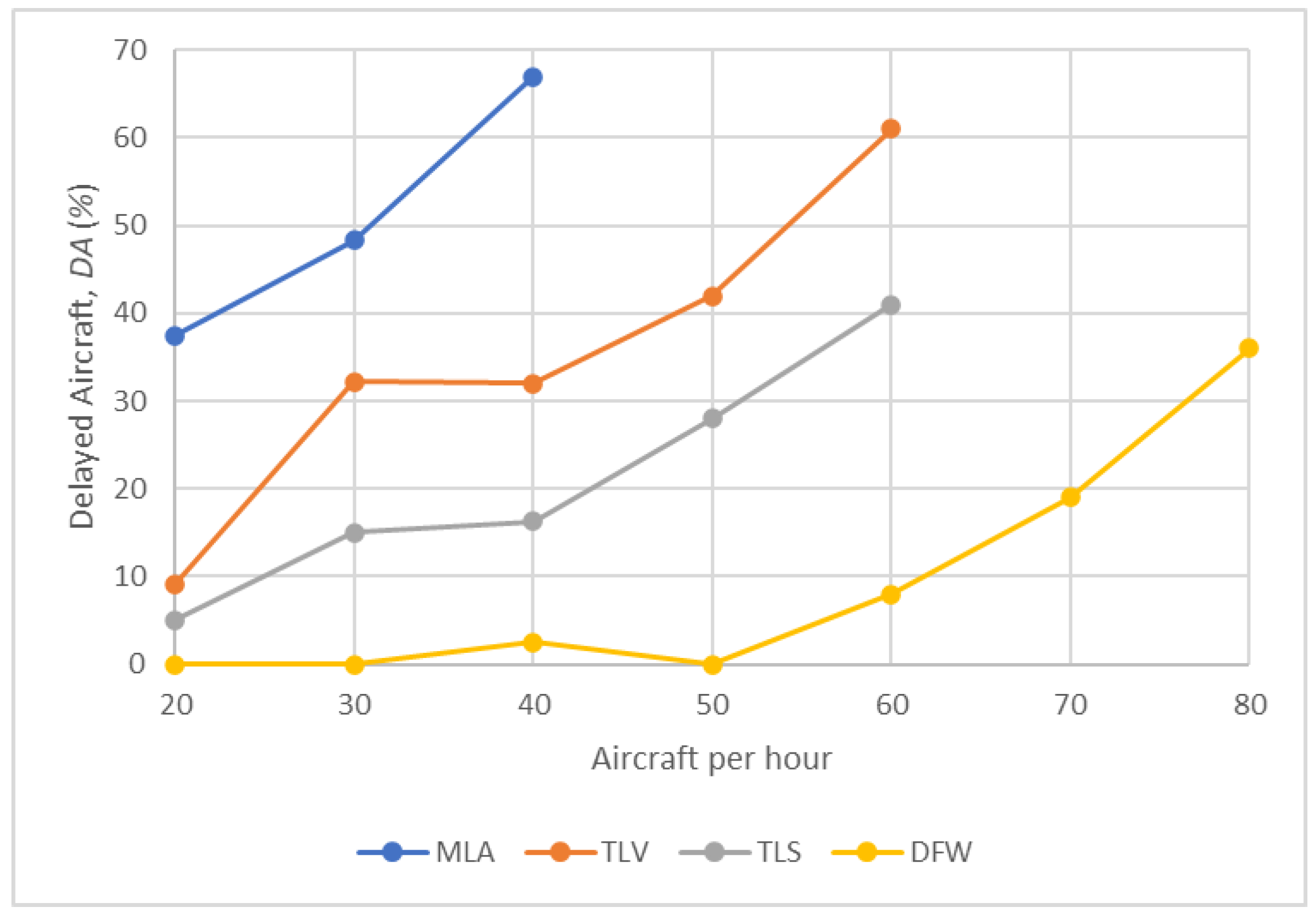
- Results for Test Scenario 1
- 2.
- Results for Test Scenario 2
- 3.
- Results for Test Scenario 3
- 4.
- Results for Test Scenario 4
- 5.
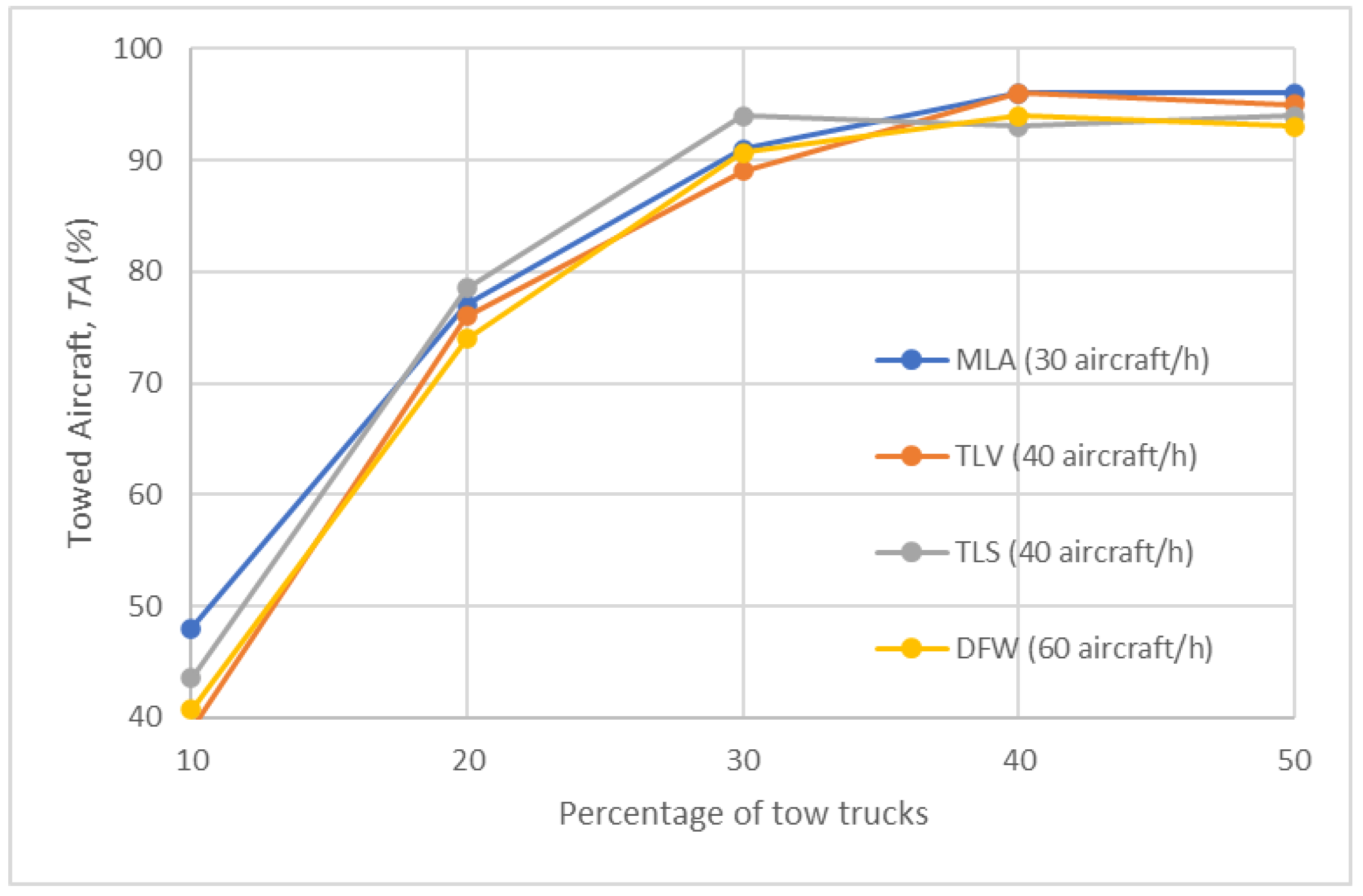
- Results for Test Scenario 5
- 6.
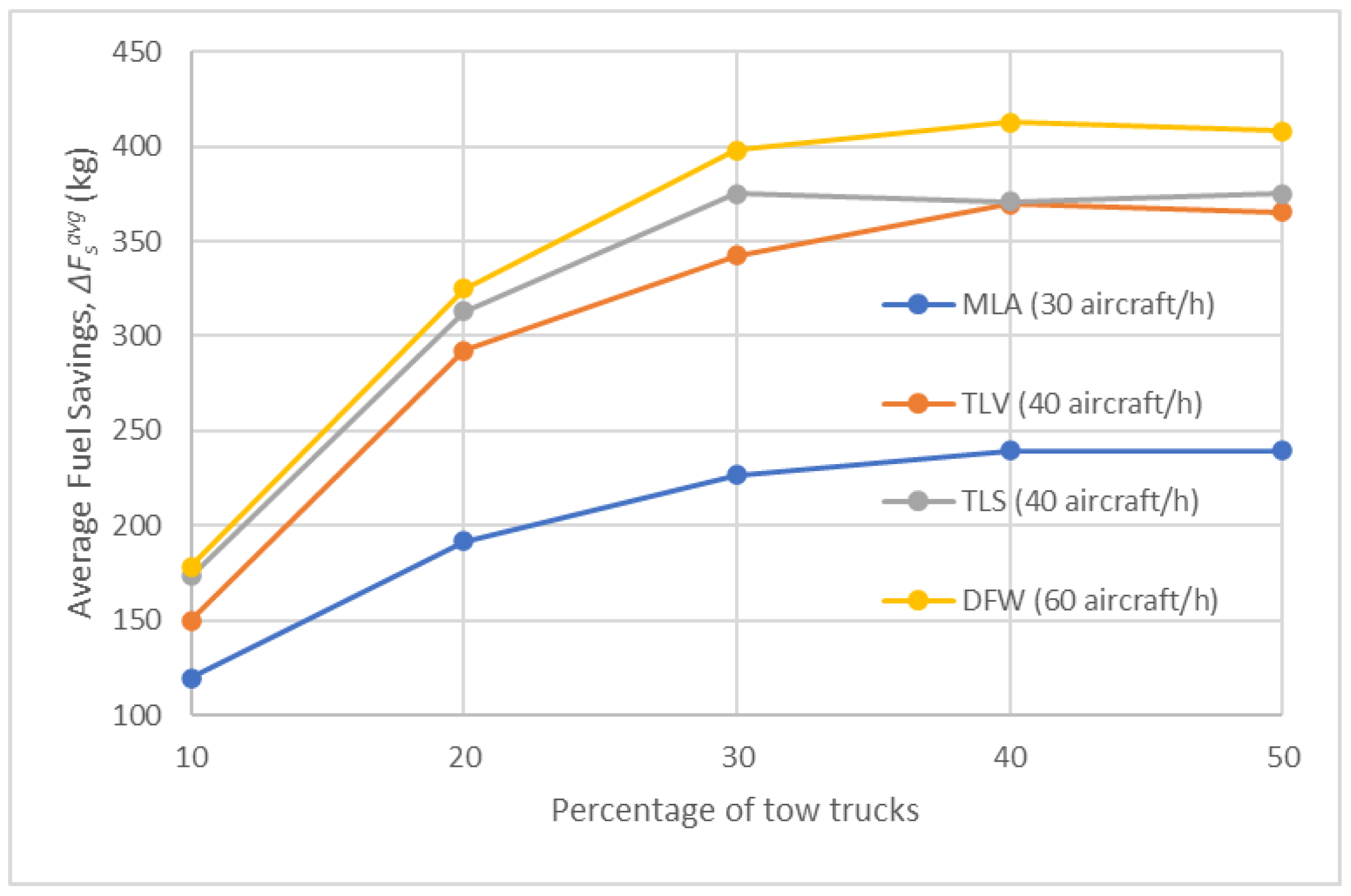
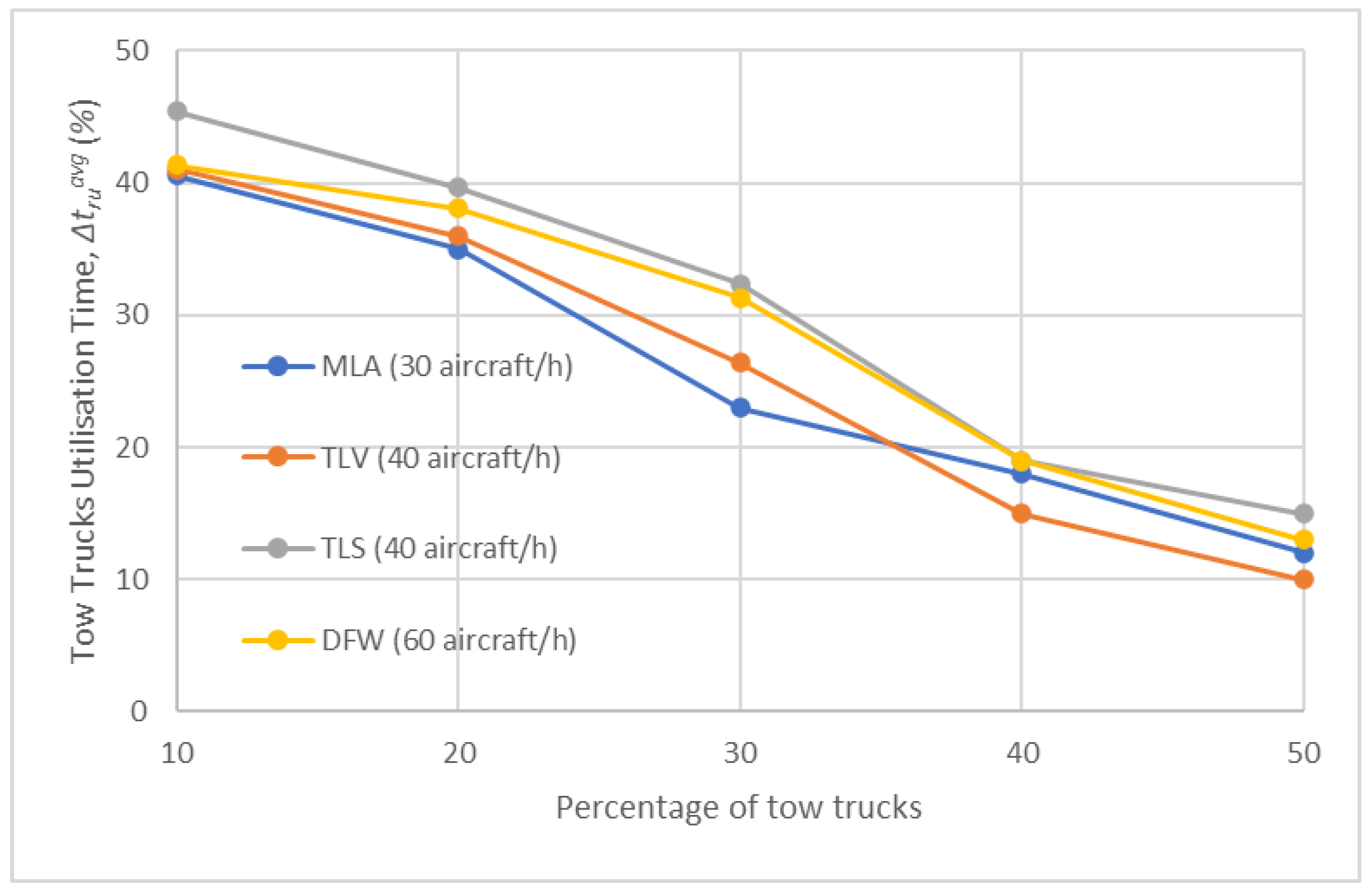
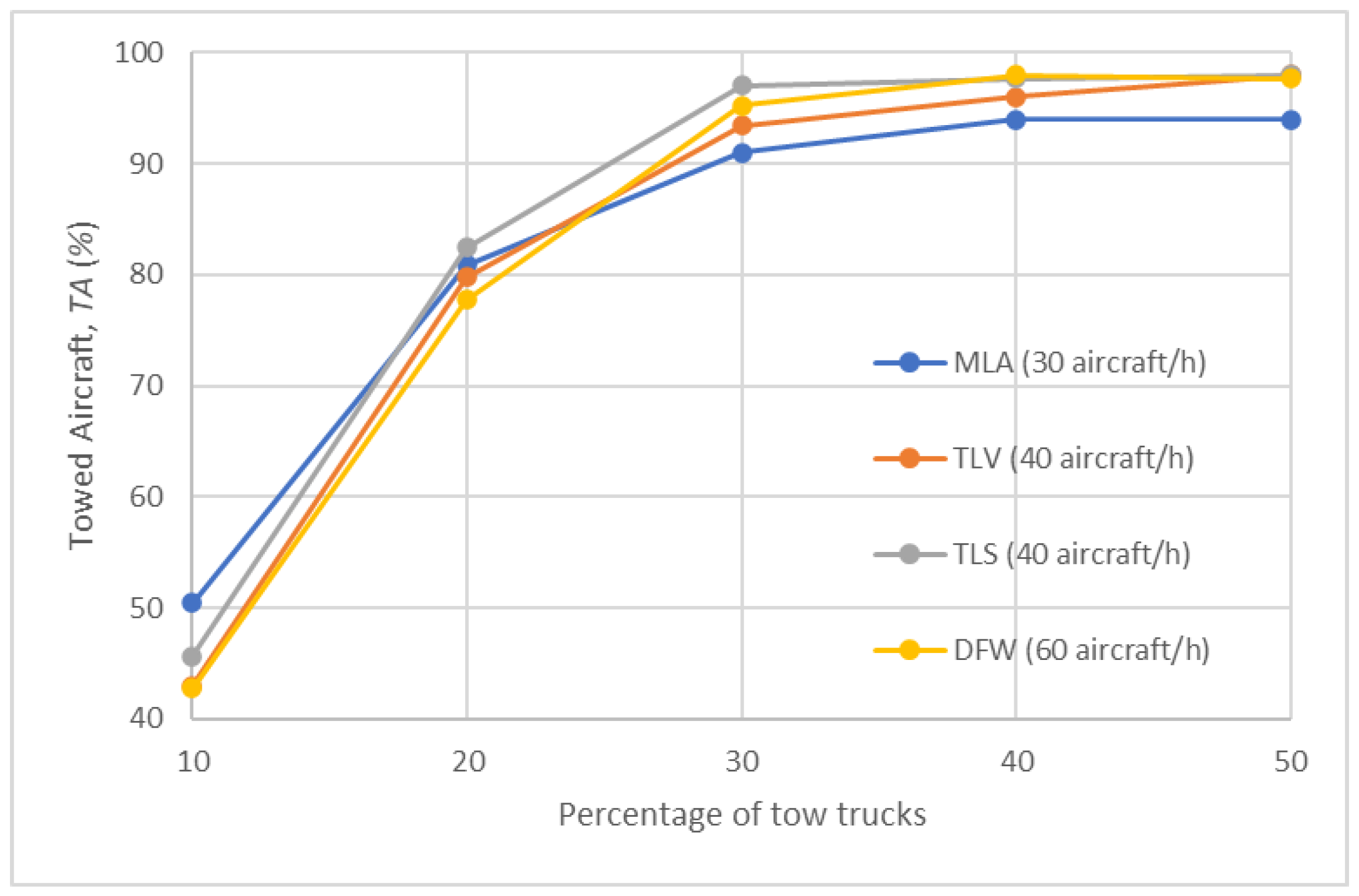
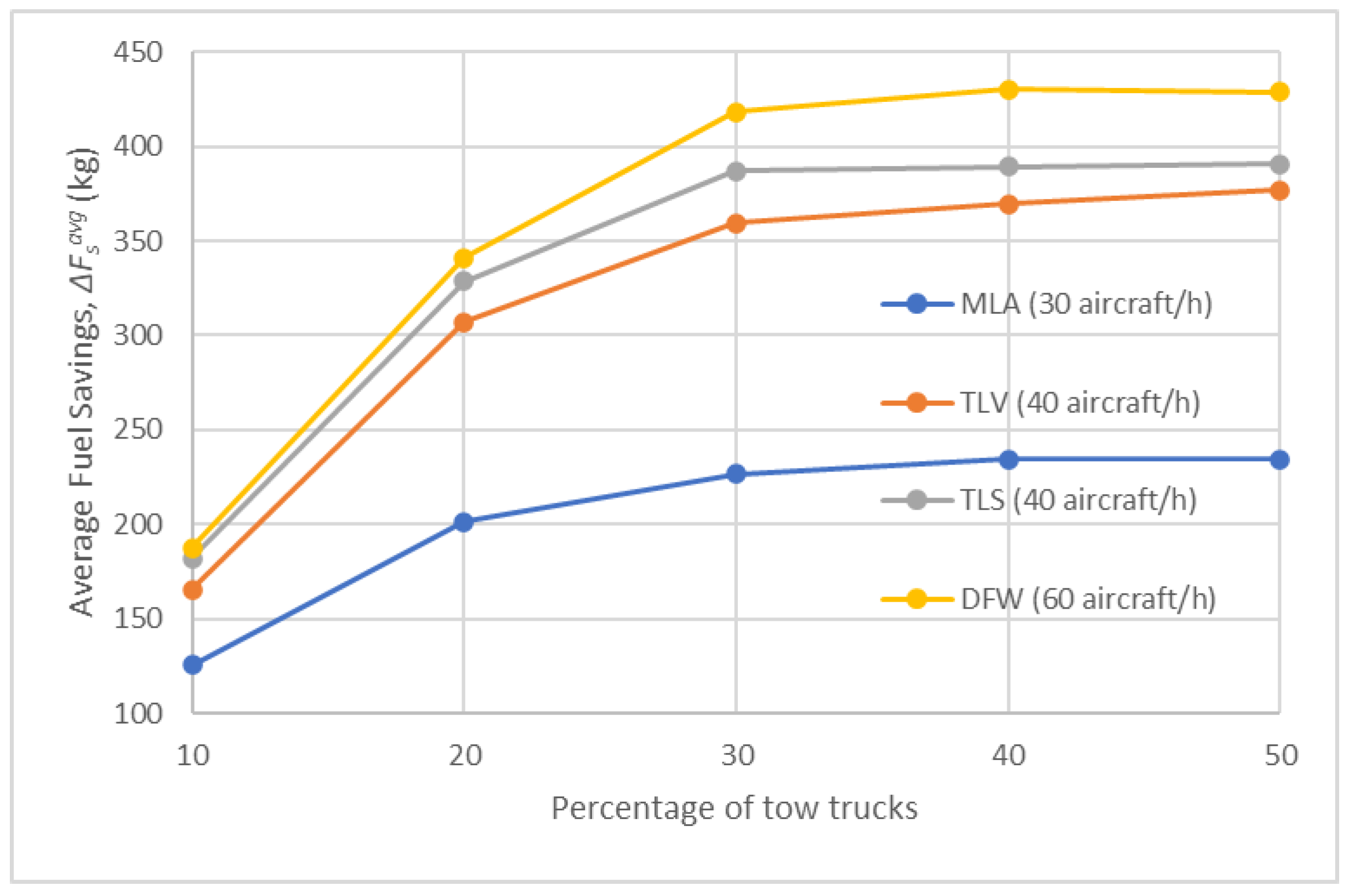
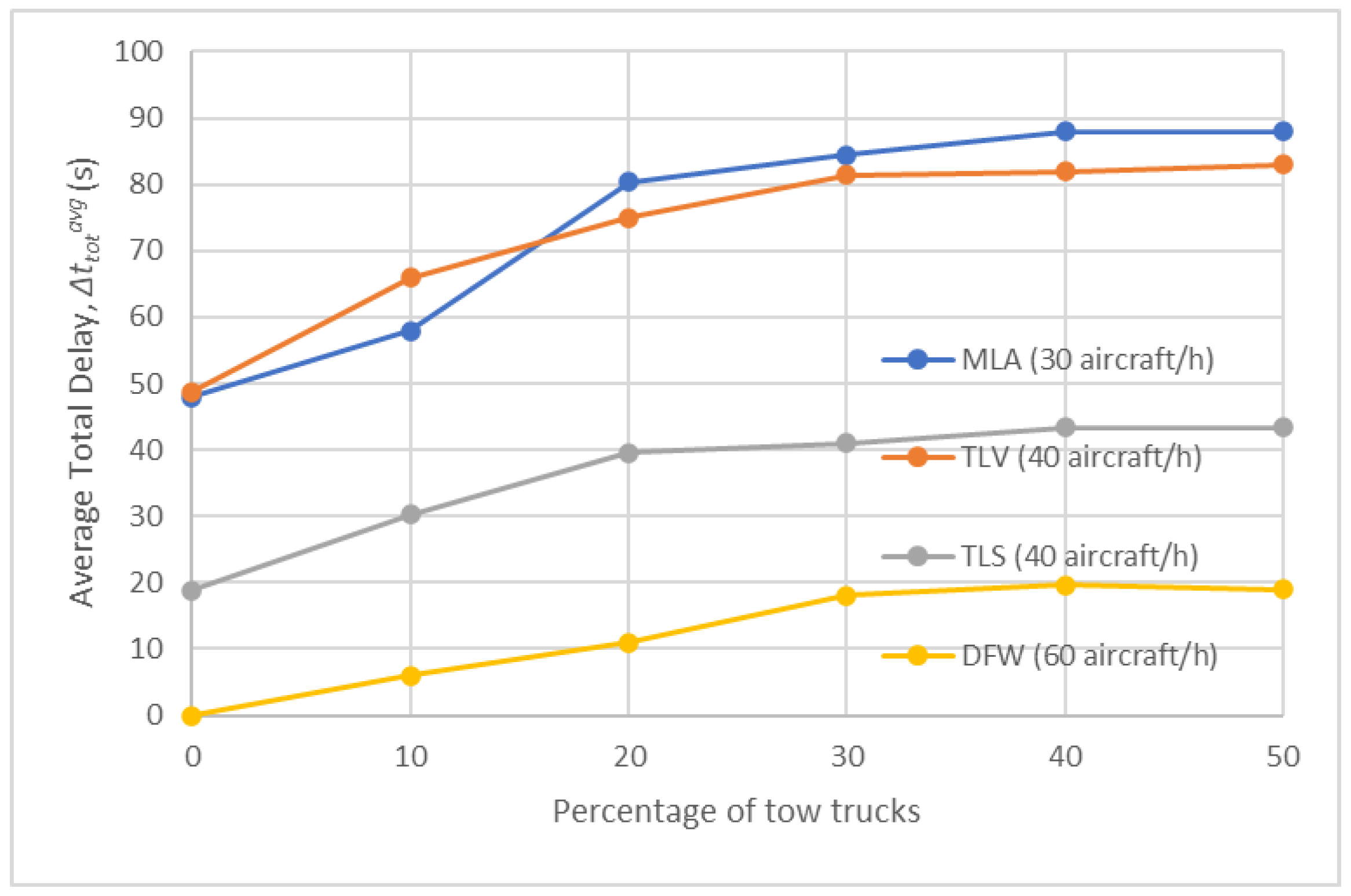
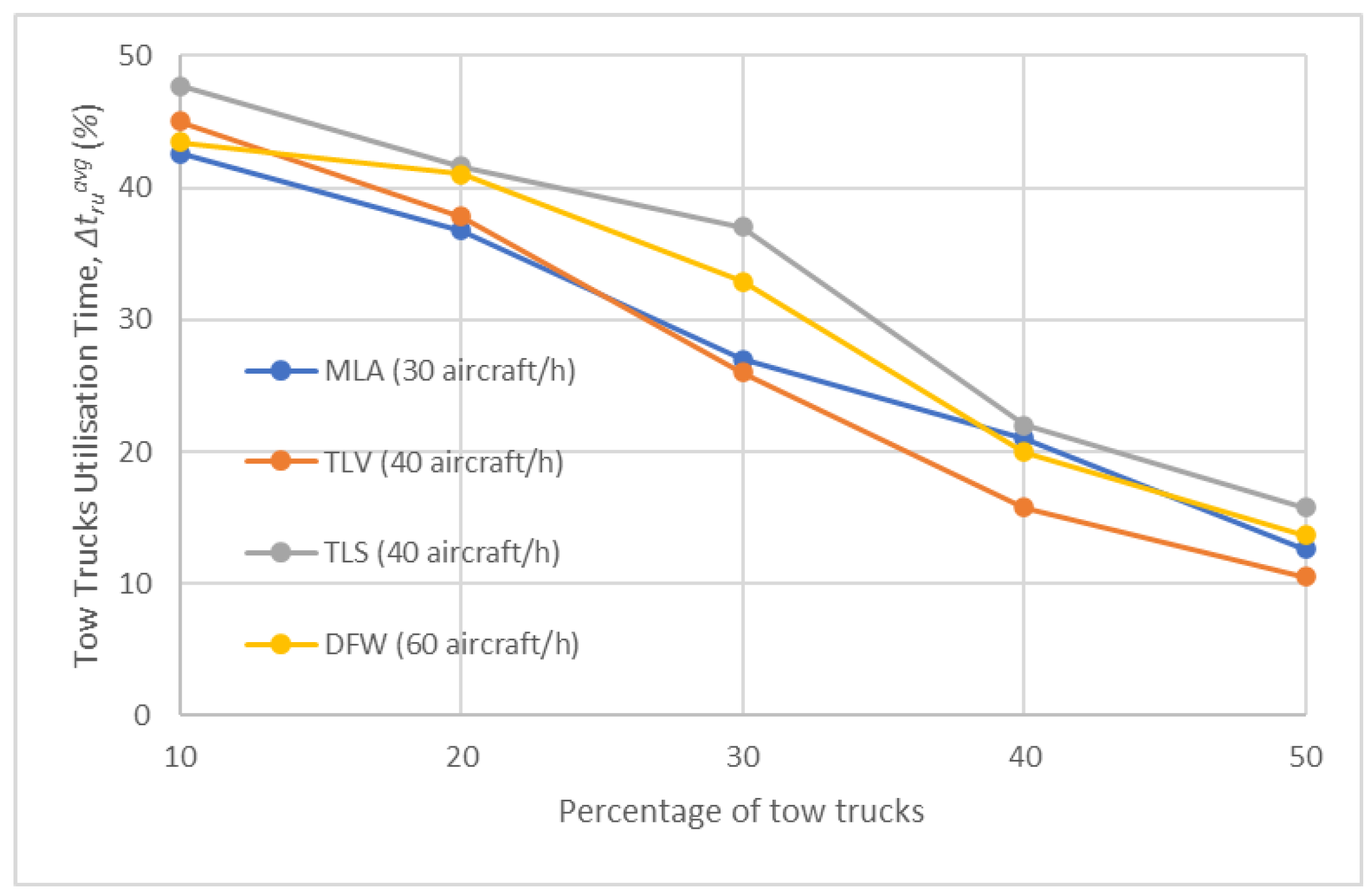
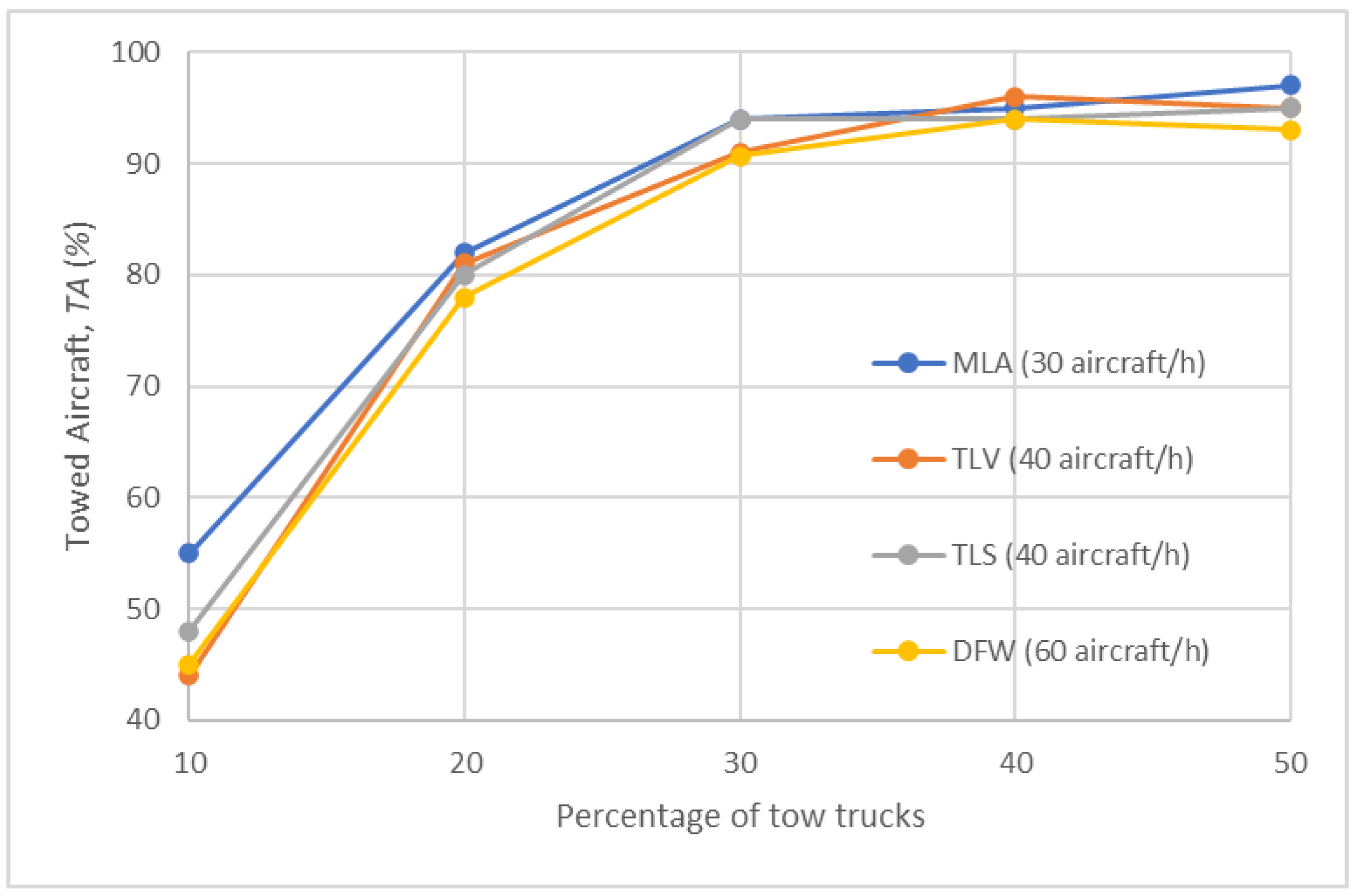
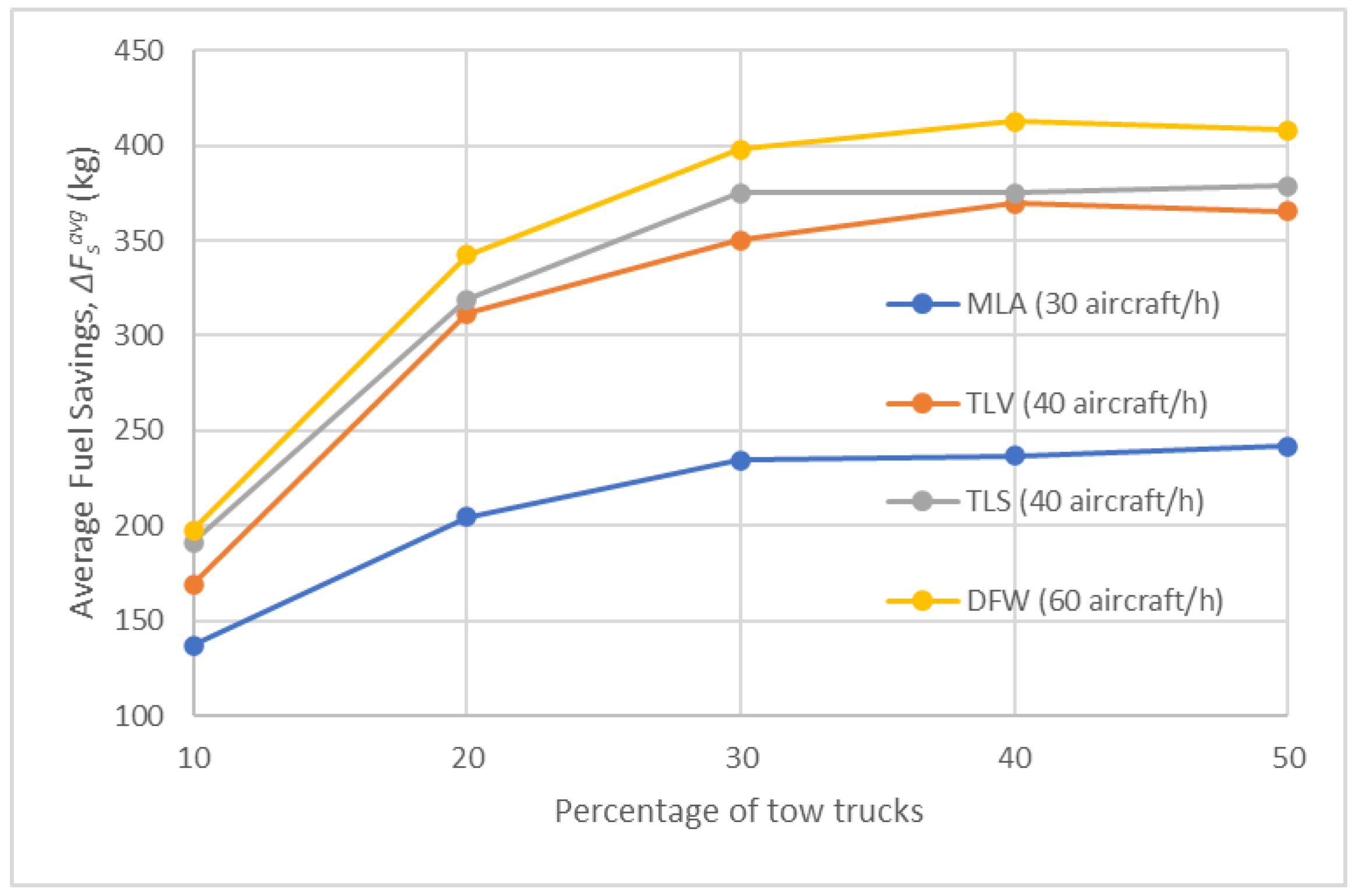
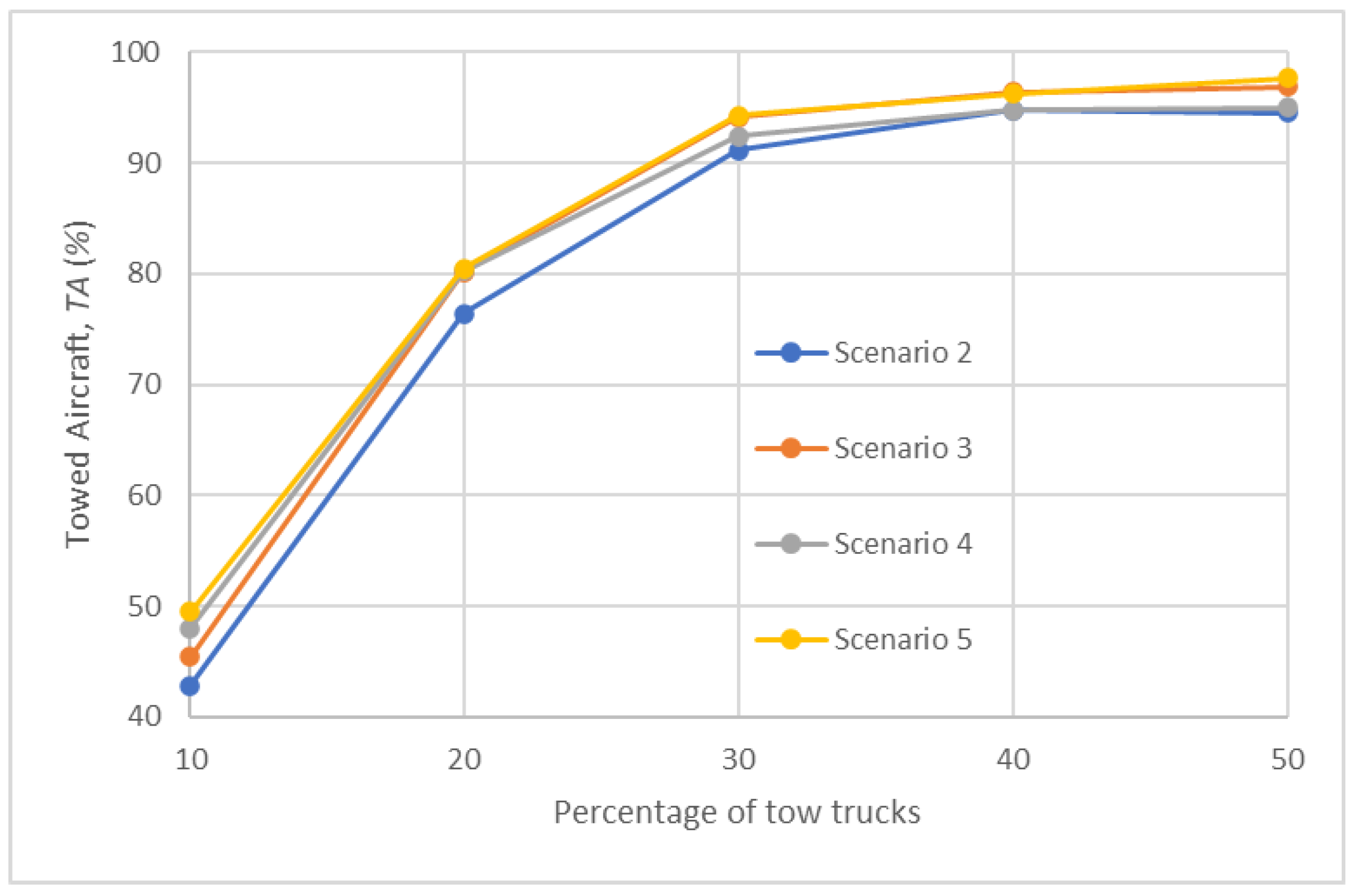
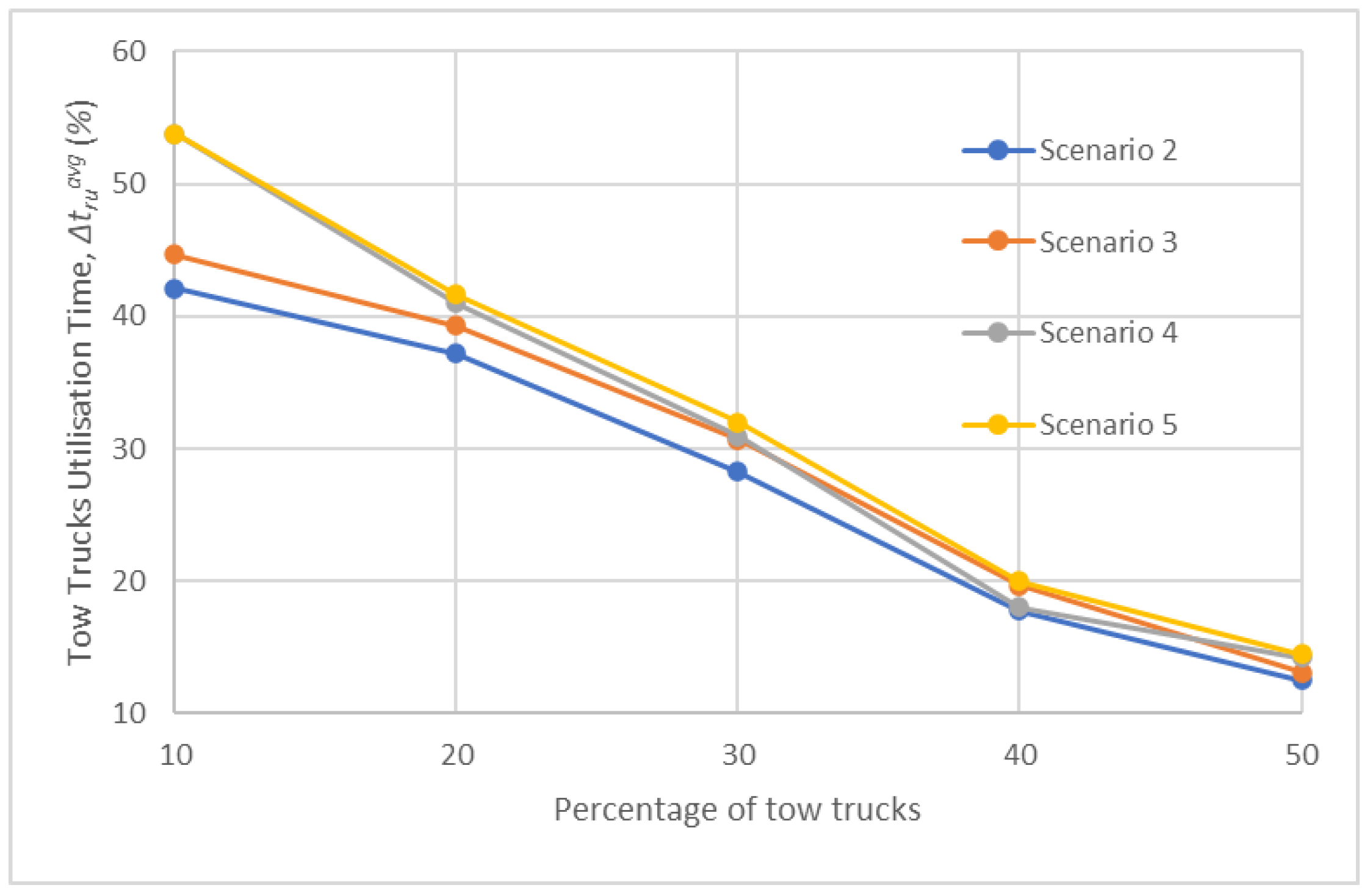
- Comparison of results of Test Scenarios 2–5
- 7.
- Results for Test Scenario 6
5. Discussion
6. Conclusions and Future Work
6.1. Conclusions
6.2. Potential Areas of Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| OBT | Off-Block Time (-) |
| TOA | Time of Arrival (-) |
| number of parking slots at a depot (-) | |
| total number of tow trucks (-) | |
| total number of depots (-) | |
| ToP | takeoff point (-) |
| LEP | landing entry point (-) |
| Average Vehicle Velocity (m/s) | |
| buffer area (m2) | |
| Buffer Distance (m) | |
| aircraft (-) | |
| (-) | |
| (-) | |
| time to start taxiing | |
| total delay (s) | |
| delay experienced by an aircraft while waiting (s) | |
| delay accumulated by an aircraft while taxiing (s) | |
| ideal taxi time (s) | |
| VOT | Vehicle Occupation Table (-) |
| ECL | Edges in Conflict List (-) |
| GOT | Global Occupation Table (-) |
| Total Mission Cost (s) | |
| tow truck (-) | |
| needs to complete the mission (-) | |
| over all the tow trucks (s) | |
| maximum battery charge (%) | |
| minimum allowed battery charge (%) | |
| (%) | |
| Higher Battery Discharging Rate (%) | |
| Lower Battery Discharging Rate (%) | |
| Battery Charging Rate (%) | |
| average total delay (s) | |
| delayed aircraft (%) | |
| towed aircraft (%) | |
| average fuel savings (kg) | |
| average tow truck utilisation time (%) |
References
- www.eurocontrol.int. Eurocontrol, 10 March 2023. Available online: https://www.eurocontrol.int/publication/eurocontrol-data-snapshot-40-taxi-times#:~:text=Typically%2C%20flying%20from%20one%20of,time%20of%20over%2020%20minutes (accessed on 12 May 2023).
- Zhang, M.; Huang, Q.; Liu, S.; Li, H. Assessment Method of Fuel Consumption and Emissions of Aircraft during Taxiing on Airport Surface under Given Meteorological Conditions. Sustainability 2019, 11, 6110. [Google Scholar] [CrossRef]
- Nikoleris, T.; Gupta, G.; Kistler, M. Detailed estimation of fuel consumption and emissions during aircraft taxi operations at Dallas/Fort Worth International Airport. Transp. Res. Part D 2011, 16, 302–308. [Google Scholar] [CrossRef]
- Dzikus, N.; Fuchte, J.; Lau, A.; Gollnick, V. Potential for Fuel Reduction through Electric Taxiing. In Proceedings of the 11th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference, Virginia Beach, VA, USA, 20–22 September 2011. [Google Scholar]
- Fleuti, E.; Maraini, S. Taxi-Emissions at Zurich Airport. 2017. Available online: https://www.flughafen-zuerich.ch//jssmedia/airport/portal/dokumente/das-unternehmen/politics-and-responsibility/environmental-protection/technische-berichte/2017_taxi_study_zurichairport.pdf?vs=1 (accessed on 15 March 2023).
- op.europa.eu. European Commission. 2011. Available online: https://op.europa.eu/en/publication-detail/-/publication/296a9bd7-fef9-4ae8-82c4-a21ff48be673 (accessed on 15 March 2023).
- ec.europa.eu. European Commission. 2020. Available online: https://ec.europa.eu/clima/policies/transport/aviation_en (accessed on 15 March 2023).
- www.iata.org. International Air Transport Association, December 2022. Available online: https://www.iata.org/en/iata-repository/pressroom/fact-sheets/fact-sheet---fuel/ (accessed on 4 April 2023).
- www.fitchratings.com. Fitch Ratings, 25 February 2022. Available online: https://www.fitchratings.com/research/corporate-finance/oil-price-shock-is-a-material-risk-for-us-european-airlines-25-02-2022 (accessed on 4 April 2023).
- www.statista.com. Statista. 2023. Available online: https://www.statista.com/statistics/591285/aviation-industry-fuel-cost/ (accessed on 4 April 2023).
- WheelTug. Available online: https://www.wheeltug.com/ (accessed on 15 March 2023).
- tec.ieee.org. IEEE TRansportation Electrification Community, 2014. Available online: https://tec.ieee.org/newsletter/march-april-2014/electric-green-taxiing-system-egts-for-aircraft (accessed on 15 March 2023).
- TaxiBot. 2020. Available online: https://www.taxibot-international.com/ (accessed on 15 March 2023).
- Di Mascio, P.; Corazza, M.V.; Rosa, N.R.; Moretti, L. Optimization of Aircraft Taxiing Strategies to Reduce the Impacts of Landing and Take-Off Cycle at Airports. Sustainability 2022, 14, 9692. [Google Scholar] [CrossRef]
- Abreu, P.H.; Oliveira, E. Comparing a Centralized and Decentralized Multi-Agent Approaches to Air Traffic Control. In Proceedings of the 28th European Simulation and Modelling Conference, Porto, Portugal, 22–24 October 2014. [Google Scholar]
- Chiang, Y.J.; Klotowski, J.T.; Lee, C.; Mitchell, J.S.B. Geometric algorithms for conflict detection/resolution in air traffic management. In Proceedings of the 36th IEEE Conference on Decision and Control, San Diego, CA, USA, 12 December 1997. [Google Scholar]
- Wang, X.; Peng, H.; Liu, J.; Dong, X.; Zhao, X.; Lu, C. Optimal control based coordinated taxiing path planning and tracking for multiple carrier aircraft on flight deck. Def. Technol. 2022, 18, 238–248. [Google Scholar] [CrossRef]
- Udluft, H. Decentralization in Air Transportation. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2017. [Google Scholar]
- Gawrilow, E.; Köhler, E.; Möhring, R.H.; Stenzel, B. Dynamic Routing of Automated Guided Vehicles in Real-Time; Institut für Mathematik, Technische Universität Berlin: Berlin, Germany, 2007. [Google Scholar]
- Ibrahim, M.F.; Bakar, A.Z.A.; Hussain, A. Genetic Algorithm-Based Robot Path Planning; Department of Electrical, Electronics and Systems Engineering, Universiti Kebangsaan Malaysia: Bangi, Selangor, Malaysia, 2009. [Google Scholar]
- Zhang, M.; Huang, Q.; Li, H. Multi-Objective Optimization of Aircraft Taxiing on the Airport Surface with Consideration to Taxiing Conflicts and the Airport Environment. Sustainability 2019, 11, 6728. [Google Scholar] [CrossRef]
- Morris, R.; Chang, M.L.; Archer, R.; Cross, E.V.I.; Thompson, S.; Franke, J.L.; Garrett, R.C.; Malik, W.; McGuire, K.; Hermann, G. Self-Driving Aircraft Towing Vehicles: A Preliminary Report. In Proceedings of the Workshops at the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Morris, R.; Chang, M.L.; Archer, R.; Cross, E.V., II; Thompson, S.; Franke, J.; Garrett, R.C.; Pasareanu, C.; Malik, W.; Hemann, G. SafeTug Semi-Autonomous Aircraft Towing Vehicles; NASA: Washington, DC, USA, 2016. [Google Scholar]
- Montoya, J.; Wood, Z.; Rathinam, S.; Malik, W. A Mixed Integer Linear Program for Solving a Multiple Route Taxi Scheduling Problem. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Toronto, ON, Canada, 2–5 August 2010. [Google Scholar]
- Du, J.Y.; Brunner, J.O.; Kolisch, R. Planning towing processes at airports more efficiently. Transp. Res. Part E Logist. Transp. Rev. 2014, 70, 293–304. [Google Scholar] [CrossRef]
- Ahmadi, S.; Akgunduz, A. Airport operations with electric-powered towing alternatives under stochastic conditions. J. Air Transp. Manag. 2023, 109, 102392. [Google Scholar] [CrossRef]
- van Oosterom, S.; Mitici, M.; Hoekstra, J. Dispatching a fleet of electric towing vehicles for aircraft taxiing with conflict avoidance and efficient battery charging. Transp. Res. Part C 2023, 147, 103995. [Google Scholar] [CrossRef]
- Zoutendijk, M.; van Oosterom, S.J.; Mitici, M. Electric Taxiing with Disruption Management: Assignment of Electric Towing Vehicles to Aircraft. In Proceedings of the AIAA Aviation 2023 Forum, San Diego, CA, USA, 12–16 June 2023. [Google Scholar]
- Adacher, L.; Flamini, M.; Romano, E. Rerouting Algorithms Solving the Air Traffic Congestion; Università Degli Studi Roma Tre: Rome, Italy, 2017. [Google Scholar]
- Li, L.; Jiawei, G. Research on aircraft taxiing path optimization based on digraph model and Dijkstra algorithm. In Proceedings of the IOP Conference Series Materials Science and Engineering, Xi’an, China, 8–11 October 2020. [Google Scholar]
- Jordan, R.; Ishutkina, M.A.; Reynolds, T.G. A Statistical Learning Approach to the Modeling of Aircraft Taxi TIme. In Proceedings of the Digital Avionics Systems Conference, Salt Lake City, UT, USA, 3–7 October 2010. [Google Scholar]
- Yang, L.; Yin, S.; Han, K.; Haddad, J.; Hu, M. Fundamental diagrams of airport surface traffic: Models and applications. Transp. Res. Part B Methodol. 2017, 106, 29–51. [Google Scholar] [CrossRef]
- Khadilkar, H.; Balakrishnan, H. Estimation of Aircraft Taxi-out Fuel Burn using Flight Data Recorder Archives. Transp. Res. Part D Transp. Environ. 2012, 17, 532–537. [Google Scholar] [CrossRef]
- ACI World. Airports Council International, 2022. Available online: https://aci.aero/2022/04/11/the-top-10-busiest-airports-in-the-world-revealed/ (accessed on 27 April 2023).

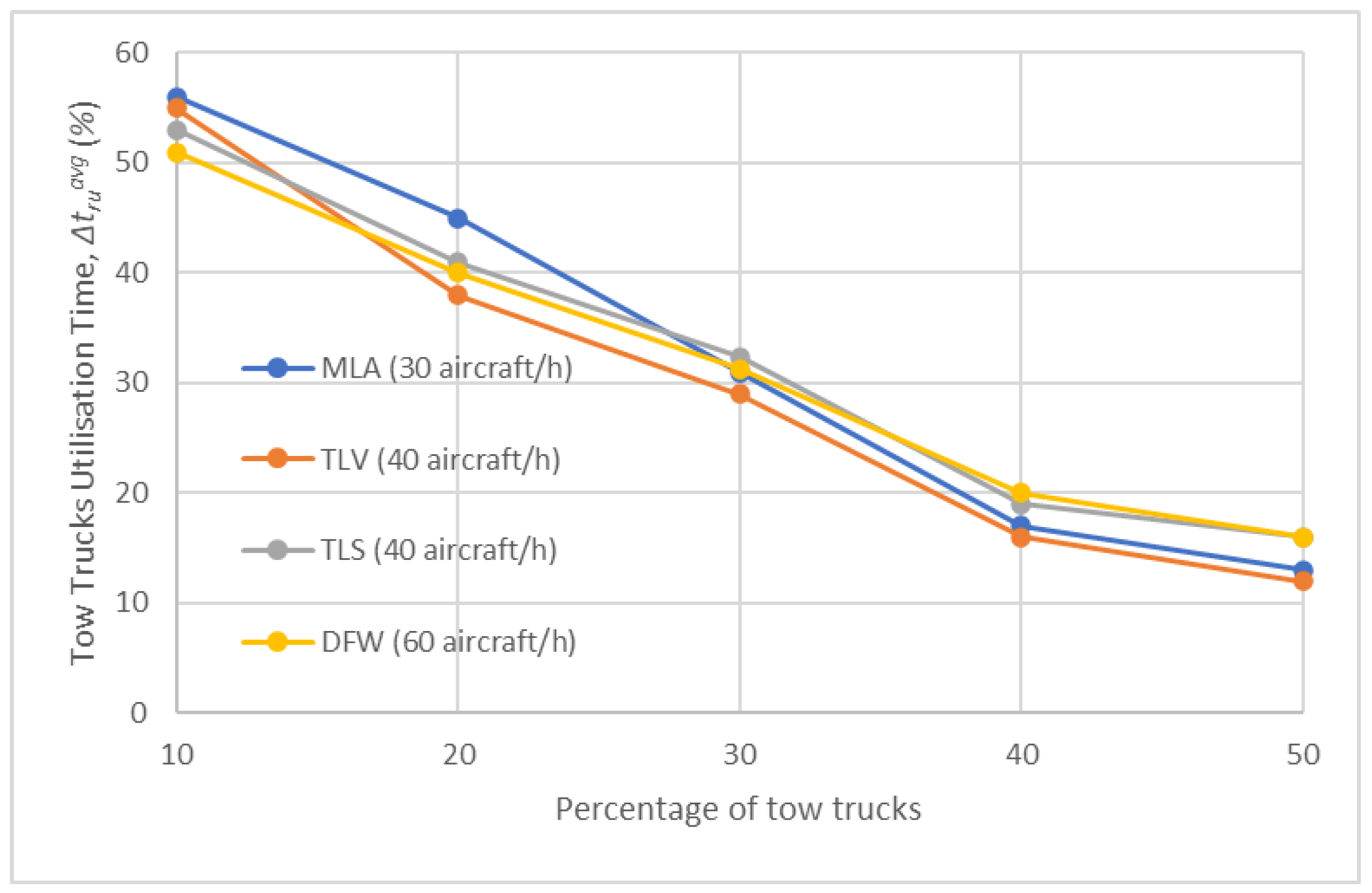
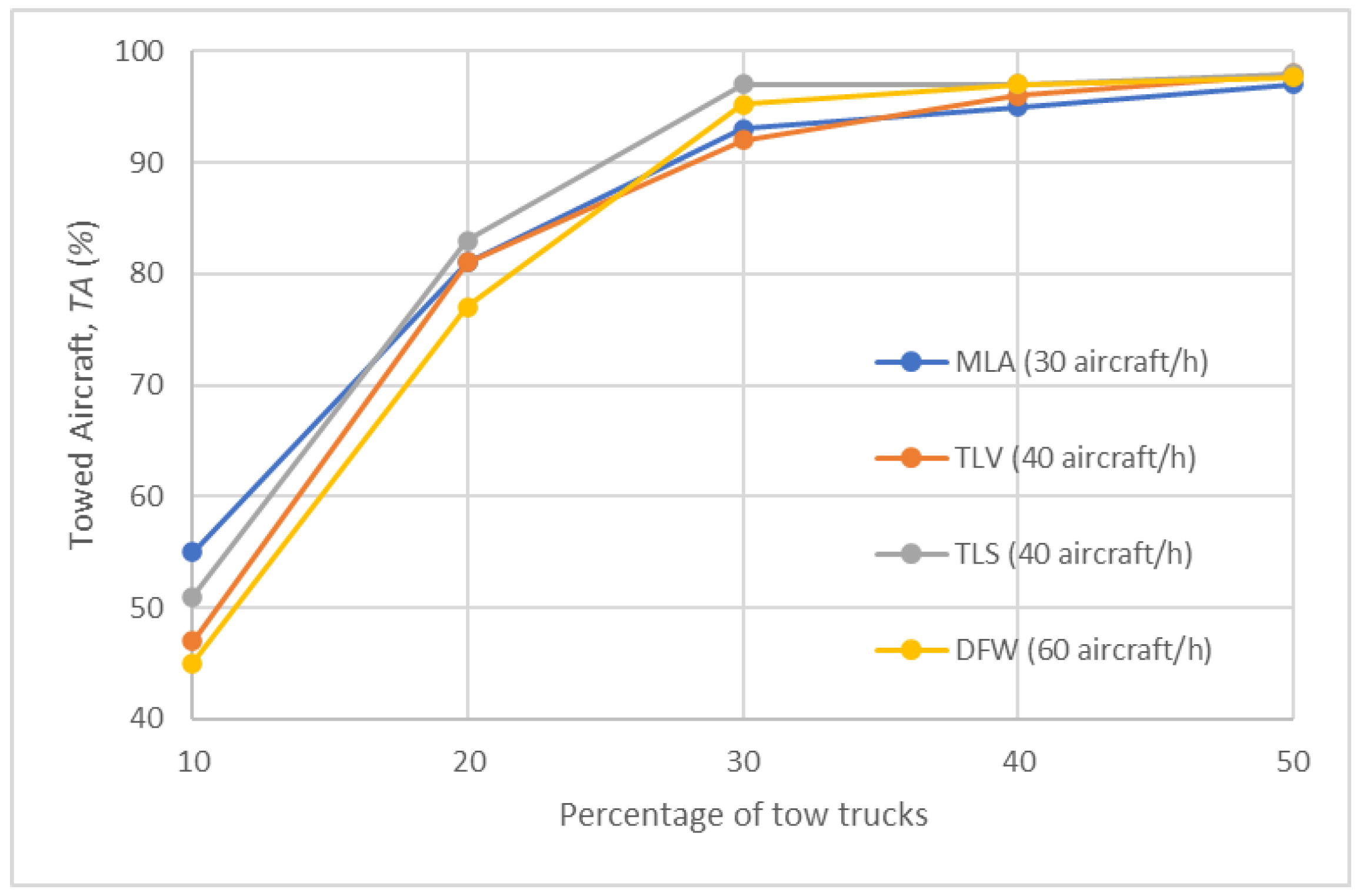
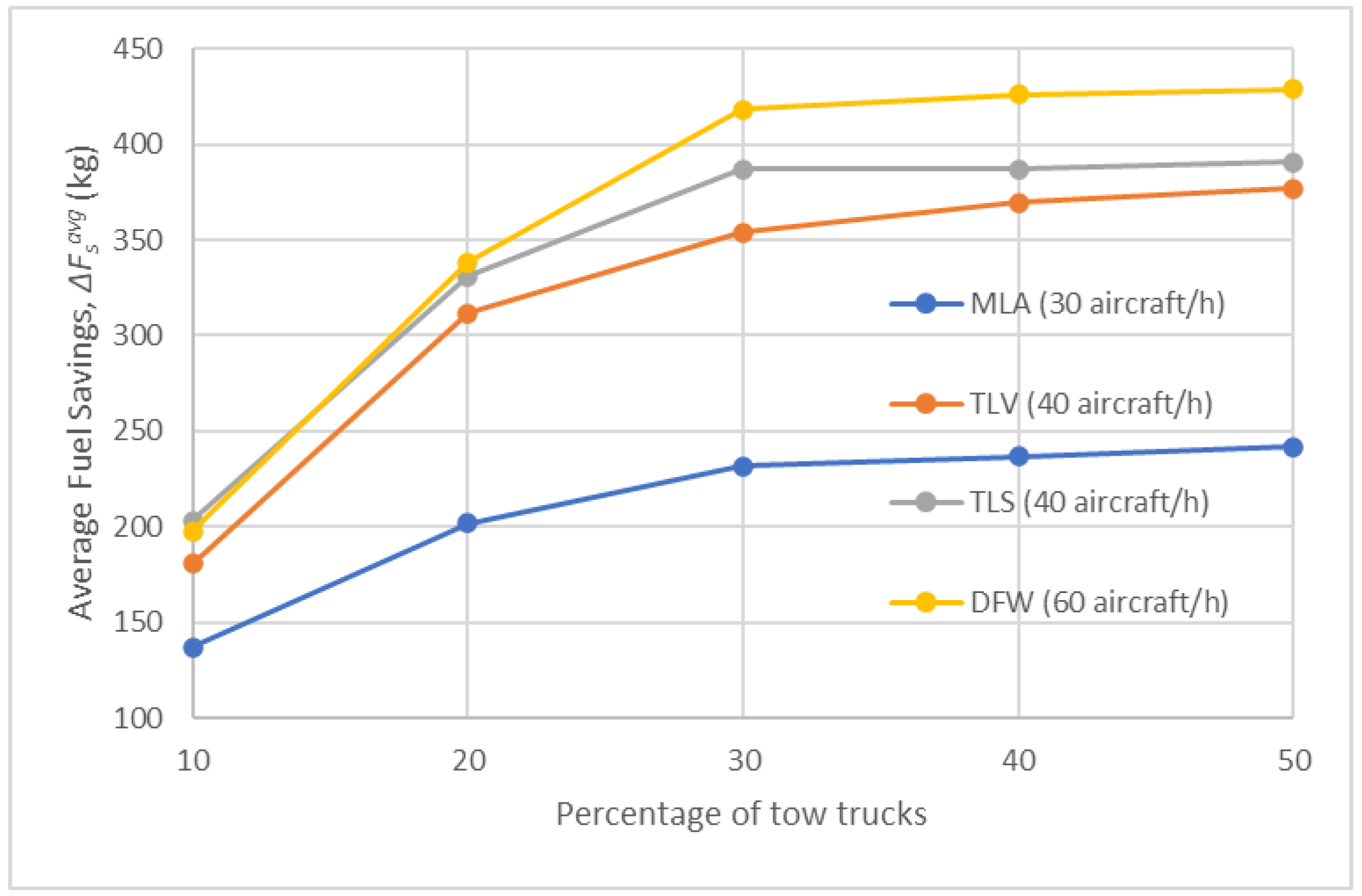
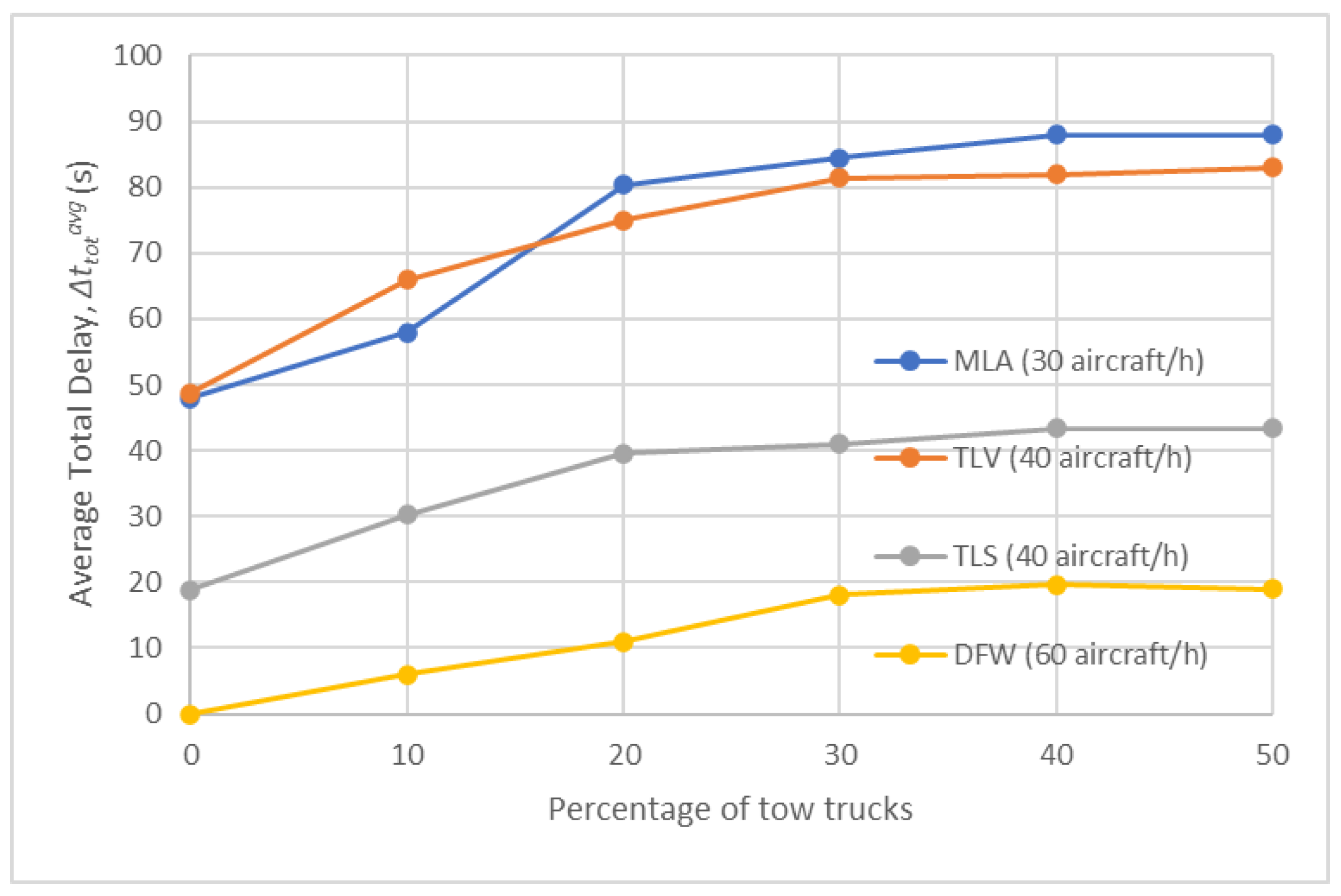


| Test Scenario | Description | Number of Simulations |
|---|---|---|
| 1 | No tow trucks | 66 |
| 2 | Tow trucks with Static Allocation and Time-Wise Approach | 210 |
| 3 | Tow trucks with Static Allocation and Fuel-Wise Approach | 210 |
| 4 | Tow trucks with Dynamic Allocation and Time-Wise Approach | 210 |
| 5 | Tow trucks with Dynamic Allocation and Fuel-Wise Approach | 210 |
| 6 | Modelling different battery discharge rates with Dynamic Allocation and Time-Wise Approach | 7 |
| Discharge Rates Percentage Variation (%/min) | rbdh (%/min) | rbdl (%/min) | TA (%) | ΔFsavg (kg) | Δtruavg (%) |
|---|---|---|---|---|---|
| −0.75 | 1.25 | 0.25 | 85 | 337 | 45 |
| −0.50 | 1.50 | 0.50 | 83 | 329 | 44 |
| −0.25 | 1.75 | 0.75 | 82 | 325 | 42 |
| 0 | 2.00 | 1.00 | 78 | 315 | 40 |
| +0.25 | 2.25 | 1.25 | 75 | 305 | 39 |
| +0.50 | 2.50 | 1.50 | 72 | 288 | 37 |
| +0.75 | 2.75 | 1.75 | 65 | 258 | 31 |
| +1.00 | 3.00 | 2.00 | 55 | 221 | 27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaninotto, S.; Gauci, J.; Zammit, B. An Autonomous Tow Truck Algorithm for Engineless Aircraft Taxiing. Aerospace 2024, 11, 307. https://doi.org/10.3390/aerospace11040307
Zaninotto S, Gauci J, Zammit B. An Autonomous Tow Truck Algorithm for Engineless Aircraft Taxiing. Aerospace. 2024; 11(4):307. https://doi.org/10.3390/aerospace11040307
Chicago/Turabian StyleZaninotto, Stefano, Jason Gauci, and Brian Zammit. 2024. "An Autonomous Tow Truck Algorithm for Engineless Aircraft Taxiing" Aerospace 11, no. 4: 307. https://doi.org/10.3390/aerospace11040307
APA StyleZaninotto, S., Gauci, J., & Zammit, B. (2024). An Autonomous Tow Truck Algorithm for Engineless Aircraft Taxiing. Aerospace, 11(4), 307. https://doi.org/10.3390/aerospace11040307






