Abstract
Recently, non-orthogonal multiple access (NOMA)-based space–air–ground integrated networks (SAGINs) have gained increasing attention due to their robust communication, broader coverage, and resource-saving advantages. However, it is imperative to consider physical layer security as a crucial performance metric in NOMA-based SAGINs. This study addresses this concern by constructing a NOMA-based free space optical (FSO)/radio frequency (RF) dual-hop SAGIN system with eavesdroppers on both links. The two new fading channel models were proposed, considering the FSO link’s fog absorption and the RF link’s stochastic distribution based on Málaga and shadowed Rician distributions. The closed-form expressions for the secrecy outage probability are derived for the SAGIN system. Monte Carlo simulations were conducted to validate the theoretical findings. The results revealed the influence of fog absorption and the stochastic geometry distribution on the SAGIN system.
1. Introduction
The non-orthogonal multiple access (NOMA)-based space–air–ground integrated network (SAGIN) has recently gained increasing attention for its role in enhancing channel capability, expanding communication coverage, and improving system performance [1,2]. Several studies, such as [3,4,5], have explored the outage probability, average bit error rate, and ergodic capacity of NOMA-based SAGIN systems. However, with the recent increase in communication coverage, the vulnerability of the SAGIN system signal to attacks has become a concern, prompting a heightened focus on signal security for NOMA-based SAGIN. Certain attacks, notably those involving jamming and intercepting, are inherently linked to the physical layer, posing challenges to the physical layer security (PLS) [6]. Therefore, evaluating the PLS of NOMA-based SAGIN systems has emerged as a challenging topic.
1.1. Methodology
NOMA-based SAGIN often involves constructing free space optical (FSO)/radio frequency (RF) and RF/FSO dual-hop systems. Various channel models have been employed to portray the fading of RF and FSO links. Traditional studies focused on the static conditions of nodes in the RF link, with the shadowed Rician (SR) distribution effectively portraying the influence of shadowing and multipath effects on the space-to-terrestrial link [7]. Tegos et al. constructed a NOMA-based uplink, employing the SR distribution to characterize the channel between satellite and terrestrial users [8]. The small-scale fading has been considered in many studies, with the Nakagami-m distribution serving as a generic statistical channel model for non-terrestrial networks [9]. Additionally, Rayleigh distribution can be applied to describe amplitudes of scatter and line-of-sight (LOS), effectively portraying small-scale fading [8]. Yan et al. modeled relay-to-user links as the Nakagami-m distribution in a NOMA-based SAGIN system [10]. Guo et al. used the Rayleigh distribution to represent fading in relay-to-users links [11]. For the non-geostationary orbit (NGSO) satellites, various channel models consider different orbits, frequency bands, user equipment, use-case, and scenario peculiarities [12]. Based on the different criteria, there are many different channel models, including a channel model proposed for constellations such as Globalstar and ICO, a narrowband channel model based on a shadowed Rician distribution, a Markov-based channel model to determine the LOS state transitions, and so on. In [13], many criteria were proposed to evaluate the performance of satellite communications. Thereafter, Baeza et al. investigated the placement of the gateway stations based on multiple criteria of the system with NGSO satellites [14]. In [15], an approach was described for beam pattern synthesis applied to geostationary satellite communication systems, considering latitude and longitude, required EIRP, minimum and maximum side love levels for the two principal cuts, and nulling direction. However, the traditional channel model must account for the stochastic geometry distribution of terminals, especially for the NOMA-based SAGIN system with increased moving terminals [16,17].
1.2. Motivation
To illustrate the stochastic geometry distribution of terminals, various studies have employed different distribution conditions. For instance, Okati et al. proposed a downlink SAGIN with plenty of satellites, considering users located on the surface of a sphere [18]. Similarly, Zhang et al. established a satellite–terrestrial downlink, assuming that the locations of legitimate receivers and eavesdroppers followed a uniform distribution in a circle [19]. They also derived the closed-form expressions of SOP for the constructed system. Homssi et al. proposed a downlink SAGIN, using a homogeneous Poisson point process to depict the stochastic geometry distribution of both satellites and terrestrial base stations [20]. In practical engineering applications where destinations are often mobile terminals, a circular distribution of locations aligns more consistently with typical scenarios, warranting further investigation for NOMA-based SAGINs.
Various channel models also portray the influence of atmospheric turbulence conditions on the FSO link. The Gamma–Gamma and Málaga distributions can model the moderate-to-strong, and weak-to-strong turbulence conditions [21,22,23]. However, fog absorption dramatically influences the FSO link [24]. The size of droplets in fog, close to the same order of magnitude as the length of the optical wave, reduces the performance of FSO communication systems due to fog absorption [25]. Therefore, it is necessary to investigate the influence of fog absorption on the FSO link, but to the best of our knowledge, it is ignored in NOMA-based SAGIN systems.
1.3. Background
In recent years, researchers have concentrated on PLS investigations for NOMA-based SAGIN, specifically focusing on secrecy performance metrics, like secrecy rate, secrecy outage probability (SOP), and the probability of non-zero secrecy capacity (PNSC). Yin et al. constructed a frequency-domain NOMA-based SAGIN system consisting of multiple user clusters with an eavesdropper in each cluster and investigated the secrecy rate of the system [26]. Bankey et al. derived SOP and the probability of positive secrecy capacity for NOMA-based SAGIN with an amplify-and-forward relay [27]. Li et al. proposed a joint beamforming scheme for cognitive SAGIN, employing orthogonal multiple access and NOMA techniques [28]. They presented the sum rate maximation with the imperfect channel state information, satisfying the data rate requirement and system transmit power constraint. Guo et al. derived the SOP of NOMA-based SAGIN under channel estimation errors and hardware impairments, considering multiple eavesdroppers [29]. Li et al. proposed an unmanned aerial vehicle (UAV)-assisted SAGIN and demonstrated that the NOMA technique can improve spectral efficiency. The average secrecy rate was derived as a measure of the NOMA-based SAGIN’s secrecy performance [30].
Therefore, a UAV-aided NOMA-based FSO/RF SAGIN system with two independent eavesdroppers was constructed in this study. This construction considered fog absorption and the stochastic geometry distribution of the locations for terrestrial users on FSO and RF links, respectively. The satellite-to-UAV and satellite-to-eavesdropper links undergo the atmospheric turbulence modeled by the Málaga distribution. Additionally, pointing error impairments and fog absorption are considered for the FSO link. For the RF link, the UAV-to-users and UAV-to-eavesdropper links suffer from the shadowing condition characterized by SR distribution, accounting for the stochastic distribution of terrestrial users. This approach, to the best of our knowledge, has not been explored yet. Based on the constructed SAGIN system, the cumulative distribution function (CDF) and probability density function (PDF) for the channel are derived. Additionally, closed-form expressions of the SOP in the proposed SAGIN system are presented, offering valuable insights for engineering applications.
1.4. Contribution
The major contributions of this study are outlined as follows:
- •
- An FSO/RF dual-hop system for the SAGIN system using the DF relaying protocol is constructed. As a classical scenario, the paper considers that there is an eavesdropper intercepting the signals on each link, respectively. In addition, the NOMA technique is used to improve the secrecy performance of the proposed system.
- •
- Considering the fog absorption for the FSO link and the stochastic geometry distribution for the RF link, the two fading channel models are proposed based on the Málaga and shadowed Rician distribution, respectively.
- •
- The closed-form expressions of SOP for the NOMA-based SAGIN system are derived, and their accuracy is verified by Monte Carlo simulations.
- •
- The influence of various system and channel parameters on the PLS of the NOMA-based SAGIN system is investigated, especially the impact of fog absorption and stochastic geometry distribution.
The structure of this paper is organized as follows: Section 2 proposes the system and channel models of the NOMA-based SAGIN system with stochastic geometry distribution. Section 3 presents closed-form expressions for the CDF and PDF of the FSO and RF links, along with the expressions for secrecy capacity and SOP. Section 4 provides the numerical and simulation results, and Section 5 concludes the study.
2. System and Channel Models
As illustrated in Figure 1, the NOMA-based SAGIN system comprises a satellite (S), UAV relay (R), near user () and far user (), and two eavesdroppers ( and ). The satellite transmits signals to the terrestrial users through the UAV relay, with eavesdropping occurring on both links. Notably, the UAV relay employs the decode-and-forwarding (DF) protocol, and its altitude is H. The near user is randomly located within a disc, centered on the ground projection of the UAV, with a radius of . Eavesdropper intercepts signals only from due to its proximity. Without loss of generality, we assume that the R– link exhibits superior channel quality compared to the R– link. Furthermore, and operate independently, intercepting signals at different working frequencies. Furthermore, and operate independently, intercepting signals at different working frequencies. System performance indicators, such as outage probability, average bit error rate, and ergodic capacity, are well-studied in traditional works. However, this paper mainly considers the physical layer security, including the secrecy capacity and the secrecy outage probability (SOP). The secrecy capacity is the difference between the channel capacity of the legitimate link and that of the eavesdropping link [29], and SOP represents the probability that the secrecy capacity falls below the capacity threshold rate [31], evaluating the secrecy performance of the system under physical layer attack. The multi-eavesdroppers scenario is more possible for the engineering application, but it will be our future work.
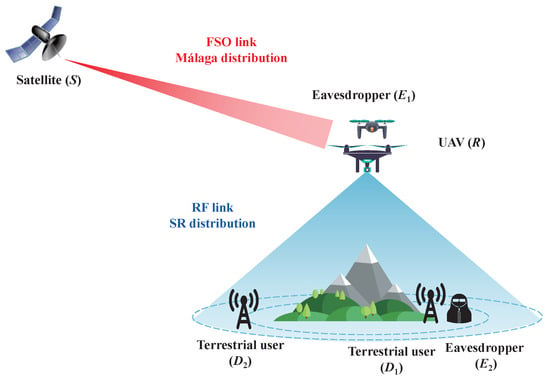
Figure 1.
Architecture of the NOMA-based SAGIN system with stochastic geometry distribution considering eavesdroppers.
In this study, the Málaga distribution model was employed to characterize the fading of the FSO link [23]. Additionally, pointing errors and fog absorption were considered in the FSO link. According to approaches outlined in [23,24], the PDF and CDF of the signal-to-noise ratio (SNR) for the FSO link can be deduced as follows:
where
where , is the distance of the foggy channel, and are the scale and shape parameters, respectively, represents and is the average SNR of the link. The parameters in (1) and (2) are the same as those outlined in [32]. Additionally, detailed illustrations of these parameters can be found in [32,33]. Note that the values of and are the atmospheric turbulence conditions, and r is the detection technique of the FSO link, where and are the heterodyne detection and intensity modulation/direct detection (IM/DD) techniques, respectively. The symbol in (1) and (2) is the Meijer G-function, defined in [34], Equation (9.301). , , and include terms, while comprises terms.
In the case of plane waves, and can be expressed as follows [35]:
where represents a unitless Rytov variance, is the refractive-index structure parameter, is the distance of the propagation link, and is the wavelength.
Additionally, the shadowed Rician (SR) fading model was used to evaluate the fading condition of the RF link. The PDF and CDF of the SR fading channel for the RF link can be expressed as follows [7,36]:
where and are the parameters of the R-, R-, and R- links, respectively. In (6) and (7), , , is the average SNR of the link, in (6) is the confluent hypergeometric function of the first kind [34], Equation (9.14/1). The values and descriptions of other parameters can be found in [36]. Note that , , and are the shadowing conditions, and and are the Gamma and incomplete Gamma functions, respectively [34], Equations (8.310) and (8.350).
In the RF link, the stochastic geometry distribution of terrestrial users was considered. Without loss of generality [37], we assume that the location of the near user is uniformly distributed in a disc centered at the ground projection of the UAV. Therefore, the PDF and CDF of the transmission distance () of the R– link can be expressed as follows:
Additionally, we assume that intercepts signals only from since operates at the same frequency as , i.e., also denotes the distance of the R– link. The location of the far user is uniformly distributed within an annulus with radii ranging from to , also centered at the ground projection of the UAV. Therefore, the PDF and CDF of the transmission distance between R and can be expressed as follows:
The entire transmission process includes two-time slots. In the first slot, the signal is transmitted from S to R using the FSO technique. Since is in proximity to R, it can intercept the signal from the legitimate link. In the second time slot, the UAV relay employs the RF technique to transmit the signal to terrestrial users ( and ). The detailed transmission process is as follows.
In the first time slot, signal is transmitted from satellite S to the UAV relay. satisfies , where is the expectation function. Here, and are the signals transmitted to and , respectively, and and are the power distribution factors of and , respectively, satisfying . To ensure fairness in the NOMA technique, we assume the channel quality of the R– link is better than that of the R– link, thereby setting . In this time slot, the received signal at R can be expressed as follows:
where is the transmitting power of satellite S, is the electrical-to-optical conversion coefficient, is the channel fading coefficient of the S-R link, obeying the Málaga distribution considering the foggy channel, and is the additive Gaussian white noise (AWGN) of the S-R link, following a normal distribution with a mean of zero and variance of .
Using (12), the instantaneous SNR of at the relay can be written as follows:
Meanwhile, the signal received by the can be expressed as follows:
where is the channel fading coefficient of the S– link, which follows the Málaga distribution considering the foggy channel, and is the AWGN at following a normal distribution with a mean of zero and a variance of .
The instantaneous SNR of at is expressed as follows:
In the second time slot, R decodes the signal and then forwards it to terrestrial users. Therefore, the signals received by and can be expressed as follows:
where is the transmitting power of relay R, and are the channel fading coefficient of the R– and R– links, respectively, is the distance between R and , and is the path loss factor. The channel fading coefficients for the R–, R–, and R– links are assumed to follow the SR distribution, while and are the AWGN at and , respectively, obeying a normal distribution with the same mean of zero and different variance ( and ).
The successive interference cancellation (SIC) technique is employed at R to decode the signal . Initially, is deciphered and removed from the obtained signal, followed by decoding from the remaining signal. Consequently, the signal-to-interference plus noise ratio (SINR) of and at can be expressed as follows:
where is the instantaneous SNR of the R– link.
When the far user receives the signal, can obtain by treating as noise. Therefore, the SINR at is expressed as
where denotes the instantaneous SNR of the R– link.
For the eavesdropper , intercepting information in the RF link, the received signal can be expressed as follows:
where is AWGN, which follows a normal distribution with a mean of zero and variance of , and is the channel fading coefficient of the R– link, following the SR distribution as mentioned above.
At eavesdropper , the SIC technique is also used to decode the received signal. The SINR of and at can be expressed as follows:
where is the instantaneous SNR of the R– link.
3. Performance Analysis
In this section, the CDF and PDF of the RF link and the SOP of the SAGIN system were scrutinized. The SOP was derived to evaluate the secrecy performance of the SAGIN system with eavesdroppers.
3.1. Cumulative Distribution Function and Probability Distribution Function
3.2. Secrecy Capacity
The secrecy capacity is the difference between the channel capacity of the legitimate link and that of the eavesdropping link [29]. Therefore, the secrecy capacity of the FSO and RF links can be expressed as:
where , , , and are the channel capacity of the S–R, S–, R–, and R– links, respectively.
3.3. Secrecy Outage Probability
The SOP represents the probability that the secrecy capacity falls below the capacity threshold rate [31,38]. In this subsection, the SOP expression of the NOMA-based SAGIN system with a stochastic distribution of terrestrial users considering eavesdroppers was deduced.
According to the definition of SOP, the SOP of the SAGIN system can be expressed as follows:
The expression of SOP is related to three parts, i.e., , , and . In subsection A, the CDF of was given, resulting in the expression of by setting . Therefore, there is a need to derive the expressions of and . Based on [39], Equation (4), the expression of can be expressed as follows:
where and is the SNR threshold. Note that the integral of polynomial power impedes us from obtaining the closed-form expression of (32). Based on [39], the integration part in (32) can be simplified by an approximate method, which can be expressed as follows:
Substituting (1) and (2) into (33) and based on [40], Equation (2.24.1.1), (33) can be finally derived as
Similarly, utilizing the definition of SOP, can be expressed as follows:
It is worth noting that (36) is the result of a finite integral, and the closed-form expression of (36) can be precisely approximated using Gaussian–Chebyshev quadrature to convert the integral to the sum of finite terms [41]. Based on [42], Table (25.4), (36) can be recast as follows:
where is the Gaussian weight, is the qth zero of Legendre polynomials, and and are derived from [42], Table (25.4).
4. Numerical Results and Discussions
In this section, we present simulation and analysis results for the secrecy performance of the NOMA-based SAGIN system, considering the stochastic distributions of terrestrial users. The FSO link was evaluated under three typical atmospheric turbulence conditions: strong, moderate, and weak turbulence. Additionally, three fog intensities (thick, moderate, and light) were employed to portray the influence of the fog absorption on the FSO link. The specific values of these parameters can be found in [23,24,43]. For simplicity, we assume specific values , , , , and [23]. Additionally, three shadowing conditions, frequent heavy shadowing (FHS), average shadowing (AS), and infrequent light shadowing (ILS), were used to portray the shadowing effects of the RF link, with specific parameter values found in [36,38]. Unless otherwise specified, the average SNRs of the RF and FSO hops are assumed to be 30 and 50 dB, respectively. For ease of calculation, we assume that the shadowing conditions of R– and R– links are the same, abbreviated as links. Moreover, we conducted Monte Carlo simulations to certify the accuracy of the proposed NOMA-based system, which uses randomness to solve problems that may theoretically be deterministic.
Figure 2 investigates the relationship between the average SNR of the FSO hop () and different detection techniques (r). The SOP decreases as increases. However, this decreasing trend slows down at larger , caused by the DF protocol, which determines the SOP performance of the dual-hop system based on the worst link. Moreover, as increases, the SOP also increases due to intercepting more signals from the legitimate link. Furthermore, the SOP under heterodyne detection is lower than that under the IM/DD technique. For example, when dB and dB, the SOP decreases from 0.19 to 0.015 as the detection technique shifts from the IM/DD technique to heterodyne detection. This can be attributed to the higher conversion gain and improved filtering performance associated with heterodyne detection.
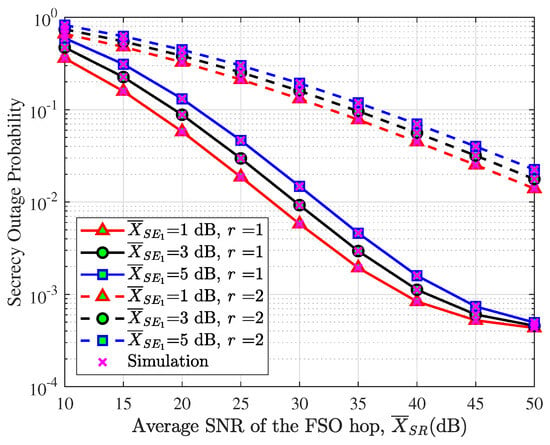
Figure 2.
SOP versus SNR of the eavesdropping link and detection technique.
Figure 3 shows the impact of various turbulence conditions and fog intensities on the SOP. The Monte Carlo simulation results align with the numerical results. Similar to Figure 2, the SOP decreases with increasing . Additionally, more severe turbulence conditions increased the SOP. For instance, the SOP increases from to when the turbulence condition transitions from weak to moderate with light fog intensity and at 30 dB. This is because the more severe atmospheric turbulence condition leads to a higher outage probability, resulting in less signal received by the receiver. Although the signal obtained at both the legitimate and eavesdropping receivers decreases, the impact on the legitimate link is greater than that on the eavesdropping link due to the larger signal received at the legitimate receiver. Furthermore, an increase in fog intensity results in a higher SOP. For instance, when the turbulence condition is weak and dB, the SOP increases from to with the fog intensity transitioning from light to moderate. This is explained by the reduction in fog intensity, which decreases the signal intensity at the receiver, thereby leading to a higher SOP.
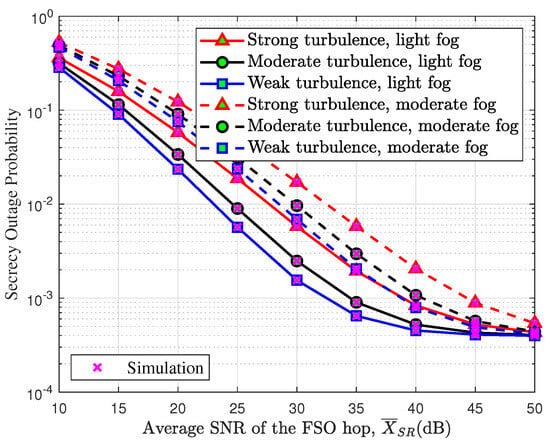
Figure 3.
SOP versus atmospheric turbulence and fog intensity.
Figure 4 presents the SOP versus , which considers the different threshold SNRs , the radius of the disc for near user , the SNR of the eavesdropping link , and the radius of the annulus . Obviously, the larger radius of the disc increases the SOP. For instance, the SOP increases from to as increases from 100 to 150 m when dB and dB. This phenomenon can be interpreted as the larger radius extending the range of the ground user, resulting in lower RF link stability. Similarly, the larger radius also increases the SOP. Additionally, a higher threshold SNR induces a higher SOP. For instance, with m and dB, the SOP increases from to as rises from 1 to 3 dB. This is because more signals will be treated as noises when is smaller than . Therefore, the larger leads to less signal obtained by the receiver, resulting in a degraded SOP performance. Furthermore, an enlarged SNR of the eavesdropping link also increases the SOP, aligning with the trend observed in Figure 2.
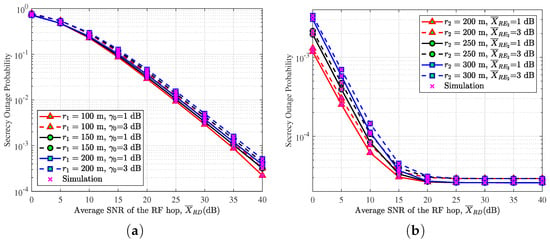
Figure 4.
SOP versus (a) threshold SNR and the radius of the disc for near users and (b) eavesdropping SNR and the radius of the annulus .
5. Conclusions
In this study, the NOMA-based SAGIN system with a stochastic geometry distribution of the terrestrial users was constructed, featuring two eavesdroppers intercepting signals in the FSO and RF links. Based on the Málaga and SR distributions, new channel models of FSO and RF links were derived, considering fog absorption and stochastic user locations. Furthermore, an exact closed-form expression of the SOP for the entire system was proposed, which was validated through Monte Carlo simulations. Finally, the influence of channel and system parameters on the NOMA-based SAGIN system was investigated. The results prove that increased fog intensity and radius contribute to higher SOP. Additionally, a higher SNR in the eavesdropping link increases the SOP.
Author Contributions
Conceptualization, X.W., J.H. and G.X.; methodology, X.W. and G.X.; software, X.W.; validation, X.W., J.C. and G.X.; formal analysis, X.W. and G.X.; investigation, X.W. and G.X.; resources, X.W. and G.X.; data curation, X.W., J.C. and G.X.; writing—original draft preparation, X.W. and G.X.; writing—review and editing, X.W., J.C., J.H. and G.X.; visualization, X.W. and G.X.; supervision, J.C. and G.X.; project administration, J.C. and G.X.; funding acquisition, J.C., Y.G. and G.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China of grant number 62271202 and 62027802, and in part by the Open Foundation of State Key Laboratory of Integrated Services Networks Xidian University of grant number ISN23-01.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Liu, Q.; Fu, M.; Li, W.; Xie, J.; Kadoch, M. RIS-Assisted Ambient Backscatter Communication for SAGIN IoT. IEEE Internet Things J. 2023, 10, 9375–9384. [Google Scholar] [CrossRef]
- Sun, G.; Xu, G.; Shao, Y.; Zhang, Q.; Song, Z. Phase fluctuations-induced bit error ratio of deep-space optical communication systems during superior solar conjunction. Opt. Express 2024, 32, 7105–7118. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Chen, Y.; Xue, P.; Lv, G.; Shu, M. Outage Performance for Satellite-Assisted Cooperative NOMA Systems With Coordinated Direct and Relay Transmission. IEEE Commun. Lett. 2020, 24, 2285–2289. [Google Scholar] [CrossRef]
- Gao, Z.; Liu, A.; Liang, X. The Performance Analysis of Downlink NOMA in LEO Satellite Communication System. IEEE Access 2020, 8, 93723–93732. [Google Scholar] [CrossRef]
- Chu, J.; Chen, X.; Zhong, C.; Zhang, Z. Robust Design for NOMA-Based Multibeam LEO Satellite Internet of Things. IEEE Internet Things J. 2021, 8, 1959–1970. [Google Scholar] [CrossRef]
- Angueira, P.; Val, I.; Montalb, J.; Seijo, Ó.; Iradier, E.; Fontaneda, P.S.; Fanari, L.; Arriola, A. A Survey of Physical Layer Techniques for Secure Wireless Communications in Industry. IEEE Commun. Surv. Tutor. 2022, 24, 810–838. [Google Scholar] [CrossRef]
- Cvetkovi, A.M. Performance of dual-hop relaying over shadowed Ricean fading channels. J. Electr. Eng. 2011, 62, 244–248. [Google Scholar] [CrossRef]
- Tegos, S.A.; Diamantoulakis, P.D.; Xia, J.; Fan, L.; Karagiannidis, G.K. Outage Performance of Uplink NOMA in Land Mobile Satellite Communications. IEEE Wirel. Commun. Lett. 2020, 9, 1710–1714. [Google Scholar] [CrossRef]
- Toka, M.; Vaezi, M.; Shin, W. Outage Analysis of Alamouti-NOMA Scheme for Hybrid Satellite–Terrestrial Relay Networks. IEEE Internet Things J. 2023, 10, 5293–5303. [Google Scholar] [CrossRef]
- Yan, X.; Xiao, H.; Wang, C.X.; An, K. Outage Performance of NOMA-Based Hybrid Satellite-Terrestrial Relay Networks. IEEE Wirel. Commun. Lett. 2018, 7, 538–541. [Google Scholar] [CrossRef]
- Guo, K.; Dong, C.; An, K. NOMA-Based Cognitive Satellite Terrestrial Relay Network: Secrecy Performance Under Channel Estimation Errors and Hardware Impairments. IEEE Internet Things J. 2022, 9, 17334–17347. [Google Scholar] [CrossRef]
- Baeza, V.M.; Lagunas, E.; Al-Hraishawi, H.; Chatzinotas, S. An Overview of Channel Models for NGSO Satellites. In Proceedings of the 2022 IEEE 96th Vehicular Technology Conference (VTC2022-Fall), London, UK, 26–29 September 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Baeza, V.M.; Salor, L.C. New horizons in tactical communications: An overview of emerging technologies possibilities. IEEE Potentials 2024, 43, 12–19. [Google Scholar] [CrossRef]
- Baeza, V.M.; Ortiz, F.; Lagunas, E.; Abdu, T.S.; Chatzinotas, S. Multi-Criteria Ground Segment Dimensioning for Non-Geostationary Satellite Constellations. In Proceedings of the 2023 Joint European Conference on Networks and Communications & 6G Summit (EuCNC/6G Summit), Gothenburg, Sweden, 6–9 June 2023; pp. 252–257. [Google Scholar] [CrossRef]
- Vásquez-Peralvo, J.A.; Querol, J.; Ortíz, F.; Rios, J.L.G.; Lagunas, E.; Baeza, V.M.; Fontanesi, G.; Garcés-Socorrás, L.M.; Duncan, J.C.M.; Chatzinotas, S. Flexible Beamforming for Direct Radiating Arrays in Satellite Communications. IEEE Access 2023, 11, 79684–79696. [Google Scholar] [CrossRef]
- Lei, H.; Zhu, C.; Park, K.H.; Lei, W.; Ansari, I.S.; Tsiftsis, T.A. On Secure NOMA-Based Terrestrial and Aerial IoT Systems. IEEE Internet Things J. 2022, 9, 5329–5343. [Google Scholar] [CrossRef]
- Ma, Y.; Lv, T.; Pan, G.; Chen, Y.; Alouini, M.S. On Secure Uplink Transmission in Hybrid RF-FSO Cooperative Satellite-Aerial-Terrestrial Networks. IEEE Trans. Commun. 2022, 70, 8244–8257. [Google Scholar] [CrossRef]
- Okati, N.; Riihonen, T.; Korpi, D.; Angervuori, I.; Wichman, R. Downlink Coverage and Rate Analysis of Low Earth Orbit Satellite Constellations Using Stochastic Geometry. IEEE Trans. Commun. 2020, 68, 5120–5134. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, J.; Pan, G.; Alouini, M.S. Secrecy Outage Analysis for Satellite-Terrestrial Downlink Transmissions. IEEE Wirel. Commun. Lett. 2020, 9, 1643–1647. [Google Scholar] [CrossRef]
- Homssi, B.A.; Al-Hourani, A. Modeling Uplink Coverage Performance in Hybrid Satellite-Terrestrial Networks. IEEE Commun. Lett. 2021, 25, 3239–3243. [Google Scholar] [CrossRef]
- Tannaz, S.; Ghobadi, C.; Nourinia, J.; Mostafapour, E. The Effects of Negative Exponential and K-distribution Modeled FSO Links on the Performance of Diffusion Adaptive Networks. In Proceedings of the 2018 9th International Symposium on Telecommunications (IST), Tehran, Iran, 17–19 December 2018; pp. 19–22. [Google Scholar] [CrossRef]
- Bykhovsky, D. Simple Generation of gamma, Gamma–Gamma, and K Distributions With Exponential Autocorrelation Function. J. Light. Technol. 2016, 34, 2106–2110. [Google Scholar] [CrossRef]
- Ansari, I.S.; Yilmaz, F.; Alouini, M. Performance Analysis of Free-Space Optical Links Over Málaga (M) Turbulence Channels With Pointing Errors. IEEE Trans. Wirel. Commun. 2016, 15, 91–102. [Google Scholar] [CrossRef]
- Yang, L.; Gao, X.; Alouini, M.S. Performance Analysis of Relay-Assisted All-Optical FSO Networks Over Strong Atmospheric Turbulence Channels With Pointing Errors. J. Light. Technol. 2014, 32, 4613–4620. [Google Scholar] [CrossRef]
- Kaushal, H.; Kaddoum, G. Optical Communication in Space: Challenges and Mitigation Techniques. IEEE Commun. Surv. Tutor. 2017, 19, 57–96. [Google Scholar] [CrossRef]
- Yin, Z.; Jia, M.; Wang, W.; Cheng, N.; Lyu, F.; Guo, Q.; Shen, X. Secrecy Rate Analysis of Satellite Communications With Frequency Domain NOMA. IEEE Trans. Veh. Technol. 2019, 68, 11847–11858. [Google Scholar] [CrossRef]
- Bankey, V.; Singh, V.; Upadhyay, P.K. Physical Layer Secrecy of NOMA-Based Hybrid Satellite-Terrestrial Relay Networks. In Proceedings of the 2020 IEEE Wireless Communications and Networking Conference (WCNC), Seoul, Republic of Korea, 25–28 May 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Li, H.; Zhao, S.; Li, Y.; Peng, C. Sum Secrecy Rate Maximization in NOMA-Based Cognitive Satellite-Terrestrial Network. IEEE Wirel. Commun. Lett. 2021, 10, 2230–2234. [Google Scholar] [CrossRef]
- Guo, K.; Tang, X.; Guo, D.; Zhu, S.; An, K.; Zhong, L.; Zhang, B. Secrecy Performance Analysis of NOMA-Based Integrated Satellite-Terrestrial Relay Networks with Multiple Colluding Eavesdroppers. In Proceedings of the 2020 International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 21–23 October 2020; pp. 648–653. [Google Scholar] [CrossRef]
- Li, H.; Li, J.; Liu, M.; Gong, F. UAV-Assisted Secure Communication for Coordinated Satellite-Terrestrial Networks. IEEE Commun. Lett. 2023, 27, 1709–1713. [Google Scholar] [CrossRef]
- Bloch, M.; Barros, J.; Rodrigues, M.R.D.; McLaughlin, S.W. Wireless Information-Theoretic Security. IEEE Trans. Inf. Theory 2008, 54, 2515–2534. [Google Scholar] [CrossRef]
- Jurado-Navas, A.; Garrido-Balsells, J.M.; Paris, J.F.; Puerta-Notario, A.; Awrejcewicz, J. A unifying statistical model for atmospheric optical scintillation. Numer. Simul. Phys. Eng. Process. 2011, 181, 181–205. [Google Scholar]
- Sandalidis, H.G.; Tsiftsis, T.A.; Karagiannidis, G.K. Optical Wireless Communications With Heterodyne Detection Over Turbulence Channels With Pointing Errors. J. Light. Technol. 2009, 27, 4440–4445. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M.; Romer, R.H. Tables of Integrals, Series, and Products, 6th ed.; Academic: New York, NY, USA, 2000. [Google Scholar]
- Khallaf, H.S.; Shalaby, H.M.H.; Garrido-Balsells, J.M.; Sampei, S. Performance analysis of a hybrid QAM-MPPM technique over turbulence-free and Gamma–Gamma free-space optical channels. J. Opt. Commun. Netw. 2017, 9, 161–171. [Google Scholar] [CrossRef]
- Abdi, A.; Lau, W.C.; Alouini, M.; Kaveh, M. A new simple model for land mobile satellite channels: First- and second-order statistics. IEEE Trans. Wirel. Commun. 2003, 2, 519–528. [Google Scholar] [CrossRef]
- Xu, M.; Xu, G.; Dong, Y.; Wang, W.; Zhang, Q.; Song, Z. UAV-assisted FSO communication system with amplify-and-forward protocol under AOA fluctuations: A performance analysis. China Commun. 2023, 20, 111–130. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, Q.; Song, Z.; Ai, B. Relay-Assisted Deep Space Optical Communication System Over Coronal Fading Channels. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 8297–8312. [Google Scholar] [CrossRef]
- Lei, H.; Gao, C.; Guo, Y.; Pan, G. On Physical Layer Security Over Generalized Gamma Fading Channels. IEEE Commun. Lett. 2015, 19, 1257–1260. [Google Scholar] [CrossRef]
- Prudnikov, A.P.; Brychkov, I.A.; Marichev, O.I. Integrals and Series: More Special Functions; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Xiang, Z.; Yang, W.; Cai, Y.; Ding, Z.; Song, Y. Secure Transmission Design in HARQ Assisted Cognitive NOMA Networks. IEEE Trans. Inf. Forensics Secur. 2020, 15, 2528–2541. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions; Dover: Downers Grove, IL, USA, 1972. [Google Scholar]
- Qu, L.; Xu, G.; Zeng, Z.; Zhang, N.; Zhang, Q. UAV-Assisted RF/FSO Relay System for Space-Air-Ground Integrated Network: A Performance Analysis. IEEE Trans. Wirel. Commun. 2022, 21, 6211–6225. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).