Abstract
A strain isolation pad is a critical connection mechanism that enables deformation coordination between the rigid thermal insulation tile and the primary structure in the thermal protection system of a reusable hypersonic vehicle. An experimental investigation has been conducted to determine the static, loading–unloading, and high-cycle fatigue (HCF) responses of the SIP with 0.2 mm adhesive under through-thickness tension at room temperature. The contributions of the rigid thermal insulation tile and metallic substructure have not been considered so far. The results indicate that the tensile behavior of the SIP joint is highly nonlinear. The static and fatigue tensile failures both initiate from the corner close to the adhesive/SIP interface due to the stress concentration and the edge effect. The uniform breakage of the aramid fiber can be seen on the cross-section. A novel method is proposed to quantify the residual strain due to the short-time ratcheting effect of the SIP joint in the initial loading–unloading tensile response. As the number of fatigue cycles increases, the thickness of the SIP joint continues to increase until failure. An explicit expression associated with the growth of SIP joint thickness, fatigue cycle number, and peak cyclic stress is established. The turning point of the thickness growth rate with the fatigue cycle number is proposed as a new fatigue failure index for the SIP joint under tensile fatigue, and a fatigue life prediction model is developed.
1. Introduction
Large-scale, heavy-duty launch vehicles, reusable space-to-ground transportation systems, and hypersonic vehicles have emerged as global research hotspots. This type of aircraft suffers from severe aerodynamic heating issues due to its hypersonic flight speed [1,2,3]. As a result, a thermal protection system (TPS) is one of the critical structures that insulates high heat flow, resists the impact of loads such as aerodynamic noise, and ensures the aircraft fuselage’s integrity. One of the thermal protection systems on hypersonic vehicles is the rigid thermal insulation tile TPS [4,5]. As shown in Figure 1, it mainly consists of four parts: coating, rigid thermal insulation tile, strain isolation pad, and fuselage skin structure. High-emissive coatings can reflect the energy generated by aerodynamic heat back into the air. Rigid thermal insulation tiles are typically made of low thermal conductivity materials, such as high-temperature-resistant ceramics with much lower failure strain, and serve mainly for heat insulation and aerodynamic load bearing. The fuselage is typically made of metallic material and is used primarily as a load-bearing structure. A 1–10 mm strain isolation pad (SIP) layer is usually bonded to the thermal insulation tile and primary structure by silicone adhesive. Because the SIP has a much lower modulus, it can coordinate the deformation of the rigid thermal insulation tile and the primary structure while avoiding damage to the thermal insulation tile due to rigid contact.
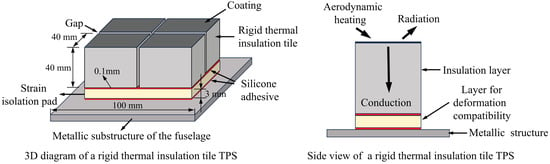
Figure 1.
A schematic illustration of a rigid thermal insulation tile thermal protection system (TPS) for a reusable hypersonic vehicle.
Most strain isolation pads are made of heat-resistant fibers, such as aramid fiber filaments, and have good deformation coordination capabilities. When subjected to external loads, the SIP’s modulus is low, resulting in significant deformation. Excessive deformation in the thickness direction may result in a gap between the rigid thermal insulation tile and the metallic structure of the fuselage. As a result, the fuselage could be exposed directly to the high-temperature thermal flow [6,7]. Understanding fundamental mechanical behavior, such as deformation and failure under through-thickness tensile loads, is critical for ensuring reusable hypersonic vehicle reliability. Reusable hypersonic vehicles must undergo a variety of load environments, such as aerodynamic force, vibration, and noise, many times during their journey between space and ground. TPS systems are prone to fatigue damage, affecting the vehicle’s durability and integrity [8,9]. To ensure the safety of reusable hypersonic vehicles, more research on the fatigue behavior of SIP, as well as the fatigue failure index and life prediction model, is required.
A few studies have been conducted on the mechanical behavior of SIP. The results are as follows: Chen et al. [10] prepared SIP with aramid fibers using the needle process. Their results show that the SIP has good coordinate deformation capacity and tensile strength. No significant change in structure occurred, and the tensile strength can reach 0.9 MPa as the temperature was less than 200 °C. Sawyer et al. [11] investigated the mechanical properties and behavior of materials used in the shuttle orbiter TPS. The materials include the LI-900 RSI tiles, the RTV-560 adhesive, and the SIP. The experimental results indicate that the SIP material exhibits highly nonlinear stress–strain behavior, increased tangent modulus and ultimate tensile strength with an increased loading rate, large short-time load relaxation, and moderate creep behavior. Phillips [12] explored the room-temperature fatigue behavior of 4.1 mm thick SIP in a series of constant-amplitude loading tests. It was found that the SIP material exhibited a monotonic increase in thickness and a monotonic increase in tensile tangent moduli. Kong et al. [13] conducted uniaxial tension, compression, and in-plane shear experiments to study the high-temperature (300 °C) mechanical properties of the SIP. The effect of temperature on the mechanical properties of SIP was investigated. The results indicate that the elasticity modulus and failure strain of the SIP exhibited obvious anisotropic characteristics, and the failure mode was related to the thicknesses of the SIP and the load types in the uniaxial tension and in-plane shear experiments. When compared with room temperature, the tensile and shear moduli were reduced by 6–9.7% and 11.6–17.5%, respectively, at elevated temperatures. Huang et al. [14] investigated the effect of different thicknesses and tensile–shear mixed-mode loadings on the failure mode of SIP through a combination of experiments and numerical simulations. They proposed that the high temperature led to a decrease in the strength of the SIP. The strength calculated by the quadratic nominal strain criterion was slightly greater than that calculated by the maximum nominal strain criterion. The nonlinear dynamic strength of the strain isolation pad (SIP) was studied using a two-degree-of-freedom nonlinear dynamic theoretical model [15]. Their results show that the nonlinear stiffness of SIP has an obvious influence on the dynamic stress of SIP, and the equivalent linear stiffness coefficient of SIP and dynamic stress of SIP decrease with an increase in the nonlinear level of the stiffness of SIP.
Some research findings have been obtained in SIP-related studies. The results, however, are primarily concerned with the mechanical behaviors of SIP joints determined by experiments, and there is a lack of understanding of the failure mechanism and damage evolution of SIP joints under alternating load. Furthermore, the SIP joint test results indicate its nonlinear constitutive behavior, but the nonlinearity has not been considered in the present numerical analysis, which results in an inconsistency with the test results. Moreover, the deformation evolution under through-thickness cyclic loading is also critical for understanding the modulus degradation of the SIP joint and the reusability evaluation of the TPS. A reliable and feasible SIP joint fatigue life prediction model is required.
To clarify the failure mechanism, develop a macroscopic constitutive model, and assess the fatigue characteristics of the SIP joint subjected to through-thickness tension, a silicone adhesive-bonded aluminum–SIP–aluminum tensile test specimen is designed first. The load–displacement response, strength, failure strain, and other mechanical properties of the SIP with 0.2 mm adhesive joint were subsequently obtained at room temperature. The deformation of the SIP joint was recorded throughout various loading stages. Second, the finite element model update method combined with the complete polynomial constitutive relationship derived using the complementary strain energy density function is proposed to determine the macroscopic uniaxial tensile stress–strain relationship of the SIP. The load–displacement response obtained using the numerical analysis with the identified model agrees well with the test results. Finally, the through-thickness tensile loading–unloading test and high cycle fatigue (HCF) test with stress ratio R = 0.1 were performed at room temperature, and the life of the SIP joint specimens under different fatigue loads was determined. An innovative data analysis method based on the modified Norton creep law is suggested to characterize the short-time creep characteristics of the SIP joint through fatigue loading and unloading responses. It is seen that the residual strain increases linearly with the number of cycles in the early stage of cyclic loading due to the short-time creep effect. Furthermore, the thickness–elongation ratio of the SIP joint is proposed as the fatigue failure index. A fatigue life prediction method is first developed based on the proposed index. The difference between the predicted life and the fatigue test results is within one standard deviation. The method provided in the work can also be extended to characterize other mechanical properties of SIP joints, such as in-plane shear, compression, and so on.
2. Experiment
2.1. Material and Specimen
The strain isolation pad (SIP) is made of aramid fiber filaments prepared by gas-phase dispersion, laminated to a specific surface density, and needle-punched into a planar fabric. The aramid fiber has excellent lightweight and high-temperature resistance properties with a density of 0.12–0.18 and a glass transition temperature of 270 °C [16,17,18]. Cut a 25 mm × 25 mm SIP, coat it evenly with silicone adhesive on both sides, bond it to the aluminum block, and vacuum pressurize it. The specific adhesive used for the tests is a modified two- or three-component room-temperature curing silicone rubber, and the mechanical and physical properties of the adhesive are strongly related to the modified coupling agent and the curing process, resulting in significant differences between batches. The supplier specifies the adhesive’s basic properties, such as density (1.0–1.3 g/cm3), tensile strength (3–5 MPa), elongation at break (100–200%), and elastic modulus (5–7 MPa). The adhesive’s glass transition temperature () was not specified, but a review of the literature revealed that the glass transition temperature of general silicone rubber ranges from −70 °C to −50 °C, indicating that the silicone rubber performs well at low temperatures. To improve the bonding strength between the Al substrate and the adhesive, the aluminum alloy’s surface was cleaned with acetone to remove oily impurities and then roughened using coarse sandpaper to improve roughness before bonding with the SIP using the adhesive. The pressure is 60 kPa, and it is cured for two days at room temperature. All of the specimen materials are supplied by Science and Technology on Reliability and Environmental Engineering Laboratory, Beijing Institute of Structure and Environment Engineering. Figure 2 depicts the dimensions of the SIP joint specimen, as well as a photograph of a typical test specimen after preparation. The SEM images indicate the microstructure of the SIP before bonding to the Al substructure with the adhesive.
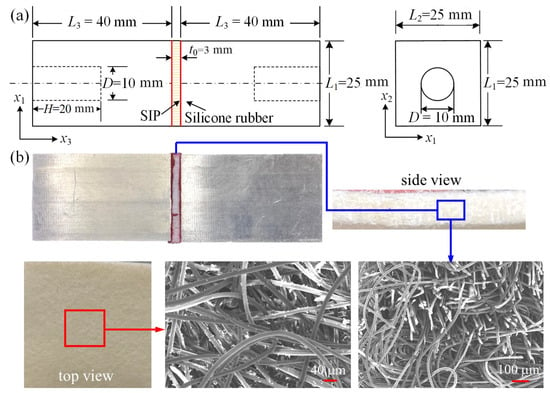
Figure 2.
(a) The dimension of the SIP joint specimen; (b) a photograph of a typical test specimen after preparation. The SEM images indicate the microstructure of the SIP before bonding to the Al substructure with the adhesive.
2.2. Experimental Setup
The SIP joint specimen and fixture are designed and installed in accordance with the monotonic tensile test standard ASTM STD C297/C297M-04 [19], as shown in Figure 3a. A universal servo-hydraulic test machine (MTS 810, MTS Ltd., Eden Prairie, MN, USA) equipped with 25 kN hydraulic grips (Model 647.02B, MTS Ltd., Eden Prairie, MN, USA) and a 10 kN load cell (Model 661.19H-02, MTS Ltd. MTS Ltd., Eden Prairie, MN, USA)was used to perform the through-thickness tensile test on the SIP joint specimen at room temperature. The monotonic loading rate was 1.0 mm/min until failure. The displacement of the SIP joint specimen was measured using a linear variable displacement transducer (Beijing Jinghaiquan Sensing Technology Co., Ltd., Beijing, China) and an MTS displacement sensor simultaneously. The comparison shows the relative deviation of the axial displacement between them is less than 1%. The deformation of the aluminum block is approximately 0.38% of the deformation of the SIP joint, indicating that the deformation of the fixture can be negligible. Similarly, when compared with the SIP joint’s through-thickness deformation, the deformation of the test fixture on the loading path can be negligible. As a result, the difference in displacements measured by LVDT and MTS appears to be insignificant. Only the data obtained by the displacement transducer of the loading machine were used to determine the deformation of the SIP joint. The same experimental setup and specimens were used in the tensile loading–unloading test and fatigue test. The fatigue stress ratio R was 0.1 with a sine wave, and the fatigue test frequency f was 10 Hz.
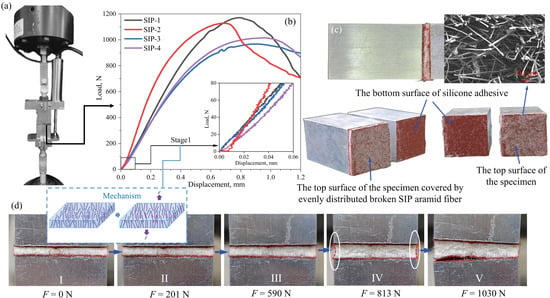
Figure 3.
(a) The experimental setup for the SIP joint’s through-thickness tensile test; (b) load–displacement curves for SIP joint tensile tests; (c) a typical failure mode of the SIP joint specimen under monotonic tension; and (d) deformation evolution for the SIP joint specimen under tension.
3. Monotonic Through-Thickness Tension
3.1. Test Results
Figure 3b depicts the load–displacement curves obtained from the four SIP joint tensile tests. The response exhibits the following two characteristics: First, the load–displacement behavior is nonlinear. When the applied displacement is low, the load increases slowly as the displacement increases. The response of different specimens varies greatly, and there is a low-modulus region for low displacement levels. As the displacement increases, the load–displacement curve exhibits linear behavior. As the displacement increases further, the load growth rate gradually decreases until the SIP joint fails. Second, the tensile behavior of different specimens varies significantly.
It is proposed that the dispersion with low tensile modulus is caused by a transition of fibers in the SIP from the randomly curved and compressed state to the straightened state, as indicated in the middle of Figure 3. The aramid fibers are curved and entangled with each other due to pressure in the curing process. The fibers change from the initial randomly curved precompressed state to the properly straightened state when subjected to a small tensile displacement ( 0.06 mm). The resulting tensile force stretches the aramid fiber from its curved and entangled state to its straightened state, resulting in the specimen’s precompression release. The majority of the fibers do not carry the tensile load, the equivalent tensile modulus is low, and deformation in the thickness direction is significant at this stage. Because fibers’ initial entangled state varies between specimens, the initial tensile behavior of different specimens is highly dispersed, as shown in the corner of Figure 3b.
As the displacement increases, the fibers gradually stretch and carry the tensile load, causing the load to rise. When all the fibers are fully loaded, the specimen’s equivalent tensile stiffness is stable, which is related to the tensile modulus of the fibers. The resultant tensile load increases linearly as the applied displacement increases. As the displacement increases, the fibers elongate and are continuously broken close to the adhesive/SIP interface, resulting in a gradual decrease in the specimen’s equivalent modulus. The fracture of SIP’s fiber gradually grows from the edge to the interior until the final failure, at which the resultant tensile load reaches its peak value due to the edge effect [20,21]. Figure 3c depicts the typical failure mode of the SIP joint test specimen. The fracture of all specimens occurred close to the adhesive/SIP interface due to higher tensile stress, which can be seen in the numerical analysis in the following section. Thus, it does not imply that the strength of the interface is weaker than other locations. The Poisson’s ratio effect causes the specimen’s cross-section to deform inwardly, as indicated in Figure 3d, and fiber damage occurs first at the free edge close to the adhesive/SIP interface. The final failure image shows that evenly broken fibers are attached to the silicone adhesive’s surface, which leads to the following statement: SIP joint’s through-thickness tensile failure is primarily manifested by aramid fiber breakage. The most critical failure location of the SIP joint specimen is near the adhesive/SIP interface.
The average equivalent tensile stress of the SIP joint specimen can be calculated using , where F denotes the resultant axial force and is the area of the cross-section area. The average normal strain along the thickness direction can be calculated as , where is the thickness variation in the SIP joint under the applied tensile force and is the initial thickness of the SIP joint. As a result, the failure stress and failure strain for the four SIP tensile tests were obtained, as shown in Table 1. The peak strain is 0.28 on average, and the failure stress is 1.71 MPa on average. The COV of the average failure strain is higher than that of the average failure stress for the SIP joint under through-thickness tensile tests.

Table 1.
Results of the through-thickness tensile tests for the SIP joint specimen.
3.2. The Nonlinear Stress–Strain Relationship under Through-Thickness Tension
The SIP joint tensile load–displacement curve exhibits obvious nonlinear characteristics. As a result, to more precisely characterize the mechanical response of the SIP, a macroscopic constitutive model based on the complementary strain energy density of the homogenous SIP material is proposed, which is given as
where and , represent the normal strain and stress components along the principal material directions. The complementary strain energy density is an analytic function of , and as . Without loss of generality, is given explicitly as [22,23].
in which , , and are unknown compliance constants of the material. Given the experiment’s feasibility and the rationality of the constitutive relation, a higher order of than six has been truncated. Due to a lack of experimental data, the model could not account for the inconsistency of material tensile and compression behavior. As a result, must be an even function of . Normal stresses in the other two orthogonal directions are significantly low in uniaxial tensile tests, resulting in the truncation of higher-order terms of and . Furthermore, the nonlinear coupling between normal stresses can be ignored. To summarize, is simplified for the through-thickness (1-axis) tension test as
Substitute Equation (3) into Equation (1),
where the nonzero coefficient is given to describe the linear normal strain–stress response, including Poisson’s ratio, and the coefficients and with one subscript are used to characterize the nonlinear strain–stress behavior of the SIP along the tensile loading direction.
Because the distributions of normal stress and strain in the test are unknown and nonuniform, it is not logical to use a least-squares fitting of the average normal stress and strain to determine the unknown coefficients in Equation (4). The resulting axial force under the applied axial displacement can be given in the experiment. As a result, the data of the resultant forces with associated applied displacements throughout the entire loading history can be used to construct the objective function for the identification of unknown coefficients in Equation (4). The first state of the load–displacement response has not been considered in the identification due to data scattering. The identification of the independent material parameters can be carried out by the finite element model updating method [24,25,26]. Assumed constitutive relations and their initial values must be given to start the simulation. The resultant forces F are collected and compared with their experimental counterparts given by the load cell. The difference is quantified with an objective error function, which could be the sum of the squared differences between experiment-measured and numerical-calculated resultant forces. The goal is to iteratively minimize this objective function concerning the constitutive parameters. Accordingly, an objective function is expressed in terms of unweighted least squares as follows:
where represents the set of unknown material parameters and N is the number of load steps at which the resulting axial force is acquired. and are the FEM-calculated and experiment-measured resultant forces at the ith loading step, respectively. It is worth noting that in order to capture the potential nonlinearity in the material behavior, a number of N load steps throughout the loading history of the specimen, all the way to the peak force, were considered in the identification procedure. To minimize the objective function, its partial derivatives with respect to the material parameters are set to zero; thus,
After substituting Equation (4) into the objective function, the objective function is now related to the FEM-calculated resultant force , the experiment-measured resultant force , and the set of unknown material constants. The finite element model updating with the extracted data points is used in solving the optimization problem to determine the unknown parameters in Equation (4). It is seen that the coefficients and , which are related to the in-plane elastic modulus, cannot be identified through the through-thickness (out-of-plane) tensile test since the axial resultant force F is not sensitive to them. The coefficients and represent Poisson’s ratio effect, and both are not sensitive to the resultant force F either. As a result, only the compliance constants , , and can be identified from the uniaxial tension along the tensile direction (the 1-axis). The initial guess of , , and can be extracted from the relationship between the average tensile stress and strain obtained from the tensile test, which can be given explicitly as
where , , F, and A are defined in Section 3.1.
To identify three unknown coefficients defined through the macroscopic uniaxial stress–strain in Equation (7), a three-dimensional numerical simulation model of the SIP joint tensile test was developed using the finite element software Abaqus, (Abaqus 2021) and the model with the meshing is shown in Figure 4a. Aluminum alloy is an isotropic material with a Poisson’s ratio of 0.3 and an elastic modulus of 72 GPa. The 0.2 mm thick adhesive layer is included in the simulation. The elastic modulus and Poisson’s ratio of 6 MPa and 0.35 are given in the model. A user subroutine, UMAT, is used to substitute the constitutive relationship of SIP given in Equation (4) and the initial parameters of the relationship into the finite element model. The model contains 27,500 8-node hexahedral C3D8 elements, with 12,500 hexahedral elements for the aluminum alloy grip and 15,000 hexahedral elements in the SIP. It is assumed that the unknown parameters and = 0.3. However, the identified results of the three coefficients , , and are not sensitive to the assumption.
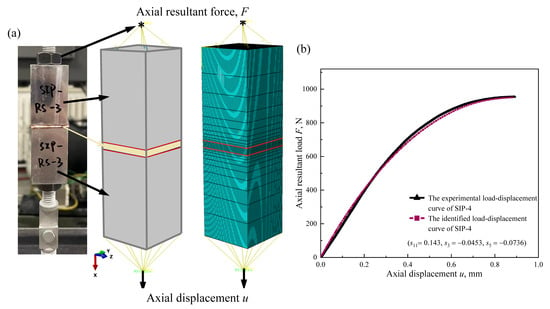
Figure 4.
(a) FEM model of the SIP joint test specimen (The symbol “*” represents reference points); (b) comparison of the typical load–displacement curves determined from the FEM simulation using the proposed constitutive model and extracted from the uniaxial tensile experiments (No-4).
The through-thickness tensile stress–strain curves for different specimens are distinct, but their nonlinear behavior characteristics are essentially similar. The comparison between the load–displacement curve calculated using the identified relationship in the FEM and the measured curve in Figure 4b indicates that the proposed stress–strain relationship can characterize the essential nonlinearity of the load–displacement for the SIP joint specimen under uniaxial tension. The stress distribution of the SIP joint under the uniaxial tensile displacement is depicted in Figure 5a–c, which is obtained through numerical simulation with the identified material parameter set −. It is seen that the distributions of the stress components , , and all have 90° rotational symmetry about the x-axis. Because of the symmetry of the structural geometry and loading conditions, the distribution is symmetric. The variation in normal stress components along different paths of the SIP specimen is demonstrated in Figure 5d–g. The results indicate that the magnitude of tensile normal stress is higher than the other two normal stress components. The stress components are higher around the edge of the adhesive/SIP interface, and it suggests that the failure of the SIP joint initiates at the edge close to the top or bottom interface. The middle section of the SIP joint specimen is the least constrained. As a result, the Poisson’s ratio effect induces an indentation in the middle section, as shown in the experimentally observed deformation in Figure 3d.
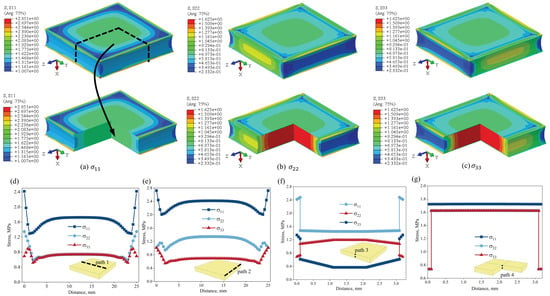
Figure 5.
The contour of the normal stress components for the SIP under uniaxial tension: (a) ; (b) ; (c) , and the variation in normal stress components along (d) path 1, (e) path 2, (f) path 3, and (g) path 4.
4. Tensile Fatigue Tests
4.1. The Loading–Unloading Tensile Response with Ratcheting Effect
In order to study the evolution of the stress–strain response at different stages under cyclic loading, Figure 6 depicts the typical tensile loading–unloading responses of the SIP joint specimen under various peak cyclic loads when the number of cycles is less than 100, which is known as very low cycle fatigue. The minimum stress remains 0.05 MPa. Given the interaction between aramid fibers, significant hysteresis occurs. It is seen that the residual strain and the area of the hysteresis loop increase rapidly in the initial few cycles, such as when the cyclic number is less than 20. The larger hysteresis loop area with higher residual strain results from strain energy dissipation caused by the SIP’s transformation from the initial precompression state to the releasing state under tensile load. Except for the initial few cyclic loads, the unloading strain at the end of the cycle nearly coincides with the loading strain at the beginning of the cycle. It is worth noting that the hysteresis loop continuously shifts to a larger strain without a noticeable change in shape, indicating that the residual strain increases significantly with an increasing number of cycles. As a result, the primary change is an increase in the SIP joint thickness.
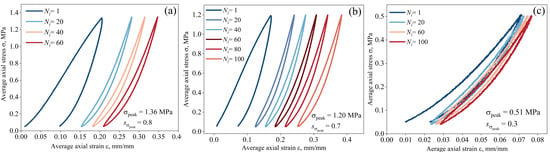
Figure 6.
The loading and unloading response of the SIP joint specimen under various cyclic loads: (a) = 0.8; (b) = 0.7; (c) = 0.3.
To characterize the effect of the loading–unloading procedure on the microstructure of the SIP material. Figure 7 demonstrates the SEM photos of the SIP material’s microstructure before and after the loading and unloading procedure. The comparison shows that the loading–unloading procedure can reduce the tightness of the entangled fibers in the SIP while increasing the gaps between the fibers, which might cause an increase in the specimen’s thickness.

Figure 7.
The comparison of SEM photos for the SIP material before loading and after the loading–unloading procedure: (a,b) show photos of the SIP’s microstructure before loading; (c,d) show images of the SIP’s microstructure after loading and unloading. The comparison indicates that the degree of entanglement of SIP fibers decreases after loading and unloading, while the gap between fibers increases.
Figure 8 illustrates the variation in the hysteresis characteristic with the number of cycles. It can be noted that except for the first 20 cycles, the area of the hysteresis loop grows gradually as the number of cycles increases and quickly as the specimen approaches failure. The variation in the secant modulus of the SIP joint is consistent with that of the area of the hysteresis loop, but it decreases with the number of cycles. Although the area of the hysteresis loop and secant modulus both change very slowly with the number of cycles, the residual strain of the material continues to increase with the number of cycles. This suggests that the SIP joint clearly exhibits a “ratcheting” effect during the loading and unloading procedure. The term “ratcheting” refers to the cyclic loading-induced inelastic stress–strain response of metallic materials, which is used to characterize the phenomenological variation in the SIP joint hysteresis. In summary, a short-time ratcheting with negligible fatigue damage is the main cause of the deformation of the SIP joint when the loading–unloading process has fewer than 100 cycles.
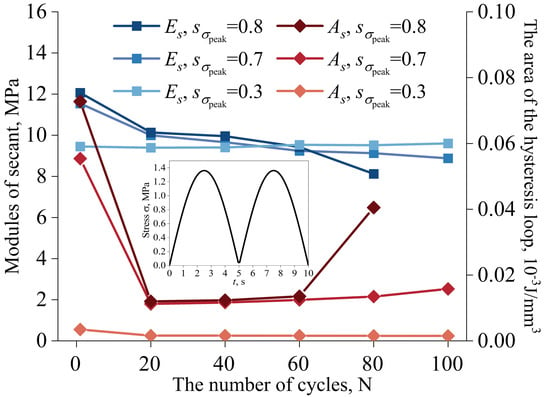
Figure 8.
The variation in the secant modulus and the hysteresis loop area with the number of cycles.
Several creep models are available to evaluate the residual strain due to the time-dependent loading history, including the Norton model [27], Burgers model [28], and Kelvin model [29], etc. For a given constant stress, the creep strain due to the stress holding time is determined using the Norton model, which is shown as
where A, B, and C are material constants. The Norton model is suitable for evaluating the time-dependent creep strain under constant stress. However, for the cyclic loading history, the stress varies continuously. The variation in the cyclic stress with time is given as follows:
in which , , and are the given fatigue amplitude, angular frequency, and mean stress, respectively. To quantify the residual strain under cyclic tensile load, the Norton model was referred to and modified to account for varying loading histories. Substituting Equation (9) into Equation (8), the residual strain at time can be expressed by the Taylor expansion as follows:
when is small enough, the second-order small quantity can be ignored.
The method for determining the residual strain due to ratcheting within one stress cycle is depicted schematically in Figure 9. It is assumed that the residual strain of the SIP joint in a short time is linearly dependent on stress holding time [11], as shown by the light orange short line in Figure 9. So, the exponential parameter of C in Equation (8) equals 1. When is a short time period with , in which T is the time for one fatigue cycle, the residual strain for the time period T can be expressed as
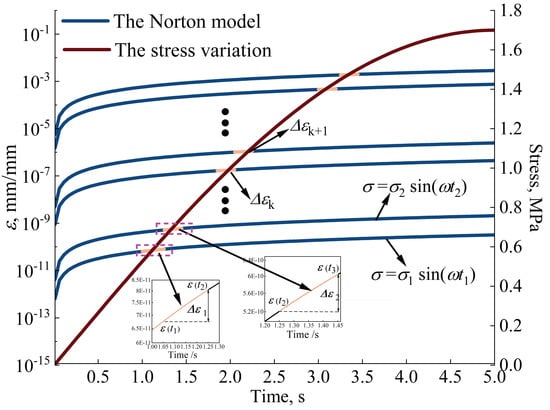
Figure 9.
A schematic diagram of the method for determining the strain due to short-time creep within a stress cycle.
The variation in stress with time t within one cycle is taken into account in Equation (11), and the residual strain in one cycle can be determined using the linear relationship between the strain and time with the Taylor expansion of Equation (8). The total residual strain can be determined by discretizing the time in one cycle T, calculating the short-time residual strain over a discrete period, and then accumulating it. The loading history can be considered by incorporating the strain from previous loading histories.
Figure 10a depicts the variation in residual strain with the number of cycles for various cyclic stress levels. When the number of cycles is fewer than 100, the residual strain increases approximately linearly with the number of cycles, where the slope k represents the residual strain growth rate with the number of cycles. In order to extract the parameters in the residual strain model, the following two sets of data were used:
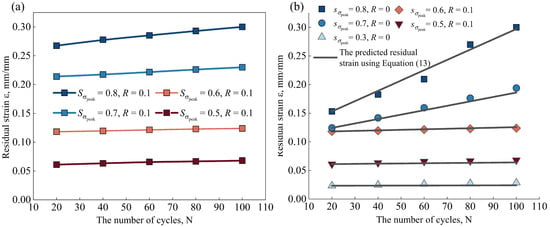
Figure 10.
(a) The variation in the residual strain with the number of cycles with 100; (b) the comparison of residual strain between the predicted model in Equation (13) and experimental result.
Equation (12) is a nonlinear equation including only one material parameter, B. It is solved using Newton’s iteration method by taking = 0.01, determining B = 5.11, and then solving the following equation: with s = 0.8. The material parameter A of 0.071 is obtained. = and are taken to verify the effect of the time step on the parameters A and B. They eventually converge to A = 0.071 and B = 5.11. As a result, the residual strain of the SIP joint caused by the short-time ratcheting can be determined as follows:
Equation (13) can be used to predict the variation in residual strain in one cycle for different peak cyclic stress with various stress ratios. Figure 10b compares the experimental results with the predicted data (black-solid line). There is good agreement between the experimental results and the residual strain predicted by the model of Equation (13). When the peak cyclic stress is high, the residual strain resulting from the short-time ratcheting grows linearly with the number of cycles, and the growth rate of the residual strain is correlated with the peak cyclic stress. Short-time ratcheting is the primary cause of residual strain, which is associated with thickness growth. Residual strain develops more quickly as the amplitude of the cyclic stress rises. To put it briefly, the deformation of the SIP joint induced by the ratcheting in the early stage of the cyclic loading history is significant and cannot be ignored.
4.2. High Cycle Fatigue Test Results
The SIP joint fatigue life was obtained using a constant-amplitude tensile fatigue test with a stress ratio of R = 0.1 and a frequency of f = 10 Hz. Peak stress ratio is defined as follows: , where is the peak cyclic stress and is the average ultimate stress obtained in the uniaxial tensile test of the SIP joint. The run-out fatigue life was set at cycles, which is much lower than the value of for high cycle fatigue. The SIP joint is used in the reusable hypersonic launch vehicle’s thermal protection system, which is the reason for the short run-out criteria given. Although the launch vehicle is reusable, its repeated service life is much shorter than that of the aircraft, so the fatigue life of can fully cover the service life of the launch vehicle. At each fatigue load level, three repeated tests were carried out, except for = 0.3. Because the run-out test was expected, only one test was performed. The results of fatigue life are listed in Table 2. The failure mode of the fatigue is the same as the monotonic tensile failure of the SIP joint specimen, as shown in Figure 3c. The fatigue failure is also caused by the breakage of the SIP aramid fiber, which occurs close to the adhesive/SIP interface. The broken fibers are evenly distributed on the surface of the silicone adhesive.

Table 2.
Tensile fatigue test results.
4.3. Prediction of Tensile Fatigue Life
When the number of cycles in the tensile fatigue test exceeds 100, material degradation caused by fatigue damage, as well as the ratcheting effect, contributes to the specimen’s deformation. Thus, the secant slope between the measured maximum and minimum axial deformations can be used to estimate the increase in SIP joint thickness with the number of fatigue cycles, as shown:
in which represents the residual deformation of the SIP joint, and is the deformation at the maximum load at fatigue cycle . Thus, can be approximately treated as the thickness growth of the SIP joint at the fatigue cycle . Accordingly, the thickness growth of the SIP joint with the number of fatigue cycles can be given, as demonstrated in Figure 11a–c. The schematic diagram of the determination for the residual deformation of the SIP joint is indicated in Figure 11a. It is seen that the SIP joint thickness continues to grow as the number of fatigue cycles increases. The growth rate is low in the early stages of the fatigue test. As the number of cycles increases, a turning point occurs, and the SIP joint thickness rapidly increases until final failure. In short, the SIP joint thickness gradually increases and then rapidly increases with the number of cycles, which is a typical uniaxial through-thickness tensile fatigue characteristic of the SIP joint.
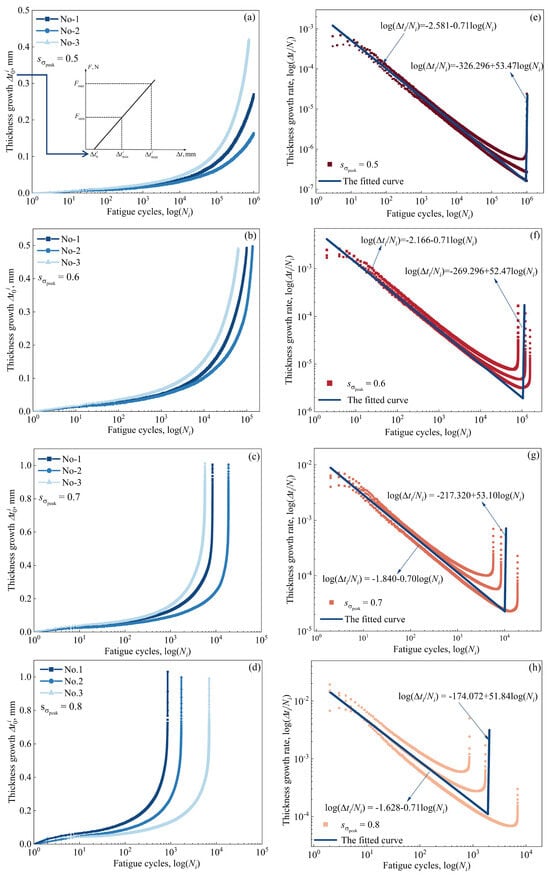
Figure 11.
The variation in the SIP joint thickness with the logarithmic number of fatigue cycles: (a) = 0.5; (b) = 0.6; (c) = 0.7; (d) = 0.8; The logarithmic variation in the thickness growth rate r with the number of fatigue cycles. (e) = 0.5; (f) = 0.6; (g) = 0.7; (h) = 0.8.
The thickness growth rate corresponding to the fatigue cycle is defined as follows: . Accordingly, the logarithmic variation in the thickness growth rate with the number of cycles can be obtained, as shown in Figure 11d–f. It is noted that the thickness growth rate shows bilinear characteristics with the number of fatigue cycles in logarithmic form. When the number of cycles is fewer than a critical threshold, the thickness growth rate decreases linearly with the number of fatigue cycles. As the number of cycles reaches the threshold, the thickness growth rate increases sharply, and there is an apparent shift in thickness growth rate between the two linear segments. It is proposed that the turning point of the number of fatigue cycles, , which is related to the amplitude of cyclic stress, can be given as the fatigue life index of the SIP joint. The fatigue life index implies that tensile failure with the debonding of the SIP joint with the substructure does not occur when the number of cycles equals , but it is expected that the thickness of the SIP joint will increase quickly, and fatal failure can arise shortly. Consequently, the number of fatigue cycles is slightly fewer than the fatigue life in Table 2. The number of fatigue cycles corresponding to the turning point of thickness growth rate is defined as the tensile fatigue life index, which is in accordance with the conservative prediction. As a result, when the number of cycles reaches the turning point , a uniaxial tensile fatigue failure will occur soon.
The bilinear variation in the total thickness growth rate with the fatigue cycles in logarithmic form can be given as follows:
where – are constants and is the fatigue life index. It is noted that and can be determined using the least-squares fitting of the experimental data, and they are insensitive to the amplitude of the fatigue stress. However, the intercepts and are related to the amplitude of the fatigue stress. To determine the fatigue life index under various fatigue stress, the relationship between and with the peak stress ratio is plotted in Figure 12. It is interesting to note that and both vary linearly with the logarithmic stress ratio . Therefore, an explicit expression between the intercept and the logarithmic stress ratio can be obtained by least-squares fitting, and the fitting results can be substituted into Equation (15). The bilinear relationship between the thickness growth rate and the fatigue cycles is given as
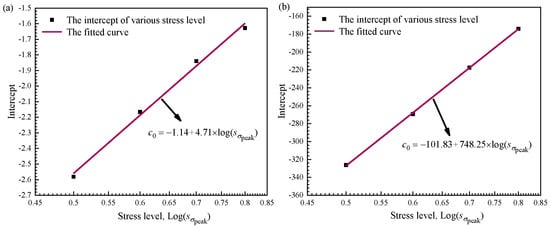
Figure 12.
(a) The variation in the intercept and (b) with the normalized fatigue stress ratio .
The relationship between the growth of SIP joint thickness, fatigue cycle number, and fatigue stress level is established by Equation (16). It elucidates how thickness increases with fatigue cycle number at any given stress level, which can be used to predict the thickness growth of the SIP joint. Additionally, the remaining fatigue life can be determined when the fatigue life index can be determined. Given that the thickness growth rate in Equation (16) is equal at , the following expression between the fatigue life index and the peak stress ratio at the turning point of the thickness growth rate curve can be obtained as follows:
As a result, Figure 13 shows a comparison between the predicted fatigue life index using Equation (17) and the failure life given from the fatigue test corresponding to different peak fatigue stress . The predicted fatigue life index appears to be in good agreement with the experimental results, which fall within one standard deviation of the error range. Using Equation (17), the tensile fatigue life index of the SIP joint is predicted to be around under the fatigue stress ratio = 0.3, implying that the specimen ran out after cycles, as we discovered in the test. The comparison results indicate that, while the fatigue life index predicted by Equation (11) is theoretically shorter than the fatigue failure life, the difference is insignificant and can be ignored. The fatigue life index proposed is better suited to conservative engineering design. By defining the fatigue life index, the thickness growth of the SIP joint can be quantified as the number of fatigue cycles increases, and the remaining life can be estimated.
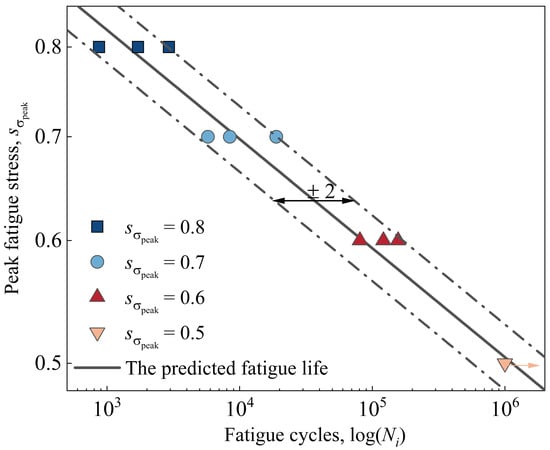
Figure 13.
The comparison of the uniaxial through-thickness tensile fatigue life between the proposed model (Equation (17)) and the experimental results.
The number of fatigue cycles corresponding to the turning point in the logarithmic variation in the thickness growth rate is defined as the SIP joint’s uniaxial tensile fatigue life index. A tensile life prediction model based on the definition is suggested, and it can be used to predict the joint’s fatigue behavior at various peak fatigue stresses. It should be noted that the prediction model must be validated further through extensive uniaxial tensile tests, as well as the fitting parameters in Equations (16) and (17) must be modified to account for data scattering. However, the feature of the thickness variation with the fatigue cycles remains unchanged, and the method to derive the model is still applicable. The SIP joint thickness growth rate and remaining fatigue life provide an evaluation method for assessing the health of the reusable aircraft thermal protection system. However, due to experimental state limitations, the methods are currently limited to low-frequency uniaxial tensile fatigue life prediction. More research into the fatigue behavior of SIP joints under high-frequency multiaxial stress states with varying fatigue stress ratios is needed.
5. Conclusions
Tensile, loading–unloading, and high cycle fatigue (HCF) tests at room temperature were conducted to investigate SIP joint through-thickness mechanical behavior. The monotonic and loading–unloading tensile stress–strain responses with tensile failure mode, as well as the fatigue failure life, have been obtained experimentally. The key findings are as follows:
Obvious nonlinearity occurs in the through-thickness tensile load–displacement response of the SIP with 0.2 mm adhesive. The tensile failure of the SIP joint specimen initiates at the corner close to the SIP/adhesive interface and propagates until final failure. The uniform breakage of the aramid fibers can be observed for tensile failure. A macroscopic equivalent nonlinear stress–strain relationship is derived using the complementary strain energy density function. Based on the identified nonlinear tensile stress–strain relationship, a finite element numerical analysis model was established to reveal the mechanism of the initial failure of the SIP joint specimen at the SIP/adhesive interface.
Under a constant-amplitude tensile fatigue load, the amplitude of the tensile strain increases continuously as the number of cycles increases. Significant residue strain can be seen when the number of cycles is less than 100. It is primarily caused by the SIP joint’s short-time ratcheting effect. The experimental results indicate that the residual strain increases linearly with the number of cycles, and the slope of the variation is related to the peak cyclic stress. A combination of the simplified Norton model and the linear relationship between ratcheting strain and stress hold time is proposed to quantify the residual strain due to the short-time ratcheting effect under the cyclic load.
The typical uniaxial tensile fatigue behavior of the SIP joint is as follows: The failure mode of uniaxial tensile fatigue is nearly identical to that of the monotonic tensile test. The SIP joint thickness gradually increases early in the fatigue test and then rapidly increases until final failure with the number of cycles. A bilinear curve can be used to describe the variation in the logarithmic SIP joint thickness growth rate and the number of fatigue cycles. Consequently, the turning point of the thickness growth rate is proposed as a new fatigue life index, and the number of cycles corresponding to the intersection point of the two slopes is defined as the uniaxial tensile fatigue life index. Accordingly, a conservative life prediction model is proposed. The thickness growth of the SIP joint can be quantified as the number of fatigue cycles increases, and the remaining life can be estimated. The predicted life appears to agree well with the experimental results, and the SIP joint fatigue test life is within one standard deviation of the error range.
Author Contributions
Conceptualization, Z.W. and M.L.; methodology, M.L. and L.L.; validation, M.L. and Z.H.; formal analysis, M.L. and Z.H.; investigation, M.L. and Z.H.; resources, Z.W. and L.L.; writing—original draft preparation, M.L. and L.L.; writing—review and editing, Z.H., Z.W. and L.L.; supervision, L.L. and Z.W.; project administration, L.L.; funding acquisition, Z.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work is sponsored by the National Natural Science Foundation of China under Grant Nos. 11472043, U2241240, and U20B2002, the National Program on Key Basic Research Project under Grant No. 2019-JCJQ-ZD-308-00, and the BIT Research and Innovation Promoting Project under Grant No. 2023YCXY016. Dr. L. Liu is supported under the Program for New Century Excellent Talents at Chinese Universities and the 111 Project (B16003). Such support is gratefully acknowledged.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to privacy reasons.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Petley, D.; Alexander, W.; Ivey, G.; Kerr, P.A. Steady Internal Flow and Aerodynamic Loads Analysis of Shuttle Thermal Protection System; Technical Report NASA/TP-1984-2255; NASA Langley Research Center: Hampton, VA, USA, 1984.
- Qin, Q.H.; Xu, J.L.; Guo, S. Fluid–thermal analysis of aerodynamic heating over spiked blunt body configurations. Acta Astronaut. 2016, 132, 230–242. [Google Scholar] [CrossRef]
- McNamara, J.J.; Thuruthimattam, B.J.; FriedFmann, P.P.; Powell, K.; Bartels, R. Hypersonic aerothermoelastic studies for reusable launch vehicles. In Proceedings of the 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Palm Springs, CA, USA, 19–22 April 2004; p. 1590. [Google Scholar]
- Glass, D.E. Ceramic matrix composite (CMC) thermal protection systems (TPS) and hot structures for hypersonic vehicles. In Proceedings of the 15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Dayton, OH, USA, 28 April–1 May 2008; p. 2682. [Google Scholar]
- Wu, D.F.; Wang, Y.W.; Gao, Z.; Yang, J. Insulation performance of heat-resistant material for high-speed aircraft under thermal environments. J. Mater. Eng. Perform. 2015, 24, 3373–3385. [Google Scholar] [CrossRef]
- Dwoyer, D.L.; Newman, P.A.; Thames, F.C.; Melson, N.D. A Tile-Gap Flow Model for Use in Aerodynamic Loads Assessment of Space Shuttle Thermal Protection System: Parallel Gap Faces; Technical Report NASA/TM-1981-83151; NASA Langley Research Center: Hampton, VA, USA, 1981.
- Walker, J.D. From Columbia to discovery: Understanding the impact threat to the space shuttle. Int. J. Impact. Eng. 2009, 36, 303–317. [Google Scholar] [CrossRef]
- Eason, T.G.; Spottswood, S. A structures perspective on the challenges associated with analyzing a reusable hypersonic platform. In Proceedings of the 54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Boston, MA, USA, 8–11 April 2013; p. 1747. [Google Scholar]
- Sanders, B.J. The Need for a Versatile & Reusable Hypersonic Vehicle. In Proceedings of the 55th International Astronautical Congress of the International Astronautical Federation, the International Academy of Astronautics, and the International Institute of Space Law, Vancouver, BC, Canada, 4–8 October 2004; p. S-5-03. [Google Scholar]
- Chen, Y.; Li, D.; Sun, C.C.; He, Y.L. Response characteristics of thermal-mechanical coupling in rigid ceramic insulation tiles. J. Eng. Thermophys. 2020, 41, 3021–3029. [Google Scholar]
- Sawyer, J.; Rummler, D. Room Temperature Mechanical Properties of Shuttle Thermal Protection System Materials; Technical Report NASA/TM-1980-81786; NASA Langley Research Center: Hampton, VA, USA, 1980.
- Phillips, E. Tension-Tension Fatigue Behavior of the Space Shuttle Strain-Isolation-Pad Material; Technical Report NASA/TM-1980-83183; NASA Langley Research Center: Hampton, VA, USA, 1981.
- Kong, B.; Yang, J.Y.; Wang, M.; Zhang, Q.; Huang, J.; Yao, W. Experiments on high temperature mechanical properties and stress distribution laws on strain isolation pad. J. Northwestern Polytech. Univ. 2018, 36, 1162–1167. [Google Scholar] [CrossRef]
- Huang, J.; Yao, W.X. High-temperature mechanical properties of strain isolation pad for thermal protection system. J. Spacecr. Rocket. 2018, 55, 848–855. [Google Scholar] [CrossRef]
- Huang, J.; Yao, W.X.; Li, P.; Zhou, D.; Chang, C.; Lin, H. Investigation on dynamic behaviors of thermal protection system using a two degree-of-freedom nonlinear theoretical method. Acta Astronaut. 2018, 151, 828–835. [Google Scholar] [CrossRef]
- Villar-Rodil, S.; Martińez-Alonso, A.; Tascón, J.M. Studies on pyrolysis of Nomex polyaramid fibers. J. Anal. Appl. Pyrol. 2001, 58, 105–115. [Google Scholar] [CrossRef]
- Perepelkin, K.E.; Andreeva, I.V.; Pakshver, E.A.; Morgoeva, I.Y. Thermal characteristics of para-aramid fibres. Fibre Chem. 2003, 35, 265–269. [Google Scholar] [CrossRef]
- Cao, K.K.; Liu, Y.F.; Yang, Y.Y.; Yuan, F.; Wang, J.; Liu, H.; Jiang, M.; Yang, J. The preparation and characterization of a heterocyclic meta-aramid fiber with outstanding thermal stability. High Perform. Polym. 2021, 33, 554–567. [Google Scholar] [CrossRef]
- ASTM C297/C297M-04; Standard Test Method for Flatwise Tensile Strength of Sandwich Constructions. ASTM International: West Conshohocken, PA, USA, 2004.
- Cognard, J.Y. Numerical analysis of edge effects in adhesively-bonded assemblies application to the determination of the adhesive behaviour. Comput. Struct. 2008, 86, 1704–1717. [Google Scholar] [CrossRef]
- Cognard, J.Y.; Devaux, H.; Soheir, L. Numerical analysis and optimisation of cylindrical adhesive joints under tensile loads. Int. J. Adhes. Adhes. 2010, 30, 706–719. [Google Scholar] [CrossRef]
- Wang, W.X.; Takao, Y. A nonlinear elastic stress-strain relation of orthotropic composite plates. Acta Mech. Solida Sin. 1991, 12, 253–358. [Google Scholar]
- Ji, X.H.; Hao, Z.Q.; Su, L.J.; He, T.; Liu, L. Characterizing the constitutive response of plain-woven fibre reinforced aerogel matrix composites using digital image correlation. Compos. Struct. 2020, 234, 111652. [Google Scholar] [CrossRef]
- Lecompte, D.; Snits, A.; Vantomme, J.; Vantomme, J.; Van Hemelrijck, D. Mixed numerical–experimental technique for orthotropic parameter identification using biaxial tensile tests on cruciform specimens. Int. J. Solids Struct. 2007, 44, 1643–1656. [Google Scholar] [CrossRef]
- Ereiz, D.; Duvnjak, I.; Jiménez-Alonso, J.F. Review of finite element model updating methods for structural applications. Structures 2022, 41, 684–723. [Google Scholar] [CrossRef]
- Girardi, M.; Padovani, C.; Pellegrini, D.; Robol, L. A finite element model updating method based on global optimization. Mech. Syst. Signal Process. 2021, 152, 107372. [Google Scholar] [CrossRef]
- Xiao, H.R.; Cai, L.X.; Han, G.Z. A novel theoretical model for obtaining Norton’s law of creep materials using different small specimens. Int. J. Mech. Sci. 2023, 261, 108677. [Google Scholar] [CrossRef]
- Wu, K.; Shao, Z.; Qin, S.; Zhao, N.; Chu, Z. An improved nonlinear creep model for rock applied to tunnel displacement prediction. Int. J. Appl. Mech. 2021, 13, 2150094. [Google Scholar] [CrossRef]
- Sun, S. Study on the creep behavior of recombinant bamboo based on a modified generalized Kelvin model. Wood Sci. Technol. 2022, 56, 589–601. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).