1. Introduction
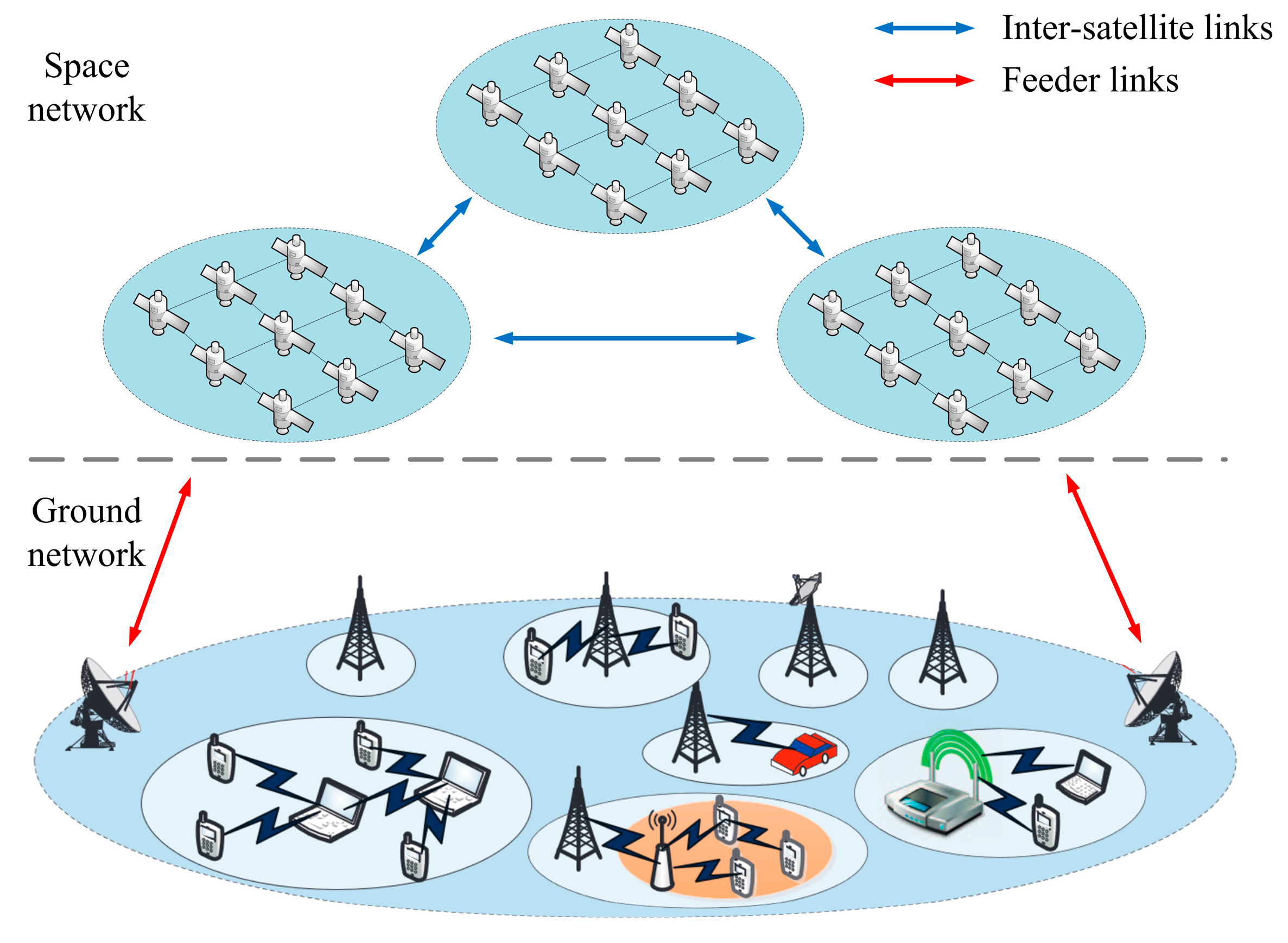
LEO mega-constellation networks demonstrate excellent communication capabilities, including wide geographic coverage, low delay, large bandwidth and uninterrupted service provision, highlighting their significant role in space–air–ground integrated networks (SAGINs) [
1]. In recent years, with the construction of LEO mega-constellations such as Starlink, OneWeb and Kuiper [
2], the explosive growth of Internet-connected devices and traffic demand have increased drastically. However, on-board computing and storage resources are limited by power consumption and the size of satellites. Thus, LEO mega-constellations face challenges in capacity and quality of service (QoS) [
3]. Due to continuous inter-satellite links (ISLs) switching between adjacent satellites, the network topology changes drastically over time. Meanwhile, satellite network traffic shows temporal and spatial heterogeneity, i.e., traffic demands may vary greatly in different geographical locations or in different time slots [
4]. In the case of expanding user scale and traffic demand, the above challenges result in increased congestion in LEO mega-constellations.
Through traffic forecasting, the change in network traffic can be analyzed in advance. The control of network traffic can be changed from reactive response to proactive perception. On the one hand, by forecasting the traffic demand for the next time slot, traffic transmission paths can be planned in advance to proactively avoid congestion. On the other hand, for bandwidth-sensitive services, always reserving peak bandwidth will inevitably reduce resource utilization. On the basis of traffic forecasting, bandwidth allocation can be dynamically adjusted according to service demand to achieve the efficient utilization of bandwidth resources.
The priority of satellite network traffic forecasting is to build network traffic models that represent the network properties accurately. Traffic demand at different geographic locations is usually cyclical [
5]. Meanwhile, the self-similarity of traffic is prevalent in terrestrial networks [
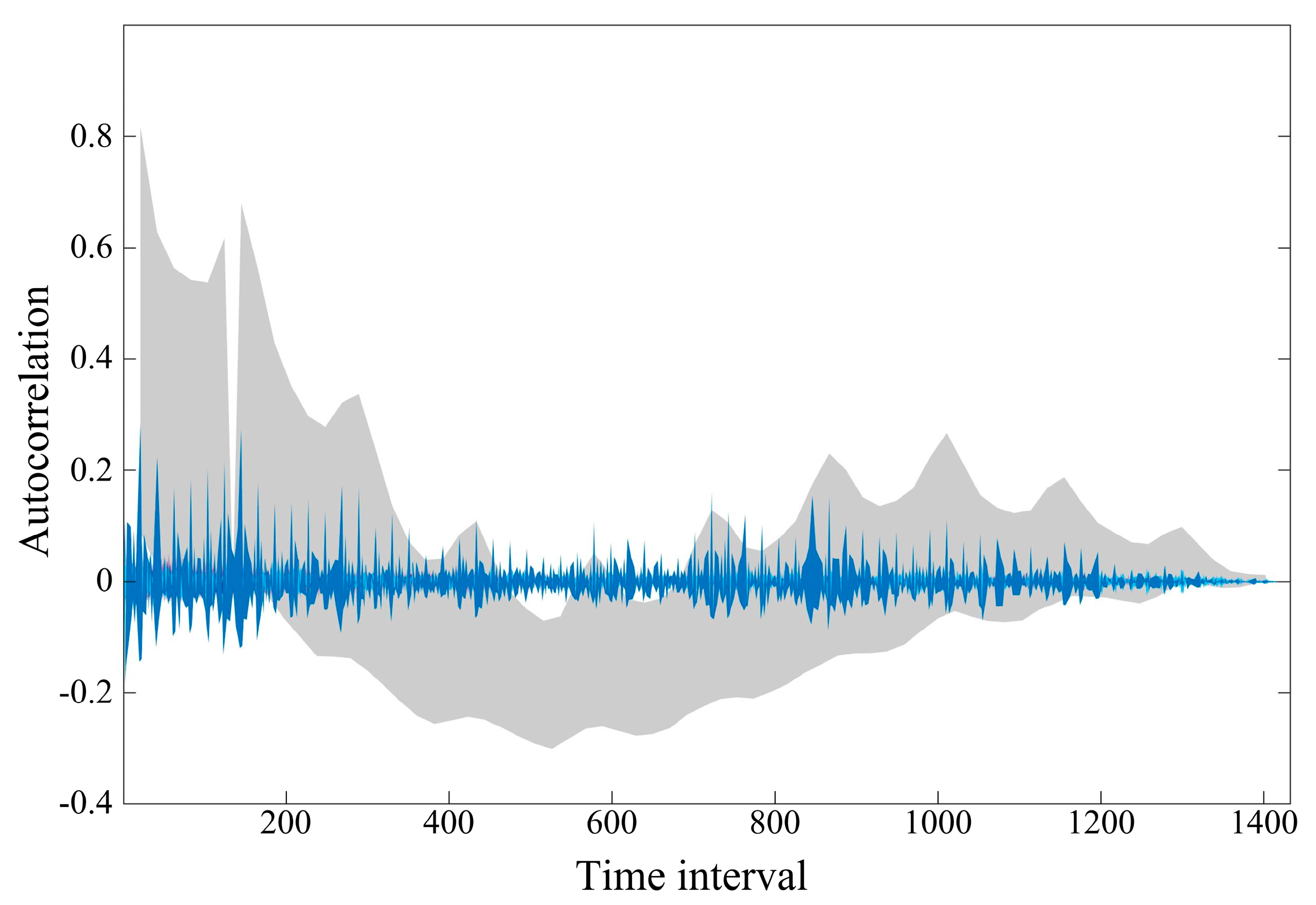
6]. In a satellite network, the traffic is aggregated through terrestrial gateways, which will not change the basic properties, i.e., long-range dependence (LRD) on a large scale and self-similarity on a small scale [
7], as shown in
Figure 1. The actual traffic demand can be divided into long-range baseline and short-range fluctuations; baseline traffic has LRD properties, whereas fluctuations are short-range dependent. Therefore, forecasting models with high precision and low complexity that can demonstrate self-similarity are essential for network traffic forecasting. Traditional network traffic forecasting models, i.e., Poisson models and Markov models, can only deal with short-range dependence (SRD) traffic. Meanwhile, due to the limited on-board computing resources of satellite networks, the computational complexity of a satellite network’s traffic forecasting model needs to be reduced [
8]. So, the traffic prediction models of terrestrial networks are not suitable for satellite networks with LRD properties.
In order to establish a high-precision and low-complexity traffic forecasting model, it is necessary to first decompose network traffic to extract the long-range correlation traffic and short-range fluctuation traffic. Moreover, the computational complexity of the forecasting models for LRD traffic in terrestrial networks is considerable. Due to the limited on-board computing and storage resources of LEO satellites, it is necessary to reduce the computational complexity. Therefore, the forecasting models of terrestrial networks cannot be adopted to constellation networks directly. It is necessary to establish a high-precision and low-complexity forecasting model for mega-constellation network traffic.
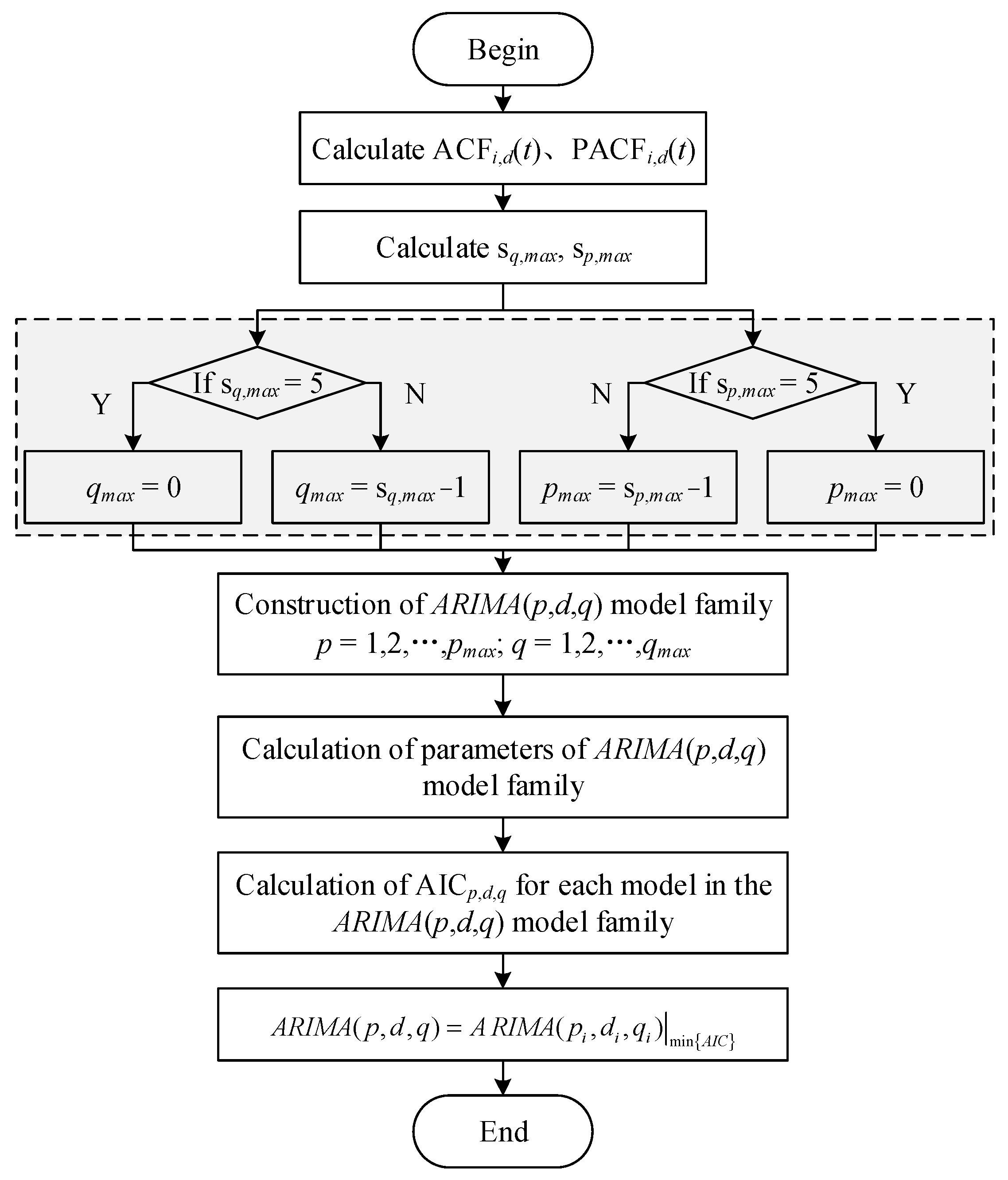
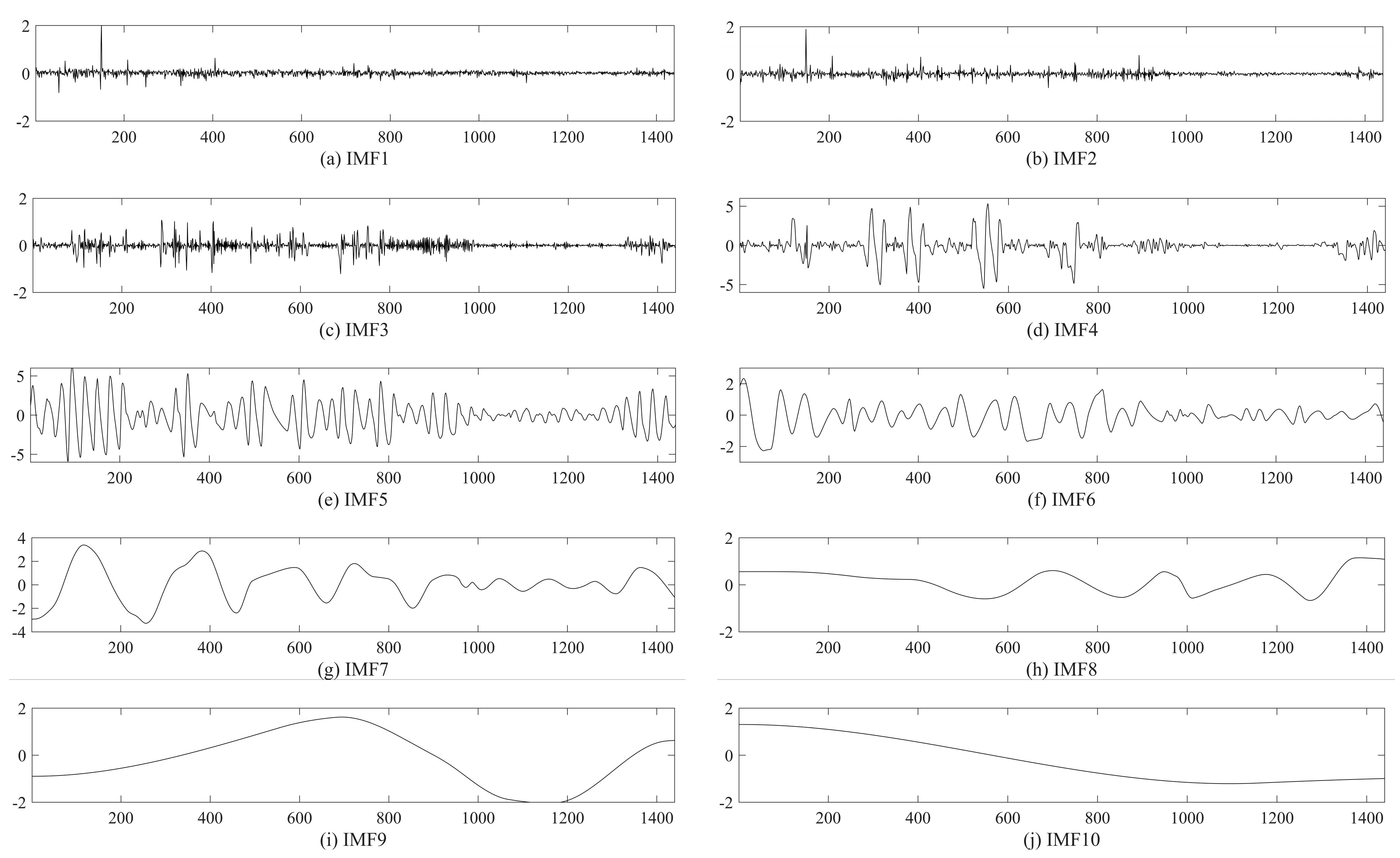
To address the above issues, constellation network traffic is decomposed into multi-order intrinsic mode functions (IMFs) with empirical mode decomposition (EMD). Given the high accuracy of short-term forecasts, the differential integrated moving average autoregressive model (ARIMA) is utilized to forecast IMFs [
9]. A back-propagation neural network (BPNN), as a traditional neural network model, has better non-linear fitting ability and performs well in terrestrial network traffic forecasting [
10]. BPNNs are utilized to forecast the residual from the ARIMA. However, numerous hyperparameters in BPNNs result in several problems, i.e., slow convergence and local optima [
11]. The grey wolf optimization algorithm (GWO) is a group intelligence algorithm derived from the social hierarchy and hunting mechanisms of grey wolves [
12]. It has been proved that GWO has a more reasonable global optimum search mechanism, which makes it more suitable for parameter optimization problems. Therefore, GWO is utilized to optimize the hyperparameters of the BPNN and prevent the BPNN from local optimality. Thus, the self-similar satellite network traffic hybrid forecasting model based on EMD-ARIMA-BPNN is proposed.
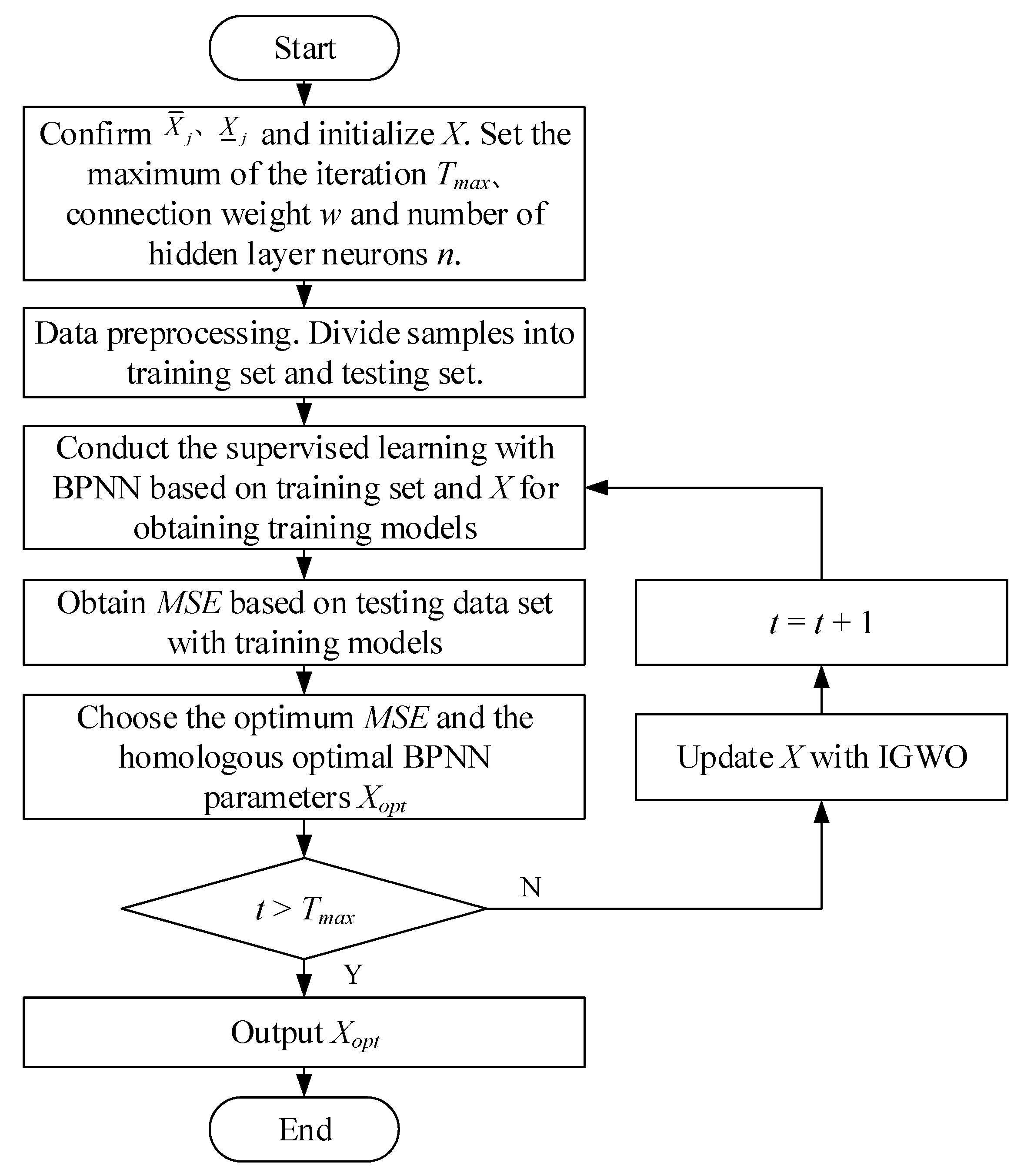
In the proposed EMD-ARIMA-BPNN model, constellation network traffic is first decomposed into multi-order IMFs with EMD. Secondly, IMFs are reconstructed to obtain network traffic residuals, which are utilized as the input for a BPNN optimized by GWO. The LRD properties in residuals can be adequately captured by the GWO-BPNN. Finally, the reconstructed IMFs and forecasted residuals are combined as satellite network traffic forecasting results. The main contributions of this paper are described as follows:
Firstly, the LRD properties of satellite network traffic can result in deteriorated forecasting accuracy and increased computational complexity. Empirical mode decomposition (EMD) is utilized to decompose LRD traffic into multi-order IMFs with single frequencies and SRD to reduce forecasting complexity;
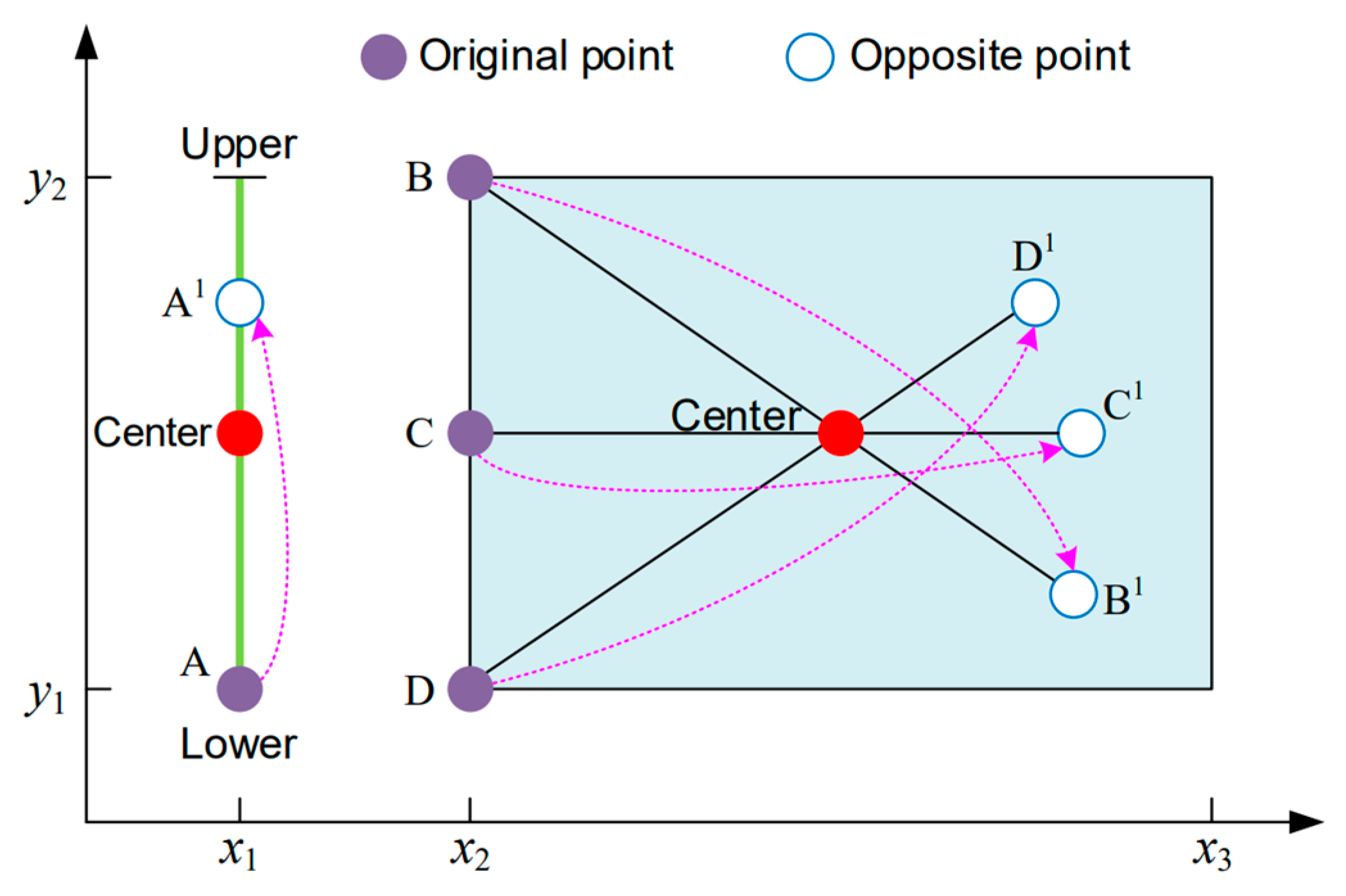
Secondly, to address the problems of the uneven initial population distribution and slow convergence rate of the standard GWO, an opposition-based learning strategy (OBL) and cosine-based non-linear convergence factor are utilized to improve the GWO, i.e., IGWO. The forecasting accuracy of the BPNN is improved by utilizing IGWO to optimize the hyperparameters;
Finally, we design the total flow of the LEO mega-constellation traffic forecasting process based on OMNET++. The effectiveness of the proposed satellite network traffic forecasting model is verified through comparative experiments.
The rest of the paper is organized as follows:
Section 2 introduces the current research status of satellite network traffic forecasting.
Section 3 constructs the satellite network traffic generation model and proposes the EMD-based network traffic decomposition.
Section 4 proposes the ARIMA-based IMFs forecasting model and BPNN-based residual forecasting model. The LEO mega-constellation network traffic hybrid forecasting model is constructed.
Section 5 summarizes this paper and proposes future work.
2. Materials and Methods
Traditional network traffic models are generally derived from Poisson processes, including the Poisson and Markov models [
13], which can only describe SRD properties. For satellite network traffic with LRD properties, it is difficult for traditional models to accurately characterize the network. Since the discovery of the self-similarity properties of network traffic in 1994 [
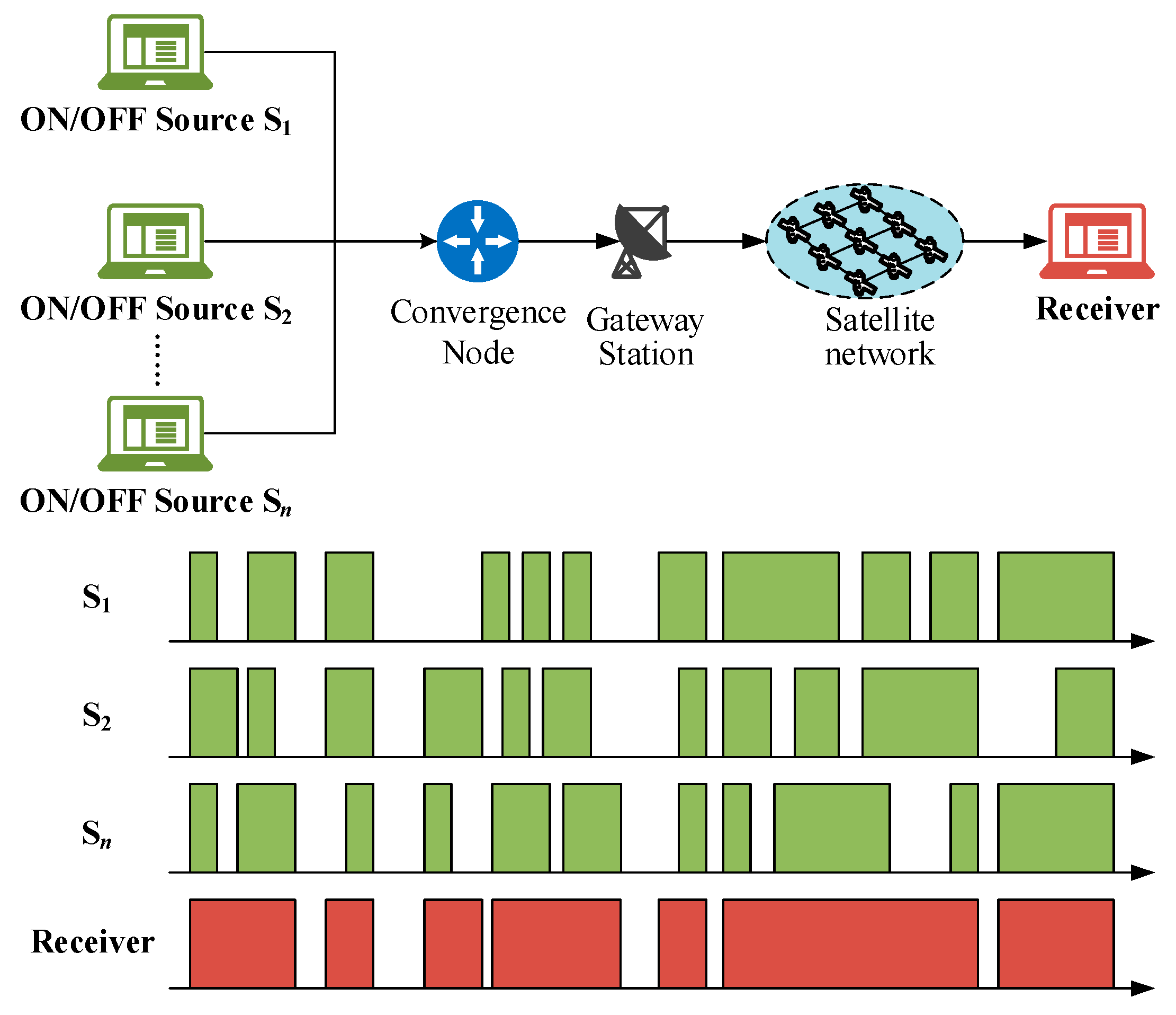
14], various self-similarity-based traffic forecasting models have been proposed. One class of models describe the observed traffic by constructing physical models, including ON/OFF models with heavy-tailed distribution [
15],
queuing models [
7], etc. Another category is statistics-based models, which attempt to simulate network traffic through data fitting. Statistics-based models mainly include linear models and non-linear models. Linear models, i.e., the autoregressive model (AR), moving average model (MA), autoregressive moving average model (ARMA) and autoregressive integrated moving average model (ARIMA) [
8], need to set a variety of parameters based on experience. Linear models are only suitable for short-term forecasting and find it difficult to deal with the self-similarity and LRD properties of satellite network traffic.
Due to the limitations of linear models, non-linear models such as the fractional autoregressive integration moving average model (FARIMA), wavelet model and grey model are utilized to forecast network traffic. Zhu et al. [
16] proposed the Markov-modulated deterministic model to simulate satellite network traffic, which converts the acquisition, storage and transmission of network traffic into an MMDP/D/1/K queued model. Yan et al. [
17] proposed a satellite network traffic forecasting model based on ARMA, which represents current traffic through the weighted summation of multiple historical traffic data. Considering the limited onboard computing and storage capacity, ARMA(2, 1) is adopted to reduce the computational complexity. Chen et al. [
18] established a traffic forecasting model with two variables: the geographic longitude of ascending nodes and the time from passing ascending nodes. A prediction method based on a surrogate model is adopted to solve the traffic prediction problem with a time-independent ground traffic distribution. According to the above analysis, statistics-based forecasting methods have limitations in describing the self-similarity, SRD and LRD laws of satellite network traffic [
16].
In view of the limitations of statistics-based models, neural network models are applied to forecast network traffic. Compared with statistics-based models, neural network models outperform them in terms of non-linear mapping capabilities [
19]. Zhou et al. [
20] proposed a forecasting method, SSA-AWELM, by combing singular spectrum analysis (SSA) and an AdaBoost weighted extreme learning machine (AWELM). In the proposed method, SSA decomposes raw traffic into three parts: trend, periodicity and residual. The AWELM is designed to predict each part separately. Fan et al. [
10] combined a recurrent neural network (RNN) and a gated recurrent unit (GRU). The experiment results demonstrated that the proposed RNN-GRU model had advantages in forecasting accuracy. Vinchoff et al. [
21] combined a graph convolutional neural network (GCN) and a generative adversarial network (GAN). In GCN-GAN, a GCN is utilized to extract the complex properties of network traffic, whereas a GAN is utilized to model the data structures. Li et al. [
22] proposed a forecasting model (LA-ResNet) that utilizes attention mechanism to solve spatiotemporal modeling and predict wireless network traffic. However, the computation complexity of LA-ResNet is too considerable to be applied in LEO mega-constellations.
According to the above analysis, increasing the number of hyperparameters will greatly increase the complexity of neural networks. In order to reduce the computation complexity and improve forecasting accuracy, Cai et al. [
23] improved long short-term memory (LSTM) using a genetic algorithm (GA), in which the GA is utilized to optimize the LSTM hyperparameters. Sudhakaran et al. [
24] proposed a deep learning approach for cellular traffic forecasting with deep neural networks (DNNs) to model cellular traffic. Traffic volume data are treated as tensors, similar to images, which are then fed to a convolutional neural network. Li et al. [
25] proposed the GRU neural network traffic prediction algorithm based on transfer learning. The proposed method combines transfer learning to solve the problem of insufficient online traffic data. The particle filter online training algorithm is adopted to reduce the computation complexity. The above network traffic forecasting methods are comprehensively compared in terms of computation complexity and forecasting accuracy, as shown in
Table 1.
To address the above issues, this paper decomposes satellite network traffic with self-similarity into multi-order IMFs with short-range correlation using EMD. The ARIMA, improved using an adaptive fixed-order search operator, is utilized to forecast IMFs with low computation complexity. IGWO is utilized to optimize the hyperparameters of a BPNN, which forecasts the residuals of the EMD-ARIMA. With the enhancement of the global optimization capability of the BPNN, the proposed EMD-ARIMA-BPNN hybrid model can fully realize the potential of mining the linear and non-linear laws of satellite network traffic, hence improving the forecasting accuracy.
6. Conclusions
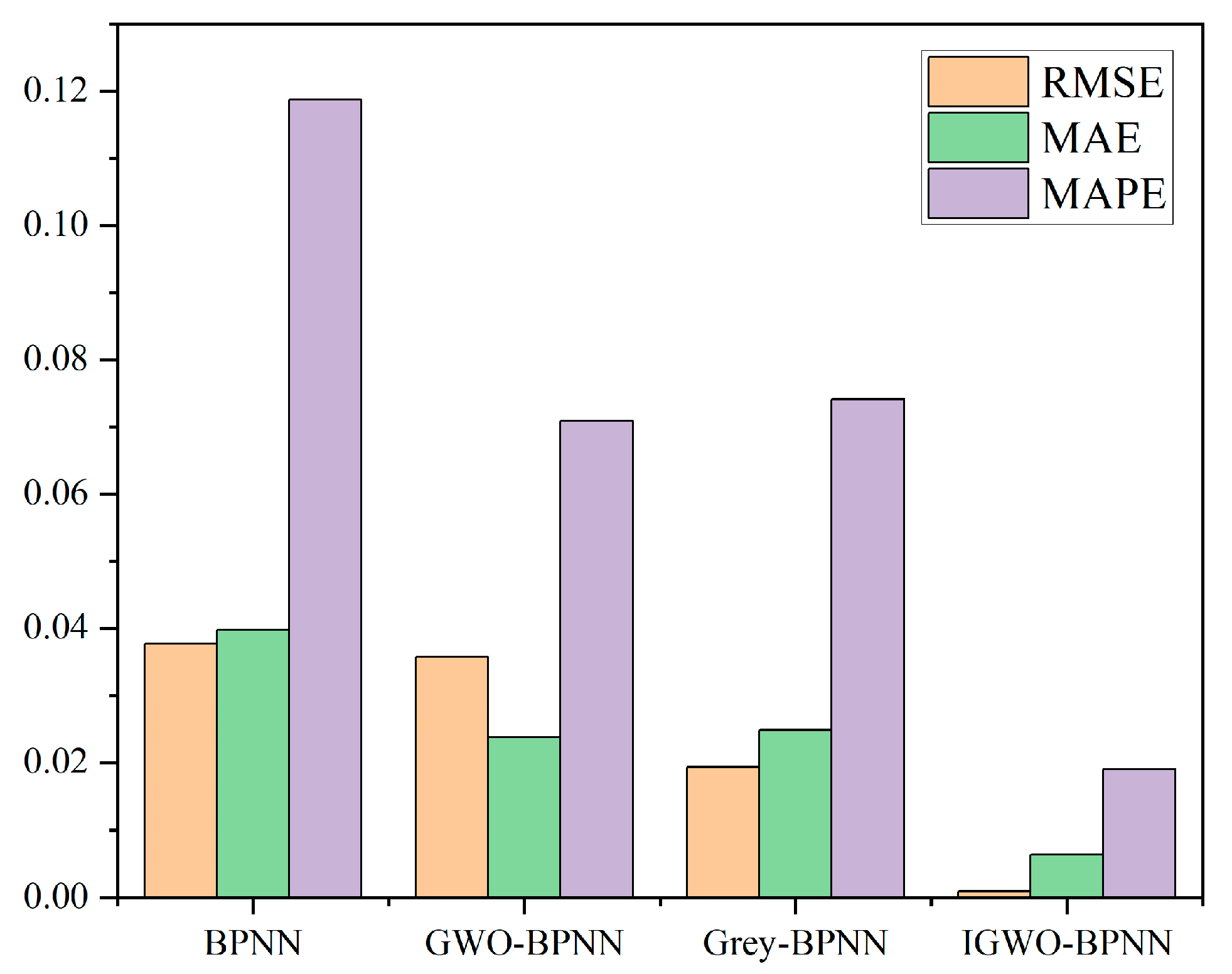
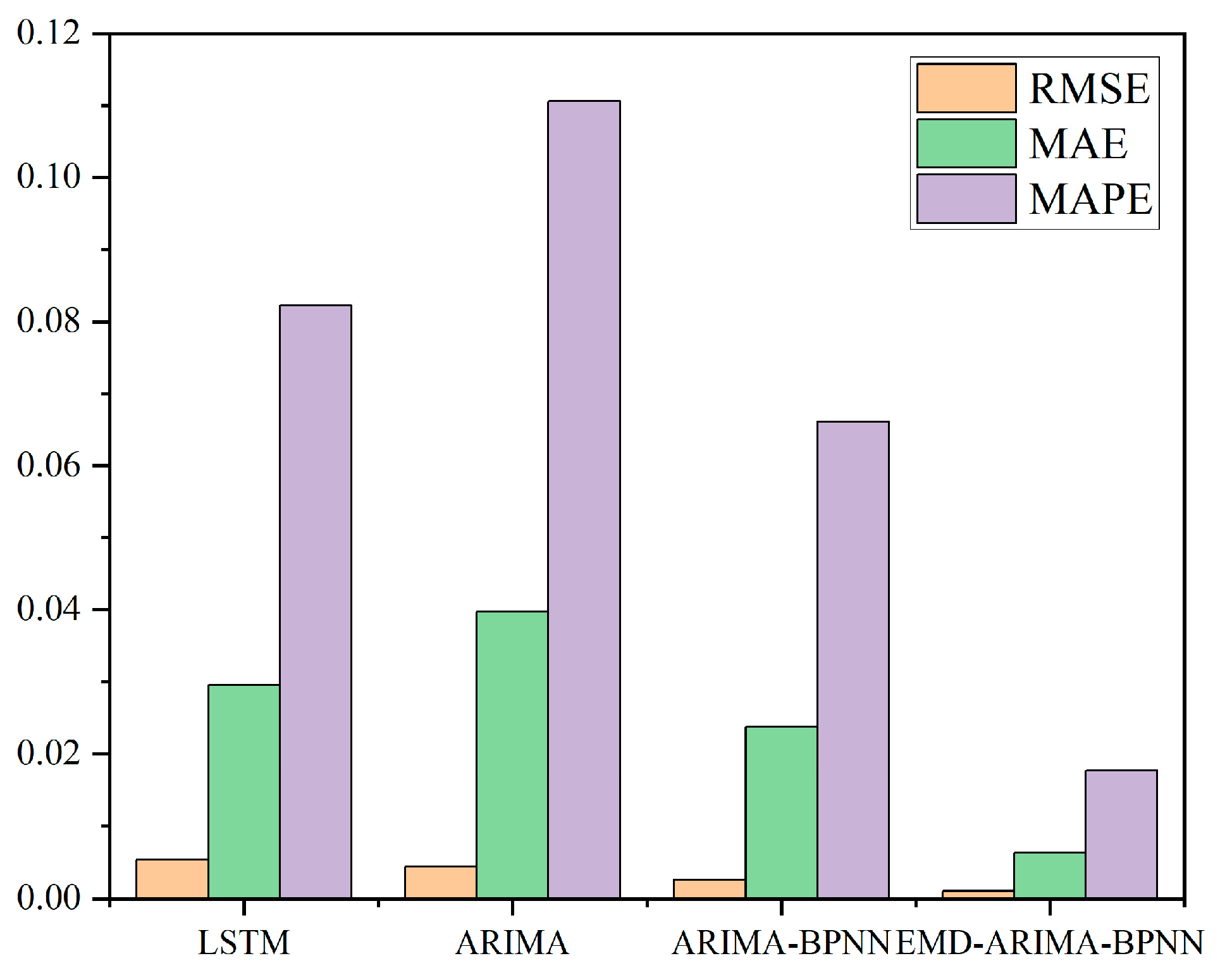
Satellite network traffic is characterized by self-similarity, long-range dependence and non-linearity, which makes it difficult to describe the traffic characteristics well with traditional single or hybrid models, resulting in low forecasting accuracy. This paper proposes an improved method for forecasting satellite network traffic by combining a BPNN with EMD-ARIMA. Different from traditional forecasting methods, we quantitatively analyze the self-similarity of satellite network traffic. Through theoretical analysis and experiments, the multi-order IMFs obtained from satellite network traffic via EMD have been proved to have short-range dependence. Thus, self-similar satellite network traffic is decomposed into multiple-order IMFs with short-range dependence using EMD. IMFs are forecasted by ARIMA and improved via an adaptive fixed-order search operator to reduce the computational complexity. At the same time, IGWO is adopted to optimize the hyperparameters of the BPNN. The residuals of EMD-ARIMA are forecasted using the optimized BPNN to finally obtain the forecasted satellite network traffic. Comparison experiments with traditional traffic forecasting models and hybrid models prove that the proposed EMD-ARIMA-BPNN model outperforms the traditional satellite network traffic forecasting methods, with several improvements in forecasting accuracy and efficiency.
In our future work, we will further apply the network traffic forecasting results to the routing of LEO mega-constellation networks. By sensing the change in traffic load, high-load ISLs can be avoided in advance, thus enhancing the load balancing ability of the mega-constellation network.