Airport Microgrid and Its Incorporated Operations
Abstract
1. Introduction
2. System Configuration
- (1)
- The DC-bus bipolar-voltage is established by the PV and the FC via unidirectional 3L boost DC-DC converters. PV is more appropriate renewable source for airports due to the special terrain limitations, while the zero-emission new energy device FC possesses the future application potential. The coordinated control scheme is proposed for the renewable PV source with MPPT and the distributed FC source, providing energy support to yield enhanced power generation characteristics. Well-regulated bus voltage is preserved by the designed controller. An OCC-based current control scheme and a robust voltage control scheme are proposed.
- (2)
- In the battery/FW HESS, the two storage devices are respectively connected to the common DC-bus via a bidirectional 3L boost converter and a bidirectional 3L three-phase switch-mode rectifier (SMR). The droop control scheme is developed to yield good current sharing characteristics between the energy-type and the power-type storage devices.
- (3)
- A chopped dump load is equipped across the DC-bus to prevent overvoltage.
- (4)
- A 3L NPC bidirectional three-phase inverter is used to conduct the G2M and M2G energy complementary operations. The droop control approach is also proposed to handle the G2M/M2G operations. The grid-connected airport microgrid can possess increased resilience and power-supply reliability.
- (5)
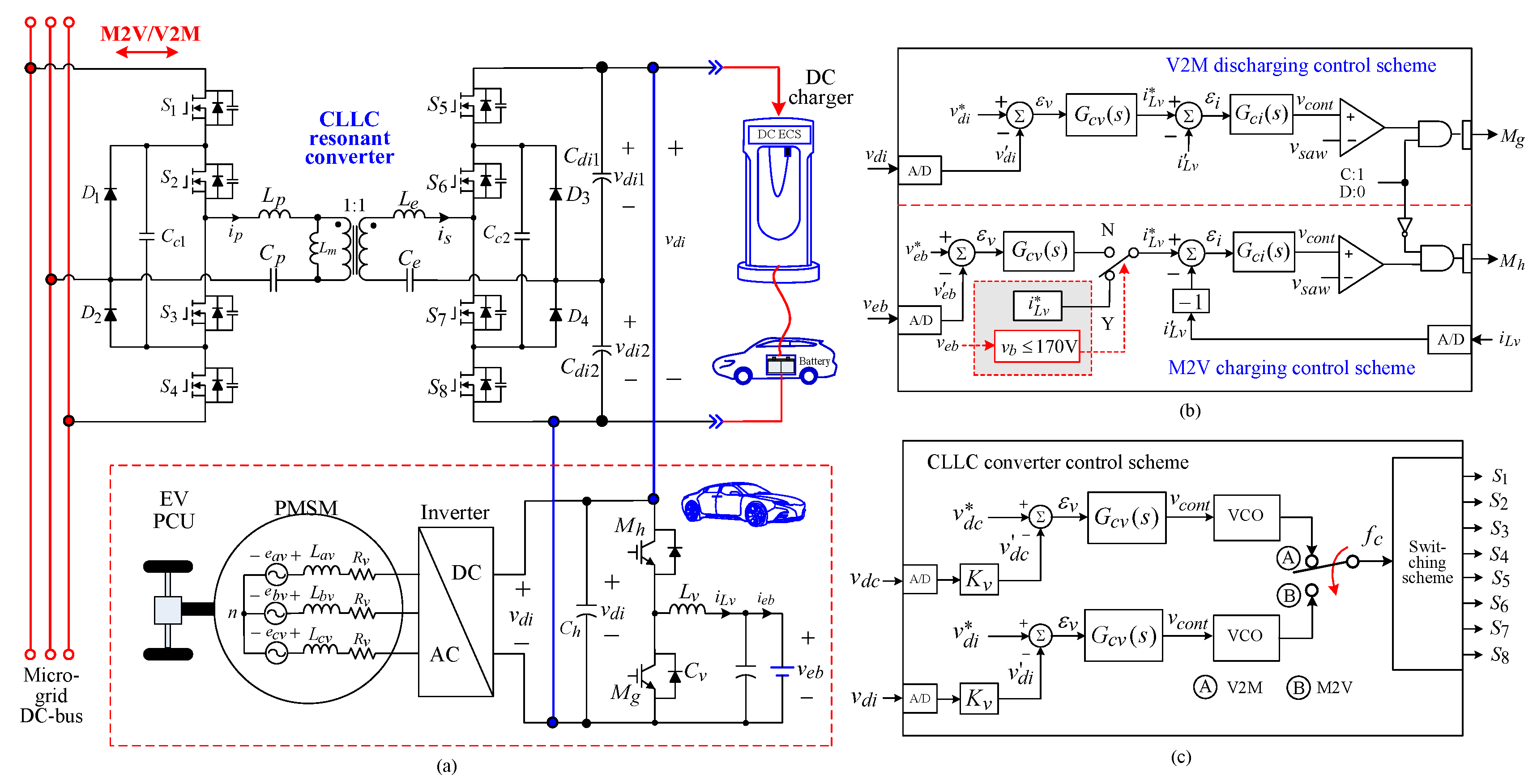
- The microgrid-to-vehicle (M2V) and the vehicle-to-microgrid (V2M) operations can be performed via the off-board DC fast charger or the on-board charger. The galvanic isolation is provided by the 3L CLLC resonant converter. The total energy utilization is further enhanced by considering the EV as a movable storage facility. This effectiveness is more obvious in the airport microgrid compared to the conventional microgrid.
- (6)
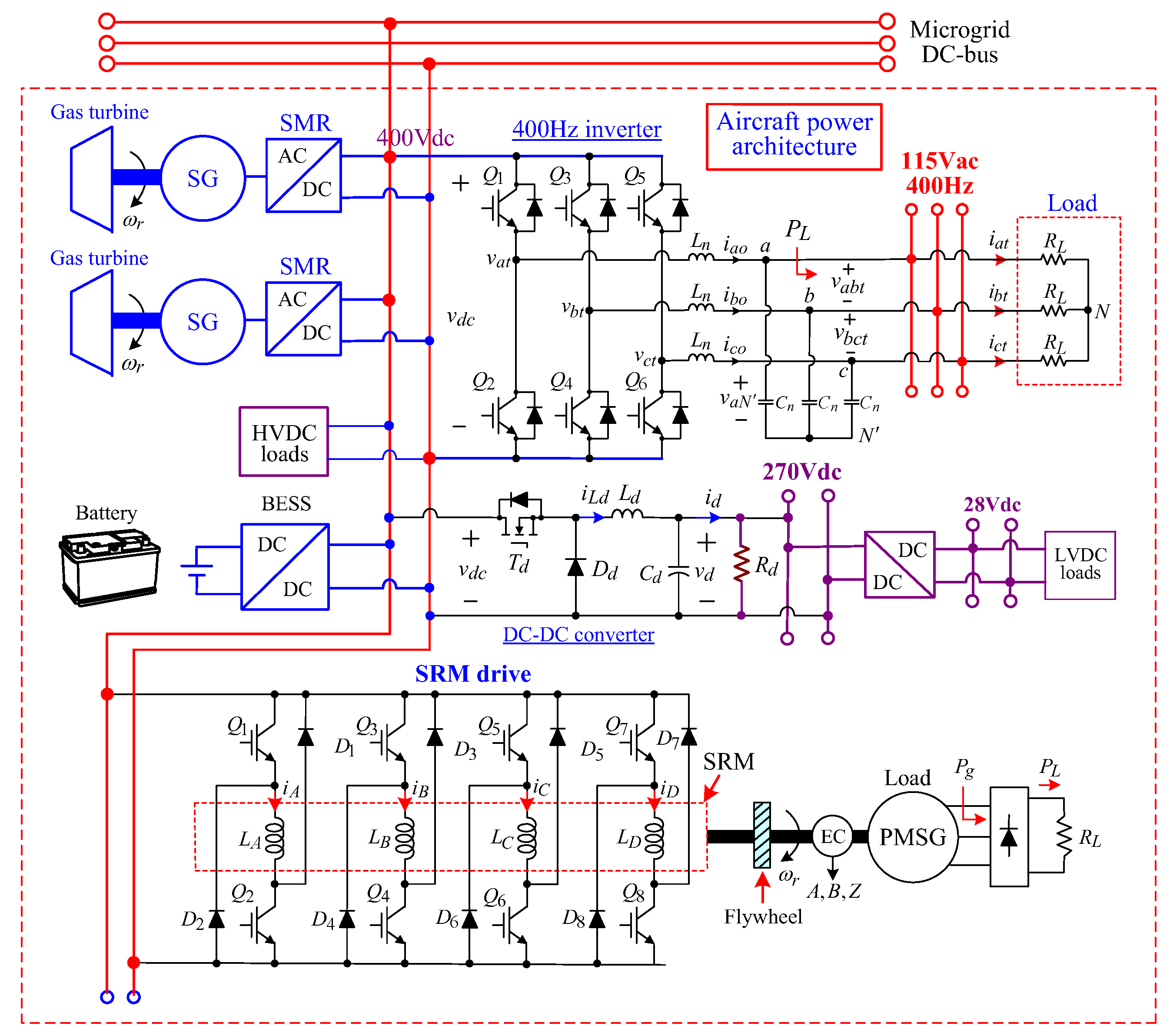
- As the aircraft is grounded, its bidirectional operations to microgrid can be conducted. Taking the more electric aircraft (MEA) electric power architecture (EPA) presented in [40,41] as an application example, the aircraft on-board facilities can be powered by the developed microgrid. The functions of a ground power unit are preserved. The arranged test facilities include the 115 V/400 Hz AC-bus, the 270 V DC-bus, and the example SRM drive [41]. The aircraft can also provide energy support to the microgrid.


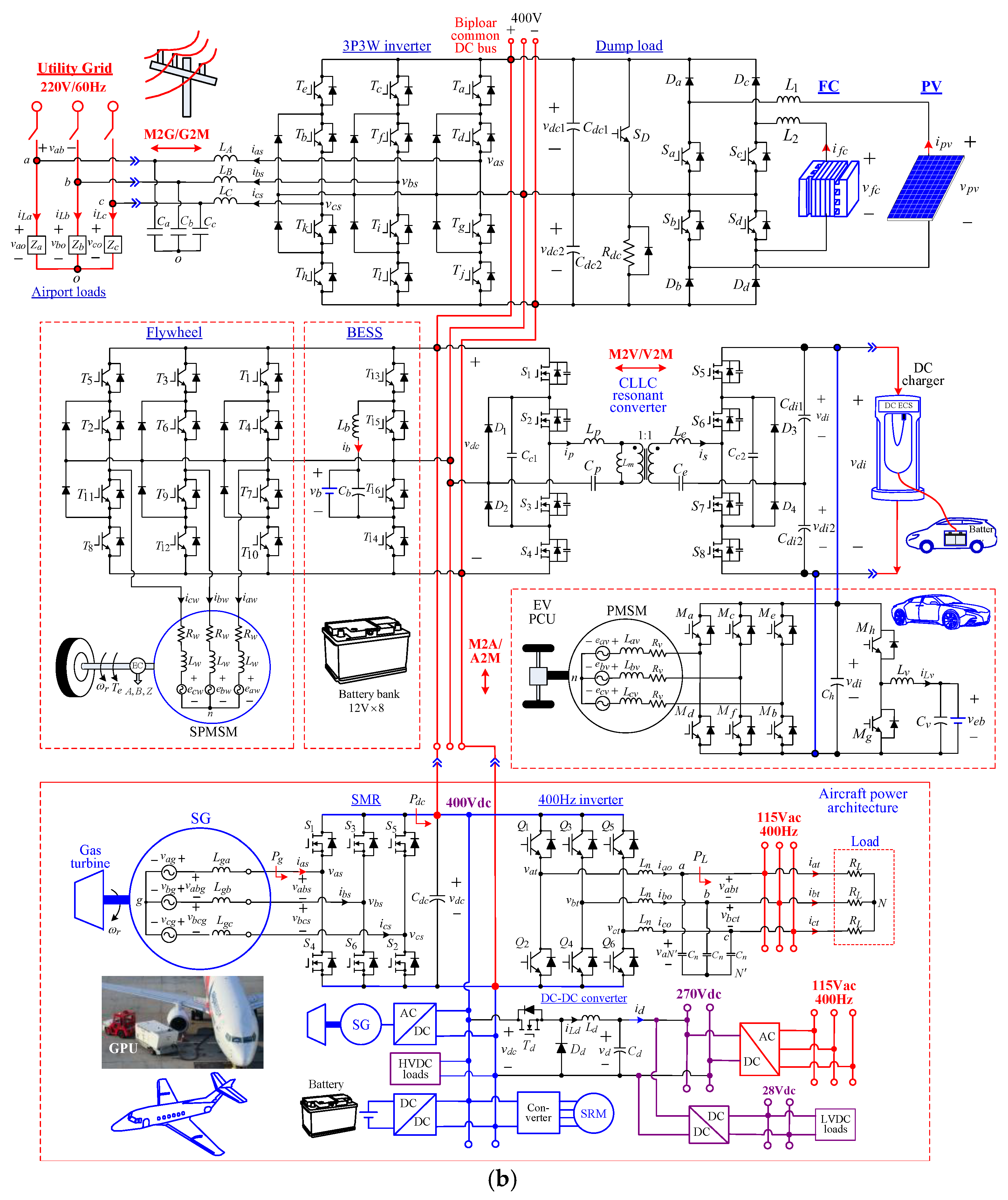
3. The Established PV and FC-Powered Microgrid
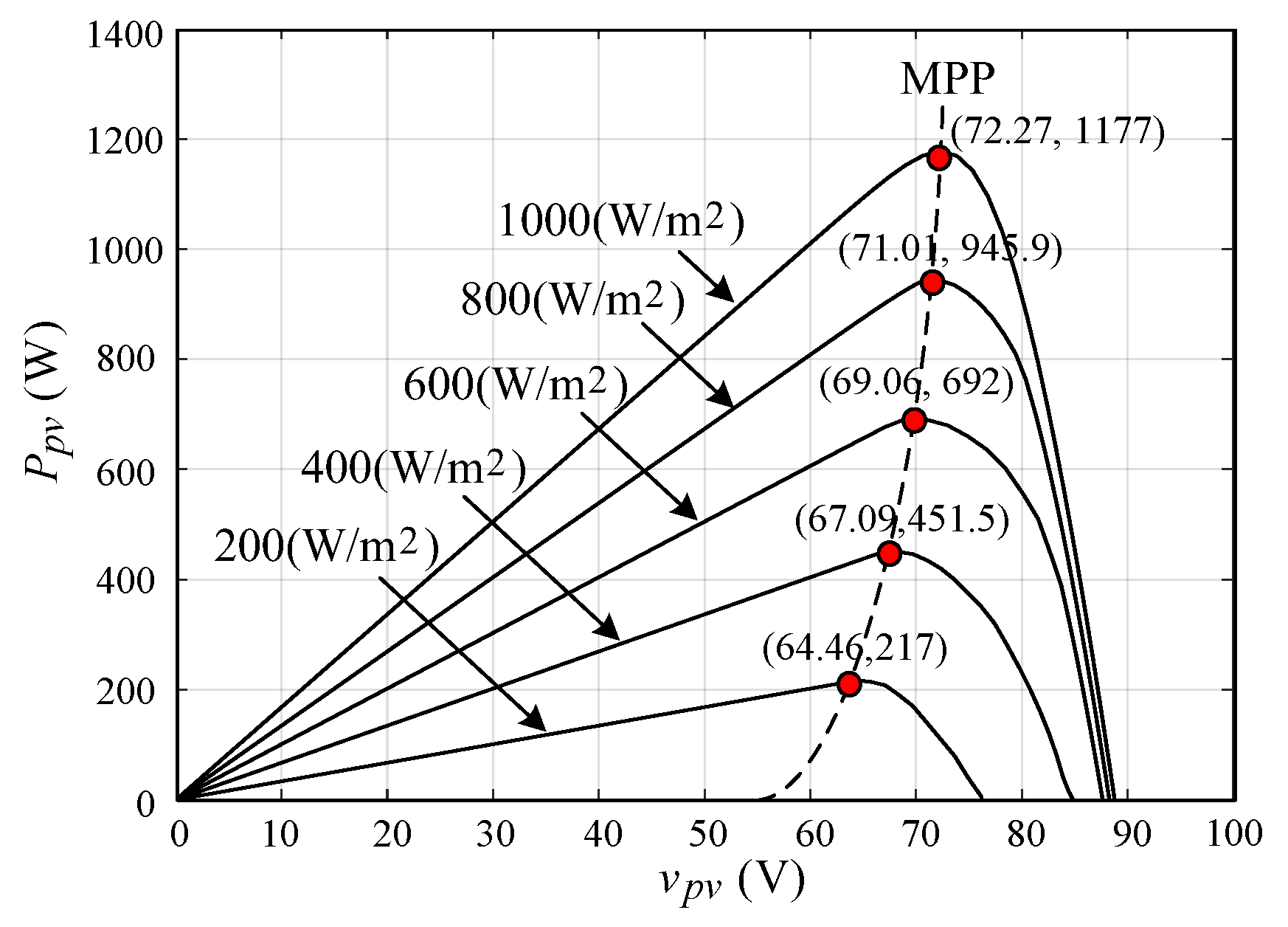
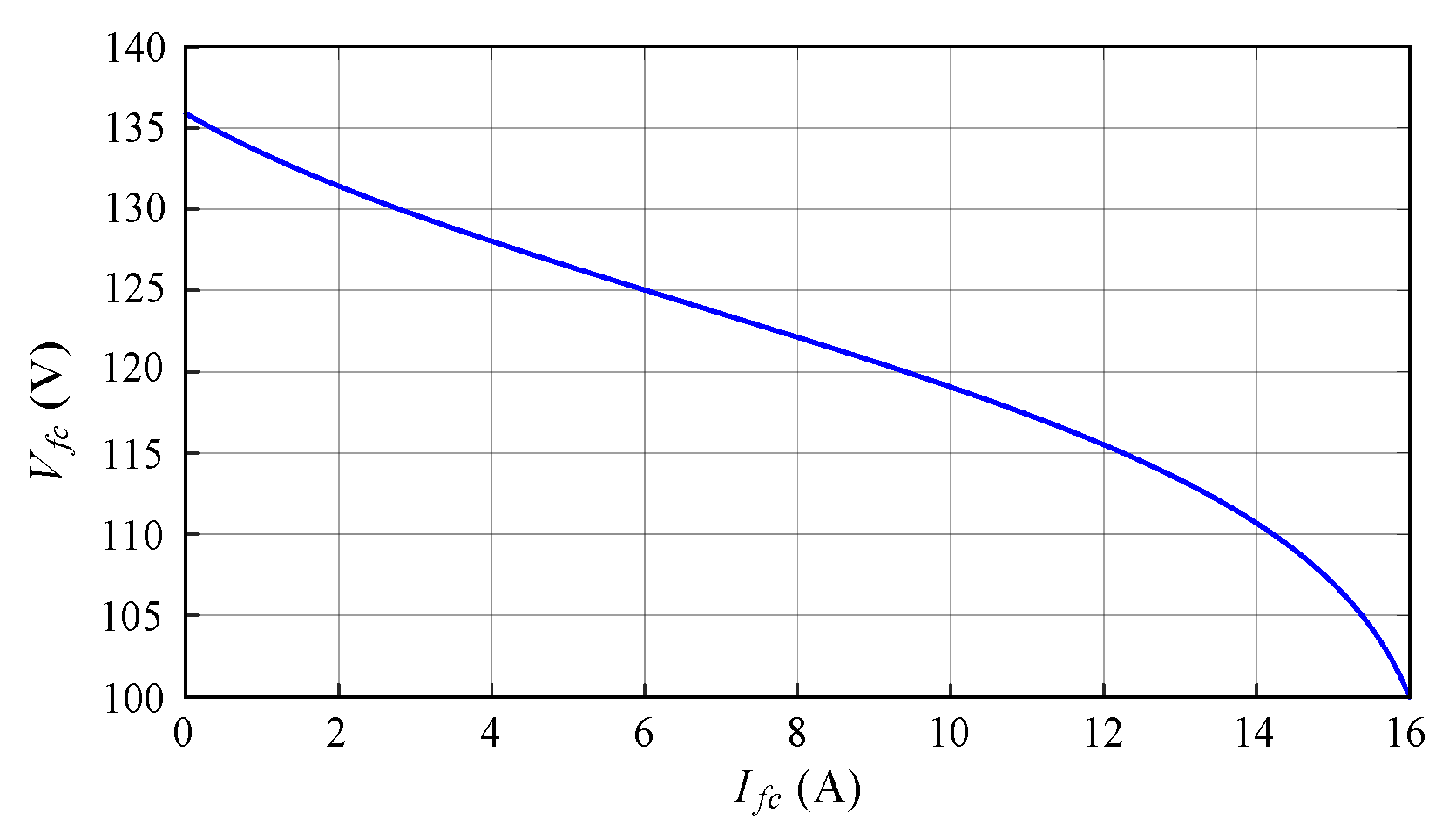
3.1. The Adopted PV Array and FC
3.2. Three-Level Boost Interface Converters
3.2.1. Circuit Components
- , where the unity efficiency is assumed;
- Switching frequency
- The IGBT module SK30MLI066 by Semikron Corp. is used to form the developed 3LBC.
- Energy storage inductor
- DC output filtering capacitor
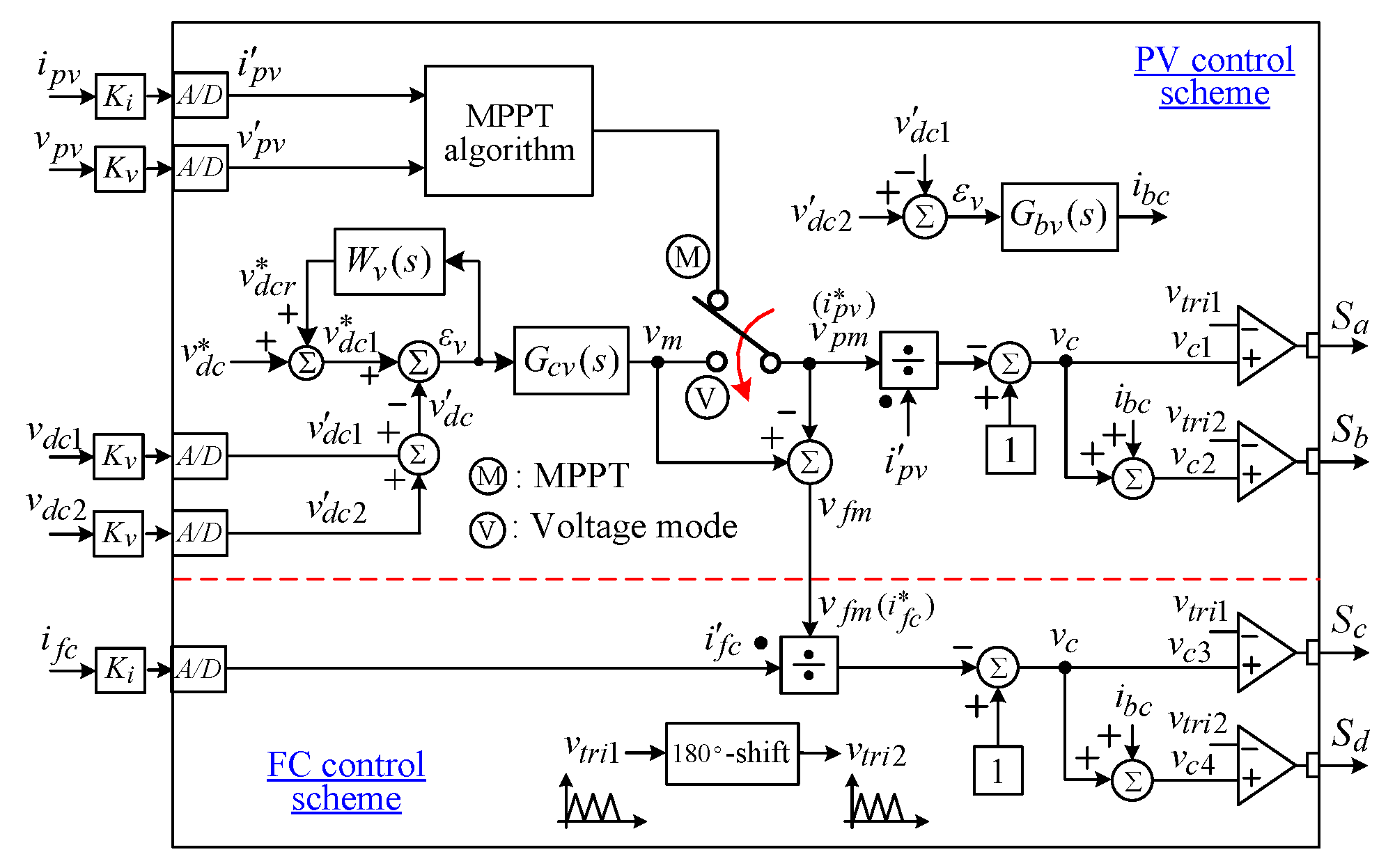
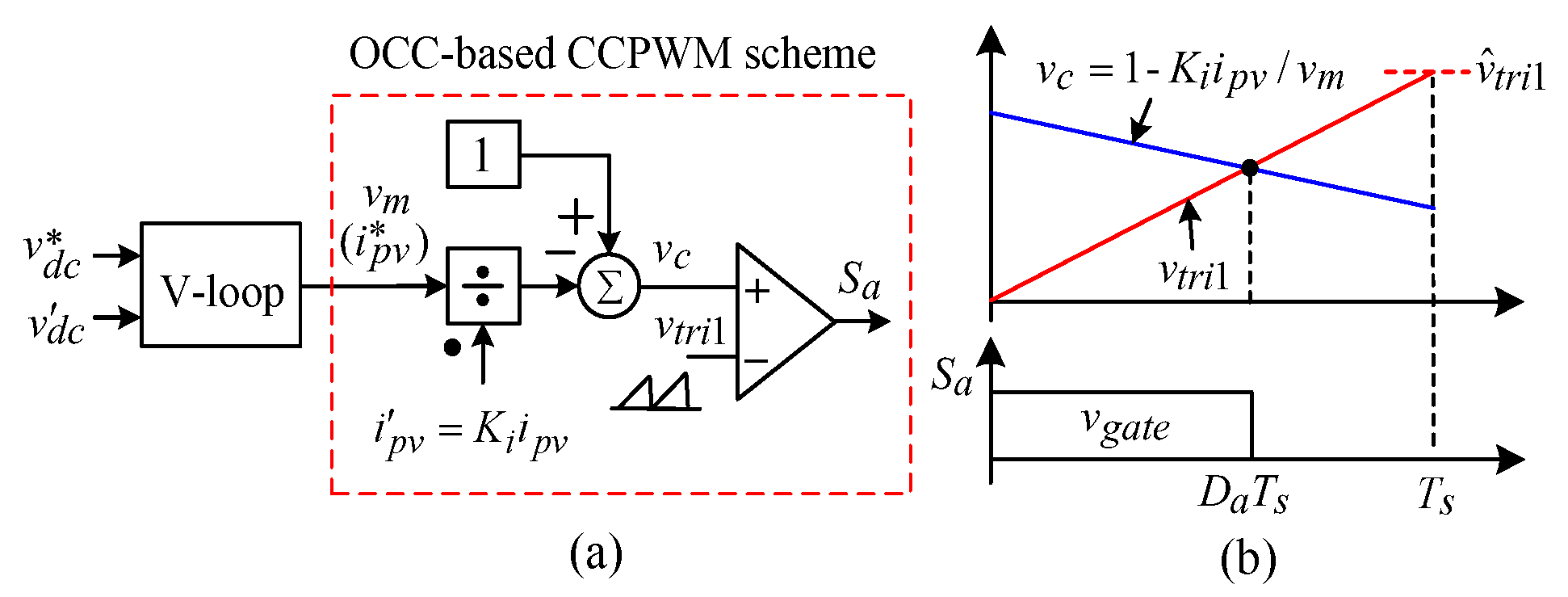
3.2.2. The Proposed OCC-Based CCPWM Scheme
3.2.3. Bipolar Voltage Balancing Controller
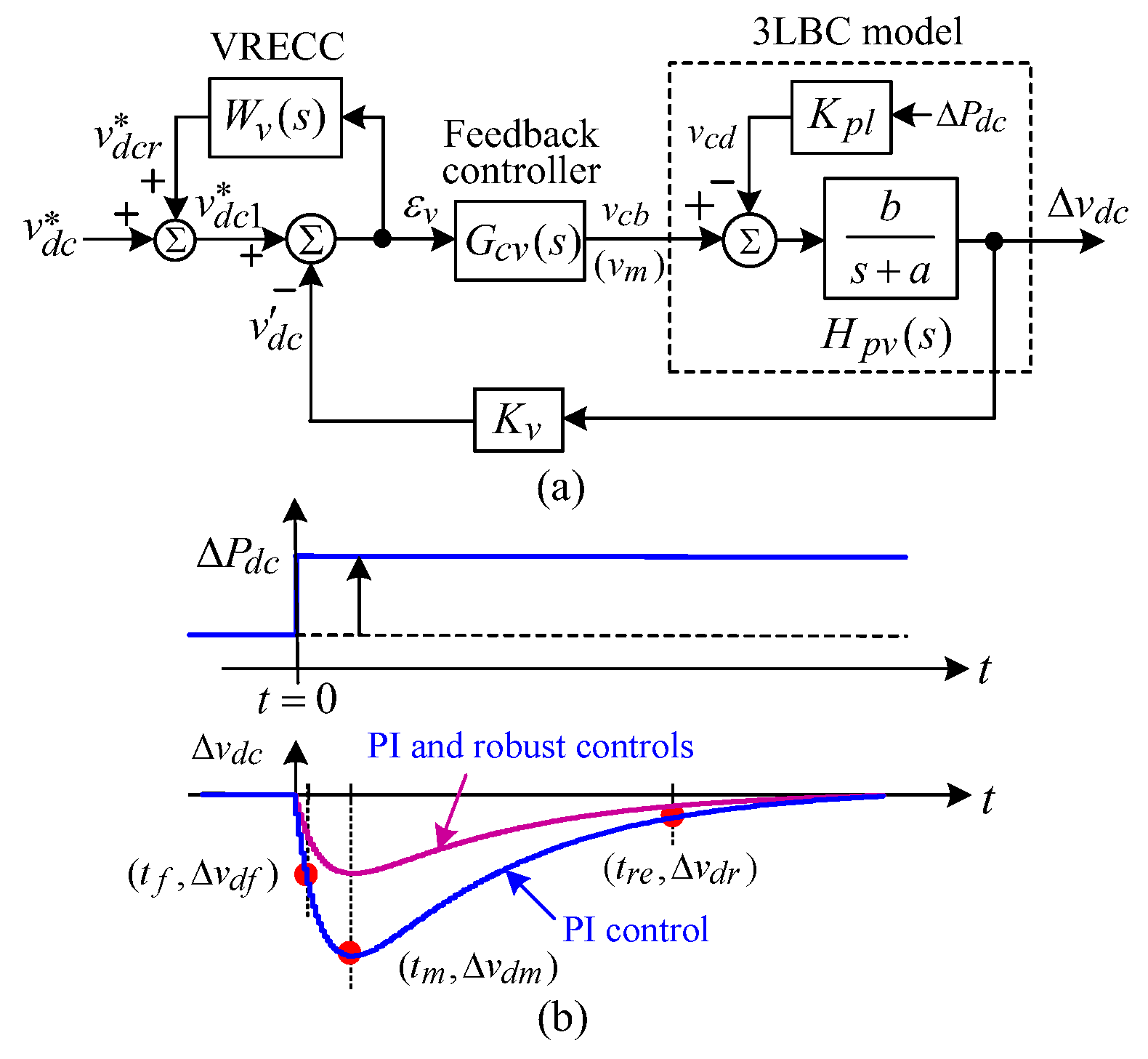
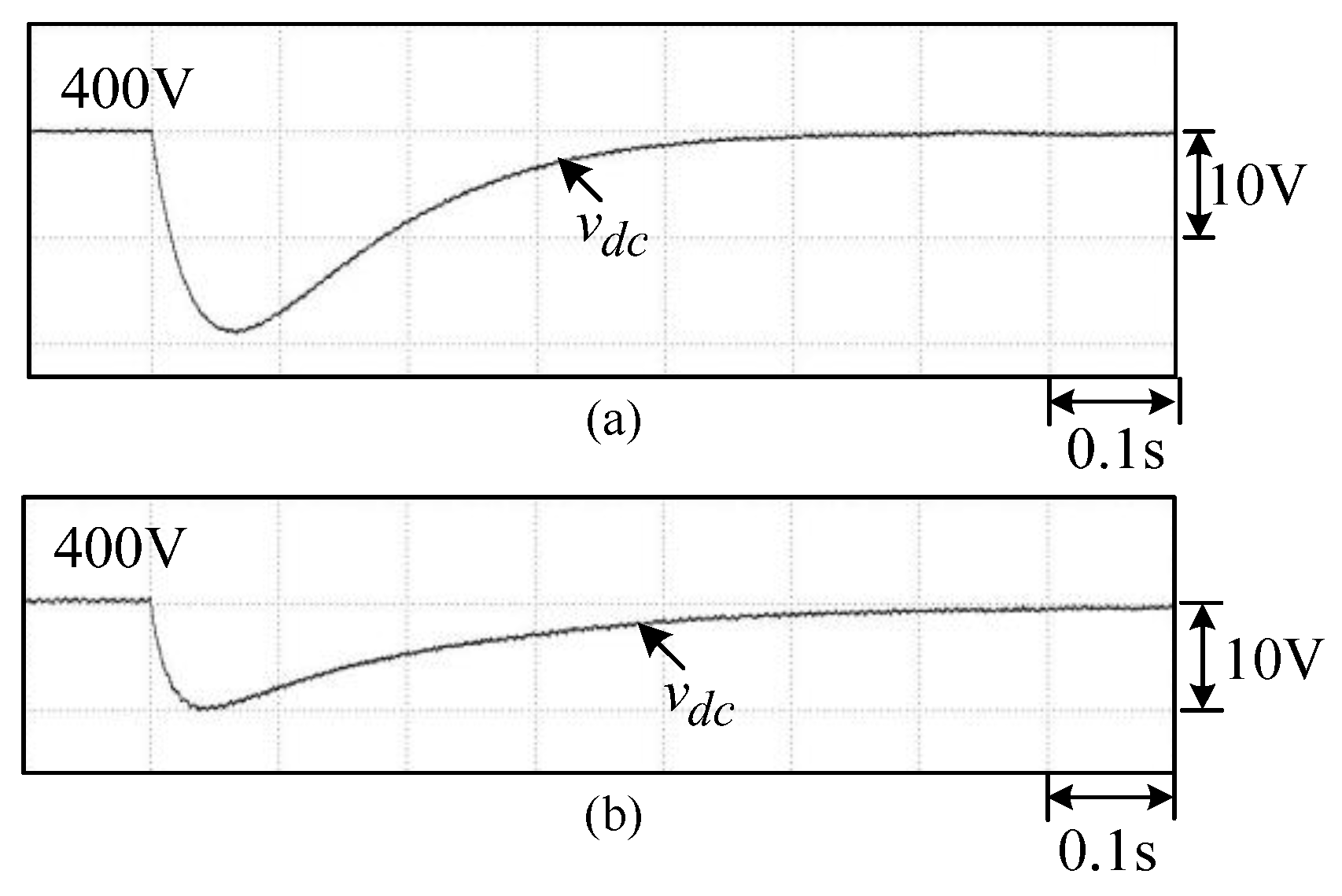
3.2.4. Voltage Control Scheme
- Dynamic model estimation:
- Quantitative controller design:
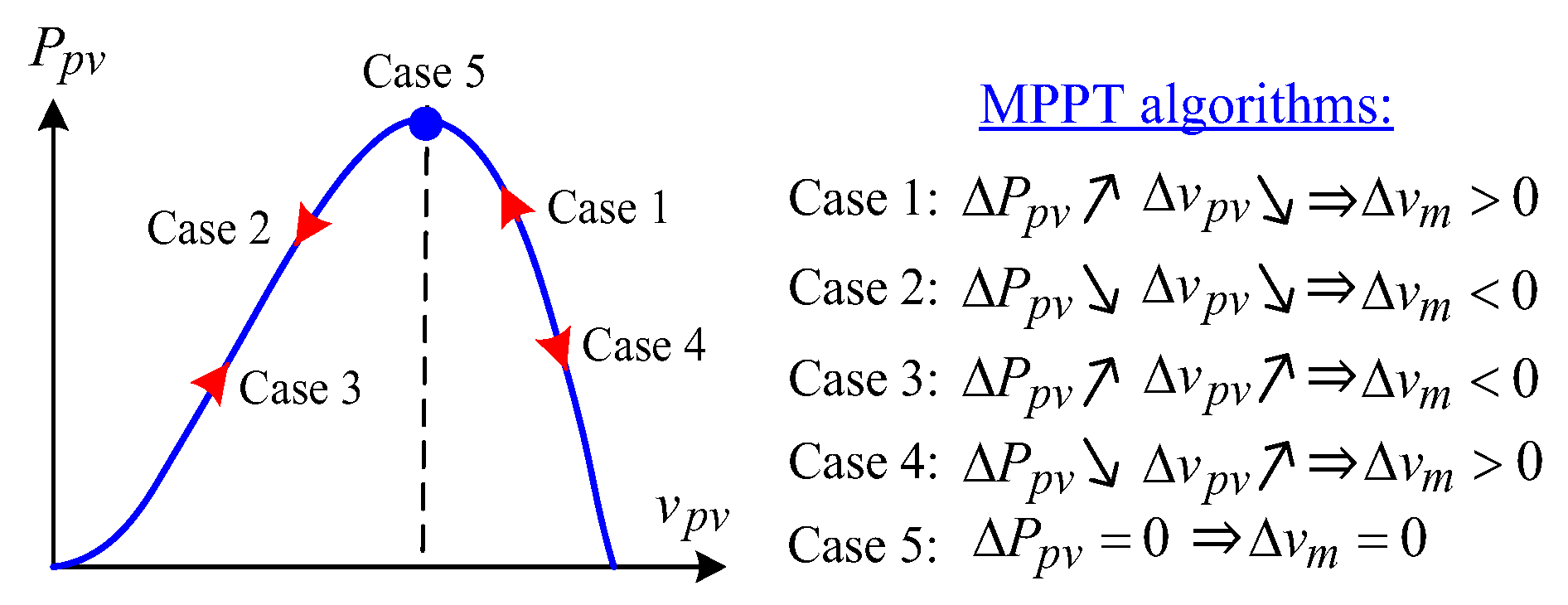
3.2.5. MPPT Control Scheme
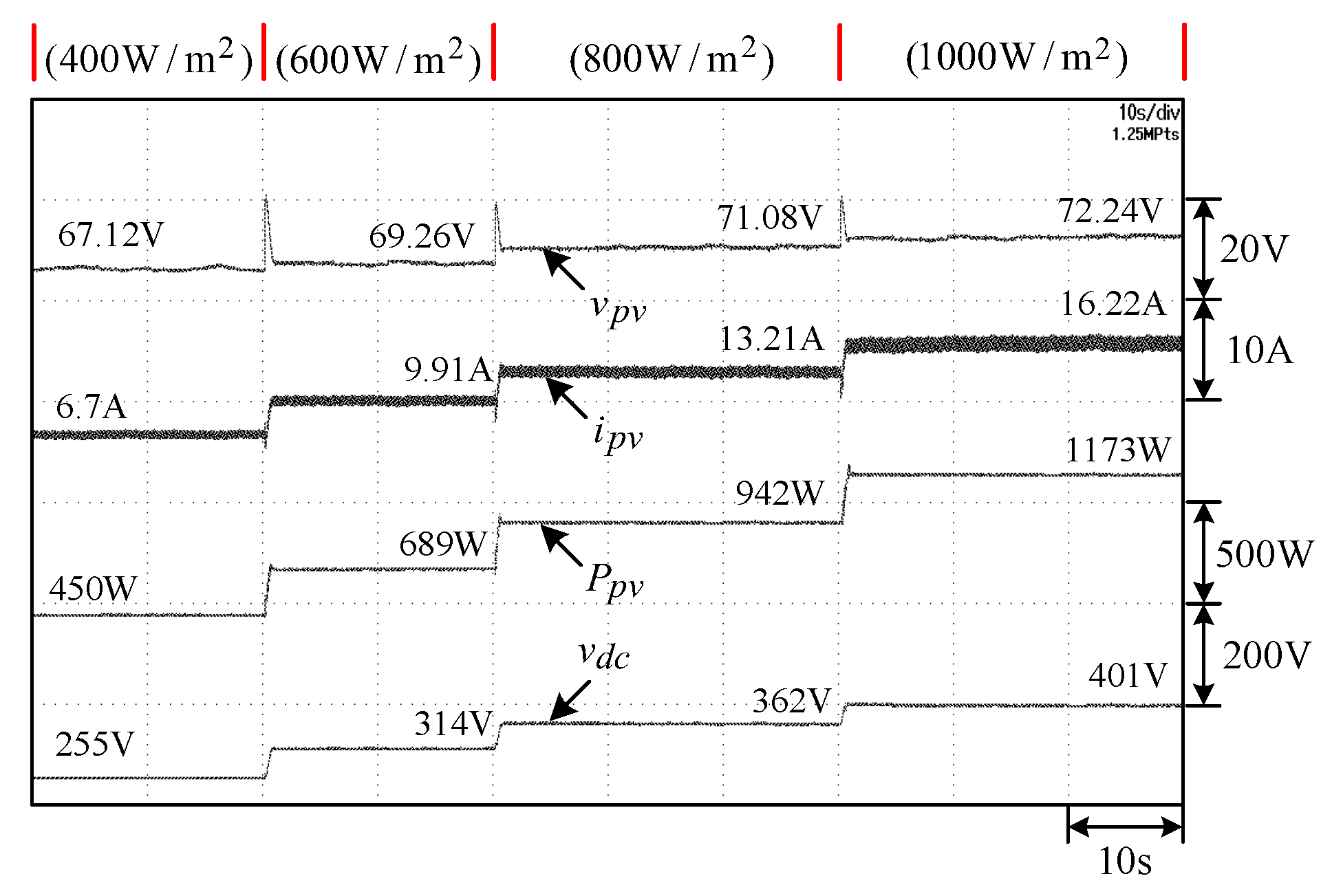
3.2.6. Measured Results
4. Grid-Connected Inverter
4.1. Power Circuit
- Output AC line rms voltage:
- Switching frequency: .
- Power devices: The IGBT module SK30MLI066 (600 V, 30 A) by Semikron Corp., Nuremberg, Germany.
- Output filter: (i) capacitors: ; (ii) inductors: measured inductances at 60 Hz are and
- Current and voltage sensing factors: . .
4.2. Control Scheme
- PLL mechanism:
- PI current feedback controller:
- PI voltage controller in M2H mode:
- Droop control scheme in M2G/G2M operations: As indicated in Figure 14, the q-axis current command based on droop control varies from −8 A to 8 A within .
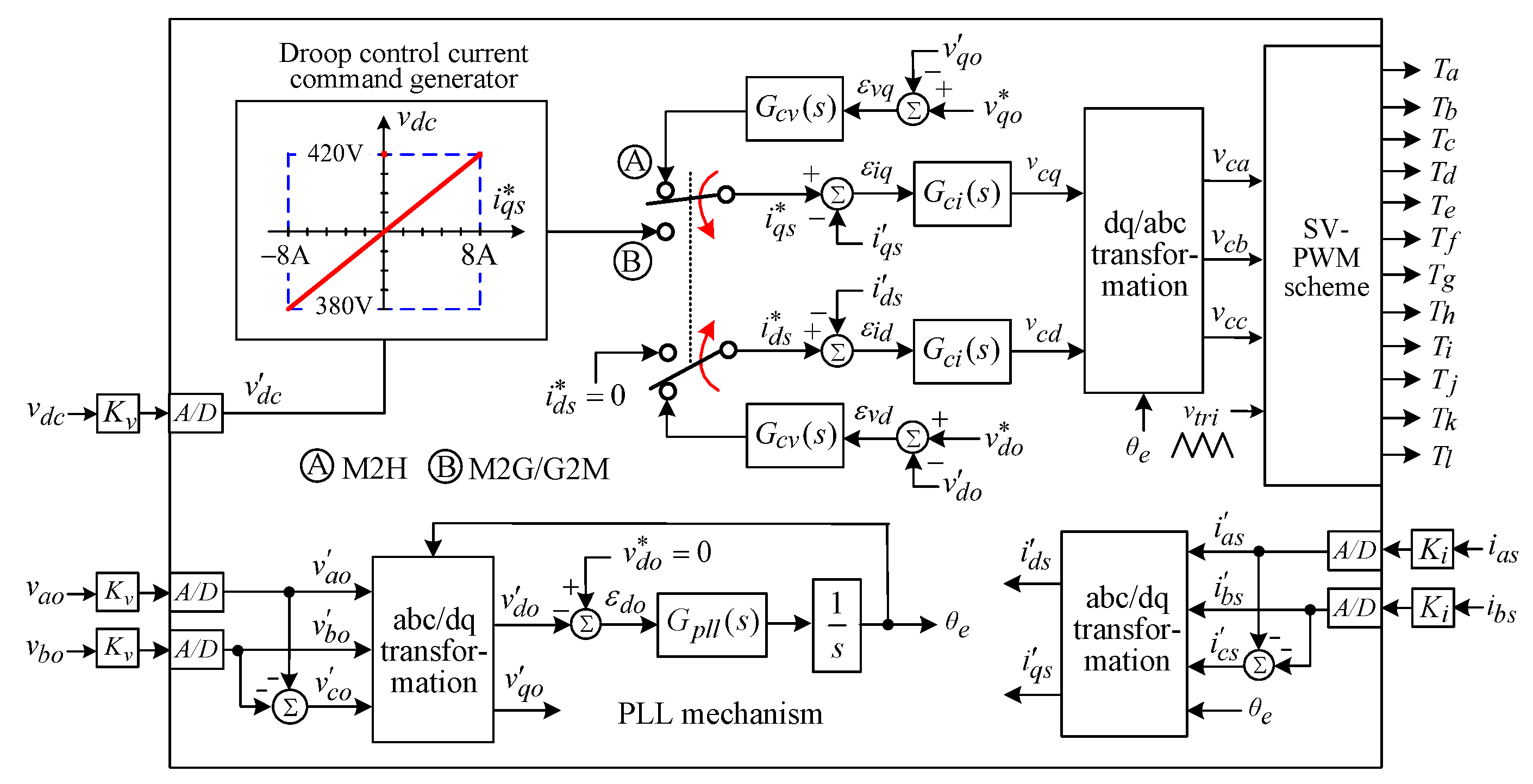
5. Energy Storage System
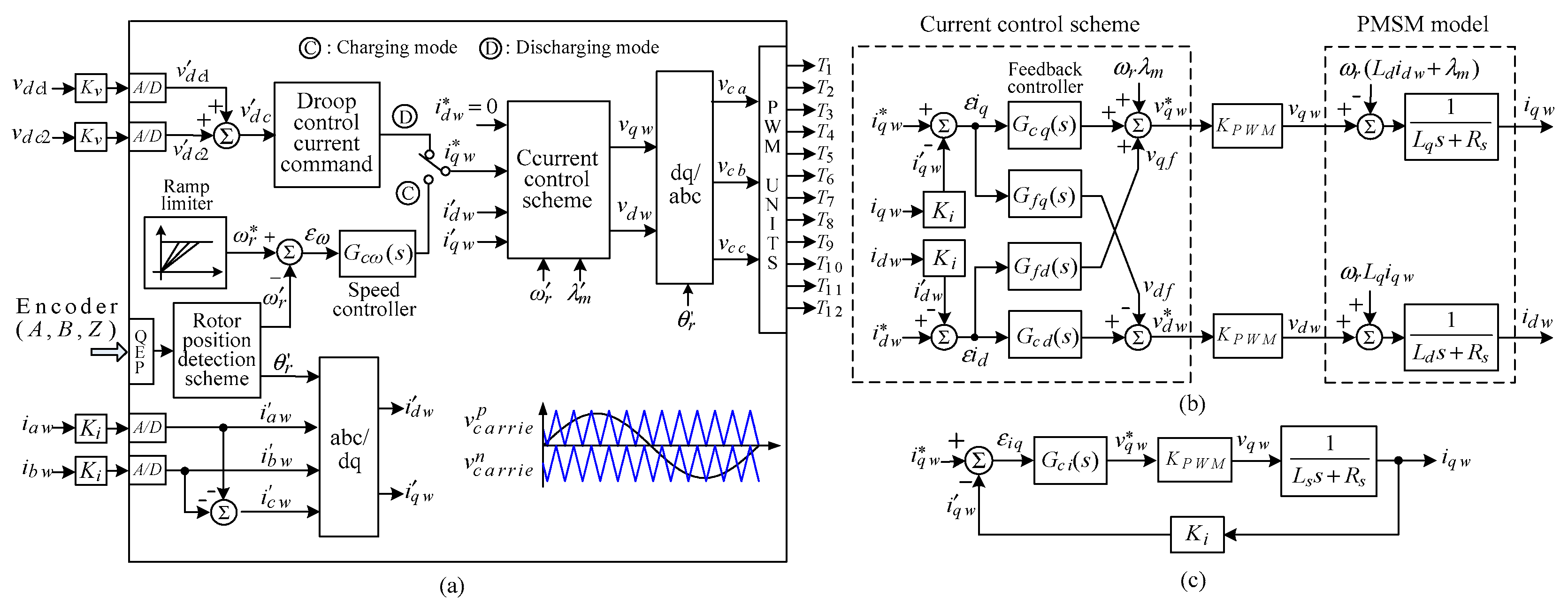
5.1. PMSM-Driven Flywheel System
5.1.1. Power Circuit
5.1.2. Control Schemes
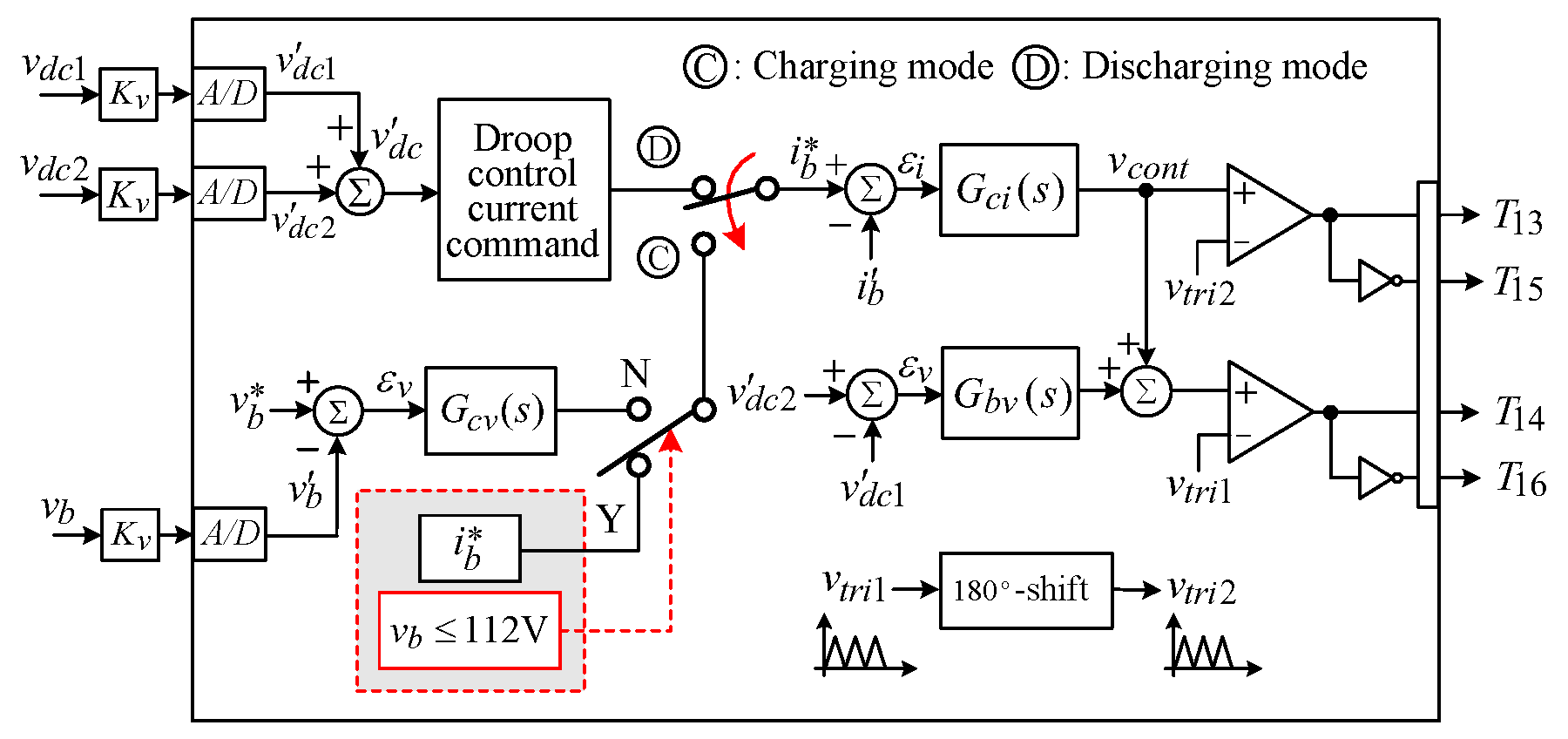
5.2. Battery Energy Storage System
5.2.1. Power Circuit
- Lead-acid battery bank: , 14 Ah (1344 wh).
- Energy storage inductor:
- Filtering capacitors: .
- Switching frequency: .
- Current and voltage sensing factors: , .
- Power devices: The power MOSFET IXFN160N30T (,) by IXYS Corporation.
5.2.2. Control Scheme
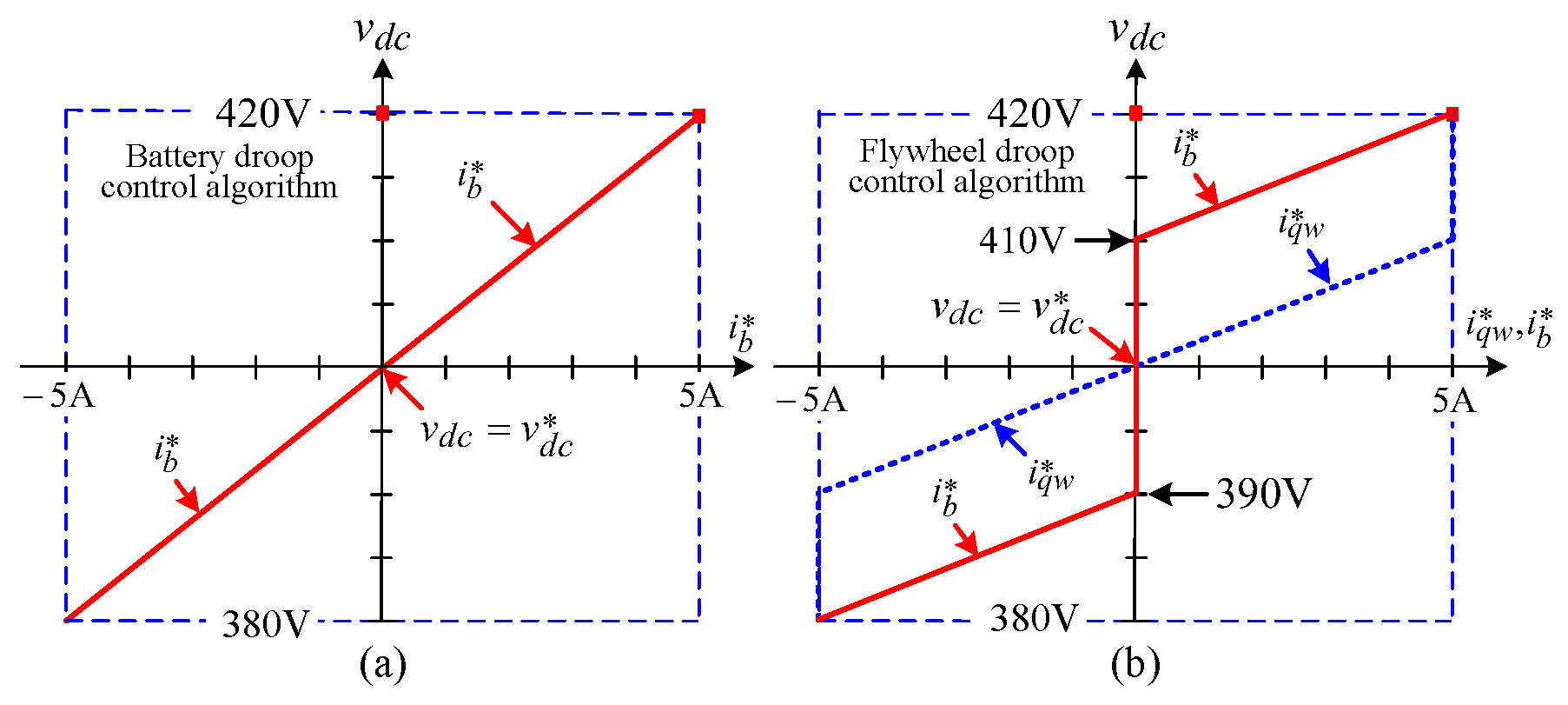
5.3. Droop Control Scheme and Measured Results
5.3.1. Battery/Flywheel Droop Control Scheme
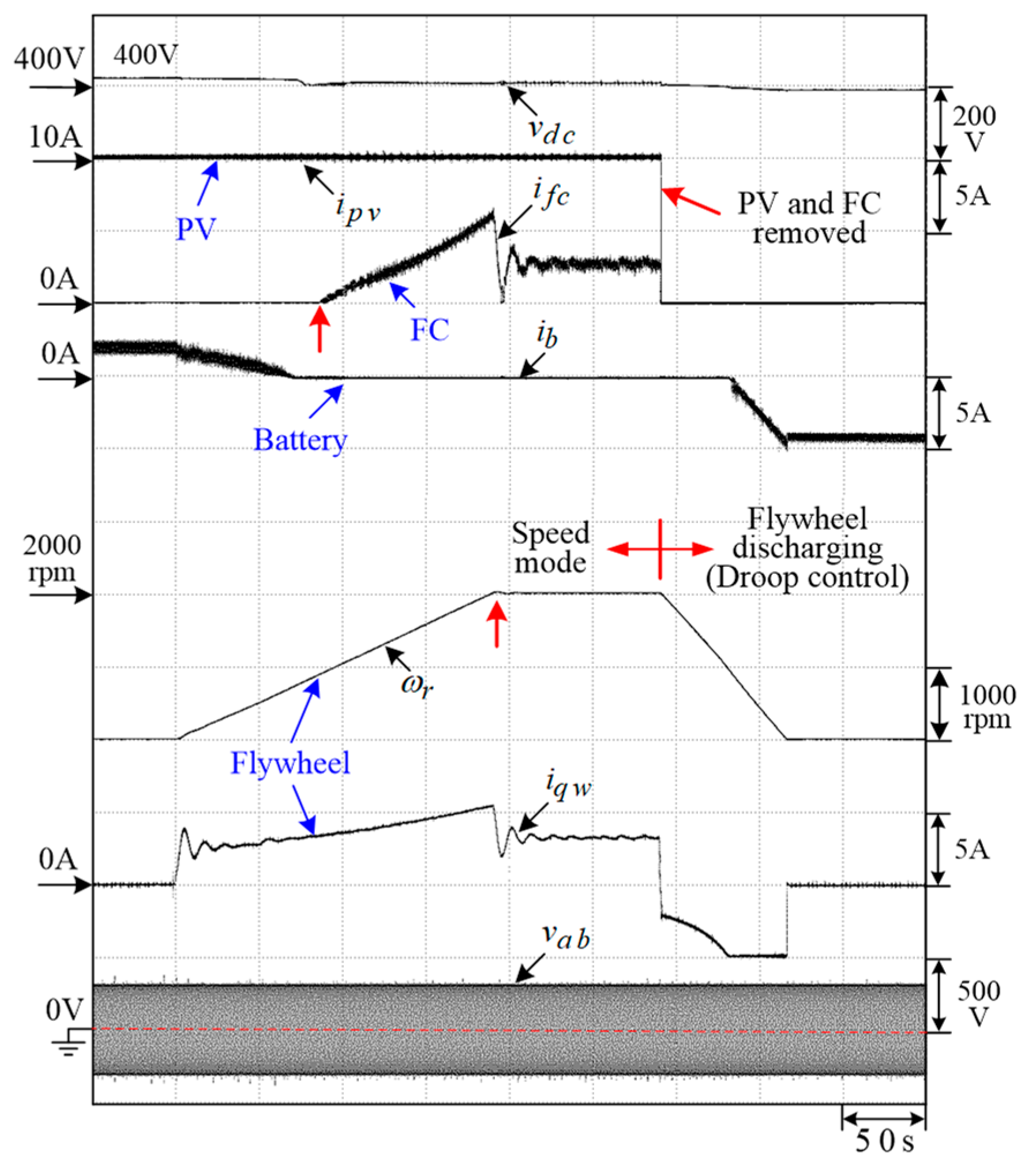
5.3.2. Measured Results
6. Integrated Operation of EVs
6.1. EV Battery System
6.1.1. Power Circuit
- Battery bank: , 2 serially connected cells (UC Battery PS40138, 72 V–30 Ah).
- Bidirectional converter: It is constructed using the IGBT module CM100DY-12H () by Mitsubishi Company, Tokyo, Japan.
- Energy storage inductors: .
- Filter capacitor: .
- Switching frequency: .
6.1.2. Control Scheme
6.2. Three-Level CLLC Resonant Converter
6.2.1. Power Circuit
- , .
- Power switches: power MOSFET IPW65R019C7, manufactured by Infineon Company.
6.2.2. Control Scheme
6.2.3. Measured Results
- (i) PV irradiance is ; (ii) the microgrid without exhausting electricity and sends power to the grid (M2G mode, ).
- (i) EV battery is start to charge with ; (ii) the grid and PV in microgrid provide the charging power (G2M + M2V modes, ).
- (i) PV irradiance is changed from to ; (ii) the power supplied from the grid is reduced (G2M + M2V modes).
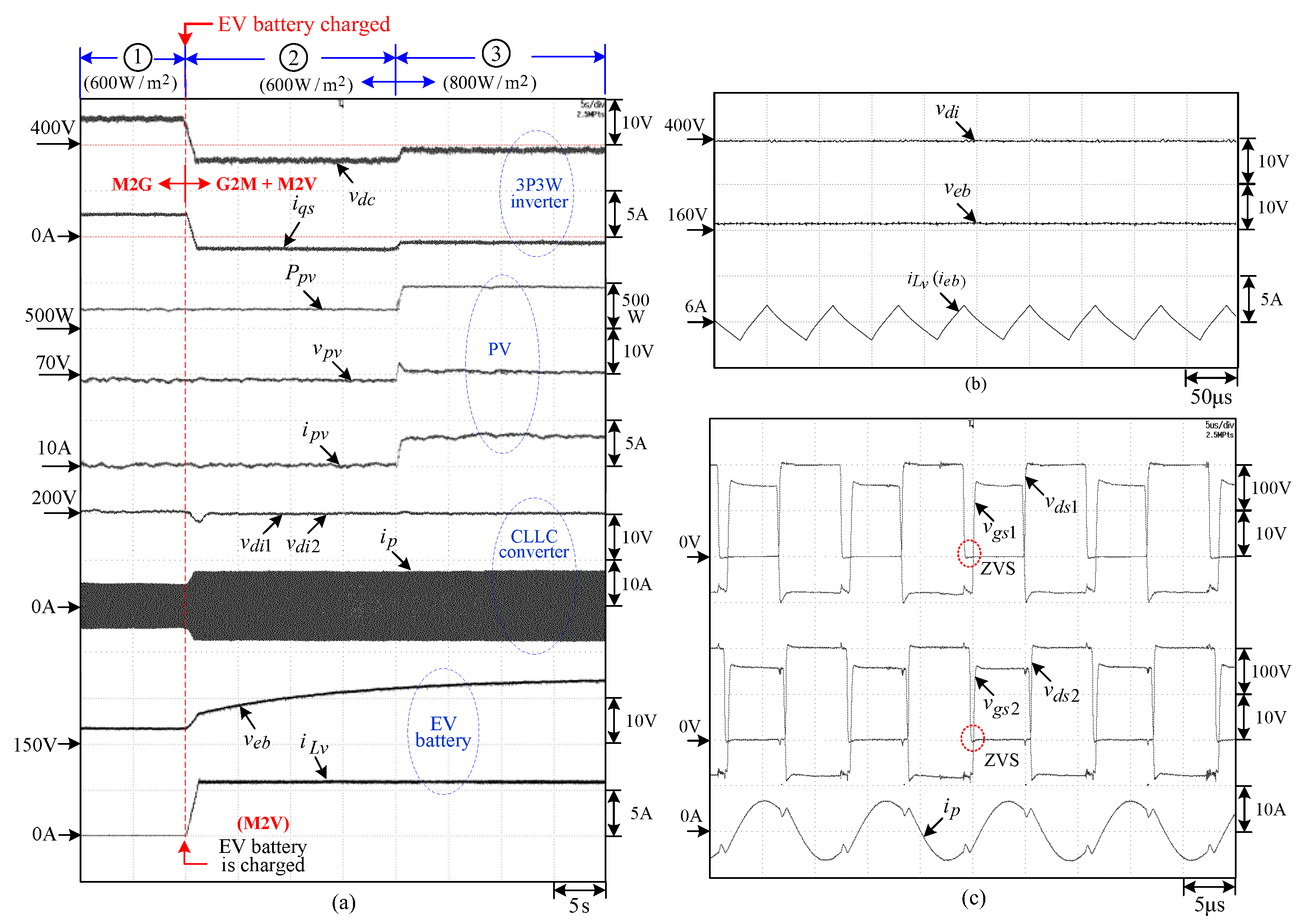
7. Integrated Operation of MEA
7.1. 270 Vdc Converter
7.1.1. Power Circuit
- Input voltage: .
- Output voltage: .
- Switching frequency: .
- Energy storage inductor: .
- Output filtering capacitor: .
7.1.2. Control Scheme
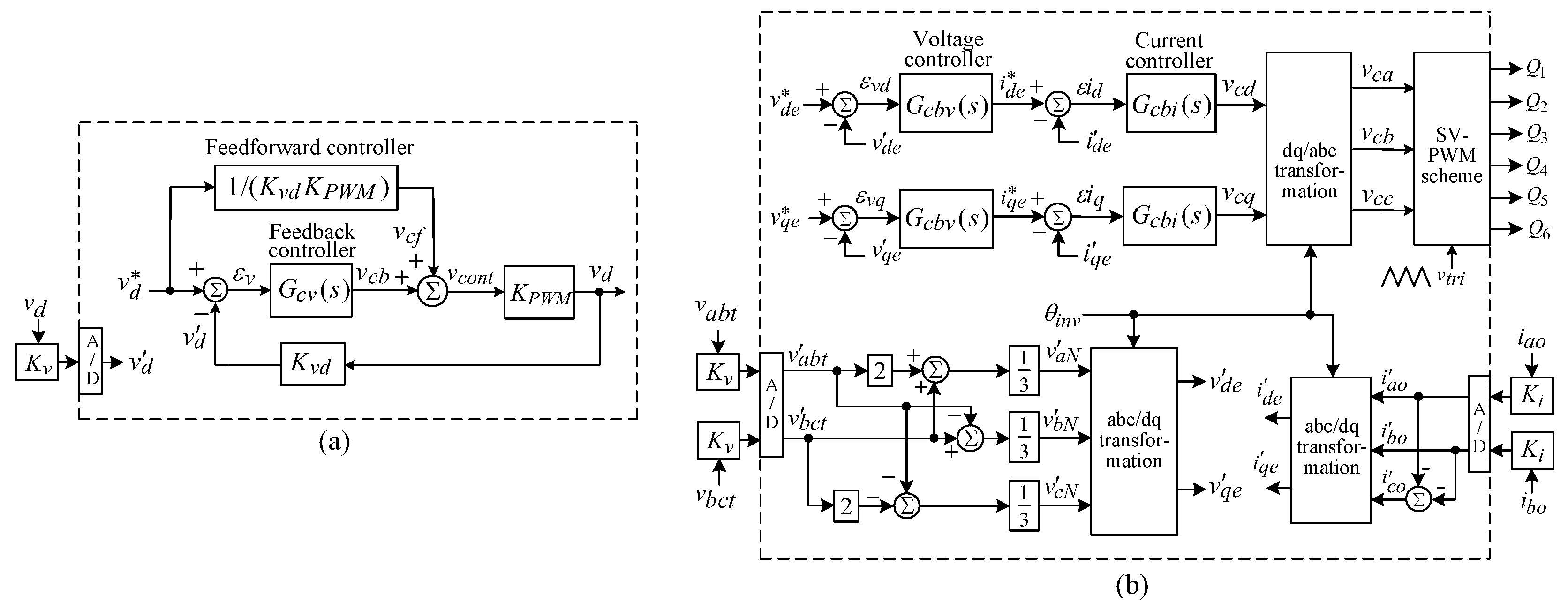
7.2. 115 V/400 Hz High-Frequency Inverter
7.2.1. Power Circuit
- Three-phase HFAC bus voltage: Phase rms voltage .
- PWM switching frequency: .
- Current and voltage sensing factors: . .
- Output filters: and
7.2.2. Control Schemes
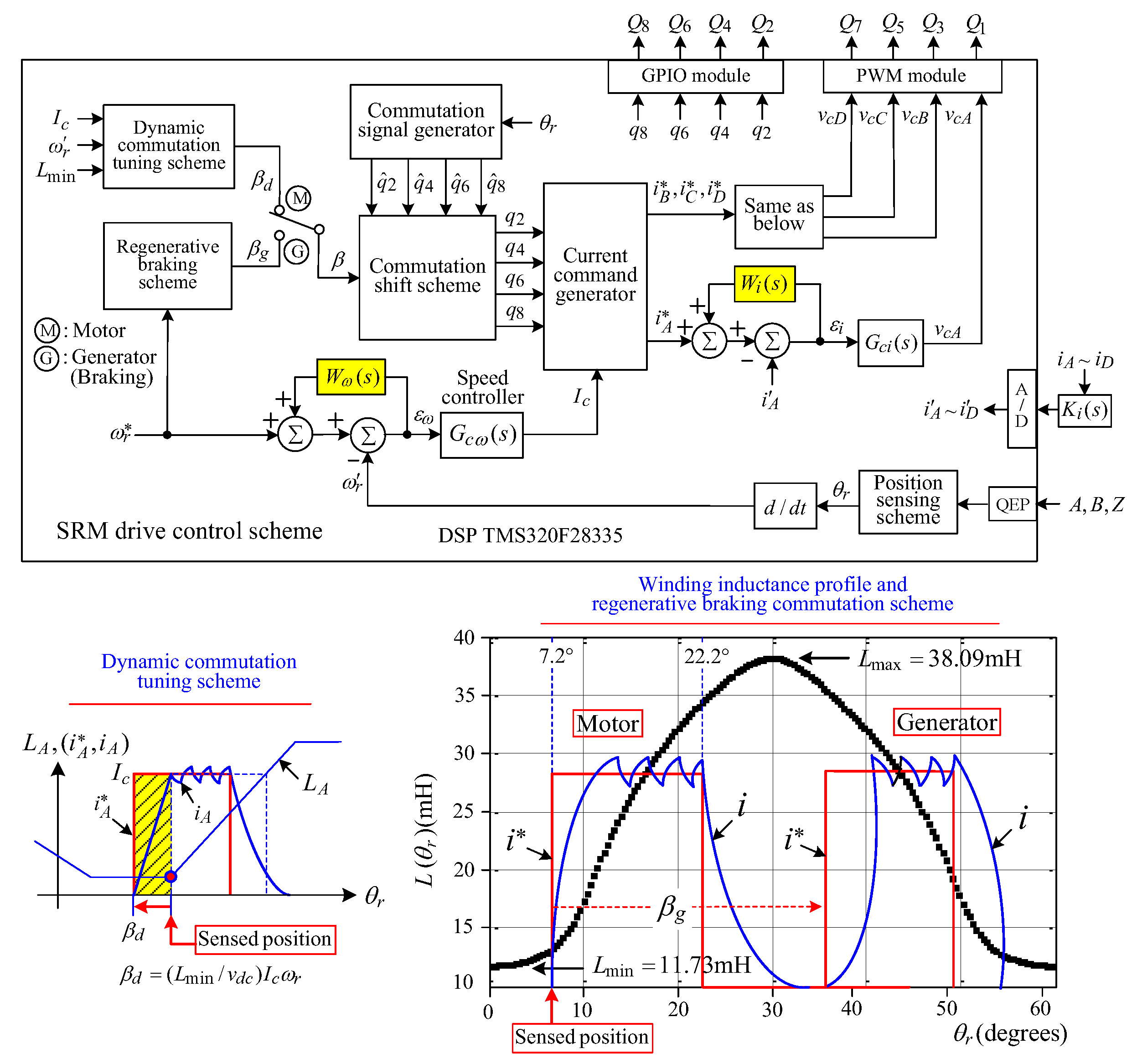
7.3. Switched-Reluctance Motor Drive
7.3.1. Power Circuit
- SRM: four-phase, 8/6 teeth, 400 V, 4 kW, 1500 rpm (TASC Drives Ltd., UK). The measured winding inductance profile and the arranged commutation mechanisms are shown in Figure 24.
- PMSG: three-phase, 24 A, 4.5 kW, 2000 rpm.
- Dynamic load: rectifier with load resistance .
- Flywheel: .
- Asymmetrical bridge converter: It is constructed by two IGBT modules, CM100RL-12NF (Mitsubishi).
7.3.2. Control Scheme
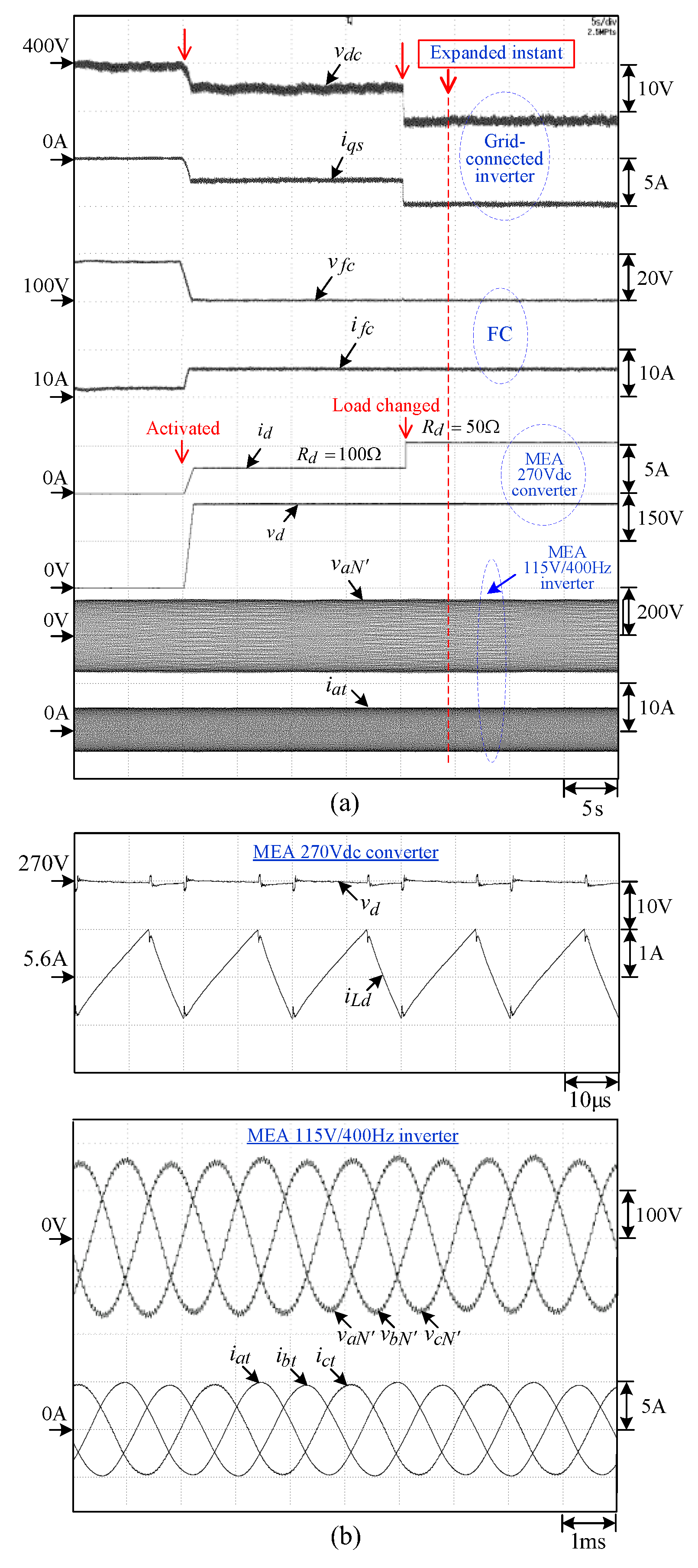
7.4. Measured Results
7.4.1. MEA Major AC Bus and DC Bus
7.4.2. SRM Drive
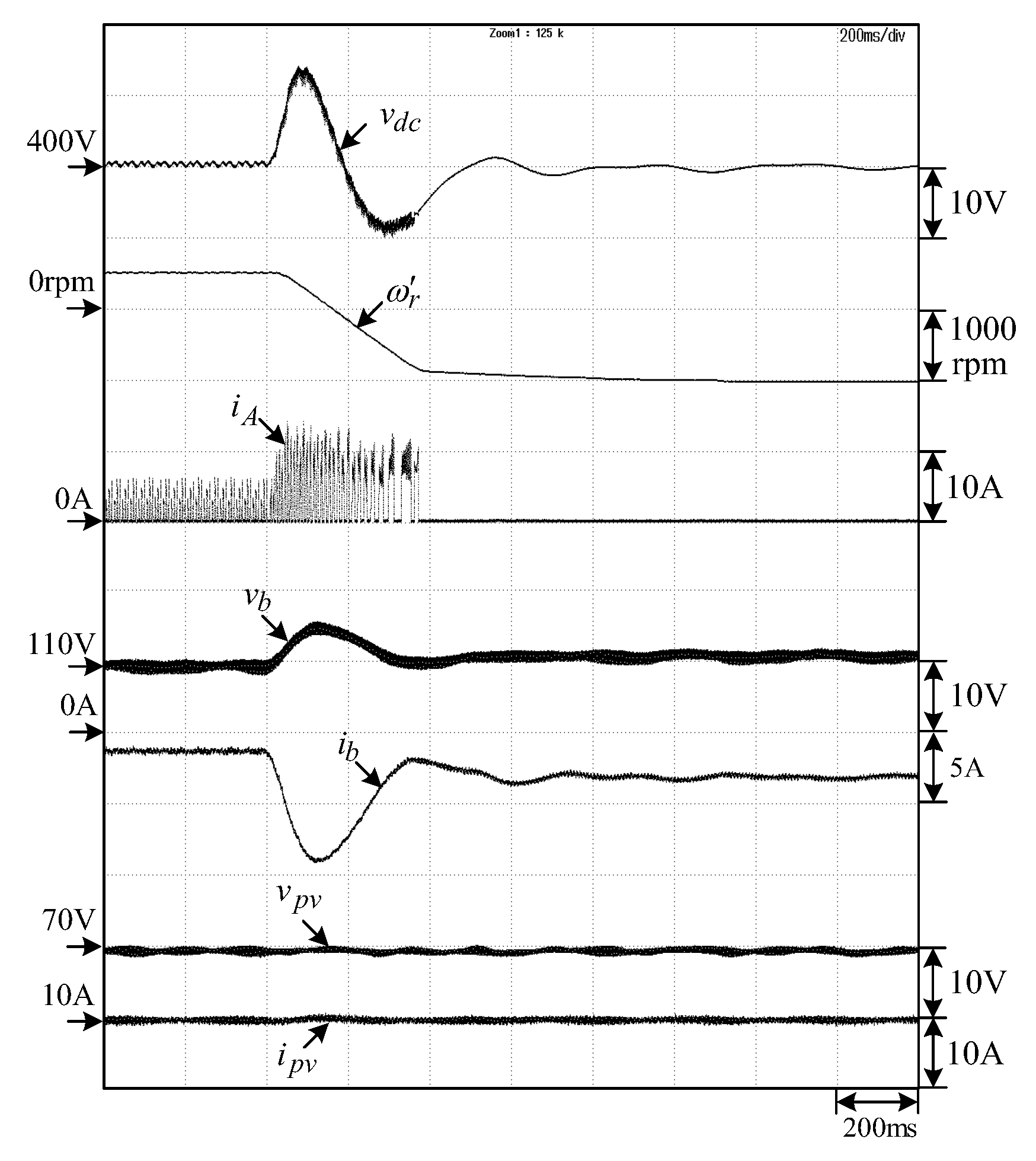
- (i) The SRM drive does not work; (ii) PV irradiance is ; (iii) the microgrid does not exhaust electricity and sends power to the BESS ().
- (i) The SRM drive is operated from ; (ii) the BESS () and PV () in the microgrid provide the power to the SRM drive.
- (i) The SRM drive is operated from ; (ii) the BESS () and PV () in the microgrid continuously provide power to the SRM drive.

8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hatziargyriou, N.; Asano, H.; Iravani, R.; Marnay, C. Microgrids. IEEE Power Energy 2007, 5, 78–94. [Google Scholar] [CrossRef]
- Emadi, A.; Lee, Y.J.; Rajashekara, K. Power electronics and motor drives in electric, hybrid electric, and plug-in hybrid electric vehicles. IEEE Trans. Ind. Electron. 2008, 55, 2237–2245. [Google Scholar] [CrossRef]
- De Santiago, J.; Bernhoff, H.; Ekergård, B.; Eriksson, S.; Ferhatovic, S.; Waters, R.; Leijon, M. Electrical motor drivelines in commercial all-electric vehicles: A review. IEEE Trans. Veh. Technol. 2012, 61, 475–484. [Google Scholar] [CrossRef]
- Wheeler, P.; Bozhko, S. The more electric aircraft: Technology and challenges. IEEE Electrif. Mag. 2014, 2, 6–12. [Google Scholar] [CrossRef]
- Nasirian, V.; Moayedi, S.; Davoudi, A.; Lewis, F.L. Distributed cooperative control of DC microgrids. IEEE Trans. Power Electron. 2015, 30, 2288–2303. [Google Scholar] [CrossRef]
- Patterson, M.; Macia, N.F.; Kannan, A.M. Hybrid microgrid model based on solar photovoltaic battery fuel cell system for intermittent load applications. IEEE Trans. Energy Convers. 2015, 30, 359–366. [Google Scholar] [CrossRef]
- Dragičević, T.; Lu, X.; Vasquez, J.C.; Guerrero, J.M. DC microgrids—Part I: A review of control strategies and stabilization techniques. IEEE Trans. Power Electron. 2016, 31, 3528–3549. [Google Scholar]
- Xu, L.; Guerrero, J.M.; Lashab, A.; Wei, B.; Bazmohammadi, N.; Vasquez, J.C.; Abusorrah, A. A review of DC shipboard microgrids—Part I: Power architectures, energy storage, and power converters. IEEE Trans. Power Electron. 2022, 37, 5155–5172. [Google Scholar] [CrossRef]
- Merabet, A.; Ahmed, K.T.; Ibrahim, H.; Beguenane, R.; Ghias, A.M. Energy management and control system for laboratory scale microgrid based wind-PV-battery. IEEE Trans. Sustain. Energy 2017, 8, 145–154. [Google Scholar] [CrossRef]
- Kakigano, H.; Miura, Y.; Ise, T. Low-voltage bipolar-type DC microgrid for super high quality distribution. IEEE Trans. Power Electron. 2010, 25, 3066–3075. [Google Scholar] [CrossRef]
- Lin, S.; Huang, Y.; Liaw, C. Wind SRG-based bipolar DC microgrid with grid-connected and plug-in energy supporting functions. Energies 2023, 16, 2962. [Google Scholar] [CrossRef]
- Jin, Z.; Sulligoi, G.; Cuzner, R.; Meng, L.; Vasquez, J.C.; Guerrero, J.M. Next-generation shipboard DC power system: Introduction smart grid and dc microgrid technologies into maritime electrical networks. IEEE Electrif. Mag. 2016, 4, 45–57. [Google Scholar] [CrossRef]
- Hirose, K. DC microgrid for telecommunications service and related application. In Proceedings of the 2018 IPEC-Niigata 2018-ECCE Asia, Niigata, Japan, 20–24 May 2018; pp. 593–597. [Google Scholar]
- Matsumoto, A.; Fukui, A.; Takeda, T.; Yamasaki, M. Development of 400-Vdc output rectifier for 400-Vdc power distribution system in telecom sites and data centers. In Proceedings of the 2010 IEEE INTELEC, Orlando, FL, USA, 6–10 June 2010. [Google Scholar]
- Ganji, M. Airport microgrids: Transportation energy as a service. IEEE Electrif. Mag. 2020, 8, 121–124. [Google Scholar] [CrossRef]
- Kilimi, M.G.R.; Motjoadi, V.; Bokoro, P.N. Improvement of an off-grid electricity supply system: A case study in Corisco international airport. In Proceedings of the IEEE ICECCME, Mauritius, 7–8 October 2021; pp. 1–8. [Google Scholar]
- Zhao, H.; Xiang, Y.; Shen, Y.; Guo, Y.; Xue, P.; Sun, W.; Cai, H.; Gu, C.; Liu, J. Resilience assessment of hydrogen-integrated energy system for airport electrification. IEEE Trans. Ind. Appl. 2022, 58, 2812–2824. [Google Scholar] [CrossRef]
- Fagundes, T.A.; Fuzato, G.H.F.; Ferreira, P.G.B.; Biczkowski, M.; Machado, R.Q. Fuzzy controller for energy management and SoC equalization in DC microgrids powered by fuel cell and energy storage units. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 3, 90–100. [Google Scholar] [CrossRef]
- Pires, V.F.; Cordeiro, A.; Foito, D.; Silva, J.F.A. Dual output and high voltage gain DC-DC converter for PV and fuel cell generators connected to DC bipolar microgrids. IEEE Access 2021, 9, 157124–157133. [Google Scholar] [CrossRef]
- Gao, Y.; Jausseme, C.; Huang, Z.; Yang, T. Hydrogen-powered aircraft: Hydrogen–electric hybrid propulsion for aviation. IEEE Electrif. Mag. 2022, 10, 17–26. [Google Scholar] [CrossRef]
- Vazquez, S.; Lukic, S.M.; Galvan, E.; Franquelo, L.G.; Carrasco, J.M. Energy storage systems for transport and grid applications. IEEE Trans. Ind. Electron. 2010, 57, 3881–3895. [Google Scholar] [CrossRef]
- Boicea, V.A. Energy storage technologies: The past and the present. Proc. IEEE 2014, 102, 1777–1794. [Google Scholar] [CrossRef]
- Hino, M.; Hara, D. Application of an energy storage system using lithium-ion batteries for more effective regenerative energy utilization. JR East Tech. Rev. 2014, 31, 23–26. [Google Scholar]
- Rocabert, J.; Capó-Misut, R.; Muñoz-Aguilar, R.S.; Candela, J.I.; Rodriguez, P. Control of energy storage system integrating electrochemical batteries and supercapacitors for grid-connected applications. IEEE Trans. Ind. Appl. 2019, 55, 1853–1862. [Google Scholar] [CrossRef]
- Kenny, B.H.; Kascak, P.E.; Jansen, R.; Dever, T.; Santiago, W. Control of a high-speed flywheel system for energy storage in space applications. IEEE Trans. Ind. Appl. 2005, 41, 1029–1038. [Google Scholar] [CrossRef]
- Abdeltawab, H.H.; Mohamed, Y.A.I. Robust energy management of a hybrid wind and flywheel energy storage system considering flywheel power losses minimization and grid-code constraints. IEEE Trans. Ind. Electron. 2016, 63, 4242–4254. [Google Scholar] [CrossRef]
- Murayama, M.; Kato, S.; Tsutsui, H.; Tsuji-Iio, S.; Shimada, R. Combination of flywheel energy storage system and boosting modular multilevel cascade converter. IEEE Trans. Appl. Supercond. 2018, 28, 1–4. [Google Scholar] [CrossRef]
- Wirasingha, S.G.; Emadi, A. Classification and review of control strategies for plug-in hybrid electric vehicles. IEEE Trans. Veh. Technol. 2011, 60, 111–122. [Google Scholar] [CrossRef]
- Williamson, S.S.; Rathore, A.K.; Musavi, F. Industrial electronics for electric transportation: Current state-of-the-art and future challenges. IEEE Trans. Ind. Electron. 2015, 62, 3021–3032. [Google Scholar] [CrossRef]
- Alagarsamy, T.; Moulik, B. A review on optimal design of hybrid electric vehicles and electric vehicles. In Proceedings of the IEEE I2CT, Mangalore, India, 27–28 October 2018; pp. 1–5. [Google Scholar]
- Kumar, G.V.; Zhuang, J.X.; Lu, M.Z.; Liaw, C.M. Development of an electric vehicle synchronous reluctance motor drive. IEEE Trans. Veh. Technol. 2020, 69, 5012–5024. [Google Scholar] [CrossRef]
- Kramer, W.; Chakraborty, S.; Kroposki, B.; Hoke, A.; Martin, G.; Markel, T. Grid Interconnection and Performance Testing Procedures for Vehicle-to-Grid (V2G) Power Electronics; Technical Report NREL/CP-5500-54505; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2012. [Google Scholar]
- Ustun, T.S.; Ozansoy, C.R.; Zayegh, A. Implementing vehicle-to-grid (V2G) technology with IEC 61850-7-420. IEEE Trans. Smart Grid 2013, 4, 1180–1187. [Google Scholar] [CrossRef]
- Monteiro, V.; Pinto, J.G.; Afonso, J.L. Operation modes for the electric vehicle in smart grids and smart homes: Present and proposed modes. IEEE Trans. Veh. Technol. 2016, 65, 1007–1020. [Google Scholar] [CrossRef]
- Hsu, Y.C.; Kao, S.C.; Ho, C.Y.; Jhou, P.H.; Lu, M.Z.; Liaw, C.M. On an electric scooter with G2V/V2H/V2G and energy harvesting functions. IEEE Trans. Power Electron. 2018, 33, 6910–6925. [Google Scholar] [CrossRef]
- MMasrur, M.A.; Skowronska, A.G.; Hancock, J.; Kolhoff, S.W.; McGrew, D.Z.; Vandiver, J.C.; Gatherer, J. Military-based vehicle-to-grid and vehicle-to-vehicle microgrid-system architecture and implementation. IEEE Trans. Transp. Electrif. 2018, 4, 157–171. [Google Scholar] [CrossRef]
- Lu, M.Z.; Guo, Z.W.; Liaw, C.M. A battery/supercapacitor hybrid powered EV SRM drive and microgrid incorporated operations. IEEE Trans. Transp. Electrif. 2021, 7, 2848–2863. [Google Scholar] [CrossRef]
- Buticchi, G.; Bozhko, S.; Liserre, M.; Wheeler, P.; Al-Haddad, K. On-board microgrids for the more electric aircraft-technology review. IEEE Trans. Ind. Electron. 2019, 66, 5588–5599. [Google Scholar] [CrossRef]
- Yeoh, S.S.; Rashed, M.; Sanders, M.; Bozhko, S. Variable-voltage bus concept for aircraft electrical power system. IEEE Trans. Ind. Electron. 2019, 66, 5634–5643. [Google Scholar] [CrossRef]
- Yang, C.W.; Lu, M.Z.; Liaw, C.M. Development of an aircraft electric power architecture with integrated ground power unit. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3446–3459. [Google Scholar] [CrossRef]
- Liaw, C.M.; Jhou, P.H.; Yang, C.W. Switched-reluctance motor drive for more electric aircraft with energy storage buffer. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 7423–7439. [Google Scholar] [CrossRef]
- Bhaskar, M.S.; Ramachandaramurthy, V.K.; Padmanaban, S.; Blaabjerg, F.; Ionel, D.M.; Mitolo, M.; Almakhles, D. Survey of DC-DC non-isolated topologies for unidirectional power flow in fuel cell vehicles. IEEE Access 2020, 8, 178130–178166. [Google Scholar] [CrossRef]
- Jung, J.; Kim, H.; Ryu, M.; Baek, J. Design methodology of bidirectional CLLC resonant converter for high-frequency isolation of DC distribution systems. IEEE Trans. Power Electron. 2013, 28, 1741–1755. [Google Scholar] [CrossRef]
- Zou, S.; Lu, J.; Mallik, A.; Khaligh, A. Bi-directional CLLC converter with synchronous rectification for plug-in electric vehicles. IEEE Trans. Ind. Appl. 2018, 54, 998–1005. [Google Scholar] [CrossRef]
- Marquardt, R. Modular multilevel converters: State of the art and future progress. IEEE Power Electron. Mag. 2018, 5, 24–31. [Google Scholar] [CrossRef]
- Ruan, X.; Li, B.; Chen, Q.; Tan, S.C.; Tse, C.K. Fundamental considerations of three-level DC-DC converters: Topologies, analyses, and control. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 55, 3733–3743. [Google Scholar] [CrossRef]
- Kan, Z.; Li, P.; Yuan, R.; Zhang, C. Interleaved three-level bi-directional DC-DC converter and power flow control. In Proceedings of the IEEE IGBSG, Yilan, Taiwan, 22–25 April 2018; pp. 1–4. [Google Scholar]
- Zhang, X.; Wang, B.; Manandhar, U.; Gooi, H.B.; Foo, G. A model predictive current controlled bidirectional three-level DC/DC converter for hybrid energy storage system in DC microgrids. IEEE Trans. Power Electron. 2019, 34, 4025–4030. [Google Scholar] [CrossRef]
- Schweizer, M.; Friedli, T.; Kolar, J.W. Comparative evaluation of advanced three-phase three-level inverter/converter topologies against two-level systems. IEEE Trans. Ind. Electron. 2013, 60, 5515–5527. [Google Scholar] [CrossRef]
- Barater, D.; Concari, C.; Buticchi, G.; Gurpinar, E.; De, D.; Castellazi, A. Performance evaluation of a three-level ANPC photo-voltaic grid-connected inverter with 650-V SiC devices and optimized PWM. IEEE Trans. Ind. Appl. 2016, 52, 2475–2485. [Google Scholar] [CrossRef]
- Lin, X.; Dong, D. SiC three-level neutral-point-clamped converter with clamping diode volume reduction using quasi-two-level operation. IEEE Trans. Power Electron. 2023, 38, 9839–9851. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Liang, X.; Huang, B. Event-triggered-based distributed cooperative energy management for multienergy Systems. IEEE Trans. Ind. Inform. 2019, 15, 2008–2022. [Google Scholar] [CrossRef]
- Vašak, M.; Banjac, A.; Hure, N.; Novak, H.; Marušić, D.; Lešić, V. Modular hierarchical model predictive control for coordinated and holistic energy management of buildings. IEEE Trans. Energy Convers. 2021, 36, 2670–2682. [Google Scholar] [CrossRef]
- Yang, L.; Li, X.; Sun, M.; Sun, C. Hybrid policy-based reinforcement learning of adaptive energy management for the energy transmission-constrained island group. IEEE Trans. Ind. Inform. 2023, 19, 10751–10762. [Google Scholar] [CrossRef]
- Zhang, N.; Sun, Q.; Yang, L.; Li, Y. Event-triggered distributed hybrid control scheme for the integrated energy system. IEEE Trans. Ind. Inform. 2022, 18, 835–846. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liaw, C.-M.; Yang, C.-W.; Jhou, P.-H. Airport Microgrid and Its Incorporated Operations. Aerospace 2024, 11, 192. https://doi.org/10.3390/aerospace11030192
Liaw C-M, Yang C-W, Jhou P-H. Airport Microgrid and Its Incorporated Operations. Aerospace. 2024; 11(3):192. https://doi.org/10.3390/aerospace11030192
Chicago/Turabian StyleLiaw, Chang-Ming, Chen-Wei Yang, and Pin-Hong Jhou. 2024. "Airport Microgrid and Its Incorporated Operations" Aerospace 11, no. 3: 192. https://doi.org/10.3390/aerospace11030192
APA StyleLiaw, C.-M., Yang, C.-W., & Jhou, P.-H. (2024). Airport Microgrid and Its Incorporated Operations. Aerospace, 11(3), 192. https://doi.org/10.3390/aerospace11030192






