Maneuvering Decision Making Based on Cloud Modeling Algorithm for UAV Evasion–Pursuit Game
Abstract
1. Introduction
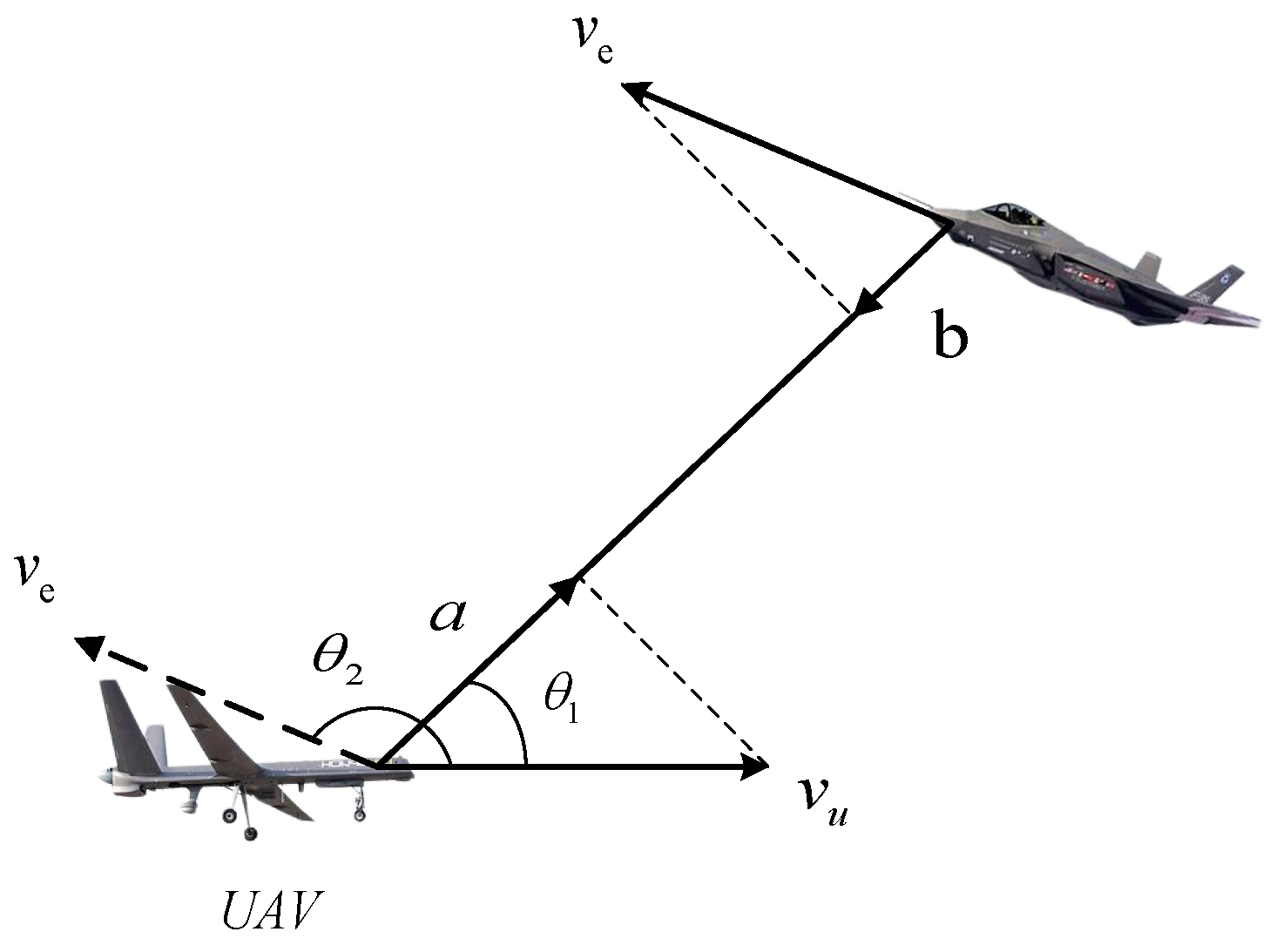
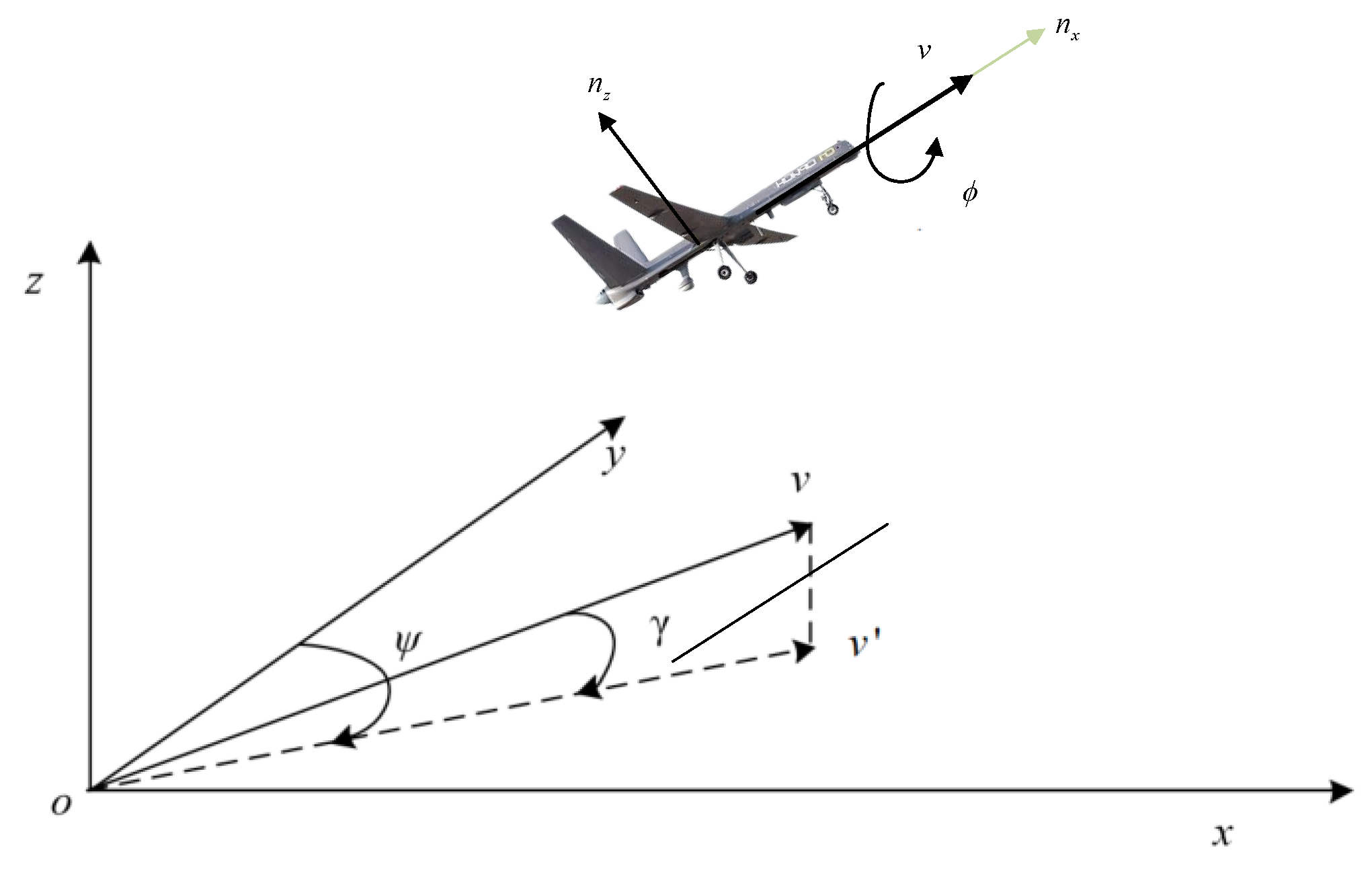
2. UAV Evasion–Pursuit Modeling
2.1. Mathematical Modeling of Fugitive-Tracing Dynamics
- (1)
- UAV location: . It indicates the position of the UAV in the inertial coordinate system;
- (2)
- Approaching rate: . It indicates the difference between the velocity vectors of the two airplanes projected on the target line-of-sight angle formed by the line of sight between the UAV and the target; when it is greater than 0, it means that the two airplanes are approaching each other, and when it is less than 0, it means that the two airplanes are moving away from each other;
- (3)
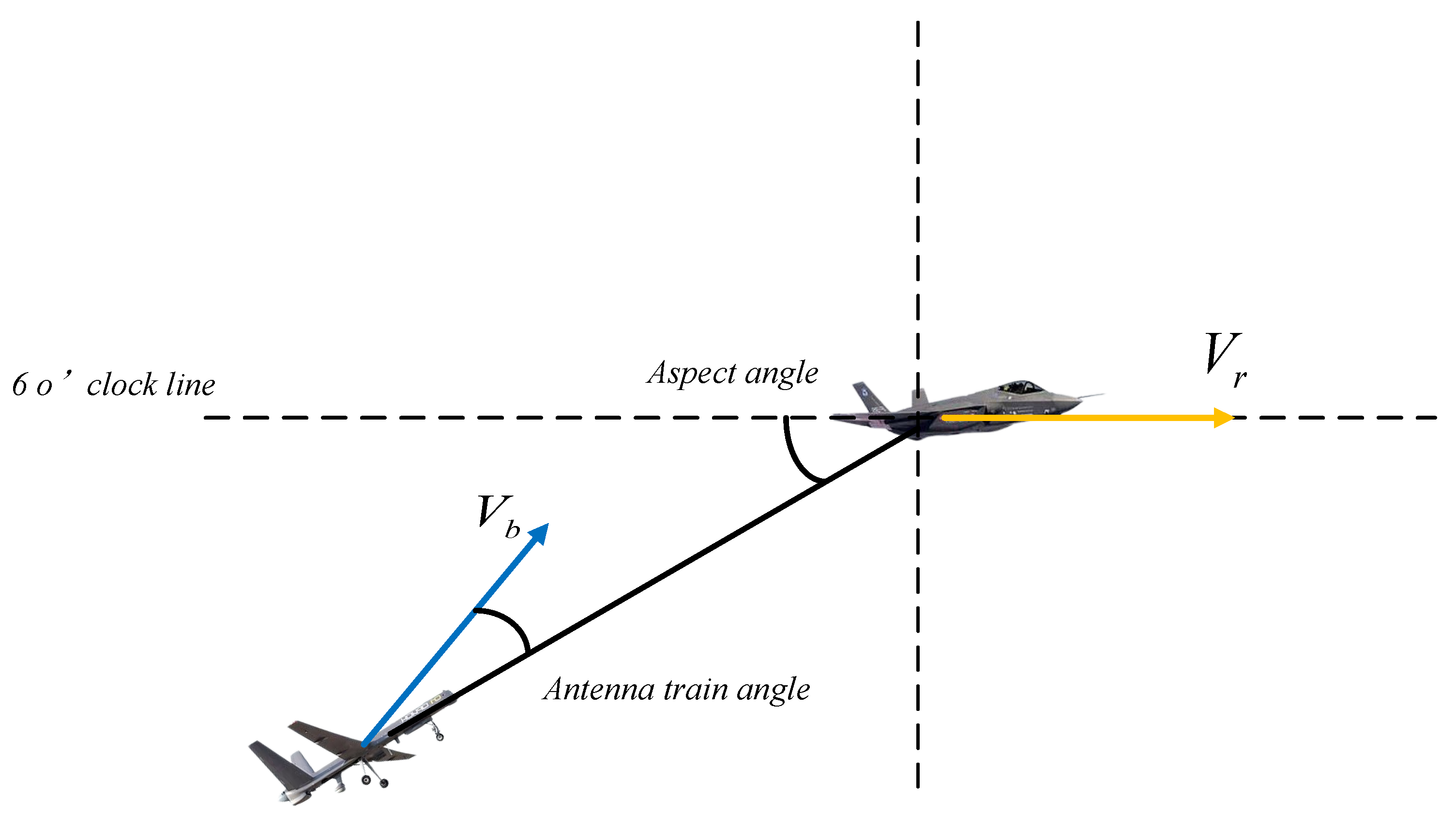
- Relative positions of the enemy and UAV: , where denotes the relative distance between the enemy and the UAV at moment t, denotes the azimuth of the enemy aircraft on the horizontal plane at moment t, and denotes the azimuth of the enemy aircraft in the lead hammer plane at moment t. The relative positions of the enemy aircraft and the UAV are determined based on these three data;
- (4)
- (5)
- Enemy radar system status: , where , for enemy radar locking status, indicates whether the aircraft is locked by the enemy radar irradiation, where 0 indicates not locked and 1 indicates locked; indicates the electronic countermeasures, where 0 indicates that the enemy has not implemented electronic interference and 1 indicates that the enemy has implemented electronic interference. Therefore, the mathematical model of UAV decision making can be expressed as follows:
2.2. Cloud Modeling-Based Assessment of UAV Aerial Pursuit Position
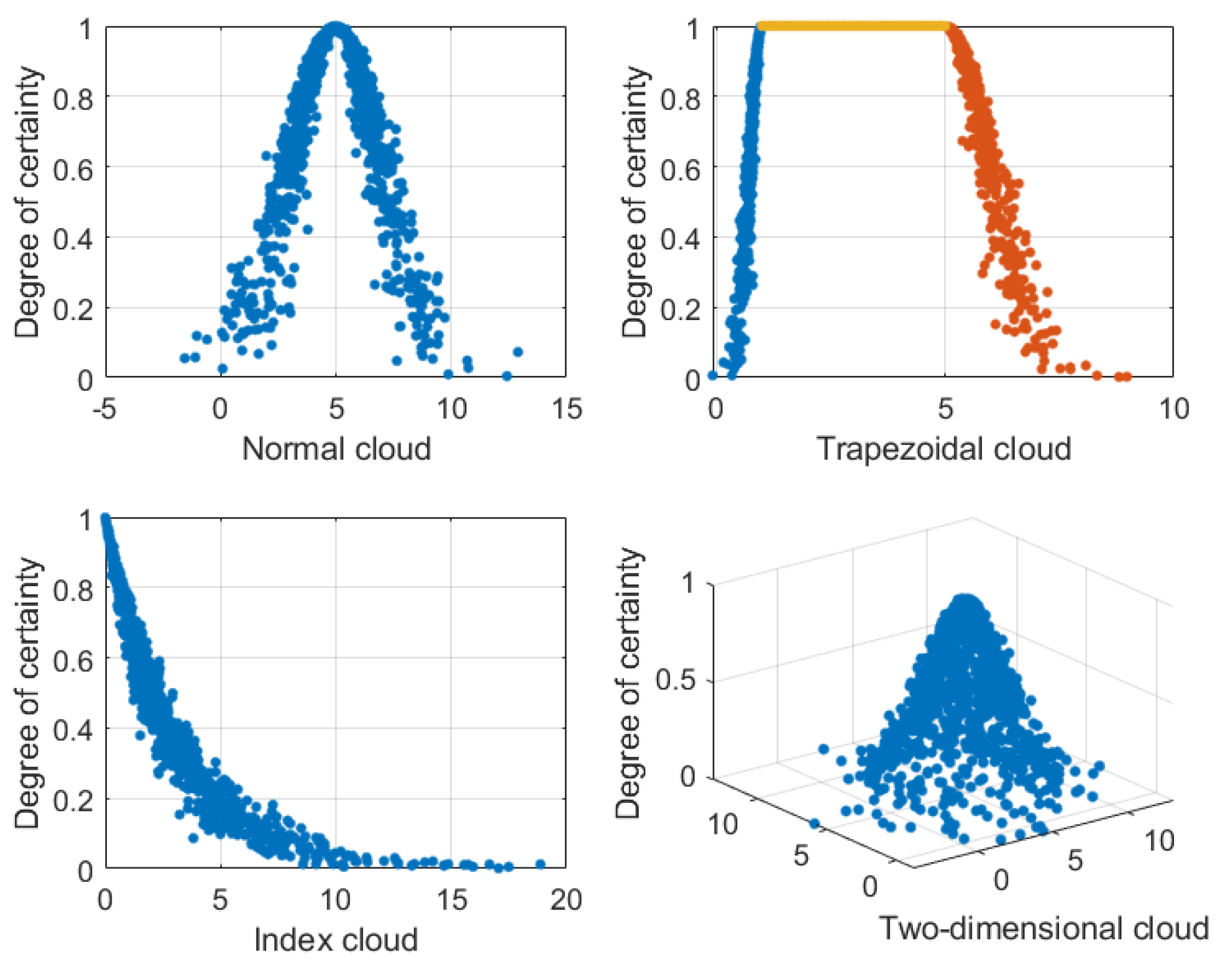
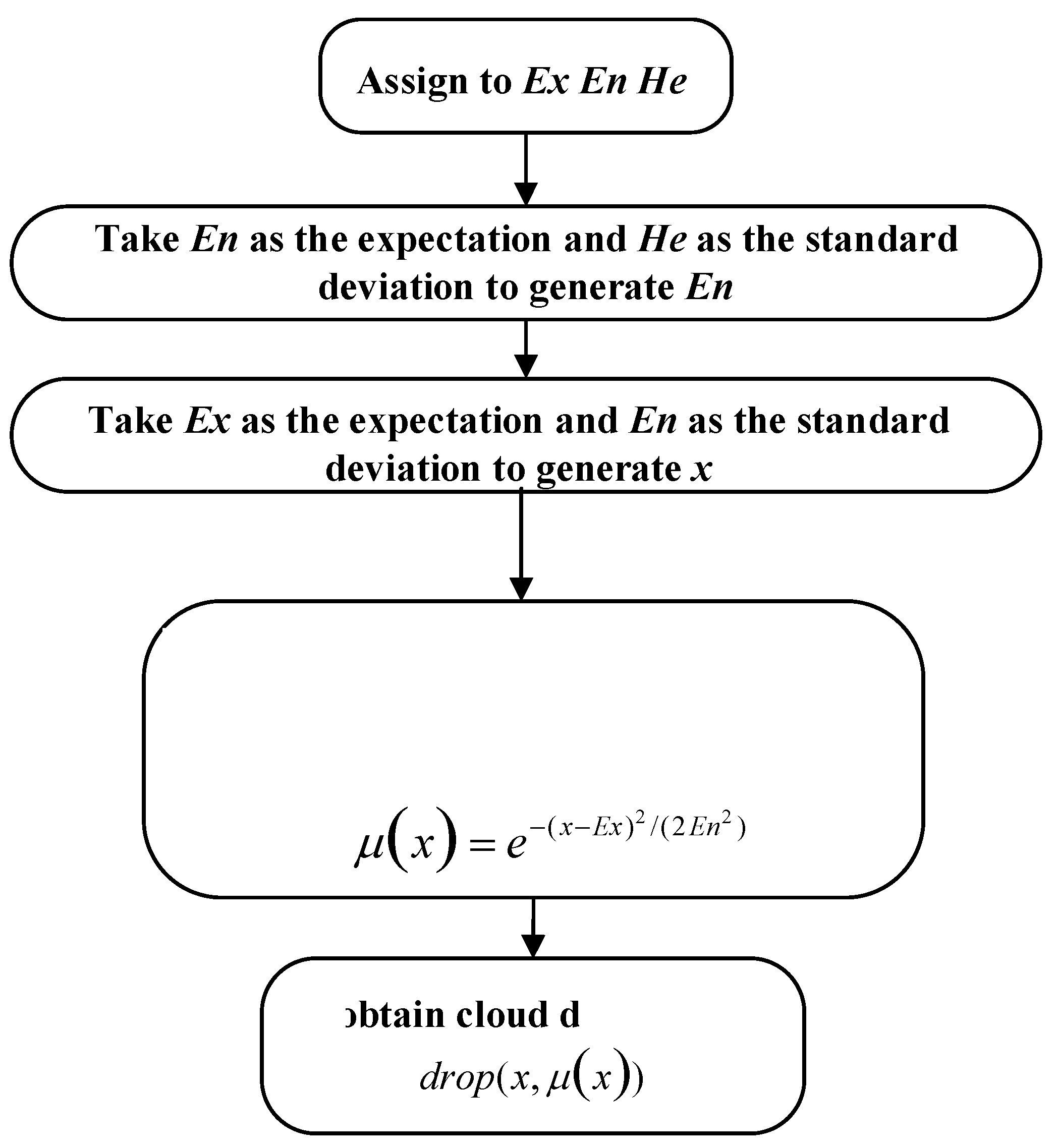
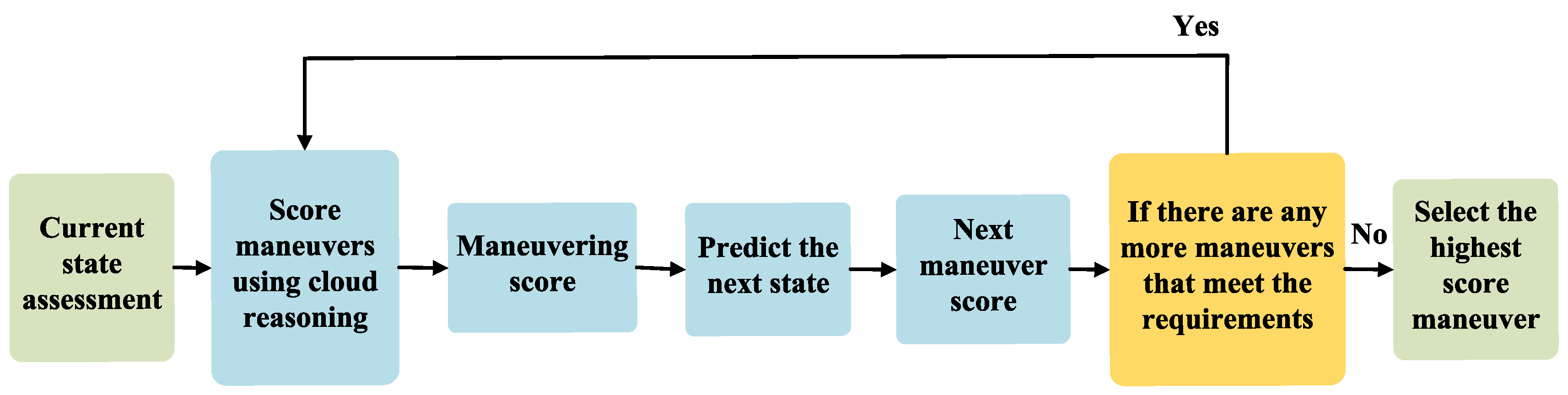
3. Cloud Model-Based Aerial Pursuit Maneuvering Decision Making
UAV Modeling
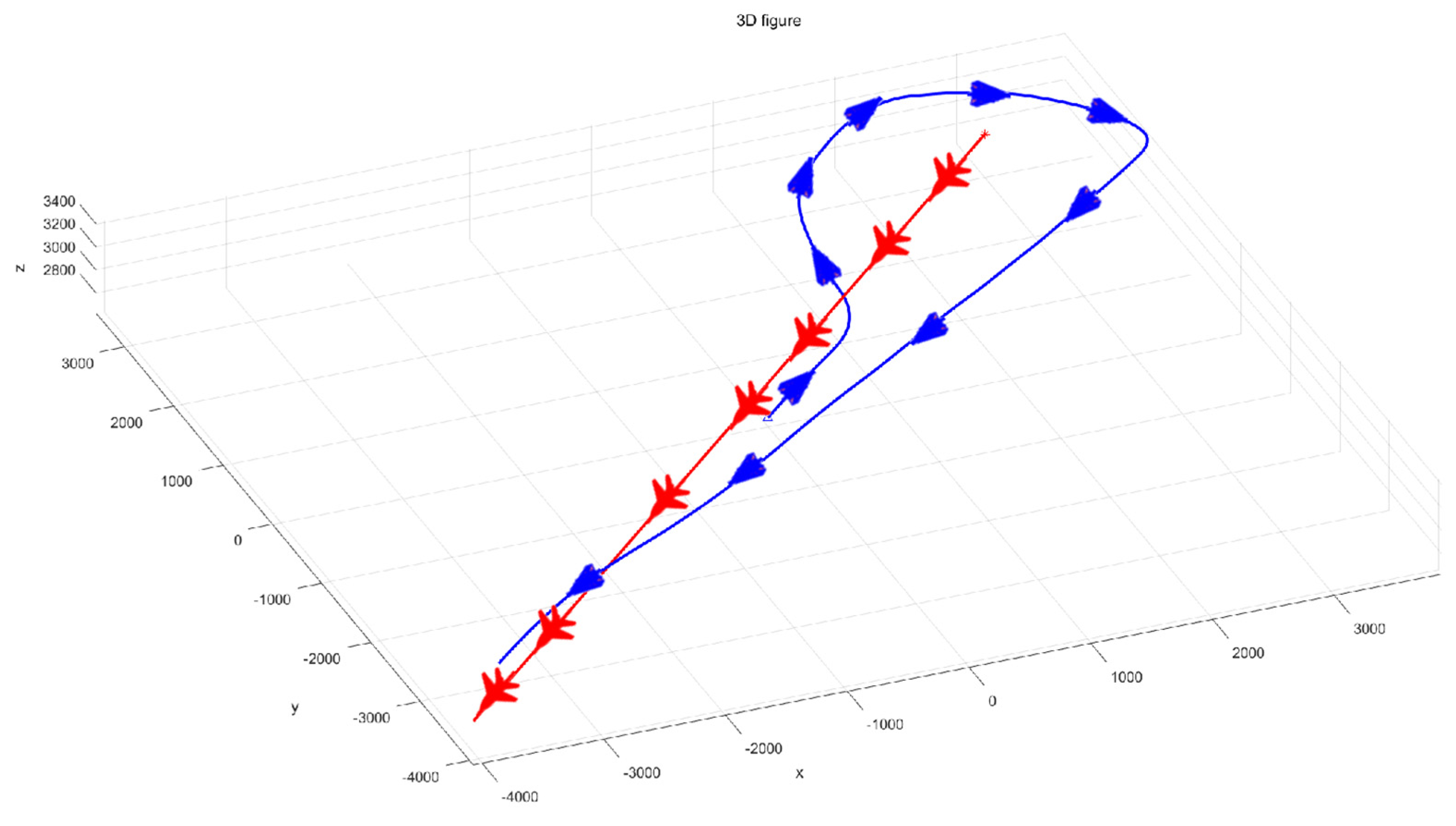
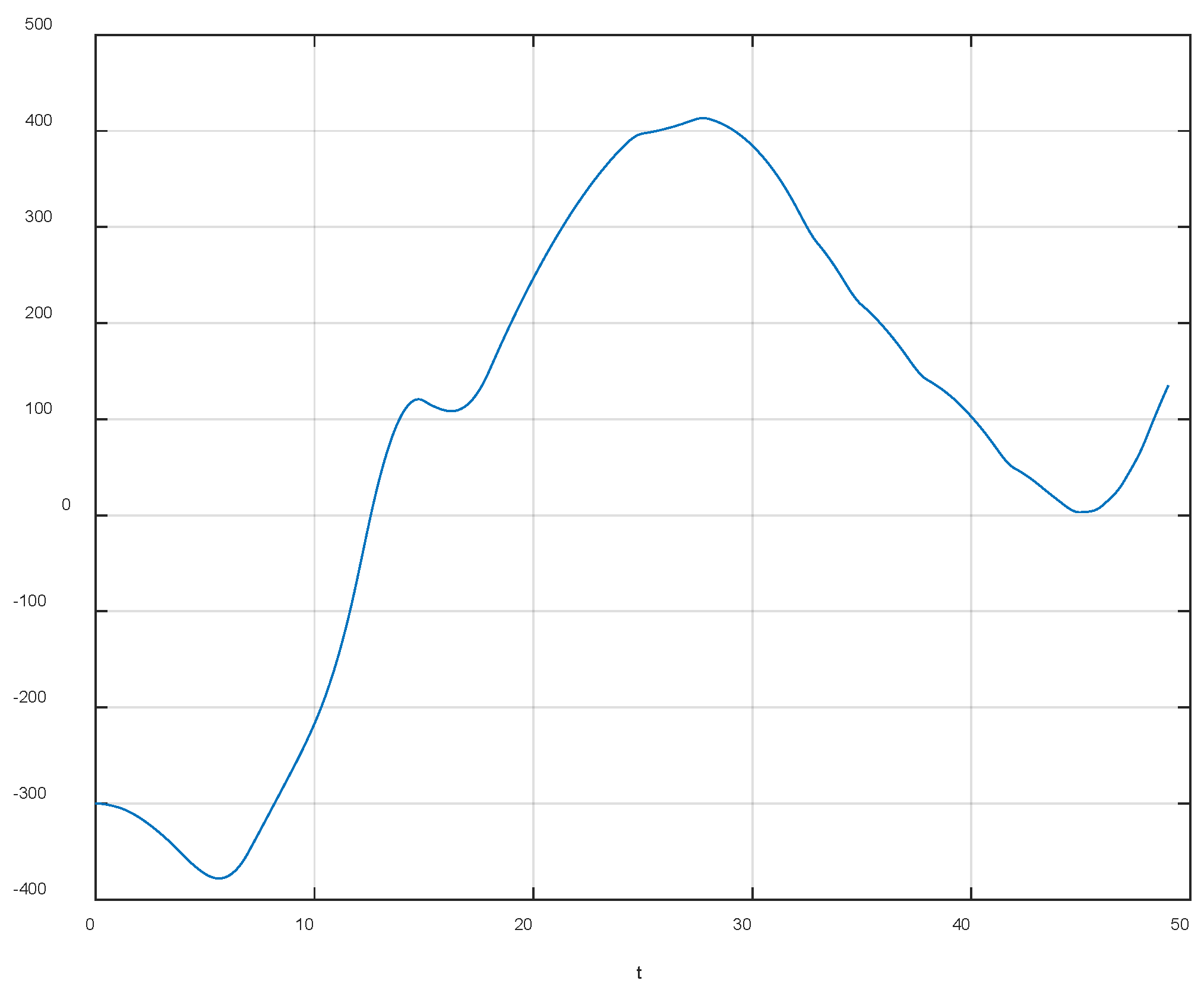
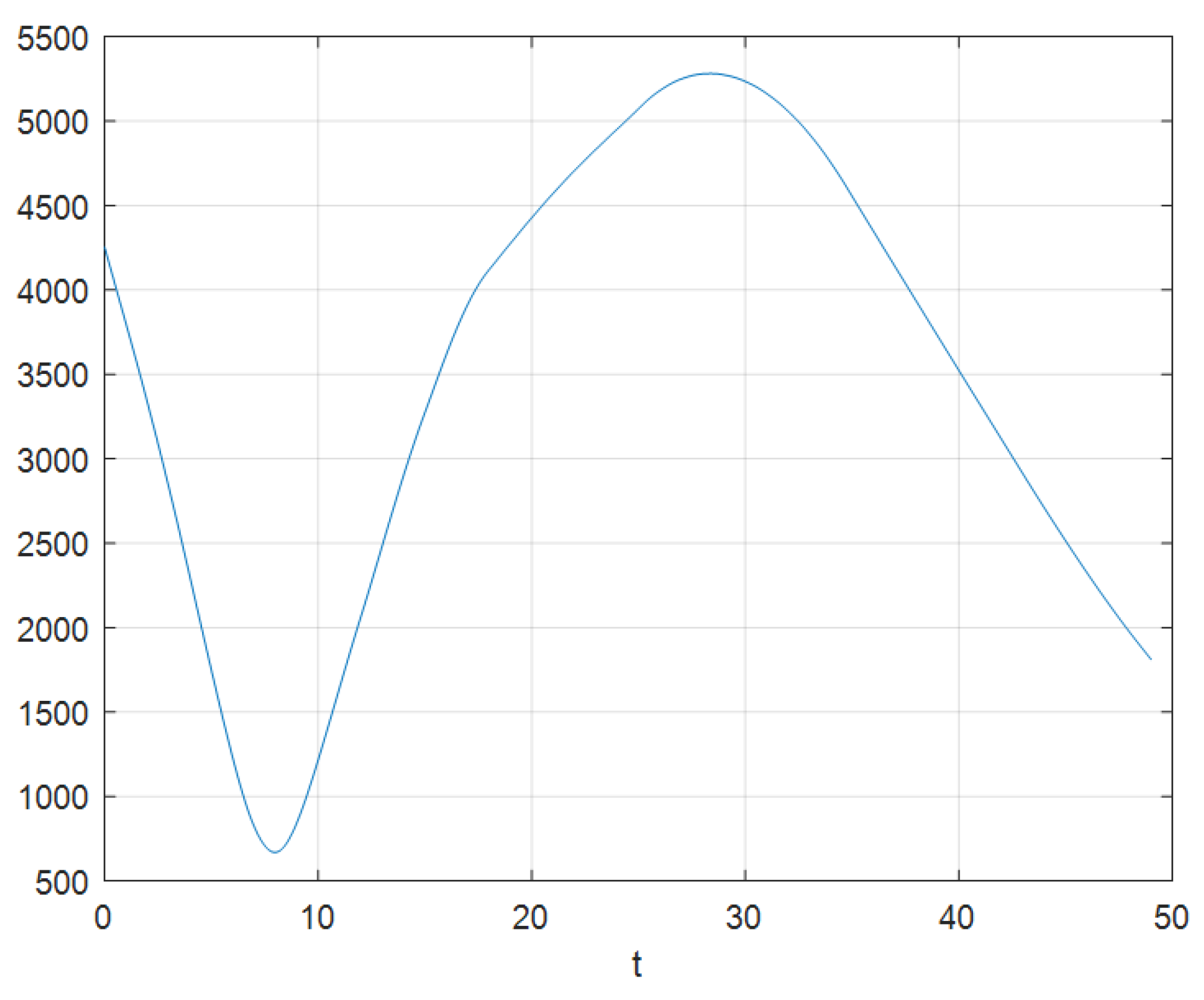
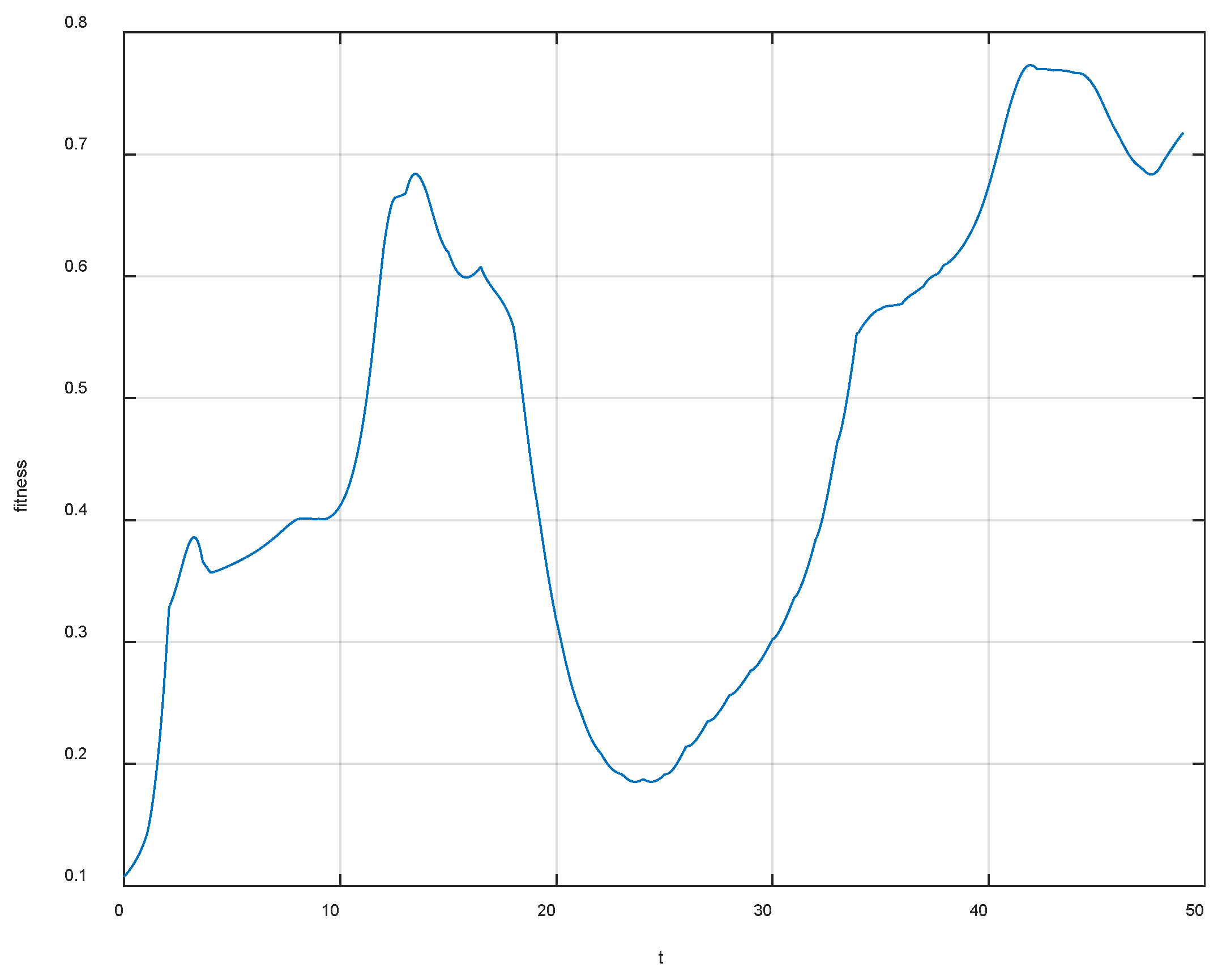
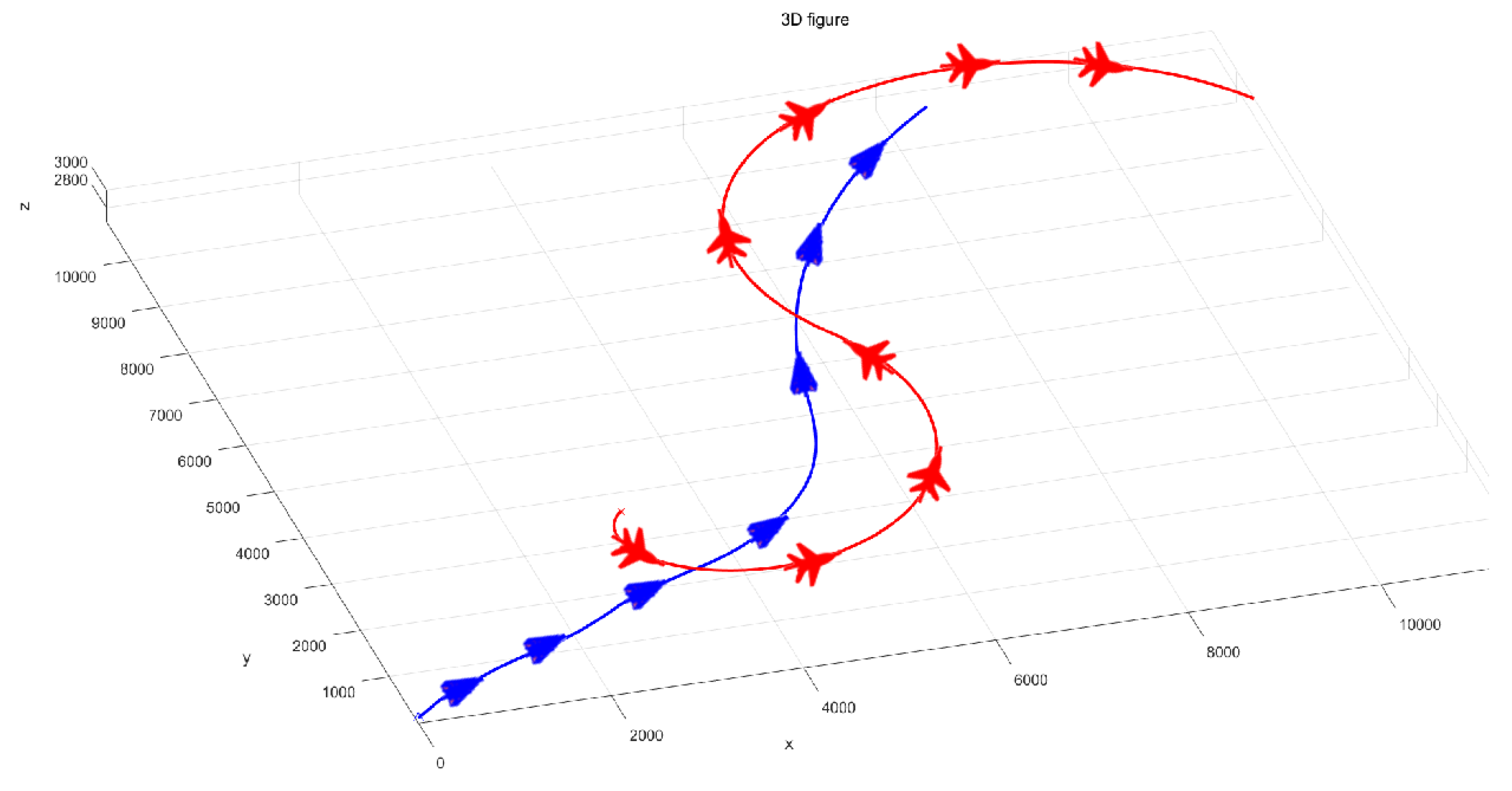
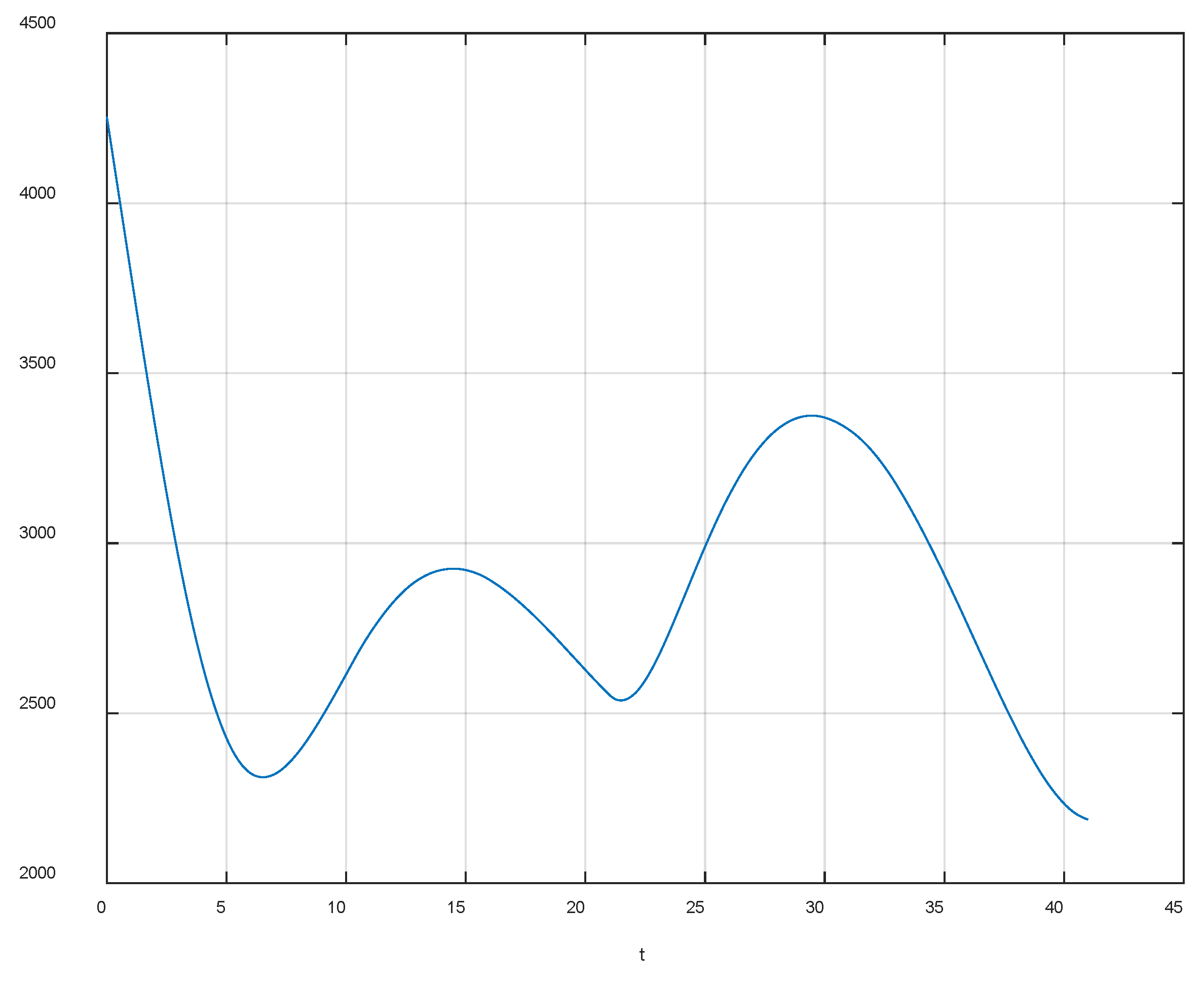
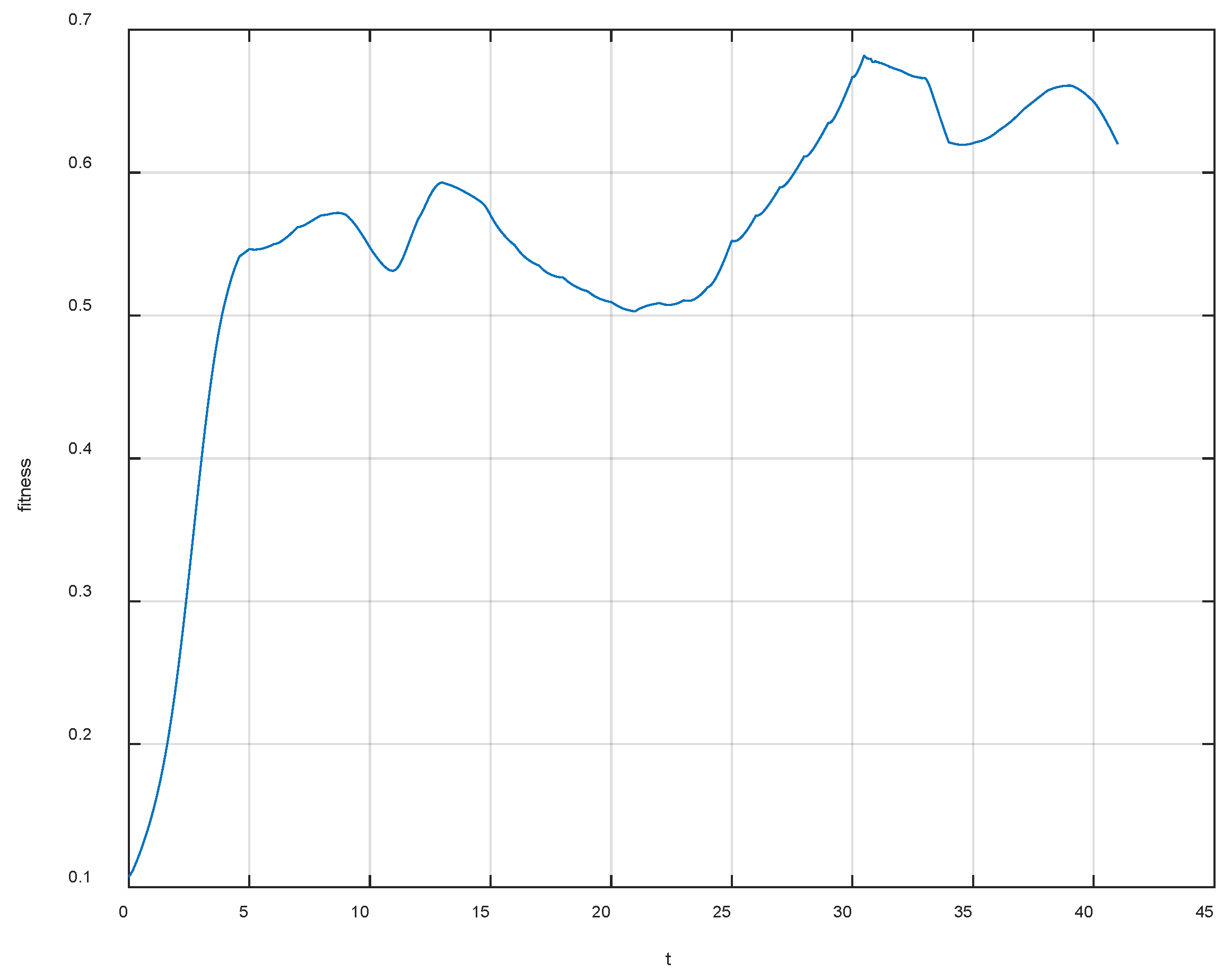
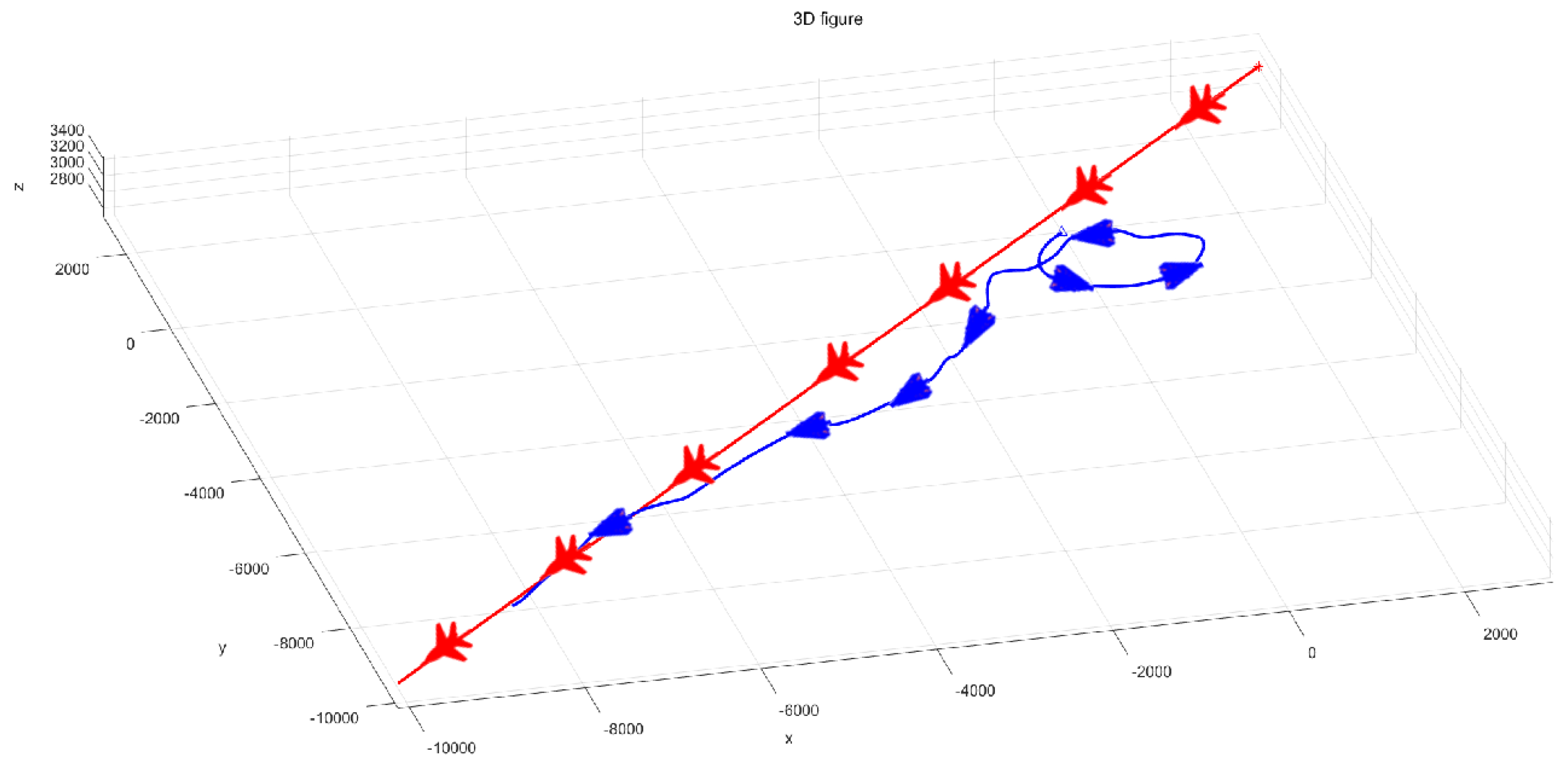
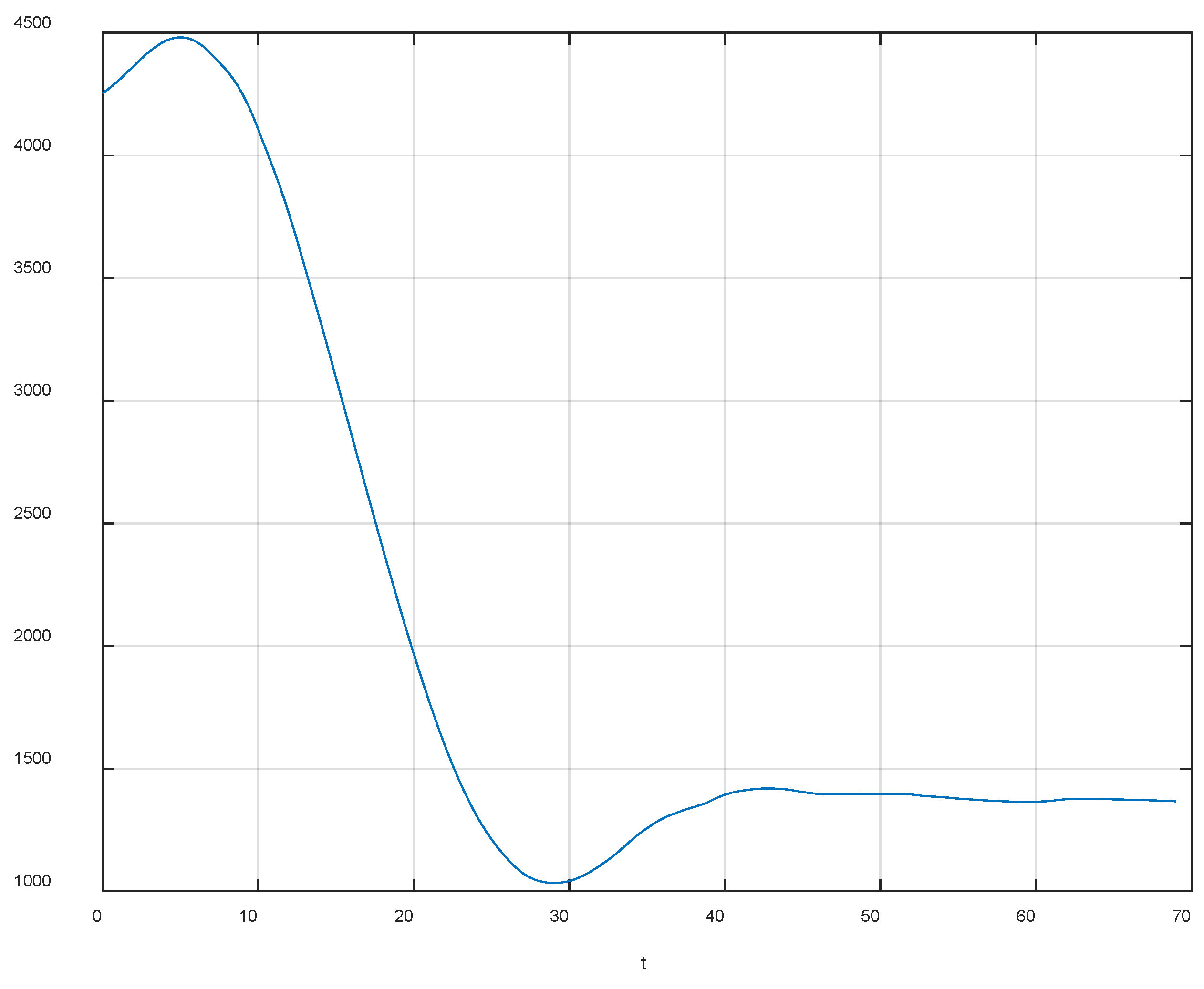
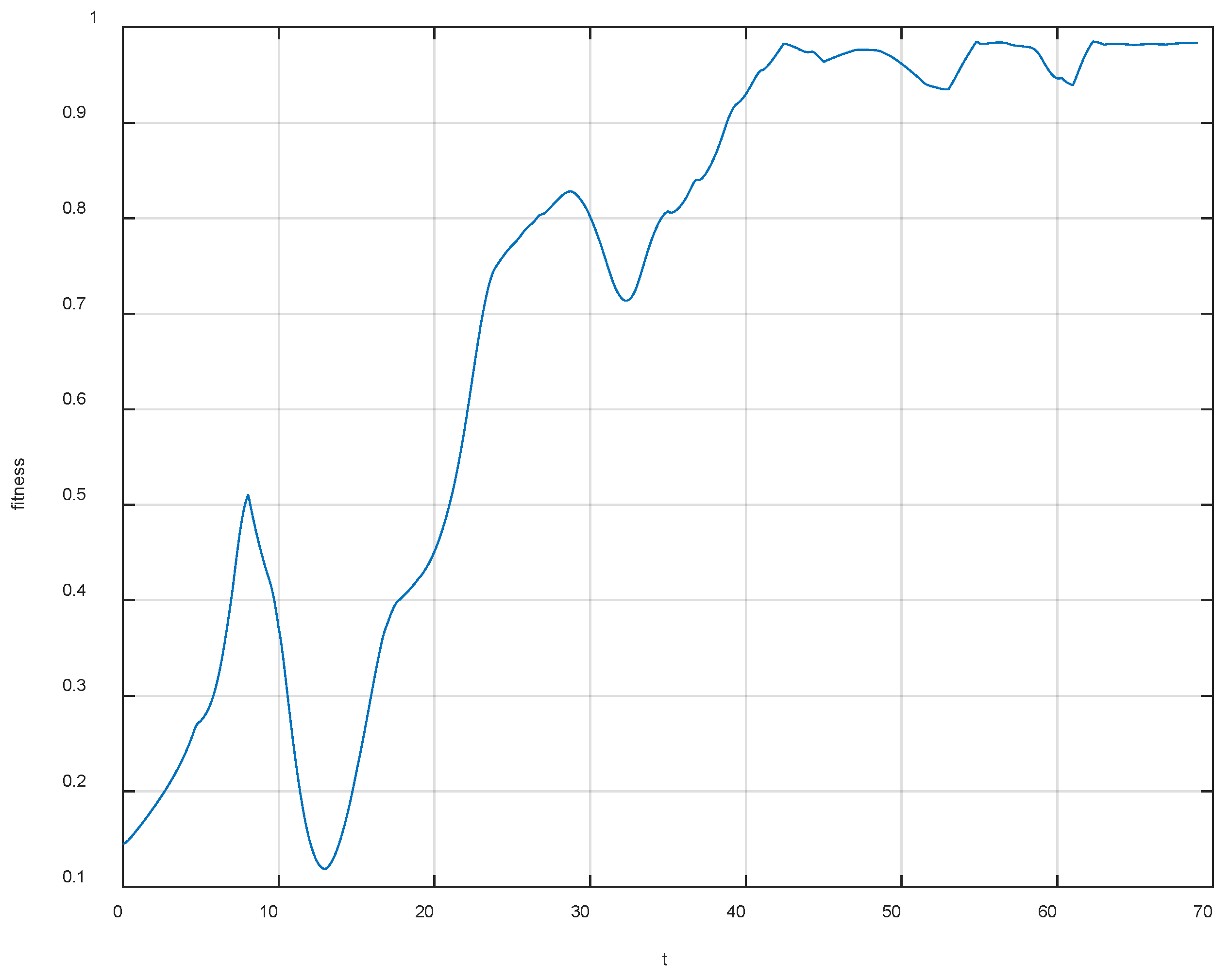
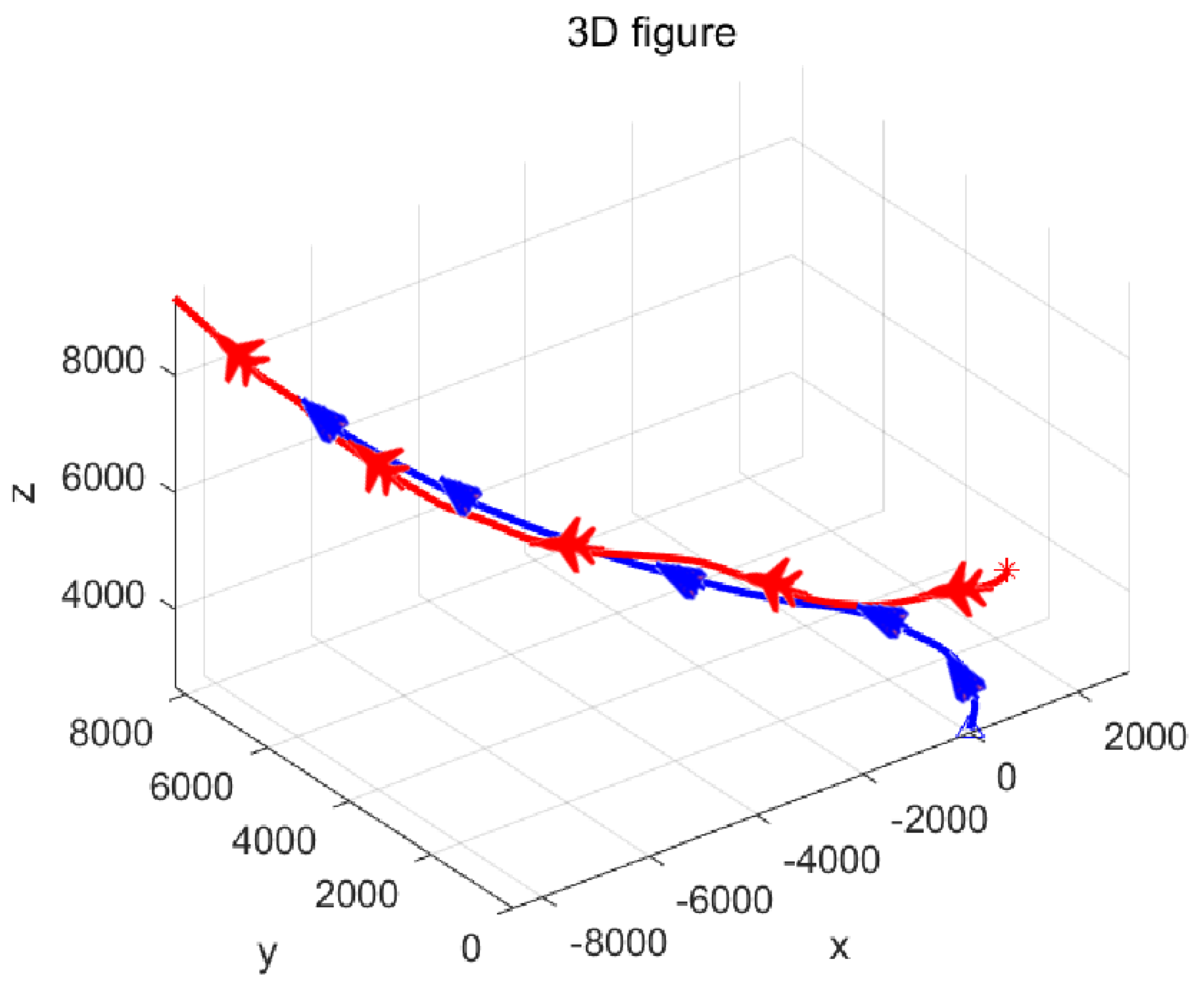
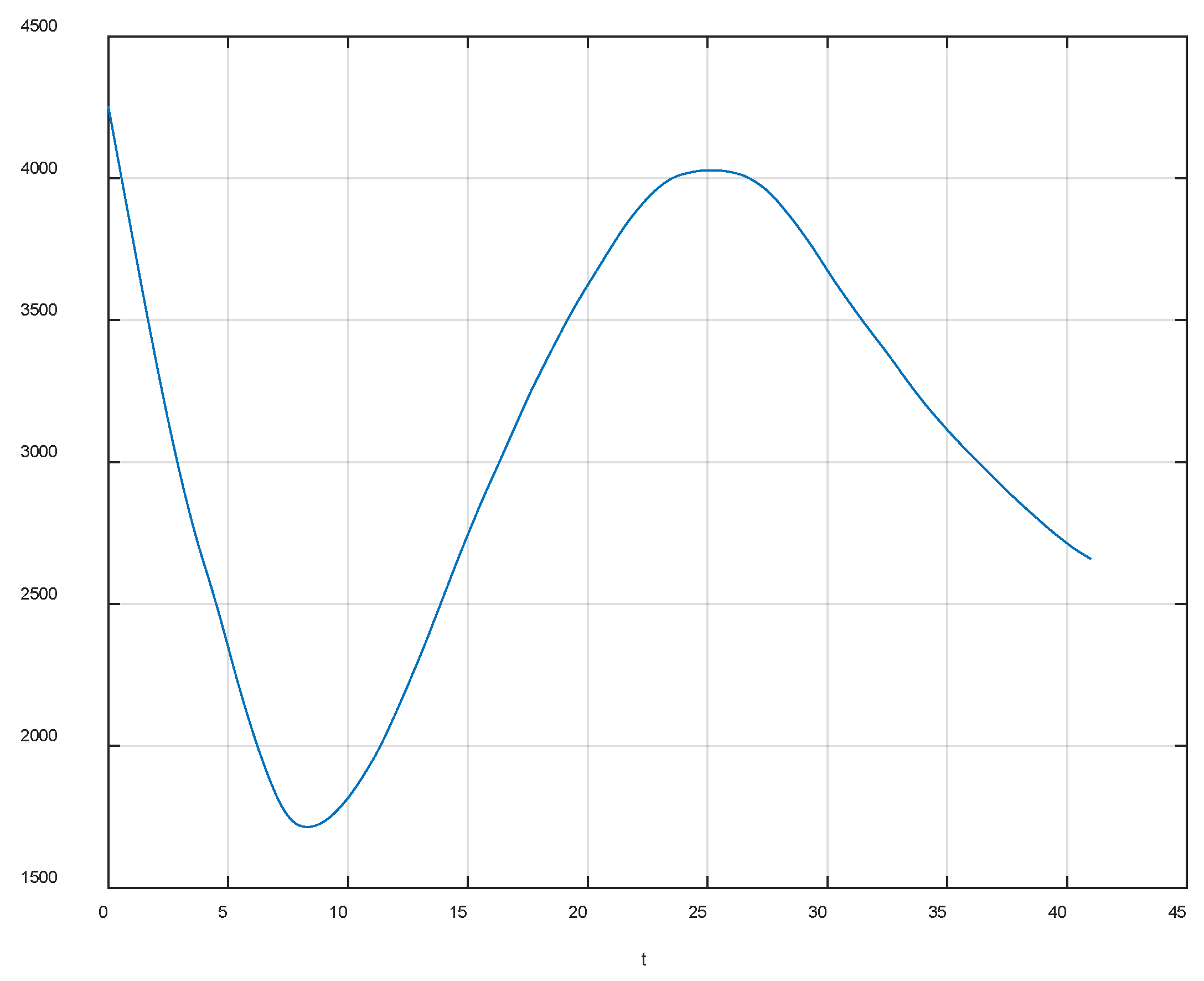
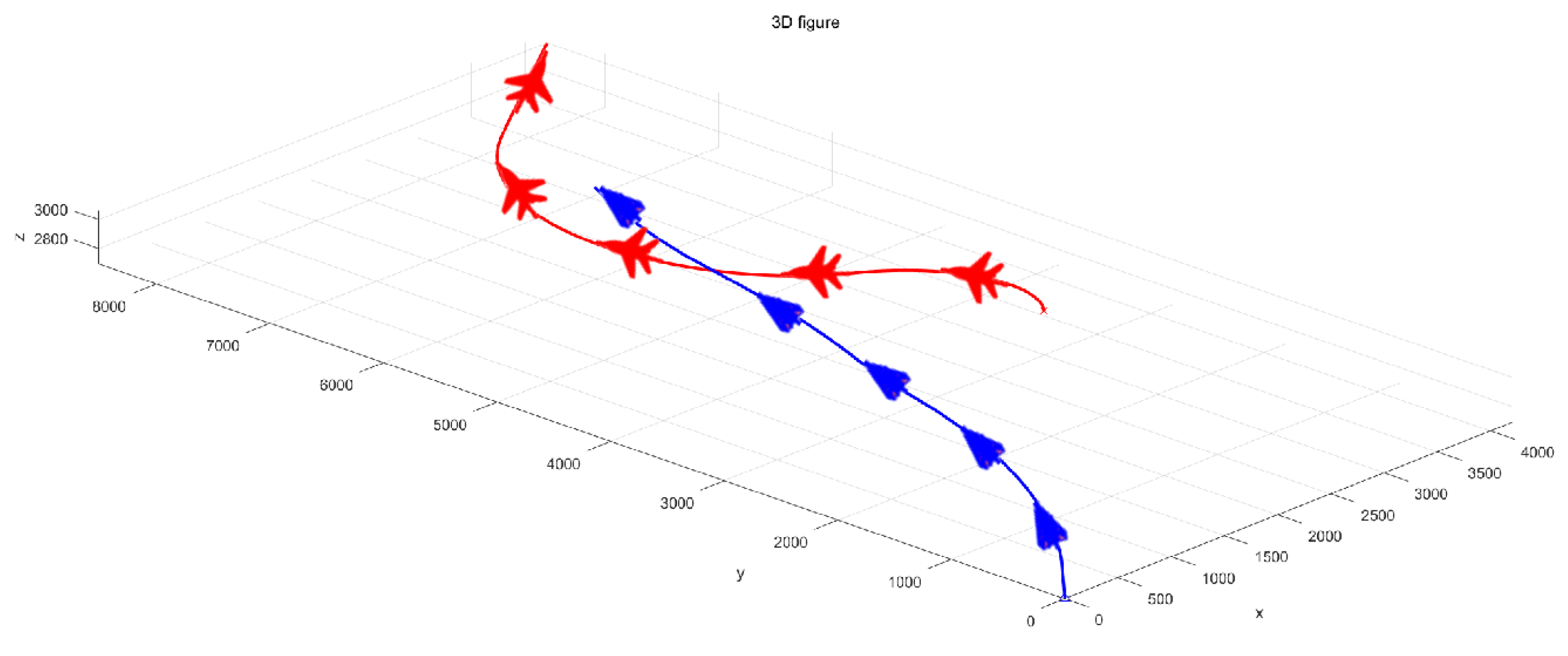
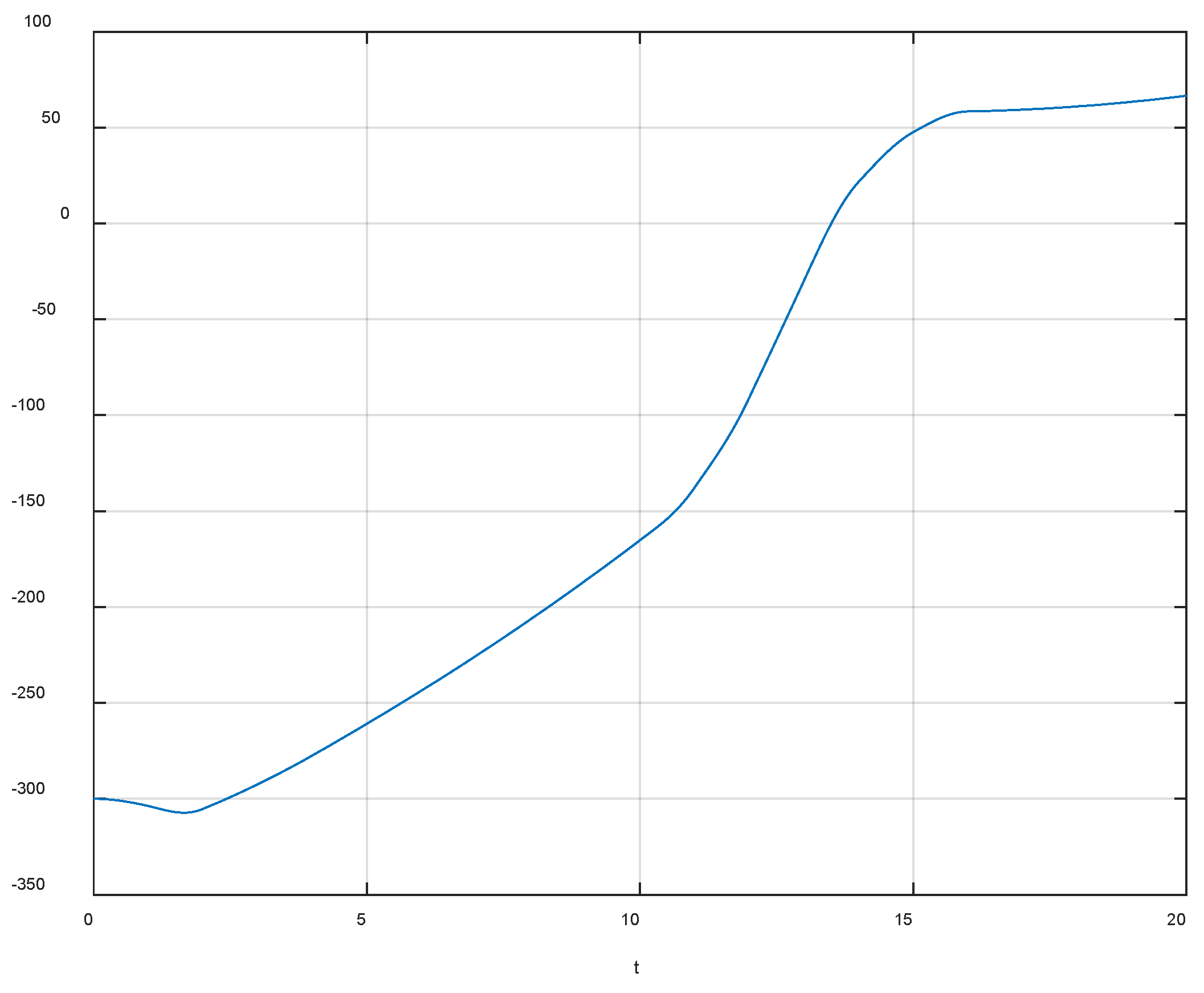
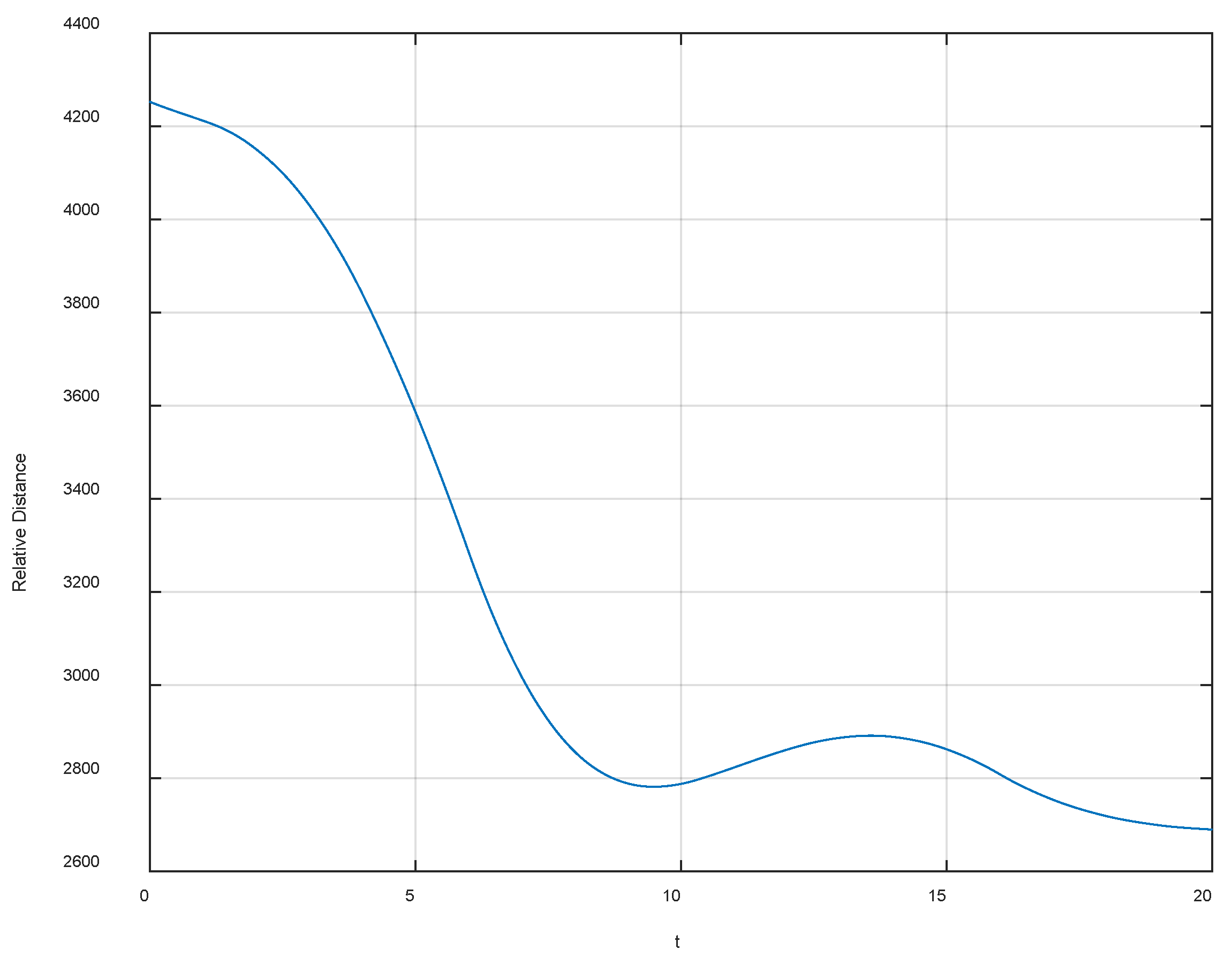
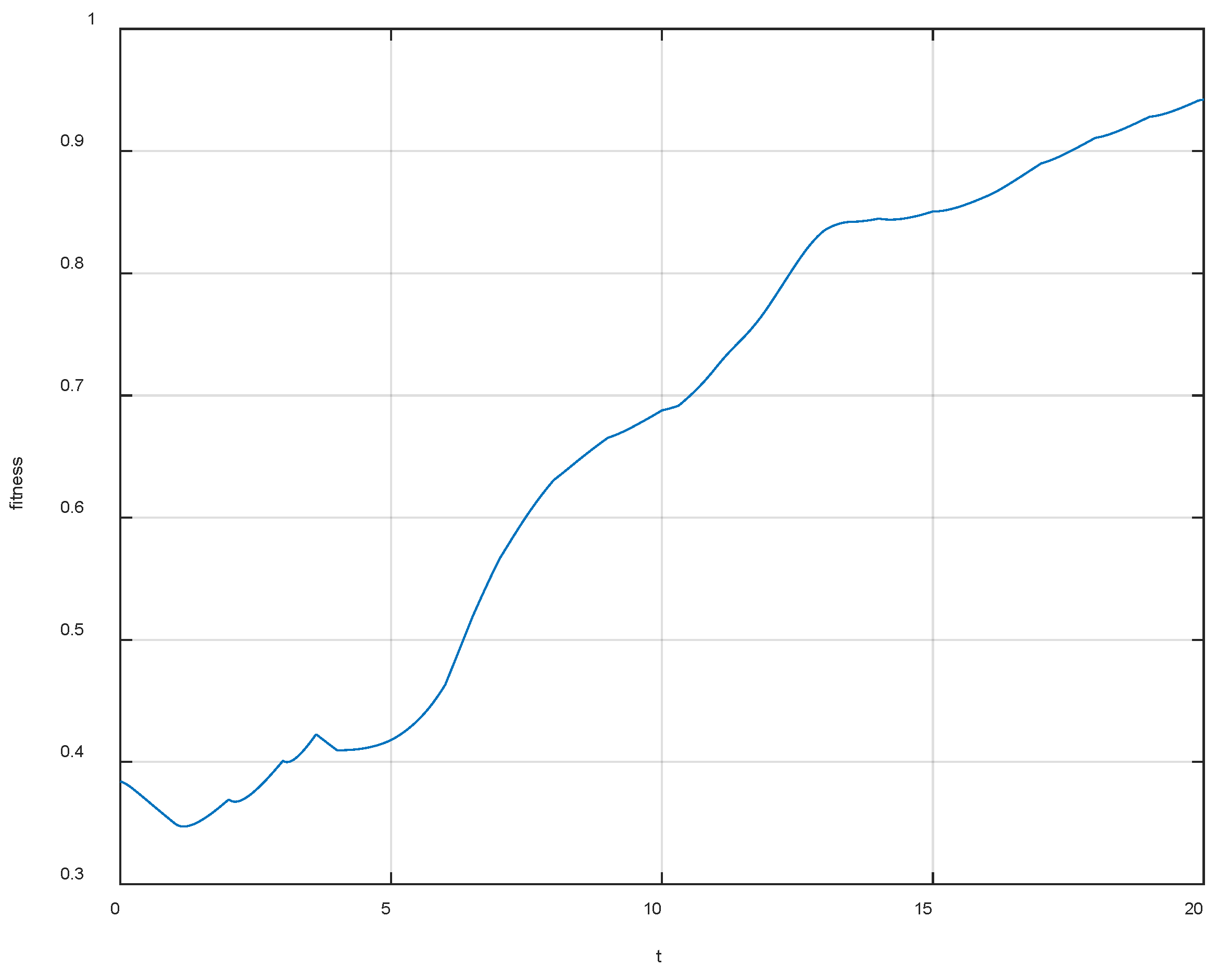
4. Simulation Example
4.1. Simulate Scenario 1
4.2. Simulation Scenario 2
4.3. Simulation Scenario 3
4.4. Simulation Scenario 3
4.5. Simulation Scenario 4
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Byrnes, M.W. Nightfall: Machine autonomy in air-to-air engagement. Air Space Power J. 2014, 28, 48–75. [Google Scholar]
- Boyd, J.R. The Essence of Winning and Losing [EB/OL]. Excerpts in Presentation Format Dated August 2010. Available online: www.dnipogo.org (accessed on 6 February 2024).
- Guierrez, L.; Vachtsevanos, G.; Heck, B. An Approach to the Adaptive Mode Transition Control of Unmanned Aerial Vehicles. In Proceedings of the American Control Conference, Denver, CO, USA, 4–6 June 2003. [Google Scholar]
- Oshman, Y.; Arad, D. Differential-game-based guidance law using target orientation observations. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 316–326. [Google Scholar] [CrossRef]
- Li, Y.F.; Shi, J.P.; Jiang, W.; Zhang, W.G.; Lyu, Y.X. Autonomous tactical decision-making of UCAVs in air combat. Electron. Opt. Control 2012, 19, 92–96. [Google Scholar]
- Nusyirwan, I.F.; Bil, C. Fatorial analysis of a real time optimization for pursuit-evasion problem. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 7 January–10 January 2008; pp. 195–198. [Google Scholar]
- Kai, V.; Janne, K.; Tuomas, R. Modeling air combat by a movinghorizon influence diagram gamel. J. Guid. Control. Dyn. 2006, 29, 1080–1091. [Google Scholar]
- Zhang, T.; Yu, L.; Zhou, Z.L.; Liu, H. Decision-making for air combatmaneuvering based on variable weight pseudo parallel genetic algorithm. Flight Dyn. 2012, 30, 470–474. [Google Scholar]
- McGrew, J.S.; How, J.P. Air combat strategy using approximate dynamic programming. In AIAA Guidance, Navigation and Control Conference; AIAA: Reston, VA, USA, 2008; pp. 1–20. [Google Scholar]
- Holsapple, R.; Baker, J.; Chandler, P.; Girard, A.; Pachter, M. Autonomous decision making with uncertainty for an urban intelligence, surveillance and reconnaissance (ISR) scenario. In AIAA Guidance, Navigation and Control Conference; AIAA: Honolulu, HI, USA, 2008; pp. 1–14. [Google Scholar]
- Trsek, R.B. The Last Manned Fighter: Replacing Manned Fighters with Unmanned Combat Air Vehicles; Air University: Montgomery, AL, USA, 2008. [Google Scholar]
- Unmanned Systems Integrated Roadmap 2013–2038; Department of Defense Office: Washington, DC, USA, 2013.
- Zhang, Y.; Li, B. Method of Target Threat Assessment Based on Cloudy MIN–MAX Center of Gravity Reasoning. J. Syst. Simul. 2014.
- Pal, M.; Foody, G.M. Feature selection for classification of hyperspectral data by SVM. IEEE Trans Geosci. Remote Sens. 2010, 48, 2298–2306. [Google Scholar] [CrossRef]
- Li, D.; Liu, C. Artificial Intelligence with Uncertainty. J. Softw. 2004, 15, 1583–1594. [Google Scholar]
- Liu, C.; Li, D.; Pan, L. Uncertain Knowledge Representation Based on Cloud Model. China Acad. J. Electron. Publ. House 2004. Available online: https://kns.cnki.net/kcms2/article/abstract?v=1TlORdBtwpYgencVCuvvBoki1Q3pPZgmjRHnAxGpExtgyYArBFpC_Rb9EuyqtOdnbk80dN3QJSiZOEZz6B8IFUta7Fkj_Eze1MaMpiE8JF_JYeO2Yt11AkoUFPUqmsj4rOdIJEadQD0=&uniplatform=NZKPT&language=CHS (accessed on 6 February 2024).
- Studer, R.; Benjiamins, V.R.; Fensel, D. Kmowledge engineering: Principles and methods. Dataknowl. Eng. 1998, 161–197. [Google Scholar]
- Montani, S. Case based representation and retrieve with Time dependant features. In International Conference on Cased Based Reasoning; Springer: Berlin/Heidelberg, Germany, 2005; pp. 353–367. [Google Scholar]
- Jurisica, I. Data mining for case-based reasoning in high-dimensional biological domains. IEEE Trans. Knowl. Data Eng. 2005, 17, 1127–1137. [Google Scholar]
- Hoffren, J.; Sailaranta, T. Maneuver Autopilot for Realistic Performance Model Simulations. In Proceedings of the AIAA Modeling and Simulation Technologies Conference and Exhibit, Montreal, QC, Canada, 6–9 August 2001. AIAA-2001-4376.2001. [Google Scholar]
- Austin, F. Automated maneuvering decisions for air-to-air combat. In Proceedings of the Guidance, Navigation and Control Conference, Monterey, CA, USA, 17–19 August 1987; pp. 659–669, AIAA Paper 87-2393. [Google Scholar]
- Liu, X. Study on Maneuver Decision and Control in Automatic Air Combat Simulation. Master’s Thesis, Northwestern Polytechnical University, Xi’an, China, 2006; pp. 15–30. [Google Scholar]
- Richardson, M. Markov logic networks. Mach. Learn. 2006, 62, 107–136. [Google Scholar] [CrossRef]
- You, L.; Liu, T.; Liu, K. Chinese frame net and OWL representation. In Proceedings of the 6th International Conference on Advanced Language Processing and Web Information Technology, Luoyang, China, 22–24 August 2007. [Google Scholar]
- Mazurkiewicz, A. Petri net languages revisited. Theor. Comput. Sci. 2012, 45, 459–467. [Google Scholar] [CrossRef][Green Version]
- Salameh, W.A. Detection of intrusion using neural networks: A customized study. Stud. Inform. Control 2004, 30, 135–143. [Google Scholar]
- Zhang, Q. Dynamic uncertain causality graph for knowledge representation and reasoning: Discrete DAG cases. J. Comput. Sci. Technol. 2012, 27, 1–23. [Google Scholar] [CrossRef]
- Day, M.Y.; Tsai RT, H.; Sung, C.L.; Hsieh, C.-C.; Lee, C.-W.; Wu, S.-H.; Wu, K.-P.; Ong, C.-S.; Hsu, W.-L. Reference metadata extraction using a hierarchical knowledge representation framework. Decis. Support Syst. 2007, 43, 152–167. [Google Scholar] [CrossRef]
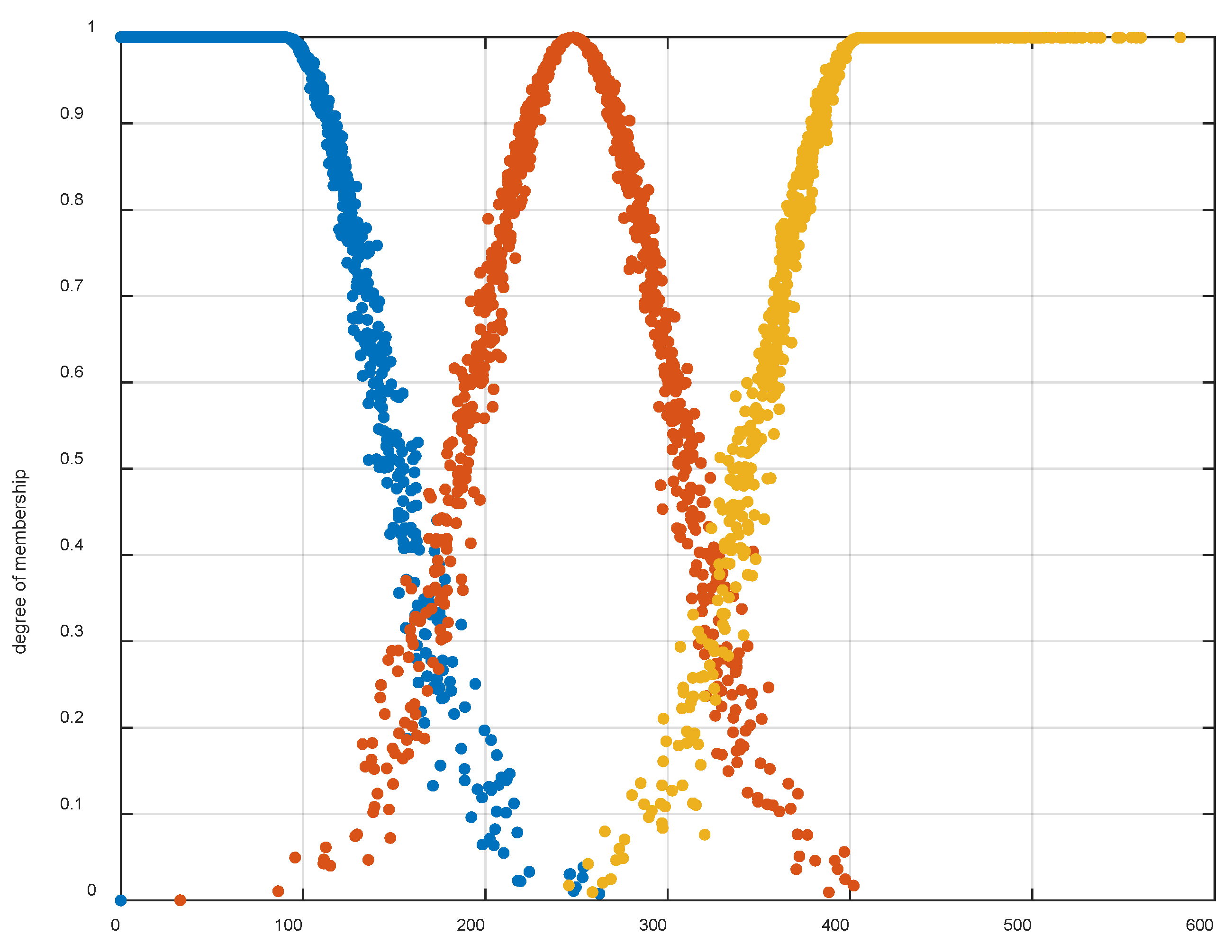
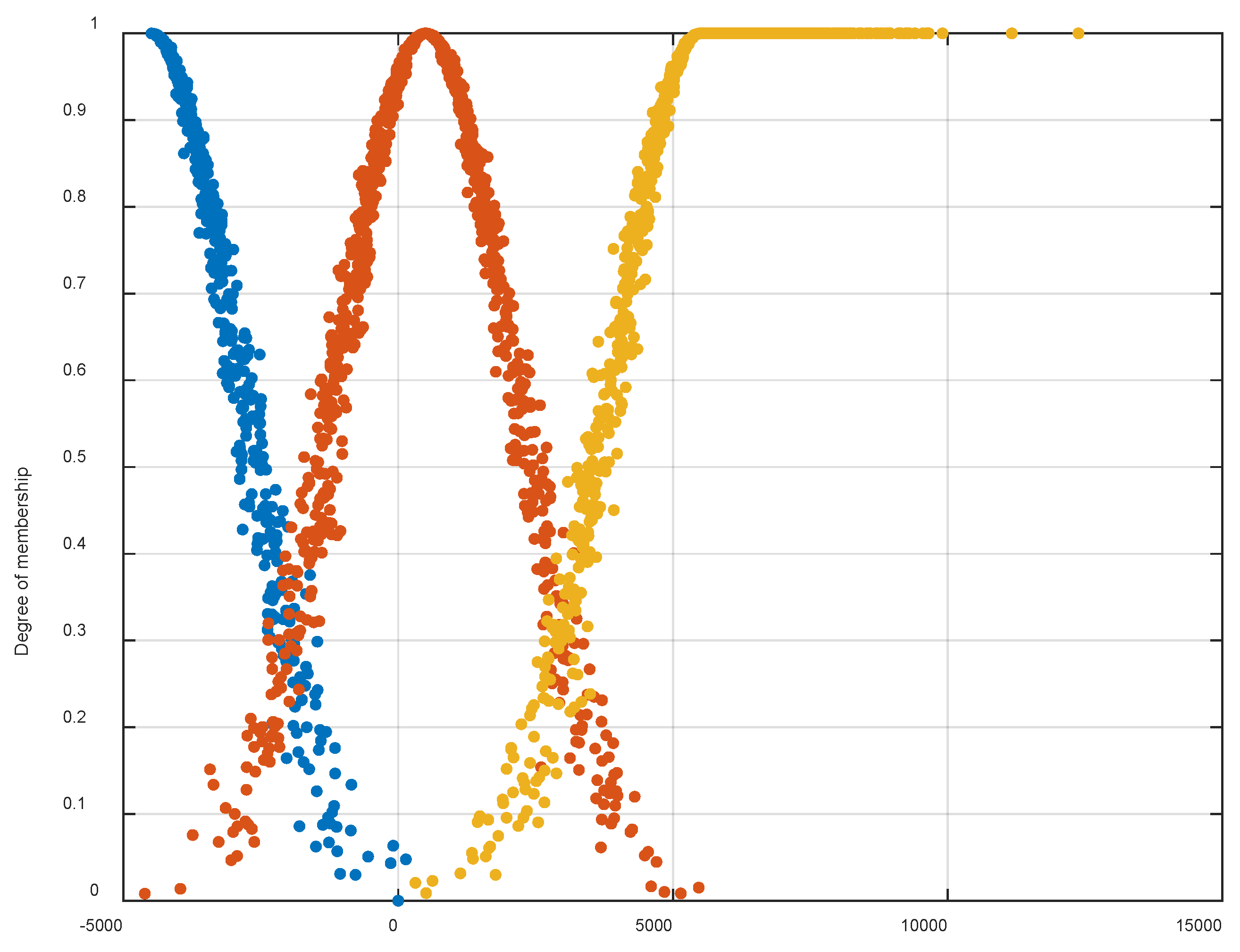

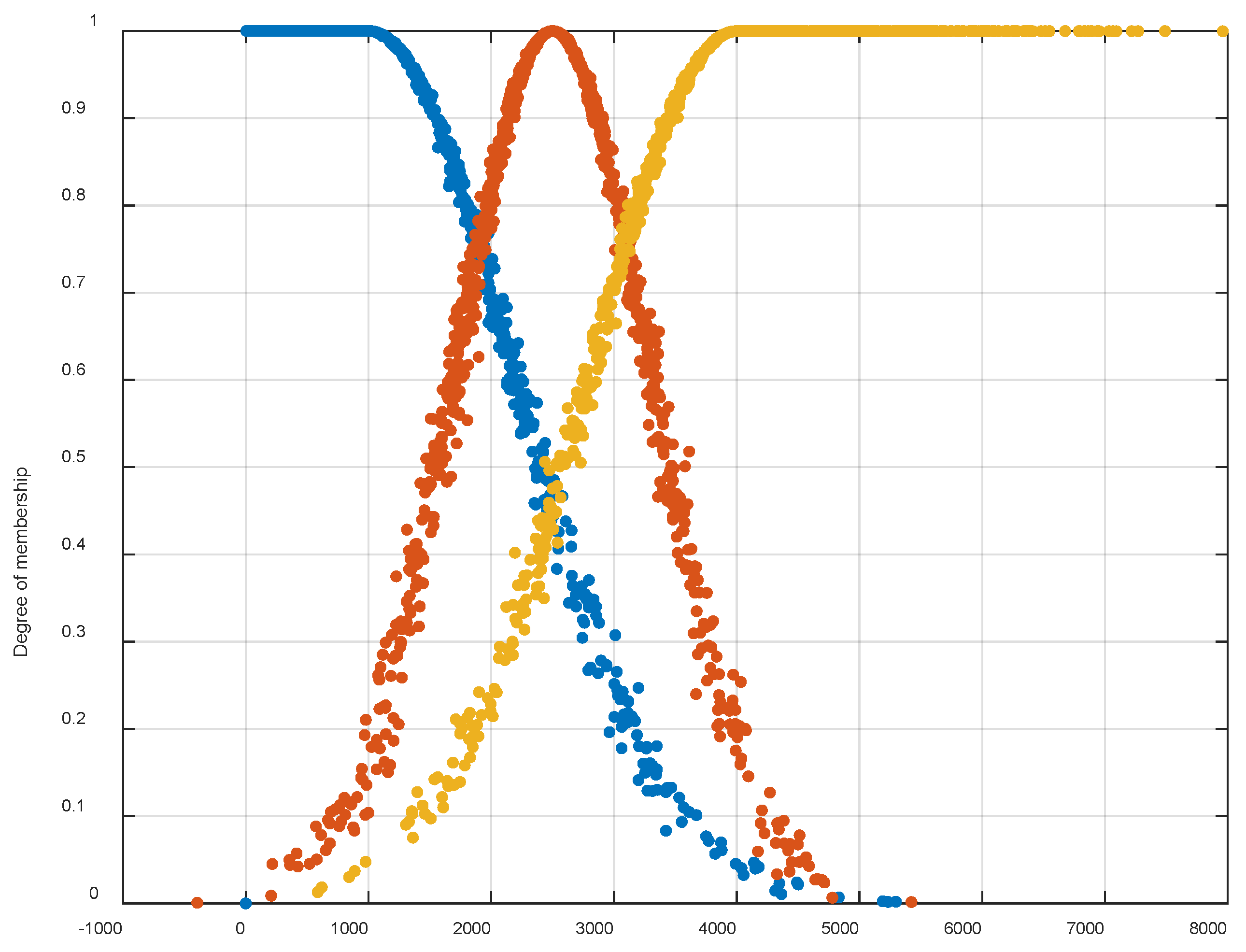





| Left turn | |||||
| Acceleration | |||||
(Rapid climb) | (Constant-velocity flight) | (Fast dive) | |||
(Swooping down) | (Climb) | (Horizontal plane) | |||
| taper | taper | ||||
| 1 Left turn, acceleration, and rapid climb | 2 Left turn, acceleration, and constant dive | 3 Left turn, acceleration, and constant climb | 4 Horizontal acceleration and left turn | 5 Left turn, acceleration, and fast dive | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Weng, W.; Zhou, H.; Jiang, Z.; Dong, Y. Maneuvering Decision Making Based on Cloud Modeling Algorithm for UAV Evasion–Pursuit Game. Aerospace 2024, 11, 190. https://doi.org/10.3390/aerospace11030190
Huang H, Weng W, Zhou H, Jiang Z, Dong Y. Maneuvering Decision Making Based on Cloud Modeling Algorithm for UAV Evasion–Pursuit Game. Aerospace. 2024; 11(3):190. https://doi.org/10.3390/aerospace11030190
Chicago/Turabian StyleHuang, Hanqiao, Weiye Weng, Huan Zhou, Zijian Jiang, and Yue Dong. 2024. "Maneuvering Decision Making Based on Cloud Modeling Algorithm for UAV Evasion–Pursuit Game" Aerospace 11, no. 3: 190. https://doi.org/10.3390/aerospace11030190
APA StyleHuang, H., Weng, W., Zhou, H., Jiang, Z., & Dong, Y. (2024). Maneuvering Decision Making Based on Cloud Modeling Algorithm for UAV Evasion–Pursuit Game. Aerospace, 11(3), 190. https://doi.org/10.3390/aerospace11030190







