Topology Optimization of a Single-Point Diamond-Turning Fixture for a Deployable Primary Mirror Telescope

Abstract

CubeSats, known for their compact size and cost effectiveness, have gained significant popularity. However, their limited size imposes restrictions on the optical aperture and, consequently, the Ground Resolution Distance in Earth Observation missions. To overcome this limitation, the concept of deployable optical payloads with segmented primary mirrors which can unfold like petals has emerged, enabling larger synthetic apertures and enhanced spatial resolution. This study explores the potential benefits of leveraging Additive Manufacturing (AM) and Topology Optimization (TO) in the realm of ultra-precision machining, specifically single-point diamond machining. The goal is to reduce fixture weight while improving stiffness to minimize deformations caused by rotational and cutting forces which compromise optical performance. Through Finite Element Analysis, this research compares conventionally machined fixtures with those produced using AM and TO techniques. The results reveal that concept designs created via TO can achieve a remarkable 68% reduction in weight. This reduction makes the assembly, including the machining fixture and 12 U deployable segments, manageable by a single operator without the need for specialized lifting equipment. Moreover, these innovative designs lead to substantial reductions of up to 86% and 51% in deformation induced by rotational and cutting forces, respectively.

1. Introduction

With the availability and lower cost of small satellite platforms such as CubeSat, there has been a constant effort among the instrumentation community to miniaturize all the components, including the optical payload, to fit in the confined space defined by the elementary CubeSat Unit (U) 10 × 10 × 10 cm in a platform ranging from 1 U up to 16 U. However, the limited size of the platform also restricts the optical aperture of the payload, which in turn limits the achievable Ground Resolution Distance (GRD), a key parameter in Earth Observation (EO) missions. Diffraction and sensor pixels’ size, when projected on the ground, contribute to the GRD. The diffraction is only defined by the aperture diameter, orbital altitude, and the wavelength. A 1 U or 3 U CubeSat with a 10 cm aperture diameter in a Low Earth Orbit (500 Km), working in the visible region at a 500 nm wavelength, will deliver at least a GRD of 3 m, while a 12 U with a 20 cm aperture diameter typically achieves a 1.5 m GRD.

Considering the launch cost scale with the spacecraft mass and volume [1], an optical payload with a deployable optics and telescope therefore becomes an attractive concept to benefit from lower launch platform costs, without compromising on the telescope aperture size. A space telescope equipped with a deployable primary mirror can, in principle, recreate, with actuated individual segments, a larger synthetic aperture than the launch vehicle size, enabling higher spatial resolution than what a non-deployable telescope would have delivered.

Historically, the James Webb Space Telescope remains the only deployable telescope currently in operation [2]. Its successful launch and operation have confirmed the viability and potential of deployable optics in space. Efforts are now being made to adapt this principle to smaller, more cost-effective platforms, such as CubeSats. Various design proposals and associated alignment concepts have been detailed in recent publications. In [3,4], concepts of a deployable secondary mirror mechanism have been described, with an extendable barrel linking the primary and secondary mirrors. In [5], a deployable primary mirror composed of four petals reconstruct a 1.5 m diameter aperture. A phasing concept for the four segments is also described, maximizing the image sharpness metric. In [6], a mechanical design of a large non-imaging deployable telescope is described. In [7], a 200 mm diameter synthetic primary mirror deployed from a 1 U CubeSat bus is described along with the holographic method to phase the three segments together using laser point sources In [8], an advanced concept of a 300 mm synthetic primary mirror fitting in a 1.5 U CubeSat space enveloped is described with the phasing principle. The paper also gives a preliminary conceptual design for a deployable secondary mirror. In [9], a similar concept is extended to a 6 U platform.

Topology Optimization (TO) and Additive Manufacturing (AM) have gained increasing prominence as tools for designing and directly 3D printing optics [10,11,12,13,14]. Furthermore, the application of this technology shows great potential in enhancing ultra-precision machining. The potential advantages they bring include faster prototyping, increased design flexibility, reduced material waste, and the ability to create complex geometries that were previously unattainable. When machining the optical surfaces of deployable primary mirrors, two distinct strategies can be considered:

The first strategy involves machining each segment independently and sequentially ‘on-axis’, with the blank centered on the polishing or diamond-turning spindle axis, and the tool describing the equivalent freeform component of the off-axis segment with three synchronized axes. The second option is to machine the four segments in their operational position, forming the synthetic aperture in its deployed configuration. This configuration offers several advantages:

• it is faster, as all segments are machined in one go rather than sequentially as in the first option;
• it requires fewer axes, thereby minimizing potential sources of error;
• it presents a primary mirror arrangement identical to the operational configuration, thus facilitating post-machining metrology when the mirrors are phased together.

However, the main drawback of this off-axis configuration is that the assembly could become large and heavy, making it challenging for a single operator to handle. Additionally, there may be specific limitations, especially with large diameters, related to possible distortion induced by rotational forces on an ultra-precise lathe.

This paper focuses on the design aspects of a machining fixture and conducts a comparative analysis of the advantages offered by AM and TO when compared to a Conventionally Machined (CM) fixture. Both types of fixtures (AM and CM) are intended for use with a single-point diamond-turning ultra-precise lathe. They have been specifically designed to accommodate four identical segments, each with dimensions of approximately 200 × 200 mm and a mass of around 1 kg. These segments, when deployed, collectively form a synthetic aperture with a diameter of $\varphi$ 600 mm. Our findings highlight the advantages of AM and TO, offering a fresh perspective on fixture design.

The folded segments fit within a 16 U CubeSat structure, with a 12 U volume nominally allocated for the optical system and an additional 4 Units (4 U) for potential avionics and satellite bus systems.

To assess the effectiveness of the proposed improvements, both the CM and AM designs are evaluated using Finite Element Analysis (FEA) against three requirements:

• The mass of the fixture;
• The deformation induced by the rotational force during machining;
• The deformation induced by the diamond tool cutting.

In the following section, we describe the conventional design fixture case study and provide background information about the modeling of rotational and cutting forces. In Section 3, we detail the topology optimization parameters, including the starting design and the boundary constraints applied during the optimization process. Moving on to Section 4, we present the results of two AM designs and discuss their performance improvements compared to the CM design. Finally, in Section 5, we engage in a discussion of the results and the opportunities they offer for future high-precision machining of large, segmented apertures.

2. Case Study—Conventional Fixture

The objective of a machining fixture is to accurately position and securely hold the four segments, which collectively form a rotationally symmetrical master surface, in their designated locations. Additionally, the fixture must ensure a reliable interface transfer between the off-axis segments and the backing plate.

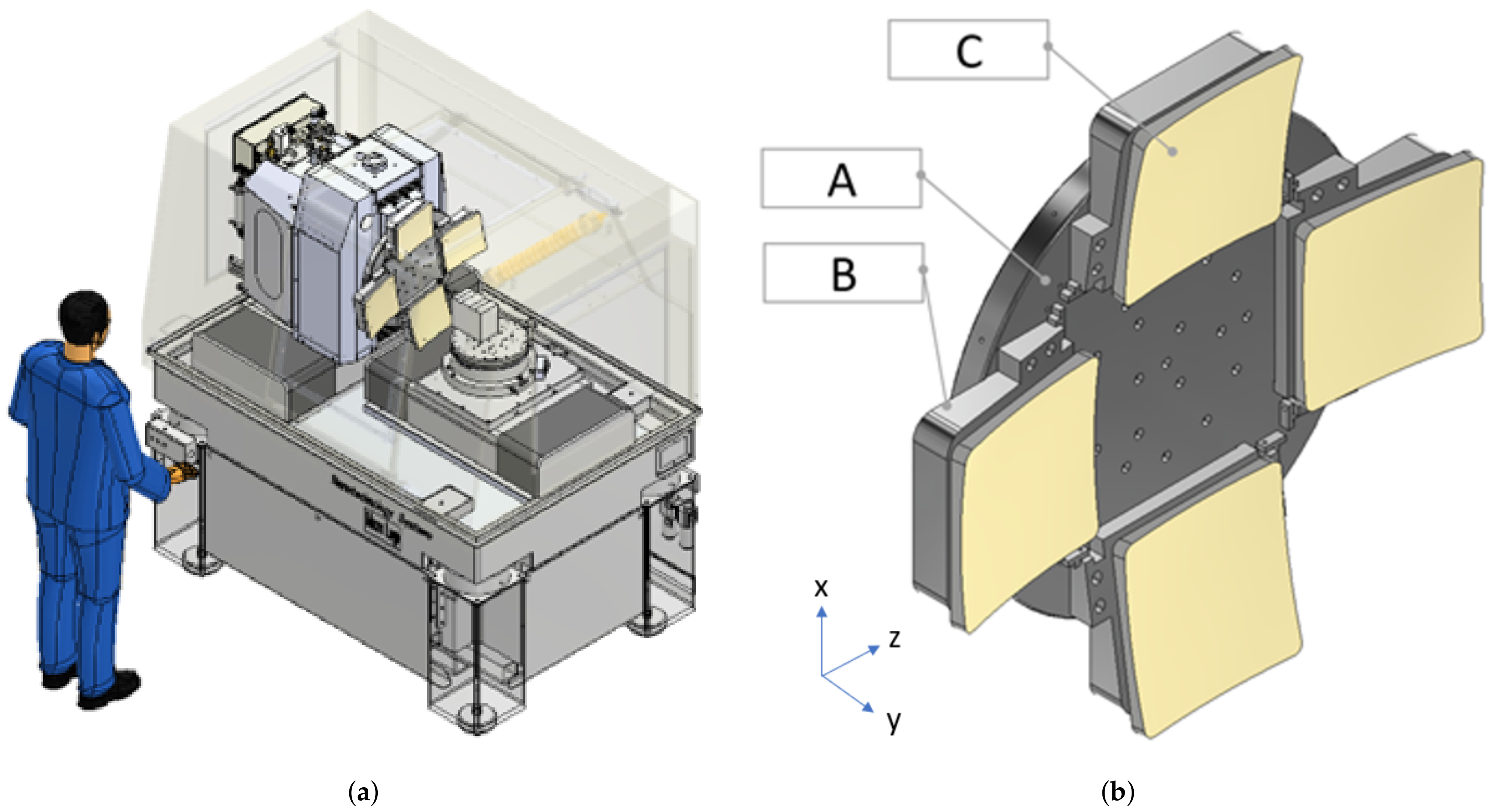
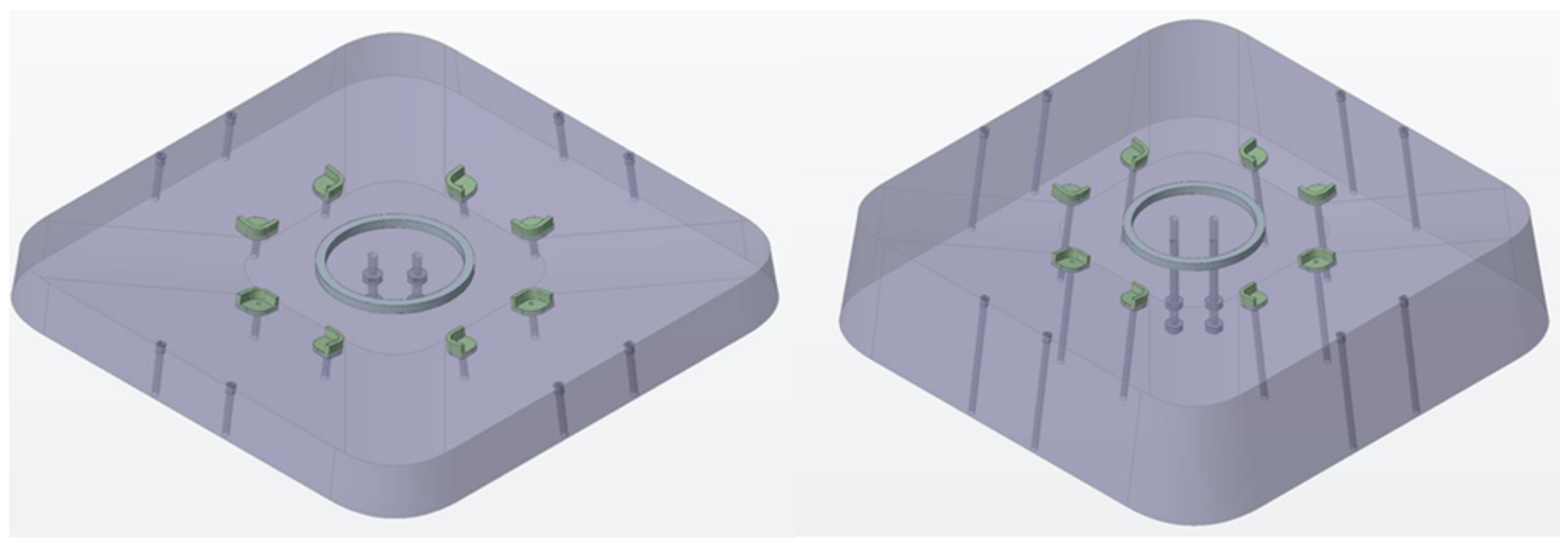
To accomplish this, the conventionally designed fixture, depicted in Figure 1, comprises three discrete components:

• Part A: The backing plate, which is affixed to the machine spindle via the central set of counterbored holes.
• Part B: Removable wedges that serve to connect the mirror segments to the backing plate. These wedges also adjust the tilt of the segments according to their off-axis values and can be positioned in the X and Z directions via shims (Axis labels differ from the conventional machine ones; instead, they align with the FEA conducted in Section 4).
• Part C: The four individual segments themselves.

Figure 1. (a) Example of a conventional fixture during machining on a Moore Nanotech 350FG at the Centre for Advanced Instrumentation at Durham University. (b) Conventional machining fixture composed of three elements. Element A is the backing plate, B are four wedges used to apply the off-axis angle on each segment and finely position each mirror on the backing plate, and C are the four segments.

Figure 1. (a) Example of a conventional fixture during machining on a Moore Nanotech 350FG at the Centre for Advanced Instrumentation at Durham University. (b) Conventional machining fixture composed of three elements. Element A is the backing plate, B are four wedges used to apply the off-axis angle on each segment and finely position each mirror on the backing plate, and C are the four segments.

As the layout of the four segments has been designed with the constraint of maintaining a thin profile to fit within the limited space of the platform, their rear faces have been aligned parallel to the tangential plane to the center of the aperture. Consequently, the use of wedges becomes necessary to compensate for this tilt. The presence of this tilt, which complicates the interface and introduces possible sources of misalignment, justifies the use of TO and its associated benefits.

2.1. Mechanical Target Requirements

The list of requirements, which defines the design objectives, is given in

Table 1. Design objectives of the fixture.

Requirement Type	Target Requirement
Mass of assembly excluding mirrors	<15 Kg
Deformation induced by centrifugal force at 400 RPM	as low as possible 1
Deformation induced by cutting forces of 10 N	as low as possible 1

¹ This requirement should be in line with the residual wavefront error requirement of the optics or telescope and should be informed via a proper tolerance analysis.

.

The first requirement concerns the mass of the fixture, stipulating that it should not exceed 15 kg. This specification underscores the need for the fixture to be lightweight enough to be easily lifted onto the spindle of the machine by an operator, without relying on a crane. Since the part is machined in a vertical position as shown on Figure 1, a heavier mass imposes additional load (bending moment) on the spindle. This increased load can potentially limit the spindle’s rotational speed, thereby extending the overall machining time. Moreover, a greater weight distributed over a larger diameter amplifies the moment and, consequently, the centrifugal force. This increase in centrifugal force induces displacements on the part during machining that give rise to form errors in the recovered mirror shape when the part is removed from the machine; hence, it is the second requirement to minimize these forces. 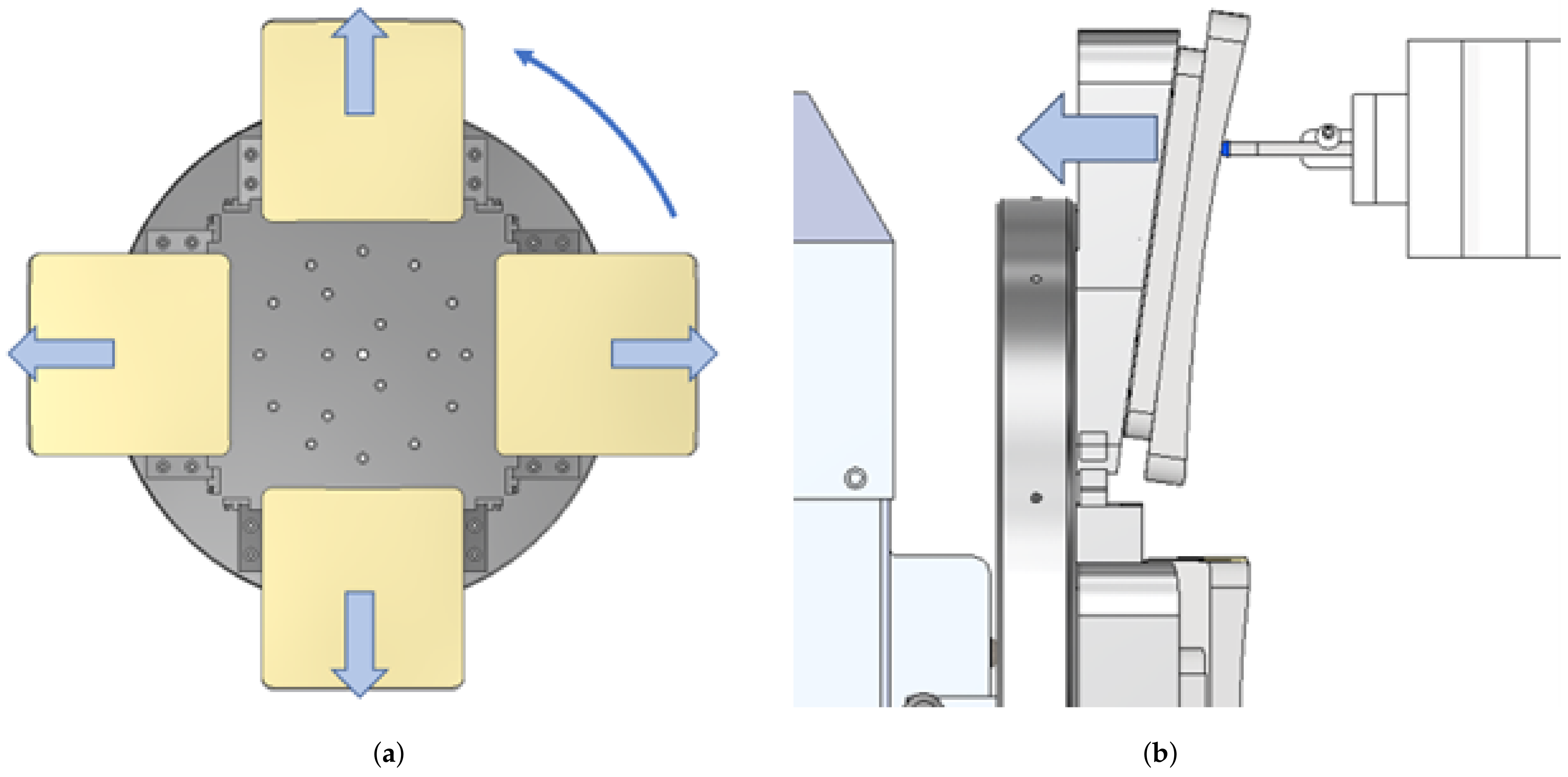Figure 2a provides a visual representation of the force vectors applied to each segment during the machining process. The centrifugal force acting on an object can be expressed using the following equation:

$$F_{rotation}={\omega }^2·r·m,$$

(1)

Here, $\omega$ represents the rotational speed in radians per second (rad/s), r signifies the distance from the object to the axis of rotation, and m denotes the mass of the object. While the primary force is applied radially to the segment, it is anticipated that a substantial portion of this force will translate into a component along the spindle axis due to the overhang of the wedges. This localized load will induce surface deformations on the mirror, similarly to the cutting force and shown on Figure 2b, governed by Hooke’s law, with surface displacement varying linearly with the applied force:

$$F_{cutting}={\displaystyle \frac{\Delta L}{L}}·A·E,$$

(2)

In this equation, $\Delta L$ represents the surface displacement, L stands for the thickness of the part where the force is applied, A denotes the surface area on which the force is exerted, and E signifies the modulus of elasticity. Consequently, the surface displacement along the spindle axis ($ϵ$) can be understood as both (i) a linear function of the tool cutting force:

$${ϵ}_{cutting}={\displaystyle \frac{\Delta L}{L}}\propto F_{cutting},$$

(3)

and (ii) a quadratic function of the rotational speed:

$${ϵ}_{rotation}={\displaystyle \frac{\Delta L}{L}}\propto {\omega }^2·r·m,$$

(4)

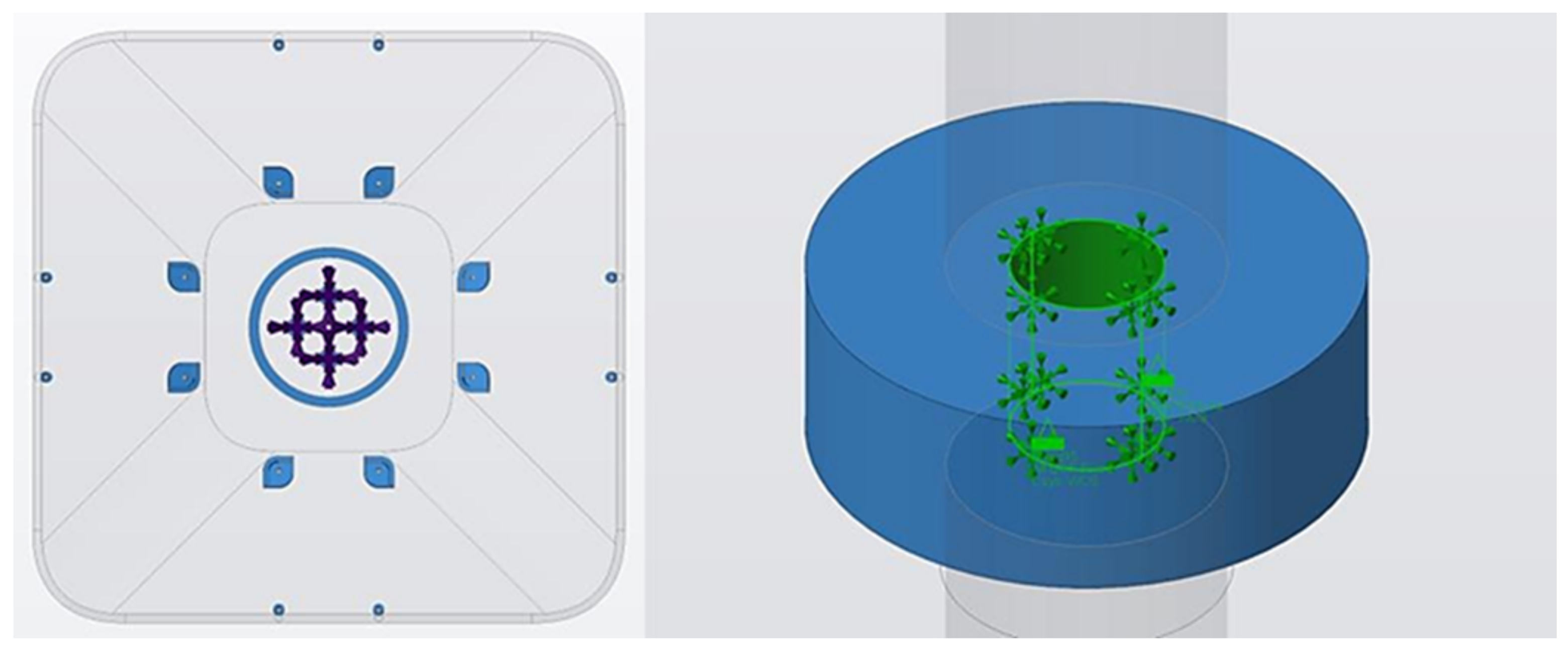
Figure 2. (a) Direction of the force induced by centrifugal force when the fixture rotates at high speed. (b) Diamond tool exerting a cutting force on the segment and machining fixture.

Figure 2. (a) Direction of the force induced by centrifugal force when the fixture rotates at high speed. (b) Diamond tool exerting a cutting force on the segment and machining fixture.

2.2. Finite Element Analysis Parameters

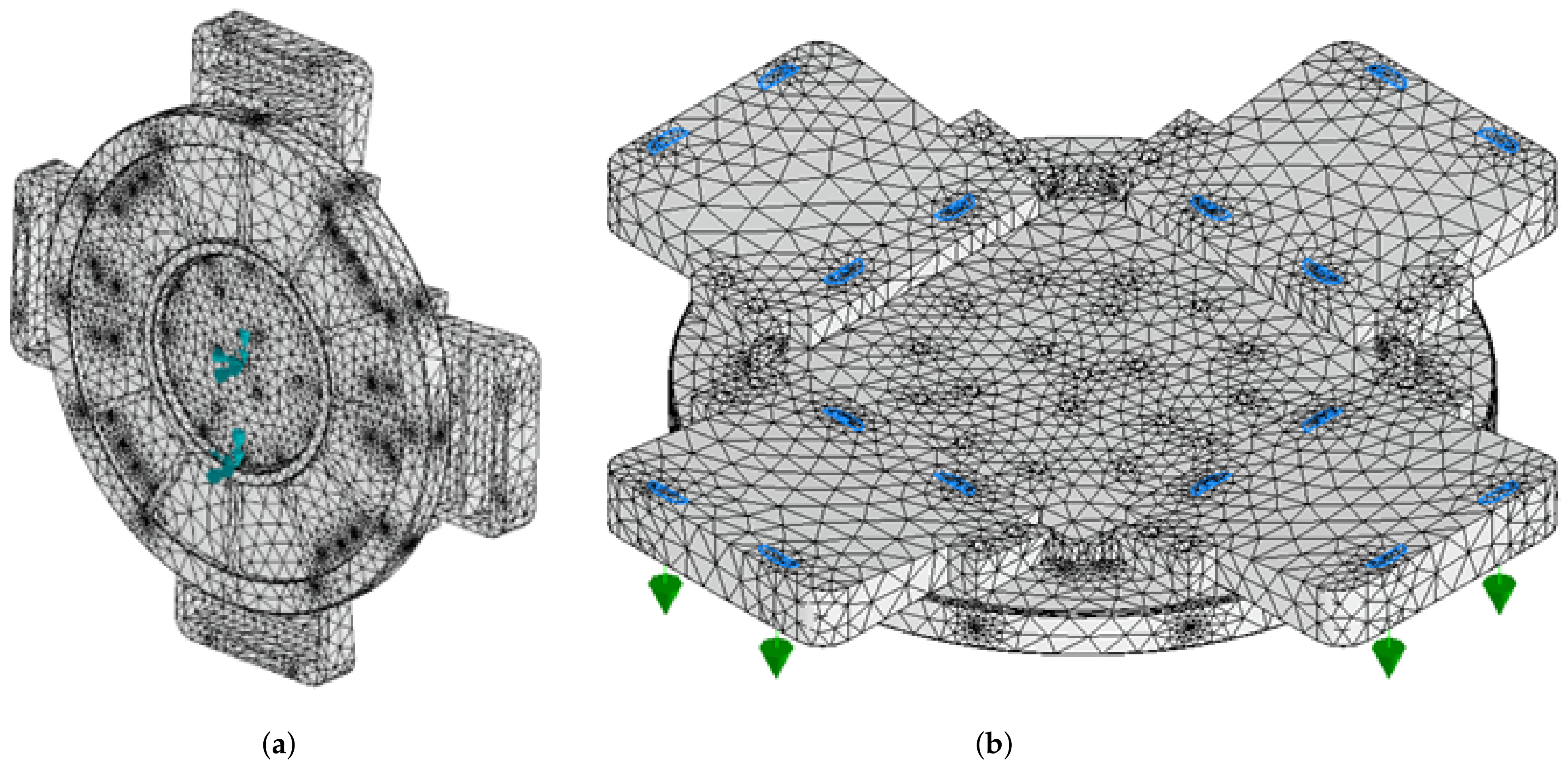
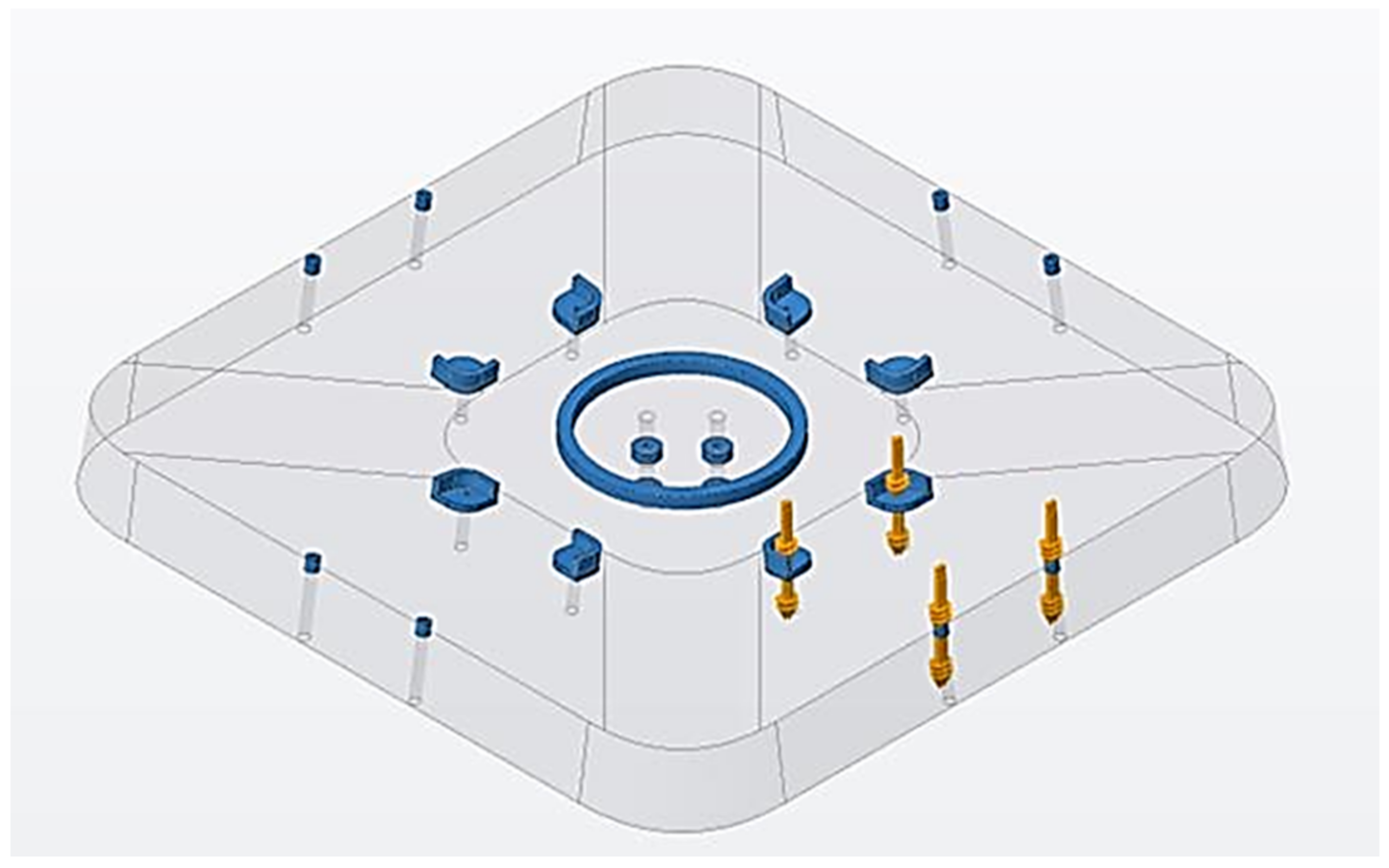
FEA using Nastran [15] was used to simulate the displacement occurring on the mating faces of the fixture subjected to stress from both cutting and rotational forces. We isolated a single body part from the assembly file to simplify the transfer of deformations from the backing plate to the wedges. A mesh with element sizes of 20 mm was generated for the analysis. Fixed constraints were imposed on the bore located on the rear face of the fixture and the face in contact with the spindle, as illustrated in Figure 3a. To represent the cutting force, a 10 N load was applied along the spindle axis to the 16 raised pads situated on top of the wedges, as depicted in Figure 3b.

The cutting force, as described by [16], is directly linked to the chip area and is influenced by parameters such as the depth of the cut, tool radius, and feed rate. Further investigation has revealed that tool quality and wear also play a significant role in determining the tool force [17]. Typical cutting forces have been measured to range between 0.1 N and 1 N in the spindle’s axis of rotation. We used a value of 10 N in our simulation, applying a safety factor. Equation (3) demonstrates that due to the linear relationship between displacement and force, the displacement results can be scaled proportionally when using a different cutting force.

In a similar manner to the approach followed by [18], we modeled the rotational forces applied to the fixture in Nastran using a rotation force and a velocity of 7 rev/s. It is important to note that the modeling focused exclusively on the fixture, without considering the mirror segments, in order to isolate only the fixture’s contribution.

When defining the structural material parameters, a representative material with a mass density of 2.7 g/cm³. and an Elastic Modulus of 68 GPa was selected as the material for both CM and AM cases. It is worth noting that alloys commonly used in AM, such as AlSi10Mg, or traditional aluminum alloys like 6061, exhibit very similar structural properties.

It would make sense to use a similar material for the telescope’s primary mirror segment and the telescope structure to enable homogeneous thermal expansion in different temperature regimes, especially for machining, alignment, integration, and in-orbit operation.

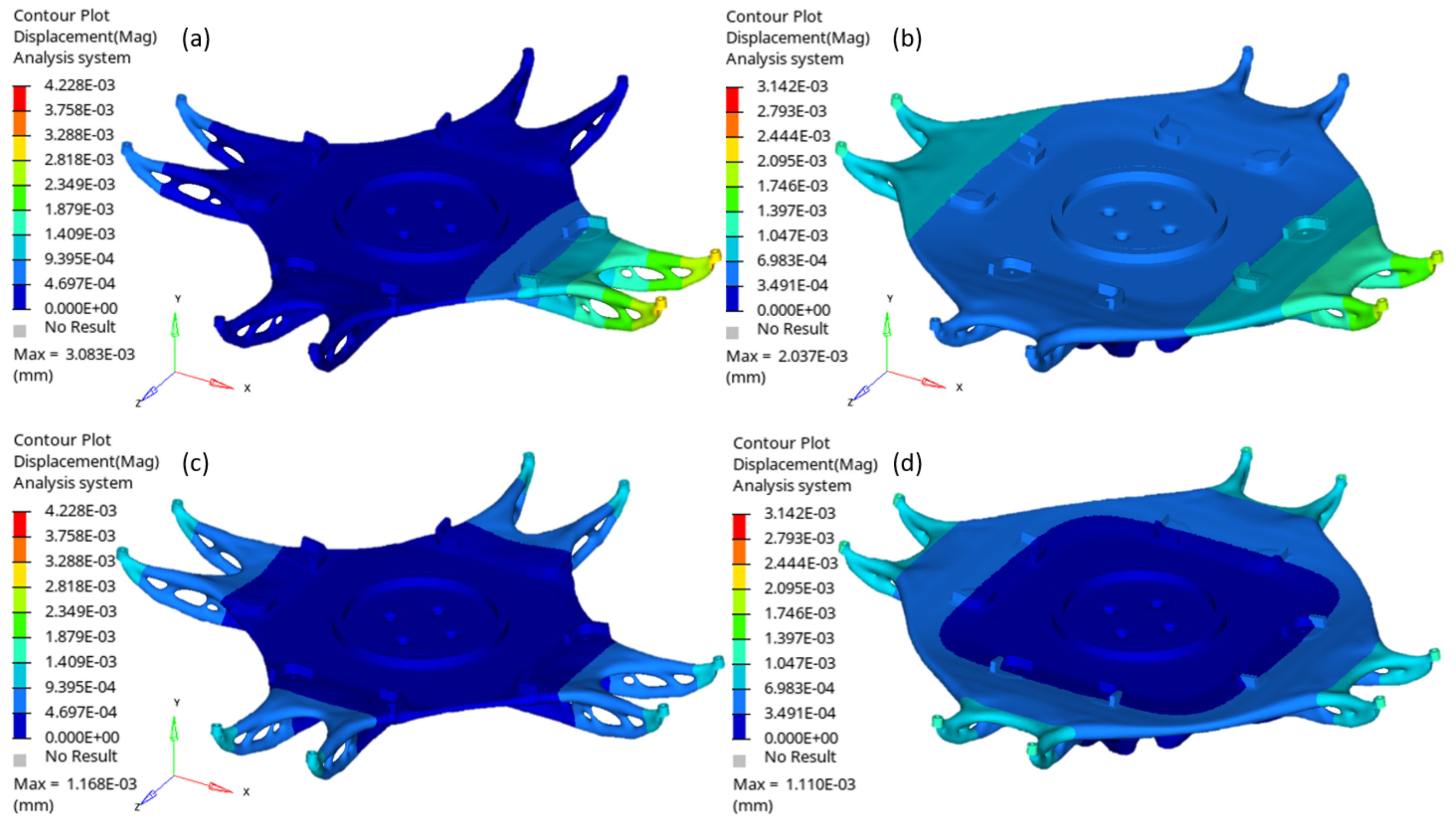
2.3. FEA Results—Conventional Fixture

The total mass of the assembly comprising the backing plate and the wedges is 15.5 kg.

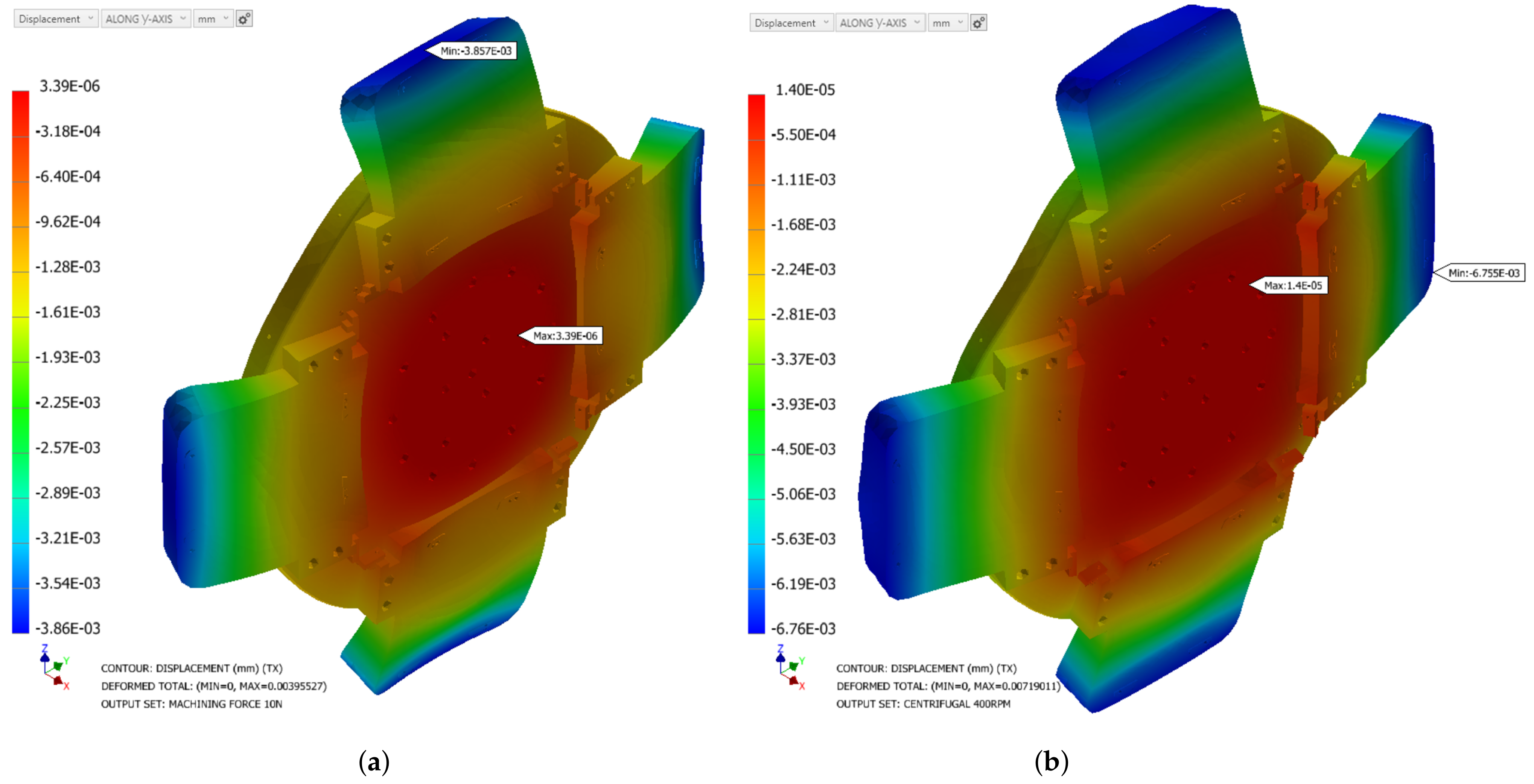
The FEA results are presented in Figure 4 and

Table 2. FEA results obtained for the conventionally machined fixture.

Requirement Type	Target Requirement
Mass of assembly excluding mirrors	15.5 Kg
Deformation induced by centrifugal force at 400 RPM	6.8 $\mathsf{\mu }$m
Deformation induced by cutting forces of 10 N	3.9 $\mathsf{\mu }$m
Deformation induced by gravity	0.56 $\mathsf{\mu }$m

, showcasing the deformation along the axis corresponding to the optical axis. With a cutting force of 10 N in Figure 4a, the deformation measures approximately 3.9 $\mathsf{\mu }$m PV. Notably, the maximum deformation is observed above the overhang, highlighting the need for a significantly stiffer and more rigid support in that area. With a more realistic cutting force of 1 N, the deformation would be around 390 nm, which would become acceptable for a IR telescope, especially considering that the distortion would also be limited to the area of the pads and not the entire fixture, which is how it has been considered here. Figure 4b illustrates the displacement outcome caused by rotational forces of 400 RPM, again along the spindle axis. As significant displacement is observed at approximately 6.8 $\mathsf{\mu }$m, it is advisable to refrain from using the fixture at rotational speeds exceeding 90 RPM, which would induce a residual deformation around 350 nm.

Due to the lower deformation induced by gravity, our subsequent optimization will primarily focus on reducing the deformation caused by cutting and rotational forces.

3. Topology Optimization

The TO was undertaken at the Advanced Manufacturing Research Centre (AMRC) and focused on a fixture design that harmonizes structural resilience with weight efficiency, suitable for deployable primary mirrors in CubeSat telescopes. For the design space, the setup was configured to optimize the fixture’s design for maximum stiffness, targeting specific mass constraints. Two mass targets were explored, 5 kg and 10 kg, to drive the optimization. In addition, two design envelopes were used to explore the design variability: a short and a long design envelope. As can be seen in Figure 1a, there is free space to allow for a larger envelope along the tool axis.

Table 3. Mechanical design requirements.

Design Requirement	Target Values
Mass of assembly excluding mirrors	<15 Kg
Deformation due to axial cutting load (10 N)	as good or better than CM (≤3.9 $\mathsf{\mu }$m)
Deformation due to acceleration at 400 RPM	as good or better than CM (≤6.8 $\mathsf{\mu }$m)

lists the primary mechanical requirements used for the fixture design space configuration.

Methodology

The CAD ‘Generative Design’ tool within PTC Creo (version 9.0.2.0) [19] was used for the TO outputs shown in this study. Altair HyperWorks (version 2022.3) [20] was also used to run final structural analysis of the concepts. The baseline geometry, comprising the base plate, wedges, and shims, is depicted in Figure 1b. This assembly formed the reference for load direction definitions, aligned with the lathe spindle axis (Y-axis) and perpendicular axes (X and Z).

The optimization process involved delineating both a design space and a non-design space. The design space, shown in Figure 5, is where material could be added or removed, shaped by local constraints and objectives. This space was defined around the original concept, ensuring no interference with essential features like fasteners or adjacent components. Conversely, the non-design space encompassed critical interface regions and functional features that were necessary to retain. Two design space sizes were explored, including a variant that integrated the backing plate into the fixture base. The fixture’s dimensions, particularly an added 200 mm length, were tailored to fit within the Single-Point Diamond Machine lathe constraints, allowing for future adjustments in design.

The fixture’s theoretical fabrication was planned to use an AM process such as Laser Powder Bed Fusion (LPBF), chosen for its ability to facilitate complex and lightweight designs not possible using methods of manufacture. For this purpose, the aluminum alloy AlSi10Mg, frequently used in AM applications, was selected. The specific properties of AlSi10Mg, for guiding the design and optimization of the fixture, are detailed in

Table 4. Material properties used for structural optimization and analysis.

Material	Young’s Modulus (GPa)	Density (Kg·m−3)	Poisson’s Ratio	Yield Stress (MPa)	Allowable Stress (MPa)
AlSi10Mg (stress relieved)	66.0	$2.68·{10}^{-6}$	0.33	174	116

.

All degrees of freedom were fixed at the lathe spindle bolting location in four positions, as shown in Figure 6. These constraints are applied on the preserve geometries (non-design space).

All components of the assembly, including the metal optics, were consolidated into a single entity, eliminating the need for joints or connectors. The metal optics were represented as point loads at their interface points. The load analysis comprised two categories: rotational loads at 400 RPM and an axial load of 10 N, applied at the metal optics fastener locations around the fixture’s periphery. This 10 N load, an exaggerated estimate for safety, was distributed across four fastener positions as depicted in Figure 7. These forces were applied to preserved geometries (non-design spaces) such as constraints. Notably, previous analyses undertaken at Durham University (DU) included gravity loads in a vertical orientation; however, these were omitted in this study since their impact was significantly lesser compared to rotational forces. The metal optics’ bodies themselves were excluded from this load evaluation to ensure direct comparability with the CM case. It is acknowledged that the inclusion of these masses in the fixture assembly will impact the study results. The primary objective of this study was to isolate and compare the effects of cutting and rotation forces on the two types of fixture.

PTC Creo’s ‘Generative Design’ tool, differing from its typical p-element method with automatic polynomial adjustment, utilized an h-element-type mesh. For maximum detail, the setting generated approximately 512,000 tetrahedral elements, averaging 3.1 mm in size. Conversely, Altair HyperWorks, which also employs the h-element method, focused on mesh convergence via element sizing. The structural analysis reporting deflections used a global average mesh size of 10 mm. An automatic surface deviation method refined the mesh for curvature, reducing it to as low as 10% of the global size (1 mm minimum). An illustrative section through the utilized mesh is shown in Figure 8. To achieve manageable outputs from the TO setup, the studies were limited to 1000 iterations, with any cases reaching this limit reported as inconclusive.

4. Results

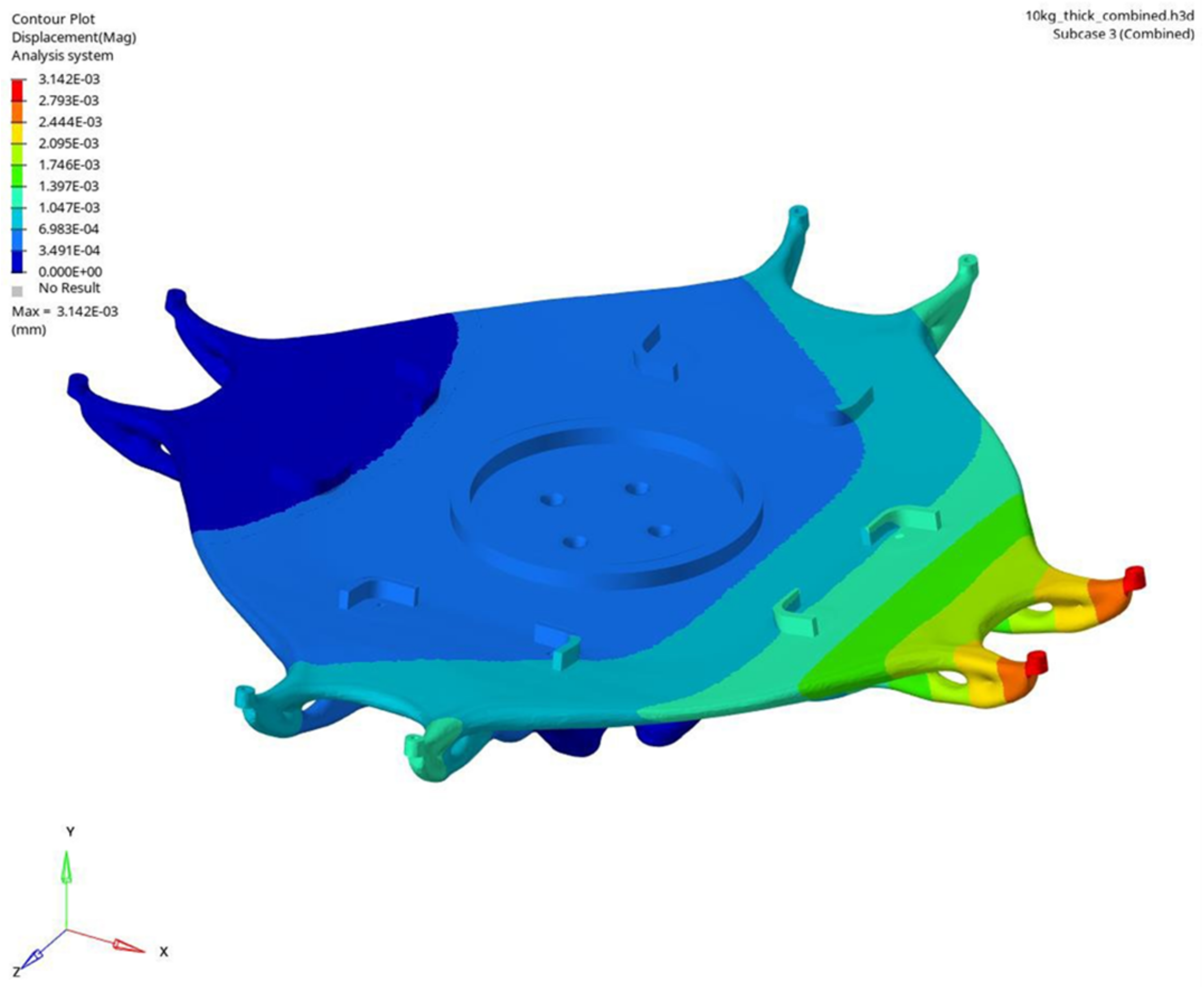
Two TO outputs were successfully produced and met the specified design criteria, as highlighted in

Table 5. Results of short and long design envelopes with 5 kg and 10 kg mass targets.

Concept	Mass, kg	Peak Deflection—400 RPM, µm	Peak Deflection—10 N, µm	Peak Deflection—Combined, µm	Peak Stress, MPa
Design Criteria	<15	As good or better than CM	As good or better than CM	As good or better than CM	<116
Short Envelope	5.2	1.17	3.08	4.23	1.24
Long Envelope	10.2	1.11	2.04	3.14	1.59

. An additional load case, combining both rotational and axial loads, was evaluated to better approximate the real machining setup. This combined load case resulted in the greatest deflection, with the findings presented in the subsequent figures. The TO outputs are shown in Figure 9 and Figure 10. Detailed deflection plots for each individual load case are shown in Figure 11, Figure 12 and Figure 13. Although peak stress levels were recorded, it is important to note that prior studies have determined that stress is not a significant concern for the materials selected for these designs.

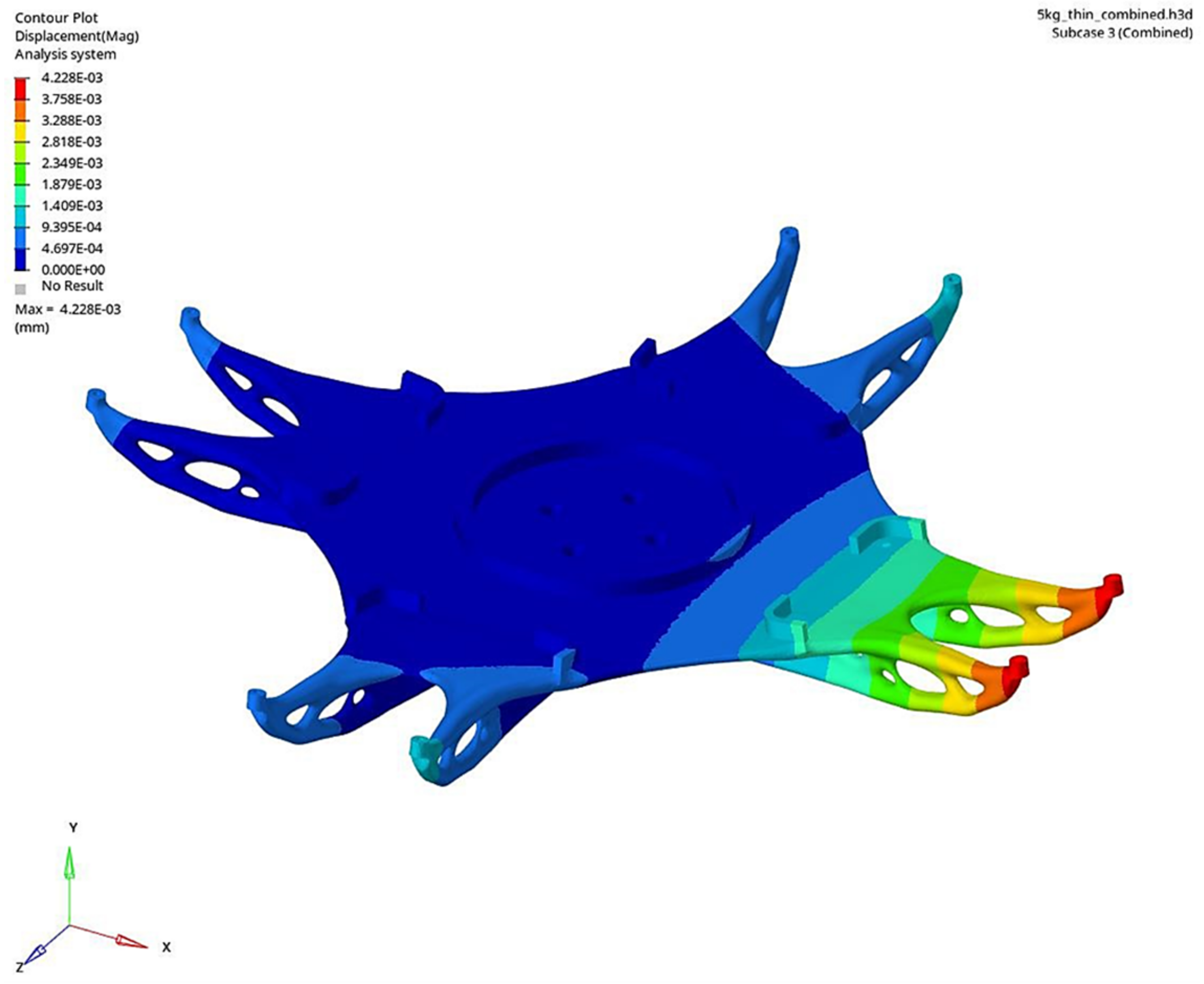
The output of the TO with the shorter design envelope and 5 kg mass target, as well as the peak deflection contour plot, are shown in Figure 9 and Figure 11.

The output of the TO with the longer design envelope and 10 kg mass target, as well as the peak deflection contour plot, are shown in Figure 10 and Figure 12.

Comparing the results of the design envelopes, the short envelope design, with a mass of 5.2 kg, demonstrated peak deflections slightly higher than the long envelope design, which weighed 10.2 kg. Specifically, under combined load conditions, the short envelope recorded a peak deflection of 4.23 µm compared to 3.14 µm for the long envelope. This difference highlights the long envelope’s slightly superior performance in minimizing deflection under load, which could be attributed to its increased mass and altered geometry. Moreover, the peak stress in the long envelope design was marginally higher (1.59 MPa) compared to the short envelope (1.24 MPa), yet both values were significantly lower than the stress limit of 116 MPa, confirming the robustness of both designs. Unlike the CM design, the TO outputs account for the stiffness of the mirror in the optimization. The resultant geometries are truss-like and have members directly connecting the mounting pads on the mirrors to the spindle. Note how the plane of the trusses acts to reduce the displacement along the spindle axis. These designs also feature reinforced support at critical points to minimize deformation under various applied loads.

The summarized results are presented in

Table 6. Mass and FEA Results for the three Case Studies (Nominal CM Design, Design 1 AM, and Design 2 AM). The percentages represent the reduction in mass or reduction in surface displacement along the spindle axis.

	Nominal CM	TO1 AM Short Envelope	TO2 AM Long Envelope
Mass of assembly excluding mirrors	15.5 kg	5.2 kg	10.2 kg
		66.45%	34.19%
Deformation induced by centrifugal force at 400 RPM	6.8 µm	1.17 µm	1.11 µm
		82.79%	83.68%
Deformation induced by cutting forces of 10 N	3.9 µm	3.08 µm	2.04 µm
		21.03%	47.69%

, where the mass and performance of the CM design are taken as a reference and compared with both TO₁ and TO₂. In addition to the actual mass and deformation values for TO₁ and TO₂, an ‘improvement’ factor is provided as a percentage, reflecting the reduction in mass or displacement achieved.

A significant 80% reduction in deflection was achieved when the assembly was subjected to rotational force, while improvements of 21% and 47% were observed in the deflection induced by cutting forces for the 5 Kg and 10 Kg TO, respectively. As mentioned, the recorded stress levels, though monitored, were not a primary concern, primarily due to the high stress tolerance of the AlSi10Mg material used in the designs. This material offers a favorable combination of strength and flexibility, making it well suited for applications requiring both lightness and durability.

5. Discussion

TO and AM have the potential to enhance the precision and efficiency of the Single-Point Diamond-Turning manufacturing process by optimizing fixture rigidity and resilience to the manufacturing stress. They also have the potential to further reduce the weight of large assembly and aperture, especially for cases such as deployable primary mirrors, helping with the handling of parts and the iteration between machining and “off-machine” metrology.

Although there are some clear benefits to using AM, 3D printing of large parts, such as the ones presented in this paper with a diameter of 600 mm and a thickness of 200 mm, can be challenging and the process may be long and costly. The volume capacity of current LPBF machines can also be limited to smaller dimensions. One solution could be to split the whole assembly into four rotationally symmetrical sections (one section is shown in Figure 14), which could therefore be printed on conventional LPBF machines. This segmentation not only facilitates printing but could also significantly reduce the stress and potential thermal distortions typically encountered in large-scale LPBF printing. Each section could be designed to be self-supporting at a 45-degree critical angle, optimizing the printing process by minimizing the need for additional support structures and streamlining post-processing, despite a possible increase in Z height and print time. The four subassemblies can then be reassembled on a backing plate and positioned on the machine spindle as one single unit. The flat interface with the segment can be prepared and rectified with a high-speed ball end mill [21] so that all planes are post-processed in the same setup, minimizing potential errors induced by removing and reattaching the fixture to the machine’s spindle.

An alternative method of manufacture could be explored using investment wax casting [22], a process renowned for its accuracy. It involves creating a wax model of the entire TO fixture (or a sand mold). This model is then encased in a refractory material to form a mold. Once the mold is heated, the wax melts away, leaving a cavity in the shape of the fixture. Molten metal is then poured into this cavity, creating a single, unified piece that mirrors the intricate design of the TO fixture. This method could be beneficial for producing complex geometries and large-scale components, which are often challenging or impractical with LPBF due to size limitations and the need for support structures. Additionally, casting the fixture as one piece significantly reduces the risks associated with segmenting and reassembling multiple parts. It eliminates potential misalignments or inconsistencies that might arise from assembling several printed sections. This ensures a higher degree of structural integrity and uniformity in the final product.

6. Conclusions

The topology optimization process at AMRC yielded two distinct outputs, primarily focused on reducing mass while maximizing stiffness. These designs feature reinforced supports at crucial points, balancing lightweight construction with enhanced structural integrity. FEA revealed that both designs significantly outperformed the reference CM model. Specifically, TO₁ demonstrated a 66.45% mass reduction and substantial decreases in deformation (82.79% under centrifugal forces at 400 RPM and 21.03% under 10 N cutting forces). Similarly, TO₂ achieved a 34.19% mass reduction, an 83.68% reduction in deformation from centrifugal forces, and a 47.69% reduction in deformation from cutting forces. In-depth examination of the topology optimization for the metal optics fixture presented an innovative design that not only minimized mass but also met or surpassed deflection standards. Both design variants shared key structural features, such as truss-like arms extending from the spindle interface to the metal optics interfaces, enhancing bending stiffness. A distinctive plate-like feature on the design envelope’s upper surface, formed in response to rotational loads, was also observed. Both designs exceeded mechanical requirements, suggesting that a more aggressive optimization approach could further reduce weight. However, our conservative strategy incorporated additional factors like rotational symmetry and dynamic acceleration criteria, ensuring compatibility with PTC Creo Version 9.0.2.0. This approach, combined with additive manufacturing considerations, underscores the transformative potential of TO and AM in refining Ultra-Precision manufacturing processes.