Abstract
The present study theoretically investigated the linear instability of a liquid film sheared by gas flow under acoustic oscillations. In this work, the velocity oscillations of the gas are used to approximately characterize the acoustic oscillations, and the ratio of the conduction heat flux to the evaporation heat flux is used to characterize the heat and mass transfer. Considering the much stronger impact of the heat convection than the heat conduction in practical cases, a correction factor is introduced to satisfy the heat flux ratio within a reasonable range. Because of the oscillatory velocity of gas, several unstable regions, involving the KHI region and the parametric instability (PI) region, appear. The impact of the velocity oscillations on the KHI is related to the forcing frequency. Increasing the oscillatory velocity amplitude promotes the KHI when the forcing frequency is large, while the KHI is restrained with the increase in the oscillatory velocity amplitude when the forcing frequency is small. Since the viscous dissipation is enhanced when the forcing oscillations frequency increases, the PI is suppressed. In addition, when the surface tension decreases, the interfacial instability is also promoted. Increasing the gas–liquid density ratio can destabilize the surface. However, the impact of the heat and mass transfer on the interfacial instability is neglectable as the gas–liquid density ratio is large. Furthermore, the heat and mass transfer have a promoting impact on the PI and KHI, while their destabilizing effect on the indentation between unstable regions is greater. It is significant to note that the location of the maximum growth rate would be in the most unstable region.
1. Introduction
Liquid film cooling is an effective cooling method, which can prevent the wall of the combustor from overheating, oxidation, and destruction. Experimental results have predicted that the detachment of droplets from the liquid layer of the liquid film cooling cannot be neglected [1]. The entrainment is a significant reason for the mass loss of the liquid film, which can result in a decrease in the liquid film cooling efficiency. This entrainment phenomenon is related to the Kelvin–Helmholtz instability (KHI) [2,3], and it can be regarded as the process of droplets being peeled from liquid film, similar to the atomization process, as the liquid film is sheared by the gas stream. As the liquid is surrounded by the gas stream, the velocity of which is higher than that of the liquid, the momentum transfer from the high-speed gas to the liquid dominates the breakup process. Various theoretical and experimental studies [4,5,6,7,8,9] of the atomization process have been carried out. The typical examples of Lasheras and Hopfinger [10] showed that the interfacial instability was the main factor of the atomization process, and the instability was suppressed by the surface tension. The KHI plays a significant role in the atomization mechanism [11,12,13,14,15,16,17]. Rayana et al. [18] extended the theoretical method of Varga et al. [11] to study the process of the droplet peeling from liquid film. It should be noted that there was only gas on the upper side of the liquid film, the lower side of the liquid film was limited by the wall rather than the free liquid film on both sides, and the results obtained by the linear stability theory agreed well with those of the experiments.
In summary, the generation of droplets can still be attributed to the general growth of the perturbation wave, and the KHI has an important impact on the process of air-assisted or air-blast atomization. The process of droplet production under the acoustic oscillations can result in combustion instability. For example, in an F-1 liquid rocket engine, the pulse combustion of liquid fuel peeled from the liquid layer of film cooling under acoustic oscillation was considered to be a main factor of the combustion instability [19]. Baillot et al. [20] considered that the pressure oscillations may reach 10% or even higher, as the combustion instability appears in the combustion chamber, which inevitably affects the atomization process. Even though the fuel injection systems are extremely insensitive to pressure oscillations in the combustion chamber, combustion instability with acoustic oscillations can also occur [21]. The pressure oscillations in the combustion chamber were mainly reflected in oscillations of the gas velocity [22]. Jia et al. [23,24,25,26] investigated the instability of coaxial jets and sheets, and the oscillatory gas velocity was used to characterize the acoustic fluctuations. Due to the oscillatory gas velocity, parametric instability (PI) appeared, and the surface waves were also oscillatory [27]. Because the viscous damping effect is enhanced when the frequency of oscillatory gas velocity increases, the PI is restrained. However, the KHI is enhanced when the frequency of oscillatory gas velocity increases. The KHI of the liquid jet is more impressionable to the rotating velocity of gas than the PI [28].
The present study focuses on the K-H instability of viscous liquid film with a co-flowing gas stream under acoustic oscillations. The acoustic oscillations are expressed as the oscillations of gas velocity. In addition, considering that the phase change caused by the temperature difference may affect the growth of the disturbance amplitude [29,30,31], the heat and mass transfer are also taken into account based on the simplified model of Hsieh [32,33]. The ratio of the conduction heat flux to the evaporation heat flux is used to characterize the heat and mass transfer. Considering that the heat convection is much stronger than the heat conduction in practical cases, a correction factor is introduced to satisfy the heat flux ratio within a reasonable range. The viscous potential flow theory is used to obtain a dispersion relation, which has been used to investigate the KHI in previous studies [34,35,36,37,38,39,40]. The dispersion relation between the temporal growth rate and the disturbance wave number is obtained. Furthermore, the effects of the acoustic oscillations, Weber number, heat and mass transfer, as well as other key parameters on the interfacial instability are discussed.
2. Program Formulation
Figure 1 shows that a two-dimensional channel is set horizontally, and the gas is over the liquid. The density, viscosity coefficients, surface tension coefficient, and the thickness of the liquid film are , , , and , respectively. The density, viscosity coefficient, and thickness of the gas stream are , , and , respectively. As the gas velocity is higher than that of the liquid, the KHI appears due to the velocity discontinuity. Hence, a coordinate system that moves with the liquid film is considered in this work. The basic velocities of gas and liquid in the and directions are and , respectively. The temperatures at the upper and lower walls are and , respectively, and represents the temperature at the surface. When the acoustic oscillations are taken into account, the expression of the gas velocity in the direction is
where is the basic axial velocity, represents the forcing oscillations amplitude, denotes the forcing oscillations frequency, and is the time.
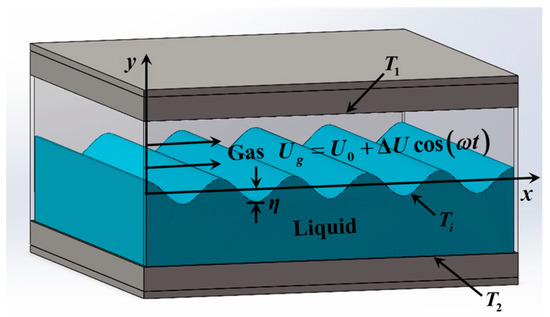
Figure 1.
Schematic of the model.
The temperature difference can lead to Marangoni effects [41], and it significantly affects the interfacial instability. Various articles have examined the Marangoni effects on the instability of liquid jets, sheets, and droplets [42,43,44,45,46,47,48,49,50,51]. It should be noted that the previous work has focused on the instability behavior dominated by the surface tension, which is named capillary instability or Rayleigh–Plateau instability, and the aerodynamic effect was neglectable. In this case, the Marangoni effects are obvious. However, as the liquid film is sheared by co-flowing gas stream, the instability behavior is driven by the aerodynamic force. In this case, the surface tension restrains the instability. The results of a recent study [52] predicted that the impact of the Marangoni effects would be weak, as the aerodynamic force dominates the instability behavior. In this work, the surface tension coefficient is a constant. Therefore, the Marangoni effects are not taken into account.
The expression of the interfacial displacement as the surface is disturbed in the present study is
where is the wavenumber.
As , and the continuity equation , the perturbation potentials satisfy the Laplace equation, which is
where the right subscripts represent the gas and liquid phases, respectively. The Laplace operator is .
The pressure disturbance can be calculated by the Lagrange integral, which is given by
The boundary condition when is
The boundary condition when is
The normal stress must be balanced at , and the boundary condition is given by
The solutions to Equation (3) are
where , , , and are coefficients, which are determined by the boundary conditions. Substituting Equations (11) and (12) into Equations (6)–(9) yields
Utilizing Equations (4) and (5), the normal stress balance boundary condition (i.e., Equation (10)) is
Substituting the expressions of the perturbation potentials into the normal stress balance boundary condition yields
where
The Hill’s equation can be obtained using the following transformation [23,25]:
Considering Equation (20), the expression of the growth rate can be written as
where is a characteristic exponent, which is introduced to obtain the dispersion relation (i.e., Equation (29)), and the equation to obtain is
The nondimensionalized dispersion relation is
where
where is a nondimensional wavenumber, is the thickness ratio, denotes the density ratio, represents the nondimensional temporal growth rate, is the viscosity ratio between the gas and liquid phases, is the nondimensional forcing frequency, is the nondimensional oscillations amplitude, is the Weber number, and denotes the Reynolds number. is the heat flux ratio between the conduction heat flux from the wall to the interface and the evaporation heat flux at the gas–liquid interface.
3. Results and Discussion
Funada et al. [53] studied the KHI of a liquid film in a channel, and the dispersion relation without gravitational acceleration is
Equation (39) is obtained in a fixed coordinate system. Under the coordinate system of the present study, it is written as
The nondimensionalized Equation (40) is
where represents the nondimensional complex growth rate, the imaginary part predicts the nondimensional disturbance frequency, and the real part denotes the nondimensional growth rate. is the wavenumber, and the wavelength . is the imaginary unit.
As the phase change and acoustic oscillations are ignored, the liquid layer is sheared by the high-speed gas stream, and this simplified model is similar to that of Funada et al. [53]. Figure 2 shows the results obtained by Equation (41) and the dispersion relation of the present study without the phase change and acoustic oscillations (i.e., and ). The curves shown in Figure 2 are normal. Before a maximum value was reached, the curves increased firstly with the wavenumber. After the maximum value, the curves decreased due to the impact of the viscosity of the liquid and the surface tension, and an abscissa-crossing point was reached. The dominant wavenumber is the wavenumber corresponding to the maximum growth rate. In addition, the range of the wavenumber from 0 to the abscissa-crossing point is known the unstable range. It can also be observed that the interfacial instability was promoted as the surface tension decreased. Figure 3 displays the results of this work compared with that of Asthana and Agrawal [34] when the heat and mass transfer were considered. In addition, the results of the simplified model in this work were in good agreement with previous studies, and the correctness of the dispersion relation obtained in this work was verified to a certain degree.
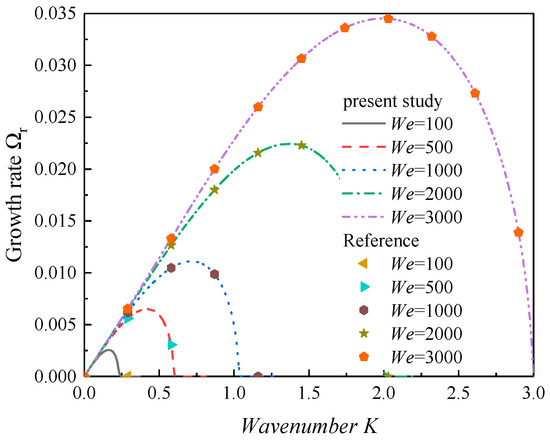
Figure 2.
The results compared with Funada et al. [53] when the Weber number varies (Re = 3000, ξ = 0.001, ρ = 0.001, α = 2).
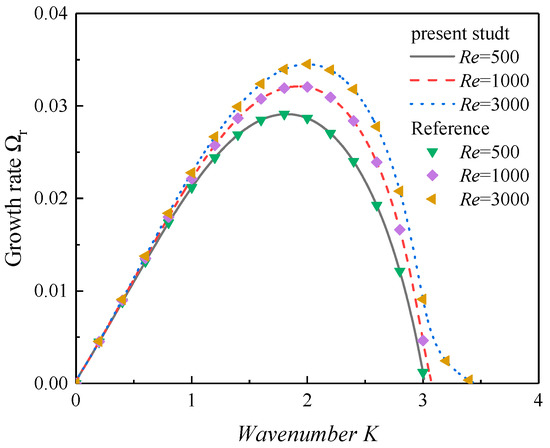
Figure 3.
The results compared with Asthana and Agrawal [34] by varying the Reynolds number (We = 3000, ξ = 0.001, Λ = 0.0001, ρ = 0.001, α = 2).
According to previous studies [1,54], the values of the typical physical parameters are shown in the following: the liquid density is , the gas density is , , , the thermal conductivity coefficient of the liquid is , the thermal conductivity coefficient of the gas , the latent heat is , the velocity difference between the gas and the liquid is , the viscosity of the liquid is , the surface tension coefficient is , the viscosity of the gas is , the thickness of the liquid film is , the thickness of the gas stream is , and the frequency of the acoustic oscillations is . The values of the typical nondimensional parameters are calculated as the reference state in the following: , , , , , , and the heat flux ratio is . In fact, the heat flux on the combustor wall of a liquid rocket can reach or higher, and the heat convection is much stronger than heat conduction. In this case, the heat flux ratio . Therefore, setting is not reasonable, and a correction factor should be introduced to satisfy within a reasonable range, i.e., . The heat flux ratio was set to 0.002 in the following.
Figure 4 shows the effect of the nondimensional oscillations amplitude of the gas velocity on the interfacial instability. As shown in Figure 4, only one unstable region occurred as the acoustic oscillations were ignored (i.e., ), without a phase transition. This unstable region is inherent, driven by aerodynamic force, and it is named the KHI region. As the oscillations of the gas velocity were neglected, the expression of the growth rate is . This means that this unstable region is dominated by . However, several unstable regions appeared without a phase transition when the oscillation amplitude of the gas velocity . According to Equations (30) and (31), these unstable regions after the first unstable region, which are named the parametric instability (PI) region, are governed by and . The full wavelength assumption of Mayer [13] indicted that the unstable disturbed waves in unstable regions can grow generally and break up into droplets. Therefore, the appearance of the PI is beneficial for the formation of smaller droplets. More importantly, Figure 4 shows the most unstable PI region was the second unstable region. Hence, the first and second unstable region only are discussed in the following. Furthermore, the location of the dominant wavenumber would be in the first unstable region as the oscillation amplitude is larger than a critical value , and it would be in the second unstable region as . Because the growth rate increases faster in the PI region than in the KHI region, as observed in Figure 4, the PI was more impressionable to the oscillations of the gas velocity than the KHI. Moreover, the results in Figure 4b show that the KHI was enhanced when the oscillatory velocity amplitude increased in the case of . However, the KHI was restrained with the increase in the oscillatory velocity amplitude when , as observed in Figure 4a. It can be concluded that the impact of the velocity oscillations on KHI is related to the forcing frequency. The KHI is enhanced with an increasing oscillatory velocity amplitude when the forcing frequency is large, while the KHI is restrained as the oscillatory velocity amplitude increases in the case when the forcing frequency is small.
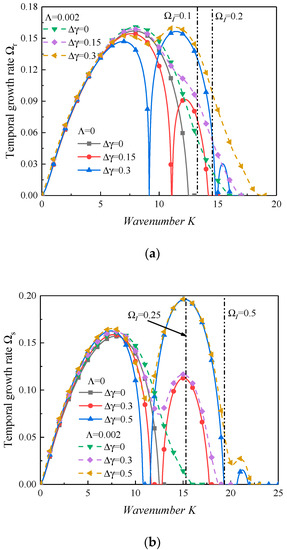
Figure 4.
The dispersion curves with varied oscillations amplitude (We = 10,000, Re = 5000, ρ = 0.00125, α = 6.25, ξ = 0.001, Λ = 0.002). (a) Ωs = 0.2. (b) Ωs = 0.5.
The inherent frequency can be calculated by Equation (20), the expression of which can be written as
The results of a previous study [55] predicted that the waves at half or harmonic frequencies were stimulated by the velocity oscillations, and the resonant wavenumber around the parametric instability regions is , where . In the present study, the resonant wavenumbers should be 13.26, 14.53, …, ·as the forcing frequency is 0.2. When the forcing frequency is 0.5, the resonant wavenumbers should be 15.30, 19.34, …, and these wavenumbers have been marked in Figure 4. However, because the variation in the inherent frequency of the system is limited, the parametric instability region would not be located at these resonant wavenumbers [55]. Furthermore, the wavenumbers around which the parametric instability appears are related to the forcing frequency, as can be seen in Figure 5 and Equation (40).
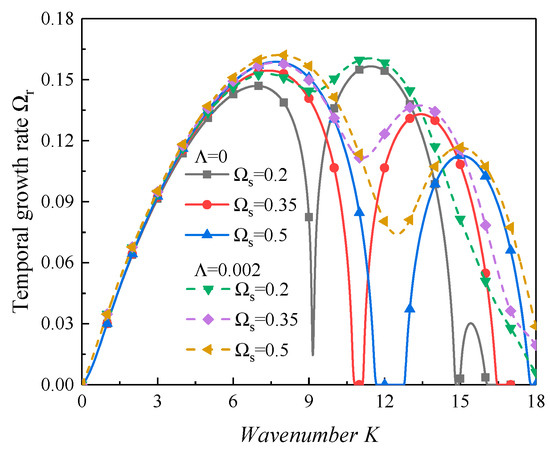
Figure 5.
The dispersion curves with varied forcing oscillations frequencies (We = 10,000, Re = 5000, ∆γ = 0.3, ρ = 0.00125, α = 6.25, ξ =0.001).
Figure 5 exhibits the influence of the forcing oscillations frequency. Obviously, as the forcing oscillations frequency increased, the instability of the surface was enhanced with an increasing forcing oscillations frequency, while the parametric instability was prevented. Meanwhile, the stabilizing effect of the increasing forcing oscillations in the parametric instability region was greater than the stabilizing effect in the KHI region, as observed in Figure 5. According to the dispersion relation equation of the present study (i.e., Equation (30)), the contribution of the viscous dissipation is
The term in Equation (41) denotes the damping effect of the liquid viscosity on the interfacial instability, and the term represents the contribution of the gas viscosity. As the wavenumber , , the viscous dissipation of the liquid phase can be proportional approximately to , as . In this case, the viscous dissipation was enhanced with an increasing wavenumber. According to Equation (42), the resonant wavenumber of the PI region increased because of the increase in the forcing oscillations frequency. Therefore, the PI was restrained because of the strongly viscous dissipation, and the regions of the PI moved to the right, as shown in Figure 5. In addition, it can be observed obviously that there was a critical forcing oscillations frequency ; the location of dominant wavenumber would be in the second unstable region when , and it would be in the first unstable region when .
As can be observed in Figure 6, the KHI as well as the PI were enhanced when the gas–liquid density increased. Meanwhile, the unstable regions expanded when the gas–liquid density ratio increased. Even though the heat and mass transfer were neglected, the gaps between unstable regions disappeared when the gas–liquid density ration was large enough. This suggests that the increases in the gas–liquid density ratio may have accelerated the breakup process of the liquid film. Due to the increase in the gas–liquid density ratio, the aerodynamic force effect was enhanced. Therefore, the interface between the gas and liquid phases tended to be more unstable with an increasing gas–liquid density ratio. In addition, it is worth noting that the growth rate in the PI region increased faster than that in the KHI region when the gas–liquid density ratio rose. It can be concluded that the PI was more susceptible to the gas–liquid density than the KHI. Furthermore, the inherent frequency of the system increased because of the increase in the gas–liquid density ratio, and it led the parametric unstable regions to move to the right, as shown in Figure 6a. Moreover, the dispersion curves with and without the heat and mass transfer were very approximate as the gas–liquid density ratio was large, as observed in Figure 6b. In this case, the effect of the heat and mass transfer could be neglected.
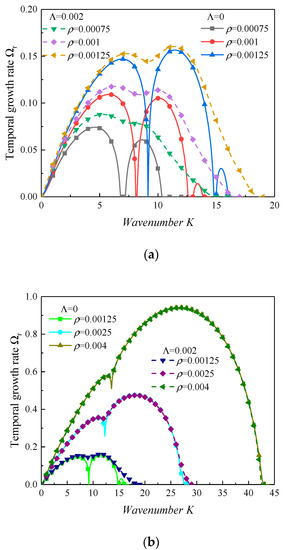
Figure 6.
The dispersion curves with varied gas–liquid density ratios (We = 10,000, Re = 5000, ∆γ = 0.3, Ωs = 0.2, α = 6.25, ξ = 0.001).
Figure 7 exhibits the influence of the surface tension on the interfacial instability of the viscous liquid film. As observed in Figure 7, with the increase in the Weber number, the maximum growth rate as well as the dominant wavenumber increased. The KHI was dominated by the aerodynamic effect, and it was suppressed by the surface tension. Hence, increasing the Weber number made the gas–liquid interface tend to be more unstable. According to the study of Varga et al. [11,12,14,15,16], the droplets after the breakup process may become smaller in this condition. In addition, the results in Figure 7 show that the growth rate in the PI region increased faster than that in the KHI region. This predicted that the impact of the oscillatory velocity on the KHI would be weaker than that on the parametric instability. One can also observe, in Equation (32), the term , which denotes the effect of surface tension on the interfacial instability. The damping effect of the surface tension would become stronger with an increasing wavenumber .
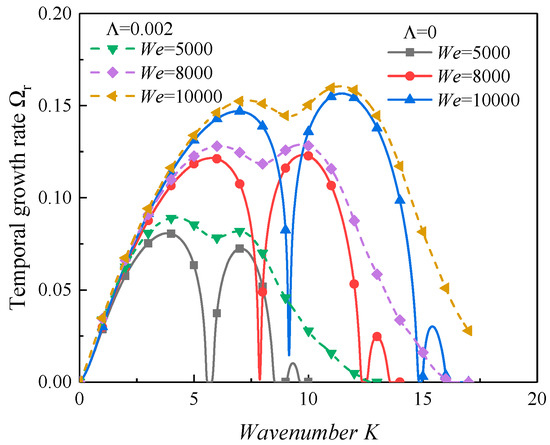
Figure 7.
The dispersion curves with varied Weber numbers (Re = 5000, ∆γ = 0.3, Ωs = 0.2, ρ = 0.00125, α = 6.25, ξ = 0.001).
Then, the effect of the viscosity of the liquid film on the surface instability was examined. It is obvious in Figure 8 that the both the inherent and PI regions increased when the Reynolds number increased. This predicted that the viscosity of the liquid would play a stabilizing role. Jia et al. [23] examined a two-dimensional liquid jet exposed to gas, as the longitudinal acoustic oscillations were considered, and the authors reported that the liquid viscous dissipation was proportional to . According to Equation (40) in this work, the damping effect of the viscosity of the liquid film was proportional approximately to , similar to the study of Kumar [56]. Moreover, it can also be concluded that there is a critical Reynolds number , the location of the maximum growth rate is in the KHI region as , and it shifts to the second unstable region when , as shown in Figure 8. A larger wavenumber corresponds to a shorter wavelength because of . According to recent studies [11,12,14,15,16], the atomization quality may be improved in the breakup process when the Reynolds number increases.
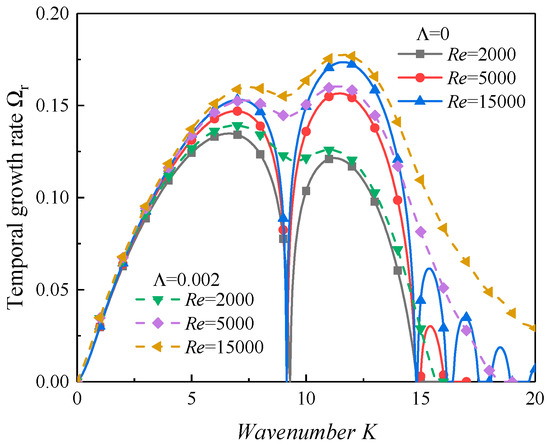
Figure 8.
The dispersion curves with varied Reynolds numbers (We = 10,000, ∆γ = 0.3, Ωs = 0.2, ρ = 0.00125, α = 6.25, ξ = 0.001).
Figure 9 shows the influence of the viscosity of the gas medium on the interfacial instability of the liquid film. It is clear that the growth rate of the inherent and parametric regions increased as the gas–liquid viscosity increased. The results predicted that increasing the viscosity of the gas would promote the KHI and PI. This conclusion is consistent with that reported by Funada et al. [57], who examined the linear stability of a viscous liquid jet exposed to a viscous gas phase. However, its destabilizing effect is neglectable because the gas–liquid viscosity ratio .
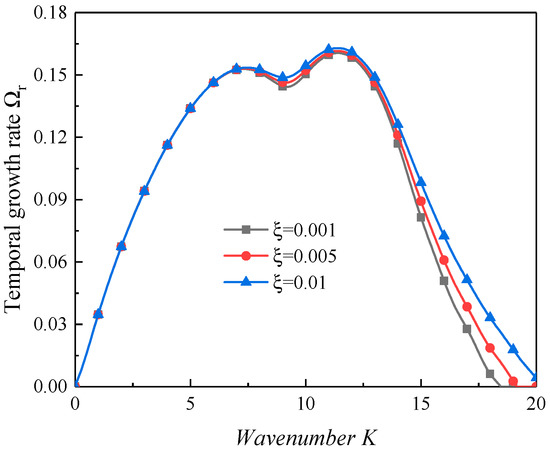
Figure 9.
The dispersion curves when the gas–liquid viscosity ratio varies (We = 10,000, Re = 5000, ∆γ = 0.3, Ωs = 0.2, ρ = 0.00125, α = 6.25, Λ = 0.002).
Figure 10 shows the variation in the growth rate by varying from 0 to 0.003 as the acoustic oscillations are taken into account. In this work, represents the ratio between the conduction heat flux and the evaporation heat flux, and it is employed to characterize the heat and mass transfer. As displayed in Figure 10, the interfacial instability was promoted as the heat and mass transfer were enhanced. It can be concluded that the heat and mass transfer had a destabilizing effect. Furthermore, the unstable regions expanded obviously as the phase transition appeared. Zeng et al. [58] investigated the primary breakup process numerically with the evaporation effect. The results suggested that the phase change could promote the KHI. Chan et al. [59] examined the mass transfer on the KHI at the gas–liquid interface. The authors concluded that the evaporation enhanced the wave instability. Although the physical model of the present study was somewhat different from those of Zeng et al. [58] and Chan et al. [59], the qualitative tendency was consistent.
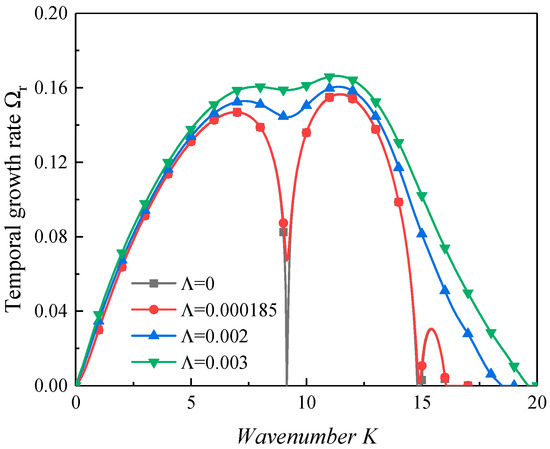
Figure 10.
The effect of the heat and mass transfer (We = 10,000, Re = 5000, ∆γ = 0.3, Ωs = 0.2, ρ = 0.00125, α = 6.25, ξ = 0.001).
4. Conclusions
This study investigated the instability of a planner liquid film theoretically when the phase change and acoustic oscillations were taken into consideration. The gas velocity oscillations were employed to characterize the acoustic oscillations. The results showed that the parametric instability (PI) appeared when the acoustic oscillations were taken into account. The impact of the velocity oscillations on the Kelvin–Helmholtz instability (KHI) was related to the forcing frequency. The results suggest that the KHI was enhanced with an increasing oscillatory velocity amplitude when the forcing frequency was large, while the KHI was restrained as the oscillatory velocity amplitude increased in the case of the small forcing frequency. In addition, the PI was more susceptible to the oscillations of the gas velocity than the KHI. Due to the enhancement of the viscous damping effect, the PI was prevented when the forcing oscillations frequency increased. Furthermore, the resonant wavenumber and frequency varied with the forcing oscillations frequency. Both the KHI and PI were promoted with the enhancement of the heat and mass transfer. More importantly, the inherent frequency of the system increased with an increase in the gas–liquid density ratio, and it led to an increase in the wavenumber of the PI. As the gas–liquid density ratio was large enough, the influence of the heat and mass transfer could be neglected. Moreover, the dominant wavenumber could be transferred from the KHI region to the PI region when the Weber number increased. The liquid viscosity restrained the interfacial instability. Although the gas viscosity destabilized the surface of the liquid film, its destabilizing impact was neglectable because of the low viscosity. Considering Mayer’s full wavelength assumption [13], which indicates that the unstable disturbed waves in unstable regions can grow generally and break up into droplets, the acoustic oscillations are beneficial for obtaining smaller droplets. In addition, increasing the Weber number, Reynolds number, and gas–liquid density ratio not only accelerates the breakup process of the liquid film but also improves the atomization quality.
Author Contributions
X.D.: Methodology; Formal Analysis; Writing—Original Draft Preparation. B.S.: Validation; Writing—Review and Editing. Y.T.: Validation; Writing—Review and Editing. N.W.: Validation; Writing—Review and Editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Natural Science Foundation of China (Grant No. 52106129) and the Science Center for Gas Turbine Project (Grant No. P2022-A-II-006-002).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| undetermined coefficients | |
| undetermined coefficient | |
| undetermined coefficient | |
| undetermined coefficient | |
| undetermined coefficient | |
| a function of time | |
| thickness of gas | |
| thickness of liquid | |
| wavenumber | |
| nondimensional wavenumber | |
| pressure disturbance | |
| disturbed pressure of gas | |
| disturbed pressure of liquid | |
| Reynolds number | |
| time | |
| axial gas velocity in coordinate system moving with liquid jet | |
| axial gas velocity in fixed coordinate system | |
| axial velocity of liquid | |
| axial velocity of gas | |
| axial basic velocity of liquid | |
| axial basic velocity of gas | |
| oscillations amplitude of gas velocity | |
| velocity vector | |
| wavelength | |
| Weber number | |
| thickness ratio between gas and liquid | |
| perturbation potential of gas | |
| perturbation potential of liquid | |
| nondimensional oscillations amplitude | |
| disturbed amplitude | |
| gas viscosity | |
| liquid viscosity | |
| gas–liquid density ratio | |
| gas density | |
| liquid density | |
| surface tension coefficient | |
| heat flux ratio | |
| nondimensional complex growth rate | |
| nondimensional inherent frequency | |
| nondimensional disturbance frequency | |
| nondimensional temporal growth rate | |
| nondimensional forcing oscillation frequency | |
| contribution of viscosity to the instability | |
| complex growth rate | |
| complex disturbance frequency | |
| temporal growth rate | |
| forcing oscillations frequency | |
| gas–liquid viscosity ratio |
Appendix A
The mass transfer, which occurs with the heat transfer, changes the amplitude of the disturbance at the interface through the phase change between gas and liquid. To obtain the kinematic boundary conditions of the disturbance wave including the effect of the mass transfer, Heish [32,33] built the mass transfer balance and heat transfer balance conditions. The mass transfer is approximated by the ratio of the conduction heat flux and the evaporation heat flux in kinematic boundary conditions. As in the studies of Hsieh [32,33], the mass transfer flux balance is
When the phase transition appears, the heat absorbed by the phase transition [32,33] is
where in Equation (A2) is the latent heat released by evaporation, and represents the heat flux. In the simplified physical model of Hsieh et al. [32,33], represents the temperature of the upper wall, denotes the temperature of the lower wall, represents the temperature of the surface, and should be the saturation temperature when the phase transition appears. We assume that the heat transfer from the upper wall to the surface is by heat conduction, and the heat transfer from the surface to the lower wall is by heat conduction. Thus, the heat flux at the disturbed interface is
where and are the thermal conductivity coefficients of liquid and gas, respectively. Obviously, Equation (A3) is not a linear expression of the disturbed amplitude . Therefore, Equation (A3) should be linearized by the Taylor series. Expanding the in the Taylor series at , the following equation can be obtained:
To represent as a function of the disturbed amplitude , the case of was assumed as an equilibrium state in previous work [32,33], and the heat flux should be zero.
It can be obtained from Equation (A5) as follows
where is a constant. Taking Equations (A3)–(A5) into Equation (A6), the linearized expression is
Utilizing the Equations (A1), (A2), and (A7), the result is
where , and the Equations (A8) and (A9) are the boundary conditions at the disturbed surface.
Appendix B
Taking Equations (20) and (21) into Equation (16) yields
Considering that
the expressions of , , and are
For the cosine function, there is
Taking Equations (A13)–(A16) into Equation (A10), the results are
where
References
- Gater, R.A.; L’Ecuyer, M.R. A Fundament Investigation of the Phenomena That Characterize Liquid-Film Cooling. Int. J. Heat Mass Transf. 1970, 13, 1925–1939. [Google Scholar] [CrossRef]
- Petrarolo, A.; Kobald, M.; Schlechtriem, S. Understanding Kelvin–Helmholtz instability in paraffin-based hybrid rocket fuels. Exp. Fluids 2018, 59, 62. [Google Scholar] [CrossRef]
- Petrarolo, A.; Kobald, M.; Schlechtriem, S. Optical analysis of the liquid layer combustion of paraffin-based hybrid rocket fuels. Acta Astronaut. 2019, 158, 313–322. [Google Scholar] [CrossRef]
- Yang, L.J.; Fu, Q.F.; Qu, Y.Y.; Gu, B.; Zhang, M.Z. Breakup of a power-law liquid sheet formed by an impinging jet injector. Int. J. Multiph. Flow 2012, 39, 37–44. [Google Scholar] [CrossRef]
- Fu, Q.F.; Yang, L.J.; Qu, Y.Y. Measurement of annular liquid film thickness in an open-end swirl injector. Aerosp. Sci. Technol. 2011, 15, 117–124. [Google Scholar] [CrossRef]
- Fu, Q.F.; Yang, L.J.; Qu, Y.Y.; Gu, B. Linear Stability Analysis of a Conical Liquid Sheet. J. Propul. Power 2010, 26, 955–968. [Google Scholar] [CrossRef]
- Fu, Q.F.; Yang, L.J.; Wang, X.D. Theoretical and Experimental Study of the Dynamics of a Liquid Swirl Injector. J. Propul. Power 2010, 26, 94–101. [Google Scholar] [CrossRef]
- Yang, L.J.; Qu, Y.Y.; Fu, Q.F.; Gu, B. Linear Stability Analysis of a Non-Newtonian Liquid Sheet. J. Propul. Power 2010, 26, 1212–1224. [Google Scholar] [CrossRef]
- Yang, L.J.; Fu, Q.F.; Qu, Y.Y.; Zhang, W.; Du, M.L.; Xu, B.R. Spray characteristics of gelled propellants in swirl injectors. Fuel 2012, 97, 253–261. [Google Scholar] [CrossRef]
- Lasheras, J.C.; Hopfinger, E.J. Liquid Jet Instability and Atomization in a Coaxial Gas Stream. Annu. Rev. Fluid Mech. 2000, 32, 275–308. [Google Scholar] [CrossRef]
- Varga, C.M.; Lasheras, J.C.; Hopfinger, E.J. Initial breakup of a small-diameter liquid jet by a high-speed gas stream. J. Fluid Mech. 2003, 497, 405–434. [Google Scholar] [CrossRef]
- Aliseda, A.; Hopfinger, E.J.; Lasheras, J.C.; Kremer, D.M.; Berchielli, A.; Connolly, E.K. Atomization of viscous and non-Newtonian liquids by a coaxial, highspeed gas jet. Experiments and droplet size modeling. Int. J. Multiphase Flow. 2008, 34, 161–175. [Google Scholar] [CrossRef]
- Mayer, E. Theory of liquid atomization in high velocity gas streams. ARS J. 1961, 31, 1783–1785. [Google Scholar]
- Qin, L.Z.; Yi, R.; Yang, L.J. Theoretical breakup model in the planar liquid sheets exposed to high-speed gas and droplet size prediction. Int. J. Multiph. Flow 2018, 98, 158–167. [Google Scholar] [CrossRef]
- Fu, Q.F.; Yao, M.W.; Yang, L.J.; Xie, L. Atomization Model of Liquid Jets Exposed to Subsonic Crossflows. AIAA J. 2020, 58, 2347–2351. [Google Scholar] [CrossRef]
- Yang, L.J.; Gao, Y.P.; Li, J.X.; Fu, Q.F. Theoretical atomization model of a coaxial gas–liquid jet. Phys. Fluids 2020, 32, 124108. [Google Scholar] [CrossRef]
- Yang, L.J.; Fu, Q.F. Stability of Confined Gas–Liquid Shear Flows in Recessed Shear Coaxial Injectors. J. Propul. Power 2012, 28, 1413–1424. [Google Scholar] [CrossRef]
- Rayana, F.B.; Cartellier, A.; Hopfinger, E.J. Assisted Atomization of a Liquid Layer: Investigation of the Parameters Affecting the Mean Drop Size Prediction. In Proceedings of the International Conference on Liquid Atomization and Spray Systems (ICLASS), Kyoto, Japan, 27 September 2006; pp. 1–8. [Google Scholar]
- Anderson, W.E.; Yang, V. Liquid Rocket Engine Combustion Instability. In Progress in Astronautics and Aeronautics; AIAA: Washington, DC, USA, 1995; pp. 1–78. [Google Scholar]
- Baillot, F.; Blaisot, J.B.; Boisdron, G.; Dumouchel, C. Behaviour of an air-assisted jet submitted to a transverse high-frequency acoustic field. J. Fluid Mech. 2003, 640, 305–342. [Google Scholar] [CrossRef]
- Ćosić, B.; Moeck, J.P.; Paschereit, C.O. Nonlinear Instability Analysis for Partially Premixed Swirl Flames. Combust. Sci. Technol. 2014, 186, 713–736. [Google Scholar] [CrossRef]
- Kheirkhaha, S.; Cirtwill, J.D.M.; Saini, P.; Venkatesanb, K.; Steinberga, A.M. Dynamics and mechanisms of pressure, heat release rate, and fuel spray coupling during intermittent thermoacoustic oscillations in a model aeronautical combustor at elevated pressure. Combust. Flame 2017, 185, 319–334. [Google Scholar] [CrossRef]
- Jia, B.Q.; Xie, L.; Cui, X.; Yang, L.J.; Fu, Q.F. Linear Stability of Confined Coaxial Jets in the Presence of Gas Velocity Oscillations with Heat and Mass Transfer. Phys. Fluids 2019, 31, 092101. [Google Scholar] [CrossRef]
- Jia, B.Q.; Xie, L.; Cui, X.; Yang, L.J.; Fu, Q.F. Linear instability of viscoelastic planar liquid sheets in the presence of gas velocity oscillations. J. Non-Newton. Fluid Mech. 2019, 273, 104169. [Google Scholar] [CrossRef]
- Jia, B.Q.; Yang, L.J.; Xie, L.; Fu, Q.F.; Cui, X. Linear stability of confined swirling annular liquid layers in the presence of gas velocity oscillations with heat and mass transfer. Int. J. Heat Mass Transf. 2019, 138, 117–125. [Google Scholar] [CrossRef]
- Guan, X.Y.; Jia, B.Q.; Yang, L.J.; Fu, Q.F. Linear instability of an annular liquid jet with gas velocity oscillations. Phys. Fluids 2021, 33, 054110. [Google Scholar] [CrossRef]
- Deng, X.D.; Jia, B.Q.; Cui, X.; Wang, N.F.; Shi, B.L. Temporal Instability of Liquid Jet in Swirling Gas with Axial Velocity Oscillations. AIAA J. 2022, 60, 3852–3862. [Google Scholar] [CrossRef]
- Deng, X.D.; Wang, H.R.; Cui, X.; Xie, L.; Jia, B.Q. Temporal instability of confined three-dimensional liquid jet with heat and mass transfer under longitudinal acoustic oscillations. Phys. Fluids 2022, 34, 102107. [Google Scholar] [CrossRef]
- Fu, Q.F.; Deng, X.D.; Yang, L.J. Kelvin–Helmholtz Instability of Confined Oldroyd-B Liquid Film with Heat and Mass Transfer. J. Non-Newton. Fluid Mech. 2019, 267, 28–34. [Google Scholar] [CrossRef]
- Fu, Q.F.; Deng, X.D.; Jia, B.Q.; Yang, L.J. Temporal instability of a confined liquid film with heat and mass transfer. AIAA J. 2018, 56, 2615–2622. [Google Scholar] [CrossRef]
- Mohanta, L.; Cheung, F.B.; Bajorek, S.M. Stability of coaxial jets confined in a tube with heat and mass transfer. Phys. A 2016, 443, 333–346. [Google Scholar] [CrossRef]
- Hsieh, D.Y. Effects of heat and mass transfer on Rayleigh-Taylor instability. J. Fluid Eng. T. ASME 1972, 94, 156–160. [Google Scholar] [CrossRef]
- Hsieh, D.Y. Interfacial stability with mass and heat transfer. Phys. Fluids 1978, 21, 745–748. [Google Scholar] [CrossRef]
- Asthana, R.; Agrawal, G.S. Viscous potential flow analysis of Kelvin–Helmholtz instability with mass transfer and vaporization. Phys. A 2007, 382, 389–404. [Google Scholar] [CrossRef]
- Asthana, R.; Agrawal, G.S. Viscous potential flow analysis of electrohydrodynamic Kelvin–Helmholtz instability with heat and mass transfer. Int. J. Eng. Sci. 2010, 48, 1925–1936. [Google Scholar] [CrossRef]
- Awasthi, M.K.; Asthana, R.; Agrawal, G.S. Pressure corrections for the potential flow analysis of Kelvin–Helmholtz instability with heat and mass transfer. Int. J. Heat Mass Transf. 2012, 55, 2345–2352. [Google Scholar] [CrossRef]
- Awasthi, M.K.; Asthana, R.; Agrawal, G.S. Viscous correction for the viscous potential flow analysis of Kelvin–Helmholtz instability of cylindrical flow with heat and mass transfer. Int. J. Heat Mass Transf. 2014, 78, 251–259. [Google Scholar] [CrossRef]
- Awasthi, M.K. Kelvin-Helmholtz instability of viscoelastic liquid-viscous gas interface with heat and mass transfer. Int. J. Therm. Sci. 2021, 161, 106710. [Google Scholar] [CrossRef]
- Moatimid, G.M.; Obied Allah, M.H.; Hassan, M.A. Kelvin-Helmholtz instability for flow in porous media under the influence of oblique magnetic fields: A viscous potential flow analysis. Phys. Plasmas 2013, 20, 102111. [Google Scholar] [CrossRef]
- Awasthi, M.K.; Asthana, R.; Uddin, Z. Nonlinear Study of Kelvin-Helmholtz instability of cylindrical flow with mass and heat transfer. Int. J. Commun. Heat Mass 2016, 71, 216–224. [Google Scholar] [CrossRef]
- Scriven, L.E.; Sternling, V.S. The Marangoni effects. Nature 1960, 187, 186–788. [Google Scholar] [CrossRef]
- Oron, A.; Deissler, R.T.; Duh, J.C. Marangoni instability in a liquid sheet. Adv. Space Res. 1995, 16, 83–86. [Google Scholar] [CrossRef]
- Dávalos-Orozco, L.A. Thermocapillar instability of liquid sheets in motion. Colloids Surf. A 1999, 157, 223–233. [Google Scholar] [CrossRef]
- Funada, T. Marangoni instability of thin liquid sheet. J. Phys. Soc. Jpn. 1986, 55, 2191–2202. [Google Scholar] [CrossRef]
- Tong, M.X.; Yang, L.J.; Fu, Q.F. Thermocapillar instability of a two-dimensional viscoelastic planar liquid sheet in surrounding gas. Phys. Fluid 2014, 26, 033105. [Google Scholar] [CrossRef]
- Zhang, S.; Lan, X.D.; Zhou, M. Thermocapillary instability of a liquid sheet with centrifugal force. J. Braz. Soc. Mech. Sci. 2018, 47, 40–47. [Google Scholar] [CrossRef]
- Hu, K.X.; He, M.; Chen, Q.S. Instability of thermocapillary liquid layers for Oldroyd-B fluid. Phys. Fluid 2016, 28, 033105. [Google Scholar] [CrossRef]
- Hu, K.X.; He, M.; Chen, Q.S.; Liu, R. Linear stability of thermocapillary liquid layers of a shear-thinning fluid. Phys. Fluid 2017, 29, 073101. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Hydrodynamic and Hydro-Magnetic Stability; Dover publications, Inc.: New York, NY, USA, 1961. [Google Scholar]
- Hasegawa, K.; Manzaki, Y. Marangoni fireworks: Atomization dynamics of binary droplets on an oil pool. Phys. Fluids 2021, 33, 034124. [Google Scholar] [CrossRef]
- Moezzi, M.; Sajjadi, M.; Hossein Hejazi, S. Thermally driven Marangoni effects on the spreading dynamics of droplets. Int. J. Multiph. Flow 2023, 159, 104335. [Google Scholar] [CrossRef]
- Cui, X.; Jia, B.Q. Thermal Effect on the Instability of Annular Liquid Jet. Aerospace 2021, 8, 382. [Google Scholar] [CrossRef]
- Funada, T.; Joseph, D.D. Viscous potential flow analysis of Kelvin-Helmholtz instability in a channel. J. Fluid Mech. 2001, 445, 263–283. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, Q.; Zhang, H.Q.; Wang, B. Numerical investigation on the performance of internal flow and atomization in the recessed gas-centered swirl coaxial injectors. Aerosp. Sci. Technol. 2022, 129, 107858. [Google Scholar] [CrossRef]
- Benjamin, T.B.; Ursell, F. The stability of the plane free surface of a liquid in vertical periodic motion. Proc. R. Soc. Lond. Ser. A 1954, 225, 505–515. [Google Scholar] [CrossRef]
- Kumar, K. Linear Theory of Faraday Instability in Viscous Liquids. Proc. R. Soc. A 1996, 452, 1113–1126. [Google Scholar] [CrossRef]
- Funada, T.; Joseph, D.D.; Yamashita, S. Stability of a Liquid Jet into Incompressible Gases and Liquids. Int. J. Multiph. Flow 2004, 30, 1279–1310. [Google Scholar] [CrossRef]
- Zeng, P.; Sarholz, S.; Iwainsky, C.; Binninger, B.; Peters, N.; Herrmann, M. Simulation of Primary Breakup for Diesel Spray with Phase Transition. In Recent Advances in Parallel Virtual Machine and Message Passing Interface: 16th European PVM/MPI Users’ Group Meeting, Espoo, Finland, 7–10 September 2009; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Chan, S.H.; Wang, Y.S.; Tan, C.C. The effect of mass transfer on Kelvin-Helmholtz instability at the gas-liquid interface of a sonic reacting and non-reacting gas jet submerged in a liquid. Int. J. Heat Mass Transf. 1994, 37, 1123–1132. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).