Abstract
The flight dynamics of a compound aircraft are highly coupled and significantly different from those of a single aircraft. In this paper, the characteristic flight dynamics of a three-unit connected aircraft are analyzed in detail. By distinguishing the aircraft’s modes into a symmetric mode group and an asymmetric mode group, the mechanisms by which the relative roll modes of the compound aircraft significantly impact the rigid-body modes of the vehicle become clear. The trim configuration of a compound aircraft has a profound influence on its stability and flight modes. In addition, the relative roll modes can be separated from the full-state model by appropriate simplifications, and the modal coupling mechanism and evolution law can be analytically derived. The key parameters which have a significant influence on the trim configuration and flight modes of the aircraft are pointed out in this paper. Finally, the common failure modes of compound aircraft are identified. A flight experiment with test data verifies the correctness of the above theoretical analysis.
1. Introduction
High-altitude long-endurance (HALE) aircraft and aerial robot swarms are among the important embodiments of future unmanned aerial vehicles (UAV). Wingtip-connected compound multi-body aircraft represent a practical scheme with the potential to become a swarm when separated in the air and an efficient aircraft with a high aspect ratio when combined [1], while reducing the difficulty of structural design compared with an entire large aircraft. The purpose of wingtip-connected aircraft is to enhance the endurance of the individual aircraft, as implemented in 1950s by the U.S. Air Force [2]. The Distributed Flight Array project adapts modular vehicle concepts, and has performed a successful flight test [3]. There are two other advantages of wingtip-connected multi-body aircraft. First, they have the ability to use modular combinations. Because the compound aircraft can be considered as a combination of several separate unit aircraft, modular payload combinations can be carried out according to the specific functions of the unit aircraft; for example, one unit aircraft can act as the power producer while its neighbors carry the task payload. Such an aircraft has almost no scale constraints in the span direction, and can carry large-scale distributed equipment such as antennas, synthetic aperture radars, and optical reconnaissance equipment.
Second, these aircraft have an extra degree of freedom in terms of their spanwise bending. This provides a compound aircraft with the ability to change its shape as needed during flight, which produces advantages in reducing the structural load and improving task flexibility. From an energy perspective, wings with solar panels can be folded and deformed to maximize the projection area towards the sun, as is the case for Aurora Flight Sciences’ “Odysseus” solar-powered high-altitude vehicle.
In recent years, Zhou et al. [4] have summarized the research progress of compound fixed-wing aircraft and analyzed the relationship between the aerodynamic performance of compound aircraft and the number of connected aircraft. Mcgill et al. [1] have shown that a compound aircraft with a wingtip-docked configuration can realize aerodynamic benefits (20–40%) based on the lift force in a configuration with an F-84 and transport situated wingtip-to-wingtip.
Montalvo [5] put forward the concept of “meta-aircraft” (called unit aircraft in this paper) and analyzed the corresponding flight dynamics in a wingtip-to-wingtip configuration and tip-to-tail configuration, together with an analysis of the number of connected individual aircraft. The controllability [6] and connection control law [7] of the compound aircraft were investigated as well. Finally, Montalvo connected two identical aircraft [8] and conducted a flight test of the feedback control law that included both take-off and landing.
Köthe et al. [9] studied the dynamics of multi-body high-altitude aircraft using the Kane method and potential flow theory (vortex lattice method); their results pointed out that the stiffness and location of the joint between both wingtips is a key factor in the flight mechanics of connected aircraft. Control allocation and eigenstructure assignment was adapted [10] to transfer the dynamics of a highly flexible multi-body aircraft into those of one classic-like rigid-body aircraft. For further investigation, a flight path controller was developed [11] and an experiment [12] was carried out.
Yang et al. conducted numerical simulation and stability analysis on compound multi-body aircraft consisting of two and three individual aircraft connected by wingtips [13]. They proved the inherent instability of compound aircraft through modal analysis, and proposed a feedback controller to eliminate this instability.
Research on the flight dynamics of compound aircraft has mainly focused on wingtip-connected multi-body aircraft, with the results mainly reflecting the aspects of modeling and time-domain simulations, linear analysis, and aerodynamic characteristics. Simulations and flight tests have been conducted to verify the feasibility of compound aircraft consisting of two and three identical unit aircraft, although detailed dynamic characteristics have not been determined. Detailed flight dynamics analysis and flight testing are mainly available for highly flexible aircraft, and are largely absent for compound aircraft [14,15,16]. The current research on the dynamics of compound aircraft is limited by the fact that most studies are numerical and focused on specific vehicles. There is a lack of quantitative and analytical analyses that comprehensively explore the dynamics of compound aircraft in general. Therefore, the cause of the modes and how the key parameters of the aircraft affect its dynamic characteristics are not yet sufficiently clear.
To provide guidance for conceptual design and control law deployment of compound aircraft, a generalized method for describing the flight characteristics of multi-body aircraft must be developed, nonlinear analysis must be performed, and an analytical expression of the flight dynamics based on reasonable simplification should be derived. Compared to compound aircraft consisting of two identical aircraft, those with three or more unit aircraft introduce extra span-wise asymmetry into the dynamics; therefore, knowledge of the flight mechanics of such aircraft is of high value.
This paper focuses on studying the flight dynamics of a three-unit connected aircraft; however, the obtained results have reference value for compound vehicles incorporating additional unit aircraft. New parameters such as the generalized spring stiffness, generalized inertia, etc., were defined in order to obtain universal analytical expressions to reveal the causes and coupling relations of each mode of the compound aircraft. This paper points out the differences in method between research on compound aircraft and traditional aircraft analysis, and points out the main factors that most highly affect the flight modes and stability of compound aircraft. Finally, valid flight data are used to prove the correctness of the theory presented in this paper.
The remainder of this paper is organized as follows. Section 2 introduces our research platform and its mathematical model; Section 3 describes the flight dynamics and modal analysis; Section 4 provides an the analytical treatment of the different modes; finally, the main contributions and conclusions of the paper are presented in Section 5.
2. Mathematical Model of 8-DOF Compound Multi-Body Aircraft
The compound multi-body aircraft studied in this article consists of three identical conventional-layout vehicles connected by spring hinges at the wingtips. The compound aircraft can only rotate around the x-axis due to the constraint of the hinge, ignoring gaps and undesired movements in other directions introduced by manufacturing error. The spring is assumed to be linear over the operating range (±40 degrees). While not all multi-body aircraft require spring hinges, some do, and most are single-degree-of-freedom spring hinges. To maintain generality, when modeling aircraft without spring hinges the spring coefficient is set to 0. For brevity, the individual aircraft are called “unit aircraft” and the unit aircraft at the center is named “the reference aircraft”. The configuration design of the compound aircraft is as shown in Figure 1. The definition of the relative roll angle of the compound aircraft is as shown in Figure 2. The total span of the prototype is 3.0 m, and the total weight is 2.25 kg. The moments of inertia along the X, Y, and Z axes of the unit aircraft are 0.027 kg/m, 0.023 kg/m, and 0.0041 kg/m, respectively. There are four actuators in the unit aircraft: one elevator, two ailerons, and one propeller thruster. For better manipulation performance, the elevator occupies 46% of the area of the horizon tail, and each aileron surface takes up 18% of the area of the main wing.
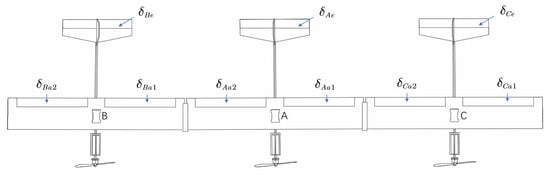
Figure 1.
Schematic of compound aircraft with three individual aircraft.
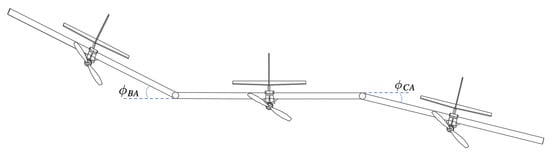
Figure 2.
Definition of relative roll angle and of the compound aircraft.
The Lagrange equations are employed in terms of the quasi-coordinates [17] to derive the equations of motion of the compound aircraft, which has the advantages of removing the constraint equations at the hinge and simplicity in comparison with the standard Lagrange equations.
Relevant CFD simulations and wind tunnel tests illustrate [18] that when two wing sections are joined the aerodynamic forces on the respective wings change somewhat compared to flying alone, which is mainly due to the aerodynamic coupling effect at the hinge on both wing surfaces and the disappearance of the corresponding wingtip vortices caused by the wingtip docking. The aerodynamic coefficient on each unit aircraft can be expressed as
where represents the original aerodynamic coefficients of the unit aircraft and denotes the impact factor, which can be expressed as a function of the relative roll angle and the angle of attack (AoA) , and where the index X represents lift (L) and drag (D) while the index Y denotes the identifier of the , , and unit aircraft
Coefficients (for example, and ) were calculated when analyzing the unit aircraft (omitted here); thus, the modeling of the compound aircraft turns on the determination of . This idea is improved from [19].
The following section explains the modeling process for , taking the impact factor of the lift coefficient , , and as an example.
First, we calculate , , and using a program based on lift-line theory under a series of relative roll angles ( ) and angles of attack (), as shown in Figure 3 (note that and share the same coefficients).
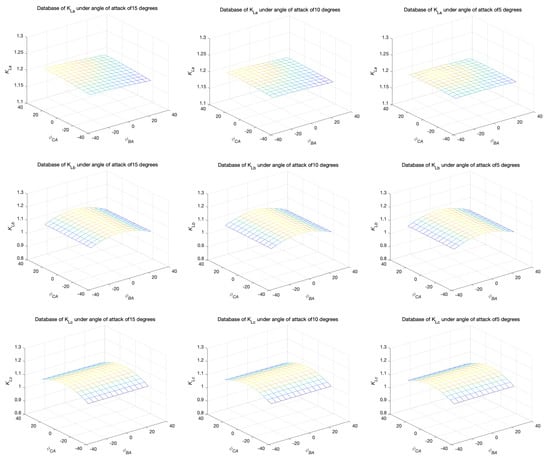
Figure 3.
Aerodynamic database of , , and under AoAs of 5, 10, and 15 degrees.
It is worth noting that while the lift coefficient changes significantly with the AoA, the impact factor is insensitive to it. This can be obtained by comparing the three subplots in each row of Figure 3. The last two rows of Figure 3 show that and are mainly affected by and , respectively. Further, the upper and lower deflections of the bank angle have nearly the same negative effects on the corresponding . These characteristics help in reducing the dimensionality of the aerodynamic database.
Next, polynomials are employed to fit the aerodynamic data. When fitting the data, the physical meaning of the form of the polynomials and the accuracy should both be taken into account, and the simplest expression should be chosen under the condition that the accuracy of the fit is guaranteed and the sum of the squared errors (SSE) is minimized.
Because the effects of and on are equivalent, the expressions of can be constructed as in Equation (2):
In fact, the CFD simulations suggest that is greater in dihedral configuration than in anhedral configuration; however, because this difference is minor, it is ignored in the expression.
Similarly, expressions of and are obtained as Equation (4):
In this paper, nearly all impact factors () of aerodynamic coefficients are studied, and it is found that the most influential ones are the factors for the lift and drag coefficients ( and ). This is because wingtip docking has a much greater influence on the main wing than on the horizontal and vertical stabilizers.
In practice, the relative roll angles and have a relatively small effect on . In most cases, can be approximated as constants rather than polynomials.
As shown in Figure 2, the quasi-velocity vector and the quasi-motion vector can be expressed as
where , , and denote the translational velocity in the body frame of the reference aircraft and , , and mean the angular velocity. The variables and represent the relative roll rate of the bank angle between the individual unit aircraft. Similarly, , , and represent the translocation of the reference aircraft and , , and are the Euler angles of the reference aircraft. Finally, and denote the bank angle.
The equations of motion in Lagrange’s method are formulated as follows:
In the above formula, L represents the Lagrange function, H and B are the assistant coefficient matrix, and denotes the generalized force and moments. The expressions of the above matrix are listed below:
The expressions of the generalized forces and moments are shown in Equations (11)–(13):
where and denote the kinetic energy and potential energy of the vehicle, respectively, represents the anti-symmetric matrix of vector , and C is the coordinate transformation matrix from the inertial coordinate to the body coordinate of the reference vehicle. The matrix transforms the Euler angle rate to the angle rate represented in the body axis. Moreover, and denotes the generalized forces and moments, means the transform matrix from frame a to frame b, k means the spring stiffness, and is the gravity of the unit aircraft.
3. Flight Dynamics and Modal Analysis
The longitudinal and lateral dynamics of a traditional aircraft are decoupled, with the short period and phugoid modes governing the longitudinal dynamics and the dutch roll, spiral, and roll modes making up the lateral dynamics. However, for a compound multi-body aircraft with extra degrees of freedom in relative roll motion, additional modes called flapping modes come into play [6]. Although classic flight dynamic modes are present for this type of aircraft, they are influenced by the flapping modes. This chapter begins by trimming and linearizing the compound aircraft, followed by modal analysis in different trimming configurations. It then delves into the mechanisms by which the different modes form and interact with each other. Finally, the nonlinear response and stability of the aircraft are studied.
3.1. Trimming, Linearization, and Mode Analysis
The trim state refers to a steady level flight of the compound aircraft without relative motion between the constituent unit aircraft. Assuming that each unit aircraft in the compound aircraft can stay in level flight without deflection of the control surface at neutral pitch, then the nonlinear dynamics from Equation (1) can be expressed in the form of Equation (14) with and as state vectors and as the control input.
Let and solve Equation (14); it is assumed that the AoAs of all unit aircraft remain neutral, while the velocity can vary. The solution of Equation (14) provides results that indicate a symmetric configuration. The compound aircraft can be trimmed under both anhedral and dihedral configurations, as shown in Figure 4.

Figure 4.
Anhedral and dihedral configurations of the compound aircraft.
Compared to the elevators and throttle, the ailerons play the most important role in trimming, allowing the aircraft to be balanced within a certain range of configurations between symmetrical anhedral and symmetrical dihedral, instead of just two trim points, which is the case without involving ailerons. The extension of the trimming range is related to the maneuverability of the aircraft’s ailerons and its maximum flight speed. Table 1 shows a series of trimming configurations for the compound aircraft, ranging from dihedral to anhedral configurations. In this table, the bank angle is assigned while the speed and control surfaces deflections are calculated. A bank angle of −3 deg represents a dihedral configuration of 3 deg, whereas a bank angle of 3 deg represents an anhedral configuration of 3 deg.

Table 1.
Trim configurations.
A compound aircraft in a anhedral or dihedral configuration always operates at a higher airspeed compared to a planar configuration. The main reason for this is that the deflections of the unit aircraft on both sides decrease the projected wing area, requiring a higher airspeed to generate sufficient lift.
Trim states with downward deflection of the side unit aircraft (anhedral configuration) result in a stable configuration, while upward deflection (dihedral configuration) can lead to configuration divergence (positive eigenvalues of flapping mode 1). Although anhedral configurations can harm the lateral stability of the compound aircraft with a positive eigenvalue of the spiral mode, this configuration is chosen as the operational state to ensure a stable configuration of the compound aircraft.
An anhedral configuration without deflection of the ailerons is chosen here as the operation configuration, though other anhedral configuration make sense as well. In the chosen stable trimming state, the Jacobian matrices can be derived and the eigenvectors and eigenvalues can be obtain to investigate the flight modes and stability of the compound aircraft. The full-state dynamic equations contain sixteen variables, meaning that there should be sixteen eigenvalues; however, four of these are located at the origin, and as such can be ignored. The remaining twelve eigenvectors and eigenvalues, corresponding to seven modes of the compound aircraft, are listed in Table 2 and Table 3.

Table 2.
Flight mode group 1 and corresponding eigenvalues.

Table 3.
Flight mode group 2 and corresponding eigenvalues.
A comparison investigation of the eigenvectors carried out with the help of the MAC matrix leads to
By evaluating the dot product of two analyzed vectors, The MAC matrix can be applied to analyze of the degree of coupling between the eigenvectors (in this case, the flight modes) for greater simplicity and intuitiveness [10]. Here, values the correlation of the and vector x, with as the eigenvector of the reference case and as the eigenvector of the currently considered case. The shading on the squares in the graph represent the strength of the correlation, with 1 indicating a perfect correlation and 0 indicating no correlation. An MAC matrix in diagonal form indicates low coupling between the investigated vectors. Figure 5 shows the MAC matrix for the compound aircraft in anhedral equilibrium configuration. Additionally, the MAC matrix indicates a division of the modal groups of the full-state flight dynamics into a symmetric mode group and asymmetric mode group.
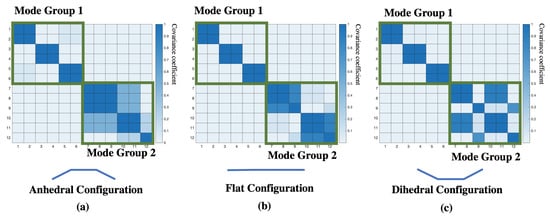
Figure 5.
MAC matrix of different trimming configurations. Modes 1 and 2: short period; modes 3 and 4: phugoid; modes 5 and 6: flapping mode 1; modes 7 and 8: flapping mode 2; mode 9: quasi-roll; modes 10 and 11: dutch roll; mode 12: spiral.
The relative roll motion (flapping modes) is the crucial mode of the compound aircraft. There are two types of flapping mode in the three-wingtip-docked compound aircraft, called flapping mode 1 and flapping mode 2, as shown in Figure 6 and Figure 7.

Figure 6.
Flapping mode 2 (anti-symmetric flapping mode).
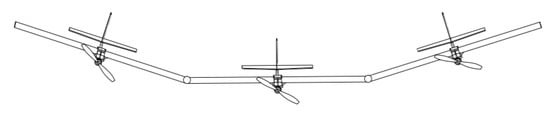
Figure 7.
Flapping mode 1 (symmetric flapping mode).
The division of longitudinal and lateral modes adapted in classic flight dynamics cannot be applied due to the addition of relative roll modes. The MAC matrix is basically presented in the form of a block diagonal matrix, indicating that the modal division of group 1 (symmetric motion) and group 2 (asymmetric motion) is reasonable. The symmetric mode group includes the short period, phugoidm and symmetric flapping (flapping mode 1) modes. The longitudinal motion (short period and phugoid) of the wingtip-docked compound aircraft analyzed in this study is not significantly different from that of a conventional aircraft [6]. In symmetric mode, the reference aircraft should be free of rolling motion. Flapping mode 1 presents a motion in which the side aircraft engages in synchronous up and down flapping motions with the same amplitudes while the reference aircraft remains horizontal. Flapping mode 1 inspires an entirely vertical velocity variation and an induced pitch.
In anti-symmetric flapping mode, here flapping mode 2, the unit aircraft on both sides roll at the same angles while the reference aircraft rolls in the opposite direction. This behavior is coupled with the lateral motion of the entire aircraft in terms of lateral velocity, yaw rate, and roll rate. During anti-symmetric flapping motion, the direction of the resultant lift vector deviates from the plane of the wind axis.
Dutch roll mode, spiral mode, anti-symmetric flapping mode (flapping mode 2), and quasi-roll mode form the asymmetric mode group. Under the anhedral operating configuration, spiral mode is unstable. Spiral mode can be easily excited, inducing instability of the entire vehicle in terms of rigid body motion and relative roll under lateral disturbances such as a slide-slip. Quasi-roll mode is an evolutionary version of the roll mode of a single aircraft in a three-wingtip-docked compound aircraft. The coupling effect of the rigid body motion and relative roll motion are illustrated in detail in Section 3.
Symmetrical motion does not stimulate asymmetrical motion; however, if asymmetrical motion is excited, symmetrical motion is excited as well. Strictly speaking, pure symmetrical motion does not exist in reality; if the initial condition is a symmetrical state, it can be easily disrupted in both numerical simulations and actual flight. When the roll attitude of the reference aircraft is not theoretically level enough, the vehicle enters a motion dominated by flapping mode 2 and dutch roll mode. In an anhedral configuration, all the flapping modes have an eigenvalue with a negative real part, guaranteeing the dynamic stability of relative roll motion. Figure 5b,c indicates that the trimming configuration influences the degree of coupling between modes.
Figure 8 shows the change in modes as the trim state of the aircraft shifts from dihedral configuration to anhedral configuration.
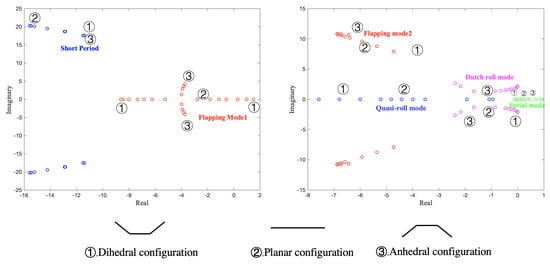
Figure 8.
Modal evolution as the configuration varies from dihedral to anhedral in the symmetric mode group (left subplot) and anti-symmetric mode group (right subplot).
The damping of the short period mode first increases and then decreases as the trim configuration changes. When the aircraft is completely planar, the damping of the short period mode is the largest. Under anhedral or dihedral configuration, the reduction of the projection area of the horizontal tail and the increase in the moment of inertia of the pitching axis cannot compensate, causing a decrease in damping of the longitudinal motion. The eigenvalues in phugoid mode vary on a scale of 10 × 10, and it is trivial compare this to other modes. For brevity, the eigenvalues in phugoid mode are not included in Figure 8.
Symmetric flapping motion varies from divergence to convergence as the configuration changes from dihedral to anhedral. This is because the aircraft on both sides tend to retract inward due to the torque generated by the lift with respect to the hinge point, resulting in configuration divergence. Symmetric flapping mode (flapping mode 1) changes from monotonic convergence to oscillatory convergence. This can be seen from Figure 8; the two eigenvalues meet on the negative real axis, then symmetrically separate along the imaginary axis direction and become a pair of conjugate complex eigenvalues.
The stability of anti-symmetric flapping motion (flapping mode 2) increases as the configuration moves from dihedral to anhedral, which is reflected in the fact that the real part of the pair of conjugated eigenvalues becomes smaller. There is no significant change in the eigenvectors in flapping mode 2. As the bank angles of the unit aircraft on both sides increase, the roll motion of the compound aircraft causes larger lateral velocity on the unit aircraft on both sides, which excites the lateral mode of the unit aircraft. therefore, the coupling of the rigid body motion (mainly dutch roll mode and spiral mode) with the relative roll motion becomes exacerbated (represented as quasi-roll mode for the compound aircraft).
The characteristics of spiral mode for compound aircraft are similar to those of a rigid aircraft in either anhedral or dihedral configuration. This reveals a contradiction in the stability of the flapping modes and spiral mode, in that dihedral configurations lead to instability of flapping mode 1 while guaranteeing the stability of spiral mode, while in anhedral configurations the opposite is true.
The dutch roll mode is worth studying as well. When the anhedral and dihedral angles of the configuration are large enough, dutch roll mode is coupled with anti-symmetric flapping mode (flapping mode 2) due to the mismatch between the roll and yaw rates of each individual aircraft in rigid body motion (represented in Figure 5a,c). Here, dutch roll mode no longer inherits the same meaning as it has for rigid aircraft; instead, it represents a motion that combines the relative roll motion and lateral flight mechanics. During a change in configuration, dutch roll mode changes from slight divergence to oscillatory convergence. This is because the equivalent and of the entire aircraft experience the process of sign change, with the absolute value of increasing as well. In addition, it is reasonable to presume that the flapping modes have an impact on the flight mechanics when the gap between the frequencies of both modes becomes narrow.
3.2. Nonlinear Dynamic Response and Stability
Nonlinear dynamic analysis provides an overview of the dynamic response of the compound aircraft. Here, the dynamic characteristics of the compound aircraft under disturbance of the AoA, side-slip angle, symmetric relative roll angle, and asymmetric relative roll angle are provided. The nonlinear dynamic response of the compound aircraft reflects a different phenomenon from that of conventional rigid-body aircraft. This phenomenon and its mechanism are introduced and explained below.
For disturbance of the AoA, the response of the wingtip-connected compound multi-body aircraft is roughly the same as that of a single-body aircraft, which is due to the fact that the hinge of the wingtip around the x-axis has little effect on the longitudinal characteristics, while the AoA response of the aircraft on both sides increases the oscillation frequency due to the coupling of flapping motion, as shown in Figure 9. How the flapping modes affect the short-period mode is explained in detail in the next chapter.
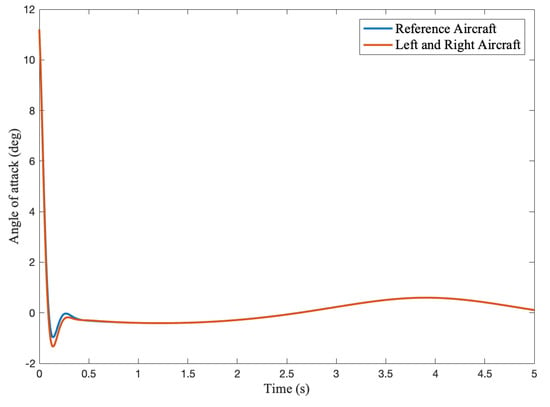
Figure 9.
Time domain response under unit impulse AoA disturbance without control input.
Lateral mode is considerably affected by the interaction of each unit aircraft, as shown in Figure 10. The side-slip angle response of the compound multi-body aircraft is convergent at first, reflecting the same lateral stability as a single-unit aircraft. However, as time passes it begins to oscillate. The lateral aerodynamic coefficient dominates the lateral stability by transferring side-slip motion to roll motion; meanwhile, the reference aircraft is forced to roll in the direction opposite the side aircraft under the same side-slip motion, stimulating anti-symmetric flapping mode in oscillation. Finally, unstable spiral mode increases the roll angle of the compound aircraft.
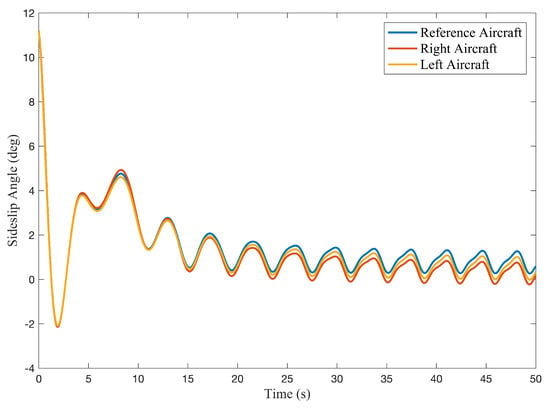
Figure 10.
Time domain response under unit impulse side-slip disturbance without control input.
The results of our nonlinear simulation of the symmetric relative roll are shown in Figure 11. Unit impulse disturbances of the symmetric relative roll angle were applied while the reference aircraft stayed in a level attitude; Figure 11a,c shows the convergent results for anhedral and dihedral disturbance, respectively, while in Figure 11b the relative roll angle response diverges rapidly under larger dihedral disturbance. This phenomenon can be seen more clearly in the phase diagram plot in Figure 12.
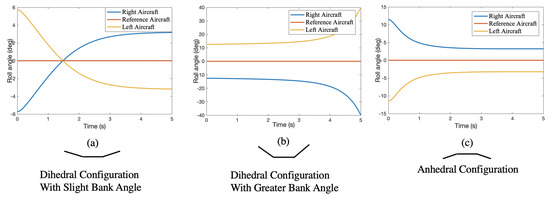
Figure 11.
Symmetric relative roll response under unit impulse disturbance without control input.
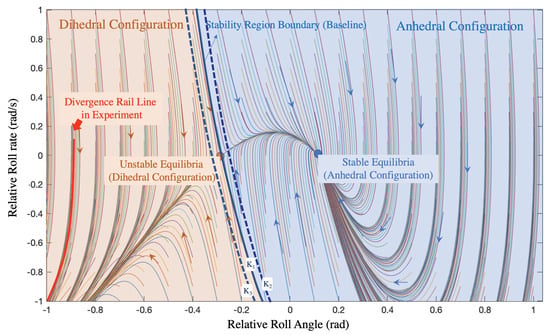
Figure 12.
Phase diagram of symmetric relative roll and roll rate.
Trim states are always in the symmetric anhedral or dihedral configuration. Thus, the X axis of the phrase diagram is the symmetric relative roll angle, with a positive value indicating an anhedral configuration and a negative value a dihedral configuration. The Y axis represents the corresponding deflection angular velocity.
The phase diagram shows that the two equilibrium configurations of the compound aircraft have different properties. The blue dot on the diagram represents the anhedral equilibrium configuration, which is a stable equilibrium point, while the brown dot represents the equilibria in dihedral configuration, which is a saddle point. This state represented by the brown dot is called the critical dihedral configuration, and the blue curve is the stability boundary dividing the attraction zone (in blue) and divergence area (in brown). A state point in the attraction area represents anhedral and slight dihedral configurations, both of which are stable in relative roll motion, while a state point outside the attraction area indicates that the relative roll angle of the compound aircraft will rapidly diverge; in the case of excessive upper deflection of the two aircraft on the sides, this means that the compound aircraft will be involved in a dangerous situation. This situation is recorded in flight experiments, shown in sequence from a to d in Figure 13. The deflection angles of the aircraft on both sides diverge rapidly, while the reference aircraft stays level. This state corresponds to the red line labeled in the phase diagram. As illustrated by this example, compound aircraft should not operate outside the attraction zone.

Figure 13.
Series of snapshots recording the divergence process.
Extension of the attraction zone can expand the operation boundary of the aircraft by introducing extra rolling aerodynamic torque, either by aileron deflection or by enhancing the spring stiffness of the hinge, corresponding to a leftward shift of the baseline. The dotted blue line beside the baseline in Figure 12 represents a shift in the stability region boundary under different K where . In this case, . As enhancing the spring stiffness of the hinge is contrary to the original intention of reducing the aircraft’s structural strength, aerodynamic design should instead be employed to add additional aerodynamic rolling torque to the aircraft on both sides, thereby extending the attraction zone.
During flight tests, it is often observed that the configuration of the compound aircraft diverges rapidly when it is disturbed by flying upwind, resulting in a situation similar to that shown in Figure 13. This is because the attraction zone narrows (a rightward shift of the baseline in the phase diagram) under the influence of upwind disturbance. As a result, a state point that would normally be within the attraction zone may fall into the divergence area. This highlights the sensitivity of compound aircraft to gusts.
4. Analytical Analysis of Modes and Flight Data Collection
This chapter introduces the unique modes of the compound aircraft and provides simplified analytical expressions for them in order to obtain the relationship between the aircraft motion and key parameters. The validity of the modes is demonstrated by flight tests, while the correctness of the simplified analytical expressions is verified using the eigenvalues. This section is an extension of the first two sections, and represents an important innovation of this paper.
From the perspective of flight performance, we hope that the aircraft is able to operate in a completely planar configuration. Therefore, the simplifications below are carried out under a planar configuration. While this assumption has a slight impact on the degree of modal coupling, it does not affect the modal mechanisms.
The compound aircraft has a set of controllers (pixkawk2 with built-in mpu6050 sensor and M8n GPS) that perform the basic flight functions and data recording. No pitot tube was mounted, as precise flight speed was not the focus of recording for this test. In order to measure the relative roll angle of the aircraft at both sides, two potentiometers were mounted at each hinge at the wingtips. Arduino with an ATmega328P processer was employed to convert the analog signals captured by the potentiometers to a digital signal sent to the flight controller. As the flight controller was responsible for running the PX4 software, an individual PX4 app module was developed to record and process the additional data. There were two flight modes in the fight programme, namely, stabilized mode and experimental mode. Stabilized mode activates during takeoff, landing, and hover flight, ensuring proper flight of the aircraft, while experimental mode is switched on when collecting free-response data; in experimental mode, all the control surfaces except thrust are disabled. For reliability, all data were subjected to Gaussian filtering in order to eliminate discontinuity and noise.
Snapshots of symmetric flapping mode and anti-symmetric flapping mode are demonstrated in Figure 14 and Figure 15 while corresponding experimental data and simulation data are compared in Figure 16 and Figure 17; it can be seen that while the two set of data show the same trends, there are a number of discrepancies. In Figure 16, the experimental data agree with the simulation data in the trend of damped oscillation. The three unit aircraft restore a level attitude at nearly the same time, leading to the compound aircraft being in a planar configuration. In Figure 17, the experimental data and simulation data show that under symmetric roll angle disturbance (anhedral configuration disturbance) the relative roll angle declines quickly, corresponding to the stability of flapping mode 1. The simulation is treated as the ideal condition, with the four most important reasons for the discrepancies (mainly frequency) between the simulation data and experimental data listed as follows:

Figure 14.
Snapshot of flapping mode 2.

Figure 15.
Snapshot of flapping mode 1.
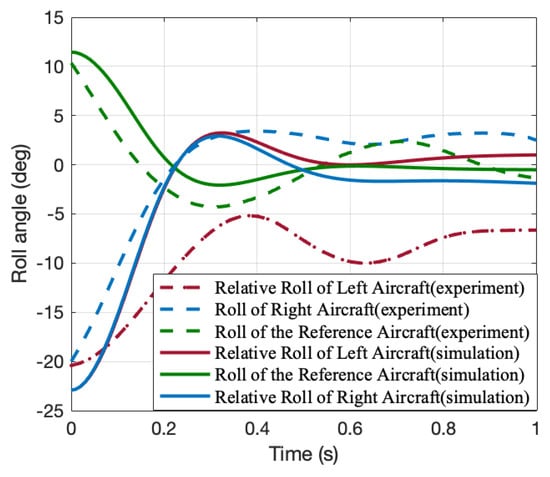
Figure 16.
Validation of flapping mode 2 by experimental data with no control input.
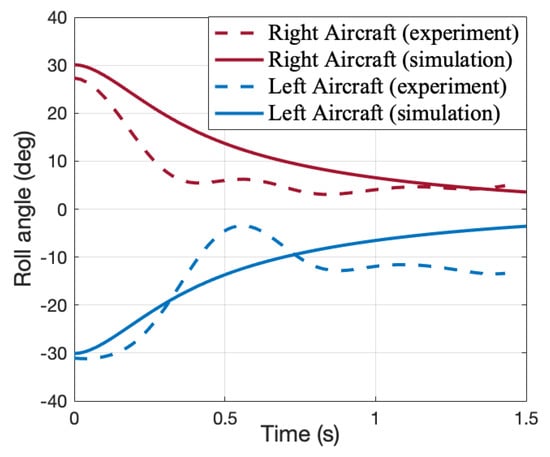
Figure 17.
Validation of flapping mode 1 by experimental data.
- (1)
- The three unit aircraft in the experiment are not exactly identical in terms of their inertia, mass, and aerodynamic characteristics. Further, the unit aircraft are assumed to be perfectly rigid in the simulation, while this is not the case in the experiment.
- (2)
- Neither complex aerodynamic forces nor the moments at the hinges are taken into account in the modeling and simulation.
- (3)
- Persistent and hard-to-measure disturbances in atmospheric gusts are present in the experiment.
- (4)
- It is not possible to apply unit impulse in the experiment.
4.1. Key Mode Analysis: Anti-Symmetric Flapping Mode
In this part, the anti-symmetric flapping mode is assessed analytically for further investigation, with new parameters defined. Figure 14 shows a snapshot of the recorded video displaying the aircraft in anti-symmetric flapping mode (flapping mode 2). The snapshot clearly demonstrates that the unit aircraft on both sides roll at the same attitude while the roll of the reference aircraft is opposite, corresponding to the eigenvectors of flapping mode 2.
The Jacobian matrix describing the dynamics of the critical flight modes is derived from equation [6]. It is assumed that:
- (1)
- Flapping mode motion only occurs spanwise;
- (2)
- No rigid body motion is stimulated except for the lateral velocity ;
- (3)
- The aircraft on both sides have the same relative roll angles in terms of the direction and amplitude ();
- (4)
- The local dynamic pressure differences between each meta-aircraft are ignored.
The derivation process includes simplifying the high-order and trigonometric terms. Further, by removing the states that are not couple with the critical modes, the number of equations can be decreased.
The dynamics of the anti-symmetric flapping motion can be expressed in state space as follows:
with
where represents the equivalent inertia, which consists of the inertia , mass M, and span of the unit aircraft b, K is the equivalent stiffness of the hinge spring, P is the dynamic pressure of the reference aircraft, and S denotes the reference wing area of the unit aircraft.
The eigenvalues of the simplified model and full state model are listed in Table 4. The simplification of flapping mode 2 is satisfactory.

Table 4.
Eigenvalues of the simplified model and full state model.
4.2. Key Mode Analysis: Symmetric Flapping Modes and Longitudinal Modes
This section mainly focuses on the analytical expression of symmetric motion; in addition, it covers the formation mechanism of symmetric mode and the coupled effect of symmetric flapping motion and longitudinal pitching motion. Photos representing symmetric flapping mode were captured, with an example in Figure 15 showing the symmetrical upward deflection of the two side unit aircraft while the reference aircraft remains horizontal.
The analysis was based on the following assumptions:
- (1)
- No rigid body motion is stimulated except for vertical translational motion and pitching motion;
- (2)
- The two aircraft on the sides have the same relative roll angle in terms of amplitude and opposite roll angles in terms of direction ();
- (3)
- The local dynamic pressure differences between the meta-aircraft are ignored.
Taking the state vector x of the symmetric motion and expressing the dynamics equation in the form of state space, the Jacobian matrix is expressed as Equation (22):
with
Table 5 indicates that the simplified dynamic model restores the dynamic characteristics of the full-state model in short period and flapping mode 1. For further simplification, the eigenvalues for flapping mode 1 can be derived as shown below.

Table 5.
Eigenvalues of the simplified model and full state model.
The influence of flapping mode on the pitching motion is mainly reflected in the term of the Jacobian matrix, which due to its representing the interaction between the pitch rate q and the relative roll angle. It is clear that the flapping motion induces a greater AoA of the wing sections, which finally leads to an increased pitch rate. Item shows that the slower a compound aircraft flies and the longer the wingspans of the unit aircraft, the greater the impact of flapping mode 1 on pitching motion.
The longitudinal response of the reference aircraft is affected by the longitudinal stability and the symmetric flapping motion, as shown in Figure 18. According to flight dynamics theory, symmetrical flapping motion causes change in AoA of the outer wing segment, and this change in the AoA causes the pitching moment to stimulate the overall pitching motion through the coefficient . The analysis can be simplified as follows: the flapping mode motion is the input excitation of the pitching motion (the longitudinal dynamics of the aircraft can be simplified into a second-order system); according to the second-order system properties, the output frequency of the pitching motion should be equal to the input frequency. Similar results have been found for flapping wing aircraft [20].
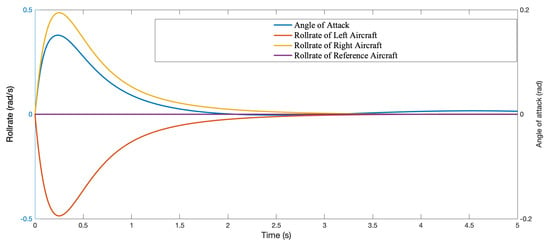
Figure 18.
Response of relative rolling and pitching motion in simulation.
The term of the Jacobian matrix dominates the influence of the pitching motion on the flapping mode. When the aircraft is in a planar configuration, the pitching motion has no influence on the flapping mode, which means that . In general, however, is listed as
with
The presence of the term in provides evidence for the previous statement that the influence of the pitching motion on the flapping mode is related to the deflection configuration.
Meanwhile, is the key factor that causes coupling. This is because in an anhedral or dihedral configuration the pitching motion of the aircraft affects the unit aircraft on both sides and introduces a yawing motion for them. Due to the presence of the lateral stability derivative , this yaw motion generates a roll moment (as well a a relative roll moment). When the compound aircraft pitches up, the roll moment weakens the deflection angle of the two aircraft on the sides. Conversely, when the vehicle pitches down, the deflection is intensified. Furthermore, kinematic theory predicts that the overall pitching velocity will result in the motion of the two aircraft on the sides exacerbating the relative roll angle under centrifugal force.
The K parameter appears in the analytical expression of the eigenvalues of the flapping mode, and has an important influence on the flapping mode. This parameter is independent of the aircraft design, and an appropriate value can be selected based on the expected characteristics of the flapping modes. Figure 19 shows the impact of K on the key modes of the aircraft; note that the spring stiffness k is not meaningful, and should be replaced by the equivalent stiffness K. With an increase in K, flapping mode 1 changes from monotone convergence to damped oscillation. The amplitude and oscillation frequency of flapping mode 2 both increase, while the quasi-roll mode degenerates into the same rolling mode as in classic rigid-body aircraft.
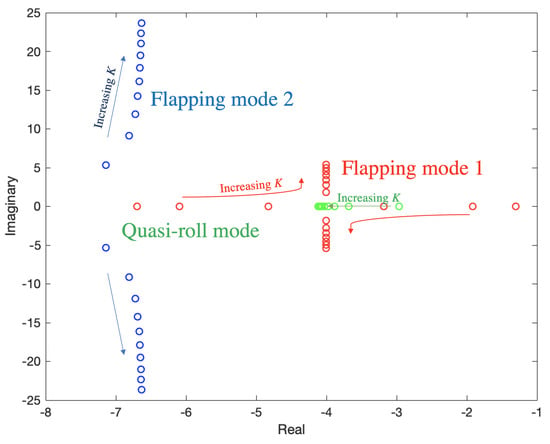
Figure 19.
Changes in flapping modes with increasing equivalent spring stiffness K.
5. Conclusions
This paper provides an analytical study of the flight dynamics of a compound aircraft from both linear and nonlinear perspectives, with a focus on the differences between compound aircraft with wingtip connection and classic individual aircraft. The findings of this study have important implications for the overall design and control law development of compound aircraft. The main results of this paper are listed below.
- (1)
- By adding degrees of freedom for the relative rotation of the two unit aircraft on the sides, the number of modes of the compound multi-body aircraft is increased from six rigid-body modes to eight. The flight modes can be divided into symmetric mode (phugoid, short period, and flapping mode 1) and asymmetric mode (spiral mode, dutch roll mode, flapping mode 2, and quasi-roll mode) groups. The additional degrees of freedom allow for dihedral and anhedral trimming configurations under neutral control surface deflection. In dihedral configurations, flapping mode 1 becomes divergent and spiral mode converge, while the opposite is true in anhedral configurations. Because the relative roll angle diverges much faster than the spiral mode, the aircraft should be operated near anhedral trimming configuration. The longitudinal mode of the compound aircraft is similar to that of a single vehicle, while most lateral modes are coupled with flapping mode 2 and quasi-roll mode.
- (2)
- The divergence of aircraft configuration becomes the main reason for the instability of the compound aircraft. By increasing the spring stiffness, the range of the stability region of the aircraft can be enlarged.
- (3)
- The flight modes of an aircraft can be affected by changes in the trimming configuration and equivalent connection stiffness, with flapping modes and dutch roll mode being the most susceptible. When the aircraft configuration is nearly planar and the equivalent stiffness is relatively high, the flapping modes and flight mechanics become distinct.
- (4)
- Expressions of state space and eigenvalues for both symmetric and asymmetric modes have been derived, from which we can infer the following: the longitudinal motion of the compound aircraft is affected by flapping mode 1, the dominant parameter is the equivalent stiffness K, and the aerodynamic derivatives are and . The lateral motion is affected by the coupling of flapping mode 2, quasi-roll mode, and dutch roll mode, with the dominant parameter being the equivalent stiffness K, with aerodynamic derivatives and . The spiral mode determines the divergence of the free response of the aircraft over a long time range.
The proposed research method and the parameters defined in this paper are extendable for wingtip-connected vehicles generally. In addition, the control laws applicable to the separation and recombination of compound aircraft will be the focus of our future research.
Author Contributions
Conceptualization, Z.Z. and E.Z.; Methodology, E.Z.; Software, H.L.; Validation, E.Z. and H.L.; Formal Analysis, H.L.; Draft Preparation, H.L. and E.Z.; Writing – Review & Editing, H.L., E.Z. and Z.Z.; Supervision, Z.Z.; Project Administration, Z.Z.; Funding Acquisition, Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Defence Fund of funder grant number 2021-JCJQ-JJ-0790 and 2022-JCJQ-JJ-1137.
Data Availability Statement
No data is availble due to secrecy.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| The collective term for the original aerodynamic coefficients of a single aircraft (dimensionless) | |
| C | The collective term for the aerodynamic coefficients of a single aircraft after being revised |
| (dimensionless) | |
| Aerodynamic coefficients correction factor (dimensionless) | |
| Relative roll angle between unit aircraft A and unit aircraft B (rad) | |
| Relative roll angle between unit aircraft A and unit aircraft C (rad) | |
| Relative roll rate angle between unit aircraft A and unit aircraft B (rad/s) | |
| Relative roll rate angle between unit aircraft A and unit aircraft C (rad/s) | |
| Quasi-velocity vector | |
| Quasi-motion vector | |
| P | Dynamic pressure (Pa) |
| S | Wing surface area (m) |
| b | Wing span (m) |
| k | Spring stiffness (N·m) |
| K | Equivalent spring stiffness (newly defined parameter) ()dimensionless) |
| M | Mass of the unit aircraft (kg) |
| Inertia along the y-axis of the unit aircraft (kg·m) | |
| Inertia along the x-axis of the unit aircraft (kg·m) | |
| Equivalent inertia (newly defined parameter) (kg·m) | |
| AoA | Angle of Attack (rad) |
| SSE | Sum of Squared Errors |
References
- McGill, S. Compound aircraft transport study: Wingtip-docking compared to formation flight. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Hampton, VR, USA, 6–9 January 2003; p. 607. [Google Scholar]
- Anderson, C.E. Dangerous Experiments: Wingtip Coupling at 15,000 Feet. Flight J. 2000, 5, 64. [Google Scholar]
- Oung, R.; Ramezani, A.; D’Andrea, R. Feasibility of a distributed flight array. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC) Held Jointly with 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; pp. 3038–3044. [Google Scholar]
- Zhou, W.; Ma, P.; Guo, Z.; Wang, D.; Zhou, R. Research progress of combined fixed-wing unmanned aerial vehicle based on wingtip chained. Acta Aero-Naut. Astronaut. Sin. 2022, 43, 325946. (In Chinese) [Google Scholar] [CrossRef]
- Montalvo, C.; Costello, M. Meta aircraft flight dynamics. J. Aircr. 2015, 52, 107–115. [Google Scholar] [CrossRef]
- Troub, B.; Montalvo, C.J. Meta aircraft controllability. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Washington, DC, USA, 13–17 June 2016; p. 3395. [Google Scholar]
- Montalvo, C.; Costello, M. Meta Aircraft Connection Dynamics. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Minneapolis, MN, USA, 13–16 August 2012; p. 4677. [Google Scholar]
- Carithers, C.; Montalvo, C. Experimental control of two connected fixed wing aircraft. Aerospace 2018, 5, 113. [Google Scholar] [CrossRef]
- Köthe, A. Flight Mechanics and Flight Control for a Multi-Body Aircraft. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2019. [Google Scholar]
- Köthe, A.; Luckner, R. Applying Eigenstructure Assignment to Inner-Loop Flight Control Laws for a multi-body Aircraft. CEAS Aeronaut. J. 2022, 13, 33–43. [Google Scholar] [CrossRef]
- Köthe, A.; Luckner, R. Flight Path Control for a Multi-body HALE Aircraft. In Advances in Aerospace Guid-Ance, Navigation and Control; Springer: Cham, Switzerland, 2018; pp. 421–442. [Google Scholar]
- Köthe, A.; Behrens, A.; Hamann, A.; Nagel, P.; Nowka, D.; Luckner, R. Closed-loop flight tests with an un-manned experimental multi-body aircraft. In Proceedings of the International Forum on Aeroelasticity and Structural Dynamics (IFASD), Como, Italy, 25–28 June 2017. [Google Scholar]
- Yang, M.E.; Chao, A.N.; Changchuan, X.I.; Chao, Y.A. Conceptual design and flight test of two wingtip-docked multi-body aircraft. Chin. J. Aeronaut. 2022, 35, 144–155. [Google Scholar]
- Cesnik, C.E.; Senatore, P.J.; Su, W.; Atkins, E.M.; Shearer, C.M. X-HALE: A very flexible unmanned aerial vehicle for nonlinear aeroelastic tests. AIAA J. 2012, 50, 2820–2833. [Google Scholar] [CrossRef]
- Bertolin, R.M.; Guimarães Neto, A.B.; Barbosa, G.C.; Paulino, J.A.; Silvestre, F.J. Design of Stability Augmen-tation Systems for Flexible Aircraft Using Projective Control. J. Guid. Control Dyn. 2021, 44, 2244–2262. [Google Scholar] [CrossRef]
- Guimarães Neto, A.B.; Barbosa, G.C.; Paulino, J.A.; Bertolin, R.M.; Nunes, J.S.; González, P.J.; Cardoso-Ribeiro, F.L.; Morales, M.A.; da Silva, R.G.; Bussamra, F.L.; et al. Flexible Aircraft Simulation Validation with Flight Test Data. AIAA J. 2021, 61, 285–304. [Google Scholar] [CrossRef]
- Meirovitch, L.; Stemple, T. Hybrid equations of motion for flexible multi-body systems using quasicoordinates. J. Guid. Control Dyn. 1995, 18, 678–688. [Google Scholar] [CrossRef]
- Baldelli, D.H.; Lee, D.H.; Pena, R.S.; Cannon, B. Modeling and control of an aeroelastic morphing vehicle. J. Guid. Control Dyn. 2008, 31, 1687–1699. [Google Scholar] [CrossRef]
- Liu, D.; Xie, C.; Hong, X. Dynamic characteristics of wingtip-jointed composite aircraft system. J.-Beijing Univ. Aeronaut. Astronaut. 2021, 47, 2311–2321. [Google Scholar] [CrossRef]
- Xue, D.; Song, B.F.; Song, W.P.; Yang, W.Q. Advances in coupling aeroelasticity and flight dynamics of bird inspired FMAV. Acta Aerodyn. Sin. 2018, 36, 88–97. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).