Abstract
Concerned with the problem of interceptor midcourse guidance trajectory online planning satisfying multiple constraints, an online midcourse guidance trajectory planning method based on deep reinforcement learning (DRL) is proposed. The Markov decision process (MDP) corresponding to the background of a trajectory planning problem is designed, and the key reward function is composed of the final reward and the negative step feedback reward, which lays the foundation for the interceptor training trajectory planning method in the interactive data of a simulation environment; at the same time, concerned with the problems of unstable learning and training efficiency, a trajectory planning training strategy combined with course learning (CL) and deep deterministic policy gradient (DDPG) is proposed to realize the progressive progression of trajectory planning learning and training from satisfying simple objectives to complex objectives, and improve the convergence of the algorithm. The simulation results show that our method can not only generate the optimal trajectory with good results, but its trajectory generation speed is also more than 10 times faster than the hp pseudo spectral convex method (PSC), and can also resist the error influence mainly caused by random wind interference, which has certain application value and good research prospects.
1. Introduction
The midcourse guidance phase of the interceptor takes the longest proportion of time in the composite guidance process, which directly determines the range and distance of the interceptor and plays an important role in determining whether the interceptor can have a good interception situation at the initial stage of the terminal guidance phase [1]. However, due to the influence of target maneuver, especially regarding the high-altitude, the high-speed and strong maneuvering targets, midcourse guidance trajectory needs online real-time planning to cope with real-time changing terminal constraints.
At present, the research of trajectory online planning mainly faces the following difficulties: (1) The real-time performance of the online planning method is difficult to guarantee; (2) In order to ensure the efficiency of online planning, it is difficult to generate the real optimal trajectory with high accuracy; (3) Dynamic pressure, heat flow density, overload and other constraints restrict the efficiency of trajectory planning, which brings great difficulties to engineering implementation. In order to solve the difficulties encountered in online trajectory planning, a large number of researchers have conducted in-deep research, References [2,3,4,5,6] introduced convex optimization theory into the online reentry trajectory planning of aircrafts, making it easy to solve the trajectory and providing a new idea for online trajectory planning. However, this method requires a specific simulated flight trajectory as the initial value, which leads to strong restrictions. The trajectory planning problem can also be regarded as an optimal control problem, and the pseudo spectral method is very popular in the numerical solution of optimal control problems [7,8]. Typical methods include the Gauss pseudo spectral method [9], Radau pseudo spectral method [10], etc. References [11,12,13] have applied various improved pseudo spectral methods in optimal trajectory generation design and achieved a good optimization performance. However, the pseudo spectral method cannot be directly applied to engineering practice due to an uncertain solution time [14]. References [15,16] proposed a new hybrid guidance method for the guidance problem of reusable launch vehicles during the descent and landing stages, combining convex optimization theory and the improved transcription of the generalized hp pseudo spectral method. It not only satisfies the constraints acting on the system and reduces optimization time, but also is more accurate than standard convex optimization, providing the possibility for the real-time online resolution of guidance problems. References [17,18,19,20] used an inverse dynamics in the virtual domain (IDVD) method, which transforms the trajectory planning problem from the time domain to the virtual domain by virtual factors and then optimizes the trajectory using the dynamic inversion method. It not only has good real-time and robust performance, but can also meet the process constraints. However, the accuracy problem that restricts the effectiveness of the method has not been well solved.
The foothold of the traditional trajectory online generation algorithm is based on the offline trajectory or discrete waypoints, which strictly limits the effective improvement of the real-time performance of the algorithm and increases the degree of nonlinear violation of the trajectory online planning problem. With the development of telemetry technology and simulation technology, more and more data can be observed and applied in the field of aircraft guidance and control, which provides a new design mode for trajectory online planning methods, that is, trajectory planning methods based on data-driven approaches, which are expected to solve problems that cannot be solved by traditional methods. In recent years, artificial intelligence (AI) has flourished in various fields of society, and is regarded as the main innovative technology to solve high-dimensional complex systems [21], which is the best way to achieve such methods. In particular, the technology of deep reinforcement learning (DRL), which combines reinforcement learning (RL) and deep learning (DL), has attracted extensive attention in various fields and it has been applied in the research of auto driving [22,23,24], UAV path planning [25,26,27] and robot motion control [28,29]. With the development of telemetry technology and simulation technology, more and more data can be observed and applied in the field of aircraft guidance and control, providing a new design mode for trajectory planning methods, namely that of trajectory planning methods based on a data-driven approach, and the DRL is the best way to achieve such methods. As a classical DRL algorithm, the deep Q network (DQN) algorithm [30] first introduced the deep neural network into RL as a function approximator, which enhanced the ability to fit functions, mastered the method of learning control strategies directly from high-dimensional inputs and successfully solved the continuous state space problem, but it could not be applied to the continuous action control and the training effect was unstable. In order to solve the problem of continuous action space, reference [31] proposed a deterministic policy gradient (DPG) algorithm, which used deterministic behavior strategies instead of random strategies, reducing the amount of sampled data and improving the computational efficiency. The deep determination strategy gradient algorithm adds the DQN algorithm idea to DPG algorithm [32] and better solves the problem of the actor–critic network convergence, making the training process more stable. Moreover, it solves the problem that the actor–critic network is difficult to converge, which also increases the stability of the training process. Reference [33] proposed the proximal policy optimization (PPO) algorithm, which mainly aims to improve the efficiency of the algorithm by updating the policy. The advantage of this method is that it can utilize the sampled samples multiple times, to some extent solving the problem of low sample utilization. References [34,35,36] applied the PPO algorithm to planetary power descent and landing phase guidance, missile terminal guidance and hypersonic strike weapon terminal guidance tasks, providing a reference for the application of DRL technology in the field of trajectory planning generation.
The algorithm design of trajectory online planning generation can be used as a control decision problem. The speed, position and part of the target information can be obtained through sensors, which can better describe the state of the dynamic environment. The control quantity acting on the friendly missile can be regarded as an action. Thus, the online trajectory planning problem can be studied under the reinforcement learning framework, and it is expected to overcome some difficulties of traditional algorithms. In addition, applying DRL to solve this problem can jump out of the limitations of traditional models and find potential performance and more excellent online trajectory planning methods. This can also provide a new algorithm model reference for experts in this field.
In conclusion, for the complex and high-dimensional midcourse guidance trajectory planning model, this paper selects the DDPG algorithm to train the interceptor for trajectory planning, and obtains the midcourse guidance online trajectory planning method according to the set training strategy. The main contributions are summarized as follows:
- (1)
- The Markov decision process (MDP) is designed according to the characteristics of the midcourse guidance trajectory planning model. The reward function is designed using the negative feedback reward contrary to the traditional positive reward, which makes the agent learning more consistent with the interceptor guidance mechanism;
- (2)
- The trajectory planning task training strategy is set based on the idea of course learning (CL) to deal with the low convergence of the direct training of the DDPG algorithm. The algorithm convergence is significantly improved by replacing the training task from easy to difficult, which is verified by simulation experiments;
- (3)
- The trajectory planning of midcourse guidance is investigated using the DDPG algorithm. The optimality of the trajectory it solves is similar to the traditional optimization algorithm, which has higher efficiency and is more suitable for online trajectory planning, as verified by simulation experiments.
The work in this paper is arranged as follows. This section describes the research status of the online trajectory generation algorithm and expounds the innovation of this paper. The second section describes the problem of midcourse guidance trajectory online planning. The third section gives the MDP design method. The fourth section gives the DDPG algorithm model. The fifth section describes the online planning method of the medium-guided trajectory. The sixth section performs the simulation verification for the research content. The last section summarizes the contents of this paper and looks forward to the next research direction.
2. Online Trajectory Planning Problem Formulation
2.1. Model Build
The context of this paper includes the ground-based interceptor and high-altitude high-speed strong maneuvering target, as shown in Figure 1.
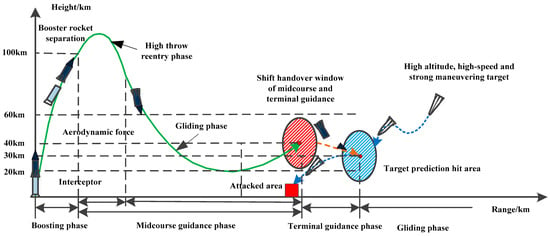
Figure 1.
Full-range trajectory of ground-based interceptor.
The whole trajectory of the interceptor is mainly divided into four phases: the boosting phase, midcourse guidance–high throw reentry phase, midcourse guidance–gliding phase and terminal guidance phase. In the boosting phase, the interceptor will be launched vertically, the rocket booster will send the interceptor to the designated altitude quickly and give it a fast flight speed. After the rocket booster completes the task, the booster stage of the interceptor falls off and turns into the midcourse guidance–high throw reentry phase. The interceptor continues to fly up to the high throw point relying on inertia and reenters the adjacent space by adjusting its attitude. In the midcourse guidance–gliding phase, the interceptor glides freely with the help of the aerodynamic rudder of the correction stage and aerodynamic force. After flying to the shift handover window of the midcourse and terminal guidance, the correction stage of the interceptor falls off and enters the terminal guidance phase. The time of the terminal guidance phase is generally short. When the interceptor flies to the predicted hit area, the seeker starts to capture the target and the interceptor intercepts the target under the guidance of the terminal guidance law through the direct/air composite control. The research of midcourse guidance trajectory planning in this paper is mainly focused on midcourse guidance–gliding trajectory.
The simplified midcourse guidance motion model of the interceptor [37] is as follows:
where , and are the coordinates of the interceptor’s center of mass under the northeast sky coordinate system, respectively, is interceptor speed, is the trajectory inclination angle, is the trajectory deflection angle, is the drag acceleration, is the lift acceleration, is the gravity acceleration, is the angle of bank, is the Earth’s radius with a value of 6371.2 km.
The calculation of , and is as follows,
where is the drag coefficient, is the lift coefficient, is dynamic pressure, is the characteristic area of the interceptor, is the interceptor mass, is the gravity acceleration at sea level and its value is 9.81 m/s2.
The calculation of and is the function formula containing the angle of attack ,
The calculation of is as follows,
where is the air density and its calculation formula is as follows,
where = 1.226 km/s3 is the air density at sea level and H = 7254.24 m is the reference height.
For the convenience of calculation, all the above variables can undergo dimensionless treatment by the normalization method, as follows:
where , and represent dimensionless coordinate positions; represents the dimensionless speed; represents dimensionless time; , and represent dimensionless lift, drag and gravity.
2.2. Problem Formulation
According to the model analysis in Section 2.1, the state equation of the interceptor can be expressed as
where represents the state variable of the interceptor and represents the control variable of the interceptor.
In order to meet the requirements of fast interception, the performance index is selected as the shortest time to reduce the escape probability of the target and relieve the pressure of long-term target trajectory prediction.
In the midcourse guidance phase, the interceptor flies at high altitude and high speed for a long time, which will inevitably be restricted by the constraints of heat flow density , dynamic pressure , overload and control input . The optimized trajectory should satisfy the following constraints:
where C = 1.291 × 10−4 is the calculation constant of and represents the maximum limit of the constraints.
In addition, the boundary conditions of the midcourse guidance phase are composed of the high throw reentry point of the trajectory and the position of the predicted handover point. The trajectory planning needs to meet the following boundary conditions
where and represent the initial value and terminal value of the variable, respectively.
The online trajectory planning problem in the midcourse guidance phase can be expressed as follows: under the conditions of Equations (7), (9) and (10), the online trajectory planning with the requirements can be solved, and the value of Equation (8) should be as optimal as possible.
3. MDP Design
The interaction between the agent and environment in DRL follows the MDP, which mainly includes the state set S, the action set A, the reward function R, the discount coefficient γ and the transition probability. This paper uses the modeless DRL method, so the transfer probability is not considered. To facilitate the training and learning of the RL algorithm, the corresponding <S, A, R, γ> is designed based on the background of the midcourse guidance trajectory planning problem.
3.1. State Set
When designing the state set, the principle of taking information that is helpful to solve problems as much as possible and discarding information that may interfere with decisions is followed. According to the guidance mechanism of the interceptor, based on the original interceptor state variable, this paper defines the remaining distance of interceptor , the longitudinal plane component and the transverse plane component of the velocity leading angle of interceptor; their expressions are
where and are the components of the line-of-sight angle of the interceptor target in the longitudinal and transverse planes, respectively. Therefore, the state set of interceptors is defined as S = .
3.2. Action Set
As the input of the interceptor guidance control, the action set is composed of control variables and . According to the interceptor control constraint, the control set of the interceptor is defined as A = .
3.3. Reward Function
The design of the reward function is the key to affect the learning convergence of the algorithm. In order to make the interceptor find the target point better, this paper not only gives the final reward, but also designs the feedback reward of the corresponding simulation step according to the prior knowledge, that is, and should be as small as possible, so that the interceptor can always fly towards the direction near the target. The reward functions are given by
where is constant, is the simulation step, and are, respectively, the velocity leading angle component of the corresponding . represents the final reward obtained by the interceptor when it meets the condition , and the final reward is inversely proportional to the sum of the simulation steps, that is, the interceptor is encouraged to complete the task in the shortest time. represents the feedback reward of corresponding , and its negative value is to encourage the interceptor to keep the speed direction always towards the target so as to optimize the shortest flight time; represents the termination condition. In combination with the background of interceptor head-on interception mode in practice, is set as
Combining Equations (14) and (15), the reward function is the sum of the final reward and feedback reward, that is, .
3.4. Discount Coefficient
The discount coefficient γ is between 0 and 1, which represents the degree of impact of future rewards on current rewards. γ = 0 refers to the current reward only relying on the reward from the next moment, γ = 1 refers to the future rewards that are equally important for the current state, regardless of how far they are from the present. In practical applications, γ generally does not choose 1 for the following reasons: (1) It is difficult to mathematically ensure the convergence of the formula; and (2) Future behavior is uncertain. Usually, the farther the future behavior is from the present, the less impact it should have on the present. To enable the obtained trajectory to comprehensively consider the overall performance, based on experience, the value of γ is set as 0.99.
4. DDPG Algorithm Model
The DDPG algorithm adopts an actor–critic network architecture, and it creates a mutually independent actor target network (hereinafter referred to as network) and the critical target network (hereinafter referred to as the network) as copies of the actor online network (hereinafter referred to as the network) and the critic online network (hereinafter referred to as a Q network), respectively, as shown in Figure 2.
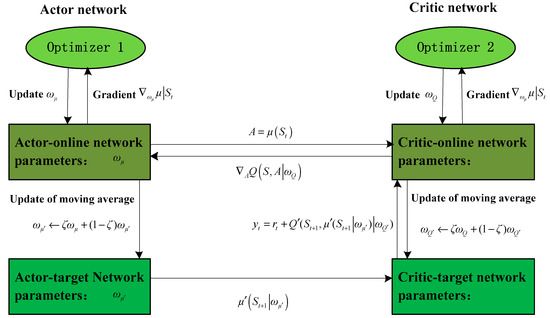
Figure 2.
Network structure of DDPG algorithm.
The Q network updates the parameter using the temporal difference error method of the DQN algorithm, and the loss function L is represented by the minimum mean square error
where N is the number of samples, is an accurate label of the network, which is obtained using the Bellman optimal equation. In order to make the learning process of parameter more stable and improve the convergence performance, the network is also used in its calculation
Based on the standard back propagation method, the parameter is optimized and updated according to the gradient ,
where is the learning rate of the Q network.
The update of parameter in the network follows deterministic strategy,
where is the learning rate of the network.
The parameters of the network and network are updated in the way of moving average
where is the update parameter and the value of is 0.01. This makes the target network parameters update slowly and improves the stability of learning.
To ensure the effective exploration of agents in the continuous space learning process, the DDPG algorithm introduces the Ornstein–Uhlenbeck stochastic process as the random noise
To deal with different dimensional problems, the DDPG algorithm also uses batch standardized DL technology, which can normalize each dimension in small batch samples to obtain the unit mean and variance so as to improve the learning efficiency of the algorithm.
In addition, the DDPG algorithm uses the experience playback mechanism of the DQN algorithm for reference. When generating sample data, the data obtained from the environment will be stored in the memory with a state transition sequence as the unit (St, At, Rt, St+1) to deal with the Markov problem of RL data.
5. Online Trajectory Planning Method for Midcourse Guidance
In this section, based on the midcourse guidance motion model, the MDP design and DDPG algorithm model, the interceptor is trained and the midcourse guidance trajectory planning method is obtained.
5.1. Training Strategy Based on CL
The CL refers to the method of gradually increasing the difficulty of tasks in machine learning to increase the learning speed. Agents are more likely to obtain the final reward in simple tasks, and the idea of CL is to transfer the strategy of completing simple tasks to complex tasks to gradually achieve the desired learning effect. Its advantage is that it can effectively reduce the exploration difficulty of complex tasks and improve the convergence speed of the algorithm.
The midcourse guidance trajectory planning problem is a complex nonlinear optimization problem, which not only needs to meet various constraints, but also needs to ensure the optimal performance as far as possible. If the above problem is not handled and the DDPG algorithm is used directly to learn and train the problem, it is likely to cause the interceptor to be difficult to reach the termination condition and the algorithm cannot converge. Therefore, the CL method is extended to the midcourse guidance phase trajectory training strategy.
Regarding the steps of the training task setting of the strategy, we first arbitrarily give the position of the handover point at the end of midcourse guidance phase; with the termination condition as = 5 km and does not consider process constraints of the trajectory. Furthermore, we consider the process constraints and set the termination condition as = 0.5 km. Note that arbitrarily giving the position of the handover point at the end of midcourse guidance phase is mainly reflected in the changes of and caused by the target maneuver. Process constraints are expressed in the form of termination conditions in the algorithm, as follows
In the training process, the learning task from easy to difficult is set by adding the process constraints and improving the convergence criteria, and the midcourse guidance trajectory planning ability of the interceptor is trained step by step, which has a good effect upon improving the generalization of the model.
Therefore, a training strategy combining the CL idea and the DDPG algorithm is proposed for the midcourse guidance trajectory planning training task. The training network is shown in Figure 3, and the specific training strategy process is as follows:
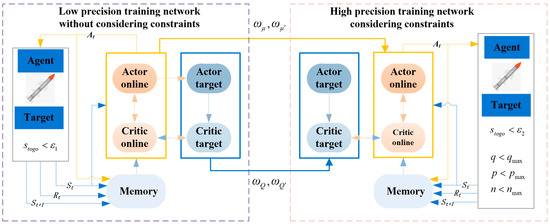
Figure 3.
Training network for trajectory planning task in the midcourse guidance phase.
The low-precision training network without process constraints and the high-precision training network with process constraints are designed;
The interceptor is trained in low-precision network to learn to complete simple tasks and obtain network parameters;
The low-precision network parameters are transferred to the high-precision network, and the interceptor continues to be trained in the high-precision network to learn to complete complex tasks.
5.2. Online Trajectory Planning Method
The main limitation of online trajectory planning is the real-time problem of the algorithm, especially when the interceptor and target speed are very fast, many optimization algorithms do not meet the constraint requirements of the problem. Therefore, this paper applies the above offline training strategy to train the interceptor trajectory planning capability, and proposes an online trajectory planning method based on this. The specific process is as follows:
- (1)
- Transform the interceptor midcourse guidance trajectory planning model into the corresponding MDP of the DDPG algorithm;
- (2)
- Based on the DDPG algorithm model, refer to Section 3 for details, and set the offline algorithm training process. The pseudocode is detailed in Algorithm 1.
| Algorithm 1. Offline DDPG algorithm training. |
| Initialize critic network and actor with weights Initialize target network with weights Initialize the memory capacity for episode = 1, M do Initialize the random process (as exploration noise) Set the initial state of interceptor Randomly select the target point position for t = 1, T do Select the action of the interceptor according to the current strategy and exploration noise Execute At, calculate the current reward Rt, integrate the next state St+1 Store the state transition sequence (St, At, Rt, St+1) in the memory Randomly sample small batch training data of N sequences (St, At, Rt, St+1) form memory Update according to the DDPG network model (Equations (16)–(22)) end for end for |
- (3)
- Set the low-precision training network without considering constraints, substitute the interceptor into the offline training process of step (2) and obtain the optimal parameters of the network;
- (4)
- Set high-precision training network considering constraints as well as substitute the interceptor into the offline training process of step (2), note that the optimal parameters trained in step (3) are taken as the initial parameters of the network and obtain the optimal parameters of the network;
- (5)
- Based on the offline trained network parameters, the midcourse guidance planning trajectory is quickly generated online. The pseudocode is detailed in Algorithm 2.
| Algorithm 2. Online trajectory planning. |
| Input the initial state of interceptor and the target point position Import optimal network parameters to the network Select the action of the interceptor according to the optimal strategy Integral calculation of the state sequence of the interceptor Output interceptor midcourse guidance planning trajectory |
6. Simulation Verification
6.1. Experimental Design
Assuming that the interceptor has completed the trajectory planning of the boost phase and the middle guidance high throw phase before the middle guidance gliding phase, the mass of the interceptor is 900 kg and the characteristic area of the interceptor is 0.7 m2. The initial state parameters and process constraint parameters are set as shown in Table 1 and Table 2.

Table 1.
Initial state parameters.

Table 2.
Process constraint parameters.
The change range of the forecast handover point needs to fully consider the impact of the target maneuver, mainly reflected in the change of hf and zf, and the terminal position parameters are set as shown in Table 3.

Table 3.
Terminal position parameters.
This paper uses Python language for simulation the experiment programming, MATLAB software for simulation drawing and Pytorch module to support DRL. The input layer of the network and network has 9 nodes, and the output layer has 2 nodes, the input layer of Q network and network has 11 nodes and the output layer has 1 node, all networks contain a hidden layer with 300 nodes, and the learning rate of all networks is set to 0.0001. The Adam Optimizer is used as the optimizer of the network parameters in the simulation. The memory capacity is set to 1 × 106, the number of samples for random N is set to 2000, and the maximum number of workouts is set to 1 × 105. The value of the simulation step in this paper is 1.
In addition, except for the algorithm anti-interference verification in Section 6.5, all other simulation experiments in this article do not add disturbances.
6.2. Algorithm Convergence Verification
Define two training strategies, one of which is the training strategy based on CL, and the other is the direct training strategy. The average reward index (that is, the average of the total rewards of 50 rounds, when the round is less than 50 rounds, use the average of the total rewards of total rounds as the average reward) is used to observe the convergence of the algorithm. The simulation data are shown in Figure 4.
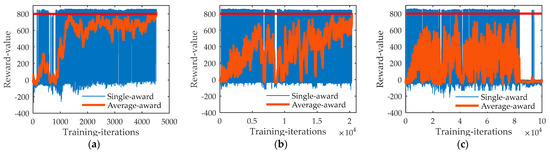
Figure 4.
Comparison of the convergence between two training strategies: (a) Step 1 training in CL training strategy; (b) Step 2 training in CL training strategy; and (c) Direct training strategy.
In the simulation, when the average reward reaches 800, the training achieves the desired effect, and the algorithm converges. It can be seen from the simulation results in Figure 4 that when the training strategy based on CL is adopted for training, the DDPG algorithm achieves the training effect when the number of training iterations in the step 1 task training is 4536,and the training effect when the number of training iterations in step 2 task training is 20,368. When the training strategy based on direct training is adopted, the DDPG algorithm is trained to the maximum number of iterations (1 × 105), but the expected effect was not achieved. By comparing the training effects of the two training strategies, the convergence based on the CL training strategy is more prominent. In addition, the training strategy of the direct training significantly declines in the training effect during the late training period, as shown in Figure 4c; this shows that the method of direct training from scratch is not suitable for the complex high-dimensional interceptor midcourse guidance trajectory planning task, and it is easy to lead to the interceptor, which cannot find a feasible solution to the problem.
6.3. Algorithm Effectiveness Verification
In order to verify whether the trajectory generated by the algorithm meets the constraint requirements, the Monte Carlo experiment method is used to conduct simulation experiments on the networks trained in two strategies, the terminal position parameters are randomly generated and 10,000 Monte Carlo tests are conducted, respectively; the simulation data are shown in Table 4.

Table 4.
Test results of two training strategies.
According to the test results in Table 4, the success rate and average reward of the training strategy based on CL designed in this paper are far greater than direct training, and its standard deviation is also less than direct training, which shows that the DDPG algorithm combined with the CL idea has more effective training effect than direct training. In addition, this paper only divides the trajectory planning task into two steps of training, whilst the stage training task can be further refined in the future to improve the success rate and convergence of the training strategy.
6.4. Algorithm Optimization Performance Verification
In order to verify the optimization performance of the method in this paper, the trajectory online planning method in this paper (CLDDPG) is used to optimize the trajectory online, and the terminal position parameters are random. At the same time, under the same simulation conditions, the hp pseudo spectral convex method (PSC) in the literature [15] is used to compare with the method in this paper, and the PSC method selects 100 nodes. The simulation data are shown in Figure 5 and Table 5.
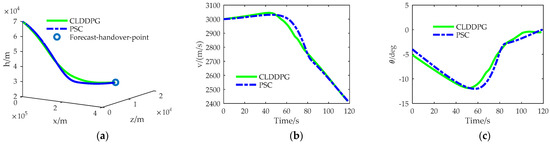
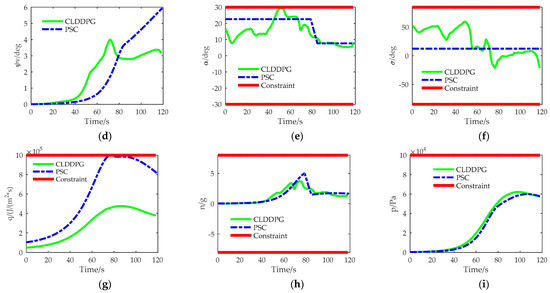
Figure 5.
Comparison of two trajectory optimization performance: (a) Simulation trajectory diagram; (b) Speed diagram; (c) Trajectory inclination angle diagram; (d) Trajectory deflection angle diagram; (e) Angle of attack diagram; (f) Angle of bank diagram; (g) Heat flow density diagram; (h) Overload diagram; and (i) Dynamic pressure diagram.

Table 5.
Comparison of simulation results of two methods.
It can be seen from Figure 5 that the two optimized trajectories can meet the guidance requirements (see Figure 5a). The final speed of the two optimized trajectories are almost the same (see Figure 5b). Compared to the trajectory inclination angle (see Figure 5c), the difference in their trajectory deflection angle is greater (see Figure 5d), because their angle of attack changes have the same trend (see Figure 5e), the bank angle of the PSC trajectory has always been positive, while the bank angle of the CLPPDG trajectory is negative for a period of time in the later stage (see Figure 5f), which directly leads to a much larger increase in the trajectory deviation angle of PSC compared to CLDDPG. They can all meet the constraints of heat flux density (see Figure 5g), overload (see Figure 5h), and dynamic pressure (see Figure 5i), but the heat flux density of the PSC trajectory is relatively high, which is caused by the lower height of the PSC trajectory compared to the CLPPDG trajectory. It can be seen from Table 5 that the flight time of the CLPPDG trajectory is almost the same as that of the GPM optimized trajectory, but CLPPDG is far superior to PSC in the time required for optimizing the trajectory, which may benefit from CLPPDG’s extensive offline training experience. The simulation results show that the online planning method based on deep reinforcement learning proposed in this paper can not only generate a trajectory with good optimization performance online, but also have excellent real-time performance.
6.5. Algorithm Anti-Interference Verification
In the course of an interceptor midcourse guidance flight, it will be affected by many interference factors, such as atmospheric random interference, measurement noise, etc. To verify the anti-interference of the method in this paper, random wind interference is added to the experiment in Section 6.4. The interference model is shown in Equation (25).
where is the control variable after interference, represents a function that generates random numbers between 0 and 1, is the interference intensity and the value selected in this paper is 2°. The simulation results are shown in Figure 6.
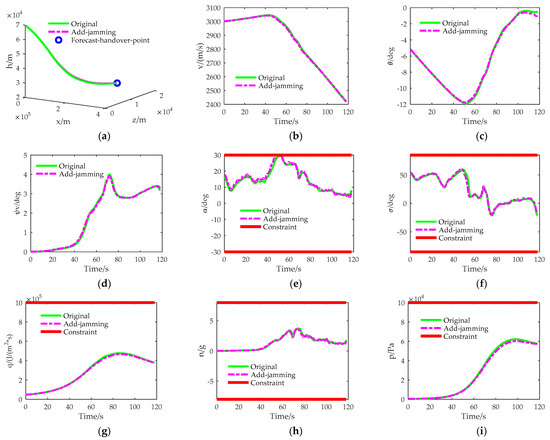
Figure 6.
Comparison of trajectory performance with and without jamming: (a) Simulation trajectory diagram; (b) Speed diagram; (c) Trajectory inclination angle diagram; (d) Trajectory deflection angle diagram; (e) Angle of attack diagram; (f) Angle of bank diagram; (g) Heat flow density diagram; (h) Overload diagram; and (i) Dynamic pressure diagram.
It can be seen from Figure 6 that the interceptor can still meet the guidance requirements with the addition of random wind interference (see Figure 6a). The change in speed (see Figure 6b) shows slight fluctuations, and there is a slight deviation in the final values of the trajectory inclination angle (see Figure 6c) and trajectory deviation angle (see Figure 6d), all of which are within a controllable range and almost do not affect the trajectory. Due to the direct effect of random wind interference on the control variables, the fluctuations in the angle of attack (see Figure 6e) and angle of bank (see Figure 6f) are more pronounced. At the same time, it can be clearly seen that the trajectory with increased random wind interference can still meet the constraints of heat flux density (see Figure 6g), overload (see Figure 6h) and dynamic pressure (see Figure 6i). The simulation results show that the online trajectory planning method based on deep reinforcement learning proposed in this paper has strong anti-interference characteristics.
7. Conclusions
This paper aims to solve the online planning problem of the interceptor midcourse guidance trajectory, and the main conclusions of this paper are as follows:
- (1)
- An MDP designed according to the characteristics of the midcourse guidance trajectory planning model can enable the interceptor to use the DDPG algorithm for offline learning training;
- (2)
- The training strategy based on CL is proposed, which greatly improves the training convergence of the DDPG algorithm;
- (3)
- The simulation results show that the online trajectory planning method based on the deep reinforcement learning proposed method has a good optimization performance, strong anti-interference and an outstanding real-time performance.
In addition, with the deepening of learning and training, adjusting the training strategy becomes very important to improve the convergence of the algorithm. For future research, the training strategy should be further investigated to improve the rate of convergence of the algorithm.
Author Contributions
Conceptualization, W.L. and J.L.; methodology, W.L., J.L. and M.L.; software, W.L.; validation, W.L. and J.L.; writing—original draft preparation, W.L.; writing—review and editing, L.S. and N.L.; supervision, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant no. 62173339).
Institutional Review Board Statement
No applicable.
Informed Consent Statement
No applicable.
Data Availability Statement
All data generated or analyzed during this study are included in this published article.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Magnitude | Meaning | Units |
| Coordinate position of the interceptor | M | |
| Velocity of the interceptor | m/s | |
| Trajectory inclination angle | rad | |
| Trajectory deflection angle | rad | |
| Radius of the Earth | M | |
| Lift and drag force of the interceptor | N | |
| Gravity acceleration | m/s2 | |
| Gravity acceleration at sea level | m/s2 | |
| Air density | kg/m3 | |
| Air density at sea level | kg/m3 | |
| Reference height | M | |
| , | Lift coefficient and drag coefficient | |
| S | State set of MDP | |
| A | Action set of MDP | |
| R | Reward function of MDP | |
| Discount coefficient of MDP | ||
| Remaining distance of interceptor | m | |
| Longitudinal plane component and transverse plane component of velocity leading angle | rad | |
| Heat flow density | W/m2 | |
| Dynamic pressure | Pa | |
| Overload | ||
| Attack angle | rad | |
| Bank angle | rad | |
| Objective function | ||
| Updates the parameter of network | ||
| Updates the parameter of network |
References
- Zhou, J.; Lei, H. Optimal trajectory correction in midcourse guidance phase considering the zeroing effort interception. Acta Armamentarii 2018, 39, 1515–1525. [Google Scholar]
- Liu, X.; Shen, Z.; Lu, P. Entry trajectory optimization by second-order cone programming. J. Guid. Control Dyn. 2016, 39, 227–241. [Google Scholar] [CrossRef]
- Roh, H.; Oh, Y.; Kwon, H. L1 penalized sequential convex programming for fast trajectory optimization: With application to optimal missile guidance. Int. J. Aeronaut. Space 2020, 21, 493–503. [Google Scholar] [CrossRef]
- Bae, J.; Lee, S.D.; Kim, Y.W.; Lee, C.H.; Kim, S.Y. Convex optimization-based entry guidance for space plane. Int. J. Control Autom. 2022, 20, 1652–1670. [Google Scholar] [CrossRef]
- Zhou, X.; He, R.Z.; Zhang, H.B.; Tang, G.J.; Bao, W.M. Sequential convex programming method using adaptive mesh refinement for entry trajectory planning problem. Aerosp. Sci. Technol. 2020, 109, 106374. [Google Scholar] [CrossRef]
- Liu, X.; Li, S.; Xin, M. Mars entry trajectory planning with range discretization and successive convexification. J. Guid. Control Dyn. 2022, 45, 755–763. [Google Scholar] [CrossRef]
- Ross, I.M.; Sekhavat, P.; Fleming, A.; Gong, Q. Optimal feedback control: Foundations, examples, and experimental results for a new approach. J. Guid. Control Dyn. 2012, 31, 307–321. [Google Scholar] [CrossRef]
- Garg, D.; Patterson, M.; Hager, W.W.; Rao, A.V.; Benson, D.A.; Huntington, G.T. A unified framework for the numerical solution of optimal control problems using pseudo spectral methods. Automatica 2010, 46, 1843–1851. [Google Scholar] [CrossRef]
- Benson, D.A.; Huntington, G.T.; Thorvaldsen, T.P.; Rao, A.V. Direct trajectory optimization and costate estimation via an orthogonal collocation method. J. Guid. Control Dyn. 2006, 29, 1435–1440. [Google Scholar] [CrossRef]
- Sagliano, M.; Theil, S.; Bergsma, M.; D’Onofrio, V.; Whittle, L.; Viavattene, G. On the Radau pseudospectral method: Theoretical and implementation advances. CEAS Space J. 2017, 9, 313–331. [Google Scholar] [CrossRef]
- Zhao, J.; Zhou, R.; Jin, X. Reentry trajectory optimization based on a multistage pseudo-spectral method. Sci. World J. 2014, 2014, 878193. [Google Scholar]
- Zhu, Y.; Zhao, K.; Li, H.; Liu, Y.; Guo, Q.; Liang, Z. Trajectory planning algorithm using gauss pseudo spectral method based on vehicle-infrastructure cooperative system. Int. J. Automot. Technol. 2020, 21, 889–901. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, Y.; Wu, Z.; Cheng, C. The intelligent trajectory optimization of multistage rocket with gauss pseudo-spectral method. Intell. Autom. Soft Comput. 2022, 33, 291–303. [Google Scholar] [CrossRef]
- Malyuta, D.; Reynolds, T.; Szmuk, M.; Mesbahi, M.; Acikmese, B.; Carson, J.M. Discretization performance and accuracy analysis for the rocket powered descent guidance problem. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Sagliano, M.; Heidecker, A.; Macés Hernández, J.; Farì, S.; Schlotterer, M.; Woicke, S.; Seelbinder, D.; Dumont, E. Onboard guidance for reusable rockets: Aerodynamic descent and powered landing. In Proceedings of the AIAA Scitech 2021 Forum, online. 11–15 & 19–21 January 2021. [Google Scholar]
- Marco, S. Generalized hp pseudospectral-convex programming for powered descent and landing. J. Guid. Control Dyn. 2019, 42, 1562–1570. [Google Scholar]
- Ventura, J.; Romano, M.; Walter, U. Performance evaluation of the inverse dynamics method for optimal spacecraft reorientation. Acta Astronaut. 2015, 110, 266–278. [Google Scholar] [CrossRef]
- Yazdani, A.M.; Sammut, K.; Yakimenko, O.A.; Lammas, A.; Tang, Y.; Zadeh, S.M. IDVD-based trajectory generator for autonomous underwater docking operations. Robot. Auton. Syst. 2017, 92, 12–29. [Google Scholar] [CrossRef]
- Yakimenko, O. Direct method for rapid prototyping of near-optimal aircraft trajectories. J. Guid. Control Dyn. 2000, 23, 865–875. [Google Scholar] [CrossRef]
- Yan, L.; Li, Y.; Zhao, J.; Du, X. Trajectory real-time optimization based on variable node inverse dynamics in virtual domain. Acta Aeronaut. Astronaut. Sin. 2013, 34, 2794–2803. [Google Scholar]
- Minh, D.; Wang, H.X.; Li, Y.F.; Nguyen, T.N. Explainable artificial intelligence: A comprehensive review. Artif. Intell. Rev. 2021, 55, 3503–3568. [Google Scholar] [CrossRef]
- He, R.; Lv, H.; Zhang, H. Lane Following Method Based on Improved DDPG Algorithm. Sensors 2021, 21, 4827. [Google Scholar] [CrossRef] [PubMed]
- Yin, Y.; Feng, X.; Wu, H. Learning for Graph Matching based Multi-object Tracking in Auto Driving. J. Phys. Conf. Ser. 2021, 1871, 012152. [Google Scholar] [CrossRef]
- Joohyun, W.; Chanwoo, Y.; Nakwan, K. Deep reinforcement learning-based controller for path following of an unmanned surface vehicle. Ocean Eng. 2019, 183, 155–166. [Google Scholar]
- You, S.; Diao, M.; Gao, L.; Zhang, F.; Wang, H. Target tracking strategy using deep deterministic policy gradient. Appl. Soft Comput. 2020, 95, 106490. [Google Scholar] [CrossRef]
- Hu, Z.; Gao, X.; Wan, K.; Zhai, Y.; Wang, Q. Relevant experience learning: A deep reinforcement learning method for UAV autonomous motion planning in complex unknown environments. Chin. J. Aeronaut. 2021, 34, 187–204. [Google Scholar] [CrossRef]
- Yu, Y.; Tang, J.; Huang, J.; Zhang, X.; So, D.K.C.; Wong, K.K. Multi-Objective Optimization for UAV-Assisted Wireless Powered IoT Networks Based on Extended DDPG Algorithm. IEEE Trans. Commun. 2021, 69, 6361–6374. [Google Scholar] [CrossRef]
- Hua, J.; Zeng, L.; Li, G.; Ju, Z. Learning for a Robot: Deep Reinforcement Learning, Imitation Learning, Transfer Learning. Sensors 2021, 21, 1278. [Google Scholar] [CrossRef]
- Li, X.; Zhong, J.; Kamruzzaman, M. Complicated robot activity recognition by quality-aware deep reinforcement learning. Future Gener. Comput. Syst. 2021, 117, 480–485. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic policy gradient algorithms. In Proceedings of the 31st International Conference on Machine Learning (ICML 2014), Beijing, China, 21–26 June 2014. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Brian, G.; Richard, L.; Roberto, F. Deep reinforcement learning for six degree-of-freedom planetary landing. Adv. Space Res. 2020, 65, 1723–1741. [Google Scholar]
- Gaudet, B.; Furfaro, R.; Linares, R. Reinforcement learning for angle-only intercept guidance of maneuvering targets. Aerosp. Sci. Technol. 2020, 99, 105746. [Google Scholar] [CrossRef]
- Gaudet, B.; Furfaro, R. Terminal adaptive guidance for autonomous hypersonic strike weapons via reinforcement learning. arXiv 2021, arXiv:2110.00634. [Google Scholar]
- Sagliano, M.; Mooij, E. Optimal drag-energy entry guidance via pseudospectral convex optimization. Aerosp. Sci. Technol. 2021, 117, 106946. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).