Optimization of the Wire Diameter Based on the Analytical Model of the Mean Magnetic Field for a Magnetically Driven Actuator
Abstract
1. Introduction

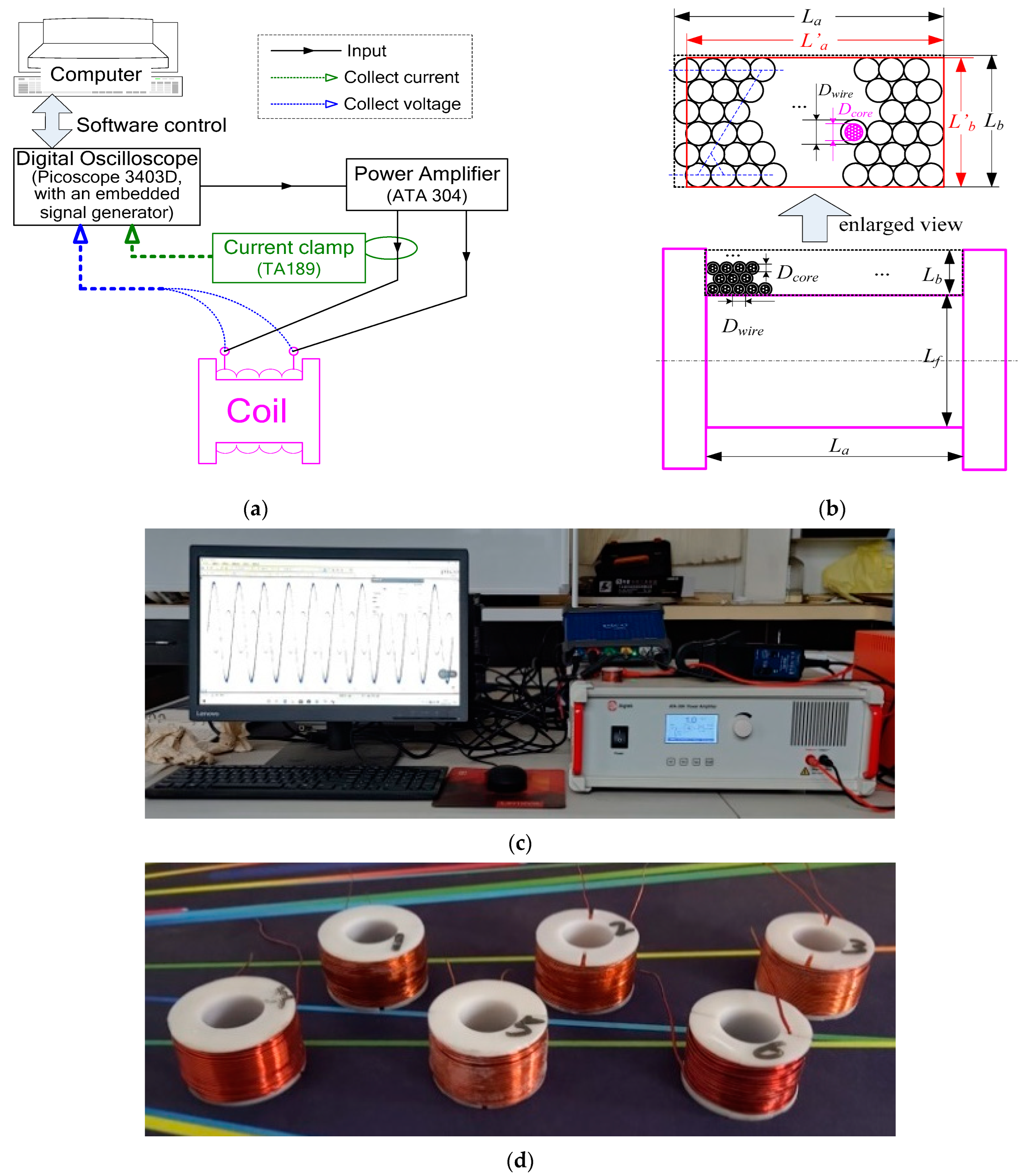
2. Experimental Methods
2.1. Test Principle
2.2. Experiment Setup and Parameters
3. Data Processing and Analysis
3.1. Inherent Characteristic Parameters of Coils
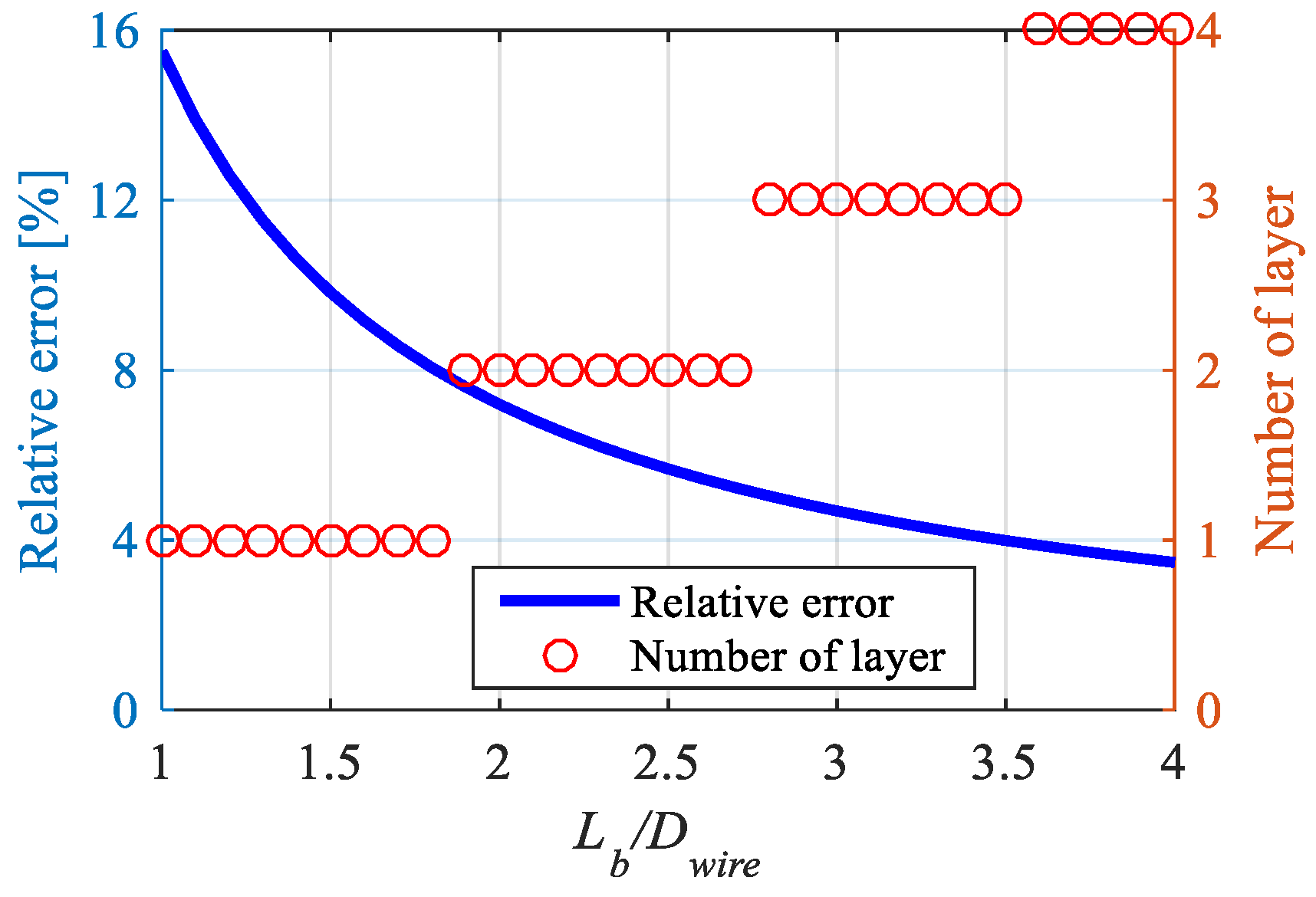
3.1.1. Dimension Parameters
3.1.2. Static Resistance and Static Inductance
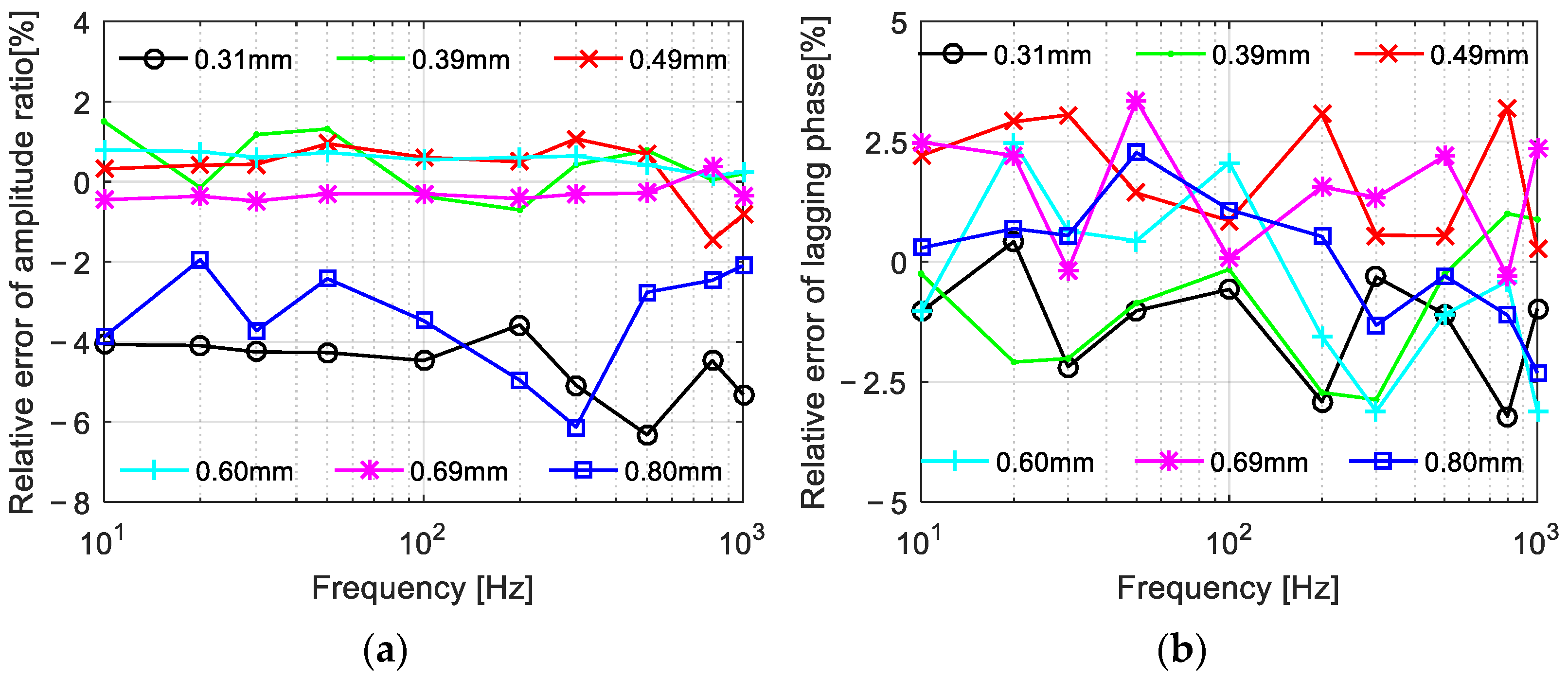
3.2. Sinusoidal Response
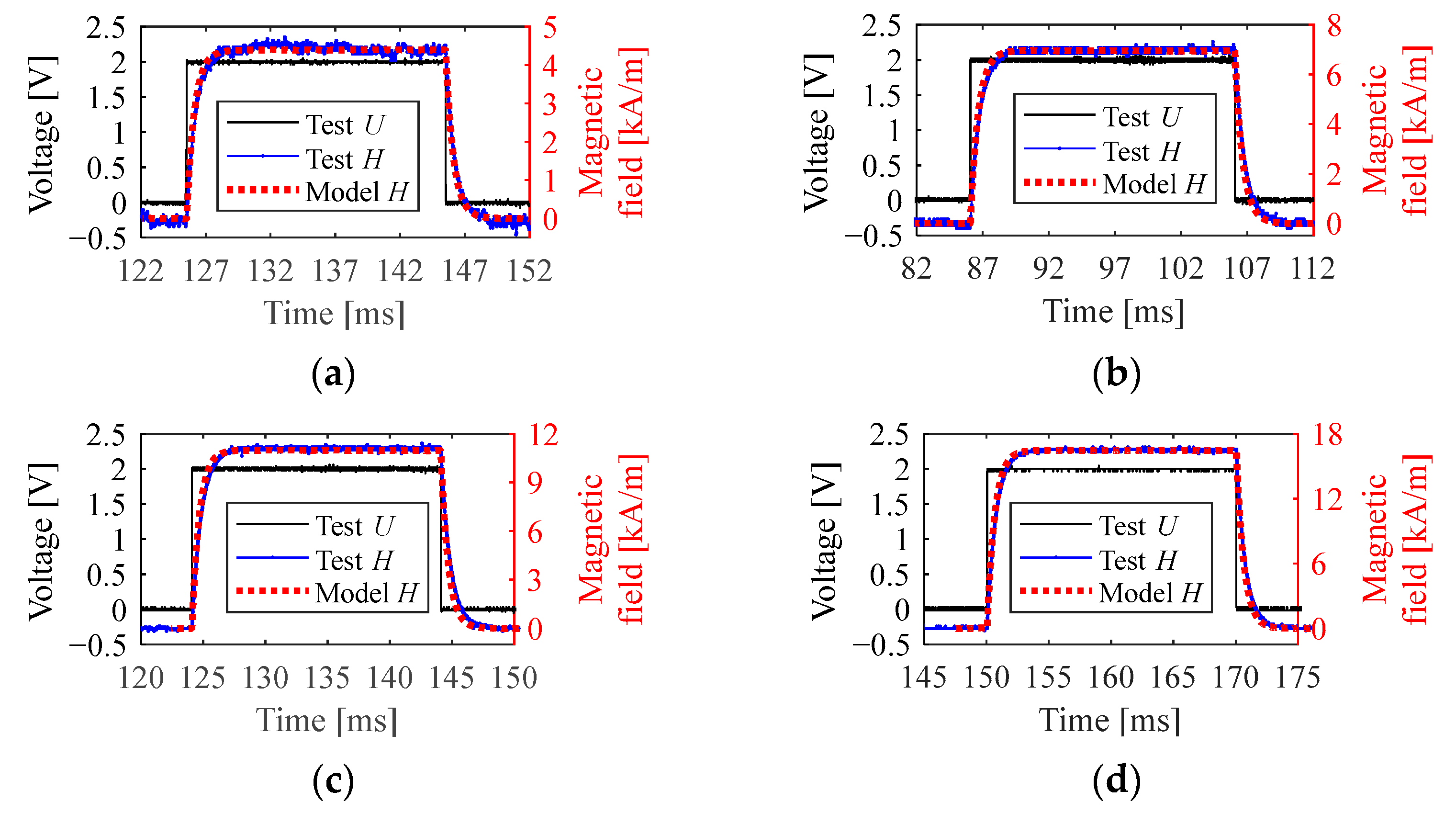
3.3. Square-Wave Response
3.3.1. Time-Domain Response
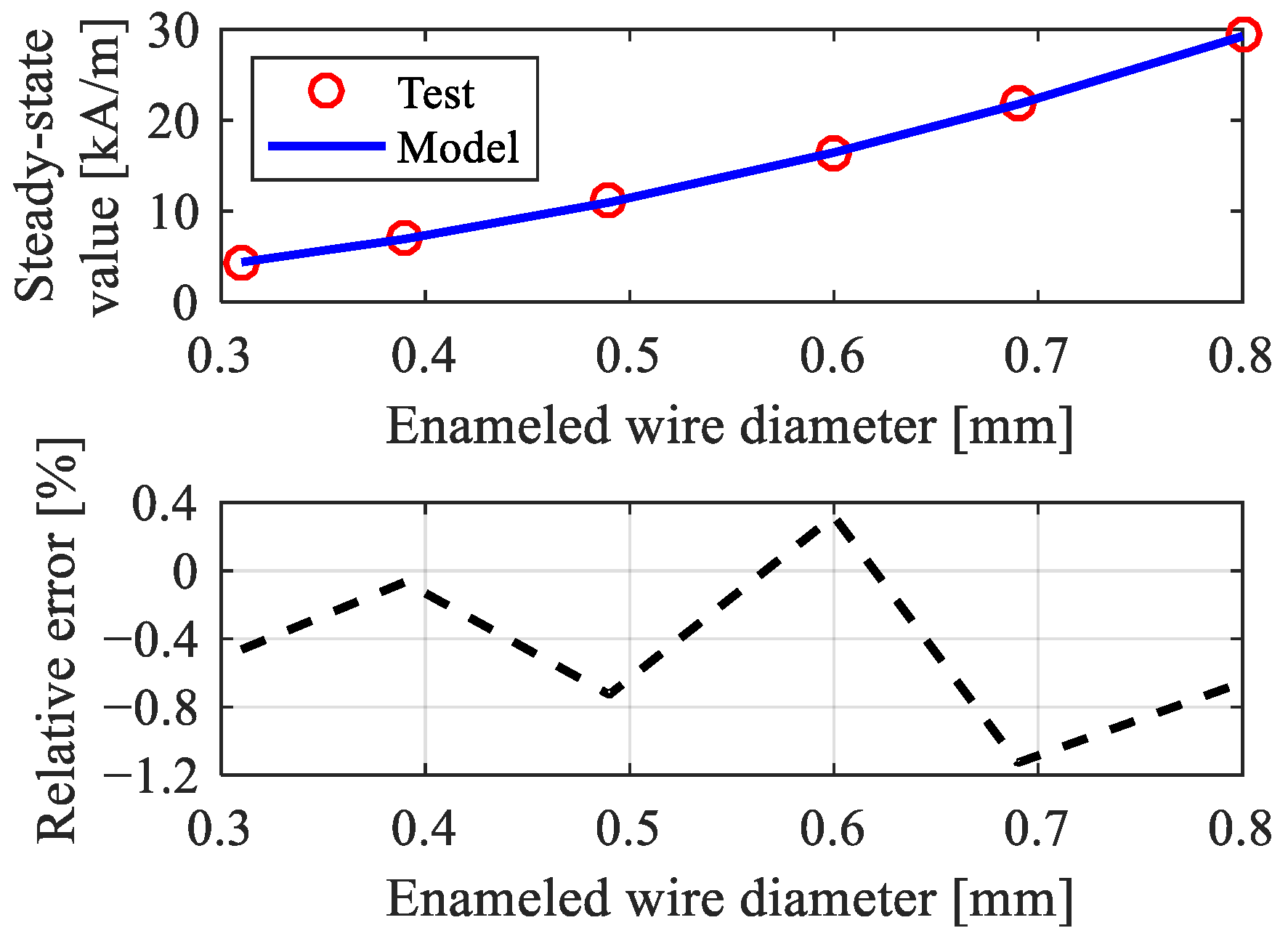
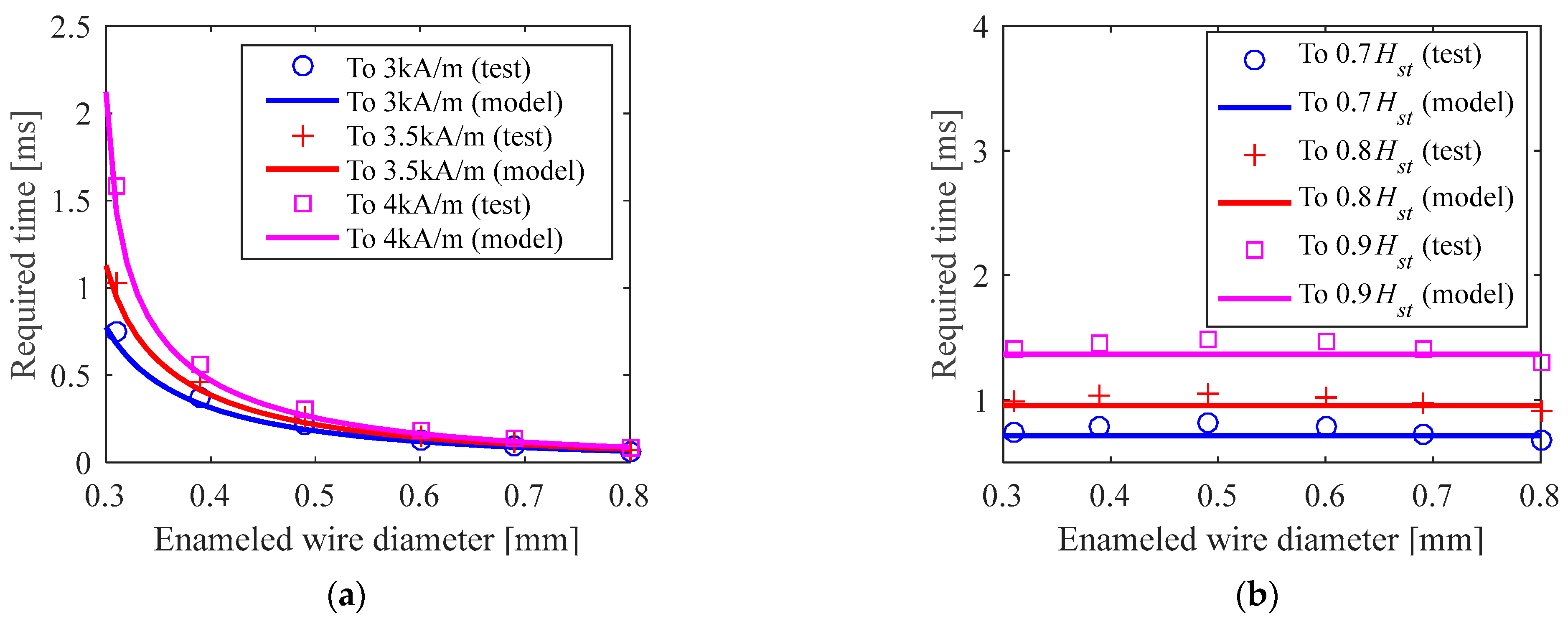
3.3.2. Steady-State Value and Response Time
4. Conclusions
- (1)
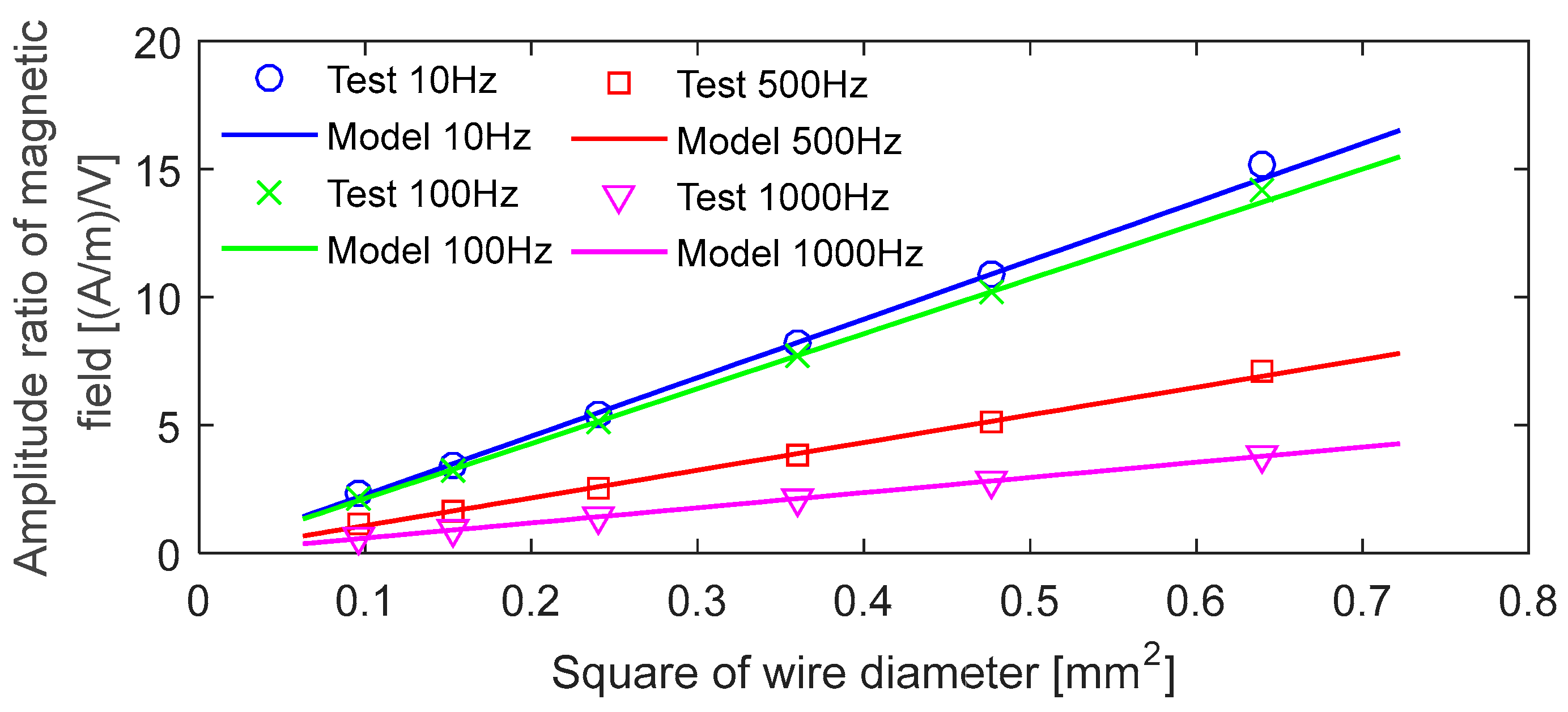
- The resistance and inductance are inversely proportional functions vs. the quartic of the enameled wire diameter. Under the sinusoidal voltage, a wider wire diameter is quite helpful for a higher magnetic field amplitude while it has little influence on the phase lag of the magnetic field. Under the square-wave voltage, the steady-state magnetic field was positively proportional to the square of the wire diameter, as a wider wire diameter is helpful for a higher steady-state magnetic field. Regarding the response speed, increasing the wire’s diameter is helpful for reducing the response time from 0 to the specified intensity, while it is helpless to improve the response speed from 0 to the steady-state or any other proportional value.
- (2)
- The proposed model was verified as the calculated results from the model were in good agreement with the experimental results. Specifically, the relative errors of the model in computing the resistance and the inductance were lower than 3.1% and 2.8%, respectively. For predicting the sinusoidal response, the errors were lower than 6.4% (lower than 2.0% under most conditions) in computing the amplitude and lower than 3.2% in computing the lagging phase. For predicting the square-wave response, the model calculated the amplitudes with errors lower than 1.2% and described the curve shape effectively.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, T.; Yuan, H.; Pan, H.; Li, B. Study on the rare-earth giant magnetostrictive actuator based on experimental and theoretical analysis. J. Magn. Magn. Mater. 2018, 460, 509–524. [Google Scholar] [CrossRef]
- Xue, G.; Zhang, P.; Li, X.; He, Z.; Wang, H.; Li, Y.; Ce, R.; Zeng, W.; Li, B. A review of giant magnetostrictive injector (GMI). Sensor. Actuat. A-Phys. 2018, 273, 159–181. [Google Scholar] [CrossRef]
- Braghin, F.; Cinquemani, S.; Resta, F. A model of magnetostrictive actuators for active vibration control. Sensor. Actuat. A-Phys. 2011, 165, 342–350. [Google Scholar] [CrossRef]
- Sobczyk, M.; Wiesenhütter, S.; Noennig, J.R.; Wallmersperger, T. Smart materials in architecture for actuator and sensor applications: A review. J. Intell. Mater. Syst. Struct. 2022, 33, 379–399. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y.; Guo, Y.; Li, L. Engineering Vibration Control Based on Rotating Actuator. J. Nanjing Univ. Aeronaut. Astronaut. 2018, 50, 601–610. [Google Scholar]
- McIvor, B.; Chahl, J. Energy Efficiency of Linear Electromagnetic Actuators for Flapping Wing Micro Aerial Vehicles. Energies 2020, 13, 1075. [Google Scholar] [CrossRef]
- Li, Y.; Wu, J.; Hu, J.; Wang, Q.; Liu, C. Analysis of Factors Influencing Peak Torques and Peak Losses of Rotary Voice Coil Actuators Used in Aerospace. IEEE Access 2021, 9, 57120–57126. [Google Scholar]
- Li, W.; Shi, G.; Asme. Review of Aerospace Actuator Technology. In Proceedings of the 33rd Bath/ASME International Symposium on Fluid Power and Motion Control (FPMC), Electr Network, Longboat Key, FL, USA, 9–11 September 2020. [Google Scholar]
- Kang, J.G.; Kwon, J.Y.; Lee, M.S. A Dynamic Power Consumption Estimation Method of Electro-mechanical Actuator for UAV Modeling and Simulation. Int. J. Aeronaut. Space Sci. 2022, 23, 233–239. [Google Scholar] [CrossRef]
- Ashpis, D.E.; Thurman, D.R. Dielectric Barrier Discharge (DBD) Plasma Actuators for Flow Control in Turbine Engines: Simulation of Flight Conditions in the Laboratory by Density Matching. Int. J. Turbo Jet-Engines 2019, 36, 157–173. [Google Scholar] [CrossRef]
- Roussel, J.; Budinger, M.; Ruet, L. Preliminary Sizing of the Electrical Motor and Housing of Electromechanical Actuators Applied on the Primary Flight Control System of Unmanned Helicopters. Aerospace 2022, 9, 473. [Google Scholar] [CrossRef]
- Misra, R.; Wisniewski, R.; Zuyev, A. Attitude Stabilization of a Satellite Having Only Electromagnetic Actuation Using Oscillating Controls. Aerospace 2022, 9, 444. [Google Scholar] [CrossRef]
- Yang, X.; Zhu, Y.; Ji, L.; Fei, S.; Guo, Y. Experimental investigation and characteristic analysis of a giant magnetostrictive materials-based electro-hydrostatic actuator. AcAAS 2016, 37, 2839–2850. [Google Scholar]
- Yang, X.; Zhu, Y.; Fei, S.; Ji, L.; Guo, Y. Magnetic field analysis and optimization of giant magnetostrictive electro-hydrostatic actuator. JAerP 2016, 31, 2210–2217. [Google Scholar]
- Fang, S. Research on Robotic Motion Planning and Compliance Control for Ultrasonic Strengthening of Aviation Blade Surface; Beijing Jiaotong University: Beijing, China, 2021. [Google Scholar]
- Grunwald, A.; Olabi, A.G. Design of a magnetostrictive (MS) actuator. Sensor. Actuat. A-Phys. 2008, 144, 161–175. [Google Scholar] [CrossRef]
- Shi, X.; Ren, C.; Li, Y.; Ding, G. Design, Modeling, and Optimization of a Bistable Electromagnetic Actuator with Large Deflection. IEEE Magn. Lett. 2021, 12, 2102505. [Google Scholar] [CrossRef]
- Lu, Y.W.; Yang, Y.; Zhang, M.; Wang, R.M.; Zhu, B.L.; Jiang, L. Magnetic Enhancement-Based Multi-Objective Optimization Design of the Large-Scale High-Intensity Homogeneous Magnetic Field Coil System. IEEE Trans. Magn. 2022, 58, 9. [Google Scholar] [CrossRef]
- Yan, H.; Gao, H.; Hao, H.; Zhang, Z.; Zhuang, F. Design and Simulation of Exciting Coil in Rare Earth Giant Magnetostrictive Actuator. Mech. Sci. Technol. Aerosp. Eng. 2019, 38, 1569–1575. [Google Scholar]
- Yan, L.; Wu, Z.; Jiao, Z.; Chen, C.-Y.; Chen, I.M. Equivalent energized coil model for magnetic field of permanent-magnet spherical actuators. Sensor. Actuat. A-Phys. 2015, 229, 68–76. [Google Scholar] [CrossRef]
- Kim, H.; Kim, H.; Gweon, D. Magnetic field analysis of a VCM spherical actuator. Sensor. Actuat. A-Phys. 2013, 195, 38–49. [Google Scholar] [CrossRef]
- Olabi, A.G.; Grunwald, A. Computation of magnetic field in an actuator. Simul. Model. Pract. Theory 2008, 16, 1728–1736. [Google Scholar] [CrossRef]
- Geng, H.; Zhang, X.; Yan, S.; Tong, L.; Ma, Q.; Xu, M.; Zhang, Y.; Han, Y. Magnetic field analysis and performance optimization of hybrid excitation generators for vehicles. Sustain. Energy Technol. Assess. 2022, 52, 102200. [Google Scholar] [CrossRef]
- Lee, J.; Dede, E.M.; Banerjee, D.; Iizuka, H. Magnetic force enhancement in a linear actuator by air-gap magnetic field distribution optimization and design. Finite Elem. Anal. Des. 2012, 58, 44–52. [Google Scholar] [CrossRef]
- Yang, X.; Zhu, Y.; Zhu, Y. Characteristic investigations on magnetic field and fluid field of a giant magnetostrictive material-based electro-hydrostatic actuator. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 232, 847–860. [Google Scholar] [CrossRef]
- Golda, D.; Culpepper, M.L. Modeling 3D magnetic fields for precision magnetic actuators that use non-periodic magnet arrays. Precis. Eng. 2008, 32, 134–142. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, X.; Li, S.; Zhang, Z.; Chen, Y. Dynamic modeling of stack giant magnetostrictive actuator with magnetic equivalent network considering eddy current effect. J. Appl. Phys. 2022, 131, 224503. [Google Scholar] [CrossRef]
- Chen, L.; Zhu, Y.; Ling, J.; Zhang, M. Development and Characteristic Investigation of a Multidimensional Discrete Magnetostrictive Actuator. IEEE-ASME T. Mech. 2022, 27, 2071–2079. [Google Scholar] [CrossRef]
- Ramirez-Laboreo, E.; Roes, M.G.L.; Sagues, C. Hybrid Dynamical Model for Reluctance Actuators Including Saturation, Hysteresis, and Eddy Currents. IEEE-ASME T. Mech. 2019, 24, 1396–1406. [Google Scholar] [CrossRef]
- Lyu, Z.; Zhang, J.; Wang, S.; Zhao, X.; Li, T. Optimal design of multi-coil system for generating uniform magnetic field based on intelligent optimization algorithm and finite element method. J. Beijing Univ. Aeronaut. 2019, 45, 980–988. [Google Scholar]
- Sun, J.; Ren, J.; Le, Y.; Wang, H. Analysis of Air-Gap Magnetic Field and Structure Optimization Design of Hollow-Cup Motor. Aerospace 2022, 9, 549. [Google Scholar] [CrossRef]
- Niu, M.; Yang, B.; Yang, Y.; Meng, G. Modelling and parameter design of a 3-DOF compliant platform driven by magnetostrictive actuators. Precis. Eng. 2020, 66, 255–268. [Google Scholar] [CrossRef]
- Zhou, J.; He, Z.; Shi, Z.; Song, J.; Li, Q. Design and experimental performance of an inertial giant magnetostrictive linear actuator. Sensor. Actuat. A-Phys. 2020, 301, 111771. [Google Scholar] [CrossRef]
- Liu, H.; Jia, Z.; Wang, F.; Zong, F. Research on the constant output force control system for giant magnetostrictive actuator disturbed by external force. Mechatronics 2012, 22, 911–922. [Google Scholar] [CrossRef]
- Xue, G.; Zhang, P.; He, Z.; Li, D.; Yang, Z.; Zhao, Z. Displacement model and driving voltage optimization for a giant magnetostrictive actuator used on a high-pressure common-rail injector. Mater. Des. 2016, 95, 501–509. [Google Scholar] [CrossRef]
- Bright, C.B.; Garza, J.C. Possible Very High Speed Rate Shaping Fuel Injector; SAE Technical Paper 2007-01-4113; SAE: Warrendale, PA, USA, 2007. [Google Scholar]
- Xue, G.; Zhang, P.; He, Z.; Li, D.; Huang, Y.; Xie, W. Design and experimental study of a novel giant magnetostrictive actuator. J. Magn. Magn. Mater. 2016, 420, 185–191. [Google Scholar] [CrossRef]
- Xue, G.; Ge, J.; Ning, P.; Zhou, J.; Wang, K.; Cheng, Z.; Pei, G. Simulation studies on the boot shape injection of a giant magnetostrictive injector. Sci. Rep. 2021, 11, 22999. [Google Scholar] [CrossRef]
- Hoang, M.C.; Kim, J.; Park, J.-O.; Kim, C.-S. Optimized magnetic field control of an electromagnetic actuation system for enhanced microrobot manipulation. Mechatronics 2022, 85, 102830. [Google Scholar] [CrossRef]
- Pang, H.Y.; Duan, L.H.; Quan, W.; Wang, J.; Wu, W.F.; Fan, W.F.; Liu, F. Design of Highly Uniform Three Dimensional Spherical Magnetic Field Coils for Atomic Sensors. IEEE Sens. J. 2020, 20, 11229–11236. [Google Scholar] [CrossRef]
- Tang, Y.D.; Jin, T.; Flesch, R.C.C.; Gao, Y.M. Improvement of solenoid magnetic field and its influence on therapeutic effect during magnetic hyperthermia. J. Phys. D-Appl. Phys. 2020, 53, 6. [Google Scholar] [CrossRef]
- Rong, C.; He, Z.B.; Xue, G.M.; Zhou, J.T.; Zhao, Z.L. Physics-based modeling and multi-objective parameter optimization of excitation coil for giant magnetostrictive actuator used on fuel injector. Meas. Control 2022, 55, 421–436. [Google Scholar] [CrossRef]
- Fang, S.; Chen, Y.; Yang, Y. Optimization design and energy-saving control strategy of high power dc contactor. Int. J. Electr. Power Energy Syst. 2020, 117, 105633. [Google Scholar] [CrossRef]
- Bright, C.B.; Faidley, L.; Witthauer, A.; Rickels, E.; Donlin, T. Programmable Diesel Injector Transducer Test Results; SAE Technical Paper 2011-01-0381; SAE: Warrendale, PA, USA, 2011. [Google Scholar]
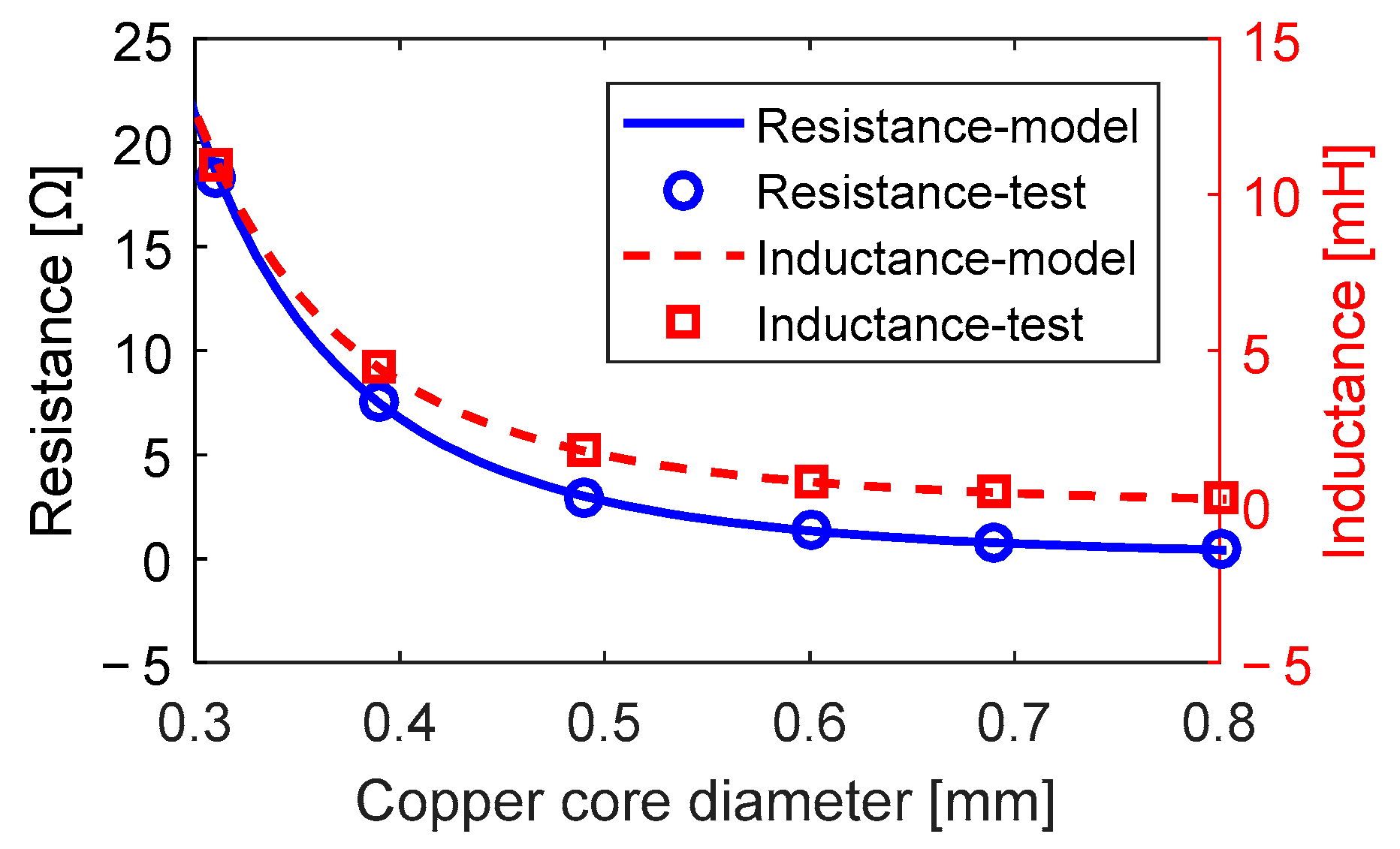

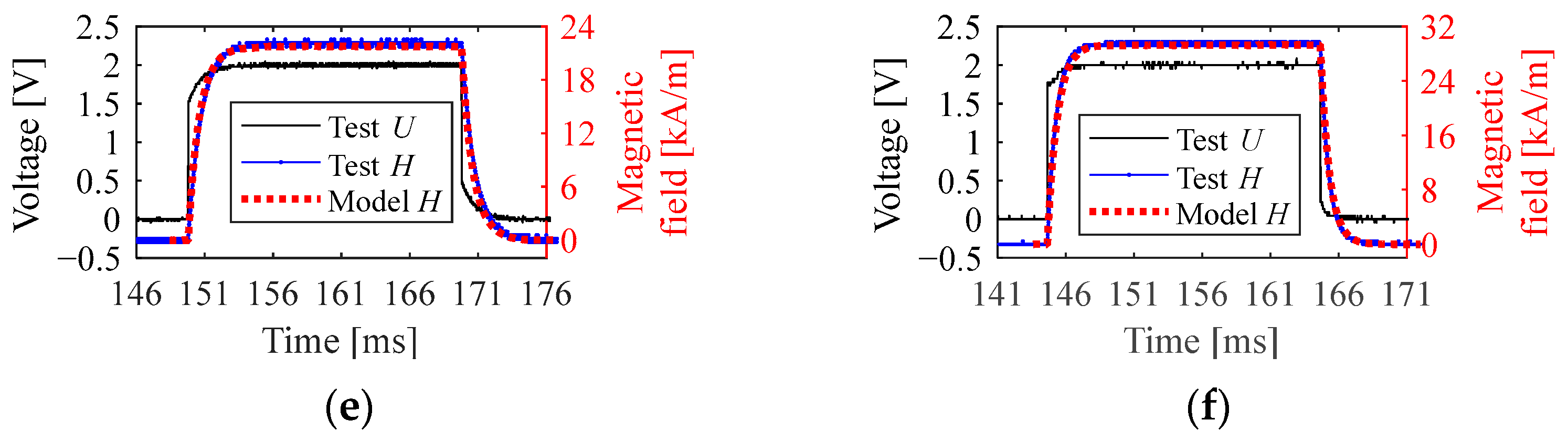
| Coil Label | External Diameter (Dwire) [mm] | Core Diameter (Dwire) [mm] | Number of Coil Turns (N) [Null] | Resistance (R) [Ω] | Inductance (L) [mH] |
|---|---|---|---|---|---|
| Coil 1 | 0.31 | 0.27 | 837 | 18.325 | 10.933 |
| Coil 2 | 0.39 | 0.35 | 537 | 7.472 | 4.487 |
| Coil 3 | 0.49 | 0.44 | 342 | 2.994 | 1.789 |
| Coil 4 | 0.60 | 0.55 | 229 | 1.342 | 0.801 |
| Coil 5 | 0.69 | 0.64 | 175 | 0.767 | 0.459 |
| Coil 6 | 0.80 | 0.74 | 124 | 0.410 | 0.243 |
| Parameter (Variable) [Unit] | Value |
|---|---|
| Coil length (La) [mm] | 16.5 |
| Coil thickness (Lb) [mm] | 6.8 |
| Diameter of skeleton shaft (Lf) [mm] | 18.2 |
| Resistivity of copper (ρ) [Ω·m] | 1.71 × 10−8 |
| Proportional coefficient (CHI) [null] | 0.8 |
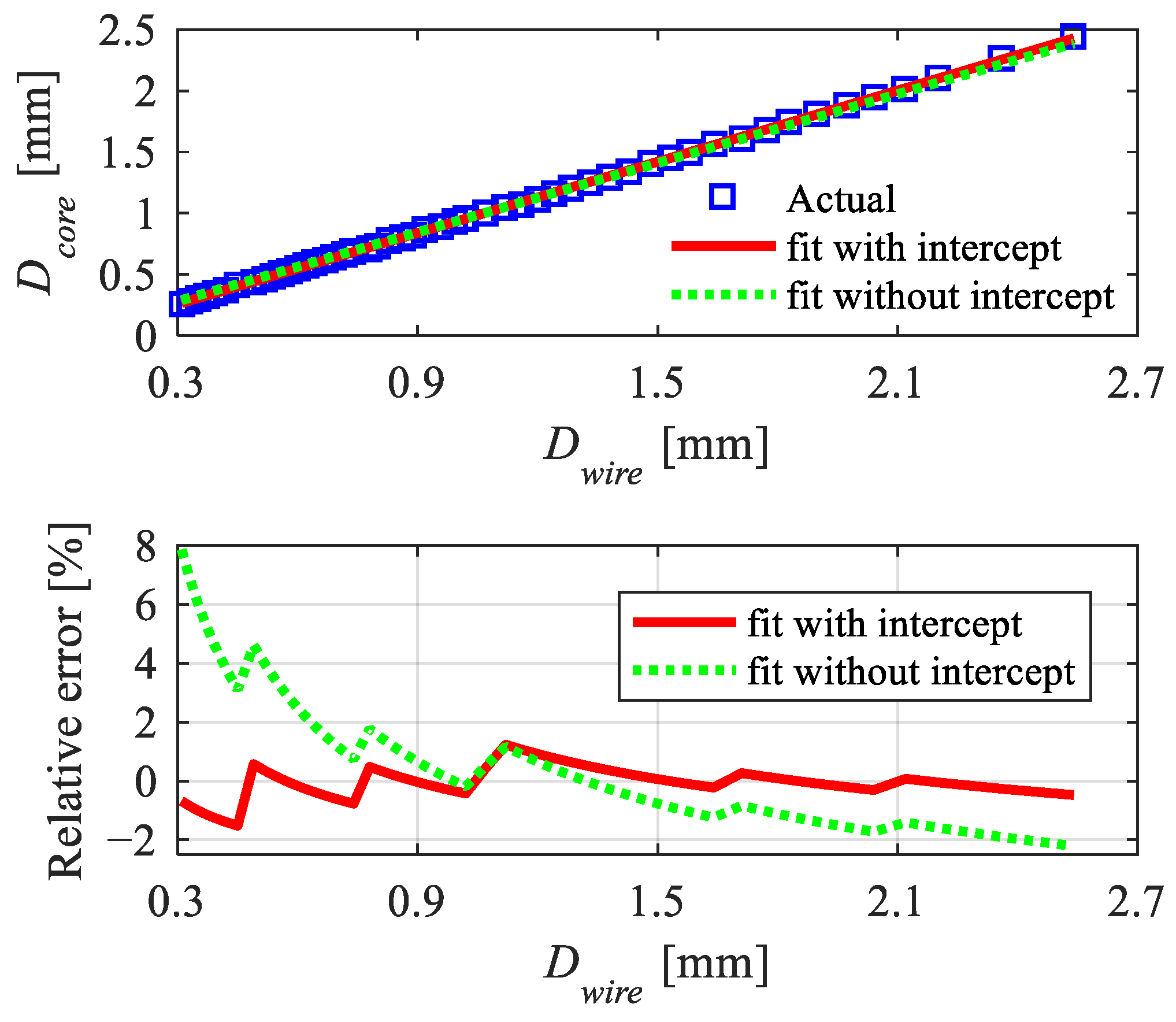
| Dwire | Tested Dcore | Dcore from 0.962 Dwire − 0.0277 | Relative Error of 0.962 Dwire − 0.0277 (%) | Dcore from 0.898 Dwire | Relative Error of 0.898 Dwire (%) |
|---|---|---|---|---|---|
| 0.31 | 0.27 | 0.2705 | 0.1926 | 0.2784 | 3.1037 |
| 0.39 | 0.35 | 0.3475 | −0.7200 | 0.3502 | 0.0629 |
| 0.49 | 0.44 | 0.4437 | 0.8364 | 0.4400 | 0.0045 |
| 0.6 | 0.55 | 0.5495 | −0.0909 | 0.5388 | −2.0364 |
| 0.69 | 0.64 | 0.6361 | −0.6125 | 0.6196 | −3.1844 |
| 0.8 | 0.74 | 0.7419 | 0.2568 | 0.7184 | −2.9189 |
| Coil Label | Coil Turns from Test | Coil Turns from Model 1 | Relative Error (%) |
|---|---|---|---|
| 1 | 837 | 847.33 | 1.23 |
| 2 | 537 | 535.36 | −0.30 |
| 3 | 342 | 339.15 | −0.83 |
| 4 | 229 | 226.19 | −1.23 |
| 5 | 175 | 171.03 | −2.27 |
| 6 | 124 | 127.23 | 2.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Bai, H.; Xue, G.; Ren, Z. Optimization of the Wire Diameter Based on the Analytical Model of the Mean Magnetic Field for a Magnetically Driven Actuator. Aerospace 2023, 10, 270. https://doi.org/10.3390/aerospace10030270
Wu Z, Bai H, Xue G, Ren Z. Optimization of the Wire Diameter Based on the Analytical Model of the Mean Magnetic Field for a Magnetically Driven Actuator. Aerospace. 2023; 10(3):270. https://doi.org/10.3390/aerospace10030270
Chicago/Turabian StyleWu, Zhangbin, Hongbai Bai, Guangming Xue, and Zhiying Ren. 2023. "Optimization of the Wire Diameter Based on the Analytical Model of the Mean Magnetic Field for a Magnetically Driven Actuator" Aerospace 10, no. 3: 270. https://doi.org/10.3390/aerospace10030270
APA StyleWu, Z., Bai, H., Xue, G., & Ren, Z. (2023). Optimization of the Wire Diameter Based on the Analytical Model of the Mean Magnetic Field for a Magnetically Driven Actuator. Aerospace, 10(3), 270. https://doi.org/10.3390/aerospace10030270







